Золотое сечение композиция: Золотое Сечение в Искусстве (Живописи) Основы Композиции • ИзоКурс, Мск — Главная

Содержание

Рисуем вместе » Что такое золотое сечение.

Опубликовано 19 Дек 2010 в рубрике «Немного теории»

«Золотое сечение» уже давно стало синонимом слова «гармония». Словосочетание «золотое сечение» обладает просто магическим действием. Если вы выполняете какой-то художественный заказ (неважно, картина это, скульптура или дизайн), фраза «работа сделана в полном соответствии с правилами золотого сечения» может стать прекрасным аргументом в вашу пользу – проверить заказчик скорее всего не сможет, а звучит это солидно и убедительно. При этом немногие понимают, что же скрывается под этими словами. Между тем, разобраться, в том, что такое золотое сечение и как оно работает, достаточно просто.

Золотое сечение – это такое деление отрезка на 2 пропорциональные части, при котором целое так относится к большей части, как большая к меньшей. Математически эта формула выглядит так: с :

b = b : а или a : b = b : c.

Итогом алгебраического решения данной пропорции будет иррациональное число Ф (Ф в честь древнегреческого скульптора Фидия).

Я не буду приводить само уравнение, чтобы не загружать текст. При желании, его можно легко найти в сети. Скажу только, что Ф будет приблизительно равным 1,618. Запомните эту цифру, это числовое выражение золотого сечения.

Итак, золотое сечение – это правило пропорции, оно показывает соотношение частей и целого.

На любом отрезке можно найти «золотую точку» — точку, которая делит этот отрезок на части, воспринимаемые как гармоничные. Соответственно, так же можно разделить любой объект. Для примера построим прямоугольник, поделенный в соответствии с «золотой» пропорцией:

Отношение большей стороны получившегося прямоугольника к меньшей будет приблизительно равно 1,6 (заметьте, меньший прямоугольник, получившийся в результате построений, также будет золотым).

Вообще, в статьях, объясняющих принцип золотого сечения, встречается множество подобных рисунков. Объясняется это просто: дело в том, что найти «золотую точку» путем обычного измерения проблематично, поскольку число Ф, как мы помним, иррациональное. Зато, такие задачи легко решаются геометрическими методами, с помощью циркуля и линейки.

Однако, наличие циркуля для применения закона на практике совсем не обязательно. Есть ряд чисел, которые принято считать арифметическим выражением золотого сечения. Это ряд Фибоначчи. Вот этот ряд:

0 1 1 2 3 5 8 13 21 34 55 89 144 и т.д.

Запоминать эту последовательность не обязательно, ее можно легко вычислить: каждое число в ряду Фибоначчи равно сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618.

Один из самых древних (и не потерявших свою привлекательность до сих пор) символов, пентаграмма – прекрасная иллюстрация принципа золотого сечения.

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении (на приведённом рисунке отношение красного отрезка к зелёному, так же как зелёного к синему, так же как синего к фиолетовому, равны). (цитата из Википедии).

Почему же «золотая пропорция» представляется такой гармоничной?

У теории золотого сечения есть масса как сторонников, так и противников. Вообще, идея о том, что красоту можно измерить и просчитать с помощью математической формулы, симпатична далеко не всем. И, возможно, эта концепция действительно казалась бы надуманной математической эстетикой, если бы не многочисленные примеры природного формообразования, соответствующие

золотому сечению.

Сам термин «золотое сечение» ввел Леонардо да Винчи. Будучи математиком, да Винчи также искал гармоничное соотношение для пропорций человеческого тела.

“Если мы человеческую фигуру – самое совершенное творение Вселенной – перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию от того же пояса до макушки, как весь рост человека к длине от пояса до ступней”.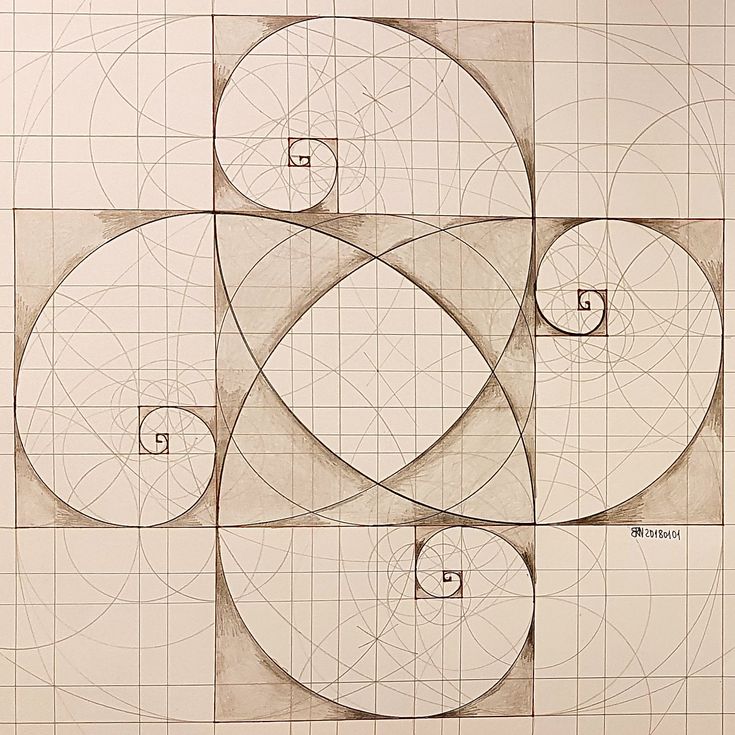

Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции

золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Постепенно, золотое сечение превратилось в академический канон, и когда в искусстве назрел бунт против академизма, про золотое сечение на время забыли. Однако, в середине XIX века эта концепция вновь стала популярной благодаря трудам немецкого исследователя Цейзинга. Он проделал множество измерений (около 2000 человек), и сделал вывод, что золотое сечение выражает средний статистический закон.

Помимо людей, Цейзинг исследовал архитектурные сооружения, вазы, растительный и животный мир, стихотворные размеры и музыкальные ритмы. Согласно его теории, золотое сечение является абсолютом, универсальным правилом для любых явлений природы и искусства.

Принцип золотой пропорции применяется в разных сферах, не только в искусстве, но и в науке и в технике. Будучи настолько универсальной, она, конечно, подвергается множеству сомнений. Часто проявления золотого сечения объявляются результатом ошибочных вычислений или простого совпадения, (а то и подтасовки). В любом случае, к любым замечаниям, как сторонников теории, так и противников, стоит относиться критически.

А о том, как этот принцип применять на практике, можно прочитать здесь.

Вернуться на главную страницу

Золотое сечение — презентация, доклад, проект

Вы можете изучить и скачать доклад-презентацию на тему Золотое сечение. Презентация на заданную тему содержит 11 слайдов.

Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

Презентации» Математика» Презентация Золотое сечение

Слайды и текст этой презентации

Слайд 1

Описание слайда:

Золотое сечение Презентацию разработала Родионова Надежда Владимировна Учитель математики, ГОУ Гимназия № 157, г. Санкт-Петербург

Слайд 2

Описание слайда:

Золотое сечение Сегодня мы познакомимся с необычной пропорцией, называемой золотым сечением и даже “божественной пропорцией”. Вы узнаете какую роль играет эта пропорция в окружающем мире, как она связана с понятием гармонии и как и почему она используется в искусстве (живописи, архитектуре, фотографии…), дизайне…

Слайд 3

Описание слайда:

Золотое сечение в живописи, фотографии, дизайне. Основы композиции В живописи, фотографии, дизайне золотое сечение очень часто используется в виде классических приемов композиции, о чем вы можете прочитать, заглянув на любой сайт, посвященный этим видам искусства.] Основная рекомендация заключается в следующем. Объект, являющийся центральной фигурой в композиции, далеко не всегда должен располагаться в центре. Определенные точки в композиции автоматически привлекают внимание. Таких точек 4, и расположены они на расстоянии 3/8 и 5/8 от краев картины. Нарисовав сетку, получим эти точки в местах пересечения линий (см. фотографию).

Слайд 4

Описание слайда:

Золотое сечение. История вопроса. Под золотым сечением понимается такое пропорциональное деление отрезка на неравные части. При котором длина всего отрезка так относится к его большей части, как длина большей части относится к длине меньшей. Это отношение равно иррациональному числу Ф=1.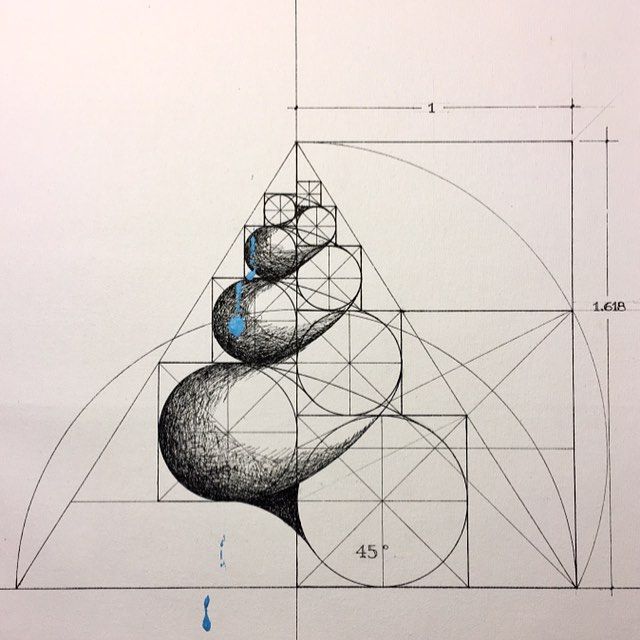 618033989.. Впервые золотое сечение встречается в «Началах» Евклида (300 лет до н.э.). Лука Пачоли, современник Леонарда да Винчи, назвал его «божественной пропорцией». Золотое сечение обозначают символами PHI или Ф (в честь древнегреческого скульптора Фидия, всегда использовавшего в своих работах золотое сечение). Математик Фибоначчи впервые получил последовательность чисел, названной в его честь числами Фибоначчи 1,1,2,3,5,8,13,21,34,55 … Особенностью этого числового ряда является то, что каждый его член, начиная с третьего, равен сумме двух предыдущих : 1+1=2; 1+2=3; 2+3=5; 3+5=8 …При этом отношение двух соседних членов равно золотому сечению, т.е. числу Ф. Рассматривая закономерности, связанные с проявлением золотого сечения, обычно используют обратную величину числа Ф : 1/1,618 = 0,618

Слайд 5

Описание слайда:

Золотая спираль Вопрос: Что общего в расположении полипептидных цепей нуклеиновых кислот, лепестков розы, раковин моллюсков, рогов млекопитающих, подсолнуха, далеких космических галактик? Ответ: в основе их структуры лежит золотая (логарифмическая) спираль.

Эта спираль вписывается в золотой прямоугольник (отношение длины и ширины которого равно числу Ф). Последовательно отрезая от него квадраты и вписывая в каждый из них по четверти окружности, мы и получим золотую спираль (см. фото)

Слайд 6

Описание слайда:

Золотая спираль

Слайд 7

Описание слайда:

Золотая спираль Явление филлотаксиса

Слайд 8

Описание слайда:

Золотое сечение в искусстве Архитектура Золотое сечение пронизывает всю историю искусства: пирамиды Хеопса, знаменитый греческий храм Парфенон, большинство греческих скульптур памятников, непревзойденная Джоконда Леонарда да Винчи, картины Рафаэля, Шишкина, этюды Шопена, музыка Бетховена, Чайковского, стихи Пушкина … вот далеко не полный перечень выдающихся произведений искусства, наполненных чудесной гармонией основанной на золотом сечении.

Слайд 9

Описание слайда:

Пропорции тела человека и золотое сечение Идеальным, совершенным считается тело, пропорции которого составляет золотое сечение. Основные пропорции были определены Леонардо да Винчи, и художники стали сознательно их использовать. Основное деление человеческого тела – это деление точкой пупа. Отношение расстояния от пупа до ступни к расстоянию от пупа до макушки составляют золотое сечение. Идеальной женской фигурой считается фигура Афродиты Милосской (см. рисунок).

Слайд 10

Описание слайда:

Пропорции золотого сечения в природе Форма птичьих яиц описывается золотым сечением. Сегодня уже установлено, что при такой конфигурации прочностные характеристики оболочки оказываются наиболее высокими. Совершенная форма тела стрекозы создана по законам золотого сечения: отношение длины хвоста и корпуса равно отношению общей длины к длине хвоста.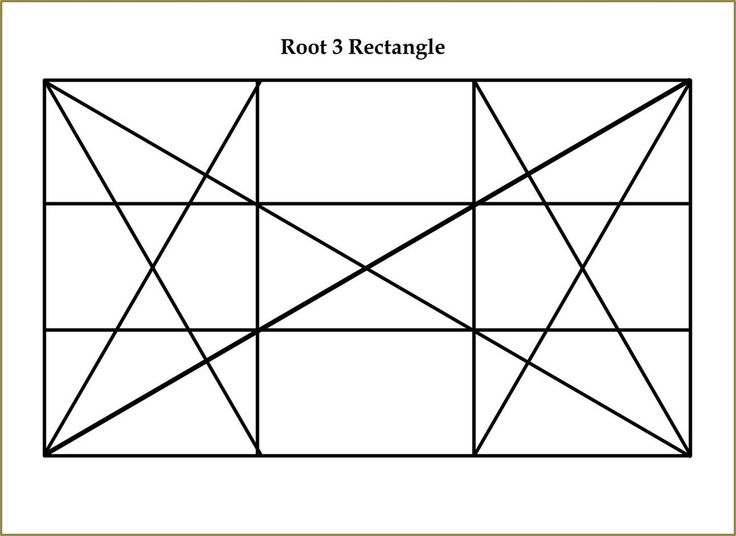

Слайд 11

Описание слайда:

Практические задания 1. Разделите отрезок длиной 16 см в отношении “золотого сечения”. Используйте числа Фибоначчи 1 вариант – 3 и 5 2 вариант — 2 и 3 2. Длина прямоугольника равна 20 см (1 вариант), 15 см(2 вариант). Найдите такую ширину прямоугольника, чтобы отношение длины к ширине составило “золотое сечение” Ф=1,6 Решите задачу, составив уравнение 3. Проверьте, насколько идеально одно из отношений вашей ладони: отношение длины указательного пальца к длине двух его фаланг от конца пальца. Измерьте с помощью линейки указанные длины и найдите их отношение. Округлите полученное число до десятых и сравните с Ф=1,6 (определите, насколько оно больше или меньше числа Ф )

Tags Золотое сечение

Похожие презентации

Презентация успешно отправлена!

Ошибка! Введите корректный Email!

Пропорции.

Золотое сечение. Измеритель золотого сечения

Размеры и пропорции — одна из главных задач в поисках художественного образа любого произведения пластического искусства. Понятно, что вопрос о размерах решается с учетом помещения, где оно будет находиться, и окружающих его предметов.

Говоря о пропорциях (соотношении размерных величин), мы учитываем их в формате плоского изображения (картина, маркетри), в соотношениях габаритных размеров (длина, высота, ширина) объемного предмета, в соотношении двух различных по высоте или длине предметов одного ансамбля, в соотношении размеров двух явно выделяющихся частей одного и того же предмета и т. д.

В классике изобразительного искусства на протяжении многих веков прослеживается прием построения пропорций, называемый золотым сечением, или золотым числом (этот термин введен Леонардо да Винчи).

Принцип золотого сечения, или динамичной симметрии, заключается в том, что «отношение между двумя частями единого целого равно отношению ее большей части к целому» (или соответственно целого к большей части).

Математически это число выражается как —¹^±₂^?5— что дает 1,6180339… или 0,6180339…

В искусстве за золотое число принимается 1,62, т. е. приближенное выражение отношения большей величины в пропорции к ее меньшей величине.

От приближенного к более точному это отношение может быть выражено: и т. д., где: 5+3=8, 8+5=13 и т. д. Или: 2,2:3,3:5,5:8,8 и т. д., где 2,2+3,3—5,5 и т. д.

Графически золотое сечение можно выразить соотношением отрезков, получающихся различными построениями.

Удобнее, на наш взгляд, построение, показанное на рис. 169: если к диагонали полуквадрата добавить его короткую сторону, то получится величина в отношении золотого числа к его длинной стороне.

Рис. 169. Геометрическое построение прямоугольника в золотом сечении 1,62 : 1. Золотое число 1,62 в отношении отрезков (а и Ь)

Рис. 170. Графическое построение функции золотой пропорции 1,12: 1

Пропорция двух величин золотого сечения

Рис.

171. Золотые пропорции гармонично развитого человека. Масштабный график золотого числа 1.62 для проверки пропорций. Каждая пара отрезков, обозначенных на рисунке а и Ь, находятся в пропорциональной зависимости 1,62: 1

создает зрительное ощущение гармонии и равновесия. Есть и другое гармоничное соотношение двух смежных величин, выражаемое числом 1,12. Оно является функцией золотого числа: если взять разность двух величин золотого сечения, разделить ее также в золотой пропорции и каждую долю добавить к меньшей величине исходного золотого сечения, то получится соотношение 1,12 (рис. 170).

В таком отношении, например, проводится средний элемент (полочка) в буквах Н, Р, Я и т. д. в некоторых шрифтах, берутся пропорции высоты и ширины для широких букв, также встречается это отношение и в природе.

Золотое число наблюдается в пропорциях гармонично развитого человека (рис. 171): длина головы делит в золотом сечении расстояние от талии до макушки; коленная чашечка также делит расстояние от талии до подошвы ног; кончик среднего пальца вытянутой вниз руки делит в золотой пропорции весь рост человека; отношение фалангов пальцев — тоже золотое число.

Это же явление наблюдается и в иных конструкциях природы: в спиралях моллюсков, в венчиках цветков и др.

Рис. 172. Золотые пропорции резного листа герани (пеларгонии). Построение: 1) С помощью масштабного графика (см. рис. 171) строим ? ABC,	Рис. 173. Пятилепестковый и трехлепестковый лист винограда. Отношение длины к ширине составляет 1,12. Золотой пропорцией выражается

На рис. 172 и 173 показано построение рисунка листа герани (пеларгонии) и листа винограда в пропорциях золотых чисел 1,62 и 1,12. В листе герани базой построения являются два треугольника: ABC и CEF, где отношение высоты и основания каждого из них выражается числами 0,62 и 1,62, а расстояния между тремя парами наиболее удаленных точек листа равны: AB=CE=SF.

Построение указано на чертеже. Конструкция такого листа является типичной для герани, имеющей подобные резные листья.

Обобщенный лист платана (рис. 173) имеет пропорции так же, как и лист винограда, в отношении 1,12, но большую долю у листа винограда составляет его длина, а у листа платана — его ширина.

Лист платана имеет три пропорциональных размера в отношении 1,62. Такое соответствие в архитектуре называется триадой (для четырех пропорций — тетрада и далее: пектада, гексода).

Рис. 174. Форма кленового листа: а — десять гармоничных пропорций листа клена; б — пропорции молодого листа клена; в — лист остролистого клена в натуре; г — упрощенное и приближенное построение листа клена

На рис. 174 показан способ построения в пропорциях золотого сечения листа клена.

При соотношении ширины к длине в 1,12 он имеет несколько пропорций с числом 1,62. За основу построения взяты две трапеции, у которых отношение высоты и длины основания выражается золотым числом.

Построение показано на чертеже, также приведены варианты формы листа клена.

В произведениях изобразительного искусства художник или скульптор осознанно или подсознательно, доверяя своему тренированному глазу, часто применяет соотношение размеров в золотой пропорции.

Так, работая над копией с головы Христа (по Микеланджело), автор данной книги заметил, что смежные завитки в прядях волос по своим размерам отражают отношение золотого сечения, а по форме — спираль Архимеда, эвольвенту.

Читатель сам может убедиться, что в ряде картин художников-классиков центральная фигура расположена от сторон формата на расстояниях, образующих пропорцию золотого сечения (например, размещение головы как по вертикали, так и по горизонтали в портрете М. И. Лопухиной В. Боровиковского; положение по вертикали центра головы в портрете А. С. Пушкина кисти О. Кипренского и др.).

То же самое иногда можно видеть и с размещением линии горизонта (Ф. Васильев: «Мокрый луг», И. Левитан: «Март», «Вечерний звон»).

Конечно, указанное правило не всегда есть решение проблемы композиции, и оно не должно подменять в творчестве художника интуицию ритма и пропорций. Известно, например, что некоторые художники применяли для своих композиций отношения «музыкальных чисел»: терции, кварты, квинты (2:3, 3:4 и др.).

Искусствоведы не без основания отмечают, что конструкцию любого классического памятника архитектуры или скульптуры при желании можно подогнать под какое угодно отношение чисел.

Нашей же задачей в данном случае и особенно задачей начинающего художника или резчика по дереву является научиться строить обдуманную композицию своего произведения не по случайным соотношениям, а по гармоничным пропорциям, проверенным практикой.

Эти гармоничные пропорции надо уметь выявить и подчеркнуть конструкцией и формой изделия.

Рассмотрим в качестве примера поиска гармоничной пропорции определение размеров рамки к работе, показанной на рис. 175. Формат помещаемого в нее изображения задан в пропорции золотого сечения.

Внешние размеры рамки при одинаковой ширине ее сторон золотой пропорции не дадут. Поэтому отношение длины и ширины ее (ЗЗ0X220) принято несколько меньше золотого числа, т. е. равным 1,5, а ширина поперечных звеньев соответственно увеличена по сравнению с боковыми сторонами.

Это позволило выйти на размеры рамки в свету (для картины), дающие пропорции золотого сечения.

Отношение же ширины нижнего звена рамки к ширине его верхнего звена подогнано к другому золотому числу, т. е. к 1,12. Также отношение ширины нижнего звена к ширине бокового (94:63) близко к 1,5 (на рисунке — вариант слева).

Рис. 175. Размеры рамки, построенной по двум различным закономерностям: слева — приближенные к зависимости пропорций двух золотых чисел (1,62 и 1,12), справа — отражающие точные пропорции золотого числа 1,62

Таким образом, удалось сохранить пропорции кадра изображения, формата рамки и ее элементов приближенными к классической гармонии.

Теперь сделаем эксперимент: увеличим длинную сторону рамки до 366 мм за счет ширины нижнего звена (она будет 130 мм) (на рисунке — вариант справа), чем приблизим не только отношение но и к золотому числу 1,62 вместо 1,12.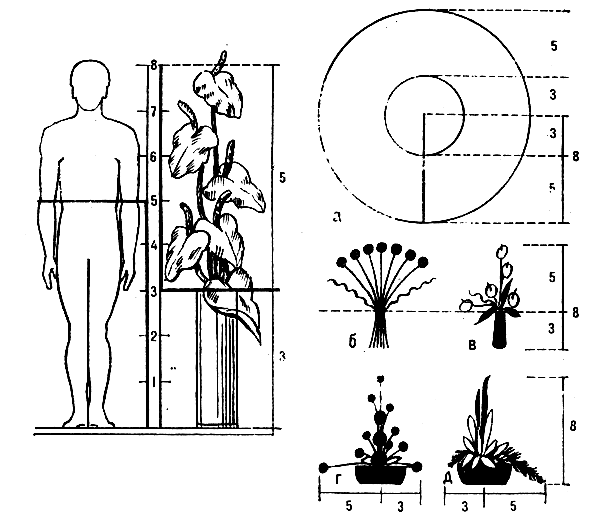

В результате получилась новая композиция, которая может быть применена в каком-либо ином изделии, но для рамки возникает желание сделать ее короче.

Закройте нижнюю часть ее линейкой настолько, чтобы глаз «принял» получившуюся пропорцию, и мы получим ее длину 330 мм, т. е. подойдем к исходному варианту.

Так, анализируя различные варианты (могут быть и другие кроме двух разобранных), мастер останавливается на единственно возможном с его точки зрения решении.

Применение принципа золотого сечения в поисках нужной композиции лучше делать, используя несложный прибор, принципиальная схема конструкции которого показана на рис. 176.

Две линейки этого прибора могут, вращаясь вокруг шарнира В, образовывать произвольный угол.

Если при любом растворе угла разделить точкой К расстояние АС в золотом сечении и смонтировать еще две линейки: КМ\\ВС и КЕ\\АВ с шарнирами в точках К, Е и М, то при любом растворе АС это расстояние будет делиться точкой К в отношении золотого сечения.

Рис. 176. Прибор — измеритель пропорций золотого сечения. Принципиальная схема конструкции (сторона МК и ВС, а также КЕ и АВ соответственно параллельны)

Как вам поделка?

Золотой прямоугольник Композиция

На сегодняшнем уроке композиции мы обсудим Золотой прямоугольник.

Золотой прямоугольник основан на «золотом сечении», идее о том, что существует золотое сечение (1,168), которое повторяется в природе.

Я не буду слишком много говорить о научных или математических подробностях; но с практической точки зрения в фотографии это хороший способ создать более сильные и сбалансированные композиции.

Скачать

PDF
Сетка наложения Photoshop (.psd)
Презентация Powerpoint (.pptx)
Основная презентация Apple

—

1. Нарисуйте стандартный видоискатель (3:2) с соотношением сторон:

Прежде всего, представьте ваш видоискатель со стандартным соотношением сторон 3:2.

2. Начертите диагональную линию

3. Нарисуйте перпендикулярную красную линию под углом 90 градусов:

4. Пересечение

Обратите внимание на пересечение красных линий, это то же самое, что и спираль Фибоначчи.0003

Давайте применим диагонали к другим направлениям:

И давайте поработаем в разных направлениях:

Давайте вернемся к основам, с чистого листа.

Затем добавим красные диагонали и посмотрим, какую сетку они образуют:

Доступ к золотому прямоугольнику в Lightroom

Откройте Lightroom
Нажмите «D», чтобы перейти к модулю разработки
Нажмите «R», чтобы перейти в режим cRop
Нажмите «O», чтобы изменить наложение
Нажмите «Shift+O», чтобы изменить ориентацию наложения
Продолжайте переключать, пока не получите Золотой прямоугольник:

Пример моей фотографии:

Теперь я собираюсь засыпать вас несколькими изображениями, надеюсь, вы сможете следовать за мной. Обратите внимание, как золотой прямоугольник и спираль Фибоначчи следуют друг за другом:

Почему Золотой прямоугольник?

Не знаю, почему это работает; но это работает.

Золотой прямоугольник намного динамичнее стандартного правила третей. Это связано с тем, что правило третей слишком много внимания уделяет горизонтальным и вертикальным линиям, которые не так динамичны, как диагональные линии.

Как я могу применить это к своей фотографии?

По сути, вам нужно знать следующее:

Рисование красных/синих линий полезно для оценки ваших композиций после того, как вы сделали фотографии. Это поможет лучше проинформировать вашу композицию и кадрирование в следующий раз, когда вы пойдете фотографировать.
Когда я снимаю, я стараюсь думать о диагоналях . Я намеренно пытаюсь получить диагональ, идущую от угла моего кадра. Это делает мои фотографии более динамичными .
Думайте о диагоналях, а не о спирали Фибоначчи. И если на ЖК-экране вашей камеры есть наложение диагональной сетки, включите его.
Больше наклоняйте камеру. Используйте «Голландский угол» для создания более драматичных изображений.
При кадрировании сосредоточьтесь на краях кадра и убедитесь, что края образуют диагонали.

В конечном счете, цель композиции — создать более сбалансированные, динамичные и интересные кадры. И чем сильнее ваша композиция, тем больше вы можете сосредоточиться на эмоциях и душе фотографии.

Скоро будет больше.

Всегда,

Эрик

Поднимите свою композицию на новый уровень:

Центральный глаз
Низкоугольный
Голландский угол
Глубокая глубина
Расстояние
Силуэт
Направляющие линии
Фигура на землю
Спираль Фибоначчи
Обрезка
Эмоции
Композиция Эрика Кима

Композиция для уличной фотографии 101

Чтобы получить подробные уроки по композиции, прочтите бесплатную электронную книгу: « Руководство по композиции для уличной фотографии ».

Дополнительные статьи для улучшения ваших композиций в фотографии:

Урок композиции №1: Треугольники
Композиция Урок №2: Фигура на земле
Урок композиции №3: Диагонали
Урок композиции #4: Ведущие линии
Урок композиции #5: Глубина
Композиция Урок №6: Обрамление
Урок композиции № 7: Перспектива
Урок композиции #8: Кривые
Урок композиции #9: Автопортреты
Урок композиции №10: Городские пейзажи
Композиторский урок №11: «Найди то, что нельзя»
Композиция Урок №12: Теория цвета
Урок композиции №13: несколько предметов
Урок композиции №14: Квадратный формат

Теория композиции

Изучите теорию композиции:

Почему композиция важна?
Не думайте о композиции при съемке уличной фотографии
Как использовать пустое пространство
Композиция для уличной фотографии 101
Теория композиции в уличной фотографии: 7 уроков от Анри Картье-Брессона

Лекции по композиции

Уроки композиции от мастеров искусства

Уроки композиции Рафаэль может научить вас фотографии
В процессе: Леонардо да Винчи

В процессе

Золотой прямоугольник

Школа искусств

Grays — И.Т. Интернет

Композиция и золотое сечение

Что такое композиция?

Композиция используется для направления взгляда по изображению и влияет на то, как зритель интерпретирует визуальную информацию.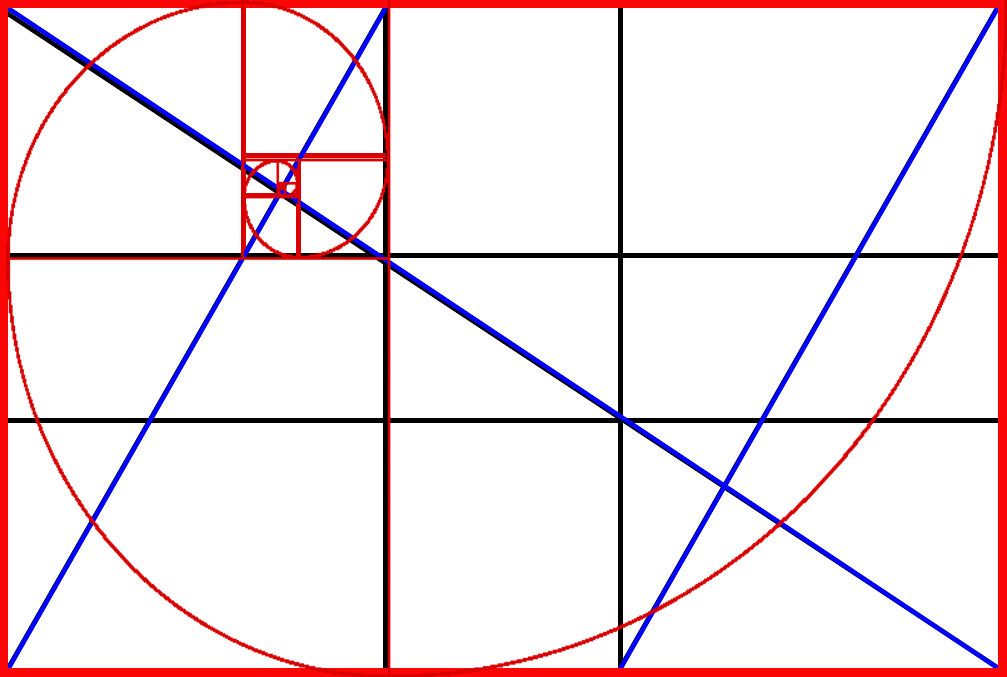

Композиция может относиться к размерам, положениям и пространственным отношениям различных элементов в изображении.
Его можно использовать как способ организации элементов на странице или экране или для создания ощущения динамического визуального напряжения.

В зависимости от расположения элементов общий эффект будет либо эстетически приятным, либо эстетически неприятным.

Какой из приведенных ниже прямоугольников кажется вам наиболее удачным?

Нажмите на изображение выше

Золотое сечение — 1:1,618 (также известное как Золотое сечение)

Большинство людей, независимо от их культурного происхождения, находят эти композиционные пропорции эстетически приятными.

В конце 19 века немецкий психолог Густав Фехнер исследовал реакцию человека на прямоугольные формы на основе золотого сечения.

Он измерил тысячи прямоугольных предметов — например, книг, газет, коробок, зданий и т. д. — и обнаружил, что большинство людей предпочитают смотреть и использовать прямоугольные предметы с пропорциями 1:1,618

Подобные эксперименты были проведены и достигли примерно таких же результатов.

Геометрия дизайна, книга графического дизайнера по имени Кимберли Элам ссылается на это.
(The Geometry of Design, Princeton Architectural Press, New York, 2001)

Щелкните здесь, чтобы увидеть, как рисуется прямоугольник золотого сечения

Божественная пропорция

Внешний вид прямоугольников, созданных с использованием Золотого сечения, основан на Божественной пропорции .

Соотношение 1 : 1,618 также известно как греческая буква фи.
http://en.wikipedia.org/wiki/Image:Phi_uc_lc.svg

(Математическая формула Божественной пропорции: (AB разделить на AC) = (AC разделить на CB)

Похоже, что структура на основе (или приблизительно на основе) измерения божественной пропорции будут выглядеть эстетично.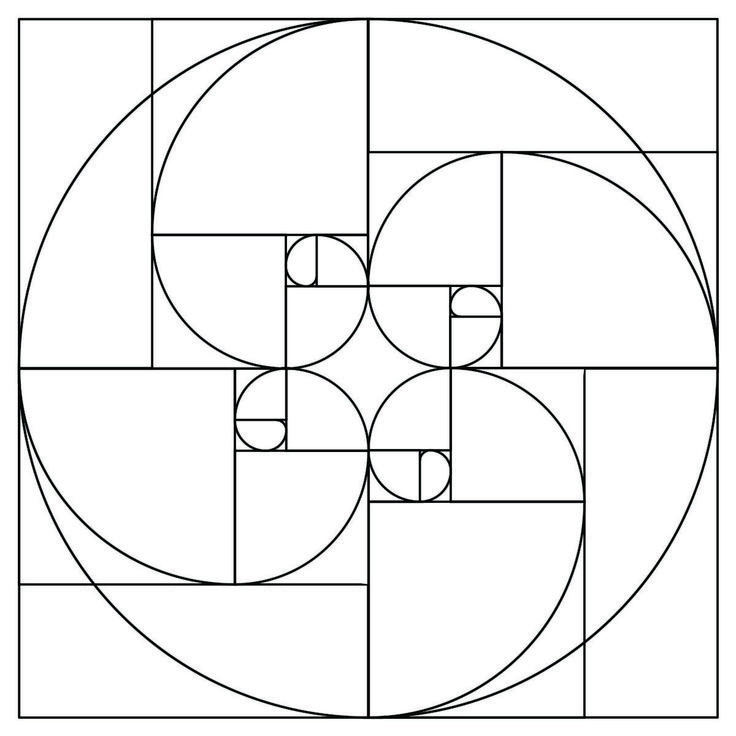

Дизайнеры могут использовать это понимание пропорций, чтобы сделать свою работу более визуально привлекательной.

Многие дизайнеры сознательно не используют Божественную Пропорцию в своей повседневной работе.
Однако может случиться так, что люди, тяготеющие к областям искусства и дизайна, интуитивно понимают эту систему пропорций и используют ее неосознанно.

Примеры золотого сечения в том виде, как оно проявляется в человеческом теле

Возможно, люди предпочитают пропорции золотого сечения и находят их использование визуально привлекательным потому, что на подсознательном уровне мы привыкли видеть эти пропорции в себе и друг друга.
• Отношение кисти к предплечью приблизительно равно Золотому сечению.
(Обратите внимание, что на практике соотношение может быть ниже.)

——

• Каждая кость указательного пальца руки приблизительно в 1,618 раза больше, чем предыдущая кость
(От кончика указательного пальца к ладони).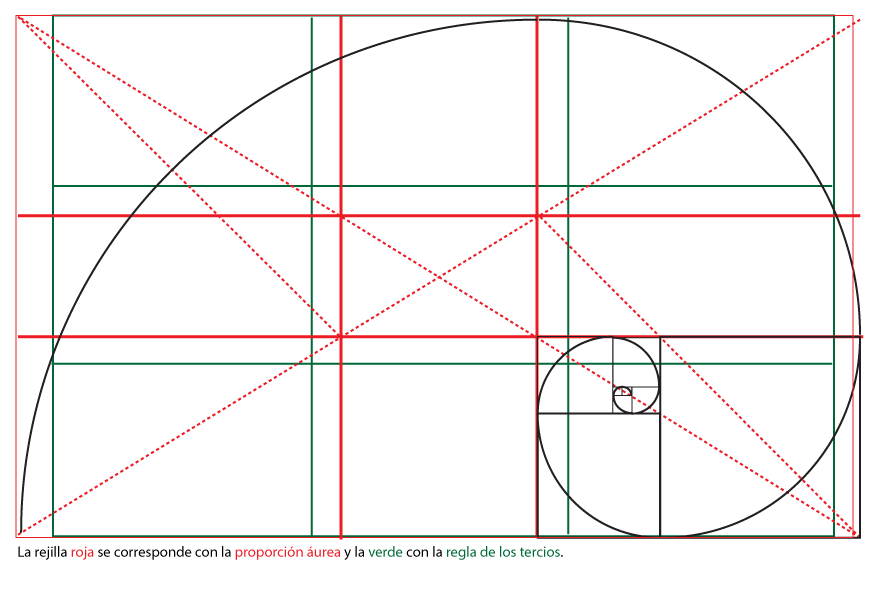 в «раскладке» наших лиц.
http://goldennumber.net/images/face-phi.png

——

• Профессор Стивен Марквардт считает, что человеческая привлекательность может быть связана с золотым сечением.
Он разработал «маски для лица» на основе математики золотого сечения и утверждает, что лица людей, которых можно назвать «привлекательными», кажутся вписывающимися в очертания, появляющиеся на масках.

http://www.beautyanalysis.com/index2_mba.htm
(Идеальное лицо > Маски)

http://www.intmath.com/Numbers/mathOfBeauty.php
Попробуйте наложение интерактивных масок Flash «game»

Последовательность Фибоначчи

Леонардо Пизанский (также известный как Фибоначчи) был итальянским математиком XII-XIII веков.

Он познакомил Европу с индо-арабскими цифрами, которые имели значение для десятичной системы счисления, посредством публикации своей книги Liber Abacci .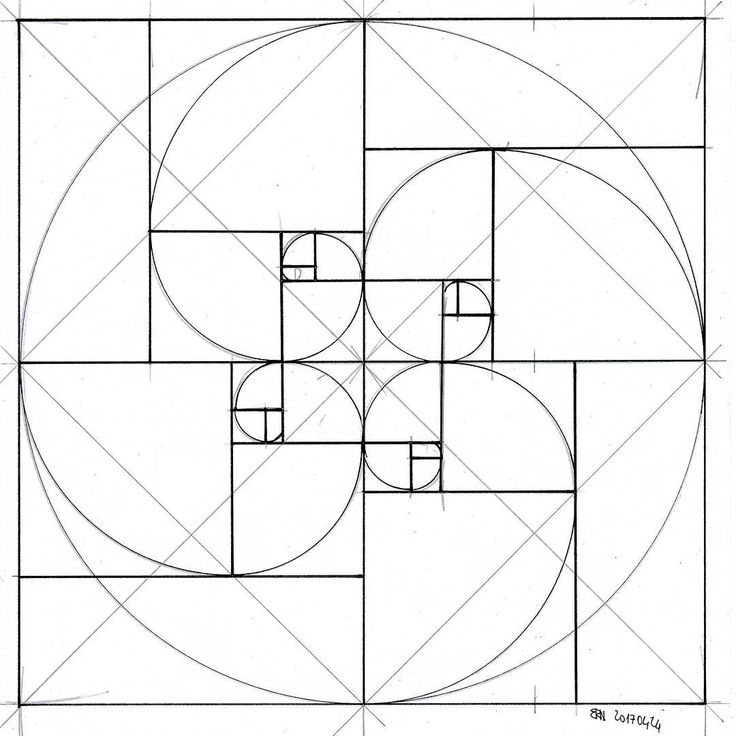 (что означает Книга Чисел или Книга Расчетов. )

Последовательность Фибоначчи представляет собой серию чисел, названную в его честь и которую он тщательно изучал.
(На самом деле он не открыл свойства чисел сам, хотя последовательность теперь названа в его честь.)

В приведенной ниже последовательности Фибоначчи каждое третье число получается путем сложения двух предыдущих чисел.

т.е.

1
1
2 (1+1)
3 (1+2)
5 (2+3)
. )
13 (5+8)
21 (8+13)
34 (13+21)
etc

Говорят, что последовательность Фибоначчи связана с золотым сечением.
Начиная с числа «3», все числа в последовательности — если они делятся на предыдущее число — дают результат, равный 9. 0098 приблизительно 1,618

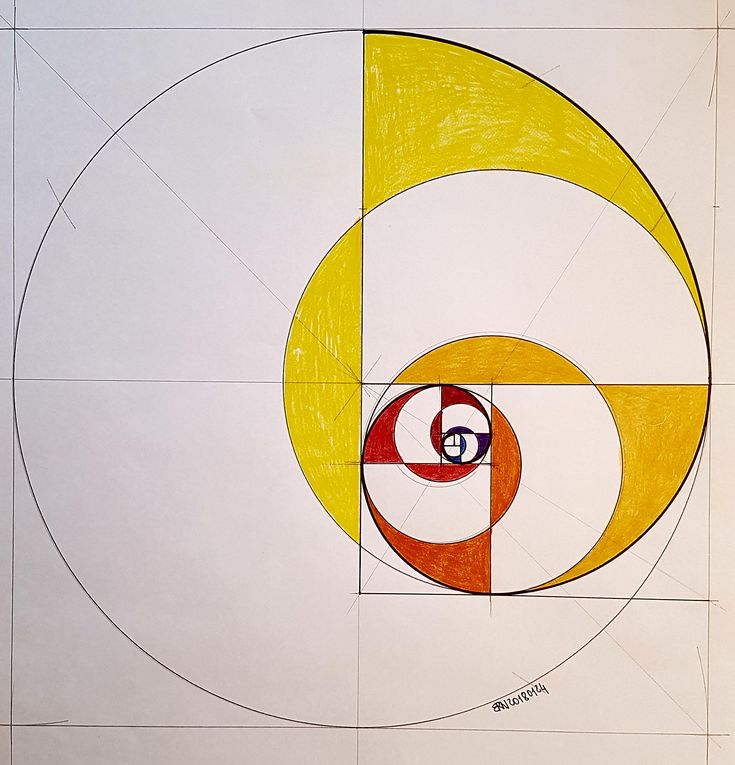
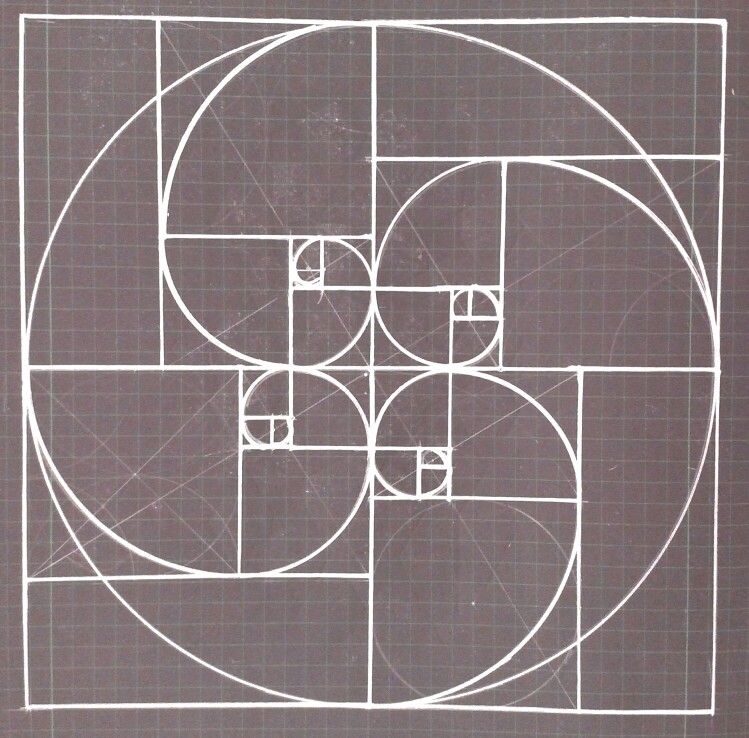
Когда мы рисуем квадрат внутри прямоугольника золотого сечения, оставшаяся прямоугольная форма также имеет пропорции золотого сечения.

Эта оставшаяся прямоугольная форма примерно в 1,618 раза меньше, чем предыдущий прямоугольник Золотого сечения, в котором он находится.

Этот процесс можно повторять бесконечно, как показано ниже.

——

Когда мы рисуем спираль на основе прямоугольников золотого сечения, повторяющихся внутри больших прямоугольников золотого сечения,
мы обнаруживаем, что форма этой спирали напоминает формы, наблюдаемые в мире природы.

например, морская раковина.
Морские раковины вырастают примерно в 1,618 раза больше на каждой фазе своего роста. >>

http://en.wikipedia.org/wiki/Image:Fibonacci_spiral.svg

Говорят, что золотое сечение 1:1,618 встречается во многих других областях.
Древние греки считали золотое сечение эстетически привлекательным и писали об этом еще в 5 веке. Они предположили, что мы можем найти примеры Божественной Пропорции в рукотворном мире, а также в мире природы.
• Парфенон в Афинах, Греция
Структура фасада Парфенона разделена с использованием пропорций золотого сечения.
• Внешняя форма Парфенона вписывается в прямоугольник с соотношением сторон 1:1,618
• Фасад был разделен таким образом, чтобы соответствовать шаблону, появляющемуся, когда прямоугольник Золотого сечения рисуется, а затем повторяется внутри себя.
Другие примеры —
• http://goldennumber.net/
• http://goldennumber.net/acoustics.htm
• http://goldennumber.net/music.htm
Канон Витрувия
Маркус Витрувий Поллион (известный как Витрувий) был греческим ученым и архитектором, который работал примерно между 80 г.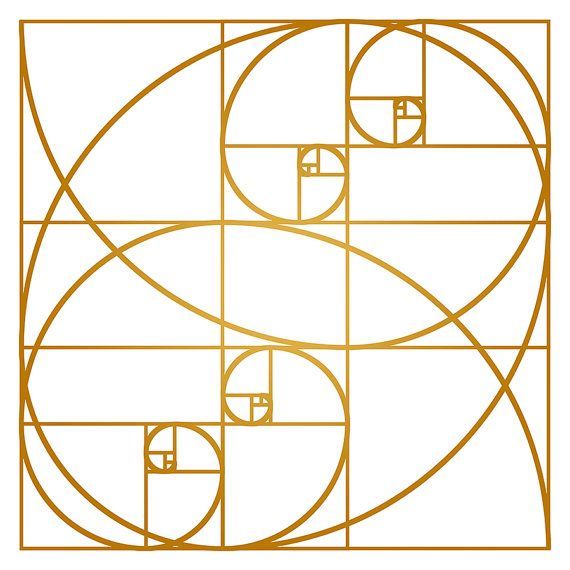 до н.э. и 25 г. до н.э. Он считал, что архитектурные пропорции греческих храмов должны основываться на визуально гармоничных пропорциях человеческого тела.
Художники эпохи Возрождения Леонардо да Винчи и Альбрехт Дюрер использовали Витрувий Канон в конце 15 века и в начале 16 века.
По ссылке ниже показано одно из самых известных изображений идеализированных пропорций. «Витрувианский человек» Леонардо да Винчи.
http://en.wikipedia.org/wiki/Image:Da_Vinci_Vitruve_Luc_Viatour.jpg
Он отметил ряд особенностей пропорций человеческого тела —
• Высота от ступней до макушки примерно равна длине рук, если вытянуты
• Высота туловища и длина вытянутых рук равны, Таким образом, на основе этих измерений можно нарисовать квадрат, который заключает в себе все тело
• Если фигура стоит с широко расставленными ногами и вытянутыми/поднятыми вверх руками все они будут соприкасаться с точками на окружности, если их начертить используя расстояние между пупком и ступнями в качестве радиуса
• Фигуру можно разделить по золотому сечению на уровне пупка
• Если расстояние между пупком и ступнями разделить на расстояние между пупок и голова, получаем число примерно 1,618
Однако . . .
Не все, особенно математики, убежден в этой экстраполяции математических формул — особенно с подразумеваемыми «мистическими» свойствами — из явлений природы.
Как и в большинстве источников информации, утверждающих, что «красота» может быть измерено, есть противоположная информация, которая говорит, что это не может
Выписка:
http://www.lhup.edu/~dsimanek/pseudo/fibonacc.htm
http://www.umcs.maine.edu/~markov/GoldenRatio.pdf
Корень 2 прямоугольника

Корень 2 прямоугольника имеет пропорциональное соотношение размеров 1:1,41 A4, A3 и т. д.
Любой лист, сложенный пополам по самому длинному краю, имеет следующий размер A меньше или, если его сложить вдвое по самому длинному краю, это следующий размер A больше.
Рисунок, образованный делениями на спинке и сиденье стула «Барселона» Миса ван дер Роэ 1929 года, основан на прямоугольниках Root 2. Со стороны сама конструкция опирается на 3 простых кривых. Длина основания стула такая же, как и его высота (поэтому сбоку вся конструкция может быть заключена в квадрат).
http://en.wikipedia.org/wiki/Image:Mies-Barcelona -Chair-and-Ottoman.jpg
Нажмите здесь, чтобы увидеть, как рисуется прямоугольник корня 2
(прямоугольники Root 3, Root 4, Root 5 и т. д. основаны на аналогичной структуре)

Традиционное расположение текста на печатной странице
Говорят, что ранние рукописи были размещены с использованием пропорций, аналогичных приведенному ниже примеру.
Базовая структура, на которой размещены элементы на странице, помогает странице выглядеть хорошо сбалансированной и упорядоченной.

Общая общая пропорция страницы составляет 2:3
• Измерения здесь приблизительно основаны на пропорциях золотого сечения.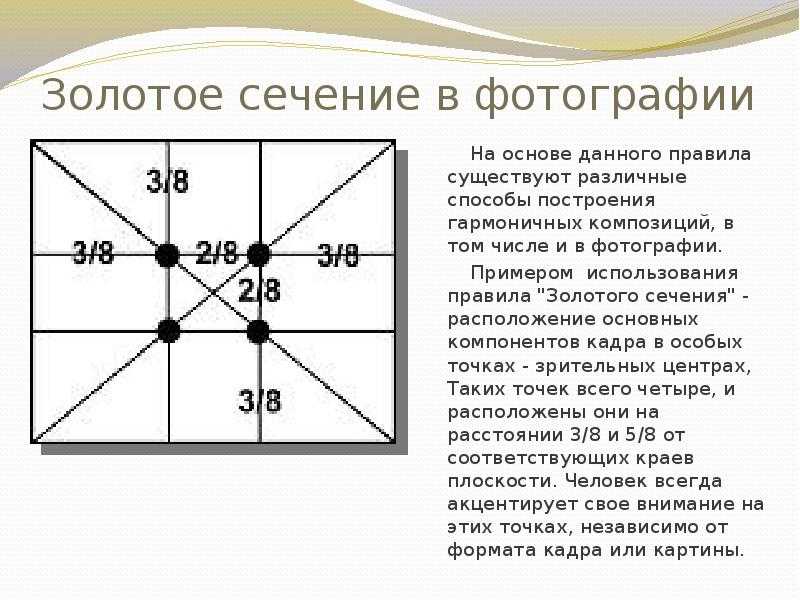
Размер каждого блока текста пропорционально размеру страницы, на которой он расположен, т. е. 2:3
• Текст размещается так, чтобы он совпадал с диагональными линиями.
• Высота каждого блока текста равна ширине каждой страницы.
Глядя на страницу слева —
• Правое поле составляет примерно 1/9 ширины страницы.
• Левое поле составляет примерно 2/9 ширины страницы.
Все еще глядя на левую страницу —
Каждое поле в два раза больше ширины поля напротив.
• Ширина левого поля в два раза больше ширины правого поля, а ширина нижнего поля в два раза больше ширины верхнего поля.
• Это дает соотношение 1 : 1,5 : 2 : 3
——
Эта система пропорций названа Канон Ван де Граафа в честь человека, который ее открыл.
Щелкните здесь, чтобы увидеть, как создается двойная страница.
——
Бумага формата «A»
Хотя приведенный выше макет считается хорошо сбалансированным, сегодня мы редко видим его в использовании.
Бумага формата «A» (например, A3/A4/A5) стала «стандартным» форматом. Любой лист, сложенный пополам по самому длинному краю, соответствует следующему размеру «А» по размеру меньше, или, если он сложен вдвое по самому длинному краю, это следующий размер «А» по размеру.
• Печатать на бумаге формата «A» экономически выгодно, так как это легко доступный и стандартизированный размер бумаги.
• Макет, использованный при создании рукописей (см. выше), оставляет большую часть страницы пустой. Это означает, что на каждой странице можно разместить меньше текста. По этой причине книга, оформленная таким образом, потребует большего количества страниц и, следовательно, будет стоить дороже.
Современные размеры бумаги «А» вместе с производственными и экономическими требованиями могут привести к результату, больше похожему на изображение ниже.

Золотое сечение также может быть применено к макету веб-страниц
Ниже приведен скриншот веб-сайта BBC.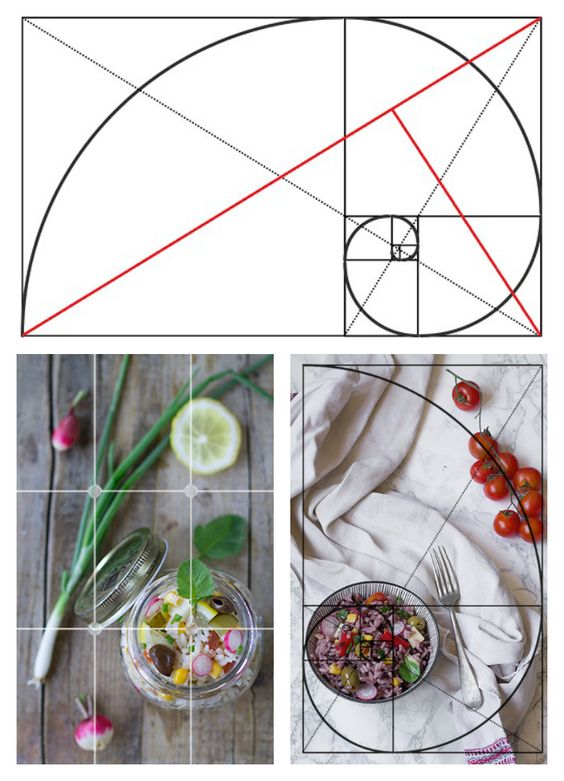 Нажмите на изображение ниже.
Было бы довольно необычно найти веб-страницу, которая была бы выложена точно с пропорциями 1:1,618.
Однако мы можем найти некоторые примеры веб-страниц, где области страниц расположены таким образом, что приблизительно соответствует Золотому сечению, пропорции которого указаны выше.
Такое использование асимметрии помогает сделать макет визуально более интересным.
Компания, ссылка на которую приведена ниже, разработала инструмент компоновки, помогающий разрабатывать веб-страницы на основе пропорций золотого сечения. http://www.atrise.com/golden-section/screenshots.php

Золотое сечение: искусство создания сбалансированных композиций в дизайне
Айеша Амбрин
Для создания визуальной привлекательности или гармонии дизайнеры комбинируют связанные элементы, такие как цвета, формы, текстуры и так далее. В то время как визуальные эффекты создают ощущение баланса, симметрии и равновесия, они должны следовать определенному шаблону, который сводит все в одну точку.
Понятие гармонии также коренится в законе дизайна об эстетическом удобстве использования, который гласит, что люди «часто воспринимают эстетически приятный дизайн как дизайн, который более удобен в использовании». Короче говоря, дизайн, который кажется красивым, считается функциональным. Итак, есть ли надежный способ помочь дизайнеру создать визуально приятный дизайн? Золотое сечение может помочь. В этой статье я постараюсь помочь вам понять золотое сечение, как оно влияет на дизайн и где его можно применять.
Что такое золотое сечение
Золотое сечение — математический принцип, обозначаемый фи (?), — использовался на протяжении тысячелетий. Считается, что ранние египтяне использовали его для строительства пирамид Гизы. Греческий скульптор и математик Фидий (500 г. до н.э. – 432 г. до н.э.) применил фи к дизайну Парфенона.
Точно так же Платон считал его универсальным связующим математических отношений. Евклид (отец геометрии) связал золотое сечение со структурой пентаграммы.
От Да Винчи и Микеланджело до Сальвадора Дали художники, скульпторы, математики и архитекторы начали использовать это общепринятое понятие баланса в своей работе.
Итак, как они использовали фи?
Золотое сечение (также известное как Золотое сечение или Золотое сечение) — это особое число (1,618…), полученное делением Золотого прямоугольника на более длинную и более короткую части. Его можно просто рассчитать следующим образом: сумма более длинной части (A) при делении на более короткую часть (B) равна сумме обеих частей (A+B), деленной на более длинную часть (A), т. е. ? или 1,618…, что ведет к бесконечности.
Формы существуют в соотношении 1:1,618 и могут быть представлены формулой, показанной на рисунке ниже.
Золотое сечение часто связывают с последовательностью Фибоначчи, где каждое последующее число является суммой двух предыдущих чисел.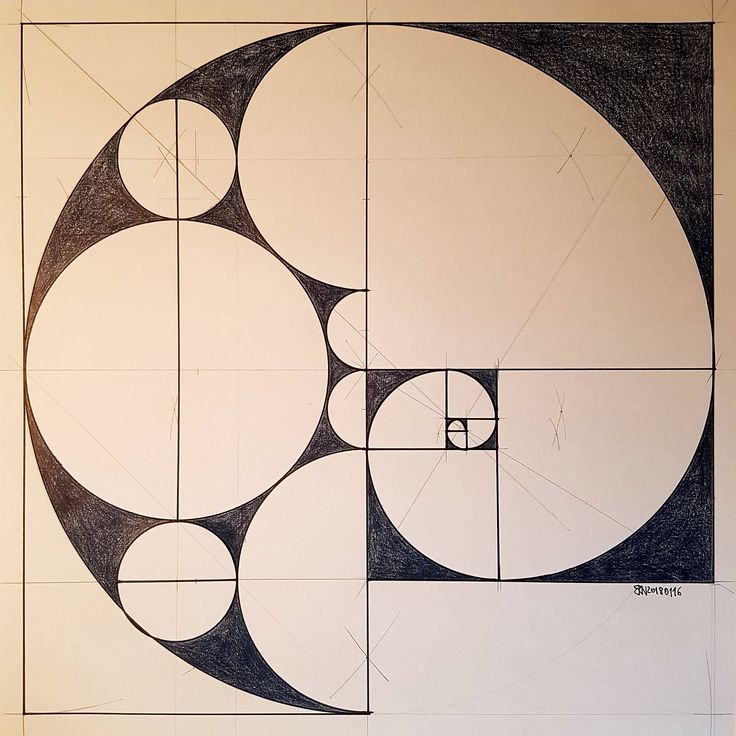 Начиная с нуля, последовательность идет как 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… и этот список можно продолжать и продолжать. При подстановке в ту же формулу золотого сечения числа из последовательности дают сумму, близкую к фи.
Божественная пропорция
Графические дизайнеры могут использовать золотое сечение и производные от него размеры для создания привлекательных дизайнов. Они могут просто умножить или разделить размер элемента на 1,618, чтобы получить идеальные размеры элемента дизайна, или использовать золотую спираль для управления макетами в своих проектах всех типов. Adobe Photoshop и Lightroom предлагают наложения кадрирования с использованием «Золотой спирали» и «Золотого сечения», чтобы помочь вам составить идеальное изображение.
Как использовать золотое сечение в графическом дизайне
Вы можете подумать, что использование золотого сечения каким-то образом замедлит или ограничит ваше творчество. Но на самом деле это дает вам возможность заставить ваш дизайн летать.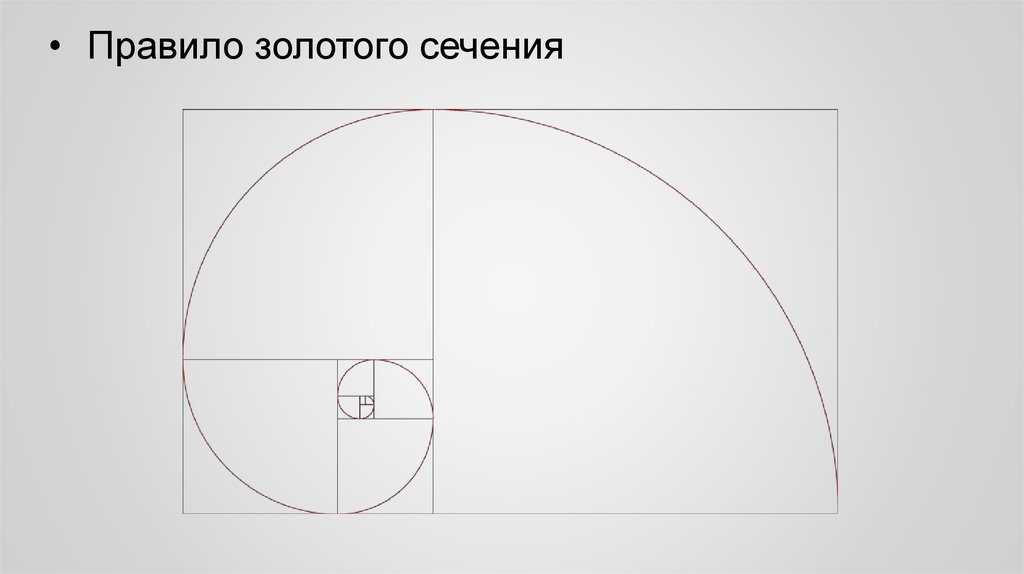 Вот несколько примеров того, как его можно использовать в различных типах дизайна, и советы по началу работы.
Дизайн логотипа
Когда вам нужно придумать дизайн логотипа, подумайте об использовании золотого сечения. Это может помочь вам мгновенно распознавать и создавать закономерности, которые установят гармонию.
Изображение: Twitter/RabiaaIqbal
Совет : Вы можете взять основные формы из золотого сечения. Это поможет сохранить гармоничные пропорции. Затем объедините фигуры и выровняйте их с помощью сетки. Вы также можете определить высоту, ширину, размещение, размер и даже длину элементов логотипа. Просто не забудьте начать с одного золотого сечения и взять пропорции из него. Использование более одного загромождает ваш дизайн.
Лучшими примерами являются логотипы Twitter, Apple и Pepsi, которые без особых усилий сохраняют пропорции гармонии. Каждый из них использует одну спираль и берет пропорции для создания форм, составляющих логотипы.
Источник: Behance
Веб-дизайн
Веб-дизайн, созданный с помощью Золотого сечения, подчеркивает эстетику и качество визуальной иерархии. Некоторые сайты разработаны с использованием золотых пропорций, чтобы создать значимый опыт для пользователей, добавив при этом повышенное чувство очарования.
Например, 2ndSTREET использует золотую пропорцию для своей домашней страницы, которая представляет собой концептуальный взгляд на предметы одежды. Когда вы посещаете веб-сайт, вы видите традиционный макет веб-сайта с четко разграниченными разделами A и B. Причина, по которой он выглядит очень убедительно, заключается в прогрессивном дизайне с золотой сеткой для динамического макета.
Источник: 2 ^nd Street
Другим примером является Гарвардский киноархив. С заголовком справа и занимающим большую часть пространства, меньшие пропорции используются для выделения CTA. Причина, по которой это удовлетворяет глаз, заключается в передышке между содержанием. Это демонстрирует, что сайт может иметь исключительную компоновку, используя золотую середину.
Источник: Harvard Film Archive. Симметрия и баланс часто остаются незамеченными, но создают исключительный вид. Взгляд зрителя притягивается к центру спирали, где размещение композиционной модели выглядит привлекательно и эффектно.
Хорошим примером является обложка книги «Помощь » Кэтрин Стокетт, разработанная с использованием золотого сечения. Обложка привлекает внимание идеально подобранными пропорциями.
Источник: Википедия
Другим примером, где активно используется спираль золотого сечения, является журнал Feld. Мелкий текст и подробное содержание сконцентрированы к центру спирали, направляя взгляд извилистым образом.
Источник: Canva.com
Фотография
Профессиональные изображения не создаются случайным образом. Фотографы используют золотое сечение и правило третей для создания эстетичных фотографий.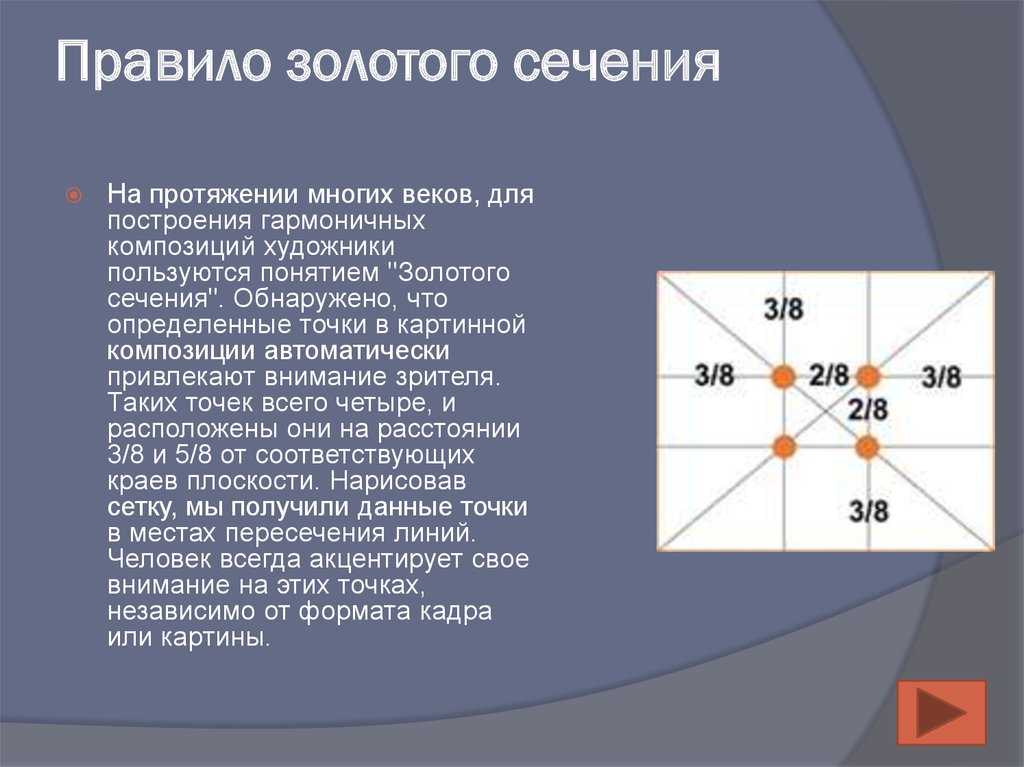 Это помогает сконцентрировать внимание на отдельных элементах изображения, не теряя общей привлекательности.
Используя золотое сечение, изображение разбивается на неравные части, где изображение строится по линиям и пересечениям. Следующее соотношение составляет 1,618 к 1. Спираль должна использоваться для направления взгляда зрителя на важный элемент, пример которого показан ниже.
Изображение: Flickr/John Lemieux
При использовании правила третей вы делите изображение на 3 части по горизонтали и по вертикали в равной пропорции 1:1:1. Сюжеты изображения вдоль пересекающихся точек и линий создают композицию для идеального баланса в изображении. Вот пример.
Изображение: SLR Lounge
Золотое сечение повсюду вокруг нас
Когда вы осознаете это, вы можете начать замечать, что золотое сечение проявляется повсюду. Он описывает естественную и бессознательную реакцию, которая заставляет глаза находить точку притяжения и фокусироваться.
Золотое сечение композиция: Золотое Сечение в Искусстве (Живописи) Основы Композиции • ИзоКурс, Мск