Фокусное расстояние объектива в масштабе фотографии Калькулятор
✖Масштаб фотографии определяется фокусным расстоянием камеры и высотой полета над землей.ⓘ Масштаб фото [P] | +10% -10% | ||
✖Высота полета самолета над исходной точкой (обычно средним уровнем моря) определяется как средняя высота полета над землей.ⓘ Высота полета самолета [H] | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Отметка точки, линии или площади относительно нулевой точки. | створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% |
|
✖Фокусное расстояние объектива обычно выражается в миллиметрах (мм), что является основным описанием фотографического объектива. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
⎘ копия |
👎
Формула
сбросить
👍
Фокусное расстояние объектива в масштабе фотографии Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1.
Масштаб фото: 2 —> Конверсия не требуется
Высота полета самолета: 11 метр —> 11 метр Конверсия не требуется
Высота точки: 10 метр —> 10 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
2 метр —> Конверсия не требуется
< 4 Фотограмметрия Калькуляторы
Фокусное расстояние объектива в масштабе фотографии формула
Фокусное расстояние объектива = (Масштаб фото*(Высота полета самолета-Высота точки))
f = (P*(H-h1))
Что такое фокусное расстояние?
На самом деле для каждой линзы есть две точки фокусировки, на одинаковом расстоянии от линзы, на противоположных сторонах. Расстояние от объектива до фокальной точки называется фокусным расстоянием.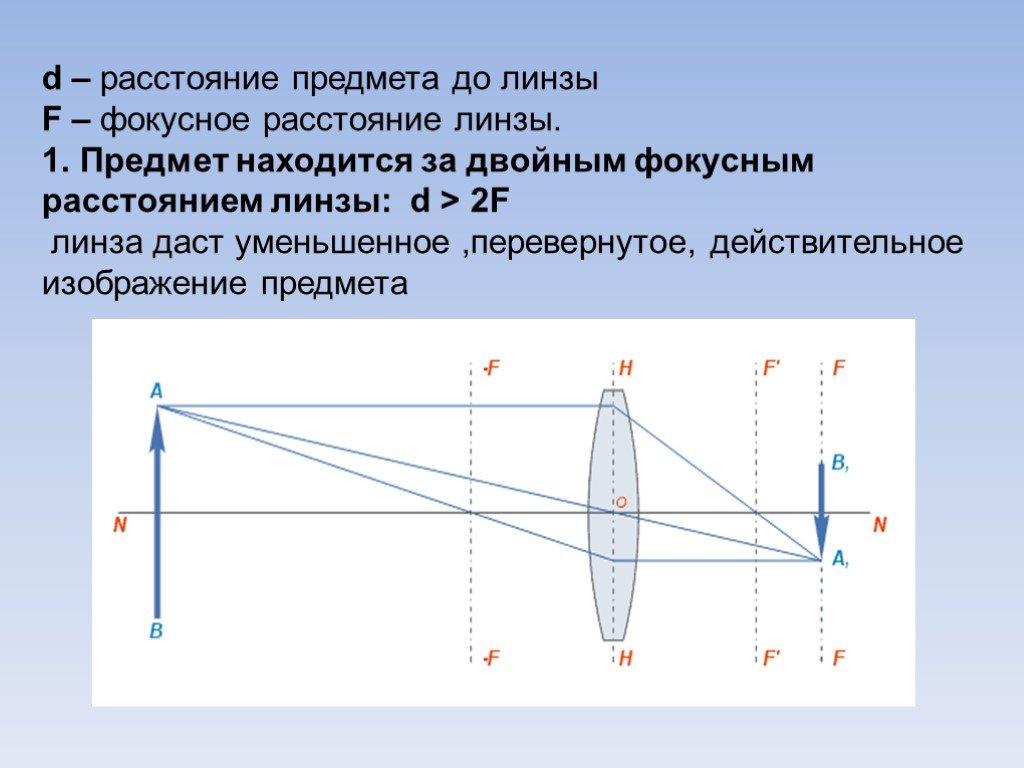
Share
Copied!
|
Основные формулы, показывающие на что примерно способен телескоп.
Сначала три основных понятия:
Сами формулы: Кратность или увеличение телескопа (Г)Г=F/f F вы изменить чаще всего не можете, но имея окуляры с разным f, вы сможете менять кратность или увеличение телескопа Г. 
Максимальное увеличение (Г max)
Максимальное увеличение телескопа ограничено диаметром объектива.
Принято считать, что Г max=2*D, но из-за поправок на искажения, точности изготовления и настройки, лучше немного занизить эту величину:
Светосила
Светосила телескопа определяется в виде отношения D:F. Разрешающая способность (b)
Разрешающая способность телескопа — наименьший угол между такими двумя близкими звездами, когда они уже видны как две, а не сливаются зрительно в одну.
Проще говоря, под разрешающей способностью можно понимать «чёткость» изображения (да простят меня профессионалы-оптики…).
Из-за атмосферы эта величина нечасто бывает меньше 1″ (1 секунды). Например, на Луне 1″ соответствует кратеру диаметром около 2 км. Для длиннофокусных объективов, со значением светосилы 1:12 и более длинных, формула немного другая: b=116/D (по Данлопу). Из сказанного выше видно, что в обычных условиях минимальная разрешающая способность в 1″ достигается при апертуре 150мм у рефлекторов
и около 125мм у планетников-рефракторов. Так что, нет особого смысла ограничиваться 150-ю миллиметрами 😉 Предельная звёздная величина (m)
Предельная звёздная величина, которая видна в телескоп, в зависимости от апертуры:
На деле значения будут немного отличаться из-за разницы световых потерь в разных конструкция телескопов. Выходной зрачок
Выходной зрачок телескопа = D/Г
Поле зрения телескопа
Поле зрения телескопа = поле зрения окуляра / Г
Теперь, когда примерно ясна взаимосвязь характеристик телескопа, можно другими глазами посмотреть на то, что можно увидеть в телескопы разных размеров. Начинающему астроному Николай Курдяпин, kosmoved.ru или расскажите друзьям: Помогите подобрать прибор под задачу. Как решить эту задачу,не понимаю. Как определить (по какой формуле) диапазон телескопа, если он необходим для наблюдения за звездами с атмосферной температурой, например, 10000:К? В тексте ошибка: «Г max=1,5*D, где D — фокусное расстояние объектива». Думаю должно быть: D — апертура объектива или главного зеркала. А мой телескоп наверное самый такой простой. Вы пишете в статье: «6 мм. — примерный диаметр человеческого зрачка в темноте». Но, я встречала упоминания, что в темноте зрачок у нас 8 мм. Так сколько же на самом деле? Большое спасибо за статью и другие статьи вашего сайта, очень понятно и подробно, спасибо!!! Замечательная статья. Благодарю. Celestron 120/1000 OMNI Очень интересно и подробно всё описано. Для меня это очень нужная статья, т.к. недавно начал заниматься астрономией. Мой телескоп: Sturman HQ1400150EQ. Спасибо вам большое!
Ответ: |
|
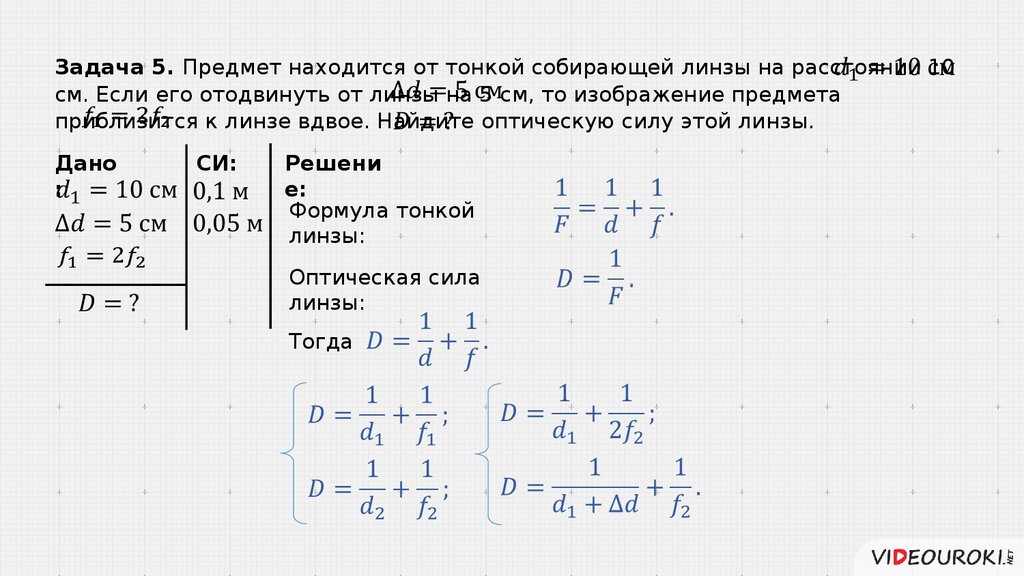
Формула тонкой линзы
Формула тонкой линзы|
Ниже показана обычная гауссовская форма уравнения линзы. Эта форма используется в большинстве вводных учебников. Форма, использующая соглашение о декартовых знаках, часто используется в более сложных текстах из-за преимуществ, связанных с системами с несколькими линзами и более сложными оптическими инструментами. Любая форма может использоваться с положительными или отрицательными линзами и предсказывает формирование как реальных, так и виртуальных изображений. Он справедлив только для параксиальных лучей (лучей, близких к оптической оси) и не применяется к толстым линзам. Если уравнение линзы дает отрицательное расстояние изображения, то изображение является виртуальным изображением на той же стороне линзы, что и объект. Если это дает отрицательное фокусное расстояние, то линза является рассеивающей, а не собирающей линзой на иллюстрации. Уравнение линзы можно использовать для расчета расстояния до изображения как для реальных, так и для виртуальных изображений, а также для положительных и отрицательных линз. Отношение линейного увеличения позволяет предсказать размер изображения.
|
Index Концепции объективов | ||
|
Назад |
|
Если используется декартово соглашение о знаках, гауссова форма уравнения линзы становится  Расстояние до объекта o тогда является отрицательным числом, потому что для перемещения от линзы к объекту вы должны двигаться в направлении, противоположном движению света. Уравнение тонкой линзы
также иногда выражается в ньютоновской форме. Вывод
гауссовой формы исходит из геометрии треугольника. Для тонкой линзы оптическая сила P представляет собой сумму поверхностных оптических оптических сил. Для более толстых линз можно использовать уравнение Гуллстранда, чтобы получить эквивалентную силу. Расстояние до объекта o тогда является отрицательным числом, потому что для перемещения от линзы к объекту вы должны двигаться в направлении, противоположном движению света. Уравнение тонкой линзы
также иногда выражается в ньютоновской форме. Вывод
гауссовой формы исходит из геометрии треугольника. Для тонкой линзы оптическая сила P представляет собой сумму поверхностных оптических оптических сил. Для более толстых линз можно использовать уравнение Гуллстранда, чтобы получить эквивалентную силу.
|
Index Концепции объективов | ||
|
Назад |
Поскольку направление движения света является постоянным и существует постоянное соглашение для определения знака всех расстояний в расчетах, это соглашение о знаках используется во многих текстах. Он имеет некоторые преимущества при работе с многообъективными системами и более сложными оптическими приборами.
|
Index Lens concepts Meyer-Arendt, 2nd Ed | |||
|
Назад |
|
В ньютоновской форме уравнения линзы используются расстояния от точек фокусного расстояния до объекта и изображения, а не расстояния от линзы. Ньютон использовал «внефокальные расстояния» x o и x i в своей формулировке уравнения тонкой линзы. Это эквивалентная обработка, но в этом ресурсе будет использоваться форма Гаусса.
|
Index Концепции объективов | ||
|
Вернуться назад |
Тонкие линзы
Тонкие линзы Единый сферический интерфейс между двумя прозрачными
средства массовой информации могут привести к формированию имиджа. Но просмотр этих изображений не
всегда возможно. Рассмотрим интерфейс воздух-стекло. Когда
объект находится со стороны воздуха, изображение можно просматривать только изнутри
стекло. Придание стеклу конечной толщины и добавление второго
сферическая граница между стеклом и воздухом создаст изображение,
может быть просмотрен кем-то в воздухе. Кусок стекла конечной толщины с
две сферические границы — линза. Если толщина линзы
намного меньше диаметра объектива, мы называем его тонкая линза .
Но просмотр этих изображений не
всегда возможно. Рассмотрим интерфейс воздух-стекло. Когда
объект находится со стороны воздуха, изображение можно просматривать только изнутри
стекло. Придание стеклу конечной толщины и добавление второго
сферическая граница между стеклом и воздухом создаст изображение,
может быть просмотрен кем-то в воздухе. Кусок стекла конечной толщины с
две сферические границы — линза. Если толщина линзы
намного меньше диаметра объектива, мы называем его тонкая линза .
Тонкие линзы могут быть собирающими или
расходящиеся . Собирающие линзы это
в середине толще, чем по краям, а рассеивающие линзы
ближе к краям толще, чем в середине. Тонкая линза имеет два фокусных
точки, расположенные на оптической оси, на расстоянии f от центра линзы на
по обе стороны линзы. Лучи, параллельные оптической оси, проходящие через тонкую собирающую линзу
сходятся в фокусе f на противоположной стороне линзы, а лучи
параллельные оптической оси, проходящие через рассеивающую линзу, расходятся как
если бы они уходили из фокуса на падающую сторону по прямой
путь.
| Собирающая линза | |
| Рассеивающая линза |
Плоскость, проходящая через фокус перпендикулярно оптической оси, называется фокальная плоскость. Параллельные лучи сходятся в фокальной плоскости или расходятся от фокальной плоскости, независимо угла, который они образуют с оптической осью.
Реальное изображение
Виртуальное изображение
Тонкие линзы могут формировать реальные и мнимые изображения.
Пусть x o обозначает перпендикулярное расстояние объекта от осевой линии линзы и пусть x o положительно. Пусть х я обозначают перпендикулярное расстояние изображения от центральной линии линзы. Тогда x i можно найти из уравнения линзы
1/x o + 1/x i = 1/f,
при условии, что мы используем следующее соглашение о знаках.
- x o положительно для объекта перед объективом.
- x i положительно, если x o и x i находятся на противоположные стороны линзы.
- x i является отрицательным, если x o и x i находятся на с той же стороны объектива.
- f положительно для собирающей линзы.
- f отрицательно для рассеивающей линзы.
- Увеличение M = -x i /x o .
Если М отрицательно, изображение перевернуто.
Мы можем найти положение и размер изображения геометрически. Только два луча должны быть нарисованы.
- Нарисуйте оптическую ось и центральную линию линзы.
- Отметьте положение фокусов.
- Нарисуйте объект перед линзой. Нарисуйте падающий луч параллельно
оптическая ось от точки на объекте до центральной линии линзы,
и преломленный луч от центральной линии через f.
- Для собирающей линзы проведите преломленный луч через фокус на
сторону выхода, а для рассеивающей линзы нарисуйте преломленный луч так, чтобы
его продолжение проходит через фокус на падающей стороне.

- Для собирающей линзы проведите преломленный луч через фокус на
сторону выхода, а для рассеивающей линзы нарисуйте преломленный луч так, чтобы
его продолжение проходит через фокус на падающей стороне.
- Нарисуйте второй луч, падающий через f, и преломленный луч, параллельный
оптическая ось.
- Падающий луч или продолжение падающего луча должны пройти через ф. Для собирающей линзы нарисуйте падающий луч или его продолжение. через фокус на падающей стороне, а для рассеивающей линзы нарисуйте падающий луч так, что его продолжение проходит через фокус на сторона выхода.
- Пересечение двух лучей отмечает положение изображения.
- Чтобы проверить точность вашего рисунка, проведите третий луч через центр объектива. Этот луч не искривлен. Он должен пройти через пересечение других лучей, которые вы нарисовали.
Собирающие линзы образуют реальные
перевернутые изображения, если x o > f, и виртуальные прямые изображения, если x или
< ф.
Рассеивающие линзы формируют только мнимые изображения.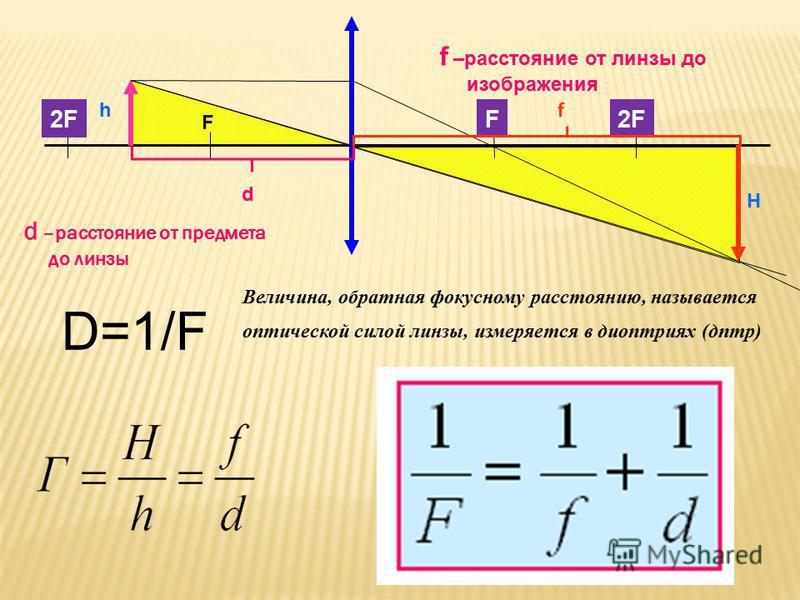
Ссылка:
Приложение для трассировки лучей формирования изображения
Перетаскивайте стрелки и линзу, пока приложение выполняет трассировку лучей.
Уравнение линзы и уравнение зеркала
записываются как
1/х или + 1/х i = 1/ф.
Но знак
условности для х o , x i и f отличаются для линз и
зеркала.
- Зеркала отражают свет, поэтому реальные изображения формируются с одной стороны на котором находится объект. Если x i и f лежат на с этой стороны они положительные.
- Линзы пропускают свет, поэтому реальное изображение формируется на стороне линза напротив предмета. Если x i и f лежат на с этой стороны они положительные.
Вот несколько вещей, которые всегда подходят для тонкой линзы.
- Реальное изображение <--> перевернутое image <--> x i положительный <--> M отрицательный
- Виртуальный образ <--> вертикальное изображение <--> x i отрицательное <--> M положительное
Виртуальное изображение, создаваемое собирающей линзой <--> M > 1, (изображение больше, чем объект)
Виртуальное изображение, создаваемое рассеивающей линзой <--> M < 1, (изображение меньше объекта)
Фокусное расстояние тонкой линзы связано с радиусами кривизны двух ее
поверхности.
1/f = (n 2 — n 1 )(1/R 1 — 1/R 2 ).
- R i положительно, если x o и кривизна центра лежит на противоположные стороны соответствующей поверхности.
- R i отрицательно, если x o и кривизна центра совпадают сторону соответствующей поверхности.
- R 1 радиус поверхности, ближайший к x o .
Проблема:
Контактная линза изготовлена из пластика с показателем преломления 1,5. Линза имеет внешний радиус кривизны 2 см и внутренний радиус искривление 2,5 см. Чему равно фокусное расстояние линзы?
Решение:
- Рассуждение:
Фокусное расстояние тонкой линзы связано с радиусами кривизны двух ее поверхности.
1/f = (n 2 — n 1 )(1/R 1 — 1/R 2 ). - Детали расчета:
Оба R 1 и R 2 положительны. Поэтому
Поэтому
1/f = (n 2 — n 1 )(1/R 1 — 1/R 2 ) = (1,5 — 1)(½ — 1/2,5) = 0,05. ф = 20 см.
Уравнения линзы и зеркала действительны для параксиальных лучи. Если все световые лучи, участвующие в формировании изображения, малыми углами с оптической осью, так что sinθ ≈ тангенс ≈ θ, то в местах, предсказываемых этими уравнениями, формируются почти идеальные изображения. Для внеосевых или косых лучей изображение точки становится размытым, и мы наблюдаем аберрации.
Применение линзы
уравнения для тонких линз, мы можем с уверенностью предположить, что свет преломляется в
центр линзы и пренебречь толщиной линзы. За
толстые линзы мы должны быть более осторожными.
Нужно вычислить местоположение
главные плоскости , от которых измерять
расстояния до объекта, изображения и фокуса
точки.
Многие оптические приборы имеют более одного оптического элемента. Сочетание
зеркала и линзы можно анализировать, рассматривая изображение первого элемента как
объект второго элемента и так далее. Если образ первого элемента
отстает от второго элемента, мы все еще можем использовать уравнение линзы или зеркала,
но тогда мы должны использовать отрицательное расстояние до объекта x или .
Сочетание
зеркала и линзы можно анализировать, рассматривая изображение первого элемента как
объект второго элемента и так далее. Если образ первого элемента
отстает от второго элемента, мы все еще можем использовать уравнение линзы или зеркала,
но тогда мы должны использовать отрицательное расстояние до объекта x или .
Проблема:
Тонкая линза имеет фокусное расстояние 25 см. Найдите изображение, когда
объект находится
(а) 26 см
(б) 24 см
перед линзой. Опишите изображение в каждом случае.
Решение:
Проблема:
Лупа представляет собой собирающую линзу с фокусным расстоянием 15 см. При чем расстояние от почтовой марки, если вы держите этот объектив, чтобы получить увеличение +2?
Решение:
- Рассуждение:
Используйте уравнение линзы. 1/х или + 1/х и = 1/ф. М = -х i /х о . - Детали расчета:
M = -x i /x o = 2, x i = -2x o .
1/х или — 1/(2x o ) = 1/(2x o ) = 1/f = 1/15.
х о = 7,5 см.
Проблема:
В качестве лупы используется собирающая линза с фокусным расстоянием 4 см. Если объект находится на расстоянии 3 см от объектива, какое увеличение?
Решение:
- Рассуждение:
Используйте уравнение линзы. 1/х или + 1/х и = 1/ф. М = -х i /х о . - Детали расчета:
1/х о + 1/x i = 1/f, 1/3 + 1/x i = 1/4, x и = -12 см.
М = -х i /х о = 12/3 = 4.
Проблема:
Предположим, две тонкие собирающие линзы с фокусным расстоянием f 1 и f 2 ,
соответственно, очень близко друг к другу, поэтому можно пренебречь расстоянием
между ними. Они фокусируют свет далекой звезды в фокусе на расстоянии
f eff от линз.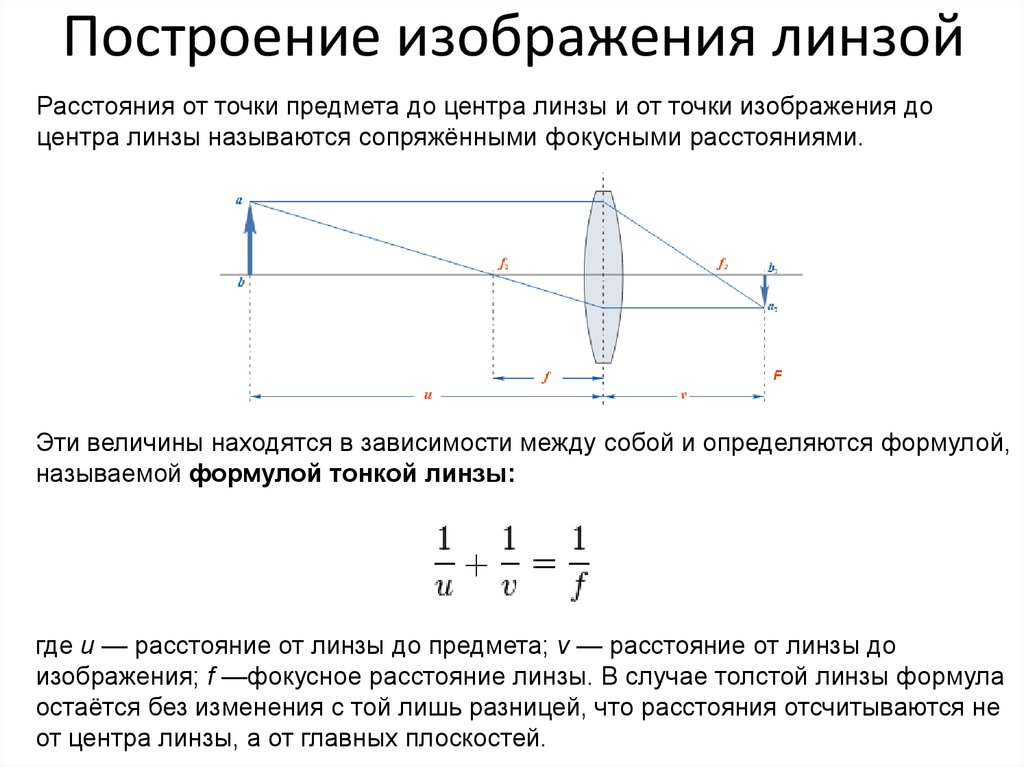 Найти f eff через f 1
и ф 2 .
Найти f eff через f 1
и ф 2 .
Решение:
- Рассуждение:
Используйте уравнение линзы. 1/х или + 1/х и = 1/ф. - Детали расчета:
x o = бесконечность, поэтому для первой линзы 1/x i = 1/ф 1 , х i = f 1 . Изображение первой линзы становится объект второй линзы. Он находится за второй линзой, поэтому расстояние до объекта для второй линзы -f 1 .
Для второй линзы имеем -1/f 1 + 1/x i = 1/f 2 , 1/x i = 1/f 1 + 1/f 2 .
Но расстояние изображения второго объектива равно фокусному расстоянию f eff всей системы.
Следовательно, 1/f эфф = 1/f 1 + 1/f 2 .
Встроенный вопрос 1
У вас есть увеличительное стекло? Если нет, есть ли у вас доступ к некоторым
очки по рецепту? Сделайте несколько наблюдений с помощью одного объектива.
- Держите линзу на расстоянии вытянутой руки от глаз и смотрите на свое яркое
экран компьютера с текстом на нем. Переместите объектив ближе к или
подальше от экрана, держа его на расстоянии вытянутой руки от вашего
глаза. Какой тип изображения вы видите? Кажется ли это в
спереди или сзади объектива?
Помните: увеличительные стекла представляют собой собирающие линзы с относительно короткое фокусное расстояние. Линзы для очков могут быть собирающими или расходящиеся, и они имеют относительно большие фокусные расстояния. - Найдите точечный источник света, например светодиодный фонарик, держите его 2-3
футах от линзы и светит через линзу.
Посмотрите на изображения, образованные отражением от передней и задней сторон линзу, глядя на линзу со стороны источника света. поверхности линз действуют как зеркала.
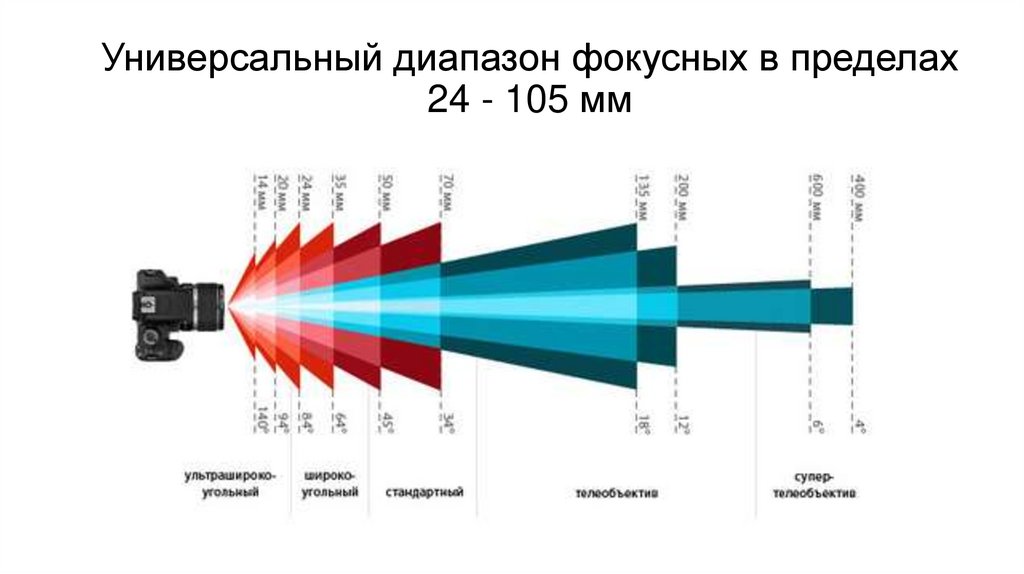
Какие типы изображений вы видите? Они кажутся впереди или за объективом? Если вы используете очки, переверните их, чтобы вы можете наблюдать отражения от выпуклых и вогнутых поверхностей. Фокусное расстояние объектива формула: Фокусное расстояние объектива что это такое и на что влияет
Фокусное расстояние объектива формула: Фокусное расстояние объектива что это такое и на что влияет

 ⓘ Высота точки [h1]
ⓘ Высота точки [h1]
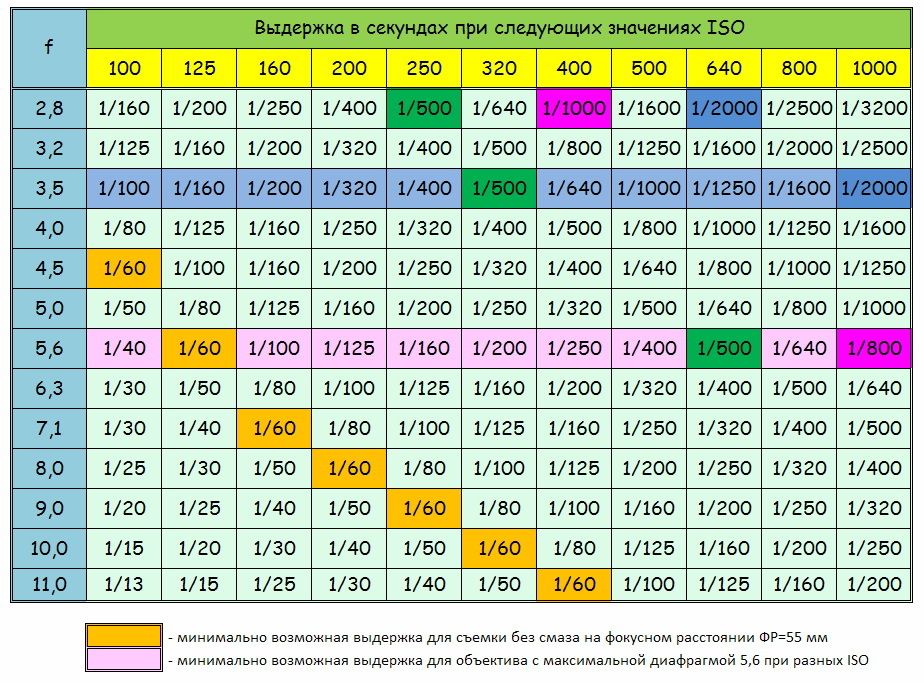 Если не особо заморачиваться, то чем меньше это отношение, тем лучше телескоп подходит для наблюдения галактик и туманностей (например 1:5).
А более длиннофокусный телескоп с соотношением вроде 1:12 лучше подходит для наблюдения Луны.
Если не особо заморачиваться, то чем меньше это отношение, тем лучше телескоп подходит для наблюдения галактик и туманностей (например 1:5).
А более длиннофокусный телескоп с соотношением вроде 1:12 лучше подходит для наблюдения Луны.
 Более апертуристые телескопы дают более чёткое изображение только в теории, ну или высоко в горах, где чистая атмосфера,
либо в те редкие дни, когда «с погодой везёт»…
Более апертуристые телескопы дают более чёткое изображение только в теории, ну или высоко в горах, где чистая атмосфера,
либо в те редкие дни, когда «с погодой везёт»…
 Более слабые объекты ищутся через фотографирование и последующую компьютерную обработку кадров.
Более слабые объекты ищутся через фотографирование и последующую компьютерную обработку кадров.


 «Г» уже нашли: 41,67 крат.
«Г» уже нашли: 41,67 крат.

 Лампа накаливания в помещении олеблется под действием акустической речевой волны. Амплитуда колебаний на частоте 600 Гц спектрального ядра речи составляет 100 мкм. С какими параметрами нужен телескоп для того, чтобы увидеть колебания с расстояния 10 м извне помещения через окно
Лампа накаливания в помещении олеблется под действием акустической речевой волны. Амплитуда колебаний на частоте 600 Гц спектрального ядра речи составляет 100 мкм. С какими параметрами нужен телескоп для того, чтобы увидеть колебания с расстояния 10 м извне помещения через окно ..Levenhuk Skyline 76*700AZ очень обидно то,что я могу посмотреть только окружность звезды я середина её тёмная. почему?ответьте если можно…
..Levenhuk Skyline 76*700AZ очень обидно то,что я могу посмотреть только окружность звезды я середина её тёмная. почему?ответьте если можно… Успехов!
Успехов!

 3
3