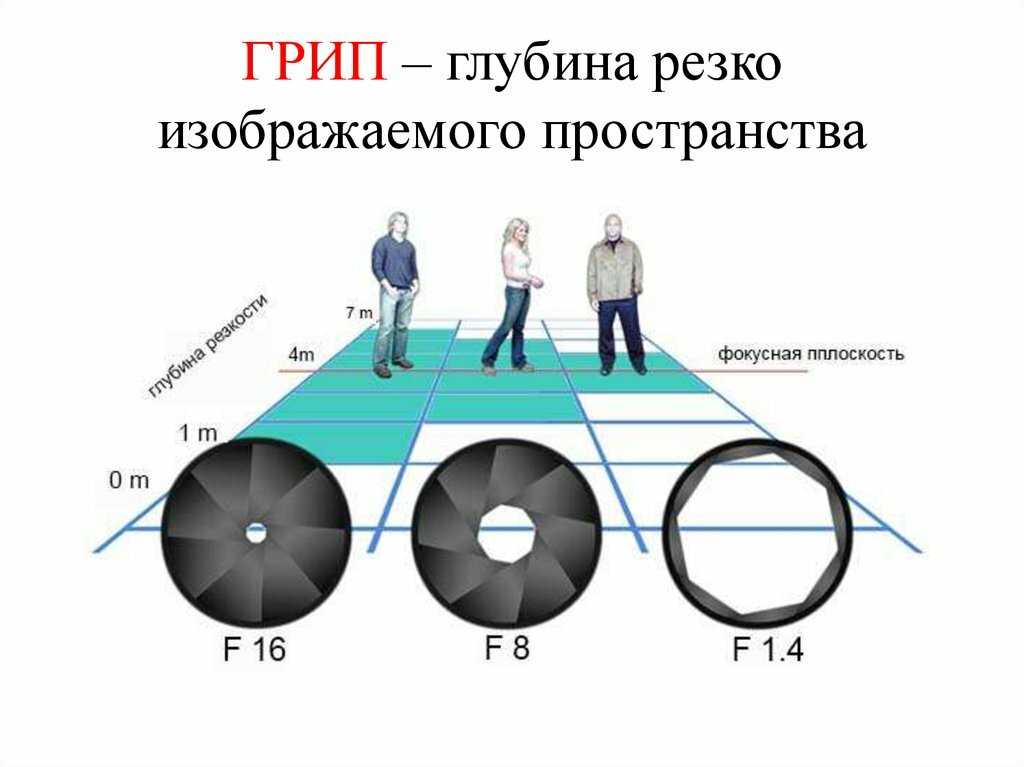
С самолета, летящего на высоте 12 км, сфотографирована местность в масштабе 1:16000
Условие задачи:
С самолета, летящего на высоте 12 км, сфотографирована местность в масштабе 1:16000. Каково фокусное расстояние объектива?
Задача №10.5.68 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(d=12\) км, \(\Gamma=\frac{1}{16000}\), \(F-?\)
Решение задачи:
В фотоаппарате установлена собирающая линза, поскольку только она может давать действительное изображение. При этом, очевидно, что предмет расположен левее относительно переднего фокуса линзы (\({d} > {F}\)).
Чтобы построить изображение точки A в собирающей линзе, нужно провести через точку A два луча: один параллельно главной оптической оси, а второй через главный оптический центр O. Первый луч, преломившись в линзе, пройдет через задний фокус линзы. Второй луч проходит через линзу, не преломляясь. На пересечении этих лучей и будет находиться точка A1. Проекция этой точки на главную оптическую ось есть точка B1. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей), перевернутым и уменьшенным (так как \({d} > {2F}\)).
Проекция этой точки на главную оптическую ось есть точка B1. Вот и все, изображение построено. Как мы видим, оно получилось действительным (поскольку получается на сходящемся пучке лучей), перевернутым и уменьшенным (так как \({d} > {2F}\)).
Запишем формулу тонкой линзы:
\[\frac{1}{F} = \frac{1}{d} + \frac{1}{f}\;\;\;\;(1)\]
В этой формуле \(F\) – фокусное расстояние линзы, знак перед ним “+”, поскольку линза – собирающая, \(d\) – расстояние от линзы до предмета, знак перед ним “+”, поскольку предмет – действительный (в случае одиночной линзы предмет всегда действительный, оно бывает мнимым в случае системы линз), \(f\) – расстояние от линзы до изображения, знак перед ним “+”, поскольку изображение – действительное (то есть образуется на сходящемся пучке лучей – смотрите рисунок).
Из подобия треугольников AOB и A1OB1 по трем углам следует, что (при этом эти две дроби ещё равны и поперечному увеличению (хотя в этом случае корректнее назвать уменьшением) линзы \(\Gamma\)):
\[\Gamma = \frac{f}{d} = \frac{h}{H}\]
\[\Gamma = \frac{f}{d}\;\;\;\;(2)\]
Тогда из формулы (1) выразим неизвестное расстояние от линзы до изображения \(f\):
\[\frac{1}{f} = \frac{1}{F} – \frac{1}{d}\]
\[\frac{1}{f} = \frac{{d – F}}{{dF}}\]
\[f = \frac{{dF}}{{d – F}}\;\;\;\;(2)\]
Подставим выражение (3) в формулу (2):
\[\Gamma = \frac{{dF}}{{d\left( {d – F} \right)}}\]
\[\Gamma = \frac{F}{{d – F}}\]
Чтобы найти искомое фокусное расстояние фотоаппарата, нам нужно решить полученное уравнение:
\[F = \Gamma \left( {d – F} \right)\]
Раскроем скобки в правой части уравнения:
\[F = \Gamma d – \Gamma F\]
Перенесем все члены с \(F\) в левую сторону, тогда:
\[F + \Gamma F = \Gamma d\]
\[F\left( {1 + \Gamma } \right) = \Gamma d\]
Окончательно получим такое решение представленной задачи в общем виде:
\[F = \frac{{\Gamma d}}{{1 + \Gamma }}\]
Если подставить в эту формулу значения величин из условия задачи, то мы получим ответ (не забываем переводить эти значения в систему СИ):
\[F = \frac{{\frac{1}{{16000}} \cdot 12000}}{{1 + \frac{1}{{16000}}}} = 0,75\;м = 75\;см\]
Ответ: 75 см.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.5.67 Линзой пользуются как лупой. Первоначально изображение было в 4 раза больше
10.5.69 При фотографировании предмета с расстояния 1 м высота изображения равна 6 см
10.5.70 Светящаяся точка приближается к собирающей линзе вдоль ее главной оптической оси
1 2 3 4 5 6 7 8 9 … 154 Bog’liq
1 2 3 4 5 6 7 8 9 … 154 Ma’lumotlar bazasi mualliflik huquqi bilan himoyalangan ©hozir.org 2023 |
Bosh sahifa fanidan mustaqil sog’liqni saqlash uzbekistan coronavirus respublikasi sog’liqni coronavirus covid koronavirus covid covid vaccination vazirligi koronavirus qarshi emlanganlik risida sertifikat vaccination certificate sertifikat ministry haqida umumiy o’rta ta’lim matematika fakulteti fanlar fakulteti pedagogika universiteti ishlab chiqarish moliya instituti fanining predmeti |
Снимок фотографии: сила объективов
Цветные рефераты объектива камеры предоставлены вам Snoron. com
com
WIRED Staff
Эта статья является третьей в серии обучающих основам фотографии. Мы начали с изучения свойств света и того, как создается изображение, мы также узнали, как линза преломляет свет, чтобы сфокусировать отдельные лучи в одно яркое изображение. На этом уроке мы закончим изучение научной теории линз и того, как использовать линзы для увеличения в дополнение к яркости.
Эта статья является третьей в серии обучающих основам фотографии. Мы начали с изучения свойств света и того, как создается изображение, а также узнали, как линза преломляет свет, чтобы сфокусировать отдельные лучи в одно яркое изображение. На этом уроке мы закончим изучение научной теории линз и того, как использовать линзы для увеличения в дополнение к яркости.
Связь между диаметром объектива и диафрагмой. (с сайта Panasonic.com)
(с сайта Panasonic.com)
На прошлом уроке мы провели эксперимент по фокусировке света свечи через линзу. Мы также узнали, что для определения фокусного расстояния системы мы перемещаем фокусировочный экран вперед и назад, пока изображение пламени не окажется в фокусе. Давайте на мгновение рассмотрим эту систему свечи/линзы. Как вы думаете, что произойдет, если мы заменим линзу на линзу вдвое большего диаметра с тем же фокусным расстоянием? Будет ли изображение в два раза ярче? Изображение в два раза больше? Если бы вы предположили, что линза большего размера сделает изображение ярче, вы были бы правы. Большая линза имеет большую площадь для сбора света, что на самом деле соответствует изображению, яркость которого более чем в два раза превышает яркость при соотношении, равном πr², где r равно радиусу линзы. Однако изображение не будет больше, поскольку фокусное расстояние линзы такое же.
Диаграмма уменьшения диафрагмы, т. е. увеличения числа f, с шагом в одну ступень; каждая апертура имеет вдвое меньшую площадь сбора света, чем предыдущая.
(Изображение с Wiki Commons)
В фотографии вы часто слышите, как объективы описываются фокусным расстоянием и их коэффициентом f. Отношение f описывает соотношение между диаметром объектива и фокусным расстоянием и рассчитывается путем деления фокусного расстояния на диаметр объектива. Например, если объектив должен иметь фокусное расстояние 50 мм и диаметр 10 мм, то коэффициент f будет равен 50 мм/10 мм = 5 или иначе будет называться f5. Если бы вы удвоили диаметр объектива, 50 мм / 20 мм = 2,5, коэффициент f был бы f2,5. Как вы, вероятно, уже сделали вывод, более низкое или «более короткое» значение f-соотношения означает, что больше света фокусируется на изображении, и, следовательно, изображение становится более ярким. Отношение f и фокусное расстояние объектива почти всегда будут напечатаны на кольце, окружающем стекло. Если вы когда-либо слышали, как кто-то называет свой объектив «быстрым» или «медленным», они имеют в виду коэффициент f камеры.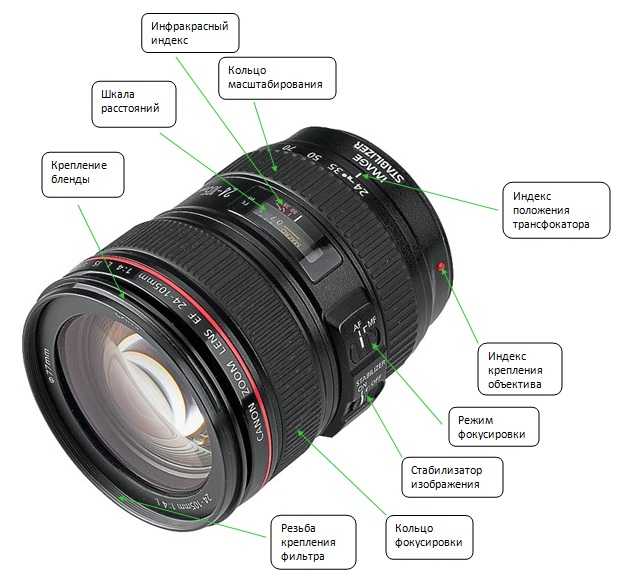
Когда мы обсуждали камеру-обскуру в начале этой серии статей, мы отметили, что хотя большая апертура, пропускающая свет, увеличит ее яркость, но также снизит четкость изображения. После добавления объектива в эксперимент с камерой-обскурой вы сможете немного лучше понять взаимосвязь между этими двумя переменными. Более светосильный объектив (с меньшим коэффициентом f) будет иметь меньшую глубину резкости (меньшую плоскость фокусировки). Современные цифровые зеркальные камеры позволяют фотографу изменять апертуру своего объектива, тем самым изменяя коэффициент f или скорость своей камеры.
Фотопоток Flickr)
В то время как больший диаметр диафрагмы может увеличить яркость и повысить резкость фокуса, увеличение увеличения объектива увеличит фокусное расстояние и, таким образом, увеличит изображение. Величина фокусного расстояния, которое вы желаете, будет определять, какое увеличение необходимо вашему объективу. Думайте об увеличении с точки зрения того, насколько сильно изгибается ваш свет. Чем больше кривизна вашего объектива, тем больше ваш свет будет отклоняться к центральному фокусу. Создание большей кривой в линзе означает увеличение толщины линзы, таким образом добавляя больше материала для замедления света, когда он проходит через линзу. Как видите, увеличение влияет не только на фокусное расстояние, но и на яркость изображения. Мы говорили об увеличении с точки зрения увеличения размера изображения, когда почти на всех фотографиях изображение, которое вы создаете, значительно меньше, чем исходный объект. Один тип фотографии, в которой вы хотите увеличить размер создаваемого изображения, называется макросъемкой. Специальные объективы разработаны именно для этой специализированной цели, построены с большим фокусным расстоянием и очень близким объектом для фотографирования.
Величина фокусного расстояния, которое вы желаете, будет определять, какое увеличение необходимо вашему объективу. Думайте об увеличении с точки зрения того, насколько сильно изгибается ваш свет. Чем больше кривизна вашего объектива, тем больше ваш свет будет отклоняться к центральному фокусу. Создание большей кривой в линзе означает увеличение толщины линзы, таким образом добавляя больше материала для замедления света, когда он проходит через линзу. Как видите, увеличение влияет не только на фокусное расстояние, но и на яркость изображения. Мы говорили об увеличении с точки зрения увеличения размера изображения, когда почти на всех фотографиях изображение, которое вы создаете, значительно меньше, чем исходный объект. Один тип фотографии, в которой вы хотите увеличить размер создаваемого изображения, называется макросъемкой. Специальные объективы разработаны именно для этой специализированной цели, построены с большим фокусным расстоянием и очень близким объектом для фотографирования.
Макрообъективы описываются коэффициентом увеличения. Это означает, что объектив 1:1 будет давать реалистичное изображение на детекторе. 19,05-миллиметровая копейка будет давать 19,05-миллиметровое изображение на детекторе, занимая более половины полного 35-миллиметрового детектора или почти 80% сенсора с кадрированием кадра (что вы найдете в большинстве камер нижнего уровня). Коэффициент увеличения 1: 1, как правило, является минимальным, чтобы считаться макрообъективом, а другие объективы достигают диапазона 1: 10 (увеличение объекта диаметром 1 мм в изображение диаметром 10 мм).
Это означает, что объектив 1:1 будет давать реалистичное изображение на детекторе. 19,05-миллиметровая копейка будет давать 19,05-миллиметровое изображение на детекторе, занимая более половины полного 35-миллиметрового детектора или почти 80% сенсора с кадрированием кадра (что вы найдете в большинстве камер нижнего уровня). Коэффициент увеличения 1: 1, как правило, является минимальным, чтобы считаться макрообъективом, а другие объективы достигают диапазона 1: 10 (увеличение объекта диаметром 1 мм в изображение диаметром 10 мм).
Оптическая диаграмма, показывающая влияние фокусного расстояния и размера сенсора на поле зрения.
(Изображение с WikiCommons)
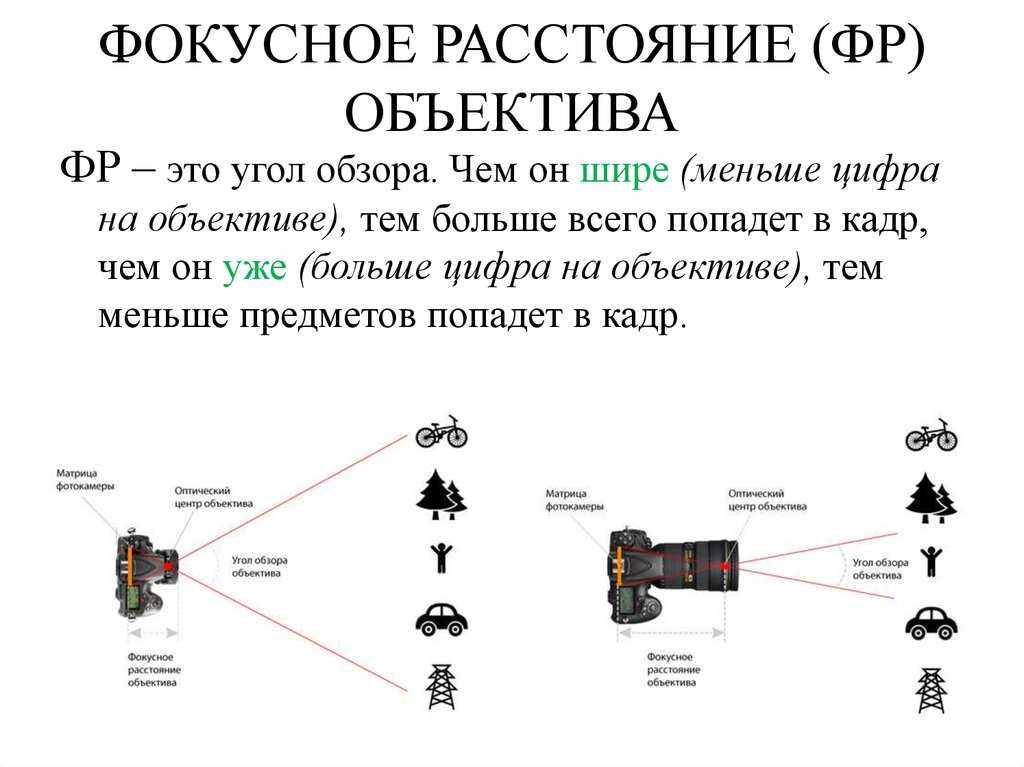
Последняя часть оптической головоломки — это то, что называется полем зрения (FOV), другими словами, какую часть мира может видеть детектор. FOV объектива зависит от его фокусного расстояния и размера поверхности обнаружения или детектора камеры. Давайте рассмотрим возможность фотографирования одного и того же объекта, изменяя только фокусное расстояние системы. По мере увеличения фокусного расстояния поле зрения сужается, увеличивая размер изображения на детекторе. Поле зрения довольно просто визуализировать, просто проследив траекторию луча в оптической системе. Одним из специализированных типов линз является линза типа «рыбий глаз». Эти линзы отличаются чрезвычайно коротким фокусным расстоянием, от 10 мм до 20 мм, и выпуклым стеклом, которое выглядит как рыбий глаз. Эти объективы имеют поле зрения 180 градусов или больше, что делает их особенно удобными для захвата всего ночного неба на одном изображении.
По мере увеличения фокусного расстояния поле зрения сужается, увеличивая размер изображения на детекторе. Поле зрения довольно просто визуализировать, просто проследив траекторию луча в оптической системе. Одним из специализированных типов линз является линза типа «рыбий глаз». Эти линзы отличаются чрезвычайно коротким фокусным расстоянием, от 10 мм до 20 мм, и выпуклым стеклом, которое выглядит как рыбий глаз. Эти объективы имеют поле зрения 180 градусов или больше, что делает их особенно удобными для захвата всего ночного неба на одном изображении.
Пять изображений с использованием функции ступенчатого масштабирования, эквивалентной 24, 28, 35, 50 и 72 мм, для иллюстрации углов обзора.
(Изображение с WikiCommons)
Изображение с Wiki Commons
Хотя фокусное расстояние объектива влияет на поле зрения, другим фактором поля зрения является размер детектора. В DSLR у вас обычно будет либо «обрезанный» датчик, либо датчик с полным кадром 35 мм. Кроп-сенсор определяется его кроп-фактором или множителем фокусного расстояния (FLM); отношение диагонали кадра 35 мм к (43,3 мм) к длине диагонали на «обрезанном» датчике. В зеркальных фотокамерах Canon кроп-фактор равен 1,6, в то время как у большинства других марок кропнутых сенсоров этот коэффициент равен 1,5. Это отношение умножается на фокусное расстояние, чтобы определить фокусное расстояние объектива, обеспечивающего такое же поле зрения. Например, 50-миллиметровый объектив на кроп-сенсоре Canon будет давать изображения, аналогичные полнокадровой камере с прикрепленным объективом с фокусным расстоянием 80 мм. Обрезанные изображения всегда будут «выглядеть» более увеличенными, однако это увеличение просто вызвано вышеупомянутым фактором кадрирования.
Кроп-сенсор определяется его кроп-фактором или множителем фокусного расстояния (FLM); отношение диагонали кадра 35 мм к (43,3 мм) к длине диагонали на «обрезанном» датчике. В зеркальных фотокамерах Canon кроп-фактор равен 1,6, в то время как у большинства других марок кропнутых сенсоров этот коэффициент равен 1,5. Это отношение умножается на фокусное расстояние, чтобы определить фокусное расстояние объектива, обеспечивающего такое же поле зрения. Например, 50-миллиметровый объектив на кроп-сенсоре Canon будет давать изображения, аналогичные полнокадровой камере с прикрепленным объективом с фокусным расстоянием 80 мм. Обрезанные изображения всегда будут «выглядеть» более увеличенными, однако это увеличение просто вызвано вышеупомянутым фактором кадрирования.
Зум-объектив сочетает в себе форму, диаметр и фокусное расстояние линзы, а также их соответствующие расстояния друг от друга для изменения диафрагмы и увеличения в системе. В то время как некоторые зум-объективы имеют около 30 различных оптических элементов, которые взаимодействуют для создания изображения, большинство зум-объективов имеют одинаковую базовую конструкцию, они состоят из нескольких отдельных линз, которые могут быть либо фиксированными, либо скользящими в осевом направлении вдоль корпуса объектива. Одна из наиболее распространенных конструкций зум-объективов делит оптическую сборку на две части: фокусирующую линзу с фиксированным фокусным расстоянием и систему афокального увеличения, состоящую из ряда фиксированных и подвижных линз. Целью афокальной системы является не создание сфокусированного изображения, а простое изменение размера изображения, попадающего на детектор. В результате получается сфокусированное изображение, которое меняет размер на детекторе.
Одна из наиболее распространенных конструкций зум-объективов делит оптическую сборку на две части: фокусирующую линзу с фиксированным фокусным расстоянием и систему афокального увеличения, состоящую из ряда фиксированных и подвижных линз. Целью афокальной системы является не создание сфокусированного изображения, а простое изменение размера изображения, попадающего на детектор. В результате получается сфокусированное изображение, которое меняет размер на детекторе.
Простая система зум-объектива. Три линзы афокальной системы: L1, L2, L3 (слева). L1 и L2 могут перемещаться влево и вправо, изменяя общее фокусное расстояние системы.
(Изображение с Wiki Commons)
Упрощенный зум-объектив в работе
(GIF через Wiki Commons)
В моем следующем выпуске «Снимок фотографии» мы еще больше отойдем от теории фотографии и исследуем треугольник экспозиции, начиная с диафрагмы. Мы начнем учиться вручную контролировать изображения, которые вы формируете, и мы начнем давать короткие домашние задания, чтобы вы могли снимать на камеру.
ТемыобразованиеЭксперименты и наукаобъективыАктивный отдых на свежем воздухеФототехникаGeekMom
PHY1160C, Глава 26 Домашнее задание
Гл. 26: 2, 3, 5, 9, 13, 15, 20, 25, 27
| Вернуться к главе 26 Домашняя страница (ToC) |
26.2 Камера с точечным отверстием используется для съемки фотография студента ростом 1,8 м. Студент стоит 2,7 м перед камерой. Пленка размещается на 10 см позади булавочное отверстие. Определяем высоту изображения произведено.
Треугольник, образованный объектом (точкой ученика), а лучи от головы и ног ученика идут к отверстие и треугольник, образованный изображением и лучами идущие от отверстия для булавки к голове и ногам изображения подобных треугольников, то отношения соответствующих сторон этих треугольники равны. То есть
г i = 0,067 м = 6,7 см
26. 3 Расстояние от роговицы до
размер сетчатки конкретного глаза составляет 2,1 см. Найдите эффективное
фокусное расстояние этого глаза для объекта, расположенного
3 Расстояние от роговицы до
размер сетчатки конкретного глаза составляет 2,1 см. Найдите эффективное
фокусное расстояние этого глаза для объекта, расположенного
(а) на бесконечности,(б) для объекта, расположенного на расстоянии 10 м далеко, и
(c) для объекта, расположенного на расстоянии 25 см прочь.
Мы можем напрямую применить изображение Уравнение
Расстояние изображения, di, это расстояние от роговицы до сетчатки 2,1 см.
Для (а) расстояние до объекта, d o , бесконечно,
f = 2,1 см
Для (b) расстояние до объекта равно d o = 10 м
Смотреть
единицы измерения! Нельзя добавлять счетчики и
сантиметры; нельзя добавлять обратные метры и обратные
сантиметры. Два термина справа должны иметь одинаковые единицы измерения.
прежде чем вы сможете добавить их!
Два термина справа должны иметь одинаковые единицы измерения.
прежде чем вы сможете добавить их!
f = 2,096 см 2,1 см
Для (c) расстояние до объекта равно д o = 25 см
f = 1,94 см
26,5 Предмет находится на 35 см левее собирающей линзы с фокусным расстоянием 20 см. 75 см до справа — вторая собирающая линза с фокусным расстоянием 15 см. Найдите и охарактеризуйте конечное изображение.
Лучевая диаграмма всегда хороший способ начать. Обычно более реальное понимание доступно в лучевую диаграмму, чем при «просто» численном решении задачи. Кроме того, хорошая диаграмма предоставляет место для хранения всех размеры проблемы.
Для первого объектива начнем с Уравнение изображения,
или
А мы знаем ф 1 = 20 см и д o1 = 35 см,
д i1 = 46,7 см
Это изображение (реальное, перевернутое и увеличен) становится объектом для второй линзы, поскольку мы снова применяем Уравнение изображения,
или
Поскольку линзы находятся на расстоянии 75 см друг от друга, изображение, сформированное на 46,7 см правее линзы №1, расположено 28,3 см слева от линзы № 2, поэтому расстояние до объекта
д i2 = 31,9 см
То есть итоговое изображение расположено 31.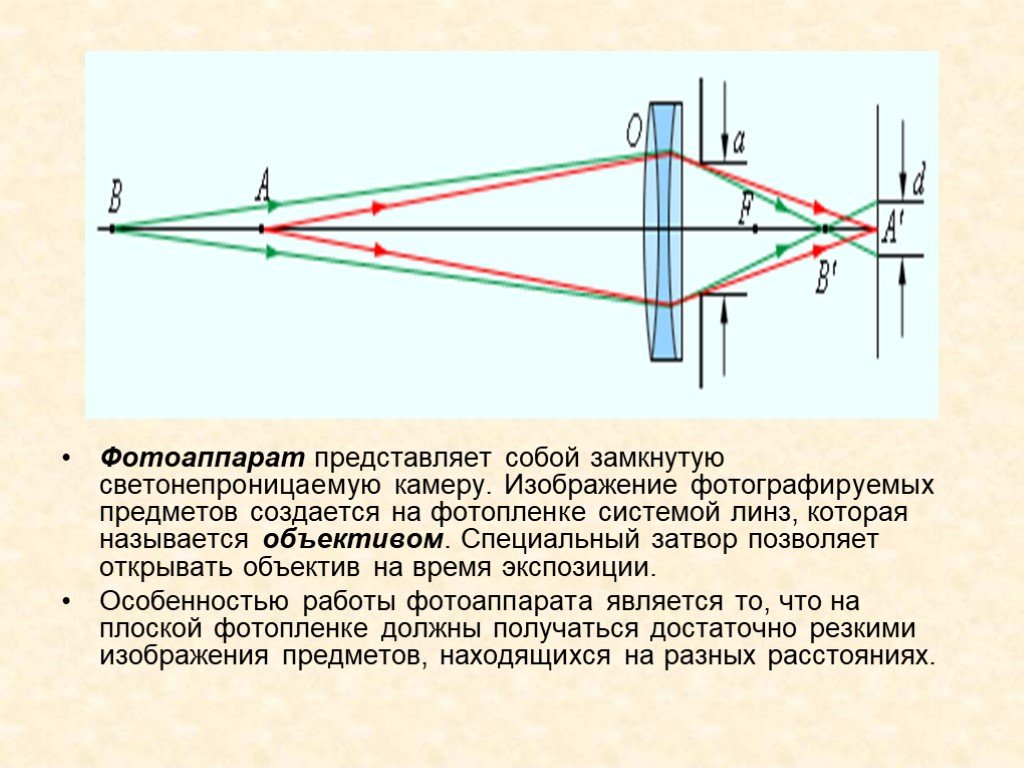 9
см справа от второй линзы. Поскольку d i2 > 0
(то есть, поскольку d i2 = +), мы знаем, что это изображение
реальное . Он перевернут по сравнению с объектом для объектива №2.
Но это было перевернутое изображение исходного объекта. Поэтому,
это последнее изображение вертикальный .
9
см справа от второй линзы. Поскольку d i2 > 0
(то есть, поскольку d i2 = +), мы знаем, что это изображение
реальное . Он перевернут по сравнению с объектом для объектива №2.
Но это было перевернутое изображение исходного объекта. Поэтому,
это последнее изображение вертикальный .
Общее увеличение является произведением увеличения двух объективов,
М к = (1,33)(1,13)
М до = 1,5
26.9 Глаз пациента может фокусироваться только на предметы выше 100 см. Какое слово характеризует этот тип зрения проблема? Что такое фокусное расстояние и сила контактной линзы необходимо исправить эту проблему?
У этого пациента дальнозоркость или дальнозоркость.
У этого пациента проблемы с чтением книги на комфортном расстоянии
— например, 25 см — поэтому мы должны найти объектив, который возьмет
объект на 25 см (d o = 25 см) и создать изображение (a
виртуальное изображение) на 100 см (d i = — 100 см).
Диаграмма может помочь четко установить что нам нужно
д я = — 100 см
Важно помнить или осознавать что сформированный образ является виртуальным образом. Это с левой стороны объектива на схеме выше. Это означает, что расстояние до изображения отрицательный. Как только мы знаем do и di, легко найти фокусное расстояние. длина линзы из уравнения изображения,
f = 33,3 см
Для описания объектива с точки зрения «мощности». (в единицах дптр ) нам нужно взять обратное фокусное расстояние в метрах,
P = 1/f = 3 диоптрии
26.10 Определенный глаз может фокусироваться только на предметы ближе 50,0 см. Какое слово характеризует это тип проблемы со зрением? Какие контактные линзы (описаны оба по фокусному расстоянию и мощности) это исправит проблема?
Этот глаз близорук или близорук. Мы
нужно найти линзу, которая будет снимать объект на бесконечности
(д или = )
и создать мнимое изображение на расстоянии 50,0 см (d i = — 50,0 см
= — 0,50 м).
Мы
нужно найти линзу, которая будет снимать объект на бесконечности
(д или = )
и создать мнимое изображение на расстоянии 50,0 см (d i = — 50,0 см
= — 0,50 м).
Теперь мы знаем изображение и объект расстояния —
д я = — 50,0 см
Важно помнить или осознавать что сформированный образ является виртуальным образом. Это с левой стороны объектива на схеме выше. Это означает, что расстояние до изображения отрицательный. Как только мы узнаем д o и d i тогда это легко найти фокусное расстояние объектива по изображению Уравнение,
f = — 50,0 см
ф = — 0,50 м
Р = 1 / ф = — 2 диоптрии
Примечание: Эти проблемы начались в
книга с дальней точкой 500 см или 5,0 м. Как мы увидим, что
не требует очень большой коррекции, чтобы иметь возможность что-то увидеть
на бесконечности. Это не кажется разумным или интересным
проблема. Поэтому я изменил задачу. Тем не менее, давайте вперед
и решить это для исходного случая —
Как мы увидим, что
не требует очень большой коррекции, чтобы иметь возможность что-то увидеть
на бесконечности. Это не кажется разумным или интересным
проблема. Поэтому я изменил задачу. Тем не менее, давайте вперед
и решить это для исходного случая —
д и = — 500 см
ф = — 500 см = — 5 м
P = 0,20 диоптрии
26.11 Конкретный глаз может фокусироваться только на объекты дальше 150 см. Какое слово характеризует это тип проблемы со зрением? Какое фокусное расстояние и мощность корректирующие линзы, необходимые для исправления этой проблемы? Объектив должен быть носится на 2,0 см перед глазами?
Использование линзы, находящейся на расстоянии 2 см от глаза, но небольшое отличие от задачи 26.9, в которой использовалась контактная линза. Для этой ситуации у нас есть
д и = — 148 см
Важно помнить или осознавать
что сформированный образ является виртуальным образом. Это с левой стороны
объектива на схеме выше. Это означает, что расстояние до изображения
отрицательный. Как только мы знаем do и di, легко найти фокусное расстояние.
длина линзы из уравнения изображения,
Это с левой стороны
объектива на схеме выше. Это означает, что расстояние до изображения
отрицательный. Как только мы знаем do и di, легко найти фокусное расстояние.
длина линзы из уравнения изображения,
f = 27,2 см = 0,272 м
P = 1 / f = 3,7 диоптрии
26.20 Алмаз рассматривается с Ювелирная лупа с фокусным расстоянием 5,0 см. Где должны поставить алмаз, чтобы обеспечить виртуальное изображение в бесконечности? Что будет угловым увеличением этого простого лупа?
Алмаз должен быть размещен в фокусе точки линзы (ювелирной лупы), т. е. в 5,0 см от объектив.
Увеличение дано
М = 5
26.25 У микроскопа есть объектив и окуляр на расстоянии 18 см друг от друга. Если f obj = 0,40 см и f глазок = 5,0 см, где должен располагаться образец для создать окончательное виртуальное изображение на бесконечности? Какова общая увеличение этого микроскопа?
Чтобы иметь финальное изображение на d и
= , нам нужно, чтобы реальное изображение, формируемое объективом, располагалось
в фокусе окуляра. С целью и
линзы окуляра на расстоянии 18,0 см это означает,
С целью и
линзы окуляра на расстоянии 18,0 см это означает,
д я + 5,0 см = 18,0 см
д я = 13,0 см
Теперь мы снова можем применить изображение Уравнение,
d o = 0,41 см
26.27 Астрономический телескоп используется для просмотра объекта в бесконечности. Объектив имеет фокусное длина 15,0 см. Где должен быть установлен окуляр 0,5 см, чтобы сформировать изображение на бесконечности? Какой общий угол увеличение?
Реальное изображение, формируемое объективом
линза будет расположена в фокусе этой линзы,
д я = f obj = 15,0 см от этой линзы. К
создать мнимое изображение на бесконечности, окуляр должен быть расположен
так что это изображение, которое действует как объект для окуляра,
находится в фокусе линзы окуляра,
d o = f глаз = 0,5
см.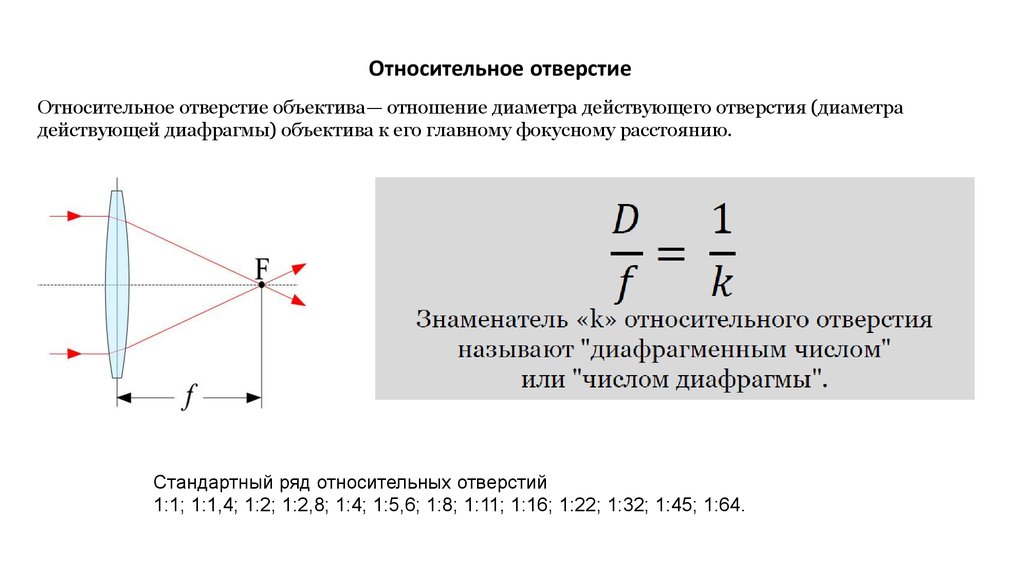

 ХАБИБУЛЛАЕВ, А. БОЙДЕДАЕВ, А. БАХРАМОВ, М. ЮЛДАШЕВА
ХАБИБУЛЛАЕВ, А. БОЙДЕДАЕВ, А. БАХРАМОВ, М. ЮЛДАШЕВА