Частотное разложение 2.0. По горячим следам мастер-класса
?
| ||||
| |||||||||||||||||||||||||||||||||||||
Частотное разложение в предметной фотографии: мышь или планшет?
Обработка любой предметной фотографии строится по одному и тому же принципу. Как всегда, мы начинаем с RAW-конвертации, работаем с балансом белого, контрастом и цветом. Эти базовые настройки имеют отношение не только к предметной фотографии, но и к остальным фото- жанрам. Данные процедуры довольно простые, и если нет привычки к работе с графическим планшетом, то легко выполняются с помощью компьютерной мыши.
Как всегда, мы начинаем с RAW-конвертации, работаем с балансом белого, контрастом и цветом. Эти базовые настройки имеют отношение не только к предметной фотографии, но и к остальным фото- жанрам. Данные процедуры довольно простые, и если нет привычки к работе с графическим планшетом, то легко выполняются с помощью компьютерной мыши.
Главная задача обработки — сделать картинку красивой и цепляющей взгляд смотрящего. А в коммерческой предметной съемке – еще и продающей. Поэтому на следующих этапах основные задачи обработки — убрать ненужное, акцентировать внимание на самом важном. И прежде всего в предметной фотографии важно правильно и красиво отделить предмет от фона. Уметь его грамотно изменить. Убрать пыль и царапины с предмета.
Открыв изображение в Adobe Photoshop, создаю пустой слой над обрабатываемой фотографией и, увеличив масштаб, начинаю аккуратно убирать пылинки «Восстанавливающей (Лечащей) кистью». Пером графического планшета это выходит очень аккуратно и быстро.
Зачастую в моей работе предметы небольшие, не больше спичечного коробка или кольца, и вопрос, что же удобней использовать — мышку или графический планшет – очень актуален.
Наверняка вы уже знаете, что чем сильнее закрыта диафрагма, тем больше объектов в кадре попадет в зону резкости. В предметной и ювелирной фотографии мы выполняем Фокус стэкинг – это промежуточный этап обработки, который сочетает в себе использование камеры и программного обеспечения для постобработки, проще говоря Брекетинг по фокусу. Для этого мы закрываем диафрагму до значения f9 и начинаем снимать сверху вниз, смещая фокус на 1 шаг с помощью управления фокусом с компьютера. Делаем от 40 до 80 кадров по зоне резкости, затем загружаем их в Photoshop, выбираем команду Sсripts, далее — Load files into stack. В открывшемся окне выбираем все эти кадры и нажимаем OK. Так у нас склеивается картинка по зоне резкости.
После этого в палитре Liers выбираем все слои с помощью клавиши Shift, и нажимаем в выпадающем меню команду Auto-Blend Laers команду Edit.
В процессе создания такого количества кадров у нас проявляются все, даже мелкие, детали и царапины. И нам требуется сделать две вещи: освободить предмет от фона и очистить от этих самых деталей и царапин сам объект съемки.
Если при обработке, например, кольца взять компьютерную мышку и попытаться сделать его выделение, то сделать это ровно и красиво не получиться. Причины основные две:
— у мыши нет возможности более точного позиционирования, как есть у пера графического планшета
— мышкой мы вынуждены работать кистью так, что рука быстро устаёт от постоянного напряжения.
Получается, что если работать с кривой и точками обычной мышкой, то процесс очень нудный и неудобный. Приходится делать много лишних движений и плюс нужна большая площадь для манипуляций мышкой.
Лично я уже давно сделал для себя выбор в пользу графического планшета. А тут заполучил для работы XP-PEN Artist 15.6 Pro – опыт для меня оказался новый и очень интересный.
Для меня он оказался удобнее обычного планшета сразу по нескольким параметрам:
— работаешь на цветном дисплее с высоким разрешением. Самое прекрасное, что картинка у меня сразу на дисплее и мне не нужно работать вслепую.
— смотришь при работе не на мотор, а на экран дисплея
— используешь активно кнопки и колеса управления: левой рукой, вращая колесо, мы либо увеличиваем, либо уменьшаем картинку для просмотра отдельных областей или, наоборот, очень плавно смещаем картинку по полю, чтобы аккуратно делать обводку. Горячие клавиши можно назначить на 8 кнопок на дисплее. Я сразу настроил их под себя, назначив первые 2 клавиши для увеличения/уменьшения размера кисти. Еще одной клавишей переключаюсь между пером и ластиком. Остальные свободные клавиши чтобы не залезать постоянно в меню и не пользоваться клавиатурой использовал под следующие команды: копировать, вставить, запуск Бриджа, «схлопнуть» слои.
— более точно и аккуратно убираешь пыль и царапины, особенно на ювелирных изделиях.
Еще одно преимущество работы на дисплее (да и на любом графическом планшете) становится очевидным при работе с микс-кистью при частотном разложении. Я вижу каждую деталь на большом увеличении на камнях и аккуратно сглаживаю тон и разводы, а мягкость и степень давления пера позволяет мне контролировать толщину штрихов и мазков. Тем самым достигается идеальный коммерческий результат. Мышкой подобное сделать нереально, что уже проверчено многолетним опытом и практикой.
Давайте более детально рассмотрим пример частотного разложения:
1. Подготавливая предмет под частотное разложение: создаем 3 дубликата слоя. Первый слой называем Hi, второй Mid, третий Low.
2. Отключаем первые 2 слоя, слой Low размываем командой «Размытие по Гауссу».
3. К слою Mid применяется команда Apply Image. В качестве исходного слоя выбираем Low, режим наложения «Add», шаг (scale) 2, обязательно ставим галочку «Инвертировать».
4. Далее к слою Hi применяем фильтр High Pass со значением 2. Применяем наложение слоя в режиме Linear Light к слою Hi, создаем корректирующий слой кривых со значениями белая точка 192, черная — 64. И привязываем его к слою Hi
Применяем наложение слоя в режиме Linear Light к слою Hi, создаем корректирующий слой кривых со значениями белая точка 192, черная — 64. И привязываем его к слою Hi
5. Создаем пустой слой и привязываем его к слою Mid, и размываем слой mid «Размытием по Гауссу» со значением 2
6. Создаем пустой слой над слоем Low и начинаем работать Mixer brush по пустому слою над слоем Low. В настройках кисти ставим следующие параметры: Wel 20, Load 20, Mix 20, Flow 21, обязательно поставить галочку Sample All Laers
Вот тут начинается магия планшета и она становится видна сразу. Работая Mix Brash кистью, мы можем очень аккуратно работать с верхним цветовым тоном! С помощью пера мы очень мягко и плавно сравниваем тон делаем ровной и гладкой поверхность предмета, убирая разные дефекты отражений и световых бликов. То, как плавно и аккуратно это делает перо планшета, мышка к сожалению не сможет. Так как мы, работая пером-ручкой по дисплею, видим то, что делаем в реальном времени, контролируя степень нажатия пера и толщину штрихов.
Выпустив не один обучающий курс по работе в Adobe Photoshop, и обработав не одну сотню кадров, я каждый раз убеждаюсь: ретушь предмета, да и портретная тоже, с графическим планшетом на 50% быстрее и аккуратнее, чем мышкой. Ведь рисовать ручкой/карандашом нам привычнее с детства, чем елозить мышкой по всему столу.
Добавлю еще одну плюшку от интерактивного дисплея. Я решил попробовать Artist 15.6 PRO в монтаже видео. Скажу честно — это потрясающе. Использовал его как второй монитор и перевел на него Timelines. Общие панели для просмотра на втором мониторе. ЭТО СКАЗКА. Дальше пером я более аккуратно передвигал слайды и видеокуски по Timelines. Колесо управления на дисплее настроил на перемотку Timelines. Чуть коснулся его – и оно плавно плывёт.
Подводя итоги, хочу сказать: перо графического планшета в десятки раз мощней, удобней и практичней, чем любая мышка, даже самая дорогая. Мышка хороша в игрушках))) Но для работы в графике планшет незаменим хотя бы потому, что он может помочь контролировать в ретуши степень нажатия, тем самым регулируя толщину штриха кисти. И это здорово сэкономит время и нервы.
И это здорово сэкономит время и нервы.
Автор: Жан Гаспарян
Частотно-временное разложение — SEG Wiki
Содержание
- 1 Преобразование Фурье
- 2 Частотно-временное представление
- 3 Продолжить изучение
- 4 Автор, ответственный за переписку
- 5 Благодарностей
- 6 Внешние ссылки
Рассмотрим форму волны или сигнала s как функцию времени t . Например, синусоида с некоторой амплитудой a и с некоторой частотой f может быть определен как
s (t) = asin (2πft) {\ displaystyle s (t) = a \ sin (2 \ pi ft)}.
Мы можем реализовать эту математическую функцию как подпрограмму, обычно также называемую функцией , на языке программирования Python. Поскольку компьютеры живут в дискретном мире, мы необходимо оценить функцию в течение некоторого времени и с некоторой частотой дискретизации:
по определению sine_wave(f, a, продолжительность, частота дискретизации):
t = np. arange(0, продолжительность, 1/sample_rate)
вернуть * np.sin (2 * np.pi * f * t), т
arange(0, продолжительность, 1/sample_rate)
вернуть * np.sin (2 * np.pi * f * t), т Теперь мы можем вызвать эту функцию, передав ей частоту f = 261,63 Гц. Мы попросим 0,25 с с частотой дискретизации 10 кГц.
с, t = sine_wave(f=261,63,
а=1,
продолжительность=0,25,
sample_rate=10e3) Это приводит к следующему сигналу, обычно называемому временным рядом , который мы визуализируем путем построения графика s в зависимости от времени t :
Я изобразил результирующий массив в виде линии, но на самом деле это ряд дискретных точек, представленных в Python в виде массива чисел, начиная с этих четырех:
array([ 0. , 0.1636476 , 0.32288289, 0.47341253])
Построим первые 80 точек:
Когда воздух вибрирует на этой частоте, мы слышим среднее До или До4. Вы можете прослушать примечание для себя в Jupyter Notebook, сопровождающем эту статью, по адресу https://github. com/seg/tutorials-2018.
(Блокнот также содержит весь код для создания графиков.) Код для вывода массива s в виде звука очень короткий:
com/seg/tutorials-2018.
(Блокнот также содержит весь код для создания графиков.) Код для вывода массива s в виде звука очень короткий:
из IPython.display import Audio фс = 10e3 Аудио(и, скорость=fs)
Этот сигнал длится всего 0,25 с, а покачиваний уже много. Мы бы хотели иметь сейсмические данные на этой частоте! Большинство сейсмических данных воспроизводятся только на нижних 20–30 клавишах 88-клавишного фортепиано — действительно, самая нижняя клавиша — это A0, что на частоте 27,5 Гц превышает пиковую частоту многих старых съемок.
Если бы мы хотели узнать частоту этого сигнала, мы могли бы предположить, что это чистый тон, и просто подсчитать количество циклов в единицу времени. Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
f = np.массив ([261,6, 329,6, 392,0]) а = np.массив ([1,5, 0,5, 1]) s, t = sine_wave (f = f.reshape (3, 1), а=а.изменить(3, 1), продолжительность=0,25, sample_rate=10e3)
Результатом является набор из трех синусоидальных кривых длиной 0,25 с:
Общий сигнал определяется суммой трех кривых:
s = np.sum(s, axis=0)
Преобразование Фурье
Хотя это смешанное или политонный сигнал представляет собой просто сумму трех чистых тонов, разобраться в компонентах уже не тривиально. Здесь в дело вступает преобразование Фурье.
Мы не будем вдаваться в подробности того, как работает преобразование Фурье. Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Сначала мы конусность сигнала путем умножения его на функцию окна . Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.
Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.
s = s * np.blackman(s.size)
Оконная функция (зеленая) оказывает сужающее действие на сигнал:
Поскольку функция s определена для данного момента времени t , мы называем это представление сигнала временем 9(е) {\ Displaystyle {\ шляпа {s}} (е)}). Это новое представление называется частотной областью. Он состоит из массива коэффициентов Фурье :
S = np.fft.fft(s)
Вспомогательная функция fftfreq() возвращает массив частот, соответствующих коэффициентам. Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
freq = np.fft.fftfreq(s.size, d=1/10e3)
Результатом является массив из коэффициентов Фурье , большинство из которых равны нулю. Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.
Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.
Это называется спектром сигнала s . Он показывает величину каждой частотной составляющей.
Частотно-временное представление
Теперь мы знаем, как расплетать политонические сигналы, но давайте введем еще одно усложнение — сигналы, компоненты которых меняются со временем. Такие сигналы называются нестационарный . Например, подумайте о монотонном сигнале, тон которого меняется в какой-то момент (см. Блокнот для кода, который генерирует этот сигнал):
Мы можем вычислить преобразование Фурье этого сигнала, как и раньше:
с *= np.blackman(s.size) S = np.fft.fft(s) freq = np.fft.fftfreq(s.size, d=1/10e3)
И постройте амплитуду S в зависимости от массива частот freq :
Он очень похож на спектр, который мы сделали раньше, но без средней частоты. Пики немного более рассредоточены, потому что продолжительность каждого сигнала вдвое меньше, чем была. (Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)
(Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)
Дело в том, что нет большой разницы между спектром двух смешанных сигналов и спектром двух последовательных сигналов. Если мы заботимся о локализации сигналов во времени (мы делаем!), это проблема. Одним из решений является обращение к частотно-временным представлениям . Пытаясь разделить сигнал одновременно по времени и частоте, они предлагают способ одновременного использования преимуществ обеих областей.
Библиотека для построения графиков Python matplotlib предлагает удобный способ построения графика время-частота, также известного как спектрограмма . В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
_ = plt.specgram(s, Fs=1/10e3,
NFFT=512, noverlap=480) Немного поработав, мы можем получить очень богатое представление наших данных:
График использует алгоритм, называемый кратковременным преобразованием Фурье, или STFT. Это просто делает преобразование Фурье в скользящем окне длиной
Это просто делает преобразование Фурье в скользящем окне длиной NFFT с перекрытием точек, перекрывающихся в предыдущем окне. Мы хотим NFFT должен быть длинным, чтобы получить хорошее разрешение по частоте, и мы хотим, чтобы nooverlap был большим, чтобы получить хорошее разрешение по времени.
Обратите внимание, что мы не можем точно увидеть точную частоту компонентов — они не служат достаточно долго, чтобы их можно было зафиксировать. И есть некоторая неопределенность в отношении сроков перехода, потому что для получения приличного разрешения по частоте нам нужен длинный сегмент сигнала (в данном случае 512 отсчетов) — поэтому мы теряем информацию о времени. Но в целом этот сюжет лучше, чем только спектр: мы видим, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.
Фрагмент фортепианной музыки может напоминать такой сюжет. Поскольку клавиши пианино могут воспроизводить только одну ноту, спектрограмма фортепианной музыки выглядит как серия горизонтальных линий:
Существует большое сходство между этим частотно-временным разложением и нотной записью:
Оказывается, самые интересные сигналы — и, возможно, все естественные сигналы — политонны и нестационарны. По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот несколько примеров; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).
По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот несколько примеров; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).
Человеческий голос произносит «SEG». Сонорные гласные имеют гармоники (горизонтальные полосы), а шипящие звуки «С» и первой части «Г» — шумоподобные. спектральные отклики.
На этой спектрограмме показана 5-секундная серия чириканий летучих мышей. Я указал 18 кГц, приблизительный предел человеческого слуха, оранжевой линией, и если вы слушаете звук этого сигнала в Ноутбук, можно убедиться, что чириканье еле слышно при нормальной скорости воспроизведения; только при замедлении клипа они могут быть отчетливо слышны.
Наконец, вот вулканический «крик» — гармонический толчок, предшествующий взрывному извержению на горе Редут, Аляска, в марте 2009 года. На слух это звучит невероятно, но спектрограмма
тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.
На слух это звучит невероятно, но спектрограмма
тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.
Продолжить изучение
Все рисунки в этой записной книжке можно воспроизвести с помощью кода в записной книжке Jupyter, прилагаемой к этой статье, на https://github.com/seg/tutorials-2018. Вы даже можете запустить код в облаке и поиграть с ним в браузере. Ничего не сломаешь — не волнуйся!
В хранилище вы также найдете больше сигналов, синтетических и естественных, от сердцебиения и загадочного подводного щебетания до гравитационных волн и сейсмических следов. Мало того, есть записная книжка, показывающая, как использовать другой алгоритм — непрерывное вейвлет-преобразование — для проведения частотно-временного анализа другого типа.
Счастливого разложения!
Автор, ответственный за переписку
- Автор, ответственный за переписку: Matt Hall, Agile Scientific, Mahone Bay, Новая Шотландия, Канада.
 Электронная почта:
Электронная почта: mattagilescientific.com
Благодарности
Фортепианная запись из BWV846 Баха лицензирована Кимико Ишизака CC-BY на http://welltemperedclavier.org. Данные чириканья летучих мышей лицензированы CC-BY-NC пользователем http://freesound.org klankschap. Спасибо Алисии Хотовек-Эллис за ее помощь с данными о горе Редут, записанными вулканической обсерваторией Геологической службы США на Аляске.
Внешние ссылки
| найти литературу о Частотно-временное разложение |
- Мадагаскарский рабочий процесс — воспроизводимый с помощью Мадагаскарского программного обеспечения с открытым исходным кодом
Частотно-временное разложение — SEG Wiki
Рассмотрим форму волны или сигнала s как функцию времени t . Например, синусоидальная волна с некоторой амплитудой a и с некоторой частотой f может быть определена как
Например, синусоидальная волна с некоторой амплитудой a и с некоторой частотой f может быть определена как
s (t) = asin (2πft) {\ displaystyle s (t) = a \ sin (2 \ pi ft)}.
Мы можем реализовать эту математическую функцию как подпрограмму, обычно также называемую функцией , на языке программирования Python. Поскольку компьютеры живут в дискретном мире, мы необходимо оценить функцию в течение некоторого времени и с некоторой частотой дискретизации:
по определению sine_wave(f, a, продолжительность, частота дискретизации):
t = np.arange(0, продолжительность, 1/sample_rate)
return a * np.sin(2 * np.pi * f * t), t Теперь мы можем вызвать эту функцию, передав ей частоту f = 261,63 Гц. Мы попросим 0,25 с с частотой дискретизации 10 кГц.
с, t = sine_wave(f=261,63,
а=1,
продолжительность=0,25,
sample_rate=10e3) Это приводит к следующему сигналу, обычно называемому временной ряд , который мы визуализируем путем построения графика s в зависимости от времени t :
Я изобразил результирующий массив в виде линии, но на самом деле это ряд дискретных точек, представленных в Python в виде массива чисел, начиная с этих четырех:
array([ 0., 0.1636476 , 0.32288289, 0.47341253])
Построим первые 80 точек:
Когда воздух вибрирует на этой частоте, мы слышим среднее До или До4. Вы можете прослушать примечание для себя в Jupyter Notebook, сопровождающем эту статью, по адресу https://github.com/seg/tutorials-2018. (В блокноте также содержится весь код для построения графиков.) Код для отображения массива s , так как звук очень короткий:
из IPython.display import Audio фс = 10e3 Audio(s, rate=fs)
Этот сигнал имеет длину всего 0,25 с, а шевелений уже много. Мы бы хотели иметь сейсмические данные на этой частоте! Большинство сейсмических данных воспроизводятся только на нижних 20–30 клавишах 88-клавишного фортепиано — действительно, самая нижняя клавиша — это A0, что на частоте 27,5 Гц превышает пиковую частоту многих старых съемок.
Если бы мы хотели узнать частоту этого сигнала, мы могли бы предположить, что это чистый тон, и просто подсчитать количество циклов в единицу времени. Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
Но естественные сигналы редко бывают монотонными, так что давайте сделаем более интересный сигнал. Мы можем использовать нашу функцию, чтобы создать до-мажорный аккорд с тремя нотами (C4, E4 и G4), передав векторы-столбцы (изменив форму массивов) для частоты 9.0021 f и амплитуда a :
f = np.массив ([261,6, 329,6, 392,0])
а = np.массив ([1,5, 0,5, 1])
s, t = sine_wave (f = f.reshape (3, 1),
а=а.изменить(3, 1),
продолжительность=0,25,
sample_rate=10e3) Результатом является набор из трех синусоидальных кривых длиной 0,25 с:
Общий сигнал определяется суммой трех кривых:
s = np.sum(s, axis=0)
Преобразование Фурье
Хотя это смешанное или политонный сигнал представляет собой просто сумму трех чистых тонов, разобраться в компонентах уже не тривиально. Здесь в дело вступает преобразование Фурье.
Мы не будем вдаваться в подробности того, как работает преобразование Фурье. Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Лучшее объяснение, которое я видел за последнее время, — это вводное видео Гранта Сандерсона. Дело в том, что преобразование описывает сигналы как смеси периодических составляющих. Попробуем на нашем аккорде.
Сначала мы конусность сигнала путем умножения его на функцию окна . Идеальные чистые тона имеют бесконечную продолжительность, а сужение помогает предотвратить влияние краев нашего конечного сигнала на преобразование Фурье.
s = s * np.blackman(s.size)
Оконная функция (зеленая) оказывает сужающее действие на сигнал:
Поскольку функция s определена для данного момента времени t , мы называем это представление сигнала временем 9(е) {\ Displaystyle {\ шляпа {s}} (е)}). Это новое представление называется частотной областью. Он состоит из массива коэффициентов Фурье :
S = np.fft.fft(s)
Вспомогательная функция fftfreq() возвращает массив частот, соответствующих коэффициентам. Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
Интервал выборки частоты определяется длительностью сигнала с : чем длиннее сигнал, тем меньше интервал выборки частоты. (Точно так же короткие интервалы выборки по времени соответствуют широкой полосе пропускания по частоте.)
freq = np.fft.fftfreq(s.size, d=1/10e3)
Результатом является массив из коэффициентов Фурье , большинство из которых равны нулю. Но на частотах аккорда и вблизи них коэффициенты велики. Результат: «рецепт» аккорда с точки зрения синусоидальных монотонов.
Это называется спектром сигнала s . Он показывает величину каждой частотной составляющей.
Частотно-временное представление
Теперь мы знаем, как расплетать политонические сигналы, но давайте введем еще одно усложнение — сигналы, компоненты которых меняются со временем. Такие сигналы называются нестационарный . Например, подумайте о монотонном сигнале, тон которого меняется в какой-то момент (см. Блокнот для кода, который генерирует этот сигнал):
Мы можем вычислить преобразование Фурье этого сигнала, как и раньше:
с *= np.blackman(s.size) S = np.fft.fft(s) freq = np.fft.fftfreq(s.size, d=1/10e3)
И постройте амплитуду S в зависимости от массива частот freq :
Он очень похож на спектр, который мы сделали раньше, но без средней частоты. Пики немного более рассредоточены, потому что продолжительность каждого сигнала вдвое меньше, чем была. (Общий принцип неопределенности распространяет сигналы по частоте по мере того, как они становятся более компактными во времени.)
Дело в том, что нет большой разницы между спектром двух смешанных сигналов и спектром двух последовательных сигналов. Если мы заботимся о локализации сигналов во времени (мы делаем!), это проблема. Одним из решений является обращение к частотно-временным представлениям . Пытаясь разделить сигнал одновременно по времени и частоте, они предлагают способ одновременного использования преимуществ обеих областей.
Библиотека для построения графиков Python matplotlib предлагает удобный способ построения графика время-частота, также известного как спектрограмма . В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
В одной строке кода он создает график 2D-изображения, показывающий зависимость частоты от времени.
_ = plt.specgram(s, Fs=1/10e3,
NFFT=512, noverlap=480) Немного поработав, мы можем получить очень богатое представление наших данных:
График использует алгоритм, называемый кратковременным преобразованием Фурье, или STFT. Это просто делает преобразование Фурье в скользящем окне длиной NFFT с перекрытием точек, перекрывающихся в предыдущем окне. Мы хотим NFFT должен быть длинным, чтобы получить хорошее разрешение по частоте, и мы хотим, чтобы nooverlap был большим, чтобы получить хорошее разрешение по времени.
Обратите внимание, что мы не можем точно увидеть точную частоту компонентов — они не служат достаточно долго, чтобы их можно было зафиксировать. И есть некоторая неопределенность в отношении сроков перехода,
потому что для получения приличного разрешения по частоте нам нужен длинный сегмент сигнала (в данном случае 512 отсчетов) — поэтому мы теряем информацию о времени. Но в целом этот сюжет лучше, чем
только спектр: мы видим, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.
Но в целом этот сюжет лучше, чем
только спектр: мы видим, что есть по крайней мере два сильных сигнала с частотами около 250 и 400 Гц, и что изменение происходит примерно через 0,125 с.
Фрагмент фортепианной музыки может напоминать такой сюжет. Поскольку клавиши пианино могут воспроизводить только одну ноту, спектрограмма фортепианной музыки выглядит как серия горизонтальных линий:
Существует большое сходство между этим частотно-временным разложением и нотной записью:
Оказывается, самые интересные сигналы — и, возможно, все естественные сигналы — политонны и нестационарны. По этой причине, хотя временные ряды часто полезны, частотно-временная декомпозиция может быть очень показательной. Вот несколько примеров; в каждом случае частота отложена по вертикальной оси, а время по горизонтальной оси. Цвета указывают мощность от низкой (синий) до высокой (желтый) (пропорционально квадрату амплитуды).
Человеческий голос произносит «SEG». Сонорные гласные имеют гармоники (горизонтальные полосы), а шипящие звуки «С» и первой части «Г» — шумоподобные. спектральные отклики.
спектральные отклики.
На этой спектрограмме показана 5-секундная серия чириканий летучих мышей. Я указал 18 кГц, приблизительный предел человеческого слуха, оранжевой линией, и если вы слушаете звук этого сигнала в Ноутбук, можно убедиться, что чириканье еле слышно при нормальной скорости воспроизведения; только при замедлении клипа они могут быть отчетливо слышны.
Наконец, вот вулканический «крик» — гармонический толчок, предшествующий взрывному извержению на горе Редут, Аляска, в марте 2009 года. На слух это звучит невероятно, но спектрограмма тоже интересно. В отличие от чириканья летучей мыши, этот 15-минутный временной ряд нужно ускорить, чтобы его услышать.
Продолжить изучение
Все рисунки в этой записной книжке можно воспроизвести с помощью кода в записной книжке Jupyter, прилагаемой к этой статье, на https://github.com/seg/tutorials-2018. Вы даже можете запустить код в облаке и поиграть с ним в браузере. Ничего не сломаешь — не волнуйся!
В хранилище вы также найдете больше сигналов, синтетических и естественных, от сердцебиения и загадочного подводного щебетания до гравитационных волн и сейсмических следов.



 В чем может быть проблема?
В чем может быть проблема? Сама была только на ч.р. 1.0, интересно переработали подход.
Сама была только на ч.р. 1.0, интересно переработали подход.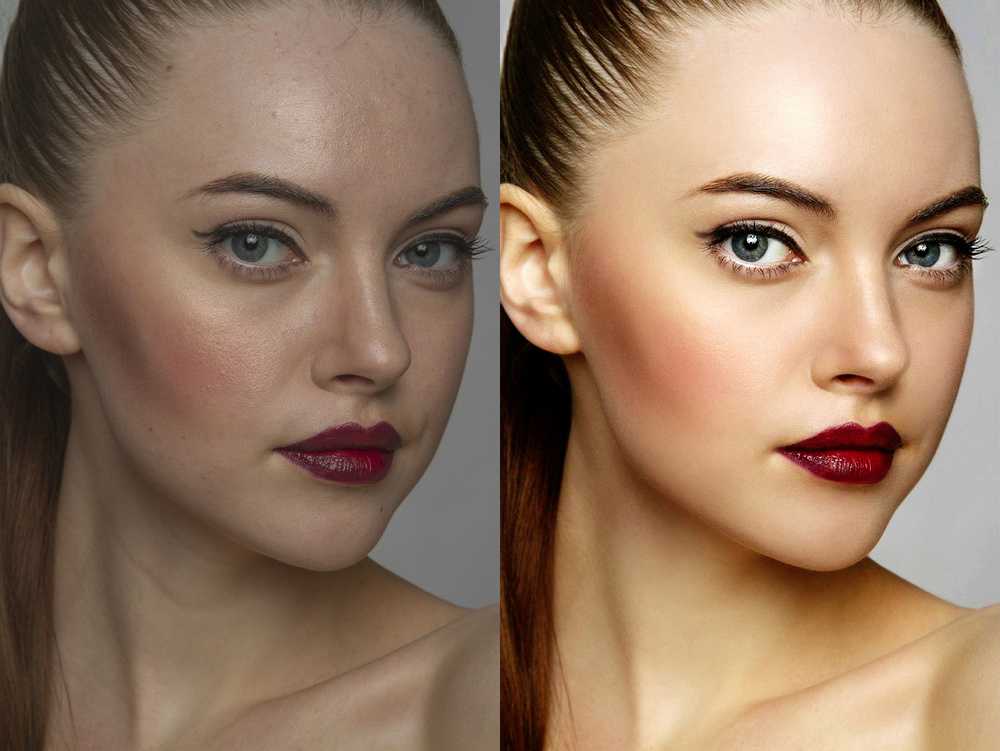 В завершении разложения остаётся всего лишь привычным образом через Apply Image получить недостающую высокочастотную составляющую.
В завершении разложения остаётся всего лишь привычным образом через Apply Image получить недостающую высокочастотную составляющую.