Частотное разложение. ULTIMATE | Виртуальная школа Profile
Частотное разложение. ULTIMATE
Цикл завершен. Начавшаяся 4 года назад история подошла к логическому концу. Я не изобретал этот прием, мне просто удалось вытащить его из узкого кулуарного круга «крутых профи» и запустить в широкие массы. Само название «частотка» — яркое тому доказательство. Огромное спасибо Александру Миловскому за подсказку, позволившую мне открыть Америку через форточку (так мой дед называл изобретение для себя лично чего-либо уже известного окружающим). Именно из его статьи шагнул в массы термин «частотное разложение».
1. ТЕОРИЯ
Разложение в спектр.
В 1807 году Жан Батист Жозеф Фурье подготовил доклад «О распространении тепла в твёрдом теле», в котором использовал разложение функции в тригонометрический ряд
При таком преобразовании функция представляется в виде суммы синусоидальных колебаний (гармоник) с различной амплитудой
Любой сигнал может быть представлен в таком виде, а все образующие его гармоники вместе называются спектром
В 1933 году Владимир Александрович Котельников сформулировал и доказал теорему, согласно которой любой сигнал с конечным спектром может быть без потерь восстановлен после оцифровки, при условии, что частота дискретезации будет как минимум в два раза выше частоты верхней гармоники сигнала
Что такое пространственные частоты.
Частота с которой меняется яркость при перемещении по горизонтали или вертикали
Изображение — это двумерный сигнал (яркость меняется при перемещении по горизонтали и вертикали), поэтому общая решетка образуется из двух решеток различных ориентаций — горизонтальной и вертикальной
Чем выше частота, тем быстрее меняется яркость, тем мельче детали которые она задает
Самые мелкие детали — это перепады яркости на контрастных контурах
Разложение на полосы частот.
Для эффективной обработки сигнала нет необходимости раскладывать его в спектр, достаточно разложить его на несколько полос, содержащих все гармоники ниже или выше определеной частоты
Самые низкие частоты задают общее распределение яркости и, как следствие, цвета
Средние частоты уточняют эту картинку принося основные объемы объектов
Верхние частоты добавляют самую мелкую детализацию — фактуру поверхностей
Дополнительные материалы:
Алексей Шадрин. «Управление визуальным объемом изображений»Александр Миловский. «Муар нам только снится»
«Муар нам только снится»2. ПРОСТОЕ РАЗЛОЖЕНИЕ НА 2 ПОЛОСЫ ЧАСТОТ
Фильтры нижних и верхних частот.
Gaussian Blur — фильтр нижних пространственных частот
Чем больше Raduis, тем более крупные детали убираются, тем ниже оставшиеся частоты
High Pass — фильтр верхних пространственных частот, дополнительный к Gaussian Blur
High Pass показывает детали, которые убрал Gaussian Blur при том же значении Radius
Эти детали отображаются в виде отклонения от средне-серого цвета (отклонения от средней яркости в каждом канале)
Сложение исходного изображение из частотных полос.
Добавить эти отклонения к исходному изображению может режим Linear Light
Контраст ВЧ-слоя надо понизить в два раза вокруг средней яркости (тон 128), чтобы скомпенсировать заложенное в Linear Light удвоение
Это можно сделать при помощи кривых (Curves) подняв черную точку в позицию (0; 64) и опустив белую в позицию (255; 192)
Можно понизить контраст при помощи Brightness/Contrast с установкой Contrast -50 и активированным ключем Use Legacy
Вместо понижения контраста можно уменьшить до 50% непрозрачность слоя, но в этом случае регулятор Opasityиспользовать нельзя, а нужно воспользоваться регулятором Fill
Дополнительные материалы:
Андрей Журавлев. «Ретушь портрета на основе частотного разложения»
«Ретушь портрета на основе частотного разложения»3. DODGE & BURN
Идеология Dodge & Burn.
Основная идея этой техники: ручное осветление излишне темных и затемнение слишком светлых участков для придания объекту более гладкой и правильной формы
Таким же образом усиливаются или дорисовываются недостающие объемы
Классически реализуется при помощи инструментов Dodge Tool и Burn Tool, но эти инструменты допускают только деструктивную обработку
Может быть реализована при помощи режимов наложения или корректирующих кривых с рисованием по макске слоя
Реализация Dodge & Burn при помощи режимов наложения.
Для сильной перерисовки свето-теневого рисунка используются режимы наложения Multiply и Screen
Рисование производится на пустых или залятых нейтральными для данных режимов цветом слоях
Основным преимуществом такой работы является большая сила воздействия: Multiply способен затемнять даже белый объект, а Screen осветлять даже черный
Дополнительным плюсом является возможность работать разным цветом на одном слое и простота выбора цвета: его можно брать с самого изображения
Минусом (особенно для начинающих) является уже упомянутая сила воздействия, заставляющая точно контролировать свои движения
Для легкой финальной правки применяют слой в режиме Soft Light (прозрачный или залитый средне-серым)
Плюсами являются: мягкость и визуальная однородность воздействия; ограниченный диапазон воздейстывий; отсутствие воздействия на белые и черные участки
Реализация Dodge & Burn при помощи кривых.
Затемнение и осветление производится при помощи корректирующих слоев кривых (Curves), а необходимые участки прорисовываются по их маскам
При затемнении происходит повышение, а при осветлении понижение, насыщенности изображения. Для их компенсации к каждому слою кривых через маску вырезания (Create Clipping Mask) добавляется слой Hue/Saturation
К плюсам метода можно отнести большую (по сравнению с использованием режимов наложения) гибкость последующих настроек
Минусом является невозможность вносить разные оттенки цвета при помощи одного корректирующего слоя
Для самостоятельного изучения:
Алиса Еронтьева и Дмитрий Никифоров. «Портретная ретушь»4. ИНСТРУМЕНТЫ ИХ НАСТРОЙКИ
Почему выгодно править частотные полосы по отдельности.
При ретуши необходимо согласовывать цвет и его переходы с одной стороны и фактуру поверхности с другой
При исправлении формы крупных объектов выгодно использовать пониженную непрозрачность
Для сохранения мелких объектов (фактура поверхности) необходимо использовать 100% непрозрачность
Мягкая граница кисти у штампа — вынужденный компромисс между этими двумя требованиями
Жесткий стык между однородными однотипными фактурами заметен не будет
Выбор радиуса при разложении на две полосы частот.
Для Gaussian Blur выгодно задавать большой радиус, чтобы максимально убрать фактуру
Для High Pass выгодно задавать малый радиус, чтобы не пропустить объемы
Конкретное значение выбирается как компромиссный вариант между этими двумя условиями
При этом учитывается детали какой крупности мы относим к фактуре
Визуализация при выборе радиуса разложения.
Радиус Gaussian Blur удобнее подбирать плавно увеличивая его, пока не исчезнут ненужные детали
Радиус High Pass удобнее подбирать плавно уменьшая его, пока не пропадут ненужные объемы
Если более важной является форма, радиус удобнее подбирать ориентируясь на содержимое НЧ (размытая картинка)
Если более важной является фактура поверхности, радиус удобнее подбирать ориентируясь на содержимое ВЧ («хайпасная» картинка)
Зависимость радиусов от размера лица и крупности дефектов.
Пропорции среднего лица (ширина к высоте) составляют примерно один к полутора
При вычислении радиусов удобнее отталкиваться от высоты лица, так как она меньше зависит от ракурса съемки
Для удаления аккуратной фактуры кожи необходимо взять значение Radius порядка 1/280 — 1/250 от высоты лица
Для удаления мелких дефектов (прыщи, морщины и т. п.) необходимо взять значение Radius порядка 1/100 — 1/120 от высоты лица
п.) необходимо взять значение Radius порядка 1/100 — 1/120 от высоты лица
Для удаления крупных дефектов (подглазины, шрамы и т.п.) необходимо взять значение Radius порядка 1/50 — 1/60 от высоты лица
5. РЕТУШЬ ПРИ РАЗЛОЖЕНИИ НА 2 ПОЛОСЫ ЧАСТОТ
Ретушь НЧ-составляющей — исправление формы.
Находящуюся на НЧ слое форму удобно ретушировать при помощи инструментов Clone Stamp, Brush и Mixer Brush
Штампом работаем с мягкой кистью и пониженной непрозрачностью
Можно работать на новом прозрачном слое с настройкой штампа Sample: Current & Below
При этом на экран можно вывести общий вид картинки, а не только НЧ слоя.
Кисть (Brush Tool) удобно использовать для закрашивания локальных дефектов (пробойные блики, проваальные тени и т.п.) телесным цветом
Mixer Brush используется для быстрого разглаживания лишних объемов
Ретушь ВЧ-составляющей исправление фактуры.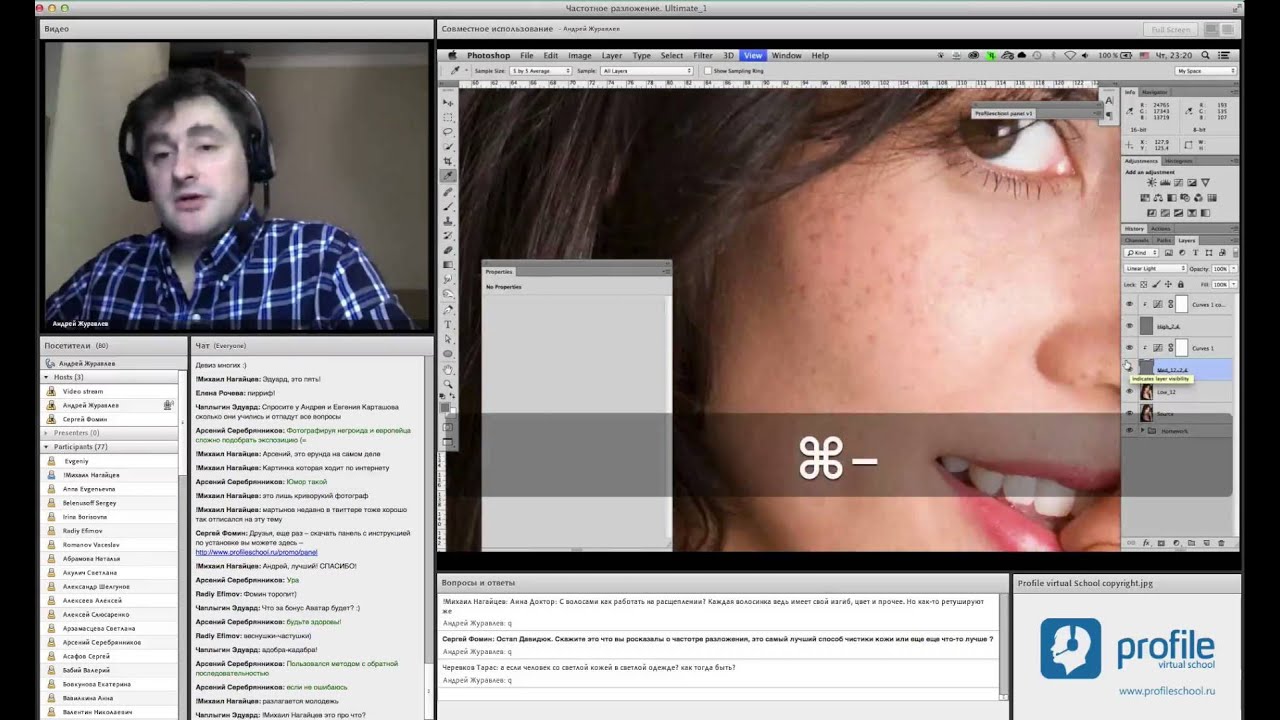
Работаем штампом с жесткой кистью и 100% непрозрачностью
Можно работать на новом прозрачном слое с настройкой штампа Sample: Current & Below и отображением только ВЧ слоя
Чтобы ретушировать глядя на финальную картинку надо работать на самом ВЧ слое (его копии) с настройкой штампа Sample: Current Layer
Чтобы иметь возможность откатиться к исходному состоянию ретушь проводят на копии слоя ВЧ с применением к нему команды Create Clipping Mask
Для лучшего контроля над деталями можно временно включить корректирующий слой кривых, повышающий контраст ВЧ составляющей
При отсутствии на изображении необходимой текстуры можно перенести ее с другой фотографии
Как работает Healing Brush.
На НЧ слое после размытия на участках рядом с контрастной границей появляется цвет соседней области
На ВЧ слое вдоль контрастных границ появляются ореолы противоположных цветов
Если в процессе ретуши ВЧ слоя убрать ореол на финальной картинке на этом участке появится цвет соседней области
Healing Brush переносит фактуру с донорской области, подгоняя цвет и яркость под ретушируемого участка под цвет и яркость его окрестностей
Его работа построена на алгоритме частотного разложения, а значение радиуса привязано к размер кисти
6. ОТДЕЛЬНЫЕ ПРИЕМЫ РЕТУШИ
ОТДЕЛЬНЫЕ ПРИЕМЫ РЕТУШИ
Как побрить человека.
Вынести волоски (щетину) на ВЧ слой и заменить их фактурой чистой кожи
Если щетина была темная, поправить цвет на НЧ слое
Внимательно следите за фактурой, она сильно отличается на разных участках лица
«Брить» мужчину тяжело, поскольку на лице не хватает нужной фактуры
При необходимости нужную фактуру кожи можно взять с другой фотографии
Борьба с пробойными бликами. Ретушь НЧ.
Изображение раскладывается на две полосы с установками обеспечивающими полный переход фактуры кожи на ВЧ слой
На НЧ слое участки пробойных бликов закрашиваются цветом кожи
При необходимости на них наносится свето-теневой рисунок передающий объем объекта
Борьба с пробойными бликами. Ретушь ВЧ.
Если блик пробойный и вообще не содержал фактуры, она переносится с целых участков кожи
Если блик близок к пробойному и фактура кожи все-таки содержится, после ретуши НЧ она визуально усилится
Чтобы смягчить этот эффект можно наложить на нее фактуру с более гладких участков на отдельном слое с пониженной непрозрачностью
7. «ЧЕСТНОЕ» РАЗЛОЖЕНИЕ НА 2 ПОЛОСЫ ЧАСТОТ
«ЧЕСТНОЕ» РАЗЛОЖЕНИЕ НА 2 ПОЛОСЫ ЧАСТОТ
Ошибка High Pass.
Максимальный диапазон разностей яркости от -256 (вычитаем белый из черного) до 256 (вычитаем черный из белого) составляет 512 тоновых уровней
Максимально возможные отклонения от средней яркости от -128 (затемнение) до 127 (осветление)
При наличии мелких деталей на массивном фоне отличающихся по яркости более чем на 128 уровней High Pass ошибается
Обычно это случается на точечных бликах расположенных на темном объекте
Чем больше радиус размытия, тем больше сама ошибка и вероятность ее появления.
На практике, при малых радиусах разница является «гомеопатической» и рассматривать ее как реальную проблему можно только с академической точки зрения
При больших радиусах ошибка составляет реальную проблему, поскольку «гасит» мелкие блики
Создание ВЧ составляющей вычитанием НЧ из оригинала.
Альтернативой High Pass является наложение на исходное изображение размытой версии при помощи команды Apply Image в режиме Subtract с установками Scale:2 Offset:128
В поле Offset (смещение) задается значение яркости вокруг которого будет откладываться результат вычитания
В поле Scale устанавливается во сколько раз будет уменьшаться результат вычитания перед добавлением к значению Offset
Диапазон установок Scale от 1 до 2, то есть контраст можно понизить максимум в 2 раза
Применять корректирующий слой понижающий контраст в этом случае не нужно, поскольку он уже понижен установкой Scale:2
Особенности разложения 16-битных изображений.
При вычислении ВЧ через команду Subtract у 16-битных изображений появляется ошибка величиной в 1 восьмибитный (128 шестнадцатибитных) уровень
Вероятно, это связано с тем, что реально вычисления происходят в пятнадцатибитном виде
Чтобы избежать этой ошибки при работе в 16-битном режиме вместо команды Subtract используют команду Add с активированным ключом Invert и установками Scale:2 Offset:0
Использование Surface Blur для получения НЧ составляющей.
В случае применения для получения НЧ составляющей Gaussian Blur вдоль контрастных границ создаются сильные ореолы
Ретушь в области ореолов может привести к «затягиванию» на объект цвета соседнего фона
Проблема проявляется тем более сильно, чем больше радиус размытия, поскольку в этом случае ореолы становятся более массивными и плотными
Чтобы избежать такой проблемы НЧ составляющую можно создавать при помощи фильтра Surface Blur
Границы, имеющие перепад яркости больше уровня установленного регулятором Threshold, не размываются
На практике удобнее всего подобрать значение Radius при установленном на максимум Threshold, а потом уменьшать значение Threshold до восстановления контрастных границ
8. АВТОМАТИЗАЦИЯ ПРОЦЕССА
Запись универсального экшена для разложения на 2 полосы частот.
Все операции выполняются со слоями, созданными самим экшеном
Слой создается командой Layer > New Layer и сразу переименовывается
Текущее изображение помещается на него при помощи команды Image > Apply Image с установкой Layer: Merged
Переключения между слоями выполняются при помощи шоткатов «Alt»+«[» и «Alt»+«]»
Для возможности переключения вместо отключения видимости слоя его непрозрачность уменьшается до нуля
При необходимости перемещение слоев выполняются командами Layer > Arange
В качестве подсказки перед применением Gaussian Blur в экшен вставляется команда Stop с комментариями по подбору радиуса
При регулярном применении Stop можно деактивировать или удалить
Преимущества «честного» разложения при работе с экшенами.
При записи экшена количество стандартных операций не является критичным
При этом важно минимизировать количество операций, требующих участия пользователя
Вычисление ВЧ составляющей через наложение НЧ на копию исходного слоя избавляет пользователя от задания радиуса для фильтра High Pass
Дополнительным плюсом такого метода является возможность применить для размытия не Gaussian Blur, а какой-нибудь другой фильтр
Создание набора экшенов для разложения на 2 полосы.
Сделать набор экшенов с жестко заданными значениями радиуса можно на основе универсального экшена
Для этого нужно убрать команду Stop, отключить диалоговое окно в Gaussian Blur и настроить его радиус на требуемый
Для удобства последующей работы с файлом к названиям слоев Low и High можно сразу добавить приписку со значением радиуса размытия
Экшен для пакетной обработки с настройкой по первому кадру.
При обработке серии фотографий с одинаковой крупностью объектов было бы удобно один раз вручную подобрать нужный радиус разложения, а потом применять его ко всей серии
Это можно сделать, если вместо прямого вызова конкретного фильтра вписать в экшен команду вызова последнего использовавшегося фильтра
Теперь достаточно один раз вызвать нужный фильтр (в рамках стандартного экшена или отдельно), настроить его параметры и он будет применяться при всех следующих запусках экшена
9. РАЗЛОЖЕНИЕ НА 3 ПОЛОСЫ ЧАСТОТ
РАЗЛОЖЕНИЕ НА 3 ПОЛОСЫ ЧАСТОТ
Зачем раскладывают картинку на три полосы.
Чаще всего задача такого разложения — вынести все дефекты в среднюю полосу частот
Таким образом можно бороться с объектами определенного типоразмера, например веснушками
Кроме того, в средних частотах находится большинство «старящих» элементов: глубина морщин, жилистость, вены, провисания, мешки под глазами и т.п.
Реже ретушируются все три полосы, в этом случае процесс аналогичен разделению на 2 полосы, но позволяет проще работать объектами разного типоразмера
Как это сделать.
Для НЧ увеличиваем радиус Gaussian Blur пока не останется чистая форма
Для ВЧ уменьшаем радиус High Pass пока не останется чистая фактура
Создаем между нами слой средних частот применив к нему сначала High Pass с радиусом который использовался для создания НЧ, а потом Gaussian Blur с радиусом который использовался для создания ВЧ
Универсальное правило: High Pass следующего слоя имеет такой же радиус, как Gaussian Blur предыдущего
Теперь можно ретушировать средние частоты не обращая внимание не только на фактуру, но и на разницу цвета исходной и ретушируемой области
При «честном» разложении средние частоты получаются вычитанием из исходного изображения низких и высоких
Автоматизация разложение на три полосы.
Для создания ВЧ удобно использовать High Pass, поскольку он позволяет более наглядно подобрать радиус
В процессе подбора уменьшаем радиус High Pass пока на ВЧ не останется чистая фактура
Вместо High Pass можно использовать Gaussian Blur с визуализацией ВЧ составляющей
Слой средних частот можно получить вычитая из исходного изображения верхние и нижние частоты
10. УПРОЩЕННЫЙ МЕТОД РЕТУШИ СРЕДНИХ ЧАСТОТ (INVERTED HIGH PASS)
Почему можно упростить ретушь средних частот.
Ретушируя средние частоты мы прежде всего убираем лежащие в них излишние локальные объемы
Это можно сделать проще, не раскладывая изображение на три полосы, а выделить среднюю и вычесть ее из исходника
Вычитание должно быть локальным: только на участках где присутствует лишний объем, пропорционально степени его подавления
Как это сделать.
Подбирать радиус для High Pass удобнее через Gaussian Blur (через НЧ составляющую) и наоборот
Делаем копию исходного слоя
Вызываем Gaussian Blur, плавно увеличиваем радиус пока не исчезнут ненужные детали, запоминаем его значение и нажимаем Cansel
Вызываем High Pass, плавно уменьшаем радиус пока не пропадут ненужные объемы, запоминаем его значение и вводим радиус подобранный на предыдущем шаге
Применяем Gaussian Blur с радиусом подобранным на предыдущем шаге
Инвертируем изображение
В два раза понижаем контраст вокруг средней точки
Переключаем режим наложения на Linear Light
На слой вычитающий средние частоты из исходного изображения набрасываем черную маску
Белой кистью по маске прорисовываем те участки, на которых нужно подавить крупные детали
Автоматизация процесса.
Все рутинные операции записываются в экшен
Полоса средних частот получается вычитанием из исходного изображения НЧ и ВЧ полос с подобранными пользователем радиусами
За счет этого визуализация оказывается наиболее комфортной
Подбор верхнего радиуса можно делать после наложения на исходное изображение инвертированной СЧ+ВЧ составляющей. В этом случае используется Gaussian Blur и на размытой картинке начинает проступать чистая фактура
Чем приходится расплачиваться за скорость.
Результат ручной ретуши выглядите естественно прежде всего из-за сохранения мелких неоднородностей
За скорость и простоту приходится расплачиваться механистически правильной формой объектов, что визуально удешевляет работу
Соотношение радиусов обычно выбирают 1:3 или меньше, иначе результат будет выглядеть слишком неестественным
Для более тонкой работы соотношение радиусов берут примерно 1:2 и производят несколько циклов разложения с разными значениями вилки
При ретуши второстепенных участков можно брать соотношение 1:4 и даже больше
Для самостоятельного изучения:
Евгений Карташов. «Рецепты частотного разложения»
«Рецепты частотного разложения»11. ЧАСТОТНОЕ РАЗЛОЖЕНИЕ И ДРУГИЕ ИНСТРУМЕНТЫ PHOTOSHOP
Средние частоты и Clarity.
Алгоритм работы Clarity строится на усилении (ослаблении) средних пространственных частот
При этом работа идет только по яркостной составляющей изображения
Повышение и ослабление Clarity не симметрично
Инструмент использует интеллектуальное размытие с сохранением контрастных контуров напоминающее Surface Blur, но не совпадающее с ним
При умеренных значениях можно рекомедовать использование Clarity в конвертере, при условии, что в дальнейшем изображение не будет подвергаться «сильной» обработке
Высокие частоты и повышение резкости.
Искусственное повышение резкости есть ни что иное, как усиление самых верхних из содержащихся в изображении частот.
При подготовке пейзажей основной проблемой является замыливание (исчезновение) сверх мелкой детализации (трава) вследствии нехватки разрешения.
Аналогичная проблема встает при подготовке изображений с мелкими деталями для размещения в интернете
Создать визуально ощущение наличия сверх мелких деталей можно добавив в изображение мелкий шум, согласованный с его элементами
Для этого повышаем резкость классическим способом, но оставляем это повышение только на низко контрастных областях
Проще всего это сделать используя Surface Blur в качестве фильтра, создающего нерезкую маску
12. В ЗАВЕРШЕНИИ РАЗГОВОРА
Для чего еще можно применять частотное разложение
Частотное разложение — это универсальный метод применимый к любому жанру фотографии
Убирать складки на ткани или других материалах
С его помощью можно смягчать слишком жесткие тени
Избавляться от разводов оставшихся после общей ретуши
Решать любые задачи, требующие различной работы с общей формой и мелкими деталями
Почему после частотного разложения картинка выглядит плохо?
Ретушь — это процесс не поддающийся автоматизации
Частотное разложение не делает ретушь за вас, оно лишь упрощает решение некоторых проблем
Увлекшись возможностью решить все «несколькими размашистыми мазками», при использовании частотного разложения ретушеры нередко позволяют себе работать халтурно
Будьте честны перед собой, не сваливайте собственные ошибки и халтуру на «плохую методику»
Чтобы избежать такой ловушки можно разделить процесс на два этапа
При помощи частотного разложения быстро поправить форму и разобраться с сильными огрехами фактуры (пробойные блики, грубая фактура и т. п.)
п.)
Последующую доработку производить при помощи привычных реализаций Dodge & Burn, чтобы обеспечить остаточную неоднородность и естественность изображения
Для самостоятельного изучения:
ModelMayhem.com — RAW! Beauty Robot.Сергей Брежнев «Частотное разложение vs Dodge&Burn»Все про резкость. Часть 7. Дэн Маргулис против Андрея Журавлева.: skitalets_san — LiveJournal
Все про резкость. Часть 7. Дэн Маргулис против Андрея Журавлева.
Сначала, лирическое отступление. Сейчас, только ленивый, наверное, не слышал про частотное разложение. В свое время получилось так, что и я, и Андрей Журавлев стали независимо друг от друга углубленно заниматься изучением этого метода. Помню даже, как он обращался ко многим с просьбой предоставить ему портрет небритого мужчины, чтобы «побрить» его. Андрея Журавлева, по его же словам, вдохновила на эти изыски статья Александра Миловского. И он ушел с головой в исследование этого метода. В бОльшей степени применительно для портретной ретуши. Результатом его огромной работы в течении 4 лет стал 5-ти часовой мастер-класс, который я рекомендовал бы посмотреть всем и каждому, если кто еще не умеет пользоваться этим методом. Ибо там не просто все разложено по полочкам и разжевано, но даже и в рот положено.
Результатом его огромной работы в течении 4 лет стал 5-ти часовой мастер-класс, который я рекомендовал бы посмотреть всем и каждому, если кто еще не умеет пользоваться этим методом. Ибо там не просто все разложено по полочкам и разжевано, но даже и в рот положено.
Частотное разложение. Ultimate. Конспект и видео
Моим же вдохновителем детального исследования частотного разложения был Стефан Марш. После публикации его экшена по повышению резкости в сообществе Colortheory в яху-группах. Но в отличии от Андрея Журавлева я не занимался исследованием областей применимости метода частотного разложения, сосредоточившись только на повышении резкости. А потом и вообще года на 4 выпал из обоймы.
Так вот, а при чем тут вообще частотное разложение? А при том, что даже в самом примитивном случае использования, метод High Pass (цветовой контраст) плюс Overlay (перекрытие), как раз и является примером частотного разложения. Я в свое время пошел дальше. Решил попытаться восстановить (без образования ореолов) размытый контур с использованием только Unsharp Mask (контурная резкость) и частотного разложения. Суть идеи была проста. Разложить изображение на несколько высоких частот (я использовал радиусы 0,4 0,8 1,2 и 1,6) и к каждому высокочастотному слою применить Unsharp Mask (контурная резкость) с различными настройками таким образом, чтобы и контур восстановился и ореолы, за счет того, что имели различную ширину и интенсивность, взаимно погасили друг друга, оставив только восстановленный контур. Причем, приходилось все это делать еще и в несколько проходов. Реализовать идею удалось, но… для этого потребовались многочасовые пляски с бубнами с подбором параметров почти вслепую. Естественно, такой метод не применим для практического использования и не имеет никакого смысла. Потому что в Photoshop имеется уже не один инструмент (как было 5 лет назад), а целых три, которые справляются с задачей восстановления размытого контура намного быстрее и наглядней. Об этих инструментах и о методах их использования поговорим в последующих статьях. Если хватит творческого запала и не одолеет непроходимая лень, чисто для академического интереса, попробую описать все свои пляски с бубном более подробно и с картинками.
Суть идеи была проста. Разложить изображение на несколько высоких частот (я использовал радиусы 0,4 0,8 1,2 и 1,6) и к каждому высокочастотному слою применить Unsharp Mask (контурная резкость) с различными настройками таким образом, чтобы и контур восстановился и ореолы, за счет того, что имели различную ширину и интенсивность, взаимно погасили друг друга, оставив только восстановленный контур. Причем, приходилось все это делать еще и в несколько проходов. Реализовать идею удалось, но… для этого потребовались многочасовые пляски с бубнами с подбором параметров почти вслепую. Естественно, такой метод не применим для практического использования и не имеет никакого смысла. Потому что в Photoshop имеется уже не один инструмент (как было 5 лет назад), а целых три, которые справляются с задачей восстановления размытого контура намного быстрее и наглядней. Об этих инструментах и о методах их использования поговорим в последующих статьях. Если хватит творческого запала и не одолеет непроходимая лень, чисто для академического интереса, попробую описать все свои пляски с бубном более подробно и с картинками.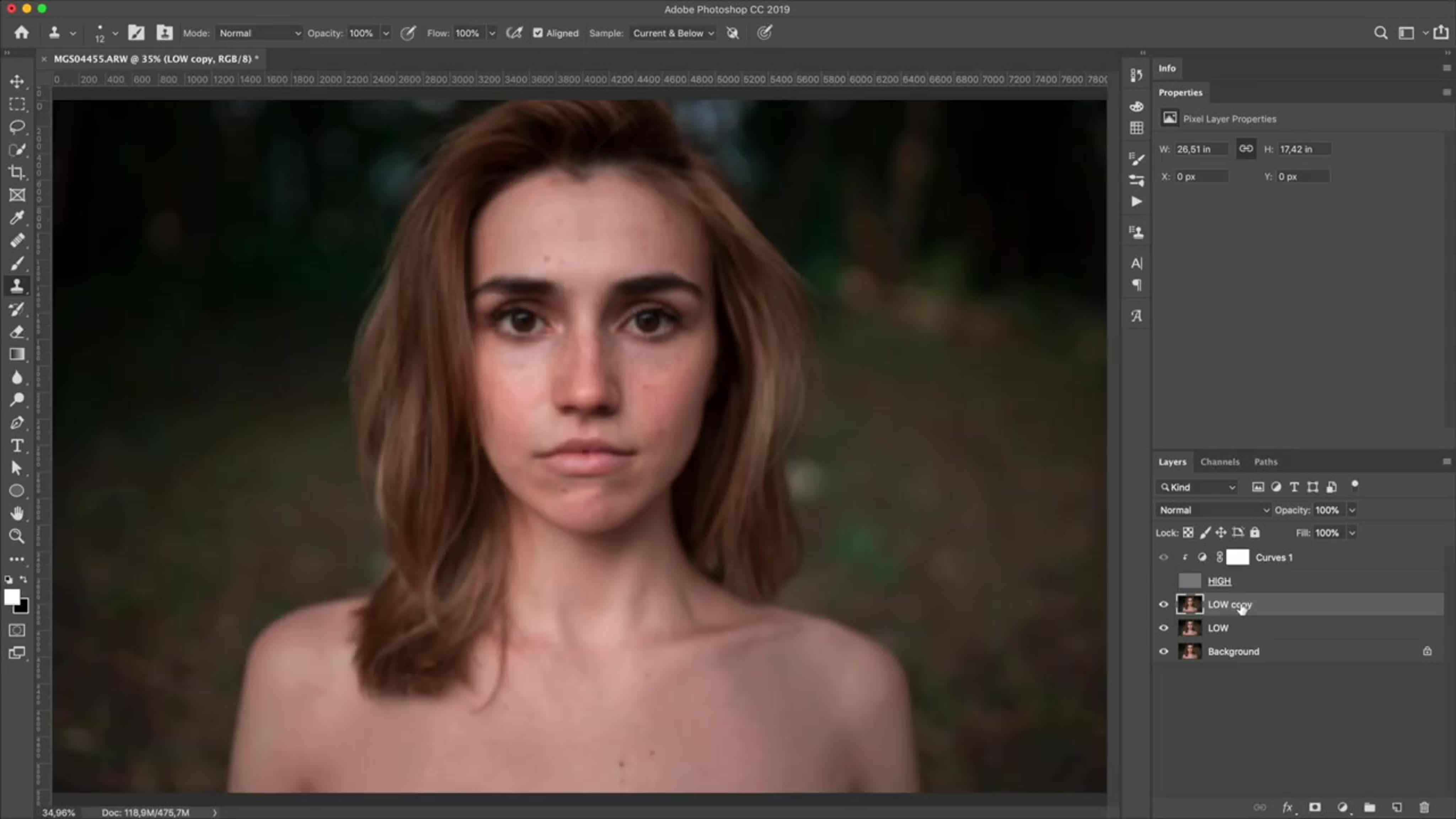
И все же, как соотносится название статьи и частотное разложение? Самым непосредственным образом. Дело в том, что, когда Андрей Журавлев заканчивал свой цикл статей по повышению резкости, он остановился только на High Pass (цветовой контраст) плюс Overlay (перекрытие) и не пошел дальше. Почему, я могу только предполагать. Само собой не потому, что не хватало знаний. Это точно не про него. Осмелюсь предположить, что виной тому стало его новое увлечение. Частотное разложение. И он с головой ушел в него не завершив начатое с резкостью. Больше того, где-то в публикациях у него мелькало, что он больше и не хочет возвращаться к вопросам резкости.
Чтобы была более понятна суть полемики, приведу цитаты из его статьи посвященной плюсам и минусам метода High Pass (цветовой контраст) плюс Overlay (перекрытие), где он описывает свою переписку с Дэном Маргулисом. Желающие могут ознакомиться с оригиналом:
Искусственное повышение резкости. Минусы и плюсы метода «High Pass – Overlay»
Минус первый: отсутствие Threshold (порога срабатывания). Как я уже писал выше, Threshold не решает всех проблем, связанных с усилением шумов при нерезком маскировании, и если основным критерием работы является качество, нерезкое маскирование все равно требует серьезной ручной доработки. Однако если во главе угла стоит скорость обработки, регулятор Threshold оказывается серьезным подспорьем. Вот мнение Дэна Маргулиса на эту тему, высказанное им в книге «Photoshop LAB Color» (врезка на стр. 135 русского издания):
Как я уже писал выше, Threshold не решает всех проблем, связанных с усилением шумов при нерезком маскировании, и если основным критерием работы является качество, нерезкое маскирование все равно требует серьезной ручной доработки. Однако если во главе угла стоит скорость обработки, регулятор Threshold оказывается серьезным подспорьем. Вот мнение Дэна Маргулиса на эту тему, высказанное им в книге «Photoshop LAB Color» (врезка на стр. 135 русского издания):
«Некоторые пользователи, пытаясь получить альтернативный эффект, дублируют слой, задают режим наложения Overlay и применяют фильтр High Pass из меню Filter \ Other. Этот способ не только более громоздкий, но и менее гибкий, поскольку в нем отсутствует параметр Threshold, что затрудняет подбор оптимального значения Radius».
С такой оценкой я категорически не согласен. Ниже будет показано, что метод «High Pass» является гораздо более гибким, чем Unsharp Mask, и открывает такие возможности обработки, которые даже не снились последнему. Да, он более громоздкий и долгий, чем простой вызов фильтра Unsharp Mask, но качество конечного результата того стоит.
Да, он более громоздкий и долгий, чем простой вызов фильтра Unsharp Mask, но качество конечного результата того стоит.
………………………………….
Рассматривать «громоздкость» данного метода в качестве минуса несерьезно: при незатейливом скоростном применении время, затрачиваемое на него, равно (или как минимум сравнимо) времени работы с Unsharp Mask, а при серьезной вдумчивой обработке результат настолько превосходит «конкурента», что сравнение становится просто некорректным.
………………………………….
После прочтения этихстрок у меня сразу же возник закономерный вопрос. Как оказалось, как будет видно ниже, не у меня одного. А кто мешает проделать абсолютно все то же самое с использованием Unsharp Mask (контурная резкость)? Применим к копии изображение нерезкое маскирование и из него вычтем оригинал. Получим абсолютно то же самое, что и в случае использования High Pass (цветовой контраст), только включая еще и работу Threshold. Причем, это не обязательно должен быть Unsharp Mask. Можно использовать и более продвинутые фильтры. Для меня не совсем понятно, почему Андрей так зациклился именно на High Pass.
Причем, это не обязательно должен быть Unsharp Mask. Можно использовать и более продвинутые фильтры. Для меня не совсем понятно, почему Андрей так зациклился именно на High Pass.
Замечание от Дэна Маргулиса.
«Сравнение High Pass и традиционного USM сделано сильно, но не произвело на меня впечатления, потому что аргументы выглядят примерно так:
a) имеются красная и зеленая машины, обе без бензина;
b) поскольку бензина нет, мы должны толкать их чтобы заставить двигаться;
c) красная машина меньше, поэтому ее легче толкать;
d) однако, если заправить зеленую машину, можно было бы поехать на ней и анализ ситуации показал бы, что управляя зеленой машиной, можно добраться до многих мест, куда невозможно было бы попасть толкая красную;
e) таким образом, зеленая машина лучше чем красная, Ч.Т.Д.
Мой коментарий в книге, косающийся сравнения High Pass и USM, сделан в контексте традиционного рабочего потока, когда повышение резкости делается быстро. Если, скажем, мы согласимся с тем, что повышение резкости должно быть сделано максимум за 20 секунд без применения каких-либо скриптов или экшенов, тогда, я полагаю, мы согласимся и с тем, что High Pass не выдерживает соревнования. В этом случае можно:
Если, скажем, мы согласимся с тем, что повышение резкости должно быть сделано максимум за 20 секунд без применения каких-либо скриптов или экшенов, тогда, я полагаю, мы согласимся и с тем, что High Pass не выдерживает соревнования. В этом случае можно:
a) сдублировать слой;
b) применить к нему USM с Amount 500%, Radius и Threshold по вкусу;
c) наложить поверх всего копию исходного слоя в режиме Darken с непрозрачностью 50%;
d) добавить настройки Blend If если необходимо управлять ореолами в тенях;
e) настроить непрозрачность слоя по вкусу
Можно получить аналогичный результат используя High Pass или, что то же самое, Gaussian Blur. Однако, каждый из этих путей потребует дополнительных шагов и в обоих случаях будет тяжело оценить, какими должны быть начальные настройки. Таким образом, при ограничении времени, нет смысла использовать High Pass.
Если есть больше времени, вы предлагаете ряд интересных вещей, которые можно реализовать используя результат действия фильтра High Pass. Все зависит от того, имеем ли мы карту ореолов.
Используя USM (или Gaussian Blur), можно легко создать такую же карту ореолов, просто вычтя оригинал из отшарпленной версии. С этой картой можно добиться всего того, что вы предложили сделать при помощи High Pass.
Примеры таких карт можно найти в обоих экшенах, ссылки на скачивание которых я давал на семинаре. Эти экшены понадобились, чтобы реализовать два заключения, которые я сделал после публикации последней книги.
1) Я пришел к выводу, что насыщеный цвет — это аргумент против повышения резкости, а нейтральный — аргумент за. Поэтому мне понадобилось каким-то образом автоматизировать создание маски цетовой насыщенности.
2) Сегодня мы часто встречаемся с необходимостью вычищать грязь, которая возникает в результате избыточного шарпа в камере или в Raw-конвертере, когда мы не имеем исходной (не шарпленной) версии изображения. Это требует метода, который позволяет подчеркивать более слабые ореолы не затрагивая более сильные, этакой «обратной отсечки» («Reverse Threshold»).
Экшены делают это, как и многое другое, например, создание темных и светлых ореолов с различными радиусами. Однако они построены не на прямом применении USM, а на создании карт ореолов, подобных той, которую делает High Pass. RGB-экшен создает два слоя с ореолами на средне-сером фоне, наложенные в режиме Linear Light (так же, как делает High Pass). Ореолы создаются при помощи Gaussian Blur.
Lab-экшен, представляющийся более практичным, использует USM для создания темных ореолов на белом фоне и светлых на черном. Они накладываются на изображение в режимах Multiply и Screen.
По этой причине ваши выводы кажутся мне не очевидными, а возможность создания карты ореолов при помощи USM — невыявленной. Однако, это не должно умалять общую ценность статьи, которая весьма значительна.»
При моем искреннем уважении к Дэну, у него есть одна скверная привычка: в споре он ставит такие граничные условия, которые априори делают его позицию беспроигрышной. А кто сказал, что у меня «нет бензина»? Почему мы должны отводить на повышение резкости всего 20 секунд и обходиться при этом без экшенов?
Как оказалось, я подумал точно о том же, о чем говорит Ден Маргулис. Андрей Журавлев абсолютно прав в том, что касается использования экшенов. Поэтому, мне тем более непонятно его упрямство в отстаивании преимуществ метода High Pass (цветовой контраст) плюс Overlay (перекрытие). Как я писал выше, думаю, тут дело в том, что он просто переключился на другую заинтересовавшую его тему и не пошел дальше. В целом, в этом споре, я в бОльшей степени на стороне Андрея Журавлева. Я полностью согласен с его идеями по практическому применению High Pass. Но… сам инструмент то куцый. Куцый и кастрированный. В этом пункте я полностью на стороне Дэна Маргулиса. Абсолютно все, о чем говорит Андрей полностью применимо и к другим инструментам. Так зачем пользоваться самокатом, если можно ехать даже не на велосипеде, а на машине?
Андрей Журавлев абсолютно прав в том, что касается использования экшенов. Поэтому, мне тем более непонятно его упрямство в отстаивании преимуществ метода High Pass (цветовой контраст) плюс Overlay (перекрытие). Как я писал выше, думаю, тут дело в том, что он просто переключился на другую заинтересовавшую его тему и не пошел дальше. В целом, в этом споре, я в бОльшей степени на стороне Андрея Журавлева. Я полностью согласен с его идеями по практическому применению High Pass. Но… сам инструмент то куцый. Куцый и кастрированный. В этом пункте я полностью на стороне Дэна Маргулиса. Абсолютно все, о чем говорит Андрей полностью применимо и к другим инструментам. Так зачем пользоваться самокатом, если можно ехать даже не на велосипеде, а на машине?
Таким образом получается, что все хвалебные оды, которые пелись методу High Pass (цветовой контраст) плюс Overlay (перекрытие) в предыдущей статье справедливы, но… за исключением самого инструмента. Сам я не придумал ничего нового. Для меня идейным вдохновителем явился экшен Стефана Марша. После него я стал выносить на высокочастотные слои действия абсолютно всех фильтров повышающих резкость. Включая и деконволюционные. Так как это действительно очень удобно и дает огромную гибкость. Поэтому, в свете всего выше сказанного, считаю использование именно инструмента High Pass (цветовой контраст) для повышение резкости не только совершенно бессмысленным, но и сильно ограничивающим возможности. Все, что можно делать с «картой ореолов» (термин прижившийся с легкой руки Андрея Журавлева) полностью применимо к любому фильтру повышающему резкость, которые имеют существенно больше возможностей по сравнению с примитивным High Pass (цветовой контраст). Огромной заслугой High Pass является не то, что он делает, ибо это можно сделать и другими методами и, зачастую, лучше, а в том, что этот инструмент дает идейный толчок для дальнейших исследований людям пытливым и любознательным. Лично мне, к сожалению, этого «толчка» не хватило. Потребовался дополнительный «толчок» в лице экшена Стефана Марша, чтобы дальше уже с головой уйти во всю эту «кухню».
Так что, при всем моем огромном уважении к Андрею Журавлеву, я в корне не согласен с его финальным подходом к повышению резкости, основанным на методе High Pass (цветовой контраст) плюс Overlay (перекрытие).
Ретушь портрета на основе частотного разложения изображения
Андрей ЖуравлевКонспект Лекции «Ретушь портрета на основе частотного разложения изображения.»
И так, частотное преобразование (wavelet) изображения, инструмент уже есть в программе Gimp (графический редактор)
Что мы подразумеваем :
- Низкие частоты — информация в изображении о общей форме
- Средние частоты — о деталях
- Высокие частоты — о мелких деталях придающих изображению «резкость»
Зачем нам это нужно — разделение изображения по такому принципу позволит редактировать отдельно каждую «частотную полосу»,
что по идее должно помочь ретушировать раздельно дефекты форм, дефекты изображения связанного с муаром, фактурой, убирать мелкий шум или вносить его, производить монтаж изображений получая новые художественные эффекты.
| Задача — разложить картинку на частотные составляющие, а затем сложить вместе и получить приемлемый результат. Что считаем за частоту (как критерий), нас интересует размер элементов — это и будет критерием. Поясним — считаем, что чем больше размер тем ниже частота, но размер подразумеваем как размер размытия по Гауссу. Получается, чтобы выделить низкочастотную составляющую изображения, к нему нужно применить Гауссово размытие, для выделения верхней частоты полосы нам нужно применить высокочастотный фильтр, в Фотошопе это фильтр HighPass. Хорошо, разделить изображение не сложно, как его собрать обратно ? Если говорить о фотошопе, то на основе ВЧ фильтра HighPass смотрим для каждого пиксела, на сколько его яркость отличается от средне серого (127) и нужно внести эти данные в изображение полученное с помощью НЧ фильтра Gaus Blure. Для этого в режиме наложения слоев есть интересный режим Linear Light. Есть одна особенность в работе этого режима, а именно коэффициент 2, откуда появляется — формула по которой работает режим L = A + 2 * (B — 128), где L — результат наложения, A — цвет нижнего слоя, B — цвет накладываемого слоя. Формула применяется по каналам раздельно. | |
| Если нижним слоем будет изображение после НЧ фильтра, а верхним после HighPass, получим изображение с удвоенными по силе деталями. Значит, результат после ВЧ фильтра нужно ослабить, т. е. вдвое уменьшить контраст. Для этого создадим корректирующий слой с кривыми где выставим яркости темной точки в 64 а для светлой 192 (форма кривой — возрастающая прямая). Редактирование результата НЧ фильтрации позволяет поправить — плохой макияж, ошибки света, мешки под глазами и т.п., при этом фактура кожи остается не затронутой поскольку мелкие детали у нас в ВЧ слое. Результат ВЧ фильтрации позволяет аккуратно убрать веснушки, шрамы, морщины. Рецепт редактирования женского портрета : разделим на 3-и частотные полосы, так чтобы на НЧ части нежелательные детали (в примере -веснушки) исчезли, для этого из копии исходного изображения создаем SmartObject к нему применяем фильтр Gaus Blure, подбираем радиус радиус размытия как компромисс между НЧ фильтром и ВЧ фильтром (в примере получили = 9). Создаем SmartObject для ВЧ части к нему применяем фильтр HighPass с радиусом ~ 2, так чтобы стали проявляться веснушки. Для СЧ части — фильтр HighPass должен цепляться за нижнюю и верхнюю части предыдущих частей. Поправляем результаты согласно нашим представлениям о красоте. От чего отталкиваться при выборе значений для фильтров : для размытия по Гауссу, радиусы : ~2 уходит мелкая фактура, ~10 ухоит детализация лица (речь идет о портретной съемке), морщины, шрамы и т.д. ~20-25 — остается только освещение ~4 в ВЧ части тонкая фактура кожи и мелкая детализация. Рецепт простого варианта ретуши : Создаем СЧ фильтр, так чтобы в него входили детали которые нам ненужны в итоговом результате применяем фильтры Gaus Blure (10) + HighPass (~24), итог инвертируем и создаем из него SmartObject + корректирующая кривая учитывающая коэффициент 2 и наложение LinearLight. Далее создаем маску скрывающую ненужные детали. |
Послесловие и начало эксперимента :
Я честно пытался повторить все, что было показанно на лекции, но результат не получался, не получался тем который нужен
изображение после фильтров оставалось мутным с некоторыми деталями.
Разбираясь, что не так, пришел к рецепту который изложу ниже.
Источники информации :
Андрей Журавлев «Цветокоррекция. Режимы наложения»
Александр Миловский «Муар нам только снится»
WiKi «Дискретное вейвлет-преобразование»
Вооружившись информацией приступим к действию, и для начала поясню некоторые детали
SmartObject — позволит нам изменять изображение, при этом надстройки над ним, такие как фильтры, режимы наложения остануться нетронутыми и будут действовать на результат изменений, кроме того появляется возможность попровлять режимы фильтров.
Создание групп — позволит нам группировать объекты, создавать более сложные обработки, уменьшить количество дублей слоев…
Первым делом разделим изображение на полосы низкой частоты и высокой частоты, для этого создаем 2-е копии слоя оригинального изображения, делаем из каждой SmartObject, создаем группу «Разложение изображения» куда переносим копии.К первой копии применяем фильтр Gaus Blure (размытие по Гаусу) например с значением 10. | |
| Внутри группы «Разложение изображения» создаем группу «ВЧ часть фильтра» в которую перенесем вторую копию изображения, к ней применим фильтр HighPass с значением 10, создадим корректирующий слой с кривыми для коррекци контраста (прямая 64 — 192) и изменим режим наложения группы «ВЧ часть фильтра» на LinearLight. Проверим, что наши действия приводят к адекватному результату. Изменяя видимость группы «Разложение изображения» сравниваем ее с исходным слоем, если все сделано правильно разницы не заметим. | |
| Смысл проделанных действий — мы провели границу частотного разделения по радиусу 10, теперь все что касается Нижних частот будет находиться в слое с размытием по Гаусу, а все что связанно с Высокими частотами будет внутри группы «ВЧ часть фильтра» Если нам понадобиться разделить на три полосы частот, НЧ СЧ ВЧ, то нам нужно будет внутри группы «ВЧ часть фильтра», произвести действия аналогичные для получения группы «Разложение изображения», а именно сделать две копии результата фильтра HighPass (10), к первой применить размытие по Гаусу с меньшим радиусом размытия (2,4), к второй применить фильтр HighPass с радиусом 2.4, создать вложенную группу в «ВЧ часть фильтра» куда поместить результат HighPass (2,4) c корректирующими кривыми (прямая 64-192) и изменить режим наложения группы на LinearLight. |
Нетрудно заметить, что тут возникает рекурсия, так в принципе и должно быть.
Редактируя SmartObject мы вносим изменения в соответствующие полосы частот, добиваясь нужного нам результата.
Видео, сейчас это группа Pink Floyd «Paint Box»
Экшн для ретуши в Photoshop на основе частотного разложения
Эта статья написана для тех, кто хочет погрузится в ретушь кожи при помощи частотного разложения.Детальное описание сути метода частотного разложения, определений частотного разделения и примеров есть у Андрея Журавлева, вот в этом посте, за что ему оргомное спасибо. Я также уверен, что если вам интересна цвето-коррекция, то вы сможете найти у Андрея Журавлёва массу полезных и хорошо написанных статей.
Я же, всего лишь, создал экшн для ретуши в Photoshop, использующего метод частотного разложения изображения описаного Андреем.
Основная суть метода:
Разнеся разные частоты изображения на различные слои, мы сможем редатктировать крупные детали на слове НЧ, сглаживая картинку по яркости, при этом не убивать сверх-мелкую и среднюю детализацию, к примеру поры.
И наоборот, замазывая шрамы, вы можете больше не боятся за яркостную и цветовую составляющие, вы работете на ВЧ слое где только детализация.
Для упрощения работы, я сделал экшн для ретуши в Photoshop, он должен работать как в русской версии так и в английской.
Разложение частот выполнено только на 2 канала: Детали (Retouch Details) и Тон\Яркость ( Retouch Tone)
Как пользоваться экшенами в фотошопе:
- Открыли изображение
- Нажали Alt + F9 — показать окно Экшенов (Операций по русски)
- Загрузили экшн в список
- Теперь выбираем в списке Retouch -> Retouch Fourier 2ch и жмём в нижней части треугольничек play
- Появилась куча слоёв, но нам нужно работать всего с двумя:
- Retouch Tone — НЧ составляющая
- Retouch Details — ВЧ составляющая.
Как выполнить ретушь в фотошопе на основе метода частотного разложения :
Ретушь необходимо выполнять на новом прозрачном слое (в экшене это слои Retouch Tone и Retouch Details), включив для штампа режим Sample: Current & Below (Образец: Текущий и Предыдущий.
1) Начинаем с деталей
Убираем все артефакты которые нам не нравятся на слое Retouch Details.
Используем штамп (S) или Healing Brush tool — Восстанавливающая кисть (J)
2) Смотрим что получилось
Выбираем слой «Details Group — Linear Light» и ставим ему режим наложения Linear Light.
Зажимаем Alt и жмём по глазику на против слоя Background \ Задний План — тем самым отключаются все слои, кроме самого начального — тоесть видно картинку до \ после.
3) Если надо что-то доделать на слое с деталям — ставим режим наложения группы «Details Group — Linear Light» в Pass Through ( Пропустить) и опять работаем на слое Retouch Details пока не достигнем желаемого результата
4) Неровности освещения — правим на слое Retouch Tone c помощью тех же инструментов + обычная кисть.
5) Смотрим что получилось — См Шаг 2. Если всё окей, оставляем всё как есть.
6) Так как слои использовались как смарт-объекты, то мы можем подогнать настройки разделения частот под себя — изменив значения смар-фильтров.
Кликаем 2 раза по слою Gaussian Blur (размытие по Гаусу) и изменяем значение размытия.
Такое же значение необходимо выставить в слое High Pass (Цветовой контраст).
Полностью согласен с Андреем, что для каждого отдельного изображения должен быть свой подход, так что значения ниже, не более чем ориентир:
Radius 1-2 — мелкая фактура кожи
Radius 4-5 — полная фактура кожи за исключением глубоких морщин и подобных дефектов
Radius 10-12 — полная фактура кожи с крупными дефектами
Radius 25-30 — практически все локальные блики и тени (мешки под глазами, носогубные складки, второй и прочие подбородки и т.п.)
Пост написан, дабы не забыть, да поделится с колегами из Фото-Клуба: «Просвіт»
Adobe Photoshop 1 ступень
Привет, меня зовут Андрей Журавлев, и я помогу Вам начать работать в программе Adobe Photoshop. Дальше нужно было бы написать о просторном классе, красивых компьютерах iMac, проекторе с правильной цветопередачей и огромной проекцией на целую стену. Все так и есть, но, на мой взгляд, не это является залогом успешного обучения.
Освоение Photoshop очень напоминает обучение вождению автомобиля. Сначала страшно от количества кнопок, команд и инструментов. После освоения первых инструментов страх проходит, но начинаешь в них путаться. К настройкам привык, и вот уже следующий вопрос: «А какой инструмент применять вот к этой картинке?»
Ничего не напоминает? Сначала тяжело тронуться с места, потому что ноги путаются в педалях. Трогаться научились, выехали на площадку, и все бы хорошо, но машина не всегда едет туда, куда задумывалось. Площадку освоили хорошо, пора выезжать в город, и тут даже не вопрос появляется, а паника: «Куда мне ехать сейчас?»
Можно ли «поехать» в Photoshop всего за 8 занятий? Можно, если рядом будет хороший инструктор. Главный плюс живых занятий — преподаватель всегда под рукой. Что-то не получается, сразу задал вопрос, сразу получил ответ. И чем проще объяснения, тем лучше. Я умею объяснять сложные вещи просто. А еще студенты говорят, что вживую я выгляжу не таким строгим, как на видео.
ПО ОКОНЧАНИИ КУРСА СТУДЕНТ ДОЛЖЕН УМЕТЬ:
- Организовывать грамотное хранение файлов на диске.
- Управлять файлами через программу Adobe Bridge.
- Конвертировать raw-файлы средствами Adobe Camera Raw.
- Кадрировать снимок и исправлять геометрию объектов.
- Устанавливать и менять хроматический баланс изображения при помощи инструмента Curves (кривые).
- Создавать и дорабатывать выделения, производить через них выборочные коррекции.
- Эффективно использовать слои и маски слоя, уметь работать в не разрушающей манере.
- Понимать логику работы и эффективно применять основные инструменты ретуши.
- Делать выборочную коррекцию без применения масок.
- Переводить фото в ч/б, тонировать цветное и ч/б изображение.
- Сохранять изображение для печати и размещения в интернете.
О ПРЕПОДАВАТЕЛЕ:
Андрей Журавлев — профессиональный цветокорректор и специалист по допечатной подготовке. Обработкой изображений в Adobe Photoshop занимается с 1996 года.
С 2009 года проводит авторские семинары и курсы по обработке изображений. В 2010 году провел авторский мастер-класс в рамках конференции Adobe Creative Future, открыв для широкой русскоязычной аудитории «частотное разложение» — профессиональную методику быстрой ретуши, основанную на разложении изображения на частотные полосы.
Автор цикла статей, посвященных работе с режимами наложения, опубликованных в журнале «Фотомастерская». Ведет свой собственный блог, где можно найти много полезных материалов по цветокоррекции, повышению резкости, автоматизации обработки, работе с режимами наложения и многим другим вопросам работы в Adobe Photoshop.
- ПРИ ЕДИНОВРЕМЕННОЙ ПОКУПКЕ 1 И 2 СТУПЕНИ СУММА ОПЛАТЫ СОСТАВИТ 34 900р.
Частотное разложение. Ultimate.
El-Dar «Почему 7 утра?»
El-Dar «Классика из выступлений Михаила Николаевича…»
andersen «Вот поэтому я не хожу по кафе…»
nezke «Замечательно! Очень понравилось. Действительно…»
andersen «Лучше чем Анжела )))»
zmeij «Пацаки должны носить цак! И не важно как он…»
optrnk «Бугага!!! Да 60 летний мерседес дороже 20…»
Razvedalnik «Смяшно»
|
|||||||||||||
Человеческая личность отражает пространственно-временную и частотно-временную структуру ЭЭГ
Характеристики ЭЭГ
Для анализа особенностей электрической активности мозга были рассчитаны значения по формуле (7) для n = 1,… 19 каналов ЭЭГ. Полученные коэффициенты определяют процентное отношение спектральной энергии к дельта-, тета-, альфа-, бета-1, бета-2 и гамма-диапазонам частот, а также характеризуют степень участия нейронного ансамбля, расположенного в окрестности n -й регистрирующий электрод, в генерации соответствующего вида деятельности [56].
Далее для описания нейродинамики в левом и правом полушариях мы рассмотрели коэффициенты ε LH (12) и ε RH (13), полученные усреднением коэффициентов ε , рассчитанных для каналов ЭЭГ, принадлежащих в левое и правое полушария соответственно. Согласно методу иерархической кластеризации (см. Материал и методы), субъектов можно сразу разделить на три группы. На рис. 3 (а) мы наносим на график значения ε RH и ε LH для каждого из 22 участников в активной (закрытые точки) и пассивной (светлые точки) фазах (каждая группа показана на отдельный подсюжет).
Рис. 3. Три сценария познавательной деятельности при умственном обработка задачи.
(а) Соотношение энергий высокочастотных и низкочастотных спектральных компонент в левом ( ε LH ) и правом ( ε RH ) полушариях, рассчитанное для активного (темные точки) и пассивного ( открытые точки) экспериментальные фазы. Распределения показаны для трех субъектов, принадлежащих к разным группам. (б) Коэффициент ε , показывающий соотношение между энергиями высокочастотных и низкочастотных спектральных компонентов, вычисленных для каждого канала ЭЭГ во время активной (левые столбцы) и пассивной (правые столбцы) фаз.Группы I и III содержат n = 8 предметов, а группа II содержит n = 6 предметов.
https://doi.org/10.1371/journal.pone.0197642.g003
Исходные данные, содержащие значения ε RH и ε LH для каждого предмета, показаны в таблице 1. Это Из рисунка 3 (а) ясно видно, что поведение ε RH и ε LH в каждой группе отличается. В группе I значения ε RH и ε LH имеют практически одинаковые значения во время активной и пассивной фаз.Во II группе активная фаза связана с увеличением высокочастотной активности в правом полушарии, а пассивная фаза — с повышением высокочастотной активности в левом полушарии. В группе III переход от активной к пассивной фазе связан с выраженным увеличением ε RH и уменьшением ε LH .
Таблица 1. Особенности ЭЭГ, выявленные в активной фазе (выполнение таблицы Шульте) и пассивной фазе, в терминах коэффициентов ε LH, RH и k .
ε LH, RH — соотношение между высокочастотной и низкочастотной активностью в левом и правом полушарии и k = ε RH / ε LH — степень полушария асимметрия.
https://doi.org/10.1371/journal.pone.0197642.t001
Рис. 3 (b) представляет пространственно-временную активность мозга в единицах ε в активной и пассивной фазах для каждой из трех групп. В группе I активность мозга в активной фазе характеризуется полушарной симметрией, тогда как в пассивной фазе полушарная симметрия сохраняется, хотя пространственно-временная структура меняется.
В группе II пространственно-временная структура существенно отличается. Можно заметить асимметрию полушарий как в активной, так и в пассивной фазах. Однако характер асимметрии в этих фазах иной: высокочастотная активность преобладает в правом полушарии во время активной фазы и перемещается в левое полушарие во время пассивной фазы.
В группе III испытуемые также демонстрируют асимметрию полушария как в активной, так и в пассивной фазах.В отличие от группы II характер асимметрии остается одинаковым в обеих фазах. Как видно из рис. 3 (б), асимметрия в обеих фазах проявляется в преобладании высокочастотной активности в правом полушарии. В то же время разница между активным и пассивным состояниями выявляет уменьшение ε в правом полушарии при переходе от активной фазы к пассивной.
Чтобы проверить, действительно ли группы существенно отличаются друг от друга, мы применили многомерный дисперсионный анализ (MANOVA).В качестве критерия принадлежности к одной из трех групп мы выбрали межсубъектный фактор (независимая переменная). С другой стороны, значения ε RH и ε LH , рассчитанные для активной и пассивной фаз, считались внутрисубъектными факторами (зависимыми переменными). В результате этого анализа мы обнаружили существенные различия между группами. Множественные сравнения выявили значительные различия по всем факторам, за исключением ε LH ( p = 0.858) рассчитано в активной фазе в группах 1 и 3.
Отличительные особенности активности мозга во время активной и пассивной фаз, наблюдаемые в трех группах, показаны на рис. 4 (а). Горизонтальные желтые полосы показывают медианное значение ε , рассчитанное для левого (LH) и правого (RH) полушарий во время активной и пассивной фаз. В группе I значения ε остаются практически одинаковыми для разных полушарий как в активной, так и в пассивной фазах ( p = 0.123 и p = 0,889 с помощью непараметрического знакового рангового критерия Вилкоксона (NPWSRT), n = 8). Во II группе активная фаза характеризуется резким увеличением ε в правом полушарии (медиана ε RH > 0,5 против медианы ε LH <0,35) ( p <0,05 по данным NPWSRT , n = 6). В пассивной фазе динамика обратная: в левом полушарии наблюдается увеличение ε (медиана ε RH <0.4 против медианы ε LH > 0,45) ( p <0,05 через NPWSRT, n = 6). Наконец, в группе III во время активной фазы ε в правом полушарии немного выше, чем в левом (медиана ε RH > 0,45 против медианы ε LH <0,45) ( p <0,05 через NPWSRT, n = 8). Во время пассивной фазы такая разница становится больше (медиана ε RH > 0.6 против медианы ε LH <0,35) ( p <0,05 через NPWSRT, n = 8).
Рис. 4. Статистические показатели для трех сценариев познавательной деятельности.
(а) Отношение ε между энергиями высокочастотных и низкочастотных спектральных компонент, рассчитанных для каналов ЭЭГ, принадлежащих левому (LH) и правому (RH) полушариям во время активной и пассивной фаз. (b) Отношение k между значениями ε , рассчитанными для левого и правого полушарий во время активной и пассивной фаз.Желтые полосы, прямоугольники и усы обозначают, соответственно, медианы, 25–75 процентилей и контуры. Группы I и III содержат n = 8 предметов, а группа II содержит n = 6 предметов. * p <0,05 с помощью непараметрического знакового рангового критерия Вилкоксона.
https://doi.org/10.1371/journal.pone.0197642.g004
Известно, что выполнение умственных задач связано с изменениями нейронной активности, которые можно обнаружить по спектру мощности ЭЭГ.Роль низкочастотной дельта-активности в умственных задачах изучалась в [57], где авторы сообщили об увеличении дельта-активности на ЭЭГ во время умственных задач, связанных с усилением внимания. Позже [58] также была выявлена связь между дельта-колебаниями и выполнением умственных задач. С другой стороны, в более ранних работах [59, 60] подчеркивалось увеличение тета-активности во время умственных усилий. В последнее время для оценки динамики умственной нагрузки использовали изменение уровня активности в низкочастотном диапазоне θ [61].
Связь между альфа-активностью и завершением умственных задач была продемонстрирована еще в 1984 году Осакой [62], который обнаружил изменения в амплитуде и местоположении пиковой альфа-частоты в спектре мощности. Позднее была выявлена значительная роль альфа-активности в памяти и когнитивных процессах [63]. Изменения энергии высокочастотных ритмов мозга обычно связаны с познавательной деятельностью, в частности с выполнением умственной задачи [64]. Например, учет гамма-активности для классификации умственных задач повышает точность [65].
Согласно рис. 4 (а), можно видеть, что электрическая активность мозга в каждой группе следует определенному сценарию, определяемому, с одной стороны, латерализацией функции мозга, а с другой стороны, определенными переходами между активным и пассивным. фазы. Для количественного описания наблюдаемых сценариев мы вычислили k = ε RH / ε LH , что отражает степень полушарной асимметрии. Эти значения нанесены для каждой группы на рис. 4 (б).Видно, что для группы I характерна полусферическая симметрия в активной и пассивной фазах, которая остается неизменной при фазовом переходе активно-пассив (Δ k ≈ 0), где Δ k = k пассивный — k активный . Для других групп асимметрия и переход наблюдаются между активной и пассивной фазами и отображаются на графике в единицах k , которые можно описать как Δ k <0 и Δ k > 0, соответственно.
Взаимосвязь между особенностями ЭЭГ и умственными способностями
Участники, принадлежащие к каждой из трех групп, были подвергнуты психодиагностическим тестам (см. Методы). В результате для каждого предмета были оценены значения WE , WU и PS , которые определяют среднее время выполнения задачи, среднюю производительность и сохранение внимания соответственно (см. Таблицу 2).
Результаты психодиагностических тестов представлены на рис. 5, где каждый участок иллюстрирует значения WE (a), PS (b) и WU (c) для каждой из трех групп.Данные представлены как среднее ± стандартное отклонение. Статистически сравнивали различия результатов психодиагностических тестов между группами испытуемых. Мы применили непараметрический критерий Крускала – Уоллиса H для нескольких независимых выборок для количественной оценки изменения значений WE , WU и PS по группам. В результате мы получили p <0,05 для средней производительности WU , среднего времени выполнения задачи WE и настойчивости внимания PS .
Рис. 5. Результаты психодиагностических тестов.
Меры, характеризующие умственные способности испытуемого во время выполнения теста Шульте. (a) Среднее время выполнения задачи WE (рассчитано по формуле 1, измерено в секундах). (b) Настойчивость внимания PS (рассчитывается по формуле 3, измеряется в безразмерных единицах). (c) Средняя производительность WU (рассчитана по формуле 2, измерена в безразмерных единицах). Данные представлены в виде среднего значения ± стандартное отклонение (стандартное отклонение — стандартное отклонение).
https://doi.org/10.1371/journal.pone.0197642.g005
Испытуемые I группы продемонстрировали двустороннюю активность ЭЭГ в обоих полушариях во время тестов с таблицами Шульте. При этом эти испытуемые продемонстрировали средне-низкую эффективность при выполнении задания. Для них среднее время выполнения задачи составило WE = 40,2 ± 0,68 секунды, а средняя производительность составила WU = 1,07 ± 0,08 (целевое значение — 1). Стойкость внимания была высокая PS = 0.97 ± 0,045 (целевое значение — 1). Испытуемые из этой группы могли сразу выполнять неизвестные задачи и поддерживать свою работоспособность на относительно высоком уровне, выше среднего или низкого уровня. Психологическая расшифровка тестов включала замечания о творческом подходе к выполнению тестов и быстром переходе к новым заданиям. В личном тесте такие испытуемые обладали ярко выраженной склонностью к работе в одиночку, высоким интеллектом, аналитическим складом ума, критическим мышлением, нетерпимостью к неопределенности и задержкой в принятии решений.Более того, они демонстрировали самоконтроль, отсутствие тревожности, ярко выраженное лидерство и желание доминировать в группе. Мы предполагаем, что творческий подход и попытка оптимизировать их работу привели к снижению их эффективности работы.
Испытуемые из II группы пытались разработать стратегию упрощения выполнения задания. При выполнении первой задачи присутствовала максимальная латерализация высокочастотной активности, т. Е. Активность в правом полушарии была гораздо более выраженной.Это означает, что при выполнении первой задачи стратегия еще не была разработана. При выполнении следующих заданий нагрузка на правое полушарие у этих испытуемых была снижена. В результате испытуемые из группы II продемонстрировали более высокую работоспособность, чем испытуемые из группы I. Среднее время выполнения задания составило WE = 33,6 ± 1,58 секунды. Стойкость внимания ПС = 0,86 ± 0,02 (целевое значение — 1). Средняя производительность составила WU = 1,07 ± 0,09 (целевое значение — 1).Этим испытуемым требовалось мало времени на адаптацию и они не утомлялись, будучи способны длительное время эффективно поддерживать высокую работоспособность. В их личных профилях гармонично сочетаются высокие показатели интеллекта, эмоциональной зрелости и самоконтроля.
В отличие от группы II, испытуемые из III группы выполнили задание без каких-либо попыток разработать стратегию его упрощения. Это подтвердил психологический тест. Их эффективность работы оставалась высокой; среднее время выполнения задания составило WE = 33 ± 1.35 секунд. Стойкость внимания составила PS = 0,9 ± 0,02 (целевое значение — 1). Средняя производительность составила WU = 1,24 ± 0,06 (целевое значение — 1). Мы предполагаем, что испытуемым из этой группы трудно поддерживать высокую работоспособность в течение длительного времени. Их личные тесты показали явное предпочтение работать в одиночку с низким самоконтролем, нетерпимостью к неопределенности и задержкой в принятии решений, которая может проявляться тревогой. Они также продемонстрировали высокий интеллект, аналитический склад ума, критическое мышление и дух экспериментов.
Взаимосвязь с личностными качествами
Участники, принадлежащие к каждой из трех групп, были подвергнуты тесту по 16 личностным факторам Кеттелла. На диаграмме на рис. 6 (а) показаны результаты теста «16 факторов личности» Кеттелла для трех групп. Данные отображаются в виде значений всех основных факторов анкеты 16PF, усредненных по всем предметам в каждой группе. Видно, что большинство факторов имеют схожие значения в каждой группе. В то же время для некоторых факторов соответствующие значения существенно различаются от группы к группе.Среди этих факторов можно выделить теплоту (A), рассуждения (B), эмоциональную стабильность (C) и доминирование (E). Чтобы количественно оценить различия между группами по каждому из анализируемых личностных факторов, мы применили непараметрический H-критерий Краскела-Уоллиса для нескольких независимых выборок. Значения p , рассчитанные для каждой из 16 личностных шкал, показаны на рис. 6 (b). Можно видеть, что для 4 факторов (A, B, C, E) p -значение относительно мало ( p ≤ 0,05), в то время как для других факторов p -значение значительно больше.Исходя из этого, мы рассмотрели эти 4 фактора более подробно и сравнили, насколько они различаются внутри групп. Мы применили непараметрический U-критерий Манна – Уитни, чтобы статистически проанализировать разницу между факторами в каждой паре групп. В результате мы обнаружили, что группа 1 и группа 2 не демонстрируют значительного изменения факторов A ( p = 0,218) и C ( p = 0,39). В то же время эти группы достоверно различаются по факторам B и E ( p <0.01). С другой стороны, различия между группами 1–3 и 2–3 значимы для всех рассмотренных факторов (Рис. 6 (c) –6 (f)).
Рис. 6. Опросник по шестнадцати личностным факторам.
(a) Основные факторы анкеты 16PF, усредненные по предметам в каждой группе (группа I — пунктирная линия, группа II — сплошная линия, группа III — пунктирная линия). Пунктирной областью выделены факторы, по которым наблюдаются значительные изменения между группами. (b) p -значения, рассчитанные для этих групп для различных факторов анкеты 16PF с помощью H-критерия Краскела – Уоллиса для нескольких независимых выборок.На вставке подробно показаны низкие значения p , рассчитанные для коэффициентов A, B, C, E. (c-e) Значения A, B, C, E рассчитаны для трех групп (данные показаны как среднее ± стандартное отклонение). Группы I и III содержат n = 8 субъектов, а группа II n = 6 субъектов, * p > 0,05, ** p > 0,01 по непараментрическому U-критерию Манна-Уитни.
https://doi.org/10.1371/journal.pone.0197642.g006
На диаграмме на рис. 6 (а) показаны результаты теста «16 факторов личности» Кеттелла для трех групп.Данные отображаются в виде значений всех основных факторов анкеты 16PF, усредненных по всем предметам в каждой группе. Видно, что большинство факторов имеют схожие значения в каждой группе. В то же время для некоторых факторов соответствующие значения существенно различаются от группы к группе. Среди этих факторов можно выделить теплоту (A), рассуждения (B), эмоциональную стабильность (C) и доминирование (E), которые представлены в таблице и сравниваются с результатами исследования ЭЭГ и психодиагностического теста на рис. (б).
По результатам классификации личности на основе психодиагностического теста различные особенности структуры ЭЭГ, а именно латерализация и соотношение энергии высокочастотных и низкочастотных волн, отражают разные личностные качества. Важно отметить, что, хотя активность ЭЭГ варьировалась в разных группах, внутри каждой группы она представляла один и тот же сценарий. Подобное поведение наблюдалось в психологической классификации, где были выделены три группы субъектов со схожими личными профилями.
Обычно в большинстве научных публикаций, направленных на выявление ЭЭГ-сигнатур когнитивной деятельности, описывается сценарий, повторяющийся от одного испытуемого к другому. В то же время мы показываем, что различия, возникающие от одного предмета к другому, также могут быть систематизированы. Среди испытуемых можно выделить разные сценарии познавательной деятельности в зависимости от личности.
Наши результаты подтверждают гипотезу, выдвинутую Вингиано и Уильямом [66] о существовании связи между полушарием мозга и личностью.Наши результаты также согласуются с работой [67], где было показано, что связанные с тревожностью свойства личности, оцененные по методике Кэттела, коррелируют со спектральной плотностью мощности (СПМ) ритмов ЭЭГ, в частности, бета – 1 и бета – 2. Авторы утверждали, что интенсивный ритм бета-ЭЭГ коррелирует с высокой ситуативной и индивидуальной тревогой. В то же время было обнаружено, что эмоциональная устойчивость человека связана с силой альфа-ритма.
Таким образом, полученные результаты дают новые знания в понимании особенностей личности человека путем анализа взаимосвязи пространственно-временной и частотно-временной структуры ЭЭГ.
Следует отметить, что в целом, чтобы делать точные прогнозы относительно личности, требуется гораздо больший размер выборки. При этом в нашем исследовании мы постарались создать максимально однородную группу добровольцев, чтобы исключить неизбежное влияние дополнительных, плохо учтенных факторов на результаты наших оценок. Планируется дальнейшее расширение группы испытуемых на произвольно выбранных лиц (с разным физическим состоянием, полом, уровнем образования и т. Д.).Это должно быть достигнуто, во-первых, за счет увеличения числа испытуемых, а, во-вторых, за счет добавления различных техник психологического тестирования и личных психологических интервью каждого испытуемого, проводимых психологом.
Ab initio расчеты термодинамических параметров оксидов лития, натрия и калия под давлением
Google ученый
R. H. Lamoreaux, D. L. Hildenbrand, J. Phys. Chem. Ref. Данные 13 , 151 (1984).
ADS Статья Google ученый
П. Гоэль, Н. Чоудхури, С. Л. Чапло, Phys. Ред. B: Конденс. Дело 70 (17), 174307 (2004).
ADS Статья Google ученый
Т. Курасава, Т. Такахаши, К. Нода, Х. Такешита, С. Насу и Х.Watanabe, J. Nucl. Матер. 107 , 334 (1982).
ADS Статья Google ученый
S. Hull, T. W. D. Farley, W. Hayes, M. T. Hutchings, J. Nucl. Матер. 160, , 125 (1988).
ADS Статья Google ученый
X.-F. Ли, X.-R. Чен, Ч.-М. Мэн, Г.-Ф. Цзи, Solid State Commun. 139 , 197 (2006).
ADS Статья Google ученый
R. Weiyi, W. Feng, Z. Zhou, X. Pingchuan, S. Weiguo, J. Nucl. Матер. 404 (2), 116 (2010).
Артикул Google ученый
В. Н. Жарков, В. А. Калинин, Уравнения состояния твердых тел при высоких давлениях и температурах, (Наука, М., 1968; Консультативное бюро, Нью-Йорк, 1971).
Google ученый
Ф. Берч, Дж.Geophys. Res. 57 , 227 (1952).
ADS Статья Google ученый
K. Kunc, I. Loa, K. Syassen, Phys. Ред. B: Конденс. Дело 68, , 094107 (2003).
ADS Статья Google ученый
П. Винет, Дж. Х. Роуз, Дж. Ферранте и Дж. Р. Смит, J. Phys .: Condens. Дело 1 , 1941 (1989)
ADS Статья Google ученый
W. B. Holzapfel, Rep. Prog. Phys. 59 , 29 (1996).
ADS Статья Google ученый
С. С. Кушва, Дж. Шанкер, Physica B (Амстердам) 253 , 90 (1998).
ADS Google ученый
R. E. Cohen, O. Gülseren, R. J. Hemley, Am. Минеральная. 85 , 338 (2000).
Google ученый
А. Б. Алчагиров, Дж. П. Пердью, Дж. К. Боттгер, Дж. К. Альберс, Р. К. Фиолхайс, Phys. Ред. B: Конденс. Дело 63 , 224115 (2001).
ADS Статья Google ученый
A. K. Pandey, Pharma Chem. 1 , 78 (2009).
Google ученый
Ландау Л.Д., Станюкович К.П. // Докл. Акад. АН СССР 46, , 399 (1945).
Google ученый
И. К. Слейтер, Введение в химическую физику (McGraw-Hill, Нью-Йорк, 1935).
Google ученый
Дж. С. Дагдейл, Д. К. Макдональд, Phys. Ред. 89 (4), 832 (1953).
ADS Статья Google ученый
В. Н. Зубарев, В.Я. Ващенко, Сов. Phys. Твердотельный 5 (3), 653 (1963).
Google ученый
Z. Wu, E. Zhao, H. Xiang, X. Hao, X. Liu, J. Meng, Phys. Ред. B: Конденс. Дело 76 , 054115 (2007).
ADS Статья Google ученый
Беломестных В. Н., ЖТФ. Phys. Lett. 30 (2), 91 (2004).
ADS Статья Google ученый
Панков В.Л., Науки Земли 1 (1), 11 (1998).
Google ученый
Фортов В. Е., Ломоносов И. В., Физика открытой плазмы. J. 3 , 122 (2010).
Google ученый
Оганов А.Р., Бродхольт Дж., Прайс Г. Д., Phys. Планета Земля. Интер. 122 , 277 (2000).
ADS Статья Google ученый
Д. Чен, К.-М. Сяо, Ю.-Л. Чжао, Б.-К. Сюн, Б.-Х. Ю., Д.-Х. Ши, Чин. Phys. Lett. 25 , 4352 (2008).
ADS Статья Google ученый
Х. Фу, В. Лю и Т. Гао, Can. J. Phys. 87 , 169 (2009).
ADS Статья Google ученый
М. А. Бланко, А. М. Пендас, Э. Франциско, Дж. М. Ресио и Р. Франко, J.Мол. Структура: ТЕОХИМА 368 , 245 (1996).
Артикул Google ученый
С.-Н. Луо и Т. Дж. Аренс, J. Geophys. Res. 108 , 2421 (2003).
ADS Статья Google ученый
В.Ю. Бодряков В.А., Повзнер А.А., Зелюкова О.Г. // УФН. Твердотельный 40 (9), 1433 (1998).
ADS Статья Google ученый
А. М. Молодец, Горючая, Explos. Ударные волны 31 (5), 620 (1995).
Артикул Google ученый
Л. Бураковский, Д. Л. Престон, Ю. Ван, Solid State Commun. 132 , 151 (2004).
ADS Статья Google ученый
Д. Т. Морелли и Дж. П. Хереманс, Appl. Phys. Lett. 81 , 5126 (2002).
ADS Статья Google ученый
Н. Кокер, Планета Земля. Sci. Lett. 292 , 392 (2010).
ADS Статья Google ученый
R. Dovesi, VR Saunders, C. Roetti, R. Orlando, CM Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, and NM Harrison, CRYSTAL09: A Computational Tool for Solid Государственная химия и физика. Руководство пользователя (Туринский университет, Турин, Италия, 2009 г.).
Google ученый
J. P. Perdew, Y. Wang, Phys. Ред. B: Конденс. Дело 45, , 13244 (1992).
ADS Статья Google ученый
www.crystal.initio.it/Basic-Set/ptable.html.
C. G. Broyden, J. Appl. Математика. 6, , 222 (1970).
MathSciNet МАТЕМАТИКА Google ученый
Р. Вайкофф, Кристаллическая структура (Интерсайенс, Нью-Йорк, 1963).
Google ученый
A. Lazicki, C.-S. Yoo, W. J. Evans, W. E. Pickett, Phys. Ред. B: Конденс. Дело 73 , 184120 (2006).
ADS Статья Google ученый
Y. Duan, D. C. Soerescu, Phys. Ред. B: Конденс. Дело 79 , 014301 (2009).
ADS Статья Google ученый
Ž. Чанчаревич, Й. К. Шен, М. Янсен, Phys. Ред. B: Конденс. Дело 73 (22), 224114 (2006).
ADS Статья Google ученый
М. Моакафи, Р. Хената и А. Бухемаду, Eur. Phys. J. B 64 , 35 (2008).
ADS Статья Google ученый
X.-F. Li, X. Chen, G. Ji, and C. Meng, Chin. Phys. Lett. 23 , 925 (2006).
ADS Статья Google ученый
M. M. Elcombe, W. Pryor, J. Phys. C: Физика твердого тела. 3 , 492 (1970).
ADS Статья Google ученый
T. Tanifugi, K. Shiozawa, S. Nasu, J. Nucl. Матер. 78, , 422 (1978).
ADS Статья Google ученый
M. F. Sarry, Tech. Phys. 43 (10), 1137 (1998).
Артикул Google ученый
М. Кумар и М. Кумар, Indian J. Pure Appl. Phys. 45 , 256 (2007).
Google ученый
Z.-Y. Цзэн, К.-Э. Ху, X.-R. Чен, X.-L. Чжан, Л.-К. Цай и Ф.-К. Цзин, Phys. Chem. Chem. Phys. 13 , 1669 (2011).
Артикул Google ученый
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности.Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Перейти к основному содержанию Поиск
Поиск
- Где угодно
Поиск Поиск
Расширенный поиск- Войти | регистр
- Подписка / продление
- Учреждения
- Индивидуальные подписки
- Индивидуальные продления
- Библиотекари
- Чикагский пакет
- Полный охват и охват содержимого
- Файлы KBART и RSS-каналы
- Разрешения и перепечатки
- Инициатива развивающихся стран Чикаго
- Даты отправки и претензии
- Часто задаваемые вопросы библиотекарей
- заказы, тарифы
- и платежи
- О нас
- Публикуйте у нас
- Недавно приобретенные журналы
- tners
- Подпишитесь на уведомления eTOC
- Пресс-релизы
- СМИ
- Книги издательства Чикагского университета
- Распределительный центр в Чикаго
- Чикагский университет
- Положения и условия
- Заявление об издательской этике
- Уведомление о конфиденциальности
- Доступность Chicago Journals
- Доступность университета
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
- Свяжитесь с нами
- Медиа и рекламные запросы
- Открытый доступ в Чикаго
- Следуйте за нами на facebook
- Следуйте за нами в Twitter
Решения в закрытом виде для осцилляторов с неупругими ударами
Journal of Sound and Vibration 359 (2015) 154–167Списки содержания доступны на ScienceDirect
Домашняя страница журнала Journal of Sound and Vibration: www.elsevier.com/locate/jsvi
Решения в замкнутой форме для осцилляторов с неупругими ударами В.Н. Пилипчук п. Машиностроение, Государственный университет Уэйна, 5050 Anthony Wayne Dr. Редактор: LN Virgin Доступно онлайн 26 сентября 2015 г.
Рассматривается класс колебательных систем с идеально жесткими ограничителями амплитуды посредством негладких временных замен.Движение представлено как комбинация колеблющейся составляющей, которая возникает из-за циклических столкновений с ограничителями, и медленного затухания, вызванного постепенной потерей энергии во время столкновений. Используется конкретная модификация двух переменных разложений, где негладкий (треугольная волна) временной аргумент рассматривается как быстрое время, в то время как спад энергии описывается в медленной шкале времени. В результате получаются аналитические решения в замкнутой форме, автоматически удовлетворяющие условиям столкновения с потерей энергии.Рассмотрены три качественно различных основных типа колебаний: периодические, частотно-модулированные и амплитудно-частотно-модулированные движения. & 2015 Elsevier Ltd. Все права защищены.
1. Введение Структурные колебания со столкновениями между различными частями колебательной системы представляют значительный теоретический и практический интерес. Сопровождаемая дребезжащим шумом такая динамика может указывать на нежелательные структурные изменения в механических системах, такие как ослабление соединений и / или образование зазоров.В качестве альтернативы динамика виброударов рассматривается как полезное явление для поглощения или сбора энергии. Однако доступные инструменты соответствующего анализа ограничены сильно нелинейным характером динамики виброударов. Это связано с тем, что традиционные методы асимптотического интегрирования требуют дифференцируемости характеристик осциллятора [27]. Для преодоления математических препятствий были разработаны различные подходы [1–5,7–10,15–20,24–26,28–31,35–41,43,45,47].С физической точки зрения, большинство предложенных теорий предполагают идеальную пространственно-временную локализацию событий столкновения. Согласно такому предположению, внезапные скачки восстанавливающих силовых характеристик представляются абсолютно жесткими связями, предположительно движение между ограничениями легко описывается. В результате динамика системы дискретизируется с точки зрения отображений и сопоставления различных частей решений. Поскольку время столкновения априори неизвестно, численные алгоритмы требуют согласования на основе событий.Если части решений между ограничениями доступны в аналитической форме, то время столкновения все же должно быть определено из типично нелинейных алгебраических задач. Другая группа методов следует идее предварительных преобразований координат, эффективно устраняя жесткие ограничения (барьеры) от ударных систем. С геометрической точки зрения такие преобразования напоминают преобразования развертывания пространства, предложенные Шварцем для выпрямления биллиардных траекторий [13]. В [46,47] показано, что соответствующие аналитические манипуляции приводят дифференциальные уравнения движения к такой форме, которая оправдывает использование различных процедур усреднения без необходимости отслеживания событий столкновения.Это связано с тем, что условия ограничения выполняются автоматически с помощью определенных негладких функций, участвующих в
n
Тел .: þ1 313 608 1245. Адрес электронной почты: [электронная почта защищена]
http: / /dx.doi.org/10.1016/j.jsv.2015.08.023 0022-460X / & 2015 Elsevier Ltd. Все права защищены.
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
155
трансформации. Обратите внимание, что, поскольку соответствующие аналитические манипуляции по существу нелинейны (нелокальны), более высокий класс гладкости обычно достигается за счет более сильной нелинейности получаемых дифференциальных уравнений движения.Далее идея негладкого преобразования координат была распространена на пространство состояний за счет рассмотрения ударных осцилляторов с односторонними барьерами [21]. Эта версия по-прежнему разворачивает конфигурационное пространство, однако скорость также участвует в преобразовании. Такое обобщение учитывает потери энергии каждый раз, когда система взаимодействует с барьером. Как было отмечено в [42], этот элегантный подход не получил большой популярности в инженерных приложениях. Возможно, это связано с некоторой технической сложностью соответствующих выводов и полученных уравнений.В частности, воспроизведение преобразования предполагает определенные знания о нелинейных манипуляциях с особенностями, которые выходят за рамки стандартных алгебраических правил [11,12]. Однако, если коэффициент восстановления близок к единице, консервативный вариант [46,47] также может применяться асимптотически, как описано в [42]. Важно, что методологии, предложенные в [46,21], генерируют дифференциальные уравнения движения на всем временном интервале, автоматически включающие в себя события столкновений из-за проектирования преобразований.В результате решения могут быть получены в замкнутой (а не кусочно) форме. Тем не менее, соответствующие процедуры асимптотического интегрирования могут столкнуться со значительными техническими проблемами из-за существенно нелинейного характера преобразованных систем. К сожалению, результирующие уравнения выглядят сильно нелинейными даже в тех случаях, когда исходная модель между ограничениями является линейной. В настоящей работе рассматривается класс задач виброударов с помощью негладких временных замен [32,33].Несмотря на наличие подобных типов негладких функций, этот подход отличается от негладких преобразований координат своим физическим содержанием и математической формализацией. В частности, если исходная модель линейна между барьерами, то результирующие уравнения остаются линейными. Это происходит потому, что негладкие временные замены эффективно устраняют препятствия, меняя направление стрелки времени, тогда как системные координаты трансформируются линейным образом; см. раздел 2 для получения более подробной информации.Отметим, что первоначальная формулировка этого подхода была разработана для класса сильно нелинейных, но все же гладких колебательных систем, а затем применена к виброударным системам, однако, в условиях столкновения без потерь энергии [34]. Более того, на первый взгляд, описание потерь энергии удара в рамках такого подхода невозможно, так как соответствующая подстановка времени не влияет на стрелку времени. Тем не менее, в этой работе показано, что «гиперболическая комплексификация» переменных состояния обеспечивает адекватный способ описания эффекта потери энергии через конкретные граничные условия, налагаемые на новый временной аргумент.Затем разрабатываются аналитические алгоритмы решения краевых задач. В дополнение к удобству расчетов без учета переменных во время столкновений, предлагаемый тип решений в замкнутой форме может быть разумным выбором для описания нестационарной динамики так называемых стоков энергии виброударов [14,44]. Хотя широко известно, что виброгасители вибрации допускают интерпретацию с помощью различных методологий [3,47], нестационарные динамические компоненты обычно усложняют соответствующий анализ.Эта статья организована следующим образом. В первой части раздела 2 приведены необходимые подробности идеи негладких преобразований времени. Затем формулируются граничные условия для области новой временной переменной, описывающие эффект потери энергии во время столкновения. Наконец, в разделе 3 описаны соответствующие аналитические алгоритмы с иллюстрациями на различных примерах периодических, частотно-модулированных и амплитудно-частотно-модулированных колебаний. Примеры служат для проверки алгоритмов.Предполагается, что приложения к более сложным моделям могут вызвать некоторые технические, а не методологические сложности. 2. Генерация модели и базисных функций 2.1. Основные тождества негладкого преобразования времени Чтобы дать некоторое представление о технических особенностях негладких временных замен, рассмотрим случай периодических движений, когда новая временная переменная задается волновой функцией треугольника (t для 1 rt r1 8t τðt Þ ¼; τ ðt Þ ¼ τ ð4 þ t Þ (1) t þ 2 для 1 rt r 3 Функция (1) описывает положение борта, колеблющегося между двумя идеально жесткими параллельными барьерами с отражениями от барьеров в идеалистическом случае без потерь энергии, как показано на рис.1. Расстояние между преградами и скорость равны 2Δ ¼ 2 и v ¼1 соответственно. Как показано на рис. 2, τðtÞ представляет собой треугольную волну, амплитуда которой равна единице, а период равен T ¼4,
Рис. 1. Базовый ударный осциллятор.
156
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
Рис. 2. Базовые функции, генерируемые ударным осциллятором, когда Δ ¼ 1 и v¼ 1.
, тогда как скорость осциллятора τ_ ðtÞ ¼ eðtÞ представляет собой прямоугольную волну. со ступенчатыми разрывами.Следует подчеркнуть, что такую пару функций не следует рассматривать как формальную геометрическую композицию различных прямых линий. Как только что было показано, волны треугольника и прямоугольника генерируются довольно простой физической моделью. С математической точки зрения обе такие негладкие волны относятся к классу элементарных функций, которые также можно описать в замкнутой форме: 2 πt τðt Þ ¼ arcsin sin 2 π
(2)
и
eðt Þ ¼ cos
π t 1 cos ¼ sign cos π t = 2 2 2
π t
(3)
Обратите внимание, что, в отличие от обычных тригонометрических функций синуса и косинуса, волны треугольника и прямоугольника могут быть представлены в несколько способов с разными амплитудами, периодами и фазами.В нашем случае важно, чтобы волны треугольника и прямоугольника имели ту же временную симметрию и нормализацию амплитуды, что и обычные синус и косинус. Однако период нормирован на T¼4, а не на 2π, по причине, которая объясняется ниже в настоящем разделе. По сравнению с синусом и косинусом, волны треугольника и прямоугольника вычислить проще и быстрее, поскольку не требуются таблицы или разложения в степенной ряд. Хотя наиболее важным для настоящей работы является то, что такие функции естественным образом улавливают особенности воздействия, которые потребовали бы очень длинных тригонометрических рядов для более или менее адекватного описания.Напомним, что в различных квазигармонических аналитических процедурах каждый новый член такого ряда требует нового шага аналитической итерации. Функции (2) и (3) удобны для вычислений на компьютере, так как не требуется кондиционирования. Более того, все, что используется при выводе, легко следует из диаграмм на рис.2, а именно линейная независимость элементов 1, e _ и следующих свойств и e,
τ_ ¼ e e_ ¼ 2
1 X
δðt þ 1 4kÞ δðt 1 4kÞ
k ¼ 1
e2 ¼ 1
(4)
Строго говоря, равенства (4) следует интерпретировать в терминах распределений из-за наличия особенностей, возникающих всякий раз, когда τ ¼ 7 1 .Однако методология разработана таким образом, что явного наличия типичных интегральных тождеств теории распределений не требуется. Как обсуждалось в ссылке [33], уравнение. (4) представляет собой полный набор правил для проведения необходимых аналитических манипуляций разработанной методологии. Соответствующий формализм, обобщенный в настоящей работе, реализует временную замену t-τðtÞ на основе следующего утверждения [32,33]: любой периодический процесс xðt Þ периода, нормированного на T¼4, может быть выражен через динамическое состояние удара осциллятор, fτðtÞ; eðtÞg, в виде «гиперболической» комплексной комбинации x ¼ X ðτÞ þ Y ðτÞe;
e2 ¼ 1
(5)
где обе компоненты X и Y могут быть определены через исходную функцию x (t), если она известна как X ðτÞ ¼ 12 ½xðτÞ þ xð2 τÞ Y ðτÞ ¼ 12 ½xðτÞ xð2 τÞ
(6)
Обратите внимание, что оба члена в правой части уравнения.(5) важны, поскольку ответственные за компоненты с различной временной симметрией, как показано тождеством xðt Þ ¼ A sin
πt 2
þB cos
, где τ ¼ τðt Þ, e ¼ eðt Þ, а A и B — произвольные константы.
πt 2
¼ A sin
πτ 2
þ B cos
πτ 2
e
(7)
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
157
Комбинация (5) удобна для различных аналитических манипуляций.Например, свойство так называемой «функциональной линейности» сохраняется для любой функции f: f ðX þ YeÞ ¼ RðX; YÞ þ IðX; YÞe
(8)
где RðX; Y Þ ¼ 12 f ðX þ Y Þ þ f ðX Y Þ I ðX; Y Þ ¼ 12 f ðX þ Y Þ f ðX Y Þ
Это видно из уравнения. (8) что применение функции f не влияет на алгебраическую структуру с базисом f1; например. Следующий частный случай уравнения. (8) напоминает хорошо известную формулу Эйлера (эллиптического) комплексного анализа: expðX þYeÞ ¼ expðX Þ chðYÞ þ sinhðYÞe (9), где наличие гиперболических функций объясняет термин «гиперболический», который используется в настоящем тексте.Обратите внимание, что структура гиперболических чисел, которая часто рассматривается как простой частный случай алгебр Клиффорда, была известна без отношения ни к колеблющимся системам, ни к негладким функциям в течение довольно долгого времени, в основном как формальное расширение регулярных комплексных чисел. [23]. Типичное формальное определение гиперболических чисел просто предполагает существование унипотентного u такого, что u a þ 1 и u a 1, но u2 ¼ 1. Затем, рассматривая элементы f1; ug в качестве базиса любое гиперболическое число w A H представляется в виде w ¼ x þ yu, где x и y — действительные величины.Хотя такого определения достаточно для установления соответствующих алгебраических и геометрических соотношений, любая физическая или даже ясная математическая природа унипотентного u остается неопределенной. Это может объяснить, почему гиперболические комплексные числа значительно менее популярны по сравнению с обычными эллиптическими комплексными числами. Однако в данном случае унипотентность (мнимая единица) e приобретает определенный физический смысл благодаря формуле. (5), которая обнаруживает прямую логическую связь между периодическими процессами и гиперболическими алгебрами.А именно, зависящая от времени величина e ¼ eðtÞ — это скорость ударного осциллятора (рис. 1), абсолютное значение которой сохраняется, e2 ¼ 1, но направление меняется так, что ни e ¼1, ни e ¼ 1 не сохраняется в течение всего цикла. Кроме того, наличие временного аргумента t дает возможность вводить дифференциальные и интегральные операции и, следовательно, рассматривать динамические системы в рамках набора гиперболических чисел. По этой причине, давайте рассмотрим непрерывный T-периодический процесс, период которого нормирован на T 4 относительно фазы φ ¼ φðtÞ, такой что уравнение.(5) принимает вид xðtÞ ¼ XðτðφÞÞ þ YðτðφÞÞeðφÞ
(10)
Уравнение (10) оказывается удобным для подстановок в дифференциальные уравнения, поскольку дифференцирование также сохраняет гиперболическую структуру элементов. А именно, взяв производную по времени от уравнения. (10) дает x_ ¼ Y 0 ðτÞ þ X 0 ðτÞe ω (11) _ ðtÞ, в то время как член YðτðφÞÞe0 ðφÞω имеет, где штрихи указывают дифференцирование по аргументу τ, а ωðtÞ ¼ φ исключен из уравнения. (11) путем наложения граничных условий
τ ¼ 7 1:
Y ¼0
(12)
Уравнение (12) является необходимым условием непрерывности координаты x (t), что оправдано тем, что особые точки (обобщенной) производной e0 ðφÞ совпадают с точками амплитуды треугольной волны fφ: τðφÞ ¼ 71g.Следовательно, при _ условии (12) и периодический процесс x (t), и его темпоральная скорость xðtÞ обладают одинаковой (гиперболической) алгебраической структурой с базисом f1; например. Теперь производные высокого порядка можно вычислить последовательно аналогичным образом, например, _ þ Y ″ τÞω2 þ X 0 ðτÞω _ e þ X 0 ðτÞe0 ω2 x € ¼ X ″ ðτÞω2 þY 0 ðτÞω (13) _ Если скорость xðtÞ непрерывна, то сингулярный член X 0 ðτÞe0 ω2 должен быть исключен из (13) путем наложения граничного условия: X 0 ¼ 0 при τ ¼ 7 1. Однако в настоящей работе рассматривается класс задач со ударами, такие как что скорость меняет не только свое направление, но и величину всякий раз, когда τðφÞ ¼ 71.Следовательно, условие непрерывности для скорости должно быть заменено соответствующим условием разрыва, описывающим эффект потери энергии во время столкновения и сохраняющим сингулярный член в уравнении. (13). Однако математическая структура такого условия не сразу ясна, поскольку аргумент τ симметричен во времени относительно точек его амплитуды τ ¼ 71, связанных со столкновениями (рис. 2), тогда как скорость должна изменять свое абсолютное значение при прохождении через такие точки. Условие столкновения с потерей энергии выводится в следующем разделе.В качестве отправной точки разработанной техники уравнение. (10) используется в качестве подстановки в дифференциальных уравнениях движения в предположении, что неизвестная функция x (t) описывает колебательный процесс с амплитудной и / или частотной модуляцией. Обратите внимание, что, несмотря на специфический негладкий базис {τ, e}, никаких ограничений на временные формы несущей волны не накладывается, поскольку основное тождество (5) выполняется для любого периодического процесса x (t) независимо от его класса гладкости .
158
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
2.2. Моделирование потерь энергии при идеально жестких барьерах. Настоящее моделирование основано на предположении, что как движущийся борт, так и барьеры (стены) являются идеально жесткими; см. рис. 1. Другими словами, (упругопластические) деформации столкновения считаются незначительными по сравнению со смещениями твердого тела, в то время как каждое событие столкновения происходит мгновенно. Тем не менее, даже при таких предположениях термины упругие и неупругие (пластические) столкновения обычно используются в литературе для характеристики обратимой и необратимой частей кинетической энергии соответственно.Феноменологически одномерное столкновение движущейся частицы с жесткой преградой описывается как разрыв скорости _ i þ 0Þ ¼ kxðt _ i 0Þ xðt 0 rk r1
(14)
где ti — время столкновения (удара), k — так называемый коэффициент восстановления, который далее представлен в виде k ¼ 1ε
(15)
Согласно формуле. (15), ε ¼ 0 означает совершенно «упругое» столкновение без потерь энергии, тогда как ε 1 является совершенно «пластичным» пределом, когда вся кинетическая энергия мгновенно рассеивается во время столкновения.В настоящей работе потери энергии из-за столкновений считаются небольшими, так что 0 o εÀ1
(16)
Обратите внимание, что уравнение. (14) фиксирует стрелку времени динамики, нарушая симметрию t⟶ t аналогично вязкому члену 2ζω0 x_ линейного осциллятора x ˆ þ2ζω0 x_ þ ω20 x ¼ 0. На первый взгляд такая временная асимметрия создает препятствие для описания динамика виброударов в терминах нового временного аргумента τ, который рассматривается как колеблющееся время, периодически меняющее свое направление обратимым образом.Другими словами, имея дело с временным аргументом τ, трудно указать подобласти до и после. Тем не менее, давайте покажем, что уравнение. (10) по-прежнему соответствует модели «неупругого» столкновения (14) в определенных граничных условиях на концах интервала 1 r τ r 1. По этой причине обратите внимание, что согласно фиг. 1 и 2, столкновения происходят всякий раз, когда τ ¼ 71. Если, например, время столкновения ti соответствует некоторой точке амплитуды, в которой τ ¼ 1, то при прохождении через ti функция e переключает свое значение с e ¼ 1 на e ¼ þ 1; см. схемы на рис.2. Таким образом, подставляя уравнение. (11) в уравнение. (14) с учетом уравнения. (15) и отбрасывая общий множитель ω, получаем τ ¼ 1: Y 0 þ X 0 ¼ ð1 εÞ Y 0 X 0 (17) Однако функция e меняет свое значение с e ¼ þ 1 на e ¼ 1 при прохождении через точки амплитуды, в которых
τ ¼ þ 1. Следовательно, в таких случаях
τ ¼ þ 1:
Y 0 X 0 ¼ ð1 εÞ Y 0 þ X 0
(18)
Граничные условия ( 17) и (18) представляют собой аналог модели столкновения (14), полученный путем замены временного аргумента t⟶τ.В следующем разделе показано, что уравнения. (17) и (18) адекватно описывают динамику виброударов с потерями энергии из-за столкновений с преградами. 3. Примеры и решения В этом разделе рассматриваются три различных примера, охватывающих качественно разные типы ударных движений. Это периодические, частотно-модулированные и амплитудно-частотно-модулированные колебания. В результате подстановки (10) первая задача допускает точное решение в замкнутой форме, иллюстрирующее некоторые особенности аналитических манипуляций с временным аргументом τ треугольной волны.3.1. Периодическое ступенчатое нагружение Периодические колебания виброударного генератора (рис. 1) при периодическом скачкообразном нагружении описываются уравнением x ˆ ¼ αeðφÞ;
jxj r Δ
(19)
где α — амплитуда нагрузки, φ ¼ ωt — фаза, а условия ударного взаимодействия с барьерами x ¼ 7 Δ задаются уравнением. (14). Покажем, что проблема, заданная уравнениями. Уравнение (14) и (19) допускает точное решение в замкнутой форме после перехода t⟶τ. Этот простой случай призван проиллюстрировать роль граничных условий (17) и (18) в моделировании потерь энергии.Во-первых, давайте заменим уравнение. (19) с помощью эффективной модели без ограничений: x ˆ ¼ αeðφÞ þpe0 ðφÞ
(20)
В уравнении. В (20) реакция ограничений представлена слагаемым pe ðφÞ, который представляет собой периодическую серию δ-импульсов амплитудой 2p = ω с еще неизвестным параметром p; см. (4). Обратите внимание, что исходная модель, описанная уравнениями. (19) и эффективная модель (20) не полностью эквивалентны. А именно, некоторые решения уравнения. (20) может нарушить условие jxj r Δ, поскольку эффективная система может проникать через барьеры, тогда как исходная модель не может [34].Однако это не относится к решениям, полученным в настоящей работе, в связи с условиями, принятыми ниже; см. уравнение. (26). 0
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
159
_ ¼ 0, и подставив уравнение. (13) в уравнение. Теперь поищем решение в виде (11) при (12). Принимая во внимание, что ω (20) дает X ″ ω2 þ ðY ″ ω2 αÞe þðX 0 ω2 pÞe0 ¼ 0
(21)
Задавая отдельно обе компоненты «гиперболического числа» в уравнении.(21) к нулю и исключение сингулярного члена дает уравнения и граничное условие для определения p, соответственно, как
ω2 X ″ ¼ 0 ω2 Y ″ ¼ α
(22)
и
τ ¼ 71:
ω2 X 0 ¼ p
(23)
при граничных условиях (12), (17) и (18). Кроме того, предположим, что ограничения x ¼ 7 Δ достигаются в точках амплитуды τ ¼ 7 1. Тогда уравнения. (10) и (12) дают
τ ¼ 7 1:
X ¼ 7Δ
(24)
Несмотря на сильную нелинейность исходной модели, краевая задача (12), (17), ( 18), (22) и (23) линейны и легко решаются, поскольку общее решение уравнения(22) имеет вид X ¼ Aτ þ B Y ¼ Cτ þ D þ
ατ2 2ω2
(25)
где A, B, C и D — произвольные постоянные. Подставляя уравнение. (25) в уравнения. (12), (17), (18) и (24) определяют все произвольные постоянные и конкретное условие, при котором периодическое решение действительно существует. Наконец, такое условие и соответствующее решение принимают вид соответственно r ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi ð2 εÞα ω¼ (26)
εΔ
и εð1 τ2 Þ e xðt Þ ¼ X þ Ye ¼ Δ τ 2ð2 εÞ, где τ ¼ τðωtÞ и e ¼ eðωtÞ даются уравнениями.(2) и (3). Условия (23) и (26) определяют еще неизвестный параметр
2 1 α p ¼ ω2 Δ ¼
ε
(27)
(28)
Временные формы координаты и скорости показаны на рис. 3а и б соответственно. Удобство точного решения (27) связано с его замкнутой формой, что позволяет легко использовать его в различных аналитических процедурах, включая анализ возмущений. Также компьютерные расчеты замкнутых растворов не требуют типового кондиционирования, которое необходимо в случае кусочно-раздельных решений.Кроме того, как упоминалось в разделе 2.1, форма решения (27) представляет собой определенный алгебраический элемент (10), который удобен для различных алгебраических, дифференциальных и интегральных операций. 3.2. Свободные колебания с потерями энергии при ударе. Рассмотрим модель свободного виброудара, представленную двумя различными механически эквивалентными конструкциями на рис. 4 (а) и (б). Дифференциальное уравнение движения с условием связи: 2 x ˆ Ω x ¼ 0;
jxj r Δ
(29)
с условиями потери энергии удара (14), имеющими место всякий раз, когда x ¼ 7 Δ.Соответствующая эффективная модель определяется выражением 2 x ˆ þ Ω x ¼ pe0 ðφÞ
(30)
_ ðtÞ больше не фиксируется внешней нагрузкой. Приписываемая скорости шарика, в данном случае частота ω ¼ φ величина ω определяет временной масштаб колебательного процесса. Вообще говоря, в данном относительно простом случае, когда не действуют никакие внешние силы, частота ω может считаться постоянной между любыми двумя взаимодействиями с ограничениями, чтобы найти точное кусочное решение.Это можно сделать напрямую, без перехода к осциллирующему временному аргументу τ. Однако цель настоящего подхода состоит в том, чтобы получить решение в замкнутой форме, используя идею разделения движений. По этой причине предполагается, что функция ωðtÞ является непрерывно убывающей величиной в течение всего периода
160
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
1,0 0,5
x
0,0 0,5 1,0
0
1
2
3
4
5
4
4
6
т
v
1.5 1,0 0,5 0,0 0,5 1,0 1,5 0
1
2
3
6
т Рис. барьеры: (а) координата и (б) скорость; α ¼ 0: 5, Δ ¼ 1: 0, ε ¼ 0: 5 и ω ¼ 1: 2247.
Рис. 4. Две модели виброударов: (а) масс-пружинный осциллятор с идеально жесткими ограничителями амплитуды и (б) маятник в зазоре между двумя жесткими преградами; эти модели эквивалентны, если обе пружины являются линейно упругими и геометрическая нелинейность маятника не учитывается.
временной диапазон процесса. Скорость распада связана с потерей энергии из-за столкновений с барьерами и считается относительно низкой, налагая условие (16). Подставляя уравнения. (10) и (13) в уравнение. (30) приводит к уравнениям
ω2 X ″ þ Ω2 X þY 0 ω_ ¼ 0 ω2 Y ″ þ Ω2 Y þX 0 ω_ ¼ 0
(31)
при граничном условии (23). Обратите внимание, что набор граничных условий имеет тот же вид, что и для периодического случая, рассмотренного в предыдущем пункте.Воспроизведем полный список условий при τ ¼ 71: Y ¼0 Y 0 8 X 0 ¼ ð1 εÞ Y 0 7 X 0 X ¼ 7Δ
(32)
X 0 ω2 ¼ p
(33)
Уравнение (33) служит для определения неизвестного параметра p и приводит к требованию X 0 jτ ¼ 1 ¼ X 0 jτ ¼
1
(34)
Обратите внимание, что уравнение. (34) выполняется автоматически на каждом шаге процедуры интегрирования, если X является нечетным многочленом от τ.
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
161
Будем искать решение краевой задачи (31) и (32) в виде асимптотических разложений: XðτÞ ¼ X 0 ðτÞ þ X 1 τÞε þ X 2 ðτÞε2 þ O ε3 YðτÞ ¼ Y 0 ðτÞ þY 1 ðτÞε þ Y 2 ðτÞε2 þ O ε3
τ ¼ τðφÞ
(35)
φ_ ðtÞ ωη ε3
p ¼ p0 ðηÞ þp1 ðηÞε þ p2 ðηÞε2 þO ε3
(36) (37)
где η ¼ εt — медленный временной масштаб, определяемый скоростью потери энергии, определяемой уравнением.(16). Подставляя уравнения. (35) — (37) в уравнения. Согласование (31) — (33) коэффициентов при одинаковой степени ε дает ряд следующих краевых задач. В главном приближении ε0 краевая задача задается уравнениями X ″ 0 þ λ X 0 ¼ 0 2
Y ″ 0 þ λ Y 0 ¼ 0 2
(38)
при граничных условиях при τ 7 1: X 0 7 Δ;
X 00 ¼ p0
2
λ Ω
Y 00 ¼ 0
Y 0 ¼ 0;
(39)
, где введен следующий медленно меняющийся параметр «отношения частот»:
λη ¼
Ω ω0 ðηÞ
(40)
Напомним, что период треугольной волны нормирован на T 4.Следовательно, «реальное» отношение частот равно 2 = π Þλ, однако решения выглядят менее сложными при обозначении (40) из-за формы уравнения. (38). Физический смысл величины λ будет обсужден позже. На этом этапе решение первого порядка получается из уравнений. (38) и (39) как X0 ¼ Δ
sin λτ; sin λ
Y0 0
(41)
и p0 ¼
Ω2 Δ
λ tan λ
С учетом решения (41) дает дифференциальные уравнения первого приближения в виде
Δ sin λτ Ω sin λ dλ Δ cos λτ 2 Y ″ 1 þ λ Y 1 ¼ λ dη Ω sin λ
X ″ 1 þ λ X 1 ¼ 2ω1 λ 2
3
(42)
при граничных условиях при τ ¼ 7 1: Y1 ¼ 0 1 Y 01 ¼ 7 λΔ кроватка λ 2 X1 ¼ 0
2 λ 2Δ 2ω1 λ детская кроватка λ X 01 ¼ p1
Ω
Ω
(43)
где ω1 ðηÞ , λðηÞ и p1 ðηÞ — пока неизвестные функции.Решение краевой задачи (42) и (43) имеет вид X1 ¼ 0
(44)
и
Y1 ¼ при условии, что ω1 ðηÞ 0 и p1 ðηÞ 0.
Δ dλ cos λτ sin λτ τ 2Ω dη cos λ sin λ
(45)
162
ВН Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
Второе уравнение в Ур. (43) приводит к следующему дифференциальному уравнению первого порядка для отношения частот λðηÞ:
1 dλ Ω sin 2λ 1 þ cos 2λ 1 þ ¼ dη 2 2λ
(46)
Предполагая, что λðηÞ определяется из (46 ) и с учетом уравнения.(40) дают быструю фазу
φ¼Ω
Z
t 0
dt
(47)
λðεtÞ
Наконец, принимая во внимание уравнения. (35) и (10) дает решение первого порядка
sin λτ ε dλ cos λτ sin λτ e þO ε2 τ xðt Þ ¼ Δ sin λ 2Ω dη cos λ sin λ
(48)
где τ ¼ τðφÞ и e ¼ eðφÞ определяются уравнениями. (2) и (3) соответственно. Принимая во внимание уравнение. (11) дает соответствующую скорость
cos λτ ε dλ cos λτ sin λτ sin λτ vðt Þ ¼ ΩΔ e þ þ O ε2 τ sin λ 2Ω dη sin λ λ sin λ cos λ
(49)
Хотя дифференциальное уравнение (46) отделимо, соответствующую квадратуру вряд ли можно найти в классе элементарных функций.Однако его удобно решать численно из-за медленного временного масштаба η ¼ εt. Соответствующие результаты показаны на рис. 5, где параметры выбраны как Ω ¼ 1: 0, Δ ¼ 1: 0, ε ¼ 0: 2 и ω 0 ¼ ω0 ð0Þ ¼ 5: 0. Два меньших окна фрагмента (b) показывают увеличенные части первой и последней пяти единиц времени истории скорости. В начале процесса ограничители амплитуды диктуют качественные особенности временной формы моды, которая довольно близка к прямоугольной.Это происходит потому, что начальная кинетическая энергия, которая намного выше, чем у упругой пружины, может накапливаться из-за ограничений амплитуды. Однако из-за того, что некоторая энергия теряется при каждом цикле вибрации, реакция ограничений становится менее значительной, как видно из рис. 5d. В результате частота вибрации и временные формы становятся близкими к гармоническому осциллятору. Обратите внимание, что в рамках настоящего моделирования амплитуда вибрации не может измениться, даже если интенсивность ударного взаимодействия с ограничениями уменьшается со временем; см. рис.5 (а) и (г). Причина в том, что между ограничителями не предполагается потери энергии, и система должна в конечном итоге достичь некоторого «скользящего» режима с почти нулевыми импульсами удара, но с той же амплитудой [6]. Поддержим сделанные выше замечания, рассмотрев два различных асимптотических случая, соответствующих пределам высоких и низких энергий.
1,0
4
0,5 x
2 v
0,0 0,5 1,0
2 0
10
20 т
30
4
0
8
900020 т
30
40
20
30
40
I
6
0
4
2 4
40
10
4
2 1.0
0,5 0,0
x
0,5
1,0
0
0
10
t
Рис. 5. Динамика виброударного осциллятора с потерями энергии из-за столкновений с идеально жесткими преградами: (a) и (b) смещение и скорость в зависимости от времени соответственно, (c) диаграмма фазовой плоскости и (d) частотный параметр ω и «продолженная» амплитуда импульса I ¼ 2p = ω, показанные сплошными и пунктирными линиями соответственно.
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
163
Случай 1. Рассмотрим предел λ ¼ Ω = ω0 -0, соответствующий либо очень высокой начальной кинетической энергии, либо очень слабой пружине осциллятора.В этом случае уравнение. (46) принимает вид dλ = dη ¼ Ω = 2 и дает решение λ ¼ Ωη = 2 þ λð0Þ, приводящее к
ω0 ¼ ω 0 ð1 þ 12 ω 0 ηÞ 1
(50)
и, наконец,
2 ω φ ¼ ln 1 þ 0 εt ε 2
где верхняя полоса означает начальное значение. Тогда решение (48) сводится к xðt Þ ¼ Δ τ 14 ε 1 τ2 e þ O ε2
(51)
(52)
Эта форма близка к треугольной волне постепенно нарастающего периода T ¼ ð4 = ω 0 Þð1 þ εω 0 t = 2Þ. Обратите внимание, что роль «мнимого» члена порядка ε в решении (52) заключается в компенсации отклонений от прямых линий между отражениями от барьеров.Такие отклонения связаны с непрерывным представлением фазы φðtÞ; см. уравнение. (52). Обратите внимание, что согласно решению (50) частота должна упасть до нуля по мере того, как время бежит до бесконечности. Однако этого не может произойти, потому что частота имеет свою нижнюю границу, которая является собственной частотой самого гармонического осциллятора без взаимодействия с ограничителями амплитуды. По этой причине рассмотрим динамику вблизи ее низкоэнергетического предела. Случай 2: «скользящая» динамика достигается при условии, что частота вибрации становится равной собственной частоте осциллятора, а именно λ ¼ Ω = ω0 -π = 2, в то время как амплитуда остается равной Δ.(Напомним, что числовой коэффициент π = 2 отражает различные нормировки для периода синусоидальной волны и треугольной синусоидальной волны.) Если λ-π = 2, то решение (48) описывает гармоническую временную форму относительно фазы φ: hπ i hπ i xðt Þ-Δ sin τ φ Δ sin φðt Þ (53) 2 2 Отметим, что в этом пределе член порядка ε исчезает из (48) в силу уравнения. (46) несмотря на наличие знаменателя cos λ, который приближается к нулю при λ-π = 2. Теперь, вводя «расстройку» ρ ¼ π = 2 λ и рассматривая небольшую окрестность λ ¼ π = 2, приведем уравнение.(46) к виду
1
dρ ¼ Ωρ2 þ O ρ3 dη
, где C — произвольная постоянная. с общим решением ρ ¼ Ωη þ C Затем, проводя интегрирование в уравнении. (47) дает фазу асимптотического решения (53) как
π 2 π2 2 φðt Þ ¼ Ωt þ ln 1 þ εt ω 0 Ω 2 επ 4 π
(54)
(55)
Решение (55 ) выполняется при условии ω 0 4ð2 = π ÞΩ, что означает, что изначально система должна находиться в «области удара». В этом случае фаза оценивается как ð2 = π ÞφðtÞ Ωt при t-1.В противном случае логарифмический член в (55) становится сингулярным. Обсудим некоторые особенности разработанной процедуры. Обратите внимание, что использование обычных теорем об усреднении и связанных аналитических инструментов не оправдано в данном случае из-за единичных членов, представляющих столкновения с барьерами. Тем не менее, идея разделения движения формализована здесь в некоторой степени аналогично множественным масштабам или, скорее, двухпеременным разложениям [27,22]. Однако существует значительная разница между настоящим аналитическим алгоритмом и типичными процедурами с двумя или несколькими масштабами из-за того, что быстрый масштаб времени τ ¼ τðφÞ является периодической функцией фазы.В результате «светские термины», например τ sin λτ в уравнении. (45) становятся периодическими, так что больше нет смысла накладывать условия периодичности на быстрые движения. Напомним, что условия периодичности играют важную роль в «гладких» многомасштабных методах путем генерации дифференциальных уравнений для компонентов медленного движения. Вместо этого настоящий аналитический алгоритм производит уравнения медленного масштаба из исключения сингулярных членов с помощью граничных условий; см. уравнения. (43). Другой особенностью соответствующих решений является то, что даже асимптотическое приближение первого порядка фиксирует локальные детали взаимодействия с барьерами, такие как скачки скорости, за счет использования свойств негладких функций τ ¼ τðφÞ и e eðφÞ; см. решение (48) и (49).Обратите внимание, что особенности столкновения было бы довольно сложно описать с помощью квазигармонических разложений, генерируемых обычным методом множественных масштабов. 3.3. Прыгающий мяч. Пусть z ¼ zðtÞ — вертикальная направленная вверх координата идеально жесткого маленького шарика, который падает из своего начального положения zð0Þ ¼ H 40 с нулевой начальной скоростью. При z¼0 валик отражается от идеально жесткого пола с коэффициентом восстановления k ¼ 1 ε, где 0 o ε⪡1. Затем бусинка продолжает подпрыгивать, пока вся ее энергия не будет потеряна.Дифференциальные уравнения движения между отражениями и условиями столкновения, соответственно, z ˆ ¼ g;
z Z0
(56)
164
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
и z_ ðt i þ 0Þ ¼ ð1 εÞz_ ðt i 0Þ
z ¼ 0:
(57)
где g — ускорение свободного падения. Если бы линейная вязкость присутствовала в уравнении. (56), это технически усложнило бы процесс асимптотического интегрирования, однако не сильно повлияло бы на аналитическую процедуру, которая описана ниже.Эффективная модель, в которой реакция ограничения представлена внешними импульсами, принимает вид z ˆ ¼ gp signðτðφÞÞe0 ðφÞ
(58)
По сравнению с двумя предыдущими примерами, данный случай кажется более сложным из-за к комбинированной амплитудно-частотной модуляции. Для описания такой модуляции подстановка (10) должна быть обобщена как z ¼ Xðτ; ηÞ þ Yðτ; ηÞe
(59)
где τ ¼ τðφÞ, e ¼ eðφÞ; φ ¼ φðtÞ и η ¼ εt. Дифференцируя уравнение.(59) при условии (12) дает z_ ¼
∂Y ∂X ∂X ∂Y ωþε þ ωþε e ∂τ ∂η ∂τ ∂η
(60)
Подставляя уравнение. (60) в уравнение. (58) и приравнивая по отдельности обе компоненты результирующего гиперболического « элемента » к нулю, получаем ∂2 X 2 ∂Y ∂2 Y ∂2 X ω ε2 2 g ω þ ω_ ¼ 2ε ∂τ ∂τ ∂η ∂τ2 ∂η ∂ 2 Y 2 ∂X ∂2 X ∂2 Y ω ε2 2 ω þ ω_ ¼ 2ε 2 ∂τ ∂τ∂η ∂τ ∂η
(61)
В этом случае набор граничных условий (32) и (33) при τ ¼ 7 1 необходимо изменить как τ ¼ 71: Y ¼0
∂Y ∂X ∂X ∂Y ∂X ∂X ω 8 7 þ ε ¼ ð1 εÞ ω þε ∂τ ∂τ ∂η ∂τ ∂τ ∂η
X¼0
(62)
∂X 2 ω ¼ 8p ∂τ
(63)
, где член ∂Y = ∂η был исключен из-за первого уравнения в уравнении.(62). Обратите внимание, что уравнение. (63) определяет неизвестный параметр p при условии выполнения следующего условия симметрии: ∂X ∂X j ¼ jτ ¼ ∂τ τ ¼ 1 ∂τ
(64)
1
Условие (64) отличается от условия (34). ) знаком минус в правой части, роль которого состоит в том, чтобы заставить все ударные импульсы действовать в одном направлении. Будем искать решение краевой задачи (61), (62) в виде асимптотических рядов: Xðτ; ηÞ ¼ X 0 ðτ; ηÞ þX 1 ðτ; ηÞε þX 2 ðτ; ηÞε2 þ O ε3 Yðτ; ηÞ ¼ Y 0 ðτ; ηÞ þ Y 1 ðτ; ηÞε þY 2 ðτ; ηÞε2 þO ε3 φ_ ðtÞ ω ¼ ω0 ðηÞ þ ω1 ðηÞε þ ω2 ðηÞε2 þO ε3
τ ¼ τ ðφÞ В главном приближении
(65)
ε, краевая задача 4 ∂ 0
X ¼ 2; ∂τ2 ω0τ ¼ 7 1:
Y 0 0;
∂2 Y 0 ¼0 ∂τ2 ∂Y 0 0; ∂τ
(66)
X0 ¼ 0
(67)
при условии ∂X 0 ∂X 0 j ¼ j ∂τ τ ¼ 1 ∂τ τ ¼
1
(68)
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
165
Решение краевой задачи (66) (по 68): X0 ¼
гð1 τ2 Þ; 2ω20
Y0 ¼ 0
где функция ω0 ðηÞ остается неизвестной. Тогда с учетом решения (69) получаем уравнения первого асимптотического порядка в виде
∂2 X 1 1 dω0 ∂Y 0 ∂2 Y 0 ∂2 X 0 2g ω1 ¼ 2 þ 2ω0 þ2ω0 ω1 2 ¼ 2 ∂ τ∂η ∂τ ∂τ ω0 dη ∂τ ω30
∂2 Y 1 1 dω0 ∂X 0 ∂2 X 0 ∂2 Y 0 3g τ dω0 ¼ 2 þ2ω0 þ2ω0 ω1 2 ¼ 4 ∂τ∂η ∂τ2 ∂τ ω0 dη ∂τ ω0 dðθÞη
(69)
(70)
при граничных условиях
τ ¼ 71: τ ¼ þ1: τ ¼ 1:
Y1 ¼ 0
(71)
∂X 0 ∂Y 0 ∂Y 1 ∂X 0 ∂Y 0 ¼2 þ 2 þ ω1 ∂τ ∂τ ∂τ ∂η ∂τ
∂X 0 ∂Y 0 ∂Y 1 ∂X 0 ∂Y 0 ω0 þ2 þ ω1 ¼ 2 ∂τ ∂τ ∂τ ∂η ∂τ
ω0
(72)
и
τ ¼ 71:
X1 ¼ 0
(73)
Условие симметрии (64) дает ∂X 1 ∂X 1 j ¼ j ∂τ τ ¼ 1 ∂τ τ ¼
1
(74)
Общее решение уравнения(70) получается интегрированием как g ω1 X 1 ¼ A 1 η τ þ B1 η þ 3 τ 2
ω0
g dω0 τ3 Y 1 ¼ C 1 η τ þ D1 η 4 ω0 dðθÞη 2
(75 )
где A1 ðηÞ, B1 ðηÞ, C 1 ðηÞ и D1 ðηÞ — произвольные функции медленного временного масштаба η ¼ εt. Принимая во внимание ур. (71) и (73) приводят уравнение. (75) к виду X1 ¼
г ω1
ω30
τ2 1;
Y1 ¼
gd ω0 τ τ3 2ω40 dη
(76)
Отметим, что первые два члена частотного разложения ω0 ðηÞ и ω1 ðηÞ пока неизвестны, а условия неупругого удара первого порядка (72 ) остаются неиспользованными.Теперь подставляя решения (69) и (76) в уравнение. (72) показывает, что оба уравнения в (72) (72) выполняются, если функция ω0 ðηÞ подчиняется дифференциальному уравнению dω0 1 2 ¼ ω0 2 dη
(77)
φ_ ¼ ω0 ¼ ω 0 ð1 12 ω 0 ηÞ 1
(78)
Это дает
где ω 0 ¼ ω0 ð0Þ — произвольная положительная постоянная. Как следует из решения (76), еще произвольная функция ω1 ðηÞ определяет амплитуду приближения X1. Однако параболическая форма, описываемая функцией X 1 τÞ, уже фиксируется нулевым приближением X 0 τÞ.Поэтому выберем X 1 0, положив ω1 ηÞ 0. Теперь, собирая приближения нулевого и первого порядков и принимая во внимание уравнения (59) и (77) дают
г 1 2 z¼ 1 τ ετ e (79) 1 þ 2 2ω20 p ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi Тогда, учитывая уравнение. (78) и удовлетворяя начальному условию zð0Þ ¼ H, дают ω 0 ¼ g = ð2HÞ. Наконец, подставив ω0 из уравнения. (78) в решение (79) дает r ffiffiffiffiffiffiffi 2
ε g ε t 1 τ2 1 þ τe (80) zðt Þ ¼ H 1 2 2H 2
166
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
5 4
z
3 2 1 0
0
1
2
3
4
5
t Рис.6. Вертикальная координата прыгающего мяча в зависимости от времени: решение, полученное в [5]. [47] (тонкая линия), точное кусочно-параболическое решение (штриховая линия) и негладкое решение с заменой времени (сплошная линия).
где τ ¼ τðφÞ и e ¼ eðφÞ задаются уравнениями. (2) и (3), соответственно, и φ ¼ φðtÞ получается интегрированием уравнения. (78) при начальном условии φð0Þ ¼ 0 в виде r ffiffiffiffiffiffiffi
2 ε gt (81) φ ¼ ln 1 ε 2 2H Как следует из решения (80) и (81), процесс подпрыгивания заканчивается при s ffiffiffiffiffiffiffi 2 2H t max ¼ ε g Такой же результат был получен в справочнике [47], однако с использованием другого аналитического инструмента, основанного на преобразовании координат разворачивания пространства с усреднением по быстрой фазе.Обратите внимание, что рассмотрение точного кусочно-параболического решения также дает такую же длительность процесса отскока, однако временные формы трех вышеуказанных решений несколько отличаются, как это видно из рис. 6. 4. Выводы В этой статье используется методология негладкого преобразования времени. был обобщен для учета потерь энергии из-за столкновений колебательных систем с ограничителями амплитуды. В частности, особый тип граничных условий по отношению к новой временной переменной был введен для описания потерь энергии из-за неупругих эффектов на ограничивающих барьерах.Были рассмотрены три иллюстративных примера, охватывающих периодические, частотно-модулированные и амплитудно-частотно-модулированные колебания. Помимо удобства расчетов без учета переменных состояния во время столкновений, предлагаемый тип решений в замкнутой форме, по-видимому, хорошо подходит для описания нестационарной динамики так называемых поглотителей энергии виброударов. Ссылки [1] В. Акари, Б. Брольято, Численные методы для негладких динамических систем: приложения в механике и электронике, Springer, Berlin, Heidelberg, 2008.[2] J. Awrejcewicz, C.-H. Ламарк, Бифуркация и хаос в негладких механических системах, World Scientific, Сингапур, 2003. [3] В.И. Бабицкий, Теория виброударных систем и приложения, Springer-Verlag, Берлин, 1998. [4] Б. Блазейчик-Околевска, К. Чолчински, Т. Капитаняк, Дж. Воевода, Хаотическая механика в системах с ударами и трением, World Scientific, Singapore, 1999. [5] B. Brogliato, Удары в механических системах: анализ и моделирование, Springer-Verlag, Berlin, 2000. [6] W. Chin, E.Отт, Х. Нуссе, К. Гребоги, Бифуркации скольжения в ударных осцилляторах, Physical Review E 50 (декабрь) (1994) 4427–4444. [7] Х. Данкович, М. Р. Пол, Бифуркации, вызванные разрывом в системах с гистерезисными силовыми взаимодействиями, Журнал вычислительной и нелинейной динамики 4 (2009) 1–6. Статья 041009. [8] М.Ф. Диментберг, Статистическая динамика нелинейных и изменяющихся во времени систем, John Wiley & Sons, New York, 1988. [9] B.A. Фини, А. Гуран, Н. Хинрихс, К. Попп, Исторический обзор сухого трения и явлений прерывистого скольжения, Обзоры прикладной механики ASME 51 (1998) 321–341.[10] А. Фидлин, Нелинейные колебания в машиностроении, Springer, Berlin, Heidelberg, 2005. [11] А.Ф. Филиппов, Дифференциальные уравнения с разрывной правой стороной, Kluwer Academic Publishers Group, Дордрехт, 1988. [12] С. Фучик, А. Куфнер, Нелинейные дифференциальные уравнения, Исследования по прикладной механике, Vol. 3, 1980, Эльзевир, Амстердам, Оксфорд, Нью-Йорк. [13] Г.А. Гальперин, А. Земляков, Математический бильярд, Наука, М., 1990. [14] О.В. Гендельман, Аналитическая обработка системы с виброударным нелинейным поглотителем энергии, Journal of Sound and Vibration 331 (2012) 4599–4608. [15] В. Голдсмит, Удар: теория и физическое поведение при столкновении, Courier Dover Publications, North Chelmsford, 2001. [16] А. Гуран, Ф. Пфайффер, К. Попп, Динамика с трением: моделирование, анализ и эксперименты , World Scientific, Сингапур, 2001. [17] CM Хатчинс, История исследования скрипки, Журнал Акустического общества Америки 73 (5) (1983) 1421–1440.
В.Н. Пилипчук / Journal of Sound and Vibration 359 (2015) 154–167
167
[18] R.A. Ибрагим, Динамика виброударов: моделирование, картографирование и приложения, Конспект лекций по прикладной и вычислительной механике, Vol. 43, SpringerVerlag, Берлин, Гейдельберг, 2009. [19] Р.А. Ибрагим, В. Бабицкий, М. Окума (ред.), Виброударная динамика океанских систем и связанные с ней проблемы, Springer-Verlag, Berlin Heidelberg, 2009. [20] А.П. Иванов, Динамика систем с механическими столкновениями, Международная программа образования, Москва, 1997 с.[21] А.П. Иванов, Ударные колебания: линейная теория устойчивости и бифуркации, Journal of Sound and Vibration 178 (3) (1994) 361–378. [22] Дж. Кеворкян, Дж. Д. Коул, Методы множественных масштабов и сингулярных возмущений, Springer-Verlag, New York, 1996. [23] В.В. Кисил, Индуцированные представления и гиперкомплексные числа, Успехи в прикладных алгебрах Клиффорда 23 (2) (2013) 417–440. [24] А.Е. Кобринский, Динамика механизмов с упругими связями и ударными системами, Iliffe Books, Лондон, 1969. [25] Р.I. Leine, Henk Nijmeijer, Hendrik Nijmeijer, Динамика и бифуркации негладких механических систем, Springer, Berlin, New York, 2006. [26] F.L. Льюис, Д. Доусон, К. Абдалла, Управление роботом-манипулятором: теория и практика, CRC Press, Нью-Йорк, 2004. [27] А.Х. Найфех, Методы возмущений. Чистая и прикладная математика, John Wiley & Sons, Нью-Йорк-Лондон-Сидней, 1973. [28] Ф. Петерка, Введение в колебания механических систем с внутренними ударами, Academia, Прага, 1981 (на чешском языке).[29] Ф. Пфайффер, Динамика механической системы, Springer, Берлин, Гейдельберг, 2008. [30] Ф. Пфайффер, К. Глокер, Многотельная динамика с односторонними контактами, Wiley, Нью-Йорк, 1996. [31] Ф. Пфайфер, А. Кунерт, Модели грохота от детерминированных к случайным процессам, Нелинейная динамика 1 (1) (1990) 63–74. [32] В. Пилипчук, Аналитическое исследование вибрирующих систем с сильной нелинейностью с использованием пилообразных временных преобразований, Journal of Sound and Vibration 192 (1) (1996) 43–64. [33] В.Н. Пилипчук, Нелинейная динамика: между линейным пределом и пределом удара (конспект лекций по прикладной и вычислительной механике), Springer, Berlin, Heidelberg, 2010. [34] В.Н. Пилипчук, Ударные режимы в дискретных колебательных системах с двусторонними барьерами, Международный журнал нелинейной механики, 36 (6) (2001) 999–1012. [35] К. Попп, Негладкие механические системы, Журнал прикладной математики и механики, 64 (5) (2000) 765–772. [36] П.Ф. Роват, А. Селверстон, Осцилляторные механизмы в парах нейронов, связанных с быстрыми тормозными синапсами, Journal of Computational Neuroscience 4 (1997) 103–127.[37] А. Самойленко, А.А. Бойчхук, В.Ф. Журавлев, Слабо нелинейные краевые задачи для операторных уравнений с импульсным воздействием, Украинский математический журнал, 49 (2) (1997) 272–288. [38] П. Шерц, Практическая электроника для изобретателей, McGraw-Hill, New York, 2006. [39] S.W. Шоу, К. Пьер, Динамический отклик настроенных амортизаторов для вращающихся гибких конструкций. asme., Журнал вычислительной и нелинейной динамики 1 (2005) 13–24. [40] С.В. Шоу, Р. Х. Рэнд, Переход к хаосу в простой механической системе, Международный журнал нелинейной механики 24 (1) (1989) 41–56.[41] У. Дж. Стронге, Механика удара, Cambridge University Press, Нью-Йорк, 2000. [42] Дж. Дж. Томсен, А. Фидлин, Анализ почти упругих виброударов путем прерывистых преобразований и усреднения, Journal of Sound and Vibration 311 (2008) 386–407. [43] Дж. Д. Тернер, О моделировании разрывных функций, Журнал прикладной механики 68 (сентябрь) (2001) 751–757. [44] А.Ф. Вакакис, О.В. Гендельман, Л.А. Бергман, Д. МакФарланд, Г. Кершен, Ю.С. Ли, Нелинейная целевая передача энергии в механических и конструктивных системах, Springer-Verlag, Берлин, Гейдельберг, 2009.[45] М. Верцигрох, Б. де Кракер (ред.), Прикладная нелинейная динамика и хаос механических систем с разрывами, т. 28, World Scientific, Сингапур, 2000. [46] В.Ф. Журавлев, Метод анализа виброударных систем с помощью специальных функций, Известия АН СССР Механика твердого тела 11 (2) (1976) 30–34. [47] В.Ф. Журавлев, Д. Климов, Прикладные методы в теории колебания, Наука, М., 1988 (Под ред. И с предисловием А. Ю. Ишлинского).
Bufo) с использованием вариации последовательности ДНК в митохондриальных и ядерных локусах в JSTOR
АбстрактныйНарушение среды обитания, ведущее к разрушению экологических барьеров, привело к гибридизации между многочисленными симпатрическими видами и упадку или исчезновению родительских видов.Несмотря на сильный постзиготный отбор, гибридизация происходит между двумя обычно экологически изолированными видами жаб, жабой побережья Мексиканского залива (Bufo nebulifer) и жабой Фаулера (Bufo fowleri). Эта гибридизация потенциально способствовала сокращению численности более редкого вида B. fowleri. Предполагаемые гибриды могут быть морфологически загадочными; поэтому для их идентификации использовались молекулярные методы. Мы использовали однонуклеотидные полиморфизмы (SNP) для идентификации гибридов, а вариации митохондриальной последовательности в сегменте 12S и 16S области рРНК также использовались для определения материнского происхождения гибридов и поиска доказательств направленной гибридизации и интрогрессии самцов B.nebulifer с самкой B. fowleri. Было проведено прямое секвенирование 72 особей обоих видов из девяти гнездящихся популяций. Двенадцать видоспецифичных SNP из фрагмента из 333 пар оснований в ядерном интроне гена родопсина были использованы для идентификации каждого вида, и два мужских гибрида были идентифицированы на основе гетерозиготности в этих сайтах. Обладание разными последовательностями мтДНК каждым гибридом указывало на альтернативную материнскую линию от каждого из родительских видов и идентифицировало гибриды как потомство от каждого реципрокного скрещивания.Использование митохондриальных и ядерных молекулярных маркеров позволило однозначно идентифицировать гибриды и их материнского родителя, что невозможно было бы провести без использования обоих наборов данных. Мы также исследовали филогенетические отношения между B. fowleri и его близкими родственниками в комплексе видов B. americanus, используя вариации митохондриальной последовательности.
Информация о журналеЖурнал герпетологии публикует оригинальные исследовательские статьи по биологии амфибий и рептилий с упором на поведение, сохранение, экологию, эволюцию, морфологию, физиологию и систематику.Цель журнала — расширить знания о земноводных и рептилиях и способствовать общению между герпетологами и другими биологами, интересующимися земноводными и рептилиями.
Информация об издателеОбщество изучения амфибий и рептилий (SSAR) — это некоммерческая организация, созданная для продвижения исследований, сохранение и образование в отношении земноводных и рептилий. Он был основан в 1958 году и в настоящее время является крупнейшим международным герпетологическое общество.Общество собирается ежегодно, обычно в совместных местах с другими герпетологическими обществами. Члены получать первичную исследовательскую публикацию Общества, Журнал герпетологии, и его новостной журнал, Герпетологический журнал. Рассмотрение. SSAR также издает книжные монографии, факсимиле и каталог американских рептилий и амфибий. Грантовые программы поддерживают исследования студентов. Комитеты по охране природы и образования имеют обширные информационные компоненты. Чтобы В целях содействия публикации исследований по амфибиям и рептилиям SSAR предлагает программу помощи герпетологам в редакции. для которых английский не является родным языком.
Саратовская осенняя встреча 2019: Вычисления и анализ данных: от наномасштабных инструментов к функциям мозга | (2020) | Публикации
Распознавание паттернов ЭЭГ при мысленных намерениях: сравнительное исследованиеАвторы): Дарья С. Гришина; Наталья Михайловна Куприяшкина; Ольга Н. Павлова; Анастасия Е.Runnova; Алексей Николаевич Павлов
Показать аннотацию
Распознавание определенных колебательных паттернов в электроэнцефалограммах человека (ЭЭГ) — важная проблема, которая привлекла значительное внимание при создании интерфейсов мозг-компьютер (ИМК). Некоторые из этих закономерностей легко идентифицировать различными численными методами. Однако гораздо труднее распознать мысленные намерения, которые могут быть далее преобразованы в команды управления для оборудования, и выбор соответствующего числового инструмента становится очень важным.В этом исследовании мы сравниваем несколько численных методов, примененных к многоканальным ЭЭГ, записанным у нетренированных добровольцев, которые воображали движения рук и ног. Мы показываем, что качество распознавания варьируется между разными методами и зависит от объекта. Обсуждаем возможности надежного разделения воображаемых движений разных типов.
Особенности двигательной активности мозга, выявленные с помощью количественного анализа рецидивовАвторы): Елена Пицик; Никита Фролов
Показать аннотацию
Мы предлагаем подход к анализу двигательной активности мозга, основанный на сочетании непрерывного вейвлет-преобразования и количественного анализа повторяемости (RQA).Обнаружение таких паттернов на ЭЭГ — сложная задача из-за нестационарности и сложности сигнала ЭЭГ, что приводит к высокой меж- и внутрипредметной вариабельности традиционно применяемых методов. Мы показываем, что измерения сложности RQA, такие как частота рецидивов и ламинарность, очень полезны при обнаружении переходов от фоновой к двигательной ЭЭГ. Более того, RQA измеряет временную зависимость для верхних конечностей контралатерально, что позволяет различать два типа движений.
Использование искусственных нейронных сетей для классификации кинестетических и визуальных воображаемых движений по данным МЭГАвторы): Семен Куркин; Парф Чхолак; Гиомар Нисо; Никита Фролов; Александр Писарчик
Показать аннотацию
Анализ нейрофизиологических механизмов, ответственных за воображение движения, необходим для разработки интерфейсов мозг-компьютер.Проведенные магнитоэнцефалографические (МЭГ) эксперименты с добровольными участниками подтверждают существование двух типов двигательных образов: кинестетических образов (KI) и визуальных образов (VI), отличающихся активацией и торможением различных областей мозга. Для классификации состояний мозга, связанных с образами движения, мы использовали иерархический кластерный анализ и популярный тип искусственных нейронных сетей, называемый многослойным персептроном. Применение методов машинного обучения позволяет нам классифицировать двигательные образы при поднятии правой и левой руки со средней точностью 70% как для KI, так и для VI, используя соответствующую фильтрацию входных сигналов.Такая же средняя точность достигается за счет оптимизации каналов MEG и уменьшения их количества до 13.
Когнитивное взаимодействие через интерфейс мозг-мозгАвторы): Владимир Максименко; Никита Фролов; Вадим Грубов; Владимир Недаивозов
Показать аннотацию
Мы разрабатываем неинвазивный интерфейс мозг-мозг, который позволяет динамически перераспределять когнитивную нагрузку между субъектами на основе их текущих когнитивных способностей.В результате участник, показывающий более высокую производительность, подвергается более высокой нагрузке, в то время как его / ее партнер получает меньшую нагрузку. Мы демонстрируем, что распределение нагрузки позволяет повысить когнитивные способности пары взаимодействующих субъектов.
Сетевая структура мозговой активности детей при когнитивной нагрузкеАвторы): Александр Э.Храмов; Вадим В. Грубов; Никита Сергеевич Фролов; Елена Н. Пицик; Храмова Марина Валерьевна
Показать аннотацию
Мы проанализировали нейронные взаимодействия в коре головного мозга детей, связанные с когнитивной активностью во время простой оценки когнитивной задачи (таблица Шульте) в двух различных частотных диапазонах — альфа (8-13 Гц) и бета (15-30 Гц) диапазонах с использованием линейных Пирсонов. корреляционный анализ связности.Мы наблюдали связанное с задачей подавление связности альфа-диапазона в лобной, височной и центральной областях мозга, в то время как в теменной и затылочной областях мозга связь увеличивается. Мы также продемонстрировали значительное увеличение функциональной связности в бета-диапазоне во всей распределенной корковой сети, связанное с задачами.
Поддержание состояния внимания детей при познавательной нагрузкеАвторы): Вадим В.Грубов; Максименко Владимир Александрович; Семен А. Куркин; Марина В. Храмова; Александр Евгеньевич Храмов
Показать аннотацию
Мы проанализировали ЭЭГ-сигналы детей, записанные при выполнении конкретной познавательной задачи — теста Шульте. Мы проанализировали поведенческие характеристики — интервалы времени, необходимые для нахождения испытуемым каждого последовательного номера в таблице, а также частотные характеристики сигнала ЭЭГ, рассчитанные с помощью непрерывного вейвлет-преобразования с учетом усредненных энергий вейвлетов по альфа- и бета-диапазонам частот.Мы также выполнили статистический анализ этих характеристик с помощью дисперсионного анализа, чтобы найти особенности, которые можно использовать для оценки уровня внимания и его динамики во время выполнения элементарной задачи.
Метод пространственно-временного каркаса для анализа данных ЭЭГАвторы): Анастасия Евгеньевна Руннова; Э.Ситникова; М. Журавлев
Показать аннотацию
Предлагается новый метод пространственно-временного анализа, основанный на использовании концепции непрерывного вейвлет-преобразования. Этот метод позволяет вовремя обнаружить доминирующую частоту в каждом из каналов записи ЭЭГ и визуализировать результаты. Показаны результаты применения разработанной методики к ЭЭГ-сигналам активности головного мозга крыс.Показаны различные структурные особенности колебательной активности мозга во время поведенческого сна у крыс с абсцессной эпилепсией и условно здоровых.
Анализ повторяемости графиков при обработке экспериментальных биомедицинских данныхАвторы): Анастасия Руннова; Антон Сельский; Максим Журавлев; Елизавета Емельянова; Елена Сельская
Показать аннотацию
В данной статье мы предложили метод выявления индивидуальных характеристик двигательной активности на основе анализа рецидивов применительно к энцефографии головного мозга человека.Анализ проводился по реальным и воображаемым (для МЭГ только воображаемым) движениям испытуемых и сравнивался с фоновой записью, когда испытуемый находился в состоянии покоя. Такой подход позволяет определить для каждого испытуемого каналы, в которых частота увеличивается в момент двигательной активности и / или формируется устойчивый паттерн, соответствующий этому движению. Предлагаемый метод имеет большое количество прикладных приложений в медицине и нейрофизиологии.
Определение наилучшего запаздывания внедрения для моделирования пик-волновых разрядов на основе экспериментальных данныхАвторы): Анастасия А.Грищенко; Марина Васильевна Сысоева; Клементина М. ван Рейн; Илья Васильевич Сысоев
Показать аннотацию
Цель. Произведен расчет оптимального значения задержки внедрения. Запаздывание — один из эмпирических параметров математических моделей, используемых в моделях авторегрессии для прогнозирования, анализа связи, классификации сигналов и т. Д. Методы. Обнаружен первый минимум зависимости функции взаимной информации от запаздывания.Полученные результаты. Расчет показал, что оптимальная задержка составляет около 8 интервалов выборки (1/64 с или 1/8 характерного периода колебаний для приступов отсутствия). Обсуждение. Оптимальная задержка, составляющая около 1/8 характерного периода колебаний, была получена как для эпилептиформной, так и для фоновой активности, включая преиктальную и различные стадии иктальной активности, т.е. е. эта временная шкала присутствует в сигнале на протяжении всего времени наблюдения.
Методика определения по сигналам ЭМГ предвестников начала движения конечностиАвторы): Владимир С.Хорев; Дария Д. Пушкарская; Елена Н. Пицик; Семен Анатольевич Куркин
Показать аннотацию
В этой статье мы разработали метод, позволяющий автоматически определять предвестник начала движения на основе анализа электромиографических сигналов. Методы определения начала движения и моментов планирования движения являются острой необходимостью в нейробиологии, и отдельной проблемой является использование сигналов электрической активности мышц (электромиограмм) для точного определения начала движения руки из-за сложности, малой продолжительности. и шум исходных сигналов.Мы выяснили, что в случае, когда движение начинается по определенному звуковому сигналу, момент начала движения фиксируется с некоторой задержкой по времени.
Выявление раннего рака желудка с помощью вейвлетовАвторы): Александр Петрович Хороводов; Илана М. Агранович; Никита Анатольевич Наволокин; Ольга Н. Павлова; Алексей Н.Павлов; Екатерина Борисова; Оксана Викторовна Семячкина-Глушковская
Показать аннотацию
Ранние стадии рака желудка не распознаются из-за его бессимптомного развития. Выявление патологических изменений может быть достигнуто с помощью фотодинамической диагностики, но такой подход обеспечивает довольно низкую селективность опухоли.Дополнительные возможности для улучшения выявления предраковых стадий могут быть предоставлены путем анализа кровообращения в сосудах желудка. Мы рассматриваем возможности мультиразрешающего анализа в распознавании изменений кровообращения у крыс с разными уровнями флуоресцентного сигнала в желудке, связанными с предраковыми стадиями.
Определение наиболее информативных длин волн для неинвазивной диагностики меланомы в спектральной области от 450 до 950 нм.Авторы): Дмитрий Близнукс; Юрий Чижов; Андрей Бондаренко; Дильшат Утешев; Алексей Лихачев; Илзе Лихачова
Показать аннотацию
В этом исследовании было проанализировано 300 кубиков мультиспектральных данных о поражениях кожи (включая 32 меланомы кожи).Были проанализированы многоэтапные и одношаговые подходы к машинному обучению, чтобы найти диапазоны волн, которые предоставляют наибольшую информацию, которая помогает отличить меланому кожи от других доброкачественных пигментных поражений. Подход многоэтапного машинного обучения предполагал обучение нескольких моделей, но оказался неэффективным. Причина этого — необходимость обучить модель сегментации на очень маленьком наборе данных и использование стандартного классификатора машинного обучения, которые показали низкую производительность классификации.Одношаговый подход основан на нейронной сети глубокого обучения. Мы провели 2600 экспериментов с двумя архитектурами нейронных сетей: популярным предварительно обученным анализатором изображений «InceptionV3» и простыми настраиваемыми классификаторами сверточной нейронной сети (ConvNet). Наблюдение за показателями производительности этих двух архитектур на основе глубокого обучения (DL) позволило определить комбинации трех спектральных диапазонов волн, что позволило обучить классификатор с лучшими результатами классификации. Было обнаружено, что простой классификатор ConvNet позволил нам получить лучшие результаты классификации.Результаты обучения ConvNet показали, что наиболее информативными являются диапазоны волн 450 нм, которые являются наиболее информативными для концентрации меланина на поверхности кожи, 590 нм, которые представляют собой интегральную информацию о распределении меланина и гемоглобина из слоя эпидермиса и дермы, и 950 нм, которые предоставляют информацию из более глубоких слоев кожи. . В представленном виде модель сверточной нейронной сети (CNN) была простой, но не показала большой производительности. Кроме того, мы должны изучить альтернативные архитектуры CNN. Фреймворк AutoKeras был использован для поиска архитектуры классификатора изображений с использованием найденных триплетов диапазона волн.
Особенности фазовой синхронизации сердечно-сосудистых и дыхательных колебаний у человекаАвторы): Арина Валерьевна Танканаг; Андрей А. Гриневич; Ирина В. Тихонова; Николай К. Чемерис
Показать аннотацию
Фазовые взаимодействия между сердечно-сосудистой и дыхательной системами анализировали в состоянии покоя у добровольцев.В исследовании приняли участие 22 здоровых некурящих человека с нормальным АД в возрасте от 21 до 45 лет. Одновременно регистрировались следующие физиологические сигналы: частота дыхания, вариабельность сердечного ритма (ВСР), кровоток в коже предплечья и стопы, объем крови в тканях подушечек пальцев кисти и стопы. Степень синхронизации фаз анализируемых сигналов оценивалась значением функции фазовой когерентности вейвлета. Обнаружена высокая фазовая синхронизация между дыханием и колебаниями объема крови в тканях обоих пальцев и низкая синхронизация между дыханием и колебаниями кровотока в коже обоих исследуемых участков кожи.Также была получена высокая фазовая синхронизация между колебаниями ВСР и тканевого объема крови обоих пальцев, а также низкая синхронизация между колебаниями ВСР и кожного кровотока обоих участков кожи с частотой дыхания (~ 0,3 Гц). Имеется сходство фазовых взаимодействий обоих анализируемых сигналов (кровотока и объема крови) с ВСР в низкочастотном диапазоне от 0,0095 до 0,1 Гц. Эти результаты не зависели от исследуемых конечностей. Мы полагаем, что полученные результаты могут быть использованы для разработки новых диагностических подходов к оценке состояния периферических сосудов при патологиях.
Синхронизация и когерентность низкочастотных составляющих сигналов сердечно-сосудистой системы у новорожденныхАвторы): Виктория В. Сказкина; Юлия В. Попова; Елена Н. Муреева; Антон Р. Киселев; Юрий Михайлович Ишбулатов; Ольга С. Панина; Владимир Сергеевич Хорев; Татьяна А.Галушко; Юрий В. Черненков; Анатолий Сергеевич Караваев
Показать аннотацию
В данной работе мы проанализировали сигналы вариабельности сердечного ритма и фотоплетизмограммы ног новорожденных. В серии экспериментов участвовали 10 условно здоровых испытуемых; каждая запись велась в течение 15 минут во время кормления. Использованы методы спектрального анализа и методы нелинейной динамики.В данной работе показаны некоторые особенности вегетативной нервной регуляции сердечно-сосудистой системы у новорожденных, дана оценка степени синхронизации и сцепления петель для регулирования вариабельности сердечного ритма и сосудистого тонуса с использованием методов расчета поперечного спектра, коэффициента когерентности и общего процент фазовой синхронизации.
Роль NCX в инициировании и расширении астроглиальных событий Ca2 + в распределенной моделиАвторы): Андрей Ю.Верисокин; Дарья Валерьевна Вервейко; Постнов Дмитрий Евгеньевич; Браж Алексей Р.
Показать аннотацию
Мы представляем двумерную модель динамики астроцитов Ca 2+ . Мы принимаем во внимание два основных фактора рассматриваемого процесса: опосредованное IP 3- высвобождение из внутриклеточных хранилищ Ca 2+ и двунаправленный обмен плазматической мембраны, т.е.е. Na + / Ca 2+ -обменник (NCX). Мы основывались на формализме Ходжкина-Хаксли для описания эффектов NCX и принимали во внимание опосредованное переносчиком глутамата увеличение Na + во время синаптической активности и регуляцию, зависимую от Na + — и Ca 2+ . Результаты численного решения единой модели подтверждают появление кальциевых волн, которые возникают из-за синаптической активности и распространяются по сети астроцитов. Присутствие NCX приводит к уменьшению средних площадей, на которые влияет глобальная кальциевая волна во время возбуждения.Однако обменник Na / Ca стимулирует кальциевые волны, делая возможным формирование более долгоживущих волн.
Активность кальция в модели астроцита губки с контролем параметров AVFАвторы): Дарья Валерьевна Вервейко; Андрей Ю. Верисокин; Постнов Дмитрий Евгеньевич; Браж Алексей Р.
Показать аннотацию
Мы моделируем формирование и динамику кальциевых волн в распределенной сети астроцитов.Мы учитываем объемные эффекты, вызванные реальной морфологией клетки астроцита. Астроциты представляют собой губчатые структуры, которые не занимают весь объем своего отсека: листочки астроцитов окружены нейропилем. Мы вводим параметр объемной доли астроцитов (AVF), который показывает часть 2D-шаблона, занимаемую астроцитом по сравнению с нейропилем, и коррелирует с этим соотношением в реальной 3D-структуре. Для описания разницы в процессах в ветвях и листочках астроцита и непрерывного перехода между ними мы используем параметр отношения поверхности к объему (SVR).
Функциональная модель нервно-сосудистой единицы: поиск баланса между физиологической значимостью и вычислимостьюАвторы): Постнов Дмитрий Евгеньевич
Показать аннотацию
Сосудисто-нервная единица паренхимы головного мозга называется клеточной цепью, которая обеспечивает контроль местного кровотока в зависимости от потребностей нейронов.При изменении активности нейрона активируется цепочка сигнальных механизмов, что приводит к увеличению или уменьшению радиуса ближайшего кровеносного сосуда. Разработан ряд математических моделей сосудисто-нервного взаимодействия, воспроизводящих основные сигнальные пути и позволяющих оценивать количественную сторону процессов. Однако эти модели слишком сложны в вычислительном отношении, чтобы служить основой для 2D и тем более 3D моделирования паренхимы нервной ткани. В данной статье мы предлагаем функциональную модель нервно-сосудистого блока, направленную на правильное воспроизведение динамических паттернов нервно-сосудистого ответа с минимальным количеством уравнений и управляющих параметров.Такая модель включает в себя наиболее значимые элементы клеточной схемы: сцепление объемной передачи в межклеточном пространстве паренхимы, внутриклеточную динамику концентрации кальция в астроците, а также двухфазный характер реакции клетки гладкой мускулатуры сосуда на рост концентрации калия в периваскулярном пространстве. Результаты вычислительного эксперимента показывают хорошее согласие динамики модели с известными типами нервно-сосудистого ответа.
Открытие BBB может отключить нервно-сосудистую связь: предсказание количественной математической моделиАвторы): Роберт И.Лошкарев; Постнов Дмитрий Евгеньевич
Показать аннотацию
Понятие нервно-сосудистая единица (NVU) используется для обозначения клеток и их коммуникационных механизмов, участвующих в формировании ауторегуляции кровоснабжения. Было показано, что «открытие» гематоэнцефалического барьера (ГЭБ) может быть вызвано различными эффектами, такими как сильный и продолжительный звук или лазерное излучение.Замечено, что открытие ГЭБ сопровождается периваскулярным отеком, так как проницаемость капилляров для воды также увеличивается во много раз. Таким образом, можно ожидать, что такие изменения могут существенно повлиять на режим работы нервно-сосудистого блока. Мы представляем модельное исследование, направленное на оценку влияния периваскулярного отека на функционирование нервно-сосудистой связи с использованием многомерной количественной математической модели. Наши результаты предсказывают блокировку работы нервно-сосудистой коммуникации при открытии ГЭБ.А именно, мы показываем, что относительно небольшое (в 2-3 раза) изменение периваскулярного объема имеет тонкий эффект, 10-кратное увеличение PVS заметно изменяет, но не нарушает функциональность сосудисто-нервного взаимодействия, и значительную степень отека ( увеличение ПВС более чем в 100 раз) практически полностью отключает нервно-сосудистую связь.
Синхронизация мозгового и периферического кровообращения: изменения, вызванные стрессомАвторы): Андрей В.Терсков; Ольга Н. Павлова; Аркадий Сергеевич Абдурашитов; Алексей Н. Павлов; Оксана Викторовна Семячкина-Глушковская
Показать аннотацию
Мы рассматриваем синхронизацию между динамикой кровотока в мозговых и периферических сосудах у крыс с точки зрения фиксации мгновенных частот, связанных с медленными колебаниями, вызванными нейрогенным регуляторным механизмом или, частично, метаболической активностью.Мы показываем, что степень синхронизации изменяется с развитием инсульта, вызванного сильным стрессом, что отражается в уменьшении средней продолжительности сегментов с частотной синхронизацией. Такие изменения различаются между макро- и микроцеребральной динамикой и более выражены для сети мелких сосудов, окружающих сагиттальный синус.
Математическое моделирование низкочастотных колебаний, индуцированных модулированным шумом в микрососудистой сети человека.Авторы): Андрей А.Гриневич; Арина Валерьевна Танканаг; Николай К. Чемерис
Показать аннотацию
Разработана математическая гидродинамическая модель сердечно-сосудистого ложа человека. Модель включает четырехкамерное сердце, два круга кровообращения и многоуровневую микрососудистую сеть. С помощью разработанной модели изучено влияние шума малой интенсивности на колебания кровотока в микрососудистом русле.Изучено влияние шума малой интенсивности на тонус сердечной стенки левого желудочка. Использовались немодулированный шум и шум, модулированный синусом с частотами 0,02, 0,0625 и 0,1 Гц. Немодулированный шум вызывал формирование низкочастотных колебаний микрососудистого кровотока с максимумом на частоте 0,1 Гц. Модулированный шум вызывал низкочастотные колебания кровотока с ярко выраженными пиками на частотах модуляции. Полученные результаты указывают на детектирующее свойство моделируемого сосудистого русла, что позволяет определять модулирующий сигнал.Такое поведение характерно для системы, состоящей из нелинейной и фильтрующей составляющих.
Применение кросс-рекуррентного анализа для выявления сцепления в математической модели вегетативного управления кровообращениемАвторы): Юрий Михайлович Ишбулатов; Ольга Михайловна Посненкова; Екатерина И. Боровкова; Юлия В. Попова; Данил Д.Кульминский; Елена Васильевна Навроцкая; Владимир Сергеевич Хорев; Виктория В. Кудряшова; Антон Р. Киселев; Анатолий Сергеевич Караваев
Показать аннотацию
Исследование направлено на применение анализа перекрестных рецидивов для выявления связи между петлями симпатической регуляции сердечно-сосудистой системы. Для проверки применимости метода и задания его параметров он был применен к математической модели сердечно-сосудистой системы, имеющей структуру, аналогичную структуре реальной системы.Чтобы выяснить, отражает ли анализ перекрестных рецидивов динамику вегетативного контроля, авторы провели четыре численных эксперимента с постепенно снижающейся активностью симпатической регуляции. Не было обнаружено корреляции между результатами перекрестного анализа повторений и силой сцепления.
Математическая модель сократимости лимфангионаАвторы): Ксения О.Меркулова; Постнов Дмитрий Евгеньевич
Показать аннотацию
Механизмы сократимости и пространственно-временные закономерности активности лимфатических сосудов изучены гораздо меньше, чем кровеносных сосудов. Однако понимание характеристик их динамики не менее важно для биомедицинских приложений. В этой работе мы предлагаем простую модель сократительной активности элементарного сегмента лимфатического сосуда, которую мы используем для сборки модели лимфангиона, функциональной единицы лимфатической системы, обеспечивающей перекачку лимфы.Наши результаты показывают, что этот подход является многообещающим, особенно с учетом дальнейшей параметризации модели.
Взаимодействие бистабильных нейронов, приводящее к сложной сетевой динамикеАвторы): Андрей В. Андреев; Наталия А. Малова; Екатерина И. Боровкова; Никита С.Фролов
Показать аннотацию
Мы исследуем динамику сетей из 100 идентичных бистабильных нейронов Ходжкина-Хаксли с безмасштабными, малыми мирами и случайными топологиями. Для всех из них мы обнаруживаем явление, когда одна часть нейронов находится в состоянии покоя, а другая находится в колебательном режиме в определенной области силы связи и амплитуды внешнего тока.Мы исследуем это явление и объясняем его взаимодействием нейронов, аналогичным короткому импульсу внешнего тока, который способен переключать режим нейрона с покоя на колебательный и наоборот. Мы находим различия в этом явлении для разных топологий и исследуем его эволюцию с увеличением внешнего тока.
Управление динамикой бистабильной нейронной сети внешним импульсомАвторы): Андрей В.Андреев; Никита Сергеевич Фролов; Наталия Александрова Александрова; Мария А. Чабан
Показать аннотацию
Мы исследуем динамику отдельного нейрона Ходжкина-Хаксли в мультистабильной области, где сосуществуют как стабильная фиксированная точка, так и стабильный предельный цикл. Продемонстрирована возможность управления динамикой нейрона коротким импульсом постоянного внешнего тока.В зависимости от времени, длительности и амплитуды импульса он может переключать состояние нейрона из состояния покоя в колебательное и наоборот. Мы исследуем возможность управления динамикой сети из 100 бистабильных нейронов Ходжкина-Хаксли с помощью короткого внешнего импульса тока. Мы показываем, что для определенных значений параметров импульса, таких как амплитуда, продолжительность и время приложения, импульс может заставить некоторые нейроны изменить свою динамику.
Вывод функциональной зависимости в связанных хаотических системах с использованием нейронной сети с прямой связьюАвторы): Никита С.Фролов; Макаров Владимир Васильевич
Показать аннотацию
Мы предлагаем новый безмодельный метод на основе искусственной нейронной сети с прямой связью для обнаружения функциональной связности в связанных системах. Разработанный метод, не требующий больших вычислительных затрат и способный работать с короткими испытаниями данных, может быть использован для анализа и восстановления связности экспериментальных многоканальных данных различной природы.Мы тестируем этот подход на хаотической системе Рёсслера и демонстрируем хорошее согласие с предыдущими известными результатами.
Энергообмен M-солитонного кластера в двумерной решетке МорсаАвторы): Игорь А. Шепелев; Елена А. Корзникова; Павел В. Захаров; Дмитриев Сергей Васильевич
Показать аннотацию
Краудион представляет собой разновидность межузельного дефекта, расположенного в плотно упакованных атомных рядах, может играть важную роль в релаксационных процессах, происходящих в кристаллах в неравновесных условиях, эффективно передавая массу и энергию.В последнее время динамика краудионов широко изучалась для различных типов решеток и размеров. Однако точка обмена энергией между краудионами ранее не рассматривалась. В статье представлен анализ энергообмена в комплексе краудионов, расположенных в соседнем плотно упакованном атомном ряду. Полученные результаты показывают, что близко расположенные краудионы могут интенсивно передавать энергию друг другу, что влияет на динамику и сценарий эволюции дефектной структуры в кристалле.
Динамика дыхания 2-краудионов в платинеАвторы): Айрат М. Баязитов; Елена А. Корзникова; Игорь А. Шепелев; Павел В. Захаров; Дмитриев Сергей Васильевич
Показать аннотацию
Краудионы, будучи межузельными атомами, расположенными в плотноупакованных атомных рядах, играют важную роль в релаксационных процессах, происходящих в металлах и сплавах при сильных внешних воздействиях, эффективно передавая массу и энергию.Недавно концепция сверхзвукового краудиона была расширена до N-краудиона, состоящего в одномерном движении N дополнительных атомов вдоль плотно упакованного атомного ряда. В данной работе методом молекулярной динамики изучено движение 1- и 2-краудионов в ГЦК решетке Pt. N-краудион возбуждался путем приложения одинаковой скорости к N соседним атомам вдоль плотно упакованного ряда. Установлено, что независимо от начальных условий краудион демонстрирует квазипериодическую динамику бризера, а средняя длина пробега практически не зависит от начальной скорости и конфигурации.
Обзор специально дискретизированных моделей Клейна-ГордонаАвторы): Юрий Васильевич Бебихов; Игорь А. Шепелев; Дмитриев Сергей Васильевич
Показать аннотацию
Дискретные перегибы в уравнениях Клейна-Гордона обычно имеют две равновесные конфигурации: нестабильную с максимальной потенциальной энергией и стабильную с минимальной энергией.Разница между энергиями кинка в этих двух конфигурациях дает высоту потенциала Пайерлса-Набарро. Максимальный градиент этого потенциала дает минимальную силу, необходимую для приведения изгиба в движение. Было показано, что некоторые исключительные неинтегрируемые дискретизации уравнения Клейна-Гордона имеют нулевой статический потенциал Пайерлса-Набарро. Произвольно малая внешняя сила в таких моделях приводит к ускорению кинка. Здесь будут рассмотрены несколько методов, дающих дискретные модели Клейна-Гордона с нулевым статическим потенциалом Пайерлса-Набарро.Будут упомянуты законы сохранения, которым удовлетворяют эти дискретные уравнения.
Фазовые переходы в пучках углеродных нанотрубок при боковом сжатииАвторы): Дина Юрьевна Абдуллина; Алексей А. Кудрейко; Елена А. Корзникова; Игорь А. Шепелев; Сергей В.Дмитриев
Показать аннотацию
Углеродные нанотрубки (УНТ) обладают очень высокими механическими свойствами, поэтому их используют для изготовления сверхпрочных и легких нитей, канатов, наполнителей для композитов, твердых смазок и т. Д. Механические свойства жгутов УНТ рассматривались в ряде экспериментальных и теоретические исследования. Разработка эффективных вычислительных методов для решения этой проблемы является важным шагом в разработке новых материалов на основе УНТ.В настоящем исследовании модель атомистической цепи используется для анализа механического отклика кристалла УНТ в условиях плоской деформации. Модель учитывает растяжение и изгиб стенки УНТ, а также ван-дер-ваальсовы взаимодействия. Дискретность модели позволяет описать большую кривизну стенки УНТ и разрушение УНТ при очень высоком давлении. Получены равновесные структуры кристалла УНТ при двухосном нагружении с контролируемой деформацией, а потенциальная энергия структуры разложена на энергию валентных связей, валентных углов и ван-дер-ваальсовых взаимодействий.Показано, что основной вклад в потенциальную энергию дает энергия валентных углов, связанная с изгибом стенок УНТ. Представленные результаты моделирования хорошо согласуются с существующей литературой. Предлагаемая здесь цепная модель может быть эффективно применена для анализа механических свойств однослойных или многослойных пучков УНТ в условиях плоской деформации или, при несложных модификациях, к аналогичным структурам из других 2D наноматериалов.
Масштабирование характеристик прерывистой динамики, охарактеризованных на основе наборов данныхАвторы): Ольга Н.Павлова; Алексей Николаевич Павлов
Показать аннотацию
Мы обсуждаем, как случайное переключение между двумя состояниями в динамике сложных систем влияет на характеристики колебаний на основе анализа данных.
