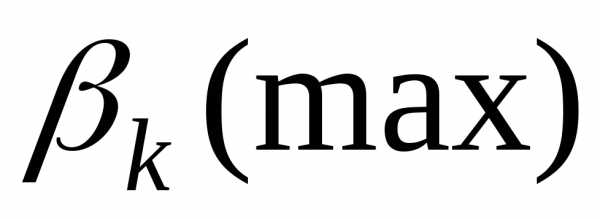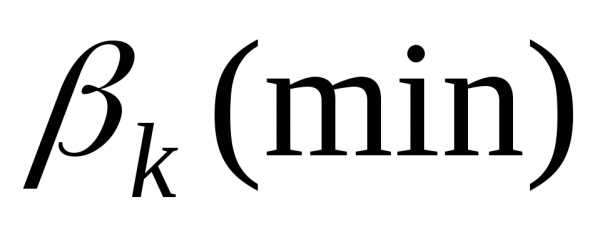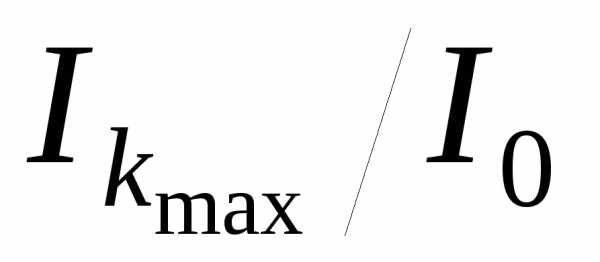Дифракция света
7
Л3-4Дифракция света
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле – любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшое отверстие в экранах и т.д.
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате наложения (суперпозиции) волн. По историческим причинам отклонение от закона независимости световых пучков, возникающее в результате суперпозиции когерентных волн, принято называть интерференцией волн. Отклонение от закона прямолинейного распространения света, в свою очередь, принято называть дифракцией волн.
Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида дифракции. Если источник света S и точка наблюдения P расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку P, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля. Дифракцию Фраунгофера можно наблюдать, поместив за источником света S и перед точкой наблюдения P по линзе так, чтобы точки S и P оказались в фокальной плоскости соответствующей линзы (рис.).
Принципиально дифракция Фраунгофера
не отличается от дифракции Френеля.
Количественный критерий, позволяющий
установить, какой вид дифракции имеет
место, определяется величиной безразмерного
параметра 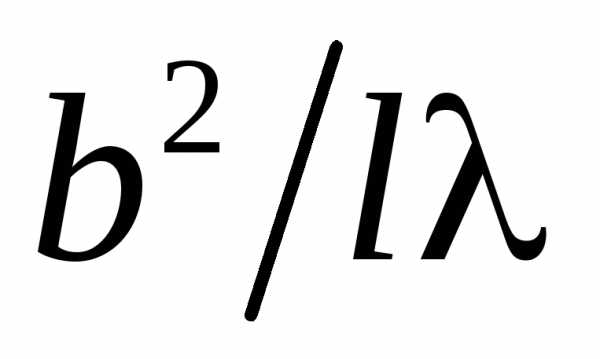
Явление дифракции качественно объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Для монохроматической волны волновая поверхность есть поверхность, на которой колебания совершаются в одинаковой фазе.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис.). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т.е. огибает края отверстия.
Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а, следовательно, и об интенсивности на фронте волны. Из повседневного опыта известно, что в большом числе случаев лучи света не отклоняются от их прямолинейного распространения. Так, предметы, освещенные точечным источником света, дают резкую тень. Таким образом, принцип Гюйгенса нуждается в дополнении, позволяющем определять интенсивность волны.
Френель дополнил принцип Гюйгенса идеей интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, излучаемых малыми элементами некоторой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому источники вторичных волн действуют синфазно. В аналитическом виде для точечного источника этот принцип записывается в виде
, (1)
где E – световой
вектор, включающий в себя временную
зависимость 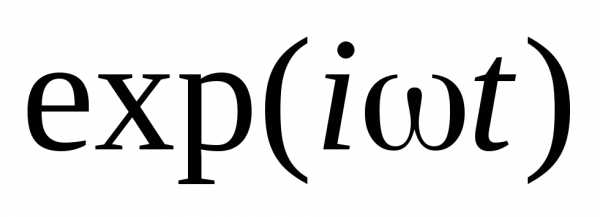 , k – волновое число, r – расстояние
от точки P на
поверхности S до точки P, K – коэффициент, зависящий от ориентации
площадки по отношению к источнику и
точке P. Правомерность
формулы (1) и вид функции K устанавливается в
рамках электромагнитной теории света
(в оптическом приближении).
, k – волновое число, r – расстояние
от точки P на
поверхности S до точки P, K – коэффициент, зависящий от ориентации
площадки по отношению к источнику и
точке P. Правомерность
формулы (1) и вид функции K устанавливается в
рамках электромагнитной теории света
(в оптическом приближении).
В том случае, когда между источником S и точкой наблюдения P имеются непрозрачные экраны с отверстиями, действие этих экранов может быть учтено следующим образом. На поверхности непрозрачных экранов амплитуды вторичных источников считаются равными нулю; в области отверстий амплитуды источников такие же, как при отсутствии экрана (так называемое приближение Кирхгофа).
Метод зон Френеля. Учет амплитуд и фаз вторичных волн позволяет в принципе найти амплитуду результирующей волны в любой точке пространства и решить задачу о распространении света. В общем случае расчет интерференции вторичных волн по формуле (1) довольно сложный и громоздкий. Однако ряд задач можно решить, применив чрезвычайно наглядный прием, заменяющий сложные вычисления. Метод этот получил название метода зон Френеля.
Суть метода разберем на примере точечного
источника света S.
Волновые поверхности представляют
собой в этом случае концентрические
сферы с центром в S.
Разобьем изображенную на рисунке
волновую поверхность на кольцевые зоны,
построенные так, что расстояния от краев
каждой зоны до точки P отличаются на 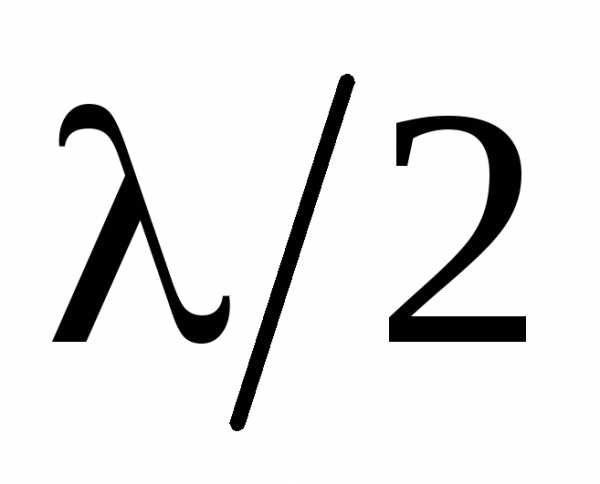 .
Обладающие таким свойством зоны
называются зонами Френеля. Из рис.
видно, что расстояние
.
Обладающие таким свойством зоны
называются зонами Френеля. Из рис.
видно, что расстояние 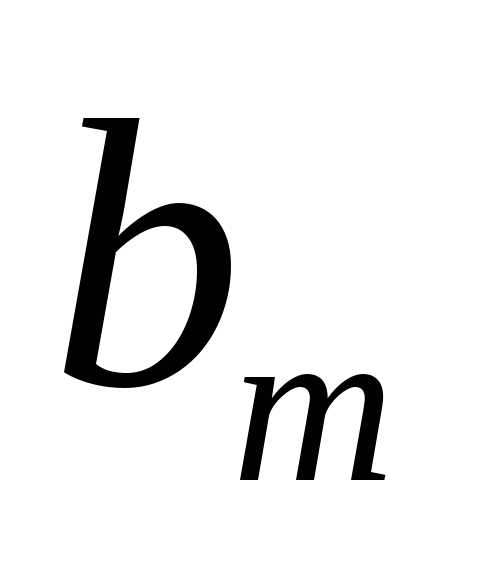 от внешнего края – m-й
зоны до точки P равно
от внешнего края – m-й
зоны до точки P равно
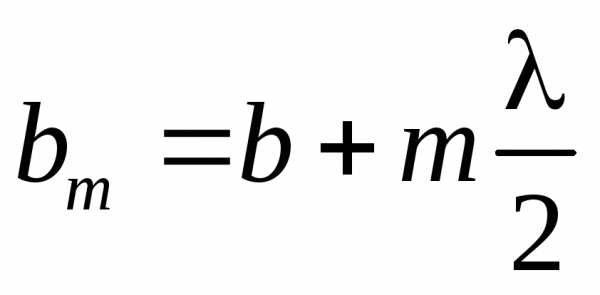 ,
где b – расстояние
от вершины волновой поверхности O до точки P.
,
где b – расстояние
от вершины волновой поверхности O до точки P.
Колебания, приходящие в точку P от аналогичных точек двух соседних зон (например, точек, лежащих в середине зон или у внешних краев зон), находятся в противофазе. Поэтому колебания от соседних зон будут взаимно ослаблять друг друга и амплитуда результирующего светового колебания в точке P
, (2)
где  ,
,  ,
… – амплитуды колебаний, возбуждаемых
1-й, 2-й, … зонами.
,
… – амплитуды колебаний, возбуждаемых
1-й, 2-й, … зонами.
Для оценки амплитуд колебаний найдем
площади зон Френеля. Пусть внешняя
граница m-й
зоны выделяет на волновой поверхности
сферический сегмент высоты 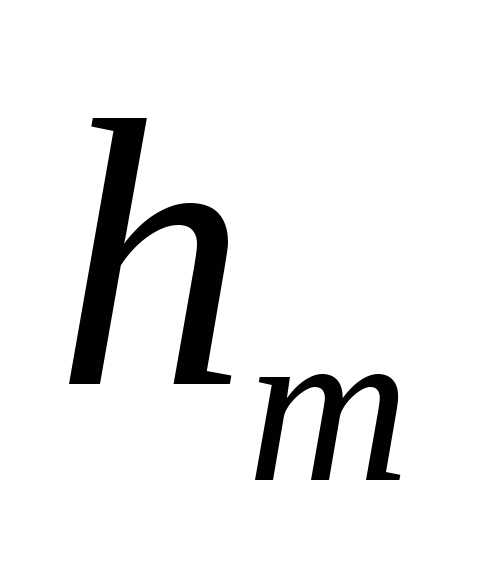
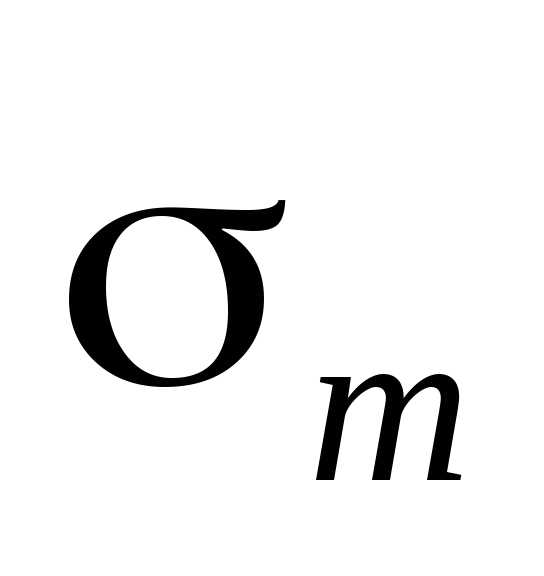 ,
найдем, что, площадь m-й
зоны Френеля равна
.
Из рисунка видно, что
.
После несложных преобразований,
учитывая
,
найдем, что, площадь m-й
зоны Френеля равна
.
Из рисунка видно, что
.
После несложных преобразований,
учитывая 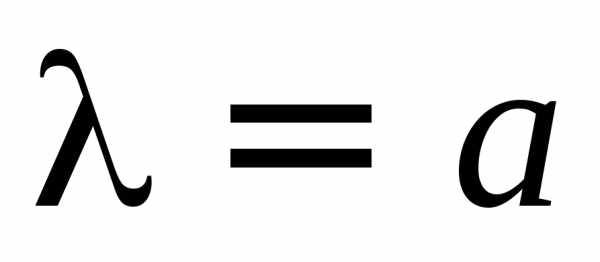 и
и 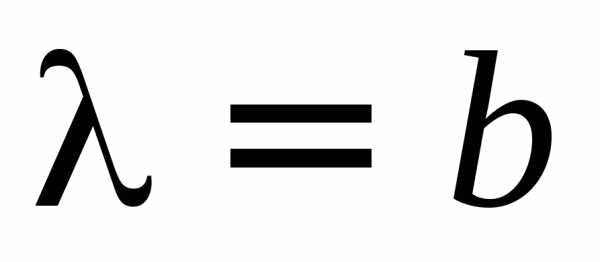 ,
получим
,
получим 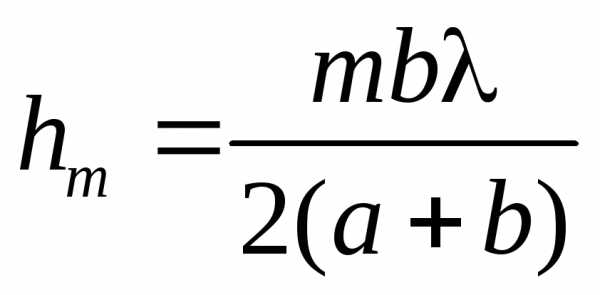 .
Площадь сферического сегмента и
площадь m-й
зоны Френеля соответственно равны
.
Площадь сферического сегмента и
площадь m-й
зоны Френеля соответственно равны
, . (3)
Таким образом, при не слишком
больших m площади зон
Френеля одинаковы. Согласно предположению
Френеля, действие отдельных зон в точке P тем меньше, чем больше
угол 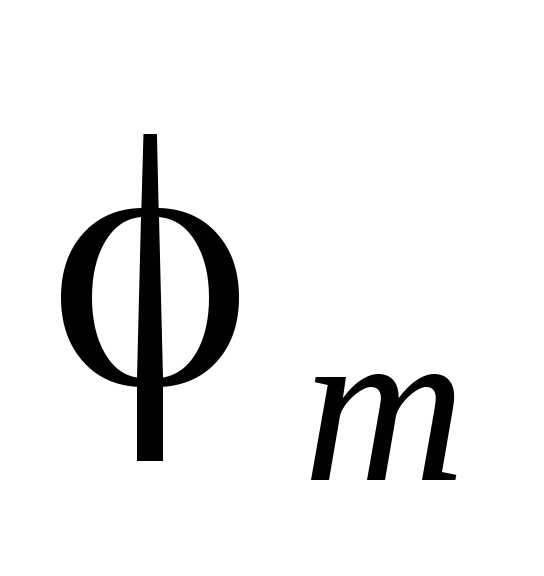 между нормалью n к поверхности зоны и направлением
на P, т.е. действие зон
постепенно убывает от центральной к
периферийным. Кроме того, интенсивность
излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от
зоны до точки P.
Таким образом, амплитуды колебаний
образуют монотонно убывающую
последовательность
между нормалью n к поверхности зоны и направлением
на P, т.е. действие зон
постепенно убывает от центральной к
периферийным. Кроме того, интенсивность
излучения в направлении точки P уменьшается с ростом m и вследствие увеличения расстояния от
зоны до точки P.
Таким образом, амплитуды колебаний
образуют монотонно убывающую
последовательность
.
Общее число зон Френеля, умещающихся на полусфере, очень велико; например, при и число зон достигает ~106. Это означает, что амплитуда убывает очень медленно и поэтому можно приближенно считать
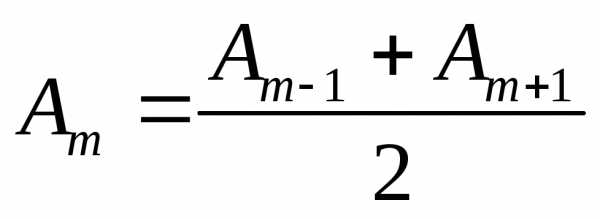 . (4)
Тогда выражение (2) после перегруппировки
суммируется
. (4)
Тогда выражение (2) после перегруппировки
суммируется
, (5) так как выражения в скобках, согласно (4), равны нулю, а вклад последнего слагаемого ничтожно мал. Таким образом, амплитуда результирующих колебаний в произвольной точке P определяется как бы половинным действием центральной зоны Френеля.
При не слишком больших m высота сегмента 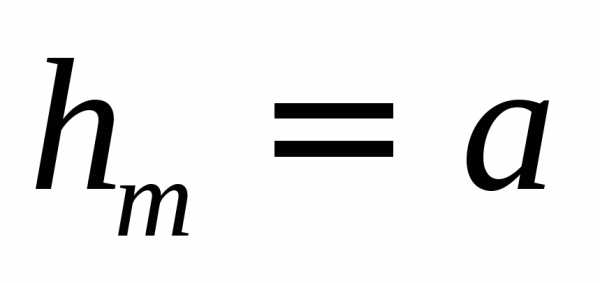
 .
Подставив значение для
.
Подставив значение для 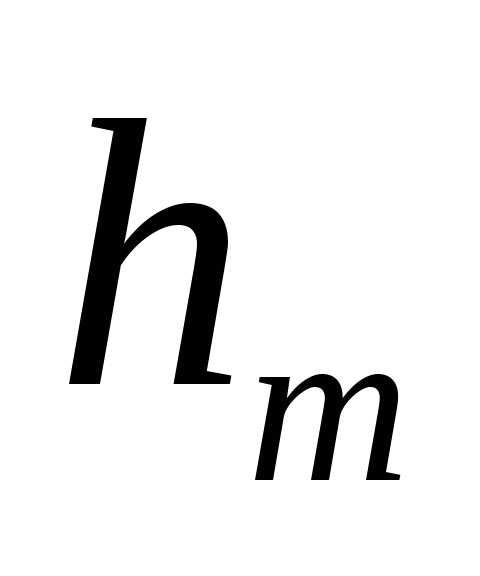 ,
получим для радиуса внешней границы m-й
зоны
,
получим для радиуса внешней границы m-й
зоны  . (6)
При и радиус первой (центральной) зоны
.
Следовательно, распространение света
от S к P происходит так, как если бы световой
поток шел внутри очень узкого канала
вдоль SP, т.е. прямолинейно.
. (6)
При и радиус первой (центральной) зоны
.
Следовательно, распространение света
от S к P происходит так, как если бы световой
поток шел внутри очень узкого канала
вдоль SP, т.е. прямолинейно.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонная пластинка – в простейшем случае стеклянная пластинка, состоящая из системы чередующихся прозрачных и непрозрачных концентрических колец, с радиусами зон Френеля заданной конфигурации. Если поместить зонную пластинку в строго определенном месте (на расстоянии a от точечного источника и на расстоянии b от точки наблюдения), то результирующая амплитуда будет больше, чем при полностью открытом волновом фронте.
Дифракция Френеля на круглом отверстии. Дифракция Френеля наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию, в данном случае экрана с отверстием. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути экран с отверстием. Дифракционная картина наблюдается на экране, параллельном экрану с отверстием. Ее вид зависит от расстояния между отверстием и экраном (для данного диаметра отверстия). Проще определить амплитуду световых колебаний в центре картины. Для этого разобьем открытую часть волновой поверхности на зоны Френеля. Амплитуда колебания, возбуждаемая всеми зонами равна
, (7) где знак плюс отвечает нечетным m и минус – четным m.
Когда отверстие открывает нечетное
число зон Френеля, то амплитуда
(интенсивность) в центральной точке
будет больше, чем при свободном
распространении волны; если четное то
амплитуда (интенсивность) будет равна
нулю. Например, если отверстие открывает
одну зону Френеля, амплитуда 
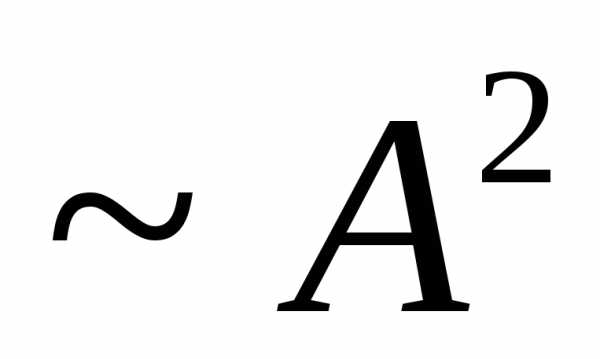 )
больше в четыре раза.
)
больше в четыре раза.Расчет амплитуды колебания на внеосевых участках экрана более сложен, так как соответствующие зоны Френеля частично перекрываются непрозрачным экраном. Качественно ясно, что дифракционная картина будет иметь вид чередующихся темных и светлых колец с общим центром (если m четное, то в центре будет темное кольцо, если m нечетное – то светлое пятно), причем интенсивность в максимумах убывает с расстоянием от центра картины. Если отверстие освещается не монохроматическим светом, а белым светом, то кольца окрашены.
Рассмотрим предельные случаи. Если
отверстие открывает лишь часть
центральной зоны Френеля, на экране
получается размытое светлое пятно;
чередования светлых и темных колец в
этом случае не возникает. Если отверстие
открывает большое число зон, то 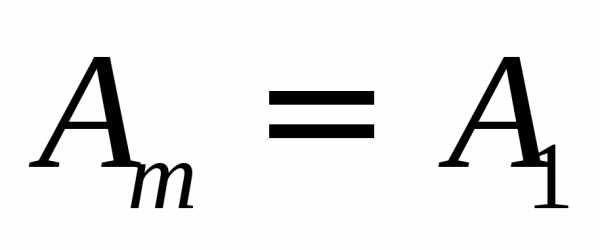 и амплитуда в центре
и амплитуда в центре 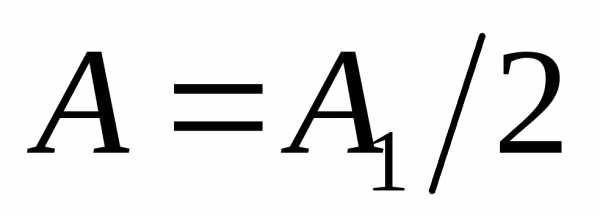 ,
т.е. такая же, как и при полностью открытом
волновом фронте; чередование светлых
и темных колец происходит лишь в очень
узкой области на границе геометрической
тени. Фактически дифракционная картина
не наблюдается, и распространение света,
по сути, является прямолинейным.
,
т.е. такая же, как и при полностью открытом
волновом фронте; чередование светлых
и темных колец происходит лишь в очень
узкой области на границе геометрической
тени. Фактически дифракционная картина
не наблюдается, и распространение света,
по сути, является прямолинейным.
Дифракция Френеля на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск (рис.). Дифракционная картина, наблюдаемая на экране, является центрально симметричной. Определим амплитуду световых колебаний в центре. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда колебаний равна
или
, (8)
так как выражения, стоящие в скобках,
равны нулю. Следовательно, в центре
всегда наблюдается дифракционный
максимум (светлое пятно), соответствующий
половине действия первой открытой зоны
Френеля. Центральный максимум окружен
концентрическими с ним темными и светлыми
кольцами. При небольшом числе закрытых
зон амплитуда 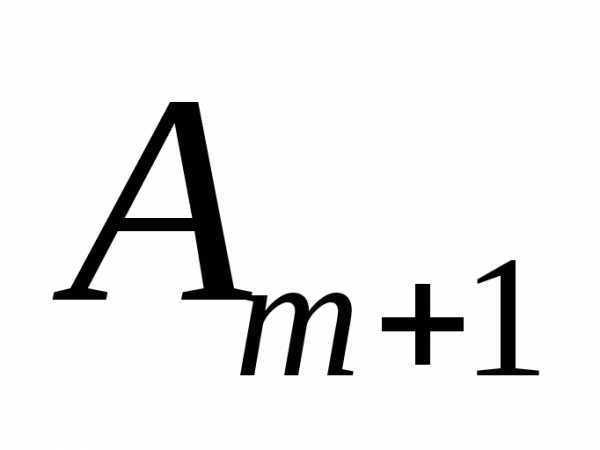 мало отличается от
мало отличается от  .
Поэтому интенсивность в центре будет
почти такая же, как при отсутствии диска.
Изменение освещенности экрана с
расстоянием от центра картины изображено
на рис.
.
Поэтому интенсивность в центре будет
почти такая же, как при отсутствии диска.
Изменение освещенности экрана с
расстоянием от центра картины изображено
на рис.
Рассмотрим предельные случаи. Если диск
закрывает лишь небольшую часть центральной
зоны Френеля, он совсем не отбрасывает
тени – освещенность экрана всюду
остается такой же, как при отсутствии
диска. Если диск закрывает много зон
Френеля, чередование светлых и темных
колец наблюдается только в узкой области
на границе геометрической тени. В этом
случае 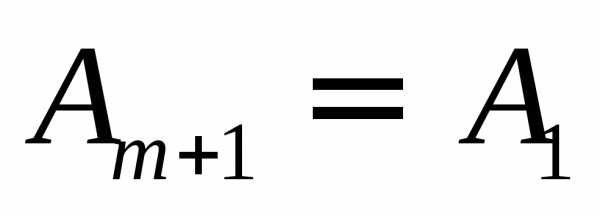 ,
так что светлое пятно в центре отсутствует,
и освещенность в области геометрической
тени практически всюду равна нулю.
Фактически дифракционная картина не
наблюдается, и распространение света
является прямолинейным.
,
так что светлое пятно в центре отсутствует,
и освещенность в области геометрической
тени практически всюду равна нулю.
Фактически дифракционная картина не
наблюдается, и распространение света
является прямолинейным.
Дифракция Фраунгофера на одной щели. Пусть плоская монохроматическая волна падает нормально плоскости узкой щели шириной a. Оптическая разность хода между крайними лучами, идущими от щели в некотором направлении
.
Разобьем открытую часть волновой
поверхности в плоскости щели на зоны
Френеля, имеющие вид равновеликих полос,
параллельных щели. Так как ширина каждой
зоны выбирается такой, чтобы разность
хода от краев этих зон была равна 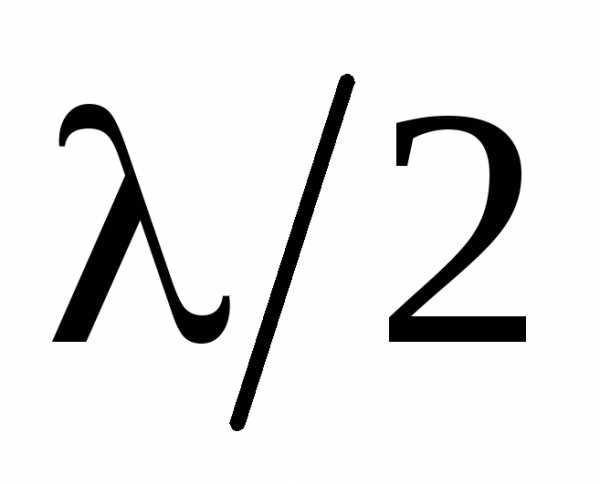 ,
то на ширине щели уместится
,
то на ширине щели уместится  зон. Амплитуды вторичных волн в плоскости
щели будут равны, так как зоны Френеля
имеют одинаковые площади и одинаково
наклонены к направлению наблюдения.
Фазы колебаний от пары соседних зон
Френеля отличаются на ,
поэтому, суммарная амплитуда этих
колебаний равна нулю.
зон. Амплитуды вторичных волн в плоскости
щели будут равны, так как зоны Френеля
имеют одинаковые площади и одинаково
наклонены к направлению наблюдения.
Фазы колебаний от пары соседних зон
Френеля отличаются на ,
поэтому, суммарная амплитуда этих
колебаний равна нулю.
Если число зон Френеля четное, то
, (9а) и в точке B наблюдается минимум освещенности (темный участок), если же число зон Френеля нечетное, то
(9б)
и
наблюдается близкая к максимуму
освещенность, соответствующей действию
одной нескомпенсированной зоны Френеля.
В направлении  щель действует, как одна зона Френеля,
и в этом направлении наблюдается
наибольшая освещенность, точке
щель действует, как одна зона Френеля,
и в этом направлении наблюдается
наибольшая освещенность, точке  соответствует центральный или главный
максимум освещенности.
соответствует центральный или главный
максимум освещенности.
Расчет освещенности в зависимости от направления дает
, (10)
где 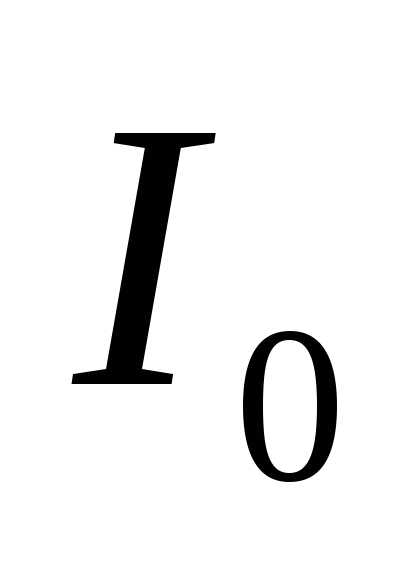 – освещенность в середине дифракционной
картины (против центра линзы),
– освещенность в середине дифракционной
картины (против центра линзы), 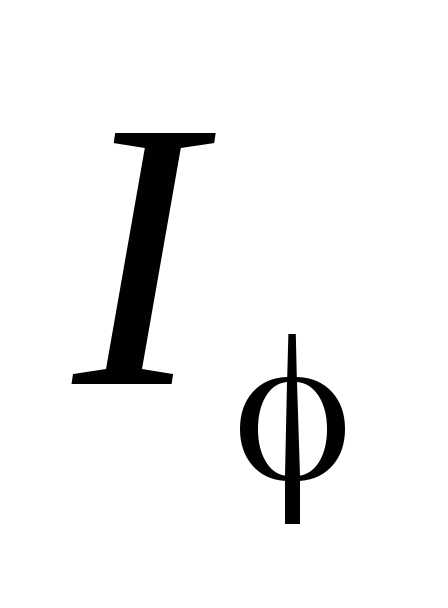 – освещенность в точке, положение
которой определяется направлением .
График функции (10) изображен на рис.
Максимумы освещенности соответствуют
значениям ,
удовлетворяющие условиям
– освещенность в точке, положение
которой определяется направлением .
График функции (10) изображен на рис.
Максимумы освещенности соответствуют
значениям ,
удовлетворяющие условиям
, , и т.д. Вместо этих условий для максимумов приближенно можно пользоваться соотношением (9б), дающим близкие значения углов. Величина вторичных максимумов быстро убывает. Численные значения интенсивностей главного и следующих максимумов относятся как
и т.д., т.е. основная часть световой энергии, прошедшей через щель, сосредоточена в главном максимуме.
Сужение щели приводит к тому, что
центральный максимум расплывается, а
его освещенность уменьшается. Наоборот,
чем щель шире, тем картина ярче, но
дифракционные полосы уже, а число самих
полос больше. При  в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
в центре получается резкое изображение
источника света, т.е. имеет место
прямолинейное распространение света.
studfiles.net
Дифракция света
Определение 1Дифракция света – это явление отклонения света от прямолинейного направления его распространения во время прохождения рядом с препятствиями.
Из опыта видно, что определенные условия влияют на захождение геометрической тени на область.
Когда на пути встречается препятствие в виде диска, шарика или круглого отверстия, тогда экран, расположенный на большом расстоянии, покажет дифракционную картину, то есть систему чередующихся светлых и темных колец. При отверстии линейного характера (щели или нити) экран показывает параллельные дифракционные полосы.
Принцип Гюйгенса-Френеля
Существование дифракционных явлений было задолго до времен Ньютона. Объяснение, основанное на корпускулярной теории, не давало должных результатов. Одним из первых объяснений явления дифракции, основанное на волновых представлениях, было дано Т. Юнгом. Еще в 1818 году была известна и развита количественная теория дифракционных явлений О. Френеля. Принцип Гюйгенса был заложен в основу. Он только дополнил при помощи идеи об интерференции вторичных волн.
Первоначальный вид данного принципа давал возможность нахождения положения фронтов в последующие моменты времени, иначе говоря, определял направление распространения волны. Это и есть принцип геометрической оптики. Впоследствии гипотеза Гюйгенса об огибающих вторичных волнах были заменены Френелем с помощью физически ясного положения, тогда вторичные волны в точке наблюдения интерферировали друг с другом.
Принципом Гюйгенса-Френеля считалась гипотеза, которая была со временем подтверждена. При решении задач, где необходимо использовать данный принцип, получение результата достаточно точное. На иллюстрации изображен принцип Гюйгенса-Френеля.
Рисунок 3.8.1 Принцип Гюйгенса-Френеля. ∆S1 и ∆S2– элементы волнового фронта, n1→ и n2→ — заданные нормали.
Предположим, что поверхность S – положение волнового фронта в некоторый момент. Из теории волн известно, что он является поверхностью, где в заданных точках происходит колебание с одинаковым значением фазы. Волновыми фронтами плоской волны считают семейством параллельных плоскостей, которые перпендикулярно направлены относительно распространения волны. Волновые фронты сферической волны, которые испускаются при помощи точечного источника, относят к концентрическим сф
zaochnik.com
Дифракция — Всё для чайников
Дифракция
- Подробности
- Категория: Оптика
ДИФРАКЦИЯ
Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.

Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.
Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.
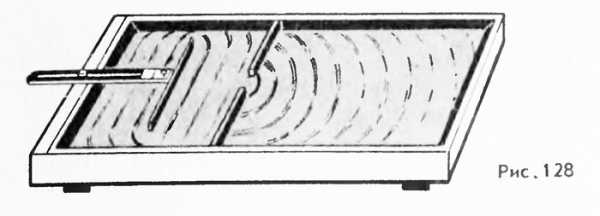
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
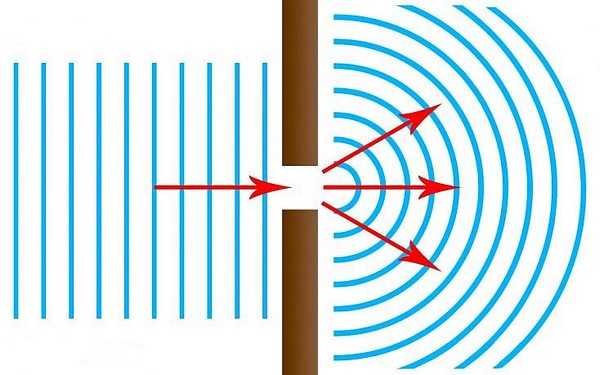
Явление дифракции волн на поверхности воды можно наблюдать, если поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны (рис. 128). Хорошо будет видно, что за экраном распространяется круговая волна, как если бы в отверстии экрана располагалось колеблющееся тело -источник волн. Согласно принципу Гюйгенса так и должно быть. Вторичные источники в узкой щели располагаются столь близко друг к другу, что их можно рассматривать как один точечный источник.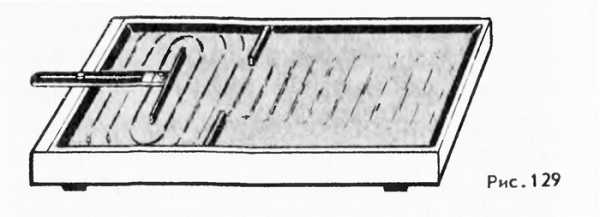
Если размеры щели велики по сравнению с длиной волны, то картина распространения волн за экраном совершенно иная (рис. 129). Волна проходит сквозь щель, почти не меняя своей формы. Только по краям можно заметить небольшие искривления волновой поверхности, благодаря которым волна частично проникает и в пространство за экраном. Принцип Гюйгенса позволяет понять, почему происходит дифракция. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.
ДИФРАКЦИЯ СВЕТА
Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.
Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.
Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.
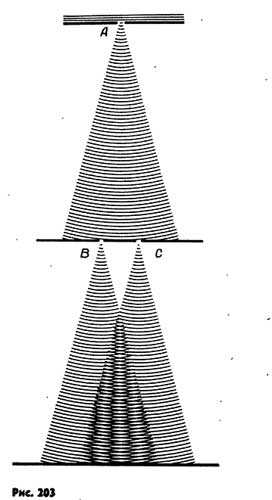
Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.
Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.
Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.
Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.
Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).

Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.
Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.
Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.
Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.
На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.
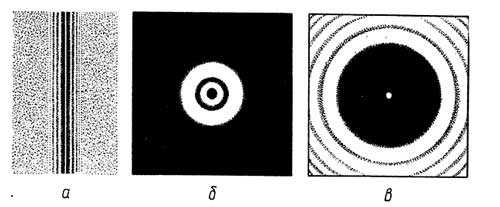
Зоны Френеля для трехсантиметровой волны
Зонная пластинка для трехсантиметровых волн
Трёхсантиметровые волны: пятно Пуассона
Трёхсантиметровые волны: фазовая зонная пластинка
Круглое отверстие. Геометрическая оптика — дифракция Френеля
Круглое отверстие. Дифракция Френеля — дифракция Фраунгофера
Сравнение картин дифракции: ирисовая диафрагма и круглое отверстие
Пятно Пуассона
Дифракция Френеля на краю полуплоскости
Трехсантиметровые волны: дифракция Френеля на двух щелях
Дифракция Фраунгофера. Щель и полоска
Дифракция Фраунгофера. Две щели
Дифракционные решетки с разными периодами
Двумерные дифракционные решетки
Трёхсантиметровые волны и очень узкая щель
Модель спирали Корню
forkettle.ru
Дифракция света и дифракционная решетка: определение простыми словами

Содержание:
Первые опыты и активные исследования природы света начались еще в далеком XVII веке, когда итальянский ученый Франческо Гримальди впервые открыл такое интересное физическое явление как дифракция света. Что же такое дифракция света? Это отклонение света от прямолинейного распространения в силу определенных препятствий на его пути. Более научное объяснение причинам дифракции света было дано в начале XIX века английским ученым Томасом Юнгом, согласно нему дифракция света возможна благодаря тому, что свет представляет собой волну, идущую от своего источника и естественным образом искривляющуюся при попадании на определенные препятствия. Им же была изобретена первая дифракционная решетка, представляющая собой оптический прибор, работающий на основе дифракции света, то есть специально искривляющий световую волну.
Дифракция и интерференция света
Изучая поведение монохроматического пучка света, Томас Юнг, разделив его пополам, получил дифракционную картину, которая представляла собой последовательное чередование ярких и темных полос на экране. Волновая теория природы света, сформированная Юнгом, прекрасно объясняла это явление. Будучи волной, пучок света при попадании на непрозрачное препятствие искривляется, меняет траекторию своего движения. Так появляется дифракция света, при которой свет может, как целиком огибать препятствия (если длина световой волны больше размеров препятствия) или искривлять свою траекторию (когда размеры препятствий сопоставимы с длиной световой волны). Примером тут может быть попадание света через узкие щели или небольшие отверстия, как на фото ниже.

Луч света в пещере, наглядная иллюстрация дифракции света в природе.
А тут на картинке показано более схематическое изображение дифракции.
Физическое явление дифракции света дополняет еще одно важное свойство световой волны — интерференция света. Суть интерференции света заключается в накладывании одних световых волн на другие. В результате может происходить искривление синусоидальной формы результирующей волны.

Так схематически выглядит интерференция.
При этом, волны, которые накладываются, могут, как усиливать мощь общей световой волны (при совпадении амплитуд), так и наоборот погасить ее.
Дифракционная решетка
Как мы писали выше, дифракционная решетка представляет собой простой оптический прибор, который искривляет световую волну.

Вот так она выглядит.

Или еще чуть более маленький экземпляр.
Также дифракционную решетку можно охарактеризовать тремя параметрами:
- Период d. Он представляет собой расстояние между двумя щелями, через которые проходит свет. Так как длина световой волны обычно находится в диапазоне нескольких десятых микрометра, то величина d обычно имеет 1 микрометр.
- Постоянная решетка а. Это количество прозрачных щелей на длине 1 мм поверхности решетки. Эта величина обратно пропорциональна периоду дифракционной решетки d. Обычно имеет 300-600 мм-1
- Общее количество щелей N. Высчитывается путем умножения длины дифракционной решетки на ее постоянную а. Обычно длина решетки имеет несколько сантиметров, а количество щелей при этом составляет 10-20 тысяч.
Виды дифракционных решеток
На самом деле есть целых два вида дифракционных решеток: прозрачная и отражающая.
Прозрачная решетка представляет собой прозрачную тонкую пластину из стекла или прозрачного пластика, на которую нанесены штрихи. Штрихи эти как раз и являются препятствиями для световой волны, сквозь них она не может пройти. Ширина штриха – это и есть, по сути, период дифракционной решетки d. А оставшиеся между штрихами прозрачные зазоры – это щели. Такие решетки наиболее часто применяются при выполнении лабораторных работ.
Отражающая дифракционная решетка – это металлическая либо пластиковая и отполированная пластина. Вместо штрихов на нее нанесены бороздки определенной глубины. Период d соответственно это расстояние между этими бороздками. Простым примером отражающей дифракционной решетки может быть оптический CD диск.

Такие решетки часто используют при анализе спектров излучения, так как благодаря их дизайну можно удобно распределить интенсивность максимумов дифракционной картины на пользу максимумов более высокого порядка.
Принцип работы дифракционной решетки
Представим, что на нашу решетку падает свет, имеющий плоский фронт. Это важный момент, так как классическая формула будет верна при условии, что волновой фронт является плоским и параллельным самой пластинке. Штрихи решетки будут вносить в этот световой фронт возмущение и как результат на выходе из решетки создаться ситуация будто бы работает множество когерентных (синхронных) источников излучения. Эти источники и являются причиной дифракции.
От каждого источника (по сути щели между штрихами решетки) будут распространяться световые волны, которые будут когерентными (синхронными) друг другу. Если на некотором расстоянии от решетки поместить экран, то мы сможем увидеть на нем яркие полосы, между которыми будет тень.
Формула дифракционной решетки
Яркие полосы, которые мы увидим на экране можно также назвать максимумами решетки. Если рассматривать условия усиления световых волн, то можно вывести формулу максимума дифракционной решетки, вот она.
sin(θm) = m*λ/d
Где θm это углы между перпендикуляром к центру пластинки и направлением на соответствующую линию максимума на экране. Величина m называется порядком дифракционной решетки. Она принимает целые значения и ноль, то есть m = 0, ±1, 2, 3 и так далее. λ – длина световой волны, а d – период решетки.
Таким образом, можно рассчитать положение всех максимумов решетки.
Разрешающая способность дифракционной решетки
Разрешающей способностью называют способность решетки разделить две волны с близкими значениями длины λ на два отдельных максимума на экране.
Применение дифракционной решетки
Какое же практическое применение дифракционной решетки, в чем ее конкретная польза? Дифракционная решетка является важным и незаменимым инструментов в спектроскопии, так с ее помощью можно узнать, например, химический состав далекой звезды. Свет, идущий от этой звезды, собирают зеркалами и направляют на решетку. Измеряя значения θm можно узнать все длины волн спектра, а значит и химические элементы, которые их излучают.
Дифракция света и дифракционная решетка, видео
И в завершение интересное образовательное видео по теме нашей статьи от заслуженного учителя Украины – Павла Виктора, на наш взгляд его видео лекции на Ютубе по физике могут быть очень полезными для всех, кто изучает этот предмет.
www.poznavayka.org
ДИФРАКЦИЯ СВЕТА • Большая российская энциклопедия
ДИФРА́КЦИЯ СВЕ́ТА, в узком, но наиболее употребительном смысле – огибание лучами света границы непрозрачных тел (экранов), проникновение света в область геометрич. тени. В широком смысле Д. с. – проявление волновых свойств света в условиях перехода от волновой оптики к геометрической. Наиболее рельефно Д. с. проявляется в областях резкого изменения плотности потока лучей: на границах геометрич. тени, вблизи фокуса линзы и др.
Д. с. тем слабее, чем меньше длина волны $λ$ света. Красный свет сильнее отклоняется на границе тел, чем фиолетовый. Поэтому последовательность цветов в спектральном разложении белого света, вызванном дифракцией, получается обратной по сравнению с получающейся при разложении света в призме за счёт дисперсии. Это различие часто бывает определяющим при выяснении природы мн. атмосферных оптич. явлений.
Проникновение света в область геометрич. тени было известно уже в 17 в.; так, Ф. М. Гримальди описал это явление в своём трактате, вышедшем в 1665. Однако объяснение Д. с. было дано лишь в 19 в. Тогда были сформулированы две, казалось бы, совершенно разные концепции Д. с. T. Юнг (1800) предположил, что Д. с. обусловлена поперечной диффузией волновых фронтов световых волн. Чередование тёмных и светлых полос на границе тени и света он считал результатом интерференции падающей плоской волны и вторичной, излучаемой границей.
Рис. 2. Дифракция света на круглом отверстии при открытом нечётном (а) и чётном (б) числе зон.

Рис. 1. Обрезание волнового фронта краями экрана.
В приближённой теории О. Френеля (1815–18) Д. с. считалась результатом интерференции вторичных волн (см. Гюйгенса – Френеля принцип). Несмотря на недостатки, эта теория сохранила своё значение и служит основой расчётов дифракционных эффектов в инструментальной оптике. В теории Френеля амплитуда $u_P$ светового поля в точке наблюдения $P$ (рис. 1) слагается из парциальных амплитуд сферич. волн, испускаемых всеми элементами $dS$ поверхности $S$, не закрытой экраном. Его метод вычисления освещённости за экраном заключался в разбиении поверхности $S$, совмещённой с фронтом падающей волны, на т. н. Френеля зоны, расстояния от края которых до точки $P$ отличаются на $λ/2$. Поэтому соседние зоны вносят в поле $u_Р$ вклады противоположных знаков, взаимно компенсирующие друг друга. Освещённость в точке $P$ зависит от местоположения и размера отверстия. Эта зависимость определяется количеством зон, доступных видению из точки $P$: если открыто чётное число зон, то в центре дифракционной картины получается тёмное пятно (рис. 2,б), при нечётном числе зон – светлое (рис. 2,а).
Метод Френеля также качественно объясняет причину освещения в области геометрич. тени круглого экрана: светлый центр (т. н. пятно Пуассона) создаётся вторичными волнами первой кольцевой зоны Френеля, окружающей экран. Метод расчёта освещённости за системой экранов с использованием зон Френеля положен в основу теории зонных пластинок.
При расчётах различают два случая Д. с. – дифракция Френеля и дифракция Фраунгофера – в зависимости от соотношения между $R,\text{ } L \text{ и } d$. [Здесь $L$ – радиус кривизны поверхности $S$, не закрытой экраном, $d$ – поперечный размер отверстия, $R$ – расстояние от точки наблюдения до центра $O$ диафрагмы (отверстия), рис. 1.] Дифракция Фраунгофера имеет место, когда $kd_2/l≪1$, т. е. $d≪\sqrt {l\lambda}$, где $𝑘$ – волновое число, $1/l=1/R+1/L$ (дифракция в дальней зоне). Если источник света расположен далеко от экрана, то фронт его волны в отверстии почти плоский $(L→∞)$, и тогда $d≪\sqrt {R\lambda}$. Дифракция Фраунгофера наблюдается, когда размер отверстия значительно меньше зоны Френеля. Картина дифракции в этом случае характеризуется угловым распределением интенсивности потока, расходящегося с углом расходимости $φ∼λ/d$. Картина дифракции Фраунгофера не меняется, если экраны превратить в диафрагмы, а последние – в экраны. Из этого следует, в частности, что маленький экран может служить фокусирующей системой в той же степени, что и отверстие в камере-обскуре.
Дифракция Френеля ($𝑘d^2/l≫1$, дифракция в ближней зоне) обусловлена изогнутостью дифрагирующего волнового фронта или его относительно большими угловыми размерами $d/r≫λ/d$, воспринимаемыми из точки наблюдения $P$ ($r$ – расстояние от $P$ до элемента поверхности $dS$). Дифракция Френеля наблюдается, когда размер отверстия сравним с размером зоны Френеля $d≈\sqrt {R\lambda}$. Расчёт этого случая сложен, он требует применения спец. функций даже при простейшей геометрии обрезания волновых фронтов.
Математически полное построение теории Френеля выполнил Г. Кирхгоф (1882). Однако в его теории не учитываются векторный характер световых волн и свойства самого материала экрана.
В строгих расчётах Д. с. рассматривается как граничная задача рассеяния света. Её точные решения позволяют выяснить пределы применимости теории Френеля – Кирхгофа и обосновывают представления Юнга. Из решений следует, что свет проникает в область тени сильнее, чем предсказано этой теорией. Световое поле вдали от острого края экрана в области тени такое же, как если бы край был источником граничной волны, что согласуется с представлениями Юнга. На самом деле, край – не бесконечно тонкий источник, хотя при приближении к нему плотность светового потока растёт. По этой причине глазу, аккомодированному на край, он кажется светящейся линией. Причём, несмотря на то что радиусы закругления краёв реальных экранов велики по сравнению с $λ$, дифракционные картины почти не зависят от формы краёв и их размеров: даже стеклянная пластинка радиусом в неск. метров, изогнутого края которой касается световая волна, создаёт структуру полос того же вида, что и лезвие бритвы.
Д. с. может проявляться и без эффекта резких границ, при плавных пространственных изменениях потоков светового поля. Напр., расплывание пучка при его распространении обусловлено дифракционной расходимостью. Расплывание пучков – яркое проявление концепции Юнга диффузии волновых фронтов.
Задачи диффузионной Д. с. связаны с исследованием распространения света в средах с крупномасштабными (по сравнению с $λ$) неоднородностями диэлектрической проницаемости: в турбулентных средах, в голографических системах, при дифракции света на ультразвуке и др. В этих случаях Д. с. часто неотделима от сопутствующей ей рефракции света.
Д. с. играет важную практич. роль: она ограничивает разрешающую способность микроскопов и телескопов, добротность открытых резонаторов и др. В лазерной технике Д. с. определяются свойства полей излучения (см. Нелинейная оптика).
bigenc.ru
Дифракция света. Дифракционная решетка. | Объединение учителей Санкт-Петербурга
Зоны Френеля
Принцип Гюйгенса — Френеля: волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.
Для того чтобы найти амплитуду световой волны от точечного монохроматического источника света А в произвольной точке О изотропной среды, надо источник света окружить сферой радиусом r=ct. Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке О, т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки О до волновой поверхности В равно r0. Первая зона Френеля ограничивается точками волновой поверхности, расстояния от которых до точки О равны: , где λ — длина световой волны. Вторая зона .
Аналогично определяются границы других зон. Если разность хода от двух соседних зон равна половине длины волны, то колебания от них приходят в точку О в противоположных фазах и наблюдается интерференционный минимум, если разность хода равна длине волны, то наблюдается интерференционный максимум.
Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно).
Расчеты позволили понять, каким образом свет от точечного источника, испускающего сферические волны, достигает произвольной точки О пространства.
www.eduspb.com
2 Дифракция света
МЧС России
Санкт-Петербургский университет государственной противопожарной службы
Утверждаю
Начальник кафедры физики и теплотехники, полковник вн.сл. Иванов А.Н.
(должность, звание, ФИО)
«13» октября 2008 года
ЛЕКЦИЯ
по учебной дисциплине «Физика»
Специальность 280104.65 — Пожарная безопасность
Заочное отделение, 6 лет
Тема № 6 «Оптика»
Обсуждена на заседании кафедры
Протокол № 2/10 от
«13» октября 2008 года
Санкт- Петербург
2008
I. Цели занятия
1. Образовательная – изучение интерференции, дифракции света и законов теплового излучения
2. воспитательные
— применение рассмотренных явлений в пожарной безопасности
— повышение квалификации сотрудников ГПС
II. Расчёт учебного времени
Содержание и порядок проведения занятия | Время, мин. |
ВВОДНАЯ ЧАСТЬ ОСНОВНАЯ ЧАСТЬ Учебные вопросы: 1.Интерференция света 2.Дифракция света 3.Тепловое излучение ЗАКЛЮЧИТЕЛЬНАЯ ЧАСТЬ | 5 260 80 90 90 5 |
III. Литература
Основная:
1. Трофимова Т.И. Курс физики. — М.: Высшая школа, 2003, с.316-375.
Дополнительная:
Савельев И.В. Курс общей физики. — М.: Наука, 1989, Т.1.
Трубилко А.И., Звонов В.С., Поляков А.С., Дятченко А.А. Электричество. Пособие для самостоятельной работы — СПб.: СПбИПБ МВД России, 1998.
IV. Учебно-материальное обеспечение
Технические средства обучения: мультимедийный проектор, интерактивная доска.
V. Текст лекции
Вводная часть. Ставятся цели занятия.
Учебные вопросы
1 Интерференция света
Явление интерференции заключается в наложении колебаний, вызванных различными источниками, с образованием упорядоченной картины чередования максимумов и минимумов интенсивности. Отметим, что интерференционная картина стационарна (не меняется во времени), хотя источники постоянно колеблются. Упорядоченная картина возникает благодаря усилению или ослаблению колебаний в точках пространства, до которых распространились возмущения от источников. Интерференция наблюдается при взаимодействии волн любой природы, в частности электромагнитных (свет, радиоволны) и звуковых. Возникновение интерференции возможно только при условии когерентности источников колебаний.
Когерентность. Источники колебаний (независимо от их природы) называются когерентными, если выполняются два условия:
1. частоты их колебаний одинаковы;
2. разность фаз колебаний не меняется во времени, т.е.
Невыполнение хотя бы одного из приведенных условий означает, что источники не будут когерентными. Стационарной устойчивой интерференционной картины в этом случае не возникает. Условия когерентности могут выполняться приближенно на определенном интервале времени и в ограниченной области пространства. В этом случае говорят о времени и длине когерентности.
При создании когерентных источников труднее всего обеспечить постоянство разности фаз. Для того, чтобы создать когерентные источники света (если в качестве источника света не используется лазер) световой луч разделяют на два. В частности, при использовании плоскопараллельной пластинки когерентными будут: луч, отраженный от передней границы, и луч, преломленный на передней и отраженный от задней границы (рис. 1). Кроме того, для получения когерентных лучей применяют бипризму Френеля и билинзу Бийе. Когерентные источники радиоволн можно получить, подавая на две или несколько антенн колебания от одного и того же генератора.
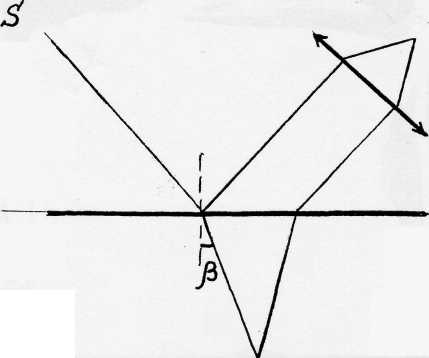
Рис.1. Получение когерентных лучей с помощью плоскопараллельной пластины
Интенсивность колебаний. Интенсивность пропорциональна квадрату амплитуды колебаний. Интенсивность колебаний в данной точке пространства при действии двух когерентных источников (рис. 2) определяется следующим соотношением
(1)
где
— амплитуда колебаний первого и второго
источников,- разность фаз колебаний от источников
в точке наблюдения, — частота колебаний,
— частота колебаний, — скорость распространения колебаний,- разность хода от источников до точки
наблюдения. Отметим, что,
где
— скорость распространения колебаний,- разность хода от источников до точки
наблюдения. Отметим, что,
где —
длина волны колебания.
—
длина волны колебания.
Если источники колебаний одинаковы, то А. Тогда из (1) будем иметь
(2)
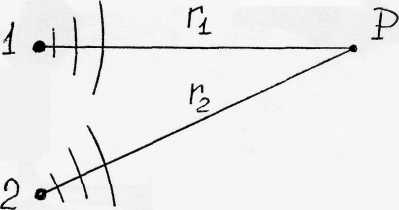
Формула (2) дает распределение интенсивности колебаний в пространстве при интерференции волн от двух источников (разность хода зависит от положения точки наблюдения). С ее помощью можно получить распределение интенсивности на экране.
Используя метод векторных диаграмм, можно получить формулу для интенсивности колебаний в случае интерференции волн от N источников, расположенных на одной линии:
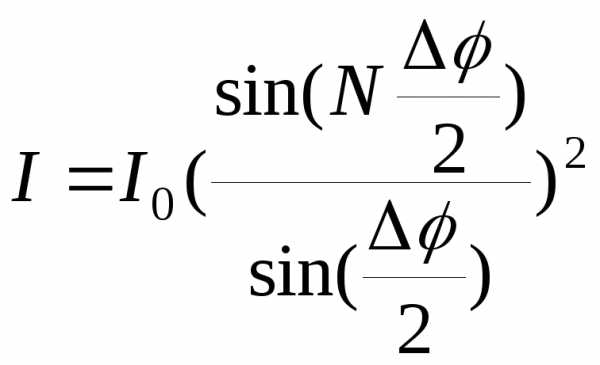 (3)
(3)
где  —
разность фаз соседних источников. При
N = 2 эта формула переходит в (2). При
—
разность фаз соседних источников. При
N = 2 эта формула переходит в (2). При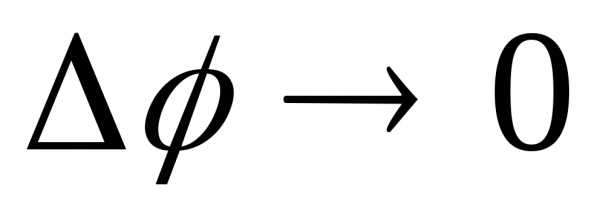 имеем
имеем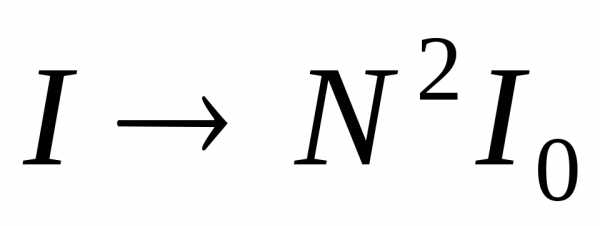 .
Таким образом, интенсивность волн,
создаваемых N источниками, оказывается
в
.
Таким образом, интенсивность волн,
создаваемых N источниками, оказывается
в раз
больше интенсивности, создаваемой
отдельным источником (рис. 2.3).
раз
больше интенсивности, создаваемой
отдельным источником (рис. 2.3).
Геометрическая
разность хода.
Характер взаимодействия двух колебаний,
вызванных разными когерентными
источниками, зависит от соотношения
расстояний 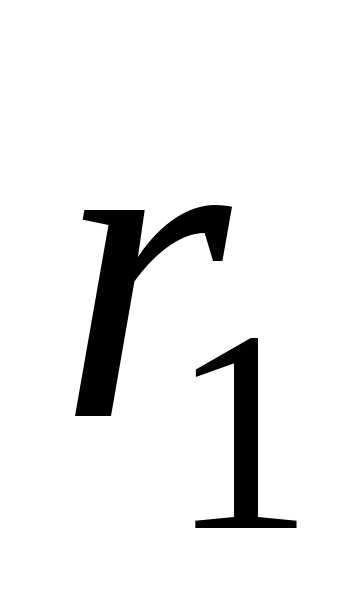 и
и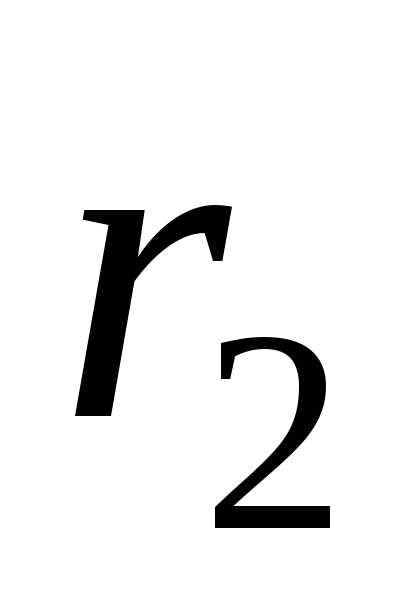 от источников до данной точки пространства.
Разностьназывается геометрической разностью
хода. В данной точке пространства Р
(рис. 2) будет наблюдаться максимальное
усиление колебаний, если разность фаз
от источников до данной точки пространства.
Разностьназывается геометрической разностью
хода. В данной точке пространства Р
(рис. 2) будет наблюдаться максимальное
усиление колебаний, если разность фаз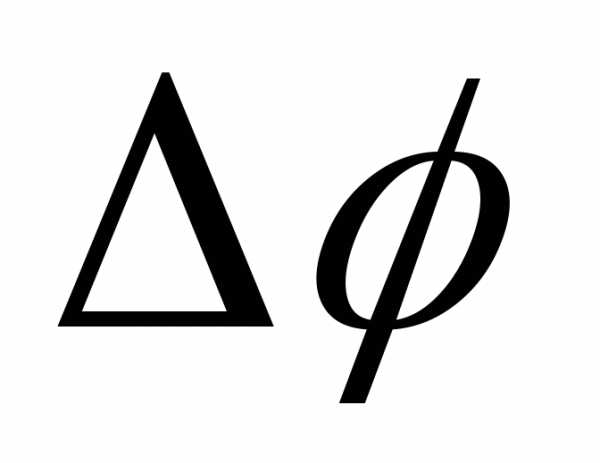 кратна
кратна .
В этом случае разность хода
.
В этом случае разность хода двух волн равна целому числу длин волн
(условие максимумов):
двух волн равна целому числу длин волн
(условие максимумов):
, (4)
Ослабление
колебаний наблюдается, если
.
При этом разность хода равна полуцелому числу длин волн (условие
минимумов)
равна полуцелому числу длин волн (условие
минимумов)
(5)
Оптическая
разность хода. Разность фаз колебаний, достигших точки
наблюдения, может быть обусловлена не
только разной длиной пути, но и разными
свойствами сред, через которые проходят
колебания. Если два когерентных луча
света прошли через среды с разными
коэффициентами преломления 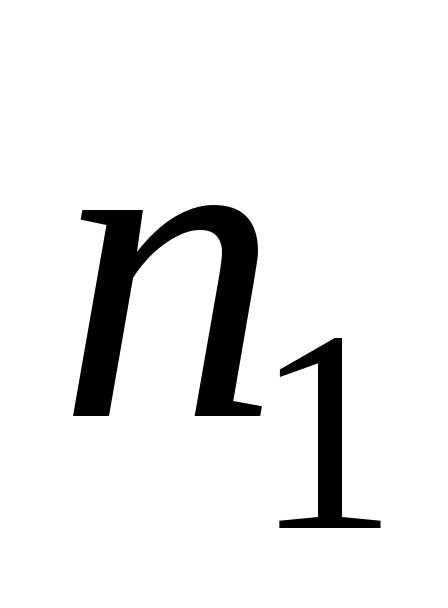 и
и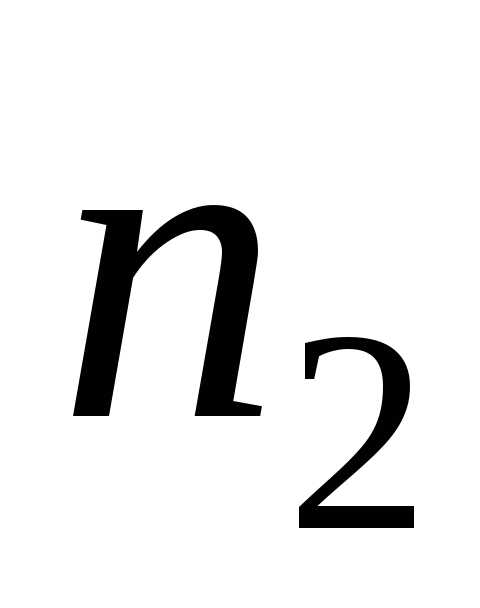 ,
то под величиной
,
то под величиной понимается оптическая разность хода,
которая определяется как:
понимается оптическая разность хода,
которая определяется как:
(6)
Условиями максимумов и минимумов по-прежнему являются соотношения (4) и (5).
Интерференция, возникающая из-за разной оптической плотности эталонной (чистый воздух) и загрязненной (воздух с примесью) газовых сред, используется в шахтном интерферометре для определения концентрации пожароопасных примесей и продуктов горения.
Интерференция
в плоскопараллельной пластинке (на
тонкой пленке). Результат интерференции света в
плоскопараллельной
пластинке толщины 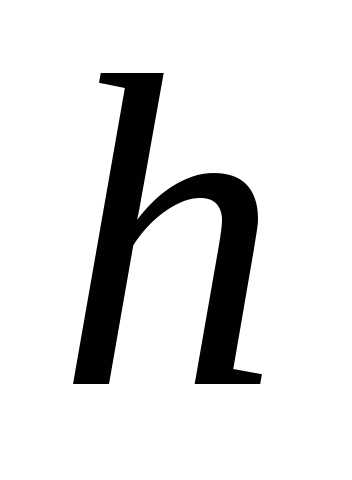 определяется следующими соотношениями.
В проходящем свете наблюдается
усиление света (условие максимумов),
если
определяется следующими соотношениями.
В проходящем свете наблюдается
усиление света (условие максимумов),
если
, (7)
где  — коэффициент преломления материала
пластинки,
— коэффициент преломления материала
пластинки, — угол преломления. Ослабление света
(условие минимумов) наблюдается, если
— угол преломления. Ослабление света
(условие минимумов) наблюдается, если
, (8)
В
отраженном свете условия максимумов и
минимумов обратны, что связано с потерей
половины длины волны при отражении от
границы оптически более плотной
среды (так как в этом случае фаза волны
меняется на  ).
).
Кольца
Ньютона. Явление
с таким названием наблюдается
при
отражении света в воздушном зазоре,
образованном плоской
пластинкой и
соприкасающейся с ней плосковыпуклой
линзой с большим радиусом кривизны  .
Пусть параллельный пучок света
падает
нормально на плоскую поверхность
линзы и частично отражается от
верхней
и нижней границ раздела между стеклом
и воздухом. Тогда
при наложении
отраженных лучей возникают полосы,
имеющие вид окружностей.
.
Пусть параллельный пучок света
падает
нормально на плоскую поверхность
линзы и частично отражается от
верхней
и нижней границ раздела между стеклом
и воздухом. Тогда
при наложении
отраженных лучей возникают полосы,
имеющие вид окружностей.
В отраженном свете радиус темных колец (условие минимумов) определяется соотношением
 ,
(9)
,
(9)
Радиус светлых колец (условие максимумов) вычисляется по формуле
, (10)
В проходящем свете условия максимумов и минимумов обратны по той же причине, что и для плоскопараллельной пластинки.
Определение
дифракции.
Дифракция — это явление огибания
волной препятствия, размер которого  сравним с длиной падающей волны
сравним с длиной падающей волны :
: .
Особенность дифракции состоит в
непрямолинейном распространении
света и проникновении световой волны
в область геометрической тени. Прямой
задачей теории дифракции является
расчет распределения интенсивности
света (дифракционной картины) на экране,
расположенном за препятствием. В
частности, требуется найти положение
максимумов и минимумов интенсивности
света. При решении обратной задачи по
положению максимумов и минимумов
восстанавливают размеры препятствия
или длину волны.
.
Особенность дифракции состоит в
непрямолинейном распространении
света и проникновении световой волны
в область геометрической тени. Прямой
задачей теории дифракции является
расчет распределения интенсивности
света (дифракционной картины) на экране,
расположенном за препятствием. В
частности, требуется найти положение
максимумов и минимумов интенсивности
света. При решении обратной задачи по
положению максимумов и минимумов
восстанавливают размеры препятствия
или длину волны.
Принцип Гюйгенса-Френеля. Принцип Гюйгенса-Френеля включает следующие два положения.
1.
Каждая точка фронта волны в момент
времени  является источником когерентных
вторичных волн. Огибающая вторичных
волн является волновым фронтом в
последующий момент времени
является источником когерентных
вторичных волн. Огибающая вторичных
волн является волновым фронтом в
последующий момент времени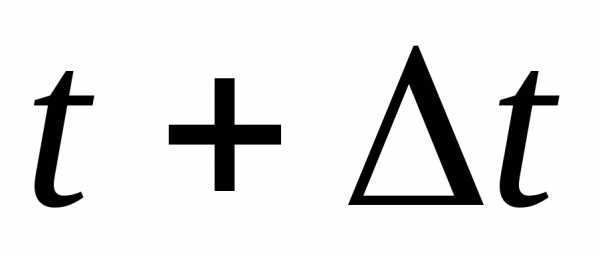 .
.
2. Вторичные волны, будучи когерентными, интерферируют друг с другом. Результирующее распределение интенсивности колебаний — результат интерференции вторичных волн.
Если между источником волн и точкой наблюдения находится препятствие с отверстием, то, в соответствии с принципом Гюйгенса-Френеля, на поверхности препятствия интенсивность колебаний равна нулю, а в отверстии — такая же, как при отсутствии экрана. Таким образом, задача заключается в суммировании вклада волн, пришедших от каждой точки отверстия.
Интерференция и дифракция — это одно и то же физическое явление волновой природы.
Метод зон Френеля. Отверстие содержит бесконечно много точек, являющихся источниками вторичных волн, поэтому проводится условное разбиение фронта волны на конечные кольцевые участки (зоны Френеля) по следующему правилу: волны от соседних зон приходят в точку наблюдения в противофазе и ослабляют друг друга. Это значит, что расстояния от границ соседних зон до точки наблюдения отличаются ровно на половину длины волны (рис. 3).
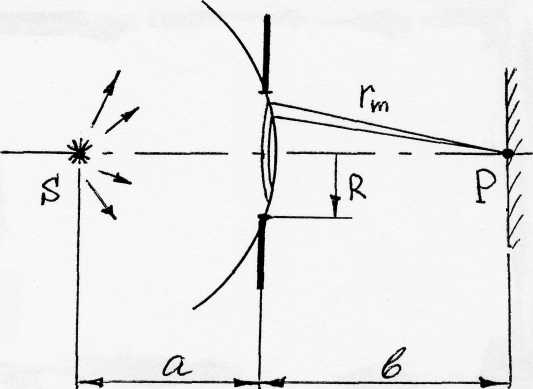
Рис.3. Дифракция Френеля на круглом отверстии
В этом случае амплитуда, создаваемая в точке наблюдения всей сферической волновой поверхностью, равна половине амплитуды, создаваемой одной центральной зоной.
Дифракция
на круглом отверстии.
Пусть в точке S находится источник
сферических волн (рис. 3), на расстоянии  от источника расположено непроницаемое
препятствие с круглым отверстием
радиуса
от источника расположено непроницаемое
препятствие с круглым отверстием
радиуса ,
а на расстоянии
,
а на расстоянии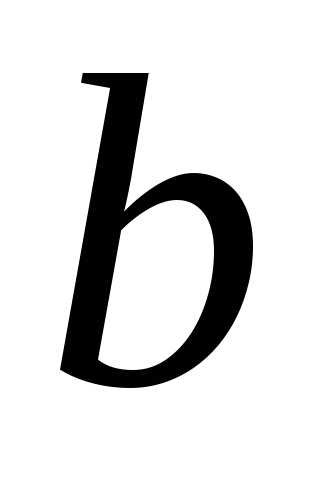 от препятствия — экран, на котором
наблюдается дифракционная картина.
Говорят, что имеет место дифракция
Френеля, если расстояние до препятствия
сравнимо с размером препятствия:
от препятствия — экран, на котором
наблюдается дифракционная картина.
Говорят, что имеет место дифракция
Френеля, если расстояние до препятствия
сравнимо с размером препятствия: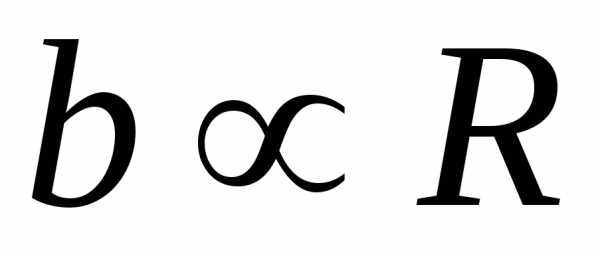 .
В этом случае волновой фронт в области
наблюдения является искривленным.
Радиус внешней границы зоны Френеля с
номером
.
В этом случае волновой фронт в области
наблюдения является искривленным.
Радиус внешней границы зоны Френеля с
номером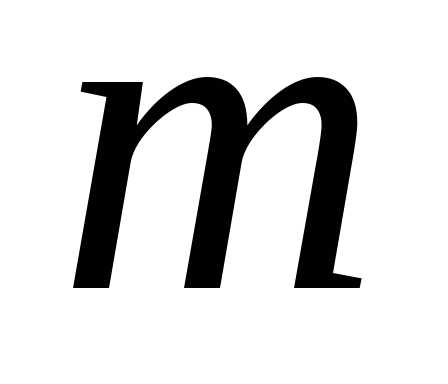 вычисляется
по формуле:
вычисляется
по формуле:
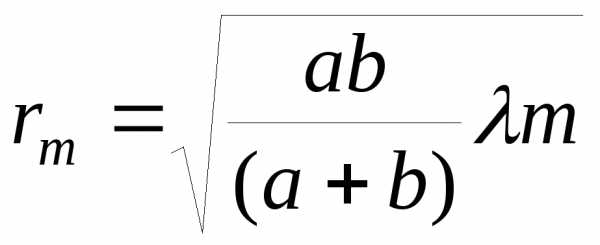 (11)
(11)
где  — длина волны. Число зон Френеля,
укладывающихся в отверстии, можно
найти из равенства
— длина волны. Число зон Френеля,
укладывающихся в отверстии, можно
найти из равенства :
:
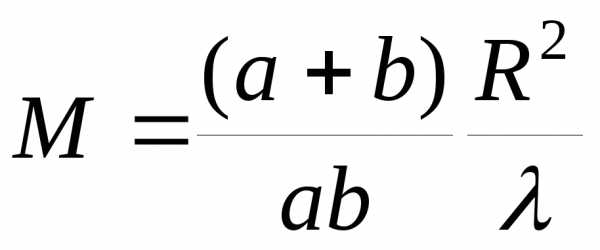 (12)
(12)
Если
отверстие открывает нечетное число
зон, то в центре экрана (точка Р на рис.3)
наблюдается усиление колебаний. В
частности, при  интенсивность колебаний в точке Р в
четыре раза больше той, которая имела
бы место в отсутствие препятствия. Если
отверстие открывает четное число зон,
то в центре экрана наблюдается
ослабление колебаний. Точка Р будет
наиболее темной, если открыто две зоны
Френеля. В любом случае вокруг точки Р
будут наблюдаться светлые и темные
концентрические окружности.
интенсивность колебаний в точке Р в
четыре раза больше той, которая имела
бы место в отсутствие препятствия. Если
отверстие открывает четное число зон,
то в центре экрана наблюдается
ослабление колебаний. Точка Р будет
наиболее темной, если открыто две зоны
Френеля. В любом случае вокруг точки Р
будут наблюдаться светлые и темные
концентрические окружности.
Из (12) видно, что число зон, открываемых отверстием, зависит как от размеров отверстия, так и от положения экрана.
Дифракция
на круглом диске. Рассмотрим противоположную ситуацию:
волновой фронт от источника  взаимодействует с непрозрачным диском
радиуса R (рис. 4). В этом случае важно,
сколько зон Френеля закрыто непрозрачным
диском. Суммирование амплитуд колебаний
от открытых зон (располагающихся вокруг
диска) показывает, что амплитуда колебания
в центре экрана равна половине
амплитуды, вызываемой первой открытой
зоной Френеля. Следовательно, в центре
экрана за диском всегда будет наблюдаться
максимум интенсивности (яркое пятно,
называемое пятном Пуассона).
взаимодействует с непрозрачным диском
радиуса R (рис. 4). В этом случае важно,
сколько зон Френеля закрыто непрозрачным
диском. Суммирование амплитуд колебаний
от открытых зон (располагающихся вокруг
диска) показывает, что амплитуда колебания
в центре экрана равна половине
амплитуды, вызываемой первой открытой
зоной Френеля. Следовательно, в центре
экрана за диском всегда будет наблюдаться
максимум интенсивности (яркое пятно,
называемое пятном Пуассона).
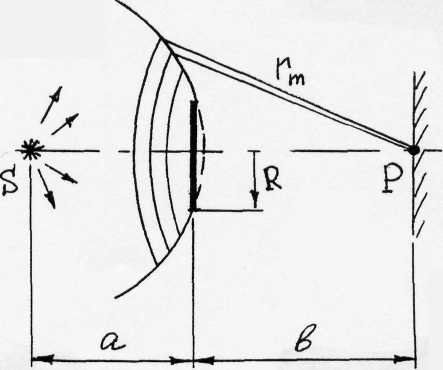
Рис.4. Дифракция Френеля на круглом диске
Центральный
максимум окружен темными и светлыми
кольцами. С увеличением размеров
диска интенсивность центрального
максимума уменьшается. В пределе 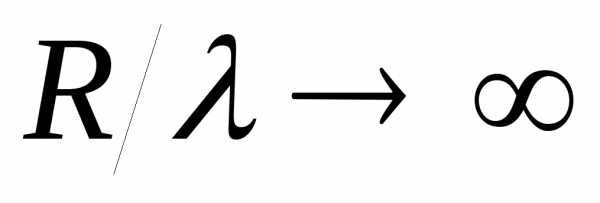 получаем
тень, определяемую по законам
геометрической оптики.
получаем
тень, определяемую по законам
геометрической оптики.
Дифракция Фраунгофера. Дифракцией Фраунгофера называют дифракцию, при которой и падающие, и вторичные волны имеют плоский фронт. Иначе говоря, речь идет о дифракции в параллельных лучах. Такая ситуация возникает, если расстояние от источника до препятствия и от препятствия до точки наблюдения значительно больше размеров препятствия (,на рис. 3, 4). Другой способ получить параллельный пучок света — использовать собирающие линзы.
Дифракция на щели. Рассмотрим длинную узкую щель, на которую падает параллельный пучок света (рис. 5). Разбивая внутреннее пространство щели на малые участки, и суммируя вклад соответствующих вторичных волн (см. принцип Гюйгенса-Френеля), получим распределение интенсивности света справа от экрана:
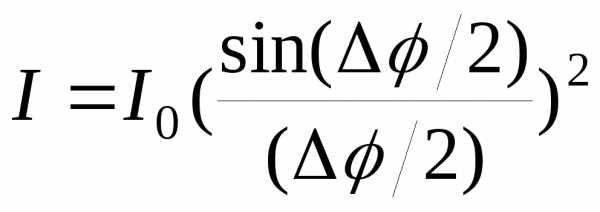 (13)
(13)
где 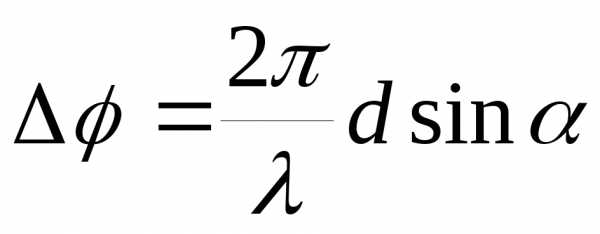 (14)
(14)
 —
длина волны,
—
длина волны,  — ширина щели,
— ширина щели, — угол между перпендикуляром к плоскости
щели и направлением к точке наблюдения
(рис. 5). Зависимость
— угол между перпендикуляром к плоскости
щели и направлением к точке наблюдения
(рис. 5). Зависимость
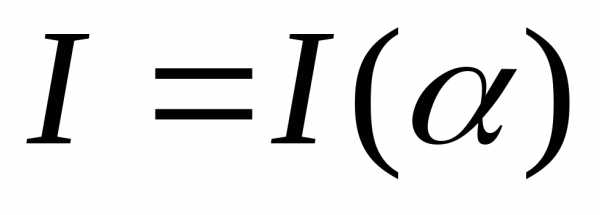 представлена
на рис. 6. Из (13) следуют условие максимумов
представлена
на рис. 6. Из (13) следуют условие максимумов
, (15)
и условие минимумов
 ,
(16)
,
(16)
интенсивности
на экране. Дифракционная картина на
экране представляет собой совокупность
из нескольких параллельных темных и
светлых полос. Яркость светлых полос
убывает по мере удаления от центра,
общее число полос конечно. Максимум,
определяемый соотношением (4.3)
называется максимумом порядка 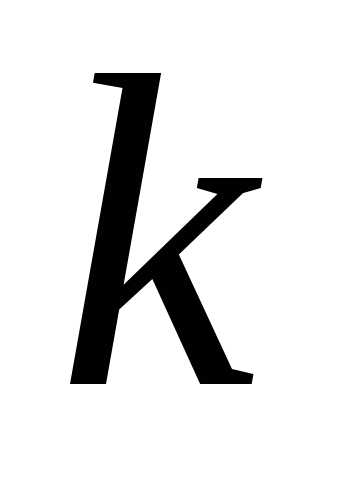 .
Отметим, что для определения расстояния
между максимумами, близкими к
центральному, следует использовать
малость угла
.
Отметим, что для определения расстояния
между максимумами, близкими к
центральному, следует использовать
малость угла .
В этом случае,
где
.
В этом случае,
где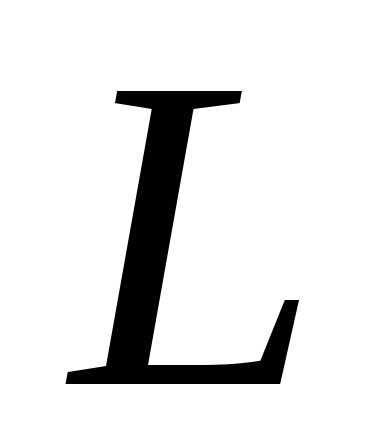 — расстояние до экрана.
— расстояние до экрана.

Рис.5. Ход лучей при дифракции на узкой щели
Расстояние между минимумами, ближайшими к центральному максимуму, можно принять за ширину изображения щели.
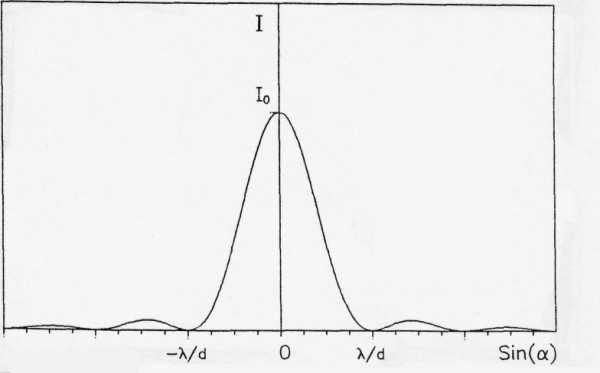
Рис.6. Распределение интенсивности на экране при дифракции на узкой щели
Дифракция на круглом отверстии. Распределение интенсивности при дифракции на круглом отверстии имеет вид:
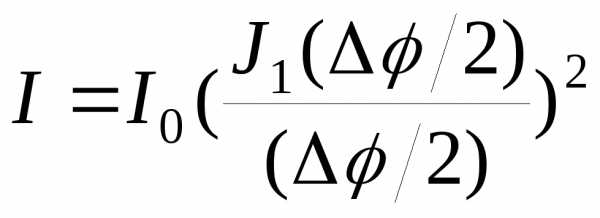 (17)
(17)
где 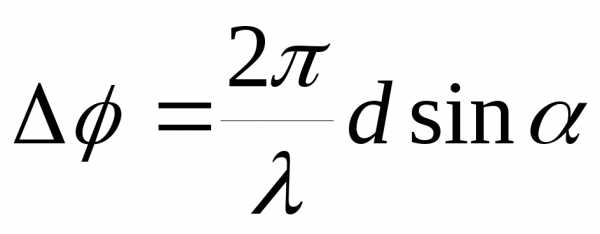 ,
, -функция
Бесселя 1-ого порядка. Дифракционная
картина представляет собой совокупность
концентрических светлых и темных
колец. Радиусы светлых и темных колец
определяются из условия максимумов и
минимумов
-функция
Бесселя 1-ого порядка. Дифракционная
картина представляет собой совокупность
концентрических светлых и темных
колец. Радиусы светлых и темных колец
определяются из условия максимумов и
минимумов
, (18)
Значения
коэффициента 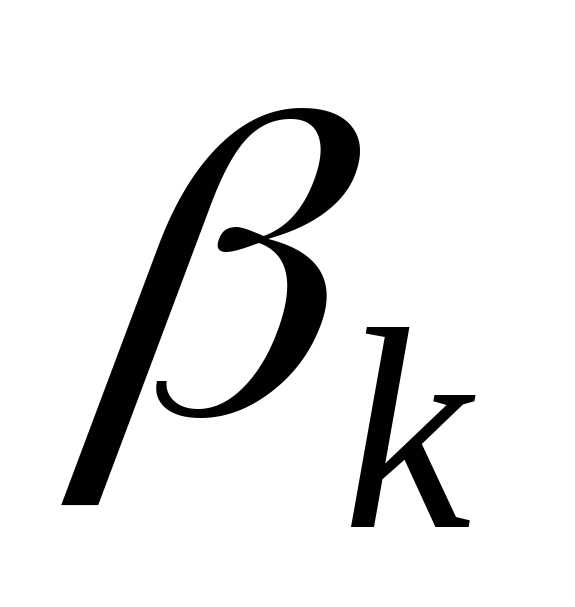 и относительных максимумов интенсивности
приведены в табл. 4.1.
и относительных максимумов интенсивности
приведены в табл. 4.1.
Таблица 1
Параметры дифракции на круглом отверстии
k | | | |
1 2 3 4 | 0 0.82 0.88 0.92 | 1.22 1. 12 1.08 1.06 | 1 0.0175 0.0042 0.0016 |
Радиусом изображения круглого отверстия можно считать радиус первого темного кольца.
Дифракция
на решетке. Спектроскопия. Дифракционная решетка — это совокупность
параллельных узких щелей в непрозрачном
препятствии. Пусть щель, пропускающая
свет, имеет размер  ,
а длина области, непропускающей свет,
равна
,
а длина области, непропускающей свет,
равна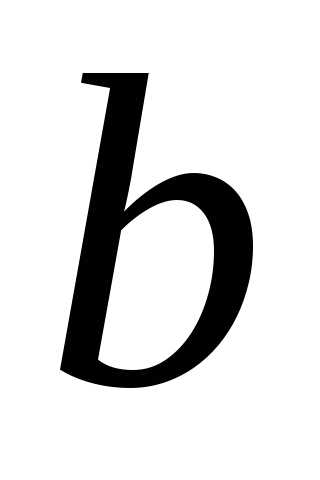 .
Если направить на эти щели параллельный
пучок монохроматического света, то
получим систему — из
.
Если направить на эти щели параллельный
пучок монохроматического света, то
получим систему — из N
когерентных источников. Для этого случая
распределение интенсивности в пределе
бесконечно узкой щели (
N
когерентных источников. Для этого случая
распределение интенсивности в пределе
бесконечно узкой щели ( )
дается соотношением (3), где
)
дается соотношением (3), где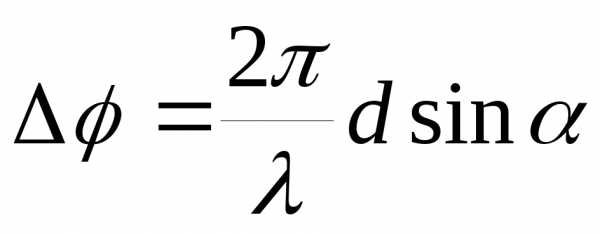 ,- расстояние между штрихами (постоянная
решетки). Интенсивность принимает
значение
,- расстояние между штрихами (постоянная
решетки). Интенсивность принимает
значение в тех случаях, когда знаменатель
обращается в нуль, т.е. при выполнении
условия максимумов
в тех случаях, когда знаменатель
обращается в нуль, т.е. при выполнении
условия максимумов
 ,
(19)
,
(19)
Отметим, что в типичных дифракционных решетках число щелей N составляет несколько тысяч.
При
учете ширины щели  уже нельзя пренебрегать дифракционными
явлениями на ней. Поэтому дифракционная
картина изменится. Условие минимумов,
называемых главными, соответствует
условию минимумов дифракции на щели
(15)
уже нельзя пренебрегать дифракционными
явлениями на ней. Поэтому дифракционная
картина изменится. Условие минимумов,
называемых главными, соответствует
условию минимумов дифракции на щели
(15)
, (20)
Условия появления главных максимумов соответствует интерференции от N когерентных источников
, (21)
При одновременном выполнении условий (20) и (21) в данной точке, на экране произойдет явление так называемого пропавшего максимума (на месте светлого пятна оказывается темное).
Будут наблюдаться также и дополнительные минимумы в тех точках, для которых
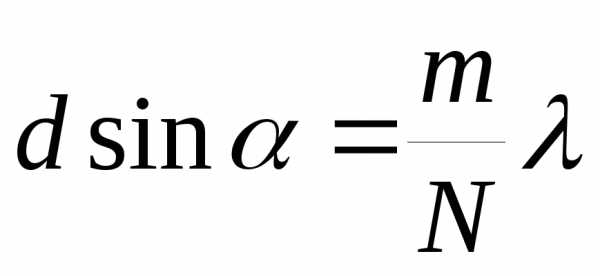 ,
(22)
,
(22)
где  m
принимает все целочисленные значения
кроме
m
принимает все целочисленные значения
кроме
Сказанное выше можно получить, рассмотрев распределение интенсивности на экране, которое будет определяться как интерференцией от N щелей, так и дифракцией на одной щели:
(23)
где 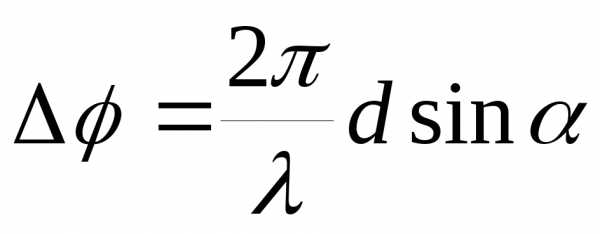 ,
,
На
рис.7 приведен график распределения
интенсивности на экране для N=4 и 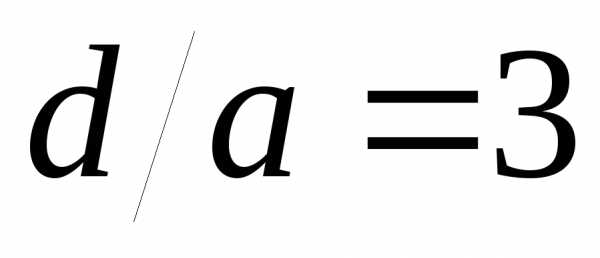 .
Пунктирная кривая, проходящая через
главные максимумы,изображает
интенсивность от одной щели, умноженную
на
.
Пунктирная кривая, проходящая через
главные максимумы,изображает
интенсивность от одной щели, умноженную
на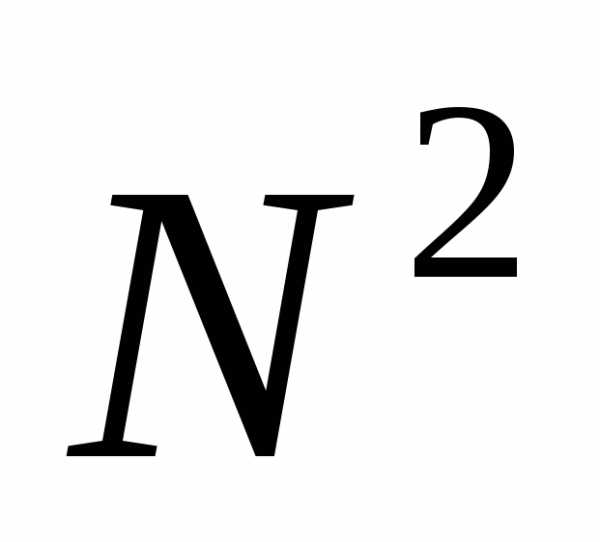 .
При выбранном соотношении (
.
При выбранном соотношении (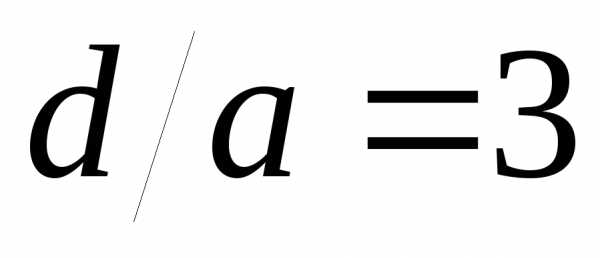 )
главные максимумы 3-го, 6-го и т.д. порядков
приходятся на минимумы интенсивности
от одной щели, вследствие чего они
пропадают.
)
главные максимумы 3-го, 6-го и т.д. порядков
приходятся на минимумы интенсивности
от одной щели, вследствие чего они
пропадают.
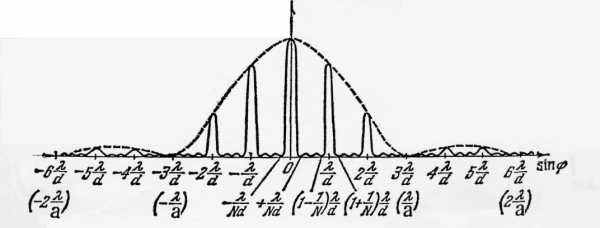
Рис. 7. Распределение интенсивности на экране при дифракции на дифракционной решетке
Угол, на который отклоняется свет, проходя через дифракционную решетку, как видно из (20), (21), (22), зависит от длины волны. Это делает дифракционную решетку мощным инструментом исследования спектрального состава светового пучка.
3.Тепловое излучение.
Тепловым излучением называется перенос энергии посредством электромагнитных волн в диапазоне, включающем видимый свет и инфракрасное излучение (длина волны 0,4 – 100 мкм).
Излучение в оптическом диапазоне становится заметным на глаз, когда температура тела превышает 500 – 550 0С. Дальнейшее увеличение температуры приводит к изменению цвета, как это показано в табл. 2.
Таблица 2
studfiles.net