Матрицы: определение и основные понятия.
Навигация по странице:
Определение матрицы
Определение.
Матрицей размера n×m называется прямоугольная таблица специального вида, состоящая из n строк и m столбцов, заполненная числами.Количество строк и столбцов задают размеры матрицы.
Обозначение
Матрица — это таблица данных, которая берется в круглые скобки:
| A = | 4 | 1 | -7 | ||
| -1 | 0 | 2 |
Матрица обычно обозначаются заглавными буквами латинского алфавитв. Матрица содержащая n строк и m столбцов, называется матрицей размера n×m. При необходимости размер матрицы записывается следующим образом: An×m.
Элементы матрицы
Элементы матрицы A обозначаются aij, где i — номер строки, в которой находится элемент, j — номер столбца.
Пример.
Элементы матрицы A4×4:| A = | 4 | 1 | -7 | 2 | ||
| -1 | 0 | 2 | 44 | |||
| 4 | 6 | 7 | 9 | |||
| 11 | 3 | 1 | 5 |
a11 = 4
Определение.
Строка матрицы называется нулевой, если все ее элементы равны нулю.Определение.
Если хотя бы один из элементов строки матрицы не равен нулю, то строка называется ненулевой.Пример.
Демонстрация нулевых и ненулевых строк матрицы:| 4 | 1 | -7 | < не нулевая строка | ||
| 0 | 0 | 0 | < нулевая строка | ||
| 0 | 1 | 0 | < не нулевая строка |
Определение.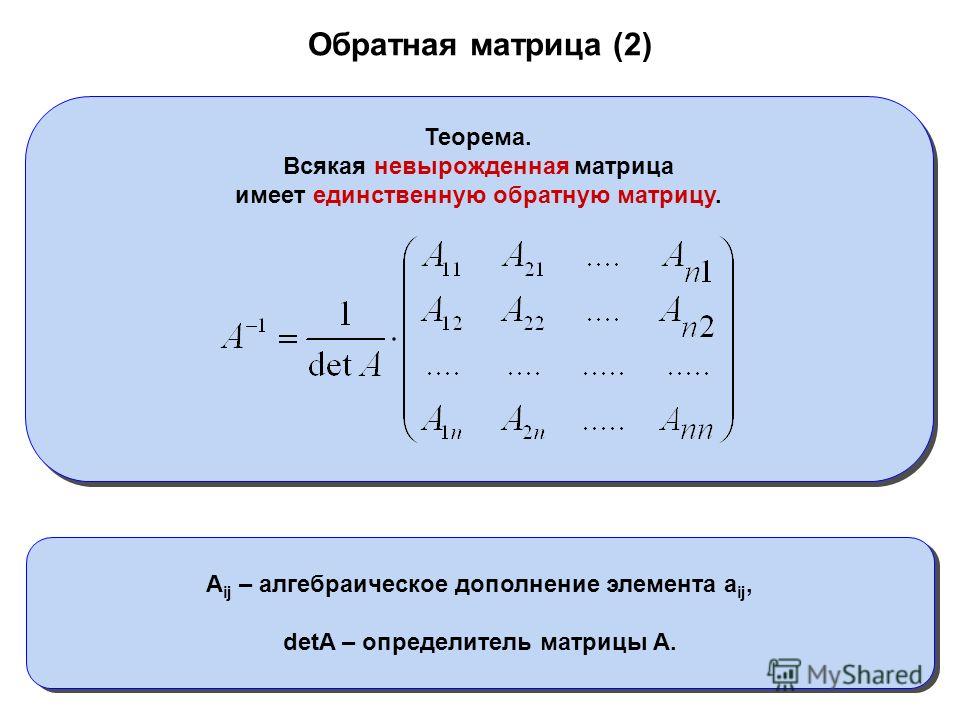
не не нулевой столбец
Диагонали матрицы
Определение.
Главной диагональю матрицы называется диагональ, проведённая из левого верхнего угла матрицы в правый нижний угол.Определение.
Побочной диагональю матрицы называется диагональ, проведённая из левого нижнего угла матрицы в правый верхний угол.Пример.
Демонстрация главной и побочной диагонали матрицы:| 0 | 1 | -7 | — главнаяпобочная диагональ | ||
| 0 | 0 | 2 |
| 0 | 1 | -7 | — главнаяпобочная диагональ | ||
| 0 | 0 | 2 | |||
| 8 | 2 | 9 |
Определение.
Следом матрицы называется сумма диагональных элементов матрицы.
Обозначение.
След матрицы обозначается trA = a11 + a22 + … + ann.Матрицы размерность — Справочник химика 21
Рассмотрим некоторые свойства и связи в матрицах Г и В. Напомним, что рангом матрицы называется максимальное Число линейно-независимых векторов — строк матрицы, и численно ранг матрицы равен порядку ее наивысшего ненулевого минора. Матрица размерности (В х X М) имеет полный ранг, если ее ранг совпадает с минимальным из чисел В, М, т. е. если выполняется условие rg Г = ш п(Д, М), Важнейшее свойство такой матрицы заключается в том, что она сохраняет свой ранг при любых достаточно малых возмущениях, а ее нормальное решение имеет непрерывный характер. Ранг стехиометрической матрицы Г никогда не может быть выше М — I), где [c.130]Техника нахождения элементов матрицы Г достаточно проста [12, 63].
 В уравнении (3.28) разобьем атомную матрицу В по столбцам на две матрицы В и В так, чтобы их размерность была соответственно (ТУ X М— )] и т -1) X I]. Для дальнейших преобразований удобно представить для матрицы В условие сохранения в виде = 0. В свою очередь В х можно разбить еще на две матрицы и перегруппировать столбцы так, чтобы получить неособенную квадратную матрицу размерности [(ТУ — —I) X М — I)]. Тогда размерность оставшейся матрицы есть [(Л/ — I) X ]. Аналогично для матрицы получим две матрицы размерностей [(ЛГ — /) X П и [/ х Л соответственно. В матричной записи имеем
В уравнении (3.28) разобьем атомную матрицу В по столбцам на две матрицы В и В так, чтобы их размерность была соответственно (ТУ X М— )] и т -1) X I]. Для дальнейших преобразований удобно представить для матрицы В условие сохранения в виде = 0. В свою очередь В х можно разбить еще на две матрицы и перегруппировать столбцы так, чтобы получить неособенную квадратную матрицу размерности [(ТУ — —I) X М — I)]. Тогда размерность оставшейся матрицы есть [(Л/ — I) X ]. Аналогично для матрицы получим две матрицы размерностей [(ЛГ — /) X П и [/ х Л соответственно. В матричной записи имеем Показатели степеней у размерностей переменных объединяются в матрицу размерностей [c.88]
Последовательный подход. Вначале рассмотрим эту проблему применительно к последовательному подходу. Здесь уменьшение размерности задачи расчета ХТС достигается методами структурного анализа [47]. При этом решаются следующие задачи 1) в схеме выделяются комплексы — совокупности блоков охваченных обратными связями [3, с. 33] 2) определение внутри каждого комплекса оптимальной с точки зрения какого-либо критерия совокупности итерируемых переменных (II, 5). Обычно совокупность итерируемых переменных (II, 5) выбирается из условия, чтобы их суммарная размерность была минимальной. Положительные и отрицательные стороны такого выбора переменных (II, 5) обсуждаются в работе [3, с. 85]. Отметим здесь, что применительно к квазиньютоновским методам это более или менее оправдано, поскольку, как мы уже отмечали, можно считать при применении этих методов, что число итераций растет пропорционально размерности системы нелинейных уравнений. Уменьшаются требования и к размеру памяти, поскольку приходится хранить одну или две матрицы размерности fix/г. При использовании ориентированного на уравнения подхода так же, как и в предыдущем случае определяются комплексы, а внутри комплексов — оптимальные совокупности разрываемых потоков [48 17 18, с. 258].
[c.61]
33] 2) определение внутри каждого комплекса оптимальной с точки зрения какого-либо критерия совокупности итерируемых переменных (II, 5). Обычно совокупность итерируемых переменных (II, 5) выбирается из условия, чтобы их суммарная размерность была минимальной. Положительные и отрицательные стороны такого выбора переменных (II, 5) обсуждаются в работе [3, с. 85]. Отметим здесь, что применительно к квазиньютоновским методам это более или менее оправдано, поскольку, как мы уже отмечали, можно считать при применении этих методов, что число итераций растет пропорционально размерности системы нелинейных уравнений. Уменьшаются требования и к размеру памяти, поскольку приходится хранить одну или две матрицы размерности fix/г. При использовании ориентированного на уравнения подхода так же, как и в предыдущем случае определяются комплексы, а внутри комплексов — оптимальные совокупности разрываемых потоков [48 17 18, с. 258].
[c.61]
Матрица, содержащая одну строку, т. е. размерности 1 X и, называется вектор-строкой, а матрица размерности и X 1, т. е. состоящая из одного столбца, называется вектор-столбцом. [c.229]
размерности 1 X и, называется вектор-строкой, а матрица размерности и X 1, т. е. состоящая из одного столбца, называется вектор-столбцом. [c.229]
Отличительной особенностью большинства соотношений, используемых для расчета коэффициентов активности многокомпонентной смеси, является то, что они являются обобщением соответствующих соотношений для бинарных смесей. Поэтому коэффициенты этих соотношений определяются по экспериментальным равновесным данным соответствующих бинарных пар. Очевидно, для системы, содержащей к компонентов, коэффициенты будут представляться в простейшем случае матрицей размерности к X к.
Для решения покомпонентного материального баланса применяются те же алгоритмы, что и при решении задачи линеаризации, однако здесь элементы являются скалярными величинами, а не матрицами размерностью (2С + I) х (2С + 1). [c.262]
Базисной матрицей называется невырожденная матрица размерности т хт, образованная из т столбцов матрицы ограничений А. [c.183]
[c.183]
Пусть (/ = 1, 2 г = 1,. . га) есть -обратные матрицы размерности I X га, удовлетворяющие соотношениям [c.67]
Пусть Nq = щ,. . Пд) — матрица размерности (п X д), столбцы которой образованы векторами и, (г = 1,. . д ). Примем, что ранг ее равен а. Алгоритм движения надо строить таким образом, чтобы поисковые направления р1 лежали внутри линейного многообразия Ьд. Очевидно, что этого можно достигнуть, образуя направления по формуле [c.192]
Здесь С = Фп, т+1-Ф , т+1 — матрица размерности (т + 1 X X т + 1) 5 = II Я,. . Я — матрица размерности (т + 1 X 1) а = 0,. . — матрица размерности (т + 1 X 1). [c.39]
Таким образом, в представлении (XI,2) векторы г/( ) и являются клеточными матрицами размерностей соответственно и х1 и т х1. Как обычно, уравнения блоков должны быть дополнены уравнениями связей [c.230]
Пусть I — матрица размерности (2/7 Хт), столбцы которой являются базисом подпространства V.
Всиомним теперь, что часть компонент вектора 6 — заданные величины, равные перемещениям на и перенесем произведения их на соответствующие элементы матрицы К в правую часть системы уравнений (4.204) вспомним также, что уравнения, соответствующие узлам на незаконны и вычеркнем их из системы (4.203). В результате этих преобразований получим вторую систему уравнений с матрицей размерности 2Х (Л/в—М в), где Мин — количество лежащих на 8и вершин. Обозначим эту матрицу через [ ], она получается вычеркиванием строк и столбцов матрицы [X] с номерами 21—1 и 21, где I пробегает номера вершин на 5 (заметим, что программная реализация этого процесса достаточно проста). [c.189]
Матрица [К], называемая глобальной матрицей жесткости, или просто матрицей жесткости системы, получается сложением локальных матриц жесткости [Я ] по следующему правилу сначала к нулевой матрице размерности МХМ добавляется матрица, в левом верхнем углу которой стоит локальная матрица жесткости 1-го элемента, к получившейся матрице добавляется матрица размерности NXN, ненулевые элементы которой расположены на пересечении 2-го и 3-го столбцов и 2-й и 3-й строк и равны соответствующим элементам локальной матрицы жесткости для
[c.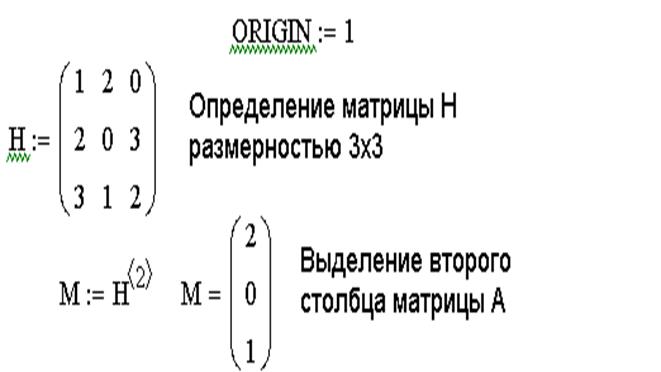 181]
181]
Для группы Сав существует только четыре разных набора матриц размерности 1 X 1, т. е. четыре НП типа Л а, В (табл. 19). [c.114]
Таким образом, матрицы представления Г суть унитарные матрицы. Можно доказать, что все возможные представления каждой группы О (в том числе и не обязательно группы точечной симметрии) эквивалентны ее унитарным представлениям, другими словами, при подходящем выборе базиса матрицы любого представления переходят в унитарные матрицы, а потому при рассмотрении представлений достаточно ограничиться лишь унитарными представлениями. Среди всех унитарных представлений всегда есть единичное, или полносимметричное, в котором каждому элементу группы отвечает одна и та же матрица размерности 1 х 1, а именно единица.
Отсюда следует, что любой объект gi е Охарактеризуется матрицей размерности [т X 1]. Каждый элемент этой матрицы принимает значение из отрезка [О, 1]. Примером таких объектов могут служить отдельные изделия выпускаемой продукции, а свойствами — характеристики качества изделий. [c.25]
[c.25]
I — единичная матрица размерности 3 х 3), согласно соотношению [c.346]
Представлением группы называется гомоморфное ютображение данной группы на группу квадратных матриц. Размерность матриц называется размерностью представления. [c.20]
Допустим, что матрицы компенсации можно представить в виде В( = (Е( где Et — единичная матрица размерности/и fXWf. Разо- [c.81]
Следовательно, проатранство решений (2) представляет собой матрицу размерностью 6 х 4. [c.143]
В результате полного цикла моделирования за время Т будет получена симуляционная матрица размерности (N 5), где N-общее число повторов, возникших с самого качала работы модели. [c.69]
Размер матрицы — Энциклопедия по экономике
Размеры матрицы можно существенно сократить за счет рассмотрения в ней лишь дефицитных материалов, оборудования, конструкций, т. е. таких, по которым
[c.101]
е. таких, по которым
[c.101]Решение. Размер матрицы произведения [c.260]
Равномерный закон распределения 34 Размер матрицы 2 Размерность пространства 270 Ранг 78 [c.304]
При больших размерах матрицы вычисление по этой формуле элементов матрицы А 1 требует громоздких расчетов. Поэтому изыскиваются различные более эффективные методы О.м. на ЭВМ. [c.233]
| Рис. 2. Окно диалога определения размеров матрицы |
Для размера матриц, отображающих re-мерное пространство в г-мер-ное, будем использовать обозначение ->г. [c.33]
Численное же нахождение оптимальных стратегий в матричных играх требует значительного объема вычислений, который быстро растет с увеличением размеров матрицы выигрышей игры. [c.59]
Матрицы — это массивы данных, имеющие прямоугольную форму. Данные располагаются в строках и столбцах. Размер матрицы выражается числом строк и столбцов, т.е. матрица с пятью строками и четырьмя столбцами будет матрицей размера 5×4. Например, следующая матрица имеет размер 3×3
[c.302]
Данные располагаются в строках и столбцах. Размер матрицы выражается числом строк и столбцов, т.е. матрица с пятью строками и четырьмя столбцами будет матрицей размера 5×4. Например, следующая матрица имеет размер 3×3
[c.302]
Заметьте, что размер матрицы Z составляет только 2 2. Это потому, что размер матрицы-произведения равен числу строк в первой матрице и числу столбцов во второй. [c.304]
Все матрицы AS(t), AS(t — 1), S(At), S (At) квадратные и одинакового размера, т. е. имеют одинаковое количество строк и столбцов, определяемое числом участников игры. В нашем примере размеры матриц имеют число строк 3 + 1=4, где + 1 — это итоговая строка, число столбцов также 3 + 1 = 4, где + 1 — это итоговый столбец. Таким образом, размер матрицы (3 + 1) х (3 + 1) или 4 х 4. В общем же случае, при числе участников игры М размеры матриц с итогами будут соответственно (М + 1) х (М + 1). [c.17]
Число строк m и число столбцов в определяют размер матрицы, который обозначают как произведение числа строк на число столбцов mxn, и поэтому говорят матрица размером mxn. [c.364]
[c.364]
Размер матрицы является важнейшей характеристикой, определяющей вид матрицы и действия над ней. [c.364]
Произведение матриц (векторов) А, 10 и В10 1 также существует, так как внутренние индексы 10 и 10 совпадают, а размер матрицы-произведения будет 1 х 1, но это уже будет не матрица, а число (скаляр) j г [c.386]
Максимальный размер матрицы-корреспонденции определяется множеством плана счетов, точнее, мощностью этого множества — количеством счетов, содержащемся в плане. [c.391]
Только для синтетических счетов, содержащихся в плане, размер матрицы будет 76 х 76, а с субсчетами и произвольно устанавливаемыми субконто размер матрицы корреспонденции будет значительно большим, хотя матрица практически необозрима уже и в том случае, когда она имеет указанный размер 76 х 76. [c.391]
Множество использованных счетов в отчетном периоде (объединенное со счетами, которые имели ненулевое сальдо на начало периода) определяет минимальный размер матрицы-корреспонденции. [c.392]
[c.392]
Всего использовано 4 счета, поэтому минимальный размер матриц-корреспонденций и матриц-проводок 4×4. Матриц-проводок будет столько же, сколько и самих проводок. Они приводятся ниже [c.394]
Матрицы, пуансоны формовочных, вырубных, вытяжных штампов ковочные штампы и прессформы сложного профиля с полированием в размер матрицы для прессформ — растачивания сферических гнезд по шаблону. [c.357]
Текст программы оценки значимости экономических показателей приводится в приложении 2. Исходной информацией программы являются веса экспертов и матрицы экспертных заключений о весомости показателей. С ЭВМ поступают следующие сообщения веса экспертов, матрицы показателей, нормированные относительные веса. Правильность расчета проверяется условием сумма относительных весов показателей равна единице . Необходимые инструктивные материалы по подготовке исходных данных и работе с программой содержатся в источнике [63, с. 130—131]. Процедура проведения экспертной оценки показателей отличается простотой. Она позволяет получить научно обоснованное коллективное заключение о сравнительной важности показателей. Каждый член экспертной группы заполняет матрицу. Размер матрицы зависит от числа ранжируемых показателей 3X3, 4X4, 5X5 и т. д. Используется метод парных сравнений. Если, по мнению эксперта, значимость показателей эквивалентна, им присваивается по 1 баллу, если один показатель более важен, чем другой,— 2 балла, менее важен —0 баллов.
[c.73]
Она позволяет получить научно обоснованное коллективное заключение о сравнительной важности показателей. Каждый член экспертной группы заполняет матрицу. Размер матрицы зависит от числа ранжируемых показателей 3X3, 4X4, 5X5 и т. д. Используется метод парных сравнений. Если, по мнению эксперта, значимость показателей эквивалентна, им присваивается по 1 баллу, если один показатель более важен, чем другой,— 2 балла, менее важен —0 баллов.
[c.73]
Модель (1) состоит из N блоков со следующими размерами матрицы каждого блока число столбцов — а = /n(./V + I) -f Jn (Pn + 1) число строк — Ъп — M — — pln + Jn(Рп + Q) + Кп [c.363]
Однако составление общей матрицы синтетического учета на ЭВМ и ее практическое применение связано с определенными трудностями. Если бухгалтерских сче тов имеется много, то соответственно и размеры матрицы крупные. При этом в матрице превалируют нулевые элементы, так как по общему правилу количество корреспондирующих счетов ограничено. В нашем примере нулевые элементы составляют от общего количества элементов матрицы 84%. По типовому счетному плану этот показатель составляет 73%, а по счетному плану ГЕНСИС —примерно 66% (см. 3.3).
[c.83]
По типовому счетному плану этот показатель составляет 73%, а по счетному плану ГЕНСИС —примерно 66% (см. 3.3).
[c.83]
Размеры матрицы групп счетов небольшие. Нулевых элементов в этих матрицах встречается немного (всего 9), так как взаимосвязи счетов одной группы, как правило, в несколько раз теснее, чем взаимосвязи всех счетов (табл. 4.4). Нулевые элементы встречаются у раздела основных средств — по выходу с пятью и по вводу с тремя разделами. Отсутствует также связь между разделами денежных средств и затрат на производство. Более обоснованные частные матрицы можно конструировать на базе общей матрицы корреспонденции синтетических счетов, сгруппировав их согласно конкретным целям. [c.87]
Для измерения силы бизнеса могут быть использованы следующие переменные доля рынка, рост доли рынка, относительная доля рынка по отношению к ведущей марке, лидерство в качестве или другие характеристики, такие, как, например, издержки, прибыльность по отношению к лидеру. При определении размера матриц очень важную роль играет выбор единиц измерения объемов, норм приведения к единой базе, временных интервалов и т. д.
[c.173]
д.
[c.173]
Разрыв между верхними и нижними уровнями в организации По матричной схеме работают нижние звенья, а «верхи» ею не пользуются Необходимо поддерживать маленький размер «матриц», чтобы вовлечь высшее руководство [c.269]
Большое значение имеет и другой параметр светочувствительной матрицы, про который обычно не упоминают, а именно — физический размер матрицы, от которого зависит и размер одной точки матрицы. Тут чем больше, тем лучше, так как больший по размеру пиксель может [c.305]
Смысл этого определения состоит в том, что доминирующая стратегия никогда не хуже, а в некоторых случаях даже лучше, чем доминируемая стратегия. Отсюда следует, что игроку нет необходимости использовать доминируемую стратегию. В самом деле, будут существовать оптимальные смешанные стратегии, при которых вероятность использования доминируемых строк и столбцов равна нулю, и при решении игры все доминируемые строки и столбцы могут быть отброшены, что позволяет уменьшить размеры матрицы. (Этот подход может использоваться также при поиске решения игры в чистых стратегиях.)
[c.226]
(Этот подход может использоваться также при поиске решения игры в чистых стратегиях.)
[c.226]
Объем выборки m Объем данных по фактору (размер матрицы по вертикали). Применяется для установления тенденций изменения фактора Не менее чем в 3 — 5 раз больше числа факторов (nxj). С увеличением числа факторов кратность должна увеличиваться [c.321]
Критерий Фишера F Математический критерий, характеризующий значимость уравнения регрессии. Применяется для выбора модели Больше табличного значения, установленного для различных размеров матрицы и вероятностей [c.322]
Еще недавно категория матричных шрифтов являлась единственной. Шрифты в этом случае создаются по так называемой bitmap технологии, или методом битовой карты. В файле с таким шрифтом хранятся точечные изображения каждого символа внутри сетки точек фиксированного размера. Чем выше разрешающая способность устройства, тем больше размер матрицы, а стало быть и качество прорисовки контуров символов. Каждый символ растрового шрифта прорисовывается вручную и его форму можно подобрать так, чтобы он выглядел наилучшим образом на конкретном дисплее или при определенном разрешении.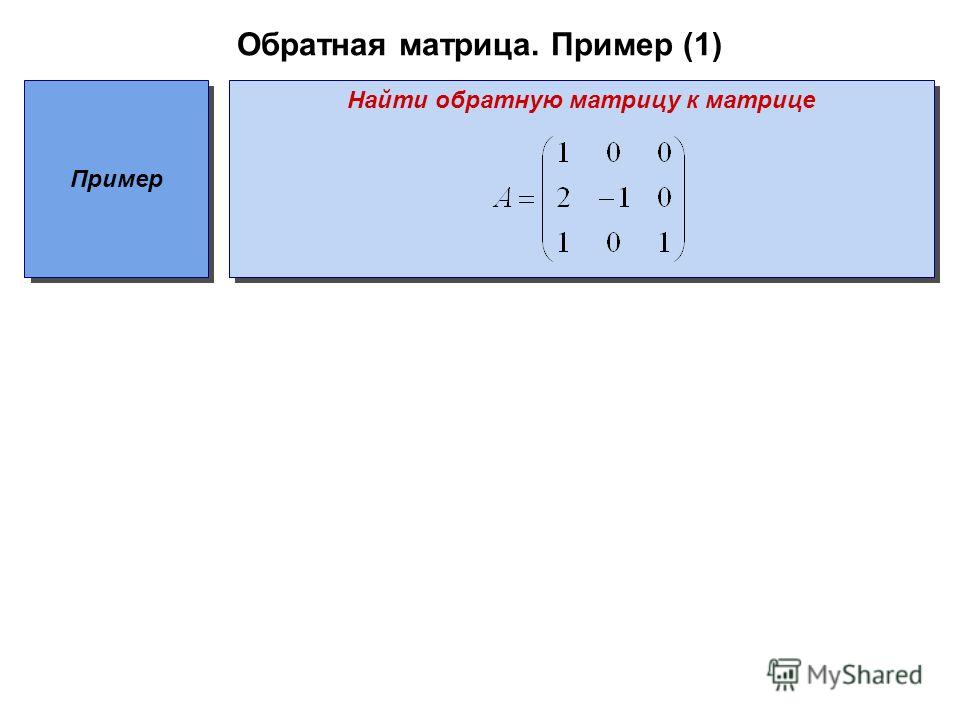 Однако разрешение обычного монитора намного хуже, чем разрешение самого слабого принтера. По этой причине нельзя добиться полного соответствия изображения на бумаге и на принтере. К недостаткам растровых шрифтов можно отнести существенное ухудшение качества изображения при изменении размера шрифта, его масштабировании. Контуры букв приобретают ступенчатую форму, возникает так называемый лестничный эффект. Принцип соответствия изображения WYSIWYG поддерживает большинство современных систем подготовки текстовой информации, поэтому возникает необходимость использования иной технологии создания шрифтов, свободной от указанных недостатков.
[c.408]
Однако разрешение обычного монитора намного хуже, чем разрешение самого слабого принтера. По этой причине нельзя добиться полного соответствия изображения на бумаге и на принтере. К недостаткам растровых шрифтов можно отнести существенное ухудшение качества изображения при изменении размера шрифта, его масштабировании. Контуры букв приобретают ступенчатую форму, возникает так называемый лестничный эффект. Принцип соответствия изображения WYSIWYG поддерживает большинство современных систем подготовки текстовой информации, поэтому возникает необходимость использования иной технологии создания шрифтов, свободной от указанных недостатков.
[c.408]
Заданные подобным образом матрицы не имеют имен. Если вы хотите ввести матрицу, имеющую имя, необходимо сначала задать имя матрицы, затем ввести двоеточие. В результате после введенного вами неполного определения появится пустая ячейка. Затем следует открыть диалоговое окно создания матрицы любым из вышеперечисленных способов, задать в нем размеры матрицы и щелкнуть на кнопке Insert (Вставить) или ОК. Будет сгенерирована матрица, уже обладающая именем. Чтобы завершить определение необходимо, разумеется, еще ввести элементы матрицы.
[c.48]
Будет сгенерирована матрица, уже обладающая именем. Чтобы завершить определение необходимо, разумеется, еще ввести элементы матрицы.
[c.48]
Указание. Для определения символьной матрицы введите с клавиатуры ее имя, символьный знак равенства (нажмите на клавиатуре одновременно клавиши и — на экране будет отображен знак равенства), определите размеры матрицы и введите ее элементы. Ввести букву греческого алфавита можно, щелкнув по кнопке с нужной буквой в панели [c.59]
Типовыми регионами являются город с населением около 1 млн. чел. (матрица 150×150), республика, край, область средних размеров (матрица 100×100), административный район с населением 50 тыс. чел. (матрица 60×60). Затраты на решение задач приведены в табл. 4.2.6. [c.171]
Тщательный учет всех названных факторов фиксации размеров матриц ифает исключительно важную роль для качественного проведения анализа портфеля бизнесов. [c.104]
АЛГЕБРА И ГЕОМЕТРИЯ Лекция 1 Матрицы Преподаватель Ананьева
АЛГЕБРА И ГЕОМЕТРИЯ Лекция 1. Матрицы Преподаватель: Ананьева М. С.
Матрицы Преподаватель: Ананьева М. С.
1. 1. Основные понятия n n Определение 1 Матрица – прямоугольная таблица, содержащая m строк и n столбцов из mn элементов
1. 1. Основные понятия n n Определение 1 Числа – элементы матрицы
1. 1. Основные понятия n n Определение 1 Числа – элементы матрицы n i – номер строки n j – номер столбца
1. 1. Основные понятия n Обозначения матриц
1. 1. Основные понятия n Размерность матрицы ¨ Кол-во n (m n) строк кол-во столбцов
1. 1. Основные понятия n n Определение 2 Матрицы A и B называются равными, если они имеют одинаковую размерность и их соответствующие элементы, т. е. стоящие на местах с одинаковыми номерами, равны
n n n Определение 2 Матрицы A и B называются равными, если они имеют одинаковую размерность и их соответствующие элементы, т. е. стоящие на местах с одинаковыми номерами, равны 1. 1. Основные понятия Обозначается А=В
е. стоящие на местах с одинаковыми номерами, равны 1. 1. Основные понятия Обозначается А=В
1. 1. Основные понятия n n Определение 3 Матрица, все элементы которой равны нулю, называется нулевой ¨ — «тета» (греч. )
n n n 1. 2. Действия над матрицами: сложение Определение 4 Суммой матриц A и B одинаковой размерности называется матрица С той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц С=A+B, где
n n n 1. 2. Действия над матрицами: сложение Определение 4 Суммой матриц A и B одинаковой размерности называется матрица С той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых матриц С=A+B, где
1. 2. Действия над матрицами: сложение n n Пример 1. Дано: а) Вычислите матрицу А+В Решение.
1. 2. Действия над матрицами: n Определение 5 вычитание n n Разностью матриц A и B одинаковой размерности называется матрица D той же размерности, каждый элемент которой равен разности соответствующих элементов матриц D=A–B , где
1. 2. Действия над матрицами: вычитание n Пример 1. Дано: n а) Вычислите самостоятельно матрицу А-В n
2. Действия над матрицами: вычитание n Пример 1. Дано: n а) Вычислите самостоятельно матрицу А-В n
1. 2. Действия над матрицами n Пример 1. Дано: n а) Вычислите самостоятельно матрицу А-В n Ответ: n
1. 2. Действия над матрицами: умножение на число n n Определение 6. Произведением матрицы A на действительное число α ( 0) называется матрица F=αА, каждый элемент которой есть произведение элементов матрицы А на α, т. е.
1. 2. Действия над матрицами: умножение на число n n Определение 6. Произведением матрицы A на действительное число α ( 0) называется матрица F=αА, каждый элемент которой есть произведение элементов матрицы А на α, т. е.
1. 2. Действия над матрицами: умножение на число n n Пример 2. Дано: а) Вычислите матрицу 5 А Решение.
1. 2. Действия над матрицами: умножение на число n n Определение 7. Противоположной к матрице А называется матрица, элементы которой получаются умножением элементов матрицы А на – 1, т. е. –А.
е. –А.
1. 2. Действия над матрицами: умножение на число n Пример 2. Дано: n Составьте противоположную матрицу n
1. 2. Действия над матрицами: умножение на число n n Пример 2. Дано: Составьте противоположную матрицу Решение.
1. 2. Свойства линейных операций над матрицами n Операции сложения и вычитание в алгебре называют операциями алгебраического сложения n Операции сложения и умножения на действительное число называют линейными операциями
1. 2. Свойства линейных операций над матрицами
1. 2. Свойства линейных операций над матрицами
1. 2. Действия над матрицами: умножение n Операция умножения матриц определяется только для согласованных матриц, когда число столбцов первой матрицы равно числу строк второй матрицы n Порядок матриц важен!
1. 2. Действия над матрицами: умножение n n Определение 8. Произведением согласованных матриц A и B размерности (m n) и (n p) называется матрица C размерности (m p), каждый элемент которой, стоящий на пересечении i-й строки и k-го столбца, получается как сумма произведений каждого элемента i-й строки матрицы A на соответствующий элемент k-го столбца матрицы B
Произведением согласованных матриц A и B размерности (m n) и (n p) называется матрица C размерности (m p), каждый элемент которой, стоящий на пересечении i-й строки и k-го столбца, получается как сумма произведений каждого элемента i-й строки матрицы A на соответствующий элемент k-го столбца матрицы B
1. 2. Действия над матрицами: умножение n n Определение 8. Произведением согласованных матриц A и B размерности (m n) и (n p) называется матрица C размерности (m p), каждый элемент которой, стоящий на пересечении i-й строки и k-го столбца, получается как сумма произведений каждого элемента i-й строки матрицы A на соответствующий элемент kго столбца матрицы B
1. 2. Действия над матрицами: умножение n n Определение 8. Произведением согласованных матриц A и B размерности (m n) и (n p) называется матрица C размерности (m p), каждый элемент которой, стоящий на пересечении i-й строки и k-го столбца, получается как сумма произведений каждого элемента i-й строки матрицы A на соответствующий элемент kго столбца матрицы B Размерность: (m n) (n p) = (m p)
1. 2. Действия над матрицами: умножение n n Определение 8. Произведение согласованных матриц A и B размерности (m n) и (n p) называется матрица C размерности (m p)
2. Действия над матрицами: умножение n n Определение 8. Произведение согласованных матриц A и B размерности (m n) и (n p) называется матрица C размерности (m p)
1. 2. Действия над матрицами: умножение
1. 2. Действия над матрицами: умножение
1. 2. Действия над матрицами: умножение
1. 2. Действия над матрицами: умножение
1. 2. Действия над матрицами: умножение
1. 2. Действия над матрицами: умножение n Примеры 4. а)
1. 2. Действия над матрицами: умножение n Примеры 4. б)
1. 2. Действия над матрицами: умножение n Примеры 4. в)
1. 2. Свойства умножения матриц
1. 2. Свойства умножения матриц n 5. Произведение ненулевых матриц может равняться нулю даже тогда, когда ни один из множителей не является нулевой матрицей
1. 2. Свойства умножения матриц n Примеры 4. г) n д)
2. Свойства умножения матриц n Примеры 4. г) n д)
1. 2. Свойства умножения матриц n 6. Коммутативный (переместительный) закон умножения для большинства матриц не выполняется АВ ВА n n Размерность АВ: (m n) (n p) = (m p) Размерность ВА: (n p) (m n) ¨ в общем случае матрицы ВА не согласованы
1. 2. Свойства умножения матриц Определение 9. n Матрицы, для которых выполняется коммутативность умножения (АВ=ВА) называются коммутативными (перестановочными) n
1. 2. Свойства умножения матриц n Произведения АВ и ВА одновременно определены только для квадратных матриц Размерность АВ: (n n) = (n n) n Размерность ВА: (n n) = (n n) n
1. 2. Действия над матрицами: возведение в степень n n Для квадратных матриц определено n-кратное умножение, т. е. операция возведения в степень Аn
1. 2. Действия над матрицами: возведение в степень n Пример 5.
1. 3. Виды матриц n Если m=n матрица называется квадратной, а число n – ее порядком. n Определение 10. Квадратной матрицей порядка n называется совокупность n 2 элементов, расположенных в квадратной схеме n
1. 3. Виды матриц n Элементы образуют главную диагональ, n элементы составляют побочную диагональ.
1. 3. Виды матриц n n n Определение 11. Квадратная матрица, у которой все элементы выше или ниже главной диагонали равны нулю, называется треугольной (верхняя и нижняя) Прямоугольная матрица, у которой элементы верхнего или нижнего углов образуют треугольник из нулей, называется трапециевидной
1. 3. Виды матриц n n Определение 12. Квадратная матрица, у которой все элементы, выше и ниже элементов главной диагонали, равны нулю, называется диагональной n на диагонали могут быть нулевые элементы ¨ не все
1. 3. Виды матриц n n Определение 13. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной
Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной
1. 3. Виды матриц n n n Определение 14. Диагональная матрица, у которой все элементы главной диагонали равны единице, называется единичной Матрица, у которой несколько первых элементов главной диагонали равны единице, а остальные элементы матрицы равны 0, называется канонической
1. 3. Виды матриц n n n Определение 15. Матрица, содержащая один столбец элементов, называется матрицей-столбцом или вектором-столбцом Матрица, содержащая одну строку элементов, называется матрицей-строкой или вектором-строкой
1. 3. Виды матриц n Любое число есть матрица размерности (1 1)
1. 4. Преобразование матриц: транспонирование n n Определение 16. Матрица, полученная из данной матрицы А заменой каждой строки столбцом с тем же номером, называется транспонированной к данной и обозначается АТ
1. 4. Преобразование матриц: транспонирование Свойства транспонирования 1. 2. 3. 4. Двойное транспонирование матрицы дает ту же матрицу Транспонированная матрица суммы матриц равна сумме транспонированных слагаемых матриц Транспонированная матрица произведения двух матриц равна произведению транспонированной второй матрицы на транспонированную первую Транспонированная матрица симметрична данной относительно главной диагонали
4. Преобразование матриц: транспонирование Свойства транспонирования 1. 2. 3. 4. Двойное транспонирование матрицы дает ту же матрицу Транспонированная матрица суммы матриц равна сумме транспонированных слагаемых матриц Транспонированная матрица произведения двух матриц равна произведению транспонированной второй матрицы на транспонированную первую Транспонированная матрица симметрична данной относительно главной диагонали
1. 4. Преобразование матриц: элементарные преобразования n n n перестановка двух строк (столбцов) присоединение строки (столбца) из нулей исключение строки (столбца) из нулей умножение всех элементов строки (столбца) на действительное число линейная комбинация строк (столбцов), т. е. прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на какое-либо число
1. 4. Преобразование матриц: элементарные преобразования n Определение 17. Матрица, полученная из данной путем элементарных преобразований, называется эквивалентной (равносильной) данной матрице. n Записывают А В или А В n n С помощью элементарных преобразований можно любую матрицу свести к треугольной (трапециевидной), единичной (канонической) матрице
n Записывают А В или А В n n С помощью элементарных преобразований можно любую матрицу свести к треугольной (трапециевидной), единичной (канонической) матрице
1. 4. Преобразование матриц: элементарные преобразования пример 6
Что такое размер матрицы фотоаппарата, видеокамеры? Как правильно определить размер матрицы?
Продавцы и производители фотоаппаратов стараются обращать внимание покупателей на количество мегапикселей и умалчивать о таком важном параметре, как физический размер матрицы. Конечно, это нечестно, однако маркетинг никто не отменял, и он успешно диктует свои условия, поэтому производители и продавцы просто вынуждены давать пользователям то, чего они хотят.
Почему так важен размер матрицы?
Количество мегапикселей вообще не влияет на качество. Оно только определяет, насколько большим будет изображение. Картинка может быть просто огромной, но плохой. А чтобы она была хорошего качества, необходим большой размер матрицы. Эта информация не нова, но про нее намеренно забывают даже в магазинах.
Эта информация не нова, но про нее намеренно забывают даже в магазинах.
Между тем хороший размер матрицы фотоаппарата (не максимальный, а просто хороший) важнее разрешения, ведь именно от него зависит качество картинки и то, насколько много света попадет на сам сенсор. Разрешение играет роль только тогда, когда планируется печать фотографий на большом носителе. Например, для печати фото на формате A1 необходимо большое разрешение, но даже здесь 4 Мп будет достаточно. Но для печати на обычной фотобумаге размером 10 х 15 см подойдет разрешение 2 Мп, не более. А вообще, большинство пользователей загружают фото в социальные сети, где они проходят предварительное сжатие.
Это соотношение фактического размера матрицы фотоаппарата к стандартному размеру пленки, который равен 35 мм. Поясним: современные камеры имеют кропнутые (обрезанные) матрицы, поэтому их размер чаще всего не равен и половине стандартного. Однако он всегда указывается в дробной величине (например, 1/3.2″), и покупатель при этом запутывается окончательно.
Часто люди видят большое значение и думают, что это хорошо, но на самом деле большое значение в знаменателе — это плохо. Ведь чем оно будет больше, тем размер матрицы видеокамеры или фотоаппарата будет меньше, а значит, и качество снимков будет хуже.
Типовые размеры
В зависимости от того, насколько дорогой или хороший фотоаппарат, размер матрицы может быть малым, средним или большим. Ниже представим типовые размеры, которые встречаются чаще всего.
Начнем с самых маленьких матриц:
- 1/3.2″ — матрицы с таким размером являются самыми маленькими. Хуже ничего на рынке быть не может. Видя такой параметр в характеристиках фотоаппарата, покупать его не стоит. Физический размер здесь равен 3,4 х 4,5 квадратных миллиметра, и ни один более-менее достойный фотоаппарат не будет оснащаться столь маленькой матрицей.
- 1/2.7″ — этот размер также мал (4 х 5,4 квадратных миллиметра) и встречается только в дешевых камерах.
- 1/2.5″ — физический размер матрицы с таким соотношением равен 4,3 х 5,8 кв.
 мм. Большинство современных «мыльниц» среднего ценового диапазона оснащаются такими сенсорами. Можно сказать, что это стандарт даже для современных беззеркальных и дешевых зеркальных фотоаппаратов.
мм. Большинство современных «мыльниц» среднего ценового диапазона оснащаются такими сенсорами. Можно сказать, что это стандарт даже для современных беззеркальных и дешевых зеркальных фотоаппаратов. - 1/1.8″ — геометрический размер сенсора равен 5,3 х 7,2 кв. мм. Отсюда начинается категория более-менее достойных фотоаппаратов. Дорогие зеркальные камеры среднего уровня могут оснащаться сенсором с такими геометрическими параметрами. Также и простые небольшие мыльницы могут иметь такие матрицы.
- 2/3″ — соотношение, при котором физический размер будет равен 6,6 х 8,8 квадратным миллиметрам. Сенсоры с таким параметром используются в дорогих зеркальных и компактных фотоаппаратах со сменной или несменной оптикой.
- 4/3″ — матрицы с таким соотношением применяются исключительно в дорогих камерах. Здесь размер равен 18 х 13,5 кв. мм.
- DX, APS-C. Редко размер указывается буквами. Если вы видите такой параметр, то это значит, что матрица в фотоаппарате больше предыдущего формата, и ее размер составляет 24 х 18 мм.
 Он соответствует полукадру 35 мм. Эти матрицы довольно популярны и часто их можно увидеть в полупрофессиональных фотоаппаратах. Они дешевые в изготовлении, а размер пикселя при этом в них остается большим даже при разрешении 11-12 Мп.
Он соответствует полукадру 35 мм. Эти матрицы довольно популярны и часто их можно увидеть в полупрофессиональных фотоаппаратах. Они дешевые в изготовлении, а размер пикселя при этом в них остается большим даже при разрешении 11-12 Мп. - Полнокадровые матрицы. По размеру они соответствуют классическому кадру 35 мм, и их размер составляет 36 х 24 кв. мм. На рынке существует мало фотоаппаратов с такими матрицами. Это профессиональные модели, которые очень дорого стоят. Сами матрицы сложны в производстве, чем и объясняется высокая стоимость фотоаппаратов, созданных на базе этих сенсоров.
Как определить размер матрицы?
Сделать это несложно. Он всегда указывается в технических характеристиках к любой камере. Но это можно даже сделать визуально. Например, цифровые фотоаппараты с матрицами размером 1/2.7″ будут небольшими, легкими. А вот камера с матрицей 1/1.8″ при прочих равных характеристиках будет немного больше и тяжелее.
Размер оказывает влияние на вес и объем камеры, ведь размеры оптики тесно связаны с геометрическими параметрами сенсоров. Профессиональные фотографы могут «на глаз» определить, какой размер матрицы используется в том или ином фотоаппарате.
Профессиональные фотографы могут «на глаз» определить, какой размер матрицы используется в том или ином фотоаппарате.
Шумы
Зернистость на фото — это один из самых распространенных дефектов, который может быть на фото. Если камера имеет небольшую матрицу, то количество света на нее попадает тоже небольшое. Из-за этого при ограниченном свете (например, в помещении) такие камеры делают фотографии с зернистостью (шумами). При равных условиях фотоаппарат с матрицей размером 1/1.8″ сделает фото с меньшим количеством шумов по сравнению с моделью с матрицей 1/2.3″. Конечно, в появлении шумов имеют место также внутренние электрические процессы, дефекты или нагрев матрицы, но это уже не относится к нашей теме.
Заключение
Помните, что фотоаппарат с разрешением 20 Мп и размером матрицы 1/2.3″ сделает фото по качеству хуже, чем камера с разрешение 8 Мп, но матрицей с размером 1/1.8″. Так что дело здесь совсем не в разрешении, которое влияет только на размер изображения. Он то вообще в нынешних условиях не играет роли, ведь в основном люди «заливают» свои фото в социальные сети, где никто не будет открывать их оригинальный размер.
Он то вообще в нынешних условиях не играет роли, ведь в основном люди «заливают» свои фото в социальные сети, где никто не будет открывать их оригинальный размер.
Помните: размером матрицы называется физический реальный размер используемого сенсора, который оказывает наибольшее влияние на качество изображения. Выбирая камеру, в первую очередь обращайте внимание именно на геометрические размеры сенсора, которые всегда указываются в характеристиках. И только затем смотрите на остальные параметры, включая разрешение.
Произведение двух матриц: формула, решения, свойства
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Определение. Произведением двух матриц А и В называется матрица С, элемент
которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов
i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В.
Из этого определения следует формула элемента матрицы C:
Произведение матрицы А на матрицу В обозначается АВ.
Пример 1. Найти произведение двух матриц А и B, если
,
.
Решение. Удобно нахождение произведения двух матриц А и В записывать так, как на рис.2:
На схеме серые стрелки показывают, элементы какой строки матрицы А на элементы какого столбца матрицы В нужно перемножить для получения элементов матрицы С , а линиями цвета элемента матрицы C соединены соответствующие элементы матриц A и B, произведения которых складываются для получения элемента матрицы C.
В результате получаем элементы произведения матриц:
Теперь у нас есть всё, чтобы записать произведение двух матриц:
.
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Произведение двух матриц АВ имеет смысл только в том случае, когда число столбцов матрицы А совпадает с числом строк матрицы В .
Эту важную особенность будет легче запомнить, если почаще пользоваться следующими памятками:
Имеет место ещё одна важная особенность произведения матриц относительно числа строк и столбцов:
В произведении матриц АВ число строк равно числу строк матрицы А , а число столбцов равно числу столбцов матрицы В .
Пример 2. Найти число строк и столбцов матрицы C, которая является произведением двух матриц A и B следующих размерностей:
а) 2 Х 10 и 10 Х 5;
б) 10 Х 2 и 2 Х 5;
в) 4 Х 4 и 4 Х 10.
Решение:
а) 2 Х 5;
б) 10 Х 5;
в) 4 Х 10.
Пример 3. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 2, число столбцов в матрице B — 2. Следовательно, размерность матрицы C = AB — 2 X 2.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 5. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 2, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 2 X 1.
Следовательно, размерность матрицы C = AB — 2 X 1.
Вычисляем элементы матрицы C = AB.
Произведение матриц запишется в виде матрицы-столбца: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Пример 6. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 3, число столбцов в матрице B — 3. Следовательно, размерность матрицы C = AB — 3 X 3.
Вычисляем элементы матрицы C = AB.
Найденное произведение матриц: .
Проверить решение этой и других подобных задач можно на
калькуляторе произведения
матриц онлайн.
Пример 7. Найти произведение матриц A и B, если:
.
Решение. Число строк в матрице A — 1, число столбцов в матрице B — 1. Следовательно, размерность матрицы C = AB — 1 X 1.
Вычисляем элемент матрицы C = AB.
Произведение матриц является матрицей из одного элемента: .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Программная реализация произведения двух матриц на С++ разобрана в соответствующей статье в блоке «Компьютеры и программирование».
Возведение матрицы в степень определяется как умножение матрицы на ту же самую матрицу.
Так как произведение матриц существует только тогда, когда число столбцов первой матрицы совпадает с
числом строк второй матрицы, то возводить в степень можно только квадратные матрицы. n-ая
степень матрицы путём умножения матрицы на саму себя n раз:
n-ая
степень матрицы путём умножения матрицы на саму себя n раз:
Пример 8. Дана матрица . Найти A² и A³.
Решение:
Найти произведение матриц самостоятельно, а затем посмотреть решение
Пример 9. Дана матрица
Найти произведение данной матрицы и транспонированной матрицы , произведение транспонированной матрицы и данной матрицы.
Правильное решение и ответ.
Свойство 1. Произведение любой матрицы А на единичную матрицу Е соответствующего порядка как справа, так и слева, совпадает с матрицей А , т.е. АЕ = ЕА = А .
Иными словами, роль единичной матрицы при умножении матриц такая же, как и единицы при умножении чисел.
Пример 10. Убедиться в справедливости свойства 1, найдя произведения матрицы
Убедиться в справедливости свойства 1, найдя произведения матрицы
на единичную матрицу справа и слева.
Решение. Так как матрица А содержит три столбца, то требуется найти произведение АЕ , где
—
единичная матрица третьего порядка. Найдём элементы произведения С = АЕ :
Получается, что АЕ = А .
Теперь найдём произведение ЕА , где Е – единичная матрица второго порядка, так как матрица А содержит две строки. Найдём элементы произведения С = ЕА :
Доказано: ЕА = А .
Проверить решение этой и других подобных задач можно на калькуляторе произведения матриц онлайн.
Свойство 2. Произведение матрицы А на нуль-матрицу является нуль-матрицей. Это свойство очевидно, так как все элементы нуль-матрицы равны нулю.
Свойство 3. Произведение матриц некоммутативно:
.
Для этого достаточно показать, что равенство АВ = ВА не выполняется для каких-либо двух матриц.
Пример 11. Найти произведения матриц АВ и ВА, если
,
,
и убедиться в том, что эти произведения не равны друг другу:
.
Решение. Находим:
И действительно, найденные произведения не равны:
.
Проверить решение этой и других подобных задач можно на
калькуляторе произведения
матриц онлайн.
Свойство 4. Произведение матриц ассоциативно: (АВ)С = А(ВС) .
Свойство 5. Для произведения матриц выполняется дистрибутивный закон: (А + В) С = АС + ВС , С (А + В) = СА + СВ .
Свойство 6. Определитель произведения двух квадратных матриц равен произведению их определителей: если С = АВ , то
.
Поделиться с друзьями
Начало темы «Матрицы»
Продолжение темы «Матрицы»
Другие темы линейной алгебры
На что влияет размер матрицы камеры смартфона?
Пока производители смартфонов устраивают гонку за мегапикселями, более важной характеристикой камеры продолжает оставаться размер матрицы. На что он влияет, а какие характеристики изображения не зависят от размера матрицы?
Матрица представляет собой микросхему со светочувствительными фотодиодами. Как известно, фотодиод под действием света формирует электрический сигнал, который впоследствии преобразуется в цифровой сигнал. Фактически матрица выполняет функцию пленки в традиционных фотоаппаратах. В дальнейшем информация об изображении поступает в процессор, который преобразует его и отправляет в хранилище смартфона. В среднем этот процесс длится 0,2-0,3 секунды.
Размер матрицы указывается в дюймах. В современных моделях используются матрицы со следующей диагональю:
При этом качество картинки напрямую зависит от размера матрицы. Во-первых, чем больше сенсор, тем больше света улавливает матрица. Благодаря этому более крупные датчики способны размывать фон с малой глубиной резкости, демонстрировать меньший шум в условиях низкой освещенности и захватывать более широкий динамический диапазон между самыми яркими и самыми темными областями изображения.
Во-вторых, большой сенсор может вместить больше мегапикселей. Чем больше мегапикселей у камеры смартфона, тем выше будет разрешение снимков. К сожалению, невозможно поместить много больших пикселей на сенсор, по крайней мере, в камере смартфона из-за физического размера матрицы. Так что чем больше пикселей у камеры, тем они меньше — на это тоже нужно обращать внимание.
А вот одно из популярных заблуждений — якобы от размера матрицы зависит красивое размытие фона и придание объектам на снимке объема. На самом деле эти моменты зависят от других характеристик, в частности, от работы программных алгоритмов в смартфоне.
Источник: //zoom.cnews.ru/b/post/tehnoblog/75657
Данный материал является частной записью члена сообщества Club.CNews.
Редакция CNews не несет ответственности за его содержание.
Размер матрицы — объяснение и примеры
Матрицы представляют собой прямоугольное расположение чисел в строках и столбцах. Иногда их называют массивами. Размеры матрицы в основном равны имени . Знание размерности матрицы позволяет нам выполнять с ними базовые операции, такие как сложение, вычитание и умножение. Начнем с определения размерности матрицы:
Размерность матрицы — это количество строк и столбцов.
В этой статье будет рассказано о размерности матрицы, о том, как найти размерность матрицы, и рассмотрены некоторые примеры размерностей матрицы. Если вы хотите узнать больше о матрице, прочтите эту статью.
Каков размер матрицы?
Размер матрицы — это количество строк и количество столбцов матрицы в указанном порядке. Рассмотрим матрицу, показанную ниже:
В ней 2 $ строк (по горизонтали) и $ 2 $ столбцов (по вертикали).Размерность этой матрицы $ 2 \ times 2 $. Первое число — это число строк , а следующее число — это число столбцов . Это должно быть именно в таком порядке. Мы произносим это как «матрица 2 на 2» . Знак $ \ times $ произносится как «на» .
Элементы $ 2, 3, -1 $ и $ 0 $ известны как элементов матрицы.
В общем случае, если у нас есть матрица с $ m $ строками и $ n $ столбцами, мы называем ее $ m \ times n $ или строк x столбцов. Должно соблюдаться соглашение о том, что сначала строки, а вторые столбцы . Это размерность матрицы. Вы можете запомнить название матрицы, используя быструю мнемонику.
Помните, RC . Сначала строки, затем столбцы.
Как найти размерность матрицы?
Чтобы найти размерность данной матрицы, мы подсчитываем количество имеющихся в ней строк. Затем мы подсчитываем количество столбцов в нем. Мы помещаем числа в этом порядке со знаком $ \ times $ между ними.Возьмем пример.
Сколько строк и столбцов в приведенной ниже матрице?
Проверяем по горизонтали, есть строки по 3 доллара. Проверяем по вертикали, есть столбцы $ 2 $. Таким образом, мы нашли размерность этой матрицы. Это матрица размером $ 3 \ times 2 $.
Что с этой матрицей?
Это может быть бит сложно. Но если вы всегда сосредотачиваетесь на подсчете сначала только строк, а затем только столбцов, у вас не возникнет никаких проблем.Мы видим, что есть только $ 1 $ строка (по горизонтали) и $ 2 $ столбца (по вертикали). Таким образом, эта матрица будет иметь размерность $ 1 \ times 2 $.
Давайте рассмотрим несколько примеров, чтобы лучше понять размеры матриц.
Пример 1
Каков размер матрицы, показанной ниже?
$ \ begin {pmatrix} 1 & {0} & 1 \\ 1 & 1 & 1 \\ 4 & 3 & 2 \ end {pmatrix} $
Решение
Напомним, что размерность матрицы — это число строк и количество столбцов в матрице, в этом порядке .Всегда помните, что сначала нужно думать горизонтально (чтобы получить количество строк), а затем думать вертикально (чтобы получить количество столбцов).
Глядя на приведенную выше матрицу, мы видим, что в ней есть строки по $ 3 и столбцы по $ 3. Следовательно, размерность этой матрицы $ 3 \ times 3 $.
Давайте посмотрим на другой пример.
Пример 2
Каков размер матрицы, показанной ниже?
$ \ begin {pmatrix} a \\ b \\ c \ end {pmatrix} $
Решение
Это небольшая матрица.Будьте осторожны при определении размеров таких матриц. Проверьте по горизонтали, вы увидите, что есть строки по 3 доллара. Отметьте вертикально, там только столбец $ 1 $. Из соглашения о записи размерности матрицы как строк x столбцов, мы можем сказать, что эта матрица является матрицей $ 3 \ times 1 $.
Обратите внимание, что элементов матрицы, будь то числа или переменные (буквы), не влияют на размерности матрицы.Размер только зависит от количества строк и столбцов. Вы можете использовать число или букву в качестве элементов в матрице в зависимости от ваших потребностей.
Теперь мы видим сложную проблему .
Пример 3
Каков размер матрицы, показанной ниже?
$ \ begin {bmatrix} {5} \ end {bmatrix} $
Решение
На первый взгляд это выглядит как число в скобках.Ну, это тоже может быть матрица. У нас есть одиночных записей в этой матрице. Количество строк и столбцов равно одному. Таким образом, это матрица размером $ 1 \ times 1 $.
Практические вопросы
-
- Как называются отдельные записи в матрице?
- Верно или неверно
Матрица имеет 5 $ строк и 2 $ столбцов. Размерность матрицы составляет $ 2 \ умножить на 5 $. - Каков размер этой матрицы?
$ \ begin {bmatrix} a & b & c \\ f & e & d \ end {bmatrix} $ - Имеет ли матрица, показанная ниже, размерность $ 1 \ times 5 $?
$ \ begin {pmatrix} 22 \\ 3 \\ {- 2} \\ 5 \\ 1 \ end {pmatrix} $
Ответы
- Отдельные элементы любой матрицы известны как элементов .Они могут быть числами или переменными.
- При наименовании матрицы , то есть размер матрицы , мы всегда ставим количество строк на первое место. Затем знак $ \ times $, за которым следует количество столбцов. Поскольку имеется $ 5 $ строк и $ 2 $ столбцов, размер матрицы должен быть $ 5 \ times 2 $. Следовательно, утверждение Ложно.
- Если имеется m строк и n столбцов, размер этой матрицы равен $ m \ times n $.Из показанной матрицы мы видим, что есть $ 2 $ строк и $ 3 $ столбцов. Таким образом, размерность этой матрицы $ 2 \ times 3 $.
- Если имеется m строк и n столбцов, размер этой матрицы равен $ m \ times n $. Глядя на матрицу, мы видим, что в ней 5 строк и 1 столбец. Следовательно, его размерность $ 5 \ times 1 $. Итак, НЕТ , матрица НЕ имеет размерности 1 $ \ 5 $.
Предыдущий урок | Главная страница | Следующий урок
Размер матрицы — обзор
Мы используем одну (или в нижнем индексе) жирную заглавную букву для обозначения матрицы (например, A , B , C 1 , C 2 ) в отличие от строчных полужирных букв, используемых для обозначения векторов.Заглавные буквы I и O обычно зарезервированы для специальных типов матриц, обсуждаемых позже.
Размер матрицы всегда указывается первым числом строк. Например, матрица 3 × 4 всегда имеет три строки и четыре столбца, а не четыре строки и три столбца.
Матрица m × n может рассматриваться как набор векторов-строк m , каждый из которых имеет n координат, или как набор из n векторов-столбцов, каждый с координатами м .Матрица с одной строкой (или столбцом) по существу эквивалентна вектору с координатами в виде строки (или столбца).
Мы часто пишем a ij для представления записи в i -й строке и j -м столбце матрицы A . Например, в предыдущей матрице A , a 23 — это запись -5 во второй строке и третьем столбце. Типичная матрица 3 × 4 C имеет элементы, обозначенные
C = [c11c12c13c14c21c22c23c24c31c32c33c34].
ℳ mn представляет собой набор всех матриц с записями действительных чисел, имеющими m строк и n столбцов. Например, ℳ 34 — это набор всех матриц, имеющих три строки и четыре столбца. Типичная матрица в ℳ 34 имеет вид предыдущей матрицы C .
главной диагонали элементов матрицы A — это a 11 , a 22 , a 33 ,…, те, которые лежат на диагональной линии рисуются вправо, начиная с верхнего левого угла матрицы.
Не знаете о тензорах, измерениях, рангах, порядках, матрицах и векторах? | Ромео Кинцлер | Центр данных с открытым исходным кодом и технологий искусственного интеллекта
Когда дело доходит до терминов _dimensionality_ , _rank_ и _order_ , вы должны различать случаи, когда термин описывает вектор или матрицу или тензор. Первые представляют собой математические свойства вектора и матрицы, вторые описывают форму структуры данных, называемой _tensor_ .
Позвольте мне объяснить…
Тензор — это не что иное, как математическая структура данных, способ организации данных и набор правил (определенных в линейной алгебре), которые определяют математические операции над ними.
_dimensionality_ , _rank_ или _order_ самого тензора определяет его расширение в пространстве. Следующая таблица иллюстрирует это:
Поскольку основные структуры данных уже рассмотрены, я представляю некоторые возможности и свойства для каждой из них.
Скаляры охватывают одномерное векторное пространство, поскольку они могут однозначно адресовать любую точку в нем. Одномерное векторное пространство также называется _line_ . Это означает, что с бесконечным количеством скалярных значений вы можете адресовать любую точку в строке.
Векторы охватывают векторное пространство любой размерности в зависимости от количества элементов в векторе, поскольку он может однозначно адресовать любую точку в произвольно большом (относительно количества измерений) векторном пространстве. Количество элементов в векторе также называется размерностью или порядком.Это означает, что с бесконечным числом векторов вы можете адресовать любую точку в любом векторном пространстве, независимо от того, сколько измерений она имеет. Двумерное пространство также называют плоскостью. В зависимости от теории, которой вы следуете, наша Вселенная имеет три, четыре (Эйнштейн, пространство-время), пять (Теодор Калуца) или одиннадцать (Эдвард Виттен, теория суперструн) измерений. Но набор данных MNIST, набор данных hello world в нейронных сетях, имеет 784 измерения, поскольку изображения имеют 28 на 28 пикселей.
Матрицы охватывают векторное пространство любой размерности, потому что в зависимости от количества столбцов они могут однозначно адресовать любую точку в произвольном большом (относительно количества измерений) векторном пространстве.Каждая строка в матрице соответствует одной точке в этом пространстве. Другими словами, матрица — это просто набор точек или векторов одинаковой длины. Количество строк говорит вам, сколько точек у вас есть в этом пространстве, а количество столбцов говорит вам, сколько измерений имеет это пространство.
Порядок матрицы — это количество строк (обычно упоминаемых первыми) и столбцов (обычно упоминаемых последними).
Ранг матрицы — это количество линейно независимых компонентов, и его часто путают с порядком матрицы.
Трехмерные тензоры охватывают несколько параллельных векторных пространств одинаковой размерности. В зависимости от количества столбцов он может однозначно адресовать любую точку в произвольно большом (относительно # размеров) векторном пространстве. Каждая строка в трехмерном тензоре соответствует одной точке в этом пространстве, и каждый слой в трехмерном тензоре можно рассматривать как отдельное векторное пространство с тем же количеством измерений и точек.
Я пока не использовал четырехмерный тензор для какого-либо практического применения, но я слышал, что они нужны вам для понимания общей теории относительности 🙂
|
Имя: Тип: Цель:
920,000 / 3 = 306666 элементов временных матриц. при выполнении матричных манипуляций. По умолчанию используйте 3000 строк и 100 столбцов. Самая большая квадратная матрица примерно 550 x 550 пикселей. РАЗМЕР МАТРИЦЫ позволяет изменять строки и столбцы для временных матриц.Количество строк не может быть установлено больше, чем максимальное количество строк для переменной (по умолчанию установлено значение 20 000). Поскольку эта команда измеряет только временные матрицы во время вычислений, вы можете вводить эту команду так часто, как вы желание во время одного сеанса Dataplot.
, где
, где <строки> — число или параметр, определяющий максимальное количество строк для временного матрицы.
РАЗМЕРНЫЕ КОЛОНКИ МАТРИЦЫ 500
ПОЗВОНИТЬ Y = НОМЕР НОРМАЛЬНОГО ДИАПАЗОНА ДЛЯ I = 1 1 500 ПОЗВОНИТЬ D = ДИАГНОНАЛЬНАЯ МАТРИЦА Y | |
|
Конфиденциальность
Уведомление о политике / безопасности
NIST — агентство США.С. Департамент торговли.
Дата создания: 05.06.2001 |
|
Многомерные массивы — MATLAB и Simulink
Многомерный массив в MATLAB® — это массив с более чем двумя измерениями. В матрице два измерения представлены строками и столбцами.
Каждый элемент определяется двумя нижними индексами: индексом строки и индексом столбца.Многомерные массивы являются расширением двумерных матриц и используют дополнительные индексы для индексации. Например, в трехмерном массиве используются три нижних индекса. Первые два похожи на матрицу, но третье измерение представляет страниц или листов элементов.
Создание многомерных массивов
Вы можете создать многомерный массив, сначала создав двухмерную матрицу, а затем расширив ее. Например, сначала определите матрицу 3 на 3 как первую страницу в трехмерном массиве.
A = [1 2 3; 4 5 6; 7 8 9]
A = 3 × 3
1 2 3
4 5 6
7 8 9
Теперь добавьте вторую страницу. Для этого присвойте еще одну матрицу 3 на 3 значению индекса 2 в третьем измерении. Синтаксис A (:,:, 2) использует двоеточие в первом и втором измерениях, чтобы включить все строки и все столбцы с правой стороны присвоения.
A (:,:, 2) = [10 11 12; 13 14 15; 16 17 18]
A =
А (:,:, 1) =
1 2 3
4 5 6
7 8 9
А (:,:, 2) =
10 11 12
13 14 15
16 17 18
Функция cat может быть полезным инструментом для построения многомерных массивов.Например, создайте новый трехмерный массив B , объединив A с третьей страницей. Первый аргумент указывает, по какому измерению следует выполнить конкатенацию.
B = cat (3, A, [3 2 1; 0 9 8; 5 3 7])
B =
B (:,:, 1) =
1 2 3
4 5 6
7 8 9
B (:,:, 2) =
10 11 12
13 14 15
16 17 18
B (:,:, 3) =
3 2 1
0 9 8
5 3 7
Еще один способ быстро расширить многомерный массив — присвоить один элемент всей странице.Например, добавьте четвертую страницу к B , которая содержит все нули.
В =
B (:,:, 1) =
1 2 3
4 5 6
7 8 9
B (:,:, 2) =
10 11 12
13 14 15
16 17 18
B (:,:, 3) =
3 2 1
0 9 8
5 3 7
B (:,:, 4) =
0 0 0
0 0 0
0 0 0
Доступ к элементам
Для доступа к элементам в многомерном массиве используйте целочисленные индексы так же, как для векторов и матриц.Например, найдите 1,2,2 элемент A , который находится в первой строке, втором столбце и второй странице A .
А =
А (:,:, 1) =
1 2 3
4 5 6
7 8 9
А (:,:, 2) =
10 11 12
13 14 15
16 17 18
Используйте вектор индекса [1 3] во втором измерении для доступа только к первому и последнему столбцам каждой страницы A .
С =
С (:,:, 1) =
1 3
4 6
7 9
С (:,:, 2) =
10 12
13 15
16 18
Чтобы найти вторую и третью строки каждой страницы, используйте оператор двоеточия для создания вектора индекса.
D =
D (:,:, 1) =
4 5 6
7 8 9
D (:,:, 2) =
13 14 15
16 17 18
Управление массивами
Элементы многомерных массивов можно перемещать разными способами, подобно векторам и матрицам. изменить форму , переместить и сжать — полезные функции для переупорядочивания элементов. Рассмотрим трехмерный массив с двумя страницами.
Изменение формы многомерного массива может быть полезно для выполнения определенных операций или визуализации данных.Используйте функцию reshape , чтобы преобразовать элементы трехмерного массива в матрицу 6 на 5.
A = [1 2 3 4 5; 9 0 6 3 7; 8 1 5 0 2]; A (:,:, 2) = [9 7 8 5 2; 3 5 8 5 1; 6 9 4 3 3]; B = изменить форму (A, [6 5])
B = 6 × 5
1 3 5 7 5
9 6 7 5 5
8 5 2 9 3
2 4 9 8 2
0 3 3 8 1
1 0 6 4 3
reshape работает по столбцам, создавая новую матрицу, беря последовательные элементы вниз по каждому столбцу A , начиная с первой страницы и затем перемещаясь на вторую страницу.
Перестановки используются для изменения порядка размеров массива. Рассмотрим трехмерный массив M .
M (:,:, 1) = [1 2 3; 4 5 6; 7 8 9]; M (:,:, 2) = [0 5 4; 2 7 6; 9 3 1]
M =
M (:,:, 1) =
1 2 3
4 5 6
7 8 9
M (:,:, 2) =
0 5 4
2 7 6
9 3 1
Используйте функцию перестановки для обмена индексами строк и столбцов на каждой странице, указав порядок измерений во втором аргументе.Исходные строки M теперь являются столбцами, а столбцы теперь строками.
P1 =
P1 (:,:, 1) =
1 4 7
2 5 8
3 6 9
P1 (:,:, 2) =
0 2 9
5 7 3
4 6 1
Аналогичным образом поменяйте местами нижние индексы строк и страниц M .
P2 =
P2 (:,:, 1) =
1 2 3
0 5 4
P2 (:,:, 2) =
4 5 6
2 7 6
P2 (:,:, 3) =
7 8 9
9 3 1
При работе с многомерными массивами вы можете столкнуться с ненужным размером 1.Функция squeeze выполняет другой тип манипуляции, который исключает размеры длины 1. Например, используйте функцию repmat для создания массива 2 на 3 на 1 на 4, каждый элемент которого равен 5, и третье измерение которого имеет длину 1.
A =
А (:,:, 1,1) =
5 5 5
5 5 5
А (:,:, 1,2) =
5 5 5
5 5 5
А (:,:, 1,3) =
5 5 5
5 5 5
А (:,:, 1,4) =
5 5 5
5 5 5
Используйте функцию squeeze , чтобы удалить третье измерение, в результате чего получится трехмерный массив.
В =
B (:,:, 1) =
5 5 5
5 5 5
B (:,:, 2) =
5 5 5
5 5 5
B (:,:, 3) =
5 5 5
5 5 5
B (:,:, 4) =
5 5 5
5 5 5
dim в программировании R (4 примера функции измерения)
Базовый синтаксис R:
Функция dim языка программирования R возвращает размерность (например, количество столбцов и строк) матрицы, массива или фрейма данных.Выше вы можете увидеть код R для применения dim в R.
Читать дальше! В следующей статье я дам вам несколько примеров кодов и практических советов .
Пример 1: Размер матрицы или фрейма данных
Давайте сначала создадим несколько примеров данных, прежде чем мы начнем с применения dim в R:
set.seed (62626) # Set Seed для воспроизводимости N <- 500 # Размер выборки x1 <- round (rnorm (N, 0, 10)) # Создаем 5 случайных величин x2 <- раунд (runif (N, 5, 10)) x3 <- раунд (runif (N, 1, 3), 1) x4 <- раунд (runif (N, 10, 20)) x5 <- rpois (N, 5) данные <- данные.frame (x1, x2, x3, x4, x5) # Фрейм данных с 5 столбцами head (data) # Первые 6 строк data.frame |
set.seed (62626) # Установить Seed для воспроизводимости N <- 500 # Размер выборки x1 <- round (rnorm (N, 0, 10)) # Создаем 5 случайных величин x2 <- раунд (runif (N, 5, 10)) x3 <- раунд (runif (N, 1, 3), 1) x4 <- раунд (runif (N, 10, 20)) x5 <- rpois (N, 5) данные <- данные.frame (x1, x2, x3, x4, x5) # Фрейм данных с 5 столбцами head (data) # Первые 6 строк data.frame
Таблица 1: Первые 6 строк нашего примера фрейма данных для применения dim в R.
Таблица 1 показывает, как выглядит наш пример data.frame. Нетрудно заметить, что данные состоят из 5 столбцов. Но сколько строк? Давайте проверим с помощью функции dim R:
dim (data) # Применить функцию dim к данным.Рамка # 500 5 |
dim (data) # Применить функцию dim к data.frame # 500 5
После применения функции dim в R (я использую интерфейс RStudio) мы получаем обратно два числа. Первое число отражает количество строк; а второе число отражает количество столбцов.
Другими словами: наш фрейм данных состоит из 500 строк и 5 столбцов.
Та же процедура может быть применена к матрице. Преобразуем наши данные в матричный формат и проверим, работает ли:
матрица_данных <- as.matrix (data) # Преобразование data.frame в матрицу dim (data_matrix) # Применить функцию dim к матрице # 500 5 |
data_matrix <- as.matrix (data) # Преобразование data.frame в матрицу dim (data_matrix) # Применить функцию dim к матрице # 500 5
Тот же результат, что и раньше - отлично!
Пример 2 (видео): размер кадра реальных данных
В предыдущем примере я показал вам, как применить dim к синтетическому набору данных.Хотите увидеть пример, основанный на более реалистичных данных ? Тогда вы можете посмотреть следующее видео с моего канала YouTube Statistical Programming . В видео я показываю еще один пример применения затемнения к кадру данных:
Пожалуйста, примите файлы cookie YouTube для воспроизведения этого видео. Принимая, вы будете получать доступ к контенту YouTube, услуги, предоставляемой сторонней внешней стороной.
Политика конфиденциальности YouTube
Если вы примете это уведомление, ваш выбор будет сохранен, и страница обновится.
Принять контент YouTube
Пример 3: размер списка в
рэндовИногда полезно использовать dim для объекта списка в R. Эту задачу легко выполнить с помощью комбинации dim () и sapply ().
Во-первых, давайте создадим список в R:
data_list <- list () # Создать объект пустого списка data_list [[1]] <- data # Первая запись списка data_list [[2]] <- data [1:10,] # Вторая запись (подмножество данных) data_list [[3]] <- data [5:67, c (1, 3, 5)] # Третья запись (другое подмножество данных) |
data_list <- list () # Создать объект пустого списка data_list [[1]] <- data # Первая запись списка data_list [[2]] <- data [1:10,] # Вторая запись (подмножество данных) data_list [[3]] <- data [5:67, c (1, 3, 5)] # Третья запись (другое подмножество данных)
Теперь давайте извлечем размеры каждого элемента списка:
sapply (data_list, dim) # Получить размер всех записей списка # [, 1] [, 2] [, 3] # [1,] 500 10 63 # [2,] 5 5 3 |
sapply (data_list, dim) # Получить размер всех записей списка # [, 1] [, 2] [, 3] # [1,] 500 10 63 # [2,] 5 5 3
Комбинация dim и sapply возвращает матрицу в консоль RStudio.Каждый столбец этой матрицы отражает размерность одного элемента списка:
- Запись в списке 1: 500 строк; 5 столбцов
- Запись в списке 2: 10 строк; 5 столбцов
- Элемент списка 3: 63 строки; 3 колонки
Пример 4: dim in R возвращает NULL - В чем проблема?
Распространенной ошибкой является применение dim к одномерному вектору или массиву. Посмотрим, что произойдет, когда мы это сделаем.
Сначала я создам пример вектора…
vec1 <- c (5, 9, - 20, 3, 17, 18, 2) # Пример вектора |
vec1 <- c (5, 9, - 20, 3, 17, 18, 2) # Пример вектора
… а затем применим функцию затемнения:
dim (vec1) # Применить функцию затемнения к вектору # NULL |
dim (vec1) # Применить функцию dim к вектору # NULL
Как видите: это не работает!
Если вы хотите получить количество элементов вектора, вы должны использовать функцию длины:
length (vec1) # Получить длину вектора или массива # 7 |
length (vec1) # Получить длину вектора или массива # 7
Дополнительная литература
/ * Добавьте свои собственные переопределения стиля формы MailChimp в таблицу стилей вашего сайта или в этот блок стилей.
Мы рекомендуем переместить этот блок и предыдущую ссылку CSS в HEAD вашего HTML-файла. * /
]]>
размеров матрицы - Thevoltreport
размер матрицы
Это тема, которую ищут многие люди. thevoltreport.com - это канал, предоставляющий полезную информацию об обучении, жизни, цифровом маркетинге и онлайн-курсах…. это поможет вам получить обзор и солидные многогранные знания.Сегодня thevoltreport.com представляет вам Размеры матрицы . Ниже приведены инструкции в видео ниже:
Матрица - это прямоугольное расположение или массив чисел, часто называемых элементами. Вот два примера матриц. Обратите внимание на то, что обе матрицы имеют шесть элементов, но их расположение совсем другое. Вот почему так важно понимать размеры матрицы.Размер или размер (m на n) матрицы определяет, сколько строк и столбцов имеет конкретная матрица. Количество строк - m, количество столбцов - n, где строки идут влево и вправо, а столбцы идут вверх и вниз. Итак, если посмотреть на эту первую матрицу, у нее одна, две строки и один, два, три столбца. И поэтому размеры этой первой матрицы будут два на три. Сравнивая это со второй матрицей, обратите внимание, что эта матрица имеет одну, две, три строки и один, два столбца. Следовательно, размеры будут три на два.Вот почему так важно понимать размеры матрицы. Обратите внимание, если мы рассматриваем конкретный элемент в матрице, например, этот элемент здесь. Обратите внимание, как он идентифицируется вторым вторым запятым, третьим, потому что позиция этого элемента - вторая строка, третий столбец.
Если мы сравним это с этим элементом во второй матрице, у нас будет три части, запятая два, потому что этот элемент находится в строке три, столбце два. Рассмотрим еще несколько примеров. Из этих четырех примеров видно, что обычно матрица обозначается заглавной буквой.Итак, если мы посмотрим на матрицу A, обратите внимание, что она имеет одну, две, три, четыре строки и один столбец. Следовательно, размеры будут четыре на один. И часто при идентификации матрицы с использованием заглавной буквы, как мы видим здесь, часто пишут заглавную A с нижним индексом для измерений, которые в этом случае будут четыре на один. И поскольку эта матрица состоит из одного столбца, ее также можно назвать матрицей столбцов. Если мы посмотрим на матрицу B, обратите внимание, что в ней одна строка и один, два, три столбца. Следовательно, размеры будут один на три.Поскольку он состоит из одной строки, его часто называют матрицей строк. И если мы идентифицируем это с помощью переменной B, то часто будем записывать размеры в нижнем индексе, так что у нас будет один за другим, вот так. Глядя на матрицу C, обратите внимание, что
у нас есть одна, две, три строки и один, два, три столбца. Таким образом, размеры будут три на три. Поскольку количество строк и столбцов одинаково, это называется квадратной матрицей, где, опять же, если мы используем заглавную букву C, у нас будет C с нижним индексом три на три.И для нашего последнего примера, для матрицы D, обратите внимание, что у нас есть одна, две строки и один, два, три, четыре столбца. Таким образом, размеры будут два на четыре. И снова, если мы используем заглавную букву D для обозначения этой матрицы, мы бы поместили размеры в качестве нижнего индекса, как мы видим здесь. Теперь я хочу закончить парой причин, почему так важно знать размеры матрицы. Как мы уже вкратце обсуждали, размеры матрицы должны быть известны, чтобы идентифицировать конкретный элемент в матрице. Например, если бы мы идентифицировали элемент во второй строке, первом столбце, мы должны понимать, что это означает, что мы искали элемент во второй строке, первом столбце.Итак, вот строка два, а вот столбец один, поэтому вторая запятая будет
до девяти. Другая причина - сложить или вычесть матрицы, размеры должны быть одинаковыми. Обратите внимание, что эта первая матрица представляет собой матрицу два на два, а вторая матрица также является матрицей два на два, поэтому, поскольку эти размеры совпадают, мы могли бы складывать эти матрицы. Если размеры не совпадают, мы не сможем складывать или вычитать матрицы. И, наконец, для умножения матриц количество столбцов в первой матрице должно быть таким же, как количество строк во второй матрице, чтобы выполнить умножение матриц.Так, например, эта первая матрица имеет две строки и один столбец, поэтому это матрица два на один. Вторая матрица состоит из одной строки и трех столбцов, поэтому это матрица размером один на три. Таким образом, мы можем умножать эти матрицы только в том случае, если это число, число столбцов в первой матрице и это число, число строк во второй матрице, совпадают. И поскольку они есть, мы можем выполнить это умножение. Если бы их не было, мы бы не смогли. О том, как выполнять матричные операции, мы поговорим в следующих видео. Надеюсь, вы нашли это полезным.
теги:
измерение, размеры, матрица, матрицы, строки, столбцы, по, элементы, обозначение, алгебра, james, sousa, mathispower4u
Спасибо за просмотр всех статей по теме Dimensions of a Matrix . Все акции thevoltreport.com очень хорошие. Надеемся, что статья вам понравилась. По любым вопросам, пожалуйста, оставьте комментарий ниже. Надеюсь, вы еще больше поддерживаете наш сайт.
