Что такое разрешение матрицы: , , MTF, , — funPhoto

Разрешение матрицы. Цифровая фотография. Трюки и эффекты

Читайте также

6.1. Разрешение экрана

6.1. Разрешение экрана Если не знаете, что такое разрешение экрана и зачем оно вообще нужно, то в данном разделе мы проведем теоретическую подготовку.Под разрешением экрана следует понимать то количество точек по горизонтали и вертикали, с помощью которых формируется

§ 69. Разрешение картинок

§ 69. Разрешение картинок 16 июня 2001Попробуем разобраться в одном из самых больших заблуждений человечества за всю историю существования экранной графики.Дело в том, что у электронного изображения вообще нет разрешения. Разрешение (точнее, разрешающая способность) может

§ 132. Низкое разрешение

§ 132. Низкое разрешение 28 мая 2006Применительно к человеку понятие разрешение может означать способность различать стили, объекты, здания, цвета, шрифты, голоса и так далее.Любое образование ставит целью повысить разрешение в выбранной области. Художники долго рисуют

R.6.8 Разрешение неоднозначности

R.6.8 Разрешение неоднозначности Существует неоднозначность в грамматике языка, касающаяся оператора-выражения и описания, а именно, оператор-выражение, содержащий как самое левое подвыражение явное преобразование типа, заданное в функциональном стиле (§R.5.2.3), может быть

8.1.8. Реализация разреженной матрицы

8. 1.8. Реализация разреженной матрицы Иногда бывает нужен массив, в котором определена лишь небольшая часть элементов, а остальные не определены вовсе или (даже чаще) равны 0. Подобная разреженная матрица потребляет так много памяти зря, что были найдены способы более

9.4.1. Реализация графа в виде матрицы смежности

9.4.1. Реализация графа в виде матрицы смежности Нижеприведенный пример основан на двух предыдущих. В листинге 9.3 неориентированный граф реализован в виде матрицы смежности с помощью класса ZArray (см. раздел 8.1.26). Это нужно для того, чтобы новые элементы по умолчанию получали

11.14. Реализация динамической матрицы

11.14. Реализация динамической матрицы ПроблемаТребуется реализовать числовые матрицы, размерности которых (количество строк и столбцов) неизвестны на этапе компиляции.РешениеВ примере 11.28 показана универсальная и эффективная реализация класса динамической матрицы,

11.15. Реализация статической матрицы

11.15. Реализация статической матрицы ПроблемаТребуется эффективно реализовать матрицу, когда ее размерность (т.е. количество строк и столбцов) постоянна и известна на этапе компиляции.РешениеКогда размерность матрицы известна на этапе компиляции, компилятор может легко

Разрешение

Разрешение Величина под названием «разрешение» является «связующим звеном» между логическим и физическим размером. Она определяет соотношение между ними и позволяет судить о качестве изображения.Измеряя разрешение, мы фактически измеряем размер одного пиксела.

Физический размер матрицы

Физический размер матрицы Выбирая цифровую камеру, неплохо поинтересоваться физическим размером ее матрицы, ведь именно эта характеристика определяет качество камеры. Чем сенсор больше, тем больше он содержит ПЗС-элементов, тем выше его разрешение и, следовательно,

Динамический диапазон матрицы

Динамический диапазон матрицы Динамический диапазон светочувствительной матрицы – это ее способность воспринимать градации каждого из цветов. Говоря проще, динамический диапазон определяет, сколько ступеней разности контраста может увидеть и зафиксировать матрица.

Облет повисшего объекта, или Эффект «Матрицы»

Облет повисшего объекта, или Эффект «Матрицы» Несмотря на современные достижения компьютерной техники, для получения некоторых визуальных эффектов используются старые проверенные методы фотографии. Казалось бы, что общего может иметь фотография с таким современным

Чистка матрицы зеркальной камеры

Чистка матрицы зеркальной камеры У владельцев зеркальных камер к радости от возможности смены объективов прибавляется забота о чистоте матрицы. Что делать, если вы заметили на снимках ровной светлой поверхности соринки и пятна? В некоторых моделях зеркальных камер

Чистка матрицы зеркальной камеры

Чистка матрицы зеркальной камеры В зеркальной камере, в отличие от компактной, приходится чистить матрицу. Хотите вы или нет, но рано или поздно на матрицу попадает пыль, мелкие соринки. Насколько скоро это произойдет, зависит от частоты смены объективов, условий

ТЕМА НОМЕРА: Реформирование матрицы

ТЕМА НОМЕРА: Реформирование матрицы Автор: Леонид Левкович-МаслюкГде-то в конце 1980-х или начале 1990-х я читал в «Независимой газете» обзор событий в мире книг. Автор отмечал, что на прилавках появилось оригинальнейшее сочинение по истории древнего мира, которое написал

что это и почему она так важна?

Поделиться статьёй:

При выборе фотоаппарата нужно учитывать множество нюансов, обращать внимание на каждую деталь. И далеко не последнюю роль в процессе выбора играют именно характеристики матрицы, которой оснащена камера. Что же представляет собой эта самая матрица и почему она так важна? Давайте это выясним! 

Содержание статьи:

 Общее представление о матрице фотоаппарата 

Если вы посмотрите в объектив камеры, вы легко найдете матрицу: видите блестящий прямоугольник в самом центре объектива? Да, это она и есть.

Матрица является важнейшим элементом фотокамеры, отвечающим за то, какое изображение мы получим в результате съемки. 

По сути она представляет собой микросхему, которая состоит из светочувствительных элементов. Когда на нее падает свет, начинается формирование электрического сигнала определенного уровня интенсивности, который зависит от степени яркости света. При съемке она фиксирует свет, который впоследствии преобразуется в фотографию. 

Кстати, количество мегапикселей, которое имеет фотокамера, также зависит именно от матрицы и может колебаться от 0.3 до 10 и более (чем дороже и качественнее фотоаппарат, тем больше мегапикселей он имеет).

Изначально матрица создает монохромное (ч.б) изображение. В цветное оно преобразуется благодаря светофильтрам, которыми покрываются ее составные части.

Особенности строения матрицы

Что касается структуры матрицы, то она является дискретной и складывается из множества частей, в совокупности преобразующих падающий на нее свет. Один фотодиод в составе создает один пиксель фотографии.

Как вы наверняка знаете, каждое цифровое изображение представляет собой что-то вроде мозаики, состоящей из множества точек, которые в совокупности и являются фотографией. Изображение не «распадается» именно потому, что этих точек очень много и они имеют высокую плотность расположения относительно друг друга. Вполне логично предположить, что если бы плотность их расположения была ниже, мы бы увидели, как изображение распадается на эти самые точки, и это было бы наглядной демонстрацией дискретного характера структуры матрицы.

Матрица как альтернатива пленки

В те времена, когда цифровой фототехники еще не существовало, светочувствительным элементов, выполняющим функции матрицы, была пленка. Если проанализировать устройство пленочных и цифровых фотоаппаратов, можно увидеть, что существенных отличий между ними не так уж много. Основным отличием как раз и будет схема приема и преобразования света.

Как именно происходит процесс приема света в фотокамере с пленкой? В тот момент, когда фотограф нажимает кнопку спуска, затвор открывается, в результате чего пленка принимает свет.  До того, как затвор вновь закрывается, идет химическая реакция, а ее итогом является формирование фотографии. 

Как вы можете заметить, процесс создания фотоснимка был совершенно иным, и в современных фотоаппаратах матрица выполняет именно функцию пленки, то есть генерирует изображение. Они выполняют совершенно одинаковые функции, разница состоит лишь в технике их выполнения и в хранилище созданного изображения, которым в первом случае выступает пленка, а во втором — карта памяти фотоаппарата.

 

Характеристики матрицы

Необходимо понимать, что матрицы бывают совершенно разными по качественным показателям. В этом вопросе важным сигналом будет цена: в том или ином ценовом сегменте матрицы имеют определенный уровень качества. Будьте готовы к тому, что бюджетные варианты фотоаппарата вряд ли будут обладать высококачественной матрицей. Поскольку матрицу можно смело назвать сердцем камеры, не стоит экономить при выборе. Вы ведь хотите, чтобы ваши снимки были на высоте? Тогда остановите свой выбор на фотоаппарате, оснащенном качественной матрицей. 

По каким параметрам следует выбирать матрицу?

1. Размер
2. Разрешение
3. Соотношение сигнал-шум
4. Уровень светочувствительности
5. Динамический диапазон

Итак, рассмотрим первый параметр из нашего списка, а именно — размер матрицы. Его определяет величина пикселей, а также плотность их расположения относительно друг друга. Меньшая плотность расположения пикселей дает меньший уровень нагрева матрицы и более сильное соотношение сигнала и шума, которое создает более четкую фотографию. 

Учтите, что именно размер матрицы является ее главной характеристикой. При выборе на него нужно обратить особое внимание. 

Что же обеспечивает размер матрицы и почему он является таким важным параметром?

Итак, размер матрицы диктует:

1. Уровень шума фотографии
2. Глубину и насыщенность ее цвета
3. Динамический диапазон
4. Размер фотокамеры

Больший размер матрицы обеспечивает:

1. Низкие показатели шума на фотографии. Матрица, имеющая большую поверхность, принимает больше света. Это будет сопряжено с меньшим нагревом, меньшей погрешностью в процессе квантования, соответственно, меньшим уровнем воздействия нежелательных шумов. Чем больше физический размер матрицы, тем меньше посторонних шумов будет на снимке, даже если съемка осуществляется при низком уровне освещения. Если говорить проще, фотография не будет пестрить лишними точками, точно не способствующими эстетике снимка.  
2. Широкий динамический диапазон
3. Насыщенные, глубокие цвета снимка

Глубина цвета является показателем, который определяет возможность камеры идентифицировать любые метаморфозы цвета, даже самые незначительные. Это особенно ценно для фотографий однотонных пейзажей, не имеющих резких цветовых переходов. Большая матрица способна уловить даже самый незначительный цветовой переход, в то время как маленькая не имеет такой возможности. 

Единственный недостаток, с которым придется смириться при выборе большой матрицы, это размер самой камеры. Чем больше матрица, тем больше размер камеры. Строго говоря, это вряд ли можно считать серьезным недостатком, учитывая широкий спектр преимуществ, которые дает матрица большого размера. 

Виды матрицы

Он определяет способ работы матрицы.

На этом основании матрицы делят на 2 технологии:

1. CMOS
2. CCD

Конечная цель является одинаковой: накопление света. Разница в том, что является элементом, составляющим структуру. В первой технологии это диод, а во второй — транзистор. 

Если говорить о качестве фотографий, то плюсом CCD-технологии были более приятные глазу цвета, а CMOS-технология выгодно отличалась гораздо меньшим уровнем шума. 

В наше время подавляющее большинство камер оснащено матрицей CMOS. 

Чувствительность матрицы

Она является очень важным параметром. Чем большую чувствительность установить, тем больше возможность зафиксировать на фотографии плохо освещенные объекты. Но при таких условиях будут также увеличиваться нежелательные шумы. 

Параметр IS0 является эквивалентным показателем чувствительности. 50 — самый низкий показатель чувствительности, при котором чистое фото не подвергается разрушению шумом. 

Сигнал-шум

Это параметр, который находится в непосредственной связи с чувствительностью.  Он определяет уровень света и шумов на снимке. 

Нужно помнить, что любое фото имеет определенный показатель шума. Светочувствительность характеризуется тем же. Она не может иметь статичных показателей. Они будут меняться, и эти изменения зависят от условий съемки. 

Даже если свет совсем отсутствует, фотодатчик все равно продемонстрирует в итоге определенное значение. Как раз это и является шумом. Чтобы получить качественную фотографию, сигнал должен побороть помехи на определенном уровне. Это явление и носит название «сигнал-шум». 

Чтобы фотография получилась четкой и не имела нежелательных шумов, нужно правильно настроить фильтры, чтобы они не пропустили эти помехи. 

Если увеличивать уровень чувствительности матрицы, действие фильтра будет ослабевать, чтобы поймать слабый сигнал. Но одновременно с этим на снимке отразятся и шумы. Поэтому, чтобы не нужно было усиливать чувствительность, необходимо правильно настроить выдержку. 

Что нужно сделать, чтобы ослабить помехи?

Чтобы уровень шума был минимальным, необходимо настраивать минимальную чувствительность матрицы. Однако эта возможность напрямую зависит от того, позволяет ли это выдержка камеры. 

Если же требуется уменьшать выдержку, то одновременно с этим необходимо увеличивать чувствительность, что в свою очередь приведет к увеличению уровня шума. Определенное значение приведет к тому, что шумы станут видны на снимке. Потому при съемке выбор стоит между уменьшенной чувствительностью и уменьшенным временем выдержки. 

Все это говорит в пользу выбора камеры с большим размером матрицы, позволяющего снижать уровень шума и уменьшать выдержку, чтобы снимать объекты в движении без ущерба качеству изображения.

Разрешение матрицы

Этот параметр для многих является очень важным при выборе камеры. Так ли это? Попробуем разобраться. 

Размер пикселя является очень важным параметром, и вот почему это так: когда пиксель больше по размеру, он способен «поймать» больше света. Матрица подобного типа будет давать меньшее количество шумов.  

Если матрица имеет большее разрешение, то размер пикселей, которые ее составляют, меньше, а это стимулирует нагрев и поднимает уровень шумов.

Отличительные черты размера пикселя:

1. Уровень шумов. Как уже было сказано выше, меньший размер пикселя предполагает высокий уровень шумов.
2. Уровень шевеления. Чем меньше размер пикселя, тем выше его чувствительность к дрожанию и смещению камеры. 
3. Высокие требования к объективу камеры. Чем меньше размер пикселя, тем более высокая разрешающая способность объектива потребуется для качественных снимков.
4. Чем больше разрешение фотоаппарата, тем большие возможности должен иметь компьютер, который будет обрабатывать снимки. Если вы хотите получить от съемки отличный результат, но не занимаетесь фотографированием в RAW, то вам предстоит довольно продолжительная и непростая работа в фоторедакторах на компьютере. А при редактировании снимков в очень высоком разрешении, например, составляющем 24 мегапикселя и выше это и вовсе может стать очень сложной задачей. 

Динамический диапазон матрицы

Он устанавливает максимальный диапазон яркости фотографии. Каждый из пикселей, составляющих матрицу, имеет свой уровень яркости. Функцией динамического диапазона является идентификация широты яркого участка снимка, который способен охватить фотоаппарат без ущерба качеству наиболее темных и наиболее ярких частей кадра. 

Динамический диапазон является статичной характеристикой матрицы. Его невозможно изменить. Правда, есть возможность сделать его более узким, если повысить чувствительность ISO, но это далеко не всегда сможет решить проблему. Строго говоря, это даже нежелательно. 

Когда фотоаппарат не справляется с трудными условиями съемки, например, если снимать нужно против солнца, мы получаем на фотографии слишком сильные контрасты, которые действительно режут глаз. При взгляде на такие фотографии даже непрофессионал вынесет кадру строжайший вердикт и, конечно, будет совершенно прав. 

При таких результатах съемки говорят, что динамический диапазон матрицы не справляется с условиями, в которых ведется съемка. Обычно для исправления этих недостатков нужно менять компоновку кадра, прибегать к разного рода профессиональным хитростям, которые сгладят досадные несовершенства, словом, делать все то, что с динамическим диапазоном фотоаппарата совершенно не связано, поскольку, как мы уже упомянули выше, менять его показатели невозможно, поскольку они статичны. 

Поделиться статьёй:

Разрешение матриц проектора и поддерживаемое соотношение сторон

Разрешением изображения называют общее количество пикселей, из которых оно состоит. Чем выше это разрешение, тем больше деталей может воспроизвести проектор и тем качественнее будет картинка. Разрешение проекторов определяется количеством ячеек и микрозеркал LCD и DLP-матриц: Ячейки бывают разного размера, поэтому разные матрицы с одной диагональю могут иметь разное разрешение. Формат изображения — это фактическое соотношение сторон кадра. Наиболее распространены форматы 4:3, 16:9 и 16:10. Формат 4:3 наиболее распространен в телевещании, однако цифровой телесигнал в качестве HDTV обычно транслируется в формате 16:9. Кроме того, форматы 16:9 и более редкий 16:10 используется в киноиндустрии. Матрицы формата 4:3 могут воспроизводить изображение с соотношением сторон 16:9 или 16:10 и наоборот. В таком случае возможны два варианта: изображение может подгоняться под стандартный для проектора формат, т.е. искажаться; изображение остается без искажений, однако используется не вся поверхность матрицы. По поддерживаемому разрешению современные проекторы можно условно разделить на несколько групп: Для просмотра телевизионного сигнала с кодировкой цветности NTSC, PAL и SECAM хватает разрешения SVGA (800х600) или XGA (1024х768). Такие проекторы, как правило, имеют базовое соотношение сторон 4:3. Для просмотра широкоформатного видео оптимально подходят проекторы формата 16:9 и 16:10 и разрешением WXGA (от 1280 x 720 до 1366х768), WXGA+ (1366 x 800), SXGA (1366 x 1024), SXGA+ (1400 x 1050), UXGA (1600 x 1200). В последнее время большинство производителей стараются выпускать проекторы с максимально возможным разрешением — Full-HD (1920×1080) и WUXGA (1920 x 1200). Такое качество изображения подходит для трансляции видео в формате HDTV и Blu-Ray и с соотношением сторон 16:9 и 16:10. Full-HD и WUXGA проекторы идеальны для использования в домашних кинотеатрах. В корпоративной сфере и в образовательных учреждениях для воспроизведения графических материалов, таблиц и презентаций чаще всего используются проекторы с соотношением сторон 4:3 и разрешением XGA (1024 х 768).

Как узнать разрешение матрицы ноутбука?

Разрешение матрицы – это поддерживаемый размер экрана. Тем больше этот показатель, тем выше качество демонстрируемого изображения. В настоящий момент пользователям ноутбуков доступен большой выбор разрешений, что позволяет найти подходящий вариант в зависимости от предпочтений, а также доступного бюджета.

К самым распространенным разрешениям можно отнести:

• XGA (1024×78).
• SXGA (1280×1024).
• WXGA (1280×720; 1280×768; 1360×768).
• WUXGA (1920×1080).

Для работы в офисе или на дому лучше подойдут ноутбуки с меньшим разрешением, в то время как киберспортсмены и просто любители компьютерных игр останавливают свой выбор на устройствах с большим размером.

Как определить разрешение матрицы ноутбука?

Проверить тип матрицы можно несколькими способами.

1. Проще всего определить разрешение, изучив информацию из пользовательской инструкции, которая предусматривается при покупке любого цифрового устройства. В большинстве случаев этот показатель указывается в разделе спецификации.
2. Также можно отправиться на сайт производителя ноутбука и найти искомые данные при помощи серийного номера и модели.
3. Самый простой способ – запустить устройство и при выходе на рабочий стол Windows нажать на пустое поле правой кнопкой мыши. После этого в меню необходимо выбрать «Параметры экрана». В появившемся разделе в поле «Разрешение экрана» будет указано рекомендуемое значение.

Более опытные пользователи могут скачать и установить приложение Everest, которое также называется AIDA64 – в нем указывается вся ключевая информация по используемому аппаратному и программному обеспечению.

Чтобы узнать разрешение матрицы с его помощью, необходимо выполнить запуск и перейти во вкладку «Отображение». В ней будет пункт с названием монитора, а также информация о производителе матрицы и ее модели. С помощью этого приложения можно точно установить размер матрицы, а также видимую область, оптимальное соотношение сторон и максимально возможное разрешение.

Замена оригинальной матрицы

Точная информация о виде матрицы и поддерживаемом разрешении пригодится в том числе при необходимости ее замены. Особенно это важно в том случае, если найти оригинальную деталь не удается, а ее аналог должен быть 100% совместим с устройством. При выборе новой матрицы для ноутбука в первую очередь внимание обращается на ее тип: TN, MVA или IPS.

TN относится к самому распространенному виду, устанавливаясь на ноутбуках бюджетного сегмента. Такая матрица обеспечивает достаточно высокое качество изображения, однако имеет небольшой угол обзора. Модели MVA обладают лучшим углом обзора, однако предрасположены к появлению битых пикселей. Матрицы IPS отличаются детализированным изображением высокого качества, а также оптимальной контрастностью и максимальным углом обзора.

При выборе матрицы для ноутбука важно учитывать множество факторов – помимо типа детали и ее разрешения это также метод крепления и наличие подсветки.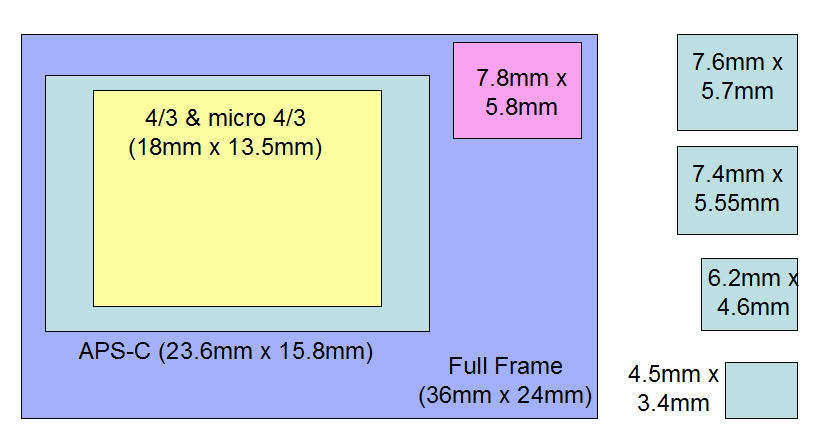 В случае возникновения сложностей с покупкой комплектующего можно обратиться к специалистам интернет-магазина Glavmag.su – здесь помогут подобрать аналог, который будет 100% совместим с используемым цифровым устройством.

Как выбрать телевизор: размер, разрешение, тип матрицы

Чтобы выбрать телевизор следует прежде всего определить оптимальный размер экрана по диагонали. Он зависит от желаемого разрешения экрана и расстояния, с которого его будут смотреть.

Выбираем разрешение экрана: Full HD или 4K?

Большинство телевизоров выпускают с разрешением экрана Full HD. Их изображение состоит из 1920×1080 точек по горизонтали и вертикали (пикселей). Экраны, которые называют Ultra HD или 4K, при тех же размерах корпуса имеют разрешение 3840×2160 пикселей. То есть в четыре раза больше!

Телевизоры Full HD оптимальны чтобы смотреть телеканалы и фильмы на дисках Blue Ray. Телевизоры 4K будут идеальны для современных фильмов, насыщенных спецэффектами. Правда, всю прелесть разрешения 4K можно увидеть лишь на экранах большого размера, от 50 дюймов и крупнее. На телевизорах с меньшей диагональю разница в сравнении с Full HD почти не видна.

В продаже ещё встречаются телевизоры с устаревшим разрешением HD (1280×720). Причём они даже бывают больших размеров, до 43 дюймов. Такого разрешения хватит разве что для просмотра эфирного телевидения или древних дисков формата DVD. Если ищете телевизор для просмотра новых фильмов, от такой покупки лучше воздержаться.

Выбираем размер экрана

Чем крупнее экран, тем больше расстояние между пикселями. Если сесть слишком близко, вы увидите точки из которых состоит изображение. Максимальная диагональ телевизора с разрешением Full HD не должна превышать 2/3 расстояния от зрителя. У экранов с разрешением 4K пиксели расположены плотнее. Их можно смотреть даже с расстояния, равного размеру диагонали.

Для простоты составим таблицу максимального размера диагонали экрана в зависимости от расстояния и выбранного разрешения:

Расстояние до экрана	Максимальная диагональ Full HD (см/дюйм)	Максимальная диагональ 4K (см/дюйм)
1,5 метра	100 см / 40 дюймов	150 см / 60 дюймов
2 метра	134 см / 53 дюйма	200 см / 80 дюймов
3 метра	200 см / 80 дюймов	300 см / 120 дюймов
4 метра	270 см / 107 дюймов

Нет смысла покупать большой телевизор, если размеры комнаты не позволяют разместить его на правильном расстоянии от дивана.

Выбираем тип матрицы: LCD, QLED или OLED?

Большинство телевизоров выпускают по технологии LCD. В ней слой кристаллов и фильтров задаёт цвет пикселя, а фоновая подсветка отвечает за его яркость. Из-за этого в них затруднено точное отображение цвета. Особенно страдает чёрный, из-за подсветки он выглядит серым.

В более новой технологии OLED источником света являются отдельные светодиоды. Чёрный цвет в них образуется простым выключением пикселя и выглядит абсолютно реалистично. Благодаря этому OLED-матрицы имеют несколько преимуществ:

• Изображение более естественное и чёткое.
• Скорость обновления кадра выше.
• Цвет картинки на OLED при взгляде под углом искажается меньше, чем у LCD.

Технология QLED – это улучшенная версия LCD. Телевизоры с таким типом матриц производит только компания Samsung. По качеству изображения QLED-экраны превосходят LCD, но несколько уступают OLED.

Если ищете большой экран для домашнего кинотеатра, лучше выбрать телевизор с матрицей OLED или QLED, но они пока ещё очень дорогие. Телевизоры, для просмотра телеканалов, можно брать с любой матрицей, главное, чтобы картинка вам нравилась.

Телевизоры Smart TV

Функционал Smart TV превращает телевизор фактически в огромный планшет! В такие модели встроены Wi-Fi, процессор, оперативная память и файловые накопители. Они могут подключаться к Интернет и отображать любые сайты. Могут напрямую скачивать фильмы по сети и проигрывать видео с Youtube. На них даже можно устанавливать игры из сетевых сервисов и подключать джойстики. По сути, вы получаете компьютер, игровую приставку и телевизор одновременно.

Стоимость “умных телевизоров” пока высока, но постепенно снижается. Несомненно, со временем все модели будут обладать подобным функционалом.

Поддержка стандарта HDR

При покупке экрана с разрешением 4K целесообразно выбрать телевизор с поддержкой технологии HDR (High Dynamic Range). Эта функция позволяет передавать с видеопотоком дополнительную информацию о яркости и цветовом балансе разных участков одной и той же сцены. В результате картинка становится ещё более насыщенной и красочной. Важно, что просматриваемое видео должно быть тоже создано с поддержкой механизма HDR. Сейчас этот стандарт поддерживают крупные западные телекомпании, занимающиеся производством сериалов. Также он внедрён в новые модели игровой приставки Sony Playstation.

Интерфейсы

Стандартный тип разъёма для подключения плееров и ресиверов – HDMI. Как показывает практика, к телевизору приходится подключать несколько источников сигнала одновременно. Поэтому, выбирайте модель у которой портов HDMI будет два или даже четыре.

Стоит ли покупать 3D-телевизор?

Нет, технология 3D мертва. Фильмов в формате 3D теперь почти не снимают. Новые модели телевизоров уже не поддерживают трёхмерное изображение. Найти такую функцию можно лишь в телевизорах прошлых лет выпуска. Не стоит за неё переплачивать.

Важна ли частота обновления экрана (Гц)?

Частота обновления (Гц) показывает, сколько раз перерисовывается кадр за секунду. По стандарту Full HD источник видеосигнала может передавать телевизору картинку с частотой максимум 60 кадров в секунду (60Гц). В формате 4K изображение передаётся с максимальной частотой 120 Гц.

Производители телевизоров придумали способы завысить этот параметр в паспортных данных. К примеру, один и тот же кадр перерисовывают два или три раза подряд, и называют это “повышением коэффициента обновления”. Некоторые указывают даже 1000 Гц.

Для мозга человека картинка, обновляемая 50 раз в секунду уже кажется постоянной и непрерывной. Лишь немногие видят разницу между 60 Гц и 120 Гц. Частота обновления более 120 Гц физически бесполезна, чтобы не утверждали продавцы в магазинах и маркетологи.

Если покупаете Full HD телевизор, выбирайте модель с частотой обновления от 60 Гц. При покупке экрана 4K лучше выбрать телевизор с частотой 120 Гц.

Изогнутый экран телевизора лучше?

Изогнутые экраны дают преимущество если зритель расположен строго по центру и на определённом расстоянии. Это подходит мониторам компьютеров, которые располагаются близко от пользователя. Телевизор же обычно смотрят сразу несколько человек. Каждый зритель видит экран немного под своим углом и с разных дистанций. Поэтому для телевизора в гостиной изогнутая форма скорее недостаток, чем преимущество.

Какой телевизор выбрать для гостиной

Оптимальным вариантом для просмотра телеканалов и фильмов в гостиной будет телевизор с диагональю экрана от 40 до 50 дюймов. Достаточно, если у него будет разрешение Full HD (1920×1080) и частота обновления от 60 Гц. Матрицы у экранов этих размеров почти всегда LCD. Располагать такой телевизор лучше на расстоянии не менее 2,5 метров от дивана.

Телевизоры 40″-50″

Какой телевизор выбрать для домашнего кинотеатра

Для просмотра фильмов со спецэффектами лучше выбрать телевизор с большим экраном и разрешением 4K. Подойдут модели с диагоналями от 50 дюймов и выше. Частота обновления экрана должна быть 120 Гц. Матрица, желательно по технологии OLED или QLED, если позволяет бюджет. Неплохо, если это будет “умный телевизор” с функционалом Smart TV. Не помешает большое количество портов HDMI и поддержка стандарта HDR, улучшающего яркость и цветопередачу. Также подумайте о приобретении вместе с телевизором для домашнего кинотеатра хорошей акустики.

Телевизоры 50″-60″ – 4K – для домашних кинотеатров

Какой телевизор выбрать для спальной

Для спальной или детской комнаты можно взять телевизор с экраном поменьше, чем в гостиной. Достаточно будет диагонали от 32 до 40 дюймов. Матрица для таких телевизоров не принципиальна, но разрешение экрана лучше выбрать Full HD.

Телевизоры 32″-39″ для спальной

Мегапиксели и размеры матрицы, цифровой шум

«Важна не столько аппаратура, которой пользуешься, сколько степень владения выбранной аппаратурой, при которой она автоматически становится продолжением твоего зрения, третьим глазом».
Эдвард Уэстон

Производители фотоаппаратов расхваливают их, упоминая количество мегапикселей. Этот параметр важен для пейзажных фотографов, но он не единственный: шумы могут испортить в остальном резкое изображение. При прочих равных условиях фотоаппараты с высоким разрешением лучше передают мелкие детали листьев, сосновых иголок, травы.
При увеличении размеров небольшого файла количество пикселей в нем увеличивается, но качество деталей не меняется; каким бы высоким ни было разрешение матрицы, для фотографа пиксели никогда не бывают лишними.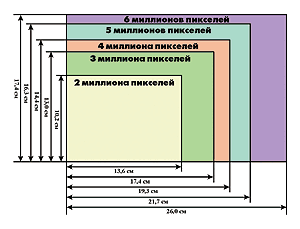 Всегда пользуйтесь самым высоким разрешением, доступным вашему фотоаппарату, и храните файлы в этом разрешении.

Для любителей всяких распродаж и желающих сэкономить был создан сайт votsale.ru, дающий возможность каждому желающему получить промокоды на скидку для покупки различных товаров и услуг.

Шумы при высоком ISO
Слабая освещенность требует довести ISO до 400, чтобы «заморозить» движение воды в водопаде. Хотя здесь шумы не бросаются в глаза, мне удалось снизить их при обработке изображения.

Шум
Шум подобен зернистости на пленке; рисунок мелких точек особенно заметен на однородных участках, таких, как небо или вода. В отличие от зернистости, шумы распределены неравномерно: на теневых участках они более заметны. При высокой ISO и длительной выдержке они усиливаются.

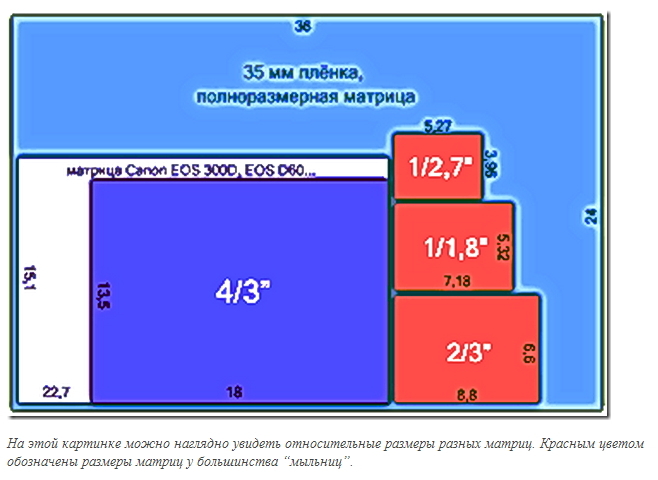
Существует три основных вида цифровых зеркальных фотоаппаратов: с полноформатными матрицами, размером с кадр 35 мм фотопленки (24×36 мм) и с матрицами величиной две трети этого размера (от 15×22 мм до 16×24 мм). В полноформатных матрицах шумов обычно бывает меньше, чем в матрицах 2/3, так как отдельные светочувствительные элементы могут быть крупнее и имеют большую концентрирующую способность.

Однако более новые матрицы формата 2/3 отлично регулируют количество шумов и дают превосходные изображения.
Фотографам, активно занимающимся пейзажной съемкой, следует задуматься о «среднеформатном» цифровом фотоаппарате. У таких матрицы еще больше, от 33×44 мм до 40×54 мм, с большим количеством мегапикселей и, как правило, низкими шумами. С другой стороны, у компактных цифровых фотоаппаратов («мыльницы») крохотные матрицы, и они больше подвержены возникновению шумов.

Шумы при длительной экспозиции
При длительной 15-секундной выдержке и ISO 100 возникают значительные шумы, особенно в тенях. Программа снижения шумов помогла лишь частично устранить их.

Снижение шумов
Устойчивый штатив даст возможность пользоваться низкой ISO и не опасаться дрожания фотоаппарата. Шумы часто проявляются при попытке осветлить темные тени при обработке снимков, поэтому следующий шаг в устранении шумов — правильный выбор экспозиции. Обычно это означает, что изображение надо сделать как можно более светлым, но без потери деталей на освещенных участках. Если изображение слишком контрастное, чтобы сохранить детали и на освещенных, и на теневых участках, при обработке придется соединить два или несколько снимков.

Во многих фотоаппаратах есть функция снижения шумов при длительной экспозиции. Обычно для этого требуется время — после экспозиции в течение 30 секунд фотоаппарат еще 30 секунд обрабатывает изображение — и в результате эта функция может оказаться бесполезной. Вам придется самому испытать фотоаппарат и посмотреть, имеет ли смысл пользоваться функцией снижения шумов. В качестве последнего средства можно обратиться к специальному программному обеспечению для снижения шумов.

Матрица тепловизора

    Матрица представляет собой микросхему с набором специальных диодов, отличающихся светочувствительностью, и свойством менять сопротивление в зависимости от интенсивности инфракрасных лучей. А размер матрицы напрямую определяет четкость тепловой фотографии объекта, так как чем больше размер ИК детектора тем больше чувствительных элементов воспринимают тепловое излучение. Чем больше разрешение матрицы тем больше температурных точек можно отследить и соответственно получается более четкая картинка.

    Например тепловизор testo 875 с матрицей 160×120 пикселей отображает тепловое изображение из 19200 точек, а модель тепловизора FLIR E60bx благодаря большей матрице 320×240 пикселей отображает 76800 значений. Чем выше разрешение там качественнее изображение, и тем дороже стоит сам тепловизор.

    Благодаря современным технологиям матрица имеет компактные размеры и отличается низким энергопотреблением. Для получения качественной картинки матрицу необходимо охлаждать. Полупроводниковые матрицы охлаждают различными способами, к примеру, жидким азотом или при помощи холодильника Стирлинга. Самые лучшие тепловизоры с охлаждаемыми датчиками могут работать на частоте до 20 кГц и измерять температуру с точностью до 0.018°, что позволяет детально рассмотреть даже очень скоротечные процессы.

    Необходимость охлаждения делает тепловизоры дорогими, громоздкими и не всегда безопасными, тем самым сильно сужая область их применения, поэтому сегодня широкое распространение получили аппараты с совершенно другим типом матриц — микроболометрических. В современных тепловизорах ПЗС-матрица заменена на микроболометрическую, которая не требует охлаждения. Изменение сопротивления элементов такой микросхемы фиксируется с большой точностью практически во всем диапазоне ИК-излучения.

    Первый коммерческий тепловизор серии Thermovision 500, в котором приемник излучения работал при комнатной температуре, был выпущен шведской фирмой AGEMA Infrared Systems.

    Важным, с точки зрения оптики, но не столько как разрешение матрицы есть оптическое разрешение. Оптическое разрешение – фактически отношение расстояния от прибора до объекта к диаметру пятна диагностики. В плане оптического разрешения важно что бы весь объект попадал в поле зрения. Фактически оно определяет с какого расстояния можно делать замеры объектов определенного размера. Но в то же время, оптическое разрешение никак не влияет на качество изображения и количество регистрируемых температурных точек. Эти показатели определяются разрешением матрицы ИК датчика.

МАТРИЦЫ РАЗРЕШЕНИЯ

МАТРИЦЫ РАЗРЕШЕНИЯ
Далее: МЕТОД ЛАНЧОСА Up: Berryman: Решение для Ланцоша Предыдущая: ВВЕДЕНИЕ

Матрицы разрешающей способности для задач линейной инверсии можно понять проще всего, рассматривая матричное уравнение вида

= и задавая вопрос: Учитывая и, что решает это уравнение? Когда матрица квадратная и обратимая, ответ на вопрос относительно прост:.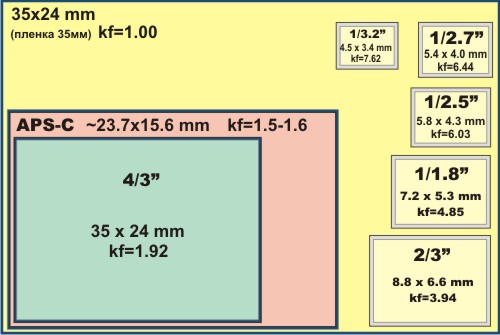 . Отклонения от единичной матрицы, определяемые матрицу, определить степень недоверия к компонентам решения вектор с наиболее плохим разрешением.

Чтобы быть более точным, рассмотрим перекрестие проблема томографии. Тогда — матрица траекторий лучей, — это вектор времени пробега первого прибытия м и медленность (обратная скорость) n -вектор. Я ищу медлительность Учитывая измеренные времена пробега в и оценки путей лучей между местоположения источника и приемника, содержащиеся в матрице [см. Berryman (1991)].Т).

В следующем обсуждении я покажу, как эти эквивалентные формулы для матриц разрешения помогают в их вычислении в процессе нахождения приближенного обратного к использованию итерационных методов.

---

Далее: МЕТОД ЛАНЧОСА Up: Berryman: Решение для Ланцоша Предыдущая: ВВЕДЕНИЕ

Стэнфордский исследовательский проект
17.11.1997

Расчет разрешающей способности и ковариационных матриц для сейсмической томографии методом LSQR | Международный геофизический журнал

Кратко обсуждается связь оценок разрешения на основе LSQR с оценками, полученными с использованием других методов.

Какой бы метод ни использовался, важны оценки разрешения и ковариации, поскольку они могут указывать на значимость и надежность инвертированной модели. Это было подчеркнуто Backus & Gilbert (1968), которые основали свою обобщенную обратную теорию на методах, разработанных для оптимизации разрешения получаемой геофизической модели, полученной из обработанных данных. Обсуждения разрешения и ковариации в сейсмической томографии также можно найти в ранней статье Аки (1977), а также во многих более поздних работах (например,грамм. Evans & Achauer 1993).

Матрицы разрешения и ковариации могут быть вычислены с помощью обобщенного обратного преобразования G ^{— g} (например, Menke 1984). Однако LSQR не дает явного обобщенного обратного преобразования; поэтому матрицы разрешения и ковариации не могут быть вычислены так же удобно, как в таких методах, как разложение по усеченным сингулярным числам (TSVD) (Nolet 1993). Основываясь на LSQR, Zhang & McMechan (1995) вывели формулы для расчета разрешающей способности и ковариационных матриц для модифицированной инверсии LSQR (LSQRA).Однако LSQRA может значительно отличаться от LSQR; Это будет обсуждаться позже.

В этой статье мы начнем с определений матриц разрешения и ковариации в обобщенной обратной теории и выведем выражения для матриц разрешения и ковариации для решателя LSQR. Поскольку LSQR настолько популярен в сейсмотомографической инверсии, расчеты разрешающей способности и ковариационных матриц для LSQR представляют практический интерес.

Поскольку существует бесконечное количество обобщенных обратных функций для решения задач наименьших квадратов в подпространстве, детали матрицы разрешения зависят от того, какой обобщенный обратный вариант выбран для обратного вычисления.= x , и параметры модели полностью разрешены в инверсии. Для предполагаемого параметра модели, то есть скорости ячейки x _i , которая разрешена хорошо, но не идеально, соответствующий диагональный элемент R ( r _{i , i} ) будет быть относительно большим. Некоторыми недиагональными элементами R , относящимися к параметру модели x _i ( r _{i , j} ), можно пренебречь, но в хорошо разрешенных случаях они обычно соответствуют ячейкам, которые пространственно близки к ячейке x _i .Находятся ли эти неотъемлемые элементы близко к диагонали в R , зависит от того, как параметры модели упорядочены в векторе x . Предполагаемая матрица R не зависит от значения x . То есть это зависит от экспериментальной конфигурации и, возможно, от используемой техники инверсии (см. Ниже), но не от скоростей в каждой ячейке.

Применяя SVD, матрица G может быть разложена на G = U Λ V ^T .Здесь U — это матрица, содержащая собственные векторы G G ^T , V — это матрица, содержащая собственные векторы G ^T G и Λ — диагональная матрица, содержащая сингулярные значения G . Если в инверсии (TSVD) используются только наибольшие сингулярные значения p , обобщенное обратное значение G может быть выражено как G ^{— g} = V _p Λ _p ^{— 1} U _p ^T (e.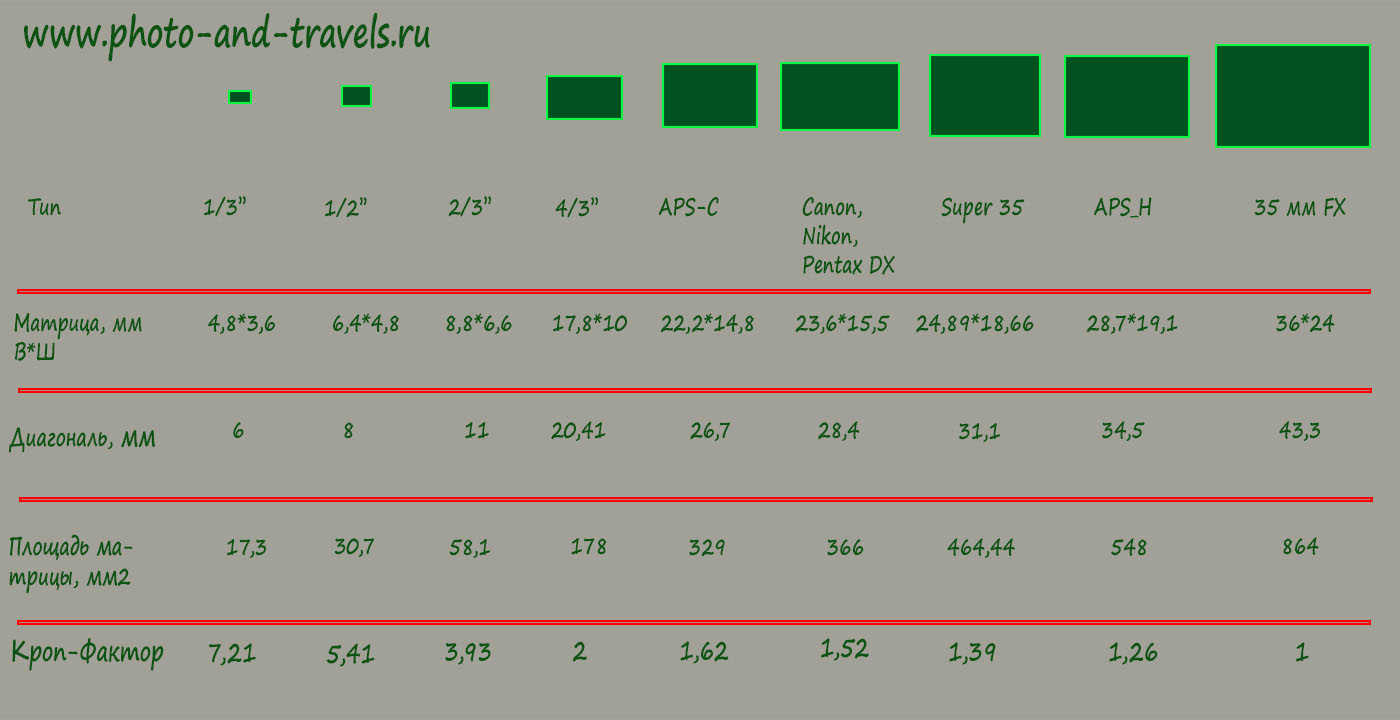 грамм. Менке 1984). Матрицы U _p и V _p состоят из первых столбцов p U и V соответственно и Λ _p (a p × p матрица) имеет соответствующие сингулярные значения. Тогда матрица разрешения может быть записана как (5), а ковариационная матрица как (например, Menke 1984) (6)

22″ data-legacy-id=»ss4″> Матрицы разрешения и ковариации

Следует отметить, что при выводе выше мы использовали ортонормированное свойство U _{k + 1} . Однако это свойство может не соблюдаться из-за конечной точности компьютеров (например, Paige 1971). Следовательно, реортогонализация необходима для U _k и V _k . Можно использовать несколько методов (например, Parlett & Scott 1979; Zhang & McMechan 1995).С реортогонализацией (см. O’Leary & Simmons 1981) мы можем вычислить векторы Ланцоша, выполнив следующие шаги. конец

1. Инициализировать β ₁ = | b | , u ₁ = b / β ₁ , v _a = G ^T u ₁ α ₁ = | v _a | , v ₁ = v _a / α ₁ . для итерации k = 1, 2

2. Реортогонализированная двудиагонализация u _a = G v _k −α _k u _{k . Реортогонализировать. u b = u a — U k ( U k ^T u a ) β k + 1 = | u b | , u k + 1 = u b / β k + 1 , v a = G u k + 1 −β k + 1 v k .Реортогонализировать. v b = v a — V k ( V k ^T v a ) α k + 1 = | v b | , v k + 1 = v b / α k + 1 .}

Размеры модели (10 × 14 км) выбраны для удобства. Проблема останется прежней, если мы соответствующим образом масштабируем задействованные переменные. Общее количество лучей 196.

Рисунок 1

Распределение лучей эксперимента.Источники находятся внизу модели, а приемники — вверху.

Рисунок 1

Распределение лучей эксперимента. Источники находятся внизу модели, а приемники — вверху.

Чтобы сгенерировать синтетические времена пробега и частные производные (элементы матрицы G ), траектории лучей аппроксимируются прямыми линиями, что делает смоделированную задачу чисто линейной. Синтетические времена пробега рассчитываются для однородной модели с постоянной скоростью 5 км с ^{— 1} .В качестве начальной модели для различных инверсий использовалась модель шахматной доски с возмущением скорости ± 0,2 км с ^{— 1} , наложенным на «истинную» модель (рис. 2). Подобные структуры шахматной доски ранее использовались различными авторами для тестирования томографических алгоритмов и экспериментальной геометрии (например, Humphreys & Clayton 1988). Сделать «истинную» скоростную модель однородной, а исходную модель — шахматной доской, удобно при исследовании ошибок в перевернутых моделях.Модель параметризована на ячейки размером 1 × 1 км, что дает 140 неизвестных параметров скорости. Мы также провели тесты, используя «истинную» модель шахматной доски и однородную стартовую модель. Результаты этих тестов по существу были такими же, как и представленные здесь.

Рисунок 2

Стартовая модель шахматной доски. Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга. Черные кружки указывают на положительные возмущения скорости, а серые кружки указывают на отрицательные возмущения скорости.

Рисунок 2

Стартовая модель шахматной доски. Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга. Черные кружки указывают на положительные возмущения скорости, а серые кружки указывают на отрицательные возмущения скорости.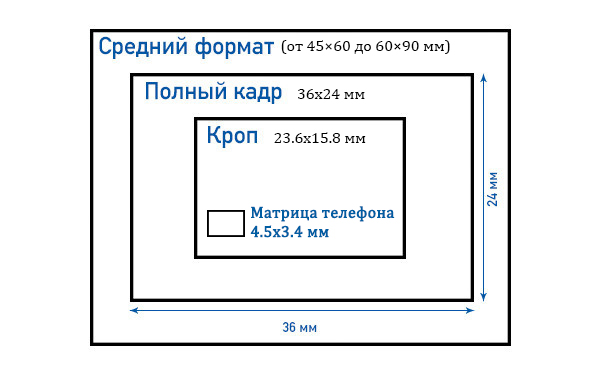

Сначала SVD был применен к матрице G , и были вычислены сингулярные значения, показанные на рис. 3. Последние 20 собственных значений практически равны нулю. Чтобы показать, как ненулевые сингулярные значения в матрице G аппроксимируются матрицей B _k , было выполнено 120 итераций с LSQR (LSQR-120) для генерации B ₁₂₀ .Сингулярные значения B ₁₂₀ , упорядоченные от большого к меньшему (рис. 3), очень хорошо аппроксимируют первые 120 наибольших сингулярных значений матрицы G . Инвертированные модели и матрицы разрешения из LSQR-120 и TSVD-120 (TSVD с сохраненными первыми 120 наибольшими сингулярными значениями) показаны на рисунках 4 и 5, которые показывают, что результаты, полученные двумя методами, очень похожи.

Рисунок 3

Распределение сингулярных значений, полученных SVD для G (сплошная линия) и B ₁₂₀ (крестики).

Рисунок 3

Распределение сингулярных значений, полученных SVD для G (сплошная линия) и B ₁₂₀ (крестики).

Рисунок 4

Перевернутые модели из TSVD-120 (а) и LSQR-120 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 4

Перевернутые модели из TSVD-120 (а) и LSQR-120 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 5

Элементы матриц разрешения для инвертированных моделей из (а) TSVD-120 и (б) LSQR-120.

Рисунок 5

Элементы матриц разрешения для инвертированных моделей из (а) TSVD-120 и (б) LSQR-120.

Для моделирования общей сейсмотомографической задачи и решения с использованием небольшого количества итераций ( k ) по сравнению с количеством параметров модели, в LSQR использовалось 14 итераций (10 процентов от количества неизвестных). Собственные значения, полученные из B ₁₄ , показаны на рис. 6, который показывает, что первые пять собственных значений почти такие же, как первые пять собственных значений, полученные из G с использованием SVD. Остальные девять собственных значений соответствуют собственным значениям G между числами 7 и 95. Инвертированные модели из LSQR-14 и TSVD-95 показаны на рис. 7. Из этого рисунка мы можем видеть, что с точки зрения несоответствия между истинными и оценочных моделей, обобщенная обратная матрица G может быть несколько лучше аппроксимирована 14 итерациями процесса Ланцоша, чем TSVD-95.Однако матрица разрешения для LSQR-14 (рис. 8) показывает, что даже пространственно удаленные параметры модели, полученные с помощью LSQR-14, сильно коррелированы. Это может привести к сильным артефактам в реальных случаях, особенно когда данные зашумлены. Два подхода могут помочь улучшить матрицу разрешения. Один — сделать больше итераций. На рис. 9 показана матрица разрешения после 28 итераций. Второй — упорядочить исходное уравнение. (1) (например, Spakman 1993). Здесь мы упорядочили уравнение. (1) с использованием метода наименьших квадратов с затуханием (например,грамм. Пейдж и Сондерс 1982b). На рис. 10 показана матрица разрешения для системы уравнений с коэффициентом затухания 0,5. Оба рисунка 9 и 10 показывают матрицы улучшенного разрешения.

Рисунок 6

Распределения сингулярных значений, полученных с помощью B ₁₄ (крестики), вместе с сингулярными значениями, полученными с помощью SVD G (сплошная линия).

Рисунок 6

Распределения сингулярных значений, полученных с помощью B ₁₄ (крестики), вместе с сингулярными значениями, созданными SVD для G (сплошная линия).

Рисунок 7

Перевернутые модели из TSVD-95 (а) и LSQR-14 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 7

Перевернутые модели из TSVD-95 (а) и LSQR-14 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 8

Матрица разрешения для модели из LSQR-14.

Рисунок 8

Матрица разрешения для модели из LSQR-14.

Рисунок 9

Матрица разрешения для модели из LSQR-28.

Рисунок 9

Матрица разрешения для модели из LSQR-28.

Рисунок 10

Матрица разрешения для модели из затухающего LSQR-14 с коэффициентом затухания, равным 0,5.

Рисунок 10

Матрица разрешения для модели из затухающего LSQR-14 с коэффициентом затухания, равным 0.5.

Численное моделирование показывает, что решение, данное LSQRA, может значительно отличаться от решения LSQR.

Концепция использования матриц разрешения на основе подпространственных решений подвергалась критике со стороны некоторых авторов (например,грамм. Нолет 1999). Этот момент вызвал широкое обсуждение в процессе рецензирования этой статьи, и поэтому мы включили конкретное обсуждение этого момента. В нашем понимании основная критика заключается в следующем.

LSQR — это метод подпространства, то есть мы (обычно) ограничиваем истинное количество степеней свободы в модели по сравнению с предопределенной моделью и регуляризацией. Алгоритм пытается подобрать данные, используя ограниченное количество векторов. Эти векторы, как правило, не обязательно являются собственными векторами, но могут близко их аппроксимировать.По мере повторения алгоритма LSQR к используемому подпространству добавляются дополнительные измерения. Теперь, из-за природы большинства проблем сейсмической томографии, хорошее соответствие данным обычно может быть получено с использованием довольно ограниченного числа измерений в нашем модельном пространстве, при условии, что эти размеры выбраны так, чтобы соответствовать наиболее значимым направлениям (в условия уменьшения несоответствия). LSQR достигает этого, и поэтому хорошее соответствие данным может быть получено с использованием довольно ограниченного подпространства, размеры которого соответствуют количеству итераций метода LSQR.То, что это разумный метод оценки моделей для сейсмической томографии, признается многими авторами, о чем свидетельствует большое количество публикаций моделей, созданных с помощью этого метода (см. Список ссылок для некоторых примеров). Отметим также, что неограниченная инверсия с использованием всех собственных векторов редко используется в сейсмической томографии: для ограничения истинного числа степеней свободы в пространстве модели применяются различные методы, такие как усеченные наименьшие квадраты и регуляризация; то есть, мы можем рассматривать концепцию моделей подпространства как таковую как общепринятый подход к томографической инверсии.

Однако можно утверждать, что ограниченное пространство модели, достаточное для создания хорошей модели Земли, может оказаться недостаточным для обеспечения разумных оценок разрешения модели, поскольку еще не исследованные направления в пространстве модели могут существенно повлиять на матрицу разрешения, но не актуальная модель. В этом рассуждении есть доля правды, о чем свидетельствуют простые примеры, представленные в этой статье. На первый взгляд, это может означать, что модели подпространства не должны использоваться для оценки разрешения.Однако этот аргумент вводит в заблуждение, и мы сейчас попытаемся его объяснить.

Нужно ли нам полностью уменьшать размер блока до исходного размера, прежде чем текущее решение будет по существу таким же (с точки зрения выводов о структуре Земли), что и исходное обращение с наименьшими блоками, зависит от характера проблемы. — конфигурация, данные и т. Д.При решении реальной проблемы, если при уменьшении размера нашего блока наступает момент, когда значительное уменьшение размера блока не приводит к значительному изменению свойств инвертированной модели и связанной с ней матрицы разрешения, то в этой точке мы, вероятно, сделаем вывод, что этого размера блока достаточно, и что дальнейшие инверсии с меньшим размером блока не требуются. Процесс уменьшения размеров блока и остановки, когда результат стабилизируется, можно рассматривать как аналогию с нашим применением подхода LSQR в том смысле, что мы пошагово увеличиваем количество степеней свободы в нашем модельном пространстве.

Можно возразить, что мы не обсуждаем ситуации, когда мы меняем размер блока нашей модели. Однако мы можем изменить «мысленный эксперимент» выше, рассмотрев случай, когда мы сохраняем размер ячейки одинаковым, но требуем взаимосвязи между параметрами модели (регуляризация, разложение по усеченным сингулярным значениям и т. Д.). Налагая ограничения, мы уменьшили истинное количество степеней свободы в модели и изменили результаты нашей инверсии, включая матрицу разрешения.

Таким образом, методы подпространства каким-то образом ограничивают пространство модели в зависимости от характера проблемы и информации в данных. Дело в том, что (в LSQR) у нас есть , ограничивающие размеры пространства модели (количество векторов), а не , как это было сделано в . Ограничивая таким образом пространство нашей модели, мы существенно переопределяем нашу модель. Как видно из ур. (3) матрица разрешения описывает в строгом математическом смысле «связь» между истинной землей и расчетными параметрами модели.Нам кажется, что прямо из этого следует, что использование одного подпространства для описания модели и чего-то еще для оценки разрешения может ввести в заблуждение. Мы не будем вычислять модель, используя один набор параметров модели, а затем анализировать разрешение, вычисленное с помощью гораздо большей сетки модели или другого набора параметров демпфирования или сглаживания. Такой подход фактически нарушил бы определение матрицы разрешения, подразумевая, что использование чего-либо, кроме того же подпространства для оценки разрешения, которое использовалось для вычисления модели, в значительной степени неверно.Правильно оцененная (подпространственная) матрица разрешения может рассматриваться как неотъемлемая часть решения.

На самом деле хорошее решение с точки зрения параметров модели, которые обеспечивают хорошее соответствие набору данных, не означает, что параметры модели не зависят друг от друга. Когда вектор в маленьком пространстве (измерениях) поворачивается к большему пространству, элементы вектора в большем пространстве неизбежно в некоторой степени коррелируют друг с другом. Два подобных решения, такие как в примере, показанном Deal & Nolet (1996), не означают, что эти два решения должны иметь одинаковые свойства.

Если номер итерации k слишком мал, может возникнуть сильная корреляция между параметрами инвертированной модели. В примере с матрицей 900 × 900 Deal & Nolet (1996) показали, что даже если решение, полученное из 50 итераций LSQR, очень похоже на решение из TSVD, включая 600 сингулярных значений, матрицы разрешения, полученные этими двумя процедурами, значительно разные. Это кажется парадоксом и инициировало дискуссию о том, действительно ли матрица разрешения может быть рассчитана с помощью процесса Ланцоша (Deal & Nolet 1996; Zhang & McMechan 1996; Nolet 1999; Yao 1999).

Из приведенных выше аргументов возникает соблазн сделать вывод, что расчеты разрешения, основанные непосредственно на LSQR, вообще говоря, подозрительны, если не совсем неверны. Однако этот вывод ошибочен. Во-первых, следует отметить, что если наш первоначальный выбор класса модели не подходит, то даже «полное» решение и соответствующая матрица разрешения могут вводить в глубокое заблуждение. Другими словами, не обязательно, чтобы модель и матрица разрешения, полученные с помощью «полной инверсии», были оптимальными; результаты могут быть улучшены, например, с помощью другой параметризации или регуляризации модели, и в таком случае модель подпространства, полученная с помощью LSQR, на самом деле может быть лучше, чем модель с полной инверсией, в том смысле, что модель LSQR может лучше аппроксимировать реальную Землю.

Теперь, если мы предположим, что наша «полная инверсия» является оптимальной, тогда решение ∂ из LSQR предоставит разумное решение, только если мы проведем достаточное количество итераций, и может быть трудно узнать, сколько итераций достаточно. . Однако это не проблема для метода расчета разрешения. То, что эти оценки разрешения могут значительно отличаться от оценок, полученных с использованием полной инверсии, не потому, что расчет разрешения неправильный, а потому, что свойства (ограниченного) решения недостаточно «хороши».Это происходит не из-за неправильной оценки матрицы разрешения, а из-за того, что решение все еще неадекватно. Другими словами, эти разрешения являются , а не попыткой описать матрицу полного разрешения, но являются полным и адекватным описанием свойств нашей модели подпространства. Проблемы, на которые может указывать матрица разрешения, реальны в том смысле, что они являются полными и истинными свойствами нашего текущего решения, что очевидно из уравнения. (3). По мере продолжения итерации наша матрица разрешения в конечном итоге будет хорошо аппроксимировать матрицу полной инверсии.Это связано с тем, что свойства решения LSQR приблизились к свойствам полной инверсии.

Сильные корреляции между компонентами решения нежелательны, поскольку они могут привести к неправильной интерпретации изображения. С увеличением размеров подпространства взаимосвязь между параметрами модели в целом уменьшается. Для стабилизации томографических инверсий обычно используются различные регуляризации, такие как затухание. Они подразумевают уровень усреднения оценочных параметров модели.Форма этого усреднения зависит от того, как применяется демпфирование, сглаживание или регуляризация. Во многих случаях результат по крайней мере частично соответствует простому пространственному сглаживанию оценочной модели. Такие процедуры часто повышают стабильность инверсии и могут помочь уменьшить дальнодействующую корреляцию в матрице разрешения R .

Поэтому мы предполагаем, что, если для инверсии был выбран LSQR, правильным путем будет исследовать решение вместе с матрицей разрешения по мере продолжения итерации.В случаях, когда оценочная модель не претерпевает значительных изменений при дальнейшей итерации, но матрица разрешения изменяется, тогда, вероятно, рекомендуется продолжить итерацию.

Наконец, по вопросу о прекращении итерации: если наша цель — аппроксимировать матрицу «полного» разрешения, а не исследовать свойства нашего фактического (LSQR) решения, то, конечно, существует риск, что «попробуем и увидеть, когда он стабилизируется »будет вводить в заблуждение. Если мы выполняем итерацию несколько раз, а решение и соответствующая матрица разрешения, кажется, не изменятся значительно при дальнейшей итерации, нет гарантии, что они не изменятся «значительно», если мы продолжим (хотя на практике это маловероятно).Однако каковы альтернативы? Из-за размера связанных с этим проблем на практике все методы оценки разрешения, которые могут использоваться вместо этого (например, Nolet 1999), не являются «полными» методами, и все они могут давать вводящие в заблуждение результаты, поскольку все они являются упрощениями или приближениями. Также обратите внимание, что большинство типов тестов на чувствительность могут, по крайней мере в принципе, вводить в глубокое заблуждение, если характер реальной Земли значительно отличается от того, что мы предполагаем (неявно или явно) в тесте (см. Ниже).Для LSQR мы можем провести параллель с методами нелинейной инверсии. Вообще говоря, мы никогда не сможем узнать, достаточно ли мы провели итерацию или поиск, чтобы найти глобальное решение, или застряли в локальном минимуме, но, тем не менее, нелинейная инверсия широко и успешно используется. Мы повторяем, что даже матрица разрешения от полной инверсии может вводить в заблуждение (с точки зрения интерпретации структуры Земли), если, например, размер нашего блока в модели слишком велик. На практике мы всегда делаем выбор при применении алгоритмов инверсии в отношении параметризации модели и (истинного) числа степеней свободы в нашей модели.LSQR с правильной связанной матрицей разрешения может помочь сделать этот выбор подходящим для данного набора данных.

Оценка надежности инвертированной модели, основанная, например, на создании синтетической модели, производстве синтетических данных, их инвертировании и сравнении синтетических и инвертированных моделей, может вводить в глубокое заблуждение, если синтетическая модель значительно отличается по характеру от реальной. Земной шар. Такие синтетические методы очень полезны и часто проливают свет, но их, вероятно, следует рассматривать как дополнение к исследованию матриц разрешения и ковариации, а не как альтернативу. В зависимости от нелинейности проблемы аналогичные аргументы могут быть применены, например, к основанным на Монте-Карло методам исследования неопределенностей томографических моделей. В сложных задачах такие методы могут на практике исследовать только небольшую часть пространства модели, и результаты, вероятно, следует рассматривать в сочетании с информацией о разрешении, основанной на линеаризации.

Если R продолжает значительно меняться по мере продолжения итерации, то, вероятно, итерацию следует продолжить.

07″> Список литературы

1

,

1977

Определение трехмерной сейсмической структуры литосферы,

J. geophys. Res.

,

82

,

277

—

296

2

,

1968

Разрешающая способность общих данных о земле,

Geophys. J. R. astr. Soc.

,

16

,

169

—

205

3

,

1996

Трехмерная структура скоростей продольных и поперечных волн вулкана Редут, Аляска,

Дж.геофизики. Res.

,

101

,

8111

—

8128

6

,

1996

Комментарий к «Оценка разрешения и ковариации для больших обращений матриц» Дж. Чжана и Г. А. МакМечана,

Geophys. J. Int.

,

127

,

245

—

250

7

,

1993

Телесейсмическая скоростная томография с использованием метода ACH: теория и применение к исследованиям в континентальном масштабе, в

319

—

360

8

,

1988

Адаптация томографии обратной проекции к задачам времени прохождения сейсмических волн,

Дж.геофизики. Res.

,

93

,

1073

—

1085

10

,

1996

Вычислительно выполнимая матрица приближенного разрешения для обратных сейсмических задач,

Geophys. J. Int.

,

126

,

345

—

359

11

,

1985

Устранение неполадок или устранение неадекватных и зашумленных томографических систем,

J. Comp. Phys.

,

61

,

462

—

482

12

,

1993

Решение больших линеаризованных томографических задач, в

248

—

264

13

,

1990

Решение больших линейных обратных задач с помощью проекции,

Geophys. J. Int.

,

103

,

565

—

568

14

,

1999

Явные приблизительные выражения для разрешения и апостериорной ковариации массивных томографических систем,

Geophys. J. Int.

,

138

,

36

—

44

15

,

1981

Процедура регуляризации бидиагонализации для крупномасштабной дискретизации некорректных задач,

SIAM J.Sci. Стат. Комп.

,

2

,

474

—

489

16

,

1971

Вычисление собственных значений и собственных векторов очень больших разреженных матриц, 17

,

1982

a

LSQR: алгоритм для разреженных линейных уравнений и разреженных наименьших квадратов,

ACM Trans. Математика. Программное обеспечение

,

8

,

43

—

71

18

,

1982

b

LSQR: разреженные линейные уравнения и задачи наименьших квадратов,

ACM Trans.Математика. Программное обеспечение

,

8

,

195

—

209

19

,

1979

Алгоритм Ланцоша с выборочной ортогонализацией,

Math. Комп.

,

33

,

217

—

38

20

,

1993

Итерационные стратегии для нелинейной томографии во времени пробега с использованием данных о глобальных землетрясениях, в

190

—

226

21

и другие. и другие. ,

1988

Алгоритмы визуализации, точность и разрешение в томографии с временной задержкой, дюйм

155

—

188

22

,

1987

Численное решение больших разреженных линейных алгебраических систем, возникающих из томографических задач, в

49

—

84

23

,

1998

Разрешение сейсмической анизотропии: методы разреженных матриц для обратных геофизических задач,

Геофизика

,

63

,

970

—

983

24

,

1999

Комментарий к «Явным приблизительным выражениям разрешения и 25

,

1995

Оценка разрешения и ковариации для больших инверсий матриц,

Geophys. J. Int.

,

121

,

409

—

426

26

,

1996

Ответ на комментарий М. М. Дила и Г. Нолета «Оценка разрешения и ковариации для больших инверсий матриц»,

Geophys. J. Int.

,

127

,

251

—

252

© 1999 РАН

Расчет разрешающей способности и ковариационных матриц для сейсмической томографии методом LSQR | Международный геофизический журнал

09″ data-legacy-id=»ss1″> Введение

Линеаризованная обратная задача может быть определена как решение матричного уравнения (1), где x ∈ Re ⁿ обозначает набор параметров модели, b ∈ Re ^m обозначает данные наблюдений, а G ∈ Re ^{m × n} — матрица, связывающая параметры модели и наблюдения. В сейсмической томографии матрица G обычно является разреженной и очень большой, и, следовательно, решение с помощью методов полной инверсии матрицы может быть трудноразрешимым с вычислительной точки зрения.

В течение последнего десятилетия метод LSQR, представленный Paige & Saunders (1982a, b), широко применялся в задачах сейсмической томографии (например, Nolet 1985, 1993; Van der Sluis & Van der Vorst 1987; Spakman & Nolet 1988; Benz 1996). Вкратце, преимущества LSQR заключаются в следующем: простые рекурсии для обновления последовательных приближений параметров модели подразумевают минимальные требования к памяти ЦП; Бидиагонализация Ланцоша хорошо подходит для вычислений с разреженными матрицами; и поскольку это метод сопряженных градиентов, сходимость последовательности приближенных решений происходит быстро.Следовательно, хорошее решение в подпространстве Крылова часто может быть получено с помощью небольшого количества итераций (например, Nolet & Snieder 1990), что делает LSQR очень эффективным с вычислительной точки зрения.

В некотором смысле, решение уравнения. (1) использование LSQR с небольшим количеством итераций ( k ) аналогично использованию частичного разложения по сингулярным числам (SVD), которое сохраняет только k сингулярных значений матрицы G . Оба метода аппроксимируют решение с использованием уменьшенного числа степеней свободы модели.Какой бы метод ни использовался, важны оценки разрешения и ковариации, поскольку они могут указывать на значимость и надежность инвертированной модели. Это было подчеркнуто Backus & Gilbert (1968), которые основали свою обобщенную обратную теорию на методах, разработанных для оптимизации разрешения получаемой геофизической модели, полученной из обработанных данных. Обсуждения разрешения и ковариации в сейсмической томографии также можно найти в ранней статье Аки (1977), а также во многих более поздних работах (например,грамм. Evans & Achauer 1993).

Матрицы разрешения и ковариации могут быть вычислены с помощью обобщенного обратного преобразования G ^{— g} (например, Menke 1984). Однако LSQR не дает явного обобщенного обратного преобразования; поэтому матрицы разрешения и ковариации не могут быть вычислены так же удобно, как в таких методах, как разложение по усеченным сингулярным числам (TSVD) (Nolet 1993). Основываясь на LSQR, Zhang & McMechan (1995) вывели формулы для расчета разрешающей способности и ковариационных матриц для модифицированной инверсии LSQR (LSQRA).Однако LSQRA может значительно отличаться от LSQR; Это будет обсуждаться позже.

В этой статье мы начнем с определений матриц разрешения и ковариации в обобщенной обратной теории и выведем выражения для матриц разрешения и ковариации для решателя LSQR. Поскольку LSQR настолько популярен в сейсмотомографической инверсии, расчеты разрешающей способности и ковариационных матриц для LSQR представляют практический интерес.

Некоторыми недиагональными элементами R , относящимися к параметру модели x _i ( r _{i , j} ), можно пренебречь, но в хорошо разрешенных случаях они обычно соответствуют ячейкам, которые пространственно близки к ячейке x _i .Находятся ли эти неотъемлемые элементы близко к диагонали в R , зависит от того, как параметры модели упорядочены в векторе x . Предполагаемая матрица R не зависит от значения x . То есть это зависит от экспериментальной конфигурации и, возможно, от используемой техники инверсии (см. Ниже), но не от скоростей в каждой ячейке.

Применяя SVD, матрица G может быть разложена на G = U Λ V ^T .Здесь U — это матрица, содержащая собственные векторы G G ^T , V — это матрица, содержащая собственные векторы G ^T G и Λ — диагональная матрица, содержащая сингулярные значения G . Если в инверсии (TSVD) используются только наибольшие сингулярные значения p , обобщенное обратное значение G может быть выражено как G ^{— g} = V _p Λ _p ^{— 1} U _p ^T (e.грамм. Менке 1984). Матрицы U _p и V _p состоят из первых столбцов p U и V соответственно и Λ _p (a p × p матрица) имеет соответствующие сингулярные значения. Тогда матрица разрешения может быть записана как (5), а ковариационная матрица как (например, Menke 1984) (6)

22″ data-legacy-id=»ss4″> Матрицы разрешения и ковариации

Следует отметить, что при выводе выше мы использовали ортонормированное свойство U _{k + 1} . Однако это свойство может не соблюдаться из-за конечной точности компьютеров (например, Paige 1971). Следовательно, реортогонализация необходима для U _k и V _k . Можно использовать несколько методов (например, Parlett & Scott 1979; Zhang & McMechan 1995).С реортогонализацией (см. O’Leary & Simmons 1981) мы можем вычислить векторы Ланцоша, выполнив следующие шаги. конец

1. Инициализировать β ₁ = | b | , u ₁ = b / β ₁ , v _a = G ^T u ₁ α ₁ = | v _a | , v ₁ = v _a / α ₁ . для итерации k = 1, 2

2. Реортогонализированная двудиагонализация u _a = G v _k −α _k u _{k . Реортогонализировать. u b = u a — U k ( U k ^T u a ) β k + 1 = | u b | , u k + 1 = u b / β k + 1 , v a = G u k + 1 −β k + 1 v k .Реортогонализировать. v b = v a — V k ( V k ^T v a ) α k + 1 = | v b | , v k + 1 = v b / α k + 1 .}

Размеры модели (10 × 14 км) выбраны для удобства. Проблема останется прежней, если мы соответствующим образом масштабируем задействованные переменные. Общее количество лучей 196.

Рисунок 1

Распределение лучей эксперимента.Источники находятся внизу модели, а приемники — вверху.

Рисунок 1

Распределение лучей эксперимента. Источники находятся внизу модели, а приемники — вверху.

Чтобы сгенерировать синтетические времена пробега и частные производные (элементы матрицы G ), траектории лучей аппроксимируются прямыми линиями, что делает смоделированную задачу чисто линейной. Синтетические времена пробега рассчитываются для однородной модели с постоянной скоростью 5 км с ^{— 1} .В качестве начальной модели для различных инверсий использовалась модель шахматной доски с возмущением скорости ± 0,2 км с ^{— 1} , наложенным на «истинную» модель (рис. 2). Подобные структуры шахматной доски ранее использовались различными авторами для тестирования томографических алгоритмов и экспериментальной геометрии (например, Humphreys & Clayton 1988). Сделать «истинную» скоростную модель однородной, а исходную модель — шахматной доской, удобно при исследовании ошибок в перевернутых моделях.Модель параметризована на ячейки размером 1 × 1 км, что дает 140 неизвестных параметров скорости. Мы также провели тесты, используя «истинную» модель шахматной доски и однородную стартовую модель. Результаты этих тестов по существу были такими же, как и представленные здесь.

Рисунок 2

Стартовая модель шахматной доски. Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга. Черные кружки указывают на положительные возмущения скорости, а серые кружки указывают на отрицательные возмущения скорости.

Рисунок 2

Стартовая модель шахматной доски. Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга. Черные кружки указывают на положительные возмущения скорости, а серые кружки указывают на отрицательные возмущения скорости.

Сначала SVD был применен к матрице G , и были вычислены сингулярные значения, показанные на рис. 3. Последние 20 собственных значений практически равны нулю. Чтобы показать, как ненулевые сингулярные значения в матрице G аппроксимируются матрицей B _k , было выполнено 120 итераций с LSQR (LSQR-120) для генерации B ₁₂₀ .Сингулярные значения B ₁₂₀ , упорядоченные от большого к меньшему (рис. 3), очень хорошо аппроксимируют первые 120 наибольших сингулярных значений матрицы G . Инвертированные модели и матрицы разрешения из LSQR-120 и TSVD-120 (TSVD с сохраненными первыми 120 наибольшими сингулярными значениями) показаны на рисунках 4 и 5, которые показывают, что результаты, полученные двумя методами, очень похожи.

Рисунок 3

Распределение сингулярных значений, полученных SVD для G (сплошная линия) и B ₁₂₀ (крестики).

Рисунок 3

Распределение сингулярных значений, полученных SVD для G (сплошная линия) и B ₁₂₀ (крестики).

Рисунок 4

Перевернутые модели из TSVD-120 (а) и LSQR-120 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 4

Перевернутые модели из TSVD-120 (а) и LSQR-120 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 5

Элементы матриц разрешения для инвертированных моделей из (а) TSVD-120 и (б) LSQR-120.

Рисунок 5

Элементы матриц разрешения для инвертированных моделей из (а) TSVD-120 и (б) LSQR-120.

Для моделирования общей сейсмотомографической задачи и решения с использованием небольшого количества итераций ( k ) по сравнению с количеством параметров модели, в LSQR использовалось 14 итераций (10 процентов от количества неизвестных).Собственные значения, полученные из B ₁₄ , показаны на рис. 6, который показывает, что первые пять собственных значений почти такие же, как первые пять собственных значений, полученные из G с использованием SVD. Остальные девять собственных значений соответствуют собственным значениям G между числами 7 и 95. Инвертированные модели из LSQR-14 и TSVD-95 показаны на рис. 7. Из этого рисунка мы можем видеть, что с точки зрения несоответствия между истинными и оценочных моделей, обобщенная обратная матрица G может быть несколько лучше аппроксимирована 14 итерациями процесса Ланцоша, чем TSVD-95.Однако матрица разрешения для LSQR-14 (рис. 8) показывает, что даже пространственно удаленные параметры модели, полученные с помощью LSQR-14, сильно коррелированы. Это может привести к сильным артефактам в реальных случаях, особенно когда данные зашумлены. Два подхода могут помочь улучшить матрицу разрешения. Один — сделать больше итераций. На рис. 9 показана матрица разрешения после 28 итераций. Второй — упорядочить исходное уравнение. (1) (например, Spakman 1993). Здесь мы упорядочили уравнение. (1) с использованием метода наименьших квадратов с затуханием (например,грамм. Пейдж и Сондерс 1982b). На рис. 10 показана матрица разрешения для системы уравнений с коэффициентом затухания 0,5. Оба рисунка 9 и 10 показывают матрицы улучшенного разрешения.

Рисунок 6

Распределения сингулярных значений, полученных с помощью B ₁₄ (крестики), вместе с сингулярными значениями, полученными с помощью SVD G (сплошная линия).

Рисунок 6

Распределения сингулярных значений, полученных с помощью B ₁₄ (крестики), вместе с сингулярными значениями, созданными SVD для G (сплошная линия).

Рисунок 7

Перевернутые модели из TSVD-95 (а) и LSQR-14 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 7

Перевернутые модели из TSVD-95 (а) и LSQR-14 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 8

Матрица разрешения для модели из LSQR-14.

Рисунок 8

Матрица разрешения для модели из LSQR-14.

Рисунок 9

Матрица разрешения для модели из LSQR-28.

Рисунок 9

Матрица разрешения для модели из LSQR-28.

Рисунок 10

Матрица разрешения для модели из затухающего LSQR-14 с коэффициентом затухания, равным 0,5.

Рисунок 10

Матрица разрешения для модели из затухающего LSQR-14 с коэффициентом затухания, равным 0.5.

55″ data-legacy-id=»ss7″> Степени свободы

Насколько мы понимаем, в критике оценки разрешения подпространства подразумевается, что существует единственная «правильная» матрица разрешения, которая связана с нашим первоначальным выбором параметризации и регуляризации модели: насколько это верно? Подумайте, что произойдет, если мы увеличим размер блоков в нашей модели, скажем, в десять раз.Размеры модельного пространства будут уменьшены в 10 раз (мы не предполагаем никаких осложнений, связанных с демпфированием, регуляризацией и т. Д.). Очевидно, что мы все еще можем инвертировать, чтобы получить модель наименьших квадратов и соответствующую матрицу разрешения (здесь предполагается полная инверсия матрицы). Матрица разрешения, которую мы получим, будет , а не , будет такой же, как матрица инверсии с исходным размером блока, но нет ни малейшего сомнения, что это полностью действительная матрица разрешения. Модель и соответствующая матрица разрешения могут по-прежнему быть хорошим описанием соответствующей структуры Земли или могут быть «плохими», вводящими в заблуждение, неадекватными и т. Д., в зависимости от проблемы. Однако это проблема с нашим выбором пространства модели и , а не с методом оценки матрицы разрешения.

Если затем мы пошагово уменьшаем размеры наших блоков, инвертируя на каждом шаге, инвертированная модель и соответствующая матрица разрешения постепенно станут более похожими на модели из полной инверсии с исходным размером блока. Нужно ли нам полностью уменьшать размер блока до исходного размера, прежде чем текущее решение будет по существу таким же (с точки зрения выводов о структуре Земли), что и исходное обращение с наименьшими блоками, зависит от характера проблемы. — конфигурация, данные и т. Д.При решении реальной проблемы, если при уменьшении размера нашего блока наступает момент, когда значительное уменьшение размера блока не приводит к значительному изменению свойств инвертированной модели и связанной с ней матрицы разрешения, то в этой точке мы, вероятно, сделаем вывод, что этого размера блока достаточно, и что дальнейшие инверсии с меньшим размером блока не требуются. Процесс уменьшения размеров блока и остановки, когда результат стабилизируется, можно рассматривать как аналогию с нашим применением подхода LSQR в том смысле, что мы пошагово увеличиваем количество степеней свободы в нашем модельном пространстве.

Можно возразить, что мы не обсуждаем ситуации, когда мы меняем размер блока нашей модели. Однако мы можем изменить «мысленный эксперимент» выше, рассмотрев случай, когда мы сохраняем размер ячейки одинаковым, но требуем взаимосвязи между параметрами модели (регуляризация, разложение по усеченным сингулярным значениям и т. Д.). Налагая ограничения, мы уменьшили истинное количество степеней свободы в модели и изменили результаты нашей инверсии, включая матрицу разрешения.

Таким образом, методы подпространства каким-то образом ограничивают пространство модели в зависимости от характера проблемы и информации в данных. Дело в том, что (в LSQR) у нас есть , ограничивающие размеры пространства модели (количество векторов), а не , как это было сделано в . Ограничивая таким образом пространство нашей модели, мы существенно переопределяем нашу модель. Как видно из ур. (3) матрица разрешения описывает в строгом математическом смысле «связь» между истинной землей и расчетными параметрами модели.Нам кажется, что прямо из этого следует, что использование одного подпространства для описания модели и чего-то еще для оценки разрешения может ввести в заблуждение. Мы не будем вычислять модель, используя один набор параметров модели, а затем анализировать разрешение, вычисленное с помощью гораздо большей сетки модели или другого набора параметров демпфирования или сглаживания. Такой подход фактически нарушил бы определение матрицы разрешения, подразумевая, что использование чего-либо, кроме того же подпространства для оценки разрешения, которое использовалось для вычисления модели, в значительной степени неверно.Правильно оцененная (подпространственная) матрица разрешения может рассматриваться как неотъемлемая часть решения.

На самом деле хорошее решение с точки зрения параметров модели, которые обеспечивают хорошее соответствие набору данных, не означает, что параметры модели не зависят друг от друга. Когда вектор в маленьком пространстве (измерениях) поворачивается к большему пространству, элементы вектора в большем пространстве неизбежно в некоторой степени коррелируют друг с другом. Два подобных решения, такие как в примере, показанном Deal & Nolet (1996), не означают, что эти два решения должны иметь одинаковые свойства.

92″ data-legacy-id=»ss9″> Выводы

Мы вывели формулы для расчета матриц разрешения и ковариации для решателя LSQR (уравнения 18–19), которые требуют лишь небольших изменений в компьютерном коде LSQR.

Самым большим преимуществом использования LSQR является то, что необходимо хранить только текущие векторы Ланцоша, что приводит к низким требованиям к памяти ЦП. Это преимущество теряется, если матрицы разрешения и ковариации вычисляются с большим номером итерации k . Кроме того, процедуры реортогонализации требуют дополнительных вычислительных затрат по сравнению с исходной процедурой LSQR (Paige & Saunders 1982a, b). Однако k обычно намного меньше, чем размеры пространства модели, и поэтому потребность в памяти для вычислений с LSQR меньше, чем для полноматричных обратных методов.Дополнительные вычислительные затраты на процедуру реортогонализации не являются чрезмерно высокими.

LSQR с ограниченным числом итераций соответствует перепараметризации пространства модели. Матрица разрешения R этого подпространственного решения может отличаться от такового для полного пространственного решения, но это правильная матрица разрешения для нашей параметризации подпространства. Матрица R предоставляет важную информацию о том, как следует интерпретировать нашу оценочную модель. Когда LSQR применяется к инверсии, следует тщательно рассмотреть подходящую регуляризацию и номер итерации.Несмотря на то, что мы не можем предоставить полные и конкретные критерии для оценки матрицы разрешения LSQR, в рамках рационального подхода к сложным процедурам инверсии мы предлагаем не только исследовать R , но и его изменения с номером итерации ( k ) следует изучить. Если R продолжает значительно меняться по мере продолжения итерации, то, вероятно, итерацию следует продолжить.

07″> Список литературы

1

,

1977

Определение трехмерной сейсмической структуры литосферы,

J. geophys. Res.

,

82

,

277

—

296

2

,

1968

Разрешающая способность общих данных о земле,

Geophys. J. R. astr. Soc.

,

16

,

169

—

205

3

,

1996

Трехмерная структура скоростей продольных и поперечных волн вулкана Редут, Аляска,

Дж.геофизики. Res.

,

101

,

8111

—

8128

6

,

1996

Комментарий к «Оценка разрешения и ковариации для больших обращений матриц» Дж. Чжана и Г. А. МакМечана,

Geophys. J. Int.

,

127

,

245

—

250

7

,

1993

Телесейсмическая скоростная томография с использованием метода ACH: теория и применение к исследованиям в континентальном масштабе, в

319

—

360

8

,

1988

Адаптация томографии обратной проекции к задачам времени прохождения сейсмических волн,

Дж.геофизики. Res.

,

93

,

1073

—

1085

10

,

1996

Вычислительно выполнимая матрица приближенного разрешения для обратных сейсмических задач,

Geophys. J. Int.

,

126

,

345

—

359

11

,

1985

Устранение неполадок или устранение неадекватных и зашумленных томографических систем,

J. Comp. Phys.

,

61

,

462

—

482

12

,

1993

Решение больших линеаризованных томографических задач, в

248

—

264

13

,

1990

Решение больших линейных обратных задач с помощью проекции,

Geophys.J. Int.

,

103

,

565

—

568

14

,

1999

Явные приблизительные выражения для разрешения и апостериорной ковариации массивных томографических систем,

Geophys. J. Int.

,

138

,

36

—

44

15

,

1981

Процедура регуляризации бидиагонализации для крупномасштабной дискретизации некорректных задач,

SIAM J.Sci. Стат. Комп.

,

2

,

474

—

489

16

,

1971

Вычисление собственных значений и собственных векторов очень больших разреженных матриц, 17

,

1982

a

LSQR: алгоритм для разреженных линейных уравнений и разреженных наименьших квадратов,

ACM Trans. Математика. Программное обеспечение

,

8

,

43

—

71

18

,

1982

b

LSQR: разреженные линейные уравнения и задачи наименьших квадратов,

ACM Trans.Математика. Программное обеспечение

,

8

,

195

—

209

19

,

1979

Алгоритм Ланцоша с выборочной ортогонализацией,

Math. Комп.

,

33

,

217

—

38

20

,

1993

Итерационные стратегии для нелинейной томографии во времени пробега с использованием данных о глобальных землетрясениях, в

190

—

226

21

и другие. и другие. ,

1988

Алгоритмы визуализации, точность и разрешение в томографии с временной задержкой, дюйм

155

—

188

22

,

1987

Численное решение больших разреженных линейных алгебраических систем, возникающих из томографических задач, в

49

—

84

23

,

1998

Разрешение сейсмической анизотропии: методы разреженных матриц для обратных геофизических задач,

Геофизика

,

63

,

970

—

983

24

,

1999

Комментарий к «Явным приблизительным выражениям разрешения и 25

,

1995

Оценка разрешения и ковариации для больших инверсий матриц,

Geophys.J. Int.

,

121

,

409

—

426

26

,

1996

Ответ на комментарий М. М. Дила и Г. Нолета «Оценка разрешения и ковариации для больших инверсий матриц»,

Geophys. J. Int.

,

127

,

251

—

252

© 1999 РАН

Расчет разрешающей способности и ковариационных матриц для сейсмической томографии методом LSQR | Международный геофизический журнал

09″ data-legacy-id=»ss1″> Введение

Линеаризованная обратная задача может быть определена как решение матричного уравнения (1), где x ∈ Re ⁿ обозначает набор параметров модели, b ∈ Re ^m обозначает данные наблюдений, а G ∈ Re ^{m × n} — матрица, связывающая параметры модели и наблюдения.В сейсмической томографии матрица G обычно является разреженной и очень большой, и, следовательно, решение с помощью методов полной инверсии матрицы может быть трудноразрешимым с вычислительной точки зрения.

В течение последнего десятилетия метод LSQR, представленный Paige & Saunders (1982a, b), широко применялся в задачах сейсмической томографии (например, Nolet 1985, 1993; Van der Sluis & Van der Vorst 1987; Spakman & Nolet 1988; Benz 1996). Вкратце, преимущества LSQR заключаются в следующем: простые рекурсии для обновления последовательных приближений параметров модели подразумевают минимальные требования к памяти ЦП; Бидиагонализация Ланцоша хорошо подходит для вычислений с разреженными матрицами; и поскольку это метод сопряженных градиентов, сходимость последовательности приближенных решений происходит быстро.Следовательно, хорошее решение в подпространстве Крылова часто может быть получено с помощью небольшого количества итераций (например, Nolet & Snieder 1990), что делает LSQR очень эффективным с вычислительной точки зрения.

В некотором смысле, решение уравнения. (1) использование LSQR с небольшим количеством итераций ( k ) аналогично использованию частичного разложения по сингулярным числам (SVD), которое сохраняет только k сингулярных значений матрицы G . Оба метода аппроксимируют решение с использованием уменьшенного числа степеней свободы модели.Какой бы метод ни использовался, важны оценки разрешения и ковариации, поскольку они могут указывать на значимость и надежность инвертированной модели. Это было подчеркнуто Backus & Gilbert (1968), которые основали свою обобщенную обратную теорию на методах, разработанных для оптимизации разрешения получаемой геофизической модели, полученной из обработанных данных. Обсуждения разрешения и ковариации в сейсмической томографии также можно найти в ранней статье Аки (1977), а также во многих более поздних работах (например,грамм. Evans & Achauer 1993).

Матрицы разрешения и ковариации могут быть вычислены с помощью обобщенного обратного преобразования G ^{— g} (например, Menke 1984). Однако LSQR не дает явного обобщенного обратного преобразования; поэтому матрицы разрешения и ковариации не могут быть вычислены так же удобно, как в таких методах, как разложение по усеченным сингулярным числам (TSVD) (Nolet 1993). Основываясь на LSQR, Zhang & McMechan (1995) вывели формулы для расчета разрешающей способности и ковариационных матриц для модифицированной инверсии LSQR (LSQRA).Однако LSQRA может значительно отличаться от LSQR; Это будет обсуждаться позже.

В этой статье мы начнем с определений матриц разрешения и ковариации в обобщенной обратной теории и выведем выражения для матриц разрешения и ковариации для решателя LSQR. Поскольку LSQR настолько популярен в сейсмотомографической инверсии, расчеты разрешающей способности и ковариационных матриц для LSQR представляют практический интерес.

19″ data-legacy-id=»ss3″> Краткий обзор Lsqr

Приведенные выше отношения являются основой алгоритма LSQR.Используя свойства нижней двудиагональной матрицы B _k , Paige & Saunders (1982a) вывели простые итерации для обновления последовательно аппроксимированных x _k . Обратите внимание, что при точном вычислении эти x _k идентичны последовательности приближений, сгенерированной методом сопряженного градиента, и, следовательно, только самые последние столбцы матриц U _k и V _k необходимо сохранить, что приводит к минимальным требованиям к памяти ЦП.

35″ data-legacy-id=»ss5″> Численное моделирование

Поскольку матрица разрешения является наиболее популярной при инверсии сейсмических данных, мы показываем анализ разрешения только в следующем примере.Мы смоделировали геометрию луча для двумерной задачи, показанной на рис. 1. 14 приемников на поверхности обнаруживают сейсмические сигналы от 14 источников на дне. Эта конфигурация актуальна для различных сейсмологических приложений (телесейсмические, региональные или межскважинные исследования). Размеры модели (10 × 14 км) выбраны для удобства. Проблема останется прежней, если мы соответствующим образом масштабируем задействованные переменные. Общее количество лучей 196.

Рисунок 1

Распределение лучей эксперимента.Источники находятся внизу модели, а приемники — вверху.

Рисунок 1

Распределение лучей эксперимента. Источники находятся внизу модели, а приемники — вверху.

Чтобы сгенерировать синтетические времена пробега и частные производные (элементы матрицы G ), траектории лучей аппроксимируются прямыми линиями, что делает смоделированную задачу чисто линейной. Синтетические времена пробега рассчитываются для однородной модели с постоянной скоростью 5 км с ^{— 1} .В качестве начальной модели для различных инверсий использовалась модель шахматной доски с возмущением скорости ± 0,2 км с ^{— 1} , наложенным на «истинную» модель (рис. 2). Подобные структуры шахматной доски ранее использовались различными авторами для тестирования томографических алгоритмов и экспериментальной геометрии (например, Humphreys & Clayton 1988). Сделать «истинную» скоростную модель однородной, а исходную модель — шахматной доской, удобно при исследовании ошибок в перевернутых моделях.Модель параметризована на ячейки размером 1 × 1 км, что дает 140 неизвестных параметров скорости. Мы также провели тесты, используя «истинную» модель шахматной доски и однородную стартовую модель. Результаты этих тестов по существу были такими же, как и представленные здесь.

Рисунок 2

Стартовая модель шахматной доски. Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга. Черные кружки указывают на положительные возмущения скорости, а серые кружки указывают на отрицательные возмущения скорости.

Рисунок 2

Стартовая модель шахматной доски. Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга. Черные кружки указывают на положительные возмущения скорости, а серые кружки указывают на отрицательные возмущения скорости.

Сначала SVD был применен к матрице G , и были вычислены сингулярные значения, показанные на рис. 3. Последние 20 собственных значений практически равны нулю. Чтобы показать, как ненулевые сингулярные значения в матрице G аппроксимируются матрицей B _k , было выполнено 120 итераций с LSQR (LSQR-120) для генерации B ₁₂₀ .Сингулярные значения B ₁₂₀ , упорядоченные от большого к меньшему (рис. 3), очень хорошо аппроксимируют первые 120 наибольших сингулярных значений матрицы G . Инвертированные модели и матрицы разрешения из LSQR-120 и TSVD-120 (TSVD с сохраненными первыми 120 наибольшими сингулярными значениями) показаны на рисунках 4 и 5, которые показывают, что результаты, полученные двумя методами, очень похожи.

Рисунок 3

Распределение сингулярных значений, полученных SVD для G (сплошная линия) и B ₁₂₀ (крестики).

Рисунок 3

Распределение сингулярных значений, полученных SVD для G (сплошная линия) и B ₁₂₀ (крестики).

Рисунок 4

Перевернутые модели из TSVD-120 (а) и LSQR-120 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 4

Перевернутые модели из TSVD-120 (а) и LSQR-120 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 5

Элементы матриц разрешения для инвертированных моделей из (а) TSVD-120 и (б) LSQR-120.

Рисунок 5

Элементы матриц разрешения для инвертированных моделей из (а) TSVD-120 и (б) LSQR-120.

Для моделирования общей сейсмотомографической задачи и решения с использованием небольшого количества итераций ( k ) по сравнению с количеством параметров модели, в LSQR использовалось 14 итераций (10 процентов от количества неизвестных).Собственные значения, полученные из B ₁₄ , показаны на рис. 6, который показывает, что первые пять собственных значений почти такие же, как первые пять собственных значений, полученные из G с использованием SVD. Остальные девять собственных значений соответствуют собственным значениям G между числами 7 и 95. Инвертированные модели из LSQR-14 и TSVD-95 показаны на рис. 7. Из этого рисунка мы можем видеть, что с точки зрения несоответствия между истинными и оценочных моделей, обобщенная обратная матрица G может быть несколько лучше аппроксимирована 14 итерациями процесса Ланцоша, чем TSVD-95.Однако матрица разрешения для LSQR-14 (рис. 8) показывает, что даже пространственно удаленные параметры модели, полученные с помощью LSQR-14, сильно коррелированы. Это может привести к сильным артефактам в реальных случаях, особенно когда данные зашумлены. Два подхода могут помочь улучшить матрицу разрешения. Один — сделать больше итераций. На рис. 9 показана матрица разрешения после 28 итераций. Второй — упорядочить исходное уравнение. (1) (например, Spakman 1993). Здесь мы упорядочили уравнение. (1) с использованием метода наименьших квадратов с затуханием (например,грамм. Пейдж и Сондерс 1982b). На рис. 10 показана матрица разрешения для системы уравнений с коэффициентом затухания 0,5. Оба рисунка 9 и 10 показывают матрицы улучшенного разрешения.

Рисунок 6

Распределения сингулярных значений, полученных с помощью B ₁₄ (крестики), вместе с сингулярными значениями, полученными с помощью SVD G (сплошная линия).

Рисунок 6

Распределения сингулярных значений, полученных с помощью B ₁₄ (крестики), вместе с сингулярными значениями, созданными SVD для G (сплошная линия).

Рисунок 7

Перевернутые модели из TSVD-95 (а) и LSQR-14 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 7

Перевернутые модели из TSVD-95 (а) и LSQR-14 (б). Скорость в каждой ячейке относительно «истинной» скорости указывается размером круга.

Рисунок 8

Матрица разрешения для модели из LSQR-14.

Рисунок 8

Матрица разрешения для модели из LSQR-14.

Рисунок 9

Матрица разрешения для модели из LSQR-28.

Рисунок 9

Матрица разрешения для модели из LSQR-28.

Рисунок 10

Матрица разрешения для модели из затухающего LSQR-14 с коэффициентом затухания, равным 0,5.

Рисунок 10

Матрица разрешения для модели из затухающего LSQR-14 с коэффициентом затухания, равным 0.5.

55″ data-legacy-id=»ss7″> Степени свободы

Насколько мы понимаем, в критике оценки разрешения подпространства подразумевается, что существует единственная «правильная» матрица разрешения, которая связана с нашим первоначальным выбором параметризации и регуляризации модели: насколько это верно? Подумайте, что произойдет, если мы увеличим размер блоков в нашей модели, скажем, в десять раз.Размеры модельного пространства будут уменьшены в 10 раз (мы не предполагаем никаких осложнений, связанных с демпфированием, регуляризацией и т. Д.). Очевидно, что мы все еще можем инвертировать, чтобы получить модель наименьших квадратов и соответствующую матрицу разрешения (здесь предполагается полная инверсия матрицы). Матрица разрешения, которую мы получим, будет , а не , будет такой же, как матрица инверсии с исходным размером блока, но нет ни малейшего сомнения, что это полностью действительная матрица разрешения. Модель и соответствующая матрица разрешения могут по-прежнему быть хорошим описанием соответствующей структуры Земли или могут быть «плохими», вводящими в заблуждение, неадекватными и т. Д., в зависимости от проблемы. Однако это проблема с нашим выбором пространства модели и , а не с методом оценки матрицы разрешения.

Если затем мы пошагово уменьшаем размеры наших блоков, инвертируя на каждом шаге, инвертированная модель и соответствующая матрица разрешения постепенно станут более похожими на модели из полной инверсии с исходным размером блока. Нужно ли нам полностью уменьшать размер блока до исходного размера, прежде чем текущее решение будет по существу таким же (с точки зрения выводов о структуре Земли), что и исходное обращение с наименьшими блоками, зависит от характера проблемы. — конфигурация, данные и т. Д.При решении реальной проблемы, если при уменьшении размера нашего блока наступает момент, когда значительное уменьшение размера блока не приводит к значительному изменению свойств инвертированной модели и связанной с ней матрицы разрешения, то в этой точке мы, вероятно, сделаем вывод, что этого размера блока достаточно, и что дальнейшие инверсии с меньшим размером блока не требуются. Процесс уменьшения размеров блока и остановки, когда результат стабилизируется, можно рассматривать как аналогию с нашим применением подхода LSQR в том смысле, что мы пошагово увеличиваем количество степеней свободы в нашем модельном пространстве.

Можно возразить, что мы не обсуждаем ситуации, когда мы меняем размер блока нашей модели. Однако мы можем изменить «мысленный эксперимент» выше, рассмотрев случай, когда мы сохраняем размер ячейки одинаковым, но требуем взаимосвязи между параметрами модели (регуляризация, разложение по усеченным сингулярным значениям и т. Д.). Налагая ограничения, мы уменьшили истинное количество степеней свободы в модели и изменили результаты нашей инверсии, включая матрицу разрешения.

Таким образом, методы подпространства каким-то образом ограничивают пространство модели в зависимости от характера проблемы и информации в данных. Дело в том, что (в LSQR) у нас есть , ограничивающие размеры пространства модели (количество векторов), а не , как это было сделано в . Ограничивая таким образом пространство нашей модели, мы существенно переопределяем нашу модель. Как видно из ур. (3) матрица разрешения описывает в строгом математическом смысле «связь» между истинной землей и расчетными параметрами модели.Нам кажется, что прямо из этого следует, что использование одного подпространства для описания модели и чего-то еще для оценки разрешения может ввести в заблуждение. Мы не будем вычислять модель, используя один набор параметров модели, а затем анализировать разрешение, вычисленное с помощью гораздо большей сетки модели или другого набора параметров демпфирования или сглаживания. Такой подход фактически нарушил бы определение матрицы разрешения, подразумевая, что использование чего-либо, кроме того же подпространства для оценки разрешения, которое использовалось для вычисления модели, в значительной степени неверно.Правильно оцененная (подпространственная) матрица разрешения может рассматриваться как неотъемлемая часть решения.

На самом деле хорошее решение с точки зрения параметров модели, которые обеспечивают хорошее соответствие набору данных, не означает, что параметры модели не зависят друг от друга. Когда вектор в маленьком пространстве (измерениях) поворачивается к большему пространству, элементы вектора в большем пространстве неизбежно в некоторой степени коррелируют друг с другом. Два подобных решения, такие как в примере, показанном Deal & Nolet (1996), не означают, что эти два решения должны иметь одинаковые свойства.

92″ data-legacy-id=»ss9″> Выводы

Мы вывели формулы для расчета матриц разрешения и ковариации для решателя LSQR (уравнения 18–19), которые требуют лишь небольших изменений в компьютерном коде LSQR.

Самым большим преимуществом использования LSQR является то, что необходимо хранить только текущие векторы Ланцоша, что приводит к низким требованиям к памяти ЦП. Это преимущество теряется, если матрицы разрешения и ковариации вычисляются с большим номером итерации k . Кроме того, процедуры реортогонализации требуют дополнительных вычислительных затрат по сравнению с исходной процедурой LSQR (Paige & Saunders 1982a, b). Однако k обычно намного меньше, чем размеры пространства модели, и поэтому потребность в памяти для вычислений с LSQR меньше, чем для полноматричных обратных методов.Дополнительные вычислительные затраты на процедуру реортогонализации не являются чрезмерно высокими.

LSQR с ограниченным числом итераций соответствует перепараметризации пространства модели. Матрица разрешения R этого подпространственного решения может отличаться от такового для полного пространственного решения, но это правильная матрица разрешения для нашей параметризации подпространства. Матрица R предоставляет важную информацию о том, как следует интерпретировать нашу оценочную модель. Когда LSQR применяется к инверсии, следует тщательно рассмотреть подходящую регуляризацию и номер итерации.Несмотря на то, что мы не можем предоставить полные и конкретные критерии для оценки матрицы разрешения LSQR, в рамках рационального подхода к сложным процедурам инверсии мы предлагаем не только исследовать R , но и его изменения с номером итерации ( k ) следует изучить. Если R продолжает значительно меняться по мере продолжения итерации, то, вероятно, итерацию следует продолжить.

07″> Список литературы

1

,

1977

Определение трехмерной сейсмической структуры литосферы,

J. geophys. Res.

,

82

,

277

—

296

2

,

1968

Разрешающая способность общих данных о земле,

Geophys. J. R. astr. Soc.

,

16

,

169

—

205

3

,

1996

Трехмерная структура скоростей продольных и поперечных волн вулкана Редут, Аляска,

Дж.геофизики. Res.

,

101

,

8111

—

8128

6

,

1996

Комментарий к «Оценка разрешения и ковариации для больших обращений матриц» Дж. Чжана и Г. А. МакМечана,

Geophys. J. Int.

,

127

,

245

—

250

7

,

1993

Телесейсмическая скоростная томография с использованием метода ACH: теория и применение к исследованиям в континентальном масштабе, в

319

—

360

8

,

1988

Адаптация томографии обратной проекции к задачам времени прохождения сейсмических волн,

Дж.геофизики. Res.

,

93

,

1073

—

1085

10

,

1996

Вычислительно выполнимая матрица приближенного разрешения для обратных сейсмических задач,

Geophys. J. Int.

,

126

,

345

—

359

11

,

1985

Устранение неполадок или устранение неадекватных и зашумленных томографических систем,

J. Comp. Phys.

,

61

,

462

—

482

12

,

1993

Решение больших линеаризованных томографических задач, в

248

—

264

13

,

1990

Решение больших линейных обратных задач с помощью проекции,

Geophys.J. Int.

,

103

,

565

—

568

14

,

1999

Явные приблизительные выражения для разрешения и апостериорной ковариации массивных томографических систем,

Geophys. J. Int.

,

138

,

36

—

44

15

,

1981

Процедура регуляризации бидиагонализации для крупномасштабной дискретизации некорректных задач,

SIAM J.Sci. Стат. Комп.

,

2

,

474

—

489

16

,

1971

Вычисление собственных значений и собственных векторов очень больших разреженных матриц, 17

,

1982

a

LSQR: алгоритм для разреженных линейных уравнений и разреженных наименьших квадратов,

ACM Trans. Математика. Программное обеспечение

,

8

,

43

—

71

18

,

1982

b

LSQR: разреженные линейные уравнения и задачи наименьших квадратов,

ACM Trans.Математика. Программное обеспечение

,

8

,

195

—

209

19

,

1979

Алгоритм Ланцоша с выборочной ортогонализацией,

Math. Комп.

,

33

,

217

—

38

20

,

1993

Итерационные стратегии для нелинейной томографии во времени пробега с использованием данных о глобальных землетрясениях, в

190

—

226

21

и другие. и другие. ,

1988

Алгоритмы визуализации, точность и разрешение в томографии с временной задержкой, дюйм

155

—

188

22

,

1987

Численное решение больших разреженных линейных алгебраических систем, возникающих из томографических задач, в

49

—

84

23

,

1998

Разрешение сейсмической анизотропии: методы разреженных матриц для обратных геофизических задач,

Геофизика

,

63

,

970

—

983

24

,

1999

Комментарий к «Явным приблизительным выражениям разрешения и 25

,

1995

Оценка разрешения и ковариации для больших инверсий матриц,

Geophys.J. Int.

,

121

,

409

—

426

26

,

1996

Ответ на комментарий М. М. Дила и Г. Нолета «Оценка разрешения и ковариации для больших инверсий матриц»,

Geophys. J. Int.

,

127

,

251

—

252

© 1999 РАН

State Resolution v2 для безнадежно нематематических

Итак, у вас нет докторской степени по математике, и вы хотите реализовать State Разрешение v2! Этот документ направлен на демистифицировать не только , как , но и , почему разрешения государственных конфликтов в Матричная комната версий 2 и более поздних, а также немного псевдокода для демонстрации реализация.

В Matrix комнаты не принадлежат определенному серверу, а реплицируются на всех серверах, участвующих в данной комнате. В результате каждый сервер в комнате должен иметь возможность самостоятельно определять состояние комнаты и все серверы в комнате должны иметь возможность прибыть, насколько это возможно, в одно и то же состояние при этом. Это то, что позволяет комнате «выглядеть» одинаково для все пользователи, независимо от домашнего сервера, с которого они подключаются.

Разрешение состояния — это принятие двух или более различных наборов состояний и выработка окончательного согласованного состояния, которое мы считаем правдивым.Идея в том, что все домашние работники согласятся, как выглядит состояние данной комнаты, следуя тем же алгоритмам разрешения состояний.

При разрешении состояния мы придерживаемся следующих рекомендаций:

1. Более высокие уровни мощности должны иметь приоритет над более низкими, например действия администратора должны отменять действия модератора
2. По возможности более ранние события должны обрабатываться раньше, чем более поздние

Стоит отметить, что такие понятия, как «раньше» и «позже», являются сложными определить в матрице, и это важная часть того, что делает состояние разрешение сделать сложно.В State Res v2 у нас есть пара новых концепций для определения, когда событие «раньше» или «позже», чем другое событие — эти описаны в разделах ниже, посвященных заказам.

Определение состояния

Прежде всего, событие состояния — это событие матрицы, которое содержит state_key . В ключ состояния определяет , к чему применяется состояние (или часто является пустой строкой, если состояние должно распространяться на всю комнату). Примеры государственных мероприятий: м., Комн. Создать , м.room.join_rules , m.room.power_level , m.room. member и т. д.

Учитывая, что события состояния также являются частью истории помещения, состояние может быть разные в разные моменты времени. Поэтому состояние на конкретном мероприятии содержит снимок всех событий состояния, которые применяются к комнате во время это данное событие и не будет включать государственные события, которые произошли после него. В случае государственных событий, состояние на момент данного события включает изменения в состоянии, предусмотренном мероприятием.

Кортеж состояний — это кортеж (тип события, ключ состояния) . Например:

• ("m.room.power_levels", "") для уровней мощности комнаты
• ("m.room.join_rules", "") для правил объединения комнат
• ("m .room.member "," @neilalexander: matrix.org ") для комнаты neilalexander членство

Каждое событие состояния пытается обновить (тип события, ключ состояния) -> событие ключ-значение отображение в данной комнате, что позволяет хранить данные «ключ-значение» для каждой комнаты.

Определение управляющих событий и событий нормального состояния

В дополнение к вышесказанному мы также определяем управляющих событий как подмножество назначать события, которые специально имеют право добавлять или удалять способности из другой пользователь. Это:

• Установка уровней мощности в помещении: m.room.power_levels , где state_key равно ""
• Установка правил объединения комнат: m.room.join_rules , где state_key равно ""
• Удаление пользователя: m.room.member с "оставить" содержимое , но где отправитель (администратор / мод) не соответствует state_key (выгнанный пользователь)
• Запрет пользователя: m.room. member с «запретить» содержимое , но где отправитель (администратор / мод) не соответствует state_key (забаненный пользователь)

Любое событие состояния , которое не соответствует приведенному выше определению, вместо этого классифицируется как обычное государственное мероприятие.К ним относятся, например:

• Настройка темы комнаты: m.room.topic , где state_key равно ""
• Настройка аватара комнаты: m.room.display_avatar где state_key равно ""
• Присоединяющиеся или уходящие пользователи: м.комн. член с "присоединиться" или "покидать" содержимое, в котором отправитель равен state_key

Конфликтные и неконфликтные наборы состояний

Конечная цель разрешения состояний — принять конфликтующих входных данных и выдавать неконфликтный выход и делать это согласованно, чтобы все серверы согласятся на то же состояние.Фактически, нам, возможно, дали несколько наборы состояния за счет вилок в комнате и, когда мы объединяем их вместе, мы может иметь несколько разных значений для одного или нескольких заданных кортежей состояний. Цель состоит в том, чтобы гарантировать, что наше конечное состояние содержит только одно значение для каждого государственный кортеж.

Форки обычно возникают, когда серверы, которые участвуют в комнате, отсутствуют больше в состоянии держать друг друга в курсе по федерации. Возможно, что пользователи на разных серверах будут продолжать отправлять любое количество событий в комната, включая события состояния, в результате чего состояние дрейфует между этими серверами.Когда серверы снова смогут объединяться, то есть после того, как сетевое подключение будет восстановлено, то мы можем разрешить конфликтное и неконфликтное состояние путем слияния вилки.

Конфликтное состояние возникает, когда:

• У нас есть более одного различных значений для данного кортежа состояния в каждой вилке
• У нас есть только одно значение для данного кортежа состояния, но это произошло только в одном fork, а не другое

Неконфликтное состояние возникает, когда:

• У нас есть только одно значение для данного кортежа состояния, потому что оно одинаково во всех вилки
• У нас есть только одно значение для данного кортежа состояния, потому что это произошло раньше вилка

События во входном наборе, которые неконфликтны , считаются правдивыми, поэтому кроме ожидания, что они пройдут аутентификацию, мы больше не делаем Государственное постановление по ним. неконфликтное событие всегда будет появиться в окончательное разрешенное состояние.

События во входном наборе, которые конфликтуют , противоположны — для начала, у нас есть несколько событий, претендующих на разные ценности, и мы не знаем, какие полагать. Мы выполняем в отношении них государственное разрешение, чтобы решить, какие из этих значений мы хотите выбрать, и только выбранных значений появляются в окончательном разрешенном государственный.

Так как мы хотим выполнить разрешение состояния только на конфликтующем наборе , начнем с работа с набором входных событий, включая их события авторизации и сортировку их в конфликтующих и неконфликтных сегментов :

  var Conflicted_events: list (event)
var unflicted_events: list (event)  

Частичное состояние

Мы называем состояние частичным , когда мы еще не завершили состояние алгоритм разрешения, поэтому результат неполный.На первом этапе частичное состояние равно неконфликтному состоянию:

  var partial_state: map (event_type -> map (state_key -> event))

для каждого Unflicted_events как e:
    partial_state [e.event_type ()] [e.state_key ()] = e  

Позже, разрешенные блоки состояний из конфликтного состояния будут наслоены на частичное состояние, что в конечном итоге приводит нас к полному разрешенному состоянию .

Решенное состояние

Окончательное разрешенное состояние комнаты определяется следующими действиями:

1. Начиная с неконфликтного состояния в качестве нашего «базового уровня»
2. Разработка последовательности управляющих событий с использованием обратного топологический упорядочивание, а затем распределение по уровням на
3. Разработка последовательности событий нормального состояния с использованием основного упорядочивания и затем наслоение их на
4. Повторное применение любых неконфликтных ключей состояния , которые могли быть перезаписаны в предыдущие шаги

Различия аутентификации

Теперь, когда у нас есть набор из конфликтующих событий , нам также необходимо убедиться, что мы иметь достаточно информации для выполнения проверок аутентификации, независимо от того, какое событие мы в конце концов решите.

Например, представьте случай, когда Алиса дает некоторую власть Бобу (в событии A ), Боб дает власть Чарли (в событии B ), а затем Чарли меняет запрет. уровень (в событии C ):

Однако в другой вилке известно событие A (значит, Боб получил питание от Алиса), а B не было, поэтому в вилке Чарли так и не получил питание и поэтому не получил разрешения на изменение уровня бана. Когда две вилки сходятся, нам нужно знать о B , чтобы успешно авторизовать С .

Разница аутентификации , таким образом, содержит все события аутентификации, которые не были общими для обе вилки — если событие аутентификации появляется только в одной вилке, но не в другой, то это событие аутентификации должно появиться в разнице аутентификации :

  var auth_difference: list (event)
var auth_sets: map (fork_id -> list (event))

для каждого конфликтующего_события как e:
    найдено = правда
    для каждого auth_sets как auth_set:
        если e не в auth_set:
            найдено = ложь

    если не найден:
        auth_difference.append (e)  

Полный конфликтующий набор фактически представляет собой конфликтующие события в сочетании с разница в авторизации:

  var full_conflicted_set: list (event)

full_conflicted_set = Conflicted_events + auth_difference  

Обратный топологический порядок управляющих событий

Теперь, когда мы вычислили полный конфликтующий набор , который также включает auth разница , теперь мы можем приступить к определению порядка, в котором мощность была отдано или отнято у конкретных пользователей.

При разрешении государственных конфликтов важно выяснить, у кого на самом деле была власть делать определенные вещи в определенный момент времени. Работа над этим для контроля события имеют приоритет над установкой порядка событий нормального состояния — те будут отсортированы по уровням мощности с этого шага.

Для отработки таймлайна управляющих событий реализована обратная топологическая упорядочение, что приводит к списку событий, в которых порядок гарантирует, что события auth всегда предшествуют событиям, которые на них ссылаются.Закончено с использованием адаптации алгоритма Кана.

Алгоритм Кана

Поскольку цепочка аутентификации события формирует ориентированный ациклический граф (DAG), мы можем сказать что каждое событие аутентификации является «узлом» на графике, и каждое отношение между двумя события — это «край». В нашем случае два узла в auth DAG связаны отношениями когда одно событие ссылается на другое событие как на событие аутентификации.

Точнее, мы бы сказали, что событие, которое относится к другим событиям авторизации имеет один или несколько исходящих ребер и это событие, на которое полагаются другие события имеет один или несколько входящих ребер .

Это позволяет нам сделать пару утверждений: что событие, не имеющее входящие ребра произошли совсем недавно, и событие, у которого нет исходящих ребер произошло не так давно.

В нашем случае алгоритм Кана работает с тремя основными компонентами:

1. Несортированный входной список событий, включая события аутентификации
2. Карта, где мы подсчитываем, сколько входящих ребер имеет каждый узел
3. Сортированный выходной список события, фактически результат алгоритма

Предполагая следующие структуры данных, мы можем заполнить карту событий и входящие ребра с начальными значениями:

  var output_events: list (event)
var event_map: map (event_id -> событие)
var incoming_edges: map (event_id -> integer)

для каждого full_conflicted_set как e:
    event_map [e.event_id] = e
    incoming_edges [e.event_id] = 0  

Специфичные для матрицы детали нашей реализации алгоритма Кана лежат в тай-брейк между событиями. Тай-брейк гарантирует, что мы получим детерминированный заказа и что мы также с самого начала соблюдаем наши два правила: всегда будем стараться отдавать предпочтение событиям от более сильных, и мы всегда будем стараться для обработки более старых событий в первую очередь. При сортировке можно утверждать, что x на выполнение следующих тестов по порядку:

1. Эффективный уровень мощности при x больше, чем эффективный уровень мощности at y
2. Отметка времени сервера происхождения события x меньше, чем источник события отметка времени сервера y (то есть событие x старше, чем y )
3. Идентификатор события x меньше, чем идентификатор события y , как вычислено лексикографическое сравнение в качестве запасного варианта

Чтобы гарантировать, что алгоритм является детерминированным (т. порядок) для данного набора входов, мы должны убедиться, что карта входящих ребер был отсортирован с использованием приведенных выше правил, прежде чем мы что-либо с ним сделаем:

  func sorted_incoming_edges () возвращает список (событие):
    sort incoming_edges, где x  y.power_level или
        x.origin_server_ts  

После сортировки входящих ребер выполните итерацию по входному списку, чтобы подсчитайте, сколько входящих ребер имеет каждое событие, и обновите карту входящих ребер с этими значениями:

  для каждого input_events как e:
    для каждого e.auth_events как:
        incoming_edges [a.event_id] + = 1  

Затем найдите события, у которых нет входящих ребер, и вставьте их в начало списка вывода - обратите внимание, что мы отличаемся от чистой реализации Алгоритм Кана здесь, поскольку мы специально требуем, чтобы карта входящих ребер была отсортировано (как указано выше):

 , а len (incoming_edges)> 0:
    для каждого sorted_incoming_edges () в качестве идентификатора подсчитать:
        если count == 0:
            output_event.prepend (event_map [id])

            для каждого event_map [id] .auth_events как auth_event:
                input_edges [auth_event.event_id] - = 1

            remove (incoming_edges, id)  

Каждый раз, когда мы добавляем узел в выходной список, мы можем «удалить» его исходящий края. Это означает, что каждое событие аутентификации, на которое ссылается это событие, имеет на один меньше входящий край. Когда он исчерпан, мы также удаляем событие из входящую карту краев, чтобы мы не пытались ее обработать снова.

Теперь мы повторяем процесс непрерывно, пока алгоритм не исчерпает вся карта входящих ребер.Как только карта станет пустой, все края будут удалены, и самые ранние события появятся в начале списка вывода.

Список вывода теперь отсортирован таким образом, что все упомянутые события теперь появляются перед события, которые относятся к ним. Он отсортирован в обратном топологическом порядке .

Итеративное применение разрешенных управляющих событий

Теперь, когда наши управляющие события отсортированы в обратном топологическом порядке, где первые события в списке являются "самыми старыми", теперь мы можем начать наложение слоев эти разрешенные управляющие события для построения частичного состояния.

Чтобы создать частичное состояние, начните с самого старого события и выполните цикл список, выполняя проверки авторизации для каждого событие с помощью текущий partial_state как разрешенный набор событий аутентификации. Мы определяем этот процесс как функция auth_against_partial_state .

Ожидается, что partial_state будет пустым списком для первой итерации, так как самое старое событие (которое является событием создания комнаты) не требует событий аутентификации. Частичное состояние (и, как следствие, выбор разрешенных событий аутентификации) будет растут с каждой итерацией.

Если событие проходит проверку аутентификации, обновите частичное состояние, чтобы включить только что авторизованное событие перед переходом к следующей итерации:

  для каждого output_event как e:
    если auth_against_partial_state (e):
        partial_state [e.event_type] [e.state_key] = e  

События, которые не проходят проверку аутентификации, должны игнорироваться и не должны распространяться. в частичное состояние.

Создание основной линии уровня мощности

После того, как управляющие события были применены к частичному состоянию, оставшаяся часть события нормального состояния должны быть упорядочены и обработаны в соответствии с порядком следования события авторизации их уровня мощности.Это делается с помощью техники, называемой mainline. заказывая .

Уровень мощности магистраль создается по пути уровня мощности события, начиная с разрешенного события m.room.power_level из частичного состояние, вернемся к тому моменту, когда комната была создана:

  var resolved_power_level_event: partial_state ["m.room.power_level"] [""] как событие
var power_level_mainline: список (событие)

func mainline_iterate (e как событие):
    power_level_mainline + = e
    для каждого е.auth_events как auth_event:
        если auth_event.event_type == "m.room.power_level":
            mainline_iterate (auth_event)  

Мы называем период времени между любыми двумя заданными событиями уровня мощности эпоха .

На иллюстрации ниже «разрешенное» событие - это событие, которое появляется в частичное состояние из предыдущего раздела.

Основной порядок событий нормального состояния

Так как основной поток будет упорядочен в зависимости от того, когда изменяется уровень мощности произошло, а другие события состояния используют события уровня мощности как события аутентификации, это можно отсортировать порядок событий нормального состояния в зависимости от того, какая магистральная мощность событие уровня, к которому они наиболее близко относятся, или, по определению, эпоху события произошло в.

Обратите внимание, что могут появиться события, относящиеся к событиям уровня мощности, которые не появляются. в основной линии, в этом случае необходимо перейти через уровень мощности события итеративно, пока вы не встретите тот, который находится на основной линии. это называется ближайшим событием основной линии :

  func get_closest_mainline_event (e как событие) возвращает событие:
    var closest_mainline_event: событие

    func closest_iterate (e как событие):
        если e в power_level_mainline:
            closest_mainline_event = e
        еще:
            для каждого е.auth_events как auth_event:
                если auth_event.event_type == "m.room.power_level":
                    closest_iterate (auth_event)

    closest_iterate (e)
    return closest_mainline_event  

На следующем рисунке Событие B происходит в более позднюю эпоху, чем Событие A как ближайшее основное событие, на которое ссылается Событие A является более ранним (ближе к событию создания комнаты), чем ближайшее основное событие, на которое ссылается по Событие B :

Для сортировки событий мы используем метод, очень похожий на тот, который используется в обратном порядке. топологическое упорядочение управляющих событий, только вместо первоначальной сортировки по уровня мощности, мы используем положение ближайшего события уровня мощности магистрали на основная линия.При сортировке вы можете утверждать, что x , запустив следующие тесты по порядку:

1. Ближайшее событие основной линии к x находится позже в основной линии, чем ближайшее событие mainline до y (например, на диаграмме выше A меньше чем B , поскольку B относится к более позднему событию уровня мощности магистрали)
2. Временная метка сервера происхождения события x меньше, чем источник события отметка времени сервера y
3. Идентификатор события x меньше, чем идентификатор события y , как вычислено лексикографическое сравнение

Чтобы алгоритм был детерминированным (т. порядок) для заданного набора входов, мы гарантируем, что события нормального состояния имеют отсортировано с использованием вышеуказанных критериев:

  func sorted_normal_state_events () как список (событие):
    сортировать normal_events, где x  

В случае, если несколько событий-кандидатов относятся к одной и той же основной мощности level, оставшиеся два теста позволят сортировке быть детерминированной.

Итеративно применять разрешенные события нормального состояния

Теперь, когда наши события нормального состояния были отсортированы в основной порядок, где первые события в списке являются "самыми старыми", теперь мы можем начать накладывать их разрешены события нормального состояния поверх частичного состояния .

Как и в случае с управляющими событиями, каждое событие нормального состояния должно быть авторизовано. против частичного состояния, перед применением действительных событий к частичному state:

  для каждого sorted_normal_state_events () как e:
    если auth_against_partial_state (e):
        partial_state [e.event_type] [e.state_key] = e  

Любое событие, не прошедшее аутентификацию в текущем частичном состоянии, следует игнорировать и не должны применяться к частичному состоянию.

Повторно применить неконфликтное состояние

Теперь, когда все события из исходного конфликтующего набора были разрешены и применив, мы завершаем последний проход по частичному состоянию, повторно применяя исходный неконфликтный набор.Обычно ничего из противоречивого набора должен перезаписывать что-либо из неконфликтного набора, но подтягивать события аутентификации может внести дополнительное состояние.

Повторно примените события неконфликтного состояния к частичному состоянию, чтобы завершить состояние:

  для каждого Unflicted_events как e:
    partial_state [e.event_type] [e.state_key] = e  

На этом этапе частичное состояние теперь эффективно завершено , поэтому теперь представляет окончательное разрешенное состояние.

Завершение

Теперь, когда вы выполнили все вышеперечисленные шаги, вы успешно реализовано Государственное разрешение v2! Если у вас есть какие-либо вопросы, не стесняйтесь присоединяйтесь к нам в Homeserver Канал разработчиков.

Дополнительная литература:

Матрица разрешения

- Изучение науки и экспертов

исследование границ синтетических полимеров эумеланина с высоким разрешением

Матрица масс-спектрометрия с лазерной десорбцией и ионизацией с ассистированной лазерной десорбцией

Журнал масс-спектрометрии, 2012 г.

Соавторы: Саманта Реале, Марчелло Кручианелли, Алессандро Пеццелла, Марко Дисчиа, Франческо Де Анжелис

Абстрактный:

Новые тенденции в материаловедении и нанотехнологиях стимулировали растущий интерес к нерастворимым биополимерам эумеланинового черного цвета, полученным путем катализируемого тирозиназой окисления тирозина через 5,6-дигидроксииндол (DHI) и его 2-карбоновую кислоту (DHICA).Эффективные антиоксидантные и фотозащитные действия, связанные с особыми оптоэлектронными свойствами, признаны важными функциями макромолекул эумеланина в пигментной системе человека и млекопитающих, что делает их уникальными кандидатами для реализации инновационных биовдохновляемых функциональных мягких материалов с физико-структурной структурой. химические свойства. Беспрецедентный прорыв в механизме накопления синтетического эумеланина стал результатом детального исследования окислительной полимеризации DHI и его N-метильного производного (NMDHI) с помощью линейной и рефлектронной масс-спектрометрии с лазерной / десорбционной ионизацией Matrix .Были раскрыты регулярные коллекции олигомеров с возрастающей массой, охватывающие весь диапазон m / z до 5000 Да (> 30-мер) и 8000 Да (> 50-мер) для двух строительных блоков, соответственно. Это первый случай, когда полимеризация дигидроксииндолов in vitro с образованием синтетических эумеланинов исследуется вплоть до ее высоких пределов по массе, давая в то же время информацию о способе полимеризации, следует ли она по ступенчатой ​​схеме (что является заключением в нашем случае ) или определение последовательности ставок малых предприятий.Т А $$ Вопрос

Теперь предположим, что я хочу понять разрешение параметров модели, предоставленных подмножествами исходных наблюдений. Мотивация здесь в том, что я хочу знать, помогают ли определенные подмножества моих данных определять определенные параметры модели или нет. Предположим, я разбиваю свой вектор наблюдения как $$ у = \ pmatrix {y_1 \\ y_2} $$ и аналогично, $$ A = \ pmatrix {A_1 \\ A_2} $$ и я хочу знать, какое разрешение модели обеспечивают $ y_1 $ и $ y_2 $ по отдельности.T A_i $

Итак, какой из этих подходов (если есть) правильный?

В качестве побочного вопроса, во многих текстах обсуждаются матрицы разрешения, но я не нашел ссылки, в которой обсуждается этот момент разделения данных на подмножества, поэтому, пожалуйста, предоставьте ссылку, если вы знаете такую.

Что такое разрешение матрицы: , , MTF, , — funPhoto