Цифры золотого сечения: Золотое сечение и пропорции Фибоначчи

Золотое сечение: применение правила

Что это? Золотое сечение – это математическая формула, соотношение двух неравных чисел. Его еще называют божественной пропорцией. Правило третей, золотая спираль – всё это визуальное отображения этого универсального правила.

Где используется? Золотое сечение применимо везде, где есть место графике, рисунку, фотографии. Сфера дизайна – не исключение. Конечно, это не единственное правило гармонии, но, пожалуй, самое известное.

В статье рассказывается:  

1. Что такое золотое сечение
2. История золотого сечения
3. Золотое сечение Фибоначчи
4. Золотое сечение в природе
5. Золотое сечение в фотографии
6. Золотое сечение в дизайне

7. Пройди тест и узнай, какая сфера тебе подходит:
   айти, дизайн или маркетинг.

   Бесплатно от Geekbrains

Что такое золотое сечение

Это отношение двух разных по величине чисел, когда большее из них относится к меньшему так же, как и общая их сумма относится к большему. Соотношение золотого сечения равняется около 1,618. Его обозначают греческой литерой Ф (читается как «фи») в честь древнегреческого скульптора Фидия, который применял эти пропорции при создании храма Парфенон.

Одним из популярных способов представления золотого сечения является прямоугольник с соотношением сторон 62 на 48 и построенной внутри спиралью.

Что такое золотое сечение

История золотого сечения

Согласно истории, данное понятие для научного использования ввел Пифагор, философ и математик Древней Греции. Предполагается, что ученый позаимствовал знание у жителей Египта и Вавилонии.

Если посмотреть на соотношение сторон пирамид, храмов и предметов домашнего обихода у древних египтян, а также на украшения из саркофага царя Тутанхамона, то очевидно, что все они создавались по принципу золотого сечения.

Архитектор из Франции Ле Корбюзье заметил, что рельеф храма египетского правителя Сети I, как и в рельефе изображения царя Рамзеса, тоже создавались по этому правилу.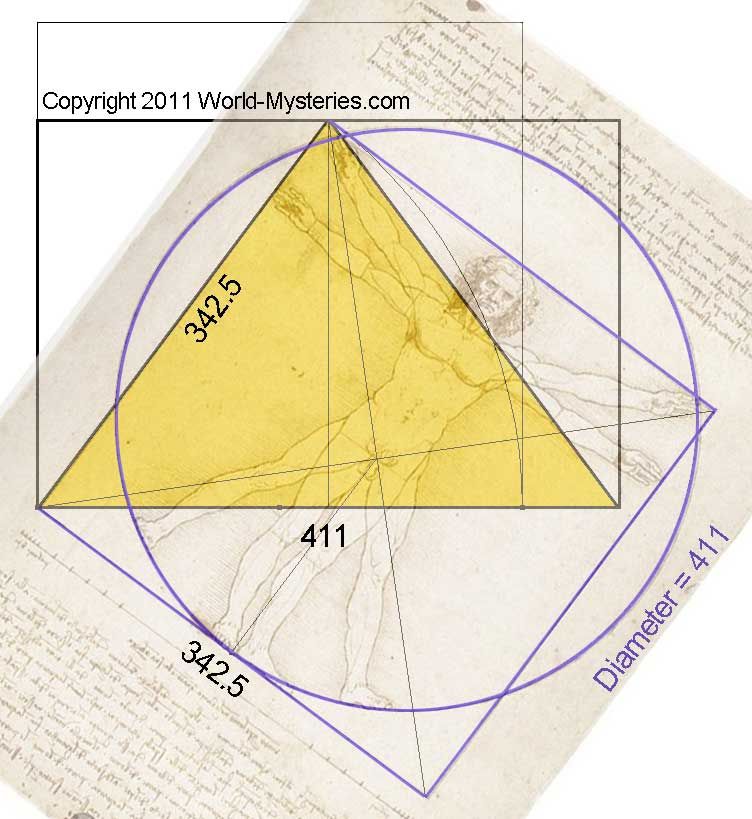 Соотношения золотого деления были обнаружены и в рельефе гробницы, на котором изображен высокопоставленный чиновник Хесира.

Жители Древней Греции хорошо владели геометрией. Арифметике, например, они учились по геометрическим фигурам уже в детстве. А квадрат Пифагора и его диагональ служили основой для создания динамических прямоугольников.

Сам термин «золотое сечение» впервые ввел в обиход математик из Германской империи Мартин Ом в 19 веке. До того времени правило имело название «божественная пропорция».

Из-за уникальных свойств она пользовалась большой популярностью. Например, в эпоху Возрождения число 1,618 было идеальным при выборе размера. Его часто применяли для создания картин и книг. А линия талии в то время считалась границей золотого сечения в теле человека.

Многие люди и сегодня уверены, что соблюдение данного правила считается залогом красоты и внешней гармонии. Эту тему активно обсуждают пластические хирурги.

Золотое сечение Фибоначчи

В конце 12 века математик из Италии Леонардо Пизанский, известный по прозвищу Фибоначчи, открыл последовательность чисел, связанных с золотой пропорцией. Суть в том, что если взять любые 2 числа из ряда итальянского математика, то соотношение между ними почти такое же, как на примерах золотого сечения. Особенность последовательности Фибоначчи в том, что каждое новое число всегда равняется сумме 2-х предыдущих. Пример: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д.

По мере увеличения ряда, отношения между числами становится все ближе к 1,618. Разделив, к примеру, 8 на 5, мы получим около 1,6. А соотношение 34 на 21 уже дает 1,619, если округлить. Каждое число ряда является логичным в последовательности Фибоначчи.

Такие соотношения из-за приближения к показателю золотого деления можно использовать при построении золотого прямоугольника. Эта фигура считается одной из самых гармоничных в геометрии, что позволяет применять пропорции Пифагора в любом виде изобразительного искусства.

Золотой прямоугольник тесно связан с золотой спиралью, которая строится методом размещения смежных между собой квадратов по алгоритму Фибоначчи.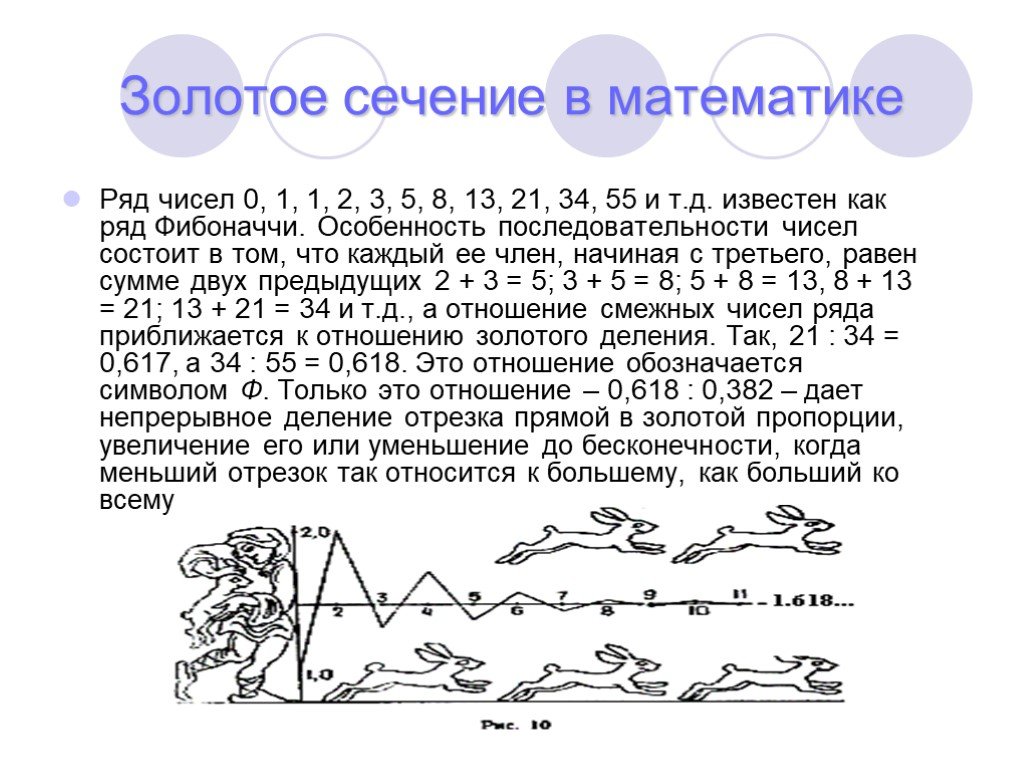

Золотое сечение в природе

Пропорции золотого сечения можно наблюдать во всех природных и научных проявлениях. В представленном списке мы рассмотрим наиболее удивительные случаи.

• Лепестки у цветов. Нередки случаи, когда их количество соответствует числовому ряду «Ф». По мнению Дарвина, все лепестки растений располагаются так, чтобы получать как можно больше солнечного света и остальных необходимых для жизни ресурсов.
• Головки у семян. Во многих случаях семена цветов начинают расти посередине головки семени и появляются снаружи, заполняя собой пространство. В качестве примера можно привести семена подсолнуха.
• Шишки у сосен. Семена, находящиеся в их семенных коробочках, произрастают вверх противоположно друг другу по спирали. Расстояние между ними обычно совпадает с соотношениями чисел из последовательности Фибоначчи.
• Ветки у деревьев. На примере их формирования и расщепления также можно заметить правило золотого ряда.
  То же самое относится и к развитию корневых систем у растений и водорослей.
• Раковины. Большинство из них демонстрируют нам правило золотого сечения. Например, это можно сказать об улитках и наутилусах.

Золотое сечение в природе

• Спиральные галактики. Млечный Путь содержит в себе несколько рукавов, представленных в виде изогональных спиралей с шагом около 12 градусов. Их форма соответствует форме золотой спирали, при том над каждой такой галактикой можно начертить золотой прямоугольник.
• Ураганы. В большинстве случаев, изнутри они устроены согласно последовательности ряда «фи».
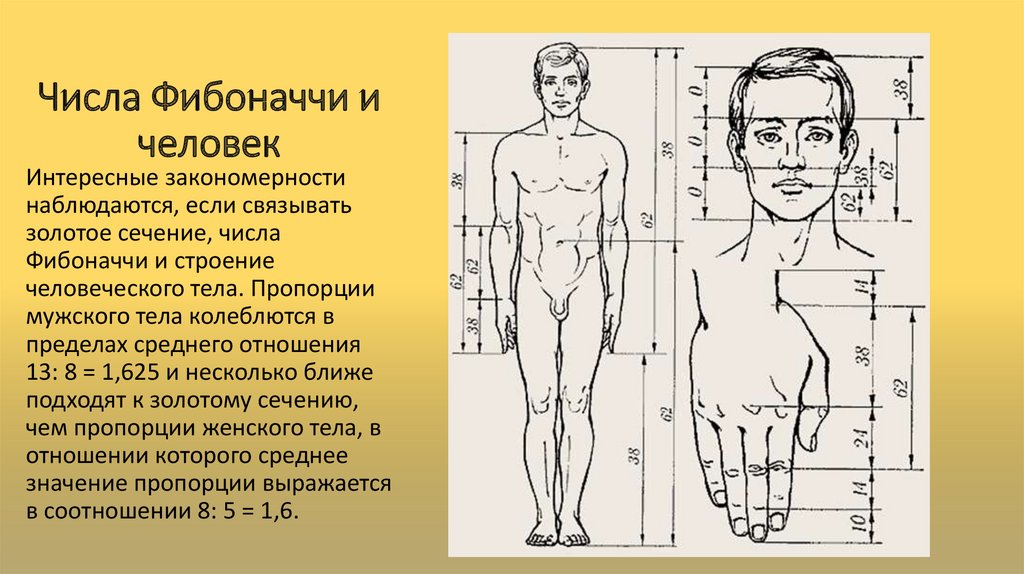
• Пальцы на руках у людей. Все участки пальцев от начала основания и до запястья увеличивается в соотношении по Фибоначчи.
• Тела людей и животных. Расстояние у людей от пупка до пола, а также от темени и до пупка — это яркий пример закона золотого сечения. Помимо человека такую пропорцию можно наблюдать и у других организмов (например, у дельфинов и пчел).
• Молекулы ДНК. Все они содержат соотношение 34 на 21 ангстрем в каждом полном спиральном цикле. А вы уже знаете, что эти цифры — часть ряда Фибоначчи.

Топ-30 самых востребованных и высокооплачиваемых профессий 2023

Поможет разобраться в актуальной ситуации на рынке труда

Подборка 50+ ресурсов об IT-сфере

Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT

ТОП 50+ сервисов и приложений от Geekbrains

Безопасные и надежные программы для работы в наши дни

pdf 3,7mb

doc 1,7mb

Уже скачали 20486

Как мы видим, примеров, где можно увидеть пропорции и соотношения по принципу золотого правила, довольно много. Помимо случаев, описанных выше, 1,618 постоянно встречается в точных науках, биологии и других областях жизни. Поэтому свое альтернативное название — божественное сечение, правило полностью оправдывает.

Ведь материальный мир словно был создан по этому закону.

Золотое сечение в фотографии

Гармоническая пропорция напрямую связана с правилом третей — другой неотъемлемой схемой для работы с визуалом. По сути, оно продолжает золотое сечение так же, как, например, фотография рождается из художественного творчества.

Основное различие заключается в соотношении сторон. Так, в принципе третей кадр разделяется на 3 одинаковые части, а в божественной пропорции он делится на 1:0.618:1.

Отсюда следует, что правило третей можно назвать более простой версией золотого сечения, но полностью рабочей.

Например, сегодня большинство камер, в том числе и в смартфонах, имеет разлинованную сетку третей, что позволяет пользователям гармонично выстраивать композицию из фото и видео.

Чем следует руководствоваться при съемке?

• Точки пересечения. Благодаря размещению нужного объекта по линиям, сделать снимок будет намного удобнее.
• Диагональная композиция. Линию можно прочертить самостоятельно из верхнего угла кадра в нижний, а можно использовать объекты, находящиеся в этой последовательности, которые формируют эту линию. Наличие разных диагоналей позволяет получить динамичный кадр. Восходящая, например, из правого нижнего угла в левый верхний придаст фотографии веселое настроение, а нисходящая — грустное.
• Пропорции. Чаще всего это относится к взаимосвязи объектов на нескольких планах снимка. Это тоже вариант золотого сечения, только представленный в соотношении объектов. Например, на заднем плане к большему объекту на переднем плане (либо наоборот).
• Линия горизонта. Когда вы делаете снимок на природе либо в городской инфраструктуре, нужно расположить горизонтальную линию кадра на одной из горизонтальных линий третей. То же самое относится и к общему плану фотографии/видео. Это даст более качественный результат.
• Правило «воздуха». Не забывайте про свободные участки между объектами. Если вы делаете фотографию человека, то оставьте немного пространства от его головы до границы кадра. А в ситуации, когда он смотрит налево, разместите человека по правым точкам пересечения линий (верно и обратное).

Золотое сечение в дизайне

Божественная пропорция делает современный дизайн более упорядоченным. Легкий и быстрый способ использования этого — умножить размер одного элемента на 1,618. Результат покажет, каким должен быть размер следующего объекта.

Только до 24.04

Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы

Список документов:

Тест на определение компетенций

Чек-лист «Как избежать обмана при трудоустройстве»

Инструкция по выходу из выгорания

Чтобы получить файл, укажите e-mail:

Подтвердите, что вы не робот,
указав номер телефона:

Уже скачали 7503

Применение формулы золотого сечения в типографике

Определяющими факторами в данной области являются 3 составляющие: размер шрифта, ширина линии и высота строки.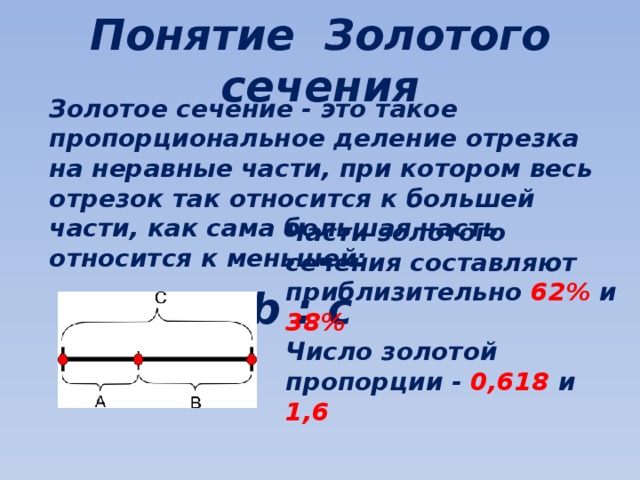 Их необходимо подбирать в правильных пропорциях.

Увеличивая и уменьшая шрифт, а также ширину текста, можно определить, какую высоту следует задать буквам. Установлено, что оптимальным для удобства читателей количеством является 70-80 символов на строку. Когда длина текста превышает этот показатель, его читабельность сильно снижается.

Для примера возьмем текст из 3 строк и определим в нем 3 части: «А», «Б» и «В». Допустим, строка «В» содержит меньше ценной информации, чем «А» и «Б». В связи с этим, текст внутри строки «В» должен иметь шрифт размером 10. Чтобы установить размер контента на строке «Б» (второй по значимости контента), надо умножить 10 на 1,618.

В разработке логотипов

Большинство популярных брендов, например, «Твиттер», «Эппл» и «Пепси», применяют знания божественного сечения, когда создают фирменный логотип.

Поэтому вы тоже можете пользоваться правилом чисел «Ф» при создании сетки. Полученный результат станет вашей опорой в разработке графического рисунка.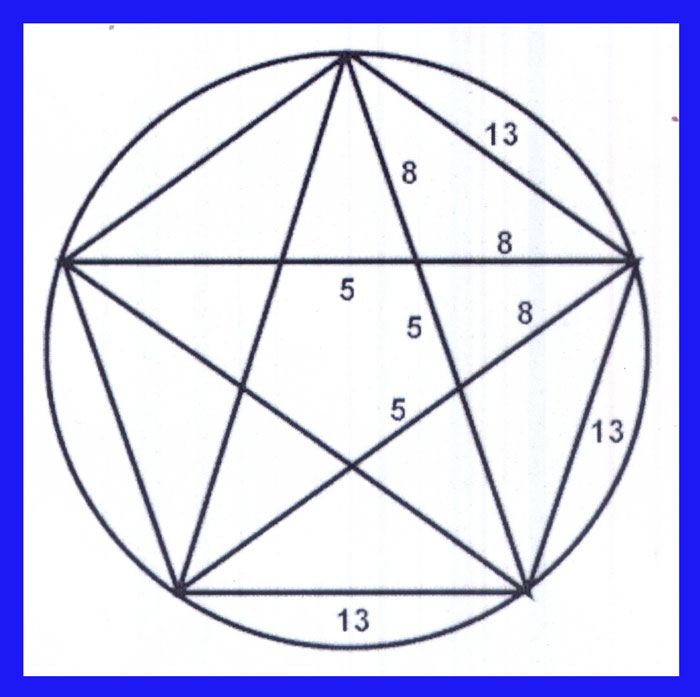

Золотое сечение в архитектуре

Зодчие прошлого применяли принцип божественного деления при создании памятников. Мавзолей-мечеть Тадж-Махал, например, относится к одному из 7 чудес света. Когда его возводили, мастера пользовались правилом золотого сечения.

Золотое сечение в архитектуре

Применение этого знания в современной архитектуре дает возможность добиться баланса между шириной и высотой сооружения. Популярным методом построить гармоничное здание является использование свойств золотого прямоугольника.

Стоит добавить, что золотое сечение дает возможность творить разнообразные формы. При их создании нет необходимости строго следовать прямоугольной структуре. Золотое деление позволяет дизайнерам применять полученные формы как основу для работы.

Разработка проектов и формирование макетов

Чтобы сделать макеты качественными, нужно учесть 2 главные составляющие: отдельные визуальные элементы и как они будут связаны между собой.

Есть много способов формирования макетов.

Например — расположение «Z». Оно дает увидеть путь, по которому проходит посетитель на веб странице, а также схему того, как он смотрит на элементы.

Еще одно востребованное правило компоновки — это применение золотой спирали. Она более эффективно, если в дизайне достаточно много элементов, различающихся между собой, но предназначенные для расположения на одном макете. Благодаря использованию правил сечения внимание посетителей ненавязчиво, но эффективно притягивается к середине спирали, в которой можно расположить главный элемент контента.

Некоторые считают, что золотое сечение в большей или меньшей степени присутствует в каждом успешном дизайне. Рассказать о востребованной концепции бывает полезным в общении с заказчиком или когда нужно показать свой проект публично. Действительно ли «божественная пропорция» очень эффективна или это мнение преувеличено? Обсуждение данного вопроса в творческой сфере продолжается и сегодня.

Продвижение блога — Генератор продаж

Рейтинг: 5

( голосов 1 )

Поделиться статьей

Просто о саженях и золотой пропорции — портфолио графического дизайнера Артёма Владимирова

Предисловие

Приветствую, Человек!
Великий Google привёл вас на эту страницу, а значит вас интересуют серьёзные темы. В этой статье я покажу, как рождается число Φ, где прячется золотая пропорция и как она применима. А также научу умножать и делить на два. Весь материал является размышлениями на заданную тему — на абсолютную истину не претендует. Призываю вместе проверить всё написанное, математика и геометрия дадут нам ключ. Все желающие приглашаются к обсуждению по электронной почте.

Наверняка вы уже имеете какое-то представление о Золотом сечении, здесь я не буду подробно останавливаться на историческом и культурном аспектах — в Интернете полно информации об этом. Здесь я хочу изучить этот феномен с помощью точной науки — математики.

---

§1. Начало. Ряд Фибоначчи

Запишем ряд чисел, начиная с единицы, в котором каждое следующее число является суммой двух предыдущих. Найдём соотношение (пропорцию) каждой пары соседних чисел друг другу, поделив следующее на предыдущее.

• 1 + 1 = 2;
• 1 + 2 = 3;
• 2 + 3 = 5;
• 3 + 5 = 8;
• 5 + 8 = 13;

• 8 + 13 = 21;
• 13 + 21 = 34;
• 21 + 34 = 55;
• 34 + 55 = 89;
• 55 + 89 = 144.

• 1 : 1 = 1;
• 2 : 1 = 2;
• 3 : 2 = 1,5;
• 5 : 3 = 1,667;
• 8 : 5 = 1,619;

• 13 : 8 = 1,618;
• 21 : 12 = 1,618;
• 34 : 21 = 1,618;
• 55 : 34 = 1,618;
• 89 : 55 = 1,618.

1 1 2 3 5 8 13 21 34 55 89

На шестой паре чисел появляется постоянное соотношение 1,618, которое остаётся неизменным до бесконечности, что само по себе уже интересно. Ряд может начинаться с любой пары чисел и соотношение всегда выравнивается до 1,618.

---

§2. Число Фи

1,618033988749894848045…

Φ — бесконечное иррациональное число. Но для наших примеров нам такая точность не нужна, достаточно 1,618.

Число Φ вычисляется по формуле (1 + √5) : 2

---

§3. Золотое сечение

Золотое сечение определяют как отношение меньшего отрезка к большему отрезку как отношение большего к их сумме:

a : b = (a + b) : a

a

b

a + b

Термин «Золотое сечение» я считаю не совсем корректным, не отражающим процесс. По-английски golden ratio дословно: золотое соотношение. Более уместен термин «Золотая пропорция».

---

§4. Метрическая система

Метр — длина пути, проходимого светом в вакууме за интервал времени 1/299 792 458 секунды

Так гласит официальное определение метра, принятое XVII Генеральной конференцией по мерам и весам в 1983 году. Метр был введён в СССР 14 сентября 1918 указом СНК РСФСР «О введении международной метрической десятичной системы мер и весов».

Расстояние, пройденное светом за одну трехсотмиллионную долю секунды. Вам это ясно? Как это применять в обычной жизни? Как проектировали и строили сооружения в более ранние века? Неужели мужик, строя дом, будет руководствоваться иррациональными числами и вычислять квадратные корни? Конечно же нет. Очевидно, что существовала другая система мер, и её отголоски сохранились в Королевской системе мер, а также в русских саженях. Нужен простой и понятный инструмент пропорционирования и соизмерения.

---

§5. Пропорции квадрата

Мы знаем, что у квадрата все стороны равны. А это значит, что квадрат можно нарисовать или построить, имея в руках лишь

одну меру любой длины: карандаш, палку и т.д. Примем его сторону за единицу.

Диагональ квадрата — редко используемая величина, но и она весьма полезна и интересна (рис. 1).
По теореме Пифагора длина диагонали квадрата (она же гипотенуза треугольника) равна корню из суммы квадратов катетов:

√ (1·1+1·1) = √2 = 1,4142

Пропорцию 1 : √2 также называют серебряным сечением. Самый известный пример этой пропорции — лист формата А4. Эта пропорция обладает интересным свойством, что сохраняется неизменной при удвоении какой-либо из сторон.

Что собой представляет корень из пяти √5 в формуле Φ = (1 + √5) ÷ 2? Это всего навсего диагональ двух квадратов (рис. 2)! Проверим по теореме Пифагора:

√ (1·1+2·2) = √5 = 2,236

Суммируем величину стороны квадрата (1) и диагональ двух квадратов (2,236). Поделим пополам и получим число Φ. Получается, что длина стороны квадрата и длина диагонали двух квадратов в сумме равны удвоенному числу Φ (рис. 3)!

Φ = 3,236 : 2 = 1,618

Удвоенный квадрат по своей сути также является половиной квадрата большего размера. А значит √5 — это также диагональ половины квадрата, а число Φ можно получить, опустив диагональ половины квадрата на продолжение его стороны (рис. 4).

---

Квадрат хранит число Φ

Нам не нужно знать иррациональные числа, математика лишь подтверждает расчёты, но не является их основой! Квадрат хранит в себе все нужные нам пропорции. Он инструмент пропорционирования! Умножая эти пропорции квадрата на целый коэффициент, мы можем получить пропорциональные величины любой нужной длины.

Построение прямоугольника в пропорции Золотого сечения

---

§6. Интересные превращения числа Φ

Теперь стало понятно, где прячется число Φ, я покажу, как оно меняется с точки зрения математики — здесь очень много волшебных превращений! Все они пригодятся нам в дальнейшней работе с саженями.

1). Если от Φ отнять единицу, получится тоже самое, если единицу поделить на Φ:

Φ − 1 = 1 ÷ Φ = 0,618

2). Если из двух Φ вычесть диагональ двух квадратов, получим единицу (рис. 2, 4):

2Φ − √5 = 1,000

3). Помним, число Φ равно половине суммы стороны квадрата и диагонали двух квадратов:

Φ = (1 + √5) ÷ 2 = 1,618

4). Если Φ умножить на диагональ двух квадратов минус единица, будет 2:

Φ · (√5 − 1) = 2,000

5). Если к Φ прибавить единицу, получится тоже самое, если Φ умножить само на себя:

Φ + 1 = Φ² = 2,618

6). Если к Φ прибавить двойку, получится тоже самое, если Φ умножить на диагональ двух квадратов:

Φ+2 = Φ²+1 = Φ·√5 = 3,618

7). Если двойку поделить на Φ получится тоже самое, если из 2Φ вычесть два:

2 ÷ Φ = 2Φ − 2 = 1,236

8). Если из 2Φ вычесть единицу, получим диагональ половины квадрата (рис. 2, 4):

2Φ − 1 = √5 = 2,236

9). Если удвоить любым способом Φ, получим 1 + √5 или 2Φ (рис. 3):

2Φ = 1 + √5 = 3,236

10). Если возвести Φ в куб, получим 2 + √5, а это две стороны квадрата + диагональ двух квадратов:

Φ³ = 2 + √5 = 4,236

Трудно не заметить, две группы чисел с одинаковыми знаками после запятой, и это не спроста!

---

§7. Система пропорций

Возвращаясь к Золотой пропорции. Суть вовсе не в том, что какой-то отрезок делит какой-то другой. Недостаточно нарисовать спираль улитки поверх фото, чтобы понять, что это означает и как этим пользоваться. Для работы на плоскости нужно два отрезка, а для построения объёма нужны три!

1 — 1,236 — 1,618

Появляется система пропорций 1 : 2÷Φ : Φ, которую уже можно использовать как коэффициенты при соизмерении. Рабочая система состоит из трех отрезков и выглядит так:

1

1,236

1,618

---

§8. Образ, подобие, мера и каравай

С математекой, должно быть ясно. Вспомним, что мы, человеки, созданы по образу и подобию Бога, или нашего Создателя, или Вселенной, или Природы, или чего-либо ещё.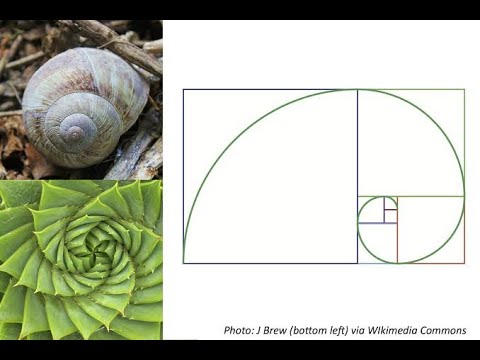 Оставим религиозные смыслы и обратимся к геометрии. Подобными в ней назвают фигуры одинаковых геометрических пропорций и свойств. Квадраты, круги и равносторонние треугольники всегда подобны таким же фигурам. А раз мы уже нашли золотую пропорцию в числах Фибоначии и в квадрате, давайте искать её в самих себе!

---

Тело человека уже хранит в себе образ и подобие — Золотую пропорцию!

---

Вспоминим русскую народную песенку про каравай:

Как на наши именины испекли мы каравай,
Вот такой вышины (поднимаем руки вверх)
Вот такой нижины (опускаем руки вниз)
Вот такой ширины (раскидываем руки вширь)
Вот такой ужины (сводим руки вместе)
Каравай, каравай, кого любишь выбирай!
Я люблю, конечно, всех, но вот (этих) — больше всех.

---

Какие движения при этом делают дети? Водят хоровод и показывают руками вышину, нижину, ширину и ужину! Проделайте сами те же движения и вы сразу поймёте, какими мерами показывают высоту, ширину и длину. Эта песенка и есть ключ!

Ключ к системе измерений саженями хранится в русской народной культуре! В простой детской песенке, которую знают все с малых лет.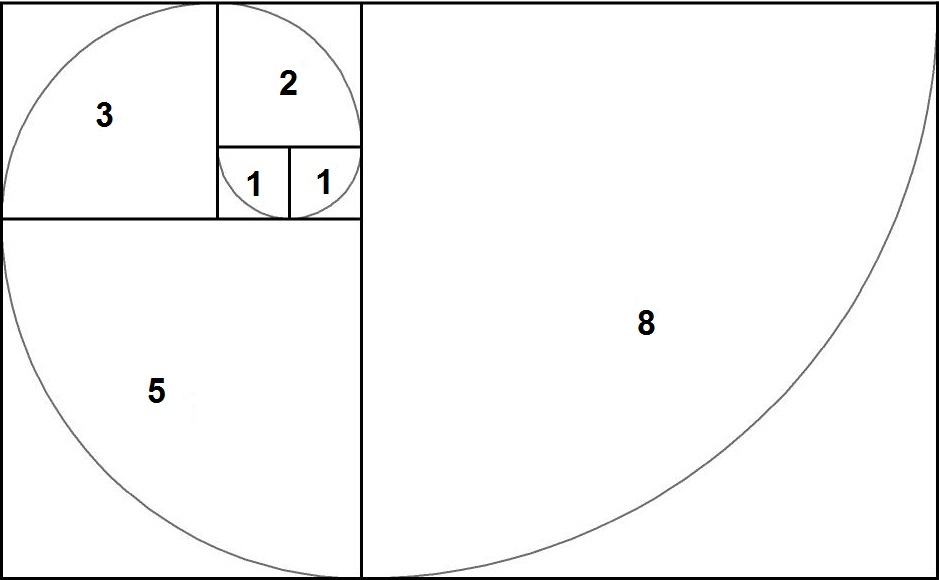 Мерить всё по себе — это правильно, логично и само собой разумеется! Однако, теперь это признак эгоизма — выбросим этот нонсенс из своей головы.

---

§9. Золотая пропорция тела человека

Рука вверх — это мера высоты (великая сажень),
Размах рук в стороны — это мера ширины (маховая сажень),
Рука вперёд — это мера длины (полсажени длины).

Эти меры являются вашими личными мерами!

Все три меры образуют единую систему соизмерений на основе пропорции 2÷Φ к 1. Разные измерения (длина, ширина, высота) должны мериться своей соответствующей мерой, то есть саженью. И тогда мы можем забыть об иррациональных числах, корнях и прочем, используя вместо них целые количества своих саженей.

---

§10. Казённая сажень отдельно

Важно отметить, что вопреки официально утверждённой казённой сажени, существовали и другие. И лишь она одна была приравнена к 7 английским футам и позже к 213 см в Российской империи и по другим источникам 218 см в СССР. На то она и являлась казённой. В корне неверно считать, что сажень была одна, как метр. Чтобы понять гармонию, не думайте о метре — это изобретение XIX века, а Вселенная со своими пропорциями вечна. 🙂

---

§11. Погрешность измерений

Я намеренно буду округлять сотые и тысячные доли чисел и подтягивать расчёты под единый вид, так как они заведомо не абсолютно точны. Иррациональные числа не делятся до конца, поэтому не везде удастся получить красивые целые числа. А мы должны увидеть картину в целом, понять всю единую систему, где тысячные доли лишь детали.

Сантиметр — это сотая доля метра, достаточно точно, поэтому предлагаю не использовать миллиметры в своих расчётах, чтобы они не создавали лишний шум. К тому же, тело гибкое и руки можно растянуть ещё шире или поднять ещё выше. Этого делать не нужно, положение должно быть комфортным.

---

§12. Измерим себя и проверим

Пора проверить всё на себе и удивиться, что всё так и есть. Я мужчина среднего роста, мой размах рук примерно 188 см.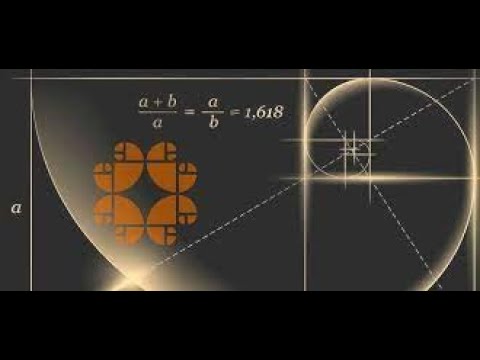 Высота поднятой руки примерно 232,5 см. Вытянутая рука вперёд (плюс столько же назад) примерно 152 см. Сначала я измерил всё рулеткой, а потом посчитал на калькуляторе. Меня поразило с какой точностью совпали все цифры.

• 188 / 152 = 1,236
• 152 / 188 = 0,809

• 232,5 / 188 = 1,236
• 188 / 232,5 = 0,809

• 232,5 / 152 = 1,529
• 152 / 232,5 = 0,655

Здесь мы видим четыре любопытных числа. Где же здесь число 1,618? Да вот же оно:

1,236 = 2 ÷ Φ

0,809 = Φ ÷ 2

1,528 = (2 ÷ Φ)²

0,655 = Φ² ÷ 4

Опишем это словами, чтобы появилось понимание, что всё это значит. Поделив сажень высоты на сажень ширины мы получим пропорцию 1 к 2 ÷ Φ, точно также как поделив сажень ширины на сажень длины. Если поменять местами величины, получится пропорция 1 к Φ ÷ 2. Пропорции остаются одинаковы. А значит мы можем подставлять сюда любые величины и любые значения в сантиметрах!

• 2 ÷ Φ / 1 = 1,236; делим большее на меньшее
• 1 / 2 ÷ Φ = 0,809; делим меньшее на большее

---

Калькулятор саженей

Чтобы посчитать ваши личные сажени, введите величину размаха рук в см:

---

Сажень высоты:

0 см

Сажень ширины:

0 см

Сажень длины:

0 см

---

0 см

0 см

0 см

---

Полсажени высоты:

0 см

Полсажени ширины:

0 см

Полсажени длины:

0 см

---

Локоть высоты:

0 см

Локоть ширины:

0 см

Локоть длины:

0 см

---

Январь 2019. Продолжение следует.

---

Другие статьи

• Комбинаторика в дизайне: цвета
• Летопись вязанного ковра
• Кухонная мебель
  из картона
• Как превратить отходы в ценности

---

Золотое сечение — самое иррациональное число.

Гетти Изображений Плюс

Эта статья адаптирована из книги Джордана Элленберга «Форма : скрытая геометрия информации, биологии, стратегии, демократии и всего остального» . © Penguin Press 2021.

Одна из величайших прелестей теории чисел — существование иррациональных чисел — таких чисел, как квадратный корень из 2 или π, которые не могут быть выражены как отношение любых двух целых чисел, нет. независимо от того, насколько большой. Легенда гласит — возможно, ложная, но, эй, она доказывает, — что открытие иррациональности √2 настолько смутило пифагорейцев, которые хотели, чтобы все числа были рациональными, что они бросили первооткрывателя в океан.

Среди загадок иррациональных чисел особое место занимает одно число: так называемое золотое сечение . Значение золотого сечения составляет около 1,618 (но не , а именно 1,618, так как тогда это было бы соотношение 1618/1000, и, следовательно, оно не является иррациональным), и оно также обозначается греческой буквой φ, которая произносится как «плата», если вы ты математик и «тьфу», если ты в братстве. Если вам нужно точное описание, золотое сечение можно выразить как (1/2)(1+√5.)

Люди веками поднимали шум вокруг этого числа. У Евклида эта пропорция носит более приземленное название «деление на крайнее и среднее». Он понадобился ему для построения правильного пятиугольника, так как золотое сечение — это пропорция между диагональю такого пятиугольника и его стороной. Золотой прямоугольник — это прямоугольник, длина которого в φ умножается на ширину; у него приятное качество: если разрезать его поперек, так что один из двух кусков будет квадратом, а другой будет меньшим золотым прямоугольником.

Вы можете сделать то же самое с этим меньшим прямоугольником, чтобы сделать новый меньший золотой прямоугольник, затем отрезать квадрат от этого маленького золотого мальчика, чтобы сделать золотой прямоугольник еще меньше, и так далее и тому подобное; в результате получается что-то вроде прямоугольной спирали:

Википедия

com/_components/slate-paragraph/instances/ckpo8chva001i3g6c4ve9kclq@published»> Золотое сечение возникает не только в геометрии; в последовательности Фибоначчи, где каждое число является суммой двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21, 34, …), отношения между последовательными членами приближаются к φ все больше и больше по мере термины становятся все больше и больше. (Но, конечно, эти соотношения никогда не0003 прибывают в φ, потому что, опять же, иррационально!)

Вокруг золотого сечения уже давно витают миазмы мистицизма. Теоретик чисел Джордж Баллард Мэтьюз жаловался на это еще в 1904 году, написав, что «божественная пропорция» или «золотое сечение» поражала невежественных и даже ученых людей, таких как Кеплер, чувством тайны и повергала их в мечтательность. видов фантастического символизма». Иногда говорят, что фигуры, длина которых находится в золотой пропорции друг к другу, по своей природе являются самыми красивыми, хотя утверждения о том, что Великая пирамида в Гизе, Парфенон и Mona Lisa были спроектированы по этому принципу, недостаточно обоснованы. В влиятельной статье 1978 года в Журнале ортопедической стоматологии говорится, что набор искусственных зубов для максимальной привлекательности улыбки должен иметь центральный резец в 1,618 раза шире бокового резца, который, в свою очередь, должен быть в 1,618 раза шире клыка. Существует небольшая, но настойчивая школа финансового анализа, которая считает, что колебания на фондовом рынке управляются золотым сечением; Ваш терминал Bloomberg, если у вас достаточно флеша, чтобы иметь его, нарисует для вас маленькие «линии Фибоначчи» на биржевых графиках.

Однажды в 90-х я ужинал с другом моего друга в закусочной Galaxy Diner в Нью-Йорке. Он сказал, что снимает фильм о математике и хочет поговорить с практикующим о том, на что на самом деле похожа математическая жизнь. Мы ели лепешки, я рассказывал ему истории, я забыл об этом, прошли годы. Друга друга звали Даррен Аронофски, а его фильм « Пи » вышел в 1998 году. Главный герой фильма — теоретик чисел по имени Макс Коэн, который очень напряженно думает и много крутит пальцами в волосах. Он встречает хасида, который заинтересовывает его еврейской нумерологией, практикой под названием 9.0003 гематрия , где слово превращается в число путем сложения числового значения содержащихся в нем еврейских букв. Еврейское слово, обозначающее «восток», дает в сумме 144, объясняет хасид, а «Древо жизни» — 233. Теперь Максу интересно, потому что это числа Фибоначчи. Он рисует еще несколько чисел Фибоначчи на страницах газеты, посвященных фондовому рынку. «Я никогда раньше такого не видел», — говорит впечатленный хасид. Макс лихорадочно программирует свой компьютер, который называется Евклид, и рисует спирали золотых прямоугольников, и довольно долго смотрит на такие же спирали молока в своем кофе. Он вычисляет 216-значное число, которое, кажется, является ключом к прогнозированию цен на акции, а также, возможно, тайным именем Бога. Он много играет в го со своим научным руководителем. («Перестань думать, Макс. Всего чувствовать . Используй свою интуицию».) У него сильно болит голова, и он еще сильнее накручивает волосы. Красивая женщина в соседней квартире заинтригована. Я забыл упомянуть, но этот фильм черно-белый. Кто-то пытается его похитить. Наконец, он просверливает дыру в собственном черепе, чтобы выпустить часть математического давления, и фильм приходит к тому, что кажется счастливым концом.

Не помню, что я говорил Аронофски о математике, но это было не то.

Золотая нумерация действительно стала популярной в 2003 году, когда Дэн Браун опубликовал свой мегахитовый роман 9.0003 Код Да Винчи , история «религиозного символиста» и профессора Гарварда, который использует последовательность Фибоначчи и золотое сечение, чтобы раскрыть заговор с участием рыцарей-тамплиеров и современных потомков Иисуса. После этого «поставить φ» было просто хорошим маркетингом. Вы могли купить джинсы, золотые пропорции которых льстили вашей задней части (они идут к вашим вставным зубам!). Существовал «Кодекс диеты», в котором утверждалось, что Леонардо хотел, чтобы вы похудели, употребляя белки и углеводы в пропорции золотого сечения. И был, пожалуй, величайший из когда-либо созданных мистических геометрических чудаков: маркетинговая фирма Arnell Group на 27 страницах объяснила новый логотип Pepsi в виде земного шара, который она разработала в 2008 году. Документ назывался «ЗАХВАТЫВАЮЩИЙ». В презентации объясняется, что Pepsi и золотое сечение являются естественными партнерами, потому что, как вы, несомненно, знаете, «словарь истины и простоты — повторяющееся явление в истории бренда». Хронология показывает, что открытие нового логотипа Pepsi является кульминацией 5000 лет науки и дизайна, включая Пифагора, Евклида, да Винчи и каким-то образом ленту Мёбиуса. Новый логотип Pepsi будет построен из дуг кругов, радиусы которых находятся в золотом сечении друг к другу, соотношение, которое, как заявляет поле, теперь, в действительно впечатляющем предложении по ребрендингу, будет известно как «Коэффициент Pepsi».

Но моя любимая вещь о золотом сечении не имеет ничего общего с пятиугольниками или Pepsi. Дело в том, что золотое сечение среди всех иррациональных чисел — это самых иррациональных чисел.

Что это может означать? Либо число является отношением двух целых чисел, либо нет*.

Оказывается, есть способы говорить о том, насколько иррационально иррациональное число. В конце концов, тот факт, что такое число, как φ, иррационально, не означает, что рядом с ним нет рациональных дробей. Конечно есть! В конце концов, десятичное расширение — это способ записи дробей, близких к числу:

com/_components/slate-paragraph/instances/ckpo8csnq001w3g6ct9nbohaf@published»> 16/10 = 1,6 (довольно близко)
161/100 = 1,61 (близко)
1618/1000 = 1,618 (еще ближе)

Десятичное расширение дает дробь со знаменателем 1000, которая находится в пределах 1/1000 от золотое сечение; если мы допустим, что знаменатель равен 10 000, мы можем получить в пределах 1/10 000 и так далее.

Мы можем лучше десятичных дробей! Помните, что отношения между числами Фибоначчи также являются дробями, которые все ближе и ближе приближаются к золотому сечению:

8/5 = 1,6
13/8 = 1,625
21/13 = около 1,615

com/_components/slate-paragraph/instances/ckpo8csnr00243g6cj6oladl9@published»> Пройдите дальше по последовательности, и вы получите:

233/144 = 1,6180555555…

… что всего лишь примерно 2 из 100 000 от золотого сечения, что значительно лучше приближения, чем 1,618/ 1000, со значительно меньшим знаменателем.

1. Мы были в Техасе на протяжении поколений. Наш транс-ребенок лечится здесь. Темнеет.
2. Удивительные недостатки использования сушильных листов
3. ФБР изъяло журнал моего брата после его ареста. То, что было внутри, рассказывает гораздо большую историю.
4. Что социальные сети на самом деле делают с детским мозгом

Некоторых иррациональных персонажей знаменитостей можно сравнить еще точнее. Цзу Чунчжи, астроном пятого века из Нанкина, заметил, что простая дробь 355/113 невероятно близка к π, всего лишь 2 из 10 миллионов. Он назвал это milü («очень близкое соотношение»). Книга Зу по математическим методам утеряна, поэтому мы не знаем, как он придумал милю. Но это была не простая находка; прошло 1000 лет, прежде чем это приближение было заново открыто в Индии, еще 100 лет, прежде чем оно стало известно в Европе, и еще столетие после этого, прежде чем было окончательно доказано, что число π на самом деле иррационально.

Один из способов получить представление о том, насколько хорошо число может быть аппроксимировано рациональными числами, — нарисовать рисунок, который я называю «штрих-код». Вот как его сделать: если х — число, посмотрите на первые, скажем, 300 кратных х — х, 2х, 3х, 4х и т. д. — и для каждого из этих кратных сделайте небольшую вертикальную отметку. в его «дробной части», которая является частью числа после запятой. То есть это число от 0 до 1; дробная часть φ, например, составляет около 0,618.

Понял? Возможно нет. Вот пример. Предположим, вы начинаете с рационального числа, например 1/7. Я получаю картинку, которая выглядит как семь тактов; потому что на что бы я ни умножал 1/7, я получаю некоторое количество седьмых, дробная часть которого равна 0, 1/7, 2/7, 3/7, 4/7, 5/7 или 6/7.

То же самое для любого рационального числа; мы можем рассматривать все больше и больше кратных, но столбцы будут ограничены конечным набором, равномерно распределенным от 0 до 1.

А как насчет π? Вот его первые 300 множителей:

Много баров. Но не 300. На самом деле, если бы вы посчитали видимые здесь полосы, вы бы увидели, что их ровно 113. То, что вы видите здесь, является подписью milü. Поскольку число π очень близко к 355/113, его первые триста кратных также очень близки к некоторому числу 113-х, а это означает, что эти столбцы будут оставаться очень близко к числам 0, 1/113, 2/113, ( сделай вид, что я записал все 113 вариантов), и 112/113. Поскольку π не совсем равно милу, его кратные числа не бьют по носу эти дроби; полосы на картинке, которые выглядят немного толще и темнее, на самом деле представляют собой несколько полос, сгруппированных так близко друг к другу, что на странице они выглядят как одна.

Что возвращает нас к золотому сечению. Штрих-код, образованный первыми 300 кратными φ, хорошо распределен, а не сгруппирован, как штрихи π:

.

Нарисуйте тысячу кратных, и это та же история, только с большим количеством полос:

И независимо от того, сколько кратных золотому сечению я возьму — тысячу, миллиард или больше — эти полосы никогда не выстроятся вдоль небольшого набора равномерно расположенных позиций, как штрих-код рационального числа. , или даже сгруппироваться рядом с этими позициями, как это делает штрих-код для π. Милю для φ не существует.

com/_components/slate-paragraph/instances/ckpo8f3ro004u3g6c2v5oydp1@published»> Вот прекрасный факт, который слишком сложно доказать здесь: вы не найдете каких-либо лучших рациональных приближений к φ, чем те, которые дает последовательность Фибоначчи. На самом деле, таким образом, который можно сделать достаточно точным (но не здесь), φ из всех чисел наименее хорошо аппроксимируется дробями; в этом смысле это самое иррациональное число . Для меня это золото.

Будущее время является партнерством Сланец, Новая Америка и Университет штата Аризона который исследует новые технологии, государственную политику и общество. 9Обновление 0007

от 9 июня 2021 г.: эта статья была обновлена, чтобы удалить потенциально недостоверную историю об этимологии слова ratio .

• Книги
• Выдержки
• История
• Математика

Что такое золотое сечение? (4 вещи, для которых он используется)

Это руководство охватывает все, что вам нужно знать о золотом сечении.

Вы когда-нибудь задумывались, почему некоторые объекты, структуры или произведения искусства кажутся красивыми и радуют глаз? Ответ может заключаться в математической концепции, известной как золотое сечение, которая веками очаровывала ученых, художников и архитекторов.

От древних цивилизаций до современного дизайна, золотое сечение было провозглашено ключом к эстетическому совершенству, но что это такое и как оно работает?

В этой статье мы с вами погрузимся в увлекательный мир золотого сечения и исследуем его значение в различных областях, включая искусство, архитектуру и природу.

Мы раскроем его историческое происхождение, углубимся в его математические свойства и раскроем его применение в дизайне и эстетике. Если вы когда-либо были заинтригованы очарованием красоты и задавались вопросом о секретах, стоящих за ней, читайте дальше, пока мы разгадываем загадочную природу золотого сечения.

Независимо от того, являетесь ли вы энтузиастом искусства, любителем математики или просто интересуетесь чудесами света, эта статья обещает раскрыть тайну золотого сечения и пролить свет на то, почему оно веками пленяло умы людей.

Мы рассмотрим следующие темы:

Содержание

Что такое золотое сечение?

С точки зрения математики, золотое сечение равно 1,618, и его представляет греческая буква Фи (Ф). Его также называют греческой буквой фи, золотым сечением и божественной пропорцией — в зависимости от того, сколько его встречается в природе. Однако, когда мы говорим о дизайне, определение золотого сечения заключается в создании органических или естественных дизайнов, на которые приятно смотреть, с пропорциями или элементами, гармонирующими друг с другом.

Золотое сечение — отличный инструмент, позволяющий сделать изображения и объекты более привлекательными.

В дизайне золотое сечение означает, что элементы сбалансированы, но при этом эстетичны.

Когда мы используем его в дизайне, он придает ему художественное преимущество, которое всегда привлекало человеческий глаз.

Золотое сечение особенное, потому что мы можем найти его повсюду, от математической геометрии, искусства и зданий до наших тел.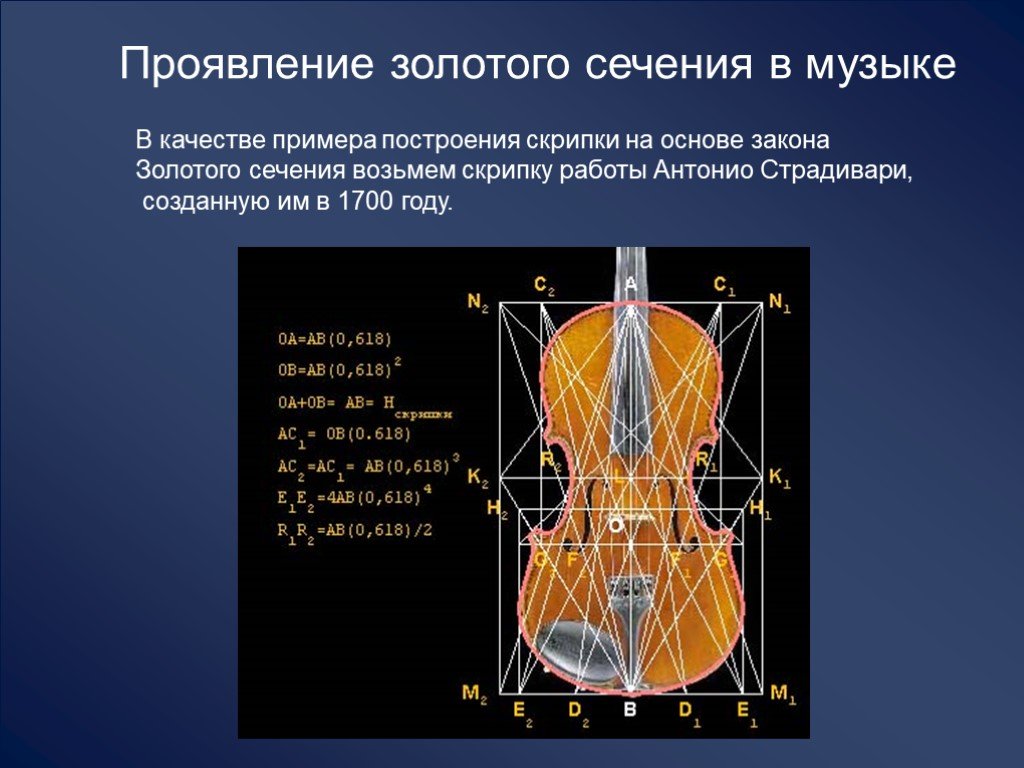 Он органично встроен в нашу повседневную жизнь. Впервые его назвали «золотым» в 1800-х годах, и с годами стало известно о его связи с фи.

Он имеет множество применений, и вы можете использовать его в типографике, изображениях, дизайне логотипов и при планировании макетов для вашей рекламы или веб-сайта.

Золотое сечение можно найти где угодно в нашем мире, в природе, живописи, музыке и архитектуре.

Отношение и число после него были получены с использованием последовательности Фибоначчи. Итак, что такое последовательность Фибоначчи?

Проще говоря, последовательность Фибоначчи — это набор чисел, существующих в природе, например, общее количество сторон банана (неочищенного) и лепестков некоторых цветов — числа Фибоначчи.

Последовательность Фибоначчи начинается с 0 и 1. Возьмем следующее число за х. Вы получите значение х, сложив два числа перед х.

В данный момент предыдущими числами являются 0 и 1, поэтому x равно 0 + 1 = 1. Вы можете получить последовательные числа, если сложите два числа перед этим числом.

Последовательность Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21… до бесконечности.

Чтобы составить отношение, мы берем два последовательных числа n и n+1 из последовательности Фибоначчи и делим n+1 на n — большее число на меньшее.

Полученный ответ близок, но не равен точно 1,618, например, 3/2 = 1,5, 5/3 = 1,667 и 21/13 = 1,615.

Золотое сечение

Почему оно называется золотым сечением?

Золотое сечение так же старо, как и сам мир, и оно распространено в окружающем нас мире.

У него было несколько других имен, прежде чем Мартин Ом назвал его «золотым» в 1800-х годах.

В своем учебнике Die rein Elementar Mathematik он описал Евклидову теорию «ныряния линии в экстремальном и главном отношении» как «золотое сечение».

Значение 1,618 называется золотым сечением, и оно может сделать любую форму, логотип, типографику и изображение приятным на вид и придать им иерархию.

Что особенного в золотом сечении?

Значение золотого сечения связано с линией – простейшей фигурой в природе.

Когда мы делим прямую на две нечетные части и берем большую часть «а» и делим ее на меньшую часть, b мы получаем отношение 1,618.

Соотношение и производные Золотой прямоугольник, и Золотая спираль все встречаются в природе, в виде цветов, папоротников, ураганов и ракушек.

Помогает сделать изображения более привлекательными.

Золотая спираль обычно используется при разработке логотипов, обрезке и изменении размера изображений и т. д.

Но что такое Золотая спираль? Золотая спираль получается, когда вы умножаете горизонтальную сторону квадрата на 1,618.

У вас получится прямоугольник, затем положите квадрат на прямоугольник.

Затем возьмите прямоугольник, не покрытый квадратом, и накройте его квадратом – разделите горизонтальную сторону на 1,618, чтобы найти размеры квадрата.

Вертикальная сторона или ширина должны оставаться одинаковыми как для квадрата, так и для прямоугольника.

Затем накройте прямоугольник квадратом. Повторите этот процесс с квадратной частью, пока не получите три маленьких квадрата.

Наложение этих двух фигур дает золотой прямоугольник.

Золотой прямоугольник

Начните рисовать спиральную арку с маленького квадрата, примыкающего ко второму квадрату, который вы использовали.

Поднимите арку на второй меньший квадрат и в квадрат внизу. Затем вытяните его во второй квадрат, который вы использовали, и вставьте его в непокрытую часть прямоугольника.

Закончите спиральную арку на одном краю квадрата, закрывающего прямоугольник. Золотая спираль покрывает перекрывающийся золотой прямоугольник.

Золотая спираль

Все, что сделано с использованием золотого сечения, становится самым живописным изображением для человеческого глаза.

Эта характеристика золотого сечения делает его особенным, и мы можем использовать его в искусстве и дизайне, архитектуре и создании веб-сайтов (макеты, типографика и т. д.) для создания элементов, которые соответствуют человеческой природе.

Для дальнейшего изучения концепций золотого сечения мы рекомендуем это видео от DavidsonArtOnline:

Для чего используется золотое сечение?

Золотое сечение использовалось на протяжении всей нашей истории в живописи, архитектуре и даже музыке, более эстетически приятной человеческому глазу.

Такие люди, как Леонардо да Винчи, использовали его в своих работах, и картина «Мона Лиза» была создана с учетом этого соотношения. В нашей повседневной жизни он также имеет множество применений.

1. Типографика

Определение золотого сечения диктует, что оно равно 1,618, и вы можете использовать это число для установки иерархии вашей типографики — искусства письма.

Вы можете использовать это соотношение, чтобы найти размер шрифта, который будет соответствовать вашим заголовкам и подзаголовкам в соответствии с размером основного текста.

Предположим, у вас есть размер основного текста 11 пикселей, и вы хотите знать, какого размера должен быть заголовок блога.

Просто умножьте 11 пикселей на 1,618, и ответ будет 17,798, поэтому вы должны использовать размер шрифта 18-19 пикселей для заголовков.

Для размера основного текста 12 пикселей ответ будет 19,416, если вы умножите 12 на 1,618, поэтому размер 19-20 пикселей будет хорошим.

Для дальнейшего изучения использования золотого сечения в типографике мы рекомендуем это видео Антона Рейеса:

2. Фотографии

Золотое сечение — эффективный инструмент для обрезки или изменения размера изображений. Вы можете использовать Золотую спираль для этой работы.

Золотая спираль тесно связана с золотым сечением, и, поместив ее на изображение, вы можете найти часть, которую хотите сохранить, или фокальную часть изображения.

С помощью золотой спирали вы сможете найти гармонию с различными элементами в образе.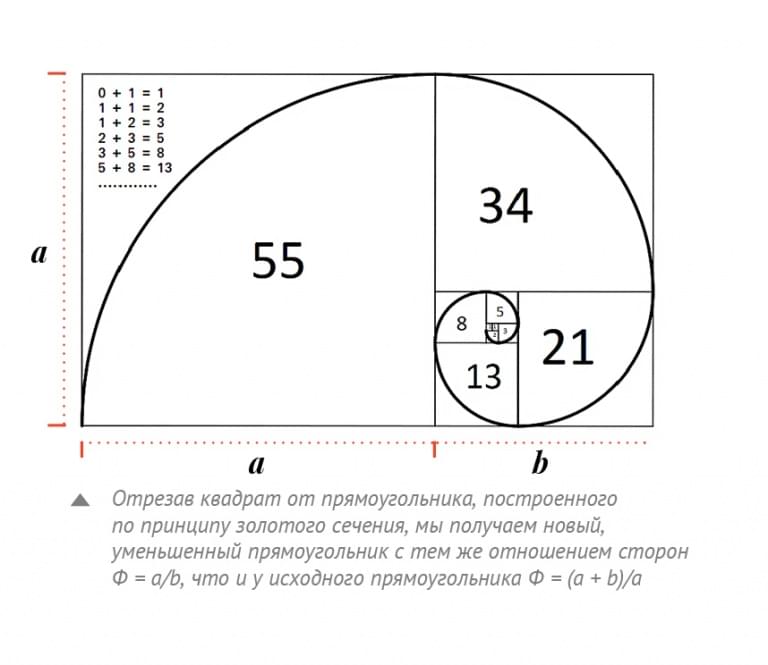

Когда вы накладываете золотую спираль на изображение, часть с наибольшим количеством деталей должна находиться в самом маленьком прямоугольнике спирали, но эта часть не обязательно должна быть в центре.

Он может быть в любой части изображения, но вам нужно будет изменить спираль в зависимости от того, где больше всего деталей.

Попробовав несколько спиралевидных наложений, вы можете убедиться, что фокусная точка вашего изображения находится в центре спирали.

Более того, вы можете перемещать объекты, пока спираль не покажет гармонию, которой она должна быть на вашем изображении.

Для дальнейшего изучения использования золотого сечения в фотографии, мы рекомендуем это видео от Reg:

3. Разработка логотипа

Вам нужен хорошо продуманный логотип, который может с первого взгляда донести идею вашего бренда. Золотое сечение может помочь вам найти правильное выравнивание и лучшую основу для вашего логотипа.

Многие крупные бренды, которые сейчас в тренде, используют божественные пропорции для создания своих логотипов, например, Pepsi, Twitter и Apple.

Вы можете использовать соотношение, чтобы найти правильную ширину и высоту, которые соответствуют вашему логотипу, и какие пропорции подходят для внутренних объектов в дизайне логотипа.

Чтобы сделать логотип, вы можете взять числа из последовательности Фибоначчи и нарисовать круги напротив каждого числа. Вы можете использовать эти круги, чтобы сделать сетку, на которой вы можете сделать свой дизайн логотипа.

Твиттер использовал этот метод, чтобы создать твит-птицу, представляющую Твиттер.

С золотым прямоугольником вы можете расположить все объекты в гармонии друг с другом или использовать круги Фибоначчи в качестве основы для логотипа.

Вы также можете использовать как золотой прямоугольник (перекрывающиеся прямоугольники и квадраты без спирали), так и круги Фибоначчи, чтобы создать сетку для вашего логотипа — Apple использовала оба для своего логотипа.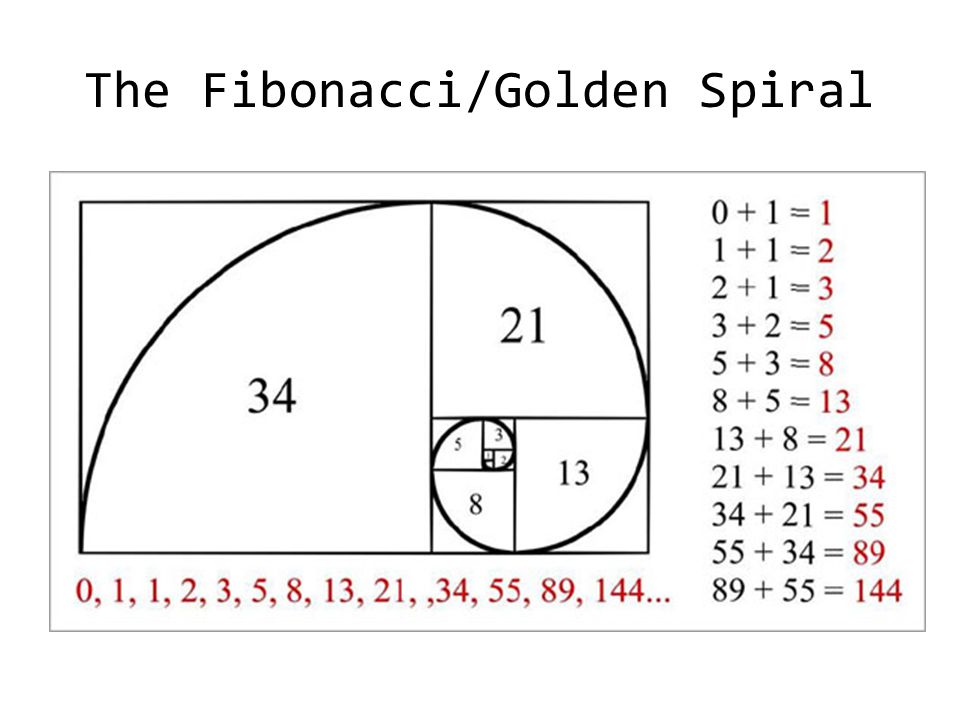

Чтобы лучше изучить использование золотого сечения в дизайне логотипов, мы рекомендуем это видео от Dansky:

4. Макет

Используя соотношение, вы можете создавать макеты, привлекательные для вашей аудитории.

Например, если вы хотите создать что-то для своего веб-сайта или блога, у которого есть основное сообщение, а затем дополнительное сообщение, вы можете использовать соотношение для расчета количества пикселей для обоих.

Для вашей инфографики, если вы хотите создать основную боковую панель шириной 667 пикселей, просто разделите ее на 1,618, чтобы найти ширину боковой панели, которая подходит для этого конкретного макета.

Соотношение может не давать точную длину в некоторых случаях, но оно может дать вам оценку того, где разместить какой элемент, чтобы сделать макет в целом более приятным на вид.

Кроме того, вы хотите сфокусировать важный элемент вашего плаката, рекламы или изображения в середине золотой спирали, потому что это место, на которое в первую очередь остановится взгляд вашей аудитории.

Кто изобрел золотое сечение и когда?

Еще до того, как Мартин Ом, немецкий математик, назвал божественную пропорцию «золотой» в 1800-х годах, исторические источники утверждают, что ее использовали греки и египтяне.

Говорят, что Великая пирамида и Парфенон были спроектированы с учетом Фи.

Художники и математики, такие как Фидий и Платон, использовали в своей работе Золотое сечение и работали над ним.

Точно так же Евклид, живший с 300 г. до н.э. по 365 г. до н.э., объяснил, что линия, разделенная на 0,6180399, называется «нырянием линии в крайнем и главном отношении», которое он позже назвал золотой серединой. В 1200 году нашей эры Леонардо Фибоначчи открыл последовательность Фибоначчи.

Перенесемся в 1500 год нашей эры. Леонардо да Винчи использовал золотую середину или Божественные пропорции, как называли в ту эпоху, в своих произведениях, например, в картине «Тайная вечеря».

Позднее, в 1900-х годах, Марк Барр, американский математик, обозначил божественную пропорцию фи, греческой буквой.

Фи — это греческая буква алфавита F, которая также является первой буквой ряда Фибоначчи, а фи — это первая половина Фидия, который, как известно, использовал золотое сечение в своих скульптурах. .

Фи или золотое сечение в наши дни используется в математике, искусстве и дизайне, архитектуре и даже ассоциируется с духовностью.

Заключительные замечания

Золотое сечение равно 1,618, и это отношение является результатом последовательности Фибоначчи, и когда последовательные числа в ряду делятся, они равны 1,618.

Это число также называется греческим Фи и является неотъемлемой частью окружающего нас мира.

Соотношение можно найти в окружающем нас мире, в природе, искусстве и архитектуре, и даже в наших телах.

Из него можно сделать Золотой прямоугольник и Золотую спираль.

Эти два элемента используются при разработке логотипов, изменении размера изображений и разработке макетов для рекламы, веб-сайтов и инфографики.