Дифракция | это… Что такое Дифракция?
Дифракция первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных максимумов
Дифра́кция во́лн (лат. diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны.
Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.
Дифракция волн может проявляться:
- в преобразовании пространственной структуры волн.
 В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении;
В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении; - в разложении волн по их частотному спектру;
- в преобразовании поляризации волн;
- в изменении фазовой структуры волн.
Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).
|
Содержание
|
Тонкости в толковании термина «дифракция»
В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её.
Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка).
Исходное ограничение волнового поля в пространстве и его определённая структура могут возникнуть не только за счёт присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.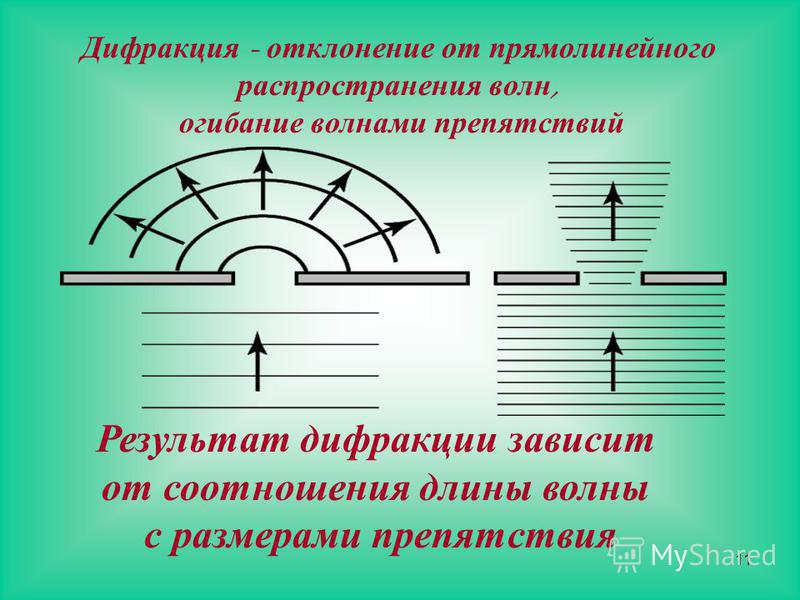
Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции.
Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на непоглощающих (прозрачных), так называемых фазовых, структурах.
Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то наблюдается тенденция понимать её проявление как любое отступление от законов геометрической оптики.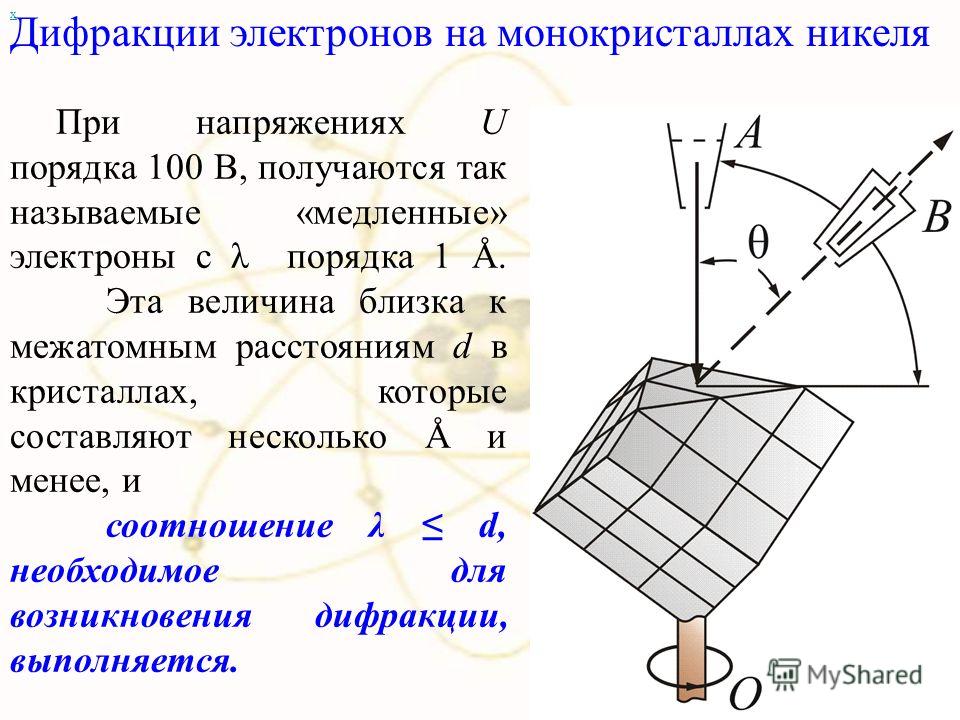
При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является.
Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.
Ещё один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).
Раздел оптики «Оптика кристаллов», имеющей дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции. В то же самое время он нуждается в корректировке используемых представлений геометрической оптики. Это связано с различием в понятии луча (как направления распространения света) и распространения волнового фронта (то есть направления нормали к нему)
Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.
Частные случаи дифракции
Исторически в проблеме дифракции сначала рассматривались два крайних случая, связанных с ограничением препятствием (экраном с дыркой) сферической волны и это была дифракция Френеля, либо плоской волны на щели или системе отверстий — дифракция Фраунгофера
Дифракция на щели
Распределение интенсивности света при дифракции на щели
В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране.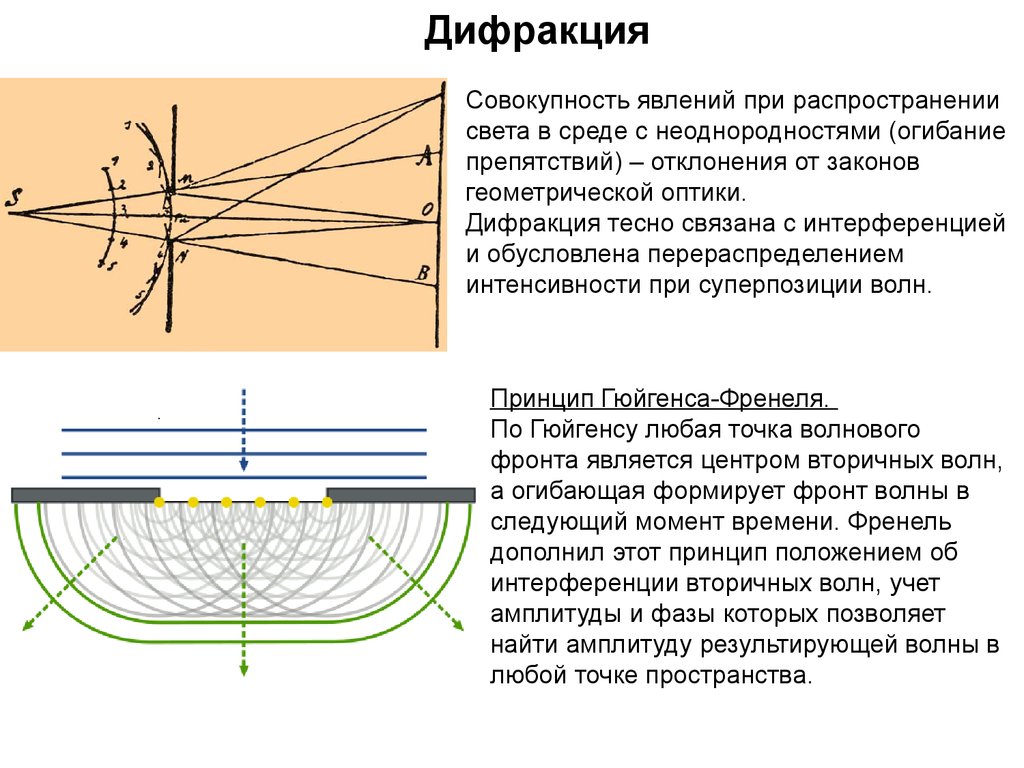
Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ, падающую на экран с щелью ширины a.
Будем считать, что щель находится в плоскости x′-y′ с центром в начале координат. Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать
пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([, ]).
Расстояние r от щели определяется как:
Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:
Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.
И тогда его можно записать приближённо как z.
Здесь мы введём некую константу ‘C’, которой обозначим все постоянные множители в предыдущем уравнении. Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.
В случае дифракции Фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:
Используя формулу Эйлера и её производную: и .
где ненормированная синкус функция определена как .
Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:
См. также Дифракция на N-щелях
Дифракция на отверстии
Дифракция лазерного луча с длиной волны 650 нм, прошедшего через отверстие диаметром 0,2 мм
Дифракция звука и ультразвуковая локация
Дифракция радиоволн и радиолокация
Исследованием дифракции радиоволн занимается геометрическая теория дифракции[2]
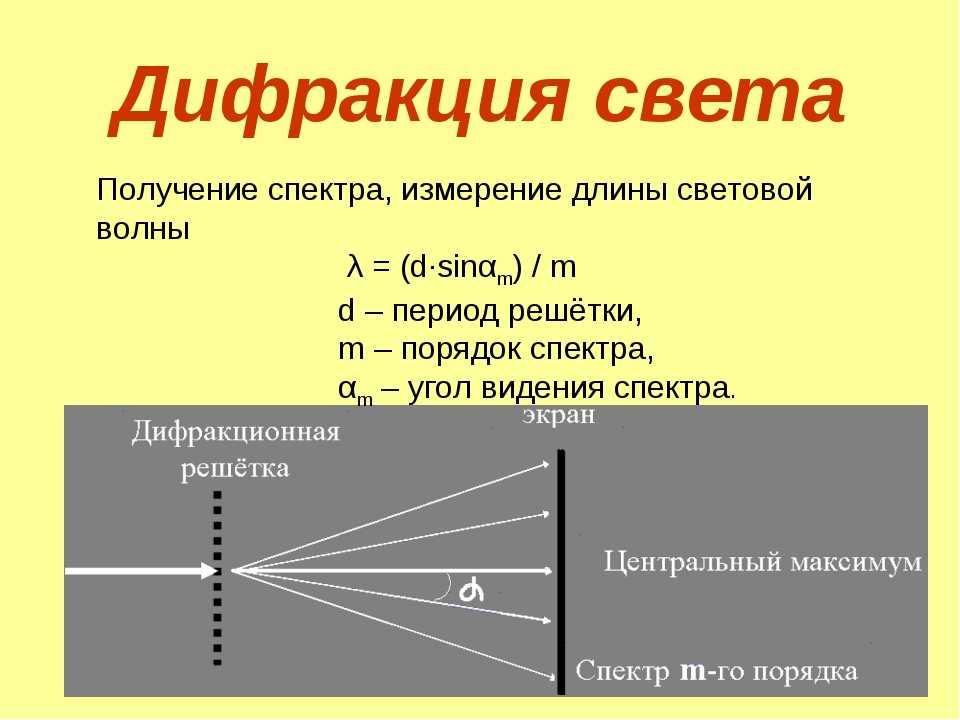
Дифракционная решётка
Основная статья: Дифракционная решётка
Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Дифракция рентгеновских лучей в кристаллах и рентгеноструктурный анализ
Дифракция света на ультразвуке
Основная статья: Акустооптика
Одним из наглядных примеров дифракции света на ультразвуке является дифракция света на ультразвуке в жидкости. В одной из постановок такого эксперимента в оптически-прозрачной ванночке в форме прямоугольного параллелепипеда с оптически-прозрачной жидкостью с помощью пластинки из пьезоматериала на частоте ультразвука возбуждается стоячая волна. В её узлах плотность воды ниже, и как следствие ниже её оптическая плотность, в пучностях — выше. Таким образом, при этих условиях ванночка с водой становится для световой волны фазовой дифракционной решёткой, на которой осуществляется дифракция в виде изменения фазовой структуры волн, что можно наблюдать в оптический микроскоп методом фазового контраста или методом тёмного поля.
Дифракция электронов
Основная статья: Дифракция электронов
Дифракция электронов — процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет свойства, аналогичные свойствам волны. При выполнении некоторых условий, пропуская пучок электронов через материал можно зафиксировать дифракционную картину, соответствующую структуре материала. Процесс дифракции электронов получил широкое применение в аналитических исследованиях кристаллических структур металлов, сплавов, полупроводниковых материалов.
При выполнении некоторых условий, пропуская пучок электронов через материал можно зафиксировать дифракционную картину, соответствующую структуре материала. Процесс дифракции электронов получил широкое применение в аналитических исследованиях кристаллических структур металлов, сплавов, полупроводниковых материалов.
Брегговская дифракция
Основная статья: Дифракция Брэгга
Согласно Закону Брэгга каждая точка (или отражение) в этой дифракционной картине формируется конструктивной интерференцией рентгеновских лучей, проходящих через кристалл. Эти данные могут быть использованы для определения атомной структуры кристаллов.
Дифракция от трехмерной периодической структуры, такой как атомы в кристалле называется дифракцией Брегга. Это похоже на то, что происходит, когда волны рассеиваются на дифракционной решётке. Брегговская дифракция является следствием интерференции между волнами, отражёнными от кристаллических плоскостей.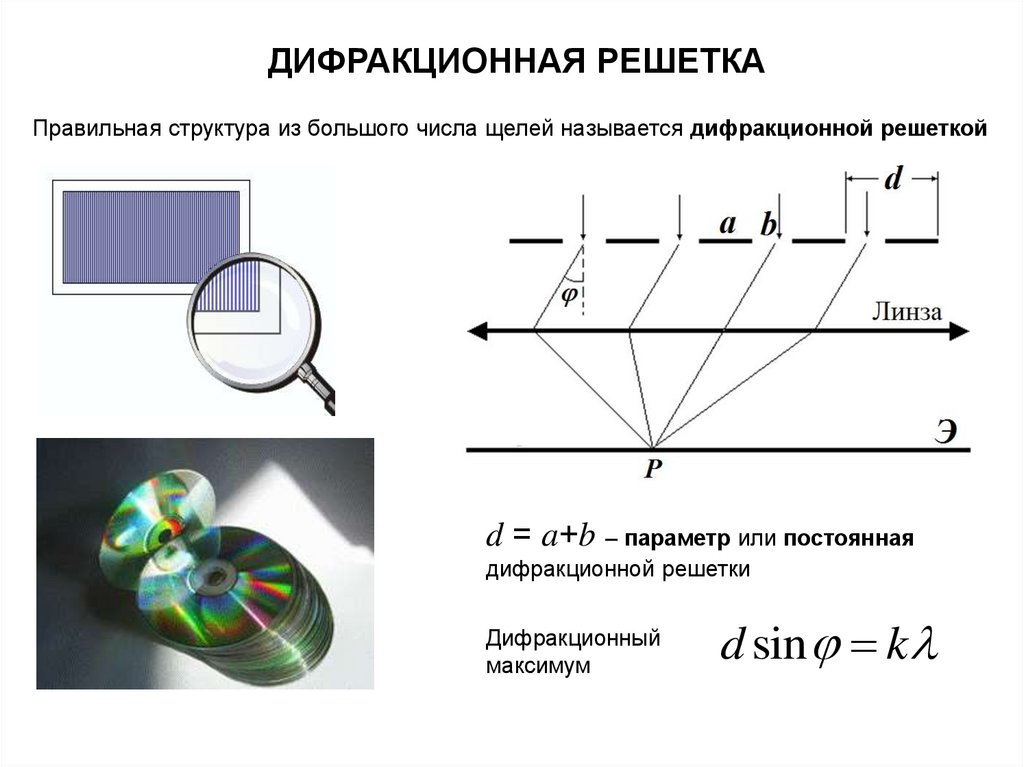
- ,
где
- d — расстояние между кристаллическими плоскостями,
- θ угол скольжения — дополнительный угол к углу падения,
- λ — длина волны,
- n (n = 1,2…) — целое число называемое порядком дифракции.
Брегговская дифракция может осуществляться при использовании света с очень маленькой длиной волны, такого как рентгеновское излучение, либо волны материи, такие как нейтроны и электроны, длины волн которых сравнимы или много меньше, чем межатомное расстояние.[3] Получаемые данные дают информацию о межплоскостных расстояния, что позволяет вывести кристаллическую структуру. Дифракционный контраст, в электронных микроскопах и рентгеновских топографических устройствах, в частности, также является мощным инструментом для изучения отдельных дефектов и локальных полей деформации в кристаллах.
Дифракция частиц (нейтронов, атомов, молекул)
История исследований
Основы теории дифракции были заложены при изучении дифракции света в первой половине XIX века в трудах Юнга и Френеля. Среди других учёных, которые внесли значительный вклад в изучение дифракции: Гримальди, Гюйгенс, Араго, Пуассон, Гаусс, Фраунгофер, Бабине, Кирхгоф, Аббе, У. Г. Брэгг и У. Л. Брэгг, фон Лауэ, Роуланд, Зоммерфельд, Леонтович, Фок, Ван-Циттерт, Цернике (см. История оптики).
Среди других учёных, которые внесли значительный вклад в изучение дифракции: Гримальди, Гюйгенс, Араго, Пуассон, Гаусс, Фраунгофер, Бабине, Кирхгоф, Аббе, У. Г. Брэгг и У. Л. Брэгг, фон Лауэ, Роуланд, Зоммерфельд, Леонтович, Фок, Ван-Циттерт, Цернике (см. История оптики).
Обнаружение дифракции частиц (электронов) в 1927 году (опыт Дэвиссона и Джермера) сыграло большую роль в подтверждении существования волн де Бройля и в подтверждении концепции корпускулярно-волнового дуализма (идеи двойственной природы волн и частиц). В XX и XXI веках продолжились исследования дифракции волн на сложных структурах.
Дифракция в фотографии
Дифракцию можно наблюдать в фотографии: чрезмерное закрытие диафрагмы (относительного отверстия) приводит к падению резкости. Поэтому для сохранения оптимально резкого изображения на фотографии не рекомендуется полностью закрывать диафрагму. Нужно отметить, что для каждого объектива существует свои границы до которых стоит закрывать диафрагму, в большинстве случаев они равны f/11. [4]
[4]
См. также
- Интерференция
- Рефракция
- Рассеяние волн
- Оптика
- Физическая оптика
- Волновая оптика
- Акустооптика
- Электронная оптика
- История оптики
- Волна
Примечания
- ↑ В явлении рассеяния на мелких неоднородностях среды сказывается не только экранирование фронта волны, но и свойства самой неоднородности (скажем, водяной капли), определяющие индикатрису рассеяния, что рассматривается, например, в научной дисциплине «Оптика атмосферы» в разделе, связанном с аэрозолем.
- ↑ Боровиков В. А., Кинбер Б. Е. Геометрическая теория дифракции. М.: Связь, 1978, 247 с.
- ↑ John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0-444-10791-6
- ↑ Что такое дифракция в фотографии. «Про Фото»
Литература
- Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное.
 — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
— М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7 - Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
- И. Г. Кондратьев, Г. Д. Малюжинец Дифракция волн // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1988—1998.
Ссылки
- Дифракция: тематические медиа-файлы на Викискладе
Дифракция | это… Что такое Дифракция?
Дифракция первого и второго порядка как интерференция волн, образованных при падении плоской волны на непрозрачный экран с парой щелей. Стрелками показаны линии, проходящие через линии интерференционных максимумов
Дифра́кция во́лн (лат.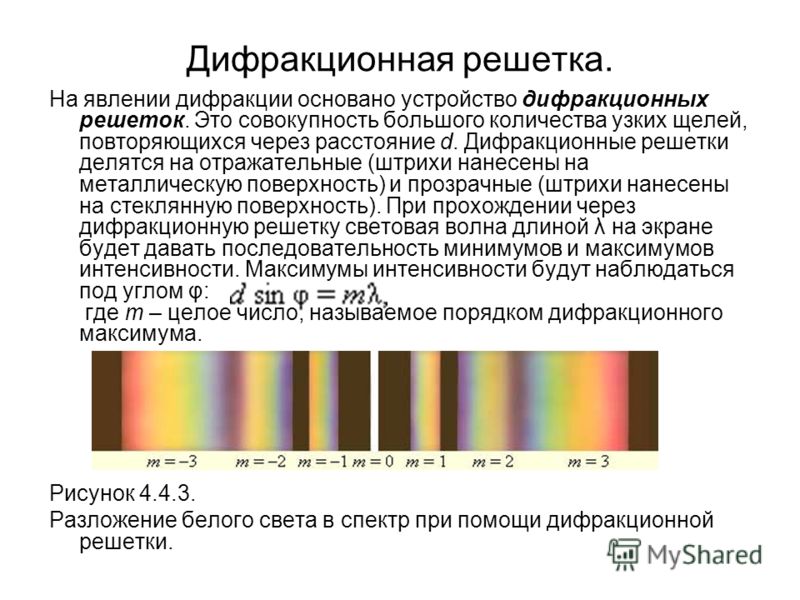 diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
diffractus — буквально разломанный, переломанный, огибание препятствия волнами) — явление, которое проявляет себя как отклонение от законов геометрической оптики при распространении волн. Она представляет собой универсальное волновое явление и характеризуется одними и теми же законами при наблюдении волновых полей разной природы.
Дифракция неразрывно связана с явлением интерференции. Более того, само явление дифракции зачастую трактуют как случай интерференции ограниченных в пространстве волн (интерференция вторичных волн). Общим свойством всех эффектов дифракции является зависимость степени её проявления от соотношения между длиной волны и характерным размером неоднородностей среды , либо неоднородностей структуры самой волны. Наиболее заметно они проявляются при размерах неоднородностей, сравнимых с длиной волны. При размерах неоднородностей, существенно превышающих длину волны (на 3—4 порядка и более), явлением дифракции, как правило, можно пренебречь. В последнем случае распространение волн с высокой степенью точности описывается законами геометрической оптики.
Изначально явление дифракции трактовалось как огибание волной препятствия, то есть проникновение волны в область геометрической тени. С точки зрения современной науки определение дифракции как огибания светом препятствия признается недостаточным (слишком узким) и не вполне адекватным. Так, с дифракцией связывают весьма широкий круг явлений, возникающих при распространении волн (в случае учёта их пространственного ограничения) в неоднородных средах.
Дифракция волн может проявляться:
- в преобразовании пространственной структуры волн. В одних случаях такое преобразование можно рассматривать как «огибание» волнами препятствий, в других случаях — как расширение угла распространения волновых пучков или их отклонение в определённом направлении;
- в разложении волн по их частотному спектру;
- в преобразовании поляризации волн;
- в изменении фазовой структуры волн.

Наиболее хорошо изучена дифракция электромагнитных (в частности, оптических) и акустических волн, а также гравитационно-капиллярных волн (волны на поверхности жидкости).
|
Содержание
|
Тонкости в толковании термина «дифракция»
В явлении дифракции важную роль играют исходные размеры области волнового поля и исходная структура волнового поля, которая подвержена существенной трансформации в случае, если элементы структуры волнового поля сравнимы с длиной волны или меньше её.
Например, ограниченный в пространстве волновой пучок имеет свойство «расходиться» («расплываться») в пространстве по мере распространения даже в однородной среде. Данное явление не описывается законами геометрической оптики и относится к дифракционным явлениям (дифракционная расходимость, дифракционное расплывание волнового пучка).
Исходное ограничение волнового поля в пространстве и его определённая структура могут возникнуть не только за счёт присутствия поглощающих или отражающих элементов, но и, например, при порождении (генерации, излучении) данного волнового поля.
Следует заметить, что в средах, в которых скорость волны плавно (по сравнению с длиной волны) меняется от точки к точке, распространение волнового пучка является криволинейным (см. градиентная оптика, градиентные волноводы, мираж). При этом волна также может огибать препятствие. Однако такое криволинейное распространение волны может быть описано с помощью уравнений геометрической оптики, и это явление не относится к дифракции.
Вместе с тем, во многих случаях дифракция может быть и не связана с огибанием препятствия (но всегда обусловлена его наличием). Такова, например, дифракция на непоглощающих (прозрачных), так называемых фазовых, структурах.
Поскольку, с одной стороны, явление дифракции света оказалось невозможным объяснить с точки зрения лучевой модели, то есть с точки зрения геометрической оптики, а с другой стороны, дифракция получила исчерпывающее объяснение в рамках волновой теории, то наблюдается тенденция понимать её проявление как любое отступление от законов геометрической оптики.
При этом следует заметить, что некоторые волновые явления не описываются законами геометрической оптики и, в то же время, не относятся к дифракции. К таким типично волновым явлениям относится, например, вращение плоскости поляризации световой волны в оптически активной среде, которое дифракцией не является.
Вместе с тем, единственным результатом так называемой коллинеарной дифракции с преобразованием оптических мод может быть именно поворот плоскости поляризации, в то время как дифрагированный волновой пучок сохраняет исходное направление распространения. Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.
Такой тип дифракции может быть реализован, например, как дифракция света на ультразвуке в двулучепреломляющих кристаллах, при которой волновые векторы оптической и акустической волн параллельны друг другу.
Ещё один пример: с точки зрения геометрической оптики невозможно объяснить явления, имеющие место в так называемых связанных волноводах, хотя эти явления также не относят к дифракции (волновые явления, связанные с «вытекающими» полями).
Раздел оптики «Оптика кристаллов», имеющей дело с оптической анизотропией среды, также имеет лишь косвенное отношение к проблеме дифракции. В то же самое время он нуждается в корректировке используемых представлений геометрической оптики. Это связано с различием в понятии луча (как направления распространения света) и распространения волнового фронта (то есть направления нормали к нему)
Отступление от прямолинейности распространения света наблюдается также в сильных полях тяготения. Экспериментально подтверждено, что свет, проходящий вблизи массивного объекта, например, вблизи звезды, отклоняется в её поле тяготения в сторону звезды. Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.
Таким образом, и в данном случае можно говорить об «огибании» световой волной препятствия. Однако, это явление также не относится к дифракции.
Частные случаи дифракции
Исторически в проблеме дифракции сначала рассматривались два крайних случая, связанных с ограничением препятствием (экраном с дыркой) сферической волны и это была дифракция Френеля, либо плоской волны на щели или системе отверстий — дифракция Фраунгофера
Дифракция на щели
Распределение интенсивности света при дифракции на щели
В качестве примера рассмотрим дифракционную картину возникающую при прохождении света через щель в непрозрачном экране. Мы найдём интенсивность света в зависимости от угла в этом случае. Для написания исходного уравнения используем принцип Гюйгенса.
Рассмотрим монохроматическую плоскую волну с амплитудой с длиной волны λ, падающую на экран с щелью ширины a.
Будем считать, что щель находится в плоскости x′-y′ с центром в начале координат.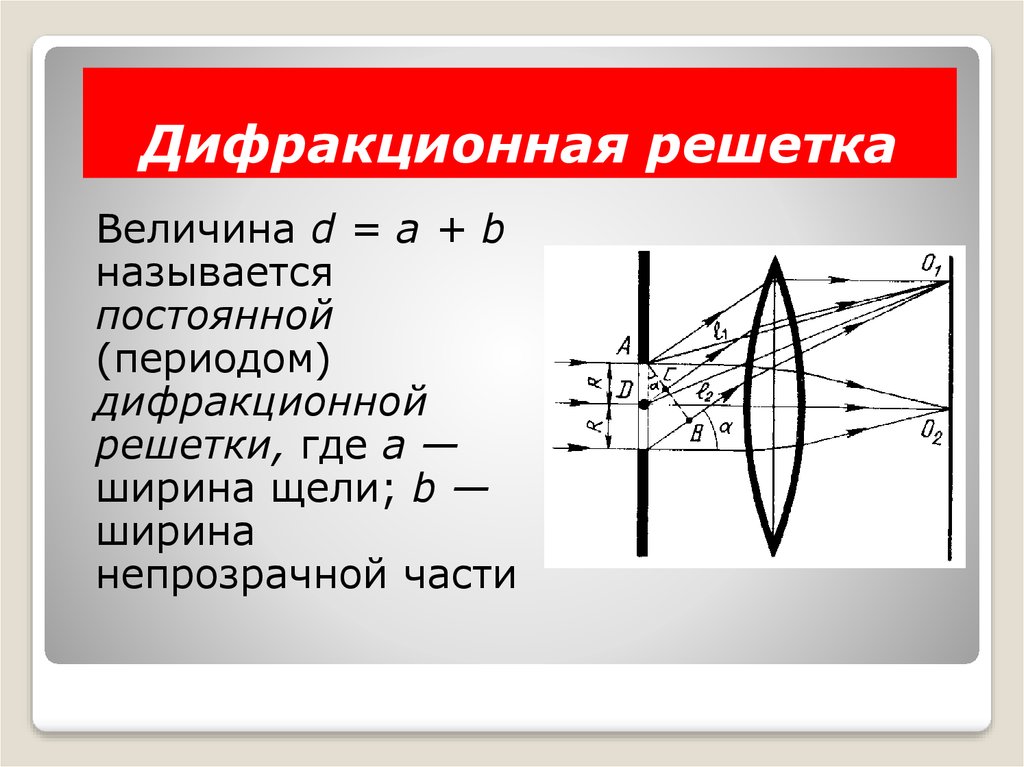 Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать
Тогда может предполагаться, что дифракция производит волну ψ, которая расходится радиально. Вдали от разреза можно записать
пусть (x′,y′,0) — точка внутри разреза, по которому мы интегрируем. Мы хотим узнать интенсивность в точке (x,0,z). Щель имеет конечный размер в x направлении (от до ), и бесконечна в y направлении ([, ]).
Расстояние r от щели определяется как:
Предполагая случай дифракции Фраунгофера, получим условие . Другими словами, расстояние до точки наблюдения много больше характерного размера щели (ширины). Используя биноминальное разложение и пренебрегая слагаемыми второго и выше порядков малости, можно записать расстояние в виде:
Видно, что 1/r перед уравнением не осциллирует, то есть даёт малый вклад в интенсивность по сравнению с экспоненциальным множителем. И тогда его можно записать приближённо как z.
Здесь мы введём некую константу ‘C’, которой обозначим все постоянные множители в предыдущем уравнении.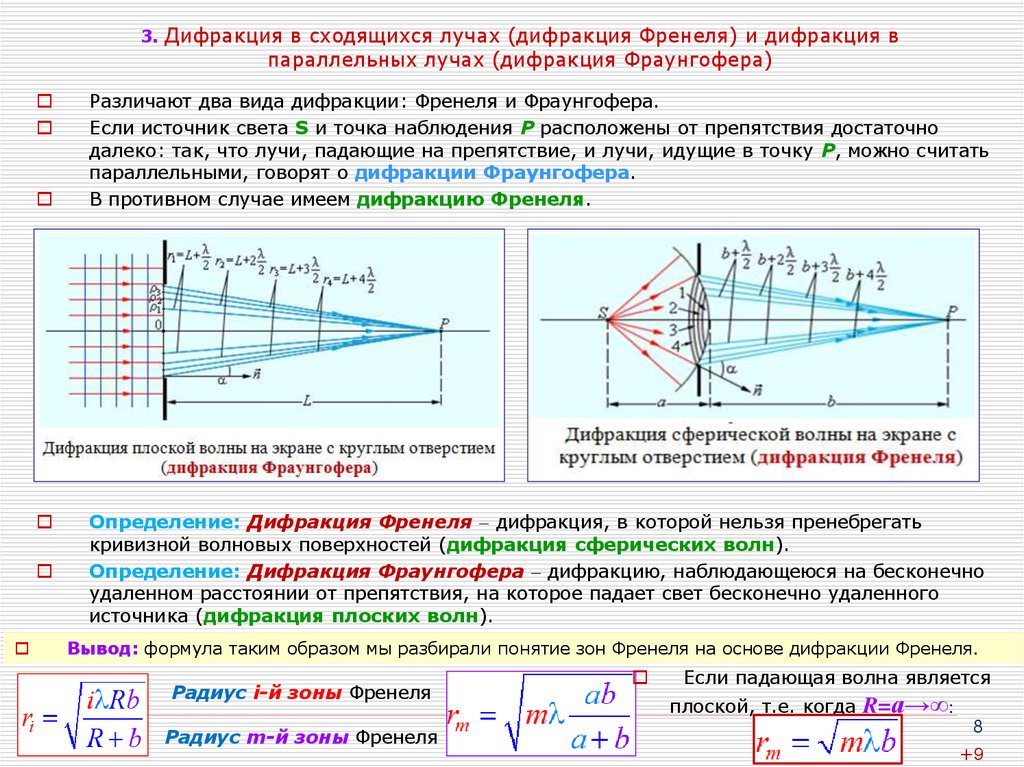 Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.
Она, в общем случае может быть комплексной, но это не важно, так как в конце нас будет интересовать только интенсивность, и нам будет интересен только квадрат модуля.
В случае дифракции Фраунгофера мало, поэтому . такое же приближение верно и для . Таким образом, считая , приводит к выражению:
Используя формулу Эйлера и её производную: и .
где ненормированная синкус функция определена как .
Подставляя в последнее выражение для амплитуды, можно получить ответ для интенсивности в виде волны в зависимости от угла θ:
См. также Дифракция на N-щелях
Дифракция на отверстии
Дифракция лазерного луча с длиной волны 650 нм, прошедшего через отверстие диаметром 0,2 мм
Дифракция звука и ультразвуковая локация
Дифракция радиоволн и радиолокация
Исследованием дифракции радиоволн занимается геометрическая теория дифракции[2]
Дифракционная решётка
Основная статья: Дифракционная решётка
Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья.
Дифракция рентгеновских лучей в кристаллах и рентгеноструктурный анализ
Дифракция света на ультразвуке
Основная статья: Акустооптика
Одним из наглядных примеров дифракции света на ультразвуке является дифракция света на ультразвуке в жидкости. В одной из постановок такого эксперимента в оптически-прозрачной ванночке в форме прямоугольного параллелепипеда с оптически-прозрачной жидкостью с помощью пластинки из пьезоматериала на частоте ультразвука возбуждается стоячая волна. В её узлах плотность воды ниже, и как следствие ниже её оптическая плотность, в пучностях — выше. Таким образом, при этих условиях ванночка с водой становится для световой волны фазовой дифракционной решёткой, на которой осуществляется дифракция в виде изменения фазовой структуры волн, что можно наблюдать в оптический микроскоп методом фазового контраста или методом тёмного поля.
Дифракция электронов
Основная статья: Дифракция электронов
Дифракция электронов — процесс рассеяния электронов на совокупности частиц вещества, при котором электрон проявляет свойства, аналогичные свойствам волны. При выполнении некоторых условий, пропуская пучок электронов через материал можно зафиксировать дифракционную картину, соответствующую структуре материала. Процесс дифракции электронов получил широкое применение в аналитических исследованиях кристаллических структур металлов, сплавов, полупроводниковых материалов.
При выполнении некоторых условий, пропуская пучок электронов через материал можно зафиксировать дифракционную картину, соответствующую структуре материала. Процесс дифракции электронов получил широкое применение в аналитических исследованиях кристаллических структур металлов, сплавов, полупроводниковых материалов.
Брегговская дифракция
Основная статья: Дифракция Брэгга
Согласно Закону Брэгга каждая точка (или отражение) в этой дифракционной картине формируется конструктивной интерференцией рентгеновских лучей, проходящих через кристалл. Эти данные могут быть использованы для определения атомной структуры кристаллов.
Дифракция от трехмерной периодической структуры, такой как атомы в кристалле называется дифракцией Брегга. Это похоже на то, что происходит, когда волны рассеиваются на дифракционной решётке. Брегговская дифракция является следствием интерференции между волнами, отражёнными от кристаллических плоскостей. Условие возникновения интерференции определяется законом Вульфа-Брегга:
Условие возникновения интерференции определяется законом Вульфа-Брегга:
- ,
где
- d — расстояние между кристаллическими плоскостями,
- θ угол скольжения — дополнительный угол к углу падения,
- λ — длина волны,
- n (n = 1,2…) — целое число называемое порядком дифракции.
Брегговская дифракция может осуществляться при использовании света с очень маленькой длиной волны, такого как рентгеновское излучение, либо волны материи, такие как нейтроны и электроны, длины волн которых сравнимы или много меньше, чем межатомное расстояние.[3] Получаемые данные дают информацию о межплоскостных расстояния, что позволяет вывести кристаллическую структуру. Дифракционный контраст, в электронных микроскопах и рентгеновских топографических устройствах, в частности, также является мощным инструментом для изучения отдельных дефектов и локальных полей деформации в кристаллах.
Дифракция частиц (нейтронов, атомов, молекул)
История исследований
Основы теории дифракции были заложены при изучении дифракции света в первой половине XIX века в трудах Юнга и Френеля. Среди других учёных, которые внесли значительный вклад в изучение дифракции: Гримальди, Гюйгенс, Араго, Пуассон, Гаусс, Фраунгофер, Бабине, Кирхгоф, Аббе, У. Г. Брэгг и У. Л. Брэгг, фон Лауэ, Роуланд, Зоммерфельд, Леонтович, Фок, Ван-Циттерт, Цернике (см. История оптики).
Среди других учёных, которые внесли значительный вклад в изучение дифракции: Гримальди, Гюйгенс, Араго, Пуассон, Гаусс, Фраунгофер, Бабине, Кирхгоф, Аббе, У. Г. Брэгг и У. Л. Брэгг, фон Лауэ, Роуланд, Зоммерфельд, Леонтович, Фок, Ван-Циттерт, Цернике (см. История оптики).
Обнаружение дифракции частиц (электронов) в 1927 году (опыт Дэвиссона и Джермера) сыграло большую роль в подтверждении существования волн де Бройля и в подтверждении концепции корпускулярно-волнового дуализма (идеи двойственной природы волн и частиц). В XX и XXI веках продолжились исследования дифракции волн на сложных структурах.
Дифракция в фотографии
Дифракцию можно наблюдать в фотографии: чрезмерное закрытие диафрагмы (относительного отверстия) приводит к падению резкости. Поэтому для сохранения оптимально резкого изображения на фотографии не рекомендуется полностью закрывать диафрагму. Нужно отметить, что для каждого объектива существует свои границы до которых стоит закрывать диафрагму, в большинстве случаев они равны f/11. [4]
[4]
См. также
- Интерференция
- Рефракция
- Рассеяние волн
- Оптика
- Физическая оптика
- Волновая оптика
- Акустооптика
- Электронная оптика
- История оптики
- Волна
Примечания
- ↑ В явлении рассеяния на мелких неоднородностях среды сказывается не только экранирование фронта волны, но и свойства самой неоднородности (скажем, водяной капли), определяющие индикатрису рассеяния, что рассматривается, например, в научной дисциплине «Оптика атмосферы» в разделе, связанном с аэрозолем.
- ↑ Боровиков В. А., Кинбер Б. Е. Геометрическая теория дифракции. М.: Связь, 1978, 247 с.
- ↑ John M. Cowley (1975) Diffraction physics (North-Holland, Amsterdam) ISBN 0-444-10791-6
- ↑ Что такое дифракция в фотографии. «Про Фото»
Литература
- Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное.
 — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
— М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7 - Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
- И. Г. Кондратьев, Г. Д. Малюжинец Дифракция волн // Физическая энциклопедия / Д. М. Алексеев, А. М. Балдин, А. М. Бонч-Бруевич, А. С. Боровик-Романов, Б. К. Вайнштейн, С. В. Вонсовский, А. В. Гапонов-Грехов, С. С. Герштейн, И. И. Гуревич, А. А. Гусев, М. А. Ельяшевич, М. Е. Жаботинский, Д. Н. Зубарев, Б. Б. Кадомцев, И. С. Шапиро, Д. В. Ширков; под общ. ред. А. М. Прохорова. — М.: Советская энциклопедия, 1988—1998.
Ссылки
- Дифракция: тематические медиа-файлы на Викискладе
Дифракция: наука о волнах и свете
Свет изгибается, когда он проходит по краю или через щель. Это искривление называется дифракцией. Вы можете легко продемонстрировать дифракцию, используя свечу или маленькую яркую лампочку фонарика и прорезь, сделанную двумя карандашами. Дифракционная картина — узор из темного и светлого, возникающий, когда свет огибает край или края — показывает, что свет обладает волнообразными свойствами.
Тема:
Физика
Свет
Waves
Ключевые слова:
Дифракция
на основе при экспонатах
Интерференция
NGSS и EP & CS:
PS
PS4
CCCS
Паттерны
и эффект
.
Инструменты и материалы
- Два чистых новых карандаша с ластиками
- Кусок прозрачного скотча (подойдет любой тонкий скотч)
- Фонарик Mini Maglite ( не заменяет другие фонари ) или свеча со спичками или зажигалкой.
- Дополнительно: Кусочки ткани, перо, пластиковая дифракционная решетка, металлический экран, человеческий волос.
Сборка
-
Зажгите свечу или, если вы используете Mini Maglite, отвинтите верхнюю часть фонарика. Крошечная лампа зажжется и будет ярко светить. ВНИМАНИЕ: если вы используете мини-светодиодный фонарь Maglite, убедитесь, что он настроен на затемнение, прежде чем отвинчивать верхнюю часть фонарика.
 Избегайте смотреть прямо на свет в течение длительного периода времени.
Избегайте смотреть прямо на свет в течение длительного периода времени.
- Оберните один слой ленты вокруг верхней части одного из карандашей, чуть ниже ластика.
Действия и уведомления
Поместите фонарь на устойчивую поверхность на расстоянии не менее одной руки от себя.
Держите два карандаша рядом, ластиком вверху. Лента, обернутая вокруг одного карандаша, должна держать карандаши немного друг от друга, образуя тонкую щель между ними, прямо под лентой. Поднесите оба карандаша к одному глазу (на расстоянии около 2,5 см) и посмотрите на источник света через прорезь между карандашами. Сожмите карандаши вместе, сделав щель меньше.
Обратите внимание, что есть линия света, перпендикулярная щели. Глядя в щель, вращайте карандаши, пока они не станут горизонтальными, и обратите внимание, что линия света становится вертикальной.
Если вы присмотритесь, то увидите, что линия состоит из крошечных пятен света.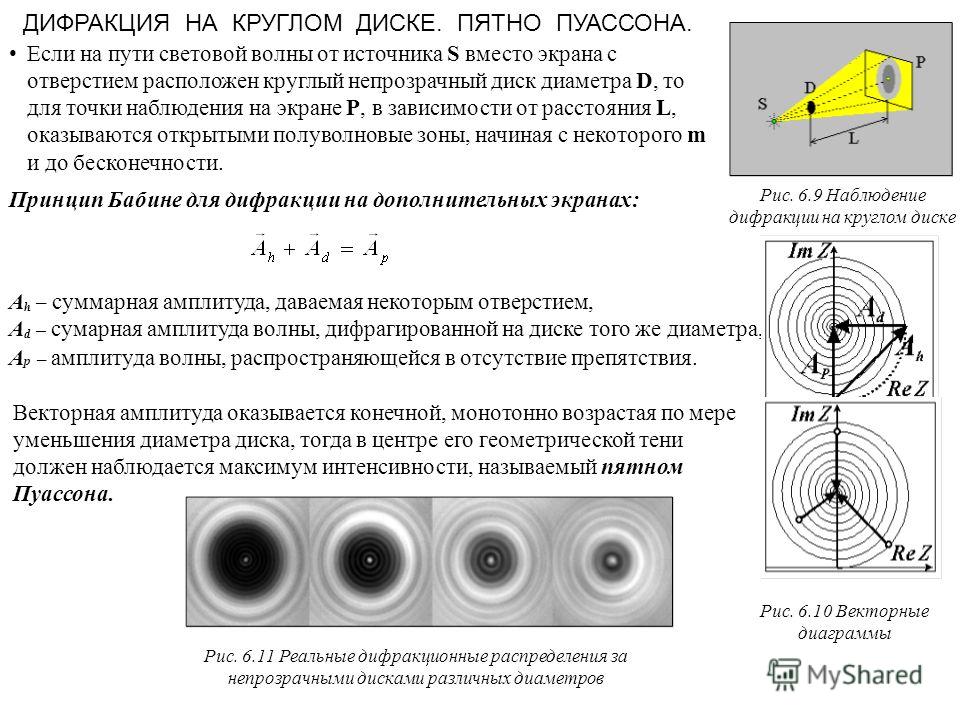 Когда вы сжимаете щель, световые пятна увеличиваются и расходятся, удаляясь от центрального источника света, и их становится легче увидеть. Обратите внимание, что у пятен есть синие и красные края, а синие края расположены ближе к источнику света.
Когда вы сжимаете щель, световые пятна увеличиваются и расходятся, удаляясь от центрального источника света, и их становится легче увидеть. Обратите внимание, что у пятен есть синие и красные края, а синие края расположены ближе к источнику света.
Туго натяните волосы и держите их на расстоянии около 2,5 см от глаз. Переместите волосы, пока они не окажутся между вашим глазом и источником света, и обратите внимание, что свет распространяется в виде линии капель от волос, точно так же, как это было от щели. Вращайте волосы и наблюдайте, как вращается линия капель.
Посмотрите на свет через кусок ткани, перо, дифракционную решетку или кусок металлического экрана. Вращайте каждый объект, пока вы просматриваете его.
Что происходит?
Черные полосы между световыми пятнами показывают, что волна связана со светом. Световые волны, проходящие через щель, распространяются, перекрываются и складываются, образуя дифракционную картину, которую вы видите. Там, где гребень одной волны пересекается с гребнем другой волны, две волны объединяются, образуя большую волну, и вы видите яркое пятно света. Там, где впадина одной волны пересекается с гребнем другой волны, волны компенсируют друг друга, и вы видите темную полосу.
Там, где гребень одной волны пересекается с гребнем другой волны, две волны объединяются, образуя большую волну, и вы видите яркое пятно света. Там, где впадина одной волны пересекается с гребнем другой волны, волны компенсируют друг друга, и вы видите темную полосу.
Угол, под которым преломляется свет, пропорционален длине волны света. Красный свет, например, имеет большую длину волны, чем синий свет, поэтому он изгибается больше, чем синий свет. Эта разная степень изгиба придает каплям цветные края: синие внутри, красные снаружи.
Чем уже щель, тем больше распространяется свет. На самом деле угол между двумя соседними темными полосами на дифракционной картине обратно пропорционален ширине щели.
Тонкие объекты, такие как прядь волос, также преломляют свет. Свет, проходящий вокруг волос, распространяется, перекрывается и создает дифракционную картину. Ткань и перья, которые состоят из множества более мелких и тонких частей, создают сложные дифракционные картины.
Дальше
В тускло освещенной комнате посмотрите одним глазом на лампочку Mini Maglite (свеча не подойдет). Обратите внимание на линии света, исходящие от источника света, как семена, исходящие из центра одуванчика.
Как найти происхождение этих линий? Вращайте источник света и обратите внимание, что линии света не вращаются. Поверните голову и обратите внимание, что линии вращаются. Держите руку или каталожную карточку перед глазами, чтобы они не закрывали вам вид на источник света (щелкните, чтобы увеличить рисунок ниже).
Обратите внимание, что вы все еще видите полный круг линий, исходящих от источника света. Эффект на самом деле происходит в вашем глазу, поскольку световые линии распространяются на сетчатку из-за дефектов в тканях вашей роговицы.
Похожие закуски
CD Spectroscope
Превратите старый компакт-диск в спектроскоп для анализа света.
Модель интерференции мыльной пленки
Смоделируйте поведение света, отражающегося от поверхностей мыльной пленки.
Мыльная пленка на банке
Почему мы видим цвета в мыльных пузырях?
Связанные экспонаты
Дифракционные тени
Тени, сделанные лазерным светом, имеют светлые и темные полосы.
Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
Атрибуция: Исследовательский педагогический институт
17.1 Понимание дифракции и интерференции — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Объяснять волновое поведение света, включая дифракцию и интерференцию, включая роль конструктивной и деструктивной интерференции в экспериментах Юнга с одной и двумя щелями
- Выполнение расчетов с учетом дифракции и интерференции, в частности длины волны света, с использованием данных двухщелевой интерференционной картины
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (7) Научные концепции.
 Учащийся знает характеристики и поведение волн. Ожидается, что студент:
Учащийся знает характеристики и поведение волн. Ожидается, что студент:
- (Д) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера
Основные термины раздела
| дифракция | Принцип Гюйгенса | однотонный | волновой фронт |
Дифракция и интерференция
Поддержка учителей
Поддержка учителей
[BL]Объясните конструктивное и деструктивное вмешательство графически на доске.
[OL]Попросите учащихся внимательно посмотреть на тень. Спросите, почему края не являются четкими линиями. Объясните, что это вызвано дифракцией, одним из волновых свойств электромагнитного излучения. Определите нанометр по отношению к другим метрическим измерениям длины.
[AL]Спросите учащихся, какие скорости, частоты и длины волн остаются неизменными, а какие изменяются при переходе луча света из одной среды в другую. Обсудите эти величины с точки зрения цветов (длин волн) видимого света.
Мы знаем, что видимый свет — это электромагнитная волна, на которую реагируют наши глаза. Как мы видели ранее, свет подчиняется уравнению
с=fλ,с=fλ,
, где c=3,00×108c=3,00×108 м/с — скорость света в вакууме, f – частота электромагнитной волны в Гц (или s –1 ), λλ – ее длина волны в м. Диапазон видимых длин волн составляет приблизительно от 380 до 750 нм. Как и для всех волн, свет распространяется прямолинейно и действует как луч, когда взаимодействует с объектами, в несколько раз превышающими его длину волны. Однако, когда он взаимодействует с более мелкими объектами, он заметно проявляет свои волновые характеристики. Интерференция — это идентифицирующее поведение волны.
На рис. 17.2 можно увидеть как лучевые, так и волновые характеристики света. Лазерный луч, испускаемый обсерваторией, отражает поведение луча, поскольку он движется по прямой линии. Пропускание чистого одноволнового луча через вертикальные щели шириной, близкой к длине волны луча, обнаруживает волновой характер света. Здесь мы видим, как луч распространяется по горизонтали в виде узора из ярких и темных областей, которые вызваны систематической конструктивной и деструктивной интерференцией. Поскольку это характерно для волнового поведения, интерференция наблюдается для водяных, звуковых и световых волн.
17.2 можно увидеть как лучевые, так и волновые характеристики света. Лазерный луч, испускаемый обсерваторией, отражает поведение луча, поскольку он движется по прямой линии. Пропускание чистого одноволнового луча через вертикальные щели шириной, близкой к длине волны луча, обнаруживает волновой характер света. Здесь мы видим, как луч распространяется по горизонтали в виде узора из ярких и темных областей, которые вызваны систематической конструктивной и деструктивной интерференцией. Поскольку это характерно для волнового поведения, интерференция наблюдается для водяных, звуковых и световых волн.
Рисунок 17.2 (а) Луч света, испускаемый лазером в обсерватории Параналь (часть Европейской южной обсерватории в Чили), действует как луч, движущийся по прямой линии. (кредит: Юрий Белецкий, Европейская южная обсерватория) (б) Лазерный луч, проходящий через сетку вертикальных щелей, создает интерференционную картину, характерную для волны. (кредит: Шимон и Слава Рыбка, Wikimedia Commons)
То, что интерференция является характеристикой распространения энергии волнами, более убедительно демонстрируется волнами на воде. На рис. 17.3 показаны водные волны, проходящие через щели между некоторыми камнями. Вы можете легко увидеть, что ширина зазоров аналогична длине волны, и это вызывает интерференционную картину, когда волны проходят за зазоры. Поперечное сечение волн на переднем плане показало бы гребни и впадины, характерные для интерференционной картины.
На рис. 17.3 показаны водные волны, проходящие через щели между некоторыми камнями. Вы можете легко увидеть, что ширина зазоров аналогична длине волны, и это вызывает интерференционную картину, когда волны проходят за зазоры. Поперечное сечение волн на переднем плане показало бы гребни и впадины, характерные для интерференционной картины.
Рисунок 17,3 Набегающие волны (вверху рисунка) проходят через щели в скалах и создают интерференционную картину (на переднем плане).
Свет имеет волновые характеристики в различных средах, а также в вакууме. Когда свет переходит из вакуума в какую-либо среду, например воду, его скорость и длина волны меняются, но его частота f остается неизменной. Скорость света в среде v=c/nv=c/n, где n — его показатель преломления. Если вы разделите обе части уравнения c=fλc=fλ на n , вы получаете c/n=v=fλ/nc/n=v=fλ/n . Следовательно, v=fλnv=fλn, где λnλn — длина волны в среде, а
λn=λn,λn=λn,
, где λλ — длина волны в вакууме, а n — показатель преломления среды. Отсюда следует, что длина волны света в любой среде меньше, чем в вакууме. Например, в воде, имеющей n = 1,333, диапазон видимых длин волн составляет от (380 нм)/1,333 до (760 нм)/1,333, или λn=λn= 285–570 нм. Хотя длины волн меняются при перемещении из одной среды в другую, цвета не меняются, поскольку цвета связаны с частотой.
Отсюда следует, что длина волны света в любой среде меньше, чем в вакууме. Например, в воде, имеющей n = 1,333, диапазон видимых длин волн составляет от (380 нм)/1,333 до (760 нм)/1,333, или λn=λn= 285–570 нм. Хотя длины волн меняются при перемещении из одной среды в другую, цвета не меняются, поскольку цвета связаны с частотой.
Голландский ученый Христиан Гюйгенс (1629–1695) разработал полезную технику для детального определения того, как и где распространяются волны. Он использовал волновые фронты, которые представляют собой точки на поверхности волны, имеющие одну и ту же постоянную фазу (например, все точки, составляющие гребень водной волны). Принцип Гюйгенса гласит: «Каждая точка на фронте волны является источником вейвлетов, которые распространяются в прямом направлении с той же скоростью, что и сама волна. Новый волновой фронт — это линия, касательная ко всем вейвлетам».
На рис. 17.4 показано, как применяется принцип Гюйгенса. Фронт волны — это длинный фронт, который движется; например, гребень или корыто. Каждая точка волнового фронта излучает полукруглую волну, которая движется со скоростью v . Они нарисованы позже в момент времени t , так что они переместились на расстояние s=vts=vt . Новый волновой фронт представляет собой линию, касательную к вейвлетам, и находится там, где волна находится в момент времени t . Принцип Гюйгенса работает для всех типов волн, включая волны воды, звуковые волны и световые волны. Это будет полезно не только при описании того, как распространяются световые волны, но и как они интерферируют.
Фронт волны — это длинный фронт, который движется; например, гребень или корыто. Каждая точка волнового фронта излучает полукруглую волну, которая движется со скоростью v . Они нарисованы позже в момент времени t , так что они переместились на расстояние s=vts=vt . Новый волновой фронт представляет собой линию, касательную к вейвлетам, и находится там, где волна находится в момент времени t . Принцип Гюйгенса работает для всех типов волн, включая волны воды, звуковые волны и световые волны. Это будет полезно не только при описании того, как распространяются световые волны, но и как они интерферируют.
Рисунок 17,4 Принцип Гюйгенса применим к прямолинейному волновому фронту. Каждая точка на фронте волны излучает полукруглый вейвлет, который перемещается на расстояние s=vts=vt. Новый волновой фронт представляет собой линию, касательную к вейвлетам.
Что происходит, когда волна проходит через отверстие, например свет проникает через открытую дверь в темную комнату? Что касается света, вы ожидаете увидеть резкую тень от дверного проема на полу комнаты, и вы ожидаете, что свет не будет огибать углы в другие части комнаты. Когда звук проходит через дверь, вы слышите его повсюду в комнате и, таким образом, понимаете, что звук распространяется при прохождении через такой проем. Чем отличается поведение звуковых волн от световых в этом случае? Ответ заключается в том, что длины волн, из которых состоит свет, очень короткие, поэтому свет действует как луч. Звук имеет длину волны порядка размера двери, поэтому он огибает углы.
Когда звук проходит через дверь, вы слышите его повсюду в комнате и, таким образом, понимаете, что звук распространяется при прохождении через такой проем. Чем отличается поведение звуковых волн от световых в этом случае? Ответ заключается в том, что длины волн, из которых состоит свет, очень короткие, поэтому свет действует как луч. Звук имеет длину волны порядка размера двери, поэтому он огибает углы.
Поддержка учителей
Поддержка учителей
[OL]Обсудите тот факт, что для того, чтобы дифракционная картина была видимой, ширина щели должна примерно равняться длине волны света. Попытайтесь дать учащимся представление о длине волны видимого света, отметив, что человеческий волос примерно в 100 раз шире.
Если свет проходит через меньшие отверстия, часто называемые щелями, вы можете использовать принцип Гюйгенса, чтобы показать, что свет изгибается так же, как и звук (см. рис. 17.5). Огибание волной краев отверстия или препятствия называется дифракцией. Дифракция — это волновая характеристика, которая имеет место для всех типов волн. Если для явления наблюдается дифракция, это свидетельствует о том, что явление вызвано волнами. Таким образом, горизонтальная дифракция лазерного луча после прохождения через щели на рис. 17.2 свидетельствует о том, что свет обладает свойствами волны.
Дифракция — это волновая характеристика, которая имеет место для всех типов волн. Если для явления наблюдается дифракция, это свидетельствует о том, что явление вызвано волнами. Таким образом, горизонтальная дифракция лазерного луча после прохождения через щели на рис. 17.2 свидетельствует о том, что свет обладает свойствами волны.
Рисунок 17,5 Принцип Гюйгенса применялся к прямому фронту волны, падающему на отверстие. Края волнового фронта изгибаются после прохождения через отверстие, этот процесс называется дифракцией. Величина изгиба является более экстремальной для небольшого отверстия, что согласуется с тем фактом, что волновые характеристики наиболее заметны при взаимодействии с объектами примерно того же размера, что и длина волны.
И снова волны на воде представляют собой знакомый пример волнового явления, которое легко наблюдать и понимать, как показано на рис. 17.6.
Рисунок
17,6
Океанские волны проходят через отверстие в рифе, образуя дифракционную картину. Дифракция возникает из-за того, что ширина отверстия аналогична длине волны.
Дифракция возникает из-за того, что ширина отверстия аналогична длине волны.
Смотреть физику
Однощелевая интерференция
В этом видео показаны математические расчеты, необходимые для прогнозирования дифракционных картин, вызванных однощелевой интерференцией.
Какие значения м обозначают место деструктивной интерференции на однощелевой дифракционной картине?
- целые числа, кроме нуля
- целых чисел
- вещественных числа без нуля
- действительные числа
Тот факт, что принцип Гюйгенса работал, не считался достаточным доказательством того, что свет является волной. Люди также не хотели принимать волновую природу света, потому что это противоречило идеям Исаака Ньютона, который все еще пользовался большим уважением. Признание волнового характера света пришло после 1801 г., когда английский физик и врач Томас Юнг (1773–1829 гг. ) провел ставший уже классическим эксперимент с двумя щелями (см. рис. 17.7).
) провел ставший уже классическим эксперимент с двумя щелями (см. рис. 17.7).
Рисунок 17,7 Эксперимент Юнга с двумя щелями. Здесь свет одной длины волны проходит через пару вертикальных щелей и создает на экране дифракционную картину — многочисленные вертикальные светлые и темные линии, разбросанные по горизонтали. Без дифракции и интерференции свет просто образовал бы две линии на экране.
Когда свет проходит через узкие щели, он преломляется в полукруглые волны, как показано на рис. 17.8 (а). Чистая конструктивная интерференция возникает там, где волны выстраиваются в линию гребень к гребню или впадина к впадине. Чисто деструктивное вмешательство происходит там, где они выстраиваются от гребня к впадине. Свет должен падать на экран и рассеиваться в наших глазах, чтобы рисунок был виден. Аналогичная картина для волн на воде показана на рис. 17.8 (b). Обратите внимание, что области конструктивной и деструктивной интерференции выходят из щелей под определенными углами к исходному лучу. Эти углы зависят от длины волны и расстояния между щелями, как вы увидите ниже.
Эти углы зависят от длины волны и расстояния между щелями, как вы увидите ниже.
Рисунок 17,8 Двойные щели создают два интерферирующих источника волн. (а) Свет распространяется (дифрагирует) от каждой щели, потому что щели узкие. Волны перекрываются и интерферируют конструктивно (светлые линии) и деструктивно (темные области). Вы можете увидеть эффект, только если свет падает на экран и рассеивается в ваших глазах. (b) Двухщелевая интерференционная картина волн на воде почти идентична таковой для света. Волновое воздействие больше всего в областях конструктивной интерференции и наименьшее в областях деструктивной интерференции. в) Когда свет, прошедший через двойные щели, падает на экран, мы видим такую картину.
Виртуальная физика
Интерференция волн
Это моделирование демонстрирует большинство волновых явлений, обсуждаемых в этом разделе. Во-первых, наблюдайте интерференцию между двумя источниками электромагнитного излучения без добавления щелей. Посмотрите, как волны воды, звук и свет демонстрируют интерференционные картины. Оставайтесь со световыми волнами и используйте только один источник. Создайте дифракционные картины с одной щелью, а затем с двумя. Возможно, вам придется отрегулировать ширину щели, чтобы увидеть рисунок.
Посмотрите, как волны воды, звук и свет демонстрируют интерференционные картины. Оставайтесь со световыми волнами и используйте только один источник. Создайте дифракционные картины с одной щелью, а затем с двумя. Возможно, вам придется отрегулировать ширину щели, чтобы увидеть рисунок.
Визуально сравните ширину щели с длиной волны. Когда вы получаете наиболее четкую дифракционную картину?
- когда ширина щели больше длины волны
- , когда ширина щели меньше длины волны
- , когда ширина щели сравнима с длиной волны
- , когда ширина щели бесконечна
Расчеты с учетом дифракции и интерференции
Поддержка учителей
Поддержка учителей
[BL] Греческая буква θθ пишется как тета . Греческая буква λλ пишется как лямда . Оба произносятся так, как вы ожидаете от правописания. Множественное число от максимальное и минимальное равно максимальное и минимальное соответственно.
Множественное число от максимальное и минимальное равно максимальное и минимальное соответственно.
[OL]Объясните, что монохромный означает одноцветный. Монохроматический также означает одну частоту . Синус угла — это противолежащая сторона прямоугольного треугольника, деленная на гипотенузу. Противоположный означает противоположный данному острому углу. Обратите внимание, что знак угла всегда ≥ 1,
Тот факт, что длина волны света одного цвета или монохроматического света может быть рассчитана по его двухщелевой дифракционной картине в экспериментах Юнга, подтверждает вывод о том, что свет обладает волновыми свойствами. Чтобы понять основу таких расчетов, рассмотрим, как две волны проходят от щелей к экрану. Каждая щель находится на разном расстоянии от заданной точки на экране. Таким образом, на каждый путь укладывается разное количество длин волн. Волны начинаются от щелей в фазе (гребень к гребню), но заканчиваются в противофазе (гребень к впадине) на экране, если пути различаются по длине на половину длины волны, создавая деструктивные помехи. Если пути различаются на целую длину волны, то волны приходят на экран синфазно (гребень к гребню), конструктивно интерферируя. В более общем случае, если пути, по которым проходят две волны, отличаются на любое полуцелое число длин волн (12λ, 32λ, 52λ и т. д.) (12λ, 32λ, 52λ и т. д.), то возникает деструктивная интерференция. Точно так же, если пути, по которым проходят две волны, отличаются на любое целое число длин волн (λ, 2λ, 3λ и т. д.) (λ, 2λ, 3λ и т. д.), возникает конструктивная интерференция.
Таким образом, на каждый путь укладывается разное количество длин волн. Волны начинаются от щелей в фазе (гребень к гребню), но заканчиваются в противофазе (гребень к впадине) на экране, если пути различаются по длине на половину длины волны, создавая деструктивные помехи. Если пути различаются на целую длину волны, то волны приходят на экран синфазно (гребень к гребню), конструктивно интерферируя. В более общем случае, если пути, по которым проходят две волны, отличаются на любое полуцелое число длин волн (12λ, 32λ, 52λ и т. д.) (12λ, 32λ, 52λ и т. д.), то возникает деструктивная интерференция. Точно так же, если пути, по которым проходят две волны, отличаются на любое целое число длин волн (λ, 2λ, 3λ и т. д.) (λ, 2λ, 3λ и т. д.), возникает конструктивная интерференция.
На рис. 17.9 показано, как определить разность длин пути для волн, идущих от двух щелей к общей точке экрана. Если экран находится на большом расстоянии по сравнению с расстоянием между щелями, то угол θθ между траекторией и линией от щелей, перпендикулярной экрану (см. рисунок), для каждой траектории примерно одинаков. Это приближение и простая тригонометрия показывают, что разность длин ΔLΔL равна dsinθdsinθ, где d — расстояние между щелями,
рисунок), для каждой траектории примерно одинаков. Это приближение и простая тригонометрия показывают, что разность длин ΔLΔL равна dsinθdsinθ, где d — расстояние между щелями,
ΔL=dsinθ. ΔL=dsinθ.
Чтобы получить конструктивную интерференцию для двойной щели, разность длин пути должна быть целым числом, кратным длине волны, или
dsinθ=mλ, для m=0,1,−1,2,−2,… (конструктивный).dsinθ=mλ, для m=0,1,−1,2,−2,…(конструктивный).
Точно так же, чтобы получить деструктивную интерференцию для двойной щели, разность длин пути должна быть кратной половине длины волны, или
dsinθ=(m+½)λ, для m=0,1,−1,2,−2,… (разрушающий).dsinθ=(m+½)λ, для m=0,1,−1,2 ,−2,…(деструктивный).
Число м порядка помех. Например, м = 4 — это помехи четвертого порядка.
Рисунок
17,9
Пути от каждой щели до общей точки на экране различаются на величину d sin θd sin θ, если предположить, что расстояние до экрана много больше, чем расстояние между щелями (здесь не в масштабе).
На рис. 17.10 показано, как уменьшается интенсивность полос конструктивной интерференции с увеличением угла.
Рисунок 17.10 Интерференционная картина для двойной щели имеет интенсивность, которая падает с углом. На фотографии видно множество ярких и темных линий или полос, образованных светом, проходящим через двойную щель.
Свет, проходящий через одиночную щель, образует дифракционную картину, несколько отличную от той, что образуется от двойных щелей. На рис. 17.11 показана картина дифракции от одной щели. Обратите внимание, что центральный максимум больше, чем с обеих сторон, и что интенсивность быстро уменьшается с обеих сторон.
Рисунок
17.11
(а) Однощелевая дифракционная картина. Монохроматический свет, проходящий через одну щель, дает центральный максимум и множество меньших и более тусклых максимумов по обеим сторонам. Центральный максимум в шесть раз выше показанного. (b) На рисунке показан яркий центральный максимум и более тусклые и тонкие максимумы по бокам. (c) Расположение минимумов показано через λλ и D .
(c) Расположение минимумов показано через λλ и D .
Анализ однощелевой дифракции показан на рис. 17.12. Если предположить, что экран находится очень далеко по сравнению с размером щели, лучи, направляющиеся к общей цели, почти параллельны. Это приближение допускает ряд тригонометрических операций, которые приводят к уравнениям для минимумов, создаваемых деструктивной интерференцией.
Dsinθ=mλDsinθ=mλ
или
DyL=mλDyL=mλ
Когда лучи движутся прямо вперед, они остаются в фазе, и получается центральный максимум. Однако, когда лучи проходят под углом θθ относительно первоначального направления луча, каждый луч проходит разное расстояние до экрана, и они могут приходиться в фазе или в противофазе. Таким образом, луч из центра проходит на расстояние λ/2λ/2 дальше, чем луч от верхнего края щели, приходят в противофазе и деструктивно интерферируют. Точно так же для каждого луча между вершиной и центром щели существует луч между центром и низом щели, который проходит расстояние λ/2λ/2 дальше от общей точки на экране и, таким образом, деструктивно интерферирует. . Симметрично ниже прямого луча будет еще один минимум под тем же углом.
. Симметрично ниже прямого луча будет еще один минимум под тем же углом.
Рисунок 17.12 Уравнения однощелевой дифракционной картины, где λ — длина волны света, D — ширина щели, θθ — угол между линией от щели до минимума и линией, перпендикулярной экрану, L — расстояние от щели до экрана, y — расстояние от центра узора до минимума, а м — ненулевое целое число, указывающее порядок минимума.
Ниже мы суммируем уравнения, необходимые для последующих расчетов.
Скорость света в вакууме c , длина волны света λλ и его частота f связаны следующим образом.
с=fλc=fλ
Длина волны света в среде, λnλn, по сравнению с его длиной волны в вакууме, λλ, равна
λn=λn.λn=λn.
17,1
Для расчета положения конструктивной интерференции для двойной щели разность длин пути должна быть целым кратным м , длины волны. λλ
λλ
dsinθ=mλ, для m=0,1,−1,2,−2,… (конструктивно), dsinθ=mλ, для m=0,1,−1,2,−2,…(конструктивно),
, где d — расстояние между щелями, θθ — угол между линией от щелей до максимума и линией, перпендикулярной к преграде, в которой расположены щели. Для расчета положения деструктивной интерференции для двойной щели разность длин пути должна быть полуцелым кратным длине волны:
dsinθ=(m+½)λ, для m=0,1,−1,2,−2,… (разрушающий).dsinθ=(m+½)λ, для m=0,1,−1,2 ,−2,…(деструктивный).
Для однощелевой дифрактограммы ширина щели, D , расстояние до первого ( м = 1) минимума деструктивной интерференции, y , расстояние от щели до экрана, L , а длина волны λλ определяется как
DyL=λ.DyL=λ.
Также для однощелевой дифракции
Dsinθ=mλ,Dsinθ=mλ,
, где θθ — угол между линией от щели до минимума и линией, перпендикулярной экрану, а м — порядок минимума.
Рабочий пример
Двухщелевая интерференция
Предположим, вы пропускаете свет гелий-неонового лазера через две щели, разделенные расстоянием 0,0100 мм, и обнаруживаете, что третья яркая линия на экране формируется под углом 10,95° по отношению к падающему лучу. Какова длина волны света?
Стратегия
Третья светлая линия обусловлена конструктивной интерференцией третьего порядка, что означает, что м = 3. Вам дано d = 0,0100 мм и θθ = 10,95º. Таким образом, длину волны можно найти, используя уравнение dsinθ=mλdsinθ=mλ для конструктивной интерференции.
Решение
Уравнение dsinθ=mλdsinθ=mλ . Решение для длины волны λλ дает
λ=dsinθm.λ=dsinθm.
17,2
Замена известных значений дает
λ=(0,0100 мм)(sin 10,95°)3=6,33×10-4 мм=633 нм. λ=(0,0100 мм)(sin 10,95°)3=6,33×10-4 мм=633 нм.
λ=(0,0100 мм)(sin 10,95°)3=6,33×10-4 мм=633 нм.
17.3
Обсуждение
В трехзначном числе 633 нм — это длина волны света, излучаемого обычным гелий-неоновым лазером. Не случайно этот красный цвет похож на тот, который излучают неоновые огни. Однако более важным является тот факт, что интерференционные картины можно использовать для измерения длины волны. Янг сделал это для видимых длин волн. Его аналитический метод до сих пор широко используется для измерения электромагнитных спектров. Для данного порядка угол конструктивной интерференции увеличивается с увеличением λλ, поэтому можно получить спектры (измерения интенсивности в зависимости от длины волны).
Рабочий пример
Однощелевая дифракция
Видимый свет с длиной волны 550 нм падает на одну щель и дает второй минимум дифракции под углом 45,0° к направлению падения света. Какова ширина щели?
Стратегия
Исходя из данной информации и предполагая, что экран находится далеко от щели, вы можете использовать уравнение Dsinθ=mλDsinθ=mλ, чтобы найти D .
Раствор
Приведены следующие величины: λλ = 550 нм, м = 2 и θ2θ2 = 45,0°. Решение уравнения Dsinθ=mλDsinθ=mλ для D и подстановка известных значений дает
D=mλsinθ=2(550 нм)sin45,0°=1,56 × 10–6 м.D=mλsinθ=2(550 нм)sin45,0 °=1,56×10-6 м.
17.4
Обсуждение
Вы видите, что щель узкая (всего в несколько раз больше длины волны света). Это согласуется с тем фактом, что свет должен взаимодействовать с объектом, сравнимым по размеру с его длиной волны, чтобы проявлять значительные волновые эффекты, такие как эта дифракционная картина с одной щелью. 9{\circ} относительно падающего луча. Какова длина волны света?
-
51,5\,\текст{нм}
-
77,3\,\текст{нм}
-
515\,\текст{нм}
-
773\,\текст{нм}
2.
Какова ширина одиночной щели, через которую проходит оранжевый свет с длиной волны 610 нм, образуя первый дифракционный минимум под углом 30,0°?
- 0,863 мкм
- 0,704 мкм
- 0,610 мкм
- 1,22 мкм
Проверьте свое понимание
Поддержка учителей
Поддержка учителей
Используйте эти задачи, чтобы оценить достижение учащимися целей обучения раздела. Если учащиеся борются с определенной целью, эти проблемы помогут определить, какие и направят учащихся к соответствующим темам.
3.
Какой аспект луча монохроматического света изменяется, когда он попадает из вакуума в воду, и как он изменяется?
-
Длина волны сначала уменьшается, а затем увеличивается.

-
Длина волны сначала увеличивается, а затем уменьшается.
-
Длина волны увеличивается.
-
Длина волны уменьшается.
4.
Выйдите на улицу на солнечный свет и понаблюдайте за своей тенью. У него нечеткие края, даже если у вас их нет. Это дифракционный эффект? Объяснять.
-
Это эффект дифракции. Все ваше тело действует как источник нового волнового фронта.

-
Это эффект дифракции. Каждая точка на краю вашей тени действует как источник нового волнового фронта.
-
Это эффект преломления. Все ваше тело действует как источник нового волнового фронта.
-
Это эффект преломления. Каждая точка на краю вашей тени действует как источник нового волнового фронта.
5.
Какой аспект монохроматического зеленого света меняется, когда он переходит из вакуума в алмаз, и как он меняется?
-
Длина волны сначала уменьшается, а затем увеличивается.
 Дифракцией называется: Дифракция | это… Что такое Дифракция?
Дифракцией называется: Дифракция | это… Что такое Дифракция?

 8 Дифракция электронов
8 Дифракция электронов