Дифракция света. Дифракционная решетка. | Объединение учителей Санкт-Петербурга
Основные ссылки
CSS adjustments for Marinelli theme
Объединение учителей Санкт-Петербурга
Форма поиска
Поиск
Вы здесь
Главная » Дифракция света. Дифракционная решетка.
|
Дифракция света |
|
|
Характерным проявлением волновых свойств света является дифракция света — отклонение света от прямолинейного распространения на резких неоднородностях среды. Дифракция была открыта Ф.Гримальди в конце XVII в. Объяснение явления дифракции света дано Т. Юнгом и О. Френелем, которые не только дали описание экспериментов по наблюдению явлений интерференции и дифракции света, но и объяснили свойство прямолинейности распространения света с позиций волновой теории. |
|
|
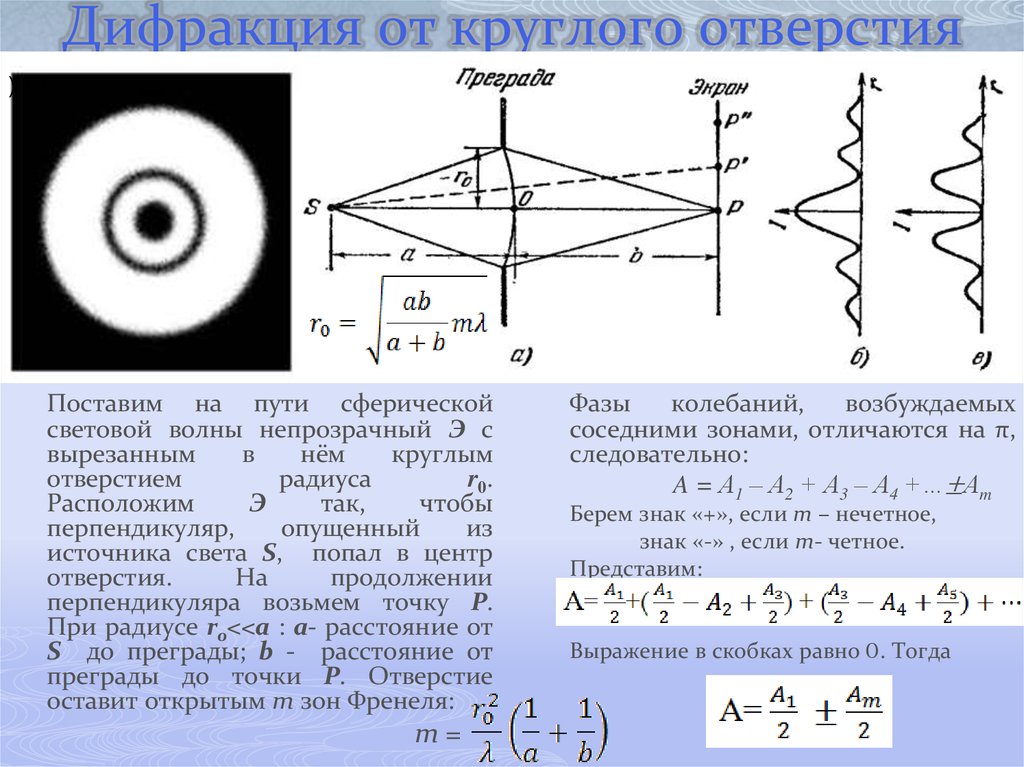
Зоны Френеля Принцип Гюйгенса — Френеля: волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции. Для того чтобы найти амплитуду световой волны от точечного монохроматического источника света А в произвольной точке О изотропной среды, надо источник света окружить сферой радиусом r=ct. Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке О, т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки О до волновой поверхности В равно r0. Первая зона Френеля ограничивается точками волновой поверхности, расстояния от которых до точки О равны: , где λ — длина световой волны. Вторая зона . Аналогично определяются границы других зон. Если разность хода от двух соседних зон равна половине длины волны, то колебания от них приходят в точку О в противоположных фазах и наблюдается интерференционный минимум, если разность хода равна длине волны, то наблюдается интерференционный максимум. Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно). Расчеты позволили понять, каким образом свет от точечного источника, испускающего сферические волны, достигает произвольной точки О пространства. |
|
|
|
|
|
Дифракция от различных препятствий:
|
|
|
Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны |
|
|
Дифракция наблюдается хорошо на расстоянии . Если , то дифракция невидна и получается резкая тень (d — диаметр экрана). Эти соотношения определяют границы применимости геометрической оптики. Если наблюдение ведется на расстоянии , где d—размер предмета, то начинают проявляться волновые свойства света. На рис. показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны. |
|
|
Интерференционные картины от разных точек предмета перекрываются, и изображение смазывается, поэтому прибор не выделяет отдельные детали предмета. Дифракция устанавливает предел разрешающей способности любого оптического прибора. Разрешающая способность человеческого глаза приблизительно равна одной угловой минуте: , где D — диаметр зрачка; телескопа α=0,02» микроскопа: увеличение не более 2-103 раз. |
|
|
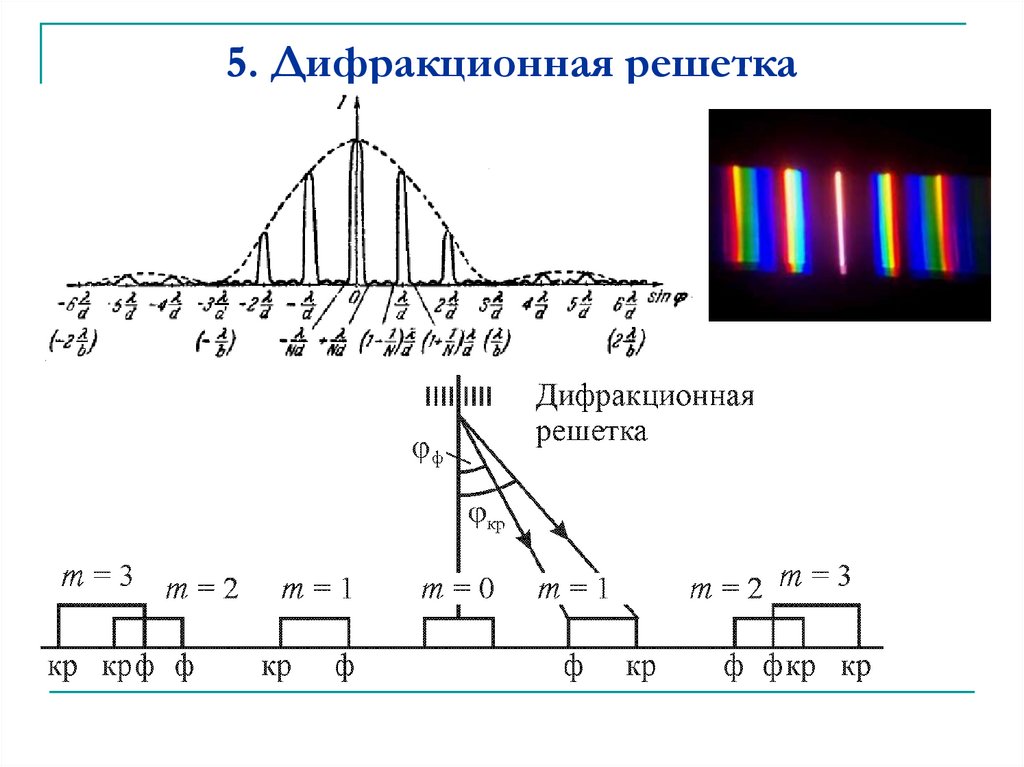
Дифракционная решетка |
|
|
Дифракционная решетка — система препятствий (параллельных штрихов), сравнимых по размерам с длиной волны. Величина d = a + b называется постоянной (периодом) дифракционной решетки ( равен 0, ± 1, ± 2 и т.д.). |
|
|
Определение λ с помощью дифракционной решетки
|
|
Теги:
конспект
|
Дифракция • Джеймс Трефил, энциклопедия «Двести законов мироздания»
200 законов мироздания > Физика
Дифракционная картина возникает в результате интерференции вторичных световых волн при огибании лучами света препятствий или их прохождении через множественные отверстия.
Идея о волновой природе света (см. Спектр электромагнитного излучения) получила серьезное подтверждение в результате открытия и изучения в начале XIX века явлений интерференции и дифракции света. Традиционное со времен Ньютона и из-за его непререкаемого авторитета долго остающееся неизменным представление о свете как о потоке частиц — так называемая корпускулярная теория света — оказалось поставленным под серьезное сомнение после открытия интерференции. А вскоре о корпускулярной теории и вовсе забыли — почти на целое столетие — в результате открытия и исследования явлений дифракции, в результате чего волновая теория света стала новым ортодоксальным и незыблемым представлением о нем. Лишь после объяснения с корпускулярной точки зрения фотоэлектрического эффекта и зарождения квантовой механики корпускулярные представления о свете получили второе рождение в рамках принципа дополнительности.
Традиционное со времен Ньютона и из-за его непререкаемого авторитета долго остающееся неизменным представление о свете как о потоке частиц — так называемая корпускулярная теория света — оказалось поставленным под серьезное сомнение после открытия интерференции. А вскоре о корпускулярной теории и вовсе забыли — почти на целое столетие — в результате открытия и исследования явлений дифракции, в результате чего волновая теория света стала новым ортодоксальным и незыблемым представлением о нем. Лишь после объяснения с корпускулярной точки зрения фотоэлектрического эффекта и зарождения квантовой механики корпускулярные представления о свете получили второе рождение в рамках принципа дополнительности.
Основы явления дифракции можно понять, если обратиться к принципу Гюйгенса, согласно которому каждая точка на пути распространения светового луча может рассматриваться как новый независимый источник вторичных волн, и дальнейшая дифракционная картина оказывается обусловленной интерференцией этих вторичных волн. При взаимодействии световой волны с препятствием часть вторичных волн Гюйгенса блокируется. Например, при падении световой волны сверху под острым углом на бритву на верхней плоскости бритвы вторичные волны Гюйгенса образовываться будут, а на нижней нет. Однако в результате конструктивной интерференции вторичные волны всё равно обогнут бритву, и мы увидим там сплошной световой луч, как если бы на пути его распространения ничего не стояло. Подобное же «огибание» волной препятствия можно наблюдать и в морском порту в шторм: суда, стоящие на якоре за волнорезом, который, казалось бы, должен полностью гасить волны, тем не менее «гуляют» вверх-вниз благодаря вторичным волнам.
При взаимодействии световой волны с препятствием часть вторичных волн Гюйгенса блокируется. Например, при падении световой волны сверху под острым углом на бритву на верхней плоскости бритвы вторичные волны Гюйгенса образовываться будут, а на нижней нет. Однако в результате конструктивной интерференции вторичные волны всё равно обогнут бритву, и мы увидим там сплошной световой луч, как если бы на пути его распространения ничего не стояло. Подобное же «огибание» волной препятствия можно наблюдать и в морском порту в шторм: суда, стоящие на якоре за волнорезом, который, казалось бы, должен полностью гасить волны, тем не менее «гуляют» вверх-вниз благодаря вторичным волнам.
Если источник света и точка наблюдения удалены от препятствия на незначительное расстояние, исходные и результирующие лучи света не параллельны друг другу — и мы наблюдаем дифракцию Френеля (дифракцию в ближней зоне). Если же источник и точка наблюдения находятся на значительном расстоянии от препятствия (точки дифракции), лучи практически параллельны, и мы наблюдаем дифракцию Фраунгофера (дифракцию в дальней зоне).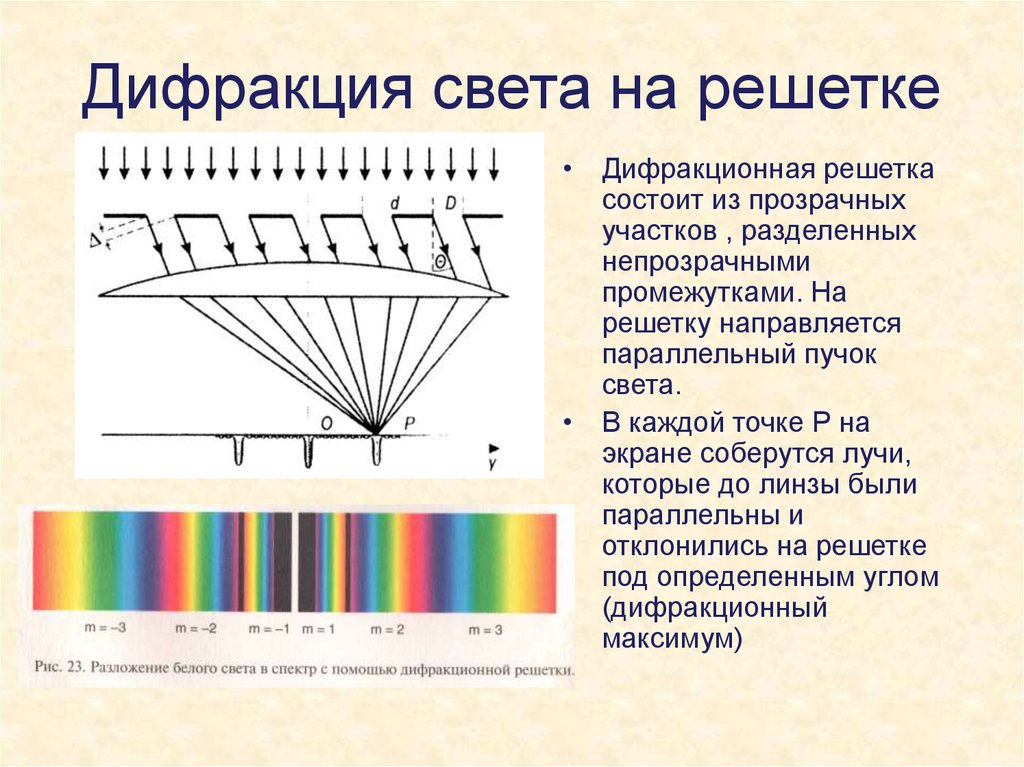 Фраунгофер, кстати, изобрел целый ряд важных прецизионных оптических приборов, включая дифракционную решетку. Она представляет собой систему расположенных на небольшом расстоянии друг от друга микроскопических линий, отражающих свет. Изначально это была затемненная стеклянная пластина с тщательно нанесенными на нее параллельными штрихами. Каждый такой штрих отражает свет, и его можно считать вторичным источником волн Гюйгенса, которые вступают в интерференцию и взаимно усиливаются под определенными углами после рассеяния на решетке.
Фраунгофер, кстати, изобрел целый ряд важных прецизионных оптических приборов, включая дифракционную решетку. Она представляет собой систему расположенных на небольшом расстоянии друг от друга микроскопических линий, отражающих свет. Изначально это была затемненная стеклянная пластина с тщательно нанесенными на нее параллельными штрихами. Каждый такой штрих отражает свет, и его можно считать вторичным источником волн Гюйгенса, которые вступают в интерференцию и взаимно усиливаются под определенными углами после рассеяния на решетке.
Начиная с середины XIX века дифракционная решетка стала важнейшим инструментом спектроскопии — с ее помощью ученые исследуют спектры излучения светящихся объектов и спектры поглощения различных веществ и по ним определяют их химический состав. Одним из важнейших открытий Фраунгофера стало обнаружение темных линий в спектре Солнца. Сегодня мы знаем, что они возникают в результате поглощения световых волн определенной длины относительно холодным веществом солнечной короны, и благодаря этому можем судить о химическом составе нашего светила.
См. также:
около 100 г. н.э. |
Закон отражения света |
1815 |
Закон Брюстера |
1896 |
Критерий Рэлея |
1912 |
Закон Брэгга |
Йозеф ФРАУНГОФЕР
Joseph von Fraunhofer, 1787–1826
Немецкий физик и оптик, уроженец Штраубинга (Straubing), сын ремесленника-стеклодува. Рано осиротев, пошел в подмастерья к стекольщику. В возрасте 14 лет серьезно пострадал при обрушении новостройки, провел несколько дней под завалом и благодаря этому несчастному случаю приобрел некоторую популярность. В частности, получил от властей Баварии денежную компенсацию, на которую открыл собственное стекольное дело, с которым в 1806 году присоединился к знаменитой баварской фирме Utzscheider, которая в те дни пользовалась славой производителя лучших в мире оптических инструментов. Явление дифракции Фраунгофер исследовал с чисто прикладной точки зрения: делом своей жизни он считал изобретение идеальных ахроматических линз, которые не давали бы радужного ореола вокруг изображения.
Явление дифракции Фраунгофер исследовал с чисто прикладной точки зрения: делом своей жизни он считал изобретение идеальных ахроматических линз, которые не давали бы радужного ореола вокруг изображения.
1
Показать комментарии (1)
Свернуть комментарии (1)
Написать комментарий
1690 |
Принцип Гюйгенса |
1807 |
Интерференция |
1818 |
Дифракция |
1970-е
Дифференциальное использование ресурсов
1924
Дисперсия: атомная теория
Новостная рассылка
«Элементы» в соцсетях:
|
телескоп Ѳ ptics.
◄
6.3.2. Аберрации и расширенные
объекты
▐
6.4.1. Телескопы для тестирования звезд
► Непосредственный эффект волнового фронта
отклонение от идеальной сферичности означает менее эффективную концентрацию энергии
в пределах дифракционной картины.
Конструктивная интерференция волн на центральном пике и на большей части
центральный диск уменьшается, а по краям увеличивается
и дальше, в районе колец. В действительности энергия
переносится из центральной части выкройки наружу. Это неблагоприятное
изменение в распределении интенсивности создает всю картину — и, таким образом,
точечное изображение, которое он представляет, кажется больше и менее контрастным. Прямой
следствием является более низкое качество как точечных, так и расширенных изображений объектов,
что можно измерить как потерю контраста/разрешения.
Изображение точечного объекта, образованное идеальным сферическим волновым фронтом, представляет собой дифракционную картину с максимально возможной
концентрация энергии ( РИС. 94 ). Диаметр первых минимумов
(примерно середина первого темного кольца) дифракционной картины
определяет « диск Эйри », в честь британского
астроном сэр Джордж Б. Эйри, который первым математически описал
явление дифракции еще в 1834 году. Диск Эйри идеального
дифракционная картина имеет линейный радиус 1,22λF,
угловой радиус 1,22λ/D
(в радианах),
и содержит 83,8% всей энергии. Второй минимальный линейный радиус равен 2,23λF,
третья 3.24λF,
и так далее. Пиковая интенсивность первого
яркое кольцо составляет 0,00175 центральной интенсивности, в то время как
второе яркое кольцо 0,00042. Эта конфигурация интенсивности определяет предел разрешения пары точечных объектов с одинаковой интенсивностью и близкий к оптимальному уровень яркости как ~λ/D в радианах (113,4/D в угловых секундах, для λ=0,55 мкм и D в мм). Хотя двойственность изображения все же можно обнаружить при меньшие расстояния, это связано с вытянутой формой двух близких точечные изображения, а не из-за того, что они визуально разделены. Радиальная симметрия паттерна не ограничивается лучшим расположением фокуса: он сохраняется и в расфокусированных паттернах. Отличительной особенностью идеальной дифракционной картины является его идентичный в- и шаблон не в фокусе для любой заданной степени расфокусировки. Хотя размер
центральный дифракционный диск определяет предел разрешения относительно
яркие точечные объекты, это количество энергии, рассеянной по диску
что критически влияет на предел разрешения деталей
на малоконтрастных протяженных объектах.
РИСУНОК 94 : Идеальная дифракция узор в его продольном (слева) и поперечном сечении (справа) с центром в лучшем фокусе. Волновая интерференция формируется радиально симметричное распределение интенсивности, состоящее из центральные максимумы и ряд последовательных пиков быстро убывающей интенсивности, разделенные минимумами интенсивности (справа). Подобные последовательные спад интенсивности также формируется в осевом направлении. Первые осевые минимумы происходит на 1 волне расфокусировки от центральных максимумов, делая центральную аксиальную пик 16λF2 длинный (слева).
Любое отклонение волнового фронта от сферического
приводит к истощению энергии из центрального диска только для того, чтобы снова появиться
в районе колец. Основной и самый вредный эффект — осветление.
принадлежащий
кольца, расширяя и смягчая изображения точечных объектов.
Увеличение самого центрального диска сравнительно
незаметны, становятся значимыми только при больших уровнях ошибок.
Так же, как форма волнового фронта
отклонение варьируется в зависимости от различных типов аберраций, поэтому
распределение интенсивности рисунка. Каждая аберрация оставляет свой уникальный
отпечаток пальца на внутри- и внеочаговом изображении узора, как показано
в РИС.
РИСУНОК 96 : Моделирование эффекта
общие аберрации на дифрактограмме беспрепятственного (слева) и 30%
закрытые апертуры, для ~ 0,95 (вверху) и ~ 0,80 Штреля, и 4λ
расфокусировать; картина в фокусе увеличена в 5 раз по сравнению с расфокусированной
шаблон.
2 —
Сбалансированная первичная (4-го порядка) сферическая
аберрация , λ/8
(вверху) и λ/4
P-V, заметно осветляет первый
яркое кольцо; внутренний рисунок крупнее и тусклее, с
интенсивность падает от центра к краю, противоположному расфокусированному
распределение интенсивности паттерна. Внефокусные паттерны меняются местами для негатива. 3 — Сбалансированный 6-й/4-й порядок сферическая аберрация , 0,2λ и 0,4λ P-V, часто наблюдаемые в апо-рефракторах и Максутов-Кассегрен телескопы, формы более отчетливо отличаются не в фокусе узоры, чем сферические более низкого порядка. Сфокусированный узор имеет первые два ярких кольца почти одинаковой яркости, отчетливо отличается от единственного яркого кольца первичной сферической формы.
4 — Кома , 0,21λ и 0,42λ P-V. вызывает асимметричную деформацию рисунка, с фокусом интенсивность распространяется в направлении, противоположном направлению увеличение интенсивности в любом из расфокусированных паттернов. С увеличение уровня ошибки, центральный диск рисунка в фокусе расширяется и децентрируется в направлении потока интенсивности.
5 — Астигматизм , 0,18λ
и 0,37λ,
создает крестообразный рисунок в фокусе с эллиптическими внефокусными рисунками
ориентированы перпендикулярно друг другу.
6 — Край загнут вниз , 0,50λ, радиус 95%,
3.4 дает почти идентичные узоры с обеих сторон
расфокусировка, за исключением того, что внутриочаговый рисунок несколько слабее и менее контрастен,
с менее выраженным внешним краем.
7 — Пережатая оптика может производить различные деформации рисунка. Представленный узор — трилистник — будет из-за опоры или удерживающих элементов (клипы) имеющие почти идеальная трехсторонняя симметрия (0,18λ и 0,36λ П-В).
8 — Форма трубы текущий где более теплый воздух скапливается ближе к верху часть трубки, имеет повышенную интенсивность в фокусе в ориентация воздушного потока, появляющаяся либо как частичная осветление колец или, с увеличением аберрации, почти расширение непрерывной интенсивности (0,26λ и 0,64λ).
9 — Атмосферный
турбулентность вызывает постоянно меняющийся случайный волновой фронт
шероховатость. Обратите внимание, что звезда довольно яркий в телескоп, с рисунком без аберраций, показывающим один яркое кольцо четкое, и намеки на второе, даже на третье. Внешний вид кольцевой структуры и размер центральных максимумов сфокусированная звезда, а также картина интенсивности расфокусированных изображений меняются в зависимости от телескопической яркости звезды. Специфический узнаваемый эффект различных аберрации на виде дифракционной картины, и ее очень высокая чувствительность даже к небольшим уровням аберраций делает возможным тестирование телескопические системы, основанные на характеристике дифракционной картины они формируют. Рассмотрение эффекта аберраций в несколько затененном трехмерном контексте помогает лучше понять дифракционные изображения в любой вертикальной плоскости изображения.
Все аберрации находятся на «дифракционно-ограниченном» уровне для среднеквадратичной ошибки волнового фронта 0,0745λ и 0,80 Штреля. Для света, движущегося слева направо, сферическая аберрация «перекорректирована», то есть краевые лучи фокусируются длиннее, чем параксиальные лучи (для «недокоррекции» паттерн зеркально перевернут, т. е. этот паттерн показывает «недостаточную коррекцию» для света, идущего справа налево) . Две асимметричные аберрации, астигматизм и кома, даны в трех ракурсах, поскольку их трехмерное дифракционное изображение не является осесимметричным. Наличие центрального препятствия изменяет все дифракционное изображение, как показано ниже. Общее изменение шаблона аналогично изменению для чистой апертуры, поэтому этот набор симуляций концентрируется на первичной сферической аберрации.
Опять же, для света, движущегося слева направо, показана «чрезмерная коррекция». В шаблоне без аберраций все лучи приходят в один и тот же лучший фокус. Аберрированные узоры имеют лучший фокус в середине, при этом краевые лучи фокусируются правее, а параксиальные лучи — слева от него (поскольку положение параксиального фокуса не меняется, это означает, что аберрированные узоры смещены влево, чем больше аберрация, тем больше). Для 1/4 волны P-V параксиальный и маргинальный фокусы разделены двумя волнами расфокусировки, с лучшим фокусом посередине между ними. Разделение пропорционально аберрации, поэтому оно вдвое меньше при 1/8 волны. Внешние лучи, фокусирующиеся за пределами внутренних лучей, приводят к тому, что внутренняя сторона фокуса (левая) имеет более широкий разброс энергии, в то время как близкие порядки дифракции делают внутреннюю часть сходящегося конуса на этой стороне более насыщенной, чем на другой. Эта функция может быть полезна для аппроксимации величины сферической аберрации закрытых апертур при тестировании звезд. ◄ 6.3.2. Аберрации и расширенные объекты ▐ 6.4.1. Телескопы для тестирования звезд ► Дом | Комментарии
|
Полученная дифрактограмма | Анализ кристаллической структуры: A Primer
Фильтр поиска панели навигации Oxford AcademicCrystal Structure Analysis: A PrimerCrystallographyBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicCrystal Structure Analysis: A PrimerCrystallographyBooksJournals Термин поиска на микросайте
Расширенный поиск
-
Иконка Цитировать Цитировать
-
Разрешения
-
Делиться
- Твиттер
- Подробнее
Cite
Glusker, Jenny Pickworth, and Kenneth N Trueblood,
‘Полученная дифрактограмма’
,
Анализ кристаллической структуры: A Primer
(
Оксфорд,
2010;
онлайн Edn,
Oxford Academic
, 12 ноября. 10.1093/oso/9780199576340.003.0014,
10.1093/oso/9780199576340.003.0014,
, по состоянию на 18 октября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicCrystal Structure Analysis: A PrimerCrystallographyBooksJournals Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicCrystal Structure Analysis: A PrimerCrystallographyBooksJournals Термин поиска на микросайте
Advanced Search
Abstract
В этой главе мы опишем те факторы, которые контролируют интенсивность брэгговских отражений, и как их выразить математически, чтобы мы могли рассчитать карту электронной плотности.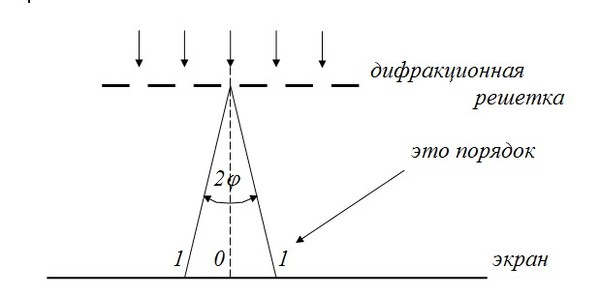 Интенсивность брэгговских отражений зависит от расположения атомов в элементарной ячейке и от того, как рентгеновские лучи, рассеянные этими атомами, интерферируют друг с другом. Поэтому дифракционная картина имеет большое разнообразие интенсивностей. Измеренные данные дифракции рентгеновских лучей состоят из списка относительной интенсивности I (hkl), ее индексов (h, k и l) и угла рассеяния 2θ для каждого брэгговского отражения. Все значения интенсивности I (hkl) находятся в одном относительном масштабе, и весь этот набор данных описывает «дифракционную картину». Он используется как часть входных данных, необходимых для определения кристаллической структуры. Как уже указывалось при изучении картин дифракции от щелей и от различного расположения молекул, угловые положения (2θ), при которых наблюдается рассеянное излучение, зависят только от размеров кристаллической решетки и длины волны используемого излучения, тогда как Интенсивности I (hkl) различных дифрагированных пучков зависят главным образом от природы и расположения атомов внутри каждой элементарной ячейки.
Интенсивность брэгговских отражений зависит от расположения атомов в элементарной ячейке и от того, как рентгеновские лучи, рассеянные этими атомами, интерферируют друг с другом. Поэтому дифракционная картина имеет большое разнообразие интенсивностей. Измеренные данные дифракции рентгеновских лучей состоят из списка относительной интенсивности I (hkl), ее индексов (h, k и l) и угла рассеяния 2θ для каждого брэгговского отражения. Все значения интенсивности I (hkl) находятся в одном относительном масштабе, и весь этот набор данных описывает «дифракционную картину». Он используется как часть входных данных, необходимых для определения кристаллической структуры. Как уже указывалось при изучении картин дифракции от щелей и от различного расположения молекул, угловые положения (2θ), при которых наблюдается рассеянное излучение, зависят только от размеров кристаллической решетки и длины волны используемого излучения, тогда как Интенсивности I (hkl) различных дифрагированных пучков зависят главным образом от природы и расположения атомов внутри каждой элементарной ячейки.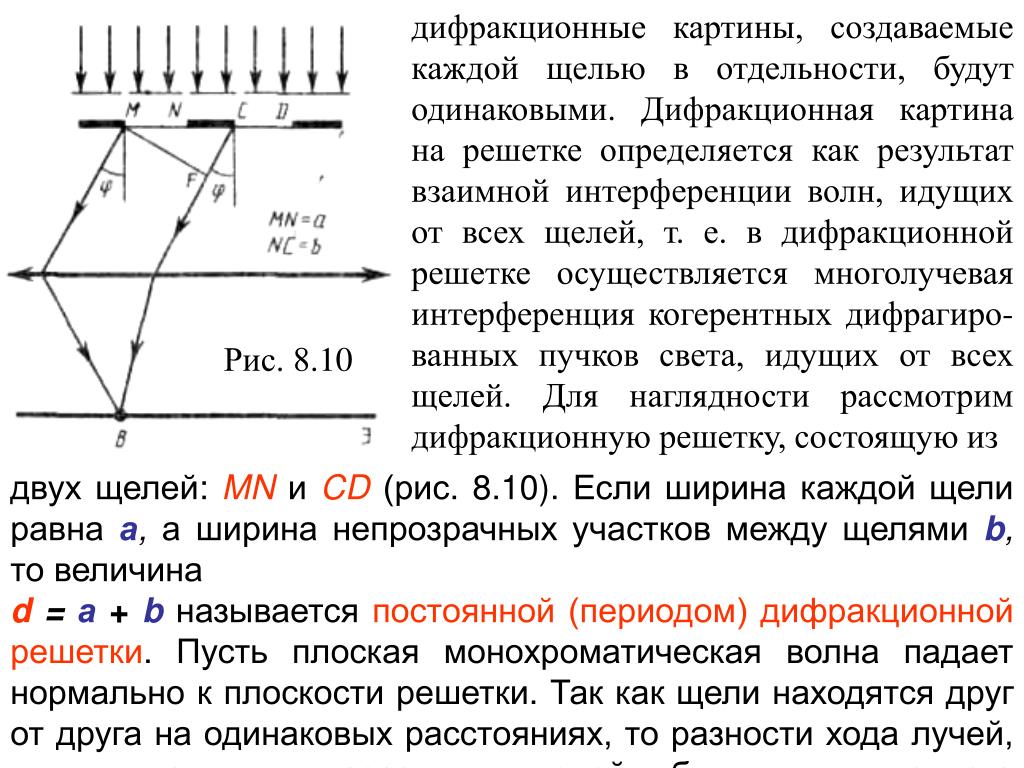 Именно эти два элемента, размеры элементарной ячейки кристалла и расположение его атомов, составляют то, что мы подразумеваем под «кристаллической структурой». Их определение является основным объектом анализа, описанного здесь. Как показано на рис. 1.1b и сопровождающем его обсуждении, а также снова упомянуто в начале главы 3, рентгеновские лучи, рассеянные электронами в атомах кристалла, не могут рекомбинироваться ни одной известной линзой. Следовательно, чтобы получить изображение рассеивающего вещества в кристалле, «структуры» этого кристалла, нам необходимо смоделировать эту рекомбинацию, а это значит, что мы должны найти способ наложения рассеянных волн с правильными фазовыми соотношениями между ними. , чтобы дать изображение материала, который произвел рассеяние, то есть электронов в атомах.
Именно эти два элемента, размеры элементарной ячейки кристалла и расположение его атомов, составляют то, что мы подразумеваем под «кристаллической структурой». Их определение является основным объектом анализа, описанного здесь. Как показано на рис. 1.1b и сопровождающем его обсуждении, а также снова упомянуто в начале главы 3, рентгеновские лучи, рассеянные электронами в атомах кристалла, не могут рекомбинироваться ни одной известной линзой. Следовательно, чтобы получить изображение рассеивающего вещества в кристалле, «структуры» этого кристалла, нам необходимо смоделировать эту рекомбинацию, а это значит, что мы должны найти способ наложения рассеянных волн с правильными фазовыми соотношениями между ними. , чтобы дать изображение материала, который произвел рассеяние, то есть электронов в атомах.
Ключевые слова: температура абсолютного нуля, координаты, дифракция, карта электронной плотности, метод тяжелого атома, интенсивность, коэффициент изотропного смещения, ортогональная система, фаза, относительный фазовый угол
Субъект
Кристаллография
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic.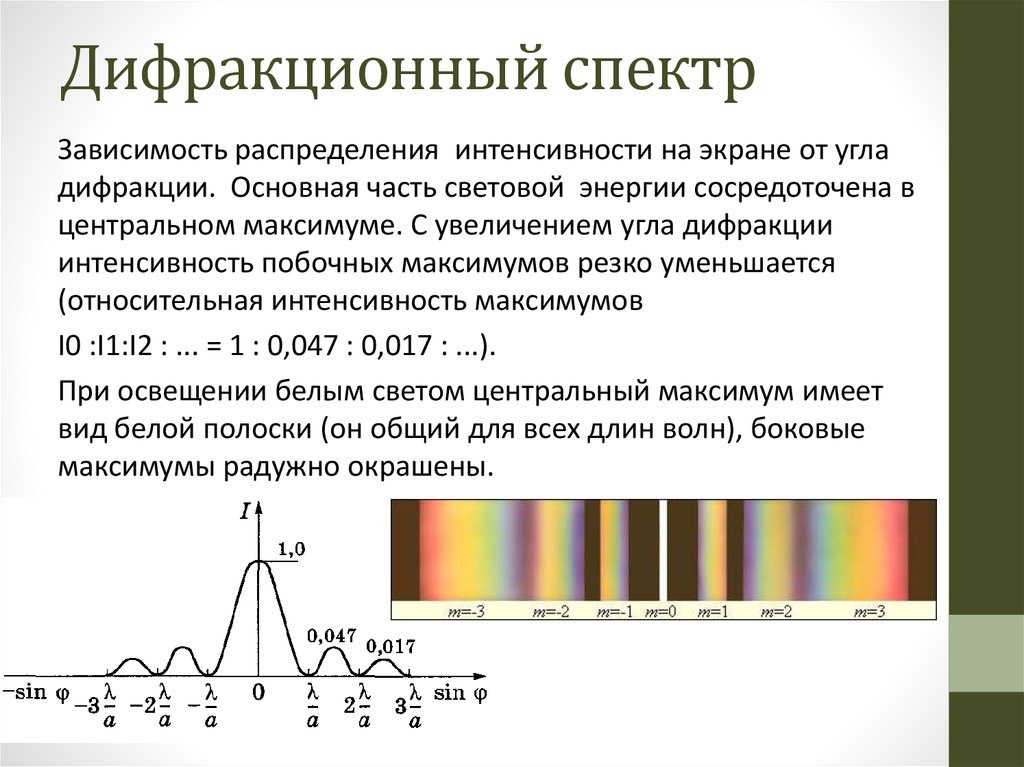 Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т.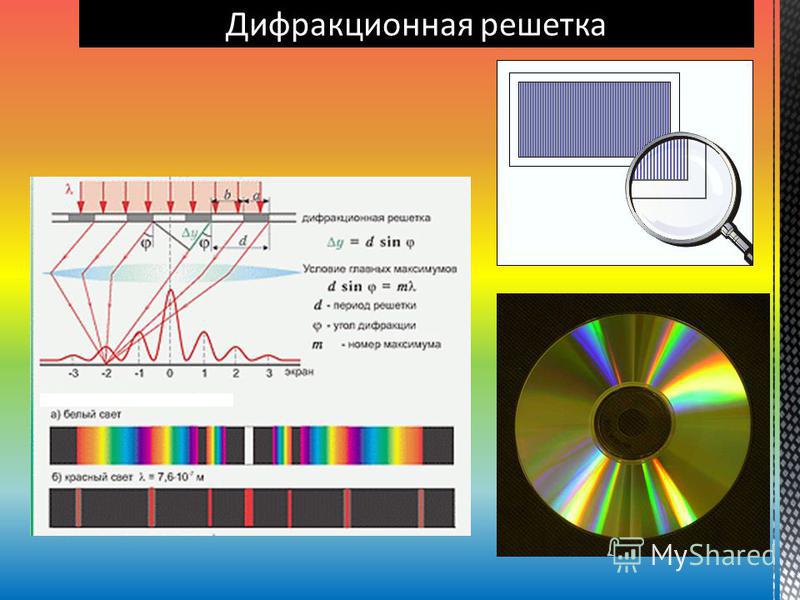 д.
д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
Использование симметрии для нахождения центра дифракционной картины
Дифракция сверхбыстрых электронов включает анализ дифракционных картин . Вот пример дифракционной картины для тонкой (<100 нм) чешуйки графита 1 :
Дифракционная картина графита (Исходный код) Дифракционная картина фактически представляет собой интенсивность преобразования Фурье. Учитывая, что кристаллы, такие как графит, хорошо упорядочены, дифракционные пики (то есть компоненты Фурье) очень велики. Вы можете видеть, что дифракционная картина шестикратно симметрична; это потому, что атомы в графите располагаются в виде сот, которые также имеют шестикратную симметрию. В этих экспериментах фундаментальная компонента Фурье настолько сильна, что нам необходимо ее заблокировать.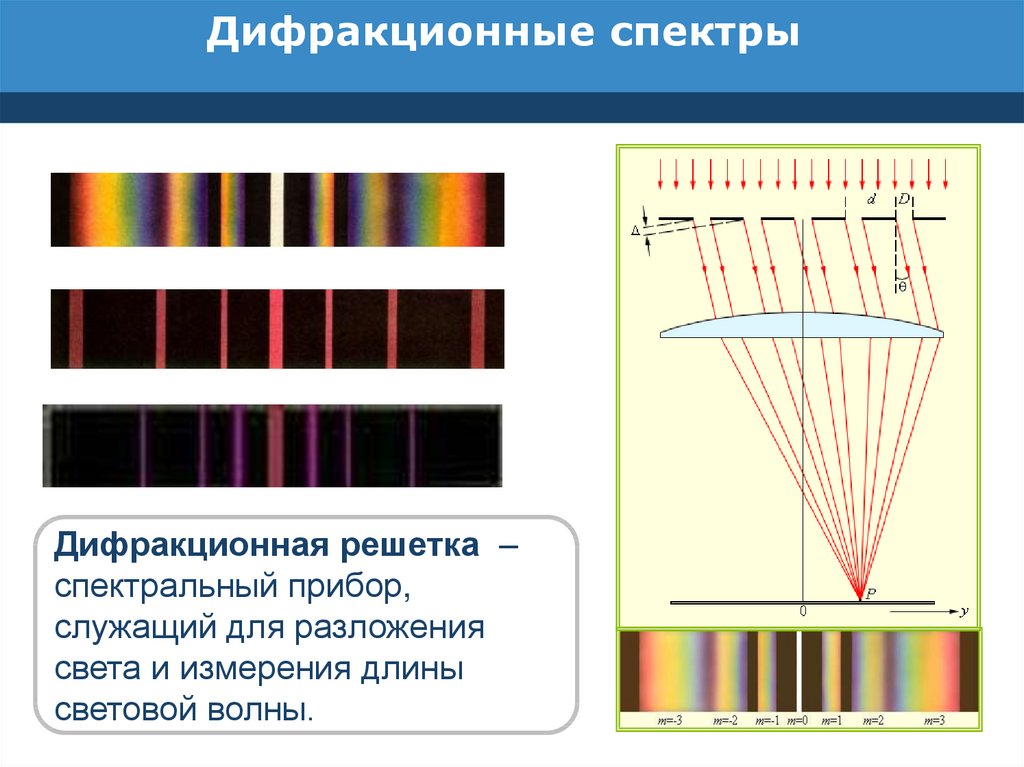 Вот что такое черное балка-блок об.
Вот что такое черное балка-блок об.
Существуют кристаллы, которые не так хорошо упорядочены, как графит. Представьте себе порошок, состоящий из множества мелких кристаллитов, размер каждого из которых составляет примерно 50 х 50 х 50 нм. Дифракция электронов через такой образец дает своего рода среднее значение всех возможных дифракционных картин. Вот пример с поликристаллическим хромом:
Дифрактограмма поликристаллического хрома (исходный код)Каждое кольцо в приведенной выше картине соответствует компоненту Фурье. Обратите внимание еще раз, насколько симметричен узор; сам материал достаточно симметричен, поэтому основная компонента Фурье должна быть заблокирована.
Для моей работы над iris-ued, пакетом анализа данных для сверхбыстрого рассеяния электронов, мне нужно было найти надежный автоматический способ получить центр таких дифракционных картин, чтобы избавиться от ручной работы, необходимой сейчас. Итак, давайте посмотрим, как!
Первая попытка: центр масс
Первая наивная попытка может начаться с центра масс , т.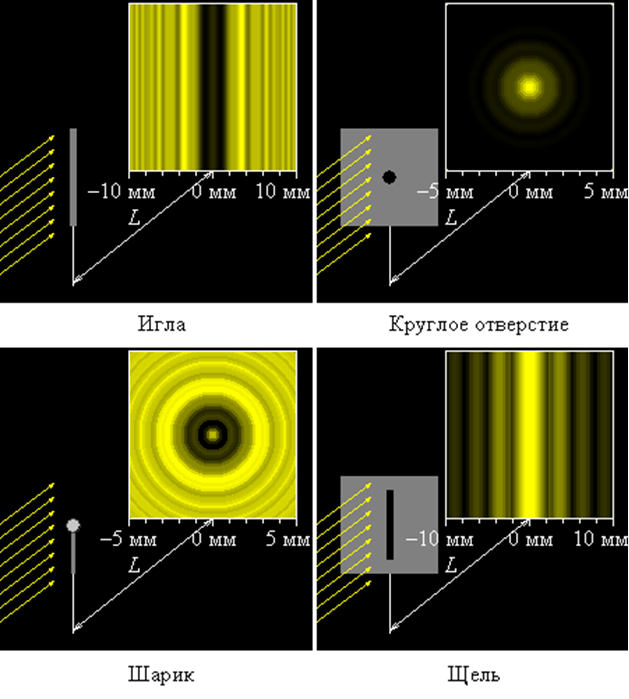 е. со средним значением позиций пикселей, взвешенных по их интенсивности. Поскольку интенсивность симметрична относительно центра, центр масс должен совпадать с фактическим физическим центром изображения.
е. со средним значением позиций пикселей, взвешенных по их интенсивности. Поскольку интенсивность симметрична относительно центра, центр масс должен совпадать с фактическим физическим центром изображения.
Хорошие новости, модуль scipy ndimage экспортирует такую функцию: center_of_mass . Давайте попробуем:
scipy.ndimage.center_of_mass для поиска центра дифракционных картин. (Исходный код) Неплохо! Особенно на первом изображении, действительно неплохая первая попытка. Но я ищу что-то идеальное по пикселям . Интуитивно понятно, что лучевой блок на каждом изображении должен мешать вычислению центра масс. Давайте определим следующие области, которые мы хотели бы игнорировать:
Яркие области определяются как замаскированные (исходный код) Маски обычно определяются как логические массивы с True (или 1), где пиксели действительны, и False (или 0), если пиксели недействительны. Поэтому мы должны игнорировать вес замаскированных пикселей.
Поэтому мы должны игнорировать вес замаскированных пикселей. scipy.ndimage.center_of_mass не поддерживает эту функцию; нам нужно расширение center_of_mass :
def center_of_mass_masked(im, mask):
rr, cc = np.indices (im.shape)
веса = im * mask.astype(im.dtype)
r = np.average (rr, веса = веса)
c = np.average (cc, веса = веса)
возврат р, с Фактически это среднее значение координат строки и столбца ( rr и cc ), взвешенное по интенсивности изображения. Хитрость здесь в том, что mask.astype(im.dtype) равно 0, где пиксели являются «недействительными»; поэтому они не учитываются в среднем! Посмотрим на результат:
center_of_mass_masked (см. выше) для нахождения центра дифракционных картин. (Исходный код) Честно говоря, я не уверен, что он выглядит лучше. Но по крайней мере у нас есть примерный центр! Это хорошая отправная точка, которая ведет к следующему шагу.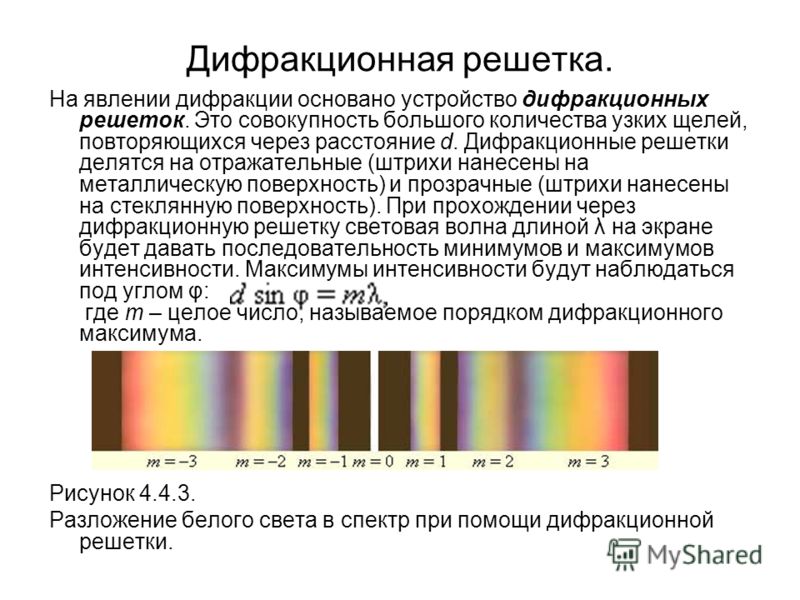
Пары Фриделя и радиальная инверсионная симметрия
В своей диссертации 2 , которая теперь также является книгой, Нельсон Лю описывает, как он это делает:
Грубая оценка его положения получается путем вычисления «центра интенсивности» или средневзвешенного по интенсивности арифметического положения > 100 случайных точек, равномерно распределенных по маскированному изображению; это используется для сопоставления дифракционных пятен с парами Фриделя среди найденных ранее. Усредняя середины линий, соединяющих эти пары точек, получают более точное положение центра.
Пары Фриделя — это пики, связанные инверсией через центр дифракционной картины. Существование этих пар гарантируется симметрией кристалла. Для поликристаллических структур пары Фриделя усредняются в кольца; кольца всегда инверсно-симметричны относительно своих центров. Вот пример двух пар Фриделя:
Пример двух пар Фриделя: белые круги образуют пару 1, а красные кружки образуют пару 2. (Исходный код)
(Исходный код) Алгоритм Лю предназначался для монокристаллических дифракционных картин с четко определенными пиками. , и не столько для колец. Однако мы можем преобразовать идею Лю в новый, более общий подход. Если приблизительный центр совпадает с фактическим центром изображения, то изображение должно быть инвариантным относительно радиальной инверсии относительно приблизительного центра. Другими словами: если образ \(I\) задан в полярных координатах \((r, \theta)\), то центр максимизирует корреляцию между \(I(r, \theta)\) и \(I( -r, \тета)\). К счастью, вычисление скрытой корреляции между изображениями — это то, над чем я работал раньше!
Давайте посмотрим, как выглядит радиальная инверсия. Есть способы сделать это с интерполяцией, например. Функция scikit-image warp . Однако в моем тестировании это невероятно медленно по сравнению с тем, что я вам покажу. Более быстрый подход состоит в том, чтобы считать, что если изображение было центрировано на массиве, то радиальная инверсия действительно меняет направление осей массива; то есть, если массив изображений I имеет размер (128, 128) и центр находится в точке (64, 64), радиальное обратное значение I — это I[::-1, ::-1] (numpy)/ flip(flip(I, 1), 2) (MATLAB)/ I[end:-1:1,end :-1:1] (Юля). Другое важное замечание заключается в том, что если приблизительный центр изображения находится далеко от центра массива, перекрытие между изображением и его радиальной инверсией ограничено. Рассмотрим это:
Другое важное замечание заключается в том, что если приблизительный центр изображения находится далеко от центра массива, перекрытие между изображением и его радиальной инверсией ограничено. Рассмотрим это:
Если бы мы обрезали яркие области вокруг кадра, то найденный примерный центр совпал бы с центром массива; тогда радиальная инверсия происходит очень быстро.
Демонстрация того, какие части изображения обрезать, чтобы центр изображения совпадал с центром массива. (Исходный код)Теперь, особенно для правого столбца изображений, совершенно ясно, что приблизительный центр не был идеальным. Поправку к приблизительному центру можно рассчитать с помощью маскированной нормализованной взаимной корреляции 3 4 :
Вверху слева : дифракционная картина. Вверху справа : радиально-инвертированная дифракционная картина приблизительно в центре. Внизу слева : замаскированная нормализованная взаимная корреляция между двумя дифракционными картинами. Внизу справа : 2-кратное увеличение кросс-корреляции показывает несоответствие трансляции между дифракционными картинами. (Исходный код)
Внизу справа : 2-кратное увеличение кросс-корреляции показывает несоответствие трансляции между дифракционными картинами. (Исходный код) Взаимная корреляция в правом нижнем углу (увеличенная в 2 раза) показывает, что истинный центр — это приблизительный центр, который мы нашли ранее, скорректированный небольшим сдвигом (белая стрелка)! Для монокристаллических дифракционных картин результат еще более поразителен:
Вверху слева : дифракционная картина. Вверху справа : радиально-инвертированная дифракционная картина приблизительно в центре. Внизу слева : замаскированная нормализованная взаимная корреляция между двумя дифракционными картинами. Внизу справа : 2-кратное увеличение кросс-корреляции показывает несоответствие трансляции между дифракционными картинами. (Исходный код)Мы можем объединить два шага и определить идеальный по пикселям центр:
(Исходный код)Бонус: низкокачественная дифракция
Вот забавное последствие: этот метод работает также для дифракционных картин, которые довольно дерьмовые и очень далеко от центра, при условии, что асимметрия фона учтена:
(Исходный код)Заключение
В этом посте, мы определили надежный способ вычисления центра дифракционной картины без каких-либо параметров, используя сильный инвариант: симметрию радиальной инверсии.




 Можно видеть предметы, размеры которых соизмеримы с длиной световой волны.
Можно видеть предметы, размеры которых соизмеримы с длиной световой волны.
 Традиционное со времен Ньютона и из-за его непререкаемого авторитета долго остающееся неизменным представление о свете как о потоке частиц — так называемая корпускулярная теория света — оказалось поставленным под серьезное сомнение после открытия интерференции. А вскоре о корпускулярной теории и вовсе забыли — почти на целое столетие — в результате открытия и исследования явлений дифракции, в результате чего волновая теория света стала новым ортодоксальным и незыблемым представлением о нем. Лишь после объяснения с корпускулярной точки зрения фотоэлектрического эффекта и зарождения квантовой механики корпускулярные представления о свете получили второе рождение в рамках принципа дополнительности.
Традиционное со времен Ньютона и из-за его непререкаемого авторитета долго остающееся неизменным представление о свете как о потоке частиц — так называемая корпускулярная теория света — оказалось поставленным под серьезное сомнение после открытия интерференции. А вскоре о корпускулярной теории и вовсе забыли — почти на целое столетие — в результате открытия и исследования явлений дифракции, в результате чего волновая теория света стала новым ортодоксальным и незыблемым представлением о нем. Лишь после объяснения с корпускулярной точки зрения фотоэлектрического эффекта и зарождения квантовой механики корпускулярные представления о свете получили второе рождение в рамках принципа дополнительности. При взаимодействии световой волны с препятствием часть вторичных волн Гюйгенса блокируется. Например, при падении световой волны сверху под острым углом на бритву на верхней плоскости бритвы вторичные волны Гюйгенса образовываться будут, а на нижней нет. Однако в результате конструктивной интерференции вторичные волны всё равно обогнут бритву, и мы увидим там сплошной световой луч, как если бы на пути его распространения ничего не стояло. Подобное же «огибание» волной препятствия можно наблюдать и в морском порту в шторм: суда, стоящие на якоре за волнорезом, который, казалось бы, должен полностью гасить волны, тем не менее «гуляют» вверх-вниз благодаря вторичным волнам.
При взаимодействии световой волны с препятствием часть вторичных волн Гюйгенса блокируется. Например, при падении световой волны сверху под острым углом на бритву на верхней плоскости бритвы вторичные волны Гюйгенса образовываться будут, а на нижней нет. Однако в результате конструктивной интерференции вторичные волны всё равно обогнут бритву, и мы увидим там сплошной световой луч, как если бы на пути его распространения ничего не стояло. Подобное же «огибание» волной препятствия можно наблюдать и в морском порту в шторм: суда, стоящие на якоре за волнорезом, который, казалось бы, должен полностью гасить волны, тем не менее «гуляют» вверх-вниз благодаря вторичным волнам. Фраунгофер, кстати, изобрел целый ряд важных прецизионных оптических приборов, включая дифракционную решетку. Она представляет собой систему расположенных на небольшом расстоянии друг от друга микроскопических линий, отражающих свет. Изначально это была затемненная стеклянная пластина с тщательно нанесенными на нее параллельными штрихами. Каждый такой штрих отражает свет, и его можно считать вторичным источником волн Гюйгенса, которые вступают в интерференцию и взаимно усиливаются под определенными углами после рассеяния на решетке.
Фраунгофер, кстати, изобрел целый ряд важных прецизионных оптических приборов, включая дифракционную решетку. Она представляет собой систему расположенных на небольшом расстоянии друг от друга микроскопических линий, отражающих свет. Изначально это была затемненная стеклянная пластина с тщательно нанесенными на нее параллельными штрихами. Каждый такой штрих отражает свет, и его можно считать вторичным источником волн Гюйгенса, которые вступают в интерференцию и взаимно усиливаются под определенными углами после рассеяния на решетке.
 Представьте себе поплавок, покачивающийся на волнах. Поднимаясь и опускаясь, поплавок повторяет движения воды, в то время как волны проходят мимо него. Явление интерференции происходит при взаимодействии двух и более волн одинаковой частоты, распространяющихся в различных направлениях.
Представьте себе поплавок, покачивающийся на волнах. Поднимаясь и опускаясь, поплавок повторяет движения воды, в то время как волны проходят мимо него. Явление интерференции происходит при взаимодействии двух и более волн одинаковой частоты, распространяющихся в различных направлениях.
 Н., Попов А. А.
Н., Попов А. А. Эта неотъемлемая часть нашей жизни, но мы все еще стараемся понять феномен света…
Эта неотъемлемая часть нашей жизни, но мы все еще стараемся понять феномен света…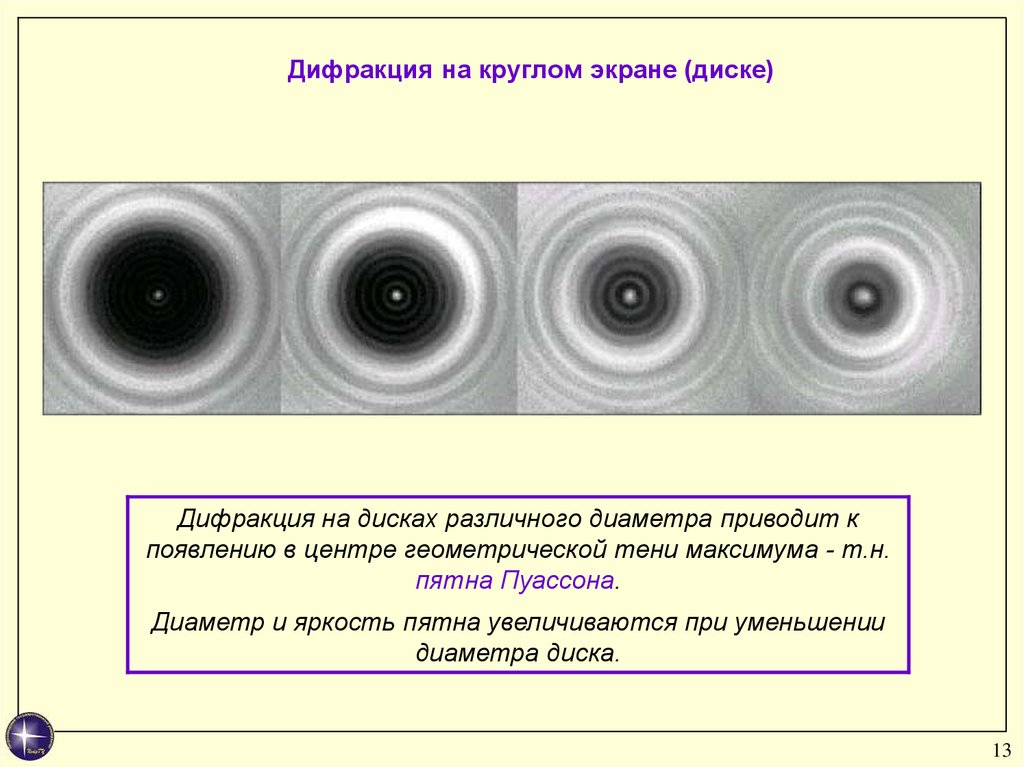 Они ведут себя и не как частицы, и не как волны, а как совершенно особые образования, проявляющие и волновые, и корпускулярные свойства в зависимости от обстоятельств. Одно дело — это заявить, и совсем другое — связать воедино волновые и корпускулярные аспекты поведения квантовых частиц, описав их точным уравнением. Именно это и было сделано в соотношении де Бройля.
Они ведут себя и не как частицы, и не как волны, а как совершенно особые образования, проявляющие и волновые, и корпускулярные свойства в зависимости от обстоятельств. Одно дело — это заявить, и совсем другое — связать воедино волновые и корпускулярные аспекты поведения квантовых частиц, описав их точным уравнением. Именно это и было сделано в соотношении де Бройля. net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ СОДЕРЖАНИЕ
net
▪
▪
▪
▪
▪▪▪▪
▪
▪
▪
▪
▪
▪
▪
▪
▪ СОДЕРЖАНИЕ 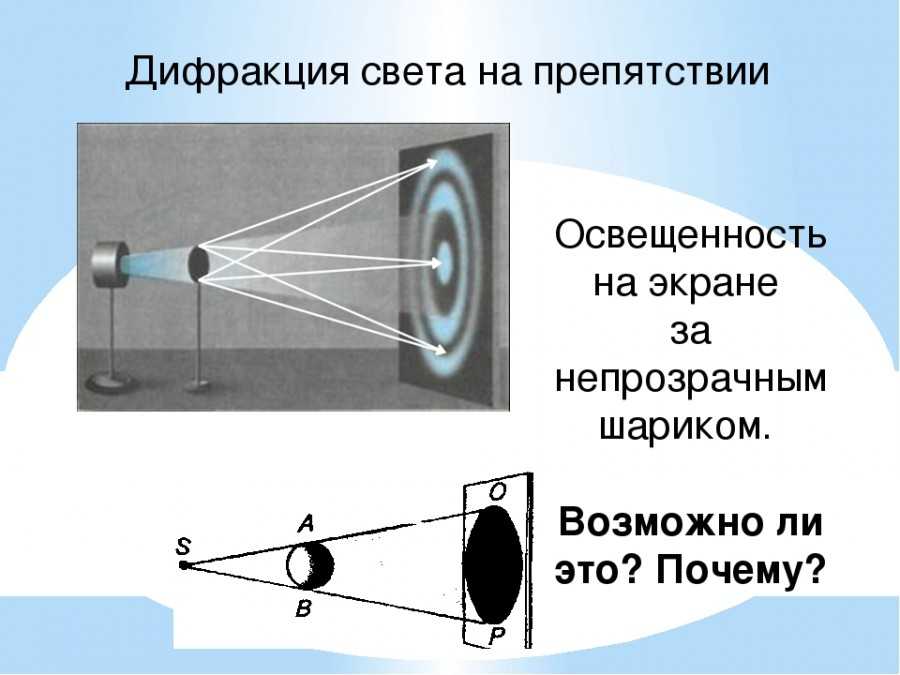 Как уже
упомянутых, два стандартных инструмента для выражения эффекта изменения в
распределение интенсивности по качеству изображения – это Коэффициент Штреля и
Передаточная функция модуляции (MTF).
Как уже
упомянутых, два стандартных инструмента для выражения эффекта изменения в
распределение интенсивности по качеству изображения – это Коэффициент Штреля и
Передаточная функция модуляции (MTF). 
 Распределение интенсивности в пределах дифракционной картины — либо идеальное, либо
аберрированный — описывается « функция разброса точек «, или
PSF ( РИС.
95 ).
Распределение интенсивности в пределах дифракционной картины — либо идеальное, либо
аберрированный — описывается « функция разброса точек «, или
PSF ( РИС.
95 ). 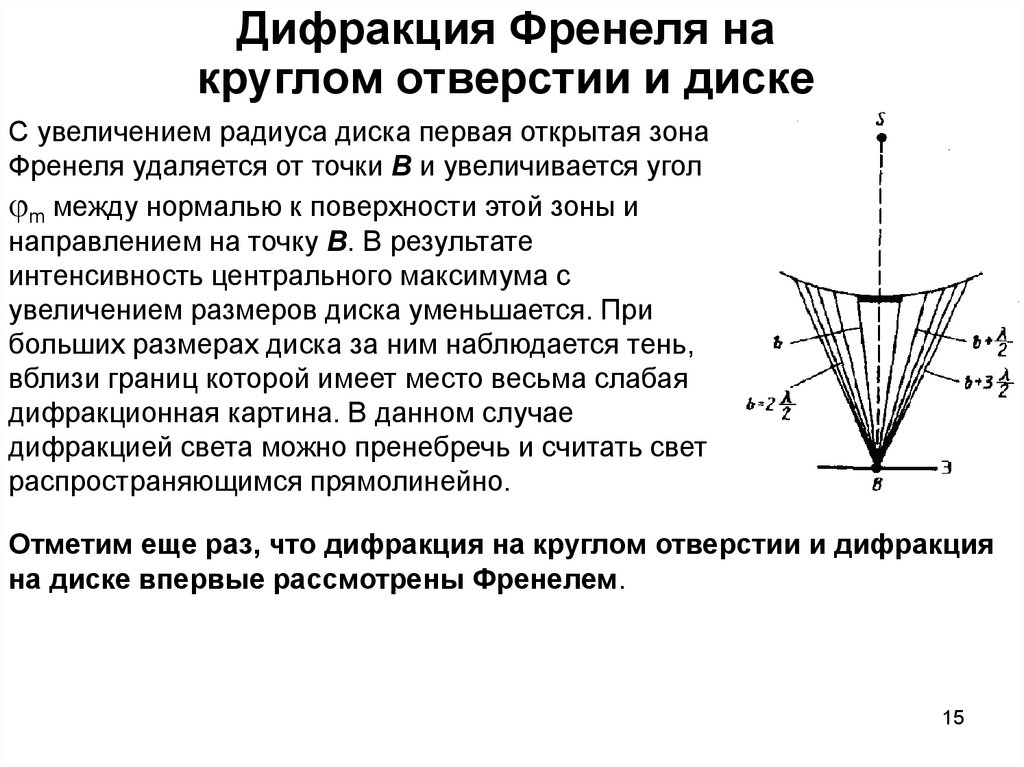 СПРАВА: Из-за логарифмической реакции глаза на свет
интенсивность, внешний вид дифракционной картины лучше
аппроксимируется графиком PSF с интенсивностью, заданной в логарифмическом
(лог10)
шкала. Этот монохроматический PSF указывает на то, что воспринимаемое падение
интенсивность центральных максимумов из-за аберраций мала по сравнению с воспринимаемой
увеличение интенсивности в (пораженной) области кольца. Однако, поскольку его
основание больше, чем у логарифмической реакции глаза
(лог2.512),
он еще больше сжимает номинальные различия в 2,5 раза. Следовательно
график, почти соответствующий кажущемуся PSF, показывает большее воспринимаемое
различия в яркости как для безаберрационного, так и для аберрированного
узор (вставка F).
СПРАВА: Из-за логарифмической реакции глаза на свет
интенсивность, внешний вид дифракционной картины лучше
аппроксимируется графиком PSF с интенсивностью, заданной в логарифмическом
(лог10)
шкала. Этот монохроматический PSF указывает на то, что воспринимаемое падение
интенсивность центральных максимумов из-за аберраций мала по сравнению с воспринимаемой
увеличение интенсивности в (пораженной) области кольца. Однако, поскольку его
основание больше, чем у логарифмической реакции глаза
(лог2.512),
он еще больше сжимает номинальные различия в 2,5 раза. Следовательно
график, почти соответствующий кажущемуся PSF, показывает большее воспринимаемое
различия в яркости как для безаберрационного, так и для аберрированного
узор (вставка F).  96 (шаблоны, сгенерированные Aberrator, Cor Berrevoets).
Обратите внимание, что яркость узора — и особенно воспринимаемая
яркость колец — зависит от размера апертуры и звездной величины.
96 (шаблоны, сгенерированные Aberrator, Cor Berrevoets).
Обратите внимание, что яркость узора — и особенно воспринимаемая
яркость колец — зависит от размера апертуры и звездной величины.  (недокорректированная) аберрация.
(недокорректированная) аберрация. 
 Увеличение аберрации приводит сначала к частичному, а
затем полный распад дифракционной картины.
Уровень ограничения дифракции (0,80 Штреля)
соответствует высокому уровню 8 по шкале Пикеринга от 1 до 10.
0,95 Уровень Штреля — это высокий уровень Пикеринга 9.
Увеличение аберрации приводит сначала к частичному, а
затем полный распад дифракционной картины.
Уровень ограничения дифракции (0,80 Штреля)
соответствует высокому уровню 8 по шкале Пикеринга от 1 до 10.
0,95 Уровень Штреля — это высокий уровень Пикеринга 9.  Моделирование ниже показывает осевое сечение в диапазоне от -8λ (в фокусе) до +8λ (вне фокуса) для чистой диафрагмы без аберраций и пяти наиболее часто встречающихся аберраций.
Моделирование ниже показывает осевое сечение в диапазоне от -8λ (в фокусе) до +8λ (вне фокуса) для чистой диафрагмы без аберраций и пяти наиболее часто встречающихся аберраций. 
 Из-за насыщенности одной стороны фокуса центральная тень мягче, вырывается на большее расстояние расфокусировки, чем с другой стороны. Оценка по своей сути затруднена из-за пониженного контраста на стороне с более яркой внутренней областью и из-за постепенного образования тени на этой стороне. Несколько проще, а значит, и точнее, должно быть сравнить диаметр тени с двух сторон при равной величине расфокусировки, при которой обе тени достаточно четко определены. Например, для 1/4 волны P-V тень при 7 волнах расфокусировки должна быть примерно на 60% больше (т.е. почти на 40% меньше) с одной стороны по сравнению с другой. С 1/8 волны примерно на 1/3 больше, а с 1/3 волны примерно вдвое больше.
Из-за насыщенности одной стороны фокуса центральная тень мягче, вырывается на большее расстояние расфокусировки, чем с другой стороны. Оценка по своей сути затруднена из-за пониженного контраста на стороне с более яркой внутренней областью и из-за постепенного образования тени на этой стороне. Несколько проще, а значит, и точнее, должно быть сравнить диаметр тени с двух сторон при равной величине расфокусировки, при которой обе тени достаточно четко определены. Например, для 1/4 волны P-V тень при 7 волнах расфокусировки должна быть примерно на 60% больше (т.е. почти на 40% меньше) с одной стороны по сравнению с другой. С 1/8 волны примерно на 1/3 больше, а с 1/3 волны примерно вдвое больше.