Диск эйри: Дифракция — Diffraction — qaz.wiki — Главная

Содержание

Дифракция — Diffraction — qaz.wiki

Не следует путать с рефракцией , изменением направления волны, переходящей из одной среды в другую.

Феномен движения волн

Дифракция относится к различным явлениям, которые происходят, когда волна встречает препятствие или проем. Он определяется как изгиб волн вокруг углов препятствия или через проем в область геометрической тени препятствия / проема. Дифрагирующий объект или апертура фактически становятся вторичным источником распространяющейся волны. Итальянский ученый Франческо Мария Гримальди придумал слово дифракция и был первым, кто записал точные наблюдения этого явления в 1660 году.

Бесконечно много точек (показаны три) вдоль длины d проецируют фазовые вклады от волнового фронта , создавая непрерывно изменяющуюся интенсивность θ на регистрирующей пластине.

В классической физике явление дифракции описывается принципом Гюйгенса-Френеля, который рассматривает каждую точку распространяющегося волнового фронта как набор отдельных сферических всплесков .

Характерная картина изгиба наиболее выражена, когда волна от когерентного источника (такого как лазер) встречает щель / апертуру, размер которой сопоставим с ее длиной волны , как показано на вставленном изображении. Это происходит из-за добавления или интерференции различных точек на волновом фронте (или, что то же самое, каждого вейвлета), которые проходят пути разной длины к регистрирующей поверхности. Однако при наличии нескольких близко расположенных отверстий может получиться сложный узор различной интенсивности.

Эти эффекты также возникают, когда световая волна проходит через среду с переменным показателем преломления или когда звуковая волна проходит через среду с переменным акустическим импедансом — все волны дифрагируют, включая гравитационные волны , волны на воде и другие электромагнитные волны, такие как X -лучей и радиоволн . Кроме того, квантовая механика также демонстрирует, что материя обладает волнообразными свойствами и, следовательно, претерпевает дифракцию (которая измеряется от субатомных до молекулярных уровней).

Дифракция и интерференция тесно связаны и почти — если не совсем — идентичны по смыслу. Ричард Фейнман отмечает, что термин «дифракция» обычно используется, когда речь идет о многих источниках волн, и «интерференция», когда рассматриваются лишь некоторые из них.

История

Эскиз Томаса Янга дифракции на двух щелях для волн на воде, который он представил Королевскому обществу в 1803 году.

Эффекты дифракции света были впервые тщательно изучены и охарактеризованы Франческо Марией Гримальди , который также ввел термин дифракция от латинского

diffringere , «разбиваться на части», имея в виду свет, распадающийся в разные стороны. Результаты наблюдений Гримальди были опубликованы посмертно в 1665 году. Исаак Ньютон изучил эти эффекты и приписал их перегибу световых лучей. Джеймс Грегори (1638–1675) наблюдал дифракционные картины, вызванные птичьим пером, которое фактически было первой обнаруженной дифракционной решеткой . Томас Янг провел знаменитый эксперимент в 1803 году, продемонстрировав интерференцию из двух близко расположенных щелей.

Объясняя свои результаты интерференцией волн, исходящих из двух разных щелей, он пришел к выводу, что свет должен распространяться как волны. Огюстен-Жан Френель провел более точные исследования и расчеты дифракции, обнародованные в 1816 и 1818 годах, и тем самым оказал большую поддержку волновой теории света, выдвинутой Христианом Гюйгенсом и усиленной Янгом против теории частиц Ньютона.

Механизм

В классической физике дифракция возникает из-за способа распространения волн; это описывается принципом Гюйгенса – Френеля и принципом суперпозиции волн . Распространение волны можно визуализировать, рассматривая каждую частицу передаваемой среды на фронте волны как точечный источник вторичной сферической волны . Волновое смещение в любой последующей точке является суммой этих вторичных волн. Когда волны складываются, их сумма определяется относительными фазами, а также амплитудами отдельных волн, так что суммарная амплитуда волн может иметь любое значение от нуля до суммы отдельных амплитуд.

Следовательно, дифракционные картины обычно имеют серию максимумов и минимумов.

В современном понимании квантовой механики распространения света через щель (или щели) каждый фотон имеет так называемую волновую функцию, которая описывает его путь от излучателя через щель к экрану. Волновая функция — путь, по которому будет двигаться фотон, — определяется физическим окружением, таким как геометрия щели, расстояние до экрана и начальные условия при создании фотона. В важных экспериментах (эксперимент с двойной щелью низкой интенсивности был впервые проведен Дж. Тейлором в 1909 г., см. Эксперимент с двойной щелью ) было продемонстрировано существование волновой функции фотона. В квантовом подходе дифракционная картина создается распределением путей, наблюдение светлых и темных полос — это наличие или отсутствие фотонов в этих областях (без интерференции!). Квантовый подход имеет поразительное сходство с принципом Гюйгенса-Френеля ; в соответствии с этим принципом свет становится серией индивидуально распределенных источников света через щель, что аналогично ограниченному количеству путей (или волновых функций), доступных для фотонов, проходящих через щель.

Существуют различные аналитические модели, которые позволяют рассчитывать дифрагированное поле, включая уравнение дифракции Кирхгофа-Френеля, которое выводится из волнового уравнения , приближение дифракции Фраунгофера уравнения Кирхгофа, которое применяется к дальней зоне, и приближение дифракции Френеля, которое применяется в ближнее поле . Большинство конфигураций не могут быть решены аналитически, но могут дать численные решения с помощью методов конечных элементов и граничных элементов .

Можно получить качественное понимание многих явлений дифракции, рассматривая, как меняются относительные фазы отдельных вторичных источников волн, и, в частности, условия, в которых разность фаз равна половине цикла, и в этом случае волны будут гасить друг друга. .

Простейшими описаниями дифракции являются такие, при которых ситуация сводится к двумерной задаче. Для волн на воде это уже так; водяные волны распространяются только по поверхности воды. Что касается света, мы часто можем пренебречь одним направлением, если дифрагирующий объект простирается в этом направлении на расстояние, намного превышающее длину волны.

В случае света, проходящего через маленькие круглые отверстия, мы должны учитывать всю трехмерную природу проблемы.

Сгенерированная компьютером картина интенсивности, сформированная на экране путем дифракции на квадратной апертуре.
Генерация интерференционной картины по дифракции на двух щелях.
Расчетная модель интерференционной картины от двухщелевой дифракции.
Оптическая дифракционная картина (лазер) (аналог рентгеновской кристаллографии)
Согласно некоторым исследованиям, цвета, видимые в паутине , частично возникают из-за дифракции.

Примеры

Круговые волны, генерируемые дифракцией от узкого входа в затопленный прибрежный карьер

Эффекты дифракции часто наблюдаются в повседневной жизни. Наиболее яркими примерами дифракции являются световые; например, близко расположенные дорожки на CD или DVD действуют как дифракционная решетка, образуя знакомый радужный узор, который можно увидеть при просмотре диска. Этот принцип может быть расширен для создания решетки со структурой, которая будет создавать любую желаемую дифракционную картину; голограмма на кредитной карте является примером. Дифракция в атмосфере на мелких частицах может привести к тому, что вокруг яркого источника света, такого как солнце или луна, будет видно яркое кольцо. Тень твердого объекта, использующая свет от компактного источника, показывает небольшие полосы по краям. Спекл , который наблюдается при лазерный луч падает на оптический неровную поверхность также явление дифракции. Когда мясные деликатесы кажутся переливающимися , это дифракция на волокнах мяса. Все эти эффекты являются следствием того, что свет распространяется как волна .

Дифракция может происходить на волнах любого типа. Океанские волны рассеиваются вокруг причалов и других препятствий. Звуковые волны могут рассеиваться вокруг объектов, поэтому можно услышать чей-то зов, даже если спрятаться за деревом. Дифракция также может быть проблемой в некоторых технических приложениях; он устанавливает фундаментальный предел разрешающей способности камеры, телескопа или микроскопа.

Другие примеры дифракции рассматриваются ниже.

Однощелевая дифракция

Численная аппроксимация дифракционной картины от щели шириной четыре длины волны падающей плоской волной. Видны главный центральный луч, нули и развороты фазы. График и изображение дифракции на одной щели.

Длинная щель бесконечно малой ширины, которая освещается светом, рассеивает свет на серию круговых волн, а волновой фронт, выходящий из щели, представляет собой цилиндрическую волну однородной интенсивности в соответствии с принципом Гюйгенса – Френеля .

Щель, ширина которой превышает длину волны, создает интерференционные эффекты в пространстве после щели. Это можно объяснить, если предположить, что прорезь ведет себя так, как если бы в ней было большое количество точечных источников, равномерно распределенных по ширине прорези. Анализ этой системы упростится, если мы рассмотрим свет одной длины волны. Если падающий свет когерентен , все эти источники имеют одинаковую фазу.

Свет, падающий в заданную точку пространства ниже щели, складывается из вкладов каждого из этих точечных источников, и если относительные фазы этих вкладов изменяются на 2π или более, мы можем ожидать найти минимумы и максимумы в дифрагированном свете. . Такие разности фаз вызваны различиями в длинах пути, по которым лучи, вносящие вклад, достигают точки от щели.

Мы можем найти угол, при котором получается первый минимум в дифрагированном свете, по следующим соображениям. Свет от источника, расположенного у верхнего края щели, разрушительно интерферирует с источником, расположенным в середине щели, когда разность хода между ними равна λ / 2. Точно так же источник чуть ниже верха щели будет деструктивно мешать источнику, расположенному чуть ниже середины щели под тем же углом. Мы можем продолжить это рассуждение по всей высоте щели, чтобы заключить, что условие деструктивной интерференции для всей щели такое же, как условие деструктивной интерференции между двумя узкими щелями, расположенными на расстоянии, равном половине ширины щели. Разность хода приблизительно такова, что минимальная интенсивность возникает под углом θ _min, определяемым формулой dгрех⁡(θ)2{\ Displaystyle {\ гидроразрыва {д \ грех (\ тета)} {2}}}

dгрех⁡θминзнак равноλ{\ displaystyle d \, \ sin \ theta _ {\ text {min}} = \ lambda}

где

d — ширина щели,
θмин{\ displaystyle \ theta _ {\ text {min}}} — угол падения, при котором возникает минимальная интенсивность, а
λ{\ displaystyle \ lambda} это длина волны света

Аналогичный аргумент можно использовать, чтобы показать, что если мы представим щель, разделенную на четыре, шесть, восемь частей и т. Д., Минимумы будут получены при углах θ _n, задаваемых формулой

dгрех⁡θпзнак равнопλ{\ Displaystyle д \, \ грех \ тета _ {п} = п \ лямбда}

где

n — целое число, отличное от нуля.

Нет такого простого аргумента, который позволил бы нам найти максимумы дифракционной картины. {2} \ left ({\ frac {d \ pi} {\ lambda}} \ sin \ theta \ right)}

где

Этот анализ применим только к дальнему полю ( дифракция фраунгофера ), то есть на расстоянии, намного превышающем ширину щели.

Из профиля интенсивности выше, если интенсивность будет мало зависеть от , следовательно, волновой фронт, выходящий из щели, будет напоминать цилиндрическую волну с азимутальной симметрией; Если бы только он имел заметную интенсивность, следовательно, волновой фронт, выходящий из щели, напоминал бы фронт геометрической оптики . d≪λ{\ displaystyle d \ ll \ lambda}θ{\ displaystyle \ theta}d≫λ{\ displaystyle d \ gg \ lambda}θ≈0{\ displaystyle \ theta \ приблизительно 0}

Когда угол падения света на щель отличен от нуля (что вызывает изменение длины пути ), профиль интенсивности в режиме Фраунгофера (то есть в дальней зоне) становится: θя{\ displaystyle \ theta _ {\ text {i}}}

я(θ)знак равноя0грех2⁡[dπλ(грех⁡θ±грех⁡θя)]{\ displaystyle I (\ theta) = I_ {0} \, \ operatorname {sinc} ^ {2} \ left [{\ frac {d \ pi} {\ lambda}} (\ sin \ theta \ pm \ sin \ theta _ {i}) \ right]}

Выбор знака плюс / минус зависит от определения угла падения . θя{\ displaystyle \ theta _ {\ text {i}}}

2-щели (вверху) и 5-ти щелевая дифракция красного лазерного света Дифракция красного лазера на дифракционной решетке. Дифракционная картина лазера с длиной волны 633 нм через сетку из 150 щелей

Дифракционная решетка

Дифракционная решетка — это оптический элемент с регулярным рисунком. Форма света, дифрагированного решеткой, зависит от структуры элементов и количества присутствующих элементов, но все решетки имеют максимумы интенсивности при углах θ _m, которые задаются уравнением решетки

d(грех⁡θм±грех⁡θя)знак равномλ.{\ displaystyle d \ left (\ sin {\ theta _ {m}} \ pm \ sin {\ theta _ {i}} \ right) = m \ lambda.}

где

θ _i — угол, под которым падает свет,
d — расстояние между элементами решетки, а
m — целое число, которое может быть положительным или отрицательным.

Свет, дифрагированный решеткой, определяется путем суммирования света, дифрагированного от каждого из элементов, и по существу представляет собой свертку дифракционных и интерференционных картин. {- i (k_ {x} x’ + k_ {y} y ‘)} \, dx’ \, dy ‘,}

В дальней зоне / области Фраунгофера это становится пространственным преобразованием Фурье распределения апертуры. Принцип Гюйгенса в применении к апертуре просто говорит, что дифракционная картина в дальней зоне является пространственным преобразованием Фурье формы апертуры, и это прямой побочный продукт использования приближения параллельных лучей, которое идентично созданию плоскости волновое разложение полей апертурной плоскости (см. Фурье-оптика ).

Распространение лазерного луча

То, как изменяется профиль лазерного луча по мере его распространения, определяется дифракцией. Когда весь излучаемый пучок имеет плоский, пространственно когерентный волновой фронт, он приближается к гауссову профилю пучка и имеет наименьшую расходимость для данного диаметра. Чем меньше выходной луч, тем быстрее он расходится. Можно уменьшить расходимость лазерного луча, сначала расширив его с помощью одной выпуклой линзы , а затем коллимируя его с помощью второй выпуклой линзы, фокус которой совпадает с точкой фокусировки первой линзы.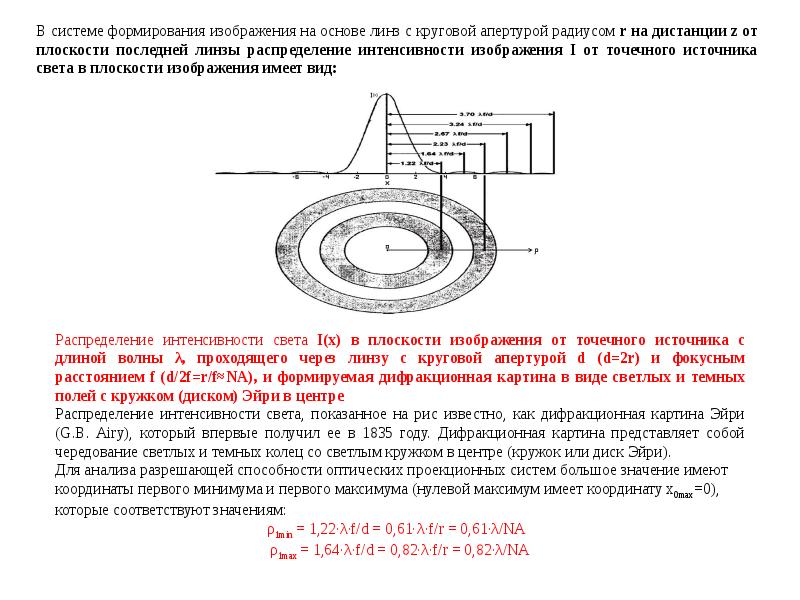 Полученный пучок имеет больший диаметр и, следовательно, меньшую расходимость. Расходимость лазерного луча может быть уменьшена ниже дифракции гауссова луча или даже обращена к сходимости, если показатель преломления среды распространения увеличивается с интенсивностью света. Это может привести к эффекту самофокусировки .

Когда волновой фронт излучаемого луча имеет возмущения, только длина поперечной когерентности (где возмущение волнового фронта составляет менее 1/4 длины волны) должна рассматриваться как диаметр гауссова луча при определении расходимости лазерного луча. Если длина поперечной когерентности в вертикальном направлении больше, чем в горизонтальном, расходимость лазерного луча будет меньше в вертикальном направлении, чем в горизонтальном.

Визуализация с ограничением дифракции

Способность системы визуализации разрешать детали в конечном итоге ограничивается дифракцией . Это связано с тем, что плоская волна, падающая на круглую линзу или зеркало, дифрагирует, как описано выше. Свет не фокусируется в точку, а образует диск Эйри с центральным пятном в фокальной плоскости, радиус которого (по измерению до первого нуля) равен

ΔИксзнак равно1,22λN{\ displaystyle \ Delta x = 1,22 \ лямбда N}

где λ — длина волны света, а N — f-число (фокусное расстояние f, деленное на диаметр апертуры D) оптики формирования изображения; это строго верно для NÀ1 ( параксиальный случай). В пространстве объектов соответствующее угловое разрешение равно

θ≈грех⁡θзнак равно1,22λD,{\ Displaystyle \ тета \ приблизительно \ грех \ тета = 1,22 {\ гидроразрыва {\ лямбда} {D}}, \,}

где D — диаметр входного зрачка изображающей линзы (например, главного зеркала телескопа).

Каждый из двух точечных источников будет давать узор Эйри — см. Фотографию двойной звезды. По мере того, как точечные источники приближаются друг к другу, узоры начинают перекрываться, и в конечном итоге они объединяются, образуя единый узор, и в этом случае два точечных источника не могут быть разрешены на изображении. В Рэлея критерий указывает , что два точечных источника, считаются «решены» , если разделение двух изображений по меньшей мере , радиус диска Эйри, т.е. если первый минимум один совпадает с максимумом другой.

Таким образом, чем больше апертура линзы по сравнению с длиной волны, тем выше разрешение системы формирования изображения. Это одна из причин, по которой астрономическим телескопам требуются большие объективы, а для объективов микроскопов требуется большая числовая апертура (большой диаметр апертуры по сравнению с рабочим расстоянием) для получения максимально возможного разрешения.

Спекл-узоры

Спекл , который виден при использовании лазерного указателя является еще одним явлением дифракции. Это результат наложения множества волн с разными фазами, которые возникают, когда лазерный луч освещает шероховатую поверхность. Они складываются вместе, чтобы получить результирующую волну, амплитуда и, следовательно, интенсивность которой изменяются случайным образом.

Принцип Бабине

Принцип Бабине — полезная теорема, утверждающая, что картина дифракции от непрозрачного тела идентична картине дифракции от отверстия того же размера и формы, но с разной интенсивностью. Это означает, что условия интерференции одиночного препятствия будут такими же, как и у одиночной щели.

Узоры

В верхней половине этого изображения показана дифракционная картина луча гелий-неонового лазера на эллиптической апертуре. Нижняя половина — это его двумерное преобразование Фурье, приблизительно восстанавливающее форму апертуры.

Можно сделать несколько качественных наблюдений за дифракцией в целом:

Угловой интервал между элементами дифракционной картины обратно пропорционален размерам объекта, вызывающего дифракцию. Другими словами: чем меньше дифрагирующий объект, тем «шире» получается дифракционная картина, и наоборот. (Точнее, это верно для синусов углов.)
Углы дифракции неизменны относительно масштабирования; то есть они зависят только от отношения длины волны к размеру дифрагирующего объекта.
Когда дифрагирующий объект имеет периодическую структуру, например, в дифракционной решетке, детали обычно становятся более резкими. Третий рисунок, например, показывает сравнение с двойной щелью узора с узором , образованный пятью прорезями, оба набором прорезей , имеющих один и тот же интервал, между центром одной щели и в следующей.

Дифракция частиц

Согласно квантовой теории каждая частица проявляет волновые свойства. В частности, массивные частицы могут интерферировать сами с собой и, следовательно, дифрагировать. Дифракция электронов и нейтронов была одним из веских аргументов в пользу квантовой механики. Длина волны, связанная с частицей, — это длина волны де Бройля.

λзнак равночасп{\ displaystyle \ lambda = {\ frac {h} {p}} \,}

где h — постоянная Планка, а p — импульс частицы (масса × скорость для медленно движущихся частиц).

Для большинства макроскопических объектов эта длина волны настолько мала, что не имеет смысла присваивать им длину волны. Атом натрия, движущийся со скоростью около 30 000 м / с, будет иметь длину волны Де Бройля около 50 пикометров.

Поскольку длина волны даже для самых маленьких макроскопических объектов чрезвычайно мала, дифракция волн материи видна только для небольших частиц, таких как электроны, нейтроны, атомы и небольшие молекулы. Короткая длина волны этих материальных волн делает их идеально подходящими для изучения атомно-кристаллической структуры твердых тел и больших молекул, таких как белки.

Было также показано, что относительно более крупные молекулы, такие как бакиболлы, дифрагируют.

Брэгговская дифракция

Следуя закону Брэгга , каждая точка (или отражение ) в этой дифракционной картине образуется в результате конструктивной интерференции рентгеновских лучей, проходящих через кристалл. Данные могут быть использованы для определения атомной структуры кристалла.

Дифракция от трехмерной периодической структуры, такой как атомы в кристалле, называется дифракцией Брэгга . Это похоже на то, что происходит, когда волны рассеиваются на дифракционной решетке . Брэгговская дифракция является следствием интерференции волн, отражающихся от разных плоскостей кристалла. Условие конструктивного вмешательства задается законом Брэгга :

мλзнак равно2dгрех⁡θ{\ Displaystyle м \ лямбда = 2d \ грех \ тета \,}

где

λ — длина волны,

d — расстояние между плоскостями кристалла,

θ — угол дифрагированной волны.

и m — целое число, известное как порядок дифрагированного луча.

Брэгговская дифракция может быть проведена с использованием либо электромагнитного излучения с очень короткой длиной волны, например рентгеновских лучей, либо волн материи, таких как нейтроны (и электроны ), длина волны которых порядка (или намного меньше) межатомного расстояния. Полученный узор дает информацию о разделении кристаллографических плоскостей d , позволяя вывести кристаллическую структуру. Дифракционный контраст, в частности в электронных микроскопах и устройствах для рентгеновской топографии , также является мощным инструментом для исследования отдельных дефектов и локальных полей деформации в кристаллах.

Согласованность

Описание дифракции основано на интерференции волн, исходящих от одного и того же источника, идущих разными путями к одной и той же точке на экране. В этом описании разница в фазе между волнами, которые прошли разные пути, зависит только от эффективной длины пути. При этом не учитывается тот факт, что волны, приходящие на экран одновременно, излучались источником в разное время. Начальная фаза, с которой источник излучает волны, может изменяться со временем непредсказуемым образом. Это означает, что волны, излучаемые источником в моменты, когда они слишком далеко друг от друга, больше не могут образовывать постоянную интерференционную картину, поскольку соотношение между их фазами больше не зависит от времени.

Длина, на которой коррелируется фаза луча света, называется длиной когерентности . Чтобы возникла интерференция, разница в длине пути должна быть меньше, чем длина когерентности. Иногда это называют спектральной когерентностью, поскольку это связано с наличием в волне различных частотных компонентов. В случае света, излучаемого атомным переходом , длина когерентности связана со временем жизни возбужденного состояния, из которого атом совершил свой переход.

Если волны испускаются из протяженного источника, это может привести к некогерентности в поперечном направлении. Если смотреть на поперечное сечение луча света, длина, на которой коррелируется фаза, называется длиной поперечной когерентности. В случае эксперимента Юнга с двойной щелью это означало бы, что если длина поперечной когерентности меньше, чем расстояние между двумя щелями, результирующая картина на экране будет выглядеть как две дифракционные картины с одной щелью.

В случае таких частиц, как электроны, нейтроны и атомы, длина когерентности связана с пространственной протяженностью волновой функции, описывающей частицу.

Приложения

Дифракция до разрушения

За последние несколько лет появился новый способ изображения отдельных биологических частиц, использующий яркие рентгеновские лучи, генерируемые рентгеновскими лазерами на свободных электронах . Эти импульсы фемтосекундной длительности позволят получить (потенциальное) изображение отдельных биологических макромолекул. Благодаря этим коротким импульсам радиационное повреждение можно избежать, и можно будет получить дифракционные картины отдельных биологических макромолекул.

Смотрите также

Ссылки

внешние ссылки

Резкость, дифракция и диафрагма

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Большинство фотографов имеют представление о том, как диафрагма влияет на резкость и о глубине резкости. Но есть так называемый диафрагменный предел, значение которого зависит как от объектива, так и от модели камеры и причиной этого является дифракция.

При съемке пейзажа или архитектуры естественным стремлением будет получение максимальной глубины резкости. Это достигается путем уменьшение отверстия диафрагмы. Легко увлечься и слишком сильно зажать диафрагму, «на всякий случай», пытаясь получить достаточную глубину поля.

При этом необходимо соблюдать разумный предел. Несмотря на то, что меньшие диафрагмы обеспечивают бо́льшую ГРИП, эффект дифракции при очень малых диафрагмах приводит к снижению общей резкости изображения.

Также неправильным будет и использование малых диафрагм для получения максимально резкого изображения, результат будет прямо противоположным. Зная пределы объектива, можно избежать этого явления, а также сопутствующих ему, таких как необходимость использования высоких ISO или длительной выдержки, необходимых для получения нормальной экспозиции при закрытой диафрагме.

Наука о дифракции света

Физики давно установили, что свет имеет корпускулярно-волновую природу. Таким образом, все свойства других видов волн, такие как звуковые колебания, волны в жидкостях и твердых телах могут быть применены к свету.

Принцип Гюйгенса-Френеля гласит, что каждую точку фронта волны можно рассматривать как источник вторичных волн, которые распространяются во все стороны со скоростью, равной скорости распространения волны.

Это означает, что свет, проходящий через диафрагму, создает новые световые волны. Крошечное отверстие диафрагмы объектива, точнее, острые края лепестков диафрагмы, создают дифракционный эффект (эффект огибания препятствия световыми волнами). К примеру, возьмем непрозрачный объект, помещенный перед источником света. Он блокирует свет, создавая тень. Посмотрите внимательно на края этой тени. Можно заметить, что даже если объект имеет острые края, края тени всегда слегка размыты

Обратите внимание на разницу в резкости спинки ножа и режущей кромки

Я использовал фотографию перочинного ножа, чтобы продемонстрировать эффект дифракции на краях. Фото было сделано в абсолютно темной комнате, единственным источником света была моя вспышка. Я также немного отрегулировал контраст в Photoshop, чтобы лучше показать эффект. Обратите внимание, что противоположная режущей кромке часть получилась очень резкой, а режущая кромка – несколько размытой, даже при таком источнике как вспышка, который можно считать точечным. Такой же эффект наблюдается и на краях лепестков диафрагмы.

Фронт световой волны, проходя через отверстие, соизмеримое с ее длиной, становится источником вторичных волн, которые взаимодействуют с основной по принципу интерференции, то есть сложения колебаний. Это создает чередование освещенных и затененных областей, а также проникновение света в затененные области. Подобные явления можно наблюдать со всеми типами волн.

Влияние дифракции на вашей камере можно имитировать, если скосить глаза. Когда вы косите глазами, мир становится расплывчатым.

Искажения световых волн при прохождении через отверстия различного диаметра.

Предположим, что у нас есть идеальный объектив с идеально круглым отверстием диафрагмы. Он называется объективом дифракционного предела, так как единственным ограничением на максимальное разрешение изображения является явление дифракции света, а не любые дефекты, смещение или разрешение сенсора.

Интерференционный узор, производимый круглой линзой при освещении пучком параллельных лучей, называется диском Эйри (в честь ученого Джорджа Эйри Биддела). При этом в центре находится так называемое дифракционное пятно, на которое приходится примерно 85% световой энергии, а окружают его светлые и темные кольца.

Диск Эйри при дифракции на круглом отверстии

Размер диска Эйри зависит только от диафрагмы и может быть приближенно рассчитан, исходя из диафрагменного числа, если его разделить на 1500. То есть, при диафрагме f/22 диаметр диска Эйри составит около 0,015 мм.

Если диаметр центрального пятна диска Эйри становится слишком большим по отношению к размеру пикселя, то изображение будет размытым. Это становится ограничивающим фактором в достижении резкого изображения. То есть, для каждой камеры есть свое значение диафрагмы, выше которого наступает ухудшение резкости изображения. Это значение носит название диафрагменного предела.

Практическое применение

Теперь, когда мы закончили со скучной теорией, давайте посмотрим, как практически применяется этот принцип. Тест на эффект дифракции очень простой. Просто возьмите набор объектов, сохраняя при этом неизменное фокусное расстояние и экспозицию, и снимайте в режиме приоритета диафрагмы, изменяя ее значение. Для получения достоверных результатов очень важно избежать любых изменений в изображении.

Примечание переводчика: для этого теста лучше использовать специальную шкалу – миру.

Для этого нужно использовать хороший штатив, дистанционный спуск затвора, блокировку зеркала, в общем, исключить все факторы, которые могут привести к малейшему дрожанию камеры.

Следующая серия изображений – это 100% кроп этикетки Crown Royal. Эти снимки были сделаны в помещении с камеры, стоящей на полу.

Отчетливо видно ухудшение резкости изображения от дифракции.

Из этого теста следует, что изображение начинает терять резкость примерно с диафрагмы f/11, сохраняя приемлемый вид до f/16. Начиная с f/22, происходит резкое ухудшение резкости, а диафрагма f/36 практически непригодна для использования.

Не забывайте также, что при использовании некоторых объективов широко открытая диафрагма также уменьшает резкость. Важно найти оптимальную величину диафрагмы для вашего объектива. Я предпочитаю использовать f/8 или f/11 в большинстве случаев.

Теперь понятно, что лучше всего не зажимать максимально диафрагму для достижения максимальной ГРИП, а строить кадр таким образом, чтобы все объекты находились в зоне глубины резкости, либо использовать гиперфокальное расстояние. Есть много способов и онлайн-калькуляторов для расчета глубины резкости.

Для этого снимка дистанция и фокусное расстояние не требуют небольшой диафрагмы для достижения большой глубины резкости.

Давайте на примере этого снимка дерева рассмотрим выбор диафрагмы для получения оптимальной ГРИП. Фотография была сделана на неполнокадровую камеру с помощью объектива с фокусным расстоянием 18 мм, расстояние до дерева примерно 20 м. Так как объект находится достаточно далеко и используется широкоугольный объектив, то даже умеренно закрытая диафрагма f/6.3 обеспечивает глубину резкости от 2,26 м до бесконечности.

Этого более чем достаточно, чтобы захватить в кадр все детали. На самом деле, с таким фокусным расстоянием даже диафрагма f/1 даст мне глубину резкости от 8,95 м до бесконечности, что опять же достаточно, чтобы дерево получилось резким.

В этой ситуации не было никакой необходимости использовать малую диафрагму, что позволило сделать снимок с меньшим ISO и более короткой выдержкой, что также вносит вклад в общую резкость картинки.

Это хорошо, когда вы знаете, что меньший диаметр диафрагмы обеспечивает большую глубину резкости, однако есть и другие факторы, оказывающие гораздо большее влияние.

Например, расстояние до объекта 25 м, а диафрагма f/8. Если используется объектив с фокусным расстоянием 100 мм, то глубина резкости будет от 17,9 до 41,6 м, общая протяженность ГРИП 23,7 м.

Однако, если вы будете использовать объектив с фокусным расстоянием 75 мм, диапазон ГРИП будет уже от 14,6 до 85,9 м, то есть 71,3 м. Это почти в три раза больше, чем при использовании объектива с фокусным расстоянием 100 мм.

Для сравнения, если мы закроем диафрагму до f/11 при фокусном расстоянии 100 мм, это даст нам глубину резкости от 16 до 57,3 м, в общей сложности 41, 3 м.

Для снимков, которые требуют более длительной выдержки, сначала лучше выбрать выдержку, которая даст вам соответствующий эффект, а затем подобрать диафрагму для нормальной экспозиции. Однако имейте ввиду, что лучше не использовать диафрагмы меньше f/8 или f/11 из-за эффекта дифракции.

Использование фильтра нейтральной плотности ND для уменьшения светового потока при съемках с длинной выдержкой даст гораздо лучший результат по резкости, чем использование для этой цели диафрагмы f/32.

Заключение

Я надеюсь, что эта статья принесет вам пользу. Знание о дифракции легко применить (хотя, в большинстве случаев этого не потребуется), но незнание может иметь плохие последствия для ваших фотографий.

Дифракционных эффектов легко избежать, если не зажимать диафрагму больше, чем до f/8.

Автор: Matthew Zhang

kapankov.ru — Дифракция и резкость

Полагаю, нет никакого секрета в том, что на средних диафрагмах (f4-f8) снимки получаются более резкими. В качестве подтверждения приведу результаты независимых измерений с сайта photozone.de для объектива Canon EF 50/1.2 USM L.

На графике отчетливо видно, что наилучшая резкость в центре достигается на диафрагме 4, а по всему полю кадра на диафрагме 5.6. При этом диафрагма 1.2 дает существенное снижение качества. Изменение резкости неизбежно происходит при смене диафрагмы при прочих равных условиях. Причина заключается в явлении дифракции. Разберемся с этим подробнее.

Свет имеет корпускулярно-волновую природу, схожую со звуком, жидкостями и т.п. Что происходит со звуком, который проходит через небольшое отверстие, при полной звукоизоляции препятствия? Звуковые волны распространяются так, словно отверстие является источником звука. И действительно, в соответствии с принципом Гюйгенса-Френеля, при прохождении волн через отверстие в препятствии, отверстие можно рассматривать как источник вторичных волн, которые распространяются во все стороны с той же скоростью, что и первичные волны.

Свет не является исключением. Свет имеет свойство как бы огибать препятствия при их прохождении. Это называется Дифракцией — явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Причем при уменьшении размера отверстия волны рассеиваются и накладываются друг на друга сильнее. При сильной закрытой диафрагме лучи рассеиваясь проходят разное расстояние до фокальной плоскости и часть лучей, соответственно, оказываются в другой фазе. В результате наблюдается эффект получения дифракционного рисунка, показанного на рисунке выше. Для идеально круглого отверстия плоский дифракционный рисунок называется «диском Эйри», в честь его первооткрывателя Джорджа Эйри. Размер кружка рассеивания (определяется как диаметр первого тёмного круга) используется в качестве определения теоретического предела разрешающей способности объектива.

Диаметр диска Эйри определяется формулой:

D = 1.22*λ*f

где

λ — длина волны света, прошедшей через объектив (в фотографических расчетах используют 546 нм)
f — диафрагменное число

А теперь, представьте, что свет проходя через объектив создает на матрице две рядом находящиеся точки (два диска Эйри), которые мы можем различить. Закрывая диафрагму, происходит расширение дисков Эйри и в какой то момент эти точки сливаются друг с другом, т.е. различие между ними исчезает. Это определяется критерием Релея: два диска Эйри воспринимаются зрением как два в том случае, если между их максимумами имеется минимум с интенсивностью на 20% меньше. Иначе наш глаз не способен их видеть как два, и говорят, что они не разрешаются.

А теперь вспомним, что в фотоаппарате разрешение определяется системой объектив-сенсор. То есть за величину принимается наибольшее значение разрешающей способности. Другими словами, пока диск Эйри меньше размера пикселя, разрешающую способность определяет разрешение матрицы, а как только диск Эйри превысит размер пикселя, то соответственно за разрешающую способность уже отвечает объектив. Так вот дифракционным пределом для системы объектив-камера принято считать размер пикселя. Когда диск Эйри становится соизмеримым с размером пикселя говорят, что достигнут дифракционный предел. Вот почему на кроп-камерах с маленьким размером пикселей так важно использовать объективы высокого качества.

Можно рассчитать теоретический дифракционный предел для камеры. Например, возьмем сенсор камеры Canon EOD 5D Mark III. Размер пикселя 6.08 мкм.

f = D/(1.22*λ)=6.08/(1.22*0.546)=9.1

Обратите внимание на то, что это теоретический дифракционный предел, которые не учитывает множество факторов, таких как, аберрации, освещенность сцены и т.п. Кроме того формула подразумевают идеально круглое отверстие, тогда как диафрагма формирует в действительности многоугольник. Также нужно помнить, что в камерах используется фильтр низких частот, размывающий изображение для борьбы с муаром.

А как же быть с открытыми диафрагмами? Ведь казалось бы, чем шире отверстие, тем резче должно быть изображение, а в самом начале статьи мы обратили внимание на то, что это вовсе на так. Дело в том, что чем больше отверстие диафрагмы, тем больше света попадает на сенсор, и свет этот собирается с большей поверхности линз и чем ближе к краям, тем больше искажений происходит при этом. Взгляните на самый первый график, приемлемая резкость у Canon EF 50/1.2 USM L начинается где-то f2.

Что же это получается? Объективы имеют предельные диафрагмы f1.2 и f22, а пользоваться ими нельзя? Да нет, можно и даже нужно при определенных условиях, когда фотограф готов пожертвовать некоторой потерей детализации для увеличения глубины резкости, например. Вопрос лишь в том, насколько готов пожертвовать фотограф резкостью. И этот момент точно нельзя доверять автоматическим режимам, по крайней мере на сегодняшний день.

Еще один замечательный вывод можно сделать, что дальнейшее увеличение мегапиксельности камер не будет приводить к увеличению детализации, поскольку не существует объективов с требуемой разрешающей способностью. Потому, можно купить хоть теоретическую 100 мегапиксельную камеру, изображения четче не станут.

В заключении хочется привести слова Энсела Адамса: «Нет ничего хуже, чем резкая фотография с нечёткой идеей». Не следует гнаться за сверхрезкими фотографиями. Во многих случаях, особенно в портретной съемке некоторая мыльность снимка только улучшит восприятие. Так или иначе, знания о влиянии различных факторов на качество снимка не являются лишними.

Практическое задание

Распечатайте две мишени: отсюда и отсюда. Снимайте их со штатива, полностью заполнив кадр с ISO 100 или 200. Меняя диафрагму изучите при каких диафрагмах резкость начинает ухудшаться для вашего объектива. Сравните результаты с тестами на photozone.de.

Дифракция света и ее влияние на качество фотографии

Дифракция света известна с 19 века и связана с волновой природой электромагнитного излучения, к которому относится и свет. Суть этого явления такова, что полностью избежать его влияния на качество фотографии невозможно, во всяком случае, на современном этапе развития физики, поэтому часто говорят о дифракционном пределе резкости снимка. Но учесть специфику дифракционных эффектов и попытаться уменьшить их вредное воздействие вполне реально.

Дифракция света проявляется в том, что при встрече с любым препятствием, световая волна отклоняется от прямолинейного движения и начинает это препятствие огибать. Это очень легко заметить, если понаблюдать за волнами на воде. После успокаивающего созерцания водяных волн станет очевидным и другой немаловажный факт: чем меньше отверстие, через которое проходит волна, тем больше она рассеивается.

Применительно к фотографии это означает, что дифракция света сильнее всего портит изображение при сильно закрытых диафрагмах, то есть именно тогда, когда увеличивается глубина резкости. Возникает такой парадокс, что наше желание получить в кадре как можно больше резких деталей приводит к обратному результату – резкость наоборот падает.

Именно здесь и возникает задача найти оптимальный баланс между глубиной резкости и ухудшением качества изображения из-за дифракции света. Иными словами, надо определить ту диафрагму, которая обеспечит нужную глубину резкости и при этом сохранится общая резкость кадра, в противном случае, глубину то мы получим, но резкость пропадет. Эту задачу мы и будем сейчас решать.

Дифракция света и критерий Рэлея

Проходя через объектив, свет фокусируется на матрице и возникает изображение, которое затем преобразуется в фотографию. Если мы фотографируем точку, то в идеальном случае мы хотели бы получить и точку на матрице. Тут-то все и портит дифракция света. Как бы хорошо не были скомпенсированы оптические аберрации объектива, мы увидим не точку, а размытый кружок рассеяния с максимумом в центре и расположенными вокруг него интерференционными кольцами, возникающими из-за наложения световых волн.

Если фотографировать две рядом расположенные точки, то из-за дифракции на матрице получатся два кружка рассеяния, и при уменьшении расстоянии между точками, в какой-то момент кружки сольются, и мы вообще не сможем понять, сфотографировали мы две точки или одну. Это и есть дифракционный предел резкости, который определяется так называемым критерием Рэлея.

Согласно критерию Рэлея считается, что два дифракционных кружка рассеяния воспринимаются зрением как два в том случае, если между их максимумами расположен минимум с интенсивностью на 20% меньше. В противном случае они не разрешаются, т. е. глаз будет видеть их как один.

Дифракция света и диафрагма фотоаппарата

Таким образом, дифракция света приводит к тому, что изображение точки, которое строит объектив, становится размытым, даже если объектив не имеет аберраций и точно на нее сфокусирован. Поскольку объектив и диафрагма имеют круглую форму, то точка приобретает вид нерезкого круга, который называется диском Эйри, в честь английского астронома, открывшего это явление. Нас интересует размер диска Эйри, поскольку именно он будет ограничивать резкость фотографии.

Но как определить размер диска, который имеет размытые края? Для этого наиболее разумно исходить из того, чтобы две точки на матрице воспринимались именно как две, т. е. удовлетворяли критерию Рэлея. Рассчитанный по критерию Рэлея диаметр диска Эйри D можно определить по формуле

где λ – длина волны прошедшего через объектив света (обычно берется зеленый свет 500 нм (= 0,0005 мм)), K – диафрагменное число.

Обратите внимание на такую особенность. Выше мы говорили, что дифракция света сильнее проявляется при малых размерах отверстия, через которое проходит световая волна. В формуле же [1] присутствует только K – диафрагменное число, а не абсолютный размер диафрагмы. В этом нет никакого противоречия, поскольку уменьшение размера диска Эйри при увеличении физического размера диафрагмы компенсируется пропорциональным его увеличением за счет фокусного расстояния, т. е. зависит только от относительного отверстия объектива, обратная величина которого и есть диафрагменное число, или просто значение диафрагмы.

Полученный результат в виде формулы [1] уже можно использовать на практике, поскольку он точно показывает, как зависит размер кружка рассеяния от диафрагмы объектива. И теперь на первое место выходит матрица.

Дифракция света и размер пикселя

Именно характеристики матрицы, а конкретно размер пикселя, определяет ту предельную диафрагму, при которой дифракция света еще не оказывает влияния на резкость. Если диаметр диска Эйри меньше размера пикселя, то разрешение системы объектив – матрица определяется матрицей (характеристики которой мы изменить не можем). А вот если больше, то диафрагмой (которую мы можем менять), что хорошо видно из соотношения [1]. Когда диаметр диска Эйри становится больше размера пикселя, дальнейшее закрытие диафрагмы приводит только к ухудшению резкости изображения.

Рассмотрим пример. Как было показано в статье про резкость в фотографии, размер пикселя матрицы формата DX (кроп фактор 1,52, 12 МПикс) фотоаппарата Nikon составляет 0,0055 мм. Определим по формуле [1] предельную диафрагму, которая еще не ухудшает резкость снимка:

Таким образом, для такой матрицы использование диафрагм больше f/9 нецелесообразно, поскольку вместо улучшения качества за счет увеличения глубины резкости, мы получим размытие из-за дифракции. Можно легко рассчитать, что для небольших компактных камер с маленькими матрицами дифракционные эффекты начинают проявляться уже на диафрагмах 4 – 5,6.

Мы получили удивительный результат! Такое объективное физическое явление как дифракция света проявляет себя в фотографии в полной зависимости от искусственно спроектированной матрицы. Говорит ли это о том, что мы можем победить дифракцию, создавая все более совершенные матрицы? Ни в коем случае. Как только размер пикселя станет равным диску Эйри на полностью открытой диафрагме идеального (т. е. без аберраций) объектива, дальнейшее наращивание «мегапиксельности» матрицы станет теоретически бессмысленным.

Дифракция света и современный фотоаппарат

Чтобы проиллюстрировать сказанное, приведу снимки испытательной миры, сделанные фотоаппаратом Nikon с матрицей, характеристики которой мы рассматривали выше. Съемка производилась на диафрагмах f/9 (которую мы получили в примере), f/16 и f/25.

Хорошо видно, что диафрагма f/9 действительно дает наиболее резкое изображение. При f/16 резкость все еще удовлетворительная, хотя если посмотреть внимательнее, то на самых мелких штрихах заметно слабое размытие. А вот f/25 никуда не годится. Мелкие штрихи разрешаются уже на пределе, а общая контрастность снимка заметно падает.

Несмотря на результаты теста, во многих случаях имеет смысл пожертвовать общей резкостью снимка, но получить одинаково резкими и передний и задний планы, например, на той же диафрагме 22. Исходя из практики, можно сказать, что для зеркальных камер предельные диафрагмы находятся в интервале 8 – 11, а для компактов 4 – 8 и этого вполне достаточно, чтобы достичь приемлемой глубины резкости без дифракционного ухудшения качества изображения. Кроме того, большинство объективов в указанных интервалах диафрагм дают наилучшее качество изображения, поскольку влияние аберраций на таких диафрагмах уже незначительно, а дифракционное размытие еще пренебрежимо мало.

Мы рассмотрели идеальный случай с точки зрения теории, в предположении, что у объектива отсутствуют аберрации. На самом деле при съемке приходится учитывать множество самых разнообразных факторов. Это и наличие штатива, и освещенность объекта и скорость его перемещения, и художественный замысел автора, и многое, многое другое. Такое знание приобретается только с опытом, поэтому точно сказать, что при предельной диафрагме 9 нельзя использовать 22, будет неправильным, но что касается максимальной резкости, то здесь дифракция света влияет однозначно, и учитывать ее надо обязательно.

Лазерная локация, доплеровские изображения и синтез апертуры / Хабр

Угловая разрешающая способность – важнейшая характеристика любой телескопической системы. Оптика утверждает, что это разрешение однозначно связано с длиной волны, на которой осуществляется наблюдение, и с диаметром входной апертуры телескопа. С большими диаметрами, как известно, большая проблема. Вряд ли когда-нибудь будет построен телескоп больше этого.
Одним из способов значительного увеличения разрешающей способности является применяемый в радиоастрономии и радиолокации метод синтезирования больших и сверхбольших апертур. В миллиметровом диапазоне самую большую апертуру — 14 км — обещают формировать 66-ю антеннами проекта ALMA в Чили.

Перенос методов апертурного синтеза в оптическую область, где длины волн на несколько порядков меньше, чем у радиолокаторов, связан с развитием техники лазерного гетеродинирования.

1.Физические основы формирования изображений.

Не будет ошибкой сказать, что изображение в любом оптическом устройстве формируется дифракцией света на входной апертуре, и более ничем. Посмотрим на изображение объекта из центра апертуры. Угловое распределение яркости изображения бесконечно удаленного точечного источника света (как, впрочем, и любого другого) будет одинаково для линзы и камеры-обскуры равного диаметра. Отличие линзы от обскуры заключается лишь в том, что линза переносит формируемое своей апертурой изображение из бесконечности в свою фокальную плоскость. Или, говоря иначе, производит фазовое преобразование входного плоского волнового фронта в сферически сходящийся. Для удаленного точечного источника и круглой апертуры изображение — это всем известная картина Эйри с кольцами.

Угловой размер диска Эйри можно в принципе уменьшить и как будто увеличить разрешение (по рэлеевскому критерию), если задиафрагмировать апертуру специальным образом. Существует такое распределение пропускания по радиусу, при котором центральный диск теоретически можно сделать произвольно малым. Однако при этом световая энергия перераспределяется по кольцам и контраст сложного изображения падает до нуля.

С математической точки зрения процедура формирования дифракционного изображения сводится к двухмерному преобразованию Фурье от входного светового поля (в скалярном приближении поле описывается комплексной функцией координат и времени). Любое изображение, регистрируемое глазом, экраном, матрицей или другим квадратичным по интенсивности приемником – не что иное, как двухмерный амплитудный спектр ограниченного апертурой светового поля, испускаемого объектом. Легко получить ту же самую картинку Эйри, если взять квадратную матрицу из одинаковых комплексных чисел (имитирующих плоский волновой фронт от удаленной точки), «вырезать» из нее круглую «апертуру», обнулив края, и сделать Фурье-преобразование всей матрицы.

Короче говоря, если каким-то образом записать поле (синтезировать апертуру) на достаточно большой области без потери амплитудной и фазовой информации, то для получения изображения можно обойтись без гигантских зеркал современных телескопов и мегапиксельных матриц, просто вычисляя Фурье-образ полученного массива данных.

2. Локация спутников и сверхразрешение.

Будем наблюдать движущийся поперек луча зрения стабилизированный объект, подсвеченный непрерывным когерентным лазерным источником. Регистрация отраженного от него излучения производится гетеродинным фотоприемником с небольшой апертурой. Запись сигнала в течение времени t эквивалентна реализации одномерной апертуры длиной vt, где v – тангенциальная скорость движения объекта. Легко оценить потенциальную разрешающую способность такого метода. Посмотрим на околоземный спутник в верхней элонгации, летящий на высоте 500 км со скоростью 8 км/сек. За 0,1 секунды записи сигнала получим «одномерный телескоп» размером 800 метров, теоретически способный рассмотреть в видимом диапазоне детали спутника величиной в доли миллиметра. Неплохо для такого расстояния.

Разумеется, отраженный сигнал на таких расстояниях ослабевает на много порядков. Однако гетеродинный прием (когерентное смешивание с опорным излучением) в значительной степени компенсирует это ослабление. Ведь, как известно, выходной фототок приемника в этом случае пропорционален произведению амплитуд опорного излучения и приходящего сигнала. Будем увеличивать долю опорного излучения и тем самым усиливать весь сигнал.

Можно посмотреть с другой стороны. Спектр записанного сигнала с фотоприемника представляет собой набор доплеровских компонент, каждая из которых есть сумма вкладов от всех точек объекта, имеющих одинаковую лучевую скорость. Одномерное распределение отражающих точек на объекте определяет распределение спектральных линий по частоте. Полученный спектр и является по сути одномерным «изображением» объекта по координате «доплеровский сдвиг». Две точки нашего спутника, расположенные на расстоянии 1 мм друг от друга в плоскости, перпендикулярной лучу зрения, имеют разность лучевых скоростей порядка 0,01-0,02 мм/сек. (Отношение этой разности к скорости спутника равно отношению расстояния между точками к расстоянию до спутника). Разность доплеровских частот этих точек для видимой длины волны 0,5 мк составит (f=2V/λ) порядка 100 Гц. Спектр (доплеровское изображение) от всего микроспутника, скажем, размером 10 см, уложится в диапазон 10 кГц. Вполне измеримая величина.

Можно посмотреть и с третьей стороны. Эта технология представляет собой не что иное, как запись голограммы, т.е. интерференционной картины, возникающей при смешивании опорного и сигнального полей. Она содержит в себе амплитудную и фазовую информацию, достаточную для восстановления полного изображения объекта.

Таким образом, подсвечивая спутник лазером, регистрируя отраженный сигнал и смешивая его с опорным лучом от того же лазера, получим на фотоприемнике фототок, зависимость которого от времени отражает структуру светового поля вдоль «одномерной апертуры», длину которой, как уже было сказано, можно сделать достаточно большой.

Двухмерная апертура, конечно, гораздо лучше и информативнее. Расставим равномерно несколько фотоприемников поперек движения спутника и запишем таким образом отраженное поле на площади vt*L, где L – расстояние между крайними фотоприемниками, которое в принципе ничем не ограничено. Например, те же 800 метров. Тем самым мы синтезируем апертуру «двухмерного телескопа» размером 800*800 метров. Разрешение по поперечной координате (L) будет зависеть от количества фотоприемников и расстояния между ними, по другой, «временной» координате (vt) – от ширины полосы излучения лазера и частоты оцифровки сигнала с фотоприемника.

Итак, мы имеем записанное световое поле на очень большой площади и можем делать с ним все, что угодно. Например, получить двухмерное изображение очень маленьких объектов на очень большом расстоянии без всяких телескопов. Или можно восстановить трехмерную структуру объекта путем цифровой перефокусировки по дальности.

Разумеется, реальная трехмерная конфигурация отражающих точек на объекте не всегда совпадает с их «доплеровским» распределением по лучевым скоростям. Совпадение будет, если эти точки находятся в одной плоскости. Но и в общем случае из «доплеровского изображения» можно извлечь много полезной информации.

3. Что было раньше.

Американская DARPA некоторое время назад финансировала программу SALTI, суть которой состояла в реализации подобной технологии. Предполагалось с летящего самолета лоцировать со сверхвысоким разрешением объекты на земле (танки, например), были получены некие обнадеживающие данные. Однако эту программу то ли закрыли, то ли засекретили в 2007 году и с тех пор про нее ничего не слышно. В России тоже кое-что делалось. Вот здесь можно посмотреть картинку, полученную на длине волны 10,6 мк.

4.Трудности технической реализации на длине волны 1,5 мк.

По зрелом размышлении я решил здесь ничего не писать. Слишком много проблем.

5. Кое-какие первичные результаты.

Пока с трудом удалось «рассмотреть» с расстояния 300 метров детали плоского диффузно отражающего металлического объекта размером 6 на 3 мм. Это был кусочек какой-то печатной платы, вот фотка:

Объект вращался вокруг оси, перпендикулярной лучу зрения, регистрация отраженного сигнала происходила примерно в момент максимального отражения (блика). Пятно от лазера, освещающее объект, имело размер около 2 см. Использовались всего 4 фотоприемника, разнесенные на 0,5 метра. Размер синтезированной апертуры оценивается величиной 0,5 м на 10 м.
Собственно, на всякий случай сами записанные сигналы (слева) и их спектры (справа) в относительных единицах:

Из предыдущей фотки объекта фотошопом выделены только интересующие нас освещаемые и отражающие участки, которые требуется увидеть:

Изображение, восстановленное двухмерным фурье-преобразованием из 4 сигналов и смасштабированное для сравнения:

Эта картинка вообще-то состоит всего из 4 строк (и около 300 столбцов), вертикальное разрешение изображения, соответственно, около 0,5 мм, однако темный уголок и обе круглые дырки вроде как видны. Горизонтальное разрешение – 0,2 мм, такова ширина токопроводящих дорожек на плате, видны все пять штук. (Обычный телескоп должен быть двухметрового диаметра, чтобы увидеть их в ближнем ИК).

По правде говоря, полученное разрешение пока далеко от теоретического предела, так что неплохо бы довести до ума эту технологию. Дьявол, как известно, кроется в деталях, а деталей здесь очень много.

Спасибо за внимание.

Королевство кривых лучей | Нанотехнологии Nanonewsnet

Обычно свет распространяется по прямой. Конечно, при помощи сред с различными коэффициентами преломления его можно отклонить. Однако новые исследования двух независимых научных групп показывают, что и сам по себе пучок света может изгибаться до 360˚.

Часто новое — это хорошо забытое, но не обязательно старое. В конце 1970-х физики Майкл Берри из Бристольского университета (Великобритания) и Нандор Балаш из Университета Стони-Брук (США) открыли, что так называемые волны Эйри могут до некоторой степени изгибаться благодаря взаимному наложению части волн.

В 2007 году исследователям из Университета Центральной Флориды в Орландо (США) впервые удалось получить лучи из волн Эйри на практике, при помощи лазера. Подтверждено экспериментально: луч слегка изгибался, до 8˚.

А изгибаются волны Эйри потому, что состоят из комбинации волн, где одна, ведущая, несёт бóльшую часть интенсивности общего луча. Другие, более слабые волны, отстают от предыдущей на половину длины. Эти волны двух видов так влияют друг на друга, что ведущая искривляется в одну сторону, а хвостовые, гасящие друг друга, — в противоположную. Луч Эйри (его видимая часть) почти не рассеивается при удалении от своего источника, превосходя в этом отношении даже довольно когерентный обычный лазерный луч.

Рис. 1. Такой изогнутый луч выглядит прерывистым, зато он почти не рассеивается. (Изображение F. Courvoisier / J. M. Dudley).

Ну а теперь Мордехай Сегев и его коллеги из Израильского технологического института в Хайфе утверждают, что нашли способ изгибать луч света под любым углом, вплоть до 360˚.

По словам г-на Сегева, прежде этого не удавалось сделать из-за ограниченности самой функции Эйри, которая позволяла рассчитывать колебания волн с высокой точностью лишь для небольших углов, после чего всё становилось слишком приближённым. Его группа обратилась к уравнениям Максвелла, которые описывают распространение электромагнитных волн (в том числе света). В итоге учёные обнаружили такие решения, которые точно описывают подбор фаз излучаемых световых волн, необходимый, чтобы добиться получения изгибающегося пучка света.

Исследование опубликовано в статье:

Ido Kaminer, Rivka Bekenstein, Jonathan Nemirovsky, and Mordechai Segev Nondiffracting Accelerating Wave Packets of Maxwell’s Equations. – Phys. Rev. Lett. 108, 163901 (2012) [5 pages].

Другая группа учёных, возглавляемая Джоном Дадли из Университета Франш-Конте (Безансон, Франция), провела эксперименты, базируясь на сходных идеях, при этом лишь модифицировав изначальную функцию Эйри. Используя пространственный модулятор света, исследователи подобрали фазы пучка лазерного излучения таким образом, что добились луча, искривлённого под углами до 60˚.

Отчёт об этом исследовании появился недавно в журнале Optics Letters.

Рис. 2. Оптические пинцеты уже сейчас могут подвешивать небольшие образцы буквально воздухе, а с изогнутыми лучами их можно будет использовать для манипуляций с клетками непосредственно в тканях или других сложных средах. (Фото ANU).

Количество потенциальных применений «кривого» лазерного луча весьма велико. Уже сейчас говорят о его использовании при создании оптического пинцета, способного без механического соприкосновения передвигать объекты по сложным траекториям (например, клетку в сложной среде), или о лазерах, выжигающих изогнутые под любыми углами отверстия. Теоретически такие лазерные лучи можно будет применять для лидарного «видения» вне прямой видимости, для связи с космическим аппаратом в точке L4 (или по ту сторону Марса) либо для наблюдения чего-то находящегося за препятствием, высокой стеной и т. д.

Чрезвычайно интересно и то, могут ли подобные решения быть применены к другим электромагнитным волнам, в частности радиоволнам и микроволнам: почти не рассеивающиеся пучки таких волн, да ещё способные огибать прежде непреодолимые для них препятствия, были бы огромным шагом вперёд для целого ряда практических задач…

Диск Эйри

Компьютерное изображение диска Эйри . Интенсивность серой шкалы была скорректирована для увеличения яркости внешних колец узора Эйри. Поверхностный график интенсивности в диске Эйри .

В оптике диск Эйри (или диск Эйри ) и узор Эйри — это описания наилучшего сфокусированного пятна света, которое может создать идеальный объектив с круглой апертурой, ограниченный дифракцией света.

Дифракционная картина, полученная от равномерно освещенной круглой апертуры, имеет яркую область в центре, известную как диск Эйри , который вместе с серией концентрических ярких колец вокруг называется узором Эйри . Оба названы в честь Джорджа Бидделла Эйри. Феномен диска и колец был известен еще до Эйри; Джон Гершель описал появление яркой звезды, видимой в телескоп при большом увеличении, для статьи о свете 1828 года для энциклопедии Encyclopedia Metropolitana :

…. тогда звезда видится (при благоприятных условиях спокойной атмосферы, постоянной температуры и т. д.) как идеально круглый, четко очерченный планетный диск, окруженный двумя, тремя или более попеременно темными и яркими кольцами, которые при исследовании внимательно видны слегка окрашенные по краям. Они следуют друг за другом почти через равные промежутки вокруг центрального диска …. ^[1]

Однако Эйри написал первую полную теоретическую трактовку, объясняющую это явление (его 1835 г. «О дифракции на предметном стекле с круглой апертурой»).^[2]

Математически дифракционная картина характеризуется длиной волны света, освещающего круглую апертуру, и ее размером. Внешний вид дифракционной картины дополнительно характеризуется чувствительностью глаза или другого детектора, используемого для наблюдения картины.

Наиболее важное применение этой концепции — камеры и телескопы. Из-за дифракции наименьшая точка, в которую линза или зеркало может сфокусировать луч света, имеет размер диска Эйри.Даже если бы можно было сделать идеальный объектив, все равно есть предел разрешающей способности изображения, создаваемого этим объективом. Оптическая система, в которой разрешение больше не ограничивается дефектами линз, а только дифракцией, называется дифракционно ограниченной.

Диск Эйри имеет важное значение в физике, оптике и астрономии.

Размер

Вдали от апертуры угол, под которым возникает первый минимум, отсчитываемый от направления падающего света, определяется по приблизительной формуле:

или, для малых углов, просто

, где θ в радианах, λ — длина волны света, а d — диаметр апертуры.Эйри написал это как

, где s, — угол первого минимума в дуговых секундах, a — радиус апертуры в дюймах, а длина волны света была принята равной 0,000022 дюйма (среднее значение видимых длин волн). ^[3] Критерий Рэлея для едва различимых двух объектов, которые являются точечными источниками света, таких как звезды, видимые в телескоп, заключается в том, что центр диска Эйри для первого объекта находится в первом минимуме диска Эйри секунда.Это означает, что угловое разрешение системы с дифракционным ограничением определяется теми же формулами.

Однако, хотя угол, под которым возникает первый минимум (который иногда называют радиусом диска Эйри), зависит только от длины волны и размера апертуры, вид дифракционной картины будет меняться в зависимости от интенсивности (яркости) света. источник. Поскольку любой детектор (глазной, пленочный, цифровой), используемый для наблюдения дифракционной картины, может иметь пороговое значение интенсивности для обнаружения, полная дифракционная картина может быть не видна.В астрономии внешние кольца часто не видны даже на сильно увеличенном изображении звезды. Возможно, ни одно из колец не видно, и в этом случае изображение звезды выглядит как диск (только центральный максимум), а не как полная дифракционная картина. Более того, более слабые звезды будут выглядеть как диски меньшего размера, чем более яркие звезды, потому что меньшая часть их центрального максимума достигает порога обнаружения. ^[4] Теоретически все звезды или другие «точечные источники» с заданной длиной волны, видимые через заданную апертуру, имеют одинаковый радиус диска Эйри, описываемый приведенным выше уравнением (и одинаковый размер дифракционной картины), различаясь только по интенсивности. («высота» графика поверхности вверху справа), более слабые источники выглядят как диски меньшего размера, а более яркие источники — как диски большего размера.^[5] Это было описано Эйри в его оригинальной работе:

Быстрое затухание света в следующих друг за другом кольцах достаточно объяснить видимость двух или трех колец с очень яркой звездой и невидимость колец со слабой звездой. Разница в диаметрах центральных пятен (или ложных дисков) разных звезд … также полностью объяснена. Таким образом, радиус ложного диска слабой звезды, где свет менее половины интенсивности центрального света не производит впечатления на глаз, определяется как [s = 1.17 / a], тогда как радиус ложного диска яркой звезды, где ощущается свет, равный 1/10 интенсивности центрального света, определяется как [s = 1,97 / a].). ^[6]

Несмотря на эту особенность работы Эйри, радиус диска Эйри часто задается просто как угол первого минимума даже в стандартных учебниках. ^[7] На самом деле угол первого минимума является предельным значением для размера диска Эйри, а не определенным радиусом. ^{[ требуется ссылка ]}

Примеры

Камеры

Если два объекта, отображаемые камерой, разделены достаточно маленьким углом, чтобы их диски Эйри на детекторе камеры начали перекрываться, объекты больше не могут быть четко разделены на изображении, и они начинают размываться вместе.Два объекта называются только что разрешенными , когда максимум первого паттерна Эйри попадает поверх первого минимума второго паттерна Эйри (критерий Рэлея).

Следовательно, наименьшее угловое разделение двух объектов, которое может иметь место до того, как они значительно размываются вместе, определяется, как указано выше как

Таким образом, способность системы разрешать детали ограничена соотношением λ / d . Чем больше апертура для данной длины волны, тем мельчайшие детали можно различить на изображении.

Поскольку θ мало, мы можем аппроксимировать это значение

, где x — это разделение изображений двух объектов на пленке, а f — расстояние от объектива до пленки. Если принять расстояние от объектива до пленки примерно равным фокусному расстоянию объектива, мы найдем

, но это f-число объектива. Типичная настройка для использования в пасмурный день — f / 8. ^[8] Для синего видимого света длина волны λ составляет около 420 нанометров.^[9] Это дает значение для x около 4 мкм. В цифровой камере уменьшение размера пикселей датчика изображения на самом деле не приведет к увеличению разрешения изображения.

Человеческий глаз

Продольные сечения сфокусированного луча с отрицательной (вверху), нулевой (в центре) и положительной сферической аберрацией (внизу). Объектив слева.

Наименьшее f-число для человеческого глаза составляет около 2,1, ^[10] соответствует функции рассеяния точки с ограничением дифракции с диаметром приблизительно 1 мкм.Однако при этом значении f сферическая аберрация ограничивает остроту зрения, а диаметр зрачка 3 мм (f / 5,7) приближается к разрешению, достигаемому человеческим глазом. ^[11] Максимальная плотность колбочек в ямке человека составляет приблизительно 170 000 на квадратный миллиметр, ^[12], что означает, что расстояние между конусами в человеческом глазу составляет около 2,5 мкм, что примерно соответствует диаметру функции рассеяния точки при f / 5.

Сфокусированный лазерный луч

Круглый лазерный луч с равномерной интенсивностью поперек круга (луч с плоским верхом), сфокусированный линзой, образует узор в виде диска Эйри в фокусе.Размер диска Эйри определяет интенсивность лазера в фокусе.

Условия наблюдения

Свет от равномерно освещенной круглой апертуры (или от равномерного плоского луча) будет демонстрировать дифракционную картину Эйри вдали от апертуры из-за дифракции Фраунгофера (дифракции в дальней зоне).

Условия для нахождения в дальнем поле и проявления паттерна Эйри следующие: падающий свет, освещающий апертуру, представляет собой плоскую волну (без изменения фазы в апертуре), интенсивность постоянна по площади апертуры и расстояние R от апертуры, где наблюдается дифрагированный свет (расстояние до экрана), велико по сравнению с размером апертуры, а радиус a апертуры не намного больше, чем длина волны λ света.Последние два условия формально можно записать как R > a ² / λ.

На практике условия для равномерного освещения могут быть выполнены, если источник освещения находится далеко от апертуры. Если условия для дальнего поля не выполняются (например, если диафрагма большая), дифракционная картина Эйри в дальней зоне также может быть получена на экране, гораздо более близком к диафрагме, с помощью линзы сразу после диафрагмы (или линзы сам может формировать проем).В этом случае узор Эйри будет сформирован в фокусе объектива, а не на бесконечности.

Следовательно, фокусное пятно однородного кругового лазерного луча (плоского луча), сфокусированного линзой, также будет узором Эйри.

В камере или системе формирования изображения удаленный объект отображается на пленку или плоскость детектора линзой объектива, и дифракционная картина в дальней зоне наблюдается на детекторе. Полученное изображение представляет собой свертку идеального изображения с дифракционной картиной Эйри из-за дифракции на диафрагме или из-за конечного размера линзы.Это приводит к конечному разрешению описанной выше системы линз.

Математические детали

Дифракция на круглом отверстии. Диаграмма Эйри наблюдается, когда R > a ² / λ (т.е. в дальней зоне) Дифракция на диафрагме с линзой. Изображение в дальней зоне будет (только) сформировано на экране на расстоянии одного фокусного расстояния, где R = f (f = фокусное расстояние). Угол наблюдения θ остается таким же, как и в безлинзовом случае.

Интенсивность дифракционной картины Фраунгофера круглой апертуры (картина Эйри) определяется квадратом модуля преобразования Фурье круглой апертуры:

, где I ₀ — максимальная интенсивность узора в центре диска Эйри, J ₁ — функция Бесселя первого рода первого порядка, k = 2π / λ — волновое число , a — радиус апертуры, а θ — угол наблюдения, т.е.е. угол между осью круглой апертуры и линией между центром апертуры и точкой наблюдения. , где q — радиальное расстояние от оси оптики в плоскости наблюдения (или фокальной), а N = R / d (d = 2a — диаметр апертуры, R — расстояние наблюдения) — f- номер системы.

Если линза используется после диафрагмы, узор Эйри формируется в фокальной плоскости линзы, где R = f (f — фокусное расстояние линзы).Обратите внимание, что предел для (или для) составляет I (0) = I ₀.

Нули J ₁ ( x ) находятся в точке. Из этого следует, что первое темное кольцо на дифракционной картине возникает там, где k a s i n θ = 3,8317 …, или

Радиус q ₁ первого темного кольца на экране связан с θ и f-числом на

где R — расстояние от апертуры, а f-число N = R / d — отношение расстояния наблюдения к размеру апертуры.Половина максимума центрального диска Эйри (где) находится при x = 1,61633 …; точка 1 / e ² (где J ₁ ( x ) = x /2 e ) происходит при x = 2,58383 …, и происходит максимум первого кольца при x = 5,13562 ….

Интенсивность I ₀ в центре дифракционной картины связана с полной мощностью P ₀, падающей на апертуру на ^[13]

, где Ε — мощность источника на единицу площади апертуры, A — площадь апертуры ( A, = π a , ²), а R — расстояние от апертуры.В фокальной плоскости линзы I ₀ = ( P ₀ A ) / (λ ² f ²). Интенсивность в максимуме первого кольца составляет около 1,75% от интенсивности в центре диска Эйри.

Выражение для I (θ), приведенное выше, можно проинтегрировать, чтобы получить полную мощность, содержащуюся в дифракционной картине внутри круга заданного размера:

, где J ₀ и J ₁ — функции Бесселя.Следовательно, доли общей мощности, содержащиеся в первом, втором и третьем темных кольцах (где Дж ₁ ( k a sin θ) = 0), составляют 83,8%, 91,0% и 93,8% соответственно. . ^[14]

Паттерн Эйри на интервале ka sin θ = [−10, 10]

Обведенная мощность отображается на графике рядом с интенсивностью.

Аппроксимация с использованием гауссова профиля

Радиальное сечение диаграммы Эйри (сплошная кривая) и аппроксимация ее гауссова профиля (пунктирная кривая).Абсцисса дана в единицах длины волны λ, умноженной на f-число оптической системы.

Рисунок Эйри довольно медленно спадает до нуля с увеличением расстояния от центра, при этом внешние кольца содержат значительную часть интегральной интенсивности рисунка. В результате среднеквадратичный размер пятна не определен (т.е. бесконечен). Альтернативным способом измерения размера пятна является игнорирование относительно небольших внешних колец диаграммы Эйри и аппроксимация центрального лепестка гауссовым профилем, так что

, где I ‘₀ — энергетическая освещенность в центре шаблона, q представляет собой радиальное расстояние от центра шаблона, а w — гауссова ширина.Если мы приравняем пиковую амплитуду паттерна Эйри и гауссовского профиля, то есть I ‘₀ = I ₀, и найдем значение w , дающее оптимальное приближение ^[15] к выкройки, получаем

, где N — f-число. Если, с другой стороны, мы хотим добиться того, чтобы профиль Гаусса имел тот же объем, что и шаблон Эйри, тогда это будет

В теории оптических аберраций обычно описывают систему формирования изображений как с ограничением дифракции , если радиус диска Эйри больше, чем среднеквадратичный размер пятна, определенный из геометрической трассировки лучей (см. Конструкция оптических линз).Поскольку среднеквадратичный размер пятна эквивалентен стандартному отклонению функции, приближение гауссова профиля обеспечивает удобное средство сравнения: здесь среднеквадратичный размер пятна — это просто параметр ширины Гаусса, w . И использование приведенного выше приближения показывает, что среднеквадратичный размер пятна гауссова приближения для диска Эйри составляет примерно одну треть от радиуса диска Эйри, то есть 0,42λ N по сравнению с 1,22λ N .

Затененный воздушный узор

Подобные уравнения также могут быть получены для затемненной дифракционной картины Эйри ^[16] ^[17], которая является дифракционной картиной от кольцевой апертуры или луча, т.е.е. равномерное круглое отверстие (луч), закрытое круглым блоком в центре. Эта ситуация актуальна для многих распространенных конструкций телескопов-рефлекторов, включающих вторичное зеркало, включая телескопы Ньютона и телескопы Шмидта-Кассегрена.

где — коэффициент затемнения кольцевой апертуры, или отношение диаметра затемняющего диска к диаметру апертуры (луча). , а x определяется, как указано выше: где R — радиальное расстояние в фокальной плоскости от оптической оси, λ — длина волны, а N — f-число системы.Дробная окруженная энергия (доля полной энергии, содержащейся в круге радиусом R с центром на оптической оси в фокальной плоскости) тогда определяется как:

Для формул уменьшите до незатененных версий выше.

Сравнение с фокусом гауссова луча

Круглый лазерный луч с равномерным профилем интенсивности, сфокусированный линзой, образует узор Эйри в фокальной плоскости линзы. Интенсивность в центре фокуса будет I _{0, A i r y} = ( P ₀ A ) / (λ ² f ²), где P ₀ — полная мощность луча, A = π D ²/4 — площадь луча ( D — диаметр луча), λ — длина волны, а f — фокусное расстояние объектива.^a ^b Mahajan, J. Opt. Soc. Am. А , 3 , 470 (1986).

Внешние ссылки

«Концепции и формулы в микроскопии: разрешение» Майкла У. Дэвидсона, Nikon MicroscopyU (веб-сайт).
- «Формирование изображения: числовая апертура и разрешение изображения» (интерактивное руководство по Java) Кеннета Р. Спринг, Брайана О. Флинна и Майкла У. Дэвидсона, Molecular Expressions (веб-сайт), 15 июня 2006 г.
- «Формирование изображения: формирование паттерна Эйри» (интерактивное руководство по Java) Кеннета Р. Спринг, Брайана О. Флинна и Майкла У. Дэвидсона, Molecular Expressions (веб-сайт), 15 июня 2006 г.
«Дифракция на круговой апертуре» Пола Пэдли, Connexions (веб-сайт), 8 ноября 2005 г. — Математические детали для вывода приведенной выше формулы.
«Диск Эйри: объяснение того, что это такое и почему его нельзя избежать», Oldham Optical UK .

Диск Эйри — Infogalactic: ядро планетарного знания

…. тогда звезда видится (при благоприятных условиях спокойной атмосферы, постоянной температуры и т. д.) как идеально круглый, четко очерченный планетный диск, окруженный двумя, тремя или более попеременно темными и яркими кольцами, которые при исследовании внимательно видны слегка окрашенные по краям. Они следуют друг за другом почти через равные промежутки вокруг центрального диска …. ^[1]

Размер

или, для малых углов, просто

, где θ в радианах, λ — длина волны света, а d — диаметр апертуры.Эйри написал это как

Быстрое затухание света в следующих друг за другом кольцах достаточно объяснить видимость двух или трех колец с очень яркой звездой и невидимость колец со слабой звездой. Разница в диаметрах центральных пятен (или ложных дисков) разных звезд … также полностью объяснена. Таким образом, радиус ложного диска слабой звезды, где свет менее половины интенсивности центрального света не производит впечатления на глаз, определяется как [s = 1.17 / a], тогда как радиус ложного диска яркой звезды, где ощущается свет, равный 1/10 интенсивности центрального света, определяется как [s = 1,97 / a]. ^[6]

Примеры

Логарифмический график зависимости диаметра апертуры от углового разрешения на дифракционном пределе для различных длин волн света по сравнению с различными астрономическими инструментами.Например, синяя звезда показывает, что космический телескоп Хаббл почти дифракционно ограничен в видимом спектре на 0,1 угловой секунды, тогда как красный кружок показывает, что человеческий глаз теоретически должен иметь разрешающую способность 20 угловых секунд, хотя обычно только 60 угловых секунд. .

Камеры

Это также может быть выражено как

где — разделение изображений двух объектов на пленке, а — расстояние от линзы до пленки. Если принять расстояние от объектива до пленки примерно равным фокусному расстоянию объектива, мы найдем

, но это f-число объектива. Типичная настройка для использования в пасмурный день — f / 8 (см. Правило Sunny 16). Для синего видимого света длина волны λ составляет около 420 нанометров (чувствительность S-колбочек см. В ячейках конуса).Это дает значение около 4 мкм. В цифровой камере уменьшение размера пикселей датчика изображения на самом деле не приведет к увеличению оптического разрешения изображения. Однако это может улучшить окончательное изображение за счет передискретизации, что позволит снизить уровень шума.

Человеческий глаз

Самое быстрое f-число для человеческого глаза — около 2.1, ^[8], что соответствует функции рассеяния точки с ограничением дифракции с диаметром приблизительно 1 мкм. Однако при этом значении f сферическая аберрация ограничивает остроту зрения, а диаметр зрачка 3 мм (f / 5,7) приближается к разрешению, достигаемому человеческим глазом. ^[9] Максимальная плотность колбочек в ямке человека составляет приблизительно 170 000 на квадратный миллиметр, ^[10], что означает, что расстояние между конусами в человеческом глазу составляет около 2,5 мкм, что приблизительно соответствует диаметру функции рассеяния точки на f / 5.

Сфокусированный лазерный луч

Круглый лазерный луч с равномерной интенсивностью поперек круга (луч с плоским верхом), сфокусированный линзой, образует узор в виде диска Эйри в фокусе. Размер диска Эйри определяет интенсивность лазера в фокусе.

Прицел

Некоторые прицельные приспособления для прицеливания оружия (например, FN FNC) требуют, чтобы пользователь выровнял визир (задний, ближний прицел, т.е. который будет не в фокусе) с наконечником (который должен быть сфокусирован и наложен на цель) в конце ствол.Глядя через визир, пользователь заметит диск Эйри, который поможет центрировать прицел над штифтом. ^[11]

Условия наблюдения

Условия для нахождения в дальнем поле и проявления паттерна Эйри следующие: падающий свет, освещающий апертуру, представляет собой плоскую волну (без изменения фазы в апертуре), интенсивность постоянна по площади апертуры и расстояние R от апертуры, где наблюдается дифрагированный свет (расстояние до экрана), велико по сравнению с размером апертуры, а радиус апертуры не намного больше, чем длина волны света.Последние два условия формально можно записать как.

На практике условия для равномерного освещения могут быть выполнены, если источник освещения находится далеко от апертуры. Если условия для дальнего поля не выполняются (например, если диафрагма большая), дифракционная картина Эйри в дальней зоне также может быть получена на экране, гораздо более близком к диафрагме, с помощью линзы сразу после диафрагмы (или линзы сам может формировать проем). В этом случае узор Эйри будет сформирован в фокусе объектива, а не на бесконечности.

Математические детали

Файл: Круглая диафрагма с lens.svg Дифракция на диафрагме с линзой. Изображение в дальней зоне будет (только) сформировано на экране на расстоянии одного фокусного расстояния, где R = f (f = фокусное расстояние). Угол обзора остается таким же, как и в безлинзовом корпусе.

где — максимальная интенсивность рисунка в центре диска Эйри, — функция Бесселя первого рода первого порядка, — волновое число, — радиус апертуры, — угол наблюдения, т.е.е. угол между осью круглой апертуры и линией между центром апертуры и точкой наблюдения. , где q — радиальное расстояние от оси оптики в плоскости наблюдения (или фокальной плоскости) и (d = 2a — диаметр апертуры, R — расстояние наблюдения) — f-число системы.

Если линза используется после диафрагмы, узор Эйри формируется в фокальной плоскости линзы, где R = f (f — фокусное расстояние линзы). Обратите внимание, что предел для (или для) равен.

Нули находятся в точке.Из этого следует, что первое темное кольцо на дифрактограмме возникает там, где, или

Радиус первого темного кольца на экране связан с числом f соотношением

где R — расстояние от апертуры, а f-число N = R / d — отношение расстояния наблюдения к размеру апертуры. Половина максимума центрального диска Эйри (где) находится в точке; точка 1 / e ² (где) встречается в, а максимум первого кольца происходит в.

Интенсивность в центре дифракционной картины связана с полной мощностью, падающей на апертуру, соотношением ^[12]

где — мощность источника на единицу площади отверстия, A — площадь отверстия (), а R — расстояние от отверстия. В фокальной плоскости линзы. Интенсивность в максимуме первого кольца составляет около 1,75% от интенсивности в центре диска Эйри.

Выражение выше можно проинтегрировать, чтобы получить полную мощность, содержащуюся в дифракционной картине в пределах круга заданного размера:

где и — функции Бесселя.Следовательно, доли общей мощности, содержащиеся в первом, втором и третьем темных кольцах (где), составляют 83,8%, 91,0% и 93,8% соответственно. ^[13]

Аппроксимация с использованием гауссова профиля

Файл: Airy vs gaus.svg Радиальное сечение диаграммы Эйри (сплошная кривая) и аппроксимация ее гауссова профиля (пунктирная кривая). Абсцисса дана в единицах длины волны, умноженной на f-число оптической системы.

Рисунок Эйри довольно медленно спадает до нуля с увеличением расстояния от центра, при этом внешние кольца содержат значительную часть интегральной интенсивности рисунка.В результате среднеквадратичный размер пятна не определен (т.е. бесконечен). Альтернативным способом измерения размера пятна является игнорирование относительно небольших внешних колец диаграммы Эйри и аппроксимация центрального лепестка гауссовым профилем, так что

где — энергетическая освещенность в центре рисунка, представляет собой радиальное расстояние от центра рисунка и является среднеквадратичной шириной по Гауссу (в одном измерении). Если мы приравняем пиковую амплитуду паттерна Эйри и гауссовского профиля, т.е.

, где N — f-число.Если, с другой стороны, мы хотим добиться того, чтобы профиль Гаусса имел тот же объем, что и шаблон Эйри, тогда это будет

В теории оптических аберраций обычно описывают систему формирования изображений как с ограничением дифракции , если радиус диска Эйри больше, чем среднеквадратичный размер пятна, определенный из геометрической трассировки лучей (см. Конструкция оптических линз). Приближение гауссова профиля обеспечивает альтернативный способ сравнения: использование приведенного выше приближения показывает, что среднеквадратичная ширина приближения Гаусса к диску Эйри составляет примерно одну треть радиуса диска Эйри, т.е.е. в отличие от.

Затененный воздушный узор

Подобные уравнения также могут быть получены для затемненной дифракционной картины Эйри ^[14] ^[15], которая представляет собой дифракционную картину от кольцевой апертуры или луча, то есть однородной круглой апертуры (луча), закрытой круглым блоком на центр. Эта ситуация актуальна для многих распространенных конструкций телескопов-рефлекторов, включающих вторичное зеркало, включая телескопы Ньютона и телескопы Шмидта-Кассегрена.

где — коэффициент затемнения кольцевой апертуры, или отношение диаметра затемняющего диска к диаметру апертуры (луча). , а x определяется, как указано выше: где — радиальное расстояние в фокальной плоскости от оптической оси, — длина волны и — f-число системы. Дробная окруженная энергия (доля полной энергии, содержащейся в круге радиуса с центром на оптической оси в фокальной плоскости) затем определяется по формуле:

Для формул уменьшите до незатененных версий выше.

Практический эффект наличия центрального препятствия в телескопе заключается в том, что центральный диск становится немного меньше, а первое яркое кольцо становится ярче за счет центрального диска. Это становится более проблематичным с телескопами с коротким фокусным расстоянием, которые требуют больших вторичных зеркал. ^[16]

Сравнение с фокусом гауссова луча

Круглый лазерный луч с равномерным профилем интенсивности, сфокусированный линзой, образует узор Эйри в фокальной плоскости линзы.Интенсивность в центре фокуса будет равна где — полная мощность луча, — площадь луча (- диаметр луча), — длина волны, — это фокусное расстояние линзы.

Гауссов пучок диаметром D, сфокусированный через апертуру диаметром D, будет иметь профиль фокуса, который близок к гауссову, а интенсивность в центре фокуса будет 0,924 раза. ^[15]

См. Также

Примечания и ссылки

↑ Herschel, J.F. W., «Свет», в « Transactions». Трактаты по физической астрономии, свету и звуку вошли в Encyclopaedia Metropolitana , Richard Griffin & Co., 1828, p. 491.
↑ Эйри, Г. Б., «О дифракции на предметном стекле с круглой апертурой», Труды Кембриджского философского общества , Vol. 5, 1835, с. 283-291.
↑ Эйри, Г. Б., «О дифракции на предметном стекле с круглой апертурой», Труды Кембриджского философского общества , Vol.5, 1835, с. 287.
↑ Сиджвик, Дж. Б., Справочник астронома-любителя , Dover Publications, 1980, стр. 39–40.
↑ Грэйни, Кристофер М., «Объекты в телескопе дальше, чем они кажутся — Как дифракция заставила Галилея неправильно измерить расстояния до звезд», Учитель физики , т. 47, 2009, стр. 362–365.
↑ Эйри, Г. Б., «О дифракции на предметном стекле с круглой апертурой», Труды Кембриджского философского общества , Vol.5, 1835, с. 288.
↑ Джанколи, Д. К., Физика для ученых и инженеров (3-е издание) , Прентис-Холл, 2000, стр. 896.
↑ Hecht, Eugene (1987). Оптика (2-е изд.). Эддисон Уэсли. ISBN 0-201-11609-X . Разд. 5.7.1
↑ Стив Чепмен, изд. (2000). Проектирование оптических систем . McGraw-Hill Professional. ISBN 0-07-134916-2 .
↑ «Плотность глазных рецепторов». Архивировано 30 апреля 2008 года. Проверено 20 сентября 2008.
↑ См. Http://en.wikibooks.org/wiki/Marksmanship, «Выравнивание прицела»
↑ Э. Хехт, Оптика , Аддисон Уэсли (2001)
↑ М. Борн и Э. Вольф, Принципы оптики (Pergamon Press, Нью-Йорк, 1965)
↑ Rivolta, Applied Optics , 25 , 2404 (1986).
↑ ^15,0 ^15,1 Mahajan, J. Opt. Soc. Am. А , 3 , 470 (1986).
↑ Сацек, Владимир (14 июля 2006 г.). «Глава 7 Эффекты препятствия (7.1. Эффект центрального препятствия)». 7. Замечания по любительской оптике телескопов . Проверено 18 мая 2013 г.

Внешние ссылки

Майкл В. Дэвидсон. «Понятия и формулы в микроскопии: разрешение». Nikon MicroscopyU (веб-сайт).
- Кеннет Р. Спринг; Брайан О. Флинн и Майкл В. Дэвидсон. «Формирование изображения: числовая апертура и разрешение изображения». Получено 15 июня 2006 г. (Интерактивное руководство по Java) Molecular Expressions (веб-сайт).
- Kenneth R. Spring; Брайан О. Флинн и Майкл В.Дэвидсон. «Формирование изображения: формирование воздушного узора». Получено 15 июня 2006 г. (Интерактивное руководство по Java) Молекулярные выражения .
Пол Пэдли. «Дифракция на круговой диафрагме». , Connexions (веб-сайт), 8 ноября 2005 г. — Математические детали для вывода приведенной выше формулы.
«Диск Эйри: объяснение того, что это такое и почему его нельзя избежать», Oldham Optical UK .
Вайсштейн, Эрик В., «Нули функций Бесселя», MathWorld .

RAPID Синтезатор

RAPID — современный полифонический гибридный синтезатор, объединяющий быстрый рабочий процесс и мощные методы синтеза. Уникальный движок слоев, на котором работает RAPID, позволяет формировать и настраивать все аспекты ваших звуков, в результате чего получаются динамические и жирные патчи, готовые для производства, исполнения или просто вдохновения.

ПОПРОБОВАТЬ ДЕМО

РУКОВОДСТВО ПО ЭКСПЛУАТАЦИИ

RAPID поставляется с большим разнообразием готовых звуков. Каждый пресет, разработанный и созданный вручную для удобства игры и творчества, прошел тщательный контроль качества. Все макросы связаны между собой, что позволяет легко управлять наиболее яркими аспектами звука.

НОВЫЙ
С последней версией 1.8.0. новый бонусный звуковой пакет Granular Elements теперь включен бесплатно.
Начиная с версии 1.7.0. дополнительный плагин RAPID FX включен. Это позволяет использовать его в качестве блока эффектов на микшере DAW, вставлять и отправлять каналы и открывает совершенно новое измерение возможностей обработки звука.

Каждый из 8 уровней синтеза может управляться отдельно и состоит из следующих элементов.
Осциллятор
Морфабельные волновые таблицы.
Множественные выборки со скоростью и / или циклическим перебором.
До 8 голосов в унисон.
Регулировка низких и высоких частот для каждой формы волны.
Дисторсия трубки и асимметричный зажим.
Фазовая модуляция и кольцевая модуляция.
Фазовая и кольцевая модуляция от других генераторов.
Phase Bend, Phase Double и Phase Mirror.
Модуляция с фазовой обратной связью.
Жесткая синхронизация и синхронизация.
Формантный сдвиг и фазовое перекрытие.
Органический дрейфовый и широтно-импульсный модулятор.
Генератор фаз хаоса и шума с плавным переходом в коричневый / белый / розовый.
Гранулированный синтез
До 100 истинных стерео зерен.
Изменяемые формы конвертов зерна.
Длина зерна от 10 миллисекунд до 1 секунды.
Хаос рандомизатор для положения зерна, скорости, объема длины и расстройки.
Может также использовать мультисэмплы стерео в качестве источника детализации.
Бесплатная бонусная библиотека Гранулярные элементы включены.
Фильтр и вставка
6, 12, 24 дБ Lowpass и Highpass.
12, 24 дБ Pro-Lowpass.
12, 24 дБ Полоса пропускания и пик.
Многополосный и многопиковый, 24 дБ.
12 дБ Notch и Multi-Notch.
Acid, Analog, Legacy и Vintage Lowpass
Xtreme Lowpass I и II.
Форманта, гласная и биткрашер.
Гребень обратной связи и задержка по времени.
Комбинация параллельного и последовательного низких / высоких частот.
Ламповый дисторшн, овердрайв и тон-фуз.
Возбудитель и усилитель атаки.
Модуляторы
4 конверта ADSR с регулируемым наклоном.
4x LFO с двойной формой волны и сдвигом фазы для сложных форм.
4x последовательности до 32 шагов, с циклическим и однократным режимами.
Различные режимы триггера для различных сценариев использования.
Арпеджиатор
32 шага шаблона с регулируемой длиной.
Вверх, вниз, случайный, очередь и режим аккордовой комбинации.
Управление октавой и перемешиванием.
Импорт / экспорт внешних файлов MIDI.
Звонок
Режим легато со скольжением нот.
Фильтрация MIDI-каналов.
Диапазон ключей на слой.
Фильтр входных нот.
Изменение порядка обработки вставок и фильтров.
Эффекты
Реверберация с 8 пространственными моделями для разных размеров.
Задержка с плавной модуляцией времени задержки.
Dual Delay с перекрестной обратной связью и режимом Ping-Pong.
Тональная задержка с настраиваемым временем задержки.
Камера для акустики с очень короткой реверберацией.
Плавное ламповое искажение с динамическим усилением эквалайзера.
Bit-Crusher, снижение скорости с джиттером.
2-полосный формирователь волны с регулируемым кроссовером.
4-полосный сатуратор с 16 различными типами вставок.
Phaser, Flanger, Chorus с точным контролем глубины модуляции.
Ансамбль Хор.
3-полосный эквалайзер с фильтром нижних и верхних частот, нижних частот, верхних полос и колоколообразным фильтром.
Talker Filter 6 формантных режимов вокала и внутреннее дробление.
Динамический компрессор с цифровым и аналоговым режимами.
Синхронизируемый выравниватель боковой цепи различной формы.
32-ступенчатый стерео Trancegate с контролем Shuffle-Rhytmn.
Маршрутизатор отправки, для параллельного микширования с другими слоями.
Tapestop с регулируемым наклоном, временем начала и остановки.
Глитч для изменения высоты тона, заикания и временных скачков, управляемый последовательностями.
Мастер
8-канальный микшер.
3-полосный динамический компрессор с различными моделями реакции.
Ограничитель выхода с автоматическим усилением подпитки.
Быстрый модификатор для одновременного управления громкостью и огибающей фильтра для всех слоев.
Пользовательские библиотеки :
Импорт одно- и многоцикловой волновой таблицы.
Импорт одной и нескольких выборок с помощью Velocity и Round Robin.
Алгоритм ресинтеза для нового поколения Multi-Sample.
Архивирование и установка автономных библиотечных пакетов.
Рабочий процесс
Drag & Drop Modulation.
пресетных файлов для модулятора, эффекта или паттерна арпеджиатора.
Копируйте и вставляйте модуляторы, узоры или целые слои.
3-макроконтроллеры.
GUI
Регулируемая графика HD с разрешением 16: 9 (1280 x 720 пикселей).
4K Готово и масштабируется до 300% (3840 x 2160 пикселей).
Десять уникальных тем пользовательского интерфейса.
Общие
Типы плагинов
Быстрый синтезатор
Rapid FX
Версия
1.8.0
Будущие обновления включены
Размер завода
Доставка
Содержание
Пресеты
660+ предустановок звука
250+ предустановок модулятора
250+ пресетов арпеджиатора
420+ пресетов эффектов
110+ пресетов Rapid FX
Аудио
250+ волновых таблиц
190+ мультивыборок
370+ образцов барабана Oneshot (44.1 кГц, стерео, 16 бит WAV)

Список содержимого
Спецификация аудио плагина
Формат плагина
Архитектура
32-разрядная (x86)
64-разрядная (x64)
Поддерживаемые хосты
Ableton Live 9-10
FL Studio 20
Cubase 9-10
Logic Pro X
Студия Один 4
REAPER 5
Bitwig Studio 3
Большинство других DAW.Чтобы убедиться, протестируйте демоверсию на совместимость!
Выход канала
Поддерживаемые частоты дискретизации
48, 96 и 192 кГц (передискретизация)
Системные требования
Операционная система
Windows 7, 8, 10
MacOS 10.7 и новее. Поддерживает MacOS Catalina.
ЦП
SSE2 доступен
Intel Core i3 / i5 / i7 / Xeon (рекомендуется)
AMD с SSE2 не ниже
Память
не менее 3 ГБ свободного места на диске
Разрешение экрана

Разное
Защита от копирования
Серийный номер / онлайн-активация
Rapid Extension
Имя XT Заводские звуки
XT ID 1
.
Диск эйри: Дифракция — Diffraction — qaz.wiki

Дифракция — Diffraction — qaz.wiki

История

Механизм

Примеры

Однощелевая дифракция

Дифракционная решетка

Распространение лазерного луча

Визуализация с ограничением дифракции

Спекл-узоры

Принцип Бабине

Узоры

Дифракция частиц

Брэгговская дифракция

Согласованность

Приложения

Дифракция до разрушения

Смотрите также

Ссылки

внешние ссылки

Резкость, дифракция и диафрагма

Наука о дифракции света

Практическое применение

Заключение

kapankov.ru — Дифракция и резкость

Дифракция света и ее влияние на качество фотографии

Дифракция света и критерий Рэлея

Дифракция света и диафрагма фотоаппарата

Дифракция света и размер пикселя

Дифракция света и современный фотоаппарат

Лазерная локация, доплеровские изображения и синтез апертуры / Хабр

Королевство кривых лучей | Нанотехнологии Nanonewsnet

Диск Эйри

Размер

Примеры

Камеры

Человеческий глаз

Сфокусированный лазерный луч

Условия наблюдения

Математические детали

Аппроксимация с использованием гауссова профиля

Затененный воздушный узор

Сравнение с фокусом гауссова луча

Внешние ссылки

Диск Эйри — Infogalactic: ядро ​​планетарного знания

Размер

Примеры

Камеры

Человеческий глаз

Сфокусированный лазерный луч

Прицел

Условия наблюдения

Математические детали

Аппроксимация с использованием гауссова профиля

Затененный воздушный узор

Сравнение с фокусом гауссова луча

См. Также

Примечания и ссылки

Внешние ссылки

RAPID Синтезатор

НОВЫЙ

Добавить комментарий Отменить ответ

Диск Эйри — Infogalactic: ядро планетарного знания