Фибоначчи числа золотое сечение: Золотое сечение и пропорции Фибоначчи

🌀 Золотое сечение на графиках Числа Фибоначчи некоторые считают «последовательностью бога», а Леон

Pulse_Official

20 октября 2022 в 11:55

🌀 Золотое сечение на графиках Числа Фибоначчи некоторые считают «последовательностью бога», а Леонардо Да Винчи утверждал, что они «руководят Вселенной». Сформированное ими золотое сечение встречалось еще в трудах 300 лет до н. э., а исследователи полагают: его пропорциями наделено все растущее и стремящееся занять свое место в пространстве. Речь идет о последовательности: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 и так далее. Она примечательна тем, что каждое третье число в ней представляет сумму двух предыдущих, а еще — при делении всех стоящих рядом чисел — за исключением некоторых первых, — получается значение близкое к 0,618 или 1,618. Это число и считается числом золотого сечения — идеальной пропорцией, которую можно встретить в тысячах природных явлений, соотношении частей тела человека, расстоянии между листьями на ветках и многих других окружающих нас явлениях. «Золотым сечением» пользуются музыканты, художники, архитекторы и трейдеры. Идея искать идеальную пропорцию на графиках впервые появилась у бухгалтера Ральфа Эллиота в прошлом веке. Занявшись этим, он не прогадал: изучив движения рынка за 75 лет, ученый пришел к выводу — они подчинены определенным ритмам — волнам, в пропорциях которых можно узнать золотое сечение. Этот вывод лег в основу теории, которая получила название волновой теории Эллиота. Именно с ней тесно связан инструмент теханализа, основанный на последовательности Фибоначчи — уровни Фибоначчи. Но обо всем по порядку. 📌 Уровни (или линии) Фибоначчи 🔹 Теория При грамотном построении на графике помогают определить уровни поддержки и сопротивления (ценовые области, где цена меняет свое направление), а с их помощью — и точки входа и выхода из сделки. Индикатор представляет собой несколько параллельных линий — технических уровней, являющихся препятствием для дальнейшего продвижения цены. То есть, подходя к ним на графике, цена актива редко беспрепятственно движется в направлении тренда и чаще — откатывается назад.

Другими словами — это уровни, от которых цена актива, скорее, оттолкнется, чем сразу пробьет. Линии выстраиваются на основании «золотой пропорции»: если любой член ряда последовательности Фибоначчи разделить на число, стоящее через одно, выйдет соотношение, близкое к 0,382. А если брать каждый третий член после исходного, — соотношение между ними будет примерно равно 0,236. Поэтому и уровни Фибоначчи выстраиваются на графике как: 0%, 23,6%, 38,2%, 61,8%, 78,6% и 100% (но некоторые трейдеры пользуются уровнями и вне этого диапазона — например, 161,8%, 261,8% и 423,6%). «Ключевыми уровнями» считаются линии 38,2% и 61,8% — при изменениях курса именно они оказывают наибольшее сопротивление и поддержку. 🔹 Практика Линии протягиваются от начала тренда к концу (или наоборот). Но обратите внимание! Для этого инструмента теханализа очень важен выраженный тренд, если его не будет, уровни Фибоначчи могут работать некорректно. 📈 Сигналом к покупке на восходящем тренде может служить снижение цены актива вниз до ключевого уровня поддержки. 📉 А сигналом к продаже (открытию позиции на понижение — в шорт) при нисходящем тренде — восстановление бумаги до ключевого уровня сопротивления. Также линии Фибоначчи инвесторы используют для поиска удачного входа в позицию при усреднении: инструмент действует на любых временных промежутках и полезен как для тех, кто торгует внутри дня, так и для тех, кто выбирает долгосрочное инвестирование. А еще с помощью этих уровней можно отслеживать точки разворота коррекции: принято считать, что коррекция в большинстве случаев останавливается на линиях Фибоначчи (ну или хотя бы демонстрирует на этих уровнях отскок). А пользуетесь ли вы линиями Фибоначчи? Опробовать этот и другие инструменты теханализа на деле можно в нашем Терминале (https://www.tinkoff.ru/invest/web-terminal/ — инструменты Ганна и Фибоначчи). #теханализ_в_пульсе #теханализ

Странная петля Фибоначчи: красота математического начала

Поговорим об удивительной последовательности Фибоначчи, золотом сечении и бактериях. Будьте готовы найти совпадения там, где не ожидали их увидеть.

Говоря об алгоритмах, нельзя не упомянуть о последовательности Фибоначчи. Она тесно связана с золотым сечением, которое мы снова и снова встречаем в природе, архитектуре, искусстве и даже романе Дэна Брауна. От раковин морских животных до сакральной геометрии, по-видимому, Золотое Сечение закодировано во многих аспектах нашей Вселенной.

Невозможно перечислить все места, где мы можем встретить эту удивительную последовательность, но самое невероятное – она появляется даже внутри самой себя. Рекурсия внутри рекурсии, математическое начало, то, что Хофштадтер мог бы назвать «странной петлей» (strange loop).

В информатике последовательность – и различные стратегии ее вычисления – это хорошие обучающие инструменты. Последовательность Фибоначчи может быть вычислена с помощью простой рекурсии:

def fib(n):
    if n <= 1:
        return 1

    return fib(n - 2) + fib(n - 1)

Один из самых замечательных моментов этой реализации в том, что код очень близко соответствует самому определению.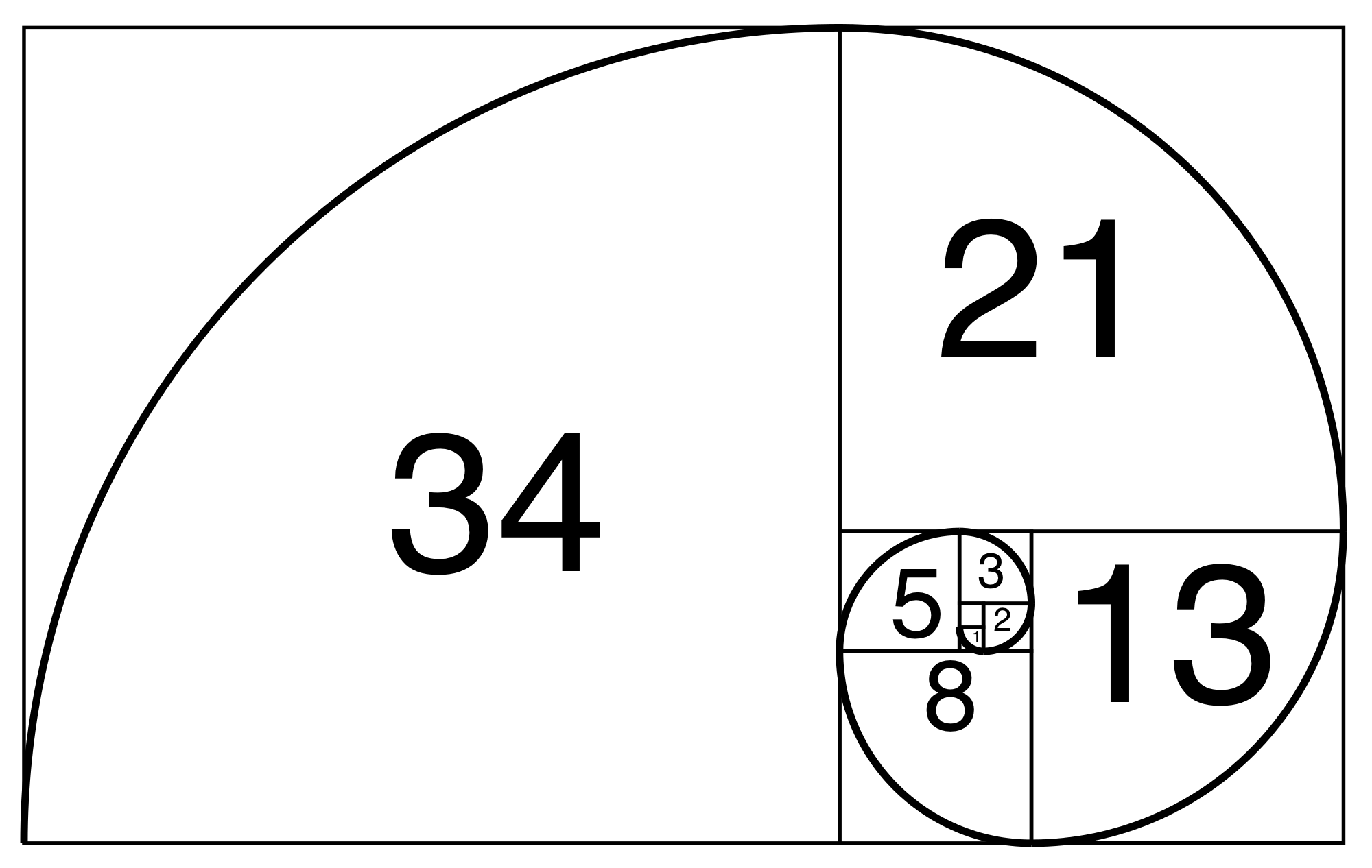

Последовательность была описана в 1202 году Леонардо Фибоначчи. Она начинается с двух единиц, а последующие члены вычисляются путем сложения двух предыдущих. Третий член 1 + 1 = 2, а четвертый 1 + 2 = 3, далее 2 + 3 = 5. Вот первые несколько цифр:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …

Рекурсивный код выше означает следующее: если n равно 0 или 1, функция вернет единицу, иначе – результат сложения fib(n-1) и fib(n-2), то есть сумму двух предыдущих членов.

Ряд Фибоначчи и золотое сечение

Кроме самой последовательности, Фибоначчи обнаружил ее связь с золотым сечением.

Золотое сечение – иррациональное число. Как и ? (число Пи), оно имеет бесконечное количество цифр после запятой, которые никогда не образуют повторяющихся шаблонов. Большинство из нас помнят ? как 3.14, а золотое сечение можно запомнить как 1.618. Буквенное представление этой величины – ? (фи, Phi).

Если взять n-ный член последовательности Фибоначчи и разделить его на (n-1)-ный, то полученный результат будет приблизительно равен золотому сечению. Чем дальше от начала, тем точнее приближение:

5/3 = 1.666
8/5 = 1.6
13/8 = 1.625
21/13 = 1.61538461538

Ряд Фибоначчи как алгоритмическая сложность

Вероятно, вы знаете, что рекурсивный код работает медленно. А знаете ли вы, что он работает медленно таким образом, который тесно связан с числом ??

Смоделируем наш пример с помощью дерева (так можно представить практически все рекурсивные функции). Каждый вызов – это внутренний узел, а базовые случаи – листья. Дерево для fib(5) выглядит вот так:

Вы можете определить сложность этой функции как O(2ⁿ). Каждый вызов по существу приводит к еще двум вызовам – практически идеальный пример экспоненциального удвоения. Другими словами, дерево, представляющее наш код, имеет коэффициент ветвления 2, каждый узел имеет 2 дочерних элемента, поэтому на каждой глубине число узлов удваивается. Из одного узла получается 2, потом 4, потом 8…

Нотация «большое O» – это нечеткая линза, где оценка одновременно рекомендуется и требуется.

Но действительно ли эта функция экспоненциально удваивается? Попробуем измерить время выполнения функции fib, определенной выше:

def time_fib(n):
    start = time.clock()
    digit = fib(n)
    stop = time.clock()

    return digit, (stop - start)


for i in range(1, 100):
    digit, time_elapsed = time_fib(i)
    print("{:3d} {:10d} {:5d}".format(i, digit, round(time_elapsed)))

Даже неуклюжий эмпирический анализ намекает на нашу странную петлю. После 32 итераций измерения приобретают знакомую форму…

n  fib(b)    time_elapsed
32 3524578   1
33 5702887   1
34 9227465   2
35 14930352  3
36 24157817  5
37 39088169  8
38 63245986  13
…

Компьютеры, часы и интерпретаторы неточны, и постепенно значение

time_elapsed становится плохим приближением ряда Фибоначчи:

n  fib(b)     time_elapsed
39 102334155  24
40 165580141  37
41 267914296  59
42 433494437  95
43 701408733  155
44 1134903170 253

Тем не менее, даже грязная реализация выявила теоретическую истину. Рекурсивный метод вычисления n-ного члена последовательности Фибоначчи имеет алгоритмическую сложность, которая отражает эту последовательность. Если бы его сложность была O(2ⁿ), количество времени бы удваивалось, но этого не происходит.

Колония бактерий и ряд Фибоначчи

Можно смоделировать сложность этой функции, используя рекуррентное отношение – формальный математический язык для описания рекурсивных функций. Не пугайтесь этого определения, тут все просто:

f (n) = f (n-1) + f (n-2)

Объем работы, который требуется для вычисления n-ного числа, – это объем работы, который требуется для вычисления предыдущих двух цифр вместе взятых. Другими словами, количество листовых узлов в рекурсивном дереве для вычисления n-ного члена последовательности отражает значение этого n-ного члена.

Возьмем конкретный пример:

f(5) = f(4) + f(3)
f(4) = f(3) + f(2)
f(3) = f(2) + f(1)
f(2) = f(1) + f(0)

И f(1), и f(0) в нашем случае постоянны, так как метод просто возвращает 1. Поэтому можно сказать, что:

f (1) = 1
f (0) = 1

Если сложить все это снизу вверх, получится следующее:

f (2) = 1 + 1 = 2
f (3) = 2 + 1 = 3
f (4) = 3 + 2 = 5
f (5) = 5 + 3 = 8

Вы уже догадываетесь, к чему все это ведет?

Давайте попробуем развернуть формулу для f(5) вместо того, чтобы вставлять в нее реальные значения:

f(5) = f(4) + f(3)
f(5) = [f(3) + f(2)] + [f(2) + f(1)]
f(5) = {[f(2) + f(1)] + [f(1) + f(0)]} + {[f(1) + f(0)] + f(1)}
f(5) = {f(1) + f(0) + f(1) + f(1) + f(0)} + {f(1) + f(0) + f(1)}

Все эти f(0) и f(1) – это листовые узлы дерева, которые имеют константное значение 1.

Можно ли смоделировать это отношение лучшим способом, чем расширение? Возможно ли создать формулу, которая описывается, сколько f(0) и f(1) будет при разложении конкретного f(n)? Оказывается, возможно! Пристегнитесь, мы входим в зону математического анализа. n f(n) = f(n — 1) + f(n — 2) = ???

Есть все основания полагать, что второе выражение также будет расти экспоненциально, но медленнее, чем 2ⁿ. С другой стороны, рекурсивное дерево для функции роста бактерий будет иметь больше узлов, чем дерево для fib, хотя в обоих деревьях у узла либо 2 ребенка, либо ни одного. Они похожи, но не идентичны.

Опять золотое сечение

Оказывается, что для «линейных гомогенных рекуррентных отношений с постоянными коэффициентами» можно использовать изящный трюк, для нахождения короткого решения. К счастью, ряд Фибоначчи является таким отношением и мы можем представить его без использования рекурсии (и даже итерации) всего в одной формуле.

Доказательство этого трюка, называемое «теоремой о различных корнях», можно найти здесь.

Мы знаем, что ряд растет по экспоненте, а этот трюк помогает найти «корни» экспоненциальной функции. Он довольно прост: нужно взять нижние индексы функции f и превратить их в экспоненты по переменной r (root – корень), для которой мы их затем решим. 2 — r — 1 = 0

Полученное уравнение можно решить для r, используя квадратичную формулу.

r = [1 +- sqrt(1 — (4*(-1)))] / 2
r = (1 + sqrt(5)) / 2
r = (1 — sqrt(5)) / 2

Произошло нечто удивительное, даже если вы этого не заметили. Посчитайте на калькуляторе 1 + sqrt(5) / 2. Вы получите … 1.618: ?, золотое сечение. Поразительно.

Чтобы не потерять лес за деревьями, отметим, что это экспериментально демонстрирует экспоненциальный рост последовательности Фибоначчи с корнем экспоненты 1.618.  Если n-ный член, разделенный на (n-1)-ный член приблизительно равен ?, то умножение (n-1)-ного члена на ? будет равно n-ному члену.

Отметим также, что второй корень – это другое замечательное число ? (Psi, пси), которое похоже на золотое сечение и примерно равно -0.618.

Конечно, технически будет правильно сказать, что верхняя граница рекурсивной функции O(2ⁿ), все же гораздо более приятно знать, что более жесткая граница – O(?ⁿ). n) / sqrt(5)

Это невероятно!

Перевод статьи Fibonacci’s Strange Loop: the beauty of mathematical inception by Tyler Elliot Bettilyon

Больше материалов по алгоритмам:

• Наиболее полный видеокурс по алгоритмам и структурам данных
• Анализ алгоритмов для начинающих: вводное руководство
• ТОП-15 алгоритмических задач, реализованных на C++
• Алгоритмы и структуры данных: развернутый видеокурс
• Как научиться решать алгоритмические задачи?

 

Природа дизайна: последовательность Фибоначчи и золотое сечение

Джонатан Кливленд | 24 сентября 2020 г. | Компетенция

Самое замечательное в работе графическим дизайнером в районе Бостона — это возможность насладиться природой Новой Англии в это время года. Подсолнухи в моем саду высокие, сильные, и они, кажется, поддерживают надежду на то, что лето еще не закончилось. Но самое лучшее в подсолнухах — это невероятное образование семян, которые вырываются из центра цветка. Это природа в лучшем виде, но также и математика в лучшем виде — это последовательность Фибоначчи в действии.

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи — одна из самых известных математических формул. Каждое число в последовательности является суммой двух предшествующих ему чисел. Итак, последовательность идет: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Его называют «секретным кодом природы» и «универсальным правилом природы». Просто взгляните на узор, который он создает, и вы сразу поймете, как эта последовательность работает в природе, как базовая универсальная сетка. Прекрасным примером этого является раковина наутилуса, чьи камеры почти идеально соответствуют логарифмической спирали последовательности Фибоначчи. Этот знаменитый узор проявляется повсюду в природе, включая цветы, сосновые шишки, ураганы и даже огромные спиральные галактики в космосе. Но последовательность Фибоначчи не ограничивается только природой. В графическом дизайне мы называем это золотым сечением. Его можно применять ко всему: от дизайна логотипа, полиграфического дизайна и дизайна веб-сайта.

Что такое золотое сечение?

Золотое сечение — это концепция дизайна, основанная на использовании последовательности Фибоначчи для создания визуально привлекательных пропорций в искусстве, архитектуре и графическом дизайне. Пропорции, размер и размещение одного элемента по сравнению с другим создают ощущение гармонии, которое привлекает наше подсознание.

Использовать или не использовать

У дизайнеров нет правил, когда дело доходит до создания эстетичного или эффективного дизайна проекта. Иногда мы обнаруживаем, что золотое сечение отлично работает на практике, а иногда нам приходит в голову отличная идея, которая не обязательно соответствует правилам. Среди графических дизайнеров, математиков и ученых продолжаются споры о том, является ли золотое сечение мифом. Но существует множество доказательств, не только в природе, но и в созданном дизайне, которые доказывают, что соотношение является надежным инструментом для нас, дизайнеров. Это может быть полезно при создании сетки для макета, поиске идеальной обрезки фотографии или определении размеров для иерархии шрифтов при отображении контента, и это лишь некоторые из них. В целом, это интересный способ взглянуть на великолепный дизайн через призму математики, и мы думаем, что интересно определить, где и как он используется в окружающем нас мире.

Заинтригованы? Вот несколько замечательных примеров золотого сечения в действии.

Эта работа компании Company Folders, Inc. находится под лицензией Creative Commons Attribution 4.0 International License.

Последовательность Фибоначчи | Imagination Station

Последовательность Фибоначчи

23 сентября 2021 г.

Последовательность Фибоначчи — это последовательность чисел, в которой каждое число является суммой двух предыдущих чисел. Например,

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …

Математически мы можем описать это как:

xn= xn-1 + xn-2

История

Многие источники утверждают, что эта последовательность была впервые обнаружена или » изобрел» Леонардо Фибоначчи. Итальянский математик, родившийся около 1170 года нашей эры, первоначально был известен как Леонардо Пизанский. В 19 веке историки придумали прозвище Фибоначчи (примерно означающее «сын клана Боначчи»), чтобы отличить математика от другого известного Леонардо Пизанского.

Другие говорят, что это не так. Кит Девлин, автор книги «В поисках Фибоначчи: поиски нового забытого математического гения, изменившего мир», говорит, что существуют древние санскритские тексты, в которых используется индийско-арабская система счисления, предшествовавшая Леонардо Пизанскому на несколько столетий.

Но в 1202 году Леонардо Пизанский опубликовал математический текст Liber Abaci. Это была «поваренная книга», написанная для торговцев о том, как делать вычисления. В тексте изложена индийско-арабская арифметика, полезная для отслеживания прибылей, убытков, остатков по кредитам и т. д., знакомящая западный мир с последовательностью Фибоначчи.

Примеры последовательности Фибоначчи:

Кролики

В книге Леонардо задумался над вопросом: при идеальных условиях сколько пар кроликов может быть получено из одной пары кроликов за один год? Ответ, как оказалось, равен 144 ¬— и соотношение, используемое для получения этого ответа, как вы уже догадались, представляет собой последовательность Фибоначчи. Этот мысленный эксперимент искусственно диктует, что самки кроликов всегда рождают пары, состоящие из одного самца и одной самки.

¬В начале двух новорожденных кроликов помещают в огороженный двор и оставляют для размножения. После первого месяца остается только первоначальная пара, так как кролики не могут размножаться, пока им не исполнится хотя бы один месяц. К концу второго месяца рождается первая пара, теперь остается две пары крольчат. На третий месяц исходная пара кроликов производит еще одну пару новорожденных, в то время как их более раннее потомство вырастает до зрелого возраста. В результате остаются три пары кроликов, две из которых рожают еще две пары в следующем месяце.

Общее количество кроликов соответствует последовательности Фибоначчи. Через 12 месяцев будет 144 пары кроликов. Через два года это число подскочило бы до 46 368 пар!

Спирали

Между числами Фибоначчи и золотым сечением существует особая связь, которая описывает, когда линия делится на две части и длинная часть (а) делится на меньшую часть (б) равно сумме (a) + (b), деленной на (a), что равно 1,618. Обозначается греческой буквой (φ). Отношение любых двух последовательных чисел Фибоначчи приблизительно соответствует значению золотого сечения ( φ = 1,6180339887…). Чем больше пара чисел Фибоначчи, тем точнее приближение. Отсюда математики могут рассчитать так называемую золотую спираль или логарифмическую спираль, коэффициент роста которой равен золотому сечению.

Используя значения последовательности в качестве длины ребер квадратов, расположенных, как показано ниже, создается спираль.

В природе

Существует множество примеров чисел Фибоначчи (числа, которые появляются в последовательности), появляющихся в естественном мире. Однако тот факт, что ряд чисел может быть применен к объекту, не означает, что существует корреляция между математикой и реальностью.

Числа Фибоначчи появляются в природе достаточно часто, чтобы доказать, что они отражают некоторые естественные закономерности. Обычно их можно заметить, изучая способ роста различных растений.

На многих семенных головках, сосновых шишках, фруктах и ​​овощах изображены спиральные узоры, которые при подсчете выражают числа Фибоначчи. Посмотрите на спирали семян в центре подсолнуха, и вы увидите узоры, изгибающиеся влево и вправо. Если вы посчитаете эти спирали, ваша сумма будет числом Фибоначчи. Разделите спирали на заостренные влево и вправо, и вы получите два последовательных числа Фибоначчи. Вы можете расшифровать спиральные узоры в сосновых шишках, ананасах и цветной капусте, которые также отражают последовательность Фибоначчи.

Фото: https://momath.org/home/fibonacci-numbers-of-sunflower-seed-spirals/

Подробнее

The Fibonacci Quarterly — это научный журнал по математическим темам, Числа Фибоначчи, публикуемые четыре раза в год. Это основное издание Ассоциации Фибоначчи, которая издает его с 1963 года.

В популярной музыке песня «Lateralus» американской прогрессив-метал-группы Tool включает последовательность Фибоначчи.