30 гармоничных фотографий с идеальной симметрией
Автор:24 июля 2015 08:29
Симметрия окружает нас везде. Посмотрите на дома и предметы что нас окружают. Вокруг так много симметрии, что порой мы забываем о ней. Вашему вниманию предлагается подборка из 30 абсолютно симметричных фотографий, радующих глаз.
Естественная симметрия

Источник:
Труба

Источник:
Метель и симметрия

Источник:
Асимметричная симметрия

Источник:
Свернуть шею

Источник:
Золотые пирамиды

Источник:
Мечеть Насир аль-Мульк

Источник:
Доброе утро, Хейло

Источник:
Праздничный блеск

Источник:
Анемона

Источник:
Теория большого взрыва

Источник:
Аллея

Источник:
Железный гигант

Источник:
Близнецы

Источник:
Вдоль и поперек

Источник:
Утренняя леди, Париж, Франция.

Источник:
Йога в Уюни

Источник:
Реинкарнация

Источник:
Отражающаяся симметрия, мечеть шейха Зайда

Источник:
Деревья

Источник:
Сближение

Источник:
Откровение

Источник:
Город Люмиоз

Источник:
Спуск в метро

Источник:
Вечный поток

fishki.net
Картинки симметрии (40 ФОТО) ⭐ Забавник
Все объекты в мире стремятся к симметрии. А идеальным симметрическим объектом является шар. Это понятие применяется в геометрии, биологии, физике, математике, химии, религии и даже в социальных взаимоотношениях.

Окружности
Лучи расходятся из многоугольника

Синяя бабочка

Симметрия спиннера

Девушка в комнате небоскрёба

Симметричное дерево

Разноцветные лепестки

Симметричная церковь

Тоннель
Симметричный рисунок клоуна
Симметрия буквы А

Симметричный значок Бетмена

Симметричная опора ЛЭП

Купол собора

Лувр в отражении

Окружности с симметрией в центре

Волнистое здание

Разноцветная симметрия

Симметричный спектр

Симметричный кот

Симметрия марки Макдональдс

Симметрия треугольника

Симметричная городская дорога

Симметричный рисунок
Модель с разноцветными узлами

2 симметричных фламинго

Красивый узор на крыше храма

Рисунок пропорций человека

Картина геометрических фигур









zabavnik.club
10 Красивых примеров симметрии в природе
Симметрия веками оставалась тем свойством, которое занимало умы философов, астрономов, математиков, художников, архитекторов и физиков. Древние греки были просто одержимы ею, и даже сегодня мы, как правило, стараемся применять симметрию во всем: от того, как мы располагаем мебель, до того, как мы укладываем наши волосы.
Никто не знает, почему это явление настолько сильно занимает наши умы, или почему математики стараются увидеть порядок и симметрию в окружающих нас вещах – как бы то ни было, ниже представлены десять примеров того, что симметрия действительно существует, а также того, что мы ею окружены.
Примите во внимание: как только вы об этом задумаетесь, вы уже постоянно будете невольно искать симметрию в окружающих вас предметах.
10. Капуста брокколи Романеско

Скорее всего, вы неоднократно проходили в магазине мимо полки с капустой брокколи Романеско и из-за её необычного вида предполагали, что это генно-модифицированный продукт. Но на самом-то деле, это всего лишь ещё один из многих примеров фрактальной симметрии в природе – хотя и безусловно поразительный.
В геометрии фрактал — это сложный узор, каждая часть которого обладает тем же геометрическим рисунком, что и весь узор в целом. Поэтому в случае капусты брокколи Романеско каждый цветок компактного соцветия обладает той же логарифмической спиралью, что и вся головка (просто в миниатюрном виде). По сути, вся головка этой капусты — это одна большая спираль, которая состоит из маленьких почек похожих на шишки, которые также растут в виде мини-спиралей.
Кстати говоря, капуста брокколи Романеско является родственницей, как капусты брокколи, так и цветной капусты, хотя её вкус и консистенция больше напоминают цветную капусту. Она также богата каротиноидами и витаминами С и К, что означает, что она является полезным и математически красивым дополнением к нашей пище.
9. Медовые соты
Пчёлы это не только ведущие производители мёда – они также знают толк в геометрии. Тысячи лет люди поражались совершенству гексагональных форм в медовых сотах и задавались вопросом о том, как же пчёлы могут инстинктивно создавать такие формы, которые человек может создавать только с линейкой и компасом. Медовые соты являются предметов обойной симметрии, где повторяющийся узор покрывает плоскость (например, плиточный пол или мозаика).
Так каким же образом и почему пчёлы так любят строить шестиугольники? Начнём с того, что математики считают, что эта совершенная форма позволяет пчёлам запасать самое большое количество мёда, используя наименьшее количество воска. При строительстве других форм у пчёл получались бы большие пространства, так как такие фигуры, как например круг – не прилегают друг к другу полностью.
Другие наблюдатели, которые менее склонны верить в сообразительность пчёл, считают, что они формируют гексагональную форму совершенно «случайно». Другими словами, пчёлы на самом деле делают круги, а воск сам по себе принимает гексагональную форму. В любом случае – это произведение природы и довольно-таки потрясающее.
8. Подсолнухи 
Подсолнухи могут похвастаться радиальной симметрией и интересным типом симметрии чисел, известным как последовательность Фибоначчи. Последовательность Фибоначчи это: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д. (каждое число определяется суммой двух предыдущих чисел).
Если не жалея времени заняться подсчётом количества семенных спиралей в подсолнечнике, мы бы обнаружили, что количество спиралей совпадает с числами Фибоначчи. Более того, огромное количество растений (включая капусту брокколи Романеско) отпускают лепестки, листья и семена в соответствии с последовательностью Фибоначчи, именно поэтому так сложно найти четырёхлистный клевер.
Считать спирали на подсолнечнике может быть довольно трудно, поэтому, если вы хотите самостоятельно проверить этот принцип, попробуйте подсчитать спирали на более крупных вещах, таких как шишки, ананасы, и артишоки.
Но почему цветы подсолнечника и другие растения подчиняются математическим правилам? Как и в случае шестиугольников в улье, всё дело в эффективности. Чтобы не углубляться в технические особенности, можно просто сказать, что цветок подсолнечника может вместить наибольшее количество семян, если каждое семечко расположено под углом, представляющим собой иррациональное число.
Оказывается, самым иррациональным числом является золотое сечение, или Фи, и так уж случилось, что, если мы разделим любое число Фибоначчи или Лукаса на предыдущее число в последовательности, мы получим число, близкое к Фи (+1,618033988749895 …). Таким образом, в любом растении, растущем в соответствии с последовательностью Фибоначчи, должен быть угол, который соответствует Фи (углу равному числу золотого сечения) между каждым из семян, листьев, лепестков, или веток.
7. Раковина Наутилуса
Помимо растений существуют также некоторые животные, демонстрирующие собою числа Фибоначчи. Например, раковина Наутилуса выросла в «Спираль Фибоначчи». Спираль образуется в результате попытки раковины поддерживать ту же пропорциональную форму по мере своего роста наружу. В случае наутилуса, такая тенденция роста позволяет ему сохранять одинаковую форму тела в течение всей своей жизни (в отличие от людей, чьи тела изменяют свои пропорции по мере взросления).
Как и следовало бы ожидать – в этом правиле существуют и исключения: не каждая раковина наутилуса вырастает в спираль Фибоначчи. Но все они растут в виде своеобразных логарифмических спиралей. И, до того как вы начнёте задумываться над тем, что эти головоногие, пожалуй, знают математику лучше вас, помните, что их раковины растут в такой форме неосознанно для них, и что они просто пользуются эволюционным дизайном, который позволяет моллюску расти, не изменяя форму.
6. Животные
Большинство животных обладает двусторонней симметрией, это означает, что их можно разделить на две одинаковые половины, если линию деления провести по их центру тела. Даже люди обладают двусторонней симметрией, и некоторые учёные считают, что симметрия человека является самым важным фактором того, будем ли мы считать его физически привлекательным или нет. Другими словами, если у вас кривобокое лицо, надейтесь, что у вас есть целая уйма компенсирующих, положительных качеств.
Одно животное, скорее всего, воспринимает важность симметрии в брачных ритуалах слишком серьёзно, и этим животным является павлин. Дарвина очень раздражал этот вид птиц, и в своём письма в 1860 году он написал, что «каждый раз, когда я смотрю на перо из павлиньего хвоста – меня тошнит!».
Для Дарвина хвост павлина казался чем-то обременительным, так как, по его мнению, такой хвост не имел эволюционного смысла, так как он не подходил под его теорию «естественного отбора». Он злился до тех пор, пока он не разработал теорию сексуального отбора, которая заключается в том, что животное развивает у себя определённые качества, которые обеспечат ему лучший шанс спариться. Очевидно, для павлинов сексуальный отбор считается невероятно важным, так как они отрастили себе различные варианты узоров, чтобы привлечь своих дам, начиная с ярких цветов, большого размера, симметрии своих тел и повторяющемся узоре их хвостов.
5. Паутины пауков
Существует примерно 5 000 видов пауков-кругопрядов, и все они создают практически совершенно круглые паутины с почти равноудаленными радиальными опорами, исходящими из центра и связанными по спирали для более эффективной ловли добычи. Ученые до сих пор не нашли ответа на вопрос, почему пауки-кругопряды делают такой большой акцент на геометрию, так как исследования показали, что округлая паутина не удерживает добычу лучше, чем паутина неправильной формы.
Некоторые ученые предполагают, что пауки строят круглые паутины из-за того, что они более прочные, и радиальная симметрия помогает равномерно распределить силу удара, когда жертва попадает в сети, в результате чего в паутине оказывается меньше разрывов. Но остается вопрос: если это действительно лучший способ создания паутины, то почему не все пауки его используют? У некоторых пауков, не являющихся кругопрядами, есть возможность создавать такую же паутину, однако они этого не делают.
Например, недавно обнаруженный в Перу паук строит отдельные части сети одинакового размера и длины (что доказывает его способность «замерять»), но затем он просто соединяет все эти части одинакового размера в случайном порядке в большую паутину, которая не обладает какой-то определённой формой. Может быть эти пауки из Перу знают что-то, чего не знают пауки-кругопряды, или же они ещё просто не оценили всю прелесть симметрии?
4. Круги на полях с урожаем
Дайте парочке приколистов доску, кусок верёвки и покров тьмы и окажется, что люди тоже хороши в создании симметричных форм. На самом деле, именно из-за невероятной симметрии и сложности дизайна кругов на полях с урожаем, люди продолжают верить, что только пришельцы из космоса способны сотворить такое, даже несмотря на то, что люди, создавшие эти круги, сознались.
Возможно, когда-то и была смесь кругов сделанных людьми с теми, которые сделали пришельцы, но прогрессирующая сложность кругов является самым явным доказательством того, что их сделали именно люди. Было бы нелогичным предположить, что пришельцы сделают свои послания ещё сложнее, учитывая то, что люди ещё толком не разобрались в значении простых посланий. Скорее всего, люди учатся друг у друга по примерам созданного и всё больше и больше усложняют свои творения.
Если отбросить в стороны разговоры об их происхождении, можно точно сказать, что на круги приятно смотреть, по большей части из-за того, что они так геометрически впечатляющи. Физик Ричард Тейлор (Richard Taylor) провёл исследование кругов на полях и обнаружил, что помимо того факта, что за ночь на земле создается по крайней мере один круг, большинство их дизайнов отображают широкий спектр симметрии и математических моделей, в том числе фракталов и спиралей Фибоначчи.
3. Снежинки
Даже такие крошечные вещи как снежинки тоже образуются по законам порядка, так как большинство снежинок формируются в виде шестикратной радиальной симметрии со сложными, идентичными рисунками на каждой из её ветвей. Понять, почему растения и животные выбирают симметрию, сложно само по себе, но неодушевлённые объекты – как же им это удаётся?
По-видимому, всё сводится к химии, и в частности к тому, как молекулы воды выстраиваются по мере своего замерзания (кристаллизуются). Молекулы воды приходят в твёрдое состояние путём образования слабых водородных связей друг с другом. Эти связи выравниваются в упорядоченном расположении, которое максимизирует силы притяжения и снижает силы отталкивания, что как раз и является причиной образования гексагональной формы снежинки. Однако всем нам известно, что двух одинаковых снежинок не бывает, так как же снежинка формируется в абсолютной симметрии сама с собой, но не похожа на другие снежинки?
По мере того как каждая снежинка падает с неба она проходит через уникальные атмосферные условия, такие как температура и влажность, которые влияют на то, как кристаллы «растут» на ней. Все ветви снежинки проходят через одни и те же условия и следовательно кристаллизуются одинаковым образом — каждая ветвь является точной копией другой. Ни одна другая снежинка не проходит через те же условия по мере своего спуска, поэтому они все выглядят немного по-разному.
2. Галактика Млечный Путь 
Как мы уже видели, симметрия и математические узоры существуют повсюду, куда бы мы ни посмотрели – но ограничены ли эти законы природы только нашей планетой? По всей видимости – нет. Недавно обнаружив новую часть Млечного Пути, астрономы считают, что наша галактика является почти совершенным отражением самой себя. Основываясь на новой информации, учёные получили подтверждение своей теории о том, что в нашей галактике есть только два огромных рукава: Персей и Рукав Центавра.
В дополнение к зеркальной симметрии, Млечный Путь обладает ещё одним удивительным дизайном – похожим на раковины наутилуса и подсолнуха, где каждый рукав галактики представляет собой логарифмическую спираль, берущую начало в центре галактики и расширяющуюся к внешнему краю.
1. Симметрия Солнца и Луны
Учитывая, что диаметр солнца составляет 1,4 миллиона километров, а диаметр луны всего 3,474 километра, очень сложно представить себе, что Луна может закрывать собой солнечный свет и давать нам около пяти солнечных затмений каждые два года.
Так как же это всё-таки происходит? По совпадению, несмотря на то, что ширина солнца примерно в четыреста раз больше ширины луны, оно расположено от нас в четыреста раз дальше, чем луна. Симметрия этого соотношения приводит к тому, что нам кажется, что солнце и луна, одинаковые по размеру, если смотреть с Земли, поэтому луна может с лёгкостью блокировать солнце, когда они находятся на одной линии по отношению к Земле.
Расстояние от Земли до солнца, конечно, может вырасти во время её выхода на орбиту, и когда в это время случается затмение, мы можем полюбоваться ежегодным или неполным затмением, так как солнце не полностью закрыто. Но каждый год или два, всё становится абсолютно симметричным, и мы можем посмотреть на великолепное событие, которое мы называем полным солнечным затмением.
Астрономы не уверены, насколько часто такая симметрия встречается между другими планетами, солнцами и спутниками, однако они думают, что это довольно редкое явление. Даже если это так, то мы не должны предполагать, что мы особенные, потому что всё, как ни странно, является делом случая. Например, каждый год луна удаляется от Земли примерно на четыре сантиметра, это означает, что миллиарды лет назад, каждое солнечное затмение было бы полным.
Если дело пойдёт так и дальше, полные затмения в конце концов исчезнут, за ними исчезнут ежегодные затмения (если планета ещё продержится настолько долго). Поэтому, можно предположить на самом деле, что мы находимся в нужном месте, в нужное время. Но так ли это? Некоторые люди выдвигают теории о том, что симметрия солнца и луны это именно тот фактор, благодаря которому жизнь на Земле стала возможной.
bugaga.ru
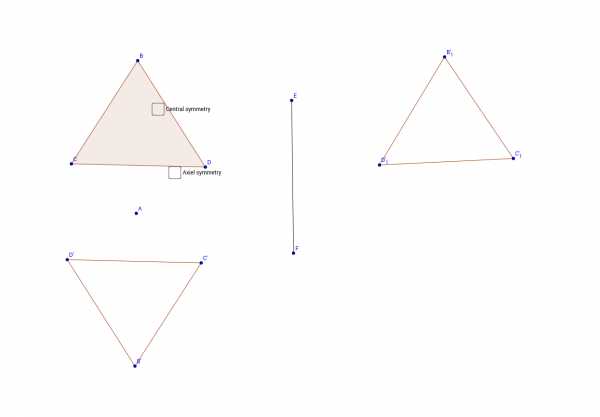
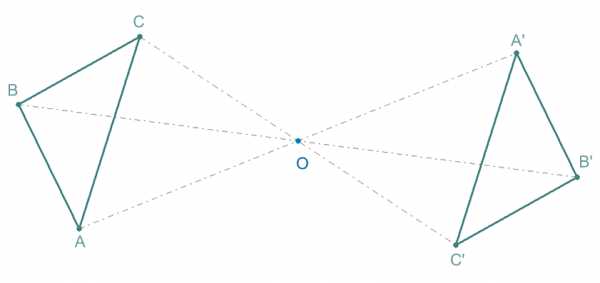
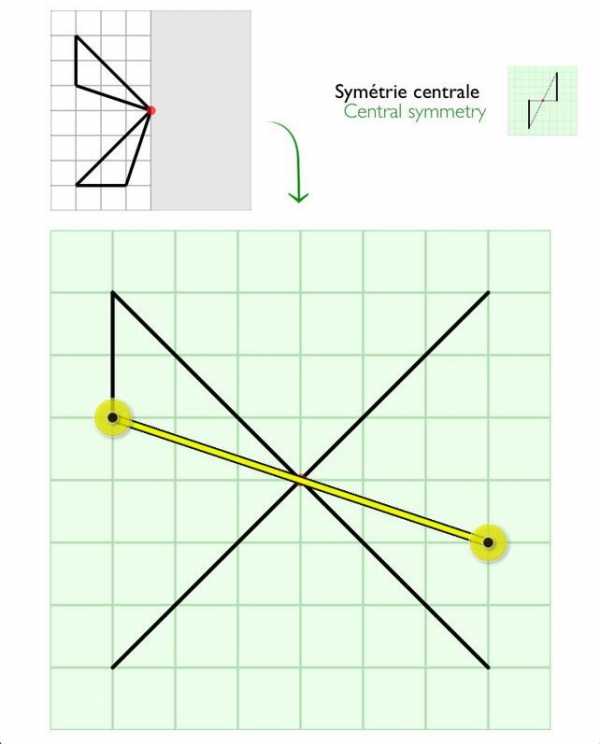
Картинки центральной симметрии (37 ФОТО) ⭐ Забавник
Центральную симметрию иногда путают с осевой симметрией. У каждой симметричной фигуры есть точка А – центр симметрии. В планиметрии под этим понятием подразумевается поворот на 180 градусов

Машина
Треугольники
Круги

Очки
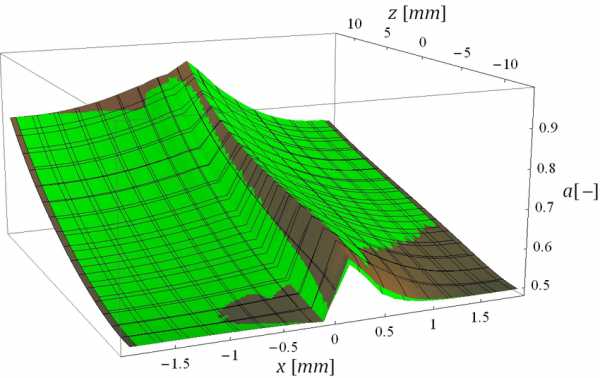
Поверхность
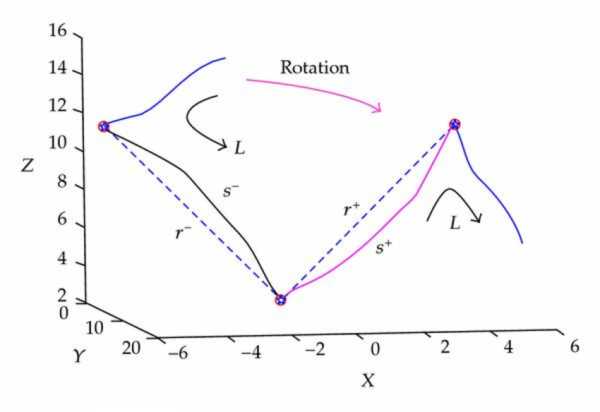
Rotation
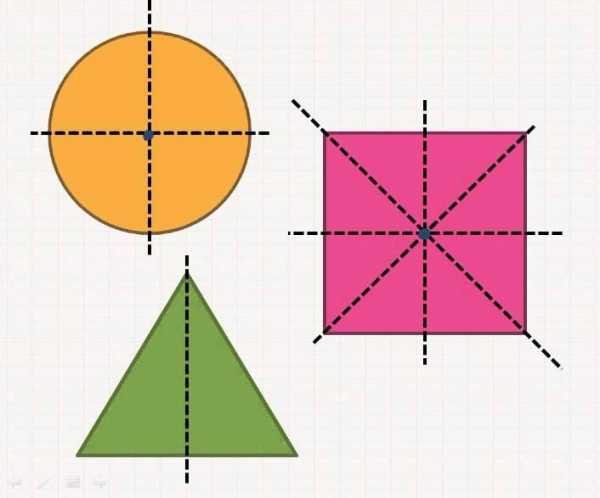
Круг, треугольник, квадрат

2 треугольника

Коктейль
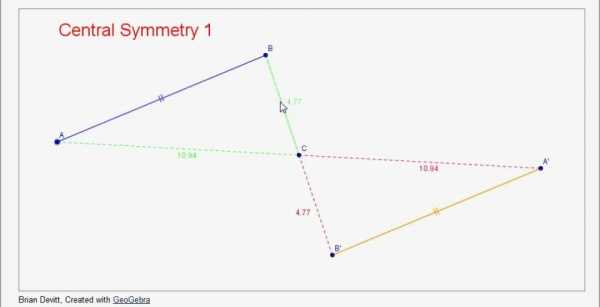
Central Symmetry

Пёс
3 треугольника
Верблюд

Купол
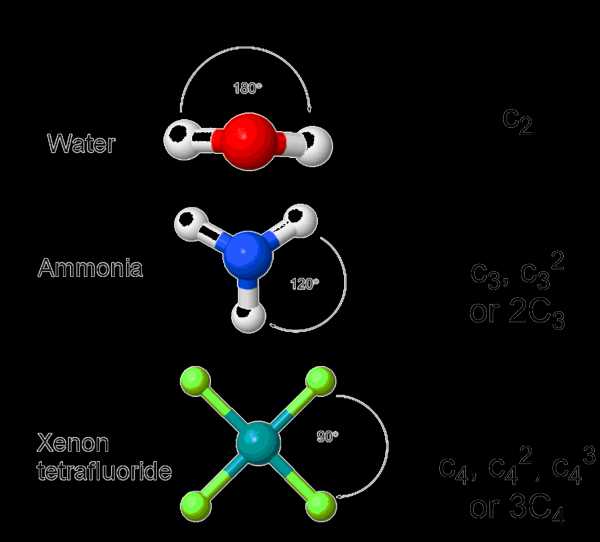
Молекулы
Колпак

Кирпичная башня в металлической башне

Пересекающиеся линии

Окно в соборе
Пересечение треугольников

Башня на фоне неба

Рисунок витража
Анимация симметрии

Central Axis Line









Ваша оценка очень важна: Загрузка…
Поделиться на Facebook
Поделиться в ВК
Поделиться в ОК
Поделиться в Twitter
zabavnik.club
Симметрия в фотографии — Фотоальбомы, креатив — ФОТОЛАБОРАТОРИЯ — Каталог статей
Уэс Андерсон хорошо известен тем, что его картины идеально симметричны. Даже есть видео из отдельных сцен разных фильмов этого режиссера, которое демонстрирует, как часто он придерживается практически идеальной центральной симметрии
++++++++++++++++++++++++++++++++++++++
Фотографии других фотографов:

1. Труба. Автор фото: Петр Дж

2. Метель и симметрия. Автор фото: Anur Shaymarov

3. Асимметричная симметрия. Автор фото: Хольгер Глааб

4. Свернуть шею. Автор фото: Джузеппе Торре

5. Золотые пирамиды. Автор фото: Джузеппе Торе

6. Мечеть Насир аль-Мульк. Автор фото: Мохаммад Реза Домири Ганжи

7. Доброе утро, Хейло. Автор фото: Аллард Шагер

8. Праздничный блеск. Автор фото: Биффи Кэт

9. Анемона. Автор фото: Марк Джонсон

10. Теория большого взрыва. Автор фото: Александр Яковлев

11. Аллея. Автор фото: Ронни Энгельман

12. Железный гигант. Автор фото: Джузеппе Торре

13. Близнецы. Автор фото: Марсель ван Остен

14. Вдоль и поперек. Автор фото: Брайан Хэммондс

15. Утренняя леди, Париж, Франция. Автор фото: Rilind H

16. Йога в Уюни. Автор фото: Эрик Паре

17. Реинкарнация. Автор фото: Роланд Шаинидзе

18. Отражающаяся симметрия, мечеть шейха Зайда. Автор фото: Джити Чадха

19. Деревья. Автор фото: Джейсон Сэвидж

20. Сближение. Автор фото: Чонг Чжэн

21. Естественная симметрия. Автор фото: Джон Уин

22. Город Люмиоз. Автор фото: Джон Чан

23. Спуск в метро. Автор фото: Хосе Рамон Сантос Москера

24. Вечный поток. Автор фото: Sairam Sundaresan

25. Облачная картина. Автор фото: Биффи Кэт

26. Альби. Автор фото: Александр Драгунов

27. Автор фото: Alfon No

28. Откровение. Автор фото: Джузеппе Торре

29. Симметричная зебра. Автор фото: Жереми Тарди

30. Симметрия. Автор фото: Фил Оуэн
www.crown6.org
Самые красивые примеры симметрии в природе (11 фото)

Самые красивые примеры симметрии в природе
Многие из нас замечали, как удивительно и необычно созданы некоторые растения, животные и т.п. вещи, которые имеют идеальную симметрию. Причем сотворена она не человеческими руками, а самой природой. Можно только позавидовать, как идеально все продумано и устроено. Давайте и мы посмотрим на самые красивые примеры симметрии в природе.

Примеры симметрии в растениях
Очень редко мы замечает идеальные углы, особенно когда они ежедневно появляются перед глазами. Примеры симметрии можно наблюдать на капусте брокколи под названием Романеско. Каждый ее цветок миниатюрного соцветия имеет форму спирали, поэтому и вся головка в целом имеет такую же форму.

Необычный пример можно понаблюдать на подсолнухах. Количество семенных спиралей в растении точь-в-точь совпадает с числами Фибоначчи. Подобным образом растут и листья, лепестки, семена на многих растений. Кроме того, если цветы или деревья имеют последовательность Фибоначчи, то обязательно должен быть определенный угол, который бы был приближен к Фи (углу, который равен золотому сечению).

Симметрия у животных
Посещая довольно интересные места нашей планеты, можно заметить симметрические примеры даже у животных. Большое количество из них обладает двусторонней симметрией, поэтому если разделить их пополам по центру тела, то можно получить две одинаковые части.
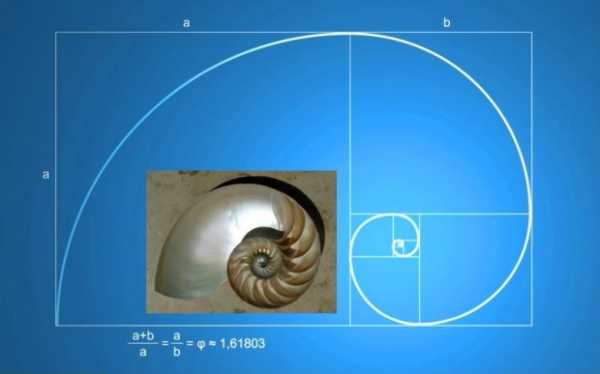
Невероятную симметрию может показать раковина Наутилуса, которая выросла «спиралью Фибоначчи». Подобная тенденция помогает наутилусу на протяжении всей жизни расти с одинаковой формой тела.

Пчелы и пауки
Мало кто из нас задумывается над тем, что достопримечательности находятся прямо у нас перед глазами. Каждый из нас наблюдал за пчелами и видел, какие соты они отводят для закладки меда. Разве это не гениальная геометрия для таких насекомых? Это обойная симметрия, так как узор, что повторяется, покрывает всю поверхность рамки. Благодаря таким шестиугольникам пчелы могут запастить огромным количеством меда.

Геометрическими ловкачами можно назвать и пауков, которые плетут ровные, круглые паутины между равномерно удаленными опорами. Ученые утверждают, что такая форма является прочной для поимки добычи

Невероятная шестикратная радикальная симметрия наблюдается и у снежинок, которые формируются со сложным, но идентичным рисунком на каждой из веток.

Законы природы раскинулись не только по нашей планете, но и далеко за ее пределами. К примеру, симметрией может похвастаться галактика Млечный Путь, которая является практически совершенным отражением самой же себя.

Наблюдать симметрию можно луны и солнца, так как нам кажется, что они одинаковые. На самом же деле ширина солнца в 400 раз больше ширины луны, но она находится в 400 раз ближе, чем солнце.

Предыдущая статья:
Морская вода: интересные факты и полезные свойства
Следующая статья:
Самые интересные сказочные существа
Похожие статьи
begin-journey.ru
Основы фотографии — симметрия, принтеры, экспозиция и цифровые датчики
Что такое симметрия в фотографии?
Удивительно, но легко сбалансированная композиция, это результат симметрии. Симметричными, считаются те фотографии, которые имеют практически идентичные элементы, по обе стороны снимка от воображаемой вертикальной, или горизонтальной линии. Такие фотографии выглядят, весьма, привлекательно для зрителя. Для начала, поместите основной элемент композиции в центре кадра, и старайтесь достигнуть баланса вдоль вертикальной, или горизонтальной оси. При таком подходе хорошо выглядят архитектурные и ландшафтные объекты, но возможно, придется добавить еще некоторые предметы в кадр, что бы сбалансировать его. Главное, что б изображение не выглядело абсолютно симметричными, иначе фотография будет выглядеть искусственно.
Что такое цифровой датчик изображения?

Автор фото : SensorCleaning.com
Когда отраженный свет от сфотографированного объекта проходит через линзы и диафрагмы, он попадает на цифровой датчик изображения.
Цифровой датчик изображения это компьютерный чип внутри камеры, который состоит из миллионов светочувствительных пикселей. В светочувствительных пикселях свет преобразуется в электрическое напряжение. Затем, в аналого-цифровом преобразователе (АЦП), электрическое напряжение преобразуется в цифровые данные. Этот процесс называется аналого-цифровым преобразованием. Полученные числовые значения формируют значения оттенков и цветов.
Каждый светочувствительный элемент цифрового датчика изображения оснащен фильтром, красного, синего, или зеленого цвета. Фильтр определяет значение каждого цвета, из полученного оттенка. Фильтров зеленого цвета в два раза больше чем красного и синего, это обусловлено особенностями человеческого зрения. Такой цветовой фильтр называется фильтром Байера. Существует два основных типа цифровых датчиков изображения, которые используются в фотоаппаратах – прибор с зарядной связью (ПЗС) и транзистор металл-оксид-полупроводник (КМОП, или CMOS).
Как работает струйный принтер?

Струйный принтер использует крошечные пиксели, что бы создать цвет, путем смешивания как минимум четырех цветов краски – синего, пурпурного, желтого и черного (CMYK). В результате печать построена из миллионов крошечных капель цвета, распыленных на разном расстоянии друг от друга, что в итоге создает иллюзию фотографического цвета.
Принтеры высокого расширения могут распылять более 2880 капель разного размера на квадратный дюйм бумаги, для создания фотореалистичных цветов.
Что такое переэкспонирование?

Автор фото : Beth Retro
Переэкспонированной считается слишком светлая, или слишком яркая фотография. С технической точки зрения это происходит потому, что на светочувствительный датчик попадает слишком много света. В цифровой фотографии это приводит к тому, что возникают слишком яркие, белые участки, без возможной детализации объекта. Иногда, переэкспонированным изображением, называют бледное, или размытое изображение.
Что такое недодержка в фотографии?

Автор фото : Richard Reader
Недодержанной считается слишком темная фотография. В таком случае, одной из проблем является отсутствие детализации объекта. Еще одной проблемой является увеличение шума в темных областях фотографии. Бывает так, что в целом снимок хорошо освещен, и только некоторые области темные, или на снимке есть слишком черные тени, такое изображение выглядит очень загроможденным, зрителю сложно рассмотреть его в деталях.
В редких случаях недоэкспонированные фотографии могут выглядеть красиво. Если кадр немного темный в некоторых местах, или на нем есть темные тени, в которых, немного, просматриваются детали, такой кадр может выглядеть богаче и ярче. Недодержанные фото могут быть более драматичными и живыми. Особенно хорошо это получается на фотографиях пейзажа.
Когда вы смотрите на гистограмму недоэкспонированной фотографии, то большая часть графика будет находиться в левой части гистограммы, это означает, что большая часть пикселей на снимке будут темными, или даже черными. Попытки исправить это во время компьютерной обработки изображения приведут к появлению лишнего шума на снимке.
cameralabs.org
