Геометрическая оптика — Оптические приборы. Фотоаппарат.
Урок 10. Оптические приборы. Фотоаппарат.
Оптические приборы, представляющие собой совокупность нескольких призм или линз, нескольких зеркал или одновременно линз, призм и зеркал, предназначены для преобразования световых пучков. С их помощью могут изменяться направления хода световых лучей, или телесные углы, в пределах которых распространяются световые пучки. Последнее обстоятельство связано с получением изображений, размеры которых отличаются от размеров предметов.
Первое, на что нужно обращать внимание при анализе действия оптической системы, — это назначение и реальные условия ее работы. Где может располагаться предмет перед системой? Какое изображение (увеличенное, уменьшенное, обратное или прямое) должна давать система? С помощью чего регистрируется полученное изображение (на экране, фотопленке, рассматривается невооруженным глазом или глазом через какую-нибудь линзовую систему)?
Все оптические приборы можно разделить на две группы:
1) приборы, при помощи которых получают
оптические изображения на экране. К ним относятся проекционные аппараты, фотоаппараты, киноаппараты и др.
К ним относятся проекционные аппараты, фотоаппараты, киноаппараты и др.
2) приборы, которые действуют только совместно с человеческими глазами и не образуют изображений на экране. К ним относится лупа, микроскоп и различные приборы системы телескопов. Такие приборы называются визуальными.
Фотоаппаратом называется оптико-механический прибор, предназначенный для получения на фотопленке или фотопластинке изображения фотографируемого предмета.
Фотография была изобретена в 30–х годах XIX века и
прошла долгий путь развития. Современная фотография, ставшая малоформатной,
моментальной, цветной, стереоскопической, нашла широчайшее применение во всех
областях нашей жизни. Велика её роль в исследовании природы. Фотография
позволяет рассматривать различные объекты (от микроскопических до космических),
невидимые излучения и т.д. Всем известное значение художественной фотографии,
детищем которой является кино.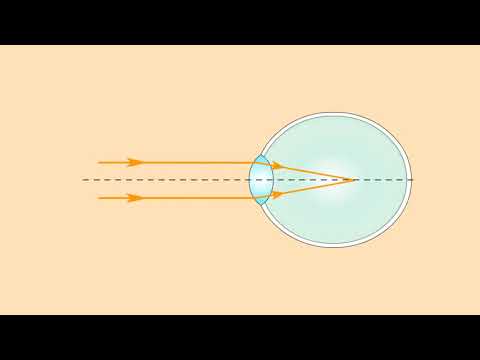
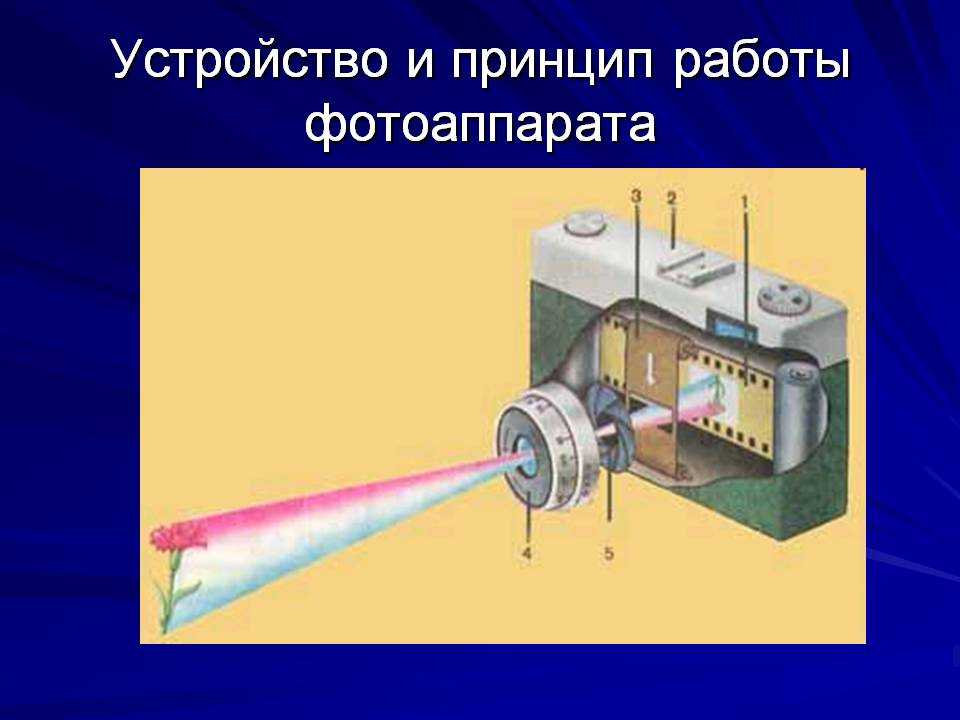
Основными частями фотоаппарата являются непрозрачная камера и система линз, называемая объективом. Простейший объектив представляет собой одну собирающую линзу. Объектив создаёт вблизи задней стенки камеры действительное перевёрнутое изображение фотографируемого предмета. В большинстве случаев предмет находится на расстоянии, большем двойного фокусного, поэтому изображение получается уменьшенным. В том месте, где получается изображение, помещается фотоплёнка или фотопластинка, покрытая слоем светочувствительного вещества – фотоэмульсией.
Фотографируемые предметы могут находиться на разных расстояниях от аппарата, следовательно, расстояние между объективом и плёнкой также необходимо изменять, что осуществляется обычно перемещением объектива.
Световая энергия, попадающая на светочувствительный
слой, дозируется фотографическим затвором, который даёт доступ свету лишь на
определённое время – время экспозиции. Время экспозиции зависит от
чувствительности фотоэмульсии и от освещённости плёнки, которая зависит, в
частности, от диаметра объектива. Диаметр действующей части объектива можно
менять с помощью диафрагмы и этим регулировать освещённость фотоплёнки. Уменьшая
отверстие диафрагмы, можно добиться того, что изображение предметов,
находящихся на различных расстояниях от аппарата, будут достаточно чёткими.
Возрастёт, как говорят, глубина резкости.
Время экспозиции зависит от
чувствительности фотоэмульсии и от освещённости плёнки, которая зависит, в
частности, от диаметра объектива. Диаметр действующей части объектива можно
менять с помощью диафрагмы и этим регулировать освещённость фотоплёнки. Уменьшая
отверстие диафрагмы, можно добиться того, что изображение предметов,
находящихся на различных расстояниях от аппарата, будут достаточно чёткими.
Возрастёт, как говорят, глубина резкости.
Диафрагма регулирует световой поток, который
попадает на пленку. Фотоаппарат дает уменьшенное, обратное, действительное
изображение, которое фиксируется на пленке. Под действием света состав пленки
изменяется и изображение запечатлевается на ней. Оно остаётся невидимым до тех
пор, пока пленку не опустят в специальный раствор — проявитель. Под действием
проявителя темнеют те места пленки, на которые падал свет. Чем больше было
освещено какое-нибудь место пленки, тем темнее оно будет после проявления.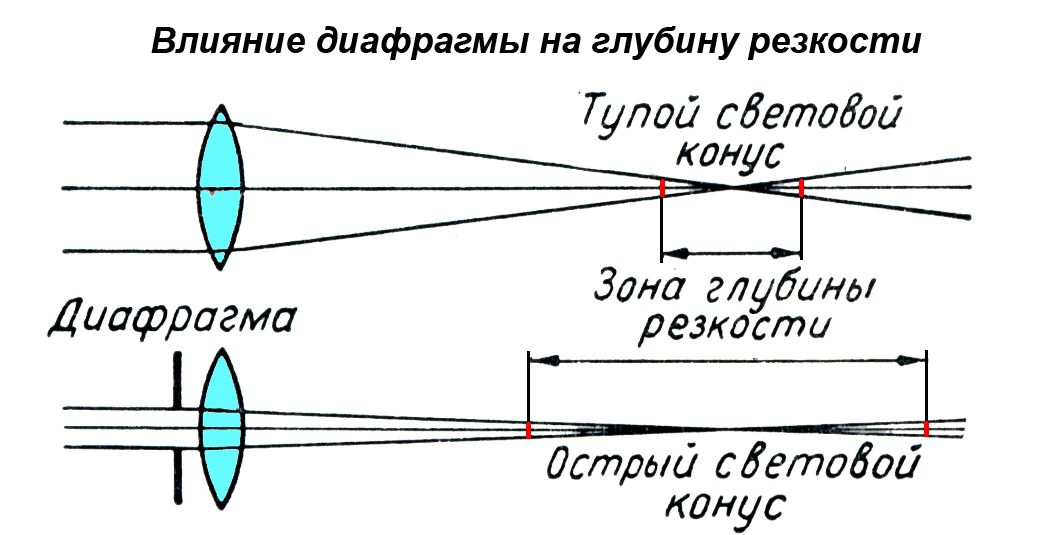 Полученное изображение называется негативом (от лат. negativus — отрицательный), на
нем светлые места предмета выходят темными, а темные светлыми.
Полученное изображение называется негативом (от лат. negativus — отрицательный), на
нем светлые места предмета выходят темными, а темные светлыми.
Чтобы это изображение под действием света не изменялось, проявленную пленку погружают в другой раствор — закрепитель. В нем растворяется и вымывается светочувствительный слой тех участков пленки, на которые не подействовал свет. Затем пленку промывают и сушат.
С негатива получают позитив (от лат. pozitivus — положительный), т. е. изображение, на котором темные места расплолжены так же как и на фотографируемом предмете. Для этого негатив прикладывают к бумаге тоже покрытой светочувствительным слоем (к фотобумаге), и освещают. Затем фотобумагу опускают в проявитель, потом в закрепитель, промывают и сушат.
После проявления пленки при
печатании фотографий пользуются фотоувеличителем, который увеличивает
изображение негатива на фотобумаге.
Проекционный аппарат (проектор) предназначен для получения на экране действительного увеличенного изображения. Следовательно, и здесь объектив представляет собой собирающую линзу, только предмет помещают между F и 2F (F<d<2F), а изображение получается на расстоянии, большем 2F (f>2F).
Проекционные аппараты — это хорошо известные фильмоскопы, эпипроекторы, диапроекторы, эпидиаскопы, киноаппараты, кодаскопы и др.
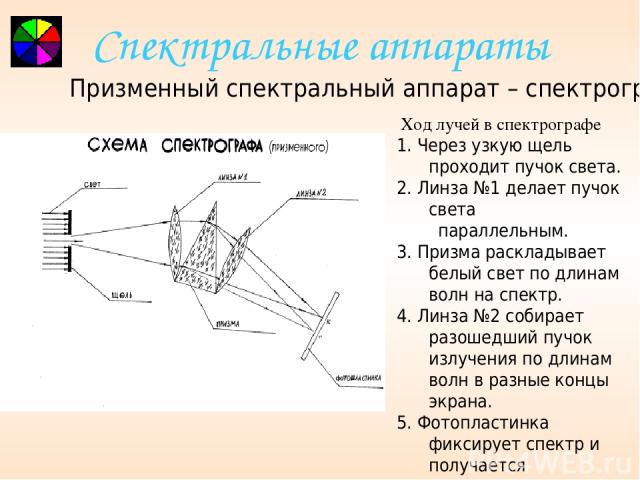
Схема оптического устройства диапроектора изображена на рисунке 1, а. Главная часть аппарата — объектив О. Предметом служит прозрачный рисунок или фотоснимок на стеклянной пластинке (или прозрачной пленке) Д. Такую пластинку называют диапозитивом.
Размеры диапозитива обычно больше размеров объектива.
Поэтому чтобы направить в объектив весь свет, идущий от диапозитива, применяют конденсор
К, который представляет
собой короткофокусную систему линз значительного размера.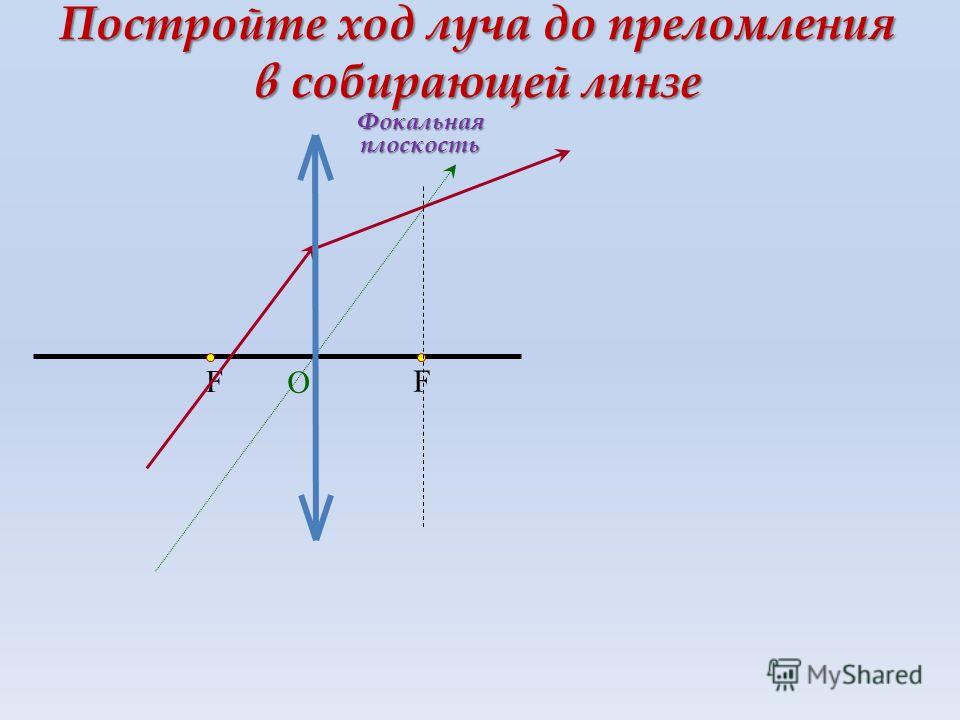
Для проецирования на экран непрозрачных предметов (чертежей, рисунков из книг и др.) используют эпипроектор (рис. 1, б). Предмет освещается сбоку светом, отраженным от вогнутого зеркала, в фокусе которого расположен источник света Л. Отраженный от предмета свет с помощью плоского зеркала З направляется на объектив О.
Аппараты, в которых устройство обыкновенного проекционного аппарата (диаскопа) и эпископа совмещено, называют эпидиаскопами (рис. 1, в).
Рис. 1
Эпидиаскоп имеет два объектива О и O1 откидную ширму Ш, отражатель и столик С для непрозрачных предметов. Когда ширма Ш опущена (рис. 1), эпидиаскоп действует как
проекционных аппарат.
Когда ширма Ш опущена (рис. 1), эпидиаскоп действует как
проекционных аппарат.
При поднятии ширмы закрываются конденсатор К и объектив О, и открывается столик С, на котором помещают непрозрачный предмет, освещаемый тем же повернутым источником света Л с рефлектором Р. Свет, отраженный от предмета, падает на зеркало 3 и от него отражается на второй объектив O1.
Лупа. Чтобы увидеть мелкие детали предмета, их нужно
рассматривать под большим углом зрения, но увеличение этого угла ограничено
пределом аккомодационных возможностей глаза. Увеличить угол зрения (сохраняя
расстояние наилучшего зрения d
Лупой называют короткофокусную собирающую
линзу или систему линз, действующих как одна собирающая линза (обычно фокусное
расстояние лупы не превышает 10 см).
Ход лучей в лупе показан на рисунке. Лупу помещают близко к глазу, а рассматриваемый предмет АВ=А1В1 располагают между лупой и ее передним фокусом, чуть ближе последнего. Подбирают положение лупы между глазом и предметом так, чтобы видеть резкое изображение предмета. Это изображение А2В2 получается мнимым, прямым, увеличенным и находится на расстоянии наилучшего зрения OB2 = d0 от глаза, а сам глаз находится непосредственно перед лупой.
Использование лупы приводит к увеличению угла зрения,
под которым глаз рассматривает предмет. Действительно, когда предмет находился
в положении А1В1 и рассматривался невооруженным
глазом, угол зрения был ϕ1. Предмет поместили между фокусом и оптическим
центром лупы в положение АВ, и угол зрения стал ϕ2 . Поскольку ϕ1> ϕ2 , то с помощью лупы на предмете можно рассмотреть
более мелкие детали, чем невооруженным глазом.
Поскольку ϕ1> ϕ2 , то с помощью лупы на предмете можно рассмотреть
более мелкие детали, чем невооруженным глазом.
Из рисунке видно также, что линейное увеличение лупы:
Так как OB2 = d0, а OB1 ≈ F (F — фокусное расстояние лупы), то где d0 = 25 см. Следовательно, увеличение, даваемое лупой, равно отношению расстояния наилучшего зрения к фокусному расстоянию лупы.
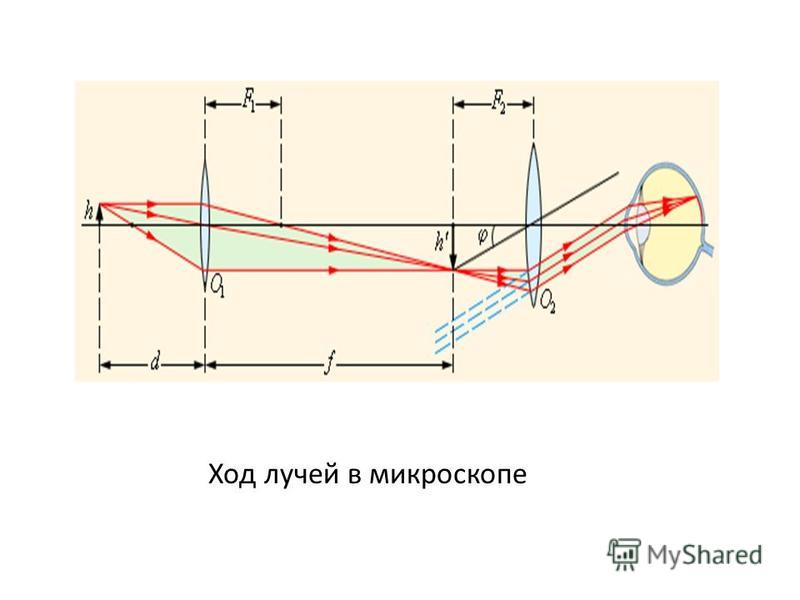
Микроскоп. Для получения больших угловых увеличений (от 20 до 2000) используют оптические микроскопы. Увеличенное изображение мелких предметов в микроскопе получают с помощью оптической системы, которая состоит из объектива и окуляра.
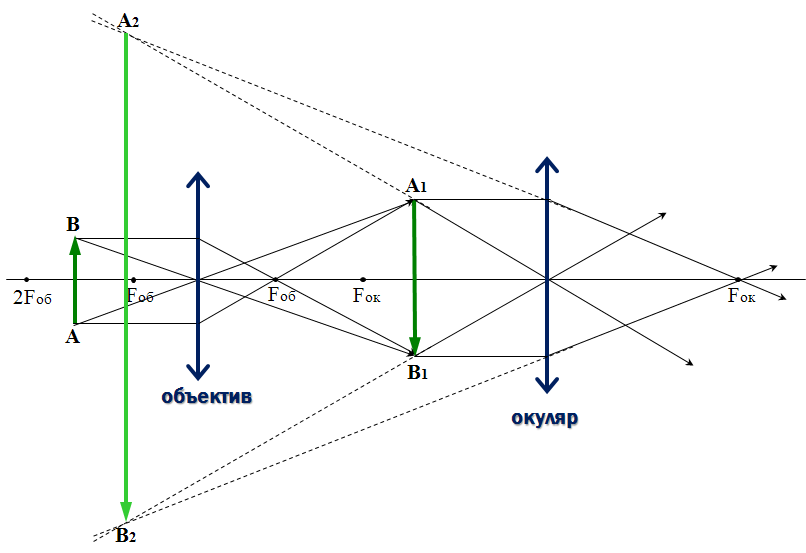
Простейший микроскоп — это система с двух линз:
объектива и окуляра. Предмет АВ размещается перед линзой, которая
является объективом, на расстоянии F1 < d < 2F1 и
рассматривается через окуляр, который используется как лупа. Увеличение Г
микроскопа равно произведению увеличения объектива Г1 на увеличение
окуляра Г2:
Увеличение Г
микроскопа равно произведению увеличения объектива Г1 на увеличение
окуляра Г2:
Г = Г1∙Г2
Принцип действия микроскопа сводится к последовательному увеличению угла зрения сначала объективом, а затем - окуляром.
читать далее
|
Получение изображения аналоговым фотоаппаратом |
||||
|
Объектив, или съёмочный объектив,
— основная и обязательная часть любого фотоаппарата. |
||||
|
Световые лучи от точечного источника распространяются во все стороны равномерно и прямолинейно. При переходе из одной среды в другую (например, на границе стекло-воздух) они преломляются, т. е. изменяют направление распространения. Для изменения направления лучей применяют
линзы, зеркала, призмы; при этом пучок лучей можно сделать сходящимся, расходящимся или параллельным.
Поверхности линз могут быть выпуклыми, вогнутыми и плоскими. Выпуклые и вогнутые поверхности имеют сферическую форму. Сферической называется форма поверхности шара (или его части). Радиус шара является радиусом кривизны линзы, а его центр-
центром кривизны. Плоские поверхности можно также рассматривать как сферические с бесконечно большим радиусом кривизны. |
||||
|
В зависимости от вида кривизны поверхностей различают линзы
двояковыпуклые, двояковогнутые, плосковыпуклые, плосковогнутые и вогнутовыпуклые. Линзы, толщина которых в середине больше, чем по краям,- собирательные и называются положительными, а те, у которых толщина больше по краям,- рассеивающими и называются отрицательными. Прямая линия, проходящая через центры кривизны поверхностей линзы, является её осью симметрии, она же — оптическая ось линзы. На рис. 3 показан ход луча через элементарный участок линзы. Его можно рассматривать как клин, если он не расположен в середине линзы. Рабочие поверхности такого участка условно можно считать плоскими. Чем ближе к краю выбран участок, тем больше будет его клиновидность, т. е. угол между рабочими поверхностями. Проходя через такой участок, луч света преломляется, т. е. отклоняется в сторону основания клина, сначала на границе воздух-стекло, а затем на границе стекло-воздух. Пучок параллельных лучей, проходящий через линзу вдоль её оптической оси, преобразуется положительной линзой в сходящийся, а отрицательной — в расходящийся. При рассмотрении тонких линз допускается, что эти плоскости совмещены в одну. Такая плоскость делит окружающее пространство на две части. На схемах принято изображать распространение света слева направо. Поэтому слева от плоскости будет пространство объектов (предметное пространство), а справа – пространство изображений. Соответственно точки и отрезки, расположенные слева, называются передними, а расположенные справа – задними.
Параллельный пучок лучей, пройдя положительную линзу, сходится в точке фокуса линзы. |
||||
|
Если перед линзой находится не точечный источник света, а некоторая поверхность, от каждой её точки на линзу будут падать световые лучи. Одиночная линза в различных участках фокальной плоскости изображает точки в виде кружков, чёрточек, запятых и точек; эти искажения называются аберрациями. Если размер искажённых изображений точек не превышает 0.1мм, то при нормальном зрении все они воспринимаются как точки. Но в фотографии изображения часто увеличивают в десятки раз и указанные искажения становятся заметными. Поэтому одиночные линзы в качестве объективов практически не используют, предпочтение отдают объективам, состоящим из 3 – 10 линз, в которых аберрации уменьшены (исправлены). Размеры изображения будут тем больше, чем больше размеры самого объекта, чем он ближе к линзе и чем больше её фокусное расстояние.
Если объект из бесконечности приблизится к области конечных расстояний, лучи, идущие от разных точек его поверхности, нельзя считать параллельными. |
||||
| Зависимость размеров изображения и его местоположения от расстояния до объекта съёмки показана на рис. 4. Чем ближе объект, тем дальше за линзой получается его изображение и тем большим будет оно по размеру. Когда объект приблизится на двойное фокусное расстояние, и его изображение окажется на таком же расстоянии за линзой. Такие условия возникают, например, макросъёмке (с близкого расстояния). Если объект удалён от линзы на расстояние, ровное фокусному расстоянию этой линзы, изображение объекта окажется в бесконечности. Одна из основных характеристик линзы – ее диоптрийность (D), которую называют также оптической силой. Она связана с фокусным расстоянием f простым соотношением D= 100 : f (где В указывается в диоптриях, а f – в см).
Оптическая сила линзы зависит от кривизны ее рабочих поверхностей и состава стекла, из которого она изготовлена. На рис. 5 показан ход лучей через объектив и обозначены основные отрезки, точки и плоскости. Задний (рабочий) отрезок объектива должен быть равен рабочему расстоянию светонепроницаемому камеры (её глубине) с точностью + 0.02 мм. К основным характеристикам объектива относится: фокусное расстояние, относительное отверстие, угловое поле зрения, угловое поле изображения и разрешающая способность. Фокусное расстояние объектива определяет масштаб изображения, т. е. степень уменьшения или увеличения изображения по сравнению с размерами фотографируемого объекта: чем больше фокусное расстояние, тем крупнее изображение «рисует» объектив (при неизменном расстоянии от фотоаппарата до объекта съемки). Обычно фокусное расстояние для каждого объектива — величина постоянная; ее значение (иногда с округлением) указывается на оправе объектива. |
||||
|
К длиннофокусным относятся также и телеобъективы, у которых оптическая система рассчитана так, что задняя оптическая плоскость находится в передней части оптической системы, и потому объектив как бы приближен к фокальной плоскости. Разновидностью телеобъективов являются зеркально-линзовые объективы типа МТО и 3М. Важная характеристика объектива — относительное отверстие, т. е. способность объектива создавать на фотопленке определенную освещенность изображения. Численно определяется как отношение диаметра светового отверстия объектива к его фокусному расстоянию. |
||||
|
Под световым отверстием объектива понимается то отверстие, через которое свет проходит внутрь фотокамеры. Величина, обратная относительному отверстию, называется диафрагменным числом. На оправе объектива и в его паспорте обычно указывается диафрагменное число, соответствующее максимальному значению относительного отверстия, которое принято называть светосилой объектива. В
современных объективах применяется так
называемая ирисовая диафрагма; она
составлена из лепестков, помещенных
между линзами объектива (примерно в
плоскости его оптического центра) и
образующих почти круглое отверстие.
Сдвигаясь или раздвигаясь, они плавно
изменяют величину действующего
отверстия объектива. |
||||
Линейная и радиальная мира. |
Угловое поле — величина, характеризующая поле зрения объектива, т. е. угол, под которым объектив «видит» фотографируемое пространство и создает его изображение в пределах кадра. Угловое поле зависит от фокусного расстояния объектива и размеров кадра: чем больше размеры кадра и меньше фокусное расстояние, тем больше угловое поле. Разрешающая способность объектива — одна из важнейших его характеристик. От нее зависит возможность получения мельчайших деталей в изображении и, следовательно, больших увеличений при печати. Она выражается числом линий (штрихов), различимых на 1 мм в изображении специальных штриховых объектов — мир. |
|||
|
Таким образом, для получения резкого изображения снимаемого предмета необходимо перед каждой съемкой установить объектив на некотором расстоянии от матового стекла, то есть произвести наводку на резкость. Матовое
стекло. Самый простой и в то же время
точный способ контроля наводки на
резкость — зрительное наблюдение по
матовому стеклу, заменяемому во время
съемки кассетой с пластинкой,
попадающей точно в плоскость матового
стекла (фотослой пластинки и матовая
сторона стекла должны быть обращены к
объективу). Шкала расстояний. Матовым стеклом пользоваться не всегда удобно и возможно по условиям съемки. Кроме того, не каждый фотоаппарат имеет матовое стекло. Поэтому все любительские аппараты для наводки на резкость снабжены шкалой расстояний, указатель которой показывает расстояние точки наводки. Наводка на резкость по матовому стеклу и по шкале расстояний должна давать одинаковые результаты. Для более простых пленочных фотоаппаратов шкала расстояний, называемая также метражной шкалой, является единственным средством наводки на резкость. Дальномер. Наилучший способ точной
наводки на резкость применение
заимствованного у артиллерийских
приборов дальномера, оптического
определителя расстояния от
фотоаппарата до снимаемого предмета. Это
оригинальная конструкция для очень
точной наводки на резкость путем
определения расстояния до объекта.
Состоит из двух простых однолинзовых
объективов, окуляра, полупрозрачного
зеркала и подвижного зеркала. Два
объектива смотрят на «объект» съемки,
образуя треугольник, подвижное зеркало
отбрасывает изображение от одного из объективов
на полупрозрачное зеркало, которое
его соединяет с изображением от второго
объектива, и все вместе отправляется
в окуляр на лицезрение фотографу.
Таким образом, фотограф видит картинку,
на которой некоторые объекты
раздвоены (их два глазка видят по-разному),
а некоторые — нет. Расстояние, на котором
некий предмет НЕ раздвоен, однозначно
определяется положением подвижного
зеркала, т. к. существует только один
прямоугольный треугольник с заданным
основанием и высотой. |
||||
|
На
главную | Предпосылки
изобретения фотографии | Камера-обскура
| Первые
снимки в мире | Дальнейшее
развитие светописи |
||||
Генерация лучей камеры (определение луча)
Большинство методов, которые мы будем изучать, начиная с этого урока, будут использовать то, что мы узнали о точках, векторах, матрицах, камерах и тригонометрии на уроке геометрии. Мы будем повторно использовать многое из того, что узнали на уроке «Вычисление пикселя 3D-точки» о различных системах координат, в которые можно преобразовать вершины и векторы. Вы также должны быть знакомы с концепциями, изучаемыми в уроке «3D-просмотр: модель камеры-обскуры». Прежде чем приступить к чтению этого урока, убедитесь, что вы рассмотрели эти основы.
Мы будем повторно использовать многое из того, что узнали на уроке «Вычисление пикселя 3D-точки» о различных системах координат, в которые можно преобразовать вершины и векторы. Вы также должны быть знакомы с концепциями, изучаемыми в уроке «3D-просмотр: модель камеры-обскуры». Прежде чем приступить к чтению этого урока, убедитесь, что вы рассмотрели эти основы.
На вводном уроке по трассировке лучей мы уже упоминали, как можно использовать трассировку лучей для решения проблемы видимости. Напомним, что определение видимой поверхности в контексте 3D-рендеринга — это процесс, используемый для определения того, какие части геометрии сцены видны через камеру. Мы можем использовать трассировку лучей для вычисления видимости (этот процесс уже объяснялся в предыдущем уроке), проводя луч через каждый пиксель изображения и ища ближайший объект, который этот луч пересекает (если он есть). Давайте также вспомним, что трассировка лучей — это метод вычисления пересечений между лучами и поверхностями.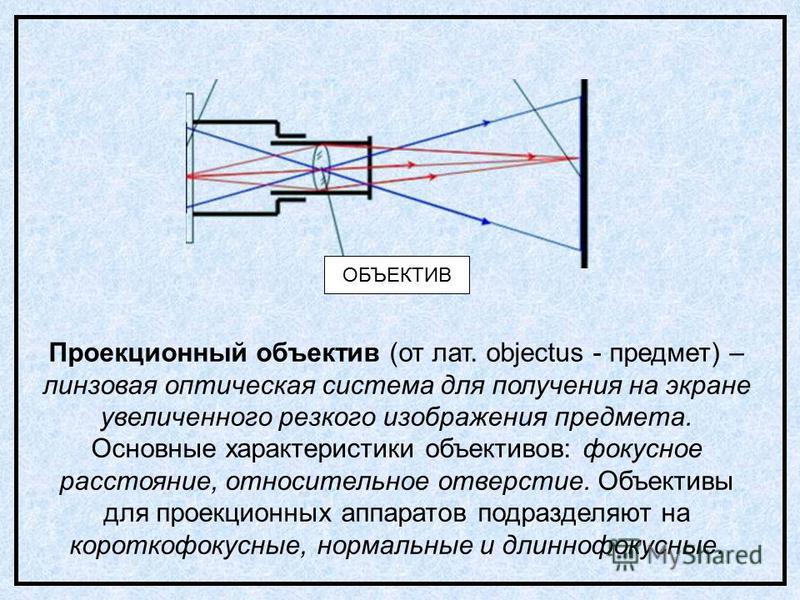 Использование трассировки лучей для вычисления видимости также называется ray-casting .
Использование трассировки лучей для вычисления видимости также называется ray-casting .
Для заданного набора препятствий в евклидовом пространстве две точки в пространстве называются видимыми друг для друга, если отрезок, соединяющий их, не пересекает никаких препятствий. (определение видимости в Википедии)
Создание изображения с использованием трассировки лучей для решения проблемы видимости требует перебора всех пикселей изображения, создания луча для каждого пикселя, наведения этого луча на сцену и поиска возможного пересечения между этот луч и любая поверхность в сцене. Эти лучи называются первичные лучи (или лучи камеры или глаза), потому что они являются первыми лучами, попадающими в сцену (вторичные лучи используются для вычисления таких вещей, как тени, отражения, преломления и т. д.). Чтобы определить, пересекает ли луч поверхность, нам нужно проверить каждый объект в сцене на возможное пересечение с этим лучом. Луч может пересекать более одной поверхности. Видимая поверхность — это поверхность с наименьшим расстоянием пересечения. Под расстоянием мы подразумеваем расстояние от начала луча (которое в случае основного луча является положением камеры) и точки пересечения.
Видимая поверхность — это поверхность с наименьшим расстоянием пересечения. Под расстоянием мы подразумеваем расстояние от начала луча (которое в случае основного луча является положением камеры) и точки пересечения.
для (int j = 0; j intersect(pimaryRay, tnear) && t
В этом уроке мы формализуем понятие луча и, что более важно, как генерируются первичные лучи для имитации камер-обскуры. Как только мы поймем, как генерируются первичные лучи, следующим шагом будет изучение нескольких методов вычисления пересечения лучей и геометрии. Это минимальные требования для создания изображения 3D-объектов с использованием трассировки лучей.
Примечание о трассировке лучей и перспективной проекции: модель камеры-обскуры проще всего моделировать в компьютерной графике. Как и в случае с растеризацией, эту модель мы также будем использовать для трассировки лучей. Изображения, сформированные с помощью этой модели. Помните, что отображение из 3D в 2D, описываемое камерой-обскурой, является перспективной проекцией.
В этой главе мы узнаем несколько полезных вещей о лучах. В следующей главе мы изучим, как вычисляются первичные лучи.
Определение лучей
Рисунок 1: луч определяется началом и направлением.
Как было сказано в предыдущем уроке,
Трассировка лучей — это метод, используемый для вычисления видимости между точками. Это просто метод, основанный на понятии луча, который может быть математически (и в компьютерной программе) определен как точка (начало луча в пространстве) и направление. Затем идея трассировки лучей состоит в том, чтобы найти математические решения для вычисления пересечения этого луча с различными типами геометрии: треугольниками, квадриками (которые мы изучаем в одном из следующих уроков), NURB и т. д. Это действительно все, что есть. к трассировке лучей.
Часть, которую мы объясним в этом уроке (и в этой главе более конкретно), — это понятие луча и то, как мы можем определить его как в теории, так и в программировании. Единственные две переменные, которые нам нужны для определения луча, — это точка и вектор. Точка (которую программно мы просто определим как vec3f) представляет собой начало луча, а вектор — его направление. Имейте в виду, что направление обычно должно быть нормализовано.
Точка (которую программно мы просто определим как vec3f) представляет собой начало луча, а вектор — его направление. Имейте в виду, что направление обычно должно быть нормализовано.
// минимальное требование для определения луча — это позиция и направление Vec3f ориг; // начало луча каталог Vec3f; // направление луча (нормализовано)
То, что эта точка и это направление вместе представляют собой полулинию. Математически любую точку на этой половине линии можно определить как:
$$P = ориг + т * реж.$$
Где \(t\) — расстояние от начала точки до точки на полуоси. Эта переменная может быть как отрицательной, так и положительной. Оно \(t\) отрицательное, точка луча находится за началом луча, а если \(t\) положительное, то точка P находится «перед» началом луча. На практике, когда мы используем трассировку лучей, нас обычно интересует только нахождение пересечения луча с поверхностями, расположенными перед началом луча. Это означает, что мы будем считать пересечение между лучом и поверхностью действительным только в том случае, если \(t\) положительно.
// определить начало и направление луча Vec3f ориг = …; Vec3f директор = …; поплавок т = БЕСКОНЕЧНОСТЬ; // пересекает ли этот луч объект? intersect() возвращает true, если пересечение было найдено if (object.intersect(origin, dir, t) && t > 0) { // это допустимое пересечение, точка попадания находится перед началом луча … }
С математической точки зрения приведенное выше уравнение называется параметрическим уравнением. Полупрямая описывается уравнением, являющимся функцией параметрической переменной \(t\) (или параметра).
Подпрограммы пересечения геометрии лучей всегда возвращают пересечение (если оно было найдено) в терминах параметра \(t\). Другими словами, если пересечение было найдено, то процедура пересечения геометрии лучей вычислит расстояние от начала луча до этого пересечения и вернет вам эту информацию. Оттуда вы можете легко вычислить положение пересечения или точки попадания в трехмерном пространстве, используя параметрическое уравнение луча, которое мы ввели выше.
// определить начало и направление луча Vec3f ориг = …; Vec3f директор = …; поплавок т = БЕСКОНЕЧНОСТЬ; // расстояние пересечения до объекта (если есть). Установите очень большое число для начала // пересекает ли этот луч объект? intersect() возвращает true, если пересечение было найдено if (object.intersect(origin, dir, t) && t > 0) { // это допустимое пересечение, точка попадания находится перед началом луча, вычислить точку попадания с помощью t Vec3f hitPoint = orig + dir * t; }
Вот и все, что нужно знать о лучах. С точки зрения программирования лучи также могут быть определены как класс C++:
class Ray { публичный: Рэй (), ориг (0), реж (0,0,-1) {} Ray(const Vec3f &o, const Vec3f &d) : orig(o), dir(d) {} // так далее. … Vec3f ориг; каталог Vec3f; };
Некоторым программистам нравится добавлять в этот класс дополнительные переменные-члены, например, расстояние \(t_{min}\) и \(t_{max}\). Они определяют диапазон допустимых значений для \(t\). Другими словами, если процедура лучевой геометрии возвращает значение для \(t\), которое не содержится в диапазоне [\(t_{min}\), \(t_{max}\)], то на самом деле будет не должно быть пересечения (даже если \(t\) больше 0).
Другими словами, если процедура лучевой геометрии возвращает значение для \(t\), которое не содержится в диапазоне [\(t_{min}\), \(t_{max}\)], то на самом деле будет не должно быть пересечения (даже если \(t\) больше 0).
класс Рэй { публичный: Луч(), ориг.(0), реж.(0,0,-1), tMin(0.1), tMax(1000) {} Ray(const Vec3f &o, const Vec3f &d): orig(o), dir(d), tMin(0.1), tMax(1000) {} // так далее. … Vec3f ориг; каталог Vec3f; поплавок tМин, tМакс; }; Рэй Рэй; // устанавливаем направление и начало луча луч.ориг = …; луч.дир = …; поплавок т = БЕСКОНЕЧНОСТЬ; if (object.intersect(ray, t) && t >= ray.tMin && t <= r.tMax) { // допустимое пересечение … }
Вы можете добавить любое количество параметров к классу Ray. Вы можете решить использовать класс Ray или нет. Это полностью оставлено на усмотрение личных предпочтений и требований. Нет никаких правил относительно того, как вы представляете эти данные в своей программе. Некоторым программистам нравится добавлять в класс Ray такую информацию, как расстояние \(t\) до ближайшей видимой поверхности (которое вы устанавливаете в подпрограмме геометрии луча при обнаружении пересечения), указатель на объект попадания и т. д. Некоторые другие программисты предпочитают отделять эту информацию от переменных луча и вместо этого хранить их в структуре или классе, например, с именем Intersection. Опять же, помимо необходимости хотя бы определить начало и направление луча, все остальное можно сделать так, как вам нравится (и это необязательно).
Некоторым программистам нравится добавлять в класс Ray такую информацию, как расстояние \(t\) до ближайшей видимой поверхности (которое вы устанавливаете в подпрограмме геометрии луча при обнаружении пересечения), указатель на объект попадания и т. д. Некоторые другие программисты предпочитают отделять эту информацию от переменных луча и вместо этого хранить их в структуре или классе, например, с именем Intersection. Опять же, помимо необходимости хотя бы определить начало и направление луча, все остальное можно сделать так, как вам нравится (и это необязательно).
Одна вещь, которая может быть полезна в программировании, это как-то пометить луч в зависимости от его типа: первичный, теневой, отраженный, преломленный и т. д. Его можно использовать для сбора статистики (если вы хотите знать, сколько теней было отброшено например, для рендеринга данной сцены) и может использоваться в коде для вызова различных функций в зависимости от типа луча. Это тоже обычная практика.
Для чего используются лучи?
Лучи можно использовать практически везде. Они используются для решения проблемы видимости, сбора информации о цветах объектов, вычисления теней и т. д. Тип лучей, о котором мы будем изучать в этом уроке, называется 9.0005 лучей камеры или первичных лучей .
Они используются для решения проблемы видимости, сбора информации о цветах объектов, вычисления теней и т. д. Тип лучей, о котором мы будем изучать в этом уроке, называется 9.0005 лучей камеры или первичных лучей .
Рисунок 2: камера или первичные лучи — это лучи, которые исходят из источника камеры и проходят через центры пикселей. Если первичный луч попадает в геометрию сцены, мы вычисляем цвет объекта в точке пересечения и присваиваем этот цвет пикселю, через который проходит луч.
Для каждого пикселя в кадре нам нужно построить один луч камеры, который мы будем направлять в сцену. Если лучи пересекают объекты, мы вычислим цвет объектов в этих точках пересечения и назначим эти цвета соответствующим пикселям. Это вкратце то, как изображение компьютерной графики создается с помощью трассировки лучей. Мы можем провести различие между первичными лучами (первыми лучами, падающими на сцену, которые имеют происхождение от камеры) и вторичных лучей (теневые, диффузные, зеркальные, пропускающие и т. д. лучи), которые мы используем при затенении. Вторичные лучи рождаются из первичных лучей в точке пересечения лучей. Направление этих вторичных лучей зависит от их типа: тень (мы бросаем луч в направлении света), отражение (мы бросаем луч в направлении отражения), преломление (мы бросаем луч в направлении преломления, которое может быть вычислено по закону Снелла) и т. д.
д. лучи), которые мы используем при затенении. Вторичные лучи рождаются из первичных лучей в точке пересечения лучей. Направление этих вторичных лучей зависит от их типа: тень (мы бросаем луч в направлении света), отражение (мы бросаем луч в направлении отражения), преломление (мы бросаем луч в направлении преломления, которое может быть вычислено по закону Снелла) и т. д.
Что дальше?
В следующей главе мы узнаем, как инициализировать лучи камеры для каждого пикселя кадра, после чего все, что нам нужно сделать, чтобы получить изображение, — это реализовать простую процедуру пересечения луча и объекта и сохранить результат в изображении. формат файла.
Трассировка лучей | NVIDIA Developer
- Домашняя страница
- Откройте для себя
- Трассировка лучей
Трассировка лучей — это метод рендеринга, который может реалистично имитировать освещение сцены и ее объектов путем рендеринга физически точных отражений, преломлений, теней и непрямого освещения.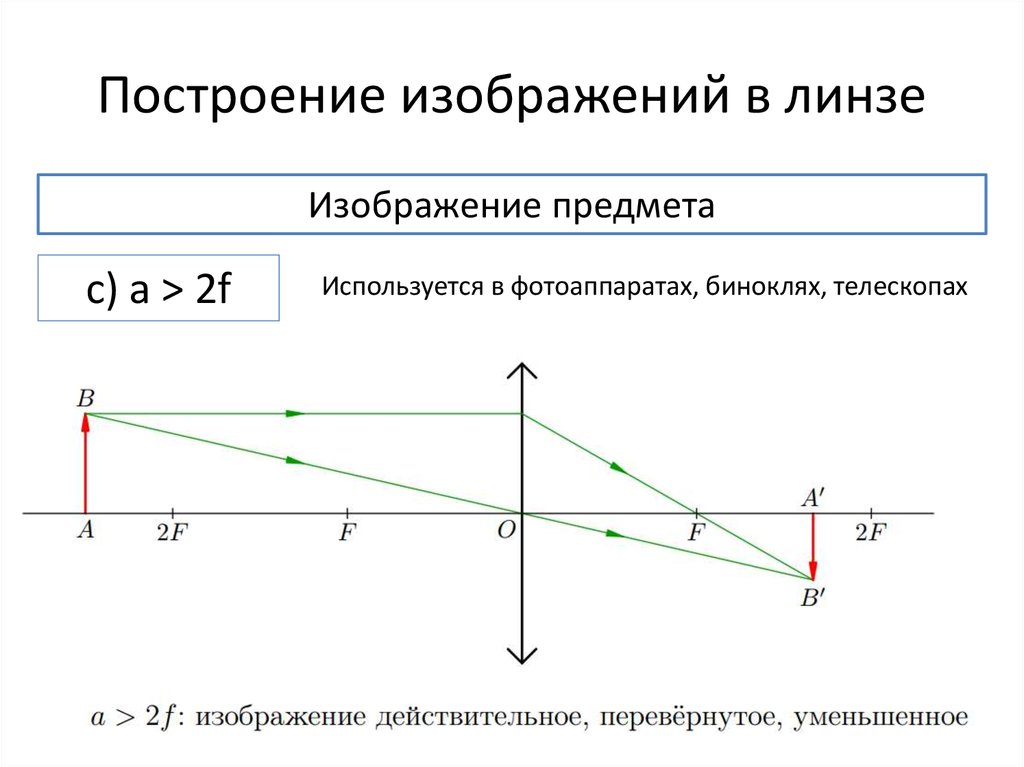 Трассировка лучей генерирует изображения компьютерной графики путем отслеживания пути света от камеры обзора (которая определяет ваш взгляд на сцену) через плоскость 2D-просмотра (плоскость пикселей), в 3D-сцену и обратно к источникам света. Проходя через сцену, свет может отражаться от одного объекта к другому (вызывая отражение), блокироваться объектами (вызывая тени) или проходить сквозь прозрачные или полупрозрачные объекты (вызывая преломление). Все эти взаимодействия объединяются для получения окончательного цвета и освещения пикселя, который затем отображается на экране. Этот обратный процесс трассировки глаза/камеры к источнику света выбран потому, что он намного эффективнее, чем трассировка всех световых лучей, испускаемых источниками света в нескольких направлениях.
Трассировка лучей генерирует изображения компьютерной графики путем отслеживания пути света от камеры обзора (которая определяет ваш взгляд на сцену) через плоскость 2D-просмотра (плоскость пикселей), в 3D-сцену и обратно к источникам света. Проходя через сцену, свет может отражаться от одного объекта к другому (вызывая отражение), блокироваться объектами (вызывая тени) или проходить сквозь прозрачные или полупрозрачные объекты (вызывая преломление). Все эти взаимодействия объединяются для получения окончательного цвета и освещения пикселя, который затем отображается на экране. Этот обратный процесс трассировки глаза/камеры к источнику света выбран потому, что он намного эффективнее, чем трассировка всех световых лучей, испускаемых источниками света в нескольких направлениях.
Другой способ представить себе трассировку лучей — это посмотреть вокруг себя прямо сейчас. Объекты, которые вы видите, освещаются лучами света. Теперь поверните его и следуйте по пути этих лучей в обратном направлении от вашего глаза к объектам, с которыми взаимодействует свет.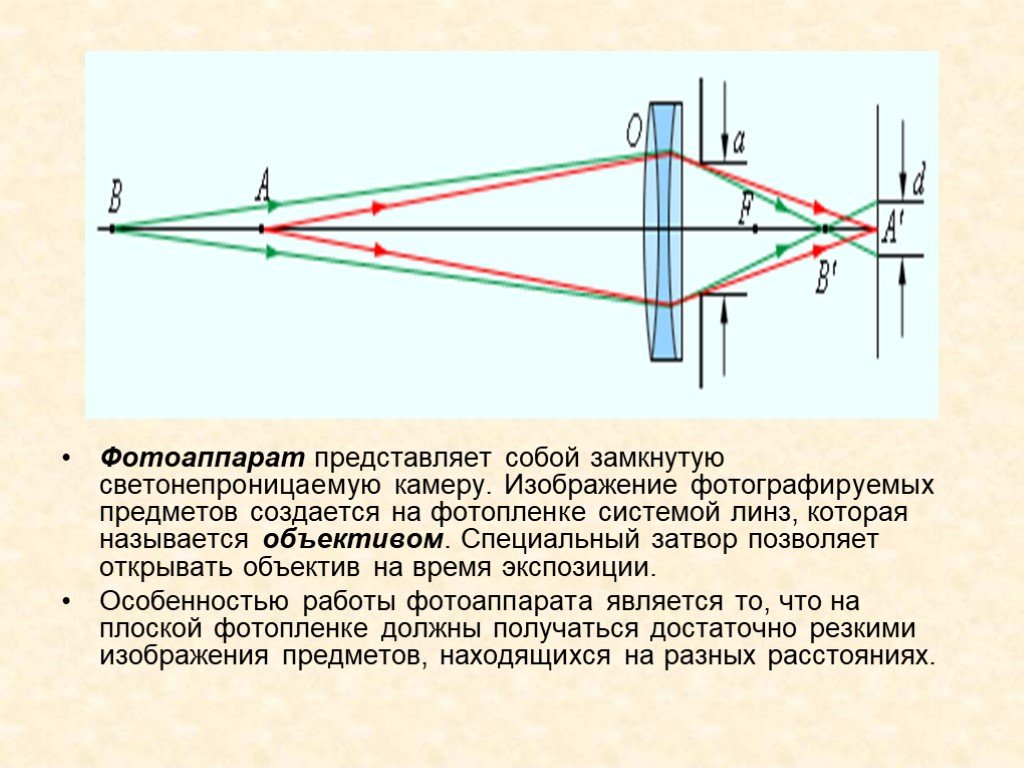 Это трассировка лучей.
Это трассировка лучей.
В основном трассировка лучей применяется в компьютерной графике, как не в реальном времени (кино и телевидение), так и в реальном времени (видеоигры). Другие приложения включают приложения в архитектуре, инженерии и дизайне освещения.
В следующем разделе представлены основы рендеринга и трассировки лучей, а также широко используемая терминология.
Рисунок 1: Основы трассировки лучей
Основы трассировки лучей
- Преобразование лучей — это процесс в алгоритме трассировки лучей, который пропускает один или несколько лучей от камеры (положение глаз) через каждый пиксель в плоскости изображения и затем проверяет, пересекают ли лучи какие-либо примитивы (треугольники) в сцене. Если луч, проходящий через пиксель и выходящий в 3D-сцену, попадает на примитив, то определяется расстояние вдоль луча от начала координат (камеры или точки наблюдения) до примитива, а данные о цвете от примитива вносят свой вклад в окончательный цвет.
 пикселя. Луч также может отражаться и поражать другие объекты и получать от них информацию о цвете и освещении.
пикселя. Луч также может отражаться и поражать другие объекты и получать от них информацию о цвете и освещении. - Трассировка пути — это более интенсивная форма трассировки лучей, которая отслеживает сотни или тысячи лучей через каждый пиксель и следует за лучами через многочисленные отражения от объектов или через объекты, прежде чем достичь источника света, чтобы собрать информацию о цвете и освещении.
- Иерархия ограничивающих объемов (BVH) — это популярный метод ускорения трассировки лучей, в котором используется древовидная «структура ускорения», содержащая несколько иерархически расположенных ограничивающих прямоугольников (ограничивающих объемов), которые охватывают или окружают различные объемы геометрии сцены или примитивов. . Тестирование каждого луча на каждом пересечении примитивов в сцене неэффективно и требует больших вычислительных ресурсов, а BVH — один из многих методов и оптимизаций, которые можно использовать для его ускорения. BVH может быть организован в различных типах древовидных структур, и каждый луч нужно проверять только на BVH с использованием процесса обхода дерева в глубину, а не на каждом примитиве в сцене.
 Перед рендерингом сцены в первый раз необходимо создать структуру BVH (называемую построением BVH) из исходной геометрии. Для следующего кадра потребуется либо новая операция сборки BVH, либо перенастройка BVH на основе изменений сцены.
Перед рендерингом сцены в первый раз необходимо создать структуру BVH (называемую построением BVH) из исходной геометрии. Для следующего кадра потребуется либо новая операция сборки BVH, либо перенастройка BVH на основе изменений сцены. - Фильтрация шумоподавления — это усовершенствованная технология фильтрации, позволяющая повысить производительность и качество изображения без необходимости испускания дополнительных лучей. Шумоподавление может значительно улучшить визуальное качество зашумленных изображений, которые могут быть созданы из разреженных данных, иметь случайные артефакты, видимый шум квантования или другие типы шума. Фильтрация шумоподавления особенно эффективна для сокращения времени рендеринга изображений с трассировкой лучей и может создавать высококачественные изображения с помощью трассировки лучей, которые выглядят визуально бесшумными. Приложения шумоподавления включают трассировку лучей в реальном времени и интерактивный рендеринг. Интерактивный рендеринг позволяет пользователю динамически взаимодействовать со свойствами сцены и мгновенно видеть результаты их изменений, обновленных в визуализируемом изображении.

Основы рендеринга
- Растеризация — это метод, используемый для отображения трехмерных объектов на двухмерном экране. При растеризации объекты на экране создаются из сетки виртуальных треугольников или многоугольников разных форм и размеров. Углы треугольников — известные как вершины — связаны с большим количеством информации, включая их положение в пространстве, а также информацию о цвете, текстуре и его «нормали», которая используется для определения формы поверхности объекта. перед. Компьютеры преобразуют треугольники 3D-моделей в пиксели или точки на 2D-экране. Каждому пикселю может быть присвоено начальное значение цвета из данных, хранящихся в вершинах треугольника. Дальнейшая обработка пикселей или «затенение», включая изменение цвета в зависимости от того, как свет попадает в сцену, и применение одной или нескольких текстур, объединяются для создания окончательного цвета, применяемого к пикселю. Растеризация используется в компьютерной графике в реальном времени, и, хотя она по-прежнему требует значительных вычислительных ресурсов, она меньше по сравнению с трассировкой лучей.

- Гибридная растеризация и трассировка лучей — это метод, который одновременно использует растеризацию и трассировку лучей для визуализации сцен в играх или других приложениях. Растеризация может определять видимые объекты и хорошо и с высокой производительностью отображать многие области сцены. Трассировку лучей лучше всего использовать для рендеринга физически точных отражений, преломлений и теней. При совместном использовании они очень эффективны для достижения высокого качества с хорошей частотой кадров.
Ускорение трассировки лучей с помощью графических процессоров
Трассировка лучей — это метод, требующий больших вычислительных ресурсов. Создатели фильмов традиционно полагались на огромное количество ферм рендеринга на базе ЦП, которым по-прежнему может потребоваться несколько дней для рендеринга сложных спецэффектов. Графические процессоры могут отображать реалистичные сцены с трассировкой лучей кинематографического качества экспоненциально быстрее, чем центральные процессоры, но они ограничены объемом встроенной памяти, который определяет, насколько сложной может быть визуализирована сцена.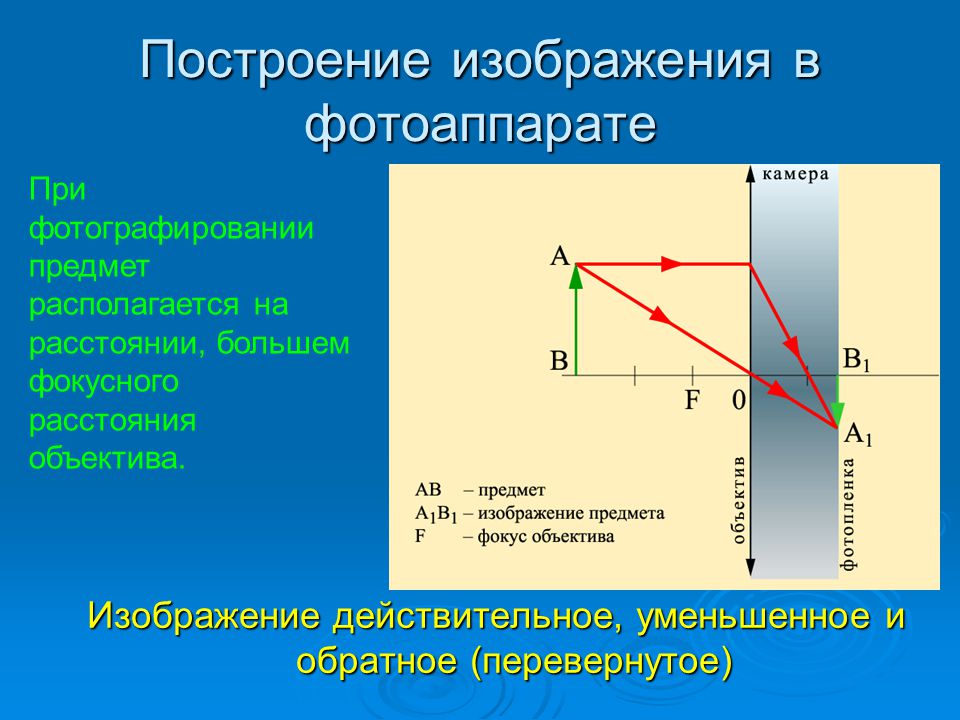



 Условно считают, что лучи пучка отклоняются на входе и на выходе из линзы, как при пересечении передней и задней оптических плоскостей.
Условно считают, что лучи пучка отклоняются на входе и на выходе из линзы, как при пересечении передней и задней оптических плоскостей. 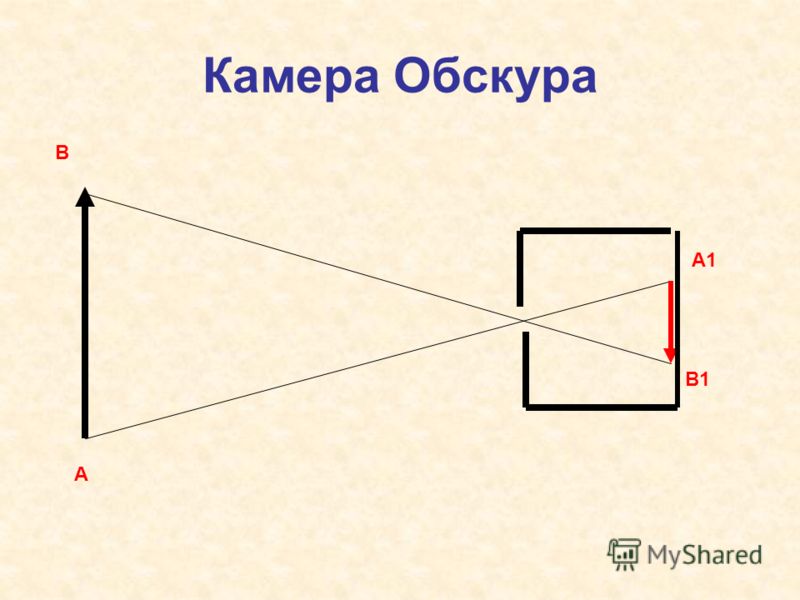 Если эта поверхность находится на расстоянии не меньшем, чем бесконечность, изображения её точек лежат в фокальной плоскости, а их совокупность образует световое изображение поверхности.
Если эта поверхность находится на расстоянии не меньшем, чем бесконечность, изображения её точек лежат в фокальной плоскости, а их совокупность образует световое изображение поверхности.  Поэтому изображения этих точек будут получать не в главной фокальной плоскости , а за ней.
Поэтому изображения этих точек будут получать не в главной фокальной плоскости , а за ней.
 Объективы, фокусное расстояние которых меньше диагонали кадра, а угол поля зрения превышает 55°, относятся к
широкоугольным, или короткофокусным. Объективы с большим, чем диагональ кадра, фокусным расстоянием и меньшим, чем 45°, углом поля зрения, относятся к
длиннофокусным.
Объективы, фокусное расстояние которых меньше диагонали кадра, а угол поля зрения превышает 55°, относятся к
широкоугольным, или короткофокусным. Объективы с большим, чем диагональ кадра, фокусным расстоянием и меньшим, чем 45°, углом поля зрения, относятся к
длиннофокусным. Это отверстие определяется
диафрагмой. Диафрагма расположена между линзами объектива и состоит из нескольких лепестков, закрепленных в оправе, имеющей наружное кольцо, посредством которого можно сдвигать и раздвигать лепестки и тем самым регулировать размер светового отверстия, т. е. изменять относительное отверстие объектива.
Это отверстие определяется
диафрагмой. Диафрагма расположена между линзами объектива и состоит из нескольких лепестков, закрепленных в оправе, имеющей наружное кольцо, посредством которого можно сдвигать и раздвигать лепестки и тем самым регулировать размер светового отверстия, т. е. изменять относительное отверстие объектива. 
 Миры монтируют на щитах и фотографируют на фоне белого освещенного экрана. Разрешающая способность может быть определена по числу штрихов в изображении, которое создает объектив, и по изображению на фотоматериале после его проявления. Первая называется визуальной разрешающей способностью, а вторая — фотографической. На фотографическую разрешающую способность влияют характеристики фотоматериала, поэтому она примерно на 50% ниже визуальной.
Миры монтируют на щитах и фотографируют на фоне белого освещенного экрана. Разрешающая способность может быть определена по числу штрихов в изображении, которое создает объектив, и по изображению на фотоматериале после его проявления. Первая называется визуальной разрешающей способностью, а вторая — фотографической. На фотографическую разрешающую способность влияют характеристики фотоматериала, поэтому она примерно на 50% ниже визуальной. Все, что глаз видит резким на
матовом стекле, таким же получится и на
пластинке. Матовое стекло служит также
для выбора кадра при съемке со штатива.
Все, что глаз видит резким на
матовом стекле, таким же получится и на
пластинке. Матовое стекло служит также
для выбора кадра при съемке со штатива.
 Дальномер может
быть автономным, т. е. просто показывать
расстояние до объекта, а может быть
сопряженным.
Дальномер может
быть автономным, т. е. просто показывать
расстояние до объекта, а может быть
сопряженным.  пикселя. Луч также может отражаться и поражать другие объекты и получать от них информацию о цвете и освещении.
пикселя. Луч также может отражаться и поражать другие объекты и получать от них информацию о цвете и освещении.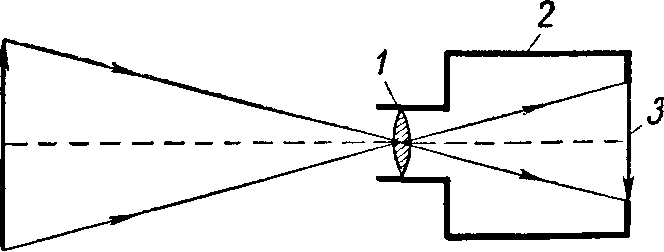 Перед рендерингом сцены в первый раз необходимо создать структуру BVH (называемую построением BVH) из исходной геометрии. Для следующего кадра потребуется либо новая операция сборки BVH, либо перенастройка BVH на основе изменений сцены.
Перед рендерингом сцены в первый раз необходимо создать структуру BVH (называемую построением BVH) из исходной геометрии. Для следующего кадра потребуется либо новая операция сборки BVH, либо перенастройка BVH на основе изменений сцены.