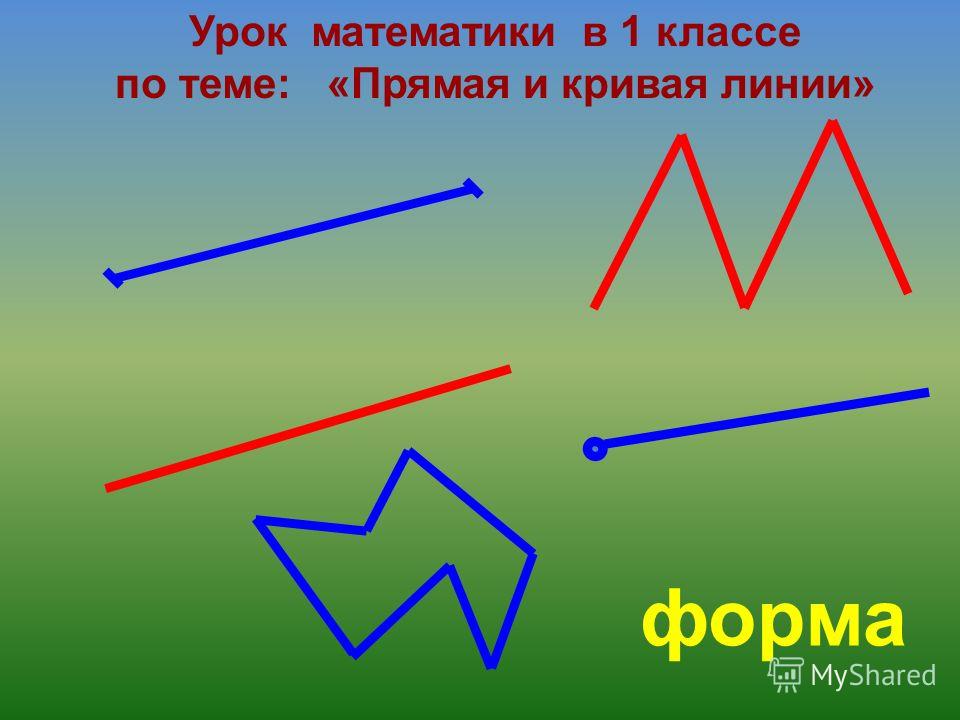
1 класс. Математика. Точка. Прямая, кривая и ломаная линии. — Прямая линия. Кривая линия. Ломаная линия.
Комментарии преподавателяНа данном уроке Вы изучите простейшие геометрические понятия, о которых вам расскажет мама дракончиков. Вместе с дракончиками Вы изучите такие основные понятия, как прямая линия, луч, отрезок, угол, ломаная и кривая линия. У Вас будет возможность изучить предложенный материал на наглядных примерах.
Тема: Наглядная геометрия
Урок: Начальные геометрические понятия
На этом уроке будут изучены простейшие геометрические понятия. Для лучшего понимания рассмотрим сказку про дракончиков.
Далеко-далеко в горах живет большая-большая семья драконов: папа-дракон, мама-дракониха и много маленьких дракончиков. Когда дракончики были маленькие, они учились ползать, бегать, летать, прыгать, узнавали, что такое снег, дождь, звёзды, учились в горах ориентироваться, учились даже огнём дышать.
Когда дракончики немножко подросли, мама решила их научить математики, в том числе геометрии. Дракончики очень удивились, они не поняли о чём идет речь. Мама предложила им сесть на площадке перед большой скалой и смотреть, что она будет рисовать. Она начала рисовать мелом на этом плоском куске скалы различные геометрические вещи, начиная с самых простых. Вначале мама-дракониха нарисовала линию, которая изображена на рисунке. (рис. 1)
Рис. 1
Мама-дракониха сказала, что эта линия называется прямая. Это такое геометрическое понятие.
Прямая линия – это линия, которая совершенно бесконечна.
Прямая линия идет бесконечно в одну сторону и в другую сторону. Есть такое даже выражение «Летит в небе по прямой».
Потом мама нарисовала точку и от неё провела линию. (рис. 2)
Рис. 2
Она объяснила, что точка – это начало, от нее идет линия в бесконечность.
Это называется луч.
Луч — это полупрямая, которая имеет точку начала и не имеет конца.
Он так называется потому, что она как луч света. У луча света всегда есть начало. Он всегда начинается либо на солнце, либо на свечки, либо в фонарике, либо на звезде далекой. Дракончики поняли, что такое луч.
Потом мама-дракониха попросила представить дракончиков, что они от прямой отрежут кусочек. Такая фигура называется отрезок. (рис. 3)
Рис. 3
Отрезок — это часть прямой, которая ограничена с двух сторон.
Отрезок может быть длинным или коротким. Дракончики сразу не поняли. Тогда мама нарисовала еще несколько отрезков: длинные и короткие. (рис. 4)
Рис. 4
Это всё отрезки. Теперь дракончики все поняли.
Потом мама-дракониха из одной точки отложила два луча, получилась фигура, которая называется угол.
(рис. 5)
Рис. 5
Причем углом называется как вся фигура, так и что находится внутри неё.
Угол – это геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Потом мама-дракониха решила нарисовать еще одну форму линии. (рис. 6)
Рис. 6
Такая линия называется ломаная линия. Потому что взяли фактически прямую линию и поломали ее. И каждый кусочек на этой линии называется звено. Ломаные линии могут быть самые разные, по разному поломанные.
Следом мама нарисовала загогулину. (рис. 7)
Рис. 7
Это кривая линия. Таких кривых линий можно нарисовать много-много самых разных.
Потом мама-дракониха спросила у маленьких дракончиков, по какой линии они летаете в небе. Дракончики задумались. И один сказал, что он летает по кривой линии, он делает всякие пируэты, закладывает спирали, петли делает.
А другой дракончик сказал, что когда они в снежки играли, он повисал в воздухе, махал крылышками, а в него кидали снежками. Он улетал от них и дёргался туда-сюда, туда-сюда. Получалась ломаная линия. Мама-дракониха сказала, что дракончики все поняли правильно. Драконы летают и по кривой линии, и по ломаной, иногда просто по прямой.
И тут мама заметила, что дракончики уже стали скучать и как-то вертеться, уже плохо её слушают. Она поняла, что пора их отпустить, она сказала, что урок закончен. Дракончики замахали крылышками, взлетели в небо, разлетелись над горами, весело кричали, смеялись. Мама смотрела на них и улыбалась, махала им лапой.
Итак, на уроке мы выучили такие простейшие геометрические понятия, как прямая линия, отрезок, луч, угол. Также мы рассмотрели ломаную и кривую линию. После изученного урока Вы будете знать простейшие геометрические понятия не хуже маленьких дракончиков.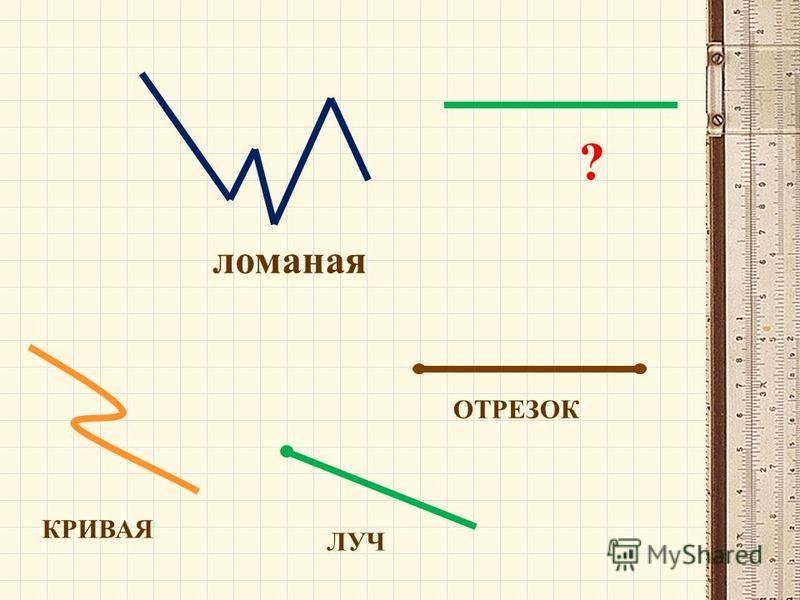
Источник конспекта: http://interneturok.ru/ru/school/matematika/1-klass/beksperimentb/nachalnye-geometricheskie-ponyatiya?seconds=0
Источник видео: https://www.youtube.com/watch?v=o8Pu_Q8YFjk
1 класс, прямая, отрезок, точка, урок и презентация по математике луч, ломанная
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Точка, прямая и кривая линии, отрезок, луч, ломаная (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 1 класса
Тренажер по Дорофееву Г.В.
Тренажер по Демидовой Т.Е.
Точка
Дорогие ребята, сегодня вместе с нашими героями мы будем изучать простейшие геометрические фигуры.
Начнем с точки. В математике точка обозначается буквой алфавита, например, буквой А.
В тетради это выглядит так. Если у вас на рисунке есть несколько точек, то их необходимо называть разными буквами, чтобы не путаться.
Линии
Если на рисунке несколько линий, то разные линии нужно обозначать разными буквами.
Прямая линия
Линия называется прямой, если она нигде не искривляется.
Вжик нарисовал несколько прямых линий разного цвета.
В математике прямая линия бесконечная, а это значит, что у неё нет ни начала, ни конца.
Кривая линия
Чип нарисовал несколько кривых линий. Каждый может их нарисовать от руки.
Отрезок
Если отрезать от прямой линии некоторую часть, то получится отрезок с началом и концом, что мы попробуем сделать. Получится отрезок AB. У данного отрезка есть длина, и обозначается она так, АB = 4 см.
На этом рисунке нарисовано 2 отрезка: АВ и СЕ.
Луч
Луч – часть прямой, которая имеет начало, но не имеет конца. Обозначается, как показано на рисунке.
Ломаная линия
Ломаная линия – это фигура, которая состоит из отрезков, последовательно соединенных своими концами.
Ломаная на рисунке обозначается $A_1A_2A_3A_4A_5A_6$.
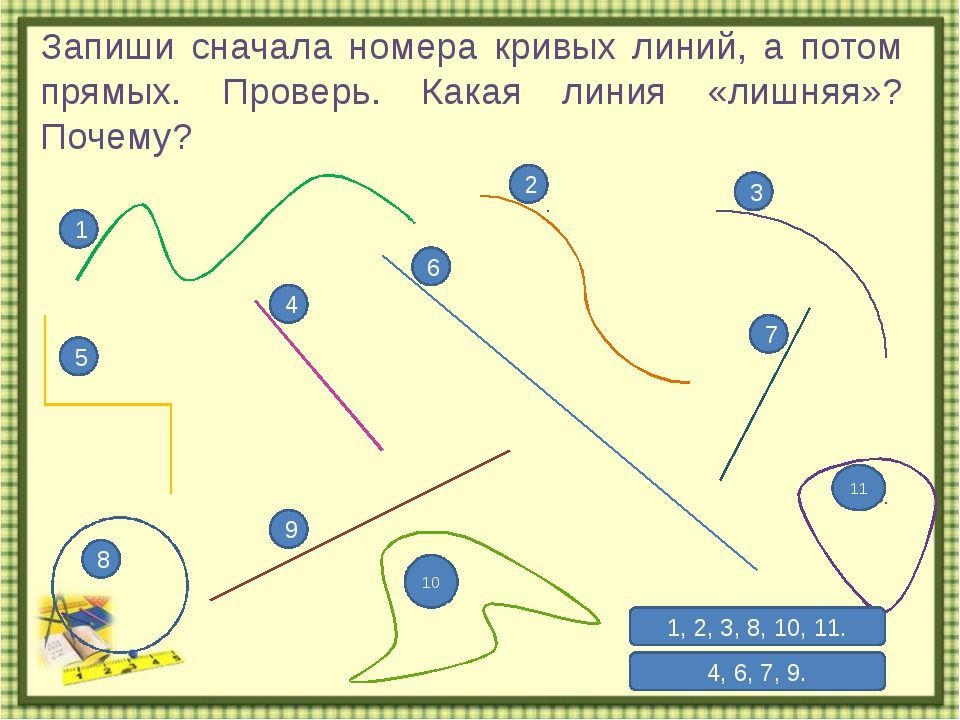
Ребята, определите, какие фигуры изображены на рисунке? Назовите каждую фигуру.
Методические указания по теме:
По программе ученики начальных классов знакомятся с плоскостными фигурами, именуемыми вообще многоугольниками; в частности с различного вида треугольниками, прямоугольниками и другими видами четырех-угольников, фигурами с большим числом сторон: пятиугольниками, шестиугольниками, которые легко можно разбить на треугольники и четырехугольники.При ознакомлении с указанными фигурами необходимо с самых первых шагов (когда дети пользуются различными фигурами как дидактическим материалом) дать практически понятие детям о том, что треугольник, четырехугольник, прямоугольник, квадрат и вообще многоугольник— это часть плоскости (поверхность бумаги, картона, фанеры, ткани), ограниченная сторонами — отрезками прямых линий, как в прямоугольнике или треугольнике, или кривой линией, как в круге, или кривой и прямой, как в полукруге.
Чтобы избежать этих ошибок, мы предлагаем знакомство с треугольником, прямоугольником и любым многоугольником начинать путем вырезывания этой фигуры из бумаги (контур фигуры очерчивается по линейке карандашом, а затем по начерченному контуру ножницами или ножичком вырезывается фигура). Вторым этапом ознакомления с такими фигурами являются чертежи на бумаге с обязательной затушевкой. Пусть ученик знает, что когда он начертил только стороны треугольника или квадрата, то это только контур (границы) фигуры, а когда он сделает затушевку, то будет видеть всю фигуру.
Если же учитель желает провести с учениками практическую работу с палочками, то им можно предложить примерно такие вопросы:
1) Сколько надо взять палочек и каких, чтобы из них сложить все стороны (или границы) квадрата? треугольника с равными сторонами?
2) Какая получится линия из сторон квадрата, если убрать одну сторону квадрата, т. е. одну палочку? (Получится ломаная линия из трех равных отрезков.) И т. п.
При изучении сотни ученики I класса знакомятся с мерами длины — сантиметром, дециметром и метром, а также с мерой массы — килограммом и с мерой емкости— литром. С мерой длины сантиметром желательно познакомить детей раньше, лучше в самом начале за¬нятий, так как знакомство с этой мерой даст возможность разнообразить занятия различными задачами практического характера.
52. Начертите три прямые линии: одну —слева направо (по строке), другую — снизу вверх, третью — наискось. Подумайте и скажите, можно ли каждую из этих линий продолжить в обе стороны.
Чертите хорошо отто-ченным карандашом по линейке слева направо. Линейку придерживайте левой рукой, а карандаш — наклонно.Указание. Надо показать, как правильно проводить прямую линию. Для этого можно листок клетчатой бумаги при¬крепить кнопками к доске и по¬казать, как держать линейку и вести карандаш. После этого необходимо проследить, как каждый из учеников выполняет это задание, и тем, кто делает неправильно, показать в тетради, как надо держать линейку и карандаш. Если этого не сделать вначале, то потом уйдет больше времени на поправки и указания.
53. Отметьте в тетради точку и проведите через нее две прямые линии. Подумайте, можно ли через эту же точку провести еще прямые линии. Проведите еще две прямые через эту точку и скажите, сколько еще можно провести прямых линий через ту же точку.
Указание. Дети должны сделать вывод, что через одну точку можно провести сколько угодно прямых.
54. Отметьте две точки и проведите через них прямую линию. Можно ли через эти две точки провести еще прямую линию, чтобы она не слилась с первой? Теперь попробуйте провести кривую линию, чтобы она прошла через те же две точки.
Можно ли еще через те же две точки провести кривую линию? А сколько кривых линий можно провести через две точки?55. Начертите 6 пар прямых линий. Всмотритесь в них внимательно и скажите, чем отличаются друг от друга 1, 3 и 6-я пары линий от 2, 4 и 5-й пар.
56. Начертите пару непересекающихся прямых и пару пересекающихся прямых. Все прямые линии на бумаге или на доске чертятся не полностью, они могут быть продолжены в обе стороны сколько угодно.
57. На этом чертеже даны две прямые линии. Какие они — пересекающиеся или непересекающиеся? Как это узнать? Как найти точку их пересечения?
Указание. Ученики должны догадаться, что обе эти прямые надо продолжить вправо.
58. Начертите две такие прямые линии, которые на чертеже не пересекаются, но должны пересечься при продолжении, и найдите точку их пересечения.
59. Начертите прямую линию и пересеките ее в двух местах черточками (штрихами). Этими черточками мы ограничиваем (отрезаем) кусочек прямой линии, и эта часть прямой линии от одной черточки до другой называется отрезком прямой линии или просто отрезком. Вокруг вас много отрезков: ребра (стороны) тетради, стекла, доски, двери — все это части прямых линий, которые ограничены с двух концов, значит, они являются отрезками.
60. Отметьте на бумаге две точки и проведите через них прямую линию. Как можно назвать ту часть линии, которая находится между точками? Можно ли провести другой отрезок между теми же точками, который не сов-пал бы с первым отрезком?
Что такое изогнутая линия? Определение, типы, примеры, факты
Что такое изогнутая линия?
Изогнутая линия, как следует из названия, представляет собой изогнутую линию.
Мы видим вокруг себя изогнутые объекты. Изогнутые линии также известны как изогнутые линии. Обратите внимание, что линия строго прямая. Кривую можно рассматривать как обобщение линии.
Вы можете заметить, что буквы A, I, T и т. д. не имеют изогнутых линий. Однако мы не можем писать такие буквы, как B, C, D и т. д., без изогнутой линии. В каких еще повседневных наблюдениях вы видите изогнутые линии? Усы, кривая линия над рядом нот в нотах, радуга, кривая дорога, кудрявые волосы!
Связанные игры
Изогнутая линия: определение
Изогнутая линия — это тип линии, которая не является прямой и изогнутой. Он непрерывный и плавный, без резких поворотов.
Мы знаем, что кривизна прямой равна нулю. Следовательно, когда кривизна линии не равна нулю, мы называем ее криволинейной линией.
Представьте, что жуку нужно переместиться из точки А в точку Б. Какими способами жук может добраться из точки А в точку Б?
Жук может добраться из пункта А в пункт Б несколькими путями.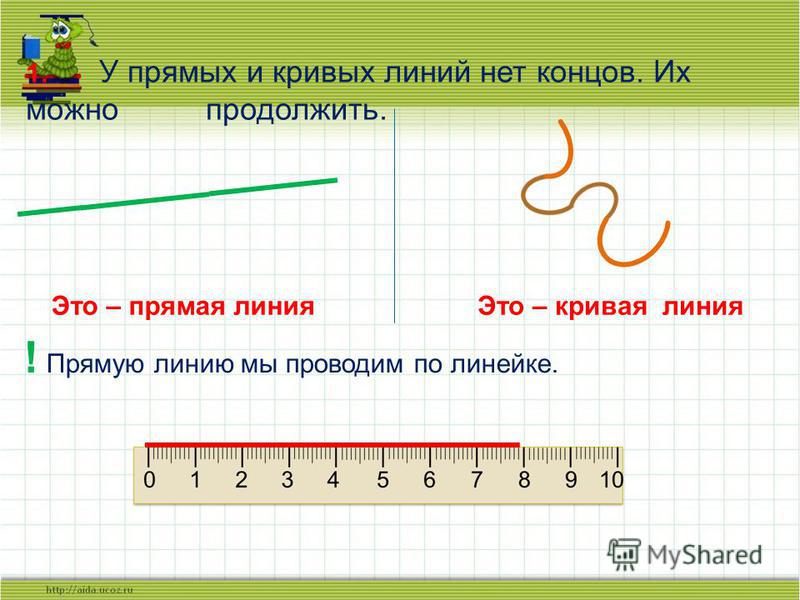
На приведенных рисунках показаны некоторые пути, по которым муравей может добраться из пункта А в пункт Б.
Мы видим, что на первых четырех рисунках муравей менял свое направление при путешествии из точки А в точку Б, то есть он не следовал одному постоянному направлению. Однако на последнем рисунке муравей двигался прямо, и расстояние, которое он прошел, было самым коротким. Движение от одной точки к другой порождает прямые или кривые линии.
Связанные рабочие листы
Примеры изогнутой линии
Приведенные выше буквы и цифры состоят только из кривых.
Прямые линии и изогнутые линии
Давайте посмотрим на разницу между изогнутыми и прямыми линиями.
Чем прямая линия отличается от кривой?
Некоторые факторы, такие как кривизна, случайный изгиб и направление, делают прямую линию отличной от кривой. Все эти различные типы кривых на графике также упоминаются.
Различные типы кривых линий
Давайте обсудим некоторые типы кривых, образованных кривыми линиями.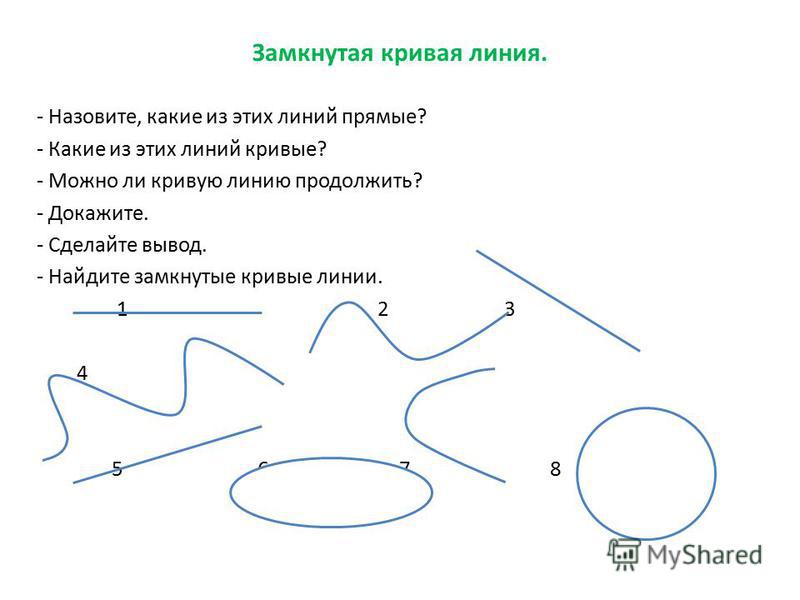
Незамкнутая кривая не заключает в себе никакой области и имеет две конечные точки. Примеры незамкнутых кривых:
Замкнутая криваяЗамкнутая кривая не имеет конечных точек и охватывает площадь (или область). Он образуется путем соединения концов открытой кривой вместе. Окружности и эллипсы формируются из замкнутых кривых. Окружность — это замкнутая кривая, образованная при движении точки по плоскости так, что она находится на постоянном расстоянии от своего центра.
Примеры замкнутых кривых:
Простая криваяПростая кривая определяется как кривая, которая не пересекает и не пересекает саму себя. Простая кривая меняет направление, но не пересекает себя при изменении направления. Он может быть открытым и закрытым.
Непростая криваяКривая, пересекающая собственную траекторию, называется сложной кривой.
Забавные факты о изогнутых линиях
- Геометрия — это раздел математики, изучающий различные фигуры и тела, состоящие из прямых и изогнутых линий.
Заключение
В этой статье мы узнали о изогнутых линиях, широко известных как кривые. Мы видели разные типы кривых. Давайте решим несколько задач для лучшего понимания.
Решенные примеры на изогнутых линиях
1. Определите незамкнутые и замкнутые кривые на рисунке ниже.
Решение:
Как мы видим, открытые кривые — это (b), (d) и (f).
Замкнутые кривые — это те, у которых конечные точки соединены вместе, (a), © и (e).
2. Какие из следующих букв обозначают открытые кривые?
O, U, C, D, S
Альтернативные теги: изогнутые линии в алфавитах
Решение:
Буквы, обозначающие две открытые кривые, U, C и S. конечные точки. Однако буквы O и D являются замкнутыми кривыми.
3. Определите простые и сложные кривые.
8, в, и, в, о
Альтернативные теги: изогнутые линии
Решение:
Простые кривые: кривые, которые не пересекаются при изменении направления.
т. е., c, o
Непростые кривые: кривые, которые пересекают собственные пути, т. е. 8, Q, &
4. Определите тип кривой на данном рисунке.
Решение:
Кривая на данном рисунке является открытой кривой.
Практические задачи
1
Буква O является примером _______ .
Непростая замкнутая кривая
Простая незамкнутая кривая
Простая замкнутая кривая
Непростая кривая
Правильный ответ: Простая замкнутая кривая
Это простая замкнутая кривая, потому что она не пересекает сама себя и ее концы сходятся заключить пространство.
2
Определите тип кривой на данном рисунке:
Открытая кривая
Простая незамкнутая кривая
Простая кривая
Непростая кривая
Правильный ответ: Непростая кривая
Кривая на данном рисунке не является простой кривой, так как она пересекает свою собственную траекторию.
3
Какая из следующих кривых является незамкнутой?
Парабола
Окружность
Эллипс
Ничего из вышеперечисленного
Правильный ответ: Парабола
Окружность и эллипс являются замкнутыми кривыми. Парабола, однако, является открытой кривой.
4
Определите тип кривой на данном рисунке:
Изокванта
Трансцендентальная кривая
Простая кривая
Непростая кривая
Правильный ответ: Непростая кривая
Кривая на данном рисунке — непростая кривая.
5
Определите тип кривой на данном рисунке:
Замкнутая
Простая кривая
Открытая кривая
Ничего из вышеперечисленного
Правильный ответ: Открытая кривая
Кривая на данном рисунке является открытой изгиб.
Часто задаваемые вопросы
Определение прямой линии.
Прямая линия может быть определена как линия, очерченная точкой, движущейся в постоянном направлении.
Что такое кривизна линии?
Кривизна показывает, насколько быстро кривая меняет направление в данной точке.
Какая польза от изогнутых линий?
Изогнутые линии обычно используются для графического представления различных типов функций.
Какие буквы английского алфавита изогнуты?
Несколько изогнутых букв английского алфавита: C, S, O и т. д.
Как называется самая высокая или самая низкая часть кривой?
Точка, в которой кривая находится на самом высоком или самом низком уровне, называется вершиной.
Изогнутые линии — значение, примеры, типы и часто задаваемые вопросы
Дата последнего обновления: 29 марта 2023 г. линия не прямая, а изогнутая. В идеале прямая линия имеет нулевую кривизну, тогда как изогнутая линия имеет ненулевую кривизну и является непрерывной и гладкой. Кривые — это выдающиеся фигуры, встречающиеся повсюду вокруг нас.
Вы можете заметить изгибы в искусстве, украшении или вообще предмете, а кривые — это фигуры, которые можно увидеть повсюду вокруг вас. Первоначально линии могли быть изогнутыми или прямыми. В сегодняшнем математическом использовании, для точного различия, кривая — это что-то изогнутое, а линия — это что-то прямое.
Кривые линии часто используются для графического представления функций, поскольку это одна из важнейших тем в области математики.
Дифференциация между изогнутыми линиями и прямыми линиями
Кричная линия | Прямая линия | 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 9044. | Кратчайшая линия, соединяющая любые две точки, называется прямой линией. |
Точки, определяющие кривую, меняют направление от одной точки к другой. | Прямая линия представляет собой последовательность нескольких точек, выровненных в одном направлении. |
Изогнутая линия всегда имеет ненулевую кривизну, которая может быть положительной или отрицательной. | Прямая линия всегда имеет нулевую кривизну. |
Изогнутые линии не двигаются в одном направлении. Направление постоянно меняется от одной точки к другой. | Прямые линии движутся в одном направлении. |
Примеры изогнутых линий
Существует множество примеров изогнутых линий. Наиболее распространенным и ярким примером изогнутых линий являются буквы алфавита C и S. Эти буквы алфавита изогнуты. Напротив, другие буквы, такие как L, N, A, Z и другие, являются подходящими примерами прямых линий, поскольку они не являются кривыми, а являются соединенными сегментами двух или более последовательных линий.
Типы изогнутых линий
Существует множество различных типов изогнутых линий. Тем не менее, есть несколько известных типов изогнутых линий:
1. Открытая кривая
Кривая или кривая называется открытой, если ее конечные точки не пересекаются. В открытой изогнутой линии конечные точки никогда не встречаются.
Парабола — прекрасный пример незамкнутой кривой.
2. Замкнутая кривая
Кривая называется замкнутой, если ее начальная точка совпадает с конечной точкой.
Круг или затмение — прекрасный пример замкнутой кривой.
3. Простая кривая
Простая кривая не пересекает сама себя. Некоторые кривые самопересекающиеся; однако простая кривая не пересекается сама с собой.
4. Алгебраическая кривая
Алгебраическая кривая — это плоская кривая, в которой множество точек размещено на евклидовой плоскости и представлено в виде многочленов.
Степень кривой обозначается степенью многочлена.
Например, C = {(a, b) ∈ R2: P(a, b) = 0}
5. Трансцендентальная кривая
изгиб. Трансцендентная кривая состоит из бесконечного числа точек перегиба и множества точек пересечения, которые будут прямыми. Это не многочлен в точках a и b.
6. Кривая изокванты
Термин «изокванта» представляет собой объединение двух терминов: «изо» означает «равно», а слово «количество» относится к количеству. Таким образом, термин изокванта определяется как кривая выпуклой формы, образованная соединением точек. Кривая изокванты помогает организациям и предприятиям регулировать затраты, чтобы максимизировать производство и прибыль.
Изогнутая линия
«Изогнутая линия» или просто «Кривая» — это непрямая линия. Кривые можно найти повсюду вокруг нас. Кривые можно найти повсюду вокруг нас, будь то искусство, декор или повседневная жизнь.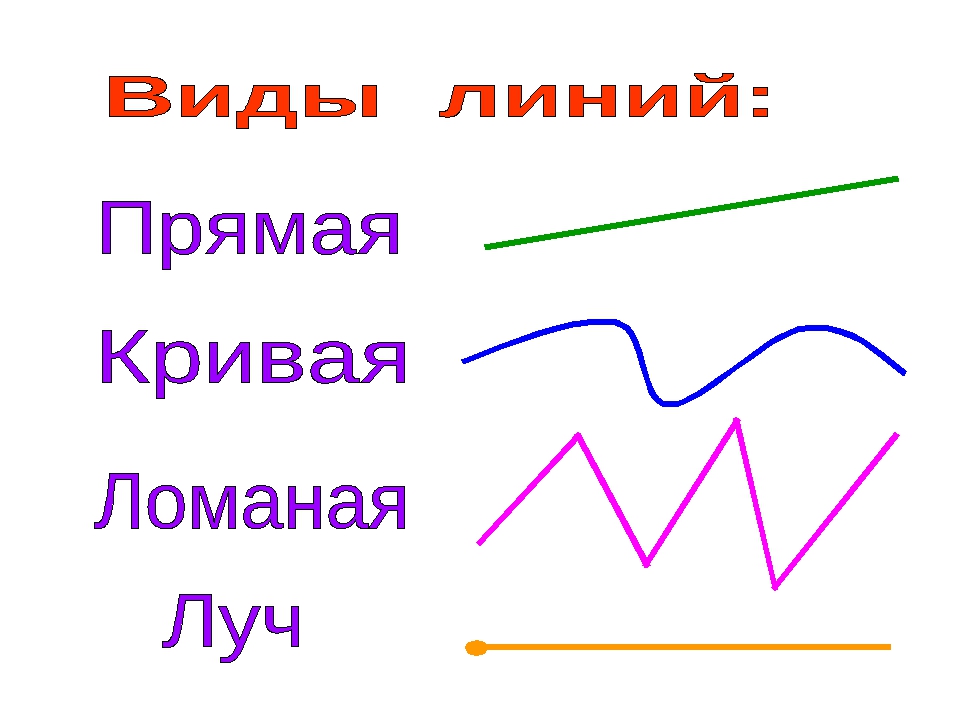
В этом посте мы изучим концепцию изогнутой линии, а также различные типы изогнутых линий и несколько экземпляров.
Что такое кривая линия?
Изогнутая линия — это изогнутая, а не прямая линия. В идеальной ситуации он должен быть плавным и непрерывным. Другими словами, кривая — это набор точек, которые напоминают прямую линию и попадают между двумя точками. Кривизна прямой линии, как известно, равна нулю. В результате мы можем назвать линию изогнутой, если ее кривизна больше нуля. Различные виды изогнутых линий изображены на диаграмме ниже.
(Изображение будет загружено в ближайшее время)
Чем прямая линия отличается от кривой?
Прямая линия
Кривая линия
Кривые линии различных типов
Кривые линии можно разделить на несколько категорий. Вот они:
Простая кривая — это кривая, не пересекающая сама себя. Мы знаем, что открытая кривая имеет два конца, а замкнутая — нет.