Как выглядит кривая: Ломаная и кривая линии

КРИВАЯ СПРОСА • Большая российская энциклопедия

Авторы: Р. М. Нуреев

Рис. 1. Зависимость величины спроса от цены.

Рис. 2. Кривая спроса.

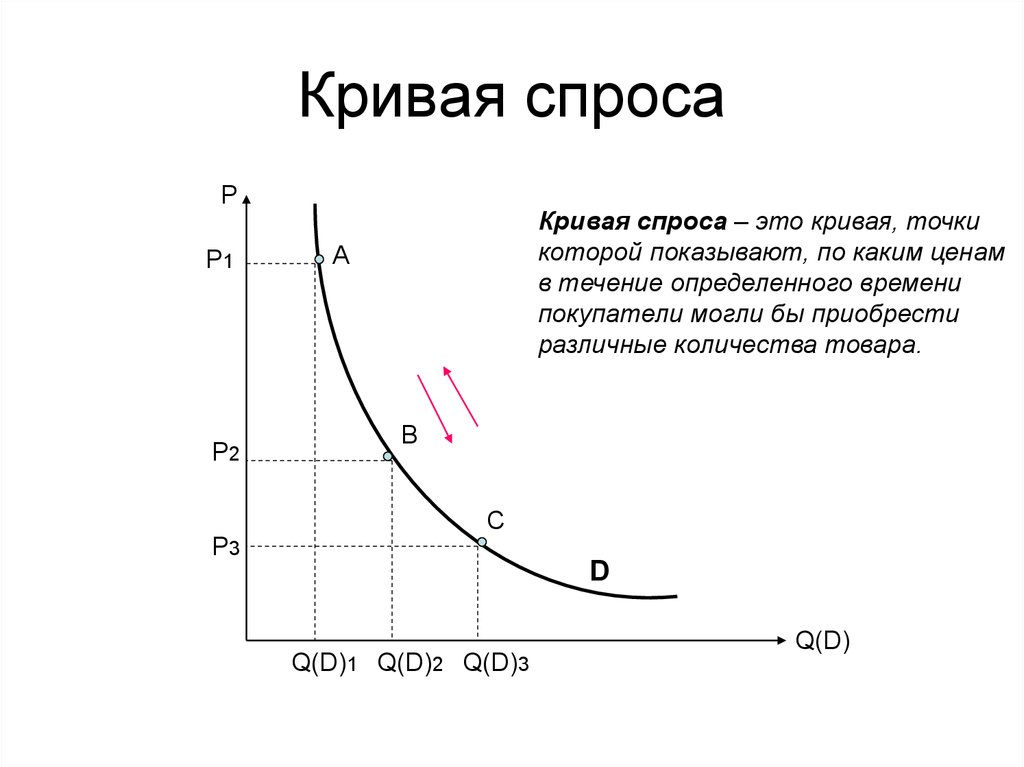
КРИВА́Я СПРО́СА, по­ка­зы­вает, ка­кое ко­ли­че­ст­во эко­но­мич. благ го­то­вы при­об­ре­сти по­ку­па­те­ли по раз­ным це­нам в дан­ный мо­мент вре­ме­ни. Ме­ж­ду це­ной то­ва­ра (P) и ко­ли­че­ст­вом про­дан­но­го (реа­ли­зо­ван­но­го) то­ва­ра (Q) су­ще­ст­ву­ет оп­ре­де­лён­ная связь. Чем ни­же це­на то­ва­ра, тем боль­шее его ко­ли­че­ст­во (при про­чих рав­ных ус­ло­ви­ях) го­то­вы ку­пить по­ку­па­те­ли, тем вы­ше на не­го спрос. Напр., при це­не в 60 долл. по­ку­па­те­ли го­то­вы ку­пить од­ну еди­ни­цу бла­га Х, при це­не в 30 долл. – три еди­ни­цы, при це­не в 20 долл. – че­ты­ре еди­ни­цы и т. д. Об­рат­ная за­ви­си­мость ме­ж­ду це­ной и ве­ли­чи­ной спро­са на­зы­ва­ет­ся за­ко­ном спро­са и мо­жет быть изо­бра­же­на гра­фи­че­ски. Не­за­ви­си­мая пе­ре­мен­ная (це­на) от­кла­ды­ва­ет­ся по вер­ти­каль­ной оси, а за­ви­си­мая (спрос) – по го­ри­зон­таль­ной оси (рис.  1). Изо­бра­жён­ная кри­вая ха­рак­те­ри­зу­ет со­стоя­ние цен и объ­ё­ма по­ку­пок про­дук­ции Х в оп­ре­де­лён­ный мо­мент вре­ме­ни. Она име­ет от­ри­ца­тель­ный на­клон, что сви­де­тель­ст­ву­ет о же­ла­нии по­тре­би­те­лей ку­пить боль­шее ко­ли­че­ст­во благ при мень­шей це­не. В об­щем ви­де: $$Q_D=f(P)$$где $Q_D$ – ве­ли­чи­на спро­са, $P$ – це­на. 

Чем ни­же це­на, тем вы­ше спрос, и на­обо­рот. Из­ме­не­ние цен оз­на­ча­ет дви­же­ние по К. с. (рис. 2).

На спрос влия­ют не толь­ко це­ны, но и иные фак­то­ры: 1) уве­ли­че­ние (или со­кра­ще­ние) до­хо­дов по­тре­би­те­ля, 2) из­ме­не­ние вку­сов и пред­поч­те­ний, 3) це­но­вые и де­фи­цит­ные ожи­да­ния, 4) ко­ле­ба­ние рас­хо­дов на рек­ла­му, 5) из­ме­не­ние цен то­ва­ров-суб­сти­ту­тов и ком­пле­мен­тар­ных то­ва­ров, 6) рост (или умень­ше­ние) ко­ли­че­ст­ва по­ку­па­те­лей и др.

Спрос яв­ля­ет­ся функ­ци­ей всех этих фак­то­ров: $$QD=f(Р, I, Z, W, P_{\mathrm{ sub}}, P_{\mathrm{com}}, N, B),$$где $Q_D$ – спрос; $P$ – це­на; $I$ – до­ход; $Z$ – вку­сы; $W$ – ожи­да­ния; $P_{\mathrm{ sub}}$ – це­на на то­ва­ры-суб­сти­ту­ты; $P_{\mathrm{com}}$ – це­на на ком­пле­мен­тар­ные то­ва­ры; $N$ – ко­ли­че­ст­во по­ку­па­те­лей; $B$ – про­чие фак­то­ры.

Рис. 3. Функция спроса (сдвиг кривой спроса).

Эти фак­то­ры спо­соб­ст­ву­ют сдви­гу К. с. впра­во или вле­во (рис. 3).

Напр., уве­ли­че­ние де­неж­ных до­хо­дов по­тре­би­те­лей (при от­сут­ст­вии ин­фля­ции) оз­на­ча­ет по­вы­ше­ние спро­са, т. е. сдвиг кри­вой $D$ в по­ло­же­ние $D_2$. При этом спрос мо­жет воз­рас­тать бы­ст­рее или мед­лен­нее рос­та до­хо­да в за­ви­си­мо­сти от ка­че­ст­ва то­ва­ра, его мес­та в бюд­же­те по­тре­би­те­ля и ря­да др. свойств. Та­кая си­туа­ция ти­пич­на для боль­шин­ст­ва то­ва­ров за ис­клю­че­ни­ем низ­ко­ка­че­ст­вен­ных. Рост до­хо­дов пе­ре­клю­ча­ет спрос по­тре­би­те­лей на то­ва­ры луч­ше­го ка­че­ст­ва, спрос же на низ­ко­ка­че­ст­вен­ные то­ва­ры сни­жа­ет­ся, т. е. кри­вая пе­ре­ме­ща­ет­ся из по­ло­же­ния $D$ в по­ло­же­ние $D_1$.

Рост цен на то­вар, яв­ляю­щий­ся суб­сти­ту­том дан­но­го то­ва­ра, по­вы­ша­ет на не­го спрос. Напр., рост цен на крас­ные гвоз­ди­ки мо­жет пе­ре­клю­чить часть спро­са на ро­зо­вые (или бе­лые) гвоз­ди­ки, вслед­ст­вие че­го це­на их так­же нач­нёт рас­ти.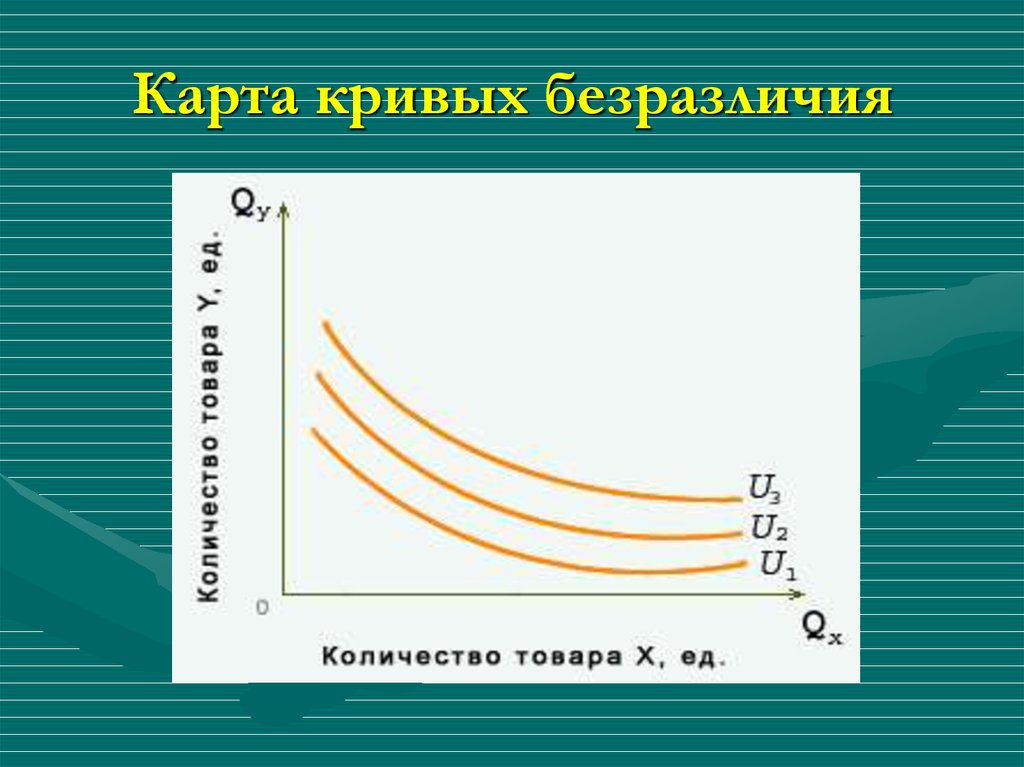 Это по­зво­ля­ет сде­лать вы­вод о том, что ес­ли два то­ва­ра взаи­мо­за­ме­няе­мы (яв­ля­ют­ся то­ва­ра­ми-суб­сти­ту­та­ми), то ме­ж­ду це­ной на один из них и спро­сом на дру­гой су­ще­ст­ву­ет пря­мая связь. Рост цен на крас­ные гвоз­ди­ки при­вёл к рос­ту спро­са на ро­зо­вые гвоз­ди­ки.

Рис. 4. Индивидуальный и совокупный спрос: а – кривые индивидуального спроса; б – совокупный спрос.

На­обо­рот, по­вы­ше­ние цен на взаи­мо­до­пол­няе­мое (ком­пле­мен­тар­ное) бла­го со­кра­ща­ет спрос на не­го. Напр., рост цен на лы­жи при­ве­дёт к умень­ше­нию объ­ё­ма их про­даж, след­ст­ви­ем че­го бу­дет па­де­ние спро­са на лыж­ные кре­п­ле­ния и это за­ста­вит про­дав­цов сни­зить на них це­ны. Т. о., ес­ли два то­ва­ра взаи­мо­до­пол­няе­мы, то ме­ж­ду це­ной на один из них и спро­сом на дру­гой су­ще­ст­ву­ет об­рат­ная связь. Важ­ным фак­то­ром, влияю­щим на спрос, яв­ля­ет­ся чис­ло по­ку­па­те­лей. До­пус­тим, име­ют­ся два по­ку­па­те­ля – Ан­д­ре­ев и Бо­ри­сов, ин­ди­ви­ду­аль­ные функ­ции спро­са ко­то­рых из­вест­ны (рис.  4а). То­гда со­во­куп­ный спрос мо­жет быть оп­ре­де­лён пу­тём сло­же­ния спро­са Ан­д­рее­ва и Бо­ри­со­ва (рис. 4б).

В ре­аль­ной ры­ноч­ной эко­но­ми­ке, ко­гда речь идёт о чис­ле по­ку­па­те­лей, чрез­вы­чай­но важ­но учи­ты­вать их по­ло­воз­ра­ст­ную струк­ту­ру, сред­ний раз­мер се­мей, до­лю лиц пен­си­он­но­го воз­рас­та и т. д. На из­ме­не­ние спро­са влия­ют и вку­сы по­тре­би­те­лей, од­на­ко их влия­ние до­воль­но труд­но оп­ре­де­лить од­но­знач­но. К то­му же один и тот же фак­тор мо­жет ока­зы­вать раз­ное (не­ред­ко пря­мо про­ти­во­по­лож­ное) влия­ние на разл. груп­пы на­се­ле­ния.

Дви­же­ние вдоль К. с. от­ра­жа­ет из­ме­не­ние ве­ли­чи­ны спро­са: чем вы­ше це­на, тем ни­же (при про­чих рав­ных ус­ло­ви­ях) ве­ли­чи­на спро­са, и, на­обо­рот, чем ни­же це­на, тем вы­ше ве­ли­чи­на спро­са (рис. 2). Сдвиг кри­вой спро­са вле­во или впра­во от­ра­жа­ет из­ме­не­ние спро­са: оно про­ис­хо­дит под влия­ни­ем фак­то­ров, оп­ре­де­ляю­щих функ­цию спро­са (рис.  3).

КРИВАЯ ПРЕДЛОЖЕНИЯ • Большая российская энциклопедия

Авторы: Р. М. Нуреев

Рис. 1. Зависимость величины спроса от цены.

КРИВА́Я ПРЕДЛОЖЕ́НИЯ, по­ка­зы­ва­ет, ка­кое ко­ли­че­ст­во эко­но­мич. благ го­то­вы про­дать про­из­во­ди­те­ли по раз­ным це­нам в дан­ный мо­мент вре­ме­ни. Обыч­но за­ви­си­мость ве­ли­чи­ны пред­ло­же­ния $(Q_S)$ от це­ны $(P)$ пря­мая: чем вы­ше це­на, тем боль­шее ко­ли­че­ст­во то­ва­ра $(Q)$ (при про­чих рав­ных ус­ло­ви­ях) го­то­вы пред­ло­жить про­дав­цы. В об­щем ви­де $QS=f(P)$.

Рис. 2. Кривая предложения (изменение величины предложения).

За­ви­си­мость ко­ли­че­ст­ва про­из­ве­дён­ных благ от уров­ня цен мож­но изо­бра­зить гра­фи­че­ски (рис. 1). Кри­вая $S$ ха­рак­те­ри­зу­ет уро­вень цен и объ­ём про­даж бла­га $X$ в оп­ре­де­лён­ный мо­мент вре­ме­ни. Она име­ет по­ло­жи­тель­ный на­клон, что сви­де­тель­ст­ву­ет о же­ла­нии про­из­во­ди­те­ля про­дать боль­шее ко­ли­че­ст­во благ по бо­лее вы­со­кой це­не. Из­ме­не­ние це­ны оз­на­ча­ет дви­же­ние по К. п. (рис. 2).

В дей­ст­ви­тель­но­сти на пред­ло­же­ние бла­га влия­ют не толь­ко це­ны са­мо­го бла­га, но и др. фак­то­ры: це­ны фак­то­ров про­из-ва (ре­сур­сов) $(Pr)$; тех­но­ло­гия $(K)$; це­но­вые и де­фи­цит­ные ожи­да­ния аген­тов ры­ноч­ной эко­но­ми­ки; раз­мер на­ло­гов и суб­си­дий $(T)$; ко­ли­че­ст­во про­дав­цов $(N)$; про­чие фак­то­ры $(B)$. Ве­ли­чи­на пред­ло­же­ния яв­ля­ет­ся функ­ци­ей всех этих фак­то­ров: $$Q_S=f(P, Pr, K, T, N, B).$$

Рис. 3. Функция предложения (сдвиг кривых предложения).

Напр., по­вы­ше­ние цен на фак­то­ры про­из-ва оз­на­ча­ет со­кра­ще­ние пред­ло­же­ния, т. е. сдвиг кри­вой $S$ в по­ло­же­ние $S_1$. В слу­чае по­ни­же­ния цен на фак­то­ры про­из-ва про­изой­дёт уве­ли­че­ние пред­ло­же­ния, что при­ве­дёт к сдви­гу кри­вой $S$ в по­ло­же­ние $S_2$ (рис. 3).

За­тра­ты в мик­ро­эко­но­ми­ке – оцен­ки, от­ра­жаю­щие цен­ность дан­ных фак­то­ров про­из-ва при их наи­луч­шем аль­тер­на­тив­ном ис­поль­зо­ва­нии.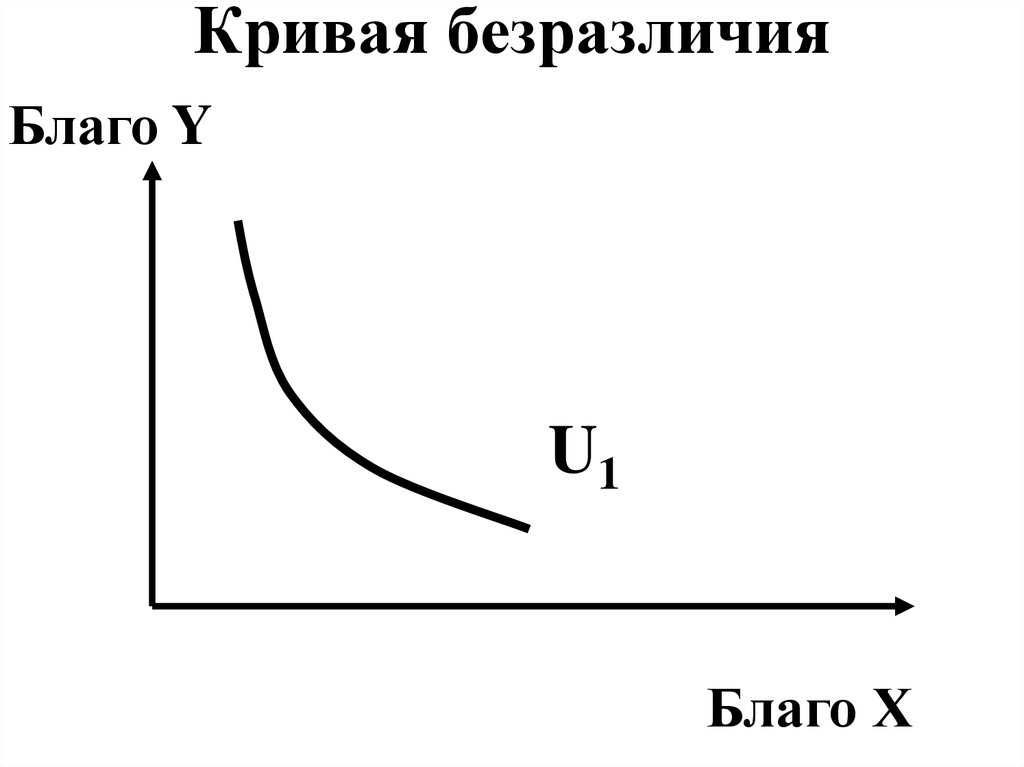 По­это­му функ­ция пред­ло­же­ния от­ра­жа­ет за­тра­ты ре­сур­сов, вла­дель­цам ко­то­рых про­из­во­ди­тель уп­ла­тил по це­не луч­шей аль­тер­на­ти­вы. Ес­ли бы он не смог это­го сде­лать, то вла­дель­цы ре­сур­сов ис­поль­зо­ва­ли бы их в про­из-ве др. то­ва­ров. Дви­же­ние вдоль К. п. по­ка­зы­ва­ет из­ме­не­ние ве­ли­чи­ны пред­ло­же­ния: чем вы­ше це­на, тем вы­ше (при про­чих рав­ных ус­ло­ви­ях) ве­ли­чи­на пред­ло­же­ния и, на­обо­рот, чем ни­же це­на, тем ни­же ве­ли­чи­на пред­ло­же­ния. Сдвиг К. п. вле­во или впра­во от­ра­жа­ет из­ме­не­ние пред­ло­же­ния: оно про­ис­хо­дит под влия­ни­ем фак­то­ров, оп­ре­де­ляю­щих функ­цию пред­ло­же­ния (рис. 3).

Рис. 4. Изменение цен и объёма предложения в кратчайший (а), короткий (б) и длительный (в) периоды.

На функ­цию пред­ло­же­ния влия­ет фак­тор вре­ме­ни. Обыч­но раз­ли­ча­ют крат­чай­ший, крат­ко­сроч­ный (ко­рот­кий) и дол­го­сроч­ный (дли­тель­ный) ры­ноч­ные пе­рио­ды. В крат­чай­шем пе­рио­де все фак­то­ры про­из-ва по­сто­ян­ны, в крат­ко­сроч­ном не­ко­то­рые фак­то­ры (сы­рьё, ра­бо­чая си­ла и др. ) яв­ля­ют­ся пе­ре­мен­ны­ми, в дол­го­сроч­ном – все фак­то­ры пе­ре­мен­ны (вклю­чая про­из­водств. мощ­но­сти, чис­ло фирм в от­рас­ли и т. д.). В ус­ло­ви­ях крат­чай­ше­го ры­ноч­но­го пе­рио­да по­вы­ше­ние (по­ни­же­ние) спро­са при­во­дит к по­вы­ше­нию (по­ни­же­нию) цен, но не от­ра­жа­ет­ся на ве­ли­чи­не пред­ло­же­ния (рис. 4а). В ко­рот­ком пе­рио­де по­вы­ше­ние спро­са обу­слов­ли­ва­ет не толь­ко рост цен, но и уве­ли­че­ние объ­ё­ма про­из-ва, т. к. фир­мы ус­пе­ва­ют из­ме­нить не­ко­то­рые фак­то­ры про­из-ва в со­от­вет­ст­вии со спро­сом (рис. 4б). В ус­ло­ви­ях дли­тель­но­го пе­рио­да уве­ли­че­ние спро­са при­водит к зна­чит. рос­ту пред­ло­же­ния при по­сто­ян­ных це­нах или не­су­ще­ст­вен­ном по­вы­ше­нии цен (рис. 4в). 

Что такое кривая? Определение, типы, формы, примеры, факты

Что такое кривая?

Кривая представляет собой непрерывную и плавную плавную линию без резких поворотов. Один из способов распознать его состоит в том, что он изгибается и меняет свое направление хотя бы один раз.

Родственные игры

Что такое изогнутые формы?

Форма, состоящая из кривых, называется изогнутой формой. Изогнутая форма может быть двухмерной, например, круги, эллипсы, параболы и дуги. Изогнутые формы также могут быть трехмерными фигурами, такими как сферы, конусы и цилиндры.

Какие существуют типы кривых?

Вот различные типы математических кривых:

1. Восходящая кривая: Кривая, которая поворачивается в восходящем направлении, называется восходящей кривой. Он также известен как вогнутая вверх или выпуклая вниз кривая.

2. Нисходящая кривая: Кривая, которая поворачивает в нисходящем направлении, называется нисходящей кривой, поскольку она изогнута вниз. Она также известна как вогнутая вниз или выпуклая вверх кривая.

  3. Открытая кривая: Открытая кривая не заключает в себе какую-либо область и имеет две конечные точки. Некоторые из незамкнутых кривых представлены на рисунке ниже:

   4. Замкнутая кривая: Замкнутая кривая не имеет конечных точек и охватывает площадь (или область). Он образуется путем соединения конечных точек открытой кривой вместе. Окружности и эллипсы формируются из замкнутых кривых.

   5. Простая кривая: Простая кривая меняет направление, но не пересекается при изменении направления. Он может быть открытым и закрытым.

  6. Непростые кривые: Кривая, пересекающая собственную траекторию, называется сложной кривой.

Изгибы вокруг нас!

• Гоночная трасса: трасса на рисунке выглядит как замкнутая кривая.
• Дороги: Дороги на холмах и горах извилистые.

Факты о кривых

Вот несколько интересных фактов о кривых:

•  Кривая состоит из множества небольших отрезков, соединенных от конца к концу. Если вы посмотрите на него очень внимательно, вы сможете увидеть линии!
• Внутренняя часть замкнутой кривой называется ее внутренней частью.
• Внешняя сторона замкнутой кривой называется ее внешней.
• Открытые кривые, такие как параболы и спирали, имеют бесконечную длину.

Решенные примеры

1. Что такое кривая?

Решение: Кривая — это непрерывная плавная линия, которая изгибается или меняет направление хотя бы один раз.

2. Является ли буква U восходящей кривой?

Решение: Да, буква U — восходящая кривая, потому что она изгибается вверх.

3. Является ли эллипс замкнутой или открытой кривой?

Решение: Эллипс — это замкнутая кривая, потому что его концы сходятся и заключают в себе пространство.

4. Является ли форма числа 8 простой или сложной кривой?

Решение: Это непростая кривая, потому что она пересекает свой путь.

5. Ваши друзья играют внутри закрытого круглого поля, а вы стоите за пределами поля.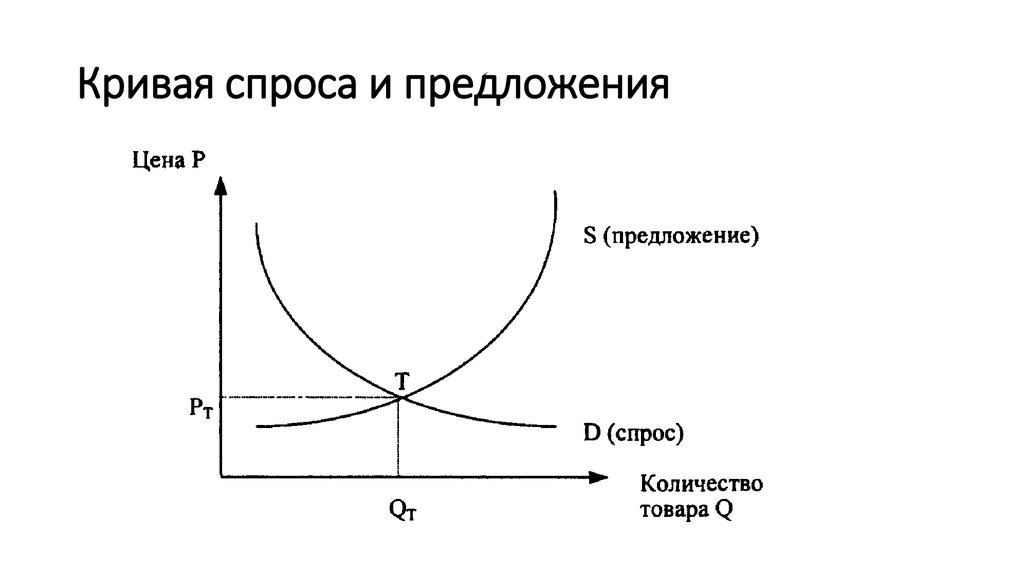 Кто находится внутри изогнутой границы детской площадки? Решение: Друзья находятся внутри, потому что они внутри замкнутой кривой, которая является границей игровой площадки.

Практические задачи

1

Что из перечисленного не является изогнутой формой?

Конус

Цилиндр

Прямоугольник

Сфера

Правильный ответ: Прямоугольник
Прямоугольник не имеет изогнутых сторон.

2

Какой из следующих типов кривых соответствует букве С?

Закрытый

Простой

Вверх

Непростая

Правильный ответ: Простая
Это простая кривая, потому что она не пересекает сама себя.

3

Какие из следующих типов кривых имеют форму нуля?

Непростая

Открытая вверх

Простая открытая

Простая закрытая

Правильный ответ: Простая замкнутая
Это простая замкнутая кривая, потому что она не пересекает сама себя и ее концы соединяются, ограничивая пространство.

4

Какая из следующих кривых является замкнутой?

Парабола

Гипербола

Эллипс

Дуга

Правильный ответ: Эллипс
Эллипс представляет собой замкнутую кривую, потому что его концы соединяются, ограничивая пространство.

5

Вы стоите на спортивной площадке, граница которой имеет форму эллипса. Ваш друг стоит за границей поля. Что из следующего верно?

Вы находитесь снаружи изогнутой границы

Вы и ваш друг оба находитесь снаружи изогнутой границы

Вы находитесь внутри изогнутой границы

Нет внутренней и внешней сторон, так как форма представляет собой эллипс

Правильный ответ: Вы находитесь на внутренняя часть изогнутой границы
Эллипс представляет собой замкнутую кривую, и вы стоите внутри замкнутого пространства.

Часто задаваемые вопросы

Является ли многоугольник кривой?

Нет. Кривая состоит из кривых линий и может быть или не быть замкнутой, тогда как многоугольник представляет собой замкнутую фигуру, состоящую из прямых линий.

Какие типы кривых вы видите на графиках?

Типы графических кривых включают следующие:

• График параболы
• График гиперболы
• График нисходящей кривой
• График восходящей кривой
• Круговая диаграмма
• График эллипса

Как называется самая высокая или самая низкая часть кривой?

Точка, в которой кривая является самой высокой или самой низкой, называется вершиной.

В чем основное отличие кривой от прямой?

В то время как обычная прямая линия непрерывно движется в линейном направлении, кривая может поворачиваться вверх, вниз, внутрь или наружу.

В чем разница между простой и сложной кривой?

Как простые, так и непростые кривые могут быть открытыми или замкнутыми, но простая кривая не пересекает сама себя, в то время как непростая кривая пересекает свой собственный путь хотя бы один раз.

Кривая — это не просто линия, она может также составлять фигуру или трехмерную фигуру. Полезно знать различные типы кривых.

Как работает оценка по кривой?

Что такое профилирование по кривой и как оно работает? Профессор колледжа объясняет, как преподаватели выставляют оценки и что это значит для студентов.

к

Женевьева Карлтон, доктор философии.

Стрелка вправо

Писатель

Удостоенный наград историк и писатель Женевьева Карлтон, доктор философии, опубликовала несколько научных статей и книгу в издательстве Чикагского университета. В настоящее время она работает писателем и консультантом. Она имеет докторскую степень. в истории с северо-запада…

Чек

Отредактировано

Ханна Муниз

Стрелка вправо

Редактор и писатель

Ханна Муниз — старший редактор BestColleges и Accredited Schools Online, специализирующаяся на планировании поступления в колледж, подготовке к экзаменам, студенческой жизни и аккредитации. Ранее работала внештатным писателем, писала статьи по SAT/ACT, высшему обра…

Опубликовано 6 апреля 2022 г.

Узнайте больше о нашем процессе редактирования

3 минуты чтения

Поделиться этой статьей

---

• Выставление оценок по кривой означает корректировку оценок учащихся после теста или задания.
• Как правило, кривая повышает средний балл и индивидуальные баллы учащихся.
• Профессора используют разные методы для кривых оценок, а некоторые вообще избегают кривых.
• В начале семестра студенты могут спросить, как их преподаватели планируют выставлять оценки.

---

После моего первого промежуточного семестра в колледже — по неорганической химии — профессор объявил, что средний балл по классу составляет 40%. Студенты вокруг меня застонали. Затем один поднял руку и спросил: «Вы оцениваете кривую?»

Еще до колледжа я слышал о криволинейных оценках. Однако только в этот момент я понял, какое огромное значение кривая оценок может иметь для моей оценки.

BestColleges.com — это сайт, поддерживаемый рекламой. Рекомендуемые или доверенные партнерские программы, а также все результаты поиска, поиска или подбора школ предназначены для школ, которые выплачивают нам компенсацию. Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.

Готов начать свое путешествие?

«Нет, — ответил профессор, — я не оцениваю по кривой». Больше стонов.

Но что такое кривая классификации? И как работает градация по кривой? Концепция криволинейного оценивания вызывает сильные отклики у студентов и преподавателей — и не всегда по одним и тем же причинам.

Что такое оценка на кривой?

Оценка по кривой означает корректировку оценок учащихся после задания.

Идея «кривой» восходит к кривой нормального распределения. В типичном классе профессора могут ожидать, что большинство оценок будет близко к среднему по классу, с меньшим количеством оценок A и неудовлетворительных оценок. Как правило, профессора стремятся получить среднюю оценку в диапазоне от C до B, в зависимости от класса.

Если преподаватель замечает, что средний балл был значительно ниже — например, средний балл не сдан — он может поставить оценку по кривой. Это означает изменение оценки каждого учащегося для повышения среднего.

В более редких случаях профессора могут скорректировать кривую, чтобы снизить среднее значение. Однако в большинстве случаев криволинейная градация повысит средний балл по классу.

Изогнутая оценка по некоторым предметам встречается чаще, чем по другим. На уроках естествознания, инженерии и математики чаще используется кривая. В классах изящных искусств и гуманитарных наук кривая используется редко. А уроки социальных наук находятся где-то посередине.

Как профессора используют кривую оценки

Не существует единственного способа реализации криволинейного профилирования. Вместо этого профессора используют несколько разных подходов.

Профессора могут повысить средний балл на заданную величину. Например, если бы средний балл по классу составлял 50 %, профессор мог бы поднять его до 75 %, фактически дав каждому студенту дополнительные 25 баллов из 100.

Точно так же, если бы средняя оценка была D, профессора могли бы изменить все оценки D на C. Таким образом, каждый учащийся получит полную буквенную оценку выше, чем его первоначальная оценка. Однако преподаватели иногда избегают этого подхода, поскольку это может означать, что учащиеся, находящиеся на вершине кривой, зарабатывают более 100% за задание.

Другой распространенный подход заключается в получении наивысшего балла на экзамене и присвоении ему 100%. Таким образом, если студент, набравший наибольшее количество баллов, набрал 85 %, профессор повысил бы каждую оценку на 15 %.

Однако этот подход не работает, если в классе есть один ученик, который стабильно получает высокие оценки.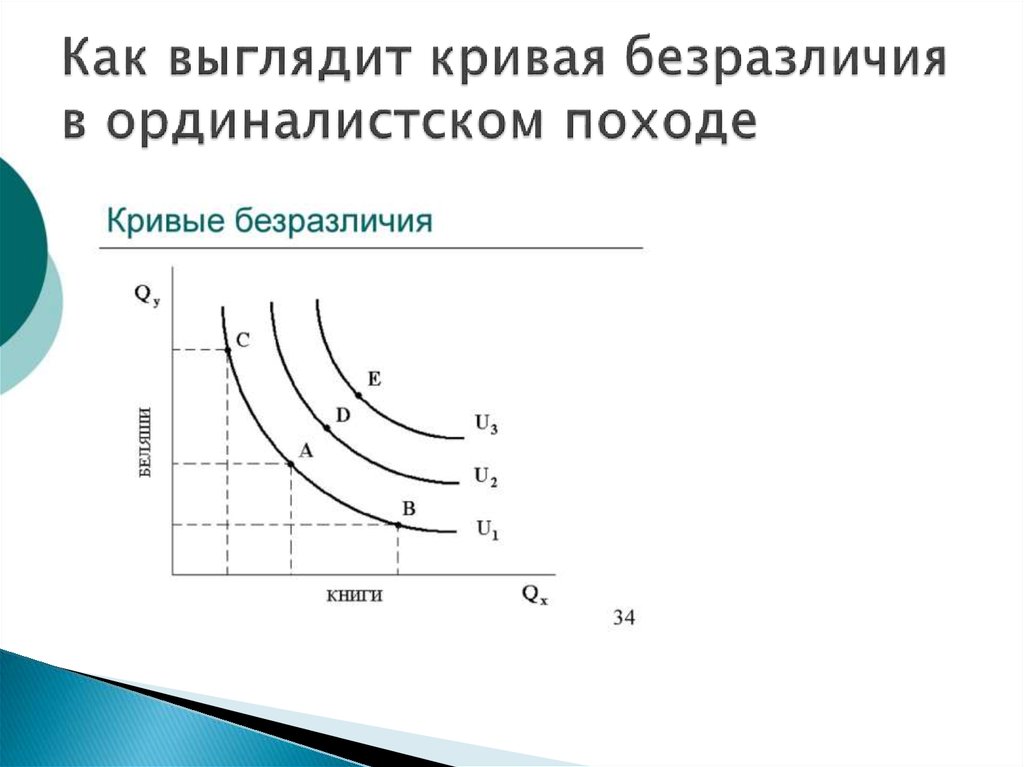 Например, предположим, что учащийся получил 96%, но средний балл по классу составил 60%. В этом случае добавление 4% не будет иметь большого значения.

Профессора используют и другие подходы. Если все учащиеся пропустили один и тот же вопрос на экзамене, профессор может исключить этот вопрос из итоговой оценки, чтобы повысить оценку. Или они могут дать учащимся возможность повторить вопросы, которые они пропустили, чтобы частично повысить свои оценки.

Наконец, старый стандарт дополнительных баллов может помочь поднять средний балл по классу.

Когда кривая классификации не работает

Градация с помощью кривой не всегда работает.

В небольших классах распределение оценок может быть достаточно случайным, поэтому кривая оценок искажает успеваемость учащихся. Большинство профессоров избегают кривых оценок в классах менее 30-40 студентов.

Классы старших классов или выпускников также могут не соответствовать стандартной кривой оценок.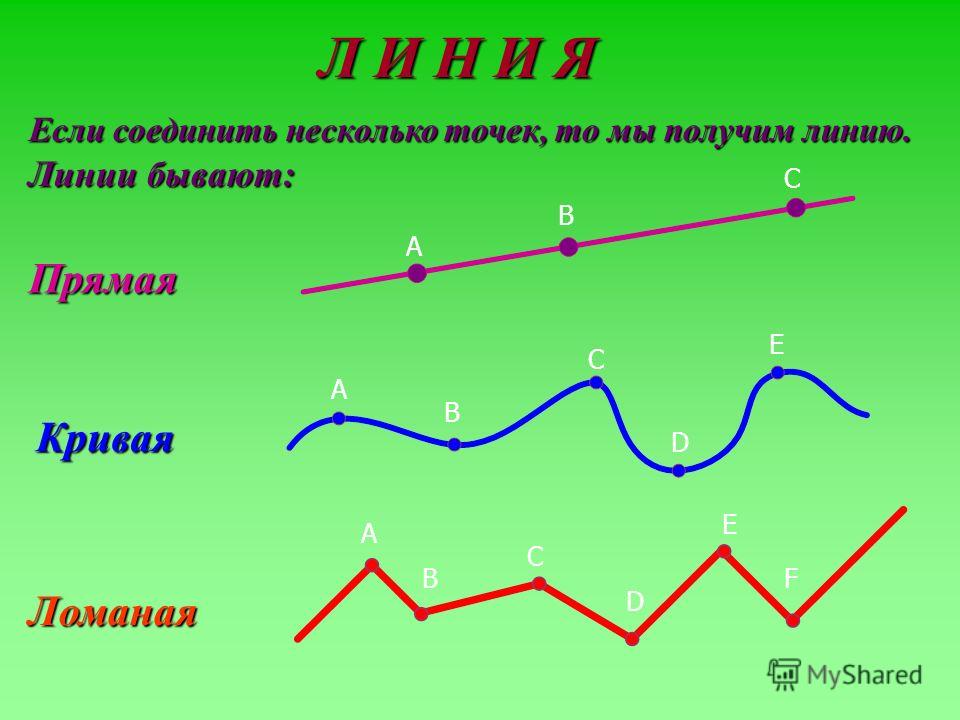

Пожилые люди, проходящие курсы по своей специальности, обычно получают более высокие оценки, чем студенты, плохо знакомые с предметом. Изгиб этих курсов может означать снижение оценок учащихся, демонстрирующих мастерство материала, чего большинство преподавателей стараются избегать.

Кривые оценок также могут создавать напряженность в классе. Если вы оцениваетесь по сравнению со своими сверстниками, вы можете начать обижаться на человека, набравшего 98% на экзаменах за то, что он «сломал кривую».

Точно так же, если вы идете на тест, предполагая, что только один человек в вашем классе получит пятерку из-за кривой профессора, у вас может быть меньше стимула к учебе.

Что означает оценка с помощью кривой для учащихся

Некоторые профессора никогда не ставят кривую оценок. И это может означать шокирующе низкие средние оценки на экзаменах. Другие профессора объявляют о своей политике в начале семестра, перечисляя, как они планируют изменять оценки в учебной программе.

А некоторые профессора решают изменить оценки только в том случае, если их студенты проваливают тест.

Как профессору, мне иногда трудно понять, будет ли тот или иной экзамен легким или сложным для студентов. Если среднее значение значительно ниже, чем ожидал профессор, он может применить кривую только к этому заданию.

Что означает для учащихся кривая оценок? В целом учащимся нравится кривая оценка, потому что она обычно означает более высокую оценку.

Но изогнутая градация также может показаться произвольной. Вместо того, чтобы получать баллы на основе ваших ответов, ваша оценка зависит от математической формулы, применяемой вашим преподавателем.

Должны ли оценки отражать вашу успеваемость по сравнению с другими в классе? Или они должны отражать ваше владение материалом? Даже профессора расходятся во мнениях по этому поводу.

Хотя я до сих пор помню боль моего профессора химии, когда он не менял оценки, я никогда не использовал кривую оценок, будучи профессором истории. Вместо этого, если я замечал, что у каждого ученика возникают проблемы с определенным вопросом, я более щедро оценивал их ответы.

Я также стремился представить итоговые оценки, которые отражали бы усвоение материала студентом в течение семестра, а не за одно задание.

В конце концов, каждый профессор решает, ставить ли оценки по кривой, и у студентов мало возможностей изменить философию оценок своего преподавателя. Криволинейные и некривые оценки подчеркивают произвольный характер классификации.

---

Характерное изображение: SDI Productions / E+ / Getty Images

Узнайте больше о ресурсах колледжа

Посмотреть все

BestColleges.com — это сайт, поддерживаемый рекламой. Рекомендуемые или доверенные партнерские программы, а также все результаты поиска, поиска или подбора школ предназначены для школ, которые выплачивают нам компенсацию. Эта компенсация не влияет на рейтинги наших школ, справочники ресурсов или другую независимую от редакции информацию, опубликованную на этом сайте.