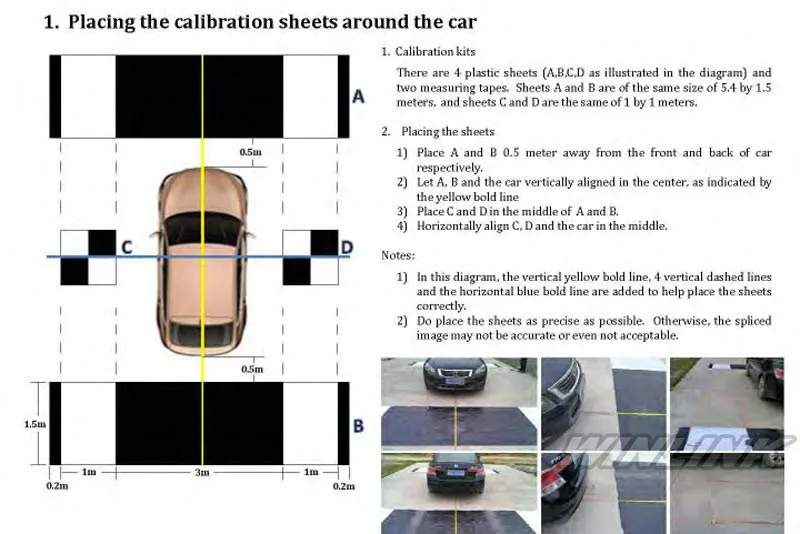
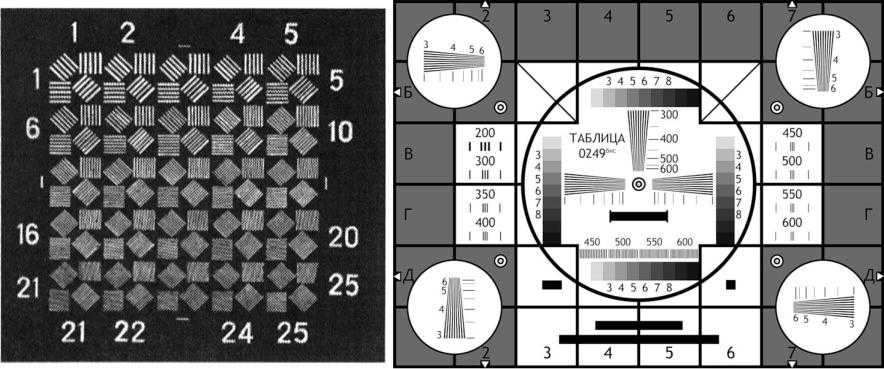
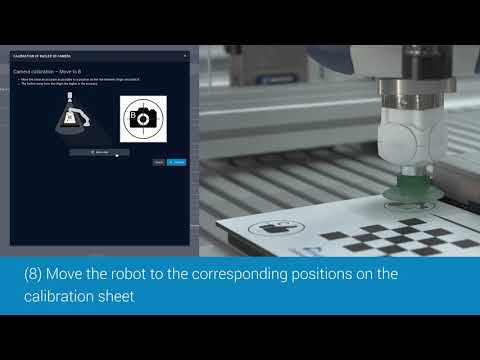
Калибровка камеры · Clover
Калибровка камеры может значительно повысить качество работы модулей, связанным с компьютерным зрением: распознавание ArUco-маркеров и Optical Flow.
При калибровке камеры подбираются параметры, наиболее хорошо описывающие конкретный установленный объектив. Данные параметры включают в себя фокусные расстояния, расположение точки principal point (которое зависит от того, насколько ровно по центру установлен объектив), коэффициенты дисторсии D. Подробнее про использующуюся модель искажений камеры можно прочитать в документации OpenCV.
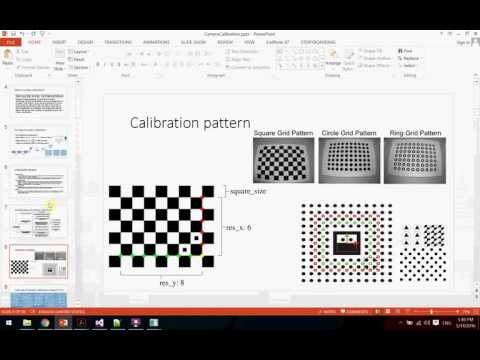
Существует несколько инструментов, которые позволяют откалибровать камеру и прописать вычисленные параметры в систему. Обычно, они используют калибровочные изображения: «шахматные доски» (Chessboard), а так же комбинации шахматной доски и сетки ArUco-маркеров (ChArUco).
Основной туториал: http://wiki.ros.org/camera_calibration/Tutorials/MonocularCalibration.
Для калибровки камеры с использованием ROS-пакета camera_calibration необходим компьютер с установленным ОС GNU/Linux и ROS Noetic.
Используя Терминал, установите на компьютер пакет
camera_calibration:sudo apt-get install ros-noetic-camera-calibration
Скачайте калибровочную доску –
chessboard.pdf. Распечатайте доску на принтере либо выведите ее на экран компьютера.Подключитесь к Wi-Fi Клевера.
Запустите калибровку (на компьютере):
ROS_MASTER_URI=http://192.168.11.1:11311 rosrun camera_calibration cameracalibrator.py --size 6x8 --square 0.108 image:=/main_camera/image_raw camera:=/main_camera
Вместо значения 0.108 укажите реальный размер квадрата на распечатанной доске или на экране (в метрах). Например, значение 0.03 будет соответствовать 3 см.
Когда программа для калибровки запустится, начните перемещать дрон таким образом, чтобы калибровочная доска попадала в кадр под разными углами.
- Перемещайте калибровочную доску в левый, правый, верхний и нижний торец кадра.
- Вращайте калибровочную доску вокруг всех 3-х осей.
- Отдаляйте и приближайте камеру к калибровочной доске.
- Перемещайте калибровочную доску в левый, правый, верхний и нижний торец кадра.
Нажмите кнопку CALIBRATE, когда она станет активной. Процесс вычисления параметров калибровки займет несколько минут.
Когда калибровка завершится, в терминале вы увидите полученные параметры. В окне отобразится изображение с выправленными искажениями. При успешной калибровке все реальные прямые линии должны остаться прямыми на полученном изображении.
Нажмите COMMIT, чтобы сохранить полученные параметры калибровки. Результат будет записан в файл калибровки основной камеры Клевера:
/home/pi/catkin_ws/src/clover/clover/camera_info/fisheye_cam.yaml
Калибровка камер — презентация онлайн
Похожие презентации:
Классический фотоальбом
Увековечение имени А. С. Пушкина в названиях городов, улиц, площадей, скверов
Проект по технологии. Подставка под горячее
Подставка под горячее
Гармоничные сочетания цветов
Иероним Босх
Внушение народу определённых чувств и мыслей средствами искусства
Кинофильмы и мультфильмы о Снегурочке
Стиль рококо в архитектуре
История русского кинематографа
Основы композиции. Правила и ошибки композиции
1. Калибровка камер
Нижникова В. С.2. Определение
Калибровка камеры — это задача получения внутренних и внешнихпараметров камеры по имеющимся фотографиям или видео, отснятыми
ею.
Калибровка камеры часто используется на начальном этапе решения
многих задач компьютерного зрения и в особенности дополненной
реальности. Кроме того, калибровка камеры помогает исправлять
дисторсию на фотографиях и видео
2
3. Дисторсии
distortio — искривление, коэффициент линейного увеличения изменяется пополю зрения объектива.
При этом нарушается геометрическое подобие между объектом и его изображением
Нулевая
дисторсия
Положительная
дисторсия
“подушка”
Отрицательная
дисторсия
“бочка”
3
Радиальные искажения возникают
в
Тангенциальные искажения возникают
в целом.

результате формы объектива
как результат
сборки камеры
4
5. Радиальные искажения
Линзы реальных камер часто искажают расположении пикселейвблизи краев фотоприёмника. Это выпуклое
явление появляется
в результате эффекта «бочка» или «рыбий глаз»
5
6. Тангенциальные искажения
возникают ввозникающих
плоскости
результате производственных
от не точно параллельно
изображения
дефектов,
установленных линз к
6
Существует ещё множество других видов искажений, которые
возникают в системах визуализации, но они,
как правило,
имеют малый эффект по сравнению с радиальным и
тангенциальным искажениями. С вязи
с эти данные (другие)
искажения далее рассматриваться не будут.
7
OpenCV предоставляет несколько алгоритмов для вычисления
внутренних параметров. Калибровка выполняется
при помощи
функции
cvCalibrateCamera2().
В данной
функции
метод калибровки предоставленной
камеры
заключаетсяв формировании структуры, содержащеймножество
индивидуальныхи идентифицируемых
точек.
 При рассмотрении
При рассмотренииданной структуры под разными
углами можно в последующем
вычислить (относительное) положение и ориентацию камеры во
время каждогополучаемого
кадра, а также внутренние
параметры камеры.Для получения набора представлений, необходимо
поворачивать
и смещать
объект,поэтому вначале необходимо
рассмотретьэти процессы
более подробно.
8
Для каждогокадра, содержащего
определенный
описать позу
данного объекта по отношению к
условиях вращения и смещения.
объект, существует возможность
системе координат камеры в
9
10. Что может быть калибровочным объектом
Калибровочным объектом в OpenCVявляется
плоская сетка с чередующимися
черными
и белыми квадратами, которую
обычно называют «шахматной
доской» (хотя
и не обязательно иметь восемь квадратов
или даже
равное количество квадратов в
каждом из направлений).
В принципе, любой достаточно
характерный
объект может быть
использован в качестве калибровочного
объекта,
однако, практичней всего
использовать
такой шаблон, как шахматная
доска.

10
11. Калибровка «Шахматной доской» в opencv
Изображениешахматной доски (или
изображение
человека, держащего
шахматную доску) можно использовать
в функции OpenCV cvFindChessboardCorners() для поиска
углов шахматной
доски
11
12. Субпиксельные углы
Углы, возвращаемые cvFindChessboardCorners()являются
приблизительными. На практике это означает, что положения точны
только в пределах
устройства обработки изображения, т.е. с
точностью до пикселя.
Функция разделения должна быть
использована для
вычисления точного расположения углов (после
получения приблизительногоположения и исходного изображения) с
точностью до субпикселя.
Для этого
необходимо использовать
функцию
cvFindCornerSubPix() т.к. углы
шахматной доски это всего на
всего частный случай более общего случая углов Harris; просто
углы шахматной доски проще найти и отследить. Пренебрежение
субписельным уточнением может
привести
к существенным
ошибкам в калибровке.
12
13. Гомография
В компьютерном зрении плоская гомография определяется какпроективное отображение из одной плоскости в другую.
Таким образом,
отображение
точек на двумерную
поверхность фотоприёмника камеры является
примером
гомографии.
плоскую
плоской
13
14. Математика преобразований
1415. Количество неизвестных
1изображение6 неизвестных
Вращение 3 угла
Перемещение 3 смещения
Это нормально, т.к. известно, что плоский объект (например, шахматная
доска) дает восемь уравнений т.е. отображение
квадрата
в
четырехугольник
можно описать четырьмя (x, y) точками
Каждый новый
шести новых
кадр
дает
восемь уравнений
внешних
неизвестных
за
счет
1 кадр
8 уравнений
15
Теперь пусть имеется N углов и K изображений
шахматной
доски (в различных позициях).
Как много представлений и
углов необходимо иметь для преодоления ограничений всех
ранее представленных параметров?
K изображений
шахматной доски обеспечивает
2NK
ограничений
(коэффициент 2 используется в связи с тем,
что каждая точка изображения
имеет две координаты (x, y)
Не принимая во внимание параметры искажения, имеется 4
внутренних параметра и 6K внешних
параметра (т.
 к.
к.необходимо найти 6 параметров положения шахматной доски
каждогопредставления K)
Для решения
также необходимо,
чтобы
(или, что эквивалентно
(N – 3)K ≥ 2)
2NK ≥
6K +
для
4
16
17. Ну и как считать?
Матрицагомографии H связывает положения точек плоскостиисходного изображения с точками плоскости конечного изображения
(какправило,
плоскости фотоприёмника) следующими
уравнениями
Существует возможность
вычислить H,
ничего не зная
о встроенных параметрах
камеры.На самом деле, вычисление
множества гомографий из нескольких
представлений это метод, которыйиспользует
OpenCV для вычисления внутренних параметров
камеры.
cvFindHomography()
Необходимо как минимум
четыре точки, чтобы найти H,
однако, всегда имеется возможность
предоставить
гораздо большее
количество точек
(при
условии рассмотрения шахматной доски размера большего, чем 3х3).
Использование большего количества точек гораздо выгоднее, т.
 к. всегда имеется шум
к. всегда имеется шум17
и иные
несоответствия, влияниекоторых необходимо сводить к минимуму.
18. А как параметры камеры вычислить?
Функциякалибровки
После получения углов от нескольких изображений
можно
вызывать
функцию cvCalibrateCamera2().
Эта функция
производит математические вычисления и предоставляет необходимую
информацию.
В
частности, в
результате будет
получена
матрицавнутренних параметров камеры,
коэффициенты искажения,
вектор вращения
и вектор
Кому интересна математика
приближенных вычислений
перемещения
Learning openCV
18
19. Не все так просто
Для того,необходимо
чтобы
воспользоваться алгоритмом в cvCalibrateCamera2().
Воспользоваться функцией cvUndistort2(), которая выполняет все
необходимое
для одного кадра, или парой функций
cvInitUndistortMap() и cvRemap(), которые позволяют обрабатывать
некоторые вещи
в видео немногоболее эффективно или ситуации,
в которых имеется множество изображений
от одной и той же
камеры
Строится карта,
которая потом
используется для
удаления искажений
19
20.
 Стереокалибровка и стереозрение1. Математически удаляются радиальные и тангенциальные
Стереокалибровка и стереозрение1. Математически удаляются радиальные и тангенциальныеискажения объектива . На выходе будет получено
неискаженное
изображение.
2. Настраиваются углы
и расстояния между камерами, так
называемый процесс уточнения. На выходе будут получены
выровненные
по строкам
3.
4. Зная
геометрическое расположение камер, развертывается
карта несоответствий за счет
триангуляции. Это так называемое
перепроецирование, в результате чего получается карта
глубины.
Ищутся особенностина представлениях левой и правой камер
(процесс
сопоставления). На выходе будет получена карта
несоответствий, где различия
будут соответствовать различиям в xкоординате плоскости изображения
для одного и тогоже
рассматриваемого признака левой и правой камер.
20
21. Как можно получить глубину?
2122. Горизонтально ровно и фронтально параллельно
2223. Эпиполярная геометрия
2 камеры обскурыКерновые точки – центр проекции
изображения другой камеры
Керновая плоскость: p el er
Эпиполярные линии: p el, р er
pl – точка материального мира
pr- проекция p на плоскость камеры 1
pr – проекция р на плоскость камеры 2
О1 и Or – центры проекций
el и er – керновые точки
23
Зачем предыдущий слайд?
Каждая трехмерная точка представлений
камер располагается на
эпиполярной плоскости, которая пересекает
каждое изображение
по
эпиполярной
линии.
Учитывая
особенностиодного
изображения, соответствующее
представление другого изображения
должно лежать вдоль соответствующей
эпиполярной
линии. Это известно,
как эпиполярное
ограничение.
Двумерный поиск становится одномерным
24
25. Еще 2 матрицы
Существенная Е — перемещение и смещение камер в пространствеФундаментальная F — как Е + информацию
относящихся
к двум
камерам
в
о внутренних параметрах,
пиксельных координатах
25
26. Как в OpenCV
Аалогично с калибровкой одной камерыпредоставляем изображения шахматной доски, снятые
правой и левой камерами
находим углы досок ()
cvFindFundamentalMat()
cvComputeCorrespondEpilines()
cvStereoCalibrate() — аналогично cvCalibrateCamera2(), но
ищется одна матрица смещений и перемещений
Применяем алгоритм стереоисправлений (Hartley или
Bouguet)
Вычисляем карты исправлений cvInitUndistortRectifyMap() для
левой и правой камер
Исправляем новые изображения для камер cvRemap()
26
27
28.
 Карты глубины трехмерного перепроецированияКарты глубинытрехмерного перепроецирования
Карты глубины трехмерного перепроецированияКарты глубинытрехмерного перепроецированияcvReprojectImageTo3D()
28
29. Фотограмметрическая калибровка
Калибровка камер производится наблюдением за калибровочнымобъектом, геометрия которого в 3D пространстве известна с большей
точностью.
Калибровка может быть сделана очень рационально. Калибровочный
объект обычно состоит из 2 или 3 плоскостей ортогональных друг другу.
Иногда плоскости подвергаются точно заданному преобразованию. Эти
подходы нуждаются в дорогих калибровочных аппаратах и их
скрупулезной установке.
29
30. по снимкам пространственного тест-объекта
3031. Установка калибровочных маркеров
3132. Съемка стенда
3233. по снимкам плоского тест-объекта
Определение параметров фотограмметрической калибровкипо полученным таким образом снимкам производится в
результате совместной обработки результатов измерений по
всем полученным снимкам, таким же образом, как и при
обработке снимков пространственного тест-объекта.
33
34. Самокалибровка
Не использует калибровочных объектов.Использует движение камеры в статической сцене. Если изображения
будут браться от тех же самых камер с фиксированными внутренними
параметрами, соответствия между тремя картинками достаточно для
получения и внутренних, и внешних параметров, которые позволят
реконструировать 3D структуру.
34
35. Технология, представленная Zhengyou Zhang
требует только камеру для наблюдения за плоским объектом,показанным с нескольких сторон
Фотограммерическая + самокалибровка
35
36. Объективом с переменным фокусным расстоянием
Способ предложила Марина Колесник в своей статье «Техника калибровкидля объективов с переменным фокусным расстоянием»
Совершаются снимки из одного
положения с изменением фокусного
расстояния(фреймы)
Затем они сопоставляются
36
37. Калибровка с помощью нейронных сетей и генетических алгоритмов
вход – искаженныеизображения
выход – выпрямленные
на практике результат хуже
стандартных методов
(www.
 sicpro.org/sicpro12/proc/p
sicpro.org/sicpro12/proc/procdngs/0547.pdf)
37
[1] Learning OpenCV (перевод на русский)
[2] C.И. Герасимов, В.И. Костин «Калибровка неметрических цифровых фотои видеокамер для фотограмметрических измерений»
[3] Zhang Z. A Flexible New Technique for Camera Calibration // Microsoft
Research, One Microsoft Way, США, Рэдмонд. — 1998.
[4] Kolesnik М. Calibration Update Technique for a Zoom Lens // CAIP, 1999, —
P.435–443
38
English Русский Правила
Калибровка камеры: принципы и процедуры
- Мириам Берни, инженер по исследованиям и разработкам EikoSim
Использование многокамерной системы для метрологии и точных измерений требует калибровки этих камер. Они могут быть представлены математически проекционной моделью в виде матрицы, позволяющей передавать положение 3D-точек в их проекцию в пространстве 2D-изображения. Процесс оценки параметров модели камеры, состоящий из набора внутренних параметров и набора внешних параметров, известен как калибровка.
Далее мы сначала представим математическую модель, описывающую камеру, затем основные семейства методов калибровки, используемые в компьютерном зрении, и, наконец, меры предосторожности, которые необходимо предпринять, чтобы ограничить ошибки, допущенные во время калибровки, и обеспечить ее успех.
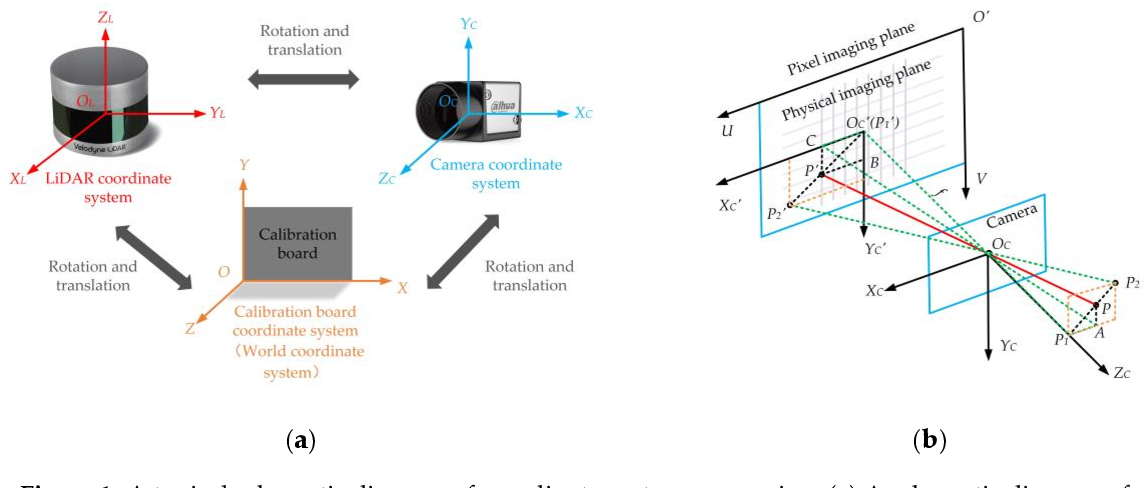
Геометрическая модель камеры, показанная на рис. 1 , основана на трех элементарных преобразованиях . Их комбинация образует так называемую модель обскуры [1].
Рисунок 1 – Проекция 3D точки на изображение с моделью камеры-обскуры (адаптировано из [2]). Положение 3D точки M сцены, определенной в мировой системе отсчета R W ее координатами ( X W , Y W , Z W 9 ), есть Выражено в локальной системе
R C Прикреплена к камере C с локальными координатами ( x C , Y C , Z C 9 666666666. Эта смена системы отсчета составляет первое преобразование и зависит только от трех поворотов и трех перемещений. это Первое преобразование между мировыми гомогенными координатами { XW } = { x W , Y W , Z W , 1} T и локальные координаты {111. = { x C , Y C , Z C , 1} T представлен A 4 × 4 MATRIX Denoted . Его можно разложить на матрицу вращения R (параметризуемый, например, тремя углами поворота) и вектор смещения
Эта смена системы отсчета составляет первое преобразование и зависит только от трех поворотов и трех перемещений. это Первое преобразование между мировыми гомогенными координатами { XW } = { x W , Y W , Z W , 1} T и локальные координаты {111. = { x C , Y C , Z C , 1} T представлен A 4 × 4 MATRIX Denoted . Его можно разложить на матрицу вращения R (параметризуемый, например, тремя углами поворота) и вектор смещения
Эти шесть параметров (три угла, три перемещения) называются внешними параметрами и поэтому определяют позиционирование камеры в трехмерном пространстве .
Второе преобразование соответствует проекции 3D точки M на плоскость сетчатки, к которой локальная система R I прилагается, в 2D точку м . Он включает только фокусное расстояние f камеры и масштабный коэффициент s в соответствии с:
Он включает только фокусное расстояние f камеры и масштабный коэффициент s в соответствии с:
Последнее преобразование выражает однородные 2D-координаты { x s } = { x s s , 1} T точки проекции м в кадре датчика R S и включает характеристики датчика:
- угол перекоса между горизонтальной и вертикальной осями датчика, принимаемый равным 90°;
- позиция оптического центра
- физический размер пикселя в обе стороны.;
Комбинация двух предыдущих преобразований может быть описана через матрицу проекции 3×4 K , которая записывается:
Таким образом, эта матрица проекции определяется четырьмя внутренними параметрами , относящимися к калиброванной камере: по горизонтали ( f x и вертикальное ( f y ) фокусные расстояния в пикселях и положение ( c x , c y ) в изображении оптического центра в пикселях.
Полная матрица проекций M , описывающая камеру, таким образом, состоит из матрицы внешних параметров
Матрица проекций M может быть выражена « неявно » как матрица 3 × 4, содержащая 12 членов ( m ij ) или « явно », через 10 независимых внешних и внутренних параметров, представленных ранее. В явной форме M записывается:
Целью калибровки камеры является оценка ее проекционной матрицы M . Когда процедура направлена на определение членов m ij , она называется неявной калибровкой , в то время как называется явной калибровкой (или «сильной» калибровкой), когда она идентифицирует внешние и внутренние параметры.
В представленной ранее модели камеры не учитываются искажения.
| (a) | (b) | (c) | (d) |
В следующем разделе будут представлены основные семейства процедур калибровки, направленные на определение параметров модели камеры.
Как выполнить калибровку камеры?
Целью калибровки камеры является определение параметров (явных или неявных) связанной с ней проекционной матрицы. Существует несколько методов, которые можно сгруппировать в три основные категории, описанные ниже:
- Калибровка благодаря мишени — классический подход к калибровке камеры;
- Самокалибровка , которая использует априорные знания номинальной геометрии изображаемого объекта для определения параметров камеры;
- Гибридная калибровка , которая объединяет два предыдущих подхода для определения отдельно внутренних и внешних параметров камеры.
Калибровка с целью основана на использовании трехмерного объекта известной геометрии (называемый калибровочной мишенью ) и его изображение, полученное камерой [1, 2]. Этот объект калибровки имеет определенные 3D-точки на своей поверхности с известным положением. Они могут соответствовать пересечению вертикальных и горизонтальных линий, когда цель представляет собой сетку (или шахматную доску), или центру кругов, когда объект калибровки состоит из точек. Положение этих трехмерных точек на изображении калибровочной мишени часто получают с помощью процедур автоматического анализа изображения [4].
Этот объект калибровки имеет определенные 3D-точки на своей поверхности с известным положением. Они могут соответствовать пересечению вертикальных и горизонтальных линий, когда цель представляет собой сетку (или шахматную доску), или центру кругов, когда объект калибровки состоит из точек. Положение этих трехмерных точек на изображении калибровочной мишени часто получают с помощью процедур автоматического анализа изображения [4].
Алгоритм, используемый в этом подходе, направлен на поиск параметров модели камеры, минимизирующих разницу между положением 3D-точек, спроецированных с помощью модели камеры, и реальным положением этих точек на изображении. Таким образом, алгоритм состоит в оптимизации проекционной матрицы до тех пор, пока квадратичная сумма этих ошибок перепроецирования не будет минимизирована. При таком подходе можно определить проекционную матрицу либо неявно, либо явно .Tutorials(2f)MonocularCalibration/mono_1.png) Характеристики искажения можно выделить и для наиболее сложных моделей [9, 10]. В случае системы стереовидения (, т.е. , с 2 камерами) этот подход позволит независимо идентифицировать параметры (внутренние и внешние) одной из двух камер, которая станет « ведущей камерой » [5]. Вторая камера, называемая «ведомой камерой », будет иметь свои внутренние параметры, идентифицированные через цель калибровки, а ее внешние параметры будут определены в зависимости от положения ведущей камеры посредством определения матрицы линейного преобразования, позволяющей перейти от камеры 1 к камере 2. Эта матрица может быть предварительно определена поставщиком системы стереозрения для систем, в которых относительное положение камер фиксировано или повторно идентифицировано по изображениям калибровочных объектов. Поскольку мишени, используемые для калибровки, должны занимать трехмерное пространство, они должны быть трехмерными или, если они плоские, они должны быть трехмерными.
Характеристики искажения можно выделить и для наиболее сложных моделей [9, 10]. В случае системы стереовидения (, т.е. , с 2 камерами) этот подход позволит независимо идентифицировать параметры (внутренние и внешние) одной из двух камер, которая станет « ведущей камерой » [5]. Вторая камера, называемая «ведомой камерой », будет иметь свои внутренние параметры, идентифицированные через цель калибровки, а ее внешние параметры будут определены в зависимости от положения ведущей камеры посредством определения матрицы линейного преобразования, позволяющей перейти от камеры 1 к камере 2. Эта матрица может быть предварительно определена поставщиком системы стереозрения для систем, в которых относительное положение камер фиксировано или повторно идентифицировано по изображениям калибровочных объектов. Поскольку мишени, используемые для калибровки, должны занимать трехмерное пространство, они должны быть трехмерными или, если они плоские, они должны быть трехмерными. 0011 перемещался в пространстве с помощью поступательно-вращательных движений [1, 11]. При таком типе калибровки необходимо получить не менее 50 изображений цели [12, 13], чтобы можно было откалибровать систему стереозрения и минимизировать влияние шумов при съемке и ошибок калибровки. Кроме того, поскольку цель калибровки является внешней, невозможно повторно откалибровать камеры во время эксперимента , что может быть необходимо, если камеры непреднамеренно перемещаются (движения штатива камеры, постепенное отвинчивание камер…).
0011 перемещался в пространстве с помощью поступательно-вращательных движений [1, 11]. При таком типе калибровки необходимо получить не менее 50 изображений цели [12, 13], чтобы можно было откалибровать систему стереозрения и минимизировать влияние шумов при съемке и ошибок калибровки. Кроме того, поскольку цель калибровки является внешней, невозможно повторно откалибровать камеры во время эксперимента , что может быть необходимо, если камеры непреднамеренно перемещаются (движения штатива камеры, постепенное отвинчивание камер…).
Второй тип калибровки называется самокалибровкой [14] и используется, в частности, в так называемых «глобальных» стереокорреляционных подходах [15], таких как предложенный EikoTwin DIC. В качестве калибровочного объекта используется весь тестовый образец , и это благодаря плотному описанию объекта ( т.е. , положение каждой точки образца параметризовано и может быть определено с помощью математической модели [16]).Tutorials(2f)MonocularCalibration/mono_0.png) Одним из возможных описаний является сетка конечных элементов [17, 18]. Следовательно, вся сетка используется как определенные точки для минимизации ошибок перепроецирования и идентификации параметров моделей камер (а не только отдельных точек калибровочной цели). Вся эта сетка будет связана со всей крапчатой тестовой выборкой, видимой на изображениях, полученных камерами, и, соответственно, со всей текстурой образца (пятнистой структурой). Цель процедуры – одновременно найти неявные параметры, параметрирующие камеры (без иерархии между камерами), минимизируя разницу в уровне серого между проекцией 3D-точек через каждую из камер (используя ее проекционную модель для оптимизации) и эталонным изображением общий для всех камер (построен из всех камер). Трехмерные точки соответствуют точкам оценки, созданным для каждого элемента сетки (равномерно разделенные подразделения внутри элемента), где уровни серого и градиенты будут оцениваться для минимизации ошибок перепроецирования.
Одним из возможных описаний является сетка конечных элементов [17, 18]. Следовательно, вся сетка используется как определенные точки для минимизации ошибок перепроецирования и идентификации параметров моделей камер (а не только отдельных точек калибровочной цели). Вся эта сетка будет связана со всей крапчатой тестовой выборкой, видимой на изображениях, полученных камерами, и, соответственно, со всей текстурой образца (пятнистой структурой). Цель процедуры – одновременно найти неявные параметры, параметрирующие камеры (без иерархии между камерами), минимизируя разницу в уровне серого между проекцией 3D-точек через каждую из камер (используя ее проекционную модель для оптимизации) и эталонным изображением общий для всех камер (построен из всех камер). Трехмерные точки соответствуют точкам оценки, созданным для каждого элемента сетки (равномерно разделенные подразделения внутри элемента), где уровни серого и градиенты будут оцениваться для минимизации ошибок перепроецирования. Таким образом, при таком подходе можно откалибровать систему стереозрения с помощью одной пары изображений , будучи устойчивым к шуму благодаря множеству точек оценки, вызванных плотным описанием тестируемого объекта. Более того, положение камер выражается в системе отсчета образца , и возможно перекалибровать камеры по желанию во время теста с использованием полученных изображений.
Таким образом, при таком подходе можно откалибровать систему стереозрения с помощью одной пары изображений , будучи устойчивым к шуму благодаря множеству точек оценки, вызванных плотным описанием тестируемого объекта. Более того, положение камер выражается в системе отсчета образца , и возможно перекалибровать камеры по желанию во время теста с использованием полученных изображений.
Однако одним из ограничений этого подхода к самокалибровке является трехмерный характер тестируемого образца , что остается условием, позволяющим избежать математических особенностей калибровки камеры [9]. В случаях, когда тестируемый объект не соответствует этим геометрическим условиям (случай плоского образца или тела вращения, такого как цилиндр), рекомендуется прибегнуть к гибридной калибровке , которая также является процедурой, предложенной EikoTwin DIC. Этот подход сочетает в себе использование калибровочного объекта ChAruCo (известной геометрии) и подхода глобальной стереокорреляции (посредством самокалибровки).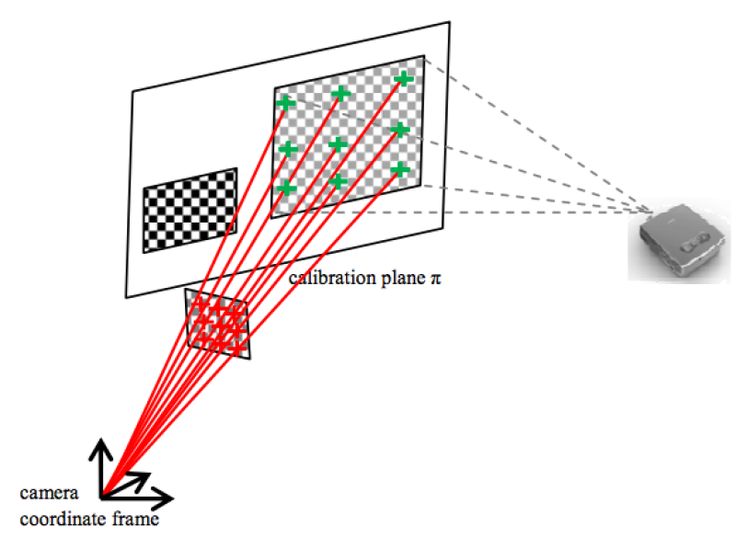 Использование мишени ChAruCo позволяет явно установить некоторые параметры проекции в фиксированные значения, а именно внутренние параметры камеры (матрица K ), а в сделать идентификацию внешней матрицы T (в неявной форме ) надежнее за счет самокалибровки. Более подробно описание этого подхода, его преимуществ и условий применения представлено в нашем блоге «Гибридная калибровка: надежная альтернатива самокалибровке».
Использование мишени ChAruCo позволяет явно установить некоторые параметры проекции в фиксированные значения, а именно внутренние параметры камеры (матрица K ), а в сделать идентификацию внешней матрицы T (в неявной форме ) надежнее за счет самокалибровки. Более подробно описание этого подхода, его преимуществ и условий применения представлено в нашем блоге «Гибридная калибровка: надежная альтернатива самокалибровке».
Как избежать ошибок калибровки камеры?
Плохая калибровка камеры очень часто приводит к ошибкам измерения перемещений и, следовательно, деформаций . Чтобы обеспечить надлежащую калибровку, может быть целесообразно получить изображения движений твердого тела (поступательного движения) с известной амплитудой и убедиться, что измерение смещения является согласованным.
Кроме того, можно принять несколько мер предосторожности, чтобы обеспечить успешное выполнение фазы калибровки :
- Воспользуйтесь « Virtual Testing », подготовив тест заранее виртуально.
 EikoTwin Virtual использует инструмент визуализации Blender, чтобы заранее определить положение камеры и оптимизировать его, чтобы иметь хорошую калибровку для измерения ожидаемых смещений (из моделирования методом конечных элементов). Более подробную информацию об этих аспектах можно найти в нашей статье «Подготовка теста корреляции цифровых изображений с помощью Blender», доступной в нашем блоге.
EikoTwin Virtual использует инструмент визуализации Blender, чтобы заранее определить положение камеры и оптимизировать его, чтобы иметь хорошую калибровку для измерения ожидаемых смещений (из моделирования методом конечных элементов). Более подробную информацию об этих аспектах можно найти в нашей статье «Подготовка теста корреляции цифровых изображений с помощью Blender», доступной в нашем блоге. - Если этот этап виртуализации не может быть выполнен, рекомендуется предупредите возможные проблемы , адаптировав положение камер в день эксперимента, выделив дополнительные 3D-точки в FOV или используя гибридную калибровку, чтобы сделать калибровку камер более надежной. Было определено несколько критериев для предварительной оценки надежности калибровки , см. нашу статью «Освоение самокалибровки с помощью Eikotwin DIC».
Выводы
Калибровка камер является первым этапом любого анализа с помощью корреляции цифровых изображений и остается этапом, который необходимо выполнять тщательно , особенно когда требуются точные измерения (формы, смещения или деформации). Все существующие подходы направлены на минимизацию ошибок репроецирования между характеристикой, связанной с проекцией конкретных трехмерных точек (положение, значение уровня серого) и их реальной характеристикой на изображении. Затем эти точки могут быть примечательными точками на калибровочной цели или точками оценки, связанными с сеткой поверхности в случае глобальных подходов. EikoTwin DIC предлагает процедуры калибровки с помощью самокалибровки и гибридной калибровки для определения надежным и одновременным способом проекционных матриц камер с использованием одной пары изображений (и около двадцати целевых изображений, если гибридная выбрана калибровка). Эти процедуры имеют много преимуществ (простота, калибровка в системе отсчета тестируемого образца, устойчивость к шуму, возможность одновременной калибровки многоракурсной системы…) и могут 0011 быть адаптированным к любому типу эксперимента .
Все существующие подходы направлены на минимизацию ошибок репроецирования между характеристикой, связанной с проекцией конкретных трехмерных точек (положение, значение уровня серого) и их реальной характеристикой на изображении. Затем эти точки могут быть примечательными точками на калибровочной цели или точками оценки, связанными с сеткой поверхности в случае глобальных подходов. EikoTwin DIC предлагает процедуры калибровки с помощью самокалибровки и гибридной калибровки для определения надежным и одновременным способом проекционных матриц камер с использованием одной пары изображений (и около двадцати целевых изображений, если гибридная выбрана калибровка). Эти процедуры имеют много преимуществ (простота, калибровка в системе отсчета тестируемого образца, устойчивость к шуму, возможность одновременной калибровки многоракурсной системы…) и могут 0011 быть адаптированным к любому типу эксперимента . Предварительно подготовив тест с помощью виртуализации или проверив соответствие некоторым критериям, можно убедиться, что камеры правильно откалиброваны , что является необходимым условием для надежного измерения перемещений и уменьшения ошибок для кинематики измерения.
Предварительно подготовив тест с помощью виртуализации или проверив соответствие некоторым критериям, можно убедиться, что камеры правильно откалиброваны , что является необходимым условием для надежного измерения перемещений и уменьшения ошибок для кинематики измерения.
Ссылки
[1] O. Faugeras, Трехмерное компьютерное зрение: геометрическая точка зрения . Кембридж, Массачусетс (США): MIT Press, 19.93.
[2] М. Саттон, Дж. Ортеу и Х. Шрайер, Корреляция изображений для измерения формы, движения и деформации: основные концепции, теория и приложения . Нью-Йорк, штат Нью-Йорк (США): Springer, 2009.
[3] G. Besnard, Характеристика и количественная оценка поверхностей с точки зрения стереокорреляции для механических исследований квазистатической сверхбыстрой динамики . Кандидатская диссертация (на французском языке), ENS de Cachan, 2010.
[4] P. Brand, Трехмерная реконструкция сцены с участием камеры в движении: влияние точности . Докторская диссертация (на французском языке), Université Claude Bernard (Lyon I), 1995.
Докторская диссертация (на французском языке), Université Claude Bernard (Lyon I), 1995.
[5] D. Garcia, Mesure de formes et de champs de déplacements tridimensionnels par séréocorrélation d’images . Кандидатская диссертация (на французском языке), Institut National Polytechnique de Toulouse (INPT), 2001.
[6] J. Heikkilä, «Геометрическая калибровка камеры с использованием круговых контрольных точек», IEEE Transactions on Pattern Analysis and Machine Intelligence , vol. 22, с. 1066 – 1077, 2000.
[7] Исходное изображение с: https://dantecdynamics.com/wp-content/uploads/2019/11/2.-Calibration-target.png
[8] Исходное изображение с: https://correlatedsolutions.com /wp-content/uploads/2016/09/3D-Calibration.jpg
[9] Р. Цай, «Универсальный метод калибровки камеры для высокоточной метрологии трехмерного машинного зрения с использованием стандартных телекамер и объективов» , IEEE J. Robotics Autom. , том. РА-3, вып. 4, pp. 323–343, 1987.
323–343, 1987.
[10] J. Heikkilä et O. Silvén, «Четырехэтапная процедура калибровки камеры с неявной коррекцией изображения», Международная конференция IEEE по компьютерному зрению и распознаванию образов , стр. 1106–1111, 1997.
[11] Z. Zhang, «Новый гибкий метод калибровки камеры», IEEE Trans. Анальный узор. Машинный интеллект. , том. 22, нет. 11, стр. 1330–1334, 2000.
[12] М. Саттон, «Бесконтактные измерения деформации на основе компьютерного зрения в механике: преобразование поколений», Appl. мех. Ред. , том. 65, нет. АМР-13-1009, с. 050802, 2013.
[13] Международное общество корреляции цифровых изображений, Руководство по эффективной практике корреляции цифровых изображений , Jones, E.M.C. et Iadicola, MA (Eds.), 2018.
[14] O. Faugeras, Q. Luong, et S. Maybank, «Самокалибровка камеры: теория и эксперименты», dans Proc. 2nd ECCV , стр. 321–334, Springer-Verlag, 1992.
[15] J.-E. Дюфур, Ф. Хильд и С. Ру, «Форма, смещение и механические свойства на основе изогеометрической многоракурсной стереокорреляции», J. Анализ деформации , vol. 50, нет. 7, стр. 470–487, 2015.
Хильд и С. Ру, «Форма, смещение и механические свойства на основе изогеометрической многоракурсной стереокорреляции», J. Анализ деформации , vol. 50, нет. 7, стр. 470–487, 2015.
[16] F. Hild et S. Roux, «Procédé de mesures tridimensionnelles par stereo-corrélation utilisant une representation paramétrique de l’objet mesuré», Dec. 6 2013. Patent n. °FR2991448.
[17] Ж.-Э. Dufour, B. Beaubier, S. Roux, et F. Hild, «Измерение смещения с использованием стереокорреляции на основе САПР с сетками», в конференции ICEM , 2014 г.
[18] L. Dubreuil, J.-E . Дюфур, Ю. Куинсат и Ф. Хильд, «Измерения формы на основе сетки со стереокорреляцией: принцип и первые результаты», Экспл. мех. , нет. 56, стр. 1231–1242, 2016 г.
Калибровка камеры — документация Navigation 2 1.0.0
Редактировать
-
Обзор
-
Требования
-
Этапы обучения
Обзор
В этом руководстве показано, как получить параметры калибровки монокулярной камеры.
Требования
1- Установите Camera Calibration Parser, Camera Info Manager и Launch Testing Ament Cmake с помощью диспетчера пакетов операционной системы:
sudo apt install ros--camera-calibration-parsers
sudo apt install ros--camera-info-manager
sudo apt install ros--launch-testing-ament-cmake
2- Image Pipeline должен быть создан из исходного кода в вашей рабочей области с помощью:
git clone – b[email protected]:ros-perception/image_pipeline.git
Также убедитесь, что у вас есть следующее:
Большая шахматная доска с известными размерами. В этом уроке используется шахматная доска 7×9 с квадратами 20 мм. Калибровка использует внутренние точки вершин шахматной доски, поэтому доска «8×10» использует параметр внутренних вершин «7×9», как в примере ниже.
Шахматную доску с заданными размерами можно скачать отсюда.
Хорошо освещенное место, свободное от препятствий и других рисунков контрольной доски
Монокулярная камера, публикующая изображения через ROS
Шаги руководства
1- Запустите терминал в графическом интерфейсе
2- Запустите драйвер ROS для вашей конкретной камеры.
3- Убедитесь, что камера публикует изображения через ROS. Это можно проверить, запустив:
Список тем ros2
4- Это покажет вам все опубликованные темы, убедитесь, что есть тема image_raw /camera/image_raw. Чтобы убедиться, что это реальная тема и действительно публикуется, проверьте тему hz:
тема рос2 хз /camera/image_raw
5- Запустить узел калибровки камеры
ros2 run camera_calibation cameracaulibator --size 7x9 --square 0.02 --ros-args -r image:=/my_camera/image_raw -p camera:=/my_camera
Имя камеры:
-c, --camera_name
имя камеры, которое будет отображаться в файле калибровки
Варианты шахматной доски:
Вы должны указать одну или несколько шахматных досок в виде пар параметров --size и --square.
-p ШАБЛОН, --pattern=ШАБЛОН
калибровочный шаблон для обнаружения - «шахматная доска», «круги», «круги», «чаруко»
-s РАЗМЕР, --size=РАЗМЕР
размер шахматной доски как NxM, считая внутренние углы (например, стандартная шахматная доска 7x7)
-q КВАДРАТ, --square=КВАДРАТ
размер шахматной доски в метрах
Варианты связи ROS:
-- приблизительно = ПРИБЛИЗИТЕЛЬНО
разрешить указанный интервал (в секундах) при сопряжении изображений с несинхронизированных стереокамер
--нет-сервис-проверить
отключить проверку сервисов set_camera_info при запуске
Параметры оптимизатора калибровки:
--fix-главная-точка
зафиксировать главную точку в центре изображения
--fix-соотношение сторон
обеспечить равенство фокусных расстояний (fx, fy)
--zero-tangent-dist
установите коэффициенты тангенциального искажения (p1, p2) равными
нуль
-k NUM_COEFFS, --k-коэффициенты=NUM_COEFFS
количество используемых коэффициентов радиальной дисторсии (до
6, по умолчанию 2)
--disable_calib_cb_fast_check
использует флаг CALIB_CB_FAST_CHECK для findChessboardCorners
Откроется окно калибровки, в котором будет выделена шахматная доска.
6- Чтобы получить хорошую калибровку, вам нужно переместить шахматную доску в кадре камеры так, чтобы:
- шахматная доска слева, справа, вверху и внизу поля зрения камеры
◦ X полоса — слева/справа в поле зрения
◦ Y полоса — верх/низ в поле зрения
◦ Полоса размера — в сторону/от камеры и наклон от камеры
шахматная доска, заполняющая все поле зрения
шахматная доска с наклоном влево, вправо, вверх и вниз (перекос)
7- По мере перемещения шахматной доски 4 полосы на боковой панели калибровки увеличиваются в длину. Когда все 4 полоски станут зелеными и будет доступно достаточно данных для калибровки, загорится кнопка CALIBRATE. Нажмите на нее, чтобы увидеть результаты. Калибровка занимает около минуты.
8- После завершения калибровки загораются кнопки сохранения и подтверждения.