Кривая фибоначчи: Спираль Фибоначчи — математика и искусство

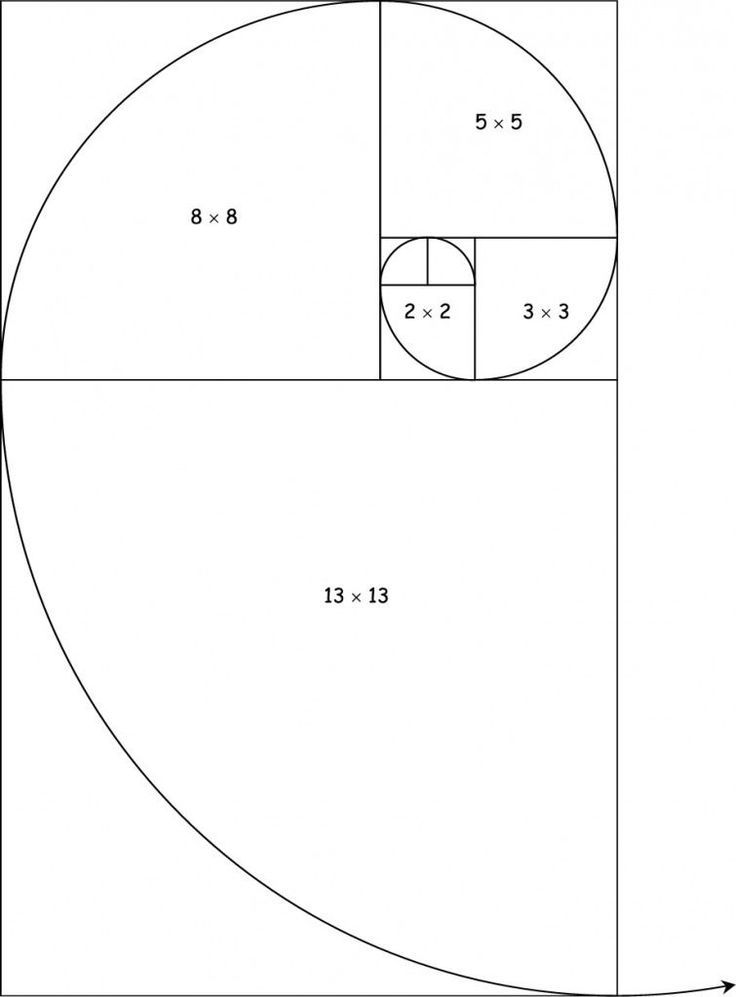
что это такое простыми словами

Человечество на протяжении многих тысяч лет сталкивалось с различными закономерностями в окружающем их мире. По мере развития науки люди начали описывать многие вещи с помощью математических инструментов. Создание моделей позволяет понять суть различных процессов, а также создает возможность прогнозирования. Один из таких способов – последовательность Фибоначчи.

Содержание

• 1 Как Леонардо Фибоначчи изобрел свою известную последовательность
• 2 Что это и для чего нужно
• 3 Где используют
• 4 Применение в трейдинге
  • 4.1 Коррекции Фибоначчи
  • 4.2 Дуги Фибоначчи
  • 4.3 Веера Фибоначчи
  • 4.4 Временные зоны Фибоначчи

Как Леонардо Фибоначчи изобрел свою известную последовательность

Леонардо Пизано по прозвищу Фибоначчи – европейский математик 12 в. Родом из Пизы, он по воле отца направился для изучения математики и торгового дела в Алжир к арабским учителям.

Фибоначчи открыл свою известную последовательность, когда задался вопросом о разведении кроликов. Суть задачи: «Пару кроликов заселяют на поляну. Сколько пар будет жить на этом месте через год?». Для решения были введены упрощения: кролики в течение года не умирают, половой зрелости достигают спустя месяц после рождения, потомки появляются только спустя месяц после зачатия.

Леонардо Фибоначчи

Таким образом, в этой задаче последовательность определяется так:

• первый месяц – 1 пара;
• второй месяц – 1+1=2 пары;
• третий месяц – 2+1=3 пары, тут рожает первая пара кроликов, так как вторая еще на третий месяц только достигла половой зрелости;
• четвертый месяц – 3+2=5 пар, здесь уже рожает и первая пара, и первые потомки, т.е. появляются на свет 2 пары.

В конце года на поляне будет 144+233=377 пар кроликов.

Что это и для чего нужно

Последовательность Фибоначчи простыми словами – это прогрессия, состоящая из целых чисел, следующих друг за другом с определенной закономерностью. Каждый последующий элемент равен сумме двух предыдущих.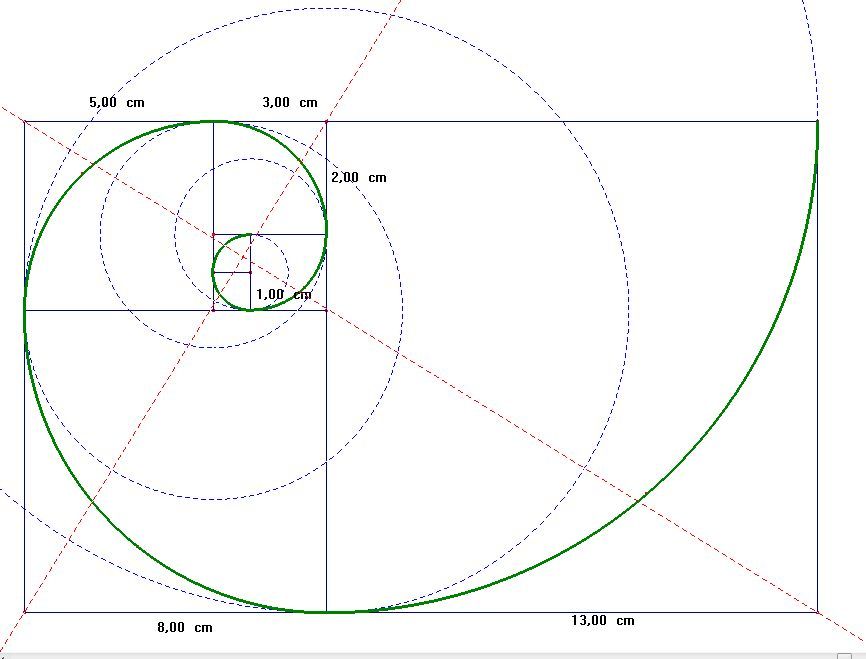

На сегодняшний день имеются многочисленные данные по проявлению ряда Фибоначчи. Модель используют в астрономии для определения новых планет и галактик, химии, квантовой механике, экономике. На основе данной последовательности даже существуют попытки создания хронологии развития человечества. 

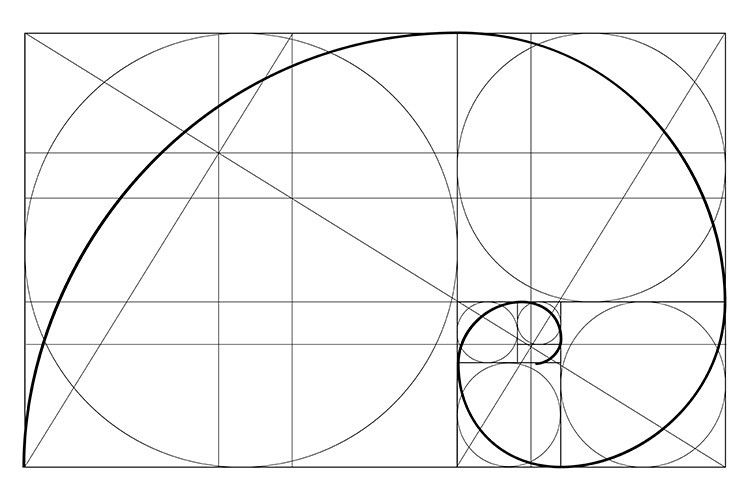
Большой интерес представляет частное двух соседних чисел, для всех элементов ряда приблизительно равное цифре 1,618. Это значение получило название «золотое сечение». Именно оно лежит в основе натуральной гармонии нашей Вселенной, присущей галактикам, цветам, животным.

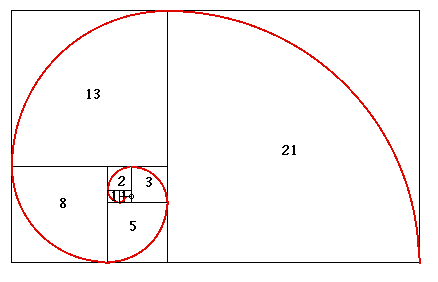
Последовательность чисел Фибоначчи

Так исторически сложилось, что первыми выявили и описали «золотое сечение» древнегреческие математики. Оно представляло собой деление отрезка АВ точкой С на части таким образом, что большая часть отрезка относится к меньшей, как весь отрезок к большей части: ВС/АС=АВ/ВС.

Позднее, в начале 13-го века, Фибоначчи привел обоснование и доказательства существования этой последовательности и «золотого сечения».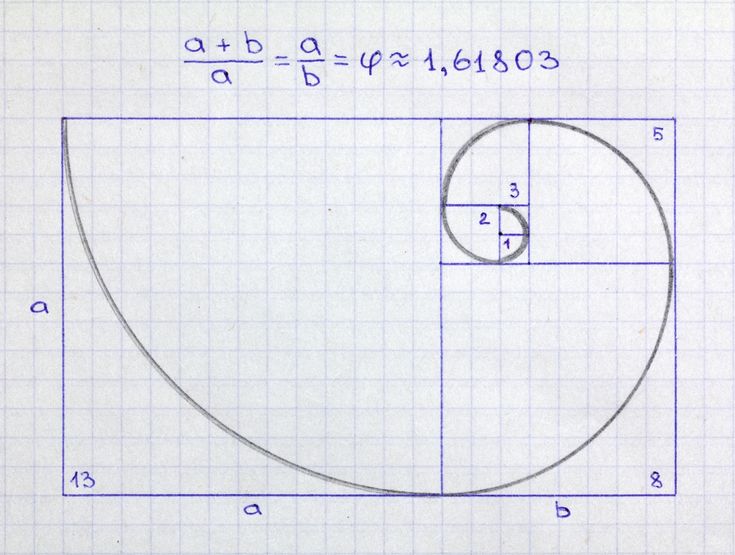 В 19 веке теоретик Эдуард Люка дал название этой прогрессии — «последовательность Фибоначчи».

Где используют

Золотое сечение наряду с загадочными свойствами чисел Фибоначчи с далеких времен и по сей день привлекают внимание ученых. Область применения последовательности довольна широка. Это может быть искусство, архитектура. Например, правило встречается на полотне И. Левитана «Сумерки. Луна» с выстроенным центром (Луной), линией горизонта, темными акцентами по правилам золотого сечения в соотношении 1,618. Соответственно, здесь и будут расположены наиболее важные части экспозиции.

В архитектуре пример «золотых» линий — знаменитая пирамида Хеопса. В древнегреческих строениях универсальное правило можно проследить, изучая Парфенон. В те времена считалось, что объекты с именно таким соотношением частей наиболее приятны для глаз человека.

Применение в трейдинге

Первым человеком, кто решил заняться изучением рынков на основе применения последовательности чисел Фибоначчи, является Ральф Нельсон Эллиот. Будучи финансистом, он смог обнаружить и определенную закономерность в поведении фондовых рынков, также поддающихся правилу золотого сечения.

Применение последовательности Фибоначчи в трейдинге

Благодаря знаменитой последовательности были созданы новые инструменты для анализа рынка — такие, как коррекции, дуги, веера и временные зоны Фибоначчи.

Коррекции Фибоначчи

Коррекции, или уровни Фибоначчи – это инструмент технического анализа, служащий для прогнозирования уровней поддержки и сопротивления.

Для построения требуется произвести следующий порядок действий:

1. Определяют экстремумы (максимальное и минимальное значение) на графике в долгосрочном периоде.
2. На основе этих точек отстраивают вертикальный отрезок и делят на коэффициенты Фибоначчи, равные 23,6%, 38,2%, 50%, 61,8%.
3. На графике рисуют горизонтальные прямые, соответствующие полученным значениям. Эти линии представляют собой уровни поддержки, что означает окончание падения цены, и сопротивления – цена не идет выше.

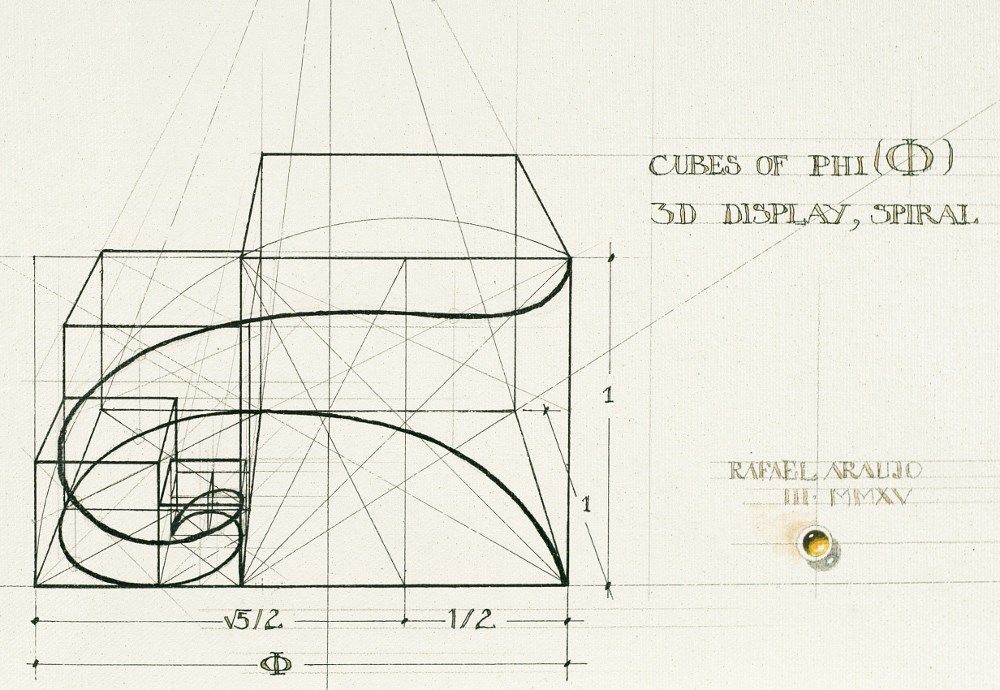
Значения коэффициентов получают по следующей формуле, согласно числам Фибоначчи (0,1,1,2,3,5,8,13,21,34,55,89,144…):

• 23,6%. Получают путем деления одного члена последовательности на число, находящееся на 3 позиции впереди от него. Например: (34/144)·100=23,6%, т. е. в последовательности берется цифра 34 и делится на число, находящееся впереди на 3 шага – это 144. Чем дальше от нулевого значения, тем точнее будет коэффициент.
• 38,2%. Деление одного числа на то, что стоит двумя позициями дальше. Например: (34/89)·100=38,2%.
• 61,8%. Частное двух соседних членов последовательности. Например: (89/144)·100=61,8%.

Существуют еще 3 уровня, не входящих в соотношения Фибоначчи:

• 0%. Означает начало отката.
• 50%. Эмпирический коэффициент, которым пользуется большое количество трейдеров. Рынок имеет тенденцию к развороту при откате в 50%.
• 100%. Это разворот рынка в противоположную сторону.

Многие трейдеры используют уровни Фибоначчи для определения оптимальных точек входа в рынок и выхода из него.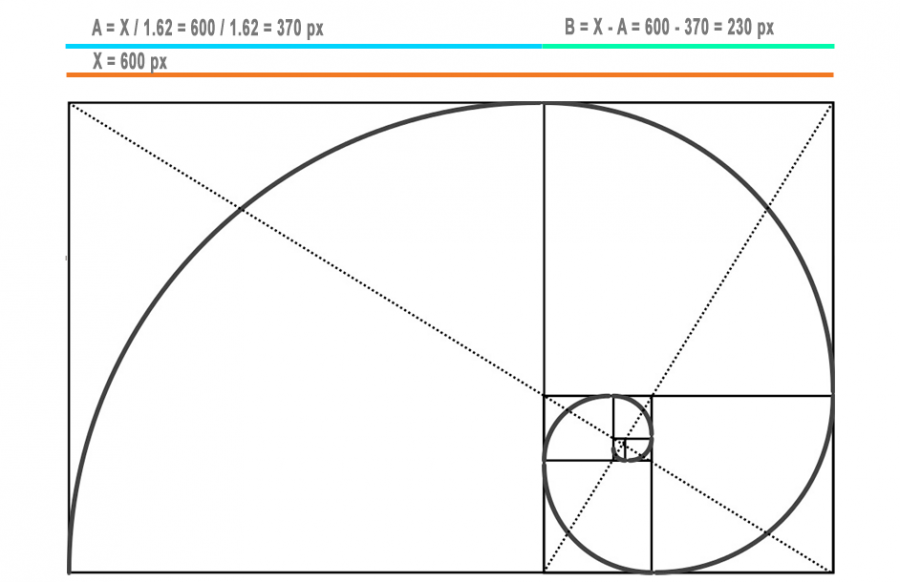

Дуги Фибоначчи

Один из индикаторов, представляющий дуги, которые могут быть уровнями поддержки и сопротивления. Трейдеры при помощи этого инструмента имеют возможность прогнозировать моменты разворота рынка, чтоб своевременно зафиксировать прибыль.

Дуги Фибоначчи

Построение производят также на основе экстремумов графика. Определяют желаемую точку. Затем от нее на расстояниях 38,2%, 50% и 61,8% отстраивают дуги.

Тем самым можно определить уровни сопротивления и поддержки цены.

При растущем тренде с помощью дуг возможно понять, до какого значения опустится цена перед ее следующим подъемом. И, наоборот, при снижении цены акции дуги показывают, как может вырасти цена до ее следующего падения.

Веера Фибоначчи

Представляют диагональные линии, исходящие из одной точки. Формой походят на веер.

Для построения требуется произвести следующие действия;

1. Определить экстремумы на графике.
2. Из выбранной точки провести наклонную линию. Если тренд возрастающий, то прямую проводят до точки с наибольшим значением, если падающий – до точки минимума.
3. От второй точки мысленно отстраивают вертикальную прямую.
4. На этой линии выделяют уровни в 38,2%, 50% и 61,8%. Далее через эти точки проводят прямые. Эти линии будут показывать на области с потенциальной силой покупателей или продавцов.

Временные зоны Фибоначчи

Это инструмент технического анализа рынка, который представляет ряд вертикальных линий, построенных в рамках числовых значений Фибоначчи. Принцип работы основан на временных отрезках, а не на движении цен.

На графике отмечают явный ценовой тренд, основанный на точках экстремума. Горизонтальное расстояние между ними – единичный отрезок. Далее строят параллельные вертикальные линии. Эти прямые будут характеризовать временные зоны, в которых с некоторой долей вероятности можно ожидать падение или взлета цен. Первый уровень должен совпадать с пиковым значением тренда на графике. Но для большей уверенности желательно, чтоб и второй уровень приходился на экстремальное значение.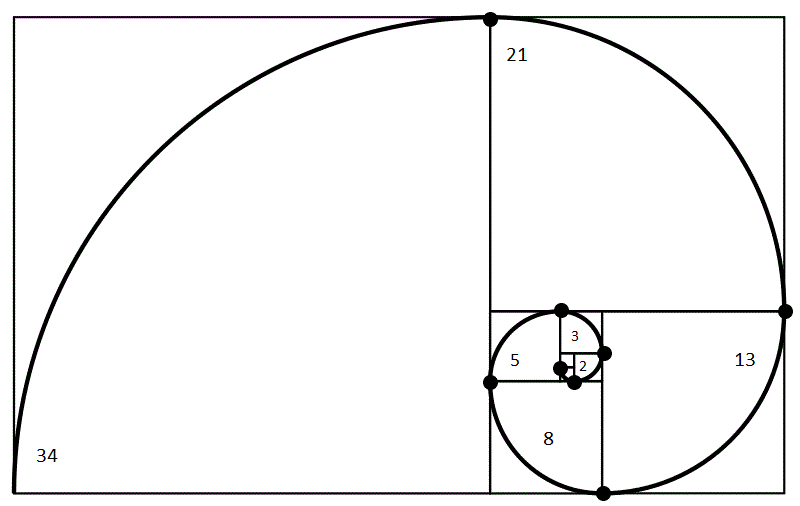

Фибоначчи слово фрактал — frwiki.wiki

Для одноименных статей см. Фибоначчи .

Три типа фрактальных кривых слова Фибоначчи.

Фибоначчи слово фрактал

представляет собой плоскость фрактальной кривой определяется из слова Фибоначчи .

Резюме

• 1 Определение
• 2 свойства
• 3 Галерея
• 4 плитка Фибоначчи
  • 4.1 чешуйка Фибоначчи
• 5 Примечания и ссылки
• 6 См. Также
  • 6.1 Связанная статья
  • 6.2 Внешняя ссылка

Определение

Первые итерации.

Эта кривая строится итеративно, применяя к слову Фибоначчи  : 0100101001001 … правило OEDR (правило нечетного-четного рисования). Для каждой цифры в позиции k  :

• если число 1: нарисуйте отрезок длиной 1 в предыдущем направлении
• если число равно 0, нарисуйте отрезок длиной 1 после поворота на четверть:
  • справа, если k четно
  • слева, если k нечетное

В длине Фибоначчи слово, которое представляет собой в н -го числа Фибоначчи, связан с кривой, сформированной из сегментов.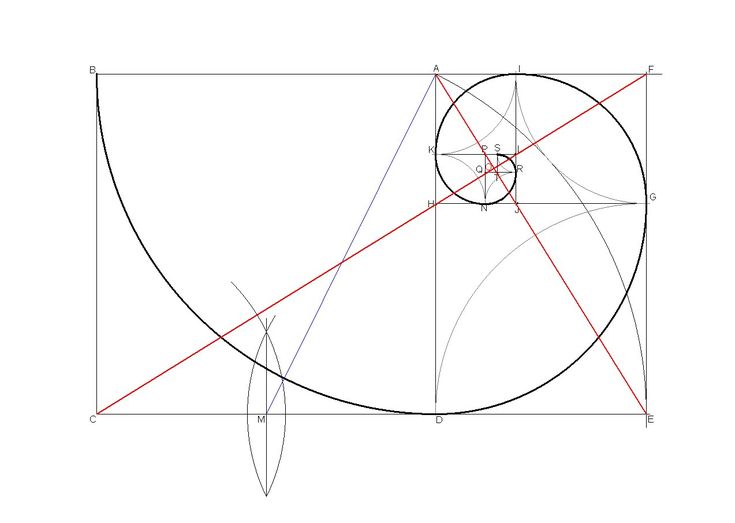

Кривая представлена ​​в трех различных аспектах в зависимости от того, имеет ли n форму 3 k, 3 k +1 или 3 k +2. Fнет{\ displaystyle F_ {n}}Fнет{\ displaystyle F_ {n}}Fнет{\ displaystyle F_ {n}}

Характеристики

Характеристики.

Числа Фибоначчи во фрактале.

• Кривая с сегментами представляет прямые и плоские углы.Fнет{\ displaystyle {\ mathcal {F}} _ {n}}Fнет{\ displaystyle F_ {n}}Fнет-1{\ displaystyle F_ {n-1}}Fнет-2{\ displaystyle F_ {n-2}}
• Кривая никогда не имеет самопересечения или двойных точек. В конечном итоге он представляет собой бесконечное количество асимптотически близких точек.
• Кривая показывает самоподобие во всех масштабах. Коэффициент уменьшения действителен . Это число, также называемое серебряным числом, присутствует во многих геометрических свойствах, обсуждаемых ниже.1+2{\ displaystyle 1 + {\ sqrt {2}}} δВграммзнак равноφ2{\ displaystyle \ delta _ {Ag} = \ varphi _ {2}}
• Число автоподобных копий в степени n — это число Фибоначчи минус 1 (точнее 🙂 . 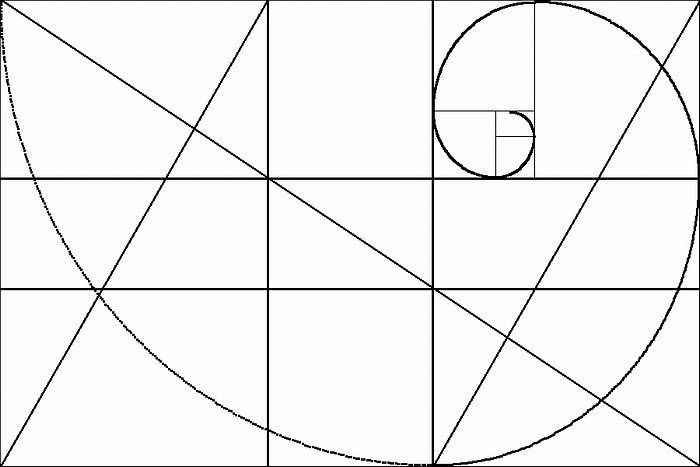{2} +1}} \ right)}}}взнак равнопотому что⁡α{\ Displaystyle а = \ соз \ альфа}
• Размерность его границы по Хаусдорфу действительна .бревно⁡3бревно⁡(1+2)≈1,2465{\ displaystyle {\ frac {\ log 3} {\ log \ left (1 + {\ sqrt {2}} \ right)}} \ приблизительно 1 {,} 2465}
• Если поменять местами «0» и «1» в слове Фибоначчи или в правиле, образуется такая же кривая, но ориентированная под углом 45 °.
• От слова Фибоначчи, мы можем определить «плотное Фибоначчи слово», на алфавите из 3 букв: 102210221102110211022102211021102110221022102211021 … (продолжение A143667 в OEIS ). Применение «естественного» правила построения графика позволяет определить бесконечное множество вариантов кривой, среди которых:
  • «диагональный» вариант;
  • вариант «свастика»;
  • «компактный» вариант.
• Мы предполагаем, что образец фрактала слова Фибоначчи можно найти для любого слова Штурма, директивная последовательность которого (следовательно, разложение наклона в непрерывные дроби ) заканчивается бесконечной последовательностью «1».

Галерея

• Кривая после итераций. F23{\ displaystyle \ textstyle {F_ {23}}}

• Самоподобие

• Габаритные размеры

• Строительство путем сопоставления (1)

• Строительство путем сопоставления (2)

• Режим построения путем повторного удаления квадратов.

• Метод построения повторяется восьмиугольниками.

• Итерационное построение из квадратов.

• С углом 60 °.

• Инверсия ролей «0» и «1».

• Варианты, порожденные плотным словом Фибоначчи.

• «Компактный» вариант

• Вариант «свастика»

• «Диагональный» вариант

• Вариант «пи / 8»

Плитка Фибоначчи

Мощение (несовершенное) плитками Фибоначчи. Непокрытое пространство стремится от нуля до бесконечности.

Идеальное мощение хлопьями Фибоначчи.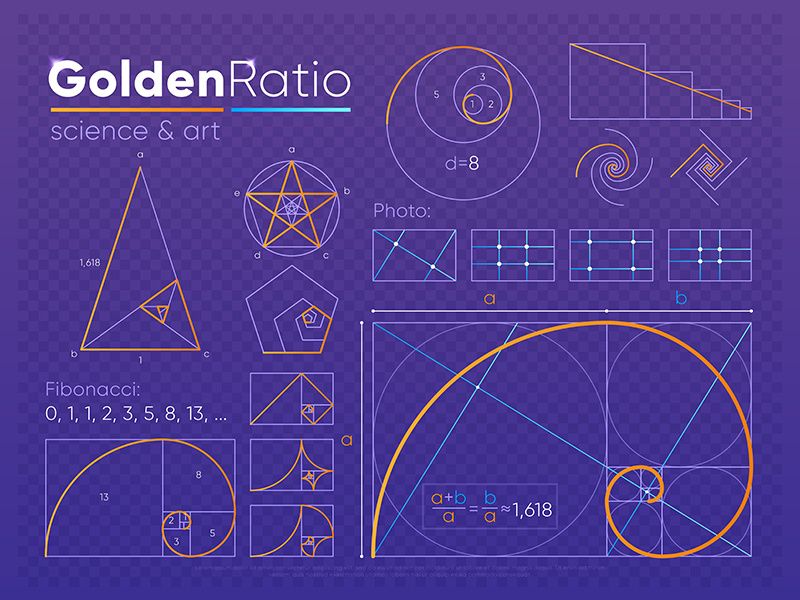

Сопоставление 4-х типов кривых Фибоначчи позволяет построить замкнутую кривую, ограничивающую соединенную поверхность ненулевой площади. Эта фигура называется «плиткой Фибоначчи». F3k{\ displaystyle F_ {3k}}

• Плитка Фибоначчи почти вымощает плоскость. Сопоставление 4 плиток (см. Иллюстрацию) оставляет в центре свободный квадрат, поверхность которого стремится к нулю, поскольку k стремится к бесконечности. В конечном итоге плитка Фибоначчи вымощает плоскость.
• Если плитка Фибоначчи вписывается в квадрат со стороной 1, то ее площадь стремится к .2-2≈0,5857{\ displaystyle 2 — {\ sqrt {2}} \ приблизительно 0 {,} 5857}

Хлопья Фибоначчи

Чешуйка Фибоначчи — это плитка Фибоначчи, определенная в соответствии со следующим правилом:

• qнетзнак равноqнет-1qнет-2{\ displaystyle q_ {n} = q_ {n-1} q_ {n-2}}если  ;нет≡2(мод3){\ Displaystyle п \ экв 2 {\ pmod {3}}}
• qнетзнак равноqнет-1qнет-2¯{\ displaystyle q_ {n} = q_ {n-1} {\ overline {q_ {n-2}}}} если не.

С помощью и, «поверните налево» и «поверните направо», и , q0знак равноϵ{\ displaystyle q_ {0} = \ epsilon}q1знак равноD{\ displaystyle q_ {1} = D}граммзнак равно{\ Displaystyle G =}Dзнак равно{\ displaystyle D =}D¯знак равнограмм{\ displaystyle {\ overline {D}} = G}

Некоторые замечательные свойства:

• Это плитка Фибоначчи, связанная с ранее определенным диагональным вариантом.
• Он прокладывает план на любой итерации (в любом порядке)
• Он проложил плоскость путем перевода двумя разными способами, так что получился двойной псевдоквадрат.
• периметр, на заказ, стоит .нет{\ displaystyle n}4F3нет+1{\ displaystyle 4F_ {3n + 1}}
• его площадь, по порядку, следует за последовательными нечетными индексами последовательности Пелла (определяемой символами, и ).нет{\ displaystyle n}п0знак равно0{\ displaystyle P_ {0} = 0}п1знак равно1{\ Displaystyle P_ {1} = 1}пнетзнак равно2пнет-1+пнет-2{\ Displaystyle P_ {n} = 2P_ {n-1} + P_ {n-2}}

Примечания и ссылки

1. ↑ (in) А. Моннеро-Дюмен, Фрактальное слово Фибоначчи, март 2009 г., на HAL .
2. ↑ ^{a и b} (ru) А. Блонден-Массе, С. Лаббе и С. Брлек, плитки Кристоффеля и Фибоначчи, сентябрь 2009 г.
3. ↑ (in) А. Блонден Масс, С. Лаббе, С. Брлек и Мендес-Франс, «  Снежинки Фибоначчи  » ^{( Архив • Wikiwix • Archive.is • Google • Что делать? )} ,2010 г..

Смотрите также

Связанная статья

Список фракталов по размерности Хаусдорфа

Внешняя ссылка

(ru) С. Брлек, Комбинаторные аспекты двойных квадратов ,июль 2009 г. (материалы конференции, с А. Блонден-Массе и С. Лаббе)

<img src=»https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>

Сколько раз вы замечали Фибоначчи в природе? Вот 7 примеров для вас…

Последовательность Фибоначчи находится путем сложения двух предыдущих чисел последовательности. Вы замечали такое в природе?

Фибоначчи (настоящее имя Леонардо Боначчи) был математиком, разработавшим последовательность Фибоначчи. Последовательность находится путем сложения двух предыдущих чисел последовательности. Выглядит это так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… И так далее. Этот шаблон также можно рассматривать как:

Последовательность Фибоначчи встречается повсюду в природе. Это естественная закономерность. Вот несколько примеров Фибоначчи в природе…

Дерево Ветви

Хотя мы все обычно видим деревья повсюду в нашей повседневной жизни, как часто вы искали в них закономерности? У деревьев Фибоначчи начинается с роста ствола, а затем расширяется по спирали по мере того, как дерево становится больше и выше.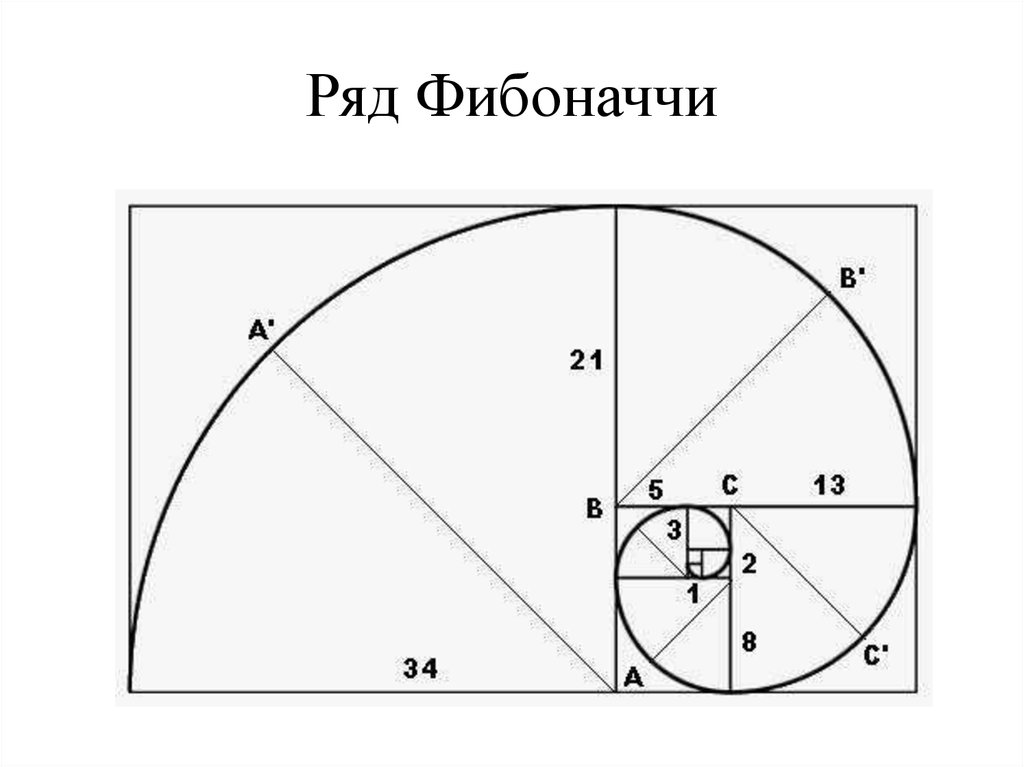

Мы также видим золотое сечение в их ветвях, поскольку они начинаются с одного ствола, который разделяется на 2, затем одна из новых ветвей делится на 2, и эта схема продолжается.

Botanica Mathematica

Штормы

Ваш глаз бури подобен 0 или 1 в последовательности Фибоначчи, когда вы продвигаетесь по спирали против часовой стрелки, вы обнаружите, что она увеличивается по последовательной схеме. Эта закономерность очень похожа на золотое сечение. Но является ли ураган на самом деле спиралью Фибоначчи?? >>

Xah Lee

Морские ракушки

При вскрытии раковины наутилусов образуют логарифмическую спираль, состоящую из секций с камерами, называемых камерами. Каждая новая камера равна размеру двух камер перед ней, что создает логарифмическую спираль. Этот пропорциональный рост происходит потому, что наутилус растет с постоянной скоростью на протяжении всей своей жизни, пока не достигнет своего полного размера.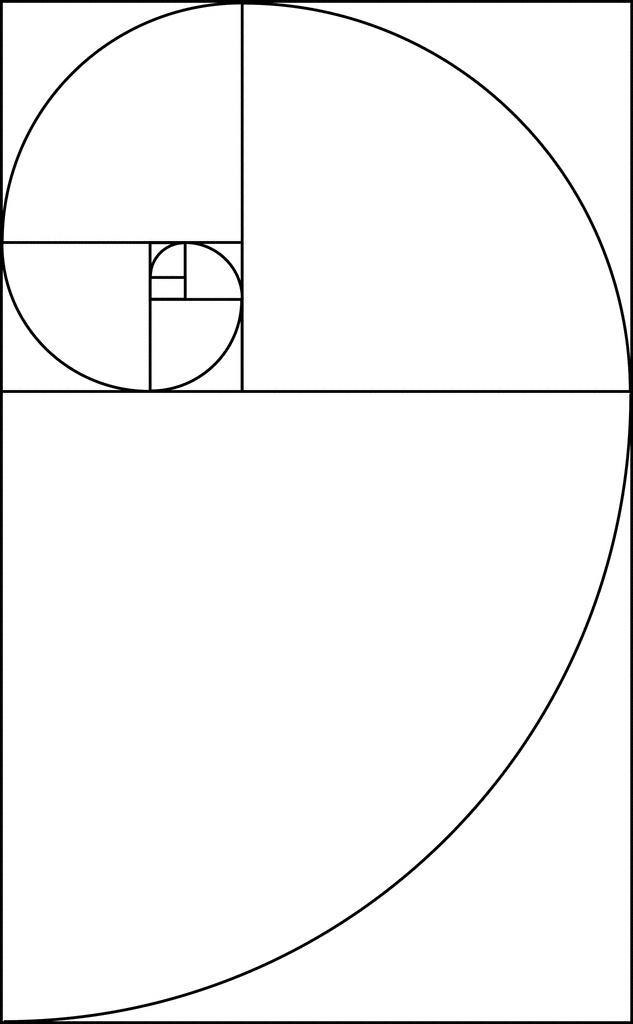

Геометрикон

Лепестки цветов

Лепестки цветка растут согласно Фибоначчи. Из наиболее заметных последовательностей Фибоначчи в растениях лилии с тремя лепестками и лютики с их пятью лепестками являются одними из наиболее легко узнаваемых.

Галактики

Золотую спираль можно найти в форме «рук» галактик, если присмотреться. Невозможно сказать, следуют ли галактики по идеальной спирали, потому что мы не можем точно измерить галактику, но на бумаге мы можем измерить ее и увидеть размер. Подробнее о Фибоначчи в галактиках читайте здесь >>

Азбука науки

Цветочные головки

В большинстве случаев семена выходят из центра цветочной головки и мигрируют наружу. Прекрасным примером этого являются подсолнухи с их спиралевидными узорами. В некоторых местах их семенные головки настолько упакованы, что их количество может быть чрезвычайно большим, иногда до 144 и более. При анализе этих спиралей почти всегда число Фибоначчи.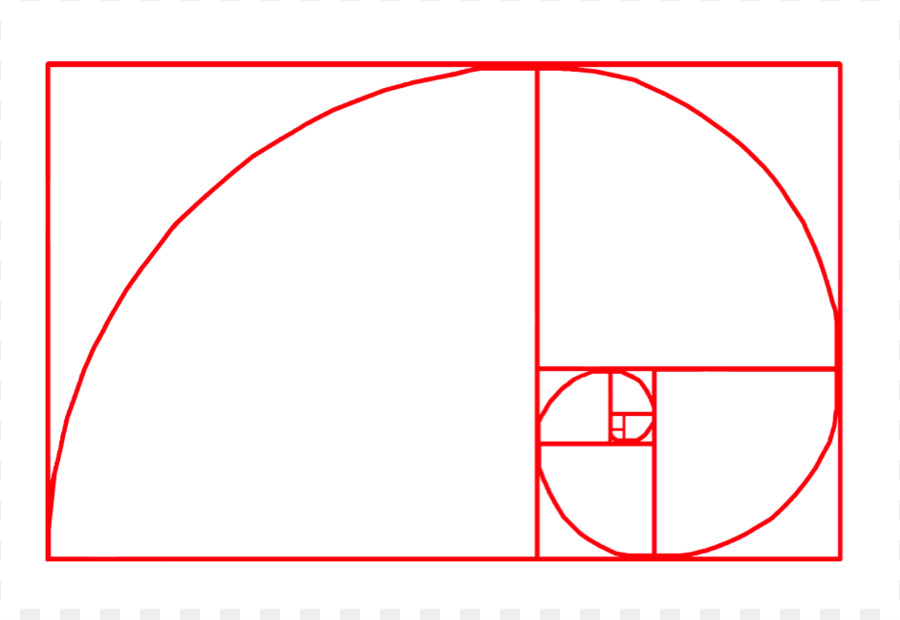

Кливленд Дизайн

ВЫ!

Вы являетесь примером красоты последовательности Фибоначчи. Человеческое тело имеет различные представления пропорций последовательности Фибоначчи, от лица до ушей и рук. Теперь было доказано, что вы математически великолепны.

Пинтерест Светящиеся блоги Золотое сечение

. В природе так много других примеров Фибоначчи, что мы не смогли бы включить их в этот список. Подробнее о Фибоначчи на Odyssey >>

Заинтересованы в STEM? Хотите найти единомышленников? Присоединяйтесь к нам в Stemet tes Society.

Вы молодая женщина или небинарный молодой человек, который ищет наставника для старта в вашей карьере STEM? Ознакомьтесь с нашей программой STS.

Изображение предоставлено Джулией Мэй | Скрыть

Искусство спирали Фибоначчи — Etsy.de

Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных.