| Оно не становится сильнее, когда квадрат расстояния между излучателем и приемником уменьшается. | |
| Радиоволны быстро уменьшаются в интенсивности на обратный квадрат расстояния, когда они распространяются от передающей антенны. | |
| Другие результаты | |
| Расстояние между двумя точками по определению равно квадратному корню из суммы квадратов разностей координат точек в трёх пространственных измерениях. | |
| Расстояние до квадрата примерно… | |
| Переместив квадрат на такое же расстояние под прямым углом к самому себе, мы получим куб. | |
| Каждый квадратный член-это нормированное расстояние, отображающее энергию символа. | |
В общем числе наименьших квадратов остаток представляет собой расстояние между точкой данных и подогнанной кривой, измеренное вдоль некоторого направления. | |
| В статистике расстояние Кука или D Кука-это обычно используемая оценка влияния точки данных при выполнении регрессионного анализа наименьших квадратов. | |
| В этом случае расстояние — это квадратная или абсолютная разница между пикселем и центром кластера. | |
| Линия проходила на довольно значительном расстоянии от скопления черных квадратов, обозначавших большие соборы или церкви. | |
| Японские и корейские пенхолдеры часто используют ракетку с квадратной головкой для игры на расстоянии от стола. | |
| Беспроводные точки доступа также часто находятся рядом с людьми, но падение мощности на расстоянии происходит быстро, следуя закону обратных квадратов. | |
| Выражая формулу Херона с определителем Кэли-Менгера в терминах квадратов расстояний между тремя заданными вершинами,. | |
Глубина резкости изменяется линейно с числом F и кругом путаницы, но изменяется пропорционально квадрату фокусного расстояния и расстоянию до объекта.
| |
| Да, да, притяжение ослабевает с квадратом расстояния. | |
| Но нам всем известен остроумный ответ на вопрос, что есть филантроп: Это человек, чье милосердие увеличивается прямо пропорционально квадрату расстояния. | |
| Это говорит нам, что сила притяжения между двумя телами … находится в прямой пропорции к их массам … и в обратной пропорции к квадрату расстояния между ними. | |
| Сила пропорциональна произведению двух масс и обратно пропорциональна квадрату расстояния между ними. | |
| И то и другое-законы обратных квадратов, где сила обратно пропорциональна квадрату расстояния между телами. | |
| Отношение расстояния между объектами, находящимися в свободном падении, к квадрату времени было недавно подтверждено Гримальди и Риччоли между 1640 и 1650 годами. | |
Интенсивность радиоволн быстро уменьшается на величину, обратную квадрату расстояния, по мере их распространения от передающей антенны. | |
| Квадрат евклидова расстояния используется в качестве метрики для декодеров мягких решений. | |
| Таким образом, вычисление расстояния в квадрате Евклидовой метрики для вычисления метрики ветви может быть выполнено с помощью простой операции сложения/вычитания. | |
| Другими словами, погрешность пропорциональна квадрату расстояния между точками данных. | |
| Как правило, алгоритм использует квадратные расстояния для сравнения, чтобы избежать вычисления квадратных корней. | |
| Кроме того, он может сэкономить вычисление, удерживая квадрат текущего наилучшего расстояния в переменной для сравнения. | |
| Квадратурные правила с равными расстояниями между точками обладают очень удобным свойством вложенности. | |
| ГУК, не имея доказательств в пользу этого предположения, мог только предполагать, что закон обратных квадратов приблизительно действителен на больших расстояниях от центра. | |
Это требует чрезвычайно чувствительных экспериментов, которые ищут отклонение от закона обратных квадратов гравитации на различных расстояниях. | |
Закон обратных квадратов
Говоря техническими терминами, закон обратных квадратов в физике утверждает, что «значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина». Вам, должно быть, интересно, что закон с подобным определением может иметь общего с фотографией (и никто вас не осудит). Закон обратных квадратов применим для множества вещей в этом мире. Сегодня, однако, мы рассмотрим лишь одну из них: свет.
Объяснение концепции
Для тех из нас, кто не слишком близко знаком с высшей математикой (или даже с основами математики, если уж на то пошло), нечто вроде закона обратных квадратов может показаться невероятно сложным. Там есть уравнения с числами и переменными, ссылки на физику и множество других вещей, которые, откровенно говоря, кажутся очень скучными. По этой причине мы постараемся охватить данную тему с практической стороны, а не с технической.
Сам закон в фотографии используется в вопросах освещения. Вообще-то, он применим по отношению к любому виду освещения, но наиболее важные области его применения касаются вне-камерного освещения. В общем, закон обратных квадратов учит нас, как работает свет на расстоянии и почему расстояние между источником света и объектом так важно.
Допустим, у нас есть источник света, включенный на полную мощность, и наша модель находится в 1 метре от него. Если мы переместим модель на удвоенное расстояние от источника (2 метра), какова будет мощность света, достигающего ее? Естественная мысль «половина мощности», — но, к сожалению, это не так, а свет работает в соответствии с законом обратных квадратов.
Согласно закону, мощность света будет обратно пропорциональна квадрату расстояния. Таким образом, если мы возьмем расстояние 2 и возведем это число в квадрат, мы получим 4, обратное значение составит ¼, то есть четверть первоначальной мощности — не половину.
Перемещение объекта на три метра от источника (3 * 3 = 9, т.е. 1/9) приведет к тому, что мощность достигающего его света составит 1/9 от первоначального значения.
На рисунке ниже показано, как уменьшается мощность света от 1 до 10 метров, помните, что каждый показатель – просто обратный квадрат расстояния свыше 1.
Закон обратных квадратов объясняет существенное снижение мощности света на расстоянии. Мы можем использовать эту информацию, чтобы лучше понимать, как наше освещение влияет на модель, и в соответствии с этим лучше контролировать его.
Практическое применение
Итак, знание о снижении мощности света забавно и все такое прочее…но как мы можем найти ему достойное применение в нашей фотографической работе? Это касается, в первую очередь, экспозиции и относительного расположения объектов. Когда свет направлен в определенном направлении, первоначально уменьшение мощности происходит очень быстро, а затем замедляется, чем дальше, тем больше.
Помните, что с законом квадратов числа увеличиваются все быстрее и быстрее, но с законом обратных квадратов они уменьшаются все медленнее и медленнее.
Если мы взглянем на уменьшение мощности света от 1 м до 10 м в процентах с точностью до целого числа, это будет выглядеть так:
Здесь мы видим падение на 75% от 1 до 2 метров, но всего 5%-ное снижение освещенности от 4 метров до 10 метров.
Экспозиция
Таким образом, мы понимаем, что близко к источнику света мощность большая, но далеко от него мы располагаем лишь очень небольшим количеством света. Исходя из этого, для получения правильной экспозиции (предполагается, что мы используем постоянную выдержку), если объект очень близко к свету, то мы должны установить нашу диафрагму примерно на F16, чтобы блокировать все излишки света.
Если, с другой стороны, объект расположен очень далеко от источника, тогда нам следует выбрать значение диафрагмы примерно F4, чтобы захватить больше света.
Исходя из этого, мы можем приблизительно оценить, какие значения диафрагмы нужно использовать на том или ином расстоянии, чтобы получить корректную экспозицию. Помните, что мощность света поначалу снижается очень быстро, а затем медленнее. По тому же принципу, мы поначалу открываем диафрагму очень резко, а потом тем медленнее, чем дальше мы от источника света.
Освещение одного объекта
Давайте переместим шкалу с диафрагменными числами на вершину диаграммы в качестве удобной точки отсчета. Теперь следующий момент: некоторые объекты не двигаются, и это означает, что как только вы поместите объект на определенном расстоянии от источника света, вы установите экспозицию, и на этом всё.
Однако если вы снимаете человека (особенно стоящего человека), он имеют тенденцию перемещаться. Если ваша модель очень близко к источнику света, и она (или он) переместится на полшага в любом направлении, то она сразу же окажется недо- или переэкспонирована.
Однако если модель находится дальше от источника, тогда она может перемещаться на несколько шагов в любом направлении, и вам вообще не нужно будет изменять настройки камеры.
Освещение группы объектов
Предыдущее правило работает очень схоже и для группы объектов. Если все ваши объекты находятся очень близко к источнику, тогда тот, что дальше от источника, окажется сильно недоэкспонированным по сравнению с тем, что ближе к свету – в диапазоне от F22 до F11.
Но если вы переместите все объекты дальше от источника, они все будут освещены достаточно хорошо на диафрагме около F4.
Освещение фона
Конечно, порой вы действительно хотите сделать так, чтобы какой-то элемент фотографии был ярким, а другой темным, как в случае с фоном. Так, если вы помещаете модель очень близко к источнику света, а фон на определенном расстоянии, тогда (предполагается, что модель экспонирована корректно) фон будет сильно недоэкспонирован.
Если вы хотите ярко осветить и модель, и фон, переместите их дальше от источника света, но близко друг к другу.
Заключение
Это было лишь небольшое введение в закон обратных квадратов и способы его применения в освещении в фотографии. Есть множество, множество переменных, которые могут быть скорректированы для получения различных эффектов, такие как выдержка, яркость источника света и использование нескольких источников.
Однако надеюсь, что теперь вы понимаете основы закона обратных квадратов и можете начать применять их в вашей фотографической работе для получения лучшего, более подходящего вам освещения.
Если у вас есть какие-то полезные советы, которые помогут людям в понимании данной темы, или что-то еще, чем вы хотите поделиться, вы можете сделать это в комментариях ниже!
Автор статьи: John O’Nolan
Закон Ньютона проверили в нанометровом масштабе с помощью рассеяния нейтронов
C. Haddock et al. / Phys. Rev. D
Haddock et al. / Phys. Rev. D
Физики из США и Японии показали, что закон обратных квадратов Ньютона работает вплоть до расстояний порядка 0,1 нанометра — сила гравитационного притяжения между телами обратно пропорциональна квадрату расстояния даже на таких маленьких масштабах. Чтобы проверить это утверждение, ученые рассеивали нейтроны на молекулах благородных газов и смотрели, какой вклад в сечение процессов вносит гравитация. Статья опубликована в Physical Review D, кратко о ней сообщает Physics, препринт работы можно найти на сайте arXiv.org.
На данный момент физикам известно четыре фундаментальных взаимодействия — электромагнитное, слабое, сильное и гравитационное. Первые три из них можно объединить с помощью перенормируемой калибровочной теории, известной как Стандартная модель, однако для гравитации этот подход не работает. Вместо этого приходится описывать ее с помощью классической (то есть не квантовой) Общей теории относительности Эйнштейна, которая в пределе малых скоростей и напряженностей гравитационного потенциала переходит в теорию гравитации Ньютона — так называемый закон обратных квадратов. Если точнее, в нерелятивистском пределе сила притяжения между двумя телами прямо пропорционально их массам и обратно пропорциональна квадрату расстояния между ними.
Первые три из них можно объединить с помощью перенормируемой калибровочной теории, известной как Стандартная модель, однако для гравитации этот подход не работает. Вместо этого приходится описывать ее с помощью классической (то есть не квантовой) Общей теории относительности Эйнштейна, которая в пределе малых скоростей и напряженностей гравитационного потенциала переходит в теорию гравитации Ньютона — так называемый закон обратных квадратов. Если точнее, в нерелятивистском пределе сила притяжения между двумя телами прямо пропорционально их массам и обратно пропорциональна квадрату расстояния между ними.
В квантовой теории поля такому закону должны отвечать переносчики взаимодействия, масса которых в точности равна нулю. Например, кулоновское (электростатическое) отталкивание между электронами можно представить как обмен виртуальным безмассовым фотоном, а потому его сила тоже обратно пропорциональна квадрату расстояния между частицами. Напротив, в теории Юкавы, которая приближенно описывает сильные взаимодействия, переносчик имеет массу, а потому интенсивность юкавских сил экспоненциально падает с увеличением расстояния между частицами. Таким образом, естественно было бы ожидать, что гипотетические гравитоны — переносчики гравитационного взаимодействия — тоже будут иметь нулевую массу. В самом деле, наблюдения за гравитационными волнами, приходящими от двойных систем сливающихся черных дыр или нейтронных звезд, позволили наложить довольно сильные ограничения на массу гравитонов (верхняя граница mg ~ 10−22 электронвольт). Таким образом, поведение гравитации на больших расстояниях довольно хорошо изучено.
Таким образом, естественно было бы ожидать, что гипотетические гравитоны — переносчики гравитационного взаимодействия — тоже будут иметь нулевую массу. В самом деле, наблюдения за гравитационными волнами, приходящими от двойных систем сливающихся черных дыр или нейтронных звезд, позволили наложить довольно сильные ограничения на массу гравитонов (верхняя граница mg ~ 10−22 электронвольт). Таким образом, поведение гравитации на больших расстояниях довольно хорошо изучено.
С другой стороны, многие альтернативные теории гравитации хорошо воспроизводят закон обратных квадратов на больших расстояниях, но предсказывают новые эффекты на расстояниях порядка нанометров. В этих теориях к безмассовым гравитонам добавляются массивные, влияние которых экспоненциально быстро затухает с расстоянием. Примером такой теории может выступать модель Аркани-Хамеда (Nima Arkani-Hamed), в которой гравитация компактифицируется путем включения в теорию дополнительных пространственных измерений. Поэтому необходимо проверить, работает ли на небольших расстояниях стандартный закон обратных квадратов, чтобы подтвердить или исключить подобные теории.
Поэтому необходимо проверить, работает ли на небольших расстояниях стандартный закон обратных квадратов, чтобы подтвердить или исключить подобные теории.
Подобную экспериментальную проверку описывает в своей статье группа ученых под руководством Тамаки Йошиока (Tamaki Yoshioka). Для этого исследователи использовали рассеяние нейтронов на молекулах благородных газов. Поскольку нейтроны и молекулы в целом электрически нейтральны, сила электрического отталкивания для них пренебрежимо мала, и тонкие эффекты, к которым может привести обмен новой массивной частицей, теоретически можно увидеть на практике. В самом деле, при включении в теорию новой массивной частицы к обычному потенциалу Ньютона добавляется экспоненциально затухающий член — следовательно, полное сечение рассеяния нейтронов на молекулах изменяется. Разумеется, чем больше масса частицы, тем слабее проявляется ее действие. Измеряя сечение рассеяния и проверяя, при каких параметрах теория лучше всего согласуется с практикой, можно определить ограничения на массу гипотетической частицы.
Схема экспериментальной установки
C. Haddock et al. / Phys. Rev. D
Именно такую проверку и провели авторы в своей работе. В качестве источника нейтронов выступала установка NOP (The Neutron Optics and Physics beam line), работающая в рамках ускорительного комплекса J-PARC. Полученные на установке нейтроны направлялись в камеру, заполненную гелием-4 или ксеноном-131, которые очищались от примесей с помощью «выпечки» (bake out) — одновременного нагревания и понижения давления в газе. Затем рассеянные нейтроны регистрировались с помощью детектора, заполненного молекулами гелия-3 и определяющего величину отклонения частицы от центра установки. Наконец, смещение нейтронов пересчитывалось в скорость, что позволяло построить зависимость сечения рассеяния от переданного молекулам импульса.
После того, как ученые завершили сбор экспериментальных данных, они проанализировали их, разделив вклад в сечение рассеяния различных взаимодействий и подобрав с помощью численных расчетов такие параметры теории, которые лучше всего объясняли измеренные значения сечений. Интересно, что несмотря на нулевой заряд нейтрона и молекул газов в целом, распределение зарядов в их объеме тоже сказывается на величине сечения, а потому физики его тоже учли. В результате ученые исключили большую область на плоскости параметров λ — α (λ — это комптоновская длина волны, то есть обратная масса частицы, а α — множитель, который описывает величину силы при фиксированном расстоянии). Если кратко, то исследователи показали, что закон обратных квадратов хорошо работает вплоть до расстояний порядка 0,1 нанометра.
Область параметров «неквадратной» части гравитационной силы, исключенные в различных экспериментах. Красным отмечены результаты текущего эксперимента
Красным отмечены результаты текущего эксперимента
C. Haddock et al. / Phys. Rev. D
В мае 2016 года японские астрономы впервые проверили работу Общей теории относительности для красных смещений z ~ 1,4, что отвечает световым лучам, шедшим до Земли более 13 миллиардов лет. В ноябре прошлого года ученые показали, что возможные нарушения лоренц-инвариантности ОТО и Стандартной модели не внесли сколько-нибудь заметный вклад в движение Луны и приливные эффекты. А в декабре французский спутник Microscope подтвердил, что гравитационная и инертная масса тел совпадает с очень хорошей точностью (их отношение может отличаться от единицы не более чем на 10−14). Ни один из перечисленных выше экспериментов не нашел отклонений от классической теории гравитации.
Дмитрий Трунин
квадрат расстояния — это.
 .. Что такое квадрат расстояния?
.. Что такое квадрат расстояния?
- квадрат расстояния
- squared distance
Большой англо-русский и русско-английский словарь. 2001.
- квадрат разности
- квадрат смешанной корреляции
Смотреть что такое «квадрат расстояния» в других словарях:
ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ — физическая теория, рассматривающая пространственно временные закономерности, справедливые для любых физ. процессов. Универсальность пространственно временных св в, рассматриваемых О. т., позволяет говорить о них просто как о .св вах пространства… … Физическая энциклопедия
Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.
 … … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
… … Энциклопедический словарь Ф.А. Брокгауза и И.А. ЕфронаДиффузия — I Диффузия (от лат. diffusio распространение, растекание) взаимное проникновение соприкасающихся веществ друг в друга вследствие теплового движения частиц вещества. Д. происходит в направлении падения концентрации вещества и ведёт к… … Большая советская энциклопедия
ТЯГОТЕНИЕ — или гравитация, свойство материи, которое состоит в том, что между любыми двумя частицами существуют силы притяжения. Тяготение универсальное взаимодействие, охватывающее всю доступную наблюдению Вселенную и потому называемое всемирным. Как мы… … Энциклопедия Кольера
Нейронный газ — Эту статью следует викифицировать. Пожалуйста, оформите её согласно правилам оформления статей … Википедия
Задача Кеплера в общей теории относительности — Общая теория относительности … Википедия
Метрика пространства-времени — У этого термина существуют и другие значения, см.
 Метрика. Схематическая двумерная иллюстрация искривления пространства времени возле массивного тела Метрика пространства времени 4 тензор, к … Википедия
Метрика. Схематическая двумерная иллюстрация искривления пространства времени возле массивного тела Метрика пространства времени 4 тензор, к … ВикипедияЧетырёхугольник — ЧЕТЫРЁХУГОЛЬНИКИ ┌─────────────┼────────────┐ невыпуклый выпуклый самопересекающийся … Википедия
Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
Частичные силы — Принятие атомической теории строения веществ (см. Вещество) влечет за собою, как необходимую принадлежность, допущение существования особых сил между молекулами в теле и между атомами в каждой молекуле. Благодаря этим силам сохраняется прочность… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Минковского пространство — четырёхмерное пространство, объединяющее физическое трёхмерное пространство и время; введено Г. Минковским (См. Минковский) в 1907 1908. Точки в М. п. соответствуют «событиям» специальной теории относительности (см.
 Относительности… … Большая советская энциклопедия
Относительности… … Большая советская энциклопедия
Кластерный анализ
Кластерный анализКластерный анализ
Основная цель
Термин кластерный анализ (впервые ввел Tryon,
1939) в действительности включает в себя набор
различных алгоритмов
классификации. Общий вопрос, задаваемый
исследователями во многих областях, состоит в
том, как организовать наблюдаемые данные в
наглядные структуры, т.е. развернуть таксономии.
Например, биологи ставят цель разбить животных
на различные виды, чтобы содержательно описать
различия между ними. В соответствии с
современной системой, принятой в биологии,
человек принадлежит к приматам, млекопитающим,
амниотам, позвоночным и животным. Заметьте, что в
этой классификации, чем выше уровень агрегации,
тем меньше сходства между членами в
соответствующем классе. Человек имеет больше
сходства с другими приматами (т.е. с обезьянами),
чем с «отдаленными» членами семейства
млекопитающих (например, собаками) и т.д. В
последующих разделах будут рассмотрены общие
методы кластерного анализа, см. Объединение
(древовидная кластеризация), Двувходовое
объединение и Метод K средних.
Человек имеет больше
сходства с другими приматами (т.е. с обезьянами),
чем с «отдаленными» членами семейства
млекопитающих (например, собаками) и т.д. В
последующих разделах будут рассмотрены общие
методы кластерного анализа, см. Объединение
(древовидная кластеризация), Двувходовое
объединение и Метод K средних.
Проверка статистической значимости
Заметим, что предыдущие рассуждения ссылаются
на алгоритмы кластеризации, но ничего не
упоминают о проверке статистической значимости.
Фактически, кластерный анализ является не
столько обычным статистическим методом, сколько
«набором» различных алгоритмов
«распределения объектов по кластерам».
Существует точка зрения, что в отличие от многих
других статистических процедур, методы
кластерного анализа используются в большинстве
случаев тогда, когда вы не имеете каких-либо
априорных гипотез относительно классов, но все
еще находитесь в описательной стадии
исследования. Следует понимать, что кластерный
анализ определяет «наиболее возможно значимое
решение». Поэтому проверка статистической
значимости в действительности здесь
неприменима, даже в случаях, когда известны
p-уровни (как, например, в методе K
средних).
Следует понимать, что кластерный
анализ определяет «наиболее возможно значимое
решение». Поэтому проверка статистической
значимости в действительности здесь
неприменима, даже в случаях, когда известны
p-уровни (как, например, в методе K
средних).
Области применения
Техника кластеризации применяется в самых
разнообразных областях. Хартиган (Hartigan, 1975) дал
прекрасный обзор многих опубликованных
исследований, содержащих результаты, полученные
методами кластерного анализа. Например, в
области медицины кластеризация заболеваний,
лечения заболеваний или симптомов заболеваний
приводит к широко используемым таксономиям. В
области психиатрии правильная диагностика
кластеров симптомов, таких как паранойя,
шизофрения и т.д., является решающей для успешной
терапии. В археологии с помощью кластерного
анализа исследователи пытаются установить
таксономии каменных орудий, похоронных объектов
и т. д. Известны широкие применения кластерного
анализа в маркетинговых исследованиях. В общем,
всякий раз, когда необходимо классифицировать
«горы» информации к пригодным для
дальнейшей обработки группам, кластерный анализ
оказывается весьма полезным и эффективным.
д. Известны широкие применения кластерного
анализа в маркетинговых исследованиях. В общем,
всякий раз, когда необходимо классифицировать
«горы» информации к пригодным для
дальнейшей обработки группам, кластерный анализ
оказывается весьма полезным и эффективным.
Объединение (древовидная кластеризация)
Общая логика
Приведенный в разделе Основная цель пример поясняет цель алгоритма объединения (древовидной кластеризации). Назначение этого алгоритма состоит в объединении объектов (например, животных) в достаточно большие кластеры, используя некоторую меру сходства или расстояние между объектами. Типичным результатом такой кластеризации является иерархическое дерево.
Иерархическое дерево
Рассмотрим горизонтальную древовидную
диаграмму. Диаграмма начинается с каждого
объекта в классе (в левой части диаграммы). Теперь
представим себе, что постепенно (очень малыми
шагами) вы «ослабляете» ваш критерий о том,
какие объекты являются уникальными, а какие нет.
Другими словами, вы понижаете порог, относящийся
к решению об объединении двух или более объектов
в один кластер.
Теперь
представим себе, что постепенно (очень малыми
шагами) вы «ослабляете» ваш критерий о том,
какие объекты являются уникальными, а какие нет.
Другими словами, вы понижаете порог, относящийся
к решению об объединении двух или более объектов
в один кластер.
В результате, вы связываете вместе всё
большее и большее число объектов и агрегируете (объединяете)
все больше и больше кластеров, состоящих из все
сильнее различающихся элементов. Окончательно,
на последнем шаге все объекты объединяются
вместе. На этих диаграммах горизонтальные оси
представляют расстояние объединения (в вертикальных
древовидных диаграммах вертикальные оси
представляют расстояние объединения). Так, для
каждого узла в графе (там, где формируется новый
кластер) вы можете видеть величину расстояния,
для которого соответствующие элементы
связываются в новый единственный кластер.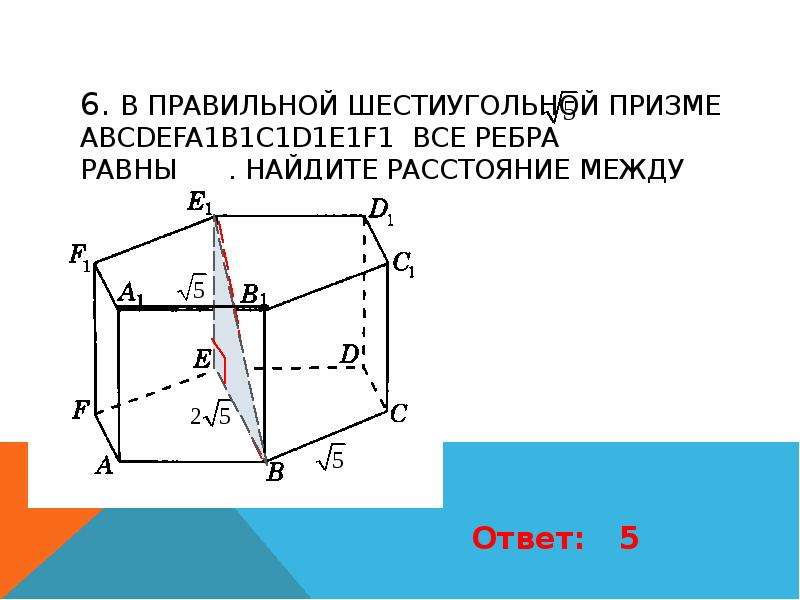 Когда
данные имеют ясную «структуру» в терминах
кластеров объектов, сходных между собой, тогда
эта структура, скорее всего, должна быть отражена
в иерархическом дереве различными ветвями. В
результате успешного анализа методом
объединения появляется возможность обнаружить
кластеры (ветви) и интерпретировать их.
Когда
данные имеют ясную «структуру» в терминах
кластеров объектов, сходных между собой, тогда
эта структура, скорее всего, должна быть отражена
в иерархическом дереве различными ветвями. В
результате успешного анализа методом
объединения появляется возможность обнаружить
кластеры (ветви) и интерпретировать их.
Меры расстояния
Объединение или метод древовидной
кластеризации используется при формировании
кластеров несходства или расстояния между
объектами. Эти расстояния могут определяться в
одномерном или многомерном пространстве.
Например, если вы должны кластеризовать типы еды
в кафе, то можете принять во внимание количество
содержащихся в ней калорий, цену, субъективную
оценку вкуса и т.д. Наиболее прямой путь
вычисления расстояний между объектами в
многомерном пространстве состоит в вычислении
евклидовых расстояний. Если вы имеете двух- или
трёхмерное пространство, то эта мера является
реальным геометрическим расстоянием между
объектами в пространстве (как будто расстояния
между объектами измерены рулеткой). Однако
алгоритм объединения не «заботится» о том,
являются ли «предоставленные» для этого
расстояния настоящими или некоторыми другими
производными мерами расстояния, что более
значимо для исследователя; и задачей
исследователей является подобрать правильный
метод для специфических применений.
Однако
алгоритм объединения не «заботится» о том,
являются ли «предоставленные» для этого
расстояния настоящими или некоторыми другими
производными мерами расстояния, что более
значимо для исследователя; и задачей
исследователей является подобрать правильный
метод для специфических применений.
Евклидово расстояние. Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:
расстояние(x,y) = {i (xi — yi)2 }1/2
Заметим, что евклидово расстояние (и его
квадрат) вычисляется по исходным, а не по
стандартизованным данным. Это обычный способ его
вычисления, который имеет определенные
преимущества (например, расстояние между двумя
объектами не изменяется при введении в анализ
нового объекта, который может оказаться
выбросом). Тем не менее, на расстояния могут
сильно влиять различия между осями, по
координатам которых вычисляются эти расстояния.
К примеру, если одна из осей измерена в
сантиметрах, а вы потом переведете ее в
миллиметры (умножая значения на 10), то
окончательное евклидово расстояние (или квадрат
евклидова расстояния), вычисляемое по
координатам, сильно изменится, и, как следствие,
результаты кластерного анализа могут сильно
отличаться от предыдущих.
Тем не менее, на расстояния могут
сильно влиять различия между осями, по
координатам которых вычисляются эти расстояния.
К примеру, если одна из осей измерена в
сантиметрах, а вы потом переведете ее в
миллиметры (умножая значения на 10), то
окончательное евклидово расстояние (или квадрат
евклидова расстояния), вычисляемое по
координатам, сильно изменится, и, как следствие,
результаты кластерного анализа могут сильно
отличаться от предыдущих.
Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом (см. также замечания в предыдущем пункте):
расстояние(x,y) = i (xi — yi)2
Расстояние городских кварталов
(манхэттенское расстояние). Это расстояние
является просто средним разностей по
координатам. В большинстве случаев эта мера
расстояния приводит к таким же результатам, как и
для обычного расстояния Евклида. Однако отметим,
что для этой меры влияние отдельных больших
разностей (выбросов) уменьшается (так как они не
возводятся в квадрат). Манхэттенское расстояние
вычисляется по формуле:
Это расстояние
является просто средним разностей по
координатам. В большинстве случаев эта мера
расстояния приводит к таким же результатам, как и
для обычного расстояния Евклида. Однако отметим,
что для этой меры влияние отдельных больших
разностей (выбросов) уменьшается (так как они не
возводятся в квадрат). Манхэттенское расстояние
вычисляется по формуле:
расстояние(x,y) = i |xi — yi|
Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как «различные», если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:
расстояние(x,y) = Максимум|xi — yi|
Степенное расстояние. Иногда желают
прогрессивно увеличить или уменьшить вес,
относящийся к размерности, для которой
соответствующие объекты сильно отличаются.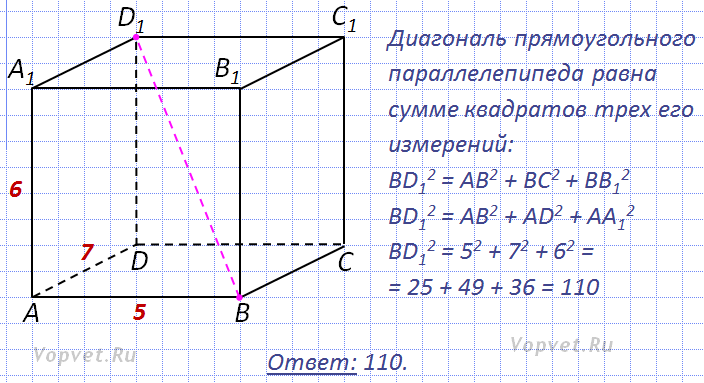 Это
может быть достигнуто с использованием
степенного расстояния. Степенное расстояние
вычисляется по формуле:
Это
может быть достигнуто с использованием
степенного расстояния. Степенное расстояние
вычисляется по формуле:
расстояние(x,y) = (i |xi — yi|p)1/r
где r и p — параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как «работает» эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра — r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.
Процент несогласия. Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:
расстояние(x,y) = (Количество xi yi)/ i
Правила объединения или связи
На первом шаге, когда каждый объект
представляет собой отдельный кластер,
расстояния между этими объектами определяются
выбранной мерой. Однако когда связываются вместе
несколько объектов, возникает вопрос, как
следует определить расстояния между кластерами?
Другими словами, необходимо правило объединения
или связи для двух кластеров. Здесь имеются
различные возможности: например, вы можете
связать два кластера вместе, когда любые два
объекта в двух кластерах ближе друг к другу, чем
соответствующее расстояние связи. Другими
словами, вы используете «правило ближайшего
соседа» для определения расстояния между
кластерами; этот метод называется методом одиночной
связи. Это правило строит «волокнистые»
кластеры, т.е. кластеры, «сцепленные вместе»
только отдельными элементами, случайно
оказавшимися ближе остальных друг к другу. Как
альтернативу вы можете использовать соседей в
кластерах, которые находятся дальше всех
остальных пар объектов друг от друга. Этот метод
называется метод полной связи. Существует
также множество других методов объединения
кластеров, подобных тем, что были рассмотрены.
Однако когда связываются вместе
несколько объектов, возникает вопрос, как
следует определить расстояния между кластерами?
Другими словами, необходимо правило объединения
или связи для двух кластеров. Здесь имеются
различные возможности: например, вы можете
связать два кластера вместе, когда любые два
объекта в двух кластерах ближе друг к другу, чем
соответствующее расстояние связи. Другими
словами, вы используете «правило ближайшего
соседа» для определения расстояния между
кластерами; этот метод называется методом одиночной
связи. Это правило строит «волокнистые»
кластеры, т.е. кластеры, «сцепленные вместе»
только отдельными элементами, случайно
оказавшимися ближе остальных друг к другу. Как
альтернативу вы можете использовать соседей в
кластерах, которые находятся дальше всех
остальных пар объектов друг от друга. Этот метод
называется метод полной связи. Существует
также множество других методов объединения
кластеров, подобных тем, что были рассмотрены.
Одиночная связь (метод ближайшего соседа). Как было описано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Это правило должно, в известном смысле, нанизывать объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными «цепочками».
Полная связь (метод наиболее удаленных
соседей). В этом методе расстояния между
кластерами определяются наибольшим расстоянием
между любыми двумя объектами в различных
кластерах (т.е. «наиболее удаленными
соседями»). Этот метод обычно работает очень
хорошо, когда объекты происходят на самом деле из
реально различных «рощ». Если же кластеры
имеют в некотором роде удлиненную форму или их
естественный тип является «цепочечным», то
этот метод непригоден.
Невзвешенное попарное среднее. В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные «рощи», однако он работает одинаково хорошо и в случаях протяженных («цепочного» типа) кластеров. Отметим, что в своей книге Снит и Сокэл (Sneath, Sokal, 1973) вводят аббревиатуру UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего — unweighted pair-group method using arithmetic averages.
Взвешенное попарное среднее. Метод
идентичен методу невзвешенного попарного
среднего, за исключением того, что при
вычислениях размер соответствующих кластеров
(т.е. число объектов, содержащихся в них)
используется в качестве весового коэффициента.
Поэтому предлагаемый метод должен быть
использован (скорее даже, чем предыдущий), когда
предполагаются неравные размеры кластеров. В
книге Снита и Сокэла (Sneath, Sokal, 1973) вводится
аббревиатура WPGMA для ссылки на этот метод, как
на метод взвешенного попарного
арифметического среднего — weighted pair-group method using
arithmetic averages.
В
книге Снита и Сокэла (Sneath, Sokal, 1973) вводится
аббревиатура WPGMA для ссылки на этот метод, как
на метод взвешенного попарного
арифметического среднего — weighted pair-group method using
arithmetic averages.
Невзвешенный центроидный метод. В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. Снит и Сокэл (Sneath and Sokal (1973)) используют аббревиатуру UPGMC для ссылки на этот метод, как на метод невзвешенного попарного центроидного усреднения — unweighted pair-group method using the centroid average.
Взвешенный центроидный метод (медиана). тот
метод идентичен предыдущему, за исключением
того, что при вычислениях используются веса для
учёта разницы между размерами кластеров (т.е.
числами объектов в них). Поэтому, если имеются
(или подозреваются) значительные отличия в
размерах кластеров, этот метод оказывается
предпочтительнее предыдущего. Снит и Сокэл (Sneath,
Sokal 1973) использовали аббревиатуру WPGMC для
ссылок на него, как на метод невзвешенного
попарного центроидного усреднения — weighted
pair-group method using the centroid average.
Снит и Сокэл (Sneath,
Sokal 1973) использовали аббревиатуру WPGMC для
ссылок на него, как на метод невзвешенного
попарного центроидного усреднения — weighted
pair-group method using the centroid average.
Метод Варда. Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Подробности можно найти в работе Варда (Ward, 1963). В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.
Для обзора других методов кластеризации, см. Двухвходовое объединение и Метод K средних.
Двувходовое объединение
Вводный обзор
Ранее этот метод обсуждался в терминах
«объектов», которые должны быть
кластеризованы (см. Объединение
(древовидная кластеризация)). Во всех других
видах анализа интересующий исследователя вопрос
обычно выражается в терминах наблюдений или
переменных. Оказывается, что кластеризация, как
по наблюдениям, так и по переменным может
привести к достаточно интересным результатам.
Например, представьте, что медицинский
исследователь собирает данные о различных
характеристиках (переменные) состояний
пациентов (наблюдений), страдающих сердечными
заболеваниями. Исследователь может захотеть
кластеризовать наблюдения (пациентов) для
определения кластеров пациентов со сходными
симптомами. В то же самое время исследователь
может захотеть кластеризовать переменные для
определения кластеров переменных, которые
связаны со сходным физическим состоянием.
Объединение
(древовидная кластеризация)). Во всех других
видах анализа интересующий исследователя вопрос
обычно выражается в терминах наблюдений или
переменных. Оказывается, что кластеризация, как
по наблюдениям, так и по переменным может
привести к достаточно интересным результатам.
Например, представьте, что медицинский
исследователь собирает данные о различных
характеристиках (переменные) состояний
пациентов (наблюдений), страдающих сердечными
заболеваниями. Исследователь может захотеть
кластеризовать наблюдения (пациентов) для
определения кластеров пациентов со сходными
симптомами. В то же самое время исследователь
может захотеть кластеризовать переменные для
определения кластеров переменных, которые
связаны со сходным физическим состоянием.
Двувходовое объединение
После этого обсуждения, относящегося к тому,
кластеризовать наблюдения или переменные, можно
задать вопрос, а почему бы не проводить
кластеризацию в обоих направлениях? Модуль Кластерный
анализ содержит эффективную двувходовую
процедуру объединения, позволяющую сделать
именно это.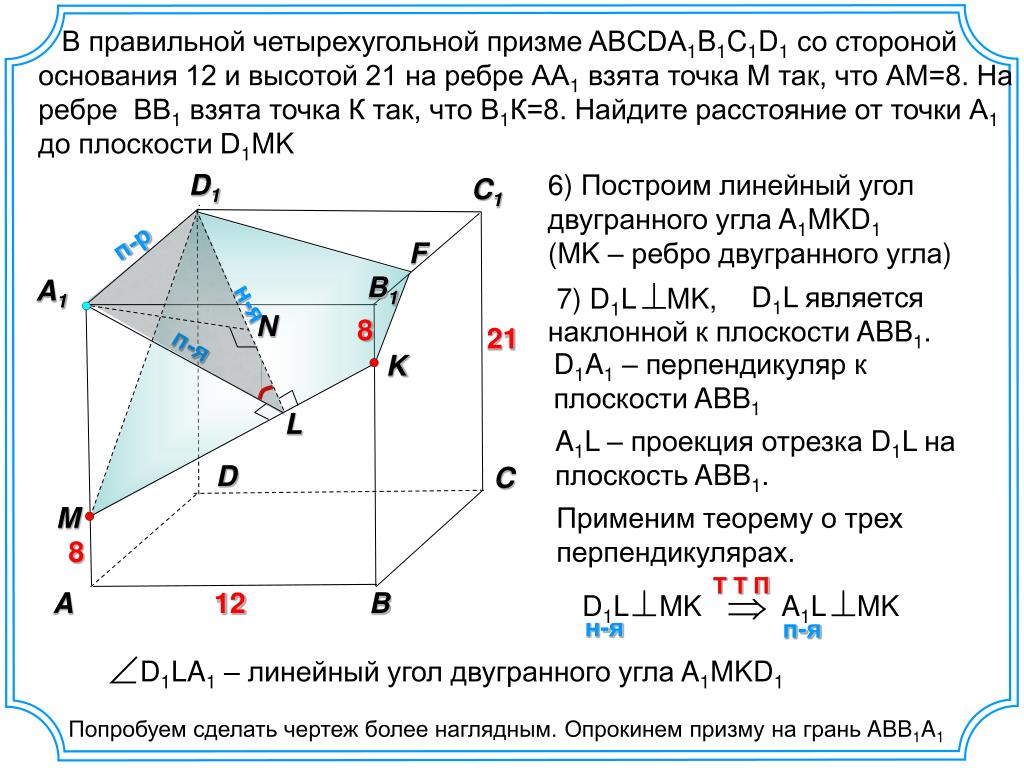 Однако двувходовое объединение
используется (относительно редко) в
обстоятельствах, когда ожидается, что и
наблюдения и переменные одновременно вносят
вклад в обнаружение осмысленных кластеров.
Однако двувходовое объединение
используется (относительно редко) в
обстоятельствах, когда ожидается, что и
наблюдения и переменные одновременно вносят
вклад в обнаружение осмысленных кластеров.
Так, возвращаясь к предыдущему примеру, можно
предположить, что медицинскому исследователю
требуется выделить кластеры пациентов, сходных
по отношению к определенным кластерам
характеристик физического состояния. Трудность
с интерпретацией полученных результатов
возникает вследствие того, что сходства между
различными кластерами могут происходить из (или
быть причиной) некоторого различия подмножеств
переменных. Поэтому получающиеся кластеры
являются по своей природе неоднородными.
Возможно это кажется вначале немного туманным; в
самом деле, в сравнении с другими описанными
методами кластерного анализа (см. Объединение (древовидная
кластеризация) и Метод K средних),
двувходовое объединение является, вероятно,
наименее часто используемым методом.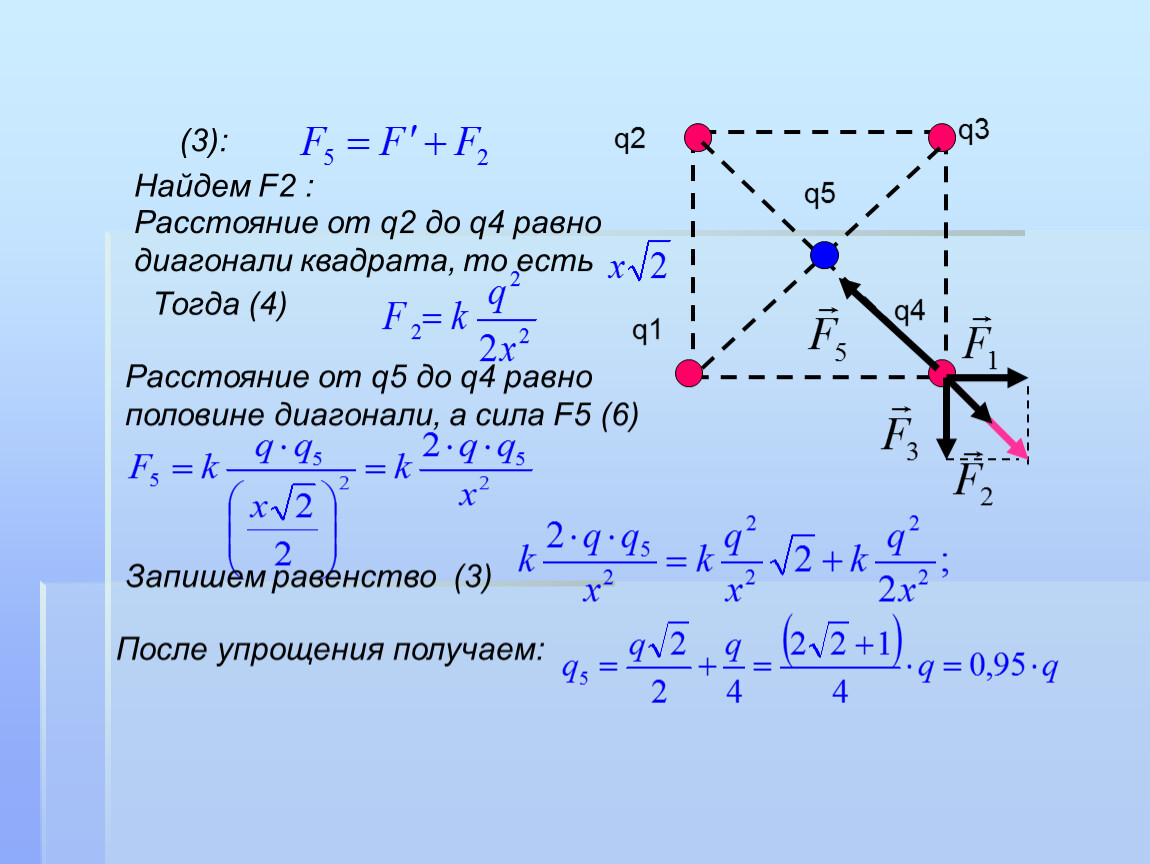 Однако
некоторые исследователи полагают, что он
предлагает мощное средство разведочного анализа
данных (за более подробной информацией вы можете
обратиться к описанию этого метода у Хартигана
(Hartigan, 1975)).
Однако
некоторые исследователи полагают, что он
предлагает мощное средство разведочного анализа
данных (за более подробной информацией вы можете
обратиться к описанию этого метода у Хартигана
(Hartigan, 1975)).
Метод K средних
Общая логика
Этот метод кластеризации существенно
отличается от таких агломеративных методов, как Объединение (древовидная
кластеризация) и Двувходовое
объединение. Предположим, вы уже имеете
гипотезы относительно числа кластеров (по
наблюдениям или по переменным). Вы можете указать
системе образовать ровно три кластера так, чтобы
они были настолько различны, насколько это
возможно. Это именно тот тип задач, которые
решает алгоритм
метода K средних. В общем случае метод K средних
строит ровно K различных кластеров,
расположенных на возможно больших расстояниях
друг от друга.
Пример
В примере с физическим состоянием (см. Двувходовое объединение), медицинский исследователь может иметь «подозрение» из своего клинического опыта, что его пациенты в основном попадают в три различные категории. Далее он может захотеть узнать, может ли его интуиция быть подтверждена численно, то есть, в самом ли деле кластерный анализ K средних даст три кластера пациентов, как ожидалось? Если это так, то средние различных мер физических параметров для каждого кластера будут давать количественный способ представления гипотез исследователя (например, пациенты в кластере 1 имеют высокий параметр 1, меньший параметр 2 и т.д.).
Вычисления
С вычислительной точки зрения вы можете
рассматривать этот метод, как дисперсионный
анализ (см. Дисперсионный анализ)
«наоборот». Программа начинает с K случайно
выбранных кластеров, а затем изменяет
принадлежность объектов к ним, чтобы: (1) -
минимизировать изменчивость внутри
кластеров, и (2) — максимизировать изменчивость между
кластерами. Данный способ аналогичен методу
«дисперсионный анализ (ANOVA) наоборот» в том
смысле, что критерий значимости в дисперсионном
анализе сравнивает межгрупповую изменчивость с
внутригрупповой при проверке гипотезы о том, что
средние в группах отличаются друг от друга. В
кластеризации методом K средних программа
перемещает объекты (т.е. наблюдения) из одних
групп (кластеров) в другие для того, чтобы
получить наиболее значимый результат при
проведении дисперсионного анализа (ANOVA).
Данный способ аналогичен методу
«дисперсионный анализ (ANOVA) наоборот» в том
смысле, что критерий значимости в дисперсионном
анализе сравнивает межгрупповую изменчивость с
внутригрупповой при проверке гипотезы о том, что
средние в группах отличаются друг от друга. В
кластеризации методом K средних программа
перемещает объекты (т.е. наблюдения) из одних
групп (кластеров) в другие для того, чтобы
получить наиболее значимый результат при
проведении дисперсионного анализа (ANOVA).
Интерпретация результатов
Обычно, когда результаты кластерного анализа
методом K средних получены, можно рассчитать
средние для каждого кластера по каждому
измерению, чтобы оценить, насколько кластеры
различаются друг от друга. В идеале вы должны
получить сильно различающиеся средние для
большинства, если не для всех измерений,
используемых в анализе. Значения F-статистики,
полученные для каждого измерения, являются
другим индикатором того, насколько хорошо
соответствующее измерение дискриминирует
кластеры.
Все права на материалы электронного учебника принадлежат компании StatSoft
Галактика в безопасности. Почему первый межзвездный астероид не врезался в Солнце
Если первый в истории межзвездный объект, попавший в Солнечную систему и замеченный астрономами, Oumuamua (в переводе с гавайского может означать «разведчик» или «посланец издалека») был привлечен в нашу систему Солнцем, почему он не врезался в эту звезду?
Как рассуждает колумнист Forbes Джиллиан Скаддер, все дело в действии гравитации на больших расстояниях. Автор объясняет, что на поверхности Земли сила тяжести в значительной степени постоянна на протяжении всей нашей жизни. «Мы признаем это как влияние, которое удерживает нас на поверхности планеты, при этом оно остается некой постоянной особенностью именно нашей планеты», — говорит она.
Дело в том, что мы все постоянно живем (более или менее) на одном и том же расстоянии от центра Земли. Если же каким-то образом расстояние между нами и центром Земли поменяется, то сила тяжести также изменится. И произойдет это довольно быстро — в правой части уравнения гравитационной силы расположена единица, деленная на квадрат расстояния между центрами двух объектов. Таким образом, если расстояние между нами и массивным объектом будет удвоено, гравитационная сила сократится в четыре раза. Если мы решим продолжать движение и еще удвоить дистанцию, без того ослабшая гравитационная сила между нами и объектом сократится еще на четверть, до одной шестнадцатой ее первоначального значения. При расстояниях в рамках Солнечной системы гравитационное влияние Земли довольно быстро сокращается до незначительного для окружающего пространства и объектов, уточняет автор.
И произойдет это довольно быстро — в правой части уравнения гравитационной силы расположена единица, деленная на квадрат расстояния между центрами двух объектов. Таким образом, если расстояние между нами и массивным объектом будет удвоено, гравитационная сила сократится в четыре раза. Если мы решим продолжать движение и еще удвоить дистанцию, без того ослабшая гравитационная сила между нами и объектом сократится еще на четверть, до одной шестнадцатой ее первоначального значения. При расстояниях в рамках Солнечной системы гравитационное влияние Земли довольно быстро сокращается до незначительного для окружающего пространства и объектов, уточняет автор.
Гравитация и расстояния
Дело в том, что в масштабах Солнечной системы вся масса Земли — это небольшой орех, например, арахис по сравнению с массой Солнца. Это логично, поскольку Земля является одной из самых небольших планет Солнечной системы. Так, например, масса Юпитера более чем в 300 раз больше массы Земли, а само Солнце в тысячу раз больше, чем Юпитер. Потому при расчете движения космических кораблей ученые учитывают и влияние Юпитера.
Потому при расчете движения космических кораблей ученые учитывают и влияние Юпитера.
Однако, если мы обратим внимание на гравитационные возмущения, возникающие от влияния Солнца, на другие объекты в нашей галактике, мы увидим, что гравитационная сила Солнца также очень быстро сокращается до незначительных значений с увеличением расстояния до объектов. Таким образом, в большей части путешествия Оумуамуа гравитационное притяжение нашего Солнца не оказывало никакого влияния на направление, в котором путешествовал космический объект.
Если бы астероид летел прямо на Солнце, то сила притяжения звезды лишь ускорила бы его. Переориентации направления движения в этом случае бы не потребовалось. Почему же все-таки он не врезался? В первую очередь, причина кроется в том, что астероид летел достаточно быстро и провел лишь короткий промежуток времени близко к Солнцу, где сила тяжести была особенно сильной. Звезда действительно немного отрегулировала движение астероида, однако Солнце «спас» тот факт, что в области сильных гравитационных возмущений, космическое тело находилось лишь короткий период времени.
Реклама на Forbes
Предыстория
Межзвездная комета С/2017 U1 (PANSTARRS), оказавшаяся впоследствии астероидом, была обнаружена 18 октября 2017 года обсерваторией США PANSTARRS 1. Наблюдения за космическим объектом показали, что он движется со скоростью около 26 км/с по незамкнутой гиперболической траектории. Ученые также установили, что космическое тело прилетело из-за пределов Солнечной системы и вскоре покинет ее. Дополнительные наблюдения с помощью телескопа VLT Европейской южной обсерватории свидетельствуют о том, что C/2017 U1 не имеет никаких признаков комы — газовой оболочки вокруг ядра, — и является скорее астероидом. В связи с этим «кометный» индекс «C» в названии изменили на астероидный «А».
Исследователи предприняли множество попыток определить, откуда именно прибыл межзвездный объект, который прилетел откуда-то из созвездия Лиры. По их мнению, его родиной могла быть Вега, одна из ярчайших звезд северного неба, которая находится в 25 световых годах от Земли. При этом сама Вега тоже перемещается, и 300 000 лет назад, когда U1 пролетал по соседству с ее нынешним положением, она была в иной точке неба.
При этом сама Вега тоже перемещается, и 300 000 лет назад, когда U1 пролетал по соседству с ее нынешним положением, она была в иной точке неба.
Объект стал первым небесным телом, которое получило новый «межзвездный» индекс — «I» (от interstellar). Малые тела Солнечной системы получают индексы A (астероид), С (комета), Р (периодическая комета). Полное название нового объекта выглядит так: 1I/2017 U1 (’Oumuamua).
Догнать астероид
Примечателен астероид еще и тем, что представляет собой вытянутое сигарообразное тело размером с половину городского квартала. Исследователи уже успели предложить догнать и изучить странный космический объект. В то же время сделать это, по их словам, можно лишь, имея современные космические технологии. «Реалистичным мог бы быть запуск через 5-10 лет (2023-2027 годы). Тогда при скорости аппарата от 33 до 76 км/с время миссии займет от 5 до 30 лет», — подсчитали авторы исследования, опубликованного в журнале Nature. Астроном Карен Мич из Гавайского института астрономии, соавтор статьи, добавил, что космическое тело имеет темно-красный оттенок, аналогичный тому, что имеют объекты во внешних частях Солнечной системы, и астрономы не нашли никаких признаков пыли вокруг него.
Работа со светом — закон обратных квадратов
В техническом плане, закон обратных квадратов является законом, который утверждает о том, что значение физической величины в определенной точке пространства является обратно пропорциональным квадрату расстояния к источнику поля, непосредственно которое и характеризует эта самая физическая величина. У многих данное определение вызовет недоумение. Казалось бы, как это относится к фотографии, и вообще, что это значит? На самом деле, это напрямую относится к фотографии, а точнее, к работе со светом.
Концепция
Данный закон позволяет легче понимать важность расстояния от объекта съемки до источника света. По сути, закон обратных квадратов поясняет степень уменьшения яркости света в зависимости от увеличения расстояния. Допустим, что есть источник света, который работает на полную мощность. Объект стоит от него на расстоянии двух метров. А как изменится освещение объекта, если он отойдет на 2 метра от источника света. многим может показаться, что освещение уменьшится в 2 раза, но на самом деле это не так.
многим может показаться, что освещение уменьшится в 2 раза, но на самом деле это не так.
Опираясь на закон обратных квадратов, можно сказать, что сила света будет обратно пропорциональна квадрату расстояния. Получается, что если взять расстояние 2 метра, то квадрат этого числа будет равняться 4, а так как нам необходимо обратно пропорциональное значение, то мы получим 1/4. Получается, что на расстоянии 2 метра от источника света освещение уменьшится на 1/4. На расстоянии 3 метра интенсивность освещенности уменьшится до значения 1/9, так как квадрат числа 3=9, а обратная пропорциональность дает значение 1/9.
Таким образом, можно построить таблицу, которая будет описывать интенсивность света в зависимости от источника света до объекта.
Практика
В фотографии описанный выше закон влияет на экспозицию. Можно говорить о том, что первоначальное падение освещенности объекта происходит быстро, но чем дальше удаляется объект, тем падение освещенности уменьшается. Для наглядности можно взглянуть на схему, которая демонстрирует процентное отношения падения освещенности на расстоянии 10 метров:
Для наглядности можно взглянуть на схему, которая демонстрирует процентное отношения падения освещенности на расстоянии 10 метров:
Можно заметить, что с первого по второй метр интенсивность света уменьшается на целых 75%, но затем, с 4 по 20 падает только лишь на 5%.
Экспонирование
Мы разобрались с тем, что чем объект съемки находится ближе к источнику света, тем сильнее он освещен, а чем он находится дальше, тем, соответственно, освещен он слабее. Основываясь на имеющихся данных, можно сказать, что для создания снимка с нормальной экспозицией при близко стоящем к источнику света объекте, следует использовать значение диафрагмы F16. Закрытая диафрагма отсечет часть света, которая в данном случае может дать переэкспонирование. В том случае, если объект расположен достаточно далеко, диафрагму желательно открыть до значения F4. Это позволит большему количеству света пройди сквозь объектив и попасть на матрицу. При одинаковой выдержке обе фотографии должны смотреться примерно одинаково, так как диафрагмой мы уравняли количество света, попадающего на сенсор камеры.
Это позволяет примерно рассчитать, на каком расстоянии от источника света какое значение диафрагмы следует использовать:
Освещение одного объекта
Теперь поместим значения диафрагмы на верхнюю часть схемы и представим, что источником света освещена модель, которая постоянно двигается в кадре. Вы наверняка заметил, что чем ближе объект съемки находится к источнику света, тем чаще происходят колебания числа F. Это значит, что если наша модель, находясь близко к источнику света, сделает шаг назад или вперед, нужно перестраивать камеру, иначе снимок получится или пересвеченный или слишком темный.
Расположив модель на расстоянии от 6 до 9 метров, можно позволить ей ходить во все стороны, а вы можете сконцентрироваться на съемке и не перестраивать камеру.
Освещение нескольких объектов
При работе с несколькими объектами или моделями может оказаться, что они окажутся неравномерно освещены. Например, расположив объекты съемки близко к источнику света, они окажутся в диапазоне от F22 до F11. Это значит, что некоторые объекты могут оказаться пересвечены, а некоторые слишком темные:
Например, расположив объекты съемки близко к источнику света, они окажутся в диапазоне от F22 до F11. Это значит, что некоторые объекты могут оказаться пересвечены, а некоторые слишком темные:
Если же переместить те же объекты на расстояние 7-9 метров от источника света, все они окажутся в одной световой зоне и будут освещены одинаково:
Освещение фона
Часто в съемке необходимо, чтобы одни предметы были светлее других. Это часто используется при работе с фоном. В таком случае можно поместить модель значительно ближе к источнику света, чем фон. При таком построении кадра фон будет казаться темным, а модель светлой.
Чтобы получить одинаковое освещение модели и фона, их необходимо расположить подальше от источника света и поставить недалеко друг от друга:
Вывод
На самом деле то, что было описано в статье — это лишь основы закона обратных квадратов. Он на самом деле намного более запутанный. Дело в том, что в нем очень много переменных. К ним относится мощность источника света, несколько источников, скорость затвора камеры, дополнительные линзы и многое другое. Зная основу, всегда можно продолжить изучение. Даже описанная выше информация, при правильном её использовании может помочь делать более качественные снимки.
На основе материалов с сайта: http://photomotion.ru
Квадратное расстояние — обзор
7.2.1 Модель линейной регрессии
Базовое уравнение прогнозирования выражает линейную связь между независимой переменной ( x , прогнозирующая переменная) и зависимой переменной ( y , критериальной переменной или человеческий ответ)
(1) y = mx + b
, где m — наклон отношения, а b — точка пересечения y . (См. Рисунок 7.11.)
Рисунок 7.11.Линейная связь между независимой переменной ( x ) и зависимой переменной ( y ).
Чтобы построить это уравнение, нам сначала понадобится набор из x-y точек выборки. Хотя подойдут любые две переменные шкалы отношений, чаще всего x-y точек объединяют настройку независимой переменной шкалы отношений ( x ) с измеренным значением реакции человека на зависимую переменную ( y ). Поскольку мы имеем дело с людьми, изменчивость неизбежна, поэтому точки выборки вряд ли окажутся на линии.Они разбегутся. Если модель хороша, точки будут достаточно близко к прямой линии. Насколько близко — ключевой вопрос.
Поиск наиболее подходящей прямой включает процесс, известный в статистике как линейная регрессия . Цель состоит в том, чтобы найти коэффициенты m и b в уравнении 1 для линии, чем минимизирует квадраты расстояний ( наименьших квадратов ) точек от линии. 7 Результатом является уравнение прогнозирования — уравнение, которое дает наилучшую оценку y в единицах x .Конечно, модель основана на точках выборки, используемых при построении уравнения. Если данные верны и модель верна, должно появиться хорошее уравнение прогноза. Также существует встроенное предположение, что связь линейна, что не обязательно так. Давайте рассмотрим пример в HCI.
В рамках эксперимента по исследованию ввода текста с помощью стилуса на программных клавиатурах Маккензи и Чжан (2001) также интересовались, можно ли предсказать скорость ввода с помощью стилуса, исходя из скорости набора пользователем сенсорного ввода со стандартной клавиатурой.В эксперименте приняли участие 12 человек. Участникам был предложен предварительный тест для измерения скорости набора текста вслепую. Во время эксперимента участники вводили текст с помощью стилуса и мягкой клавиатуры Qwerty, отображаемой на ЖК-планшете и дигитайзере. Предварительная тестовая скорость набора текста вслепую (независимая переменная) и экспериментально измеренная скорость нажатия стилусом (зависимая переменная) приведены на рис. 7.12a для каждого участника.
Рисунок 7.12. Взаимосвязь между скоростью нажатия стилусом и скоростью слепого набора: (a) Данные.(б) Диаграмма рассеяния.
(адаптировано из MacKenzie and Zhang, 2001, рис. 4)Часто перед построением уравнения прогнозирования задается более простой вопрос: существует ли связь между двумя переменными? В этом примере вопрос заключается в следующем: быстро ли машинисты нажимают стилусом? 8 Визуализация данных в виде диаграммы рассеяния помогает (см. Рис. 7.12b). Да, вроде бы отношения есть. Например, самый медленный сенсорный наборщик, P12 со скоростью 19 слов в минуту, также довольно медленно нажимал стилусом (13.1 слов в минуту). Для 12 точек на рисунке коэффициент корреляции равен r = 0,5228. 9 Это скромная положительная корреляция.
Следующим шагом является построение уравнения прогнозирования — наиболее подходящего уравнения для прямой линии, прогнозирующего скорость нажатия стилусом ( y ) на основе скорости набора текста вслепую ( x ). Это легко сделать с помощью приложения для работы с электронными таблицами, такого как Microsoft Excel. 10 Для данных на рисунке 7.12a уравнение прогнозирования:
(2) y = 0.1342 x + 15.037
Рис. 7.13 — это приукрашенная версия диаграммы на рис. 7.12b. Помимо разброса точек, он показывает линию для уравнения прогнозирования вместе с уравнением и квадратом коэффициента корреляции, R 2 = 0,2733. (По соглашению R 2 задается в верхнем регистре, r в нижнем регистре.) R 2 интерпретируется как величина вариации данных, которая объясняется моделью. Обычно это выражается в процентах.Таким образом, модель в уравнении 2 объясняет около 27 процентов вариации данных на рис. 7.12a. Это не очень много, поэтому в данном случае модель в лучшем случае является скромным предиктором скорости нажатия стилусом по сравнению со скоростью слепого набора. 11
Рисунок 7.13. График разброса на рис. 7.12b, украшенный линией линейной регрессии, уравнением прогнозирования, квадратом коэффициента корреляции ( R 2 ) и пунктирными линиями, показывающими 95% доверительный интервал.
Одним из преимуществ модели прогнозирования является возможность прогнозирования результата на основе значения предсказателя, который фактически никогда не посещался.Обратите внимание на рис. 7.12a, что ни у одного из участников скорость набора слепым шрифтом не превышала 60 слов в минуту. Даже в этом случае мы можем предположить, что пользователь со скоростью слепого набора 60 слов в минуту будет иметь скорость нажатия стилусом:
(3) y = 0,1342 (60) + 15,037 = 23,1 слов в минуту
С учетом разброса точек На рис. 7.12a явно присутствует некоторая неопределенность, связанная с этим прогнозом. Стандартная ошибка оценки ( SE ) — полезная статистика для измерения этой неопределенности. SE устанавливает доверительные интервалы вокруг прогноза.Для данных на рисунке 7.12a SE = 3,39 слов в минуту. 12 Значения в пределах -1,96 SE и +1,96 SE прогноза находятся в пределах 95% доверительного интервала. Таким образом, для модели, разработанной здесь, существует 95% уверенности в том, что пользователь, скорость набора которого составляет 60 слов в минуту, будет иметь скорость нажатия стилусом между 23,1 — (1,96 × 3,39) = 16,4 слов в минуту и 23,1 + (1,96 × 3,39) = 29,7 слов в минуту. Пунктирные линии, показывающие окно доверительной вероятности 95%, включены на рис. 7.13.
Обычно сообщают о моделях линейной регрессии, дающих уравнение и R 2 .Доверительные интервалы и SE обычно не приводятся, хотя есть исключения (Chung and Hossain, 2008; Johnsen, Raij, Stevens, Lind, and Lok, 2007; MacKenzie and Buxton, 1994). Иногда стандартная ошибка указывается отдельно для коэффициентов наклона и пересечения в модели линейной регрессии (Accot and Zhai, 2001; Cao et al., 2008; Pastel, 2006). Перейдем к популярной модели прогнозирования в HCI — закону Фиттса.
Квадрат евклидова расстояния — обзор
Далее нас интересует матрица расстояний для всех пар Δ формы m × n с использованием квадрата евклидова расстояния в качестве меры сходства:
(6.4) Δij = dist (Xtest (i), Xtrain (j)) = ∑k = 0d − 1 (Xtest (i) [k] −Xtrain (j) [k]) 2,
, где i∈ {0, …, M − 1} и j∈ {0,…, n − 1}. Мы видим, что временная сложность алгоритма O (m⋅d⋅n) почти на три порядка выше, чем его сложность памяти, равная O (m⋅n), поскольку количество пикселей на изображение d = 784 достаточно велико. Следовательно, мы ожидаем, что эта программа будет масштабироваться значительно лучше, чем ранее обсуждавшиеся примеры сложения векторов и умножения векторов матриц. Кроме того, если мы перепишем уравнение.(6.4) путем расширения его с помощью биномиальной теоремы
(6.5) Δij = ∑k = 0d − 1 (Xtest (i) [k]) 2−2∑k = 0d − 1 (Xtest (i) [k ] ⋅Xtrain (j) [k]) + ∑k = 0d − 1 (Xtrain (j) [k]) 2.
Мы наблюдаем разложение на два члена самовзаимодействия (первый и последний), которые зависят только от индекса i или j , а третий член смешивания (средний) зависит как от i , так и от j , которые на самом деле является умножением плотных матриц. Следовательно, обсуждаемые методы распараллеливания могут также применяться к другим постепенно накапливаемым мерам сходства, таким как коэффициент корреляции Пирсона двух z-нормированных (исчезающее среднее значение и единичная дисперсия) случайных величин x (i) и y (j)
( 6.6) ρ (x (i), y (j)) = ∑k = 0d − 1x (i) [k] ⋅y (j) [k] (средний член),
кросс-энтропия и расходимость Кульбака – Лейблера векторов вероятностей p (i) и q (j)
(6.7) H (p (i), q (j)) = — ∑k = 0d − 1p (i) [k] ⋅log (q (j ) [k]), KLD (p (i) || q (j)) = ∑k = 0d − 1p (i) [k] ⋅log (p (i) [k] / q (j) [k ]),
и расстояние Хэмминга между парами строк s (i) и t (j) фиксированной длины d
(6.8) Ham (s (i), t (j)) = ∑k = 0d −1 {0, если s (i) [k] == t (j) [k] 1else.
Общим для всех вышеупомянутых попарных мер является то, что они могут быть вычислены независимо для фиксированной комбинации индексов (i, j).Более того, их окончательное значение рассчитывается как сумма индивидуальных вкладов для каждого значения k . В результате у нас есть два основных варианта распараллеливания: либо мы распараллеливаем набор независимых индексов (i, j), либо выполняем параллельное сокращение суммы по внутреннему индексу k . Эффективность распараллеливания зависит от размеров матриц данных m, n, d. В дальнейшем мы будем называть распараллеливание внешних циклов «крупнозернистым» распараллеливанием, а внутреннее — «мелкозернистым».
Квадратное евклидово расстояние: статистический тест для оценки изменений растительного сообщества
Лесная служба США
Уход за землей и служение людям
Министерство сельского хозяйства США
-
Евклидово расстояние в квадрате: статистический тест для оценки изменений в растительном сообществе
Автор (ы): Раймонд Д. Рэтлифф; Сильвия Р. Мори
Дата: 1993
Источник: Res.Обратите внимание на PSW-RN-416. Олбани, Калифорния: Министерство сельского хозяйства США, Лесная служба, Тихоокеанская юго-западная исследовательская станция. 4 p.
Серия публикаций: Research Note (RN)
Station: Pacific Southwest Research Station
PDF: Download Publication (419 КБ)
Описание Описываются концепции и процедура для оценки изменения растительного сообщества с использованием функции сходства в квадрате Евклидова расстояния (SED).Анализ основан на концепции, согласно которой евклидовы расстояния составляют выборку из совокупности расстояний между единицами выборки (SU) за определенное количество раз и SU. В разное время расстояния будут внутрикластерными или межкластерными. Межкластерные расстояния представляют собой контрольную обработку. Если сообщества различаются по времени, популяция будет содержать кластеры (области высокой плотности с небольшими расстояниями между SU), которые разделены областями с низкой плотностью (большие расстояния между SU).Средние квадраты внутри и между годами из анализа дисперсии для каждого вида (sp) в матрице данных можно использовать для вычисления среднего внутрикластерного и межкластерного расстояний. Многомерный дисперсионный анализ ANOV A дает проверку гипотезы о том, что среднее внутрикластерное расстояние равно среднему межкластерному расстоянию при общей частоте ошибок, приблизительно равной ex. Статистическое распределение SED — это распределение линейной комбинации независимых случайных величин хи-квадрат. Знание этого распределения и использование обычных приближений делают возможной и надежной оценку приближенных доверительных интервалов для средних межкластерных и внутрикластерных расстояний и их разницы.Можно исследовать доверительные интервалы и принять решение относительно любого указанного изменения в сообществе. Предоставляется простой пример, позволяющий изучить вычислительные методы.
Примечания к публикации- Вы можете отправить электронное письмо по адресу [email protected], чтобы запросить печатную копию этой публикации.
- (укажите именно , какую публикацию вы запрашиваете, и свой почтовый адрес.)
- Мы рекомендуем вам также распечатать эту страницу и прикрепить ее к распечатке статьи, чтобы сохранить полную информацию о цитировании.
- Эта статья была написана и подготовлена служащими правительства США в официальное время и поэтому находится в открытом доступе.
Цитирование Ratliff, Raymond D .; Мори, Сильвия Р. 1993. Евклидово расстояние в квадрате: статистический тест для оценки изменения растительного сообщества. Res. Обратите внимание на PSW-RN-416. Олбани, Калифорния: Министерство сельского хозяйства США, Лесная служба, Тихоокеанская юго-западная исследовательская станция. 4 p
Процитировано
Ключевые слова кластеры, плотность, расстояние, многомерные методы
Связанный поиск
XML: Просмотр XML
Показать больше
Показать меньше
https: // www.fs.usda.gov/treesearch/pubs/32547
Учебное пособие по физике: Закон обратных квадратов
Наука в целом и физика в частности связаны с отношениями. Причина и следствие находятся в центре внимания науки. Природу исследуют, чтобы найти взаимосвязи и математические закономерности. Ученые модифицируют набор условий, чтобы увидеть, есть ли образец поведения в другом наборе измеримых величин. Цель состоит в том, чтобы ответить на вопрос, как изменение набора переменных или условий причинно влияет на наблюдаемый результат? В физике этот поиск причин и следствий приводит к таким вопросам, как:
Как сила влияет на ускорение объекта?Как масса объекта влияет на его ускорение?
Как скорость падающего объекта влияет на величину сопротивления воздуха, которое он испытывает?
Как расстояние от страницы до лампочки влияет на количество света, освещающего поверхность бумаги?
Как частота звуковой волны влияет на скорость движения звуковой волны?
Как расстояние между двумя заряженными объектами влияет на силу притяжения или отталкивания, с которой они сталкиваются?
Этот поиск причины и следствия часто приводит к убедительным свидетельствам того, что две переменные причинно связаны (или не связаны).Тщательное наблюдение и измерение могут указывать на то, что существует модель, в которой увеличение одной переменной всегда вызывает увеличение другой измеряемой величины. Этот тип причинно-следственной связи описывается как прямая связь . Наблюдение также может указывать на то, что увеличение одной переменной всегда вызывает уменьшение другой измеримой величины. Этот тип причинно-следственной связи описывается как обратная связь .
Обратные отношения обычны в природе.В электростатике электрическая сила между двумя заряженными объектами обратно пропорциональна расстоянию между двумя объектами. Увеличение расстояния между объектами уменьшает силу притяжения или отталкивания между объектами. А уменьшение расстояния между объектами увеличивает силу притяжения или отталкивания между объектами. Электрические силы чрезвычайно чувствительны к расстоянию. Эти наблюдения обычно производятся во время демонстраций и лабораторных экспериментов.Представьте заряженную пластиковую трубку для гольфа, которую подносят рядом с лежащими на столе обрывками бумаги. Электрическое взаимодействие настолько мало на больших расстояниях, что кажется, что трубка для гольфа не оказывает влияния на кусочки бумаги. Тем не менее, если трубку поднести ближе, наблюдается привлекательное взаимодействие, а сила настолько велика, что кусочки бумаги отрываются от стола. Подобным образом заряженные воздушные шары оказывают наибольшее влияние на другие заряженные объекты, когда расстояние между ними уменьшается.Электростатическая сила и расстояние обратно связаны.
Схема между электростатической силой и расстоянием может быть дополнительно охарактеризована как соотношение обратных квадратов . Тщательные наблюдения показывают, что электростатическая сила между двумя точечными зарядами изменяется обратно пропорционально квадрату расстояния между двумя зарядами. То есть коэффициент, на который изменяется электростатическая сила, является обратным квадрату коэффициента, на который изменяется разделительное расстояние.Таким образом, если расстояние разделения увеличивается вдвое (увеличивается в 2 раза), то электростатическая сила уменьшается в четыре раза (2 во второй степени). А если расстояние разделения утроить (увеличить в 3 раза), то электростатическая сила уменьшится в девять раз (3 во второй степени). Этот квадратный эффект делает расстояние двойным значением в его воздействии на электростатическую силу.
Обратное квадратичное соотношение между электростатической силой и разделительным расстоянием показано в таблице ниже.
| Ряд | Разделительное расстояние | Электростатическая сила |
| 1 | 20,0 см | 0,1280 с.ш. |
| 2 | 40,0 см | 0.0320 с.ш. |
| 3 | 60,0 см | 0,0142 Н |
| 4 | 80,0 см | 0,0080 Н |
| 5 | 100,0 см | 0,0051 Н |
Приведенные выше значения иллюстрируют закономерность: при удвоении разделительного расстояния электростатическая сила уменьшается в четыре раза.Например, расстояние в строке 2 вдвое больше расстояния в строке 1; а электростатическая сила в строке 2 составляет одну четверть электростатической силы в строке 1. Сравнение строк 1 и 3 показывает, что при увеличении расстояния в три раза сила уменьшается в девять раз. Расстояние в строке 3 в три раза больше, чем в строке 1, а сила в строке 3 составляет одну девятую, чем в строке 1. Аналогичное сравнение строк 1 и 4 показывает, что при увеличении расстояния в четыре раза электростатическая сила уменьшается в 16 раз.Расстояние в строке 4 в четыре раза больше, чем в строке 1, а сила в строке 4 составляет одну шестнадцатую, чем в строке 1.
Обратное квадратичное соотношение между силой и расстоянием выражается в уравнении закона Кулона для электростатической силы. В предыдущем разделе Урока 3 закон Кулона был сформулирован как
.Это уравнение часто используется как рецепт для решения алгебраических задач. Этот тип использования уравнения закона Кулона обсуждался в предыдущем разделе Урока 3.Уравнение показывает, что квадрат расстояния находится в знаменателе уравнения напротив силы. Это показывает, что сила обратно пропорциональна квадрату расстояния.
Понимание этой обратной пропорциональности позволяет использовать уравнение в качестве руководства к размышлениям о том, как изменение одной величины (например, расстояния) влияет на другую величину (Сила). Уравнения могут быть больше, чем просто рецептами для решения алгебраических задач; они могут быть «проводниками мышления».»Проверьте свое понимание закона Кулона как руководства к размышлениям, ответив на приведенные ниже вопросы. Когда закончите, нажмите кнопку, чтобы проверить свои ответы.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения по закону Кулона.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный закон Кулона позволяет учащемуся исследовать влияние заряда и разделительного расстояния на величину электрической силы между двумя заряженными объектами.
Проверьте свое понимание
Используйте свое понимание заряда, чтобы ответить на следующие вопросы. По завершении нажмите кнопку, чтобы просмотреть ответы.
Изменение размера сбора
1. Два заряженных объекта обладают силой отталкивания 0,080 Н. Если заряд одного из объектов удваивается, то какова новая сила?
2. Два заряженных объекта обладают силой отталкивания 0,080 Н. Если заряд обоих объектов удваивается, то какова новая сила?
Изменение расстояния между заряженными предметами
3.Два заряженных объекта обладают силой отталкивания 0,080 Н. Если расстояние, разделяющее объекты, удвоить, то какова новая сила?
4. Два заряженных объекта обладают силой отталкивания 0,080 Н. Если расстояние, разделяющее объекты, утроить, то какова новая сила?
5.Два заряженных объекта обладают силой притяжения 0,080 Н. Если расстояние, разделяющее объекты, увеличить в четыре раза, то какова новая сила?
6. Два заряженных объекта обладают силой отталкивания 0,080 Н. Если расстояние, разделяющее объекты, уменьшается вдвое, какова новая сила?
Изменение количества заряда и расстояния
7.Два заряженных объекта обладают силой отталкивания 0,080 Н. Если заряд одного из объектов удвоен, а расстояние, разделяющее объекты, удвоено, то какова новая сила?
8. Два заряженных объекта обладают силой отталкивания 0,080 Н. Если заряд обоих объектов удвоен, а расстояние, разделяющее объекты, удвоено, то какова новая сила?
9.Два заряженных объекта имеют силу притяжения 0,080 Н. Если заряд одного из объектов увеличивается в четыре раза, а расстояние, разделяющее объекты, увеличивается вдвое, то какова новая сила?
10. Два заряженных объекта имеют силу притяжения 0,080 Н. Если заряд одного из объектов утроился, а расстояние, разделяющее объекты, утроилось, то какова новая сила?
sklearn.metrics.pairwise.euclidean_distances — документация scikit-learn 0.24.2
Рассматривая строки X (и Y = X) как векторы, вычислите матрица расстояний между каждой парой векторов.
По соображениям эффективности евклидово расстояние между парой строк вектор x и y вычисляется как:
расст (x, y) = sqrt (точка (x, x) - 2 * точка (x, y) + точка (y, y))
Эта формулировка имеет два преимущества по сравнению с другими способами вычисления расстояний.
Во-первых, он эффективен с точки зрения вычислений при работе с разреженными данными.Во-вторых, если один аргумент меняется, а другой остается неизменным, то
точек (x, x) и / или точек (y, y) могут быть вычислены заранее.
Однако это не самый точный способ выполнения вычислений,
потому что это уравнение потенциально страдает от «катастрофической отмены».
Кроме того, матрица расстояний, возвращаемая этой функцией, может быть неточной.
симметричный, как того требует, например, scipy.spatial.distance functions.
Подробнее читайте в Руководстве пользователя.
- Параметры
-
- X {массивная разреженная матрица} формы (n_samples_X, n_features)
- Y {массивная разреженная матрица} формы (n_samples_Y, n_features), по умолчанию = None
- Y_norm_squared подобная массиву формы (n_samples_Y,), по умолчанию = Нет
-
Предварительно вычисленные скалярные произведения векторов в Y (например.грамм.,
(Y ** 2) .sum (axis = 1)) В некоторых случаях может игнорироваться, см. Примечание ниже. - в квадрате bool, по умолчанию = False
-
Возврат евклидовых расстояний в квадрат.
- X_norm_squared подобная массиву формы (n_samples,), по умолчанию = Нет
-
Предварительно вычисленные скалярные произведения векторов в X (например,
(X ** 2). Сумма (ось = 1)) В некоторых случаях может игнорироваться, см. Примечание ниже.
- Возвращает
-
- расстояния ndarray формы (n_samples_X, n_samples_Y)
Банкноты
Для достижения большей точности X_norm_squared и Y_norm_squared могут быть
не используются, если они передаются как float32 .
Примеры
>>> from sklearn.metrics.pairwise import euclidean_distances
>>> X = [[0, 1], [1, 1]]
>>> # расстояние между рядами X
>>> euclidean_distances (X, X)
массив ([[0., 1.],
[1., 0.]])
>>> # получить расстояние до исходной точки
>>> euclidean_distances (X, [[0, 0]])
массив ([[1.],
[1.41421356]])
Как работает интерполяция с обратным взвешиванием по расстоянию — ArcGIS Pro
Доступно с лицензией Geostatistical Analyst.
Интерполяция с обратным взвешиванием по расстоянию (IDW) явно предполагает, что объекты, расположенные близко друг к другу, больше похожи, чем объекты, находящиеся дальше друг от друга. Чтобы предсказать значение для любого неизмеренного местоположения, IDW использует измеренные значения, окружающие прогнозируемое местоположение. Ближайшие к прогнозируемому местоположению измеренные значения имеют большее влияние на прогнозируемое значение, чем более удаленные. IDW предполагает, что каждая измеренная точка имеет локальное влияние, которое уменьшается с расстоянием.Это дает больший вес точкам, ближайшим к месту прогноза, и веса уменьшаются в зависимости от расстояния, отсюда и название «взвешенная обратная дистанция». Веса, присвоенные точкам данных, показаны в следующем примере:
Иллюстрация области поискаОкно «Веса» содержит список весов, присвоенных каждой точке данных, которая используется для генерации прогнозируемого значения в месте, отмеченном перекрестием.
Узнайте больше о методах интерполяции, доступных в ArcGIS Geostatistical Analyst
Степенная функция
Как упоминалось выше, веса пропорциональны обратному значению расстояния (между точкой данных и местоположением прогноза), возведенному к значению мощности p .В результате с увеличением расстояния веса быстро уменьшаются. Скорость уменьшения веса зависит от значения p . Если p = 0, уменьшения с расстоянием не происходит, и поскольку все веса λ i одинаковы, прогноз будет средним для всех значений данных в окрестности поиска. По мере увеличения p веса удаленных точек быстро уменьшаются. Если значение p очень высокое, только ближайшие окружающие точки будут влиять на прогноз.
Уменьшение веса с иллюстрацией расстоянияGeostatistical Analyst использует значения мощности больше или равные 1. Когда p = 2, метод известен как взвешенная интерполяция обратного квадрата расстояния. Значение по умолчанию — p = 2, хотя нет теоретических оснований предпочитать это значение другим, и влияние изменения p следует исследовать путем предварительного просмотра выходных данных и изучения статистики перекрестной проверки.
Окрестность поиска
Поскольку объекты, которые расположены близко друг к другу, больше похожи, чем объекты, находящиеся дальше, по мере того, как местоположения удаляются все дальше, измеренные значения будут иметь мало отношения к значению прогнозируемого местоположения.Чтобы ускорить вычисления, вы можете исключить более удаленные точки, которые мало повлияют на прогноз. В результате обычной практикой является ограничение количества измеряемых значений путем указания окрестности поиска. Форма окрестности ограничивает, как далеко и где искать измеренные значения, которые будут использоваться в прогнозе. Другие параметры окружения ограничивают места, которые будут использоваться в этой форме. На следующем изображении пять измеренных точек (соседей) будут использоваться при прогнозировании значения для местоположения без измерения, желтая точка.
Пример области поискаНа форму окрестности влияют входные данные и поверхность, которую вы пытаетесь создать. Если в ваших данных нет направленных влияний, вы захотите рассматривать точки одинаково во всех направлениях. Для этого вы определите область поиска в виде круга. Однако, если в ваших данных есть направленное влияние, такое как преобладающий ветер, вы можете отрегулировать его, изменив форму области поиска на эллипс с большой осью, параллельной ветру.Корректировка этого направленного влияния оправдана, потому что вы знаете, что местоположения с наветренной стороны от прогнозируемого местоположения будут более похожими на удаленных расстояниях, чем местоположения, которые перпендикулярны ветру, но расположены ближе к прогнозируемому местоположению.
После того, как форма окружения была указана, вы можете ограничить, какие местоположения данных внутри фигуры следует использовать. Вы можете определить максимальное и минимальное количество используемых местоположений, а также можете разделить окрестности на секторы.Если вы разделите окрестность на секторы, к каждому сектору будут применены максимальные и минимальные ограничения.
Точки, выделенные в окне просмотра данных, показывают местоположения и веса, которые будут использоваться для прогнозирования местоположения в центре эллипса (местоположение перекрестия). Область поиска ограничена внутренней частью эллипса. В примере, показанном ниже, двум красным точкам будет присвоен вес более 10 процентов. В восточном секторе одному баллу (коричневому) будет присвоен вес от 5 до 10 процентов.Остальные точки в окрестности поиска получат меньшие веса.
Пример весов соседнего сектораКогда использовать IDW
Поверхность, вычисляемая с использованием IDW, зависит от выбора значения мощности ( p ) и стратегии поиска соседства. IDW — это точный интерполятор, где максимальные и минимальные значения (см. Диаграмму ниже) на интерполированной поверхности могут встречаться только в точках выборки.
Пример профиля с обратным взвешиванием по расстояниюВыходная поверхность чувствительна к кластеризации и наличию выбросов.IDW предполагает, что моделируемое явление обусловлено локальными вариациями, которые могут быть зафиксированы (смоделированы) путем определения адекватной области поиска. Поскольку IDW не предоставляет стандартные ошибки прогнозирования, обоснование использования этой модели может быть проблематичным.
Связанные темы
Отзыв по этой теме?
Расстояние между 2 точками
Краткое объяснение
Зная расстояния по горизонтали, и по вертикали, между двумя точками, мы можем вычислить расстояние по прямой следующим образом:
расстояние = √ a 2 + b 2
Представьте, что вы знаете расположение двух точек (A и B), как здесь.
Какое расстояние между ними?
Мы можем провести линии вниз от A и вдоль от B, чтобы получился прямоугольный треугольник.
И с небольшой помощью Пифагора мы знаем, что:
a 2 + b 2 = c 2
Теперь отметьте координаты точек A и B.
x A означает координату x точки A
y A означает координату y точки A
Горизонтальное расстояние a составляет (x A — x B )
Расстояние по вертикали b составляет (y A — y B )
Теперь мы можем найти c (расстояние между точками):
Начать с: c 2 = a 2 + b 2
Введите вычисления для a и b: c 2 = (x A — x B ) 2 + (y A — y B ) 2
Квадратный корень из обеих сторон: Выполнено!Примеры
Пример 1
| Введите значения: | ||
Пример 2
Неважно, в каком порядке расположены точки, потому что возведение в квадрат удаляет любые негативы:
| Введите значения: | ||
Пример 3
А вот еще пример с некоторыми отрицательными координатами… все еще работает:
| Введите значения: | ||
(при желании √136 может быть дополнительно упрощено до 2√34)
Попробуйте сами
Перетащите точки:
Три или более измерения
Отлично работает в 3 (и более!) Измерениях.
Возвести в квадрат разность для каждой оси, затем сложить их и извлечь квадратный корень:
Расстояние = √ [(x A — x B ) 2 + (y A — y B ) 2 + (z A — z B ) 2 ]
Пример: расстояние между двумя точками (8,2,6) и (3,5,7) составляет:
| = √ [(8−3) 2 + (2−5) 2 + (6−7) 2 ] |
| = √ [5 2 + (−3) 2 + (−1) 2 ] |
| = √ (25 + 9 + 1) |
| = √35 |
| Что примерно 5. Квадрат расстояния: Значение, Определение, Предложения . Что такое квадрат расстояния
|
