Матрица фильм все части 1 2 3 смотреть онлайн по порядку бесплатно в хорошем качестве hd 1080
Матрица 1999«Никто не может сказать, что такое Матрица. Вы должны увидеть это сами». — говорит Морфеус.Он разговаривает с Нео, компьютерным мастером с пустым лицом, который собирается пройти сквозь зазеркалье. Из мира конца 20-го века, каким он его знает, в настоящую, постапокалиптическую «пустыню реальности».Это реальность, когда роботы управляют планетой и держат людей подключенными к матрице виртуальной реальности. Они живут в мире снов, в то время как их энергия питает машины.Морфеус думает, что Нео — это Тот, кто является мессией, который разрушит Матрицу и воскресит человечество. В этом убеждена и один из борцов за свободу Тринити. Но Нео не уверен, и ему придется столкнуться с пагубным, могущественным подлым матриксным агентом Смитом, чтобы выяснить это.
Матрица: Перезагрузка 2003
Нео остался в реальном мире. Преследуемый кошмаром, в котором его возлюбленная, Тринити убита, он входит в конструкцию Матрицы виртуальной реальности, чтобы отыскать всезнающего Оракула.
Между тем, Сион в опасности. Машинная армия из 250 000 роботов-убийц приближается к подземному городу, в котором находятся остатки человечества.
Морфеус убежден, что Нео может спасти его, но для этого «Избранный» должен найти источник Матрицы, а это непростое дело со многими врагами на пути.
Матрица: Революция 2003
Спаситель мира, в котором доминируют машины, Нео, находится в состоянии комы. Тем временем родине человечества угрожают скопления зловещих, похожих на кальмаров, стражей, идущих в направлении Сиона. Морфеус и Тринити идут за Нео, и вынуждены заключить сделку с раздражающе культурным Меровингом, чтобы найти его. Тем временем агент Смит нашел способ сбежать из Матрицы в своем бесконечном стремлении уничтожить Нео.. Если вам понравился Матрица все фильмы смотреть онлайн, можете оставлять свои отзыв об фильме и поставить оценку этой франшизе. Приятного просмотра.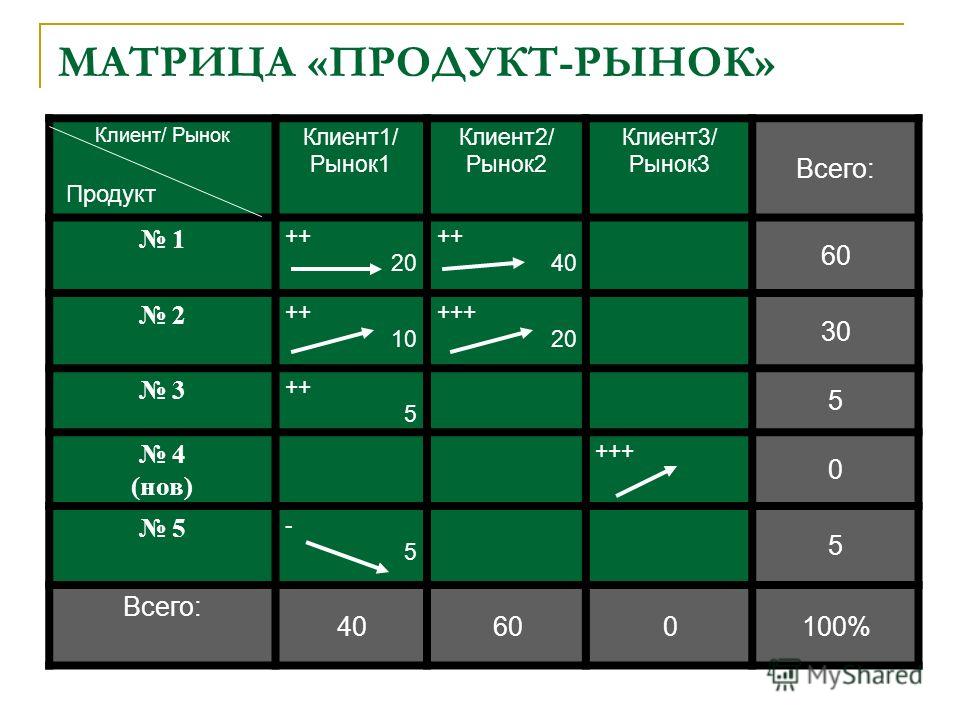
Матрица все фильмы подряд 1 2 3 смотреть онлайн в хорошем качестве hd 720 hd 1080
Смотреть онлайн!
Доступно на устройствах
Серия фильмов Матрица, все 3 фильмы можете смотреть на любых смартфонов с андроид или IOS под айфон, также на планшет и на смарт тв желаем приятного просмотра.
The Matrix
1999 — 2003СШАфантастика, боевик
- Время: 136 мин. / 02:16
- Перевод: Профессиональный (полное дублирование)
- Режиссер: Лана Вачовски, Лилли Вачовски
- В ролях: Киану Ривз, Лоренс Фишбёрн, Кэрри-Энн Мосс, Хьюго Уивинг, Глория Фостер, Джо Пантольяно, Маркус Чонг, Джулиан Араханга, Мэтт Доран, Белинда МакКлори
Сюжет Франшизы
Главный герой – обаятельный мужчина по имени Томас Андерсон. Он является офисным работником, а по ночам подрабатывает хакером, и в сети имеет прозвище Нео. Вскоре он узнает, что мир, в котором он живет всего лишь иллюзия и это всё не настоящее. Это просто матрица, а люди нужны лишь для питания искусственного разума, захватившего человечество. Нео решает изменить ситуацию и противостоять злу. Его наставник Морфеус, возлюблена Тринити и он сам продолжают свое противостояние против программ. Они готовы пожертвовать собственными жизнями, чтобы вызолить людей от рабства. Они применяют все свои умения, таланты и оружие, чтобы победить противника. Постепенно они начинают понимать, что матрица имеет более глубокое строение, чем они думали поначалу. Глубоко под землей находится небольшой город, где живут все выжившие люди, понимающие, что происходит. Они готовы любой ценой защитить свой город и последнюю надежду человечества на жизнь. Армия злобных и безжалостных машин уже на подходе и готова атаковать Зион. Машины хотят уничтожить его и всех жителей. Единственный человек, который сможет помешать этому – это отважный и непревзойденный Нео, готовый исполнить свое жизненное предназначение.
Рейтинг КиноПоиск
8.490
Голосов 375 830
Рейтинг IMDB
8.70
Голосов 1 568 562
По мнению пользователей
Реклама в плеере от нас не зависит,мы тоже против неё(((
Свет
примеры, алгоритм умножения на вектор, число, свойства произведения
Произведение двух матриц
Определение 1Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Пример 1Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+. ..+aip×bpj, i=1,…m, j=1,…m
Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Пример 2Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеУмножение матрицы на число
Определение 2Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Определение 3Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Пример 5Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Пример 6Найдем произведение матрицы А и вектора-строку В:
А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102
Преобразование матрицы m x n в матрицу n*m x 3
В настоящее время у меня есть матрица размером 479 x 729, и я хотел бы преобразовать эту матрицу в матрицу с тремя столбцами таким образом, чтобы первый столбец был записью строки исходной матрицы, второй столбец-записью столбца исходной матрицы, а третий столбец-значением в этом столбце и записи строки.
Есть ли простой способ сделать это? Я посмотрел на функцию reShape , но не понял, как применить ее здесь. Мотивация для этого состоит в том, чтобы иметь возможность создать таблицу расстояний для элементов внутри Матрицы, которая включает их местоположение.
Поделиться Источник TimColeman 19 января 2016 в 17:21
2 ответа
-
Преобразование из матрицы n x m в длинную матрицу в R
Примечание: это не вопрос графика. У меня есть матрица n x m: > m = matrix(1:6,2,3) > m a b c d 1 2 3 e 4 5 6 Я хотел бы преобразовать это в длинную матрицу: > m.l a d 1 a e 4 b d 2 b e 5 c d 3 c e 6 Очевидно, что вложенные циклы for будут работать, но я знаю, что есть много хороших…
-
Как повернуть матрицу M x N на 180 градусов?
Я видел здесь несколько вопросов, которые не совсем отвечают на мой вопрос. Я пытаюсь воспроизвести классический вопрос о вращении матрицы, который так часто используется в вопросах интервью. Вместо того чтобы сосредоточиться на квадратной матрице, меня интересуют M x N матриц. Для входной матрицы…
1
Вероятно, есть лучший или более умный способ, но это кажется достаточно прямым и быстрым:
m <- matrix(rnorm(349191), 479, 729) row_num <- as.vector(row(m)) col_num <- as.vector(col(m)) val <- as.vector(m) new_m <- as.matrix(cbind(row_num, col_num, val)) dim(new_m) # [1] 349191 3 head(new_m) # row_num col_num val # [1,] 1 1 1.0839690124 # [2,] 2 1 0.7363313818 # [3,] 3 1 0.0001195304 # [4,] 4 1 0.2123100877 # [5,] 5 1 0.1293427830 # [6,] 6 1 1.1773676868 tail(new_m) # row_num col_num val # [349186,] 474 729 -0.07942063 # [349187,] 475 729 -0.25694755 # [349188,] 476 729 -0.69421258 # [349189,] 477 729 1.24861689 # [349190,] 478 729 0.24377606 # [349191,] 479 729 0.49150676
Поделиться JasonAizkalns 19 января 2016 в 18:10
1
Вы можете использовать:
library(reshape2)
melt(M)
где M -ваша матрица
Поделиться Marat Talipov 19 января 2016 в 18:26
Похожие вопросы:
Преобразование матрицы n,m,k в матрицу a n*m k
Мне нужно изменить форму матрицы а на в, образец: A размер = [n m k] Размер B = [n*m k] Каков самый быстрый способ установить строки B со значениями A?
Инициализация матрицы N x M в python Я пытаюсь выучить python.
 В нем я пытаюсь динамически сгенерировать матрицу N x M в python, где каждая ячейка содержит значение индекса этой ячейки в python. The matrix would look like: [0,1,2,3,4…
В нем я пытаюсь динамически сгенерировать матрицу N x M в python, где каждая ячейка содержит значение индекса этой ячейки в python. The matrix would look like: [0,1,2,3,4…
Matlab, 1 x m матрица из n x M матрицы
Я пытаюсь вычесть матрицу 1 x M из матрицы N x M. допустим, моя матрица 1 x M равна [1 2] а моя матрица N x M-это [3 4; 5 4; 1 6] и то, что я хочу в результате, это [2 2; 4 2; 0 4] Я знаю, как это…
Преобразование из матрицы n x m в длинную матрицу в R
Примечание: это не вопрос графика. У меня есть матрица n x m: > m = matrix(1:6,2,3) > m a b c d 1 2 3 e 4 5 6 Я хотел бы преобразовать это в длинную матрицу: > m.l a d 1 a e 4 b d 2 b e 5 c…
Как повернуть матрицу M x N на 180 градусов?
Я видел здесь несколько вопросов, которые не совсем отвечают на мой вопрос. Я пытаюсь воспроизвести классический вопрос о вращении матрицы, который так часто используется в вопросах интервью. Вместо…
Как реализовать матрицу (N x N) x M на Matlab?
Предположим, что у нас есть сетка 2D с N точками (то есть N = N x *N y , где N x-количество точек сетки на оси x, а N y-количество точек сетки на оси y) на сетке, и у нас есть 1D-домен, встроенный в…
Умножьте матрицу a (n x 1) на коэффициент матрицы (n x m).
Я пытаюсь реализовать следующее уравнение высоты кривой Безье с помощью библиотеки Eigen : Следующий фрагмент кода работает для вычисления новых контрольных точек. В этом коде degree -переменная n…
Быстрый способ установить диагонали матрицы (M x N x N)? Einsum / n-мерный fill_diagonal?
Я пытаюсь писать быстрый, оптимизированный код на основе матриц и недавно обнаружил einsum как инструмент для достижения значительного ускорения. Можно ли использовать это для эффективной установки…
Matlab: скрытая матрица m x n в массив ячеек 1 x n
Я новичок в matlab, и мне нужна помощь в преобразовании столбцов матрицы в ячейку. Короче говоря, я хотел бы преобразовать матрицу m x n в ячейку 1 x n. Спасибо.
Короче говоря, я хотел бы преобразовать матрицу m x n в ячейку 1 x n. Спасибо.
Как сделать матрицу m by n со всеми элементами int x с помощью ArrayList?
Создание матрицы m на n с использованием ArrayList в Java. Я пытаюсь создать конструктор с функцией построения матрицы m на n со всеми элементами ‘int x’. Я объявил матрицу…
Основные сведения о матрицах
В этом разделе мы даем основные сведения о матрицах, необходимые для понимания статистики и анализа данных.
Матрицей размера m x n (читается m на n) называется прямоугольная таблица чисел, содержащая
Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,….
Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: aij, где i — номер строки, j — номер столбца.
Например, матрица:
В сокращенной записи обозначаем A=(aij); i=1,2,…m; j=1,2,…,n
Приведем пример матрицы 2 на 2:
Вы видите, что a11 = 1, a12 = 0, a21 = 2, a22=5
Наряду с круглыми скобками используются и другие обозначения матрицы:
Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, aij = bij для любых i=1,2,…m; j=1,2,…n
Виды матриц
Матрица, состоящая из одной строки, называется матрицей (вектором) — строкой, а из одного столбца — матрицей (вектором)- столбцом:
A=(a11,a12,…,a1n) — матрица — строка
B=
Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n.
Например,
Элементы матрицы aij, у которых номер столбца равен номеру строки образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a11, a22,…,ann.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
Операции над матрицами
Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые — специфические.
1. Умножение матрицы на число. Произведение матрицы А на число называется матрица B=A, элементы которой bij=aij для i=1,2,…m; j=1,2,…n
Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.
В частности, произведение матрицы А на число 0 есть нулевая матрица.
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой cij=aij+bijдля i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно).
3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.
4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц Am∙B kназывается такая матрица Cm, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:
i=1,2,…,m; j=1,2,…,n
Многие свойства, присущие операциям над числами, справедливы и для операций над матрицами (что следует из этих операций):
A+B=B+A
(A+B)+C=A+(B+C)
λ (A+B)= λA+ λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ (AB)=( λA)B=A(λB)
A(BC)=(AB)C
Однако имеются и специфические свойства матриц. Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
Так, операция умножения матриц имеет некоторые отличия от умножения чисел:
a) Если АВ существует, то после перестановки сомножителей местами произведение матриц ВА может и не существовать.
b) Если АВ и ВА существуют, то они могут быть матрицами разных размеров.
5. Транспонирование матрицы — переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А:
Из определения следует, что если матрица А имеет размер m, то транспонированная матрица А’ имеет размер n
В литературе встречаются и другие обозначения транспонированной матрицы, например, АТ
Связанные определения:
Вырожденная матрица
Обобщенная обратная матрица
Обратная матрица
Плохо обусловленная матрица
Псевдообратная матрица
Эрмитова матрица
Эрмитово-сопряженная матрица
В начало
Содержание портала
Умножение матриц
Каталин Дэвид
Чтобы можно было умножить две матрицы, количество столбцов первой матрицы должно быть равно количеству строк второй матрицы.
Алгоритм умножения матриц
Умножаем элементы в строках первой матрицы на элементы в столбцах второй матрицы.
- Умножаем элементы первой строки на элементы первого столбца.
- Умножаем первый элемент первой строки на первый элемент первого столбца.
- Умножаем второй элемент первой строки на второй элемент первого столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и первого столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет первым элементом первой строки произведения матриц.
- Умножаем элементы первой строки первой матрицы на элементы второго столбца второй матрицы.
- Умножаем первый элемент первой строки на первый элемент второго столбца.

- Умножаем второй элемент первой строки на второй элемент второго столбца.
- Делаем то же самое с каждым элементом, пока не дойдем до конца как первой строки первой матрицы, так и второго столбца второй матрицы.
- Складываем полученные произведения.
- Полученный результат будет вторым элементом первой строки произведения матриц.
- Умножаем первый элемент первой строки на первый элемент второго столбца.
- Применяя тот же самый алгоритм, умножаем элементы первой строки первой матрицы на элементы остальных столбцов второй матрицы. Полученные числа составят первую строку вычисляемой матрицы.
- Вторая строка вычисляемой матрицы находится аналогично умножением элементов второй строки первой матрицы на элементы каждого столбца второй матрицы: результаты записываются в новую матрицу после каждого суммирования.
- Делаем это с каждой строкой первой матрицы, пока все строки новой матрицы не будут заполнены.
Пример 7
$A= \begin{pmatrix} 1 & 2 & 2\\ 3 & 1 & 1 \end{pmatrix}$
$B=\begin{pmatrix} 4 & 2 \\ 3 & 1 \\ 1 & 5\\ \end{pmatrix}$
Заметим, что матрица A имеет 3 столбца, а матрица B имеет 3 строки, значит, их можно перемножить.
$A \cdot B=$ $\begin{pmatrix} \color{red}1 &\color{blue}2 & \color{green}2\\ \color{red}3 &\color{blue}1 & \color{green}1 \end{pmatrix} \begin{pmatrix} \color{red}4 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \\ \color{green}1 & \color{green}5 \end{pmatrix}=$ $\begin{pmatrix} \color{red}{1\cdot4}+\color{blue}{2\cdot3}+\color{green}{2\cdot1} & \color{red}{1\cdot2}+\color{blue}{2\cdot1}+\color{green}{2\cdot5}\\ \color{red}{3\cdot4}+\color{blue}{1\cdot3}+\color{green}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}+\color{green}{1\cdot5} \end{pmatrix}=$ $\begin{pmatrix} 12 & 14\\ 16 & 12\\ \end{pmatrix}$$B \cdot A = \begin{pmatrix} \color{red}4 &\color{blue}2 \\ \color{red}3 & \color{blue}1 \\ \color{red}1 & \color{blue}5 \end{pmatrix} \begin{pmatrix} \color{red}1 &\color{red}2 & \color{red}2\\ \color{blue}3 &\color{blue}1 & \color{blue}1 \end{pmatrix}=$
$\begin{pmatrix} \color{red}{4\cdot1}+\color{blue}{2\cdot3} & \color{red}{4\cdot2}+\color{blue}{2\cdot1} & \color{red}{4\cdot2}+\color{blue}{2\cdot1}\\ \color{red}{3\cdot1}+\color{blue}{1\cdot3} & \color{red}{3\cdot2}+\color{blue}{1\cdot1} & \color{red}{3\cdot2}+\color{blue}{1\cdot1}\\ \color{red}{1\cdot1}+\color{blue}{5\cdot3} & \color{red}{1\cdot2}+\color{blue}{5\cdot1} & \color{red}{1\cdot2}+ \color{blue}{5\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 10 & 10 & 10 \\ 6 & 7 & 7 \\ 16 & 7 & 7 \end{pmatrix}$
Заметим, что $A \cdot B \neq B \cdot A$
Пример 8
$A= \begin{pmatrix} 5 & 2 \\ 3 & 1 \end{pmatrix} B= \begin{pmatrix} 4 & 6 \\ 5 & 2 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}5 & \color{blue}2 \\ \color{red}3 & \color{blue}1 \end{pmatrix} \cdot \begin{pmatrix} \color{red}4 & \color{red}6 \\ \color{blue}5 & \color{blue}2 \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot4}+\color{blue}{2\cdot5} & \color{red}{5\cdot6}+\color{blue}{2\cdot2} \\ \color{red}{3\cdot4}+\color{blue}{1\cdot5} & \color{red}{3\cdot6}+\color{blue}{1\cdot2} \end{pmatrix} =$ $\begin{pmatrix} 30 & 34\\ 17 & 20 \end{pmatrix}$
$B \cdot A= \begin{pmatrix} \color{red}4 & \color{blue}6 \\ \color{red}5 & \color{blue}2 \end{pmatrix} \cdot \begin{pmatrix} \color{red}5 & \color{red}2 \\ \color{blue}3 & \color{blue}1 \end{pmatrix} =\begin{pmatrix} \color{red}{4\cdot5}+\color{blue}{6\cdot3} & \color{red}{4\cdot2}+\color{blue}{5\cdot1} \\ \color{red}{5\cdot5}+\color{blue}{2\cdot3} & \color{red}{5\cdot2}+\color{blue}{2\cdot1} \end{pmatrix} =$ $\begin{pmatrix} 38 & 14\\ 31 & 12 \end{pmatrix}$
Опять-таки $A \cdot B \neq B \cdot A$.
Пример 9
$A= \begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix} B= \begin{pmatrix} 5 & 2 & 1 \\ 4 & 3 & 2 \\ 2 & 1 & 5 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}{1} & \color{blue}{4} & \color{green}{3} \\ \color{red}{2} & \color{blue}{1} & \color{green}{5}\\ \color{red}{3} & \color{blue}{2} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{5} & \color{red}{2} & \color{red}{1} \\ \color{blue}{4} & \color{blue}{3} & \color{blue}{2} \\ \color{green}{2} & \color{green}{1} & \color{green}{5} \end{pmatrix}=$
$\begin{pmatrix} \color{red}{1\cdot5} + \color{blue}{4\cdot4} + \color{green}{3\cdot2} & \color{red}{1\cdot2} + \color{blue}{4\cdot3} + \color{green}{3\cdot1} & \color{red}{1\cdot1} + \color{blue}{4\cdot2} + \color{green}{3\cdot5} \\ \color{red}{2\cdot5} + \color{blue}{1\cdot4} + \color{green}{5\cdot2} & \color{red}{2\cdot2} + \color{blue}{1\cdot3} + \color{green}{5\cdot1} & \color{red}{2\cdot1} + \color{blue}{1\cdot2} + \color{green}{5\cdot5}\\ \color{red}{3\cdot5} + \color{blue}{2\cdot4} + \color{green}{1\cdot2} & \color{red}{3\cdot2} + \color{blue}{2\cdot3} + \color{green}{1\cdot1} & \color{red}{3\cdot1} + \color{blue}{2\cdot2} + \color{green}{1\cdot5} \end{pmatrix}=$
$=\begin{pmatrix} 27 & 17 & 24\\ 24 & 12 & 29\\ 25 & 13 & 12 \end{pmatrix}$
$B \cdot A = \begin{pmatrix} \color{red}{5} & \color{blue}{2} & \color{green}{1}\\ \color{red}{4} & \color{blue}{3} & \color{green}{2}\\ \color{red}{2} & \color{blue}{1} & \color{green}{5} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{4} & \color{red}{3} \\ \color{blue}{2} & \color{blue}{1} & \color{blue}{5} \\ \color{green}{3} & \color{green}{2} & \color{green}{1} \end{pmatrix}=$ $\begin{pmatrix} \color{red}{5\cdot1} + \color{blue}{2\cdot2} + \color{green}{1\cdot2} & \color{red}{5\cdot4} + \color{blue}{2\cdot1} + \color{green}{1\cdot2} & \color{red}{5\cdot3} + \color{blue}{2\cdot5} + \color{green}{1\cdot1} \\ \color{red}{4\cdot1} + \color{blue}{3\cdot2} + \color{green}{2\cdot3} & \color{red}{4\cdot4} + \color{blue}{3\cdot1} + \color{green}{2\cdot2} & \color{red}{4\cdot3} + \color{blue}{3\cdot5} + \color{green}{2\cdot1}\\ \color{red}{2\cdot1} + \color{blue}{1\cdot2} + \color{green}{5\cdot3} & \color{red}{2\cdot4} + \color{blue}{1\cdot1} + \color{green}{5\cdot2} & \color{red}{2\cdot3} + \color{blue}{1\cdot5} + \color{green}{5\cdot1} \end{pmatrix}=$
$=\begin{pmatrix} 11 & 24 & 26\\ 16 & 23 & 29\\ 19 & 19 & 16 \end{pmatrix}$
Опять-таки $A \cdot B \neq B \cdot A$.
Пример 10
$A= \begin{pmatrix} 5 & 2\\ 3 & 1\\ \end{pmatrix} I_{2}= \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}{5} & \color{blue}{2}\\ \color{red}{3} & \color{blue}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{0} \\ \color{blue}{0} & \color{blue}{1} \end{pmatrix} =\begin{pmatrix} \color{red}{5\cdot1}+\color{blue}{2\cdot0} & \color{red}{5\cdot0}+\color{blue}{2\cdot1} \\ \color{red}{3\cdot1}+\color{blue}{1\cdot0} & \color{red}{3\cdot0}+\color{blue}{1\cdot1} \end{pmatrix} = \begin{pmatrix} 5 & 2\\ 3 & 1 \end{pmatrix}$
$B \cdot A = \begin{pmatrix} \color{red}{1} & \color{blue}{0} \\ \color{red}{0} & \color{blue}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{5} & \color{red}{2} \\ \color{blue}{3} & \color{blue}{1} \\ \end{pmatrix} =\begin{pmatrix} \color{red}{1\cdot5}+\color{blue}{0\cdot3} & \color{red}{1\cdot2}+\color{blue}{0\cdot1} \\ \color{red}{0\cdot5}+\color{blue}{1\cdot3} & \color{red}{0\cdot2}+\color{blue}{1\cdot1} \end{pmatrix} = \begin{pmatrix} 5 & 2\\ 3 & 1 \end{pmatrix}$
Заметим, что $A \cdot I_{2} = I_{2} \cdot A=A$.
Пример 11
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix} I_{3}= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$
$A \cdot B = \begin{pmatrix} \color{red}{1} & \color{blue}{4} & \color{green}{3} \\ \color{red}{2} & \color{blue}{1} & \color{green}{5}\\ \color{red}{3} & \color{blue}{2} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{0} & \color{red}{0} \\ \color{blue}{0} & \color{blue}{1} & \color{blue}{0} \\ \color{green}{0} & \color{green}{0} & \color{green}{1} \end{pmatrix}=$
$\begin{pmatrix} \color{red}{1\cdot1} + \color{blue}{4\cdot0} + \color{green}{3\cdot0} & \color{red}{1\cdot0} + \color{blue}{4\cdot1} + \color{green}{3\cdot0} & \color{red}{1\cdot0} + \color{blue}{4\cdot0} + \color{green}{3\cdot1} \\ \color{red}{2\cdot1} + \color{blue}{1\cdot0} + \color{green}{5\cdot0} & \color{red}{2\cdot0} + \color{blue}{1\cdot1} + \color{green}{5\cdot0} & \color{red}{2\cdot0} + \color{blue}{1\cdot0} + \color{green}{5\cdot1}\\ \color{red}{3\cdot1} + \color{blue}{2\cdot0} + \color{green}{1\cdot0} & \color{red}{3\cdot0} + \color{blue}{2\cdot1} + \color{green}{1\cdot0} & \color{red}{3\cdot0} + \color{blue}{2\cdot0} + \color{green}{1\cdot1} \end{pmatrix}=$
$=\begin{pmatrix} 1 & 4 & 3\\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix}$
$B \cdot A = \begin{pmatrix} \color{red}{1} & \color{blue}{0} & \color{green}{0} \\ \color{red}{0} & \color{blue}{1} & \color{green}{0}\\ \color{red}{0} & \color{blue}{0} & \color{green}{1} \end{pmatrix} \cdot \begin{pmatrix} \color{red}{1} & \color{red}{4} & \color{red}{3} \\ \color{blue}{2} & \color{blue}{1} & \color{blue}{5} \\ \color{green}{3} & \color{green}{2} & \color{green}{1} \end{pmatrix}=$
$\begin{pmatrix} \color{red}{1\cdot1} + \color{blue}{0\cdot2} + \color{green}{0\cdot2} & \color{red}{1\cdot4} + \color{blue}{0\cdot1} + \color{green}{0\cdot2} & \color{red}{1\cdot3} + \color{blue}{0\cdot5} + \color{green}{0\cdot1} \\ \color{red}{0\cdot1} + \color{blue}{1\cdot2} + \color{green}{0\cdot3} & \color{red}{0\cdot4} + \color{blue}{1\cdot1} + \color{green}{0\cdot2} & \color{red}{0\cdot3} + \color{blue}{1\cdot5} + \color{green}{0\cdot1}\\ \color{red}{0\cdot1} + \color{blue}{0\cdot2} + \color{green}{1\cdot3} & \color{red}{0\cdot4} + \color{blue}{0\cdot1} + \color{green}{1\cdot2} & \color{red}{0\cdot3} + \color{blue}{0\cdot5} + \color{green}{1\cdot1} \end{pmatrix} =$
$=\begin{pmatrix} 1 & 4 & 3\\ 2 & 1 & 5\\ 3 & 2 & 1 \end{pmatrix}$
Опять-таки $A \cdot I_{3} = I_{3} \cdot A = A$.
Примечание:
- В общем случае умножение матриц некоммуникативно.
- $A\cdot I_{n} = I_{n} \cdot A = A$ для любой матрицы A, имеющей n столбцов.
Изучаем матрицы в питоне и массивы NumPy в Python
Матрица — это двухмерная структура данных, в которой числа расположены в виде строк и столбцов. Например:
Эта матрица является матрицей три на четыре, потому что она состоит из 3 строк и 4 столбцов.
Python не имеет встроенного типа данных для матриц. Но можно рассматривать список как матрицу. Например:
A = [[1, 4, 5],
[-5, 8, 9]]
Этот список является матрицей на 2 строки и 3 столбца.
Обязательно ознакомьтесь с документацией по спискам Python, прежде чем продолжить читать эту статью.
Давайте посмотрим, как работать с вложенным списком.
A = [[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]]
print("A =", A)
print("A[1] =", A[1]) # вторая строка
print("A[1][2] =", A[1][2]) # третий элемент второй строки
print("A[0][-1] =", A[0][-1]) # последний элемент первой строки
column = []; # пустой список
for row in A:
column.append(row[2])
print("3rd column =", column)
Когда мы запустим эту программу, результат будет следующий:
A = [[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]] A [1] = [-5, 8, 9, 0] A [1] [2] = 9 A [0] [- 1] = 12 3-й столбец = [5, 9, 11]
Использование вложенных списков в качестве матрицы подходит для простых вычислительных задач. Но в Python есть более эффективный способ работы с матрицами – NumPy .
NumPy — это расширение для научных вычислений, которое поддерживает мощный объект N-мерного массива. Прежде чем использовать NumPy, необходимо установить его. Для получения дополнительной информации,
- Ознакомьтесь: Как установить NumPy Python?
- Если вы работаете в Windows, скачайте и установите дистрибутив anaconda Python. Он поставляется вместе с NumPy и другими расширениями.
После установки NumPy можно импортировать и использовать его.
NumPy предоставляет собой многомерный массив чисел (который на самом деле является объектом). Давайте рассмотрим приведенный ниже пример:
import numpy as np a = np.array([1, 2, 3]) print(a) # Вывод: [1, 2, 3] print(type(a)) # Вывод: <class 'numpy.ndarray'>
Как видите, класс массива NumPy называется ndarray.
Существует несколько способов создания массивов NumPy.
import numpy as np A = np.array([[1, 2, 3], [3, 4, 5]]) print(A) A = np.array([[1.1, 2, 3], [3, 4, 5]]) # Массив чисел с плавающей запятой print(A) A = np.array([[1, 2, 3], [3, 4, 5]], dtype = complex) # Массив составных чисел print(A)
Когда вы запустите эту программу, результат будет следующий:
[[1 2 3] [3 4 5]] [[1.1 2. 3.] [3. 4. 5.]] [[1. + 0.j 2. + 0.j 3. + 0.j] [3. + 0.j 4. + 0.j 5. + 0.j]]
import numpy as np zeors_array = np.zeros( (2, 3) ) print(zeors_array) ''' Вывод: [[0. 0. 0.] [0. 0. 0.]] ''' ones_array = np.ones( (1, 5), dtype=np.int32 ) // указание dtype print(ones_array) # Вывод: [[1 1 1 1 1]]
Здесь мы указали dtype — 32 бита (4 байта). Следовательно, этот массив может принимать значения от -2-31 до 2-31-1.
import numpy as np
A = np.arange(4)
print('A =', A)
B = np.arange(12).reshape(2, 6)
print('B =', B)
'''
Вывод:
A = [0 1 2 3]
B = [[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]
'''
Узнайте больше о других способах создания массива NumPy .
Выше мы привели пример сложение, умножение матриц и транспонирование матрицы. Мы использовали вложенные списки, прежде чем создавать эти программы. Рассмотрим, как выполнить ту же задачу, используя массив NumPy.
Мы используем оператор +, чтобы сложить соответствующие элементы двух матриц NumPy.
import numpy as np A = np.array([[2, 4], [5, -6]]) B = np.array([[9, -3], [3, 6]]) C = A + B # сложение соответствующих элементов print(C) ''' Вывод: [[11 1] [ 8 0]] '''
Чтобы умножить две матрицы, мы используем метод dot(). Узнайте больше о том, как работает numpy.dot .
Узнайте больше о том, как работает numpy.dot .
Примечание: * используется для умножения массива (умножения соответствующих элементов двух массивов), а не умножения матрицы.
import numpy as np A = np.array([[3, 6, 7], [5, -3, 0]]) B = np.array([[1, 1], [2, 1], [3, -3]]) C = a.dot(B) print(C) ''' Вывод: [[ 36 -12] [ -1 2]] '''
Мы используем numpy.transpose для вычисления транспонирования матрицы.
import numpy as np A = np.array([[1, 1], [2, 1], [3, -3]]) print(A.transpose()) ''' Вывод: [[ 1 2 3] [ 1 1 -3]] '''
Как видите, NumPy значительно упростил нашу задачу.
Также можно получить доступ к элементам матрицы, используя индекс. Начнем с одномерного массива NumPy.
import numpy as np
A = np.array([2, 4, 6, 8, 10])
print("A[0] =", A[0]) # Первый элемент
print("A[2] =", A[2]) # Третий элемент
print("A[-1] =", A[-1]) # Последний элемент
Когда вы запустите эту программу, результат будет следующий:
A [0] = 2 A [2] = 6 A [-1] = 10
Теперь выясним, как получить доступ к элементам двухмерного массива (который в основном представляет собой матрицу).
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
# Первый элемент первой строки
print("A[0][0] =", A[0][0])
# Третий элемент второй строки
print("A[1][2] =", A[1][2])
# Последний элемент последней строки
print("A[-1][-1] =", A[-1][-1])
Когда мы запустим эту программу, результат будет следующий:
A [0] [0] = 1 A [1] [2] = 9 A [-1] [- 1] = 19
import numpy as np
A = np.array([[1, 4, 5, 12],
[-5, 8, 9, 0],
[-6, 7, 11, 19]])
print("A[0] =", A[0]) # Первая строка
print("A[2] =", A[2]) # Третья строка
print("A[-1] =", A[-1]) # Последняя строка (третья строка в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [0] = [1, 4, 5, 12] A [2] = [-6, 7, 11, 19] A [-1] = [-6, 7, 11, 19]
import numpy as np A = np.array([[1, 4, 5, 12], [-5, 8, 9, 0], [-6, 7, 11, 19]]) print("A[:,0] =",A[:,0]) # Первый столбец print("A[:,3] =", A[:,3]) # Четвертый столбец print("A[:,-1] =", A[:,-1]) # Последний столбец (четвертый столбец в данном случае)
Когда мы запустим эту программу, результат будет следующий:
A [:, 0] = [1 -5 -6] A [:, 3] = [12 0 19] A [:, - 1] = [12 0 19]
Если вы не знаете, как работает приведенный выше код, прочтите раздел «Разделение матрицы».
Разделение одномерного массива NumPy аналогично разделению списка. Рассмотрим пример:
import numpy as np letters = np.array([1, 3, 5, 7, 9, 7, 5]) # с 3-го по 5-ый элементы print(letters[2:5]) # Вывод: [5, 7, 9] # с 1-го по 4-ый элементы print(letters[:-5]) # Вывод: [1, 3] # с 6-го до последнего элемента print(letters[5:]) # Вывод:[7, 5] # с 1-го до последнего элемента print(letters[:]) # Вывод:[1, 3, 5, 7, 9, 7, 5] # список в обратном порядке print(letters[::-1]) # Вывод:[5, 7, 9, 7, 5, 3, 1]
Теперь посмотрим, как разделить матрицу.
import numpy as np
A = np.array([[1, 4, 5, 12, 14],
[-5, 8, 9, 0, 17],
[-6, 7, 11, 19, 21]])
print(A[:2, :4]) # две строки, четыре столбца
''' Вывод:
[[ 1 4 5 12]
[-5 8 9 0]]
'''
print(A[:1,]) # первая строка, все столбцы
''' Вывод:
[[ 1 4 5 12 14]]
'''
print(A[:,2]) # все строки, второй столбец
''' Вывод:
[ 5 9 11]
'''
print(A[:, 2:5]) # все строки, с третьего по пятый столбец
''' Вывод:
[[ 5 12 14]
[ 9 0 17]
[11 19 21]]
'''
Использование NumPy вместо вложенных списков значительно упрощает работу с матрицами. Мы рекомендуем детально изучить пакет NumPy, если вы планируете использовать Python для анализа данных.
Данная публикация является переводом статьи «Python Matrices and NumPy Arrays» , подготовленная редакцией проекта.
Что случилось с сиквелами «Матрицы»?
Трудно придумать что-либо более похожее на машину, чем двоичный выбор, который Нео и другие люди должны были сделать на протяжении всей трилогии. Красная таблетка или синяя таблетка? Спасти Троицу или спасти Сион? Победа или поражение? К тому времени, когда Нео достигает 01 и заключает перемирие с персонажем, которого буквально называют «Deus Ex Machina», (да, действительно) он уже на пути к пониманию того, что выбор между двумя абсолютами приведет лишь к повторению истории.
Красная таблетка или синяя таблетка? Спасти Троицу или спасти Сион? Победа или поражение? К тому времени, когда Нео достигает 01 и заключает перемирие с персонажем, которого буквально называют «Deus Ex Machina», (да, действительно) он уже на пути к пониманию того, что выбор между двумя абсолютами приведет лишь к повторению истории.
Если люди будут продолжать сражаться, они никогда не смогут победить, потому что Архитектор уже сказал нам, что существуют уровни выживания, которые машины готовы принять без присутствия человечества. Смит больше не готов занять свое место в ряду программ внутри Матрицы, так же, как Нео наконец понимает, что для Единого нет никакой другой роли, сбоя в системе, кроме той, которую он выбирает делать.
Нельзя сказать, что финальный бой между Нео и Смитом намеренно провален, если вы так считаете — Вачовски озорно отреагировали на эту мысль в игровой адаптации трилогии, Path Of Neo , с Четвертый уровень финального босса, разрушающий стену, завершился супербой, где Смит проявил себя как гигант, сделанный из щебня и металла, за которым последовала банальная, переработанная версия финала фильма «Мы — чемпионы» королевы, как если бы сказать: «Ой, извините, это то, что вы хотели?»
Конечно, зрители ожидали, что Нео восстанет, победит машины и приведет людей к свободе — если бы история закончилась тем, что Нео угрожал машинам по телефону, а затем улетал, эта версия могла быть у нас в голове.
Он обещает мир без границ, но в ходе построения мифологии в Reloaded и Revolutions много времени уделяется возведению стен и, как следствие, чрезмерному объяснению этих границ. С расширением сиквелов победа не может быть достигнута путем ведения войны, только путем заключения мира.
Возможно, Вачовски действительно не знали, что они снимают трилогию, когда начинали, но они знали, что они делали с этим расширением и завершением истории, когда началось производство этих двух фильмов подряд. Об этом свидетельствует бессознательный тон оригинала, но в сиквелах трилогия больше склоняется к духовному, чем к философскому.
Об этом свидетельствует бессознательный тон оригинала, но в сиквелах трилогия больше склоняется к духовному, чем к философскому.
Определитель матрицы 2×2 — ChiliMath
Предположим, нам дана квадратная матрица A с четырьмя элементами: a, b, c и d.
Определитель матрицы A вычисляется как
Если вы еще не видите узор, то вот как он выглядит, когда элементы матрицы имеют цветовую кодировку.
- Возьмем произведение элементов сверху слева направо вниз, , затем вычтем на произведение элементов сверху справа налево снизу .
Определитель матрицы 2 x 2 (анимированный)
Примеры того, как найти определитель матрицы 2 x 2
Пример 1: Найдите определитель матрицы ниже.
Это пример, когда все элементы матрицы 2 × 2 положительны.
Пример 2: Найдите определитель матрицы ниже.
Вот пример, когда все элементы отрицательны. Обязательно соблюдайте основные правила при умножении целых чисел.Помните, что произведение чисел с одинаковым знаком всегда будет положительным. Напротив, если знаки другие, продукт будет отрицательным.
Пример 3: Вычислите определитель матрицы ниже.
Обязательно запомните правила вычитания целых чисел. То есть, когда вы вычитаете целые числа, вы меняете операцию с вычитания на сложение, но вы должны переключить знак числа, которое находится непосредственно справа от него (это называется вычитанием), а затем продолжить обычное сложение целых чисел.
Пример 4: Вычислите определитель матрицы ниже.
Вы также можете столкнуться с проблемой, когда некоторые элементы в матрице являются переменными. Относитесь к этому как к обычной детерминантной проблеме. Вставьте эти переменные в обозначенные места в формуле, а затем упростите, как обычно.
Пример 5 : Найдите значение x в матрице ниже, если его определитель имеет значение -12.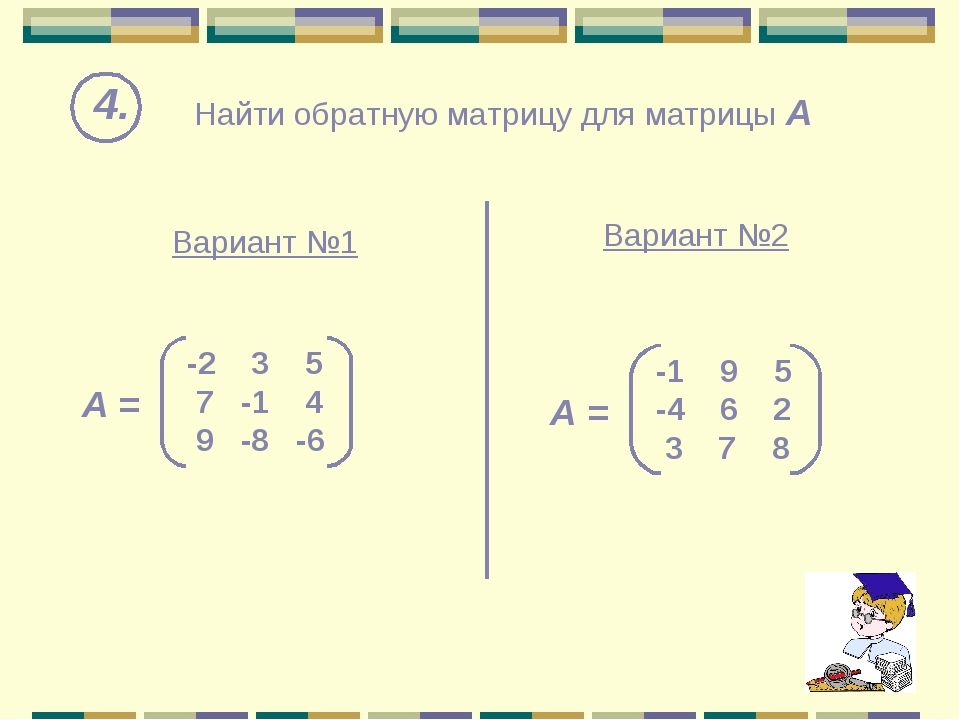
Это не вопрос с подвохом. Фактически мы можем найти такое значение x, что, применив формулу, мы получим -12.
Получите определитель данной матрицы и установите его равным -12. Поступая таким образом, мы генерируем простое линейное уравнение, которое разрешимо относительно x.
Проверяем наш ответ:
Замените x на 7, затем вычислите определитель. Ожидаем -12.
Это подтверждает правильность нашего решения!
Практика с рабочими листами
Вас также может заинтересовать:
Детерминанты матрицы 3 × 3
Операции с матрицами
Что касается линейной алгебры, две наиболее важные операции с векторами являются сложение векторов [добавление двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр).Аналогичные операции определены для матриц.
Сложение матрицы . Если A и B являются матрицами одинакового размера , то их можно складывать. (Это похоже на ограничение на добавление векторов, а именно, можно добавить только векторы из того же пространства R n ; например, вы не можете добавить 2-вектор к 3-вектору.) Если A = [ a ij ] и B = [ b ij ] — обе матрицы m x n , тогда их сумма, C = A + B , также является матрицей m x n , и ее элементы задаются формулой
Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B .
Пример 1 : Рассмотрим следующие матрицы:
Какие два можно добавить? Какова их сумма?
Поскольку могут быть добавлены только матрицы одного размера, определяется только сумма F + H ( G не может быть добавлено ни к F , ни к H ). Сумма F и H составляет
Сумма F и H составляет
Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (если оно определено) также коммутативно; то есть для любых матриц A и B одинакового размера A + B всегда будет равно B + A .
Пример 2 : Если любая матрица A добавляется к нулевой матрице того же размера, результат явно будет равен A :
Это матричный аналог оператора a + 0 = 0 + a = a , который выражает тот факт, что число 0 является аддитивным тождеством в наборе действительных чисел.
Пример 3 : Найдите матрицу B такую, что A + B = C , где
Если
, то матричное уравнение A + B = C становится
Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, из этого последнего уравнения следует
Следовательно,
Этот пример мотивирует определение вычитания матрицы : Если A и B являются матрицами одинакового размера, то элементы A — B находятся простым вычитанием элементов B из соответствующие записи A .Поскольку уравнение A + B = C эквивалентно B = C — A , вычитание матрицы, приведенное выше, даст тот же результат:
Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то
То есть матрица kA получается путем умножения каждой записи A на k .
Пример 4 : Если
, то скалярное кратное 2 A получается путем умножения каждой записи A на 2:
Пример 5 : Если A и B — это матрицы одинакового размера, то A — B = A + (- B ), где — B — скалярное кратное (−1) В .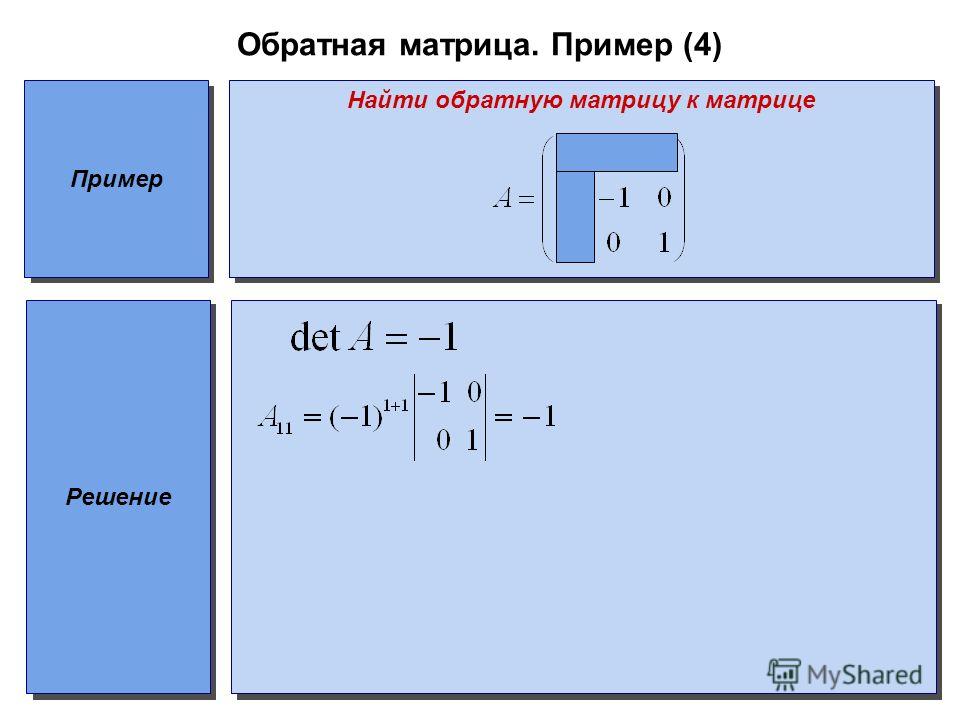 Если
Если
, затем
Это определение вычитания матрицы согласуется с определением, проиллюстрированным в Примере 8.
Пример 6 : Если
, затем
Умножение матриц . Безусловно, наиболее важной операцией с матрицами является умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя n ‐векторами. Записывая r как матрицу строк 1 x n и c как матрицу столбца n x 1, точечный продукт r и c составляет
Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей.Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом продукте: вектор-строка идет первым, вектор-столбец — вторым.
Теперь последний шаг: как умножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно соответствовать количеству строк B ; если это условие не выполняется, то продукт AB не определяется. Этот критерий следует из указанного выше ограничения для умножения матрицы-строки r на матрицу столбца c , а именно, что количество записей в r должно соответствовать количеству записей в c .Если A равно m x n и B равно n x p , то продукт AB определен, а размер матрицы продуктов AB будет m x п. . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размеры продукта:
Представление матрицы m x n A как составной из векторов-строк r 1 , r 2 ,…, r m от R n и n x p матрица B , составленная из векторов-столбцов c 1 , c 2 ,…, c p от R n ,
и
правило вычисления элементов матричного произведения AB : r i · c j = ( AB ) ij , то есть
Пример 7 : Учитывая две матрицы
определяет, какой матричный продукт, AB или BA , определен, и оценивает его.
Поскольку A составляет 2 x 3, а B — 3 x 4, продукт AB в этом порядке определяется, а размер матрицы продукта AB будет 2 x 4. Продукт BA — это , а не , поскольку первый фактор ( B ) имеет 4 столбца, а второй фактор ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно соответствовать количеству строк второй матрицы, чтобы их произведение было определено.
Произведение скалярного произведения строки 1 в A и столбца 1 в B дает запись (1, 1) в AB . С
запись (1, 1) в AB — это 1:
Скалярное произведение строки 1 в A и столбца 2 в B дает запись (1, 2) в AB ,
и скалярное произведение строки 1 в A и столбце 3 в B дает запись (1, 3) в AB :
Первая строка произведения завершается скалярным произведением строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB :
Теперь для второй строки AB : скалярное произведение строки 2 в A и столбца 1 в B дает запись (2, 1) в AB ,
и скалярное произведение строки 2 в A и столбце 2 в B дает запись (2, 2) в AB :
Наконец, взяв скалярное произведение строки 2 в A со столбцами 3 и 4 в B дает (соответственно) записи (2, 3) и (2, 4) в AB :
Следовательно,
Пример 8 : Если
и
вычислить (3, 5) запись продукта CD .
Во-первых, обратите внимание, что, поскольку C составляет 4 x 5, а D составляет 5 x 6, продукт CD действительно определен, и его размер равен 4 x 6. Однако нет необходимости вычислять все двадцать‐ четыре записи CD , если требуется только одна конкретная запись. Запись (3, 5) в CD является скалярным произведением строки 3 в C и столбца 5 в D :
Запись (3, 5) в CD является скалярным произведением строки 3 в C и столбца 5 в D :
Пример 9 : Если
убедитесь, что
но
В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; действительно, они даже не одного размера!
Предыдущий пример иллюстрирует, возможно, самое важное различие между умножением скаляров и умножением матриц.Для действительных чисел a и b всегда выполняется уравнение ab = ba , то есть умножение действительных чисел коммутативно; порядок, в котором написаны коэффициенты, не имеет значения. Однако категорически неверно, что умножение матриц коммутативно. Для матриц A и B , приведенных в примере 9, были определены оба продукта AB и BA , но они определенно не были идентичными. Фактически, матрица AB была 2 x 2, а матрица BA была 3 x 3.Вот еще одна иллюстрация некоммутативности умножения матриц: Рассмотрим матрицы
Поскольку C составляет 3 x 2, а D — 2 x 2, продукт CD определен, его размер 3 x 2 и
Продукт DC , однако, не определен, поскольку количество столбцов D (то есть 2) не равно количеству строк C (то есть 3). Следовательно, CD ≠ DC , поскольку DC даже не существует.
Из-за чувствительности к порядку записи коэффициентов обычно не говорят просто: «Умножьте матрицы A и B ». Обычно важно указать, какая матрица идет первой, а какая — второй в продукте. По этой причине выражение «Умножить A справа на B » означает получить произведение AB , а выражение «Умножить A слева на B » означает получить произведение BA . .
Пример 10 : Если
и x — это вектор (−2, 3), покажите, как A можно умножить справа на x и вычислить произведение.
Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Следовательно, если x записано как 2 x 1 столбец , матрица
, то можно вычислить произведение A x , и в результате получится еще одна матрица столбца 2 x 1:
Пример 11 : Рассмотрим матрицы
Если A умножить справа на B , получится
, но если A умножить слева на B , то получится
Обратите внимание, что оба продукта определены и имеют одинаковый размер, но не равны.
Пример 12 : Если A и B — квадратные матрицы, такие, что AB = BA , то A и B говорят, что коммутируют . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют.
Пусть
— две произвольные диагональные матрицы 2 x 2. Тогда
и
Начиная с a 11 b 11 = b 11 a 11 и a 22 b 22 09 9329 a 38 22 22 , AB действительно равно BA , как и нужно.
Хотя матричное умножение обычно не коммутативно, оно равно , иногда ; например, если
, затем
Несмотря на подобные примеры, необходимо указать, что , как правило, умножение матриц не является коммутативным .
Есть еще одно различие между умножением скаляров и умножением матриц. Если a и b являются действительными числами, то уравнение ab = 0 означает, что a = 0 или b = 0.То есть, единственный способ, при котором произведение действительных чисел может быть равным 0, — это если хотя бы один из множителей сам равен 0. Аналогичное утверждение для матриц, однако, неверно. Например, если
Аналогичное утверждение для матриц, однако, неверно. Например, если
, затем
Обратите внимание, что хотя ни G , ни H не являются нулевой матрицей, произведение GH является.
Еще одним отличием умножения скаляров от умножения матриц является отсутствие общего закона сокращения для умножения матриц.Если a, b и c являются действительными числами с a ≠ 0, то, отбрасывая множитель a , уравнение ab = ac подразумевает b = c . Для умножения матриц такого закона не существует; то есть утверждение AB = AC означает , а не , подразумевает B = C , даже если A не равно нулю. Например, если
, затем оба
и
Таким образом, даже если AB = AC и A не является нулевой матрицей, B не равно C .
Пример 13 : Хотя умножение матриц не всегда коммутативно, оно равно , всегда ассоциативно . То есть, если A, B и C — любые три матрицы, такие, что определен продукт (AB) C , то продукт A (BC) также определен, и
То есть, пока порядок факторов не меняется, то, как они сгруппированы, не имеет значения.
Проверить ассоциативный закон для матриц
Первый, с
продукт (AB) C это
Сейчас, с
продукт A (BC) равен
Следовательно, (AB) C = A (BC) , как и ожидалось.Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны, чтобы разрешить двусмысленность, потому что нет двусмысленности.
Пример 14 : Для матриц
проверьте уравнение ( AB ) T = B T A T .
Первая,
означает
Сейчас, с
B T A T действительно равно ( AB ) T .Фактически, уравнение
справедливо для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если продукт AB определен, то транспонирование продукта равно произведению перемещений в обратном порядке .
Матрицы идентичности . Нулевая матрица 0 m x n играет роль аддитивной идентичности в наборе матриц m x n так же, как число 0 в наборе действительных чисел (вспомните пример 7).То есть, если A является матрицей m x n и 0 = 0 m x n , то
Это матричный аналог утверждения, что для любого действительного числа a ,
Имея в руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как
Есть ли матрица, которая играет эту роль ? Рассмотрим матрицы
и убедитесь, что
и
Таким образом, AI = IA = A .Фактически, легко показать, что для этой матрицы I оба продукта AI и IA будут равны A для любой Матрица 2 x 2 A . Следовательно,
— мультипликативная единица в наборе матриц 2 x 2. Аналогично матрица
— мультипликативная единица в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I 3 — это матрица [δ ij ] 3 x 3 .) В общем случае матрица I n — диагональная матрица nxn с каждым диагональным элементом, равным 1 — называется единичной матрицей порядка n и служит мультипликативной единицей в наборе всех nxn матриц.
Есть ли мультипликативная идентичность в наборе всех матриц m x n , если m ≠ n ? Для любой матрицы A в M mxn ( R ) матрица I m является левой единицей ( I m A = A ) и I n — это правый идентификатор ( AI n = A ).Таким образом, в отличие от набора матриц n x n , набор неквадратных матриц m x n не обладает двусторонней идентичностью qunique , потому что I m ≠ I n , если m ≠ n .
Пример 15 : Если A — квадратная матрица, то A 2 обозначает продукт AA, A 3 обозначает продукт AAA и т. Д. Если A — это матрица
показывают, что A 3 = — A .
Расчет
показывает, что A 2 = — I . Умножение обеих частей этого уравнения на A дает A 3 = — A , если требуется. [Техническое примечание: можно показать, что в определенном точном смысле набор матриц вида
, где a и b — действительные числа, структурно идентичен набору из комплексных чисел a + bi .Поскольку матрица A в этом примере имеет следующий вид (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i , и аналогу матричное уравнение A 2 = — I , полученное выше, равно i 2 = -1, уравнение, которое определяет мнимую единицу, i .]
Пример 16 : Найдите недиагональную матрицу, которая коммутирует с
Проблема состоит в том, чтобы получить недиагональную матрицу B , такую что AB = BA . Как и A , матрица B должна быть 2 x 2. Один из способов создать такую матрицу B — сформировать A 2 , так как если B = A 2 , ассоциативность подразумевает
Как и A , матрица B должна быть 2 x 2. Один из способов создать такую матрицу B — сформировать A 2 , так как если B = A 2 , ассоциативность подразумевает
(Это уравнение доказывает, что A 2 будет коммутировать с A для любой квадратной матрицы A ; кроме того, оно предлагает, как можно доказать, что каждые интегральной степени квадратной матрицы A будет добираться на работу с A .)
В данном случае
, который недиагонален. Эта матрица B действительно коммутирует с A , что подтверждается расчетами
.
и
Пример 17 : Если
доказывают, что
для каждого натурального числа n .
Несколько предварительных расчетов показывают, что данная формула действительно верна:
Однако, чтобы установить, что формула верна для всех натуральных чисел n , необходимо дать общее доказательство.Здесь это будет сделано с использованием принципа математической индукции , который читается следующим образом. Пусть P (n) обозначает предложение относительно натурального числа n . Если можно показать, что
и
, то утверждение P (n) действительно для всех натуральных чисел n . В данном случае утверждение P (n) является утверждением
Поскольку A 1 = A , утверждение P (1) определенно верно, поскольку
Теперь, предполагая, что P (n) истинно, то есть предполагая, что
теперь необходимо установить срок действия выписки P ( n + 1), что составляет
Но это утверждение действительно верно, потому что
По принципу математической индукции доказательство завершено.
Инверсия матрицы . Пусть a будет заданным действительным числом. Поскольку 1 является мультипликативным тождеством в наборе действительных чисел, если существует число b такое, что
, то b называется , обратным или , обратным мультипликативному от a и обозначается a -1 (или 1/ a ). Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет заданной матрицей n x n .Поскольку I = I n является мультипликативным тождеством в наборе матриц n x n , если существует матрица B , такая что
, тогда B называется (мультипликативным) , обратным A и обозначается A -1 (читается « A обратный»).
Пример 18 : Если
, затем
с
и
Еще одно различие между умножением скаляров и умножением матриц заключается в существовании инверсий.Хотя каждое ненулевое действительное число имеет обратное , существуют ненулевые матрицы, у которых нет обратного .
Пример 19 : Показать, что ненулевая матрица
не имеет обратного.
Если бы эта матрица имела инверсию, то
для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка продукта также должна быть нулевой строкой:
(Когда звездочка, * появляется как запись в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку (2, 2) элемент произведения не может равняться 1, произведение не может быть равным единичной матрице. Следовательно, невозможно построить матрицу, которая могла бы служить обратной для A .
Если матрица имеет инверсию, она называется обратимой . Матрица в примере 23 обратима, а матрица в примере 24 — нет. Позже вы узнаете различные критерии для определения обратимости данной квадратной матрицы.
Пример 20 : Пример 18 показал, что
Учитывая, что
проверьте уравнение ( AB ) −1 = B −1 A −1 .
Сначала вычислим AB :
Затем вычислим B −1 A −1 :
Теперь, поскольку произведение AB и B −1 A −1 равно I ,
B −1 A −1 действительно является обратным AB . Фактически, уравнение
справедливо для любых обратимых квадратных матриц того же размера.Это говорит о том, что если A и B являются обратимыми матрицами одинакового размера, то их произведение AB также обратимо, и обратное произведение равно произведению обратных в обратном порядке . (Сравните это уравнение с уравнением с транспонированием в примере 14 выше.) Этот результат можно в общем доказать, применяя ассоциативный закон для матричного умножения. С
и
следует, что ( AB ) -1 = B -1 A -1 , как и нужно.
Пример 21 : Обратная матрица
это
Покажите, что обратное значение B T равно ( B −1 ) T .
Форма B T и ( B -1 ) T и умножьте:
Этот расчет показывает, что ( B -1 ) T является обратным B T . [Строго говоря, это показывает только то, что ( B -1 ) T — это правый обратный B T , то есть когда он умножает B T справа, продукт — это личность. Также верно, что ( B −1 ) T B T = I , что означает ( B −1 ) T — это левый обратный из . В Т .Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратное, нет различия между левым обратным и правым обратным.] Таким образом,
[Строго говоря, это показывает только то, что ( B -1 ) T — это правый обратный B T , то есть когда он умножает B T справа, продукт — это личность. Также верно, что ( B −1 ) T B T = I , что означает ( B −1 ) T — это левый обратный из . В Т .Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратное, нет различия между левым обратным и правым обратным.] Таким образом,
уравнение, которое на самом деле справедливо для любой обратимой квадратной матрицы B . Это уравнение говорит, что если матрица обратима, то ее транспонирование также является обратимым, а обратное транспонирование — это транспонирование обратного.
Пример 22 : Используйте свойство распределения для матричного умножения, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: если матрица 2 x 2 D удовлетворяет уравнение D 2 — D — 6 I = 0 , какое выражение для D −1 ?
По указанным выше распределительным свойствам D 2 — D = D 2 — DI = D (D — I) .Следовательно, уравнение D 2 — D — 6 I = 0 подразумевает D (D — I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
, что означает
В качестве иллюстрации этого результата матрица
удовлетворяет уравнению D 2 — D — 6 I = 0 , как вы можете убедиться.С
и
матрица 1/6 ( D − I ) действительно равна D −1 , как заявлено.
Пример 23 : Уравнение ( a + b ) 2 = a 2 + 2 ab + b 2 является тождеством, если a и b настоящие числа. Однако покажите, что ( A + B ) 2 = A 2 + 2 AB + B 2 — это , а не , идентичность, если A и B — это матрицы 2 x 2.[Примечание: законы распределения для матричного умножения: A ( B ± C ) = AB ± AC , данные в Примере 22, и сопутствующий закон ( A ± B ). C = AC ± BC .]
Из законов распределения для умножения матриц следует
Поскольку матричное умножение не коммутативно, BA обычно не равно AB , поэтому сумма BA + AB не может быть записана как 2 AB .В общем, тогда ( A + B ) 2 ≠ A 2 + 2 AB + B 2 . [Любые матрицы A и B , которые не коммутируются (например, матрицы в примере 16 выше), предоставят конкретный контрпример к утверждению ( A + B ) 2 = A 2 + 2 AB + B 2 , что также установит, что это не личность.]
Пример 24 : Предположим, что B обратимый. Если A коммутирует с B , покажите, что A также коммутирует с B -1 .
Доказательство . Сказать « A коммутирует с B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность:
Пример 25 : Число 0 имеет только один квадратный корень: 0.Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A такие, что A 2 = 0 .
Точно так же, как число a называется квадратным корнем из b , если a 2 = b , матрица A называется квадратным корнем из B , если A 2 = B . Пусть
— произвольная матрица 2 x 2.Возводя его в квадрат и устанавливая результат равным 0 , получаем
Записи (1, 2) в последнем уравнении подразумевают b ( a + d ) = 0, что выполняется, если (Случай 1) b = 0 или (Случай 2) d = — а .
Случай 1. Если b = 0, то диагональные записи подразумевают a = 0 и d = 0, а записи (2, 1) означают, что c произвольно. Таким образом, для любого значения c каждая матрица вида
— это квадратный корень из 0 2×2 .
Случай 2. Если d = — a , то оба недиагональных входа будут равны 0, а диагональные записи будут равны a 2 + bc . Таким образом, пока b и c выбраны так, что bc = — a 2 , A 2 будет равно 0 .
Аналогичная цепочка рассуждений, начинающаяся с записей (2, 1), приводит либо к a = c = d = 0 (и b произвольно), либо к такому же выводу, что и раньше: до тех пор, пока b и c выбираются так, что bc = — a 2 , матрица A 2 будет равна 0 .
Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет иметь свойство, состоящее в том, что ее квадрат представляет собой нулевую матрицу 2 на 2:
Поскольку существует бесконечно много значений a, b и c , таких что bc = — a 2 , нулевая матрица 0 2×2 имеет бесконечно много квадратных корней. Например, выбор a = 4, b = 2 и c = −8 дает ненулевую матрицу
Например, выбор a = 4, b = 2 и c = −8 дает ненулевую матрицу
площадью
Matrix Рейтинг
Этот урок знакомит с концепцией матрицы с рангом и объясняет, как ранг матрица раскрывается его эшелонированная форма.
Ранг матрицы
Вы можете представить себе матрицу r x c как набор строк r векторы каждый имеет c элементов; или вы можете думать об этом как о наборе c векторы-столбцы, каждый из которых содержит r элементов.
Ранг матрицы определяется как (а) максимальное количество линейно независимых столбца векторов в матрице или (б) максимальное количество линейно независимых строк векторов в матрице.Оба определения эквивалентны.
Для матрицы r x c ,
- Если r меньше c , то максимальный ранг матрицы r .
- Если r больше c , то максимальный ранг матрицы это c .
Ранг матрицы был бы равен нулю, только если бы матрица не имела элементов.Если бы матрица имела хотя бы один элемент, ее минимальный ранг был бы равен единице.
How to Find Matrix Рейтинг
В этом разделе мы описываем метод определения ранга любой матрицы. Этот метод предполагает знакомство с эшелонные матрицы и эшелонные преобразования.
Максимальное количество линейно независимых векторов в матрице равно
к количеству ненулевых строк в его
матрица эшелонов строк.
Следовательно, чтобы найти ранг матрицы, мы просто
преобразовать матрицу к ее форме эшелона строк и подсчитать количество
ненулевые строки.
Рассмотрим матрицу A и ее ряд строк. матрица, A ref .Ранее мы показывали как найти форму эшелона строк для матрицы A .
Потому что форма эшелона строки A ref имеет две ненулевые строки, мы знаем, что матрица A имеет два независимых вектора-строки; и мы знаем, что ранг матрицы A равен 2.
Вы можете убедиться, что это правильно. Ряд 1 и Ряд 2 матрицы А линейно независимый.Однако строка 3 — это линейная комбинация строк 1 и 2. В частности, строка 3 = 3 * (строка 1) + 2 * (строка 2). Следовательно, матрица A имеет только два независимых вектора-строки.
Матрицы полных рангов
Когда все векторов в матрице линейно независимый, матрица называется , полный ранг . Рассмотрим матрицы A и B ниже.
Обратите внимание, что строка 2 матрицы A является скалярным кратным ряд 1; то есть строка 2 равна удвоенной строке 1. Следовательно, строки 1 и 2 являются линейно зависимый. Матрица А имеет только одну линейно независимую row, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Теперь посмотрим на матрицу B . Все его строки линейно Независимо, поэтому ранг матрицы B равен 3.Матрица B полноразмерная.
Проверьте свое понимание
Проблема 1
Рассмотрим матрицу X , показанную ниже.
Какое у него звание?
(А) 0
(В) 1
(С) 2
(D) 3
(E) 4
Решение
Правильный ответ (С).Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля. И поскольку в нем меньше строк, чем столбцов, его максимальный ранг равен максимальному количеству линейно независимые строки. И поскольку ни одна строка не зависит линейно от другой строки, матрица имеет 2 линейно независимых строки; так что его рейтинг 2.
Проблема 2
Рассмотрим матрицу Y , показанную ниже.
Какое у него звание?
(А) 0
(В) 1
(С) 2
(D) 3
(E) 4
Решение
Правильный ответ (С). Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля. И поскольку в нем меньше столбцов, чем строк, его максимальный ранг равен максимальному количеству линейно независимых столбцы.
Столбцы 1 и 2 независимы, потому что ни один из них не может быть получен как скалярное кратное другому. Однако столбец 3 линейно зависит от столбцов 1 и 2, потому что столбец 3 равен столбцу 1 плюс столбец 2. Это оставляет матрицу максимум с двумя линейно независимые колонны; то есть столбец 1 и столбец 2. Таким образом, ранг матрицы равен 2.
Умножение матриц
Вы можете умножить только два
матрицы
если их
размеры
являются
совместимый
, что означает, что количество столбцов в первой матрице совпадает с количеством строк во второй матрице.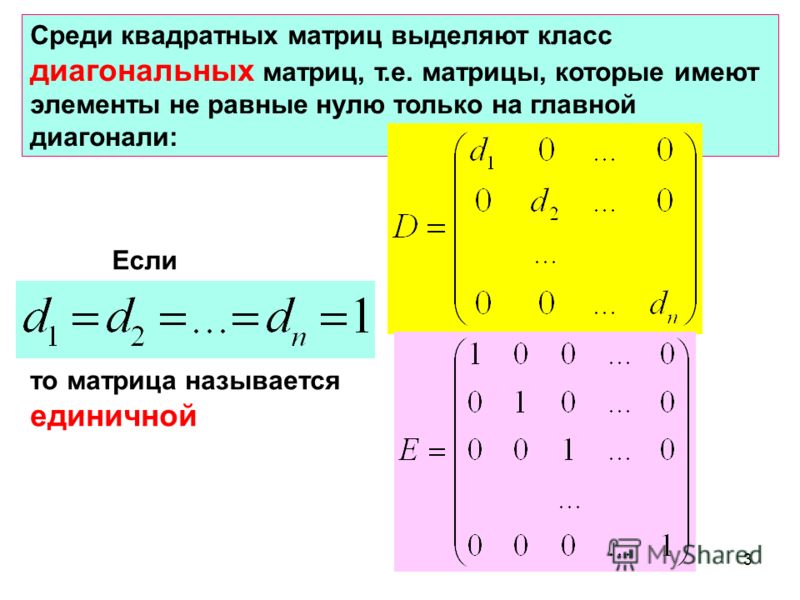
Если А знак равно [ а я j ] является м × п матрица и B знак равно [ б я j ] является п × п матрица, продукт А B является м × п матрица.
А B знак равно [ c я j ] , где c я j знак равно а я 1 б 1 j + а я 2 б 2 j + … + а я п б п j .
(Запись в я th ряд и j th столбец обозначается двойным индексом а я j , б я j , и c я j . Например, запись а 23 — запись во второй строке и третьем столбце.)
Определение матричного умножения указывает на построчное умножение, где записи в я th ряд А умножаются на соответствующие записи в j th столбец из B а затем добавляем результаты.
Умножение матриц НЕ коммутативно. Если ни то, ни другое А ни B — единичная матрица, А B ≠ B А .
Умножение строки на столбец
Мы начнем с того, что покажем вам, как умножить
1
×
п
матрица
п
×
1
матрица. Первый — это всего лишь одна строка, а второй — один столбец. По приведенному выше правилу товар является
1
×
1
матрица; другими словами, одно число.
По приведенному выше правилу товар является
1
×
1
матрица; другими словами, одно число.
Сначала назовем записи в строке р 1 , р 2 , … , р п , а записи в столбце c 1 , c 2 , … , c п . Тогда произведение строки и столбца — это 1 × 1 матрица
[ р 1 c 1 + р 2 c 2 + … + р п c п ] .
Пример:
Найдите товар.
[ 1 4 0 ] ⋅ [ 2 — 1 5 ]
Мы должны умножить 1 × 3 матрица 1 × 3 матрица.Количество столбцов в первом равно количеству строк во втором, поэтому они совместимы.
Товар:
[ ( 1 ) ( 2 ) + ( 4 ) ( — 1 ) + ( 0 ) ( 5 ) ] знак равно [ 2 + ( — 4 ) + 0 ] знак равно [ — 2 ]
Умножение больших матриц
Теперь, когда вы знаете, как умножать строку на столбец, умножать матрицы большего размера очень просто.![]() Для входа в
я
th
ряд и
j
th
столбец матрицы продукта, умножьте каждую запись в
я
th
строку первой матрицы на соответствующую запись в
j
th
столбец
второй матрицы и складываем результаты.
Для входа в
я
th
ряд и
j
th
столбец матрицы продукта, умножьте каждую запись в
я
th
строку первой матрицы на соответствующую запись в
j
th
столбец
второй матрицы и складываем результаты.
Возьмем следующую задачу, умножая 2 × 3 матрица с 3 × 2 матрица, чтобы получить 2 × 2 матрица как продукт.Элементы матрицы продукта называются е я j когда они в я th ряд и j th столбец.
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 — 1 0 2 — 1 ] знак равно [ е 11 е 12 е 21 год е 22 ]
Получить е 11 , умножить строку 1 первой матрицы по столбцу 1 второй.
е 11 знак равно [ 1 0 1 ] ⋅ [ 3 — 1 2 ] знак равно 1 ( 3 ) + 0 ( — 1 ) + 1 ( 2 ) знак равно 5
Получить
е
12
, умножить строку
1
первой матрицы по столбцу
2
второй.
е 12 знак равно [ 1 0 1 ] ⋅ [ 5 0 — 1 ] знак равно 1 ( 5 ) + 0 ( 0 ) + 1 ( — 1 ) знак равно 4
Получить е 21 год , умножить строку 2 первой матрицы по столбцу 1 второй.
е 21 год знак равно [ 0 1 2 ] ⋅ [ 3 — 1 2 ] знак равно 0 ( 3 ) + 1 ( — 1 ) + 2 ( 2 ) знак равно 3
Получить е 22 , умножить строку 2 первой матрицы по столбцу 2 второй.
е 22 знак равно [ 0 1 2 ] ⋅ [ 5 0 1 ] знак равно 0 ( 5 ) + 1 ( 0 ) + 2 ( — 1 ) знак равно — 2
Записывая матрицу продуктов, получаем:
[ е 11 е 12 е 21 год е 22 ] знак равно [ 5 4 3 — 2 ]
Таким образом, мы показали:
[ 1 0 1 0 1 2 ] ⋅ [ 3 5 — 1 0 2 — 1 ] знак равно [ 5 4 3 — 2 ]
Обратная квадратная матрица
6. 3 — Обратная квадратная матрица
3 — Обратная квадратная матрица
Реальные числа
При работе с действительными числами уравнение ax = b может быть решено относительно x путем деления обоих стороны уравнения на a, чтобы получить x = b / a, пока a не было равным нулю. Поэтому казалось бы логичным что при работе с матрицами можно взять матричное уравнение AX = B и разделить оба сторон на A, чтобы получить X = B / A.
Однако это не сработает, потому что …
Нет матричного деления!
Хорошо, скажете вы. Вычитание было определено в терминах сложения, а деление — в терминах умножение.Поэтому вместо деления я просто умножу на обратное. Так оно и есть должно быть сделано.
Обратная матрица
Итак, что есть инверсия матрицы?
Ну, в реальных числах, любое действительное число, обратное a , было числом a -1 , так что a умножить на a -1 равняется 1. Мы знали, что для действительного числа обратное число равно обратному значению число, если число не было нулем.
Обратной квадратной матрице A, обозначенной A -1 , является матрица так что произведение A и A -1 — это матрица идентичности. Единичная матрица, которая дает будет того же размера, что и матрица A. Вау, есть а много общего между действительными числами и матрицами. Это хорошо, правда — ты не хочу это быть что-то совсем другое.
A (A -1 ) = I или A -1 (A) = I
Но есть несколько исключений.Прежде всего, A -1 делает не означает 1 / A. Помните: «Матричного деления нет!» Во-вторых, A -1 делает не означает брать обратную величину каждого элемента в матрице А.
Требования к инверсии
- Матрица должна быть квадратной (одинаковое количество строк и столбцов).
- Определитель матрицы не должен быть нулевым (определители рассматриваются в разделе 6.4).
Это вместо того, чтобы действительное число не равнялось нулю, чтобы иметь обратное, определитель не должен
равняться нулю, чтобы иметь обратное.
Квадратная матрица, имеющая обратную, называется обратимым или невырожденным . Матрица, которая не у инверсии называется в единственном числе .
Матрица не обязательно должна иметь обратную, но если она есть, то обратная матрица уникальна.
Трудный путь в поисках обратного
Матрица, обратная матрице A, будет удовлетворять уравнению A (A -1 ) = I.
- Присоедините единичную матрицу к правой части исходной матрицы так, чтобы у вас есть A слева и единичная матрица справа.Это будет выглядеть так [A | I].
- Row-уменьшить (предлагаю использовать поворот) матрицу пока в левой части не появится матрица идентичности. Когда левая сторона — это личность матрица правая сторона будет Обратной [I | А -1 ]. Если вы не можете чтобы получить единичную матрицу в левой части, тогда матрица сингулярна и не имеет обратного.
- Возьмите расширенную матрицу с правой стороны и назовите ее обратной.
Ярлык для поиска инверсии матрицы 2 × 2
Обратную матрицу 2 × 2 можно найти с помощью…
- Переключить элементы по главной диагонали
- Возьмите противоположность двух других элементов
- Делим все значения на определитель матрицы (так как мы не говорили о детерминанте, для системы 2 × 2 это произведение элементов на главной диагонали за вычетом произведения двух других элементов).
Пример ярлыка
Поехали с оригинальной матрицей
Шаг 1, переключение элементов на главной диагонали повлечет за собой переключение 5 и 7.
Шаг 2, возьмите противоположность двух других элементов, но оставьте их там, где они есть.
Шаг 3, найдите определитель и разделите на него каждый элемент. Определитель
это произведение элементов на главной диагонали за вычетом произведения
элементы от главной диагонали. Это означает, что определитель этой матрицы равен
7 (5) — (-3) (2) = 35 + 6 = 41. Делим каждый элемент на 41.
Делим каждый элемент на 41.
Матрица, обратная исходной матрице …
| 5/41 | 2/41 | ||
| -3/41 | 7/41 |
Теперь, вы говорите, подождите минутку — вы сказали, что не было матричного деления.Деления по матрице нет. Вы можете умножить или разделить матрицу на скаляр (действительное число) и определитель является скаляром.
Использование калькулятора
Теперь, когда вы знаете, как найти единичную матрицу вручную, поговорим о практичности. Калькулятор сделаю это за вас.
Вход в матрицу
- Нажмите клавишу Matrix (справа под клавишей X). На TI-83 + вам понадобится на хит 2 и Матрица.
- Стрелка к подменю Правка.
- Выберите матрицу для работы. У вас есть пять вариантов на выбор с TI-82 и десять на выбор. выбирайте из с TI-83. Обычно вы будете использовать [A]. Старайтесь не использовать [E] для неуказанные причины, которые будут указаны, если вы изучаете конечную математику.
- Введите количество строк, нажмите клавишу ВВОД, а затем введите количество столбцов, а затем входить.
- Теперь вы вводите каждый элемент в матрицу, читая слева направо и сверху вниз. Нажмите введите после каждого числа.Вы можете использовать клавиши со стрелками для перемещения, если вы допустили ошибку.
- Выйдите (2 режима и ), когда закончите вводить все числа.
Использование матриц
Всякий раз, когда вам нужно получить доступ к созданной вами матрице, просто нажмите клавишу Matrix и выберите соответствующая матрица. Я бы посоветовал вам начать использовать Матрицу 1, Матрицу 2 и т. Д. Вместо Матрица, стрелка вниз, ввод. Это будет происходить быстрее, и вы будете много делать с этими матрицами.
Нахождение обратной матрицы на калькуляторе
Введите выражение [A] -1 , перейдя в Матрицу 1 и нажав клавишу x -1 . (-1).
(-1).
Возможно, вам придется использовать клавиши со стрелками вправо или влево, чтобы пролистать всю матрицу, чтобы записать ее вниз. По возможности дайте точные ответы.
Один из способов дать точный ответ — это заставить калькулятор переводить десятичные дроби в дроби для ты. В конце концов, дроби действительно ваши друзья (и я серьезно это имею в виду). Вы можете получить Калькулятор выполняет преобразование десятичной дроби в дробную, нажимая Math, Enter, Enter.
Также, если вы получите ответ типа 1.2E-12, шансы действительно хорошо, что число равно нулю, и это из-за неточности в калькуляторе что вы получаете такой ответ. Преобразуйте число до нуля.
Зачем понадобился инверс?
Я так рад, что вы спросили об этом.
Одно из основных применений обратных чисел — решение системы линейных уравнений. Вы можете записать систему в матричной форме как AX = B.
Теперь предварительно умножьте обе части на обратную величину A. Убедитесь, что вы соблюдаете эти два условия.
- Вы должны разместить инверсную матрицу рядом с матрицей. То есть потому что инверсии должны быть рядом друг с другом (математически очень расплывчато, но вернемся к функциям), чтобы уничтожить друг друга.
- Если вы умножаете, помещая что-то перед левой стороной (предварительное умножение), он должен идти впереди правой стороны. Если вы положите что-то позади (пост-умножение) левой стороны, она должна идти позади правой стороны.
Умножение матриц НЕ коммутативно!
A -1 (AX) = A -1 (B)… предварительное умножение с обеих сторон по A -1
(A -1 A) X = A -1 B … используйте ассоциативный свойство для перегруппировки факторов
I X = A -1 B … при умножении на обратное вместе они становятся единичной матрицей
X = A -1 B … единичная матрица похожа на
умножение на 1.
Если AX = B, то X = A -1 B
Итак, вы обычно цинично спрашиваете: «Вы только что решили другое уравнение, что это имеет отношение к чему-нибудь? »
Решение систем линейных уравнений
Рассмотрим систему линейных уравнений
3x + 2y - 5z = 12 х - 3у + 2z = -13 5x - y + 4z = 10
Запишите коэффициенты в матрицу A.
| х | y | z | ||
|---|---|---|---|---|
| 3 | 2 | -5 | ||
| 1 | -3 | 2 | ||
| 5 | -1 | 4 |
Запишите переменные в матрицу X.
Запишите константы в матрицу B.
| 12 | ||
| -13 | ||
| 10 |
Убедитесь, что AX = B
Этот шаг на самом деле не нужен, но я хотел показать вам, что это действительно работает.
AX будет (3 × 3) × (3 × 1) = 3 × 1 матрица. Матрица B также является матрицей 3 × 1, поэтому, по крайней мере, размеры работать правильно.
Вот A, умноженное на X.
| 3 | 2 | -5 | х | 3x + 2y — 5z | ||||||||
| 1 | -3 | 2 | г. | = | 1x — 3y + 2z | |||||||
| 5 | -1 | 4 | z | 5x — 1y + 4z |
Обратите внимание, что это левая часть системы уравнений. В
B — правая часть, значит, мы достигли равенства. Woohoo! Ты можешь написать
система линейных уравнений в виде AX = B.
В
B — правая часть, значит, мы достигли равенства. Woohoo! Ты можешь написать
система линейных уравнений в виде AX = B.
Итак, если вы можете записать систему линейных уравнений в виде AX = B, где A — коэффициент матрица, X — переменная матрица, а B — правая часть, вы можете найти решение системы X = A -1 B.
Поместите матрицу коэффициентов в [A] на калькуляторе и с правой стороны. стороной в [B].
Если вы попросили калькулятор найти обратный коэффициент матрица, это даст вам это для A -1
| 5/44 | 3/88 | 1/8 | ||
| -3/44 | -37/88 | 1/8 | ||
| -7/44 | -13/88 | 1/8 |
Вы можете сделать это, а затем умножить это на B, но было бы проще просто поместить все выражение в калькулятор и сразу получить ответ.Даже то, что показано ниже, — это больше работы, чем необходимо.
X = A -1 B = …
| х | 5/44 | 3/88 | 1/8 | 12 | 191/88 | |||||||||||
| г. | = | -3/44 | -37/88 | 1/8 | -13 | = | 519/88 | |||||||||
| z | -7/44 | -13/88 | 1/8 | 10 | 111/88 |
Итак, x = 191/88, y = 519/88 и z = 111/88. Это было бы настоящим
боль
решать вручную.
Это было бы настоящим
боль
решать вручную.
Это просто, почему мы не всегда так делаем?
Основная причина в том, что это не всегда работает.
- Инверсии существуют только для квадратных матриц. Это означает, что если вы не то же самое количество уравнений в качестве переменных, то вы не можете использовать этот метод.
- Не всякая квадратная матрица имеет инверсию. Если матрица коэффициентов A равна единственное число (не имеет обратного), тогда решения может не быть или может быть много решений, но мы не можем сказать, что это такое.
- Перевертыши сложно найти вручную. Если у вас есть калькулятор, его нет так плохо, но помните, что калькуляторы не всегда дают вам ответ, который вы находясь в поиске.
Создание, печать, добавление столбца, среза
Матричная функция в R
Матричная функция в R — это двумерный массив, имеющий m строк и n столбцов. Другими словами, матрица в программировании на R — это комбинация двух или более векторов с одним и тем же типом данных.
Примечание: Можно создать более двух массивов измерений с помощью матричной функции в R.
Как создать матрицу в R
Мы можем создать матрицу с помощью функции matrix (). Ниже приведена функция для создания матрицы в R, которая принимает три аргумента:
матрица (data, nrow, ncol, byrow = FALSE)
Аргументы:
- данные : Набор элементов, которые R разместит в строках и столбцах матрицы \
- nrow : Количество строк
- ncol : Количество столбцов
- byrow : строки заполняются слева направо.Мы используем byrow = FALSE (значения по умолчанию), если хотим, чтобы матрица заполнялась столбцами, т.е. значения заполнялись сверху вниз.
Давайте построим две матрицы 5×2 с последовательностью чисел от 1 до 10, одну с byrow = TRUE и одну с byrow = FALSE, чтобы увидеть разницу.
# Построить матрицу из 5 строк, содержащих числа от 1 до 10 и byrow = TRUE matrix_a <-matrix (1:10, byrow = TRUE, nrow = 5) matrix_a
Вывод:
Распечатать размер матрицы с помощью dim ()
Теперь напечатаем размер матрицы в R с помощью dim ().Синтаксис для печати матрицы в R с использованием dim ():
# Распечатать размер матрицы с помощью dim () dim (matrix_a)
Вывод:
## [1] 5 2
Построить матрицу из 5 строк, содержащих числа от 1 до 10, и byrow = FALSE
# Построить матрицу из 5 строк, содержащих числа От 1 до 10 и byrow = FALSE matrix_b <-matrix (1:10, byrow = FALSE, nrow = 5) matrix_b
Вывод:
Распечатайте размер матрицы с помощью dim ()
Снова напечатайте размер матрицы с помощью dim ().Ниже приведен синтаксис размера матрицы печати R:
# Распечатать размер матрицы с помощью dim () dim (matrix_b)
Вывод:
## [1] 5 2
Примечание : Использование команды matrix_b <-matrix (1:10, byrow = FALSE, ncol = 2) будет иметь тот же эффект, что и выше.
Вы также можете создать матрицу 4x3 с помощью ncol. R создаст 3 столбца и заполнит строку сверху вниз. Посмотрите пример
matrix_c <-matrix (1:12, byrow = FALSE, ncol = 3) matrix_c
Вывод:
## [, 1] [, 2] [, 3] ## [1,] 1 5 9 ## [2,] 2 6 10 ## [3,] 3 7 11 ## [4,] 4 8 12
Пример:
dim (matrix_c)
Вывод:
## [1] 4 3
Добавить столбец в матрицу с помощью cbind ()
Вы можете добавить столбец в матрицу R с помощью cbind () команда.cbind () означает привязку столбца. cbind () может объединять столько матриц или столбцов, сколько указано. Например, в нашем предыдущем примере была создана матрица 5x2. Мы объединяем третий столбец и проверяем размер 5x3
Пример:
# объединить c (1: 5) с matrix_a matrix_a1 <- cbind (matrix_a, c (1: 5)) # Проверить размер тусклый (matrix_a1)
Выход:
## [1] 5 3
Пример:
matrix_a1
Выход
## [, 1] [, 2] [, 3] ## [1,] 1 2 1 ## [2,] 3 4 2 ## [3,] 5 6 3 ## [4,] 7 8 4 ## [5,] 9 10 5
Пример:
Мы также можем добавить столбец в матрицу R более одного раза.
