Определитель матрицы 2×2, 3×3, 4×4…
Определитель (детерминант) квадратной матрицы A — это число, обладающее определенными свойствами, которое может быть получено из элементов матрицы рядом методов.
Обозначения
Пусть $ A = \begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
$det(A) = \left|A\right| = \begin{vmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{vmatrix}$
Свойства определителя
-
Если матрица имеет строку или столбец, все элементы которого равны нулю, то ее определитель равен 0.
Пример 12
$\begin{vmatrix} 1 & 4 & 2\\ 0 & 0 & 0\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 0\\ 4 & 2 & 0\\ 3 & 9 & 0 \end{vmatrix}=0$ -
Если в матрице есть две одинаковых строки или два одинаковых столбца, то ее определитель равен 0.
Пример 13
$\begin{vmatrix} 1 & 4 & 2\\ 1 & 4 & 2\\ 3 & 9 & 5 \end{vmatrix}= 0$ или $\begin{vmatrix} 1 & 4 & 1\\ 4 & 2 & 4\\ 3 & 9 & 3 \end{vmatrix}=0$ -
Если в матрице есть две пропорциональных строки или два пропорциональных столбца, то ее определитель равен 0.
Пример 14
$\begin{vmatrix} 1 & 4 & 2\\ 2 & 8 & 4\\ 3 & 9 & 5 \end{vmatrix}= 0$ (две первые строки пропорциональны)
или
$\begin{vmatrix} 8 & 4 & 7\\ 4 & 2 & 3\\ 18 & 9 & 8 \end{vmatrix}=0$ (два первых столбца пропорциональны) -
Если некоторая строка (столбец) является суммой или разностью других строк (столбцов), то определитель равен 0.
Пример 15
$\begin{vmatrix} 1 & 4 & 2\\ 7 & 2 & 3\\ 8 & 6 & 5 \end{vmatrix}= 0$ $R_{1} +R_{2} =R_{3}$ или$ \begin{vmatrix} 9 & 12 & 3\\ 1 & 8 & 7\\ 5 & 7 & 2 \end{vmatrix}=0$ $C_{1}+C_{3}=C_{2}$
-
При вычислении определителя можно выносить общие множители целых строк или столбцов.

Пример 16
В определителе
$\begin{vmatrix} 3 & 9 & 12\\ 5 & 1 & 8 \\ 7 & 4 & 2 \end{vmatrix}$, можно вынести множитель 3 из первой строки $(R_{1})$, тогда получаем:
$3 \cdot \begin{vmatrix} 1 & 3 & 4\\ 5 & 1 & 8\\ 7 & 4 & 2 \end{vmatrix}$, затем выносим 2 из третьего столбца $(C_{3})$:
$6\cdot \begin{vmatrix} 1 & 3 & 2\\ 5 & 1 & 4\\ 7 & 4 & 1 \end{vmatrix}$ - При вычислении определителя можно прибавлять (отнимать) строки к другим строкам и столбцы к другим столбцам; определитель матрицы при этом не меняется.
Пример 17
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{R_{1}+R_{2}} \begin{vmatrix} 4 & 13\\ 3 & 8 \end{vmatrix}$
Пример 18
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{C_{1}+C_{2}} \begin{vmatrix} 6 & 5\\ 11 & 8 \end{vmatrix}$ -
При вычислении определителя можно прибавлять или отнимать строки и столбцы, умноженные на произвольный коэффициент.
Пример 19
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{2R_{1}+3R_{2}} \begin{vmatrix} 11 & 34\\ 3 & 8 \end{vmatrix}$Пример 20
$\begin{vmatrix} 1 & 5\\ 3 & 8 \end{vmatrix}$ $\xlongequal{5C_{1}-C_{2}} \begin{vmatrix} 0 & 5\\ 7 & 8 \end{vmatrix}$ - Определитель матрицы равен определителю транспонированной матрицы.
- Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.
Минор матрицы
Определитель матрицы, полученной вычеркиванием некоторых строк и столбцов матрицы, называется минором этой матрицы.
Пример 21
$A=\begin{pmatrix} 1 & 4 & 2 \\ 5 & 3 & 7 \\ 6 & 2 & 1 \end{pmatrix}$
Один из миноров матрицы A есть $\begin{vmatrix} 1 & 4\\ 5 & 3 \end{vmatrix}$ (он получается вычеркиванием строки 3 и столбца 3 из матрицы A)
Другим минором является $\begin{vmatrix} 1 & 2 \\ 6 & 1 \end{vmatrix}$ (получается вычеркиванием строки 2 и столбца 2 из матрицы A)
Пример 22
$B=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix} $
Один из миноров матрицы B есть $ \begin{vmatrix} 1 & 7 & 9\\ 8 & 3 & 2\\ 8 & 1 & 4 \end{vmatrix}$ (получается вычеркиванием строки 1 и столбца 1 из матрицы B)
Другим минором является $\begin{vmatrix} 1 & 7 \\ 8 & 3 \end{vmatrix}$ (получается вычеркиванием строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Пусть $A= \begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & .
Можно определить минор $\Delta_{i,j}$, полученный вычеркиванием строки i и столбца j, для любого элемента $a_{i,j}$ квадратной матрицы A. Такой минор называется дополнительным.
Пример 23
$ A = \begin{pmatrix} 4 & 7\\ 2 & 9 \end{pmatrix}$
Определить дополнительный минор элемента 2. Так как данный элемент находится в строке 2, столбце 1, видно, что это $a_{2,1}$.
Нужно вычеркнуть строку 2 и столбец 1 из матрицы A, после чего получаем
Минор, дополнительный к элементу 2, есть $\Delta_{2,1} = 7$.
Пример 24
$B=\begin{pmatrix} 1 & 4 & 2\\ 5 & 3 & 7\\ 6 & 2 & 1\\ \end{pmatrix}$
Нужно найти минор, дополнительный к элементу 7. Так как данный элемент находится в строке 2, столбце 3, видно, что это $a_{2,3}$.
Мы должны вычеркнуть строку 2 и столбец 3 из матрицы B, после чего мы получаем
Минор, дополнительный к элементу 7, — это $\Delta_{2,3}= \begin{vmatrix} 1 & 4\\ 6 & 2 \end{vmatrix}$
Пример 25
$C=\begin{pmatrix} 2 & 5 & 1 & 3\\ 4 & 1 & 7 & 9\\ 6 & 8 & 3 & 2\\ 7 & 8 & 1 & 4 \end{pmatrix}$
Нужно найти минор, дополнительный к элементу 5. Так как данный элемент находится в строке 1, столбце 2, видно, что это $a_{1,2}$.
Мы должны вычеркнуть строку 1 и столбец 2 из матрицы C, после чего мы получаем
Минор, дополнительный к элементу 5, — это $\Delta_{1,2}= \begin{vmatrix} 4 & 7 & 9\\ 6 & 3 & 2\\ 7 & 1 & 4\\ \end{vmatrix}$
Алгебраическое дополнение элемента матрицы
Пусть $A=\begin{pmatrix} a_{1,1} & a_{1,2} & a_{1,3} & . & . & a_{1,n}\\ a_{2,1} & a_{2,2} & a_{2,3} & .
$\Delta_{1,1}= \begin{vmatrix} a_{2,2} & a_{2,3}\\ a_{3,2} & a_{3,3} \end{vmatrix} = a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2}$
$\Delta_{1,2}= \begin{vmatrix} a_{2,1} & a_{2,3}\\ a_{3,1} & a_{3,3} \end{vmatrix} = a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1}$
$\Delta_{1,3}= \begin{vmatrix} a_{2,1} & a_{2,2}\\ a_{3,1} & a_{3,2} \end{vmatrix} = a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1}$
$\left| A\right| =a_{1,1}\cdot( a_{2,2}\cdot a_{3,3}-a_{2,3}\cdot a_{3,2})-a_{1,2}\cdot(a_{2,1}\cdot a_{3,3}-a_{2,3}\cdot a_{3,1})+$ $a_{1,3}\cdot(a_{2,1}\cdot a_{3,2}-a_{2,2}\cdot a_{3,1})=$ $a_{1,1}\cdot a_{2,2}\cdot a_{3,3}-a_{1,1}\cdot a_{2,3}\cdot a_{3,2}-a_{1,2}\cdot a_{2.1}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+$ $a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-a_{1,3}\cdot a_{2,2}\cdot a_{3,1}=$ $\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+a_{1,2}\cdot a_{2,3}\cdot a_{3,1}+a_{1,3}\cdot a_{2,1}\cdot a_{3,2}-}$ $\color{red}{(a_{1,1}\cdot a_{2,3}\cdot a_{3,2}+a_{1,2}\cdot a_{2,1}\cdot a_{3,3}+a_{1,3}\cdot a_{2,2}\cdot a_{3,1})}$
Упростить получение последней формулы можно следующим образом.
Начнем с того, что перепишем первые две строки под определителем как показано ниже.
$\begin{vmatrix} \color{red}{a_{1,1}} & a_{1,2} & a_{1,3}\\ \color{red}{a_{2,1}} & \color{red}{a_{2,2}} & a_{2,3}\\ \color{red}{a_{3,1}} & \color{red}{a_{3,2}} & \color{red}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} a_{1,1} & \color{red}{a_{1,2}} & \color{red}{a_{1,3}}\\ a_{2,1} & a_{2,2} & \color{red}{a_{2,3}}\\ \end{array}$
Умножаем элементы на каждой из трех красных диагоналей (на главной диагонали и на диагоналях под ней) и складываем результаты:
$\begin{vmatrix} \color{red}{a_{1,1}} & \color{red}{a_{1,2}} & \color{blue}{a_{1,3}}\\ \color{red}{a_{2,1}} & \color{blue}{a_{2,2}} & \color{blue}{a_{2,3}}\\ \color{blue}{a_{3,1}} & \color{blue}{a_{3,2}} & \color{blue}{a_{3,3}} \end{vmatrix}$
$\hspace{2mm} \begin{array}{ccc} \color{blue}{a_{1,1}} & \color{blue}{a_{1,2}} & \color{red}{a_{1,3}}\\ \color{blue}{a_{2,1}} & \color{red}{a_{2,2}} & \color{red}{a_{2,3}}\\ \end{array}$
Умножаем элементы на каждой из трех синих диагоналей (на побочной диагонали и на диагоналях под ней) и складываем результаты:
$\color{blue}{a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1}}$
Вычитая вторую сумму из первой, получаем формулу определителя:
$\color{red}{a_{1,1}\cdot a_{2,2}\cdot a_{3,3}+ a_{2,1}\cdot a_{3,2}\cdot a_{1,3}+a_{3,1}\cdot a_{1,2}\cdot a_{2,3}-}$ $\color{red}{(a_{1,3}\cdot a_{2,2}\cdot a_{3,1}+ a_{2,3}\cdot a_{3,2}\cdot a_{1,1}+a_{3,3}\cdot a_{1,2}\cdot a_{2,1})}$
Пример 30
$A=\begin{pmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{pmatrix}$
$\begin{vmatrix} 1 & 4 & 3 \\ 2 & 1 & 5\\ 3 & 2 & 1\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 1 & 4 & 3\\ 2 & 1 & 5\\ \end{array}$
$ = 1\cdot1\cdot1 + 2\cdot2\cdot3 + 3\cdot4\cdot5 -(3\cdot1\cdot3 + 5\cdot2\cdot1 + 1\cdot4\cdot2) =$ $ 1 + 12 + 60 -(9 + 10 + 8)=73-27=46$
Пример 31
$A=\begin{pmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{pmatrix}$
$\begin{vmatrix} 3 & 5 & 1 \\ 1 & 4 & 2\\ 7 & 1 & 9\\ \end{vmatrix}$
$\hspace{2mm}\begin{array}{ccc} 3 & 5 & 1\\ 1 & 4 & 2\\ \end{array} $
$= 3\cdot4\cdot9 + 1\cdot1\cdot1 + 7\cdot5\cdot2 -(1\cdot4\cdot7 + 2\cdot1\cdot3 + 9\cdot5\cdot1) =$ $ 108 + 1 + 70 -(28 + 6 + 45)=79-79=100$
Элементы матрицы могут быть обозначены буквами. {2} \end{vmatrix}= $
{2} \end{vmatrix}= $
$\begin{vmatrix} a-c & b-c \\ (a-c)(a+c) & (b-c)(b+c) \end{vmatrix}=$ $(a-c)(b-c)\begin{vmatrix} 1 & 1\\ a+c & b+c \end{vmatrix}=$
$=(a-c)(b-c)[(b+c)-(a+c)]=$ $(a-c)(b-c)(b+c-a-c)=(a-c)(b-c)(b-a)$
Вычисление определителя матрицы 4×4
Вычислить определитель матрицы 4×4 можно с использованием общей формулы для определителя матрицы 3×3.
Но сначала надо использовать свойства определителей:
- Проверим, не выполняется ли одно из условий того, что определитель равен 0.
- Проверим, нельзя ли вынести общий множитель из одной или нескольких строк или столбцов.
- Проверим, не является ли данная матрица матрицей Вандермонде, возможно, такой, в которой некоторые строки или столбцы переставлены.
В любом из этих случаев нам пригодятся соответствующие методы вычисления определителей матриц 3×3. Модифицируем строку или столбец так, чтобы все его элементы, кроме одного, обратились в 0. Определитель будет равен произведению этого ненулевого элемента на его алгебраическое дополнение. В этом случае, алгебраическое дополнение — это определитель матрицы 3×3, который считается по уже известной формуле.
Пример 33
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 0 & 0 & 0 & 0\\ 2 & 3 & 1 & 8 \end{vmatrix}$
Замечаем, что все элементы в строке 3 равны нулю, а значит, определитель равен 0.
Пример 34
$\begin{vmatrix} 1 & 3 & 1 & 2\\ 5 & 8 & 5 & 3\\ 0 & 4 & 0 & 0\\ 2 & 3 & 2 & 8 \end{vmatrix}$
Замечаем, что $C_{1}$ равно $C_{3}$, следовательно, определитель равен 0.
Пример 35
$\begin{vmatrix} 1 & 3 & 9 & 2\\ 5 & 8 & 4 & 3\\ 10 & 16 & 18 & 4\\ 2 & 3 & 1 & 8 \end{vmatrix}$
Замечаем, что строки 2 и 3 пропорциональны друг другу, следовательно, определитель равен 0. {1+4}$
{1+4}$
Определитель матрицы: алгоритм, примеры вычисления, правила
Определение 1Определитель (детерминант) матрицы — некоторое число, с которым можно сопоставить любую квадратную матрицу А=(aij)n×n.
|А|, ∆, det A — символы, которыми обозначают определитель матрицы.
Способ вычисления определителя выбирают в зависимости от порядка матрицы.
Пример 1Определитель матрицы 2-го порядка вычисляют по формуле:
А=1-231.
Решение:
det A=1-231=1×1-3×(-2)=1+6=7
Определитель матрицы 3-го порядка: правило треугольника
Чтобы найти определитель матрицы 3-го порядка, необходимо одно из правил:
- правило треугольника;
- правило Саррюса.
Как найти определитель матрицы 3-го порядка по методу треугольника?
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
Пример 2А=13402115-1
Решение:
det A=13402115-1=1×2×(-2)+1×3×1+4×0×5-1×2×4-0×3×(-1)-5×1×1=(-2)+3+0-8-0-5=-12
Правило Саррюса
Чтобы вычислить определитель по методу Саррюса, необходимо учесть некоторые условия и выполнить следующие действия:
- дописать слева от определителя два первых столбца;
- перемножить элементы, которые расположены на главной диагонали и параллельных ей диагоналях, взяв произведения со знаком «+»;
- перемножить элементы, которые расположены на побочных диагоналях и параллельных им, взяв произведения со знаком «—».
а11а12а13а21а22а23а31а32а33=a11×a22×a33+a31×a12×a23+a21×a32×a13-a31×a22×a13-a21×a12×a33-a11×a23×a32
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Пример 3А=134021-25-11302-25=1×2×(-1)+3×1×(-2)+4×0×5-4×2×(-2)-1×1×5-3×0×(-1)=-2-6+0+16-5-0=3
Методы разложения по элементам строки и столбца
Чтобы вычислить определитель матрицу 4-го порядка, можно воспользоваться одним из 2-х способов:
- разложением по элементам строки;
- разложением по элементам столбца.

Представленные способы определяют вычисление определителя n как вычисление определителя порядка n-1 за счет представления определителя суммой произведений элементов строки (столбца) на их алгебраические дополнения.
Пример 4Разложение матрицы по элементам строки:
det A=ai1×Ai1+ai2×Ai2+…+аin×Аin
Разложение матрицы по элементам столбца:
det A=а1i×А1i+а2i×А2i+…+аni×Аni
ЗамечаниеЕсли раскладывать матрицу по элементам строки (столбца), необходимо выбирать строку (столбец), в которой(-ом) есть нули.
Пример 5А=01-132100-24513210
Решение:
- раскладываем по 2-ой строке:
А=01-132100-24513210=2×(-1)3×1-13-251310=-2×1-13451210+1×0-13-251310
- раскладываем по 4-му столбцу:
А=01-132100-24513210=3×(-1)5×210-245321+1×(-1)7×01-1210321=-3×210-245321-1×01-1210321
Свойства определителя
Свойства определителя:
- если преобразовывать столбцы или строки незначительными действиями, то это не влияет на значение определителя;
- если поменять местами строки и столбцы, то знак поменяется на противоположный;
- определитель треугольной матрицы представляет собой произведение элементов, которые расположены на главной диагонали.
А=134021005
Решение:
det А=134021005=1×5×2=10
ЗамечаниеОпределитель матрицы, который содержит нулевой столбец, равняется нулю.
Матрицы, определители, системы линейных уравнений (Лекция №12)
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так
.
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,
.
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
.
Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если
они имеют одинаковое число строк и столбцов и их соответствующие элементы равны
aij = bij. Так если и , то A=B,
если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Две матрицы A и B называются равными, если
они имеют одинаковое число строк и столбцов и их соответствующие элементы равны
aij = bij. Так если и , то A=B,
если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу B из n строк и m столбцов, у которой каждая строка является столбцом матрицы A с тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером). Итак, если , то .
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь между матрицей A и её транспонированной можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
или
Примеры. Найти сумму матриц:
- .
- — нельзя, т.к. размеры матриц различны.
- .
Легко проверить,
что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .
Для любых чисел a и b и матриц A и B выполняются равенства:
- .
Примеры.
- .
- Найти 2A-B, если , .
.
- Найти C=–3A+4B.
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В
общем случае, если мы умножаем матрицу A = (aij) размера m×n на
матрицу B = (bij) размера n×p, то получим матрицу C
размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате
произведения элементов i-ой строки матрицы A на соответствующие элементы j-го
столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
.
Примеры.
- Пусть
Найти элементы c12, c23 и c21 матрицы C.
- Найти произведение матриц.
.
- .
- — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
- Пусть
Найти АВ и ВА.
Найти АВ и ВА.
, B·A – не имеет смысла.
Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если , то
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов .
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается символом .
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
- .
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
.
Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
- .
- .
- Решите уравнение..
.
(x+3)(4x-4-3x)+4(3x-4x+4)=0.
(x+3)(x-4)+4(-x+4)=0.
(x-4)(x-1)=0.
x1 = 4, x2 = 1.
Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
Определитель матрицы 3 на 3
Определение 1
Детерминант матрицы (не путайте с дискриминантом для квадратных уравнений) — это определённая матричная характеристика. Иногда вместо термина «детерминант» также используется понятие «определитель».
Иногда вместо термина «детерминант» также используется понятие «определитель».
Детерминант можно посчитать только для квадратных матриц, поэтому при постановке вопроса о нахождении детерминанта для матрицы с размерностью 3 имеют в виду именно квадратную матрицу.
Ниже мы рассмотрим различные способы нахождения определителя 3х3.
Разложение определителя матрицы по строчке
Этот метод сложнее на словах, чем на деле.
Суть его в том, что определитель записывается как сумма произведений элементов первой или любой другой строчки и соответствующих им определителей размером 2 на 2.
Определитель для каждого произведения состоит из элементов, записанных без элементов той строчки и столбца, в которых стоит единичный элемент-множитель.
Также можно осуществлять разложение не только по первой строчке, но и по любой другой или даже столбцу.
Чтобы определить знак, который записывается перед очередным произведением, необходимо помнить, что знаки при элементах чередуются, у первого элемента первой строки — плюс.
То есть произведение при первом элементе первой строчки будет записываться положительным.
Пример 1
Вычислите определитель для $M$ разложением по любой строчке:
$M = \begin{pmatrix} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -5 & 0 & 10 \\ \end{pmatrix}$
Решение:
Рисунок 1. Пример матрицы 3х3. Автор24 — интернет-биржа студенческих работ
В последней строчке присутствует нуль, поэтому удобно будет сделать разложение именно по ней:
$Δ= (-5) \cdot \begin{array}{|cc|} 2 & 5 \\ -4 & 3 \\ \end{array} – 0 \cdot \begin{array} {|cc|} — 1 & 5 \\ 7 & 3 \\ \end{array} + 10 \cdot \begin{array}{|cc|} -1 & 2 \\ 7 & -4 \\ \end{array} = ( — 5 \cdot (6 + 20) – 0 + 10 \cdot (4 – 14) = (-5) \cdot 26 – 0 – 100 = -230$.
Способ «по-французски»: правило Саррюса
Самый легко запоминаемый способ.
Первые два столбика матрицы переписываются рядом справа с исходной матрицей, а дальше рассматриваются левые и правые образуемые диагонали.
Тройки произведений чисел с розовых диагоналей записываются с плюсом, а с синих – с минусом.
Рисунок 2. Как посчитать матрицу 3 на 3. Автор24 — интернет-биржа студенческих работ
Пример 2
Посчитайте определитель $М$ этим методом.
Решение:
$Δ = (-1) \cdot (-4) \cdot 10 + 2 \cdot 3 \cdot (-5) + 5 \cdot 7 \cdot 0 – 2 \cdot 7 \cdot 10 — (-1) \cdot 3 \cdot 0 – 5 \cdot (-4) \cdot (-5) = 40 – 30 + 0 -140 – 0 – 100 = 230$.
Мнемоническое правило с треугольниками
Несколько более сложный способ для запоминания в отличие от предыдущего.
Суть его в том, что произведения троек значений с главной диагонали и с двух треугольников, одна из сторон для каждого параллельна главной диагонали, записываются с плюсом, а с минусом записываются те произведения, что на побочной диагонали и двух треугольниках с параллельными ей сторонами (смотрите рисунок).
Рисунок 3. Как найти детерминант матрицы 3 на 3. Автор24 — интернет-биржа студенческих работ
Приведение матричной таблицы к треугольной
В этом методе нужно получить матрицу, элементы которой сверху или снизу от главной диагонали равны нулю.
Пример 3
Найти определитель для М с помощью получения треугольной матрицы.
Решение:
Вспомним свойство определителя: из любой строки или столбца можно вынести общий для этой строчки или столбца множитель.
Поэтому:
$\begin{array} {|ccc|} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -5 & 0 & 10 \\ \end{array} = \begin{array} {|ccc|} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -1 \cdot 5 & 0 \cdot 5 & 2 \cdot 5 \\ \end{array}= 5 \cdot \begin{array} {|ccc|} -1 & 2 & 5 \\ 7 & -4 & 3 \\ -1 & 0 & 2 \\ \end{array} = 5 \cdot \begin{array} {|ccc|} -1 & 1 \cdot 2 & 5 \\ 7 & -2 \cdot 2 & 3 \\ -1 & 0 \cdot 2 & 2 \\ \end{array}= 10 \cdot \begin{array} {|ccc|} -1 & 1 & 5 \\ 7 & -2 & 3 \\ -1 & 0 & 2 \\ \end{array}$.
Теперь преобразуем полученную таблицу, для этого начинаем приводить к нулям элементы крайнего левого столбца. Строчки для удобства будем записывать как (n), где n — это номер строчки.
1) (2) $\cdot \frac17$ + (3), результат запишем в третьей строчке:
$ \begin{array} {|ccc|} -1 & 1 & 5 \\ 7 & -2 & 3 \\ 0 & -\frac27 & \frac{17}{7} \\ \end{array}$ ;
2) (1) $ \cdot 7$ + (2), полученное запишем во второй строчке:
$ \begin{array} {|ccc|} -1 & 1 & 5 \\ 0 & 5 & 38 \\ 0 & -\frac27 & \frac{17}{7} \\ \end{array}$ ;
3) (2) $\cdot \frac{2}{35}$ + (3)$, пишем в 3-ью:, пишем в 3-ью:
$ \begin{array} {|ccc|} -1 & 1 & 5 \\ 0 & 5 & 38 \\ 0 & 0 & \frac{23}{5} \\ \end{array}$ ;
Получили матрицу нужного типа. Посчитаем $D$:
$Δ = 10 \cdot (-1) \cdot 5 \cdot \frac{23}{5} = -230$.
Во время использования данного способа внимательно следите за знаками, а также за порядком вычислений.
Теперь вы умеете решать определители матриц наиболее распространёнными способами.
Определитель матрицы онлайн
Данный онлайн калькулятор вычисляет определитель матрицы. Дается подробное решение. Для вычисления определителя матрицы выбирайте порядок (размер) квадратной матрицы. Введите данные в ячейки. Выберите метод решения и нажмите на кнопку «Вычислить». Теоретическую часть смотрите на странице определитель матрицы.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Примеры вычисления определителя матрицы
Пример 1. Найти определитель матрицы
. |
Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 2. При этом меняется знак определителя на «−»:
| . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/78,-2/78 соответственно:
| . |
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -5928/9048:
| . |
Мы привели матрицу к верхнему треугольному виду. Определитель матрицы равен произведению всех элементов главной диагонали (учитывая знак определителя):
| . |
Пример 2. Найти определитель матрицы A, разложением определителя по первой строке:
| . |
Для вычисления определителя матрицы методом разложения по первой строке, вычисляем произведение каждого элемента первой строки на соответствующее алгебраическое дополнение и суммируем полученные результаты:
Определитель матрицы онлайн
Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.
Этот онлайн калькулятор позволит вам определитель (детерминант) матрицы.
Для того чтобы вычислить определитель (детерминант) матрицы онлайн, выберите необходимый вам размер матрицы:
Размер матрицы: 2×23×34×45×56×67×7
Введите значения Матрицы:
Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.
Найти определительСмотрите также:
Нахождение обратной матрицы
Определитель матрицы онлайн
Определитель матрицы
Нахождение определителя матрицы является очень частой задачей в высшей математике и алгебре. Как правило, без значения определителя матрицы не обойтись при решении сложных систем уравнений. На вычислении определителя матрицы построен метод Крамера решения систем уравнений. С помощью определения детермината определяют наличие и единственность решения систем уравнений. Поэтому сложно переоценить важность умения правильно и точно находить определитель матрицы в математике. Методы решения определителей являются теоретически довольно простыми, однако с увеличением размера матрицы вычисления становятся очень громоздкими и требуют огромной внимательности и много времени. Очень легко в таких сложных математических вычислениях допустить незначительную ошибку или описку, что приведет к ошибке в окончательном ответе. Поэтому даже если вы находите определитель матрицы самостоятельно, важно проверить полученный результат. Это позволяет сделать наш сервис Нахождение определителя матрицы онлайн. Наш сервис выдает всегда абсолютно точный результат, не содержащий ни ошибок, ни описок. Вы можете отказаться от самостоятельных вычислений, поскольку с прикладной точки зрения, нахождение определителя матрицы не имеет обучающего характера, а просто требует много времени и числовых вычислений. Поэтому если в вашей задачи определение детерминанта матрицы являются вспомогательными, побочными вычислениями, воспользуйтесь нашим сервисом и найдите определитель матрицы онлайн!
Как правило, без значения определителя матрицы не обойтись при решении сложных систем уравнений. На вычислении определителя матрицы построен метод Крамера решения систем уравнений. С помощью определения детермината определяют наличие и единственность решения систем уравнений. Поэтому сложно переоценить важность умения правильно и точно находить определитель матрицы в математике. Методы решения определителей являются теоретически довольно простыми, однако с увеличением размера матрицы вычисления становятся очень громоздкими и требуют огромной внимательности и много времени. Очень легко в таких сложных математических вычислениях допустить незначительную ошибку или описку, что приведет к ошибке в окончательном ответе. Поэтому даже если вы находите определитель матрицы самостоятельно, важно проверить полученный результат. Это позволяет сделать наш сервис Нахождение определителя матрицы онлайн. Наш сервис выдает всегда абсолютно точный результат, не содержащий ни ошибок, ни описок. Вы можете отказаться от самостоятельных вычислений, поскольку с прикладной точки зрения, нахождение определителя матрицы не имеет обучающего характера, а просто требует много времени и числовых вычислений. Поэтому если в вашей задачи определение детерминанта матрицы являются вспомогательными, побочными вычислениями, воспользуйтесь нашим сервисом и найдите определитель матрицы онлайн!
Все вычисления проводятся автоматически с высочайшей точностью и абсолютно бесплатны. У нас очень удобный интерфейс для ввода матричных элементов. Но главное отличие нашего сервиса от аналогичных — возможность получения подробного решения. Наш сервис при вычислении определителя матрицы онлайн всегда использует самый простой и короткий метод и подробно описывает каждый шаг преобразований и упрощений. Так что вы получаете не просто значение детерминанта матрицы, окончательный результат, но и целое подробное решение.
Похожие сервисы:
Вычислить детерминант матрицыMatrix problem solver
Определитель матрицы.
 Определитель матрицы или детерминант матрицы — это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.
Определитель матрицы или детерминант матрицы — это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.
Определение.
Определителем матрицы n×n будет число:| det(A) = | Σ | (-1)N(α1,α2,…,αn)·aα11·aα22·…·aαnn |
| (α1,α2,…,αn) |
Обозначение
Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).Свойства определителя матрицы
Определитель матрицы с двумя равными строками (столбцами) равен нулю.
Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
- При транспонировании значение определителя матрицы не меняется:
det(A) = det(AT)
- Определитель обратной матрицы:
det(A-1) = det(A)-1
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
- Общий множитель в строке (столбце) можно выносить за знак определителя:
a11 a12 .  ..
..a1n a21 a22 … a2n . . . . k·ai1 k·ai2 … k·ain . . . . an1 an2 … ann = k a11 a12 … a1n a21 a22 … a2n . . . . ai1 ai2 … ain . . . . an1 an2 … ann - Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:
B = k·A => det(B) = kn·det(A)
где A матрица n×n, k — число. - Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
a11 a12 … a1n a21 a22 … a2n . . . . bi1 + ci1 bi2 + ci2 … bin + cin . 
. . . an1 an2 … ann = a11 a12 … a1n a21 a22 … a2n . . . . bi1 bi2 … bin . . . . an1 an2 … ann + a11 a12 … a1n a21 a22 … a2n . . . . ci1 ci2 … cin . . . . an1 an2 … ann Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
- Определитель произведения матриц равен произведению определителей этих матриц:
det(A·B) = det(A)·det(B)
Методы вычисления определителя матрицы
Вычисление определителя матрицы 1×1
Правило:
Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:∆ = |a11| = a11
Вычисление определителя матрицы 2×2
Правило:
Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:| ∆ = | = a11·a22 — a12·a21 |
Пример 1.
| A = |
|
Решение:
| det(A) = | = 5·1 — 7·(-4) = 5 + 28 = 33 |
Вычисление определителя матрицы 3×3
Правило треугольника для вычисления определителя матрицы 3-тего порядка
Правило:
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.| + | – |
| ∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33
Правило Саррюса для вычисления определителя матрицы 3-тего порядка
Правило:
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:| ∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33
Пример 2.
| A = |
|
Решение:
| det(A) = | = 5·1·3 + 7·0·2 + 1·(-4)·0 — 1·1·2 — 5·0·0 — 7·(-4)·3 = |
= 15 + 0 + 0 — 2 — 0 + 84 = 97
Вычисление определителя матрицы произвольного размера
Разложение определителя по строке или столбцу
Правило:
Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:| n | ||
| det(A) = | Σ | aij·Aij — разложение по i-той строке |
| j = 1 |
Правило:
Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:| n | ||
| det(A) = | Σ | aij·Aij — разложение по j-тому столбцу |
| i = 1 |
При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.
Пример 3.
Найти определитель матрицы A| A = |
|
Решение: Вычислим определитель матрицы разложив его по первому столбцу:
| = 2·(-1)1+1· | + 0·(-1)2+1· | + 2·(-1)3+1· | = |
= 2·(2·1 — 1·1) + 2·(4·1 — 2·1) = 2·(2 — 1) + 2·(4 — 2) = 2·1 + 2·2 = 2 + 4 = 6
Пример 4.
| A = |
|
Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):
| = -0· | + 2· | — 0· | + 0· | = |
= 2·(2·1·3 + 1·3·4 + 1·2·2 — 1·1·4 — 2·3·2 — 1·2·3) = 2·(6 +12 + 4 — 4 — 12 — 6) = 2·0 = 0
Приведение определителя к треугольному виду
Правило:
Используя свойства определителя для элементарных преобразований над строками и столбцами 8 — 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.Пример 5.
Найти определитель матрицы A приведением его к треугольному виду| A = |
|
Решение:
Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку помноженную на 2:
| det(A) = |
|
= |
Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбци:
Для этого поменяем местами 2-ой и 3-тий столбци:
Получим нули во третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец умноженный на 8:
| det(A) = — |
|
= — | = -2·1·13·1 = -26 |
Теорема Лапласа
Теорема:
Пусть ∆ — определитель n-ого порядка. Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
4. Умножение матриц
Важно: Мы можем умножать матрицы только в том случае, если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Пример 1
a) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно, и это дает матрицу 2 × 4 в качестве ответа.
b) Допускается умножение матрицы 7 × 1 на матрицу 1 × 2; это дает матрицу 7 × 2
c) НЕЛЬЗЯ умножить матрицу 4 × 3 на матрицу 2 × 3.
Как умножить 2 матрицы
Сначала мы используем буквы, чтобы увидеть, что происходит. Позже мы увидим пример чисел.
В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]`
Ответом будет матрица 2 × 2.
Умножаем и складываем элементы следующим образом. Мы обрабатываем по 1-й строке первой матрицы, поэлементно умножая на 1-го столбца второй матрицы. Складываем получившихся продуктов . Наш ответ находится в позиции a 11 (вверху слева) матрицы ответов.
Складываем получившихся продуктов . Наш ответ находится в позиции a 11 (вверху слева) матрицы ответов.
Мы делаем аналогичный процесс для 1-й строки первой матрицы и 2-го столбца второй матрицы. Результат помещается на позиции a 12 .
Теперь о 2-й строке первой матрицы и 1-м столбце второй матрицы. Результат помещается на позиции a 21 .
Наконец, мы делаем вторую строку первой матрицы и второй столбец второй матрицы. Результат помещается на позиции a 22 .
Итак, результат умножения наших двух матриц будет следующим:
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]` `= [(au + bw + cy, av + bx + cz), (du + ew + fy, dv + ex + fz)] `
Теперь давайте посмотрим на числовой пример.
Пользователи телефона
ПРИМЕЧАНИЕ: Если вы разговариваете по телефону, вы можете прокрутить любые широкие матрицы на этой странице вправо или влево, чтобы увидеть все выражение.
Пример 2
Умножить:
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
Ответ
Это 2 × 3 умножить на 3 × 2, что даст нам 2 × 2 отвечать.
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((0xx3 + -1xx1 + 2xx6,0xx-1 + -1xx2 + 2xx1), (4xx3 + 11xx1 + 2xx6,4xx -1 + 11xx2 + 2xx1))`
`= ((0-1 + 12,0-2 + 2), (12 + 11 + 12, -4 + 22 + 2))`
`= ((11,0), (35,20))`
Наш ответ — матрица 2 × 2.
Умножение матриц 2 × 2
Процесс одинаков для матрицы любого размера. Мы умножаем на строк первой матрицы и на столбцов второй матрицы поэлементно. Затем мы добавляем продукты:
`((a, b), (c, d)) ((e, f), (g, h))` `= ((ae + bg, af + bh), (ce + dg, cf + dh )) `
В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.
Пример 3
Умножить:
`((8,9), (5, -1)) ((- 2,3), (4,0))`
Ответ
`((8,9), (5, -1)) ((- 2,3), (4,0))`
`= ((8 xx -2 + 9xx4,8xx3 + 9xx0), (5xx-2 + -1xx4,5xx3 + -1xx0))`
`= ((-16 + 36,24 + 0), (- 10+ -4,15 + 0))`
`= ((20,24), (- 14,15))`
Матрицы и системы одновременных линейных уравнений
Теперь мы видим, как написать систему линейных уравнений, используя умножение матриц.
Пример 4
Система уравнений
−3 x + y = 1
6 x -3 y = −4
можно записать как:
Матрицы`((-3,1), (6, -3)) ((x), (y)) = ((1), (- 4))`
идеально подходят для компьютерного решения задач, потому что компьютеры легко формируют массивы . Мы можем опустить алгебраические символы. Компьютеру требуются только первая и последняя матрицы для решения системы, как мы увидим в разделе «Матрицы и линейные уравнения».
Примечание 1 — Обозначение
Care с записью и умножением матриц .
Следующие выражения имеют различных значений:
AB — это матричное умножение
A × B — перекрестное произведение , которое возвращает вектор
A * B используется в компьютерной нотации, но не на бумаге
A • B точечное произведение , которое возвращает скаляр .
[Дополнительную информацию о векторных и скалярных величинах см. В главе «Вектор».]
Примечание 2 — Коммутативность умножения матриц
Есть ли `AB = BA`?
Посмотрим, правда ли это на примере.
Пример 5
Если
`A = ((0, -1,2), (4,11,2))`
и
`B = ((3, -1), (1,2), (6,1))`
найдите AB, и BA.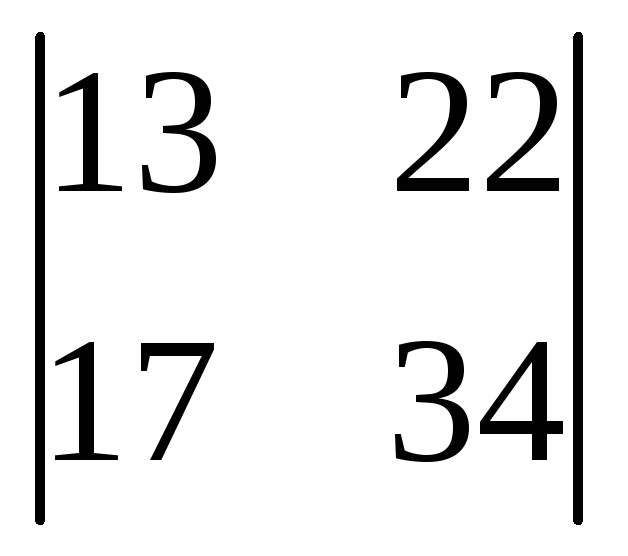
Ответ
Мы выполнили AB выше, и ответ был:
`AB = ((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((11,0), (35,20))`
Теперь BA — это (3 × 2) (2 × 3), что даст 3 × 3:
`BA = ((3, -1), (1,2), (6,1)) ((0, -1,2), (4,11,2))`
`= ((0-4, -3-11,6-2), (0 + 8, -1 + 22,2 + 4), (0 + 4, -6 + 11,12 + 2))`
`= ((-4, -14,4), (8,21,6), (4,5,14))`
Итак, в этом случае AB НЕ равно BA.
Фактически, для большинства матриц нельзя изменить порядок умножения и получить тот же результат.
В общем случае при умножении матриц закон коммутативности не выполняется, т.е. AB ≠ BA . Есть два распространенных исключения:
.- Идентификационная матрица: IA = AI = A .?
- , обратный матрицы: A -1 A = AA -1 = I.
В следующем разделе мы узнаем, как найти обратную матрицу.
Пример 6 — Умножение на идентификационную матрицу
Учитывая, что
`A = ((- 3,1,6), (3, -1,0), (4,2,5))`
найдите AI .
Ответ
`AI = ((-3,1,6), (3, -1,0), (4,2,5)) ((1,0,0), (0,1,0), (0 , 0,1)) `
`= ((- 3 + 0 + 0,0 + 1 + 0,0 + 0 + 6), (3 + 0 + 0,0 + -1 + 0,0 + 0 + 0), (4 + 0 + 0,0 + 2 + 0,0 + 0 + 5)) `
`= ((- 3,1,6), (3, -1,0), (4,2,5))`
`= A`
Мы видим, что умножение на единичную матрицу не меняет значения исходной матрицы.
То есть
AI = A
Упражнения
1. Если возможно, найдите BA и AB .
`A = ((- 2,1,7), (3, -1,0), (0,2, -1))`
`B = (4 \ \ -1 \ \ \ 5)`
Ответ
`BA = (4 \ \ -1 \ \ \ 5) ((- 2,1,7), (3, -1,0), (0,2, -1))`
`= (-8 + (- 3) +0 \ \ \ 4 + 1 + 10 \ \ \ 28 + 0 + (- 5))`
`= (- 11 \ \ 15 \ \ 23)`
AB невозможно. (3 × 3) × (1 × 3).
(3 × 3) × (1 × 3).
2. Определите, если B = A -1 , учитывая:
`A = ((3, -4), (5, -7))`
`B = ((7,4), (5,3))`
Ответ
Если B = A -1 , то AB = I.
`AB = ((3, -4), (5, -7)) ((7,4), (5,3))`
`= ((21-20,12-12), (35-35,20-21))`
`= ((1,0), (0, -1))`
`! = I`
Таким образом, B НЕ является противоположностью A.2 + 0)) `
`= ((1,0), (0,1))`
`= I`
4. Оцените следующее умножение матриц, которое используется для управления движением роботизированного механизма.
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
Ответ
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
`= ((2 (0,5) -4 (0,866) +0), (2 (0,866) +4 (0,5) +0), (0 + 0 + 0))`
`= ((- 2,464), (3,732), (0))`
Интерпретация этого заключается в том, что рука робота движется из позиция (2, 4, 0) в позицию (-2.46, 3.73, 0). То есть это перемещается в плоскости x-y , но его высота остается на уровне z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят, на сколько градусов нужно переместиться.
Интерактивные элементы умножения матриц
Ранг матрицы
Максимальное количество линейно независимых строк в матрице A называется рангом строки из A , а максимальное количество линейно независимых столбцов в A называется столбцом ранг из А .Если A является матрицей m на n , то есть, если A имеет m строк и n столбцов, то очевидно, что
Однако не так очевидно то, что для любой матрицы A
ранг строки A = ранг столбца A
Из-за этого факта нет причин различать ранг строки и ранг столбца; обычное значение просто называется ранг матрицы.Следовательно, если A равно m x n , из неравенств в (*) следует, что
, где min ( m, n ) обозначает меньшее из двух чисел m и n (или их общее значение, если m = n ). Например, ранг матрицы 3 x 5 может быть не более 3, а ранг матрицы 4 x 2 может быть не более 2. Матрица 3 x 5,
можно представить как состоящий из трех 5-векторов (строки) или пяти 3-векторов (столбцы).Хотя три 5-вектора могут быть линейно независимыми, невозможно иметь пять независимых 3-векторов. Любая коллекция из более чем трех 3-векторов автоматически зависит. Таким образом, ранг столбца — и, следовательно, ранг — такой матрицы не может быть больше 3. Итак, если A является матрицей 3 x 5, этот аргумент показывает, что
в соответствии с (**).
Процесс определения ранга матрицы можно проиллюстрировать на следующем примере.Предположим, что A — это матрица 4 x 4
.
Четыре вектора-строки,
не являются независимыми, так как, например,
Тот факт, что векторы r 3 и r 4 могут быть записаны как линейные комбинации двух других ( r 1 и r 2 , которые являются независимыми) означает, что максимальное количество независимых строк — 2.Таким образом, ранг строки — и, следовательно, ранг — этой матрицы равен 2.
Уравнения в (***) можно переписать следующим образом:
Первое уравнение здесь подразумевает, что если -2 раза эта первая строка добавляется к третьей, а затем вторая строка добавляется к (новой) третьей строке, третья строка станет 0 , строкой нулей. Второе уравнение выше говорит о том, что аналогичные операции, выполняемые с четвертой строкой, могут также произвести там строку нулей. Если после завершения этих операций первая строка будет добавлена во вторую строку -3 раза (чтобы очистить все записи ниже записи a 11 = 1 в первом столбце), эти элементарные операции со строкой уменьшат исходную матрица A в эшелонированную форму
Тот факт, что в сокращенной форме матрицы есть ровно 2 ненулевые строки, указывает на то, что максимальное количество линейно независимых строк равно 2; следовательно, ранг A = 2, что согласуется с приведенным выше выводом.В общем случае для вычисления ранга матрицы выполняет элементарные операции со строками, пока матрица не останется в эшелонированной форме; количество ненулевых строк, оставшихся в сокращенной матрице, имеет ранг . [Примечание: поскольку ранг столбца = ранг строки, только два из четырех столбцов в A — c 1 , c 2 , c 3 и c 4 — линейно независимы. Докажите, что это действительно так, проверив соотношения
(и проверка того, что c 1 и c 3 независимы).Уменьшенная форма A делает эти отношения особенно очевидными.]
Пример 1 : Найдите ранг матрицы
Во-первых, поскольку матрица имеет размер 4 x 3, ее ранг не может быть больше 3. Следовательно, по крайней мере одна из четырех строк станет строкой из нулей. Выполните следующие операции со строками:
Поскольку в этом эшелоне остаются 3 ненулевые строки, форма B ,
Пример 2 : Определите ранг матрицы шахматной доски 4 на 4
Поскольку r 2 = r 4 = −r 1 и r 3 = r 1 , все строки, кроме первого, исчезают при уменьшении ряда:
Поскольку осталась только 1 ненулевая строка, ранг C = 1.
Умножение матрицУмножение матриц
Рассмотрим произведение матрицы 2 × 3 и матрицы 3 × 4. Умножение определяется, потому что внутренние размеры (3) одинаковы. Продукт будет — матрица 2 × 4, внешние размеры.
Поскольку в первой матрице три столбца и три строки во второй матрица (внутренние размеры должны быть одинаковыми), каждый элемент в продукте будет сумма трех товары.
Ряд 1, Столб 1
Чтобы найти элемент в строке 1, столбце 1 продукта, мы возьмем строку 1 из первой матрицы и столбец 1 из второй матрицы.Мы объединяем эти значения в пары, умножаем пары значений, а затем добавляем к прибыть на 25.
р 1 : 1-2 3
× C 1 : 1-3 6
---------------
1 +6 +18 = 25
Ряд 2, столбец 3
Чтобы найти элемент в строке 2, столбце 3 продукта, возьмем строку 2 из первой матрицы и столбец 3 из второй матрицы. Мы объединяем эти значения вместе, умножьте пары значений, а затем добавьте к прибыть на 53.
р 2 : 4 5 -2
× C 3 : 4 7 -1
---------------
16 +35 +2 = 53
Понимание происхождения каждого числа в продукте полезно, когда вам нужно только конкретное значение.Вам не нужно полностью размножаться, если вы нужны только определенные элементы. Просто возьмите строку из первой матрицы и столбец из второй матрицы.
Процесс может быть завершен для остальных элементов в матрице.
| Колонка 1 | Колонка 2 | Колонка 3 | Колонка 4 | ||
|---|---|---|---|---|---|
| значений | [1, -3, 6] | [-8, 6, 5] | [4, 7, -1] | [-3, 2, 4] | |
| Ряд 1 | [1, -2, 3] | 1 (1) — 2 (-3) + 3 (6) = 1 + 6 + 18 = 25 |
1 (-8) -2 (6) + 3 (5) = -8 — 12 + 15 = -5 |
1 (4) -2 (7) +3 (-1) = 4 — 14 — 3 = -13 |
1 (-3) -2 (2) + 3 (4) = -3-4 + 12 = 5 |
| Ряд 2 | [4, 5, -2] | 4 (1) + 5 (-3) -2 (6) = 4-15-12 = -23 |
4 (-8) + 5 (6) — 2 (5) = -32 + 30-10 = -12 |
4 (4) + 5 (7) -2 (-1) = 16 + 35 + 2 = 53 |
4 (-3) + 5 (2) -2 (4) = -12 + 10-8 = -10 |
Итак, конечный продукт —
| 25 | -5 | -13 | 5 | ||
| -23 | -12 | 53 | -10 |
Умножение матриц не коммутативно
Обратите внимание, что умножение не определяется другим способом.Нельзя размножаться 3×4 и матрица 2×3 вместе, потому что внутренние размеры не совпадают.
Этот товар не определен.
Вычислить определитель матрицы Пошаговое решение математических задач
Мы знаем, что не каждая система линейных уравнений имеет единственное решение. Иногда система n уравнений от n переменных не имеет решения или бесконечное множество решений. В этом разделе мы вводим определитель матрица. В следующем разделе мы увидим, что определитель можно использовать чтобы определить, имеет ли система уравнений единственное решение.
Каждой квадратной матрице A соответствует действительное число, называемое определителем A, написано | A |.
Определитель матрицы 2 x 2 A,
определяется как
ПРИМЕЧАНИЕ Обратите внимание, что матрицы заключены в квадратные скобки, а определители обозначаются вертикальными полосами. Кроме того, матрица представляет собой массив чисел, но ее определитель — это одно число.
ОЦЕНКА A 2 X 2
ДЕТЕРМИНАНТ
Если
, затем
ОПРЕДЕЛЕНИЕ А 3 X 3 МАТРИЦА
Определитель матрицы 3 x 3 A,
определяется как
Простой метод вычисления определителей 3 X 3 находится путем перестановки и факторинг условий, приведенных выше, чтобы получить
Каждая из величин в скобках представляет определитель 2 X 2 матрица, которая является частью матрицы 3 x 3, остающейся, когда строка и столбец множитель исключается, как показано ниже.
Эти определители матриц 2 X 2 называются минорами элемента в матрица 3 x 3. Обозначение M ij представляет определитель матрица, которая получается при удалении строки i и столбца j. Следующий список дает некоторые из миноров из приведенной выше матрицы.
В матрице 4 x 4 миноры являются определителями матриц 3 X 3, а n x
Матрица n имеет миноры, которые являются определителями (n — 1) X (n — 1)
матрицы.
Чтобы найти определитель матрицы 3 X 3 или больше, сначала выберите любую строку или
столбец. Затем необходимо умножить минор каждого элемента в этой строке или столбце.
на + l или — 1, в зависимости от того, сумма номеров строк и столбцов
числа четные или нечетные. Произведение младшего и числа +1 или — l равно
называется кофактором .
КОФАКТОР Пусть M ij будет второстепенным для элемента au в матрице n x n . Кофактор ij , написано A ij , это:
Наконец, определитель матрицы n x n находится следующим образом.
ПОИСК ОПРЕДЕЛЕНИЯ МАТРИЦЫ
Умножьте каждый элемент в любой строке или столбце матрицы на его кофактор. В
сумма этих продуктов дает значение определителя.
эта сумма продуктов называется расширением по данной строке или столбцу.
НАЙТИ
КОФАКТОР ЭЛЕМЕНТА
Для матрицы
найдите кофактор каждого из следующих элементов.
(a) 6
Поскольку 6 находится в первой строке и первом столбце матрицы, i = 1 и j = 1.
Кофактор: (-1) 1 + 1 * (-6) = 1 * (-6) = -6.
(b) 3
Здесь i = 2 и j = 3.
Кофактор (-1) 2 + 3 * 10 = (-1) * 10 = -10.
(c) 8
Имеем i = 2 и j = l.
Кофактор: (-1) 2 + 1 * (-8) = (-1) * (-8) = 8.
ОЦЕНКА ДЕТЕРМИНАНТА 3 X 3
Оценить
во втором столбце.
Чтобы найти этот определитель, сначала получите миноры каждого элемента во втором
столбец.
Теперь найдите сомножитель каждого из этих младших.
Определитель находится путем умножения каждого сомножителя на его соответствующий элемент матрицы и нахождение суммы этих произведений.
ВНИМАНИЕ: Будьте очень осторожны, чтобы отслеживать все отрицательные знаки, когда оценивая детерминанты. Работайте осторожно, записывая каждый шаг, как в Примеры.Пропуск шагов часто приводит к ошибкам в этих вычислениях.
Точно такой же ответ можно найти, используя любую строку или столбец матрицы.
Одна из причин использования столбца 2 в примере 3 заключается в том, что он содержит элемент 0,
так что рассчитывать M 32 и A 32 толком не пришлось
над. Быстро понять, что нули могут быть очень полезны при работе с
детерминанты.
Вместо вычисления (-1) i + j для данного элемента следующие
можно использовать доски для проверки знаков:
Знаки чередуются для каждой строки и столбца, начиная с + в первом строка, позиция первого столбца.Таким образом, эти массивы знаков можно воспроизвести как нужный. Если мы расширим матрицу 3 X 3 около строки 3, например, первый второстепенный будет иметь знак +, связанный с ним, второй второстепенный знак — и третий минор а + знак. Эти массивы знаков могут быть расширены таким образом для определителей матриц 5 × 5, 6 × 6 и более крупных.
ОЦЕНКА ДЕТЕРМИНАНТА 4 X 4
Оценить
Расширение на несовершеннолетние около четвертой строки дает
Каждый из четырех определяющих факторов в примере 4 должен быть оценен путем раскрытия три несовершеннолетних, требующих большой работы, чтобы получить окончательную стоимость.Всегда ищите строка или столбец с наибольшим количеством нулей для упрощения работы. В следующем разделе мы ввести несколько свойств, упрощающих вычисление определителей. К счастью, детерминанты больших матриц можно оценить быстро и легко с помощью компьютера или некоторых калькуляторов.
Определитель матрицы 3 x 3 (общий и сокращенный метод)
Определитель матрицы 3 x 3 (общий и сокращенный метод)
Как мы видели в прошлых уроках, чтобы определить, что является определителем матрицы, нам нужно вернуться к нашему определению матрицы.Помните, что мы узнали, что матрица — это упорядоченный список чисел, заключенный в прямоугольную скобку. Этот список также можно назвать прямоугольным массивом, и он обеспечивает упорядоченный способ отображения «списка» информационных элементов. Если вы хотите более подробно ознакомиться с определением матрицы, вы можете вернуться к нашему уроку о нотации матриц.
Матрица описывает линейное преобразование или линейную карту, которая является своего рода транскрипцией между двумя типами алгебраических структур, такими как векторные поля.Таким образом, мы можем разрешить системы линейных уравнений, представив линейную систему в виде матрицы. Матричное представление линейной системы создается с использованием всех переменных коэффициентов, найденных в системе, и использования их в качестве элементов для построения прямоугольного массива расширенной матрицы соответствующего размера. В такой матрице результаты каждого уравнения из системы будут помещены справа от вертикальной линии, которая представляет знак равенства.
Зная это, в этом уроке основное внимание будет уделено процессу оценки определителя матрицы 3×3 и двум возможным методам, которые можно использовать.
Какой определитель матрицы
Используя знание того, что матрица представляет собой массив, содержащий информацию о линейном преобразовании, и что этот массив может быть согласован с коэффициентами каждой переменной в системе уравнений, мы можем описать функцию определителя: определитель будет масштабироваться линейное преобразование из матрицы, это позволит нам получить обратную матрицу (если таковая имеется) и поможет в решении систем линейных уравнений, создав условия, при которых мы можем ожидать определенных результатов или характеристик от система (в зависимости от определителя и типа линейной системы, мы можем знать, можем ли мы ожидать уникального решения, более одного решения или вообще ни одного решения для системы).
Но есть условие для получения определителя матрицы, матрица должна быть квадратной матрицей, чтобы ее можно было вычислить. Следовательно, упрощенное определение состоит в том, что определитель — это значение, которое может быть вычислено из квадратной матрицы, чтобы помочь в разрешении систем линейных уравнений, связанных с такой матрицей. Определителя неквадратной матрицы не существует, математически определены только определители квадратных матриц.
Определитель матрицы можно обозначить просто как det A, det (A) или | A |.Это последнее обозначение происходит от обозначения, которое мы непосредственно применяем к матрице, определитель которой мы получаем. Другими словами, мы обычно записываем матрицы и их определители очень похожим образом:
Уравнение 1: Разница между обозначениями матрицы и определителяОбратите внимание на разницу: матрица записана в прямоугольных скобках, а компоненты определителя матрицы окружены двумя прямыми линиями.
Сегодняшний урок будет сосредоточен на процессе вычисления определителя матрицы 3×3, используя подход свойств определителя матрицы, которые были кратко рассмотрены на прошлых уроках.Помните, что мы рассмотрим эту полную тему на следующем уроке, который называется: свойства детерминантов. Тем не менее, важно помнить об этих свойствах при выполнении расчетов упражнений в последнем разделе этого урока.
Как найти определитель матрицы 3×3
Существует два метода нахождения определителя матрицы 3×3: общий метод и сокращенный метод. Так же, как звучат названия каждого из них, общий метод — это «формальный» метод, который можно использовать математически, следуя всем правилам и производя некоторые второстепенные вычисления определителя матрицы по пути нахождения окончательного решения.Хотя метод быстрого доступа — это более хитрый прием, который мы можем использовать для упрощения вычислений, при этом стараясь не забыть числа, порядок, в котором они должны быть умножены, и некоторые перестановки элементов в матрице.
После того, как вы взглянете на оба метода, чтобы найти определитель матрицы 3×3, вы всегда можете выбрать тот, который вам больше всего подходит, и использовать его для своих исследований, но помните, что важно знать оба из них, на случай, если вас когда-нибудь спросят. сравнить результаты с ними.
Итак, без дальнейших задержек, давайте определим определитель матрицы 3×3 A, как показано ниже, чтобы мы могли наблюдать, как его можно вычислить обоими методами:
Уравнение 2: Определитель матрицы A- Общий метод
Общий метод получения определителя матрицы 3×3 состоит из разбиения матрицы на вторичные матрицы меньших размеров в процессе, называемом «расширением первой строки». Этот процесс использует элементы из первой строки матрицы 3×3 и использует их как множители в сумме умножений, при которой большая матрица перераспределяется.
Давайте шаг за шагом рассмотрим, как вычислить определитель матрицы 3×3:
- Сначала вы берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которому принадлежит ваш первый выбранный элемент.
Взяв в качестве ссылки определитель матрицы 3×3, показанный в уравнении 2, мы строим первую часть результата этой операции, выбирая первый элемент первой строки и столбца (который является константой «a»), а затем умножаем его на матрица, созданная из четырех элементов, которые не принадлежат ни одной строке столбца, в котором находится «a».Умножьте «a» на полученную вторичную матрицу 2×2, и это будет первый член решения.
- Второй член начинается со второго элемента верхней строки (константа «b»), сопровождаемого отрицательным знаком, который теперь умножает вторичную матрицу 2×2, которая снова получается из четырех элементов в матрице, которые не принадлежат в любой столбец строки, в которой находится «b».
- Повторяем первый шаг, но уже с третьим элементом из верхней строки матрицы.
Итак, определитель матричной формулы 3×3 для общего метода:
Уравнение 3: Уравнение для определителя матрицы 3×3 посредством общего методаПроцесс называется расширением первой строки, потому что, как вы можете видеть в уравнении 3, все элементы из первой строки исходной матрицы 3×3 остаются основными факторами в расширении, для которого необходимо решить. Все матрицы 2×2 в раскрытии — это то, что мы называем «вторичными матрицами», и их можно легко разрешить, используя уравнение, изученное на определителе на уроке по матрице 2×2.
Итак, принимая во внимание формулу для определителя квадратной матрицы размером 2×2, мы видим, что уравнение 3 дает:
Уравнение 4: Уравнение для определителя матрицы 3×3 посредством общего метода (часть 2)На этом этапе вы, возможно, заметили, что поиск определителя матрицы больше 2×2 становится долгим испытанием, но логика процесса остается той же, и поэтому сложность аналогична, единственный ключевой момент — отслеживать операции вы прорабатываете даже больше с матрицами даже большего размера, чем 3×3.
- Сначала вы берете первый элемент первой строки и умножаете его на вторичную матрицу 2×2, которая получается из элементов, оставшихся в матрице 3×3, которые не принадлежат строке или столбцу, к которому принадлежит ваш первый выбранный элемент.
- Сокращенный метод
Определитель метода быстрого доступа к матрице 3×3 — это хитрый трюк, который упрощает вычисление определителя большой матрицы путем прямого умножения и добавления (или вычитания) всех элементов в их необходимом виде, без необходимости пройти через матричное расширение первой строки и без необходимости оценивать детерминанты вторичных матриц.
Весь процесс того, как оценить определитель матрицы 3×3, используя сокращенный метод, можно увидеть в уравнении ниже:
Уравнение 5: Быстрый метод получения определителя матрицы 3×3Теперь давайте четко объясним метод быстрого доступа:
При вычислении определителя матрицы размера nxn (в данном случае матрицы 3×3), как показано выше, обратите внимание, что мы сначала переписываем матрицу, сопровождаемую повторением двух первых столбцов, которые теперь записываются снаружи с правой стороны.
Тогда значение определителя будет результатом вычитания между сложением произведений всех умножений вниз-вправо и умножений вниз-влево. Сказано яснее, всего будет три полных диагонали, идущих от верхнего левого угла до нижнего правого, и еще один набор из трех полных диагоналей, идущих от верхнего правого угла до нижнего левого угла.
Мы умножим элементы каждой диагонали вместе, а затем сложим их с результатами, полученными на других диагоналях.Есть кое-что, что нужно иметь в виду, все умножения диагоналей, идущие от верхнего левого угла к нижнему правому, имеют собственный положительный знак, умноженный на них, в то время как все умножения диагоналей, идущие сверху справа налево, имеют внутренний отрицательный знак умножения. к ним, и поэтому при сложении результатов всех умножений получится вычитание, подобное тому, которое показано в уравнении 5.
Хотя этот метод проще в применении, чем общий метод, его немного сложно объяснить из-за того, что все операции умножения и сложения выполняются одновременно, поэтому мы рекомендуем вам использовать уравнение 5 в качестве руководства и уделять пристальное внимание к видео, где демонстрируются примеры этого метода.
В последнем разделе этого урока мы проработаем набор из трех различных матриц 3×3 и их детерминанты. Мы рекомендуем вам сравнить процессы для обоих методов, чтобы лучше понять их.
Определитель большой матрицы
Процесс вычисления определителя матрицы большей размерности, чем 3×3, следует той же логике, что и то, что мы видели до сих пор. Используя общий метод на матрице A 4×4, где ее первая (верхняя) строка соответствует элементам a, b, c и d, мы вычисляем определитель матрицы следующим образом:
Уравнение 6: Определитель матрицы 4×4Мы еще раз расширили определитель на его первую строку и получили вторичные матрицы, которые в данном случае являются матрицами 3×3, каждая из которых может быть расширена и разбита на матрицы 2×2.Шаблон в процессе повторяется, вы можете продолжать работать таким образом с еще более крупными квадратными матрицами, и он всегда будет работать, но если вам больше нравится метод ярлыков, то вас ждет удовольствие, поскольку метод работает точно так же как и в случае с матрицами 3×3, он просто увеличивает количество элементов, с которыми вы работаете, но логика и перестановка точно такие же (умножение сверху слева вниз справа имеет положительный знак, умножения из верхнего правого угла в нижний левый имеют внутренний отрицательный знак).
Вы взволнованы, увидев, как сокращенный метод работает с матрицами большего размера? Мы рекомендуем вам попробовать это самостоятельно, чтобы вы могли увидеть весь процесс. Вы всегда можете вернуться и решить ту же матрицу, используя общий метод, и доказать, что ваш результат верен.
Упражнения по вычислению определителя матрицы 3×3
В следующих упражнениях мы решим определитель матрицы 3×3, предоставленной в каждом случае, с помощью соответствующего метода, а в конце мы сравним полученные результаты.
Обратите внимание, что матрицы A, B и C, представленные в обоих разделах упражнений выше, абсолютно одинаковы. Это было сделано специально, чтобы вы могли сравнить результаты обоих методов и посмотреть, как они дают одинаковые значения.
Чтобы завершить этот урок, мы хотели бы порекомендовать вам эту статью о том, как вычислить определители, и другую статью о определителе квадратной матрицы, где вы найдете гораздо больше примеров, чем приведенные здесь.
Надеемся, этот урок был интересным и полезным, до встречи в следующем!
Определитель матрицы — 2х2, 3х3, 4х4…
Автор Каталин Давид
Определение
Определитель квадратной матрицы A — это целое число, полученное с помощью ряда методов, использующих элементы матрицы.
Обозначение
Пусть $ A = \ begin {pmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {pmatrix} $
$ det (A) = \ left | A \ right | знак равно \ begin {vmatrix} 1 и 4 и 2 \\ 5 и 3 и 7 \\ 6 и 2 и 1 \ end {vmatrix} $
Свойства определителя
-
Если матрица имеет строку или столбец со всеми элементами, равными 0 , то ее определитель равен 0 .
Пример 12
$ \ begin {vmatrix} 1 и 4 и 2 \\ 0 & 0 & 0 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ или же $ \ begin {vmatrix} 1 и 4 и 0 \\ 4 и 2 и 0 \\ 3 и 9 и 0 \ end {vmatrix} = 0 $ -
Если матрица имеет две равные строки или два равных столбца , тогда ее определитель равен 0 .
Пример 13
$ \ begin {vmatrix} 1 и 4 и 2 \\ 1 и 4 и 2 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ или же $ \ begin {vmatrix} 1 и 4 и 1 \\ 4 и 2 и 4 \\ 3 и 9 и 3 \ end {vmatrix} = 0 $ -
Если матрица имеет две пропорциональные строки или два пропорциональных столбца , тогда ее определитель равен 0 .
Пример 14
$ \ begin {vmatrix} 1 и 4 и 2 \\ 2 и 8 и 4 \\ 3 и 9 и 5 \ end {vmatrix} = 0 $ (первые две строки пропорциональны)
или
$ \ begin {vmatrix} 8 и 4 и 7 \\ 4 и 2 и 3 \\ 18 и 9 и 8 \ end {vmatrix} = 0 $ (первые два столбца пропорциональны) -
Если строка или столбец является суммой или разностью других строк, соответственно столбцов , тогда определитель равен 0 .
Пример 15
$ \ begin {vmatrix} 1 и 4 и 2 \\ 7 и 2 и 3 \\ 8 и 6 и 5 \ end {vmatrix} = 0 $ $ R_ {1} + R_ {2} = R_ {3} $ или$ \ begin {vmatrix} 9 и 12 и 3 \\ 1 и 8 и 7 \\ 5 и 7 и 2 \ end {vmatrix} = 0 $ $ C_ {1} + C_ {3} = C_ {2} $
- В определителе мы можем индивидуально выделить целые числа из строк и столбцов.
Пример 16
В определителе
$ \ begin {vmatrix} 3 и 9 и 12 \\ 5 и 1 и 8 \\ 7 и 4 и 2 \ end {vmatrix} $, мы вычитаем 3 из строки 1 $ (R_ {1}) $ и получаем:
$ 3 \ cdot \ begin {vmatrix} 1 и 3 и 4 \\ 5 и 1 и 8 \\ 7 и 4 и 2 \ end {vmatrix} $, затем мы выносим 2 из столбца 3 $ (C_ {3}) $:
$ 6 \ cdot \ begin {vmatrix} 1 и 3 и 2 \\ 5 и 1 и 4 \\ 7 и 4 и 1 \ end {vmatrix} $ - В определителе мы можем добавлять или вычитать строки или столбцы из других строк, соответственно столбцов, и значение определителя остается прежним.
Пример 17
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {R_ {1} + R_ {2}} \ begin {vmatrix} 4 и 13 \\ 3 и 8 \ end {vmatrix} $
Пример 18
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {C_ {1} + C_ {2}} \ begin {vmatrix} 6 и 5 \\ 11 и 8 \ end {vmatrix} $ -
В определителе мы можем складывать или вычитать несколько строк или столбцов.
Пример 19
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {2R_ {1} + 3R_ {2}} \ begin {vmatrix} 11 и 34 \\ 3 и 8 \ end {vmatrix} $Пример 20
$ \ begin {vmatrix} 1 и 5 \\ 3 и 8 \ end {vmatrix} $ $ \ xlongequal {5C_ {1} -C_ {2}} \ begin {vmatrix} 0 и 5 \\ 7 и 8 \ end {vmatrix} $ - Определитель матрицы равен определителю ее транспонирования.
- Определитель произведения двух квадратных матриц равен произведению определителей данных матриц.
Незначительная часть матрицы
Определитель, полученный путем исключения некоторых строк и столбцов в квадратной матрице, называется минором этой матрицы.
Пример 21
$ A = \ begin {pmatrix}
1 и 4 и 2 \\
5 и 3 и 7 \\
6 и 2 и 1
\ end {pmatrix} $
Одним из миноров матрицы A является $ \ begin {vmatrix} 1 и 4 \\ 5 и 3 \ end {vmatrix} $ (получается путем исключения строки 3 и столбца 3 из матрицы A)
Другой минор — $ \ begin {vmatrix} 1 и 2 \\ 6 и 1 \ end {vmatrix} $ (получается путем исключения строки 2 и столбца 2 из матрицы A)
Пример 22
$ B = \ begin {pmatrix}
2 и 5 и 1 и 3 \\
4 и 1 и 7 и 9 \\
6 и 8 и 3 и 2 \\
7 и 8 и 1 и 4
\ end {pmatrix}
$
Одним из миноров матрицы B является $ \ begin {vmatrix} 1 и 7 и 9 \\ 8 и 3 и 2 \\ 8 и 1 и 4 \ end {vmatrix} $ (получается путем исключения строки 1 и столбца 1 из матрицы B)
Другой несовершеннолетний $ \ begin {vmatrix} 1 и 7 \\ 8 и 3 \ end {vmatrix} $ (получается путем исключения строк 1 и 4 и столбцов 1 и 4 из матрицы B)
Позволять $ A = \ begin {pmatrix} a_ {1,1} и a_ {1,2} и a_ {1,3} &.&. & a_ {1, n} \\ a_ {2,1} и a_ {2,2} и a_ {2,3} &. &. & a_ {2, n} \\ а_ {3,1} и а_ {3,2} и а_ {3,3} &. &. & a_ {3, n} \\ . &. &. &. &. &. \\ a_ {n, 1} и a_ {n, 2} и a_ {n, 3} &. &. & Анна} \ end {pmatrix} $
Мы можем связать минор $ \ Delta_ {i, j} $ (полученный путем исключения строки i и столбца j) с любым элементом $ a_ {i, j} $ матрицы A.
Пример 23
$ A = \ begin {pmatrix}
4 и 7 \\
2 и 9
\ end {pmatrix} $
Мы должны определить минор, связанный с 2.Поскольку этот элемент находится в строке 2, столбце 1, то 2 — это $ a_ {2,1} $.
Мы должны исключить строку 2 и столбец 1 из матрицы A, в результате получим
Младший из 2 равен $ \ Delta_ {2,1} = 7 $.
Пример 24
$ B = \ begin {pmatrix}
1 и 4 и 2 \\
5 и 3 и 7 \\
6 и 2 и 1
\ end {pmatrix} $
Мы должны определить младший, связанный с 7. Поскольку этот элемент находится в строке 2, столбце 3, то 7 — это $ a_ {2,3} $.
Мы должны удалить строку 2 и столбец 3 из матрицы B, в результате чего получится
Минор 7 равен $ \ Delta_ {2,3} = \ begin {vmatrix} 1 и 4 \\ 6 и 2 \ end {vmatrix} $
Пример 25
$ C = \ begin {pmatrix}
2 и 5 и 1 и 3 \\
4 и 1 и 7 и 9 \\
6 и 8 и 3 и 2 \\
7 и 8 и 1 и 4
\ end {pmatrix} $
Мы должны определить минор, связанный с 5. {i + 3} \ cdot \ Delta_ {i, 3} +.{3} \ cdot \ Delta_ {1,2} = a_ {1,1} \ cdot \ Delta_ {1,1} -a_ {1.2} \ cdot \ Delta_ {1,2}
долларов СШАОднако $ \ Delta_ {1,1} = a_ {2,2} $ и $ \ Delta_ {1,2} = a_ {2,1} $
$ \ left | А \ право | = a_ {1.1} \ cdot a_ {2,2} — a_ {1.2} \ cdot a_ {2,1} $
$ \ color {красный} { \ begin {vmatrix} а & б \\ CD \ end {vmatrix} = a \ cdot d — b \ cdot c} $
Пример 28
$ \ begin {vmatrix}
2 и 5 \\
3 и 8
\ end {vmatrix} = 2 \ cdot 8 — 3 \ cdot 5 = 16-15 = 1 $
Пример 29
$ \ begin {vmatrix}
-4 & 7 \\
-2 и 9
\ end {vmatrix} = -4 \ cdot 9 — 7 \ cdot (-2) = -36 — (- 14) = -36 + 14 = — 22 $
Вычисление определителя 3×3
Мы используем строку 1 для вычисления определителя.{4} \ cdot \ Delta_ {1,3} = $ $ a_ {1,1} \ cdot \ Delta_ {1,1} -a_ {1.2} \ cdot \ Delta_ {1,2} + a_ {1.3} \ cdot \ Delta_ {1,3} $
$ \ Delta_ {1,1} = \ begin {vmatrix} а_ {2,2} и а_ {2,3} \\ а_ {3,2} и а_ {3,3} \ end {vmatrix} = a_ {2,2} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,2} $
$ \ Delta_ {1,2} = \ begin {vmatrix} а_ {2,1} и а_ {2,3} \\ а_ {3,1} и а_ {3,3} \ end {vmatrix} = a_ {2,1} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,1} $
$ \ Delta_ {1,3} = \ begin {vmatrix} а_ {2,1} и а_ {2,2} \\ а_ {3,1} и а_ {3,2} \ end {vmatrix} = a_ {2,1} \ cdot a_ {3,2} -a_ {2,2} \ cdot a_ {3,1} $
$ \ left | А \ право | = a_ {1,1} \ cdot (a_ {2,2} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,2}) — a_ {1,2} \ cdot ( a_ {2,1} \ cdot a_ {3,3} -a_ {2,3} \ cdot a_ {3,1}) + $ $ a_ {1,3} \ cdot (a_ {2,1} \ cdot a_ {3,2} -a_ {2,2} \ cdot a_ {3,1}) = $ $ a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} -a_ {1,1} \ cdot a_ {2,3} \ cdot a_ {3,2} -a_ {1 , 2} \ cdot a_ {2.1} \ cdot a_ {3,3} + a_ {1,2} \ cdot a_ {2,3} \ cdot a_ {3,1} + $ $ a_ {1,3} \ cdot a_ {2,1} \ cdot a_ {3,2} -a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} = $ $ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {1,2} \ cdot a_ {2,3} \ cdot a_ {3, 1} + a_ {1,3} \ cdot a_ {2,1} \ cdot a_ {3,2} -} $ $ \ color {красный} {(a_ {1,1} \ cdot a_ {2,3} \ cdot a_ {3,2} + a_ {1,2} \ cdot a_ {2,1} \ cdot a_ {3 , 3} + a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1})} $
Чтобы быстрее достичь последнего отношения, мы можем использовать следующий метод.
Сначала перепишем первые две строки под определитель следующим образом.
$ \ begin {vmatrix}
\ color {красный} {a_ {1,1}} & a_ {1,2} & a_ {1,3} \\
\ color {red} {a_ {2,1}} & \ color {red} {a_ {2,2}} & a_ {2,3} \\
\ color {красный} {a_ {3,1}} & \ color {красный} {a_ {3,2}} & \ color {красный} {a_ {3,3}}
\ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc}
a_ {1,1} & \ color {красный} {a_ {1,2}} & \ color {красный} {a_ {1,3}} \\
a_ {2,1} & a_ {2,2} & \ color {красный} {a_ {2,3}} \\
\ end {array} $
Мы умножаем элементы на каждой из трех красных диагоналей (главной диагонали и тех, что под ней), и складываем результаты:
$ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {2,1} \ cdot a_ {3,2} \ cdot a_ {1,3} + a_ {3,1} \ cdot a_ {1,2} \ cdot a_ {2 , 3}} $
$ \ begin {vmatrix}
\ color {red} {a_ {1,1}} & \ color {red} {a_ {1,2}} & \ color {blue} {a_ {1,3}} \\
\ color {red} {a_ {2,1}} & \ color {blue} {a_ {2,2}} & \ color {blue} {a_ {2,3}} \\
\ color {blue} {a_ {3,1}} & \ color {blue} {a_ {3,2}} & \ color {blue} {a_ {3,3}}
\ end {vmatrix} $
$ \ hspace {2mm}
\ begin {array} {ccc}
\ color {blue} {a_ {1,1}} & \ color {blue} {a_ {1,2}} & \ color {red} {a_ {1,3}} \\
\ color {blue} {a_ {2,1}} & \ color {red} {a_ {2,2}} & \ color {red} {a_ {2,3}} \\
\ end {array} $
Мы умножаем элементы на каждой из трех синих диагоналей (вторичная диагональ и те, что под ней), и складываем результаты:
$ \ color {blue} {a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} + a_ {2,3} \ cdot a_ {3,2} \ cdot a_ {1, 1} + a_ {3,3} \ cdot a_ {1,2} \ cdot a_ {2,1}} $
Если вычесть два отношения, мы получим формулу определителя:
$ \ color {red} {a_ {1,1} \ cdot a_ {2,2} \ cdot a_ {3,3} + a_ {2,1} \ cdot a_ {3,2} \ cdot a_ {1, 3} + a_ {3,1} \ cdot a_ {1,2} \ cdot a_ {2,3} -} $ $ \ color {красный} {(a_ {1,3} \ cdot a_ {2,2} \ cdot a_ {3,1} + a_ {2,3} \ cdot a_ {3,2} \ cdot a_ {1 , 1} + a_ {3,3} \ cdot a_ {1,2} \ cdot a_ {2,1})} $
Пример 30
$ A = \ begin {pmatrix}
1 и 4 и 3 \\
2 и 1 и 5 \\
3 и 2 и 1 \\
\ end {pmatrix} $
$ \ begin {vmatrix}
1 и 4 и 3 \\
2 и 1 и 5 \\
3 и 2 и 1 \\
\ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc}
1 и 4 и 3 \\
2 и 1 и 5 \\
\ end {array} $
$ = 1 \ cdot1 \ cdot1 + 2 \ cdot2 \ cdot3 + 3 \ cdot4 \ cdot5 — (3 \ cdot1 \ cdot3 + 5 \ cdot2 \ cdot1 + 1 \ cdot4 \ cdot2) = $ 1 $ + 12 + 60 — (9 + 10 + 8) = 73-27 = 46 $
Пример 31
$ A = \ begin {pmatrix}
3 и 5 и 1 \\
1 и 4 и 2 \\
7 и 1 и 9 \\
\ end {pmatrix} $
$ \ begin {vmatrix}
3 и 5 и 1 \\
1 и 4 и 2 \\
7 и 1 и 9 \\
\ end {vmatrix} $
$ \ hspace {2mm} \ begin {array} {ccc}
3 и 5 и 1 \\
1 и 4 и 2 \\
\ end {array} $
$ = 3 \ cdot4 \ cdot9 + 1 \ cdot1 \ cdot1 + 7 \ cdot5 \ cdot2 — (1 \ cdot4 \ cdot7 + 2 \ cdot1 \ cdot3 + 9 \ cdot5 \ cdot1) = $ 108 $ + 1 + 70 — (28 + 6 + 45) = 79-79 = 100 $
Есть определители, элементами которых являются буквы. {2 }] $
Пример 32
Вычисляем определитель матрицы Вандермонда.{2}
\ end {vmatrix} = $
$ \ begin {vmatrix} а-с и б-с \\ (a-c) (a + c) и (b-c) (b + c) \ end {vmatrix} = $ $ (a-c) (b-c) \ begin {vmatrix} 1 и 1 \\ а + с и б + с \ end {vmatrix} = $
$ = (a-c) (b-c) [(b + c) — (a + c)] = $ $ (a-c) (b-c) (b + c-a-c) = (a-c) (b-c) (b-a) $
Расчет определителя 4×4
Для вычисления определителей 4×4 воспользуемся общей формулой.
Перед применением формулы, используя свойства определителей:
- Мы проверяем, выполняется ли какое-либо из условий, при которых значение определителя равно 0.
- Мы проверяем, можем ли мы исключить какую-либо строку или столбец.
- Мы проверяем, является ли определитель матрицей Вандермонда или он имеет те же элементы, но переупорядоченные, в любой строке или столбце.
В любом из этих случаев мы используем соответствующие методы вычисления определителей 3×3. Мы модифицируем строку или столбец, чтобы заполнить их 0, за исключением одного элемента. Определитель будет равен произведению этого элемента и его сомножителя. В этом случае сомножитель — это определитель 3×3, который вычисляется по его специальной формуле.
Пример 33
$ \ begin {vmatrix}
1 и 3 и 9 и 2 \\
5 и 8 и 4 и 3 \\
0 & 0 & 0 & 0 \\
2 и 3 и 1 и 8
\ end {vmatrix} $
Мы замечаем, что все элементы в строке 3 равны 0, поэтому определитель равен 0.
Пример 34
$ \ begin {vmatrix}
1 и 3 и 1 и 2 \\
5 и 8 и 5 и 3 \\
0 & 4 & 0 & 0 \\
2 и 3 и 2 и 8
\ end {vmatrix} $
Мы замечаем, что $ C_ {1} $ и $ C_ {3} $ равны, поэтому определитель равен 0.
Пример 35
$ \ begin {vmatrix}
1 и 3 и 9 и 2 \\
5 и 8 и 4 и 3 \\
10 и 16 и 18 и 4 \\
2 и 3 и 1 и 8
\ end {vmatrix} $
Мы замечаем, что строки 2 и 3 пропорциональны, поэтому определитель равен 0.
Пример 36
$ \ begin {vmatrix}
\ color {красный} {4} & 3 & 2 & 2 \\
0 & 1 & -3 & 3 \\
0 и -1 и 3 и 3 \\
0 и 3 и 1 и 1
\ end {vmatrix} $
Поскольку в столбце 1 есть только один элемент, отличный от 0, мы применяем общую формулу, используя этот столбец. {2 + 2} \ cdot
\ begin {vmatrix}
4 и 2 и 8 \\
1 и 3 и 1 \\
2 и 1 и 7
\ end {vmatrix} = $
$ = 4 \ cdot3 \ cdot7 + 1 \ cdot1 \ cdot8 + 2 \ cdot2 \ cdot1 $ $ — (8 \ cdot3 \ cdot2 + 1 \ cdot1 \ cdot4 + 7 \ cdot2 \ cdot1) = $
84 $ + 8 + 4- 48-4-14 = 30 $
Пример 38
$ \ begin {vmatrix}
1 и -2 и 3 и 2 \\
2 и 3 и 1 и -1 \\
3 и 3 и 3 и 3 \\
-1 и 4 и 2 и 1 \\
\ end {vmatrix} $
Мы можем вынести 3 из строки 3:
$ 3 \ cdot
\ begin {vmatrix}
1 и -2 и 3 и 2 \\
2 и 3 и 1 и -1 \\
1 и 1 и 1 и 1 \\
-1 и 4 и 2 и 1 \\
\ end {vmatrix} $
Поскольку в строке 3 есть только элементы, равные 1, мы можем легко сделать нули.{3 + 4} \ cdot $
$ = (- 1) \ cdot
\ begin {vmatrix}
-1 & -4 & 1 \\
3 и 4 и 2 \\
-2 и 3 и 1 \\
\ end {vmatrix} $
$ = — ((- 1) \ cdot 4 \ cdot 1 +3 \ cdot 3 \ cdot1 + (-2) \ cdot (-4) \ cdot 2 $ $ — (1 \ cdot 4 \ cdot (-2) + 2 \ cdot 3 \ cdot (-1) + 1 \ cdot (-4) \ cdot3)) $ $ = — (- 4 + 9 + 16 + 8 + 6 + 12) = -47 $
Пример 39
$ \ begin {vmatrix}
2 и 5 и 1 и 4 \\
4 и 1 и 6 и 3 \\
5 и 3 и 7 и 2 \\
1 и 0, 2 и 4
\ end {vmatrix} $
В этом примере мы можем использовать последнюю строку (которая содержит 1) и сделать нули в первом столбце.{4 + 1} \ cdot \ begin {vmatrix} 5 & -3 & -4 \\ 1 и -2 и -13 \\ 3 и -3 и -18 \ end {vmatrix} = $ $ (- 1) \ cdot \ begin {vmatrix} 5 & -3 & -4 \\ 1 и -2 и -13 \\ 3 и -3 и -18 \ end {vmatrix} $
Мы вычитаем -1 из столбца 2 и -1 из столбца 3.
$ (-1) \ cdot (-1) \ cdot (-1) \ cdot
\ begin {vmatrix}
5 и 3 и 4 \\
1 и 2 и 13 \\
3 и 3 и 18
\ end {vmatrix} = $
$ (- 1) \ cdot
\ begin {vmatrix}
5 и 3 и 4 \\
1 и 2 и 13 \\
3 и 3 и 18
\ end {vmatrix} = $
$ — [5 \ cdot 2 \ cdot 18 + 1 \ cdot 3 \ cdot 4+ 3 \ cdot 3 \ cdot 13 — (4 \ cdot 2 \ cdot 3 \ cdot + 13 \ cdot 3 \ cdot 5 + 18 \ cdot 3 \ cdot 1)] = $
$ — (180 + 12 + 117-24-195-54) = 36 $
Пример 40
$ \ begin {vmatrix}
4 и 7 и 2 и 3 \\
1 и 3 и 1 и 2 \\
2 и 5 и 3 и 4 \\
1 и 4, 2 и 3
\ end {vmatrix} $
В столбце 3 стоит 1, поэтому мы сделаем нули в строке 2. {1 + 4} $
$ = (-10) \ cdot \ begin {vmatrix} -1 и 1 и 2 \\ 2 и 3 и 1 \\ 1 и -1 и -2 \ end {vmatrix} = $ $ (- 10) \ cdot ((- 1) \ cdot 3 \ cdot (-2) +2 \ cdot (-1) \ cdot2 + 1 \ cdot 1 \ cdot 1 $ $ — (2 \ cdot 3 \ cdot 1 + 1 \ cdot (-1) \ cdot (-1) + (-2) \ cdot1 \ cdot2)) $ $ = -10 \ cdot (6-4 +1-6-1 + 4) = 0 $
Wolfram | Примеры альфа: матрицы
Свойства матрицы
Исследуйте различные свойства данной матрицы.
Вычислить свойства матрицы:
Другие примеры
Матричная арифметика
Сложение, вычитание и умножение векторов и матриц.
{{2, -1, 1}, {0, -2, 1}, {1, -2, 0}}.{x, y, z}Другие примеры
След
Вычислить след или сумму членов на главной диагонали матрицы.
Вычислить след матрицы:
Другие примеры
Детерминант
Вычислить определитель квадратной матрицы.
Вычислить определитель матрицы:
Другие примеры
Обратный
Обратить квадратную обратимую матрицу или найти псевдообратную неквадратную матрицу.
Вычислить обратную матрицу:
Другие примеры
Уменьшение строк
Привести матрицу к уменьшенной форме эшелона строк.
уменьшение строки {{2, 1, 0, -3}, {3, -1, 0, 1}, {1, 4, -2, -5}}Другие примеры
Собственные значения и собственные векторы
Вычислить собственную систему заданной матрицы.
Вычислить собственные значения матрицы:
Вычислить собственные векторы матрицы:
Вычислить характеристический полином матрицы:
Другие примеры
Другие матричные операции
Выполняет различные операции с матрицами, например сопряженное транспонирование.
Вычислите транспонирование матрицы:
Вычислить ранг матрицы:
Вычислить нулевое значение матрицы:
Вычислить адъюгат матрицы:
Другие примеры
Диагонализация
Найдите диагонализацию квадратной матрицы.
Другие примеры
Другие примеры
Матричные разложенияПреобразует матрицу в указанное разложение.
Вычислите LU-разложение квадратной матрицы:
Вычислите разложение по сингулярным числам:
Другие примеры
Другие примеры
Геометрические преобразованияНайдите матричные представления для геометрических преобразований.
Вычислите матрицу вращения 2 x 2:
Вычислите матрицу отражения 3 x 3:
Другие примеры
Типы матриц
Найдите информацию о различных типах матриц.
