Матрица цифровой камеры. Типы и размер матриц
Выбирая цифровую камеру для микроскопа или телескопа, часто обращают внимание лишь на разрешение матрицы, т.е. количество мегапикселей. Однако это не единственный важный параметр цифровой камеры, определяющий качество полученных фотоснимков и видеороликов. По каким же признакам следует выбирать цифровую камеру, и чем они могут отличаться одна от другой?
Главным элементом цифровой камеры является ее матрица, которая, собственно, и фиксирует изображение в цифровой камере. Отметим, что также в техническом описании цифровых камер часто употребляется и термин сенсор, обозначающий то же, что и матрица. Матрица состоит из массива светочувствительных ячеек, и именно от нее зависит качество изображения, полученного с помощью цифровой камеры.
Существует два основных типа матриц: CCD (ПЗС матрицы) и CMOS (КМОП матрицы), отличающиеся по применяемой технологии. И если на рынке фотоаппаратов наиболее распространены цифровые камеры с ПЗС матрицей, то большинство моделей цифровых камер для телескопов и микроскопов имеют именно КМОП матрицу.
Чем же отличается ПЗС матрица от КМОП матрицы? Основным их отличием является то, что в ПЗС матрицах информация из ячеек считывается последовательно, в то время как в КМОП матрицах информация считывается индивидуально из каждой отдельной ячейки. По этой причине в ПЗС матрицах Вы не можете сделать следующий снимок до тех пор, пока не будет целиком сформирован предыдущий. Что же касается КМОП матриц, то благодаря применяемой технологии их можно использовать не только для фотосъемки, но и для экспонометрии и работы автофокуса. Помимо этого, КМОП матрицы гораздо дешевле в производстве, и поэтому доступнее для многих пользователей. Еще одно немаловажное преимущество КМОП матриц над ПЗС матрицами – потребление меньшего количества энергии.
Первым делом при выборе цифровой камеры мы рекомендуем Вам обратить внимание на размер матрицы. Физическим размером матрицы называется ее геометрический размер, т.е. длина и ширина матрицы, выраженные в мм. Физический размер матрицы определяет ее качество. Узнать значение этого параметра можно из ее технического описания, хотя, как правило, размеры фотосенсоров производители указывают не в мм, а введя специальное обозначение типа матрицы в виде дробных частей дюйма, например: 1/4″, 1/3″, 1/2.5″, 1/2″ и пр. Сравнивая различные цифровые камеры, Вы должны понимать, что размер матрицы больше у той цифровой камеры, у которой знаменатель в указанной дроби будет меньше, т.е. сенсор 1/2″ будет больше сенсора 1/3″.
Физическим размером матрицы называется ее геометрический размер, т.е. длина и ширина матрицы, выраженные в мм. Физический размер матрицы определяет ее качество. Узнать значение этого параметра можно из ее технического описания, хотя, как правило, размеры фотосенсоров производители указывают не в мм, а введя специальное обозначение типа матрицы в виде дробных частей дюйма, например: 1/4″, 1/3″, 1/2.5″, 1/2″ и пр. Сравнивая различные цифровые камеры, Вы должны понимать, что размер матрицы больше у той цифровой камеры, у которой знаменатель в указанной дроби будет меньше, т.е. сенсор 1/2″ будет больше сенсора 1/3″.
Какая же связь между физическим размером матрицы, указанным в мм и типом матрицы, выраженном в 1/дюйм? Отметим, что введенное обозначение типа матрицы выражает не размер ее диагонали, а внешний размер колбы передающей трубки. Обратите внимание на то, что не существует конкретной математической формулы, четко выражающей взаимосвязь между устоявшимся обозначением типа матрицы, выраженного в 1/дюйм, и самим физическим размером диагонали матрицы в мм. Тем не менее, в грубом приближении принято считать, что диагональ сенсора равна двум третям его типоразмера.
|
Размеры в мм |
Тип матрицы |
|
4.5х3.4 |
1/3.2″ |
|
5.4х4.0 |
1/2.7″ |
|
5.8×4.3 |
1/2.5″ |
|
6.2×4.6 |
1/2.3″ |
|
7. |
1/1.8″ |
Вполне целесообразно задать вопрос, а на что же влияет размер матрицы? Прежде всего, сколь иронично это бы не звучало, размер матрицы цифровой камеры влияет на ее стоимость и вес.
Помимо этого, как мы уже отмечали ранее, размер сенсора влияет на качество полученных фотоснимков и видеороликов. Во-первых, от размера сенсора зависит количество цифрового шума, который передается на светочувствительные элементы матрицы вместе с основным сигналом.
Из-за цифрового шума полученные снимки получают неестественный вид, в связи с чем возникает такое ощущение, что сверху на снимок наложена маска из точек различного цвета и яркости.
Причинами возникновения шумов могут быть дефекты в структуре сенсора, токи утечки (заряд может пробивать изоляцию и переходить с одного пикселя на другой), нагрева матрицы (так называемый тепловой шум, когда при повышении температуры на 6-8 градусов шум увеличивается в 2 раза) и пр.
Конечно же, нужно понимать, что абсолютно бессмысленно рассматривать показатель шума отдельно – важно соотношение сигнал / шум.
Итак, на количество шумов главным образом влияет физический размер матрицы, а также размер пикселя. Чем больше физический размер сенсора цифровой камеры, тем больше его площадь и, соответственно тем больше света попадает на него. А, следовательно, полезный сигнал матрицы будет сильнее и, значит, мы получим лучшее соотношение сигнал / шум, что обеспечит более яркое и качественное изображение с более правильной и естественной цветопередачей.
Помимо этого, отметим, что слой изоляции, разделяющий пиксели друг от друга, будет толще для пикселей большого размера. Разумеется, что чем толще слой изоляции, тем меньше зарядов смогут пробить ее. Следовательно, токов утечки будет тоже меньше, что соответственно приведет и к уменьшению шумов.
В качестве примера предлагаем Вам представить матрицу определенного размера. Предположим, что на одной такой матрице 3000 пикселей (3 Мпикс), а на второй такой же матрице расположено 5000 (5 Мпикс). А теперь представьте толщину изоляции пикселей для первого и для второго случая!
Еще раз отметим, что чем меньше матрица, тем меньшее количество света на нее попадает. В таком случае Вы получаете слабый полезный сигнал, который приходится усиливать. А с усилением полезного сигнала естественно усиливаются и становятся более заметными шумы.
В заключение еще раз повторим, что чем больше физический размер матрицы, тем большее количество света на нее попадает, а значит, тем более качественно изображение Вы получите.
Автор статьи: Галина Цехмистро
| Шины и диски на Hyundai MatrixОстальные модели Hyundai: Hyundai Accent, Hyundai Amica, Hyundai Aslan, Hyundai Atos, Hyundai Atos Prime, Hyundai Avante, Hyundai Azera, Hyundai Celesta, Hyundai Centennial, Hyundai Click, Hyundai Coupe, Hyundai Creta, Hyundai Dynasty, Hyundai Elantra, Hyundai Elantra EV, Hyundai Elantra GT, Hyundai Elantra Langdong, Hyundai Elantra LaVita, Hyundai Elantra Lingdong, Hyundai Elantra Yuedong, Hyundai Elite i20, Hyundai Encino, Hyundai Entourage, Hyundai Eon, Hyundai Equus, Hyundai Excel, Hyundai Galloper, Hyundai Genesis, Hyundai Genesis Coupe, Hyundai Getz, Hyundai Grand i10, Hyundai Grand i10 Nios, Hyundai Grand Santa Fe, Hyundai Grand Starex, Hyundai Grandeur, Hyundai H-100, Hyundai h2, Hyundai h400, Hyundai h450, Hyundai HB20, Hyundai HB20S, Hyundai HB20X, Hyundai HR, Hyundai i10, Hyundai i20, Hyundai i20 Active, Hyundai i20 Coupe, Hyundai i25, Hyundai i30, Hyundai i30 N, Hyundai i40, Hyundai i45, Hyundai i800, Hyundai iLoad, Hyundai iMax, Hyundai Ioniq, Hyundai ix20, Hyundai ix25, Hyundai ix35, Hyundai ix55, Hyundai ix55 (Veracruz), Hyundai Kauai, Hyundai Kona, Hyundai Lafesta, Hyundai Lavita, Hyundai Matrix, Hyundai Maxcruz, Hyundai Mistra, Hyundai Nexo, Hyundai Palisade, Hyundai Porter, Hyundai Porter II, Hyundai Reina, Hyundai Santa Fe, Hyundai Santa Fe Sport, Hyundai Santa Fe XL, Hyundai Santro, Hyundai Santro Xing, Hyundai Santro Zip, Hyundai Solaris, Hyundai Sonata, Hyundai Sonata Hybrid, Hyundai Sonata NF, Hyundai Starex, Hyundai Terracan, Hyundai Tiburon, Hyundai Trajet, Hyundai Tucson, Hyundai Tuscani, Hyundai Veloster, Hyundai Veloster N, Hyundai Venue, Hyundai Veracruz, Hyundai Verna, Hyundai Verna RV, Hyundai Xcent, Hyundai XG,
Подбор шин и дисков для автомобиля Hyundai MatrixИспользуя автоматический подбор шин и дисков для автомобиля Hyundai Matrix, можно избежать множества проблем, связанных с их совместимостью и соответствием рекомендациям автопроизводителей. Ведь эти комплектующие оказывают огромное влияние на целый ряд эксплуатационных характеристик транспортного средства, начиная от управляемости и заканчивая динамическими качествами. Кроме того, шины и колесные диски в современном автомобиле являются одним из элементов активной безопасности. Именно поэтому к их выбору следует подходить максимально ответственно, т. е. со знанием о целом ряде параметров этих комплектующих. К сожалению, или, наоборот, к счастью значительная часть автолюбителей предпочитает не изучать техническое устройство собственного автомобиля досконально. Полностью автоматическая система подбора в таком случае является едва ли не единственным способом избежать неверного выбора при покупке шин и колесных дисков. А его отличает чрезвычайное разнообразие, благодаря наличию в интернет-магазине «Мосавтошина» широкого ассортимента данного вида изделий. |
Полнокадровая матрица и понятие кроп-фактор. Блог для начинающих фотографов
Матрица – это микросхема, состоящая из светочувствительных элементов, с помощью которых свет преобразуется в электрические сигналы и записываются на карту памяти в виде изображений, состоящих из цифрового кода.
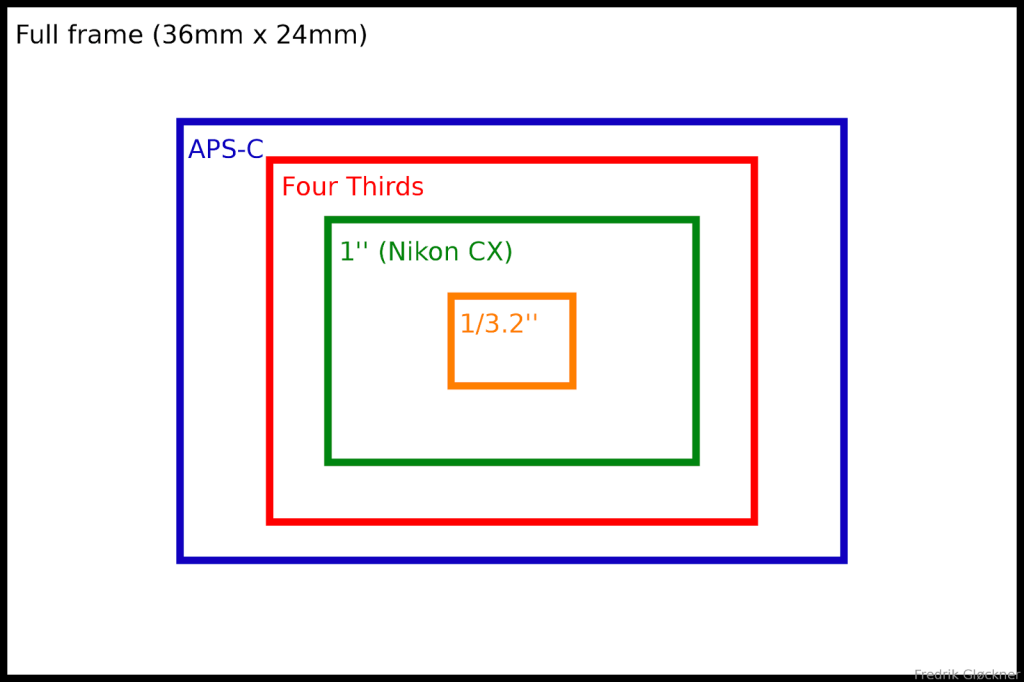
Одним из самых важных параметров цифровой фотокамеры является физический размер матрицы. Он может соответствовать размеру стандартного пленочного кадра – 24х36 мм, такие матрицы называются полноформатными (или полнокадровыми), либо быть меньше, тогда матрица будет называться «кроповой» (crop в переводе с англ.
Физические размеры матрицы, соответствующие значению кроп-фактора:
1 = 36х24
1,3 = 27х18
1,5 = 24х16
1,6 = 22,5х15
Отличие полноформатной матрицы от кроповой, преимущества полноформатной
1. Печать больших форматов.
Матрица фотокамеры состоит из светочувствительных элементов – пикселей, задача которых собирать падающий на них свет и преобразовывать его в электрический импульс. Один пиксель равен одной точке. Чем больше пикселей участвует в формировании изображения, тем выше детализация и разрешение снимка, а это позволяет осуществлять печатать в большом формате от А4 без потери качества. Количество мегапикселей имеет значение для профессиональных фотографов, т.к. именно им приходится работать с большими форматами изображений. Увеличение количества мегапикселей достигается двумя путями – увеличением размера матрицы, либо уменьшением размера самих фотоэлементов. Второй вариант более дешевый, и чаще всего приводит к ухудшению качества изображения.
2. Качество изображения
На полноформатных и кроповых матрицах пиксели отличаются по размеру. На полноформатных матрицах они крупнее, что позволяет им собирать больше фотонов света. Чем ярче пиксель, тем больший спектр яркостей может быть передан на фото, а соответственно точнее цветопередача. Этот параметр называется динамический диапазон фотокамеры, и обозначается в ступенях.
Размер полноформатных матриц позволяет размещать светочувствительные элементы на оптимальном друг от друга расстоянии. Поэтому при получение сигнала, возникающие помехи не затрагивают соседних пикселей, в связи с чем на фотографии сокращается количество шумов, а это дает возможность фотографировать на высоких значениях ИСО. И с точностью наоборот, чем меньше размер матрицы, тем меньше пиксели и их расстояние относительно друг друга, и возникающие помехи создают шумы, которые заметны даже при минимальных значениях ИСО. Помимо шумов может возникнуть эффект дифракции (замыливания).
И с точностью наоборот, чем меньше размер матрицы, тем меньше пиксели и их расстояние относительно друг друга, и возникающие помехи создают шумы, которые заметны даже при минимальных значениях ИСО. Помимо шумов может возникнуть эффект дифракции (замыливания).
3. Фокусное расстояние объектива
Фокусное расстояние (ФР) – это расстояние от оптического центра объектива до матрицы фотокамеры.
Эквивалентное фокусное расстояние (ЭФР) – это фокусное расстояние объектива, умноженное на кроп-фактор.
Один и тот же объектив на полноформатной и кроповой матрице будет иметь разный угол обзора — охватывать большую или меньшую площадь снимаемой сцены. Например, объектив с фокусным расстоянием 28 мм на камере с полноформатной матрицей имеет угол обзора 73 градуса, в то время как на камере с кроп-фактором 1,6 будет составлять всего лишь 50 градусов. Поэтому кроп-фактор иногда называют «коэффициентом увеличения». В этом есть определенное преимущество для фотографов, использующих в своей работе длиннофокусные объективы. 200-милиметровый объектив на матрице с кроп-фактором 1,5 будет давать угол обзора, соответствующий 300-милиметровому.
Вывод: чем больше физический размер матрицы, тем больше пикселей на ней можно разместить, а это позволяет печать фотографии в большом формате. Крупные пиксели собирают больше света, что расширяет динамический диапазон фотокамеры. За счет оптимального расстояния между пикселями снижается уровень шумов, поэтому высокие значения ИСО становятся рабочими. Не нужно оперировать понятием ЭФР, чтобы рассчитать реальный угол обзора объектива.
Недостаток у полноформатной камеры один — это ее высокая стоимость.
Физический размер матрицы. Цифровая фотография. Трюки и эффекты
Читайте также
3.2.1 Физический уровень
3.2.1 Физический уровень
Физический уровень (physical layer) имеет дело с физическими носителями, разъемами и сигналами для представления логических нулей и единиц.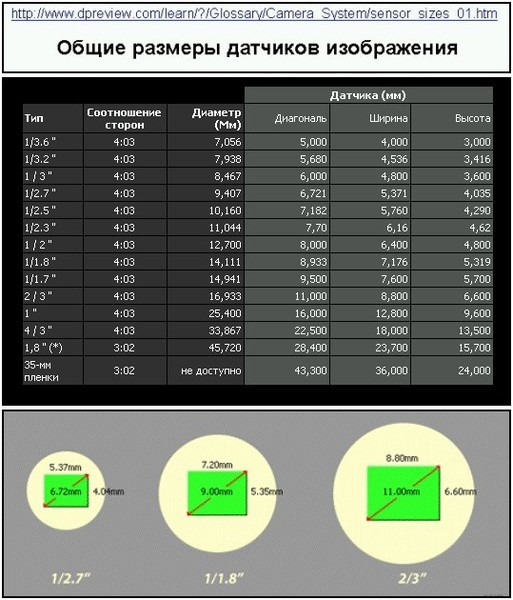 Например, адаптеры сетевого интерфейса Ethernet и Token-Ring и соединяющие их кабели реализуют функции физического
Например, адаптеры сетевого интерфейса Ethernet и Token-Ring и соединяющие их кабели реализуют функции физического
8.1.8. Реализация разреженной матрицы
8.1.8. Реализация разреженной матрицы Иногда бывает нужен массив, в котором определена лишь небольшая часть элементов, а остальные не определены вовсе или (даже чаще) равны 0. Подобная разреженная матрица потребляет так много памяти зря, что были найдены способы более
9.4.1. Реализация графа в виде матрицы смежности
9.4.1. Реализация графа в виде матрицы смежности Нижеприведенный пример основан на двух предыдущих. В листинге 9.3 неориентированный граф реализован в виде матрицы смежности с помощью класса ZArray (см. раздел 8.1.26). Это нужно для того, чтобы новые элементы по умолчанию получали
11.14. Реализация динамической матрицы
11.14. Реализация динамической матрицы ПроблемаТребуется реализовать числовые матрицы, размерности которых (количество строк и столбцов) неизвестны на этапе компиляции.РешениеВ примере 11.28 показана универсальная и эффективная реализация класса динамической матрицы,
11.15. Реализация статической матрицы
11.15. Реализация статической матрицы ПроблемаТребуется эффективно реализовать матрицу, когда ее размерность (т.е. количество строк и столбцов) постоянна и известна на этапе компиляции.РешениеКогда размерность матрицы известна на этапе компиляции, компилятор может легко
Физический размер изображения
Физический размер изображения
Физический размер изображения – это количество пикселов в изображении по ширине и по высоте. Таким образом, мы получаем размеры изображения в пикселах.Чем больше пикселов в изображении и чем больше его физический размер, тем выше может
Таким образом, мы получаем размеры изображения в пикселах.Чем больше пикселов в изображении и чем больше его физический размер, тем выше может
Размер страницы и размер кэша по умолчанию
Размер страницы и размер кэша по умолчанию При восстановлении вы можете изменить размер страницы, включив в команду переключатель -р[age_size], за которым следует целое число, задающее размер в байтах. Допустимые размеры страниц см. в табл. 38.2.В этом примере gbak восстанавливает
Числогрызы ткнулись в физический предел полупроводников. Куда дальше? Евгений Золотов
Числогрызы ткнулись в физический предел полупроводников. Куда дальше? Евгений Золотов Опубликовано 27 ноября 2013 Суперкомпьютеры всегда представлялись особенным классом вычислительной техники. Поскольку строят такие машины для решения задач
Разрешение матрицы
Разрешение матрицы Мы знаем, что матрица состоит из мельчайших светочувствительных элементов. Количество таких элементов в матрице – это и есть ее разрешение. Разрешение матрицы получают умножением количества элементов по горизонтали и вертикали. Самые
Динамический диапазон матрицы
Динамический диапазон матрицы Динамический диапазон светочувствительной матрицы – это ее способность воспринимать градации каждого из цветов. Говоря проще, динамический диапазон определяет, сколько ступеней разности контраста может увидеть и зафиксировать матрица.
Физический уровень
Физический уровень
Хотя физический доступ и не рассматривается как реальная угроза сегодняшнего дня, очевидно, что нарушение физической безопасности может привести к нарушению информационной безопасности.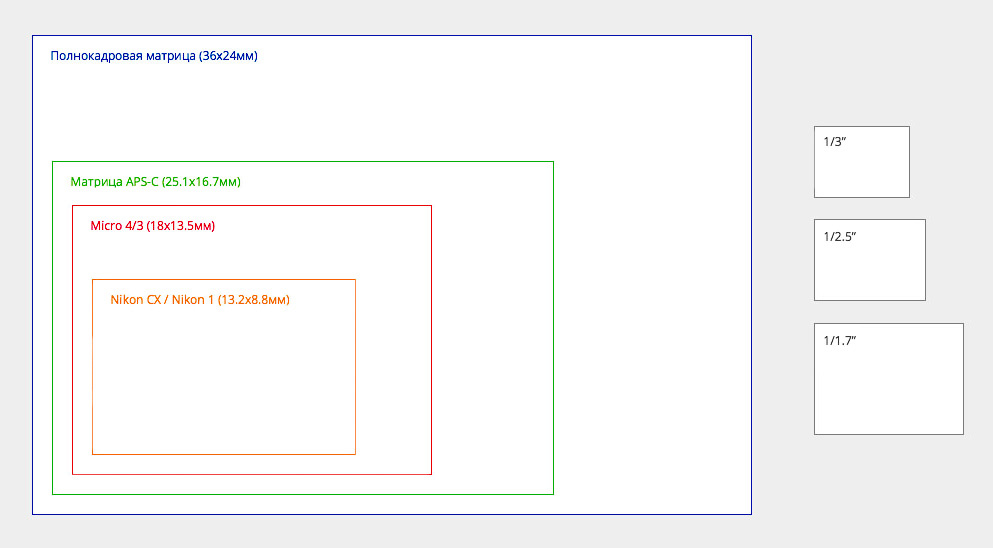 Для обеспечения высокой степени доверия к защите физического
Для обеспечения высокой степени доверия к защите физического
Чистка матрицы зеркальной камеры
Чистка матрицы зеркальной камеры У владельцев зеркальных камер к радости от возможности смены объективов прибавляется забота о чистоте матрицы. Что делать, если вы заметили на снимках ровной светлой поверхности соринки и пятна? В некоторых моделях зеркальных камер
Чистка матрицы зеркальной камеры
Чистка матрицы зеркальной камеры В зеркальной камере, в отличие от компактной, приходится чистить матрицу. Хотите вы или нет, но рано или поздно на матрицу попадает пыль, мелкие соринки. Насколько скоро это произойдет, зависит от частоты смены объективов, условий
Размер головного мозга и размер социального окружения
Размер головного мозга и размер социального окружения Дискуссии по поводу взаимосвязи между размером головного мозга какого-либо организма и размером группы, к которой этот организм принадлежит, ведутся нейробиологами уже давно. При этом взаимосвязь с социальной
ТЕМА НОМЕРА: Реформирование матрицы
ТЕМА НОМЕРА: Реформирование матрицы Автор: Леонид Левкович-МаслюкГде-то в конце 1980-х или начале 1990-х я читал в «Независимой газете» обзор событий в мире книг. Автор отмечал, что на прилавках появилось оригинальнейшее сочинение по истории древнего мира, которое написал
Типы и размеры матриц камер видеонаблюдения
Разберем характеристику первой попавшейся камеры.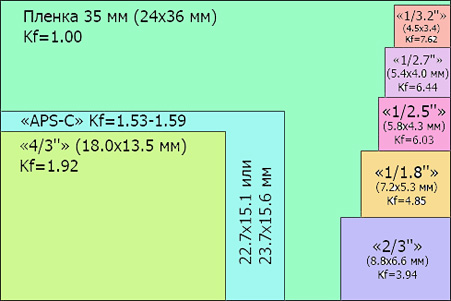
| Матрица | 1/4″ Progressive Scan CMOS |
| Эффективных пикселей | 1Мп, 1280 х 720 |
Такую таблицу вы встретите на странице каждой камеры, меняются лишь значения, подставляемые к перечню характеристик. Как понять, что вам нужно и на какие данные стоит обратить внимание в первую очередь? Ведь матрица – это и есть та главная часть камеры, которая получает изображение, как фотопленка в старых фотоаппаратах.
Рассмотрим типы матриц. И начнем от обратного. Матрицы, не использующиеся Hikvision – CCD-матрицы.
По сравнению с технологией CMOS, которую применяет в своих камерах Hikvision, CCD-матрицы позволяют создавать высококачественное изображение. В процессе съемки возникает гораздо меньше шумов, а бороться с все же возникшими намного легче, чем в матрицах CMOS.
Еще одним важным показателем является их высокая эффективность. Например, коэффициент заполнения у матриц CCD приближается к 100%, а соотношение зарегистрированных матрицей фотонов к их общему числу – 95%. Если сравнивать с нашими глазами, то при расчёте в тех же единицах соотношение составит только 1%.
К недостаткам CCD-матриц можно отнести сложность процесса. Для фиксации изображения в камере необходимо дополнительное наличие целого перечня устройств. Это приводит к более высокому энергопотреблению, делает их дороже в производстве и “капризнее” в эксплуатации.
Теперь о CMOS-матрицах.
Главное достоинство CMOS-матриц – более низкое энергопотребление и возможность произвольного считывания ячеек, а это CCD-матрице недоступно, там считывание происходит одновременно. Благодаря произвольному считыванию в CMOS-матрицах нет размазывания изображения.
Еще одно достоинство – расположение значительной части электроники непосредственно на ячейке, благодаря этому появляются широкие возможности управления матрицей и изображением.
При всех имеющихся достоинствах данной технологии, недостатков хватает. Главный – незначительный размер светочувствительного элемента в соотношении к общей площади пикселя. Одно из основных достоинств – расположения электроники на ячейке. Но из него вытекает еще один недостаток – значительная часть площади пикселя занята электроникой, а значит, уменьшена площадь светочувствительного элемента.
В то же время нельзя не отметить, что CMOS был модифицирован несколько лет назад, и для видеонаблюдения CMOS-матрицы действительно подходят лучше (благодаря чёткому изображению, низкому энергопотреблению и возможности уменьшать битрейт видео.
Как найти длину (или размеры, Размер) матрицы numpy в python?
Для матрицы numpy в python
from numpy import matrix
A = matrix([[1,2],[3,4]])
Как я могу найти длину строки (или столбца) этой матрицы? Аналогично, как я могу узнать количество строк или столбцов?
Пока что единственное решение, которое я нашел, — это:
len(A)
len(A[:,1])
len(A[1,:])
Который возвращает 2, 2 и 1 соответственно. Из этого я заключил, что len() вернет количество строк, так что я всегда могу использовать транспонирование , len(A.T), для количества столбцов. Однако это кажется неудовлетворительным и произвольным, так как при чтении строки len(A) не сразу очевидно , что это должно возвращать количество строк. На самом деле он работает иначе, чем len([1,2]) для массива 2D python, так как это вернет 2.
Итак, есть ли более интуитивный способ найти размер матрицы, или это лучшее, что у меня есть?
python matrix numpyПоделиться Источник Kyle Heuton 13 февраля 2013 в 06:07
2 ответа
- Как я могу найти размеры матрицы в Python?
Как я могу найти размеры матрицы в Python.
 Len (A) возвращает только одну переменную. Редактировать: close = dataobj.get_data(timestamps, symbols, closefield) Это (я предполагаю) генерация матрицы целых чисел (менее вероятных строк). Мне нужно найти размер этой матрицы, чтобы я мог выполнить…
Len (A) возвращает только одну переменную. Редактировать: close = dataobj.get_data(timestamps, symbols, closefield) Это (я предполагаю) генерация матрицы целых чисел (менее вероятных строк). Мне нужно найти размер этой матрицы, чтобы я мог выполнить… - матрица в степени столбца плотной матрицы с использованием numpy в Python
Я пытаюсь получить все значения в матрице beta VxK в степени всех значений в столбце Vx1, который является частью плотной матрицы VxN. Таким образом, каждое значение в бета-версии должно быть в степени соответствующей строки в столбце, и это должно быть сделано для всех K столбцов в бета-версии….
254
shape является свойством как numpy ndarray, так и матриц.
A.shape
вернет кортеж (m, n), где m-количество строк, а n-количество столбцов.
На самом деле объект numpy matrix построен поверх объекта ndarray , одного из двух фундаментальных объектов numpy (наряду с универсальным функциональным объектом), поэтому он наследуется от ndarray
Поделиться Kyle Heuton 13 февраля 2013 в 06:07
37
matrix.size согласно документам numpy возвращает надежду Number of elements in the array. , которая помогает.
Поделиться hd1 13 февраля 2013 в 06:12
Похожие вопросы:
Максимальный элемент / размер матрицы numpy?
каков максимальный элемент / случай матрицы numpy или каков максимальный размер матрицы numpy? приведенный выше код возвращает ошибку памяти при переменной матрице size…so от какой окружающей…
Размеры матрицы в C
Я должен извлечь матрицу из файла через C и вычислить ее определитель.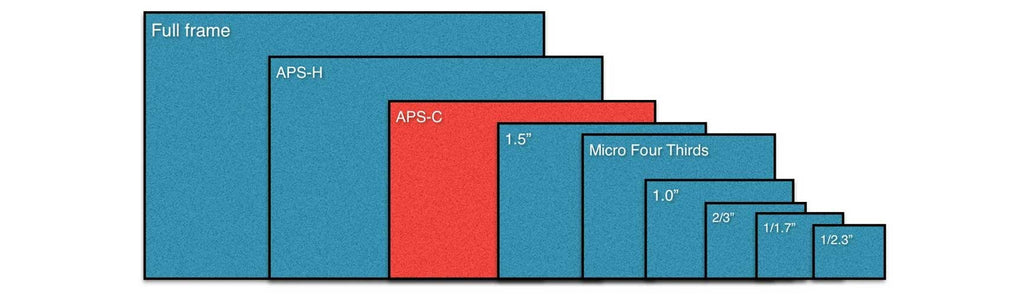 Чтобы сделать это для любой матрицы размером до 3х3, я уверен, что мне нужно знать размеры матрицы, но я довольно новичок в…
Чтобы сделать это для любой матрицы размером до 3х3, я уверен, что мне нужно знать размеры матрицы, но я довольно новичок в…
Как получить длину диагонали матрицы?
Есть ли формула, которая дала бы мне длину диагонали матрицы в единицах? Например, если матрица имеет размер 3×3, то длина диагонали будет равна 3.
Как я могу найти размеры матрицы в Python?
Как я могу найти размеры матрицы в Python. Len (A) возвращает только одну переменную. Редактировать: close = dataobj.get_data(timestamps, symbols, closefield) Это (я предполагаю) генерация матрицы…
матрица в степени столбца плотной матрицы с использованием numpy в Python
Я пытаюсь получить все значения в матрице beta VxK в степени всех значений в столбце Vx1, который является частью плотной матрицы VxN. Таким образом, каждое значение в бета-версии должно быть в…
Python numpy: «массив слишком велик»
import numpy from scipy.spatial.distance import pdist X = numpy.zeros(50000,25) C = pdist(X, ‘euclidian’) Я хочу найти: А потом numpy выдает ошибку: массив слишком велик. Я думаю, что проблема…
Преобразование матрицы numpy в массив python
Существуют ли альтернативные или лучшие способы преобразования матрицы numpy в массив python, чем этот? >>> import numpy >>> import array >>> b = numpy.matrix(1.0 2.0 3.0;…
Как получить размер матрицы?
Недавно у меня был проект, который должен был знать размер матрицы. вот раздел кода matlab. [rwn1 rwn2]=size(rtt) Тогда вы будете знать, сколько строк и столбцов он имеет в матрице под названием rtt…
Как найти значение изображения (пикселя?) в правом нижнем углу изображения с Python?
В верхней левой части изображения значение pixel всегда будет равно (0,0). Но в зависимости от разрешения камеры и различных изображений размер изображения меняется, так как же найти максимальную. ..
..
Как найти длину массива внутри кортежа
У меня есть кортеж массивов, и мне нужно найти длину массива, используя индекс кортежа. Этот кортеж генерируется из разреженной матрицы, альтернативной numpy, где я использую scipy.sparse.csr…
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или (i=1,2,…m; j=1,2,…n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Элементы расположенные на местах a11, a22 ,…, ann образуют главную диагональ матрицы. Например:
Например:
В случае m×n -матриц элементы aii ( i=1,2,…,min(m,n)) также образуют главную диагональ. Например:
Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .
Побочная диагональ матрицы
Элементы расположенные на местах a1n, a2n-1 ,…, an1 образуют побочную диагональ матрицы. Например:
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n, где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
Верхняя треугольная матрица
Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. aij=0, при всех i>j . Например:
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т. е. aij=0, при всех i<j. Например:
е. aij=0, при всех i<j. Например:
Cтроки матрицы A образуют пространство строк матрицы и обозначаются через R(AT).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
AT=−A.
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
C=A+(-1)B.
Для обозначения разности двух матриц используется запись:
C=A-B.
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
A0=E,
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=AT называется симметричной матрицей.
Для симметричных матриц имеет место равенство:
aij=aji ; i=1,2,…n, j=1,2,…n
Размер матрицы — обзор
Мы используем одну (или в нижнем индексе) жирную заглавную букву для обозначения матрицы (например, A , B , C 1 , C 2 ) в отличие от строчных полужирных букв, используемых для обозначения векторов. Заглавные буквы I и O обычно зарезервированы для специальных типов матриц, обсуждаемых позже.
Размер матрицы всегда указывается первым числом строк.Например, матрица 3 × 4 всегда имеет три строки и четыре столбца, а не четыре строки и три столбца.
Матрица m × n может рассматриваться как набор векторов-строк m , каждый из которых имеет координаты n , или как набор векторов-столбцов n , каждый имеющий координаты м . Матрица с одной строкой (или столбцом) по существу эквивалентна вектору с координатами в виде строки (или столбца).
Мы часто пишем a ij для представления записи в строке i и j -м столбце матрицы A . Например, в предыдущей матрице , , , , , 23, — это запись -5 во второй строке и третьем столбце. Типичная матрица 3 × 4 C имеет элементы, обозначенные как
C = [c11c12c13c14c21c22c23c24c31c32c33c34].
ℳ mn представляет собой набор всех матриц с записями действительных чисел, имеющими m строк и n столбцов. Например, ℳ 34 — это набор всех матриц, имеющих три строки и четыре столбца. Типичная матрица в ℳ 34 имеет форму предшествующей матрицы C .
Например, ℳ 34 — это набор всех матриц, имеющих три строки и четыре столбца. Типичная матрица в ℳ 34 имеет форму предшествующей матрицы C .
главная диагональ элементов матрицы A — это a 11 , a 22 , a 33 ,…, те, которые лежат на диагональной линии рисуются вправо, начиная с верхнего левого угла матрицы.
(функции MATLAB) Размер
(функции MATLAB)| Справочник функций MATLAB |
Размеры массива
Синтаксис
d = размер (X) [m, n] = размер (X) m = размер (
X, размер) [d1, d2, d3, ..., dn] = размер (X)
Описание
d = размер (X) возвращает размеры каждого измерения массива X в векторе d с элементами ndims (X) .Если X является скаляром, который MATLAB рассматривает как массив 1 на 1, size (X) возвращает вектор [1 1] .
[m, n] = размер (X) возвращает размер матрицы X в отдельных переменных m и n .
м = размер (X, тусклый) возвращает размер измерения X , заданный скаляром dim .
[d1, d2, d3, ..., dn] = размер (X), для n > 1, возвращает размеры измерений массива X в переменных d1, d2, d3 ,…, dn, при условии, что количество выходных аргументов n равно ndims (X) . Если n не равно ndims (X) , выполняются следующие исключения:
n | |
n> ndims (X) | size возвращает единицы в «дополнительных» переменных, то есть те, которые соответствуют значениям ndims (X) +1 от до n . |
Примечание Для массива Java size возвращает длину массива Java как количество строк. Количество столбцов всегда равно 1. Для массива массивов Java результат описывает только массив верхнего уровня. |
Примеры
Пример 1. Размер второго измерения rand (2,3,4) равен 3.
м = размер (ранд (2,3,4), 2) m = 3
Здесь размер выводится как один вектор.
Здесь размер каждого измерения присваивается отдельной переменной.
[m, n, p] = размер (rand (2,3,4)) m = 2 п = 3 p = 4
Пример 2. Если X = единицы (3,4,5), то
Но когда количество выходных переменных меньше ndims (X):
«Дополнительные» измерения свернуты в единый продукт.
Если n> ndims (X), все "дополнительные" переменные представляют одноэлементные измерения:
[d1, d2, d3, d4, d5, d6] = размер (X) d1 = d2 = d3 = 3 4 5 d4 = d5 = d6 = 1 1 1
См. Также
exist , длина , numel , whos
| sinh | срез |
© 1994-2005 The MathWorks, Inc.
Этот сайт использует файлы cookie для повышения производительности.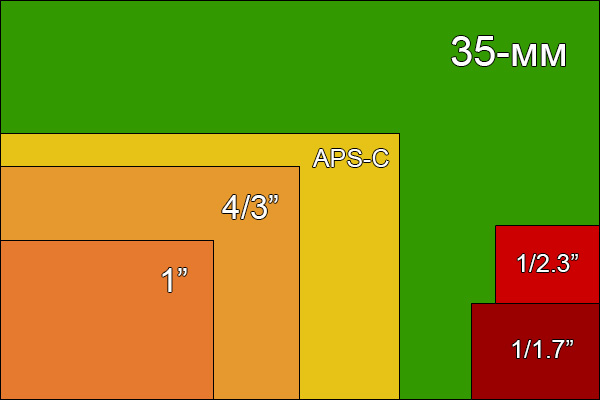 Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Есть много причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку "Назад" и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Оптимальный размер матрицы рентгенограмм грудной клетки для компьютерного обнаружения узелков или новообразований в легких с глубоким обучением
Schalekamp S, van Ginneken B, Koedam E et al (2014) Компьютерное обнаружение улучшает обнаружение легочных узелков в грудной клетке рентгенограммы за пределами поддержки изображениями с подавлением костей. Радиология 272: 252–261
Статья Google Scholar
van Ginneken B, Hogeweg L, Prokop M (2009) Компьютерная диагностика при рентгенографии грудной клетки: за пределами узелков.Eur J Radiol 72: 226–230
Статья Google Scholar
Nam JG, Park S, Hwang EJ et al (2018) Разработка и проверка основанного на глубоком обучении алгоритма автоматического обнаружения злокачественных узелков в легких на рентгенограммах грудной клетки. Радиология 290: 218–228
Статья Google Scholar
Закиров А., Кулеев Р., Тимошенко А., Владимиров А. (2015) Современные подходы к компьютерному выявлению заболеваний грудной клетки на рентгенограммах грудной клетки.Appl Math Sci 9: 4361–4369
Google Scholar
Horváth G, Orbán G, Horváth Á et al (2009) CAD-система для скрининга рентгеновской рентгенографии грудной клетки. Всемирный конгресс по медицинской физике и биомедицинской инженерии, 7-12 сентября 2009 г., Мюнхен, Германия. Springer, pp 210–213
Lodwick GS, Keats TE, Dorst JP (1963) Кодирование рентгеновских изображений для компьютерного анализа применительно к раку легких. Радиология 81: 185–200
Радиология 81: 185–200
CAS Статья Google Scholar
Leibstein JM, Nel AL (2006) Выявление туберкулеза на рентгенограммах грудной клетки с использованием методов обработки изображений. Университет Йоханнесбурга
Carrillo-de-Gea JM, García-Mateos G (2010) Обнаружение нормальности / патологии на рентгенограммах грудной клетки с использованием LBP. Int Conf BioInformatics, 20-23 января 2010 г., Валенсия, Испания, стр. 167-172
Chan YH, Zeng YZ, Wu HC, Wu MC, Sun HM (2018) Эффективное обнаружение пневмоторакса при рентгенографии грудной клетки изображения с использованием локального двоичного шаблона и машины векторов поддержки.J Healthc Eng 2018: 1-12
Dunnmon JA, Yi D, Langlotz CP, Ré C, Rubin DL, Lungren MP (2018) Оценка сверточных нейронных сетей для автоматической классификации рентгенограмм грудной клетки. Радиология 290 (2): 537-544
Chaya Devi S, Satya Savithri T (2018) Обзор: О сегментации узелков на задних и передних рентгенограммах грудной клетки. Int J Biomed Imaging 2018: 1-11
Pesce E, Withey SJ, Ypsilantis P-P, Bakewell R, Goh V, Montana G (2019) Обучение обнаружению рентгенограмм грудной клетки, содержащих поражения легких, с использованием сетей визуального внимания.Med Image Anal 53: 26–38
Статья Google Scholar
Annarumma M, Withey SJ, Bakewell RJ, Pesce E, Goh V, Montana G (2019) Автоматическая сортировка рентгенограмм грудной клетки взрослых с помощью глубоких искусственных нейронных сетей. Радиология 291: 196-202
Герас К.Дж., Вольфсон С., Шен И, Ким С., Мой Л., Чо К. (2017) Скрининг рака молочной железы с высоким разрешением с помощью глубоких сверточных нейронных сетей с несколькими проекциями. Препринт arXiv arXiv: 170307047
Wang J, Yang X, Cai H, Tan W, Jin C, Li L (2016) Дискриминация рака груди с микрокальцификациями на маммографии с помощью глубокого обучения. Научный представитель 6: 27327
Научный представитель 6: 27327
CAS Статья Google Scholar
Park S, Lee SM, Lee KH et al (2020) Система обнаружения многоклассовых поражений на рентгенограммах грудной клетки, основанная на глубоком обучении: сравнение с показаниями наблюдателя. Eur Radiol 30: 1359–1368
Статья Google Scholar
Irvin J, Rajpurkar P, Ko M et al (2019) Chexpert: большой набор данных рентгенограммы грудной клетки с метками неопределенности и экспертным сравнением. Препринт arXiv arXiv: 1031
He K, Gkioxari G, Dollár P, Girshick R (2017) Mask R-CNN. IEEE Int Conf. Компьютерное зрение, 22-29 октября 2017 г., Венеция, Италия. pp 2961-2969
Lin T-Y, Goyal P, Girshick R, He K, Dollár P (2017) Потери в фокусе для обнаружения плотных объектов. IEEE Trans Pattern Anal Mach Intell 42 (2): 318-327
Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z (2016) Переосмысление начальной архитектуры компьютерного зрения. IEEE Int Conf. Компьютерное зрение и распознавание образов, 26–1 июня 2016 г., Лас-Вегас, Невада, США. pp 2818-2826
Szegedy C, Liu W, Jia Y et al (2015) Углубление извилин. IEEE Int Conf Computer Vision and Pattern Recognition, 7-12 июня 2015 г., Бостон, Массачусетс, США. pp 1-9
обширная математическая библиотека для JavaScript и Node.js
Math.js поддерживает многомерные матрицы и массивы. Матрицы могут быть создаются, обрабатываются и используются в расчетах. Оба обычных JavaScript могут использоваться массивы, а также тип матрицы, реализованный math.js взаимозаменяемо во всех соответствующих функциях math.js. math.js поддерживает оба плотные и разреженные матрицы.
Массивы и матрицы #
Math.js поддерживает два типа матриц:
-
Массив, обычный массив JavaScript. Можно создать многомерный массив вложенными массивами.
-
Matrix, матричная реализация math.js. МатрицаArray, предоставляя служебные функции для упрощения манипуляции с матрицей, такие какподмножество,размер,изменение размера,клони другие.
В большинстве случаев тип матричного вывода функций определяется
вход функции: массив в качестве входных данных вернет массив , матрицу в качестве входных данных.
вернет Matrix .В случае смешанного ввода возвращается Matrix .
Для функций, в которых тип вывода не может быть определен из
вход, выход определяется опцией конфигурации матрицы ,
который может быть строкой «Матрица» (по умолчанию) или «Массив» .
// создаем массив и матрицу
const array = [[2, 0], [-1, 3]] // Массив
const matrix = math.matrix ([[7, 1], [-2, 3]]) // Матрица
// выполняем вычисление для массива и матрицы
математика.square (array) // Массив, [[4, 0], [1, 9]]
math.square (matrix) // Матрица, [[49, 1], [4, 9]]
// выполняем вычисления со смешанным массивом и вводом матрицы
math.add (array, matrix) // Матрица, [[9, 1], [-3, 6]]
math.multiply (array, matrix) // Матрица, [[14, 2], [-13, 8]]
// создаем матрицу. Тип вывода функциональных определяется
// параметр конфигурации `matrix`
math.ones (2, 3) // Матрица, [[1, 1, 1], [1, 1, 1]]
Создание №
Матрица может быть создана из массива с помощью функции math.матрица . В
предоставленный массив может содержать вложенные массивы для создания многомерной матрицы. При вызове без аргументов пустая матрица будет
созданный.
// создаем матрицы
math.matrix () // Матрица, размер [0]
math.matrix ([0, 1, 2]) // Матрица, размер [3]
math.matrix ([[0, 1], [2, 3], [4, 5]]) // Матрица, размер [3, 2]
Math. js поддерживает обычные массивы. Можно создать несколько размеров
путем вложения массивов друг в друга.
js поддерживает обычные массивы. Можно создать несколько размеров
путем вложения массивов друг в друга.
// создаем массивы
[] // Массив, размер [0]
[0, 1, 2] // Массив, размер [3]
[[0, 1], [2, 3], [4, 5]] // Массив, размер [3, 2]
Матрицы могут содержать разные типы значений: числа, комплексные числа, единиц или строк. Различные типы можно смешивать в одной матрице.
// создаем матрицу со смешанными типами
const a = math.matrix ([2.3, 'привет', math.complex (3, -4), math.единица измерения ('5,2 мм')])
a.subset (math.index (1)) // 'привет'
Существует ряд функций для создания матрицы определенного размера и
содержание: единиц , нулей , идентичность .
// нули создает матрицу, заполненную нулями
math.zeros (3) // Матрица, размер [3], [0, 0, 0]
math.zeros (3, 2) // Матрица, размер [3, 2], [[0, 0], [0, 0], [0, 0]]
math.zeros (2, 2, 2) // Матрица, размер [2, 2, 2],
// [[[0, 0], [0, 0]], [[0, 0], [0, 0]]]
// единицы создают матрицу, заполненную единицами
математика.ones (3) // Матрица, размер [3], [1, 1, 1]
math.multiply (math.ones (2, 2), 5) // Матрица, размер [2, 2], [[5, 5], [5, 5]]
// идентичность создает единичную матрицу
math.identity (3) // Матрица, размер [3, 3], [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
math.identity (2, 3) // Матрица, размер [2, 3], [[1, 0, 0], [0, 1, 0]]
Функции единиц , нулей и идентичности также принимают один массив
или матрица, содержащая размеры для матрицы.Когда входом является массив,
функции выведут массив. Когда входом является матрица, выход будет
быть Матрицей. Обратите внимание, что в случае чисел в качестве аргументов вывод будет
определяется опцией , матрица , как описано в разделе
Массивы и матрицы.
// Массив на входе дает массив на выходе
math.ones ([2, 3]) // Массив, размер [3, 2], [[1, 1, 1], [1, 1, 1]]
math. ones (math.matrix ([2, 3])) // Матрица, размер [3, 2], [[1, 1, 1], [1, 1, 1]]
ones (math.matrix ([2, 3])) // Матрица, размер [3, 2], [[1, 1, 1], [1, 1, 1]]
Диапазоны могут быть созданы с помощью функции диапазон .Функция диапазон есть
вызывается с параметрами start и end и, необязательно, с параметром step.
Начало диапазона включено, конец диапазона исключен.
math.range (0, 4) // [0, 1, 2, 3]
math.range (0, 8, 2) // [0, 2, 4, 6]
math.range (3, -1, -1) // [3, 2, 1, 0]
Расчеты №
Все соответствующие функции math.js поддерживают матрицы и массивы.
// выполняем вычисление по матрице
const a = математика.matrix ([1, 4, 9, 16, 25]) // Матрица, [1, 4, 9, 16, 25]
math.sqrt (a) // Матрица, [1, 2, 3, 4, 5]
// выполняем вычисление в массиве
const b = [1, 2, 3, 4, 5]
math.factorial (b) // Массив, [1, 2, 6, 24, 120]
// умножаем массив на матрицу
const c = [[2, 0], [-1, 3]] // Массив
const d = math.matrix ([[7, 1], [-2, 3]]) // Матрица
math.multiply (c, d) // Матрица, [[14, 2], [-13, 8]]
// добавляем число в матрицу
математика.add (c, 2) // Массив, [[4, 2], [1, 5]]
// вычисляем определитель матрицы
math.det (c) // 6
math.det (d) // 23
Размер и размеры #
Math.js использует геометрические размеры:
- Скаляр нульмерен.
- Вектор одномерный.
- Матрица бывает двумерной или многомерной.
Размер матрицы можно вычислить с помощью функции size .Функция размер возвращает Matrix или Array , в зависимости от параметра конфигурации matrix .
Кроме того, у матриц есть функция размером , которая всегда возвращает
массив.
// получаем размер скаляра
math.size (2.4) // Матрица, []
math.size (math.complex (3, 2)) // Матрица, []
math.size (math.unit ('5,3 мм')) // Матрица, []
// получаем размер одномерной матрицы (вектора) и строки
математика.size ([0, 1, 2, 3]) // Массив, [4]
math. size ('hello world') // Матрица, [11]
// получаем размер двумерной матрицы
const a = [[0, 1, 2, 3]] // Массив
const b = math.matrix ([[0, 1, 2], [3, 4, 5]]) // Матрица
math.size (a) // Массив, [1, 4]
math.size (b) // Матрица, [2, 3]
// матрицы имеют размер функции (всегда возвращает массив)
b.size () // Массив, [2, 3]
// получаем размер многомерной матрицы
const c = [[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]]
математика.size (c) // Массив, [2, 2, 3]
size ('hello world') // Матрица, [11]
// получаем размер двумерной матрицы
const a = [[0, 1, 2, 3]] // Массив
const b = math.matrix ([[0, 1, 2], [3, 4, 5]]) // Матрица
math.size (a) // Массив, [1, 4]
math.size (b) // Матрица, [2, 3]
// матрицы имеют размер функции (всегда возвращает массив)
b.size () // Массив, [2, 3]
// получаем размер многомерной матрицы
const c = [[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]]
математика.size (c) // Массив, [2, 2, 3]
Изменение размера #
Размер матриц можно изменить с помощью их функции resize . Эта функция называется
с массивом с новым размером в качестве первого аргумента и принимает необязательный
значение по умолчанию. По умолчанию для новых записей будет установлено значение 0 , но это возможно.
передать другое значение по умолчанию, например null , чтобы четко указать, что
записи не были заданы явно.
const a = математ.matrix () // Матрица, размер [0], []
a.resize ([2, 3]) // Матрица, размер [2, 3], [[0, 0, 0], [0, 0, 0]]
a.resize ([2, 2, 2]) // Матрица, размер [2, 2, 2],
// [[[0, 0], [0, 0]], [[0, 0], [0, 0]]]
const b = math.matrix ()
b.resize ([3], 7) // Матрица, размер [3], [7, 7, 7]
b.resize ([5], 9) // Матрица, размер [5], [7, 7, 7, 9, 9]
b.resize ([2]) // Матрица, размер [2], [7, 7]
Наружные размеры матрицы можно сжать с помощью функции сжать .Когда
получение или установка подмножества в матрице, подмножество автоматически сжимается
или без сжатия.
// сжать матрицу
const a = [[[0, 1, 2]]]
math.squeeze (a) // [0, 1, 2]
math.squeeze ([[3]]) // 3
// подмножества автоматически сжимаются
const b = math.matrix ([[0, 1], [2, 3]])
b.subset (math.index (1, 0)) // 2
Получение или замена подмножеств #
Подмножества матрицы могут быть извлечены или заменены с помощью функции subset .Матрицы имеют функцию подмножества , которая применяется к самой матрице: Matrix.. И для матриц, и для массивов
статическая функция  subset (индекс [, замена])
subset (индекс [, замена]) подмножества (матрица, индекс [, замена]) может использоваться.
Если параметр заменен на , функция заменит подмножество
в матрице, и если нет, будет возвращено подмножество матрицы.
Подмножество может быть определено с помощью индекса . Индекс содержит одно значение
или набор значений для каждого измерения матрицы.Индекс может быть
создается с помощью функции , индекс .
Матричные индексы в math.js отсчитываются от нуля, как и в большинстве языков программирования.
включая сам JavaScript.
Обратите внимание, что математические приложения, такие как Matlab и Octave, работают по-разному, поскольку они используют индексы на основе единицы.
// создаем матрицы
const a = [0, 1, 2, 3]
const b = [[0, 1], [2, 3]]
const c = math.zeros (2, 2)
const d = math.matrix ([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
const e = math.matrix ()
// получаем подмножество
математика.subset (a, math.index (1)) // 1
math.subset (a, math.index ([2, 3])) // Массив, [2, 3]
math.subset (a, math.index (math.range (0,4))) // Массив, [0, 1, 2, 3]
math.subset (b, math.index (1, 0)) // 2
math.subset (b, math.index (1, [0, 1])) // Массив, [2, 3]
math.subset (b, math.index ([0, 1], 0)) // Матрица, [[0], [2]]
// получаем подмножество
d.subset (math.index ([1, 2], [0, 1])) // Матрица, [[3, 4], [6, 7]]
d.subset (math.index (1, 2)) // 5
// заменяем подмножество.Подмножество будет применено к клону матрицы
math.subset (b, math.index (1, 0), 9) // Массив, [[0, 1], [9, 3]]
math.subset (b, math.index (2, [0, 1]), [4, 5]) // Массив, [[0, 1], [2, 3], [4, 5]]
// заменяем подмножество. Подмножество будет применено к самой матрице
c.subset (math.index (0, 1), 1) // Матрица, [[0, 1], [0, 0]]
c.subset (math.index (1, [0, 1]), [2, 3]) // Матрица, [[0, 1], [2, 3]]
e.resize ([2, 3], 0) // Матрица, [[0, 0, 0], [0, 0, 0]]
е. subset (math.index (1, 2), 5) // Матрица, [[0, 0, 0], [0, 0, 5]]
subset (math.index (1, 2), 5) // Матрица, [[0, 0, 0], [0, 0, 5]]
Итерация #
Матрицы содержат функции , отображение и для каждого для перебора всех элементов
(многомерная) матрица. Функция обратного вызова map и forEach имеет
три параметра: значение (значение текущего итерационного элемента), индекс (массив со значением индекса для каждого измерения) и матрица (
матрица повторяется).Этот синтаксис аналогичен карте и для каждого функций собственных массивов JavaScript, за исключением того, что индекс - это не число, а
Массив с числами для каждого измерения.
const a = math.matrix ([[0, 1], [2, 3], [4, 5]])
// Следующая итерация выведет в консоль следующее:
// значение: 0 индекс: [0, 0]
// значение: 1 индекс: [0, 1]
// значение: 2 индекс: [1, 0]
// значение: 3 индекс: [1, 1]
// значение: 4 индекс: [2, 0]
// значение: 5 индекс: [2, 1]
а.forEach (функция (значение, индекс, матрица) {
console.log ('значение:', значение, 'индекс:', индекс)
})
// Применяем преобразование к матрице
const b = a.map (функция (значение, индекс, матрица) {
вернуть math.multiply (math.sin (значение), math.exp (math.abs (значение)))
})
console.log (b.format (5)) // [[0, 2.2874], [6.7188, 2.8345], [-41.32, -142.32]]
// Создаем матрицу с совокупностью всех элементов
пусть count = 0
const cum = a.map (функция (значение, индекс, матрица) {
count + = значение
счетчик возврата
})
приставка.log (cum.toString ()) // [[0, 1], [3, 6], [10, 15]]
Типы складских помещений #
Math.js поддерживает как плотные, так и разреженные матрицы. Разреженные матрицы эффективны для матриц, в основном содержащих нули. В этом случае они экономят много памяти, и вычисления могут быть намного быстрее, чем для плотных матриц.
Math.js поддерживает два типа матриц:
- Плотная матрица (
«плотная»,по умолчанию) Обычная плотная матрица, поддерживающая многомерные матрицы. Это тип матрицы по умолчанию.
Это тип матрицы по умолчанию. - разреженная матрица (
'разреженная'): реализация двумерной разреженной матрицы.
Тип матрицы можно выбрать при создании матрицы с помощью функций построения: матрица , diag , identity , единиц и нулей .
// создаем разреженные матрицы
const m1 = math.matrix ([[0, 1], [0, 0]], 'разреженный')
const m2 = math.identity (1000, 1000, 'разреженный')
API №
Все соответствующие математические функции.js поддерживает матрицы и массивы. Такие функции, как math.add и math.subtract , math.sqrt , обрабатывают матрицы поэлементно. Существует набор функций, специально предназначенных для создания матриц или управления ими, например:
- Функции, такие как
math.matrixиmath.sparse,math.ones,math.zerosиmath.identityдля создания матрицы. - Функции, такие как
math.subsetиmath.индекс, чтобы получить или заменить часть матрицы - Такие функции, как
math.transposeиmath.diagдля управления матрицами.
Полный список матричных функций доступен на странице справки по функциям.
В math.js доступны два типа классов матриц для хранения плотных и разреженных матриц. Хотя они содержат общедоступные функции, задокументированные следующим образом, напрямую использовать следующий API не рекомендуется . По возможности предпочитайте использовать функции в пространстве имен «math».
.

 2×5.3
2×5.3 3 диаметром от 14 до 15, шириной от 5.5 до 5.5 и профилем от ET46 до ET46как у Mitsubishi Colt
3 диаметром от 14 до 15, шириной от 5.5 до 5.5 и профилем от ET46 до ET46как у Mitsubishi Colt Len (A) возвращает только одну переменную. Редактировать: close = dataobj.get_data(timestamps, symbols, closefield) Это (я предполагаю) генерация матрицы целых чисел (менее вероятных строк). Мне нужно найти размер этой матрицы, чтобы я мог выполнить…
Len (A) возвращает только одну переменную. Редактировать: close = dataobj.get_data(timestamps, symbols, closefield) Это (я предполагаю) генерация матрицы целых чисел (менее вероятных строк). Мне нужно найти размер этой матрицы, чтобы я мог выполнить…

 ones (math.matrix ([2, 3])) // Матрица, размер [3, 2], [[1, 1, 1], [1, 1, 1]]
ones (math.matrix ([2, 3])) // Матрица, размер [3, 2], [[1, 1, 1], [1, 1, 1]]
 size ('hello world') // Матрица, [11]
// получаем размер двумерной матрицы
const a = [[0, 1, 2, 3]] // Массив
const b = math.matrix ([[0, 1, 2], [3, 4, 5]]) // Матрица
math.size (a) // Массив, [1, 4]
math.size (b) // Матрица, [2, 3]
// матрицы имеют размер функции (всегда возвращает массив)
b.size () // Массив, [2, 3]
// получаем размер многомерной матрицы
const c = [[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]]
математика.size (c) // Массив, [2, 2, 3]
size ('hello world') // Матрица, [11]
// получаем размер двумерной матрицы
const a = [[0, 1, 2, 3]] // Массив
const b = math.matrix ([[0, 1, 2], [3, 4, 5]]) // Матрица
math.size (a) // Массив, [1, 4]
math.size (b) // Матрица, [2, 3]
// матрицы имеют размер функции (всегда возвращает массив)
b.size () // Массив, [2, 3]
// получаем размер многомерной матрицы
const c = [[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10, 11]]]
математика.size (c) // Массив, [2, 2, 3]
 subset (math.index (1, 2), 5) // Матрица, [[0, 0, 0], [0, 0, 5]]
subset (math.index (1, 2), 5) // Матрица, [[0, 0, 0], [0, 0, 5]]
 Это тип матрицы по умолчанию.
Это тип матрицы по умолчанию.