Обозначение диагонали: Основные геометрические фигуры 🟢🟨🔺 и их названия — Главная

Содержание

Диагональ телевизора в см и дюймах таблица

Диагональ экрана определяет размеры телевизора и играет большую роль при выборе телевизионного приемника. От правильности выбора размера экрана зависит комфортность просмотра видео на телевизоре.

В телевизионной индустрии принято указывать размер диагонали экрана, а не размеры телевизора. На упаковке или в инструкции вы, разумеется, найдете и размеры тв, но главным считается все-таки диагональ дисплея. Эта диагональ указывается и в названии модели. В маркировке телевизора размер диагонали экрана указывается в дюймах.

Что такое дюйм?

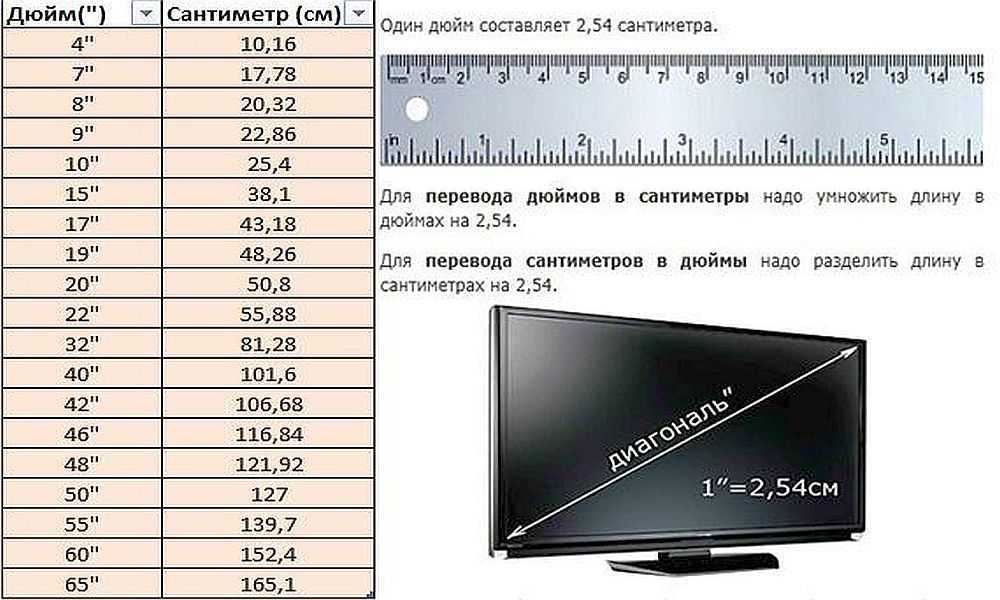
Сколько будет, если перевести 1 дюйм в см? Как известно 1 дюйм равняется 2,54 сантиметра. Дюйм (от нидерл. duim — большой палец) — название для единицы измерения расстояния в европейских неметрических системах мер. Сегодня под дюймом чаще всего понимают английский дюйм (англ. inch), равный 2,54 см ровно.

Именно с 1958 года решили принять значение дюйма ровно в 25,4 мм, а до этого после запятой было намного больше знаков. Соотношение дюймов и сантиметров следующее:

1 дюйм = 2,54 см = 25,4 мм
1 см = 0,3937 дюйма
1 м = 39,37 дюйма

В английской системе мер 1 дюйм = 12 линий = 72 точки = 1/12 фута = 1/36 ярда.

После принятия международной системы единиц измерения СИ, дюймы считаются устаревшим обозначением, которое должно быть постепенно выведена из употребления. Но, несмотря на это дюймы продолжают применяться в технике при указании калибров и форм-факторов, для совместимости с давно устоявшимися техническими решениями. При этом в качестве знака дюймов используется двойной штрих (кавычка «).

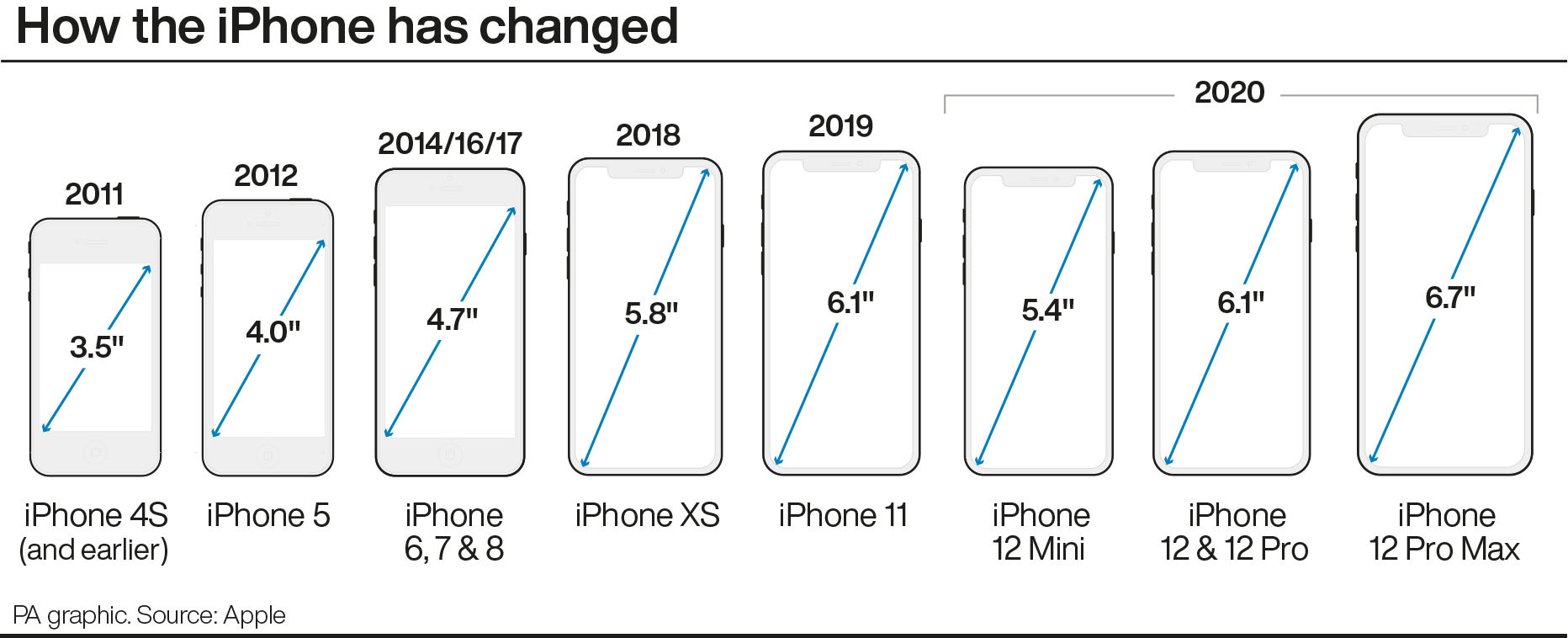
В телевизионной технике в дюймах выражают диагональ экрана, которая измеряется как расстояние между противоположными углами матрицы. Например, 37″ означает экран с диагональю в 37 дюймов или 37х2,54=93,98 см.

Простой конвертер длины для перевода дюймов в сантиметры и см в дюймы:

Размеры экрана и диагональ

Размеры телевизоров в зависимости от диагонали, таблица в см представлена ниже.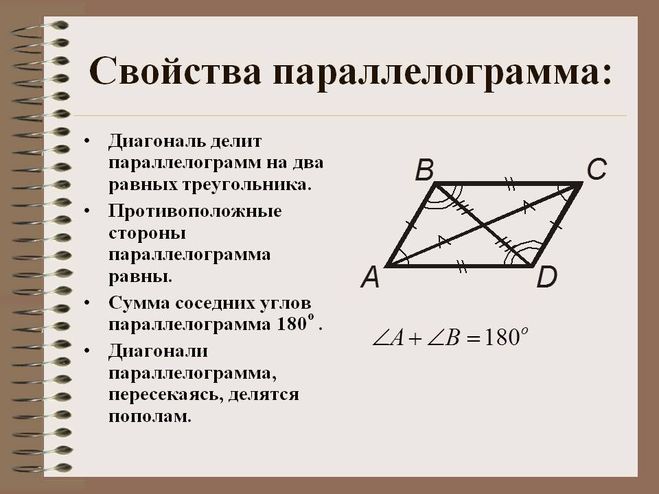 Но там размеры дисплея, а для получения размеров телевизора нужно добавить несколько миллиметров или сантиметров.

Диагональ телевизора в см и дюймах, таблица перевода величин:

Диагональ экрана дюймы и сантиметры		Ширина экрана сантиметры	Высота экрана сантиметры
10″	25.4	22.1	12.5
11″	27.9	24.4	13.7
12″	30.5	26.6	14.9
13″	33.0	28.8	16.2
14″	35.6	31.0	17.4
15″	38.1	33.2	18.7
16″	40.6	35.4	19.2
17″	43.2	37.6	21. 2
18″	45.7	39.9	22.4
19″	48.3	42.1	23.7
20″	50.8	44.3	24.9
21″	53.3	46.5	26.2
22″	55.9	48.7	27.4
23″	58.4	50.9	28.6
24″	61.0	53.1	29.9
25″	63.5	55.4	31.1
26″	66.0	57.6	32.4
27″	68.6	59.8	33.6
28″	71.0	62.0	34.9
29″	73.7	64.2	36.1
30″	76. 2	66.4	37.4
31″	78.7	68.6	38.6
Диагональ экрана дюймы и сантиметры		Ширина экрана сантиметры	Высота экрана сантиметры
32″	81.3	70.8	39.9
33″	83.8	73.1	41.1
34″	86.4	75.3	42.3
35″	88.9	77.5	43.6
36″	91.4	79.7	44.8
37″	94	81.9	46.1
38″	96.5	84.1	47.3
39″	99.1	86.3	48.6
40″	101.6	88. 6	49.8
41″	104.1	90.8	51.1
42″	106.7	93	52.3
43″	109.2	95.2	53.6
44″	111.8	97.4	54.8
45″	114.3	99.6	56
46″	116.8	101.8	57.3
47″	119.4	104.1	58.5
48″	121.9	106.3	59.8
49″	124.5	108.5	61
50″	127	110.7	62.3
51″	129.5	112.9	63.5
52″	132.1	115. 1	64.8
53″	134.6	117.3	66
54″	137.2	119.6	67.2
55″	139.7	121.8	68.5
Диагональ экрана дюймы и сантиметры		Ширина экрана сантиметры	Высота экрана сантиметры
56″	142.2	124	69.7
57″	144.8	126.2	71
58″	147.3	128.4	72.2
59″	150	130.6	73.5
60″	152.4	132.8	74.7
61″	154.9	135	76
62″	157.5	137. 3	77.2
63″	160	139.5	78.5
64″	162.6	141.7	79.7
65″	165.1	143.9	80.9
66″	167.6	146.1	82.2
67″	170.2	148.3	83.4
68″	172.7	150.5	84.7
69″	175.3	152.8	85.9
70″	177.8	155	87.2
71″	180.3	157.2	88.4
72″	182.9	159.4	89.7
73″	185.4	161.6	90.9
74″	188	163. 8	92.2
75″	190.5	166	93.4
76″	193	168.3	94.6
77″	195.6	170.5	96
78″	198.1	172.7	97.1
79″	200.7	174.9	98.4
80″	203.2	177.1	99.6
81″	205.7	179.3	100.9
82″	208.3	181.5	102.1
83″	210.8	183.8	103.4
Диагональ экрана дюймы и сантиметры		Ширина экрана сантиметры	Высота экрана сантиметры
84″	213.4	186	104. 6
85″	215.9	188.2	105.9
86″	218.4	190.4	107.1
87″	221	192.6	108.3
88″	223.5	194.8	109.6
89″	226.1	197	110.8
90″	228.6	199.2	112.1
91″	231.1	201.5	113.3
92″	233.7	203.8	114.6
93″	236.2	205.9	115.8
94″	238.8	208.1	117.1
95″	241.3	210.3	118.3
96″	243.8	212. 5	119.6
97″	246.4	214.7	120.8
98″	248.9	217	122
99″	251.5	219.2	123.3
100″	254	221.4	124.5
101″	256.5	223.6	125.8
102″	259.1	225.8	127
103″	261.6	228	128.3
104″	264.2	230.2	129.5
105″	266.7	232.5	130.8
106″	269.2	234.7	132
107″	271.8	236.9	133.2
108″	274. 3	239.1	134.5
109″	276.9	241.3	135.7
110″	279.4	243.5	137

Например, если взять телевизор 32 дюйма, то это сколько будет в см? Воспользовавшись расчетами в конверторе, получим, что 32 дюйма в сантиметрах будет 81,3. Другой пример, переводим 22 дюйма в см, получаем 55,9 сантиметра. А если взять диагональ 42 дюйма, то получим 106,7 сантиметра.

Разные размеры телевизора

Решение высшей математики онлайн

‹— Назад

Определение 14.1 Матрицей размеров называется прямоугольная таблица чисел, содержащая строк и столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Обычно принято обозначать матрицы большими буквами, а саму таблицу чисел заключать в круглые скобки. Например, — матрица размеров , — матрица размеров , или другими словами, матрица-столбец, — матрица размеров , или матрица-строка.

Иногда вместо круглых скобок в записи матрицы используют квадратные или двойные прямые линии. Например, или .

Если элементы матрицы обозначаются буквами, то для этого обозначения используется та же буква, что и для обозначения матрицы, только не большая, а малая, и эта буква снабжается двумя индексами. Например, матрицу размеров можно записать в виде

В этой записи означает, что элемент находится в строке с номером и столбце с номером , то есть первый индекс указывает номер строки, а второй — номер столбца. Например, в матрице

, .

Наряду с указанным обозначением элементов матрицы используется также обозначение , в котором номер строки указывает верхний индекс, а номер столбца — нижний.

Укажем основные типы матриц.

Если число строк матрицы равно числу столбцов, то матрица называется квадратной. Число строк или, что то же самое, число столбцов в ней называется порядком матрицы.

Если все элементы матрицы равны нулю, то матрица называется нулевой. Нулевая матрица обозначается обычной цифрой 0. Как правило, из контекста ясно, является ли этот 0 числом или матрицей.

Совокупность элементов квадратной матрицы, расположенных на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю матрицы. Например, в матрице главную диагональ образуют числа . Отметим, что при обозначении элементов матрицы буквами с двумя индексами у элементов главной диагонали и только у них индексы будут равны друг другу. Так у квадратной матрицы порядка элементами главной диагонали являются элементы , .

Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной. Примеры диагональных матриц:

Квадратная матрица называется верхней треугольной (нижней треугольной), если все ее элементы, стоящие ниже (выше) главной диагонали, равны нулю. Например, верхние треугольные матрицы:

Нижние треугольные матрицы:

Верхняя треугольная матрица иногда называется правой треугольной, а нижняя треугольная — левой треугольной.

Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны 1. Для обозначения единичной матрицы обычно используется буква . Порядок матрицы при этом обычно ясен из контекста. Например, — единичная матрица третьего порядка.

Из определения единичной матрицы видно, что ее элементы равны нулю, если индексы различны, и равны 1, если индексы совпадают. В математике таким свойством обладает величина , называемая символом Кронекера:

Поэтому .

Две матрицы называются равными, если они имеют одинаковые размеры и элементы, стоящие на одинаковых местах, равны друг другу.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Как найти диагональ матрицы?

Британский математик Артур Кейли был первым человеком, разработавшим алгебраический аспект матрицы. После этого психиат Гейзенберг использовал матрицы как инструмент для объяснения своего знаменитого квантового принципа. Изучение матриц зародилось при решении различных типов простых и сложных линейных задач, решение которых без матриц затруднительно. Прямоугольный массив mn чисел в виде m горизонтальных линий, называемых строками, и n вертикальных линий, называемых столбцами, называется матрицей порядка m x n. Эти массивы заключены в [ ] или ( ) или || || . Каждое число матрицы m x n известно как элемент матрицы. Матрица обычно обозначается заглавными буквами, а ее элемент обозначается маленькими буквами с суффиксом ij, который указывает на номер строки и столбца, т. е. aij, называется элементами матрицы A.

Элементы матрицы могут быть скалярными или векторными величинами.
Матрица — это всего лишь набор чисел; она не имеет определенного значения. т. е. [5] ≠ 5.

Некоторые важные термины, относящиеся к матрице

Элементы матрицы: Каждое из M, N чисел матрицы называется элементом или элементом матрицы.
Обозначение матрицы: Матрица обычно представлена символами [a _ij ] или (a _ij ) или ||a _ij ||. Матрица обозначается одной заглавной буквой, такой как A, B, C и т. д.
Порядок матрицы: Говорят, что матрица, имеющая m строк и n столбцов, является матрицей порядка m x n.

Диагональные элементы матрицы

Элемент aij матрицы A = [a _ij ] является диагональным элементом матрицы, если i = j, например, когда суффиксы строк и столбцов равны. Таким образом, ₁₁ , ₂₂ , a ₃₃ , a ₄₄ , … и так далее — диагональные элементы матрицы A = [a _ij ].

Главная диагональ матрицы

Главная диагональ также известна как ведущая диагональ. Диагональ квадратной матрицы, идущая от верхних левых объектов к нижним правым объектам, является главной диагональю матрицы.

Здесь элементы главной диагонали не равны нулю.

Диагональ счетчика

Также называется антидиагональю матрицы. Диагональ квадратной матрицы, идущая от верхних правых объектов к нижним левым объектам, называется встречной диагональю матрицы.

Здесь диагональные элементы счетчика не равны нулю.

Примечание: Выше мы рассмотрели примеры в главной и встречной диагонали. Элементы матрицы, отличные от диагональных, считаются нулями для лучшего понимания.

Примеры задач

Вопрос 1. Найдите диагональный элемент приведенной ниже матрицы.

Решение:

Как мы знаем, найти диагональ матрицы или диагональных элементов несложная задача; это просто базовая практика работы с матрицами. Если бы кто-нибудь сказал нам найти диагональный элемент, в результате мы нашли бы только главную диагональ. который проходит от верхних левых объектов к нижним правым объектам
Диагональный элемент матрицы,
a ₁₁ = 9, _{a ₂₂ = 8, a ₃₃ = 1}

Вопрос 2: Найдите след матрицы A, приведенный ниже.

Решение:

След матрицы: на самом деле это сумма элементов главной диагонали.
tr(A) = ₁₁ + ₂₂ + _33;
Итак, после наблюдения за матрицей
можно сказать, что ₁₁ = 1, a ₂₂ = 2, a ₃₃ = 5
tr(a) = 1 + 2 + 5 = 8

Вопрос 3. Найдите обратную диагональную матрицу :

Решение:

Определитель матрицы A,
|A| = -30
Сопряженная матрица A,
Мы знаем, что обратная матрица A равна: A ^-1 = \frac{adj(A)}{|A|}

Вопрос 4: Найдите значение ₁₁ + a ₂₃ – a ₂₂ + a ₃₁ из приведенной ниже матрицы.

Решение:

Мы знаем стандартный матричный синтаксис.

Сравнивая его с нашей матрицей, мы можем сказать, 4 31 = 5
Требуемый результат: a ₁₁ + ₂₃ – ₂₂ + a ₃₁ = 8 + 9 – 2 – 5 = 10

Вопрос 5. Найдите произведение диагонального элемента следующей матрицы:

Решение: 9001 4

Диагональный элемент матрица выше равна 2, 4 и 1 соответственно.
Произведение диагоналей: 2 × 4 × 1 = 8
Определитель матрицы A,
|A| = 5 (1 – 32) – 2 (16 – 4) + 6 (16 – 2)
|A| = 5(-31) – 2(12) + 6(14)
|A| = -155 – 24 + 84 = -95
Вопрос 7: Найдите сумму встречной диагонали матрицы , общего элемента и встречной диагонали:
Решение:
90 094
Мы знаем квадратную матрицу от верхних правых объектов к нижним левым объектам проходят встречные диагонали матрицы.
Таким образом, элементы встречной диагонали равны
a ₁₃ = 5 a ₂₂ = 2 a ₃₁ = 5
Общий элемент главной и встречной диагонали равен 2.
90 112
Идентичный, диагональный, симметричный и треугольные матрицы
Дом
О
Страницы математики и статистики
R Программирование
Предметы Python

Здравствуйте. Этот пост будет о некоторых матрицах в их специальных формах. Рассматриваемые матрицы: единичные, диагональные, симметричные и треугольные. Эти темы обычно встречаются во введении в курс линейной алгебры. Предполагается, что кто-то знает транспонирование матрицы, обратную матрицу и матричное умножение.

Темы

Матрица идентичности
Диагональные матрицы
Симметричные матрицы
Треугольные матрицы

Единичная матрица

Единичная матрица — одна из самых важных матриц в линейной алгебре. Напомним, что линейная алгебра помогает нам решать линейные системы уравнений, такие как:

\[\displaystyle \begin{array} {lcl} 2x + y & = & 2 \\ x — y & = & 1 \\ \end {массив} \]

Коэффициенты переменных \(x\) и \(y\) являются элементами матрицы 2 на 2. Когда мы решаем приведенную выше линейную систему, мы получаем такую форму, как \ (x = … \) и \ (y = … \). В матричной форме мы представляем это единичной матрицей \(I\).

\[\displaystyle I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ \end{bmatrix}\]

В общем случае единичная матрица размера n на n имеет вид :

\[\displaystyle \begin{bmatrix} 1 & 0 & 0 & \dots & 0 \\ 0 & 1 & 0 & \dots & 0 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \ddots & 0\\ 0 & 0 & 0 & \dots & 1 \end{bmatrix}\] 9{-1} = I\)). Еще одна интересная особенность заключается в том, что единичная матрица является идемпотентной. То есть \(II = I\).

Диагональные матрицы

Напомним, что матрица размера n на n имеет вид:

\[\displaystyle \begin{b матрица} x_{11} и x_{12} и x_{13} & \dots & x_{1n} \\ x_{21} & x_{22} & x_{23} & \dots & x_{2n} \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ x_{(n-1)1} & x_{(n-1)2} & x_{(n-1)3} & \ddots & x_{(n-1)n}\\ x_{n1} & x_ {n2} & x_{n3} & \dots & x_{nn} \end{bmatrix}\]

Основная диагональ идет сверху слева направо и содержит записи \(x_{11}, x_{22} \text{ to } x_{nn}\).
Диагональная матрица имеет (ненулевые) элементы только на главной диагонали, а все элементы вне главной диагонали являются элементами с 0. Примером диагональной матрицы является единичная матрица, упомянутая ранее. Диагональная матрица \(D\) показана ниже.

\[\displaystyle D = \begin{bmatrix} d_{1} & 0 & 0 & \dots & 0 \\ 0 & d_{2} & 0 & \dots & 0 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \ddots & 0\\ 0 & 0 & 0& \dots & d_{n} \end{bmatrix}\] 9{Т}\).
Например, если бы мы транспонировали матрицу, поменяв местами первую строку с первым столбцом и вторую строку со вторым столбцом матрицы A, где

\[\displaystyle A = \begin{bmatrix} 2 & 1 \\ 1 & -5 \\ \end{bmatrix}\]

мы все равно получим ту же матрицу. Вхождение единиц вне главной диагонали в этом случае одинаково.
В общем случае матрица A является симметричной, если элемент \(A_{ij}\) совпадает с элементом \(A_{ji}\), где \(i\) относится к номеру строки сверху и \( j\) — номер столбца слева направо. Записи с \(i = j\) находятся на главной диагонали.
Другой пример симметричной матрицы:

\[\displaystyle A = \begin{bmatrix} 2 & 1 & 4\\ 1 & -5 & 3 \\ 4 & 3 & 9 \\ \end{ bmatrix}\]

, где в недиагональных элементах мы имеем \(a_{12} = a_{21} = 1\), \(a_{13} = a_{31} = 4\) и \( a_{23} = a_{32} = 3\)
Если матрица \(A\) симметрична, то обратная матрица \(A\) симметрична.
Предположим, что матрицы \(A\) и \(B\) симметричны и имеют одинаковый размер, где \(k\) является скаляром, тогда мы имеем: 9{T}\) симметрична.
\(A + B\) и \(A — B\) симметричны. \(kA\) симметрична.

Треугольные матрицы (нижняя и верхняя треугольные)

Теперь рассмотрим треугольные матрицы, которые могут быть либо нижними треугольными, либо верхними треугольными. Для начала у нас есть пример нижней треугольной матрицы и верхней треугольной матрицы (вариант 5 на 5).

\[\displaystyle L = \begin{bmatrix} l_{11} & 0 & 0 & 0 & 0 \\ l_{21} & l_{22} & 0 & 0 & 0 \\ l_{31} & l_{32} & l_{33} & 0 & 0 \\ l_{41} & l_{42} & l_{43} & l_{44} & 0\\ l_{51} & l_{52} & l_ {53} & l_{54} & l_{55} \end{bmatrix}\]

\[\displaystyle U = \begin{bmatrix} u_{11} & u_{12} & u_{13} & u_{14} & u_{15} \\ 0 & u_{22} & u_{ 23} & u_{24} & u_{25} \\ 0 & 0 & u_{33} & u_{34} & u_{35} \\ 0 & 0 & 0 & u_{44} & u_{45}\ \ 0 & 0 & 0 & 0 & u_{55} \end{bmatrix}\]

Можно заметить, что и в нижней, и в верхней треугольных матрицах главная диагональ (строка \(i\) = столбец \(j\)) с ненулевыми элементами.
Обозначение диагонали: Основные геометрические фигуры 🟢🟨🔺 и их названия