что это такое и чем оно отличается от размытия объектива
Размытие может повлиять на изображение как в лучшую, так и в плохую сторону. Некоторые используют его для сокрытия областей на фотографии для конфиденциальности, а другие используют его для раскрытия красоты изображения. Между тем, вы можете использовать различные типы эффектов размытия в соответствии с вашими потребностями. Эффект размытия, который может добавить художественный эффект вашей фотографии, — это размытие по Гауссу.
Этот эффект на фото очень полезен. Это может уменьшить шум и зернистость, которые влияют на ваши изображения. Это может быть очень полезно при наложении объекта на фотографию, которая слишком занята или на изображении много чего происходит. Эффект размытия по Гауссу может помочь вам смягчить части фотографии, чтобы объект, который вы накладываете, выделялся. Узнайте больше о что такое размытие по Гауссу прочитав ниже.
- Часть 1. Что такое размытие по Гауссу
- Часть 2.
 Как вы используете размытие по Гауссу
Как вы используете размытие по Гауссу - Часть 3. Размытие по Гауссу против размытия. Сравнение размытия объектива
- Часть 4. Как удалить размытие с изображения
- Часть 5. Часто задаваемые вопросы о размытии по Гауссу
Часть 1. Что такое размытие по Гауссу
Размытие по Гауссу используется при обработке изображений, также известном как сглаживание по Гауссу. Фильтр был назван в честь ученого-математика Карла Фридриха Гаусса. Основная цель размытия по Гауссу — уменьшить шум на изображении и детализацию. Проще говоря, этот эффект размытия подходит для того, чтобы скрыть области изображения, не портя их и не выставляя напоказ красоту изображения.
Это также полезно, когда вы пытаетесь имитировать или имитировать глубину резкости. С помощью этого эффекта размытия вы сможете контролировать, что находится в фокусе, а что нет. Этот метод обычно достигается с помощью камеры высокого класса с дорогими объективами.
Часть 2. Как вы используете размытие по Гауссу
Размытие по Гауссу легко реализовать на фотографии. Фактически, некоторые инструменты для редактирования фотографий включают эту функцию для редактирования профессиональных фотографий. И инструмент для редактирования фотографий, который развивается с течением времени, — это Photoshop. Он поставляется с множеством впечатляющих функций для достижения выдающихся результатов. Что еще более важно, вы можете выполнить размытие по Гауссу с помощью этой программы. Если вы хотите применить к своим изображениям размытие по Гауссу в Photoshop, выполните следующие действия.
Шаг 1:
Перейдите на страницу загрузки программы и получите ее установщик. Вы можете получить его операционные системы Windows и macOS. Пожалуйста, соблюдайте минимальные требования и следите за тем, чтобы ваш компьютер соответствовал необходимым требованиям.
Шаг 2:
Теперь откройте новый проект и добавьте фотографию, которую хотите отредактировать или к которой хотите применить размытие по Гауссу.
Шаг 3:
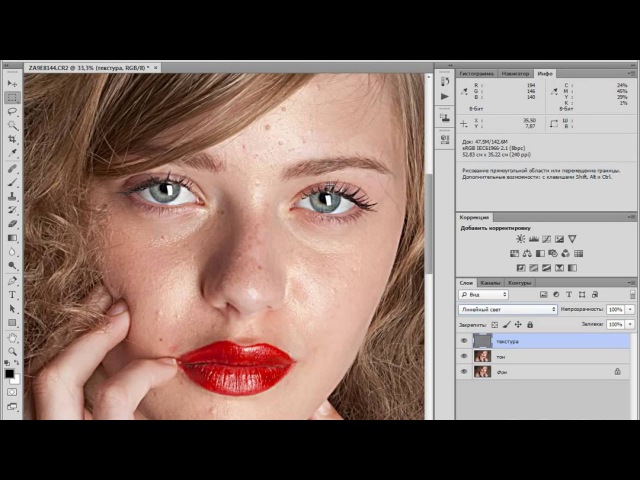
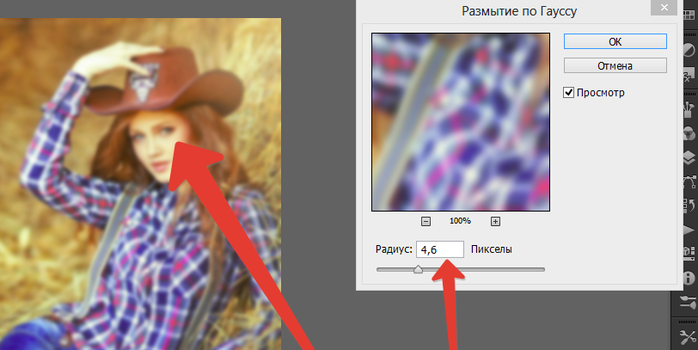
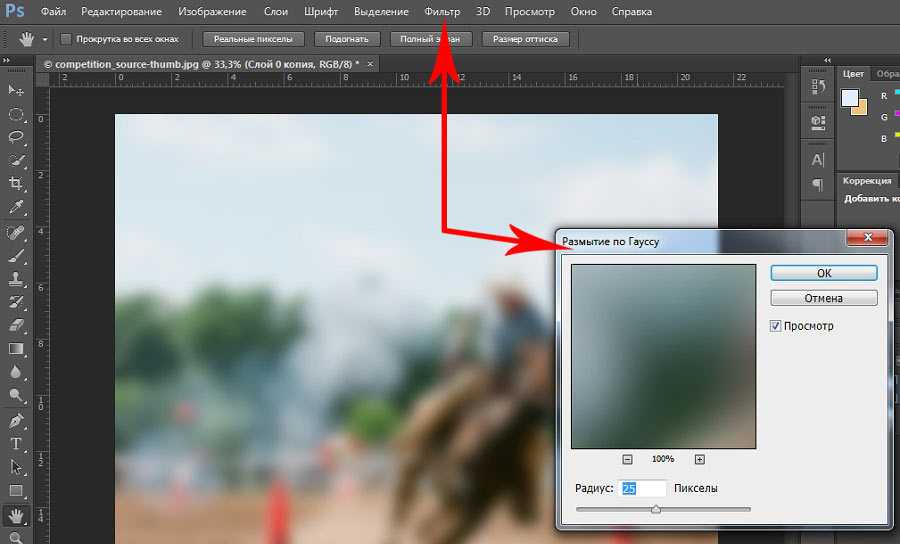
Есть два метода, с помощью которых вы можете реализовать размытие по Гауссу. Один из них заключается в применении эффекта ко всему изображению. Другой способ — выбрать объект и размыть фон. В верхнем меню нажмите на опцию «Фильтр». Затем наведите курсор на Blur и выберите Размытие по Гауссу.
Шаг 4:
Если вы уже удовлетворены результатами фотографии, экспортируйте изображение в соответствии с вашими требованиями. Перейдите к Файл> Экспорт> Экспортировать каки измените настройки экспорта в соответствии с вашими предпочтениями.
Часть 3. Размытие по Гауссу VS. Сравнение размытия объектива
В этой части основное внимание будет уделено различению эффектов Gaussian и Lens Blur. В основном, мы обсудим основы обоих эффектов фильтров. Поэтому, пожалуйста, прочитайте абзац ниже, если вы хотите понять, что такое размытие по Гауссу и размытие объектива.
Размытие по Гауссу
Размытие по Гауссу в основном смягчает все на фотографии. Это фильтр нижних частот, который включает в себя удаление экстремальных выбросов для достижения четных значений пикселей. Этот эффект размытия помогает эффективно свести к минимуму шум на фотографии, особенно когда фотография слишком занята. Он может выделить текст, объект или человека, смягчив изображение. Одна вещь, которую следует помнить о размытии по Гауссу, заключается в том, что оно реализует большую интенсивность размытия, что может снизить резкость.
Размытие линз
С точки зрения размытия объектива достигается эффект боке с малой глубиной резкости. Он выделяет передний план и размывает фон. Когда дело доходит до управления размытием, размытие объектива имеет преимущество. Он предлагает огромный контроль над эффектом. С другой стороны, Lens Blur предпочтительнее, если вы хотите добиться кремового эффекта размытия. Другими словами, это тонкое по сравнению с размытием по Гауссу.
Часть 4. Как удалить размытие с изображения
Возможно, вы сможете добиться желаемого эффекта размытия на своих фотографиях. Однако в некоторых случаях вам нужно убрать уменьшение эффекта размытия, увеличив масштаб фотографии. В других случаях вы просто хотите улучшить качество фотографии. В этом случае вы можете использовать бесплатную программу для увеличения качества изображения.
Aiseesoft Image Upscaler онлайн позволит вам улучшить качество ваших фотографий. Это обеспечивает высококачественный результат, который хорошо работает с вашими личными фотографиями, фотографиями продуктов или изображениями. Поэтому вы без колебаний поделитесь им в Интернете или с друзьями. Посмотрите ниже, чтобы узнать, как использовать этот инструмент.
Ключевая особенность:
- Это увеличивает разрешение фотографий до 800%.
- Поддержка JPEG, JPG, PNG, BMP, TIFF и многих форматов фотографий.
- Технология AI применяется для увеличения разрешения изображений.
- Улучшайте качество фотографий без ограничений.
- Настройте увеличение фотографии на 2x, 4x, 6x и 8x.
Шаг 1:
Для начала зайдите на официальный сайт программы. Вам нужно открыть браузер на своем компьютере и ввести ссылку на программу в адресной строке. После этого нажмите кнопку Загрузить фото кнопку в главном интерфейсе и загрузите целевую фотографию.
Шаг 2:
После завершения загрузки выберите уровень увеличения в соответствии с вашими требованиями. Затем просмотрите улучшенную фотографию и сравните ее с исходной фотографией. В зависимости от выбранного вами увеличения качество изменяется соответствующим образом.
Шаг 3:
Нажмите Сохраните в нижней правой части интерфейса, если вы довольны результатами. Когда вы наведете курсор на полученное изображение, вы увидите изменения. Затем вы можете с уверенностью поделиться фотографией, потому что качество уже увеличено.
Расширенное чтение:
- 3 бесплатных способа размыть фон фото
- Исправьте размытое изображение — вот полное руководство, которое вы должны знать
Часть 5.
 Часто задаваемые вопросы о размытии по Гауссу
Часто задаваемые вопросы о размытии по ГауссуМогу ли я отменить размытие по Гауссу на моих фотографиях?
Да. Многочисленные программы помогут вам как-то обратить вспять эффект размытия и сделать картинку резкой. Используя Photoshop, вы можете воспользоваться функцией High Pass, чтобы размыть фотографию.
Что такое размытие в движении?
Это техника фотографии, в которой используется длинная выдержка, которая размывает движущиеся объекты в кадре.
Как улучшить разрешение фотографий на iPhone?
Приложение «Фото» на вашем iPhone может справиться с этой задачей. Перейдите в «Правка» > «Определение». Затем меняйте определение, пока не достигнете желаемого качества.
Заключение
Гауссово размытие полезен во многих сценариях, таких как изоляция субъекта. Он может почти заменить эти высококачественные объективы камер, чтобы добиться эффекта размытия, который вы хотите для своих фотографий. Между тем, вы можете быть знакомы с некоторыми проблемами размытия и хотите их исправить. Aiseesoft Image Upscaler Online — удобная утилита, которую вы можете использовать. Идите вперед и раскройте красоту изображения, используя урок выше.
Aiseesoft Image Upscaler Online — удобная утилита, которую вы можете использовать. Идите вперед и раскройте красоту изображения, используя урок выше.
Что вы думаете об этом посте.
- 1
- 2
- 3
- 4
- 5
Прекрасно
Рейтинг: 4.9 / 5 (на основе голосов 367)Подпишитесь на нас в
Оставьте свой комментарий и присоединяйтесь к нашему обсуждению
|
Распределение ГауссаGaussian distribution Распределение Гаусса (нормальное распределение)
− плотность распределения вероятностей случайной величины n.
Функция GXσ называется функцией Гаусса.
Говорят, что результаты измерений имеют нормальное распределение, если они
описываются функцией Гаусса. Распределение Гаусса, в отличие от распределения
Пуассона, характеризуется двумя независимыми параметрами X и σ. X − среднее
число отсчетов, которое мы ожидаем получить в случае многократного повторения
измерений. σ − среднее стандартное отклонение.
На рис.
Сравним распределения Гаусса GXσ(n) и Пуассона .
Pμ(n) ≈ GXσ(n), при X = μ, σ = √μ.
|
Модель Гаусса
На восьмой неделе мы подошли к нашей последней теме в этом маленьком модуле эффективной теории поля. Здесь мы будем использовать так называемую «модель Гаусса» для расчета нашего первого вкуса критических показателей за пределами подхода среднего поля. Честно говоря, я еще не все понимаю, но думаю, что когда я начну печатать, все станет более понятным. Итак, поехали.
Зачем изучать модель Гаусса?
Помните, наша мантра с самого начала урока заключалась в том, что существует очень мало взаимодействующих систем, которые физики могут решить ровно . В первые несколько недель занятий мы видели один такой пример — одномерную модель Изинга, которую мы свели к задаче диагонализации матрицы два на два, применив прием передаточной матрицы .
Модель Гаусса — это еще одна взаимодействующая модель, которая точно решаема: мы можем начать с гамильтониана (описывающего все микроскопические детали «частей» системы), и мы получим статистическую сумму и свободную энергию, которые позволяют мы вычисляем термодинамические вещи, которые нам небезразличны.
Почему модель Гаусса разрешима?
Хитрость заключается в том, что модель Гаусса не совсем интерактивная модель: если мы преобразуем координаты в мод Фурье , то мы можем записать гамильтониан как сумму по модам без каких-либо пересечений . То есть, если мы запишем энергию в виде суммы по сайтам, то у нас будут перекрестные члены, потому что сайты взаимодействуют друг с другом, но если мы воспользуемся преобразованием Фурье, мы можем вместо этого записать энергию как сумму по невзаимодействующим модам. . С точки зрения нормальных мод модель Гаусса — это просто набор несвязанных гармонических осцилляторов.
Сложность разложения Фурье заключается в том, что обозначения становятся довольно запутанными, и трудно все уяснить. Но не бойтесь: мы уже много раз видели концепции, и основные идеи не слишком сложны. Просто как только мы составим все измерения и индексы, легко заблудиться в дебрях обозначений и забыть, что все это значит. Поэтому я постараюсь изо всех сил объяснить, что имеет физический смысл.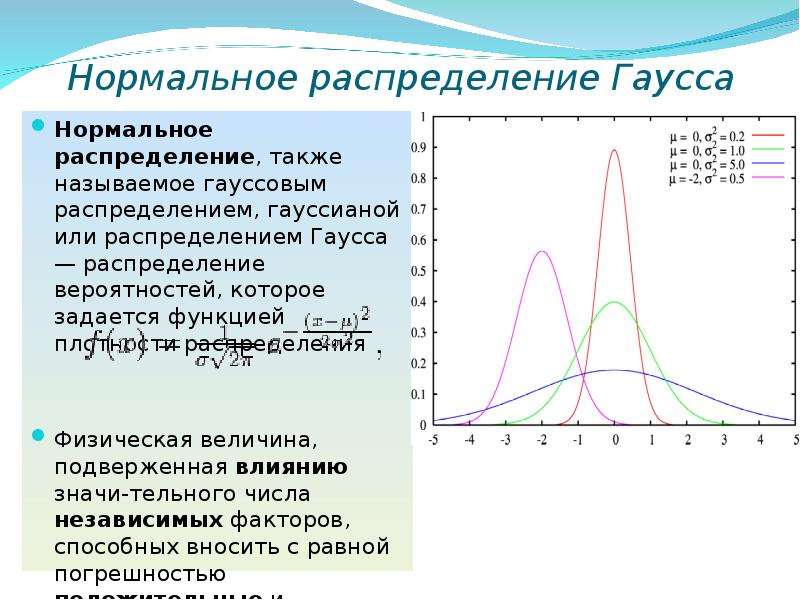
План игры
Перед тем, как перейти ко всей модели Гаусса, мы освежим нашу память о термодинамике гармонических осцилляторов и роли интеграла Гаусса. Мы также напомним себе, как мы можем описать движение связанных гармонических осцилляторов, разложив его на несвязанные нормальные моды. Имея это знание в наших карманах, это будет прямая аналогия для обобщения модели Гаусса.
Контур
-
Термодинамика гармонического осциллятора
-
Связанные генераторы и нормальные моды Фурье
-
Модель Гаусса
Гармонический осциллятор
Здесь мы решим термодинамику гармонического осциллятора. Рассмотрим частицу массы, захваченную потенциалом с жесткостью пружины . Его гамильтониан представляет собой сумму его кинетической и потенциальной энергий,
где импульс. Если бы мы изучали механику, мы бы решили уравнения Гамильтона и нашли временную траекторию движения частицы. Но мы изучаем курс термодинамики, поэтому вместо этого мы хотим понять тепловое поведение системы.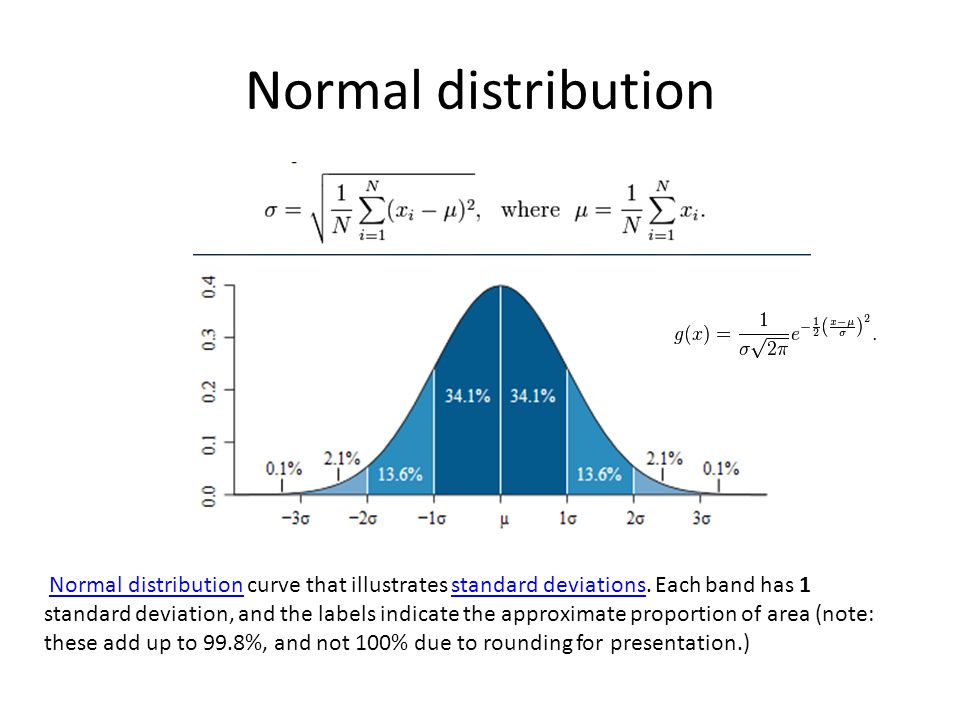 Вместо того, чтобы наблюдать, как развивается изолированная система, мы собираемся соединить ее с большой тепловой баней, подождать долгое время и задать вопрос: «Как часто она проводит время в определенной конфигурации и?» ( Физически мы можем представить себе тепловую ванну как группу молекул, натыкающихся на частицу и производящих небольшие толчки, заставляющие ее энергию колебаться.)
Вместо того, чтобы наблюдать, как развивается изолированная система, мы собираемся соединить ее с большой тепловой баней, подождать долгое время и задать вопрос: «Как часто она проводит время в определенной конфигурации и?» ( Физически мы можем представить себе тепловую ванну как группу молекул, натыкающихся на частицу и производящих небольшие толчки, заставляющие ее энергию колебаться.)
Если мы подождем достаточно долго, наша бедная бомбардируемая частица достигнет теплового равновесия , где вероятность того, что она имеет некоторую энергию, пропорциональна (с обратной температурой). Постоянная нормировки дается суммированием всех возможных конфигураций гармонического осциллятора. Поскольку мы рассматриваем классический гармонический осциллятор , мы должны просуммировать по всем позициям и всем импульсам. Мы можем думать об этом как об интеграле по фазовому пространству .
Таким образом, нам нужно выполнить следующий интеграл, чтобы найти статистическую сумму:
Подставляя квадратичную форму гамильтониана, получаем
Ого, это всего лишь произведение интегралов Гаусса, которые выглядят как , поэтому статистическую сумму найти несложно:
Нахождение спреда
В механическом равновесии частица оседает и прекращает движение при минимуме потенциальной энергии; но в термическое равновесие, оно все еще колеблется около минимума, потому что оно постоянно подвергается бомбардировке вещами в ванне с подогревом. Возникает естественный вопрос о среднем квадрате размера этих флуктуаций — тепловые флуктуации заставляют частицу отклоняться от минимума, так как далеко она склонна отклоняться?
Возникает естественный вопрос о среднем квадрате размера этих флуктуаций — тепловые флуктуации заставляют частицу отклоняться от минимума, так как далеко она склонна отклоняться?
Хорошо, мы должны сначала проверить, что частица центрирована вокруг минимума; то есть мы хотим убедиться, что . Фактически, мы можем утверждать, что среднее положение равно нулю, не выполняя интеграл, с помощью следующего аргумента симметрии. Помните, что тепловое среднее дается путем интегрирования по вероятностной мере , которая является четной функцией. Ожидаемое значение (нечетная функция!) выглядит как . Но поскольку подынтегральная функция нечетна, половина интеграла с сокращает часть с , и поэтому интеграл равен нулю. Таким образом, действительно, распределение вероятностей сосредоточено на 0,9.0003
Впрочем, второй момент никуда не исчезает. На самом деле, мы можем найти разброс, внимательно изучив фактор Больцмана. Он говорит вам, что вероятность того, что частица находится в определенном положении, равна
.
, который имеет форму Гаусса (также известного как нормальное распределение). Помните, что стандартная форма гауссианы со средним значением и дисперсией равна
.Сравнение этой стандартной формы с нашим выражением для говорит нам о том, что спред задается как = . Итак, мы нашли ответ, не производя никаких интегралов (!).
Имеет ли смысл это выражение?
-
По мере повышения температуры нагревательная ванна заставляет осциллятор крутиться все сильнее и сильнее, поэтому он имеет тенденцию к дальнейшему блужданию. Действительно .
-
По мере увеличения жесткости требуется больше энергии, чтобы выбраться дальше из потенциальной ямы, поэтому частица будет стремиться проводить время ближе к центру. Действительно .
-
Единицы правильные.
Так здорово. Среднеквадратичное колебание положения определяется как . Таким образом, мы решили одномерный гармонический осциллятор.
Обобщение на более высокие измерения
Далее мы немного обобщим, рассматривая частицы, которые движутся в кратных направлениях. (Если вы не возражаете, я также проигнорирую импульсную часть статистической суммы, так как она учитывается. Нас интересует распределение поверх. См. примечание выше.)
(Если вы не возражаете, я также проигнорирую импульсную часть статистической суммы, так как она учитывается. Нас интересует распределение поверх. См. примечание выше.)
Давайте перейдем к трем измерениям и представим, что частица движется в сферически-симметричном гармоническом колодце. Теперь он чувствует потенциал
где представляет вашу типичную радиальную координату. Если мы немного присмотримся к выражению, мы поймем, что каждое из измерений появляется независимо . То есть мы можем записать это как
, которые мы можем распознать как сумму независимых гармонических осцилляторов в каждом пространственном измерении. Таким образом, каждый компонент частицы ведет себя точно так же, как одномерный гармонический осциллятор! Например, мы можем автоматически вывести, что и, следовательно, . Мы также можем вывести, что , где 3D-сумма и 1D-сумма. (Если вы мне не верите, можете попробовать произвести расчеты и убедиться в этом сами.)
Прежде чем продолжить, давайте введем некоторые дополнительные обозначения для обобщения измерений. Вместо того, чтобы называть смещения в каждом из направлений как , , и , давайте назовем их , , и . На этом языке потенциальная энергия определяется как
Вместо того, чтобы называть смещения в каждом из направлений как , , и , давайте назовем их , , и . На этом языке потенциальная энергия определяется как
Уточним обозначения: символ представляет смещение частицы в -измерении. Индекс помечает каждое из измерений (например, в измерениях мы суммируем по , и направлениям). А величина представляет собой «радиальное» расстояние от центра гармонической потенциальной ямы по аналогии со стандартным .
Чтобы сэкономить немного места, мы также можем использовать векторную запись, в которой длина вектора определяется как . Тогда гармонический потенциал равен
Запомните это обозначение, потому что оно только еще больше запутает вас.
Обобщение на множественные гармонические генераторы
Теперь давайте представим, что у нас есть не один единственный гармонический осциллятор, а несколько гармонических осцилляторов. Что ж, мы можем пометить каждый из наших осцилляторов индексом и записать смещение ‘го осциллятора как . Если у нас есть общее количество осцилляторов, то общая потенциальная энергия определяется суммированием потенциальной энергии каждого отдельного осциллятора:
Если у нас есть общее количество осцилляторов, то общая потенциальная энергия определяется суммированием потенциальной энергии каждого отдельного осциллятора:
Теперь мы понимаем, почему обозначения получаются довольно запутанными. Индекс обозначает, какой осциллятор мы рассматриваем, тогда как векторный символ сверху относится к направлениям смещения каждого из осцилляторов. Надеюсь, это не очень запутанно.
К счастью, помимо условных головных болей, термодинамика этой проблемы очень проста, поскольку ни один из осцилляторов не взаимодействует друг с другом. Каждый из осцилляторов живет в своем собственном мире, поэтому его математические ожидания и статистические суммы точно такие же, как и в случае с одним осциллятором. Чтобы быть точным, для всех разных сайтов, потому что каждый из осцилляторов сосредоточен вокруг нулевого среднего смещения. И , где количество измерений. (Убедите себя, почему это так!)
Пока все довольно просто. Давайте сделаем вещи немного более захватывающими, позволив осцилляторам взаимодействовать друг с другом.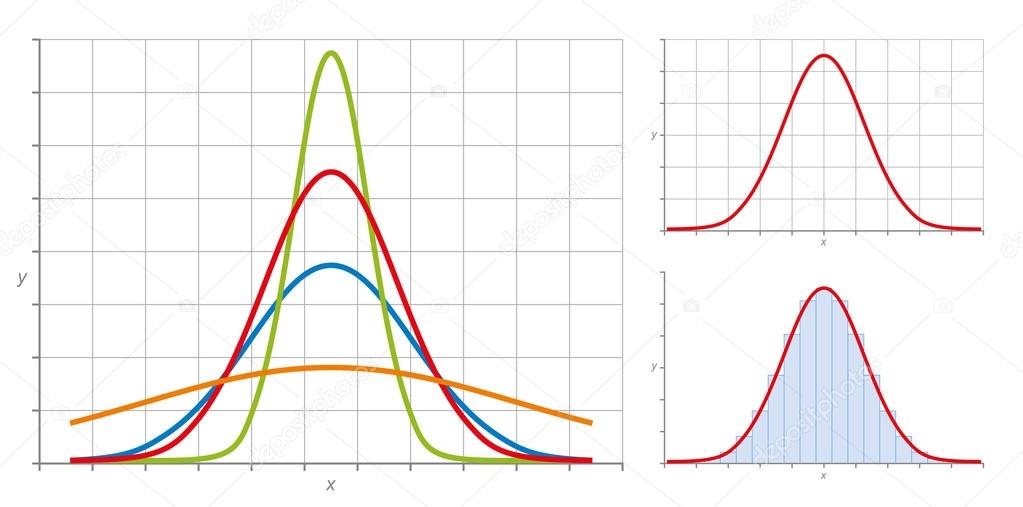
Связанные гармонические осцилляторы
Теперь мы проведем классический вывод по нахождению нормальных мод цепочки из шариков и пружин. Мы увидим, что энергия хорошо разделяется на сумму мод Фурье. Как только вы поймете, как это работает, модель Гаусса, которую мы использовали в классе, будет довольно легко следовать.
Постановка проблемы
Здесь мы рассмотрим цепочку связанных одномерных гармонических осцилляторов в одном измерении. Вы можете представить это как длинную линию масс с пружинами, соединяющими массы. Если вы возьмете одну из масс и покачаете ее, другие массы, расположенные рядом, начнут двигаться довольно сложным образом, и, в конце концов, через все соединения вся система масс и пружин будет вибрировать всевозможными сложными способами. .
Наша цель состоит в том, чтобы упростить это сложное движение до суммы простых «основных» движений.
Давайте запишем энергию более явно, чтобы иметь лучшее представление о том, что происходит.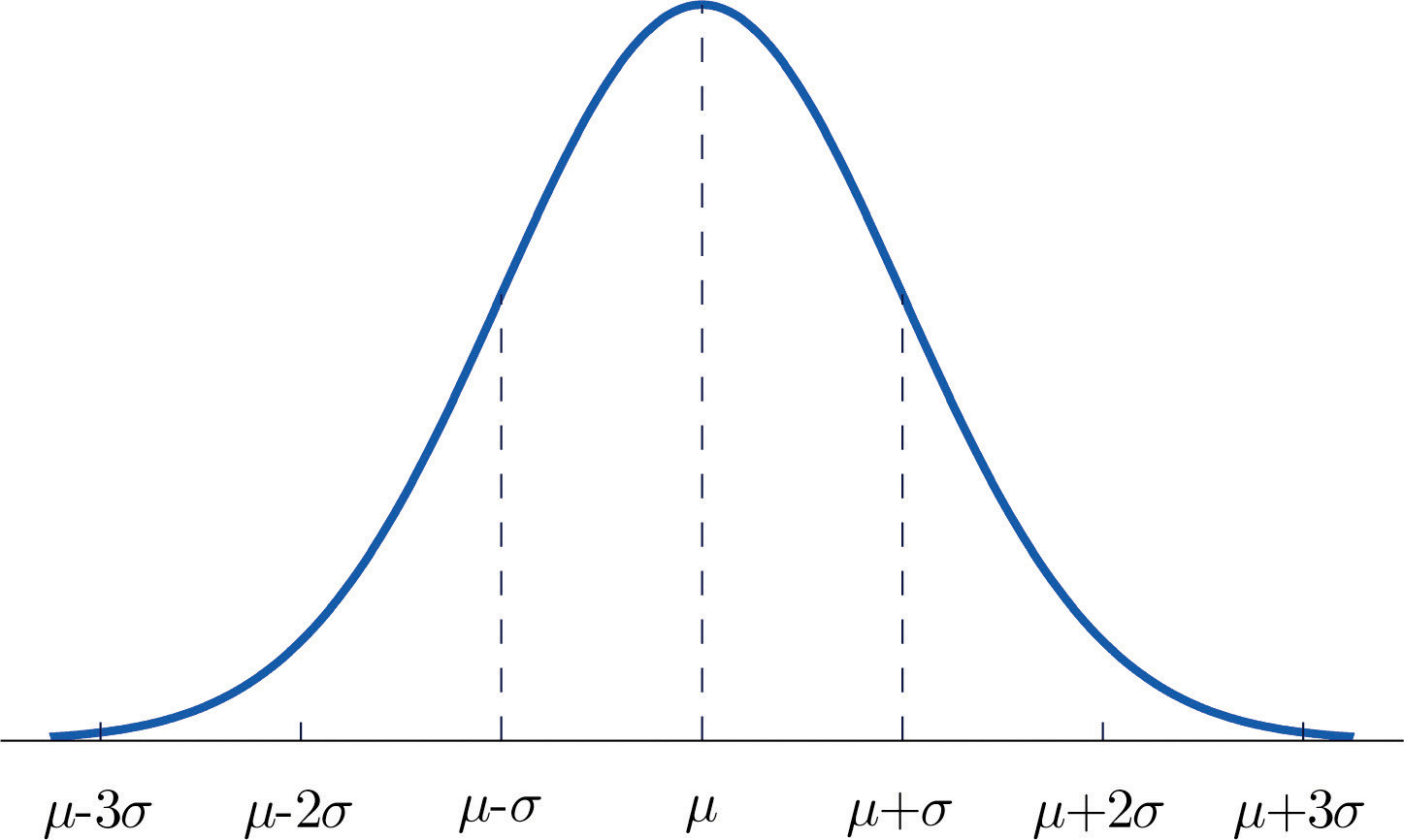 Если у нас есть массы, то это выглядит как
Если у нас есть массы, то это выглядит как
Обратите внимание, что у нас есть перекрестные термины между числами фи, такими как . Из-за этих перекрестных членов мы не сможем разложить интегралы на множители, чтобы найти статистическую сумму. Так что нам нужно найти способ переписать энергию так, чтобы больше не было пересечений.
Вот хитрость: мы выполним преобразование Фурье . Если мы запишем энергию в терминах амплитуд мод Фурье, а не смещений отдельных узлов, тогда перекрестных членов больше не будет. На языке квантовой механики гамильтониан является диагональным в импульсном базисе, а не в базисе положения.
Поскольку мы собираемся произвести замену базиса, воспользуемся языком линейной алгебры.
Мышление в терминах линейной алгебры
Конфигурация нашей системы — состояние всех пружин и масс — живет в -мерном пространстве (поскольку для полного определения ее состояния нужны разные числа). И точно так же, как любое векторное пространство, вы можете представить свое состояние в любой основе, которую пожелаете. В настоящее время мы используем базис позиции для определения состояния системы.
В настоящее время мы используем базис позиции для определения состояния системы.
Когда мы пишем нашу конфигурацию, используя базис положения, легко интерпретировать вектор состояния, потому что каждый из компонентов представляет собой просто смещения отдельных осцилляторов — первый компонент — это смещение первого осциллятора и т. д. Однако базис положения имеет тот недостаток, что гамильтониан не является диагональным в этом базисе . То есть существуют перекрестные термины между различными позициями, такими как . Эта недиагональность становится более очевидной, когда мы записываем энергию в матричных обозначениях как
В этом выражении мы явно видим, что квадратичная форма имеет недиагональные элементы, что приводит к появлению таких членов в энергии.
Если бы вместо этого мы выбрали другой базис для представления энергии, где матрица связи была бы по диагонали , то мы избавились бы от всех перекрестных членов, так что мы могли бы легко вычислить статистическую сумму. То есть если мы перешли на новый базис, где энергия выглядит как
То есть если мы перешли на новый базис, где энергия выглядит как
, тогда мы были бы в бизнесе, потому что не было бы больше перекрестных терминов, таких как . (Найдите минутку, чтобы убедить себя, почему это правда…)
В принципе, чтобы найти этот прекрасный новый диагональный базис, нам нужно найти собственные векторы матрицы связи. Однако на самом деле нам не нужно делать никакой тяжелой работы, потому что мы знаем, что ответом является базис Фурье . Возможно, я могу привести какое-то обоснование того, почему этот ответ физически разумен.
Скоро….
Модель Гаусса
Увы, мне становится немного лень, и я не уверен, что смогу набраться мотивации, чтобы закончить оставшуюся часть этой страницы. Я подытожу основные моменты, лежащие в основе этой модели, и подведу итоги.
, где структурный фактор связан с локальной структурой энергетических связей. Обратите внимание, что для малого , что означает, что как .
-
Обратите внимание, что энергия представляет собой сумму мод Фурье (обозначенных знаком ), и что амплитуда каждой моды равна в квадрате .
 Множитель перед говорит вам, насколько «жесткий» режим ‘th. Есть два вклада в жесткость: одна — внутренняя жесткость отдельных осцилляторов, а другая — член, зависящий от волнового числа, который стремится к нулю для длинноволновых возбуждений (малых).
Множитель перед говорит вам, насколько «жесткий» режим ‘th. Есть два вклада в жесткость: одна — внутренняя жесткость отдельных осцилляторов, а другая — член, зависящий от волнового числа, который стремится к нулю для длинноволновых возбуждений (малых). -
Поскольку энергия разделяется на сумму мод, мы знаем, что вибрации различных мод некоррелированы друг с другом; то есть если. Итак, как только вы посмотрите на проблему в базисе Фурье, вся эта мешанина из связанных пружин превращается в кучу невзаимодействующих гармонических осцилляторов.
-
Для определенного нормального режима длины волны энергия выглядит так , что говорит вам о том , что она действует как гармонический осциллятор с жесткостью пружины . Поскольку моды не взаимодействуют друг с другом, мы можем процитировать наш результат из более ранней задачи «простой гармонический осциллятор», чтобы сказать, что
Смотри, мам, интегралов нет!
Насколько взволнованы разные режимы?
-
Длинноволновые плоские волны (малые ) представляют собой возбуждения с наименьшей энергией, поэтому большая часть тепловой энергии уходит на эти степени свободы.
 Волны с более короткой длиной волны и более высокой частотой намного «жестче» и их сложнее возбудить, и поэтому они имеют меньшую среднеквадратичную амплитуду при тепловом равновесии.
Волны с более короткой длиной волны и более высокой частотой намного «жестче» и их сложнее возбудить, и поэтому они имеют меньшую среднеквадратичную амплитуду при тепловом равновесии. -
Обратите внимание, что среднеквадратичное возбуждение моды расходится с , когда мы устанавливаем ! (Помните это.) Поскольку флуктуации становятся все более и более важными вблизи критических точек, у нас возникает соблазн сказать, что это соответствует критической точке. Однако, поскольку модель Гаусса не имеет никакого смысла для , мы не можем фактически узнать о том, как ведет себя упорядоченная фаза из этой модели. Мы можем узнать о поведении неупорядоченной фазы только по мере ее приближения к непрерывному переходу.
Длина корреляции
-
Обратите внимание, что внизу дроби есть два термина: термин и термин. Если большое, то первое слагаемое больше; если мало, то второй член больше. Точка пересечения, когда два термина равны, происходит, когда или когда .
-
Помните, что волновое число имеет единицы обратной длины. (Например, длина волны задается как , поэтому должна иметь единицу длины, чтобы длина волны имела единицы длины.) Взятие обратного этого «пересечения» дает нам характерный масштаб проблемы, известный как корреляционная длина.
-
На самом деле, это довольно мощный результат! Поскольку корреляционная длина — единственная возможная величина, которую мы можем построить с помощью единиц длины, мы знаем, что каждых пространственно-зависимых явлений в этой задаче происходят на шкале длины . Например, корреляция между двумя точками…
Нахождение корреляционной функции в реальном пространстве
-
В реальной жизни нас интересует не только пространство Фурье, но и пространство позиций. Может быть математически удобно выражать энергии в терминах сумм по волновым числам, а не сумм по координатам, но, в конце концов, если мы хотим провести какие-либо локальные эксперименты по исследованию различных частей материалов, нам лучше выразить физические величины в терминах .
-
Одной из особенно интересных величин является , которая говорит вам о том, насколько колебания на одном участке коррелируют с колебаниями на каком-то другом участке.
-
Из-за трансляционной и вращательной инвариантности мы ожидаем, что эта корреляционная функция зависит только от расстояния между сайтами.
-
Кроме того, исходя из нашего результата с одномерной моделью Изинга, мы ожидаем, что на достаточно больших расстояниях корреляция должна затухать экспоненциально с характерной шкалой длины (потому что это единственная шкала длины в задаче)!
-
Опять же, когда мы приближаемся к критической точке, мы ожидаем, что сайты, которые все дальше и дальше, становятся все более и более коррелированными, потому что, когда мы находимся в упорядоченной фазе, далекие сайты указывают в одном направлении и, таким образом, коррелируют. Это означает, что корреляционная длина, вероятно, расходится в критической точке.

-
-
Чтобы вычислить корреляционную функцию в реальном пространстве, мы можем выразить смещения как сумму по модам Фурье, а затем использовать наши знания для упрощения результата.
Оставьте комментарий ниже!
Распределение Гаусса
Распределение Гаусса, также называемое нормальным распределением, представляет собой тип непрерывного распределения вероятностей, который симметричен относительно своего среднего значения; большинство наблюдений группируются вокруг среднего значения, и чем дальше наблюдение от среднего значения, тем ниже вероятность его появления. Как и другие распределения вероятностей, распределение Гаусса описывает, как распределяются результаты случайной величины.
Распределение Гаусса, названное так потому, что оно было впервые открыто Карлом Фридрихом Гауссом, широко используется в теории вероятностей и статистике. Во многом это связано с центральной предельной теоремой, которая утверждает, что событие, представляющее собой сумму случайных, но в остальном идентичных событий, имеет тенденцию к нормальному распределению независимо от распределения случайной величины. Многие природные явления, такие как рост, вес, результаты тестов и другие, соответствуют этому критерию и, следовательно, имеют нормальное распределение.
Многие природные явления, такие как рост, вес, результаты тестов и другие, соответствуют этому критерию и, следовательно, имеют нормальное распределение.
Функция Гаусса
График функции Гаусса образует характерную колоколообразную форму гауссовского/нормального распределения и имеет общий вид
, где a, b и c — вещественные константы, а c ≠ 0. В распределение Гаусса, параметры a, b и c основаны на среднем значении (μ) и стандартном отклонении (σ). Таким образом, функция плотности вероятности (PDF) гауссовского распределения представляет собой гауссову функцию, которая принимает форму:
Хотя графики всех гауссовских распределений имеют одинаковую общую форму колокола, параметры функции влияют на общую форму график:
Как видно из рисунка, различные μ и σ существенно влияют на форму графика, делая его выше, уже или шире и т. д. Как правило, чем больше стандартное отклонение, тем более плоской будет кривая, поскольку Вероятность данного исхода тем менее вероятна, чем дальше от кривой находится исход от среднего значения.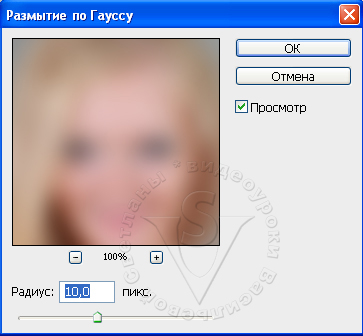 Поскольку разные нормальные распределения могут иметь такие разные формы, стандартизация часто бывает полезной. График выше, показанный синим цветом, относится к стандартному нормальному распределению.
Поскольку разные нормальные распределения могут иметь такие разные формы, стандартизация часто бывает полезной. График выше, показанный синим цветом, относится к стандартному нормальному распределению.
Стандартное нормальное распределение
Стандартное нормальное распределение — это стандартизированная форма распределения Гаусса, в которой μ = 0 и σ = 1. Стоит отметить, что любое распределение Гаусса можно преобразовать в стандартное нормальное распределение. Это важно, потому что обычно для определения вероятностей различных результатов в распределении вероятностей необходимо интегрировать функцию плотности вероятности (PDF), чтобы определить площадь под кривой; это не относится к стандартному нормальному распределению. На рисунке ниже показан график распределения Гаусса.
Заштрихованная область представляет собой площадь под кривой или вероятность того, что результат окажется между 6 и 9. Интегрирование PDF распределения Гаусса по этому интервалу дает указанную вероятность, но поскольку PDF нормального распределения относительно сложные, для вычисления этих интегралов чаще используют калькуляторы или компьютеры.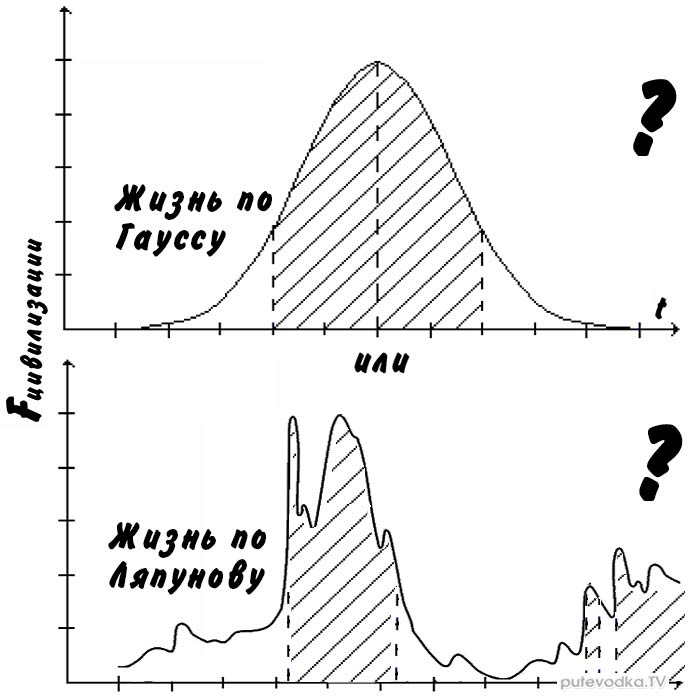
В случае стандартного нормального распределения вероятности различных исходов уже сведены в таблицы. Таким образом, вместо того, чтобы интегрировать для определения интересующих вероятностей, мы можем просто считать вероятности из того, что называется Z-таблицей. Это, в свою очередь, позволяет нам легко сравнивать различные нормальные распределения.
Преобразование в стандартное нормальное распределение
При заданной случайной величине X, имеющей гауссово распределение, отдельные значения можно стандартизировать по следующей формуле:
стандартное отклонение, а x — значение, которое нужно преобразовать. Все значения в распределении Гаусса могут быть преобразованы в Z-показатели с помощью этой формулы, и полученное распределение называется стандартным нормальным распределением или Z-распределением.
Z-показатель указывает количество стандартных отклонений данного значения от среднего. Например, Z-показатель, равный 1, указывает на то, что значение составляет 1 стандартное отклонение от среднего значения. Z-оценка может быть положительной, отрицательной или нулевой.
Z-оценка может быть положительной, отрицательной или нулевой.
- Положительный показатель Z указывает на то, что значение выше (справа) от среднего.
- Отрицательный показатель Z указывает на то, что значение ниже (слева) от среднего значения.
- Показатель Z, равный 0, означает, что значение равно среднему значению.
Z-значения используются в сочетании с Z-таблицами для определения различных вероятностей.
Пример
Средний рост пятиклассников в данном школьном округе составляет 52 дюйма со стандартным отклонением 2,4 дюйма. Предполагая, что рост пятиклассников в округе распределен нормально, найти вероятность того, что случайно выбранный пятиклассник выше 56 дюймов.
Сначала преобразуйте интересующее значение в Z-значение:
Существует несколько различных типов Z-таблиц. Таблица Z на рисунке ниже является кумулятивным из таблицы среднего Z, что означает, что значение в таблице представляет вероятность того, что результат будет лежать в интервале между средним значением (0) и выбранным Z-показателем (1,67 в данном случае).

 Как вы используете размытие по Гауссу
Как вы используете размытие по Гауссу Боттомоний
Боттомоний Чармоний
Чармоний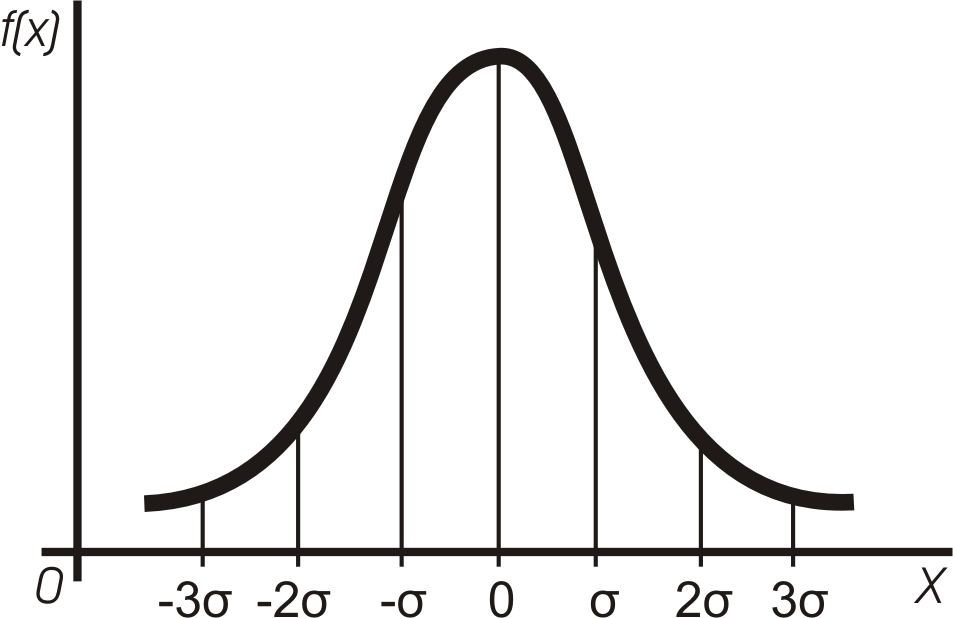
 1 показано два нормальных или
гауссовых распределения, соответствующие различным измерениям с одинаковыми
значениями X и разными σ. В первом случае X = 50, σ = 0.5, во втором случае
− X = 50, σ = 1. Величина σ в знаменателе экспоненты обеспечивает для более
узкого распределения большую высоту в максимуме.
1 показано два нормальных или
гауссовых распределения, соответствующие различным измерениям с одинаковыми
значениями X и разными σ. В первом случае X = 50, σ = 0.5, во втором случае
− X = 50, σ = 1. Величина σ в знаменателе экспоненты обеспечивает для более
узкого распределения большую высоту в максимуме. к. ширина распределения Пуассона σ автоматически определяется величиной
μ (σ = √μ).
к. ширина распределения Пуассона σ автоматически определяется величиной
μ (σ = √μ).