Полноформатная матрица: Кроп или полный кадр — что выбрать? Crop vs. FF — Главная

Содержание

Кроп-фактор: что это и как влияет на качество снимков?

Многие фотографы-любители не знают, что такое кроп-фактор. Но этот параметр важен, так как характеризует размер матрицы фотоаппарата. В данной статье мы постараемся простыми словами объяснить значение этого загадочного термина и сориентируем всех желающих купить фотокамеру в том, какой матрице отдать предпочтение.

Задавшись целью купить фотокамеру, мы идем в магазин и интересуемся у консультанта характеристиками приглянувшейся модели. Вот тут-то нас и вводят в заблуждение, выставляя главным параметром, влияющим на качество снимков, количество мегапикселей и умалчивая о размере матрицы. А ведь именно от него в большей степени зависит качество отснятого материала.

Матрица, именуемая также сенсором и фотодатчиком, представляет собой микросхему из фотодиодов, которая является важнейшей частью любой цифровой камеры. По сути, это аналог фотопленки. Во времена пленочных фотоаппаратов картинка сквозь объектив попадала на пленку, где и хранилась, а в наш цифровой век она попадает на матрицу и хранится потом на карте памяти.

Полная матрица (Full Frame) по размеру равна кадру 35-миллиметровой пленки. Такая матрица достаточна дорога в изготовлении, а камеры с ней имеют приличные размеры и вес. Используют аппараты с полной матрицей в основном профессионалы или любители, которые неплохо зарабатывают и могут себе позволить иметь дорогостоящую камеру.

Для уменьшения габаритов и цены камер современные фотомастера решили уменьшить матрицу, обрезав ее («crop» с англ. — «обрезать»), так и возникло понятие «кроп-фактор», означающее во сколько раз матрица урезана по отношению к Full Frame.

Какими матрицами оснащаются современные фотоаппараты?

Сегодня фотокамеры стали весьма популярными, большинство людей имеют в личном распоряжении и фотоаппарат, и мобильные девайсы с камерами, которые всегда под рукой. Кроп-фактор разных камер существенно отличается:

дорогие профессиональные камеры, как уже отмечалось выше, снабжаются матрицей Full Frame;
популярные любительские зеркалки имеют кроп-фактор 1,5…1,7, то есть матрица в них урезана по сравнению с полноформатной в 1,5; 1,6 или 1,7 раза;
новые беззеркальные камеры, которые уже вовсю конкурируют с зеркалками, обычно имеют кроп-фактор 2;
недорогие цифровые мыльницы оснащаются матрицей с кропом в районе 5,62;
планшеты и смартфоны наделяются камерами с кроп-фактором около 7,1.

Покупая фотоустройство, несложно и растеряться, что же предпочесть. Как понять, какая матрица подойдет именно вам, чтобы и не переплатить, и не оказаться наказанным за скупость?

Какую матрицу предпочесть?

У многих формируется мнение, что Full Frame — это идеал к которому нужно стремиться. Так ли это? Есть ли смысл гнаться за дорогой и тяжелой камерой или обойтись вариантом попроще?

Конечно, большой сенсор — это залог хорошего качества получаемых фотографий, которое проявляется в большей детализации, четкости и резкости изображения. Для полиграфии, особенно когда речь идет о многократном увеличении изображения перед печатью, использовать Full Frame не просто желательно, а обязательно. Кроме того, большой исходник намного проще кадрировать: то есть обрезать лишнее, сильно не потеряв при этом в качестве. Большая матрица лучше проявляет себя и в условиях недостаточной освещенности, обеспечивая получение снимков с меньшими шумами.

Но полноформатная матрица — это дорого и неудобно, ввиду больших размеров и веса фотоаппарата.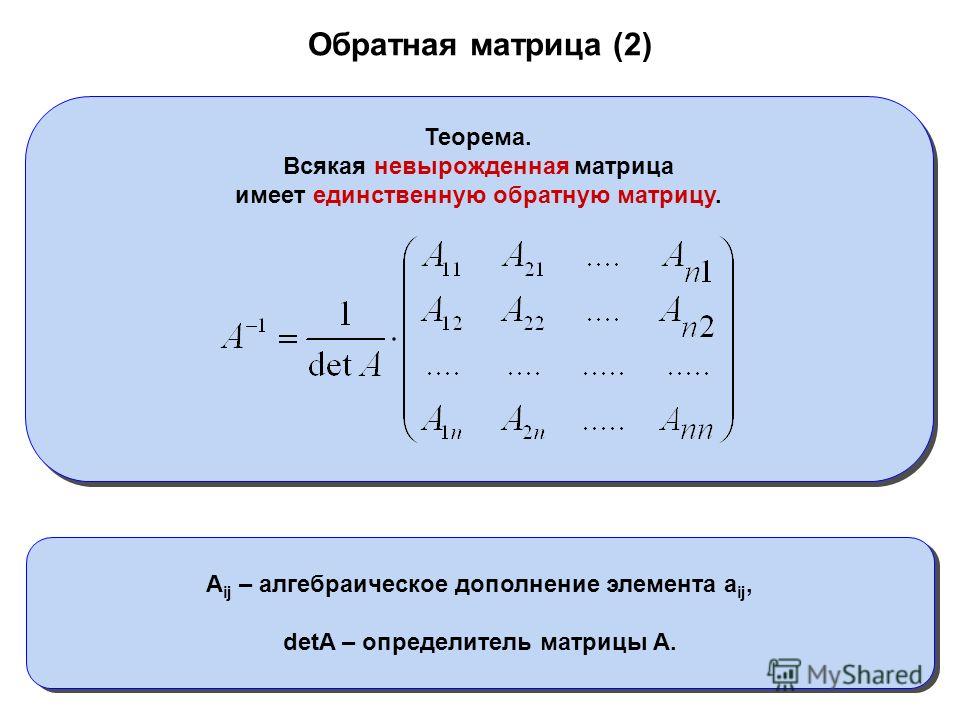 Для фотолюбителя использовать ее совсем не обязательно. Зачем тратить кучу денег и потом повсюду таскать за собой огромный аппарат, если вас вполне устроит качество, предлагаемое урезанной матрицей?

Вывод

Камеру нужно выбирать под собственные цели и кошелек. Любителям вполне подойдет мыльница, имеющая кроп 5,7, чтобы пополнять новинками семейный альбом. Продвинутым любителям лучше отдавать предпочтение зеркалкам или беззеркальным камерам с кропом 1,5…2, которые сейчас выпускаются небольшого размера и с широким функционалом. Также стоит узнать основные параметры объектива, чтобы наверняка выбрать лучшую модель.

← Вернуться к списку статей

Полноформатная зеркальная камера Canon EOS 6D Mark II

Дата публикации: 29.06.2017

Прошло почти пять лет с выхода полнокадровой зеркальной камеры EOS 6D, и Canon выпустил ей на замену модель EOS 6D Mark II. Внешне камера выглядит практически так же, но внутреннее наполнение почти полностью обновлено.

В Canon 6D II использована совершенно новая полноформатная матрица разрешения 26,2 Мп со встроенными датчиками гибридной системы автофокусировки Dual Pixel AF.

В паре с ней работает процессор обработки изображения Canon DIGIC 7. Диапазон чувствительности доходит до ISO 40000. Датчик экспозамера – 7560-зонный RGB+IR, такой же, как в модели EOS 80D. При съемке через оптический видоискатель система АФ работает с 45 точками, все они крестового типа. Скорость серийной съемки доходит до 6,5 кадров в секунду в режиме непрерывного автофокуса.

Представленный производителем видеоролик рассказывает о системе автофокуса камеры EOS 6D II:

Основное отличие в конструктиве 6D Mark II от предыдущей модели – появление полностью поворотного сенсорного монитора (с типовой диагональю 3”). Впервые полнокадровая зеркалка получает монитор такого типа.

Возможно, кто-то будет разочарован, что в систему управления не добавлен джойстик для выбора точки автофокуса – функция, которая становится всё более популярной в камерах продвинутого уровня.

Корпус имеет защиту от пыли и влаги, как и можно было ожидать от камеры стоимостью в 2000 долларов.

Что касается видеосъемки, Canon 6D II остается в рамках формата 1080@60p. Работа автофокуса должна быть уверенной за счет гибридной технологии (это предположительно, исходя из опыта с другими моделями Canon). Камера имеет разъем для подключения внешнего микрофона, а вот разъема для мониторинговых наушников нет – такую функцию предлагает старшая модель 5D Mark IV.

Canon EOS 6D II имеет полный набор встроенных беспроводных модулей – Wi-Fi с NFC и Bluetooth, а также GPS (как и у EOS 6D). Для питания используется аккумулятор NP-E6N, типовой для зеркальных камер Canon, а за $300 можно приобрести батарейную рукоятку.

Полноформатная зеркальная камера Canon EOS 6D Mark II поступит в продажу в августе 2017 года. Ориентиры цены:

$2000 за саму камеру;
$2600 за комплект с объективом 24-105/4.5-5.6 IS STM;
$3100 за комплект с объективом 24-105/4 L IS II USM.

Phase One Systems XF IQ4 150MP

Описание

Phase One XF IQ4 150MP Camera System – первая в мире 151-мегапиксельная камера. Она использует матрицу среднего формата с полным разрешением, гарантирующую, что каждое RAW-изображение содержит максимальную детализацию.

Задняя подсветка (BSI, Backside Illuminated) – еще одна новейшая технология матрицы для цифровой среднеформатной фотографии. Конструкция матрицы обеспечивает непрерывный захват света в каждом пикселе, непосредственно передавая точный рендеринг с улучшенным цветом, детализацией и обработкой шума в RAW-файле.

В основе IQ4 лежит платформа Infinity, которая обеспечивает улучшенное качество изображения, оптимизирует рабочий процесс и функциональную производительность. Редактирующее программное ядро RAW Capture One непосредственно интегрировано в платформу Infinity. Оно обеспечивает работу всех функций камеры, обработку JPEG непосредственно в камере, улучшает качество изображения и производительность во время предварительного просмотра в реальном времени.

Полноформатная матрица, используемая в XF IQ4 Camera Systems, позволяет захватывать в полтора раза больше объема изображения по сравнению с обычными матрицами.

Задник IQ 4 имеет слоты для установки различных карт памяти.

В камере реализованы три варианта организации связи с внешними устройствами – Ethernet, USB-C и Wi-Fi, способные работать с высокой пропускной способностью. Все варианты связи и используемые буферы и карты памяти могут быть объединены и работать под общим управлением.

Wi-Fi модуль может использоваться для передачи RAW-файлов непосредственно в программу Capture One, параллельно сохраняя снимки в памяти камеры.

Ethernet предоставляет возможности для полностью настраиваемого, интегрированного и динамичного рабочего процесса, обеспечивая возможность совместной работы с другими устройствами, поддерживающими Ethernet.

Порт USB-C обеспечивает стандартное подключение большинства устройств. Кроме этого, зачастую с его помощью решаются вопросы питания.

VSGO DDR-24 KIT КОМПЛЕКТ ДЛЯ ЧИСТКИ ПОЛНОФОРМАТНЫХ МАТРИЦ

Выберите категорию:

Все ПОДАРОЧНЫЕ СЕРТИФИКАТЫ Наборы оборудования для фото- видеосъёмки Кольцевые лампы » Кольцевые лампы для блогеров » Профессиональные кольцевые лампы » Аккумуляторы для кольцевых ламп Фоны хромакей » Складные фоны » Тканевые фоны хромакей » Тканевые фоны хромакей (без шва, хлопок) » Цветные фотофоны хромакей » Бумажные фоны хромакей » Системы установки фона хромакея » Т-образные стойки для фотофонов » Системы установки цветных фонов » Стойки для фонов » Аксессуары для систем установки фона » Виниловые фоны Аксессуары » Для микрофонов » Для стедикамов » Внешние аккумуляторы » Для фотоаппаратов Беспроводные колонки Беспроводные наушники Видеокамеры » Веб-камеры » Камеры для блогеров » Экшн-Камеры Геймпады Держатели для телефона » IMStick Импульсный свет » Импульсные моноблоки » Комплекты импульсного света » Накамерные вспышки Квадрокоптеры » Аксессуары для квадрокоптеров » Любительские квадрокоптеры » Профессиональные квадрокоптеры » Промышленные полетные платформы Микрофоны » Для стримов и подкастов » Беспроводные системы » Петличные микрофоны » Студийные микрофоны » Вокальные, инструментальные микрофоны » Накамерные микрофоны и микрофоны-пушки » Микрофоны для смартфонов Постоянный свет » Комплекты освещения » Лайткубы » Светодиодные светильники » Фотостолы Рекордеры Слайдеры и Краны Стедикамы Смарт-часы Стойки для баннеров » Стойки для баннеров П-образные » Стойки для баннеров Усиленные Штативы и моноподы » Напольные штативы » Настольные штативы » Моноподы Телесуфлёры и видеомониторы Фрост-рамы Видеомонтаж Вашего материала (Услуги) Циклорамы Чистящие средства для оптики и матриц Звукоизоляция Светофильтры Светоотражатели

Производитель:

ВсеAllenjoyALLOYSEEDAMAIAndoerApexelAppleArozziAUDIO-TECHNICABENROBlogerBoxBoyaContinentDeppaDgicareDigmaDJIDURACELLEKENElementsEnergizerFalcon EyeFalcon eyesFancierFangtuosiFeiyuFifineFSTFujimiGAQOUGODOXGOZHYGreenbeanGudsenHarperJBLLogitechLUMIFORMaonoMicrosoftMomaxOlympusPanasonicRekamRemaxRitmixRIVACASERODESanDiskSaramonicSAVAGESeagateSennheiserShureSJCAMSnoppaSonySymaToshibaTranscendUlanziUpperFuWeifengWO NEWXiaomiYingnuostYongNuoYuntengZhiyunZoom

Двухцветная фотоприемная матрица на диапазон 3-5 и 8-12 мкм на основе МСКЯ GaAs/AlGaAs/InGaAs

Лаборатория кинетических явлений в полупроводниках

Изготовлены и исследованы фотоприемные структуры на основе многослойных структур с квантовыми ямами чувствительные одновременно в двух спектральных диапазонах 3-5 и 8-12 мкм.

Рис. 1. Спектральная чувствительность двухцветных фотоприемных матриц.

Структуры изготовлены методом MOC гидридной эпитаксии и представляют собой выращенные на подложке GaAs последовательно в одном технологическом цикле две серии многослойных структур, чувствительных в разных спектральных интервалах и заключенных в обкладки высоколегированного GaAs n-типа для приложения электрического поля. Обе серии содержит по 30 периодов гетероструктур InGaAs/AlGaAs (квантовая яма/барьер) и GaAs/ AlGaAs (квантовая яма/барьер) с соответствующим содержанием индия и алюминия. Между сериями выращен высоколегированный n-слой GaAs (легирующая примесь — кремний с концентрацией 10¹⁸ см^-3), служащий промежуточным контактным слоем. Были изготовлены мезаструктуры с возможностью раздельного приложения электрического поля и независимого изучения каждой из фоточувствительной серии гетероструктур.

Плотность электронов в структуре, чувствительной в длинноволновой области, составляла (5-6)×10¹⁶ см^-3. В структуре, чувствительной в коротковолновой области, плотность электронов составляла (2.5-2.6)×10¹⁷ см^-3.

Спектр фоточувствительности коротковолновой и длинноволновой частей структуры показан на Рис.1. Измерения проводились раздельно на каждой структуре на тестовых элементах. Для приложения напряжения к каждой из структур использовался промежуточный контактный слой. Ввод излучения производился через подложку GaAs, скошенную под углом 45°. Кривые приведены к одному масштабу. Пиковая чувствительность составила 0.015 и 0.41 А/Вт при длине волны 4.8 и 9.2 мкм соответственно.

Nikon Z6 и Nikon Z7 Полноформатные Nikon теперь и без зеркала! — Российское фото

Компания Nikon выходит в высшую беззеркальную лигу сразу с двумя моделями — Z6 и Z7. 23 сентября в Токио мы наблюдаем исторический момент — один из ведущих мировых лидеров в области производства фототехники представляет две беззеркальные полноформатные камеры и три объектива.

<!—cke_bookmark_145E—><!&amp;mdash;cke_bookmark_145E&amp;mdash;>

Обе камеры выходят на поле хорошо всем известных Sony Alpha. В них будут использованы матрицы 24 Мп и 45 Мп, самый современный электронный OLED видоискатель на 3,6 миллиона точек, 5-осевой стабилизатор, наклонный экран тачскрин и другие фишки. Особое внимание производитель обращает на байонет, размер которого превышает прямых полноформатных конкурентов. Некоторые коллеги уже сделали предположение, что новый байонет сделан «на вырост», чтобы впоследствии можно было выпустить камеру с матрицей 44×33 мм (как у среднеформатной беззеркалки Fujifilm GFX50). Но пока речь идет о камере с «обычной» полноформатной матрицей 36×24 мм, которая, в зависимости от камеры, будет с 24 Мп или 45 Мп разрешением.

Одним из отличий между моделями будет количество точек фокусировки, размещенных на матрице (покрывают 90% площади кадра): у младшей модели их будет 273, у старшей — 493. Кроме этого, старшая модель сможет снимать Timelaps с разрешением 8к. Обе камеры смогут снимать видео в разрешении 4к. Обе камеры предлагают по одному слоту для карты памяти нового формата XQD.

Разумеется, будет и поддержка всех объективов с байонетом F, которые используются на зеркальных камерах. Для этого необходимо будет приобрести переходник. Вместе с новинками, компания показала три объектива — 24-70 mm F4, 35 mm F1,8 и 50 mm F1,8. Отдельно стоит сказать, что уже в начале следующего года нам представят сверхсветосильный объектив, который будет относиться к категории NOCT. Объектив 58 мм с диафрагмой F0.95 станет самым светосильным автофокусным объективом в линейке производителя.

	Nikon Z6	Nikon Z7
Матрица	24 Мп (6048×4024)	45 Мп (7952 × 5304)
Стабилизация	Матричная, 5-осевая	Матричная, 5-осевая
Скорость съемки	До 12 кадр/с	До 9 кадр/с
ISO	100–102400	64–25600
Видео	4К, 10-bit N-Log, Full-HD/120p	4к, 8к Timelaps, 10-bit N-Log, Full-HD/120p
Видоискатель	3,6 Мп (100%) / 0. 78х	2,4 Мп (100%) / 0.78х
Фокусировка	273 фазовых датчиков	493 фазовых датчиков
Габариты	675 грамм	675 грамм
Вес	134×101×68 мм	134×101×68 мм
Дополнительно	Встроенный Wi-Fi	Встроенный Wi-Fi

Швабе — Пресс-центр — Новости

На предприятии Холдинга «Швабе» запущен в серийное производство новый тепловизионный прицел для охотничьего стрелкового оружия, который не имеет аналогов в мире по целому ряду характеристик.

Изделие создано предприятием Холдинга – АО «Швабе – Оборона и Защита» на основе микроболометрической матрицы. Оно предназначено для наблюдения и ведения прицельной стрельбы в любое время года в любых метеорологических условиях (туман, задымленность или полная темнота).

Прибор имеет десять сменных сеток для прицеливания. Используется на различных видах оружия, пристрелянных по своей баллистике на разнообразных дистанциях с сохранением параметров выверки для каждой из десяти сеток. Кроме того, прицел позволяет фиксировать процесс на фото и видео в память устройства.

Изделие обеспечивает дальность распознавания до 700 м и обнаружения – до 1200 м. Устойчиво к ударной нагрузке оружия различного калибра, имеет малый вес и самые минимальные в своем классе габаритные размеры. Автономно в работе в течение восьми часов.

«Можно с уверенностью сказать, что на сегодняшний день это лучший тепловизионный прицел не только в России, но и за рубежом. Наша флагманская, элитная модель. Разработка не имеет аналогов в мире по полю зрения, времени автономной работы, качеству картинки и дальности обнаружения. На выставке IDEX-2015 в Абу-Даби прицел вызвал неподдельный интерес у профессионалов и знатоков. Он создавался специально для охотников-промысловиков, а также для любителей спортивной и практической стрельбы, которые ценят преимущества высоких технологий», – рассказал генеральный директор АО «Швабе» Сергей Максин.

В премиальной модели применена полноформатная матрица – именно она позволила увеличить качество распознавания удаленных объектов и повысить контрастность изображения. Среди характеристик, обеспечивших прицелу лидирующие позиции как в России, так и за рубежом, дополнительно стоит отметить прочный корпус из алюминиевого сплава и герметичное исполнение. А также — 10-секундный выход в рабочий режим, беззатворную (автоматическую) калибровку матрицы, всего три управляющие кнопки и диапазон температур от –30°С до +50°С.

В настоящее время на данную модель Холдингом получен ряд заказов из разных стран.

Источник: Пресс-релиз

MM — формат файла Matrix Market

MM — это каталог данных, который содержит файлы, хранящиеся в формате, используемом Matrix Market для хранение и обмен матриц.

Характеристики файлов MM:

Формат ASCII;
разрешить строки комментариев, которые начинаются со знака процента;
используйте «координатный» формат для разреженных матриц;
используйте формат «массив» для общих плотных матриц;

Файл в формате Matrix Market состоит из четырех частей:

Строка заголовка: содержит идентификатор и четыре текстовых поля;
Строки комментариев: позволяют пользователю сохранять информацию и комментарии;
Строка размера: указывает количество строк и столбцов, и количество ненулевых элементов;
Строки данных: указывают расположение записей матрицы (неявно или явно) и их значения.

Строка заголовка имеет вид

%% MatrixMarket  объект   формат   поле   симметрия

Строка заголовка должна быть первой строкой файла, а заголовок строка должна начинаться со строки %% MatrixMarket . Четыре поля, следующие за этой строкой,

объект обычно представляет собой матрицу , и это случай мы рассмотрим здесь.Еще одно юридическое значение вектор , формат которого аналогичен, но с некоторыми очевидные упрощения.
формат — это либо координата , либо массив ;
поле либо вещественное , двойное , сложное , целое число или шаблон .
симметрия либо общий (законный для реального, сложного, целочисленные поля или поля шаблона), симметричный (действительный, комплексный, целочисленный или шаблонный), кососимметричный (действительный, комплексный или целочисленный), или эрмитский (только комплекс).

Если поле матрицы представляет собой образец , то будут перечислены только местоположения ненулевых значений. Этот предполагает, очевидно, что мы используем координату формат!

Если симметрия матрицы равна симметрии или hermitian , то только записи на или под следует указать главную диагональ. Если симметрия кососимметричный , то только записи строго под главной диагональю должны быть указаны.

Строки комментариев, если таковые имеются, должны следовать за строкой заголовка. Единственное требование — каждая строка комментария должна начинаться с знак процента.

Если формат был задан как массив , то Линия размера имеет вид:

          м п

куда

m — количество строк в матрице;
n — количество столбцов в матрице;

Если формат был указан как координата , то Линия размера имеет вид:

          m n ненулевые

куда

m — количество строк в матрице;
n — количество столбцов в матрице;
ненулевые — количество ненулевых элементов в матрице (для общей симметрии), или количество ненулевых элементов на диагонали или ниже (для симметричной или эрмитовой симметрии), или количество ненулевых элементов ниже диагонали (для кососимметричная симметрия).

Если формат был задан как массив , должно быть точно следовать м * n строк данных, одна для каждая запись, перечисленная по столбцам, имеет форму

          значение

куда

значение — это значение записи. Если поле является комплексный , требуется пара действительных чисел.

Если формат был задан как координата , то должно быть следовать ровно ненулевых строк данных, одна для каждая запись матрицы, которая должна быть указана, имеет вид

          i j значение

куда

i — строка записи;
j — столбец записи;
значение — это значение записи.Если поле является комплексный , требуется пара действительных чисел. Если значение формата было шаблон , тогда значение не перечислены здесь; встречаются только значения i и j .

Лицензирование:

Компьютерный код и файлы данных, описанные и доступные на этой веб-странице распространяются по лицензия GNU LGPL.

Ссылка:

http: // math.nist.gov/MatrixMarket/
Веб-сайт Matrix Market.
Рональд Бойсверт, Ролдан Позо, Карин Ремингтон,
Матричные форматы рыночного обмена: первоначальный дизайн,
Технический отчет NISTIR-5935,
Национальный институт стандартов и технологий, декабрь 1996 г.

Образцы файлов:

gr_900_900_crg.mm, матрица 900 на 900 в КООРДИНАТНОЙ ИСТИННОЙ ОБЩЕЙ форме.
gre_343_343_crg.мм, матрица 343 на 343 в КООРДИНАТНОЙ РЕАЛЬНОЙ ОБЩЕЙ форме.
m_04_03_arg.mm, матрица 4 на 3 в ОБЩЕЙ форме ARRAY REAL GENERAL.
m_05_05_cch.mm, матрица 5 на 5 в КООРДИНАТНО-КОМПЛЕКСНОЙ ЭРМИЦИАНСКОЙ форме.
m_05_05_cig.mm, матрица 5 на 5 в КООРДИНАТНОЙ ЦЕЛОЙ ОБЩЕЙ форме.
m_05_05_cpg.mm, матрица 5 на 5 в ОБЩЕЙ форме КООРДИНАТНЫЙ ШАБЛОН.
m_05_05_crk.mm, матрица 5 на 5 в КООРДИНАТНОЙ РЕАЛЬНО-СИММЕТРИЧНОЙ форме.
m_05_05_crg.mm, матрица 5 на 5 в КООРДИНАТНОЙ ИСТИННОЙ ОБЩЕЙ форме.
m_05_05_crs.mm, матрица 5 на 5 в КООРДИНАТНОЙ РЕАЛЬНО-СИММЕТРИЧНОЙ форме.
wathen_29_29_adg. mm, матрица 29 на 29 в ОБЩЕЙ форме ARRAY DOUBLE GENERAL.
west_67_67_crg.мм, матрица 67 на 67 в КООРДИНАТНОЙ ИСТИННОЙ ОБЩЕЙ форме.

Вы можете подняться на один уровень до страницу ДАННЫЕ.

Последний раз редактировалось 25 марта 2006 г.

Работа с разреженной матрицей в R

Разреженные матрицы необходимы для работы с большими одноклеточными последовательностями РНК. наборы данных. Они требуют меньше памяти, чем плотные матрицы, и позволяют вычисления, чтобы быть более эффективными. В этой заметке мы обсудим внутреннее устройство класс dgCMatrix с примерами.

Давайте начнем с установки и загрузки пакета Matrix, который предоставляет классы разреженных матриц, которые мы используем в этой заметке.

  инсталляционных пакетов («Матрица»)
библиотека (Матрица)

Ниже мы рассмотрим два формата Matrix и их соответствующие классы:

Формат триплета в классе dgTMatrix
Формат сжатых столбцов в классе dgCMatrix

dgTMatrix — это класс из пакета Matrix R, который реализует:

общие числовые разреженные матрицы в (возможно избыточном) формате триплета

Формат понятен:

Предположим, что все неуказанные элементы в матрице равны нулю.
Определите ненулевые записи в триплетной форме (i, j, x) где:
- i — номер строки
- j — номер столбца
- x — это значение

Вот и все. Сделаем один:

  m <- Матрица (nrow = 3, ncol = 6, data = 0, sparse = TRUE)
m <- as (m, "dgTMatrix") # по умолчанию Matrix () возвращает dgCMatrix
м [1,2] <- 10
м [1,3] <- 20
м [3,4] <- 30
м

  ## 3 x 6 разреженная матрица класса "dgTMatrix"
##
## [1,].10 20. . .
## [2,]. . . . . .
## [3,]. . . 30. .

А давайте посмотрим, что внутри:

  ## Формальный класс 'dgTMatrix' [пакет «Матрица»] с 6 слотами
## .. @ i: int [1: 3] 0 0 2
## .. @ j: int [1: 3] 1 2 3
## .. @ Dim: int [1: 2] 3 6
## .. @ Dimnames: Список из 2
## .. .. $: NULL
## .. .. $: NULL
## .. @ x: num [1: 3] 10 20 30
## .. @ факторы: list ()

Объект имеет слоты i , j и x .

Мы можем восстановить приведенную выше разреженную матрицу следующим образом:

  d <- data.frame (
  i = m @ i + 1, # m @ i отсчитывается от 0, а не от 1, как все остальное в R
  j = m @ j + 1, # m @ j отсчитывается от 0, а не от 1, как все остальное в R
  х = м @ х
)
d

  ## i j x
## 1 1 2 10
## 2 1 3 20
## 3 3 4 30

  sparseMatrix (i = d $ i, j = d $ j, x = d $ x, dims = c (3, 6))

  ## 3 x 6 разреженная матрица класса "dgCMatrix"
##
## [1,].10 20. . .
## [2,]. . . . . .
## [3,]. . . 30. .

Мы можем преобразовать разреженную матрицу во фрейм данных следующим образом:

  as.data.frame (сводка (м))

  ## i j x
## 1 1 2 10
## 2 1 3 20
## 3 3 4 30

Поскольку м @ x дает нам доступ к значениям данных, мы можем легко преобразовать значения с log2 () :

Файлы

Matrix Market часто имеют расширение .mtx .

Запишите файл Matrix Market:

  ## NULL

Дамп содержимого файла:

  ## [1] "%% матрица MatrixMarket координата вещественная общая"
## [2] "3 6 3"
## [3] «1 2 3.4594316186372973 "
## [4] "1 3 4.3422778761"
## [5] "3 4 4.954196310386875"

Это формат файла Matrix Market:

Первая строка - это комментарий (начинается с %% ).
В следующей строке указано, что имеется 3 строки, 6 столбцов и 3 ненулевых значения.
Следующие 3 строки описывают значения в тройном формате (i, j, x) .

Прочитать файл Matrix Market:

  m <- readMM ("матрица.mtx ")
м

  ## 3 x 6 разреженная матрица класса "dgTMatrix"
##
## [1,]. 3,459432 4,3. . .
## [2,]. . . . . .
## [3,]. . . 4.954196. .

Преобразование из dgTMatrix в dgCMatrix с помощью:

  ## 3 x 6 разреженная матрица класса "dgCMatrix"
##
## [1,]. 3,459432 4,3. . .
## [2,]. . .. . .
## [3,]. . . 4.954196. .

dgCMatrix - это класс из пакета Matrix R, который реализует:

общих числовых разреженных матрицы в (отсортированном) сжатом разреженном столбце формат

Это наиболее распространенный тип матриц, с которыми мы сталкиваемся, когда имеем дело с с данными scRNA-seq.

Сделаем разреженную матрицу в формате dgCMatrix :

  библиотека (матрица)
m <- Матрица (nrow = 3, ncol = 6, data = 0, sparse = TRUE)
м [1,2] <- 10
м [1,3] <- 20
м [3,4] <- 30
м

  ## 3 x 6 разреженная матрица класса "dgCMatrix"
##
## [1,].10 20. . .
## [2,]. . . . . .
## [3,]. . . 30. .

Заглянем внутрь:

  ## Формальный класс 'dgCMatrix' [пакет «Матрица»] с 6 слотами
## .. @ i: int [1: 3] 0 0 2
## .. @ p: int [1: 7] 0 0 1 2 3 3 3
## .. @ Dim: int [1: 2] 3 6
## .. @ Dimnames: Список из 2
## .. .. $: NULL
## .. .. $: NULL
## .. @ x: num [1: 3] 10 20 30
## .. @ факторы: list ()

Объект имеет 6 слотов, включая Dim , i , x и p .

Dim имеет размеры матрицы (3 строки, 6 столбцов):

  ## [1] 3 6

x имеет значения данных, отсортированные по столбцам (сверху вниз, слева направо):

  ## [1] 10 20 30

i имеет индексы строк для каждого значения данных. Примечание: i отсчитывается от 0, а не от 1 как и все в р.

  ## [1] 0 0 2

А как насчет p ? В отличие от j , p не , а сообщает нам, в каком столбце каждое значение данных нас в.

  ## [1] 0 0 1 2 3 3 3

p имеет кумулятивное количество значений данных при переходе от одного столбца в следующий столбец слева направо. Первое значение всегда 0, а длина p на единицу больше, чем количество столбцов.

Мы можем вычислить p для любой матрицы:

  c (0, cumsum (colSums (m! = 0)))

  ## [1] 0 0 1 2 3 3 3

Поскольку p - это кумулятивная сумма, мы можем использовать diff () , чтобы получить количество ненулевые записи в каждом столбце:

  ## [1] 0 1 1 1 0 0

  ## [1] 0 1 1 1 0 0

Длина p на единицу больше, чем количество столбцов:

  ## [1] 7

  ## [1] 7

Учитывая p , мы можем вычислить j :

  rep (1: m @ Dim [2], diff (m @ p))

  ## [1] 2 3 4

В большинстве случаев проще использовать summary () для преобразования разреженной матрицы в триплет (i, j, x) формат .

  ## [1] 2 3 4

Еще один пример может помочь прояснить, как i , x и p изменяются, когда мы изменить матрицу:

  # Добавить еще значения в матрицу
м [2,2] <- 50
м [2,3] <- 50
м [2,4] <- 50
м

  ## 3 x 6 разреженная матрица класса "dgCMatrix"
##
## [1,]. 10 20. . .
## [2,]. 50 50 50. .
## [3,]. . . 30. .

  ## Формальный класс 'dgCMatrix' [пакет «Матрица»] с 6 слотами
##.. @ i: int [1: 6] 0 1 0 1 1 2
## .. @ p: int [1: 7] 0 0 2 4 6 6 6
## .. @ Dim: int [1: 2] 3 6
## .. @ Dimnames: Список из 2
## .. .. $: NULL
## .. .. $: NULL
## .. @ x: num [1: 6] 10 50 20 50 50 30
## .. @ факторы: list ()

Мы знаем, что p [1] всегда равно 0.

В столбце 1 0 значений, поэтому p [2] равно 0.

В столбце 2 2 значения, поэтому p [3] равно 0 + 2 = 2.

В столбце 3 2 значения, поэтому p [4] равно 2 + 2 = 4.

В столбце 4 2 значения, поэтому p [5] равно 4 + 2 = 6.

Столбцы 5 и 6 содержат 0 значений, поэтому p [6] и p [7] равны 6 + 0 = 6.

Вот визуальное представление м @ p для этого примера:

Вектор p имеет кумулятивное количество значений данных при переходе от одного столбец к следующему столбцу слева направо.

  # Большая матрица
set.seed (1)
m <- sparseMatrix (
  i = образец (x = 1e4, size = 1e4),
  j = образец (x = 1e4, size = 1e4),
  x = rnorm (n = 1e4)
)
pryr :: размер_объекта (м)

  ## 162 Кбайт

  pryr :: object_size (как.matrix (m)) # Плотные матрицы требуют гораздо больше памяти (RAM)

  ## 800 МБ

Вычислить разреженность матрицы:

  разреженность <- длина (м @ x) / м @ Dim [1] / м @ Dim [2]
редкость

  ## [1] 1e-04

При записи файлов Matrix Market не забудьте использовать сжатие gzip для сохранения диска Космос.

Размер несжатого файла:

  bytes_uncompressed <- file.size ("matrix.mtx")
scale :: number_bytes (несжатые байты)

  ## [1] "281 KiB"

Сжатие файла может сэкономить 50% дискового пространства:

  система ("gzip --keep matrix.mtx ")
file.size ("matrix.mtx.gz") / bytes_uncompressed

  ## [1] 0,4883699

Чтение несжатого или несжатого файла занимает примерно столько же времени Файлы Matrix Market:

  стенд :: mark (
  m <- readMM ("matrix.mtx"),
  m <- readMM ("matrix.mtx.gz")
)

  ## # Тибл: 2 x 6
## выражение min median `itr / sec` mem_alloc` gc / sec`
##      
## 1 m <- readMM ("матрица.mtx ") 6,63 мс 7,12 мс 140 626 КБ 0
## 2 m <- readMM ("matrix.mtx.gz") 7,32 мс 8,31 мс 121. 626 КБ 0

Поскольку функция writeMM () не принимает объект подключения, это не работает:

  writeMM (m, gzfile ("matrix.mtx.gz")) ## Это не работает :(

Вместо этого мы можем написать нашу собственную функцию:

  # '@param x Разреженная матрица из пакета Matrix.
# '@param file Имя файла, заканчивающееся на ".gz ".
writeMMgz <- function (x, file) {
  mtype <- "настоящий"
  if (is (x, "ngCMatrix")) {
    mtype <- "целое число"
  }
  writeLines (
    c (
      sprintf ("%%%% Координата матрицы MatrixMarket% s общая", mtype),
      sprintf ("% s% s% s", x @ Dim [1], x @ Dim [2], длина (x @ x))
    ),
    gzfile (файл)
  )
  data.table :: fwrite (
    x = сводка (x),
    файл = файл,
    append = TRUE,
    sep = "",
    row.names = ЛОЖЬ,
    col.names = ЛОЖЬ
  )
}

Подтвердите, что работает:

  writeMMgz (m, "матрица2.mtx.gz ")

all.equal (readMM ("matrix.mtx.gz"), readMM ("matrix2.mtx.gz"))

  ## [1] ИСТИНА

Сделаем плотную копию 10,000 на 10000 разреженных матриц.

Напомним, что только 10 000 (0,01%) элементов этой матрицы не равны нулю.

Многие операции с разреженными матрицами выполняются намного быстрее:

  стенд :: mark (
  colSums (м),
  colSums (d)
)

  ## # Тибл: 2 x 6
## выражение min median `itr / sec` mem_alloc` gc / sec`
##      
## 1 столбец (м) 343.6 мкс 447,5 мкс 2194. 261 КБ 0
## 2 столбца (d) 91,9 мс 92,6 мс 10,6 78,2 КБ 0

  стенд :: mark (
  rowSums (м),
  rowSums (d)
)

  ## # Тибл: 2 x 6
## выражение min median `itr / sec` mem_alloc` gc / sec`
##      
## 1 rowSums (m) 405µs 511µs 1973. 234.6KB 2.02
## 2 rowSums (d) 167 мс 169 мс 5,92 78,2 КБ 0

Предположим, мы хотим свернуть столбцы, суммируя группы столбцов в соответствии с другая переменная.

  набор. Семян (1)
y <- образец (1:10, размер = ncol (m), replace = TRUE)
таблица (y)

  ## y
## 1 2 3 4 5 6 7 8 9 10
## 980 937 972 1018 974 979 1072 1023 1015 1030

Превратим переменную в матрицу модели:

  ymat <- модель.матрица (~ 0 + коэффициент (y))
colnames (ymat) <- 1:10
голова (ymat)

  ## 1 2 3 4 5 6 7 8 9 10
## 1 0 0 0 0 0 0 0 0 1 0
## 2 0 0 0 1 0 0 0 0 0 0
## 3 0 0 0 0 0 0 1 0 0 0
## 4 1 0 0 0 0 0 0 0 0 0
## 5 0 1 0 0 0 0 0 0 0 0
## 6 0 0 0 0 0 0 1 0 0 0

  ## 1 2 3 4 5 6 7 8 9 10
## 980 937 972 1018 974 979 1072 1023 1015 1030

А теперь мы можем свернуть столбцы, принадлежащие каждой группе:

  x1 <- m% *% yмат
x2 <- d% *% ymat
все.равно (как матрица (x1), x2)

  ## [1] ИСТИНА

  all.equal (x1 [, 1], rowSums (m [, y == 1]))

  ## [1] ИСТИНА

  all.equal (x1 [, 2], rowSums (m [, y == 2]))

  ## [1] ИСТИНА

  ## [1] 10000 10

  ## 6 x 10 Матрица класса "dgeMatrix"
## 1 2 3 4 5 6 7 8 9 10
## [1,] 0 0 0 0 0 0 0,00000000 0,00000000 -0.5578692 0,0000000
## [2,] 0 0 0 0 0 0 0,74277916 0,00000000 0,0000000 0,0000000
## [3,] 0 0 0 0 0 0 0,00000000 0,00000000 0,0000000 1,5986887
## [4,] 0 0 0 0 0 0 0,00000000 0,00000000 0,0000000 0,8402201
## [5,] 0 0 0 0 0 0 0,00000000 -0,09295838 0,0000000 0,0000000
## [6,] 0 0 0 0 0 0 -0,05341102 0,00000000 0,0000000 0,0000000

На моем компьютере эта операция с данными выполняется в 100 раз быстрее с разреженным матрица, чем с плотной матрицей.

  стенд :: mark (
  m% *% ymat,
  d% *% ymat,
  check = FALSE
)

  ## # Тибл: 2 x 6
## выражение min median `itr / sec` mem_alloc` gc / sec`
##      
## 1 мкс *% ymat 603 мкс 844 мкс 1077.1,75 МБ 4,18
## 2 d% *% ymat 838 мс 838 мс 1,19 781,3 КБ 0

Вы можете попробовать эти пакеты для работы с разреженными матрицами в R:

Дополнительные сведения о дополнительных форматах матриц см. В виньетках из пакет Matrix R.

И узнайте больше о более быстрых вычислениях с разреженными матрицами в этом виньетка.

SPARSEKIT - Пакет служебных программ для разреженной матрицы

SPARSEKIT это библиотека FORTRAN90, которая выполняет ряд операции с разреженными матрицами, в частности, преобразование между различные разреженные форматы.

SPARSEKIT может работать с разреженными матрицами в различных форматах, и может конвертировать из одного в другой. Например, матрица может быть преобразован из обобщенного диагонального формата, используемого ELLPACK и ITPACK в формат, используемый разреженной матрицей Харвелла-Боинга Коллекция или в формате с полосами LINPACK.

Доступные утилиты включают преобразование структур данных, простую печать. статистика по матрице, построение профиля матрицы, выполнение основных операции линейной алгебры (аналогичные BLAS для плотной матрицы), и так далее.

Распознаваемые форматы матриц включают:

BND , формат LINPACK для стандартных ленточных матриц.
BSR , блочно-строчный разреженный формат.
COO , формат координат.
CSC , формат сжатых разреженных столбцов.
CSR , сжатый формат разреженных строк.
DIA , формат разреженной диагональной матрицы (НЕ диагональной матрицы!).
DIAG , диагональная матрица, хранящаяся как вектор.
DNS , плотное хранилище, также называемое полным хранилищем.
ELL , ELLPACK / ITPACK, формат, используемый ELLPACK и ITPACK.
HB , формат Harwell-Boeing.(Собственно, формат CSR плюс вспомогательные данные)
JAD , диагональный формат с зазубринами.
LNK , формат связанного хранилища.
MSC , модифицированный формат разреженных столбцов.
MSR , модифицированный формат разреженных строк.
SSK , Симметричный формат горизонта.
SSR , Симметричный формат разреженных строк.

Языки:

SPARSEKIT доступен в версия FORTRAN90.

Связанные данные и программы:

CSPARSE, библиотека C, которая выполняет прямое решение разреженных линейных систем.

DLAP, библиотека FORTRAN90, которая решает разреженные линейные системы.

HB_IO, библиотека FORTRAN90, которая читает и пишет разреженные линейные системы, хранящиеся в формате разреженной матрицы Harwell-Boeing.

HB_TO_ST, программа FORTRAN77, которая преобразует разреженную матричную информацию, хранящуюся в Harwell-Boeing файл в разреженный тройной файл.

МГМРЕС, г. библиотека FORTRAN90, которая применяет перезапущенный алгоритм GMRES решить разреженную линейную систему.

MM_IO, библиотека FORTRAN90, которая читает и пишет разреженные линейные системы, хранящиеся в формате Matrix Market.

SPARSE_CC, каталог данных, который содержит описание и примеры формата CC, («сжатый столбец») для хранения разреженной матрицы, включая способ записи матрицы в виде набора из трех файлов.

SPARSE_CR, каталог данных, который содержит описание и примеры формата CR, («сжатая строка») для хранения разреженной матрицы, включая способ записи матрицы в виде набора из трех файлов.

СПАРСЕПАК, библиотека FORTRAN90, которая переупорядочивает и решает разреженные линейные системы.

Ссылка:

Эфстратиос Галлопулос, Юсеф Саад,
Эффективное решение параболических уравнений Крылова методы аппроксимации,
Технический отчет RIACS, 90-14.
Ноборо Кикучи,
Методы конечных элементов в механике,
Издательство Кембриджского университета, 1986.
Дэвид Кинкейд, Томас Оппе, Джон Респесс, Дэвид Янг,
Руководство пользователя ITPACKV 2C,
Технический отчет CNA-191.
Центр численного анализа,
Техасский университет в Остине, 1984.
Дональд Кнут,
Искусство программирования,
Том 3: Сортировка и поиск,
Аддисон-Уэсли, 1973.
Оле Остерби, Захари Златев,
Прямые методы для разреженных матриц,
Springer-Verlag 1983.
Юсеф Саад,
Sparsekit: базовый набор инструментов для вычислений разреженных матриц,
Технический отчет, Департамент компьютерных наук, Университет Миннесоты
, июнь 1994 г.
Юсеф Саад,
Анализ приближения некоторых подпространств Крылова к матричный экспоненциальный оператор,
Технический отчет RIACS, 90-14.
Юсеф Саад,
Итерационные методы для разреженных линейных систем,
, второе издание,
SIAM, 2003,
ISBN: 0898715342.
Захари Златев, Кьельд Шаумбург, Ежи Васневски,
Схема тестирования подпрограмм, решающих большие линейные задачи,
Компьютеры и химия,
Том 5, номер 2-3, страницы 91-100, 1981.

Исходный код:

Примеры и тесты:

Пример задачи 1:

Пример задачи 2:

Пример задачи 3:

Пример задачи 4 берет ленточную матрицу порядка 16, сохраненную как плотная матрица, преобразует его в формат CSR и отсортированный CSR формат.

Пример задачи 5:

Пример задачи 6:

Пример задачи 7:

Пример задачи 8 генерирует три выборочные матрицы из Златев установил, и записал их в файлы формата Harwell-Boeing:

Пример задачи 9:

Пример задачи 10:

Пример задачи 11:

Пример задачи 12:

Пример задачи 13:

Пример задачи 14 генерирует образец матрицы CSR и преобразует его в NCF (несимметричный формат координат) используется NSPCG.

Список программ:

AMASK извлекает разреженную матрицу из замаскированной входной матрицы.
AMUB выполняет матрицу по матричному произведению C = A * B.
AMUBDG получает количество ненулевых элементов в каждой строке A * B.
AMUDIA выполняет матрицу по матричному произведению B = A * Diag (на месте)
AMUX умножает матрицу CSR A на вектор.
AMUXD умножает матрицу DIA на вектор.
AMUXE умножает матрицу ELL на вектор.
AMUXJ умножает матрицу JAD на вектор.
APLB выполняет матричную сумму CSR C = A + B.
APLB1 выполняет матричную сумму C = A + B для матриц в отсортированном формате CSR.
APLBDG получает количество ненулевых элементов в каждой строке A + B и общее
APLDIA добавляет диагональную матрицу к общей разреженной матрице: B = A + Diag
APLSB выполняет матричную линейную комбинацию C = A + s * B
APLSB1 выполняет операцию C = A + s B для матриц в отсортированном формате CSR.
APLSBT выполняет матричную сумму C = A + B '.
APLSCA добавляет скаляр к диагональным элементам разреженной матрицы A: = A + s I
APMBT выполняет матричную сумму C = A + B 'или C = A - B'.
АССМБ1 ???
АССМБО ???
ATMUX вычисляет A '* x для матрицы A CSR.
BLKCHK проверяет, является ли входная матрица блоком
BLKFND пытается определить, является ли ввод
BNDCSR преобразует формат Banded Linpack в формат Compressed Sparse Row.
BOUND подсчитывает количество граничных точек и
BSORT2 простая пузырьковая сортировка для получения наибольшего ncut
BSRCSR преобразует блочную разреженную строку в сжатую разреженную строку.
BSTEN вычисляет правильные значения трафарета блока для
CHECKREF возвращает ожидаемое новое количество узлов и
CHKELMT проверяет маркировку в каждом элементе и переупорядочивает
CNRMS получает нормы каждого столбца A. (выбор из трех норм)
COICSR на месте преобразует COO в CSR.
COOCSR преобразует COO в CSR.
COOELL преобразует формат координат в формат ellpack.
COPMAT копирует матрицу a, ja, ia в матрицу ao, jao, iao.
CPERM переставляет столбцы матрицы.
CSCAL масштабирует столбцы A так, чтобы их нормы были равны единице при возврате
CSORT сортирует элементы матрицы (хранящиеся в Compressed
CSRBND преобразует сжатые разреженные строки в формат с полосами (Linpack).
CSRBSR преобразует сжатую разреженную строку в блочную разреженную строку
CSRCOO преобразует сжатую разреженную строку в координаты
CSRCSC преобразует сжатую разреженную строку в сжатый разреженный столбец
CSRDIA преобразует сжатую разреженную строку в диагональный формат
CSRDNS преобразует сжатые разреженные строки в плотные
CSRELL конвертирует сжатые разреженные строки в формат Ellpack - Itpack
CSRJAD преобразует сжатые разреженные строки в хранилище JAgged Diagonal.
CSRLNK преобразует сжатую разреженную строку в формат связанного хранилища.
CSRMSR преобразует сжатую разреженную строку в измененную - разреженную строку
CSRSSK преобразует сжатую разреженную строку в формат симметричного горизонта
CSRSSR преобразует сжатую разреженную строку в симметричную разреженную строку
DCN генерирует разреженные квадратные матрицы типа D (N, C).
DCSORT вычисляет перестановку, которая при применении к
DIACSR преобразует диагональный формат в сжатую разреженную строку
DIAMUA выполняет матрицу по матричному произведению B = Diag * A (на месте)
DIAPOS возвращает позиции диагональных элементов
DINFO1 вычисляет и распечатывает матричную статистику.
DIRIC учитывает граничные условия
DLAUNY - это простой неоптимальный код триангуляции Делоне.
DNSCSR преобразует плотные в сжатые разреженные строки
DPERM переставляет строки и столбцы матрицы, хранящейся в CSR
DSCALDG масштабирует строки по диагонали, где либо указан диагноз (задание = 0)
DUMP записывает матрицу в файл, по одной строке за раз в хорошо читаемом
DVPERM выполняет перестановку действительного вектора x на месте
ECN генерирует разреженные (квадратные) матрицы типа E (N, C).
ELLCSR преобразует Ellpack-Itpack в сжатую разреженную строку.
ESTIF3 строит матрицу жесткости элементов с использованием трехузловых треугольных элементов.
EXPHES вычисляет базис Арнольди и соответствующий
EXPPRO вычисляет приближение вектора
EXPPROD вычисляет приближение вектора
EXTBDG извлекает блоки главной диагонали
ФИЛЬТР удаляет все элементы, абсолютное значение которых
GEN57BL вычисляет разреженную матрицу в сжатом
GEN57PT вычисляет разреженную матрицу в сжатом
GENFEA генерирует матрицы конечных элементов для тепла
GENFEU генерирует матрицы конечных элементов для тепла
GETBWD получает полосу пропускания нижней и верхней части A.
GETDIA извлекает заданную диагональ из матрицы, хранящейся в CSR
GETELM возвращает элемент a (i, j) матрицы A,
GETL извлекает нижнюю треугольную часть матрицы
GETSTEN вычисляет правильные значения трафарета для
GETU извлекает верхнюю треугольную часть матрицы
GRADI3 строит первую производную функций формы.
HES вычисляет exp (H dt) * y (1)
HSOURC генерирует вектор нагрузки f в собранном виде из
ILU0 - это предварительный кондиционер ILU (0).
ILUT - это предварительный кондиционер ILUT.
INFDIA получает информацию о диагоналях A.
IVPERM выполняет перестановку целочисленного вектора на месте
JADSCR преобразует хранилище с неровной диагональю в сжатые разреженные строки
LDSOL решает L x = y L = треугольный.Формат MSR
LDSOLC решает L x = y; L = без единицы Низкий. Треугольник. Формат MSC
LDSOLL решает L x = y L = треугольный. Использует формат LEVEL SCHEDULING / MSR
УРОВНИ получает структуру уровней нижней треугольной матрицы
LNKCSR преобразует формат хранения связанных списков в формат сжатых разреженных строк.
LSOL решает L x = y; L = нижний единичный треугольник. / Формат CSR
LSOLC решает L x = y; где L = нижний предел единицы. Формат CSC
LUSOL0 выполняет прямое решение с последующим обратным вычислением
MARKGEN - матричный генератор для марковской модели случайного блуждания по треугольнику. сетка
MATRF2 генерирует разреженные (прямоугольные или квадратные) матрицы.
MGSR представляет собой модифицированный грамм-шмидт с частичной реорто.
MILU0 - это простой предварительный кондиционер milu (0). *** *
MSRCSR преобразует измененную - разреженную строку в сжатую разреженную строку
PGMRES - это программа расчета GMRES с предварительной подготовкой ILUT.
PLTMT создает файл 'pic' для построения шаблона
PLTMTPS создает файл «PS» для построения шаблона
PRTMT записывает матрицу в формате Harwell-Boeing в файл.
READMT считывает матрицу Boeing / Harwell. обрабатывает правую руку
REFALL уточняет сетку конечных элементов с использованием треугольных элементов.
RETMX возвращает в формате dd (*) максимальное абсолютное значение элементов в строке *.
RNRMS получает нормы каждой строки A. (выбор из трех норм)
RPERM переставляет строки матрицы в формате CSR.
RSCAL масштабирует строки A таким образом, чтобы их нормы равнялись единице при возврате
SSKSSR преобразует формат симметричного горизонта в формат симметричных разреженных строк.
SSRCSR преобразует симметричную разреженную строку в (обычную) сжатую разреженную строку
SUBMAT извлекает подматрицу A (i1: i2, j1: j2) и помещает результат в
TRANSP выполняет процедуру транспонирования на месте.
UDSOL решает U x = y; U = верхний треугольник в формате MSR
UDSOLC Решает U x = y; U = без единицы Up. Треугольник. Формат MSC
UNASSBL ???
USOL решает U x = y U = единичный верхний треугольник.
USOLC решает U x = y; где U = верхний предел единицы.Формат CSC
SAXPY ПОСТОЯННОЕ ВРЕМЯ ВЕКТОР ПЛЮС ВЕКТОР.
SDOT ОБРАЗЫВАЕТ ТОЧЕЧНЫЙ ПРОДУКТ ДВУХ ВЕКТОРОВ.

Вы можете подняться на один уровень до исходные коды FORTRAN90.

Последняя редакция 30 августа 2005 г.

Введение в разреженные матрицы в R

Часто вы можете иметь дело с большими разреженными матрицами с несколькими ненулевыми элементами.В таких сценариях хранение данных в полной плотной матрице и работа с ней неэффективны.

Лучший способ справиться с такими разреженными матрицами - использовать специальные структуры данных, которые позволяют эффективно хранить разреженные данные. В R пакет Matrix предлагает отличные решения для работы с большими разреженными матрицами.

В этом посте мы увидим простые пошаговые примеры использования библиотеки Matrix. Мы начнем с использования разреженных матриц в R, ответив на следующие вопросы.

Как создать разреженную матрицу из плотной матрицы?
Как визуализировать разреженную матрицу?
Как создать разреженную матрицу из разреженных данных?
Как сохранить разреженную матрицу в файл?

В следующих статьях мы подробнее рассмотрим использование других функций, доступных в пакете Matrix.

библиотека (Матрица)

Создадим матрицу с разреженными данными с нуля. Сначала мы создадим данные, вектор с миллионами случайных чисел из нормального распределения с нулевым средним и единичной дисперсией.

данные <- rnorm (1e6)

Указанный выше вектор данных не является разреженным и содержит данные во всех элементах. Давайте случайным образом выберем индексы и заставим их содержать нули.

данные <- rnorm (1e6)
zero_index <- образец (1e6) [1: 9e5]
данные [нулевой_индекс] <- 0

Теперь мы создали вектор из миллиона элементов, но 90% элементов - нули. Превратим его в плотную матрицу.

mat <- матрица (данные, ncol = 1000)
мат [1: 5,1: 5]

Мы видим, что в матрице очень мало ненулевых элементов.

## [, 1] [, 2] [, 3] [, 4] [, 5]
## [1,] 0 0,000000 0 0 0
## [2,] 0 0,000000 0 0 0
## [3,] 0 1,817244 0 0 0
## [4,] 0 1.580687 0 0 0
## [5,] 0 0,000000 0 0 0

Мы можем использовать функцию R object.size и проверить размер плотной матрицы.

print (object.size (mat), units = "auto")

Плотная матрица близкая к 8Мб.

## 7.6 Мб

Как создать разреженную матрицу из плотной матрицы в R?

Давайте воспользуемся библиотекой разреженных матриц для преобразования плотной матрицы в разреженную матрицу.

mat_sparse <- Матрица (mat, sparse = TRUE)

Проверим, как данные хранятся в разреженной матрице. Мы видим, что элементы без значений показаны точками.

mat_sparse [1: 5,1: 5]

## 5 x 5 разреженная матрица класса "dgCMatrix"
##
## [1,].. . . .
## [2,]. . . . .
## [3,]. 1,817244. . .
## [4,]. 1,580687. . .
## [5,]. . . . .

Это говорит нам, что наша разреженная матрица принадлежит классу «dgCMatrix». Есть разные типы разреженных матриц. Каждый тип разреженной матрицы подходит для определенных математических операций, а также для чтения, записи и хранения. В нашем примере наши данные имеют тип double. А тип разреженной матрицы «dgCMatrix» относится к двойной разреженной матрице, хранящейся в формате CSC (сжатый разреженный столбец).Разреженная матрица в формате CSC - это формат, ориентированный на столбцы, и он реализован таким образом, что ненулевые элементы в столбцах сортируются в порядке возрастания строк.

Давайте проверим размер нашей разреженной матрицы.

print (object.size (mat_sparse), units = "auto")

## 1.1 Мб

В разреженной матрице одни и те же данные хранятся примерно на 1 Мбайт, что намного эффективнее, чем у плотной матрицы. Примерно в семь раз меньше плотной матрицы.

Как визуализировать разреженную матрицу в R?

Давайте быстро визуализируем небольшую часть разреженной матрицы с помощью функции image в R.Мы можем видеть матрицу преимущественно белого цвета, то есть разреженную без данных.

изображение (mat_sparse [1: 10,1: 10])

Визуализация разреженной матрицы в R

Как создать разреженную матрицу с нуля в R?

Наш пример создания разреженной матрицы был довольно глупым. Мы начали с плотной матрицы и преобразовали в разреженную матрицу. Мы сделали это, чтобы проиллюстрировать преимущества разреженной матрицы. В реальной жизни мы часто имеем разреженную матрицу в разреженной форме.

Лучший способ создать разреженную матрицу - начать с данных в разреженном формате.Самый простой способ сохранить данные в разреженной форме - сохранить координаты только ненулевых элементов. По сути, нам нужны три вектора одинакового размера. Первые два вектора определяют координаты (i, j) ненулевого элемента, где i - индекс строки, а j - индекс столбца. И третий вектор хранит фактические ненулевые значения.

Давайте создадим разреженную матрицу, соответствующую плотной матрице 10 × 10, такую, что матрица содержит всего 5 ненулевых элементов.

# 5 случайные индексы строк
я <- образец (10,5)
# 5 случайные индексы столбцов
j <- образец (10,5)
# 5 случайные числа
х <- rpois (5,10)

Мы можем использовать функцию sparseMatrix и задавать значения i, j и x в качестве аргументов, а также указывать размерность плотной матрицы.

sp_matrix <- sparseMatrix (i = i, j = j, x = x, dims = list (10,10))

Функция

sparseMatrix создает для нас разреженную матрицу, и мы можем видеть контент, просто распечатывая его.

sp_matrix

## 10 x 10 разреженная матрица класса "dgCMatrix"
##
## [1,]. . . . . . 11. . .
## [2,] 5. . . . . . . . .
## [3,]. . . . . . . . . .
## [4,]. . . . . . . . . .
## [5,]. 10. . . . . .. .
## [6,]. . . . . . . . . .
## [7,]. . . . . . . . . 8
## [8,]. . . 10. . . . . .
## [9,]. . . . . . . . . .
## [10,]. . . . . . . . . .

Как сохранить разреженную матрицу в файл?

Вы также хотите сохранить разреженную матрицу и использовать ее позже. Один из способов сохранить разреженные матрицы - сохранить их в виде файла Mtx, в котором матрица хранится в формате MatrixMarket.

Мы можем использовать функцию writeMM , чтобы сохранить объект разреженной матрицы в файл.В этом примере мы сохраняем нашу игрушечную разреженную матрицу в файл с именем «sparse_matrix.mtx».

writeMM (obj = sp_matrix, file = "sparse_matrix.mtx")

Мы можем загрузить сохраненные данные разреженной матрицы в разреженную матрицу, используя функцию readMM . Мы видим, что это то же самое, что и сохраненное, но на этот раз это класс dgTMatrix.

sp_matrix_read <- readMM ("sparse_matrix.mtx")
sp_matrix_read

## 10 x 10 разреженная матрица класса "dgTMatrix"
##
## [1,].. . . . . . . . .
## [2,]. . . . . . 4. . .
## [3,]. . . . . . . . . .
## [4,]. . . 18. . . . . .
## [5,]. . 10. . . . . . .
## [6,]. . . . . . . . . .
## [7,]. . . . 8. . . . .
## [8,]. . . . . . . . . .
## [9,]. . . . . . . . . .
## [10,]. . . . . . . 9. .

Таким образом, в этом посте мы узнали, как начать использовать структуру данных разреженной матрицы в R. В частности, мы научились создавать разреженную матрицу из плотной матрицы, визуализировать часть разреженной матрицы, создавать разреженную матрицу в R из трех векторов, чтобы записать разреженную матрицу в файл и загрузить разреженную матрицу, хранящуюся в формате MarketMatrix, в структуру данных разреженной матрицы.

Настройтесь на будущую публикацию о том, как использовать разреженную матрицу в распространенных статистических приложениях и приложениях машинного обучения, имеющих отношение к практике науки о данных.

Работа с данными в матрице

Загрузка данных

Наш пример данных - это измерения качества (размер частиц) при производстве ПВХ-пластика с использованием восьми различных партий смолы и трех разных операторов оборудования.

Набор данных хранится в формате значений, разделенных запятыми (CSV). Каждая строка - это партия смолы, а каждый столбец - это оператор.В RStudio откройте pvc.csv и посмотрите, что он содержит.

Подсказка

Местоположение файла указывается относительно вашего «рабочего каталога». Вы можете увидеть расположение вашего рабочего каталога в заголовке панели консоли в RStudio. Скорее всего, это «~», обозначающее ваш личный домашний каталог. Вы можете изменить рабочий каталог с помощью setwd .

Имя файла «r-intro-files / pvc.csv» означает из текущего рабочего каталога в подкаталоге «r-intro-files» файл «pvc.csv ».

Вы можете проверить, действительно ли файл находится в этом месте, используя панель «Файлы» в правом нижнем углу RStudio.

Если вы работаете на собственном компьютере, а не на нашем обучающем сервере, и загрузили и разархивировали файл r-intro-files.zip, файл может находиться в другом месте.

Мы вызвали read.csv с двумя аргументами: имя файла, который мы хотим прочитать, и столбец, содержащий имена строк. Имя файла должно быть символьной строкой, поэтому мы заключили его в кавычки.Присвоение второму аргументу row.names равному 1 указывает, что файл данных имеет имена строк и номер столбца, в котором они хранятся. Если мы не укажем row.names , результат не будет имена строк.

Подсказка

read.csv на самом деле имеет гораздо больше аргументов, которые могут оказаться полезными при импорте собственных данных в будущем.

  ## Алиса Боб Карл
## Смола1 36,25 35,40 35,30
## Смола2 35.15 35,35 33,35
## Смола3 30,70 29,65 29,20
## Смола 4 29,70 30,05 28,65
## Смола5 31,85 31,40 29,30
## Смола6 30,20 30,65 29,75
## Смола 7 32,90 32,50 32,80
## Смола8 36,80 36,45 33,15

  ## [1] "data.frame"

  ## 'data.frame': 8 набл. из 3-х переменных:
## $ Алиса: число 36,2 35,1 30,7 29,7 31,9 ...
## $ Bob: число 35,4 35,4 29,6 30,1 31,4 ...
## $ Carl: число 35,3 33,4 29,2 28,6 29,3 ...

read.csv загрузил данные как фрейм данных.Фрейм данных содержит набор «вещей» (строк), каждая из которых имеет набор свойств (столбцов) разных типов.

На самом деле эти данные лучше рассматривать как матрицу. В кадре данных столбцы содержат разные типы данных, но в матрице все элементы относятся к одному типу данных. Матрица в R похожа на математическую матрицу, содержащую все того же типа (обычно числа).

R часто, но не всегда позволяет использовать их взаимозаменяемо. При размышлении о данных также полезно различать фрейм данных и матрицу.Различные операции имеют смысл для фреймов данных и матриц. Фреймы данных занимают центральное место в R, и освоение R во многом связано с мышлением в фреймах данных. Однако любые статистические данные часто предполагают использование матриц. Например, когда мы работаем с данными RNA-Seq, мы используем матрицу счетчиков чтения. Так что стоит потратить время и на то, чтобы научиться пользоваться матрицами.

Давайте настаиваем на R, что у нас есть матрица. as.matrix «преобразует» наши данные в матричный тип.

  ## [1] "матрица"

  ## число [1: 8, 1: 3] 36.2 35,1 30,7 29,7 31,9 ...
## - attr (*, "dimnames") = Список из 2
## .. $: chr [1: 8] "Смола1" "Смола2" "Смола3" "Смола4" ...
## .. $: chr [1: 3] "Алиса" "Боб" "Карл"

Намного лучше.

Подсказка

Матрицы

можно создавать разными способами.

матрица преобразует вектор в матрицу с заданным количеством строк и столбцов.

rbind складывает несколько векторов в виде строк один поверх другого, чтобы сформировать матрицу, или он может складывать меньшие матрицы друг на друга, чтобы сформировать большую матрицу.

cbind аналогичным образом складывает несколько векторов в виде столбцов рядом друг с другом, чтобы сформировать матрицу, или может складывать меньшие матрицы рядом друг с другом, чтобы сформировать большую матрицу.

Индексные матрицы

Мы можем проверить размер матрицы с помощью функций nrow и ncol :

  ## [1] 8

  ## [1] 3

Это говорит нам, что наша матрица mat имеет 8 строк и 3 столбца.

Если мы хотим получить одно значение из матрицы, мы можем указать индекс строки и столбца в квадратных скобках:

  ## [1] 36,25

  ## [1] 30,05

Если наша матрица имеет имена строк и столбцов, мы также можем ссылаться на строки и столбцы по имени.

  ## [1] 30,05

Индекс типа [4, 2] выбирает один элемент матрицы, но мы также можем выбирать целые разделы. Например, мы можем выбрать первые два оператора (столбца) значений для первых четырех смол (строк) следующим образом:

  ## Алиса Боб
## Смола1 36.25 35,40
## Смола2 35,15 35,35
## Смола3 30,70 29,65
## Смола 4 29,70 30,05

Срез 1: 4 означает числа от 1 до 4. Это то же самое, что c (1,2,3,4) .

Срез необязательно должен начинаться с 1, например в строке ниже выбираются строки с 5 по 8:

  ## Алиса Боб
## Смола5 31,85 31,40
## Смола6 30,20 30,65
## Смола 7 32,90 32,50
## Resin8 36,80 36,45

Мы можем использовать векторы, созданные с помощью c , для выбора несмежных значений:

  ## Алиса Карл
## Смола1 36.25 35,3
## Смола 3 30,70 29,2
## Смола5 31,85 29,3

Нам также не нужно предоставлять индекс для строк или столбцов. Если мы не включаем индекс для строк, R возвращает все строки; если мы не включаем индекс для столбцов, R возвращает все столбцы. Если мы не предоставляем индекс ни для строк, ни для столбцов, например mat [,] , R возвращает полную матрицу.

  ## Алиса Боб Карл
## 31,85 31,40 29,30

  ## Смола1 Смола2 Смола3 Смола4 Смола5 Смола6 Смола7 Смола8
## 35.40 35,35 29,65 30,05 31,40 30,65 32,50 36,45

Сводные функции

Теперь давайте выполним некоторые общие математические операции, чтобы узнать о наших данных. При анализе данных мы часто хотим посмотреть частичную статистику, такую как максимальное значение на смолу или среднее значение на оператора. Один из способов сделать это - выбрать данные, которые мы хотим использовать в качестве новой временной переменной, а затем выполнить вычисление для этого подмножества:

  ## [1] 36,25

На самом деле нам не нужно хранить строку в отдельной переменной.Вместо этого мы можем объединить выбор и вызов функции:

  ## [1] 35,35

R имеет функции для других общих вычислений, например нахождение минимального, среднего, медианного и стандартного отклонения данных:

  ## [1] 28,65

  ## [1] 31,4375

  ## [1] 31,275

  ## [1] 2.49453

Задача - Подмножество данных в матрице

Предположим, вы хотите определить максимальный размер частиц смолы 5 для операторов 2 и 3.Для этого вы должны извлечь соответствующий срез из матрицы и вычислить максимальное значение. Какая из следующих строк кода R дает правильный ответ?

макс. (Мат [5,])
макс. (Мат [2: 3, 5])
макс. (Мат [5, 2: 3])
макс. (Мат [5, 2, 3])

Суммирующие матрицы

Что делать, если нам нужен максимальный размер частиц для всех смол или средний размер для каждого оператора? Как показано на диаграмме ниже, мы хотим выполнить операцию с полем матрицы:

Чтобы поддержать это, мы можем использовать функцию apply .

Подсказка

Чтобы узнать о функции в R, например apply , мы можем прочитать его справочную документацию, запустив help (apply) или ? Apply .

apply позволяет нам повторить функцию для всех строк ( MARGIN = 1 ) или столбцов ( MARGIN = 2 ) матрицы. Мы можем представить, что применяет как свертывание матрицы до размера, указанного в MARGIN , причем строки имеют размер 1, а размер столбцов 2 (напомним, что при индексировании матрицы мы даем первую строку, а второй столбец).

Таким образом, чтобы получить средний размер частиц каждой смолы, нам нужно будет вычислить среднее значение всех строк ( MARGIN = 1 ) матрицы.

И чтобы получить средний размер частиц для каждого оператора, нам нужно будет вычислить среднее значение по всем столбцам ( MARGIN = 2 ) матрицы.

Поскольку второй аргумент для apply равен MARGIN , приведенная выше команда эквивалентна apply (dat, MARGIN = 2, mean) .

Подсказка

У некоторых распространенных операций есть более сжатые альтернативы. Например, вы можете вычислить средние по строкам или столбцам с rowMeans и colMeans соответственно.

Challenge - подведение итогов матрицы

Как бы вы рассчитали стандартное отклонение для каждой смолы?

Advanced: Как бы вы рассчитали значения на два стандартных отклонения выше и ниже среднего для каждой смолы?

т испытание

R имеет множество встроенных статистических тестов.Одним из наиболее часто используемых тестов является t-тест. Значительно ли различаются средние двух векторов?

  ## Алиса Боб Карл
## 36,25 35,40 35,30

  ## Алиса Боб Карл
## 35,15 35,35 33,35

  ##
## Два образца Уэлча t-критерий
##
## data: mat [1,] и mat [2,]
## t = 1,4683, df = 2,8552, значение p = 0,2427
## альтернативная гипотеза: истинная разница в средних не равна 0
## 95-процентный доверительный интервал:
## -1.271985 3.338652
## примерные оценки:
## среднее значение x среднее значение y
## 35.65000 34.61667

Фактически, это можно считать парным выборочным t-критерием, поскольку значения могут быть объединены в пары оператором. По умолчанию t.test выполняет непарный t-тест. Мы видим в документации (? T.test ), что мы можем дать paired = TRUE в качестве аргумента для выполнения парного t-теста.

  ##
## Парный t-тест
##
## data: mat [1,] и mat [2,]
## t = 1,8805, df = 2, значение p = 0.2008 г.
## альтернативная гипотеза: истинная разница в средних не равна 0
## 95-процентный доверительный интервал:
## -1.330952 3.397618
## примерные оценки:
## среднее значение различий
## 1.033333

Challenge - с использованием t.test

Можете ли вы найти значительную разницу между любыми двумя смолами?

Когда мы вызываем t.test , он возвращает объект, который ведет себя как список . Напомним, что в R список представляет собой разнообразный набор значений.

  ## [1] "статистика" "параметр" "p.value" "conf.int" "оценка"
## [6] "null.value" "альтернативный" "метод" "data.name"

  ## [1] 0.2007814

Это означает, что мы можем написать программное обеспечение, которое использует различные результаты из t.test , например, выполняет целую серию t-тестов и сообщает важные результаты.

Совет - Типы в R под капотом

Откуда мы могли знать, что т.тест дал нам результат, который вел себя как список?

Ранее мы использовали класс , чтобы увидеть, к какому типу относятся различные значения. Здесь это говорит нам, что это «htest» , но на самом деле это просто «публичное лицо» значения. Иногда нам нужно присвоить Скуби-Ду значение и посмотреть, как R думает об этом под капотом. type of показывает, как R думает о значении внутри себя. Если мы обнаружим, что тип объекта - это «список» , тогда мы узнаем, что можем использовать $ или [[]] для доступа к его элементам.

  ## [1] "htest"

  ## [1] "список"

Попробуйте это с dat и mat .

Участок

Математик Ричард Хэмминг однажды сказал: «Цель вычислений - понимание, а не числа», и лучший способ развить понимание - часто визуализировать данные. Визуализация заслуживает отдельной лекции (или курса), но мы можем изучить некоторые особенности построения графиков R.

Давайте посмотрим на средний размер частиц смолы.Напомним, что мы уже вычисляли эти значения выше, используя apply (mat, 1, mean) , и сохранили их в переменной avg_resin . График значений выполняется с помощью функции plot .

Выше мы дали функции plot вектор чисел, соответствующих среднему значению на смолу по всем операторам. График . График создал диаграмму рассеяния, где по оси ординат показан средний размер частиц, а по оси абсцисс - порядок или индекс значений в векторе, которые в данном случае соответствуют 8 смолам.

plot может принимать множество различных аргументов для изменения внешнего вида вывода. Вот сюжет с дополнительными аргументами:

Challenge - построение данных

Создайте график, показывающий стандартное отклонение для каждой смолы.

Накопительные участки

Можно сохранить график в формате .PNG или .PDF из интерфейса RStudio с помощью кнопки «Экспорт». Однако, если мы хотим вести полную запись того, как именно мы создаем каждый график, мы предпочитаем делать это с помощью кода R.

График в R отправляется на «устройство». По умолчанию это устройство RStudio. Однако мы можем временно отправить графики на другое устройство, например, файл .PNG ( png ("filename.png") ) или файл .PDF ( pdf ("filename.pdf") ).

dev.off () очень важно. Он сообщает R прекратить вывод на устройство pdf и вернуться к использованию устройства по умолчанию. Если вы забудете, ваши интерактивные графики перестанут отображаться должным образом!

Созданный вами файл должен появиться на панели файлового менеджера RStudio, вы можете просмотреть его, щелкнув по нему.

Из чего состоит объект dgCMatrix? (формат разреженной матрицы в R)

Недавно я работал с разреженными матрицами в R (те, которые созданы с использованием Matrix :: Matrix с опцией sparse = TRUE ), и мне было трудно найти документацию о том, какие слоты в матричном объекте. Этот пост описывает слоты в объекте класса dgCMatrix .

(Щелкните здесь, чтобы получить полную документацию по пакету Matrix (а это очень много, 215 страниц).)

Фон

Оказывается, есть документация по объектам dgCMatrix в пакете Matrix . Доступ к нему можно получить, используя следующий код:

Библиотека

 (Матрица)
? `dgCMatrix-класс`

Согласно документации, dgCMatrix class

… - это класс разреженных числовых матриц в сжатом разреженном формате с ориентацией на столбцы. В этой реализации ненулевые элементы в столбцах сортируются в порядке возрастания строк. dgCMatrix - это «стандартный» класс для разреженных числовых матриц в пакете Matrix .

Пример

Мы будем использовать небольшую матрицу в качестве рабочего примера в этой публикации:

Библиотека

 (Матрица)
M <- Матрица (c (0, 0, 0, 2,
              6, 0, -1, 5,
              0, 4, 3, 0,
              0, 0, 5, 0),
            byrow = TRUE, nrow = 4, sparse = TRUE)
rownames (M) <- paste0 ("r", 1: 4)
colnames (M) <- paste0 ("c", 1: 4)
M
# 4 x 4 разреженная матрица класса "dgCMatrix"
# c1 c2 c3 c4
# r1.. . 2
# r2 6. -1 5
# r3. 4 3.
# r4. . 5.

Запуск str на x говорит нам, что объект dgCMatrix имеет 6 слотов. (Чтобы узнать больше о слотах и объектах S4, см. Этот раздел в книге Hadley Wickham Advanced R .)

 ул (М)
# Формальный класс 'dgCMatrix' [пакет «Матрица»] с 6 слотами
# [адрес электронной почты защищен] i: int [1: 7] 1 2 1 2 3 0 1
# [адрес электронной почты защищен] p: int [1: 5] 0 1 2 5 7
# [email protected] Dim: int [1: 2] 4 4
# [email protected] Dimnames: список из 2
#.. .. $: chr [1: 4] "r1" "r2" "r3" "r4"
# .. .. $: chr [1: 4] "c1" "c2" "c3" "c4"
# [адрес электронной почты защищен] x: num [1: 7] 6 4 -1 3 5 2 5
# [защита электронной почты] факторов: list ()

x , i и p

Если матрица M имеет nn ненулевых элементов, то ее слот x представляет собой вектор длины nn , содержащий все ненулевые значения в матрице. Ненулевые элементы в столбце 1 перечисляются первыми (начиная сверху и заканчивая внизу), затем идут столбцы 2, 3 и так далее.

 млн
# 4 x 4 разреженная матрица класса "dgCMatrix"
# c1 c2 c3 c4
# r1. . . 2
# r2 6. -1 5
# r3. 4 3.
# r4. . 5.

[электронная почта защищена]
# [1] 6 4-1 3 5 2 5

as.numeric (M) [as.numeric (M)! = 0]
# [1] 6 4 -1 3 5 2 5

Слот i - это вектор длиной nn . Элемент k -го элемента [защита электронной почты] является индексом строки ненулевого элемента k -го (как указано в [электронная почта защищена] ). Следует отметить, что первая строка имеет индекс ZERO, в отличие от соглашения об индексировании R. В нашем примере первая ненулевая запись, 6, находится во второй строке, то есть с индексом 1, поэтому первая запись [email protected] равна 1.

 млн
# 4 x 4 разреженная матрица класса "dgCMatrix"
# c1 c2 c3 c4
# r1. . . 2
# r2 6. -1 5
# r3. 4 3.
# r4. . 5.

[электронная почта защищена]
# [1] 1 2 1 2 3 0 1

Если матрица имеет nvars столбцов, то слот p является вектором длиной nvars + 1 . Если мы проиндексируем столбцы так, чтобы первый столбец имел индекс ZERO, , тогда [email protected] [1] = 0 и [email protected] [j + 2] - [email protected] [j + 1] дает нам количество ненулевых элементов в столбце j .

В нашем примере, когда j = 2 , [электронная почта защищена] [2 + 2] - [электронная почта защищена] [2 + 1] = 5–2 = 3 , поэтому в столбце 3 ненулевых элемента индекс 2 (т.е. третий столбец).

 млн
# 4 x 4 разреженная матрица класса "dgCMatrix"
# c1 c2 c3 c4
# r1.. . 2
# r2 6. -1 5
# r3. 4 3.
# r4. . 5.

[электронная почта защищена]
# [1] 0 1 2 5 7

С помощью слотов x , i и p можно восстановить элементы матрицы.

Размеры и Размеры

Эти два слота довольно очевидны. Dim - вектор длины 2, где первая и вторая записи обозначают количество строк и столбцов в матрице соответственно. Dimnames - это список длиной 2: первый элемент является вектором имен строк (если присутствует), а второй - вектором имен столбцов (если есть).

факторов

Этот слот, вероятно, самый необычный из всех, и его документацию было немного сложно отследить. Из документации CRAN похоже, что множителей равно

… [an] Объект класса «список» - список факторизаций матрицы. Обратите внимание, что это обычно пустое место, т.е.например, list () , первоначально и обновляется автоматически всякий раз, когда вычисляется факторизация матрицы
.

Насколько я понимаю, если мы выполняем какие-либо матричные факторизации или разложения для объекта dgCMatrix , он сохраняет факторизацию с коэффициентами , чтобы при повторном запросе факторизации он мог вернуть кешированное значение вместо повторного вычисления факторизации. Вот пример:

 [адрес электронной почты защищен]
# список()

Mlu <- lu (M) # выполнить треугольное разложение
str ([адрес электронной почты защищен])
# Список из 1
# $ LU: формальный класс sparseLU [пакет "Matrix"] с 5 слотами
#.. [электронная почта защищена] L: формальный класс 'dtCMatrix' [пакет «Матрица»] с 7 слотами
# .. .. .. [адрес электронной почты защищен] i: int [1: 4] 0 1 2 3
# .. .. .. [адрес электронной почты защищен] p: int [1: 5] 0 1 2 3 4
# .. .. .. [адрес электронной почты защищен] Dim: int [1: 2] 4 4
# .. .. .. [адрес электронной почты защищен] Dimnames: List of 2
# .. .. .. .. .. $: chr [1: 4] "r2" "r3" "r4" "r1"
# .. .. .. .. .. $: NULL
# .. .. .. [адрес электронной почты защищен] x: num [1: 4] 1 1 1 1
# .. .. .. [адрес электронной почты защищен] uplo: chr "U"
#.. .. .. [адрес электронной почты защищен] diag: chr "N"
# .. [адрес электронной почты защищен] U: Формальный класс 'dtCMatrix' [пакет «Матрица»] с 7 слотами
# .. .. .. [адрес электронной почты защищен] i: int [1: 7] 0 1 0 1 2 0 3
# .. .. .. [адрес электронной почты защищен] p: int [1: 5] 0 1 2 5 7
# .. .. .. [адрес электронной почты защищен] Dim: int [1: 2] 4 4
# .. .. .. [адрес электронной почты защищен] Dimnames: List of 2
# .. .. .. .. .. $: NULL
# .. .. .. .. .. $: chr [1: 4] "c1" "c2" "c3" "c4"
# .. .. .. [адрес электронной почты защищен] x: num [1: 7] 6 4 -1 3 5 5 2
#.. .. .. [адрес электронной почты защищен] uplo: chr "U"
# .. .. .. [адрес электронной почты защищен] diag: chr "N"
# .. [адрес электронной почты защищен] p: int [1: 4] 1 2 3 0
# .. [адрес электронной почты защищен] q: int [1: 4] 0 1 2 3
# .. [электронная почта защищена] Dim: int [1: 2] 4 4

Вот пример, который показывает, что разложение выполняется только один раз:

 набор. Семян (1)
M <- runif (9e6)
M [sample.int (9e6, size = 8e6)] <- 0
M <- Матрица (M, nrow = 3e3, sparse = TRUE)

система.время (lu (M))
# пользовательская система истекла
# 13.527 0.161 13.701

system.time (lu (M))
# пользовательская система истекла
# 0 0 0

Связанные

Нежное введение в разреженные матрицы для машинного обучения

Последнее обновление 9 августа 2019 г.

Матрицы, которые содержат в основном нулевые значения, называются разреженными, в отличие от матриц, где большинство значений ненулевые, называются плотными.

Большие разреженные матрицы широко распространены в целом и особенно в прикладном машинном обучении, например, в данных, содержащих счетчики, в кодировках данных, отображающих категории в счетчики, и даже в целых подполях машинного обучения, таких как обработка естественного языка.

Представлять разреженные матрицы и работать с ними так, как если бы они были плотными, требует больших вычислительных ресурсов, и значительное улучшение производительности может быть достигнуто за счет использования представлений и операций, которые специально обрабатывают разреженность матриц.

В этом руководстве вы узнаете о разреженных матрицах, проблемах, которые они представляют, и о том, как работать с ними непосредственно в Python.

После прохождения этого руководства вы будете знать:

Эти разреженные матрицы содержат в основном нулевые значения и отличаются от плотных матриц.
Множество областей, в которых вы, вероятно, столкнетесь с разреженными матрицами в данных, подготовке данных и подобластях машинного обучения.
Что существует множество эффективных способов хранения разреженных матриц и работы с ними, а SciPy предоставляет реализации, которые вы можете использовать напрямую.

Начните свой проект с моей новой книги «Линейная алгебра для машинного обучения», включая пошаговые руководства и файлы исходного кода Python для всех примеров.

Приступим.

Нежное введение в разреженные матрицы для машинного обучения
Фотография CAJC: в Скалистых горах, некоторые права защищены.

Обзор учебного пособия

Это руководство разделено на 5 частей; их:

Разреженная матрица
Проблемы с разреженностью
Разреженные матрицы в машинном обучении
Работа с разреженными матрицами
Разреженные матрицы в Python

Нужна помощь с линейной алгеброй для машинного обучения?

Пройдите бесплатный 7-дневный ускоренный курс электронной почты (с образцом кода).

Нажмите, чтобы зарегистрироваться, а также получите бесплатную электронную версию курса в формате PDF.

Загрузите БЕСПЛАТНЫЙ мини-курс

Разреженная матрица

Разреженная матрица - это матрица, состоящая в основном из нулевых значений.

Разреженные матрицы отличаются от матриц с в основном ненулевыми значениями, которые называются плотными матрицами.

Матрица является разреженной, если многие ее коэффициенты равны нулю. Интерес к разреженности возникает потому, что его использование может привести к огромной вычислительной экономии, а также потому, что многие проблемы с большими матрицами, которые возникают на практике, являются разреженными.

- страница 1, Прямые методы для разреженных матриц, второе издание, 2017 г.

Разреженность матрицы можно количественно оценить с помощью показателя, который представляет собой количество нулевых значений в матрице, деленное на общее количество элементов в матрице.

разреженность = подсчет нулевых элементов / всего элементов

Ниже приведен пример небольшой разреженной матрицы 3 x 6.

1, 0, 0, 1, 0, 0 А = (0, 0, 2, 0, 0, 1) 0, 0, 0, 2, 0, 0

1, 0, 0, 1, 0, 0

A = (0, 0, 2, 0, 0, 1)

0, 0, 0, 2, 0, 0

В примере 13 нулевых значений 18 элементов в матрице, что дает этой матрице показатель разреженности 0,722 или около 72%.

Проблемы с разреженностью

Разреженные матрицы могут вызвать проблемы, связанные с пространственной и временной сложностью.

Космическая сложность

Очень большие матрицы требуют много памяти, а некоторые очень большие матрицы, с которыми мы хотим работать, являются разреженными.

На практике большинство больших матриц разрежены - почти все записи нули.

- стр. 465, Введение в линейную алгебру, пятое издание, 2016 г.

Примером очень большой матрицы, которая слишком велика для хранения в памяти, является матрица ссылок, которая показывает ссылки с одного веб-сайта на другой.

Примером меньшей разреженной матрицы может быть матрица встречаемости слова или термина для слов в одной книге по сравнению со всеми известными словами в английском языке.

В обоих случаях содержащаяся матрица является разреженной и содержит намного больше нулевых значений, чем значений данных. Проблема с представлением этих разреженных матриц как плотных матриц заключается в том, что требуется память, и ее необходимо выделять для каждого 32-битного или даже 64-битного нулевого значения в матрице.

Это явно пустая трата ресурсов памяти, поскольку эти нулевые значения не содержат никакой информации.

Сложность времени

Предполагая, что очень большая разреженная матрица может уместиться в памяти, мы захотим выполнить операции с этой матрицей.3) арифметические операции, связанные с решением системы уравнений или обращением матрицы, включают нулевые операнды.

- стр. 75, Численные рецепты: искусство научных вычислений, третье издание, 2007 г.

Это проблема повышенной временной сложности матричных операций, которая увеличивается с размером матрицы.

Эта проблема усугубляется, если учесть, что даже тривиальные методы машинного обучения могут потребовать множества операций с каждой строкой, столбцом или даже по всей матрице, что приводит к значительно большему времени выполнения.

Разреженные матрицы в машинном обучении

Разреженные матрицы часто используются в прикладном машинном обучении.

В этом разделе мы рассмотрим несколько распространенных примеров, чтобы побудить вас осознавать проблемы разреженности.

Данные

Разреженные матрицы возникают в некоторых конкретных типах данных, в первую очередь в наблюдениях, которые регистрируют возникновение или количество действий.

Три примера включают:

Смотрел ли пользователь фильм в каталоге фильмов.
Приобретал ли пользователь продукт в каталоге продуктов.
Подсчет количества прослушиваний песни в каталоге песен.

Подготовка данных

Разреженные матрицы появляются в схемах кодирования, используемых при подготовке данных.

Три типичных примера:

Быстрое кодирование, используемое для представления категориальных данных в виде разреженных двоичных векторов.
Кодирование подсчета, используемое для представления частоты слов в словаре для документа
TF-IDF, используемая для представления нормализованных оценок частоты слов в словаре.

Направления обучения

В некоторых областях машинного обучения необходимо разработать специальные методы для непосредственного решения проблемы разреженности, поскольку входные данные почти всегда разрежены.

Три примера включают:

Обработка естественного языка для работы с текстовыми документами.
Рекомендательные системы для работы с использованием товаров в каталоге.
Компьютерное зрение при работе с изображениями, содержащими много черных пикселей.

Если в языковой модели 100 000 слов, то вектор признаков имеет длину 100 000, но для короткого сообщения электронной почты почти все функции будут иметь нулевой счет.

- стр. 866, Искусственный интеллект: современный подход, третье издание, 2009 г.

Работа с разреженными матрицами

Решением для представления и работы с разреженными матрицами является использование альтернативной структуры данных для представления разреженных данных.

Нулевые значения можно игнорировать, и только данные или ненулевые значения в разреженной матрице должны быть сохранены или обработаны.

Существует несколько структур данных, которые можно использовать для эффективного построения разреженной матрицы; Ниже перечислены три типичных примера.

Словарь ключей . Словарь используется там, где индекс строки и столбца сопоставляется со значением.
Список списков . Каждая строка матрицы хранится в виде списка, причем каждый подсписок содержит индекс столбца и значение.
Список координат . Список кортежей сохраняется с каждым кортежем, содержащим индекс строки, индекс столбца и значение.

Есть также структуры данных, которые больше подходят для выполнения эффективных операций; Ниже перечислены два наиболее часто используемых примера.

Сжатая разреженная строка . Разреженная матрица представлена с использованием трех одномерных массивов для ненулевых значений, экстентов строк и индексов столбцов.
Сжатая разреженная колонна . То же, что и метод сжатой разреженной строки, за исключением того, что индексы столбцов сжимаются и считываются сначала перед индексами строк.

Сжатая разреженная строка, также называемая сокращенно CSR, часто используется для представления разреженных матриц в машинном обучении с учетом поддерживаемого им эффективного доступа и умножения матриц.

Разреженные матрицы в Python

SciPy предоставляет инструменты для создания разреженных матриц с использованием нескольких структур данных, а также инструменты для преобразования плотной матрицы в разреженную матрицу.

Многие функции линейной алгебры NumPy и SciPy, которые работают с массивами NumPy, могут прозрачно работать с разреженными массивами SciPy. Кроме того, библиотеки машинного обучения, использующие структуры данных NumPy, также могут прозрачно работать с разреженными массивами SciPy, такими как scikit-learn для общего машинного обучения и Keras для глубокого обучения.

Плотная матрица, хранящаяся в массиве NumPy, может быть преобразована в разреженную матрицу с использованием представления CSR путем вызова функции csr_matrix () .

В приведенном ниже примере мы определяем разреженную матрицу 3 x 6 как плотный массив, преобразуем ее в разреженное представление CSR, а затем преобразуем обратно в плотный массив, вызвав функцию todense () .

# от плотного до разреженного из массива импорта numpy из scipy.sparse import csr_matrix # создать плотную матрицу A = массив ([[1, 0, 0, 1, 0, 0], [0, 0, 2, 0, 0, 1], [0, 0, 0, 2, 0, 0]]) печать (A) # преобразовать в разреженную матрицу (метод CSR) S = csr_matrix (A) печать (S) # восстановить плотную матрицу B = S.todense () печать (B)

# плотный к разреженному

из массива импорта numpy

из scipy.sparse import csr_matrix

# создать плотную матрицу

A = array ([[1, 0, 0, 1, 0, 0], [0, 0, 2, 0, 0, 1], [0, 0, 0, 2, 0, 0]])

print (A)

# преобразовать в разреженную матрицу (метод CSR)

S = csr_matrix (A )

print (S)

# восстановить плотную матрицу

B = S.todense ()

печать (B)

При выполнении примера сначала печатается определенный плотный массив, затем представление CSR, а затем реконструированная плотная матрица.

[[1 0 0 1 0 0] [0 0 2 0 0 1] [0 0 0 2 0 0]] (0, 0) 1 (0, 3) 1 (1, 2) 2 (1, 5) 1 (2, 3) 2 [[1 0 0 1 0 0] [0 0 2 0 0 1] [0 0 0 2 0 0]]

[[1 0 0 1 0 0]

[0 0 2 0 0 1]

[0 0 0 2 0 0]]

(0, 0) 1

(0, 3) 1

(1, 2) 2

(1, 5) 1

(2, 3) 2

[[1 0 0 1 0 0]

[0 0 2 0 0 1]

[ 0 0 0 2 0 0]]

NumPy не предоставляет функции для вычисления разреженности матрицы.

Тем не менее, мы можем легко вычислить его, сначала найдя плотность матрицы и вычтя ее из единицы. Количество ненулевых элементов в массиве NumPy может быть задано функцией count_nonzero () , а общее количество элементов в массиве может быть задано свойством размера массива. Поэтому разреженность массива можно рассчитать как

sparsity = 1.0 - count_nonzero (A) / A.size

разреженность = 1.0 - count_nonzero (A) / A. размер

Пример ниже демонстрирует, как вычислить разреженность массива.

# вычислить разреженность из массива импорта numpy из numpy import count_nonzero # создать плотную матрицу A = массив ([[1, 0, 0, 1, 0, 0], [0, 0, 2, 0, 0, 1], [0, 0, 0, 2, 0, 0]]) печать (A) # вычислить разреженность sparsity = 1.0 - count_nonzero (A) / A.size печать (разреженность)

# вычислить разреженность

из массива импорта numpy

из массива импорта numpy count_nonzero

# создать плотную матрицу

A = array ([[1, 0, 0, 1, 0, 0], [0, 0, 2 , 0, 0, 1], [0, 0, 0, 2, 0, 0]])

print (A)

# вычислить разреженность

sparsity = 1.0 - count_nonzero (A) / A.size

print (sparsity)

При выполнении примера сначала печатается определенная разреженная матрица, а затем разреженная матрица.

[[1 0 0 1 0 0] [0 0 2 0 0 1] [0 0 0 2 0 0]] 0,7222222222222222

[[1 0 0 1 0 0]

[0 0 2 0 0 1]

[0 0 0 2 0 0]]

0,7222222222222222

Расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

Разработайте свои собственные примеры преобразования плотного массива в разреженный и вычисления разреженности.
Разработайте пример для каждого метода представления разреженной матрицы, поддерживаемого SciPy.
Выберите один метод разреженного представления и реализуйте его самостоятельно с нуля.

Если вы изучите какое-либо из этих расширений, я хотел бы знать.

Дополнительная литература

В этом разделе представлены дополнительные ресурсы по теме, если вы хотите углубиться.

Книги

API

Статьи

Сводка

В этом руководстве вы узнали о разреженных матрицах, о проблемах, которые они представляют, и о том, как работать с ними непосредственно в Python.

В частности, вы выучили:

Эти разреженные матрицы содержат в основном нулевые значения и отличаются от плотных матриц.
Множество областей, в которых вы, вероятно, столкнетесь с разреженными матрицами в данных, подготовке данных и подобластях машинного обучения.
Полноформатная матрица: Кроп или полный кадр — что выбрать? Crop vs. FF

Кроп-фактор: что это и как влияет на качество снимков?

Какими матрицами оснащаются современные фотоаппараты?

Какую матрицу предпочесть?

Вывод

Полноформатная зеркальная камера Canon EOS 6D Mark II

Phase One Systems XF IQ4 150MP

Описание

VSGO DDR-24 KIT КОМПЛЕКТ ДЛЯ ЧИСТКИ ПОЛНОФОРМАТНЫХ МАТРИЦ

Двухцветная фотоприемная матрица на диапазон 3-5 и 8-12 мкм на основе МСКЯ GaAs/AlGaAs/InGaAs

Nikon Z6 и Nikon Z7 Полноформатные Nikon теперь и без зеркала! — Российское фото

Швабе — Пресс-центр — Новости

MM — формат файла Matrix Market

Характеристики файлов MM:

Лицензирование:

Ссылка:

Образцы файлов:

Работа с разреженной матрицей в R

SPARSEKIT - Пакет служебных программ для разреженной матрицы

Языки:

Связанные данные и программы:

Ссылка:

Исходный код:

Примеры и тесты:

Список программ:

Введение в разреженные матрицы в R

Как создать разреженную матрицу из плотной матрицы в R?

Как визуализировать разреженную матрицу в R?

Как создать разреженную матрицу с нуля в R?

Как сохранить разреженную матрицу в файл?

Работа с данными в матрице

Загрузка данных

Подсказка

Подсказка

Подсказка

Индексные матрицы

Сводные функции

Задача - Подмножество данных в матрице

Суммирующие матрицы

Подсказка

Подсказка

Challenge - подведение итогов матрицы

т испытание

Challenge - с использованием t.test

Совет - Типы в R под капотом

Участок

Challenge - построение данных

Накопительные участки

Из чего состоит объект dgCMatrix? (формат разреженной матрицы в R)

Нежное введение в разреженные матрицы для машинного обучения

Обзор учебного пособия

Нужна помощь с линейной алгеброй для машинного обучения?

Разреженная матрица

Проблемы с разреженностью

Космическая сложность

Сложность времени

Разреженные матрицы в машинном обучении

Данные

Подготовка данных

Направления обучения

Работа с разреженными матрицами

Разреженные матрицы в Python

Расширения

Дополнительная литература

Книги

API

Статьи

Сводка

Добавить комментарий Отменить ответ