Что такое золотое сечение и правда ли оно повсюду
18 июля 2021 Ликбез Жизнь
Спойлер: это лишь красивая математическая легенда.
Что такое золотое сечение
Это соотношение двух неравных чисел, при котором большее так же относится к меньшему, как сумма этих чисел к большему. Золотое сечение равно примерно 1,618, или 1,62, если округлить, и обозначается греческой буквой φ, «фи» — от имени древнегреческого скульптора Фидия. Считается, что он использовал такие пропорции при оформлении Парфенона.
Наиболее известные графические представления золотого сечения — это прямоугольник с соотношением сторон примерно 62:48 и построенная в нём спираль.
1 / 0
«Золотой прямоугольник» можно разделить на такие же, только меньшего размера. Изображение: Dicklyon / Wikimedia Commons
2 / 0
«Золотая спираль» (красная), вписанная в «золотой прямоугольник». Изображение: Silverhammermba & Jahobr / Wikimedia Commons
Золотое сечение тесно связано с числами Фибоначчи. Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.
Это ряд чисел, каждое из которых равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Чем дальше продолжается этот ряд, тем ближе соотношение соседних чисел в нём к 1,618. Например, 3/2=1,5; 8/5=1,6, а 34/21= 1,619.
Почему золотое сечение так популярно
Впервые им заинтересовались ещё древнегреческие математики Пифагор и Евклид. Они считали, что на числах построено всё мироздание и с их помощью можно объяснить любой феномен. Неудивительно, что элегантное соотношение так заинтересовало античных мыслителей.
Вслед за ними золотым сечением увлеклись многие выдающиеся учёные и деятели искусства. Например, Леонардо да Винчи, Альбрехт Дюрер, Иоганн Кеплер, Ле Корбюзье, Сальвадор Дали и Ричард Пенроуз.
Его считают «божественной пропорцией»
Название «золотое сечение» придумал немецкий математик XIX века Мартин Ом. До него это соотношение именовали «божественной пропорцией».
Из‑за приписываемых характеристик золотое сечение старались применять как можно чаще. Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.
Так, во времена Возрождения это число считалось идеальным способом для выбора размера. «Золотой прямоугольник», например, нередко использовали при создании книг и картин. А линию пояса называли границей золотого сечения человеческого тела.
Некоторые и поныне считают эту пропорцию секретом привлекательности и примером универсальной гармонии, приятной человеческому глазу. Например, о золотом сечении любят говорить пластические хирурги. А ещё это число популярно как никакое другое в математике.
Его можно встретить в природе
Числа Фибоначчи и спирали, подобные золотому сечению, часто обнаруживаются в природе. Например, в количестве лепестков у цветов или форме растений.
Часть растения эониума. Фото: Max Ronnersjö / Wikimedia CommonsЕго обнаруживают в произведениях архитектуры и искусства
Например, «божественные пропорции» находят в Парфеноне и египетских пирамидах. Также широко распространено заблуждение, что «Мона Лиза» написана в соответствии с числом φ.
Почему универсальность золотого сечения — миф
Однако при тщательном изучении становится понятно, что эта пропорция не так уж всеобъемлюща.
Божественность золотого сечения преувеличивается
Золотому сечению придают больше значения, чем есть в действительности. Красивые узоры и налёт таинственности сделали из обычного геометрического соотношения математический миф, который, к примеру, очень любят нумерологи.
Чаще всего вещи причисляют к золотому сечению с большими допущениями. Ни о какой точности и математической универсальности в таком случае говорить не приходится. Поэтому при желании можно обнаружить «божественные пропорции» где угодно.
В природе золотое сечение не так уж распространено
Его находят далеко не везде. Например, у маков всегда четыре лепестка, а в ряд Фибоначчи четвёрка не входит. Также нередко встречается четырёхлистный клевер. Раковины морских моллюсков похожи на спираль золотого сечения, но всё-таки другие. У них больше витков, и расстояние между ними меньше.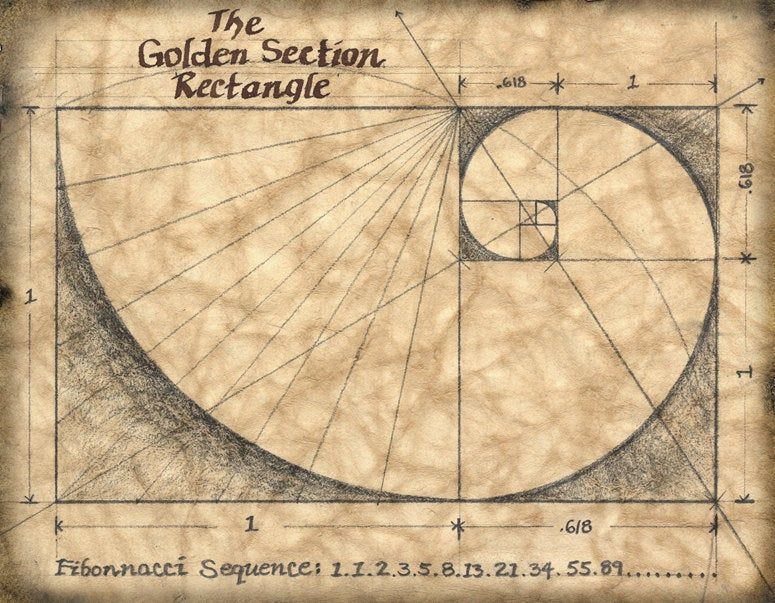 Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:
Ни у одного моллюска коэффициент скручивания раковины и близко не равен 1,62. Это видно даже невооружённым глазом:
1 / 0
Спираль морского моллюска. Изображение: Florian Elias Rieser / Wikimedia Commons
2 / 0
Спираль Фибоначчи, близкая к золотому сечению. Изображение: Jahobr / Wikimedia Commons
В человеческом теле же столько точек, от которых можно производить измерение, что при желании реально найти золотое сечение где угодно. Вот только с большой вероятностью у разных людей «божественную пропорцию» придётся искать в разных местах, так как мы можем сильно отличаться друг от друга.
В искусстве оно тоже встречается не так уж часто
Изучение 565 картин выдающихся художников показало, что в среднем соотношение сторон в работах составляет 1,34. Это явно не дотягивает до золотого сечения. Учёные не находят его даже в произведениях Леонардо да Винчи.
Археологические исследования не подтверждают и того, что древние греки могли использовать золотое сечение при постройке Парфенона. Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.
Из более чем 100 памятников древнегреческой архитектуры это число нашлось в пропорциях только четырёх объектов: башни, алтаря, гробницы и надгробия. Не могли пользоваться золотым сечением и древние египтяне, не обладавшие достаточным уровнем технологий, чтобы точно высчитывать пропорции.
Кому золотое сечение может быть полезно на самом деле
Современная математика использует золотое сечение и числа Фибоначчи при описании фракталов — фигур, которые проявляют самоподобие.
Фрактальная форма кочана капусты Романеско. Фото: Ivar Leidus / Wikimedia CommonsЗнание о числе φ играет важную роль в изучении хаоса и изменяющихся (динамических) систем. Оно помогает понять, как природа развивается и самоорганизуется.
Также числа Фибоначчи полезны при решении некоторых сложных задач. Например, с помощью этих чисел советский математик Юрий Матиясевич доказал, что не существует универсального алгоритма решения уравнений с как минимум двумя неизвестными.
Читайте также 💆♂️👩🔬
- Продолжите последовательность! 10 мини-задач для разминки мозга
- Как округлять числа
- Интересные математические факты для тех, кто хочет больше узнать о мире вокруг
- Гимнастика для ума: 10 увлекательных задач с числами
- 10 увлекательных задач от советского математика
Золотое сечение в домашнем интерьере
Есть ли практический житейский смысл в пифагоровых расчетах и числах Фибоначчи, и как их учесть на практике при создании дизайн-проекта?
В течение нескольких веков золотое сечение и ряд Фибоначчи составляют основу гармонического построения в архитектуре, живописи, музыке. Чтобы их освоить, не обязательно погружаться в сложные формулы и чертежи. Есть простые правила использования модуля и золотого сечения в домашних условиях, помня о которых, мы получим максимально комфортную среду обитания для себя и своей семьи.
Чтобы их освоить, не обязательно погружаться в сложные формулы и чертежи. Есть простые правила использования модуля и золотого сечения в домашних условиях, помня о которых, мы получим максимально комфортную среду обитания для себя и своей семьи.
Ирина Капустина
На фото: Парфенон, Акрополь в Афинах
Природная гармония
В природе существует удивительная пропорция, которая многократно повторяется в самых разных живых структурах — строении раковин, рисунке волокон деревьев, расположении лепестков цветов, строении человеческого тела и даже в расположении планет. Чудесная способность этой пропорции сообщать творению человеческих рук гармонию, заложенную в самой природе, с глубокой древности привлекала ученых, художников, строителей и философов. Мы найдем ее в пирамиде Хеопса и в афинском Парфеноне, в мечети Тадж-Махал и в европейских средневековых соборах, в работах Леонардо да Винчи и Микеланджело.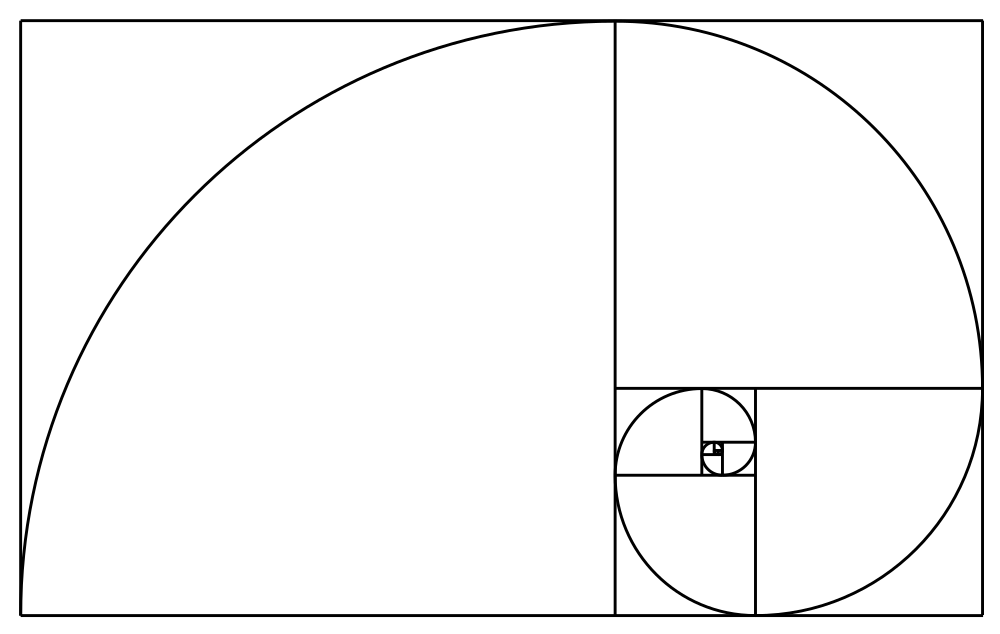
Ирина Капустина
На фото: «Мона Лиза», Леонардо да Винчи
Что же такое золотое сечение?
Великий греческий философ и математик Пифагор вывел формулу «божественной» пропорции, определив ее как деление целого на две неравные части, при котором меньшая часть относится к большей так же, как большая относится к целому. Он назвал это соотношение золотой серединой, золотым сечением, или золотым прямоугольником.
Если взять за целое единицу, то большая часть в этой пропорции будет приближена к 0,618 от целого, а меньшая — к 0,382, или 1:0,618 = 0,618:0,382. Числовое выражение этой классической пропорции 1:1,618, дающее число 0,618, а точнее, бесконечный ряд после запятой — 0,618046971…
Ирина Капустина
Спираль золотого сечения
Золотое сечение напрямую связано с рядом Фибоначчи, названным по имени открывшего его крупнейшего математика средневековой Европы (XII-XIII веков) Леонардо Пизанского, известного как Фибоначчи.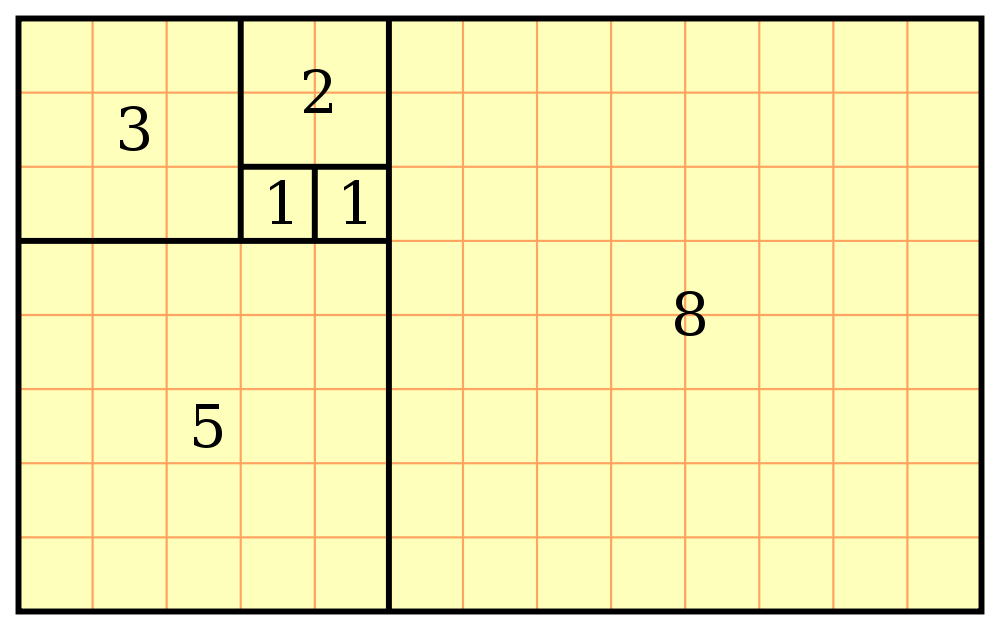
В этом ряду каждый последовательный элемент равняется сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233… Отношение каждого числа к последующему по увеличению порядкового номера все больше и больше стремится к числу 0,618, то есть к отношению золотого сечения. Собственно, золотое сечение и есть взаимосвязь между двумя числами в последовательности Фибоначчи. Построение этой последовательности в масштабе дает бесконечные спирали, нередко наблюдаемые в живой природе.
На фото: Модулор — антропометричная система пропорций, созданная Ле Корбюзье на основе золотого сечения и среднего роста человека с поднятой рукой. Использовалась для создания соразмерных человеку жилых пространств.
Соотношение чисел в золотом сечении Пифагор считал идеальным для благополучия людей. Он утверждал, что пропорции, которые выражают естественную гармонию природы, можно и нужно использовать при проектировании дома и сада: они доставляют удовольствие человеческому глазу, радуют душу и психику.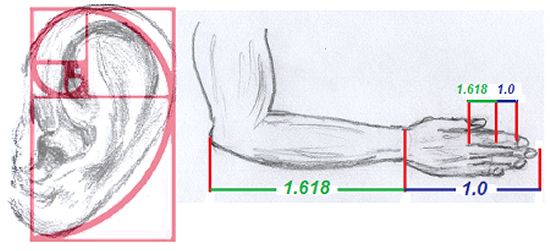
Неудивительно, что пространство, организованное в соответствии с золотым сечением, исполнено гармонии и создает тонкий, невидимый глазу настрой, который позволяет нам максимально расслабиться и почувствовать себя комфортно.
Ирина Капустина
На фото: Вилла Ла Рош в пригороде Парижа (архитектор Ле Корбюзье). Большой зал, построенный с помощью пропорций Модулора
Как использовать золотые пропорции в нашем доме?
Если мы только собираемся строить дом, можно заложить соотношения золотого сечения при проектировании. Но что делать, если уже есть жилье с заданными параметрами? Даже в этом случае можно многое изменить. Начать стоит с установки модуля — условной единицы, к которой мы привяжем основные размеры и деление пространства. Можно использовать в качестве модуля свой рост или число, приближенное к нему, и «подогнать» пространство под себя. Или взять за модуль торцевую, узкую сторону в прямоугольной комнате и на основе этого модуля вычислить остальные значения.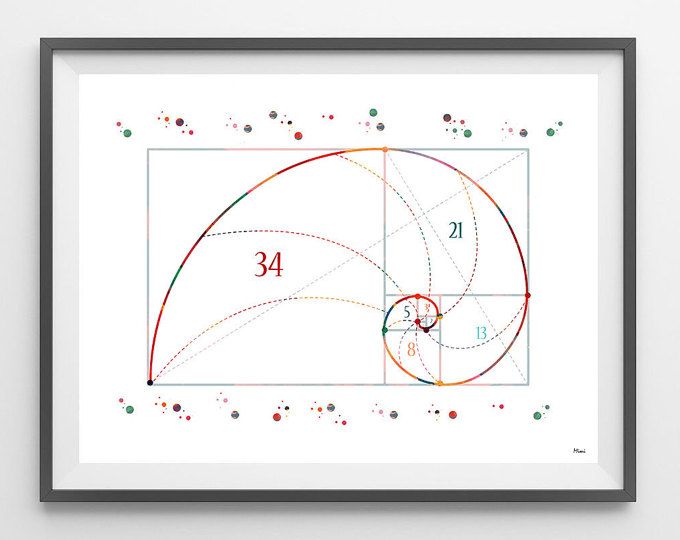 Например, сторона торца комнаты равна 3 м, или 300 см. Проще всего сразу рассчитать ряд Фибоначчи для своего помещения и оперировать полученными числами. Для этого выполним последовательное умножение нашего модуля на 0,618 (300 x 0,618). Получилась следующая цепочка чисел: 300; 185,4; 114,57; 70,8; 43,75; 27,04; 16,71; 10,33 (см) и т.д. Теперь округлим числа: 300, 185,4; 114,6; 70,8; 43,7; 27; 16,7; 10,3; 6,3 см. Полученные «золотые отрезки» можно использовать повсюду — в расстановке мебели, декорировании стен и даже при высадке растений в саду.
Например, сторона торца комнаты равна 3 м, или 300 см. Проще всего сразу рассчитать ряд Фибоначчи для своего помещения и оперировать полученными числами. Для этого выполним последовательное умножение нашего модуля на 0,618 (300 x 0,618). Получилась следующая цепочка чисел: 300; 185,4; 114,57; 70,8; 43,75; 27,04; 16,71; 10,33 (см) и т.д. Теперь округлим числа: 300, 185,4; 114,6; 70,8; 43,7; 27; 16,7; 10,3; 6,3 см. Полученные «золотые отрезки» можно использовать повсюду — в расстановке мебели, декорировании стен и даже при высадке растений в саду.
Ирина Капустина
1. Прямоугольник золотого сечения
Для выделения в прямоугольной комнате зоны золотого сечения нужно найти длину основной стороны. У нас есть торцевая стена 300 см, дальше прибавляем к модулю 300 см следующее по ряду Фибоначчи число (300 + 185,4 = 485,4) и получаем вторую сторону золотого прямоугольника — 485,4 см. Или же можно разделить число модуля 300 см на 0,618 (300 : 0,618 = 485,4).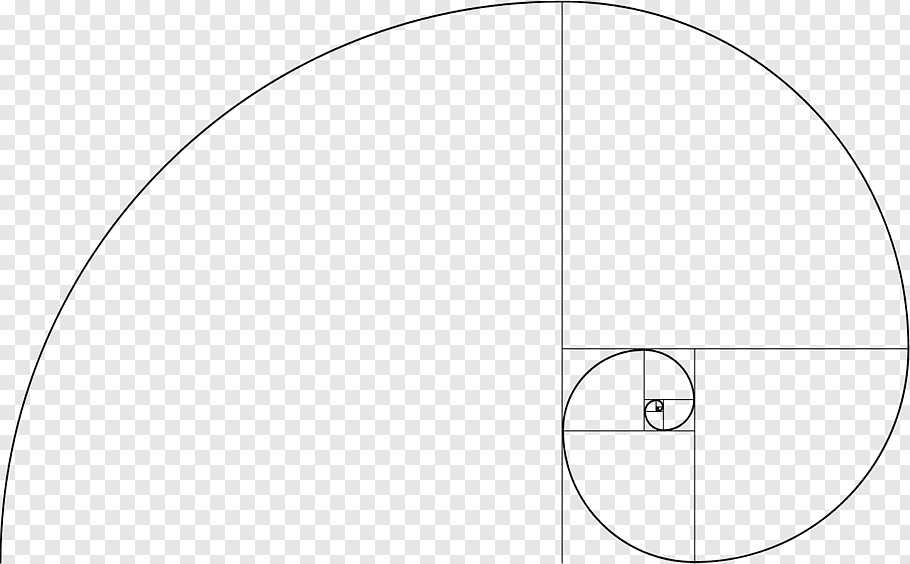
Иногда проще и быстрее построить золотое сечение графически, ничего не высчитывая. Прямоугольник золотого сечения содержит в себе квадрат и малый прямоугольник, относящиеся друг к другу как 0,618 к 0,382. Если сторона торца комнаты — 3 м, значит, на полу мы строим квадрат со стороной 3 м. Далее делим квадрат пополам вертикальной линией так, чтобы получилось два прямоугольника.
В одном прямоугольнике мы проведем линию, соединив противоположные углы. Теперь отложим циркулем отрезок, равный линии внутри прямоугольника, и развернем его на горизонтальной прямой.
Так мы построили еще один прямоугольник, который соотносится с предыдущим как 0,618:0,382. В итоге получаем общий золотой прямоугольник и деление внутри него на две неравные зоны.
J. Hirsch Interior Design, LLC
2. Соотношение цвета в комнате по правилу золотого сечения
Не стоит забывать, что использование цвета по правилу золотого сечения так же предполагает соотношение двух третей. Доминирующий цвет должен занимать около 60% комнаты, основной сопровождающий — около 30%, и последний, дополнительный — всего 10% (обычно он используется для аккомпанирующего декора).
Доминирующий цвет должен занимать около 60% комнаты, основной сопровождающий — около 30%, и последний, дополнительный — всего 10% (обычно он используется для аккомпанирующего декора).
Конечно, эти соотношения приблизительны, а дополнительные цвета могут включать несколько оттенков, но основной принцип должен сохраняться. Можно выбрать мягкий тональный переход в пределах одного цвета или яркий контрастный аккорд — все зависит от концепции дизайна помещения.
Arch Studio, Inc.
3. Пример «крещендо» в композиции интерьера
Главная фокусная точка, наибольшая насыщенность меблировки, освещения и декора должны приходиться на большую часть нашего прямоугольника. Меньшая часть может поддерживать тему, став своего рода аккомпанементом. Вообще, любая композиция должна иметь динамику.
Развитие темы происходит постепенно и поступательно, с нарастанием звучания. При этом кульминация, высшая точка сюжета приходится на вторую треть от начала темы (0,618 от всего пространства), а затем идет ее мягкое ослабление.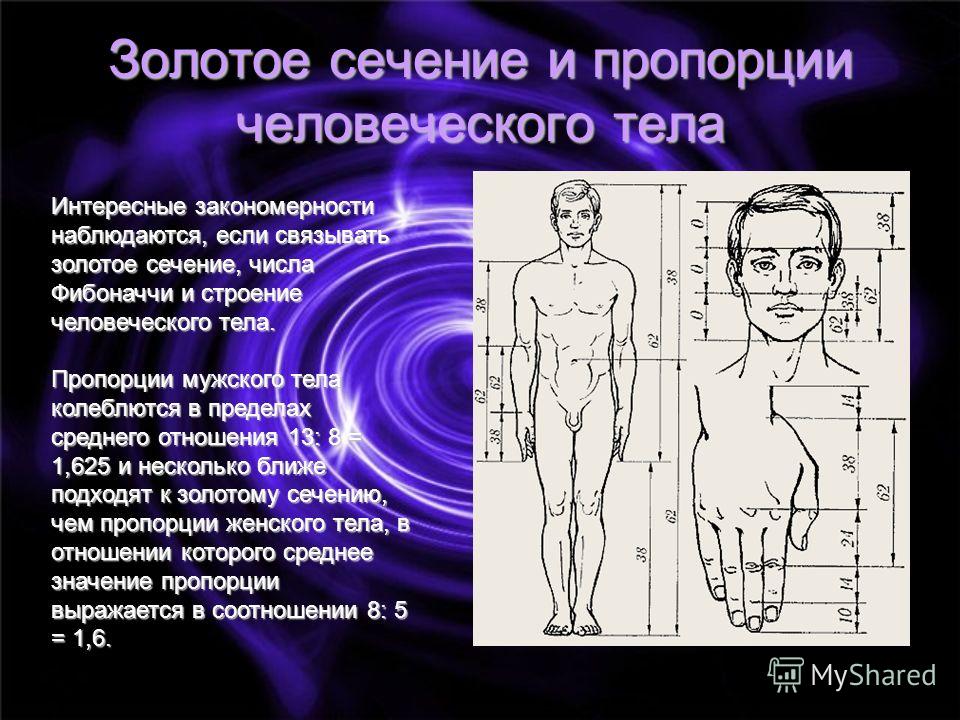
Ирина Капустина
4. Деление стены без филенок и плинтусов по принципу золотого сечения
А что делать с высотой потолка? Идеально, если при нашем модуле 300 см высота потолка тоже окажется 300 см, войдя в ряд Фибоначчи. Если вдруг высота потолка будет близкой к 280 см, то имеет смысл именно ее сделать модулем для всего помещения. В этом случае в полученный нами ряд Фибоначчи войдет значение 173 см (280, 173 и т.д.), которое является числом среднего роста человека.
Но, предположим, мы оставили модуль 300 см как приемлемый, а высота потолка — 260 см (и этого числа нет в выведенной нами последовательности). Прежде всего, нужно определиться, будет ли стена иметь какое-либо деление по горизонтали или предполагается единым целым, без карниза, фриза и плинтуса.
Если мы оставляем стену единым целым, принцип золотого сечения можно применить, например, к расстановке мебели или развеске панно. В этом случае стоит сделать основной цвет стен максимально нейтральным, тогда на первый план выйдут декоративные пятна, организованные нами с помощью золотой пропорции.
DoorsSupply
Если используется классическое деление стены — без бордюров, карнизов и плинтусов не обойтись. Тогда начните с выделения зоны, входящей в нашу пропорцию. Итак, чтобы определить высоту композиционной зоны, проще всего к числу 185,4 прибавить число 70,8. И хотя это соотношение будет несколько нарушать последовательность, вместе они дадут высоту (256 см), которая будет соотноситься с числами нужного нам ряда. На этой высоте пройдет верхняя линия карниза, а остаток (4 см) мы нейтрализуем, выкрасив одним цветом с потолком, лучше белым. Это, с одной стороны, облегчит весь верх, а с другой — отделит не вписывающийся в наш ряд отрезок от общей композиции.
Tim Hine
5. Соответствие высоты мебели линии цокольной части стены
Если мы делим стену на нижнюю часть и зону верхнего фриза, то в классическом варианте разделительный бордюр, проходящий по периметру комнаты, обычно располагается на высоте 75-100 см от пола (именно на эти размеры ориентированы мебельные фабрики). В нашем «золотом» ряду есть выбор между числами 114,6 и 70,8. Можно выбрать число 70,8, сделав его нижней линией бордюра.
В нашем «золотом» ряду есть выбор между числами 114,6 и 70,8. Можно выбрать число 70,8, сделав его нижней линией бордюра.
Сам бордюр не должен быть массивным, для его ширины вполне подойдут значения 10,3 или 16,7 см. Таким образом, к уже имеющейся нижней линии бордюра на высоте 70,8 см от пола мы получим высоту верхней линии бордюра – либо 81,1, либо 87,5. Эти линии отметят границу цокольной зоны стены. В идеале к ней должна стремиться высота кресел и стульев мебельного гарнитура, а также невысоких элементов мебели, таких, как комоды и тумбочки.
При выборе ширины плинтуса и ширины карниза мы берем числа из того же «золотого» ряда: 16,7, 10,3, 6,3 см. Выбор будет зависеть от ширины бордюра и от других элементов декора.
VersaTile Surfaces
6. Соотношение мебели и пространства
Мебель не должна занимать больше 60% композиции, чтобы не создавать ощущения тесноты и захламленности. Если мы выбираем мебель на заказ, то при ее изготовлении удобно использовать пропорции золотого сечения, высчитанные конкретно для нашей квартиры. В этом случае мебель будет выглядеть особенно гармонично, и восприниматься естественной частью единого целого.
В этом случае мебель будет выглядеть особенно гармонично, и восприниматься естественной частью единого целого.
Ирина Капустина
7. Правило 2/3
То же золотое правило двух третей (в каждом случае числа из нашего ряда Фибоначчи помогут составить более точную пропорцию) позволит правильно расположить все элементы декора интерьера. На высоте приблизительно 2/3 от общей высоты пространства наиболее гармонично будут смотреться подвесные светильники, диван не должен занимать больше 2/3 отведенного ему простенка, а журнальный столик не должен быть больше 2/3 дивана.
ВАША ОЧЕРЕДЬ…
Дизайнеры, используете ли вы золотое сечение в собственных интерьерных проектах? Поделитесь с нами в комментариях.
СТАТЬИ ПО ТЕМЕ…
Интерьер: Планировка и перепланировка | Маленькие помещения | Съемная квартира | Вопросы экономии | Хранение вещей | Секреты профи | Портреты
Спонсируемые
Innenarchitektonische Raumästhetik & Funktionalität im Rheinland
Спонсируемые
Düsseldorf I Einrichtungsberatung aus Leidenschaft
Что такое золотое сечение и как оно связано с последовательностью Фибоначчи?
Некоторая математика работает. Немного математики весело. А какая-то математика просто ошеломляет. Если это последнее описание кажется вам невероятным, то сегодня вы можете изменить свое мнение. Потому что теперь, когда мы рассмотрели достаточно материала, мы собираемся взглянуть на некоторые из удивительных, элегантных и совершенно загадочных способов, которыми последовательность Фибоначчи проявляется в окружающем вас мире.
Немного математики весело. А какая-то математика просто ошеломляет. Если это последнее описание кажется вам невероятным, то сегодня вы можете изменить свое мнение. Потому что теперь, когда мы рассмотрели достаточно материала, мы собираемся взглянуть на некоторые из удивительных, элегантных и совершенно загадочных способов, которыми последовательность Фибоначчи проявляется в окружающем вас мире.
Резюме последовательности Фибоначчи
В прошлой статье мы говорили о том, как, казалось бы, невинный вопрос о росте популяции кроликов привел Фибоначчи к последовательности чисел, которая теперь носит его имя, — последовательности Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, …
Каждое последующее число в этой последовательности получается путем сложения двух предыдущих чисел. И, за исключением нескольких усложняющих деталей, таких как тот факт, что кролики в конце концов стареют и умирают, эта последовательность прекрасно моделирует рост популяции. Но у чисел в последовательности Фибоначчи есть жизнь далеко за пределами кроликов, и они появляются в самых неожиданных местах.
Что такое золотое сечение?
Одно из таких мест особенно увлекательно: золотое сечение. Так что же это за золотое сечение? Ну, это число равно примерно 1,618. Это число теперь часто называют «фи» и выражается в письменной форме с использованием символа буквы фи из греческого алфавита. Фи не равно точно 1,618, поскольку, как и его знаменитый двоюродный брат пи, фи является иррациональным числом, а это означает, что его десятичные цифры продолжаются вечно без повторения шаблона. Если вам интересно узнать, как получается фактическое значение числа фи, ознакомьтесь с выпуском Math Dude «Video Extra!» на этой неделе. эпизод на ютубе. Но как это число стало таким важным? Как ни странно, все началось с вопроса эстетики.
Золотой прямоугольник
Какой самый красивый прямоугольник? Более конкретно: каково отношение высоты этого «самого красивого» прямоугольника к его ширине? Этот вопрос кажется странным, но это не безумие. Мы не будем сейчас вдаваться в подробности, но есть свидетельства того, что люди склонны воспринимать одну конкретную форму прямоугольника как наиболее приятную для глаз.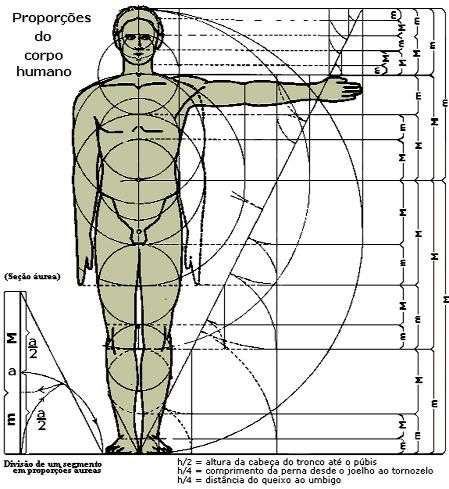 Конечно, греки знали об этом задолго до того, как это проверили современные психологи, поэтому они использовали золотые прямоугольники, а также другие золотые формы и пропорции, придерживающиеся золотого сечения, в своей архитектуре и искусстве.
Конечно, греки знали об этом задолго до того, как это проверили современные психологи, поэтому они использовали золотые прямоугольники, а также другие золотые формы и пропорции, придерживающиеся золотого сечения, в своей архитектуре и искусстве.
Например, считается, что почти 2500 лет назад греческий скульптор и архитектор по имени Фидий использовал золотое сечение для проектирования статуй, которые он изваял для Парфенона (обратите внимание на слово «фи» в имени Фидия — это не совпадение и фактически вдохновило название числа в 20-м веке). А со времен Фидия многие художники и музыканты также использовали золотое сечение в своих работах — Леонардо да Винчи, Сальвадор Дали, Клод Дебюсси и многие другие.
Но вернемся к проблеме определения формы самого приятного прямоугольника. Если вы просто нарисуете прямоугольник, который вы считаете самым красивым, затем измерите длины каждой стороны и, наконец, разделите самую длинную длину на самую короткую, вы, вероятно, обнаружите, что соотношение составляет где-то около 1,6, что является золотым сечением.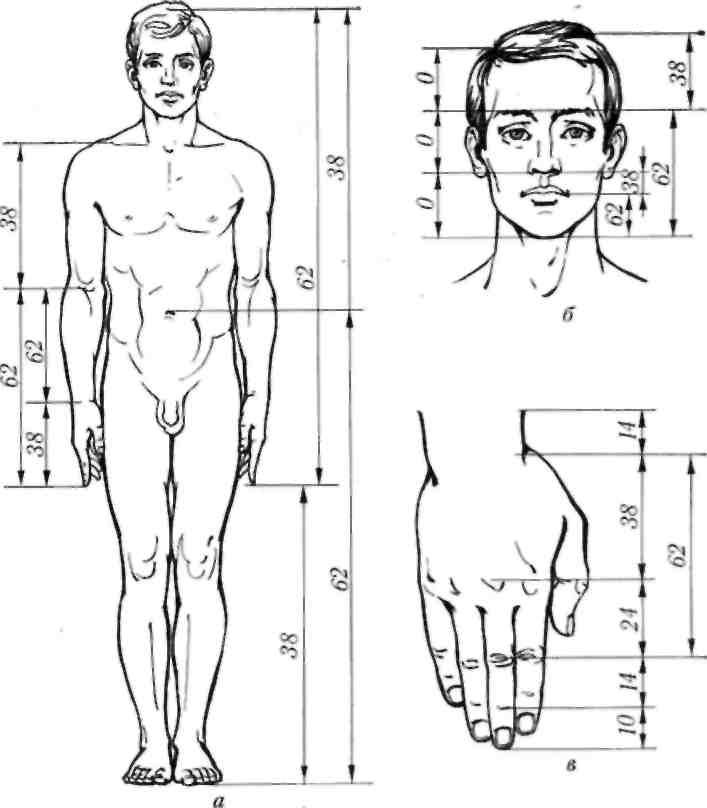 , фи, округленное до десятых. Это будет не совсем 1,6, но должно быть довольно близко. Помимо того, что она «красива», получившаяся форма имеет интригующую характеристику: если вы нарисуете золотой прямоугольник, а затем проведете внутри него линию, чтобы разделить этот прямоугольник на квадрат и другой меньший прямоугольник, этот меньший прямоугольник удивительным образом станет еще одним золотым прямоугольником! Вы можете сделать это снова с этим новым золотым прямоугольником, и вы снова получите квадрат и еще один золотой прямоугольник.
, фи, округленное до десятых. Это будет не совсем 1,6, но должно быть довольно близко. Помимо того, что она «красива», получившаяся форма имеет интригующую характеристику: если вы нарисуете золотой прямоугольник, а затем проведете внутри него линию, чтобы разделить этот прямоугольник на квадрат и другой меньший прямоугольник, этот меньший прямоугольник удивительным образом станет еще одним золотым прямоугольником! Вы можете сделать это снова с этим новым золотым прямоугольником, и вы снова получите квадрат и еще один золотой прямоугольник.
Связь между золотым сечением и последовательностью Фибоначчи
Хорошо, но как насчет последовательности Фибоначчи? Как это фигурирует в этом? Я знаю, что это может показаться совершенно не связанным, но проверьте это. Давайте создадим новую последовательность чисел, разделив каждое число в последовательности Фибоначчи на предыдущее число в последовательности. Помните, последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Таким образом, деление каждого числа на предыдущее дает: 1 / 1 = 1 , 2/1 = 2, 3/2 = 1,5 и так далее до 144/89= 1,6179….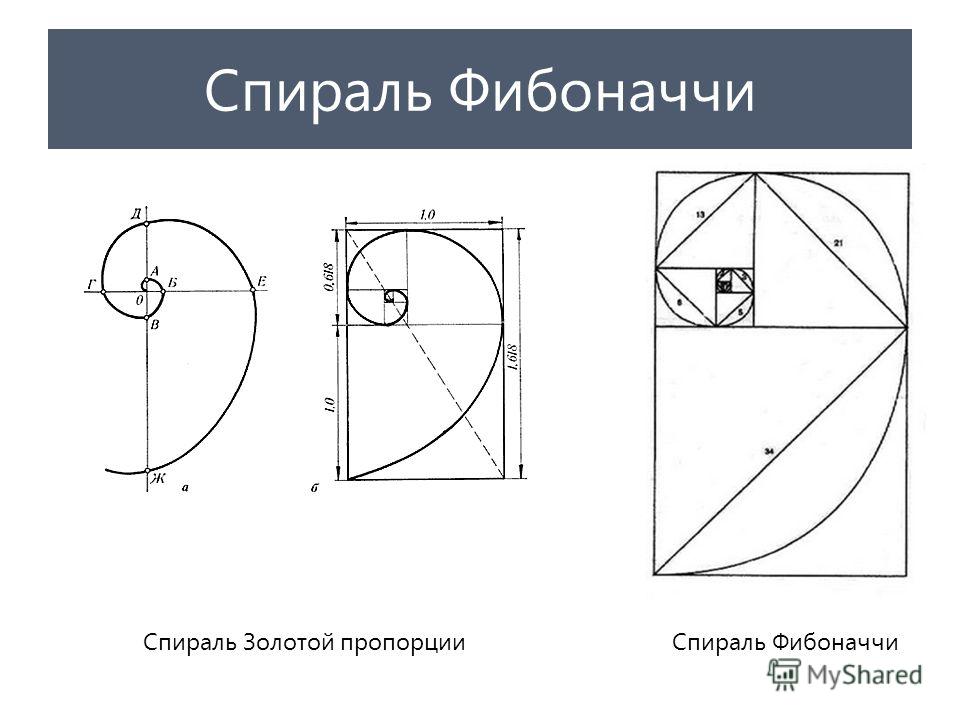 В результате получается последовательность:
В результате получается последовательность:
1, 2, 1,5, 1,666…, 1,6, 1,625, 1,615…, 1,619…, 1,6176…, 1,6181…, 1,6179…
Но заметили ли вы что-нибудь в этих числах? Возможно, из-за того, что они продолжают колебаться и дразняще приближаться все ближе и ближе к 1,618? — значению фи: золотому сечению! Действительно, без ведома Фибоначчи его решение проблемы роста популяции кроликов имеет глубокую связь с золотым сечением, которое художники и архитекторы использовали на протяжении тысячелетий!
Применение золотого сечения
Но золотое сечение предназначено не только для математиков, греческих скульпторов и художников эпохи Возрождения — его можно использовать и в жизни. На самом деле, в следующей статье мы поговорим о том, как вы можете использовать золотое сечение, чтобы делать более качественные снимки. И даже больше. Эти приятные формы проявляются не только в человеческом искусстве, но и в «искусстве» мира природы — во всем, от ракушек до подсолнухов! Обо всем этом мы тоже поговорим в следующий раз.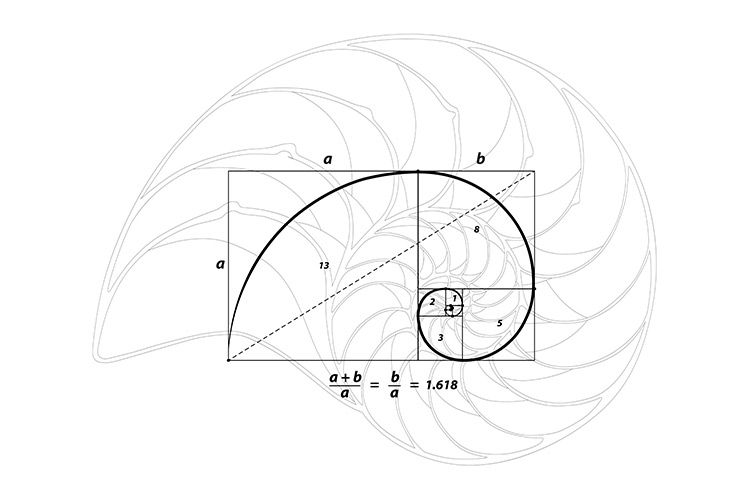
Подведение итогов
Это все математические расчеты, на которые у нас есть время на сегодня. Еще раз спасибо нашему спонсору на этой неделе, Go To Meeting. Посетите GoToMeeting.com/podcast и подпишитесь на бесплатную 45-дневную пробную версию их службы онлайн-конференций.
Пожалуйста, присылайте свои математические вопросы и комментарии по адресу , получайте обновления о шоу и моих повседневных размышлениях о математике, науке и жизни в целом, следуя за мной в Твиттере, и присоединяйтесь к нашему растущему сообществу любителей математики в социальных сетях с помощью станьте поклонником Math Dude на Facebook — это отличное место, чтобы задавать вопросы и общаться с другими любителями математики.
Если вам понравилось то, что вы прочитали, и у вас есть несколько свободных минут, я был бы очень признателен за ваш отзыв в iTunes. И пока вы там, пожалуйста, подпишитесь на подкаст, чтобы не пропустить новый выпуск Math Dude.
До встречи в следующий раз, это Джейсон Маршалл с «Быстрыми и грязными советами чувака-математика, чтобы сделать математику проще».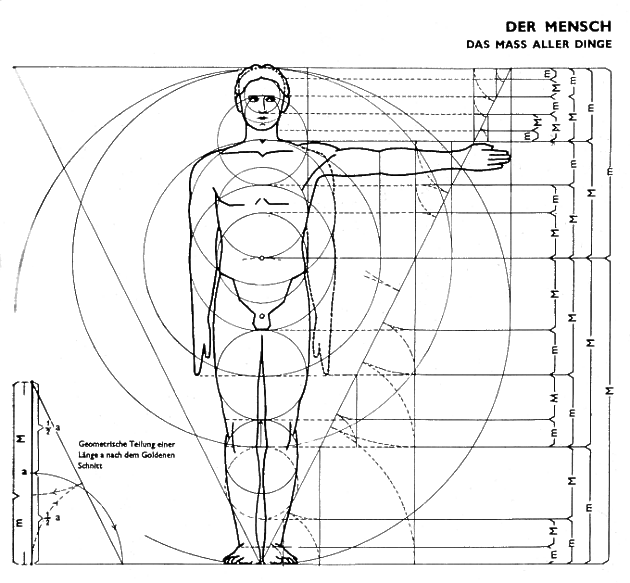 Спасибо за внимание, любители математики!
Спасибо за внимание, любители математики!
Фибоначчи и золотое сечение | Поговорим о науке
Золотая спиральная неоновая вывеска (Алина Курьянова, iStockphoto)
Неоновая вывеска «Золотая спираль» (Алина Курьянова, iStockphoto)
5,89
Узнайте о последовательности Фибоначчи и ее «золотой» связи с формами в мире красоты и природы.
Красота в глазах смотрящегоЧто делает что-то «красивым»? Красота полностью субъективна? Если да, то почему некоторые вещи долгое время считались красивыми, хотя тенденции изменились? Может ли быть в природе какая-то закономерность, на которую люди реагируют подсознательно?
Греки говорили, что вся красота сводится к математике. Философы, социологи, биологи и математики искали общее качество, которое могло бы объяснить наше восприятие красоты.
Голубая бабочка-морфо на цветке (Источник: MW через Pixabay).
Показана цветная фотография насекомого с двумя крыльями, окрашенными в оттенки синего. Узор на левом и правом крыльях является зеркальным отражением друг друга.
Крылья бабочки тёмно-синие вверху, у головы, становятся ярче до темно-синего в центре, у туловища, затем ярко-синего. Нижний край крыльев имеет толстую полосу черного цвета с рядами белых точек.
Между крыльями бабочки находится тонкое черное туловище и длинные усики. Он сидит на блестящем красном цветке с большой желтой тычинкой.
Оказывается, греки были правы насчет красоты и математики. Во многих вещах, которые люди называют красивыми, есть общий элемент. По мнению математиков еще древних греков и египтян, соотношение этого элемента равно 1:1,618. Это называется золотым сечением.
Числа Фибоначчи Так откуда взялось это «золотое» число? Соотношение основано на последовательности чисел, известных как числа Фибоначчи или последовательность Фибоначчи.
Знаете ли вы?
Леонардо Боначчи стал известен как Леонардо Пизанский, потому что он был из Пизы. Он был даже более известен как Фибоначчи, что в переводе с итальянского означает «сын Боначчи». При жизни его не называли Фибоначчи.
Фибоначчи был одним из самых важных математиков в . Он познакомил западный мир с арабской системой счисления в своей книге 9.0095 Liber Abaci . Это та же система счисления, которую мы используем до сих пор.
В той же книге Фибоначчи представил свою знаменитую задачу о кроликах:
Некий человек поместил пару кроликов в место, окруженное стеной. Сколько пар кроликов может быть получено от этой пары за год, если предположить, что каждый месяц каждая пара рождает новую пару, от которой второй месяц становится продуктивным?
(стр. 283-284, перевод с оригинальной латыни)
Его решение этой задачи привело к ряду чисел.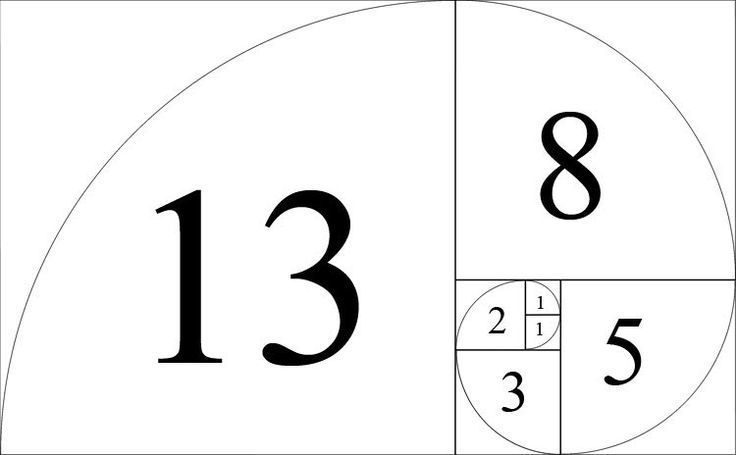 Первые два числа — это 0 и 1, а каждое последующее число — это сумма двух предшествующих ему чисел: 9.0003
Первые два числа — это 0 и 1, а каждое последующее число — это сумма двух предшествующих ему чисел: 9.0003
Это Последовательность Фибоначчи. Отдельные числа в этой последовательности называются числами Фибоначчи.
Последовательность Fibonacci также может быть выражена с использованием этого уравнения:
F N = F (N-1) + F 9007 (N-1) + F 9007 (N-1) + F 9007 (N-1) + F 9007 (N-1) + F 9007 (N-1) + F (N-1).Где n больше 1 (n>1).
Эта последовательность цифр может показаться не такой уж и большой.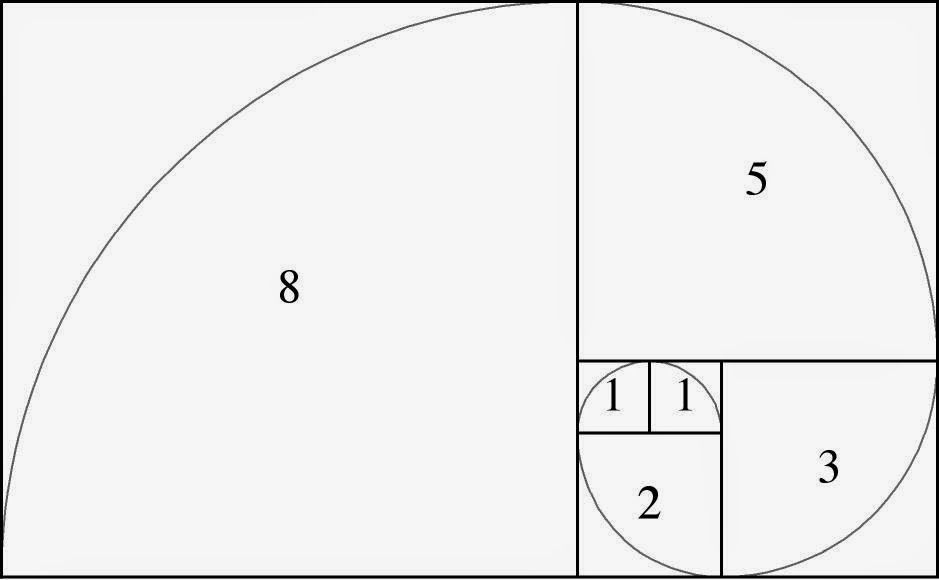
Например: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13
Для этих примеров ответы будут следующими: 1.000, 2.000, 1.500, 1.667 , 1,625 и 1,615.
Соотношения для первых семи пар чисел Фибоначчи (© Let’s Talk Science, 2022). Изображения – текстовая версияПоказана цветная гистограмма с 0–2,0 по оси Y и 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13 по оси x.
Слева направо: полоса с меткой 1/1 бледно-фиолетового цвета и достигает 1,0. Полоса с меткой 2/1 золотая и достигает 2,0. Полоса с меткой 3/2 имеет ярко-фиолетовый цвет и достигает значения 1,5. Полоса с пометкой 5/3 темно-фиолетового и достигает значения 1,667. Полоса с надписью 8/5 оранжевого цвета и достигает 1,6. Полоса с меткой 13/8 имеет бирюзовый цвет и достигает 1,625. Последний бар, помеченный 21/13, ярко-синего цвета и достигает 1,615. Эти соотношения написаны в центре каждого столбца.
Пунктирная линия проходит по графику на уровне 1,618033988749895. Это обозначено символом Phi. Горизонтальный овал с вертикальной линией через центр.
Это обозначено символом Phi. Горизонтальный овал с вертикальной линией через центр.
Золотое сечениеЗнаете ли вы?
Когда учащиеся смотрят на взаимосвязь между одним термином и следующим, они занимаются типом мышления, называемым рекурсивным мышлением .
Чем больше число Фибоначчи, тем больше отношение между каждой парой чисел приближается к 1,618033988749895. Этот номер называется Фи. Его также можно представить символом Φ, 21-й буквой греческого алфавита.
Фи — это золотое сечение. Он также обладает другими необычными математическими свойствами.
Знаете ли вы?
Золотое сечение также известно как Золотое сечение, Золотая середина и Божественная пропорция.
Золотое сечение также можно найти, используя две величины, например длины двух отрезков.
Две величины имеют золотое сечение, если их отношение равно отношению их суммы к большей из двух величин:
Соотношения отрезков в золотом сечении (© Let’s Talk Science, 2022).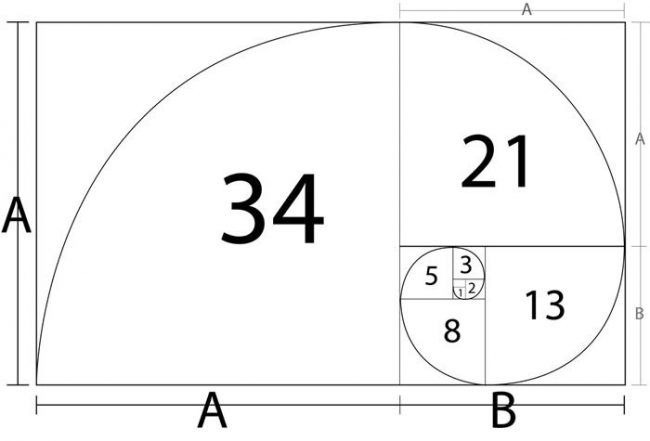 Изображение – текстовая версия
Изображение – текстовая версияНа рисунке показана цветная иллюстрация отрезков и математическое уравнение.
Вверху находится длинная черная полоса с надписью Line Segment. Ниже находится более короткая синяя полоса с надписью «Длинный сегмент». Справа находится еще более короткая зеленая полоса с надписью «Короткий сегмент». При размещении встык синяя и зеленая полосы равны по длине черной полосе.
Уравнение находится под этой иллюстрацией. Слева слова «Длинный сегмент» синего цвета разделены словами «Короткий сегмент» зеленого цвета. Справа знак равенства. Затем слова Line Segment, выделенные черным цветом, разделены словами Long Segment, выделенными синим цветом. За ним следует еще один знак равенства. Далее 1+ квадратный корень из 5 делится на два. За ним следует еще один знак равенства. Справа ответ 1,61803…
Показана цветовая диаграмма прямоугольника, разделенного на бледно-фиолетовый квадрат и меньший розовый прямоугольник.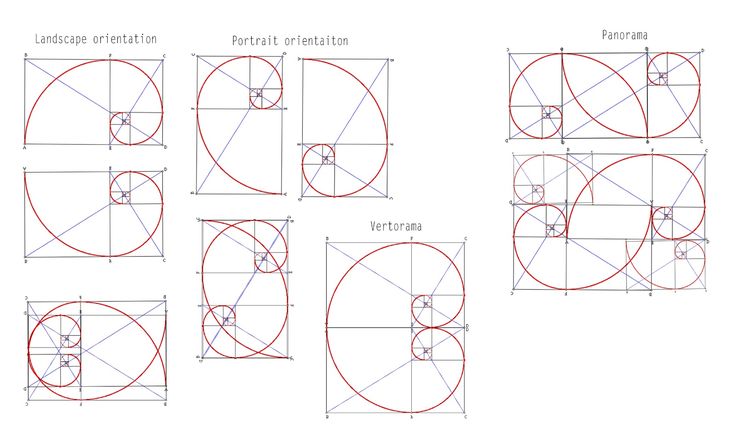
Верхний и левый края квадрата отмечены синим, строчным шрифтом, курсивом a. Верхний край меньшего прямоугольника помечен красным, строчным шрифтом, курсивом b. Весь нижний край большего прямоугольника помечен буквой a + b курсивом зеленого цвета.
Несколько золотых прямоугольников (Let’s Talk Science с использованием изображения primo-piano через iStockphoto). Изображение — текстовая версия – это черно-белая иллюстрация прямоугольника, разделенного на более мелкие квадраты и прямоугольники, которые становятся меньше по мере перемещения по странице в сторону точки в правом нижнем квадранте.Самый большой прямоугольник разделен на множество меньших фигур. Самый большой слева квадрат с цифрой 34.
Справа от квадрата находится вертикальный прямоугольник. Он разделен на квадрат с номером 21 и другой, меньший, горизонтальный прямоугольник.
Третий прямоугольник снова разделен. Квадрат справа имеет номер 13. Вертикальный прямоугольник далее делится на квадрат с номером 8 и горизонтальный прямоугольник, который снова делится.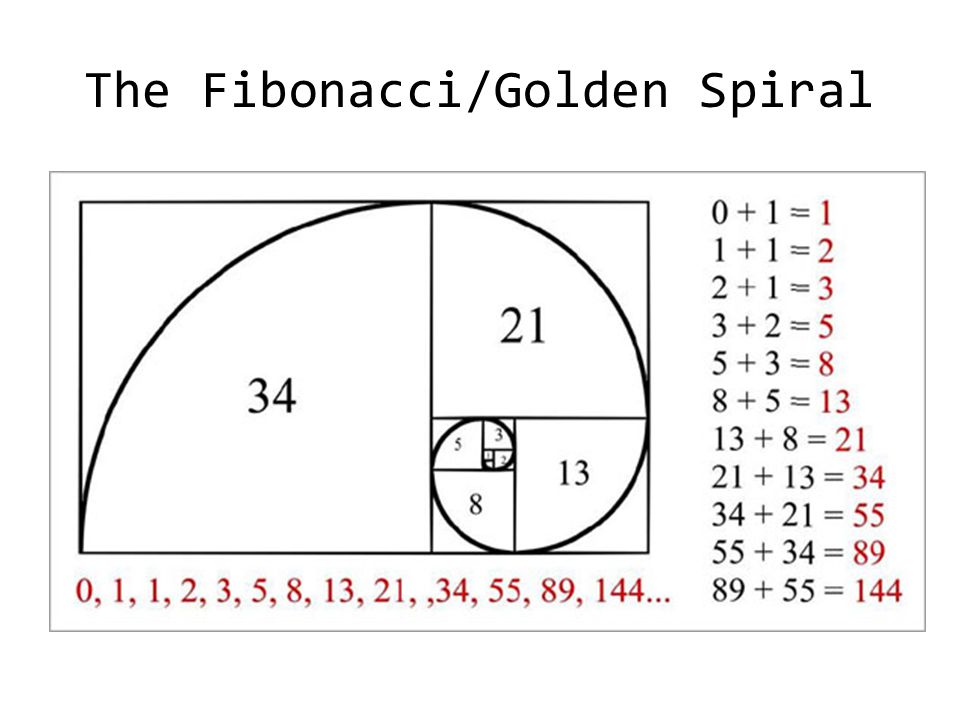 Следующий квадрат помечен 5. Рядом с ним другой вертикальный прямоугольник содержит квадрат с пометкой 3 и меньший горизонтальный прямоугольник, который, в свою очередь, содержит квадрат с пометкой 2. Наименьший квадрат не помечен, но похоже, что этот узор мог бы продолжаться, становясь все меньше и меньше с каждой итерацией.
Следующий квадрат помечен 5. Рядом с ним другой вертикальный прямоугольник содержит квадрат с пометкой 3 и меньший горизонтальный прямоугольник, который, в свою очередь, содержит квадрат с пометкой 2. Наименьший квадрат не помечен, но похоже, что этот узор мог бы продолжаться, становясь все меньше и меньше с каждой итерацией.
На черно-белом изображении прямоугольника, разделенного на более мелкие квадраты и прямоугольники, наложенные синей спиральной линией.
Самый большой прямоугольник разделен на множество меньших фигур. Самый большой слева квадрат с номером 34. Синяя линия над ним изгибается из левого нижнего угла в правый верхний, образуя четверть круга.
Справа от квадрата находится вертикальный прямоугольник. Он разделен на квадрат с номером 21 и другой, меньший, горизонтальный прямоугольник. На квадрат с номером 21 наложена еще одна четверть круга, начиная с левого верхнего и заканчивая правым нижним углом.
Третий прямоугольник снова разделен. Квадрат справа помечен цифрой 13. На него наложена изогнутая синяя линия, идущая сверху справа и снизу слева.
Вертикальный прямоугольник далее делится на квадрат с цифрой 8 и горизонтальный прямоугольник, который снова делится. Синяя линия продолжает изгибаться по этим фигурам.
Следующий квадрат имеет номер 5. Рядом с ним другой вертикальный прямоугольник содержит квадрат с номером 3 и меньший горизонтальный прямоугольник, который, в свою очередь, содержит квадрат с номером 2. Синяя линия продолжает скручиваться по этим фигурам.
Самый маленький квадрат не помечен, но это точка, где синяя спираль заканчивается тугим завитком. Узор выглядит так, как будто он может продолжаться, разделяясь на все меньшие и меньшие формы, а спираль становится все туже и туже.
Спираль Фибоначчи против Золотой спирали
Термины Спираль Фибоначчи и Золотая спираль часто используются взаимозаменяемо.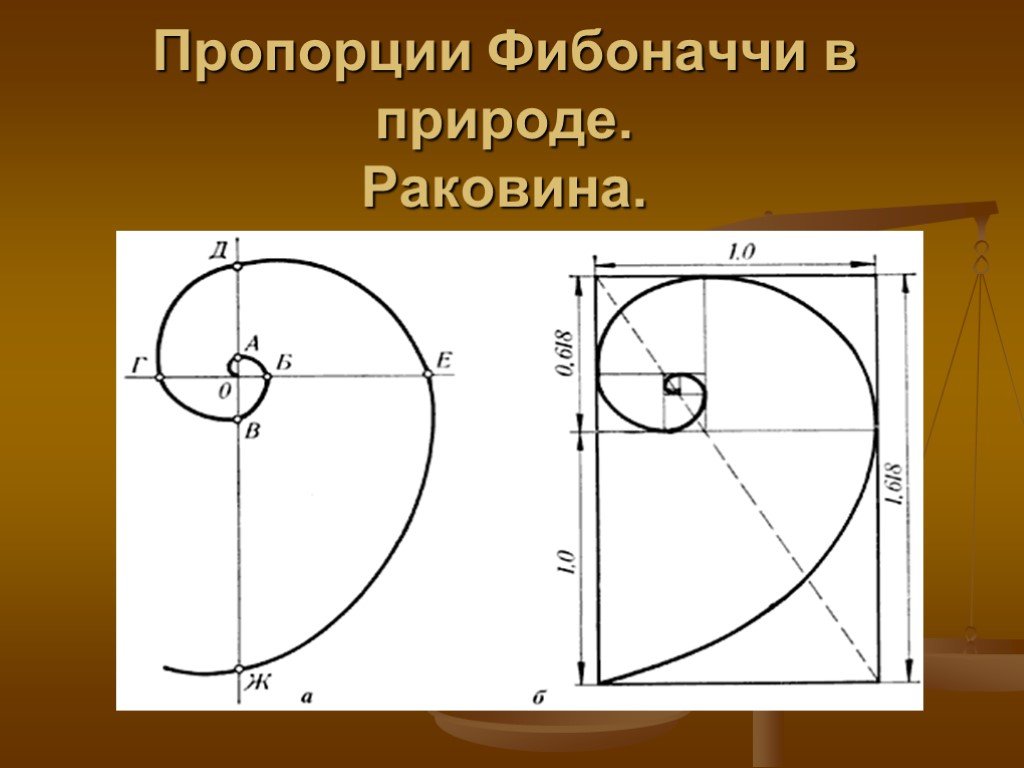
Спираль Фибоначчи создается путем создания спирали квадратов, размер которых увеличивается на числа в последовательности Фибоначчи. Итак: 1, 1, 2, 3, 5, 8, 13, 21 и т. д. Вы можете увидеть это в анимированной гифке ниже.
Как можно построить спираль Фибоначчи (© Let’s Talk Science, 2022)
Изображение – текст. Версия. Показан анимированный GIF-файл со спиралью , растущей из все более и более крупных квадратов разных цветов.
Первый квадрат крошечный и синий, с изогнутой белой линией от нижнего левого до верхнего правого угла. Второй квадрат появляется выше. Он намного больше, и линия изгибается снизу справа вверху слева. Третий квадрат снова больше. Он отображается слева от остальных, а линия изгибается от верхнего правого угла к нижнему левому. Четвертый квадрат отображается под остальными с линией, идущей сверху слева направо и снизу. Пятый квадрат оранжевого цвета и отображается справа с линией, идущей слева внизу и справа вверху.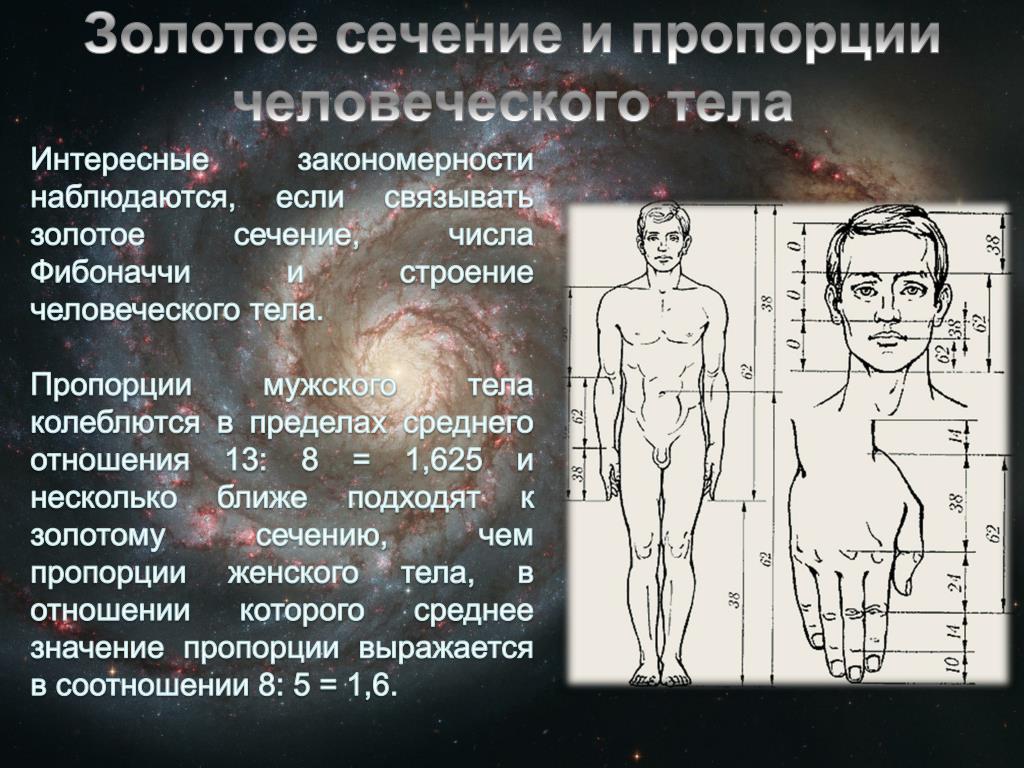 Пятый квадрат появляется поверх остальных, в розовом цвете, с линией от нижнего правого до верхнего левого. Последний квадрат настолько велик, что занимает больше половины страницы и заполняет все пространство слева от остальных. Он синего цвета с линией, изгибающейся от верхнего правого угла к нижнему левому.
Пятый квадрат появляется поверх остальных, в розовом цвете, с линией от нижнего правого до верхнего левого. Последний квадрат настолько велик, что занимает больше половины страницы и заполняет все пространство слева от остальных. Он синего цвета с линией, изгибающейся от верхнего правого угла к нижнему левому.
Когда все квадраты собраны вместе, изогнутые линии на них образуют спираль. Эта спираль вырастает из крошечного пустого квадрата в правом нижнем углу страницы.
Золотая спираль, тем не менее, создается путем вложения все меньших и меньших золотых прямоугольников в большой золотой прямоугольник. Посмотрите на разницу в GIF ниже:
Как можно сделать золотую спираль (© Let’s Talk Science, 2022)
Изображение – Текст ВерсияПоказан анимированный GIF-файл, состоящий из прямоугольников и квадратов все меньшего и меньшего размера, расположенных друг над другом в виде спирали.
Первый прямоугольник синего цвета и занимает всю панель. Он имеет изогнутую белую линию через верхний левый угол.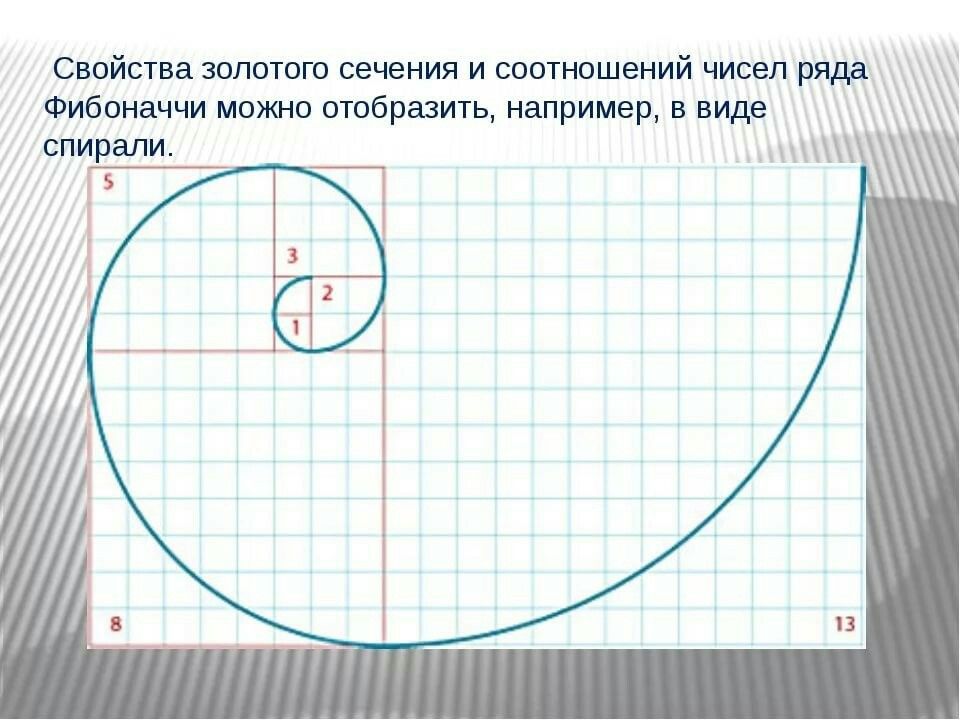 Вторая фигура — это розовый прямоугольник, который закрывает правую сторону синего, так что синяя часть теперь имеет квадратную форму. Он имеет изогнутую белую линию через верхний правый угол. Третий — оранжевый прямоугольник, который покрывает нижнюю часть розового, поэтому розовая область образует квадрат. Он имеет изогнутую белую линию в правом нижнем углу. Четвертый — фиолетовый прямоугольник, который закрывает левую часть оранжевого, образуя оранжевый квадрат. Далее идет красный прямоугольник, образующий фиолетовый квадрат, и зеленый прямоугольник, образующий красный квадрат. Наконец появляется крошечный синий квадратик рядом с белым того же размера.
Вторая фигура — это розовый прямоугольник, который закрывает правую сторону синего, так что синяя часть теперь имеет квадратную форму. Он имеет изогнутую белую линию через верхний правый угол. Третий — оранжевый прямоугольник, который покрывает нижнюю часть розового, поэтому розовая область образует квадрат. Он имеет изогнутую белую линию в правом нижнем углу. Четвертый — фиолетовый прямоугольник, который закрывает левую часть оранжевого, образуя оранжевый квадрат. Далее идет красный прямоугольник, образующий фиолетовый квадрат, и зеленый прямоугольник, образующий красный квадрат. Наконец появляется крошечный синий квадратик рядом с белым того же размера.
Когда изображение готово, все изогнутые белые линии образуют спираль, закручивающуюся к последнему белому квадрату в правом нижнем квадранте панели.
Эти спирали кажутся знакомыми? Ну должны! Мы можем наблюдать ту же закономерность в природе.
Спираль Фибоначчи на подсолнухе (Let’s Talk Science с использованием изображения Дамиана Паулоса через iStockphoto). Изображение — текстовая версияПредупреждение о неправильном представлении
Стоит отметить, что спирали, которые мы видим в природных объектах, не совсем соответствуют золотому сечению, но приближаются к нему.
Показана цветная фотография центра подсолнуха с наложенной на него синей спиралью.
Цветок с ярко-желтыми лепестками. Его центр состоит из крошечных заостренных темно-желтых структур, плотно упакованных в круг. Спираль демонстрирует, что крошечные заостренные структуры расположены по спирали.
Спираль Фибоначчи на внутренней стороне раковины наутилуса (Let’s Talk Science с использованием изображения, сделанного duncan1890 через iStockphoto). Изображение — текстовая версияПоказана цветная фотография раковины, разрезанной пополам, чтобы показать внутреннюю часть, с наложенной на нее красной спиралью. .
Стенки раковины закручиваются от центральной точки, становясь все шире и шире к внешнему краю. Эта структура разделена на изогнутые, клиновидные участки, которые также увеличиваются в размерах от центральной точки. Спираль демонстрирует, что оболочка образует спираль Фибоначчи.
Спираль демонстрирует, что оболочка образует спираль Фибоначчи.
Черный фон с белыми и золотыми точками. Центр водоворота выполнен из бледно-золотого цвета с тонкими линиями более темного золота по всему периметру. Тонкие белые хвосты вьются из центра, изгибаясь в пространство. Эти полосы полупрозрачного белого цвета перемежаются сгустками ярко-белого цвета.
Красная спираль, наложенная на фотографию, показывает, что эта галактика формирует спираль Фибоначчи.
Золотое сечение можно использовать и с другими формами. Золотые пропорции можно найти в узорах, включающих круги, треугольники, пятиугольники и другие формы.
Другие формы с их золотым сечением (Давайте поговорим о науке, используя изображение от primo-piano через iStockphoto).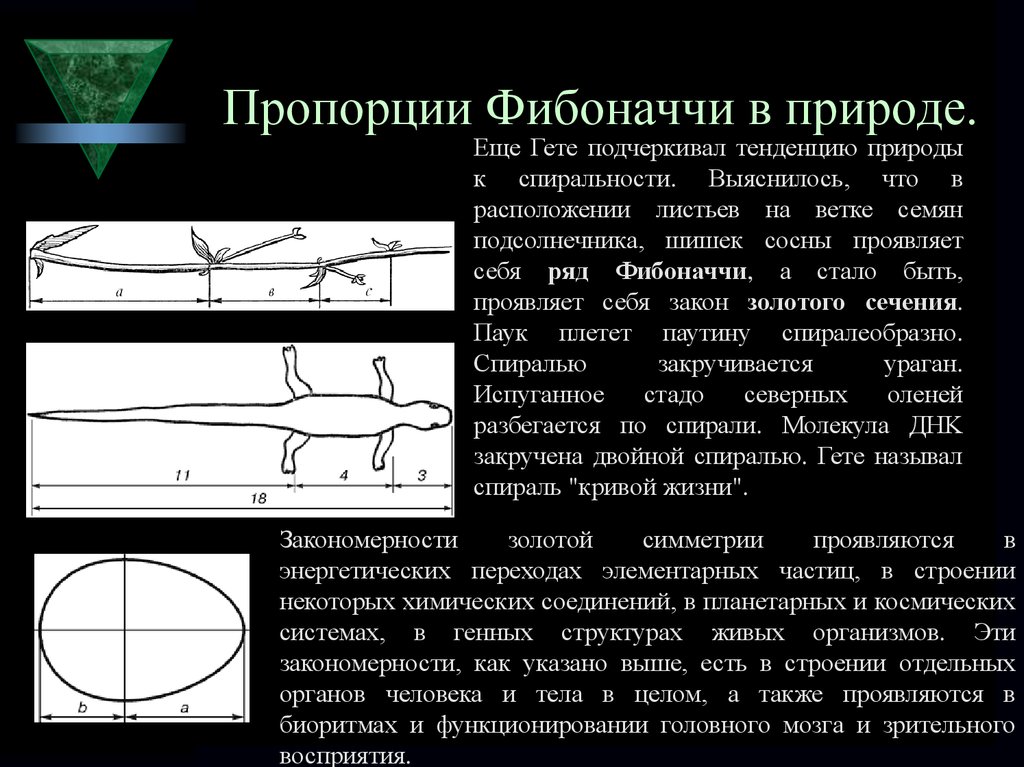 Изображение – версия текста
Изображение – версия текстаПоказана диаграмма пересекающихся треугольников, пятиугольников, квадратов и кругов с синими линиями, проведенными поверх них.
Самый большой треугольник остроугольный и содержит семь других, меньших треугольников. Его левый внешний край покрыт синей линией, обозначенной 1,618. Синяя линия поворачивает угол и продолжается на его нижнем крае, обозначенном цифрой 1. Этот треугольник разделен на равнобедренный и разносторонний треугольники. Разносторонний треугольник далее делится на еще один остроугольный и еще один равнобедренный треугольник. Синяя линия продолжается вокруг длинного, затем короткого края остроугольного треугольника. Этот треугольник снова делится на еще один остроугольный и еще один равнобедренный. Синяя линия продолжается вдоль основания остроугольного треугольника, который далее делится на еще один остроугольный и еще один равнобедренный. Синяя линия продолжается вдоль этого основания, и треугольник снова делится. Синяя линия заканчивается, когда она поворачивает за узкий угол вдоль основания наименьшего остроугольного треугольника. В целом синяя линия образует своего рода спираль с рядом острых углов и прямых краев, которые становятся короче и ближе к точке в правом нижнем углу самого большого треугольника.
В целом синяя линия образует своего рода спираль с рядом острых углов и прямых краев, которые становятся короче и ближе к точке в правом нижнем углу самого большого треугольника.
Самый большой пятиугольник помечен цифрой 8. Его нижний край обведен синей линией. Внутри него меньший пятиугольник помечен цифрой 5, а синяя линия продолжается вдоль одного из его краев. Внутри него находятся меньшие пятиугольники, обозначенные цифрами 3 и 2, где линия продолжается вдоль края каждого из них. Два еще меньших пятиугольника не подписаны, но построены по тому же образцу. Все сегменты синей линии образуют спираль с тупыми углами и прямыми краями, которые становятся короче и ближе к точке в правом нижнем углу самого большого пятиугольника.
Самый большой квадрат помечен цифрой 8. Меньший квадрат, упирающийся в него справа, помечен цифрой 5. Синяя линия проведена из левого верхнего угла большого квадрата в левый верхний угол меньшего квадрата, образуя уклон вправо. Меньшие и меньшие квадраты, помеченные 3, 2 и 1, следуют той же схеме, и синяя линия продолжается по прямому наклону вниз до самого маленького квадрата в крайнем правом углу.