Пропорции фибоначчи: Золотое сечение и пропорции Фибоначчи

Разметчик Фибоначчи

Разметчик Фибоначчи — это устройство, позволяющее вам всегда иметь под рукой соотношениие размеров для ваших изделий, удовлетворяющее принципам Золотого Соотношения. Если вы хотите, чтоб мебель, которую вы делаете, была не только функциональна, но и по-настоящему красива, то начинать нужно с пропорций предмета в целом и его частей. Если эти пропорции правильны, ваше произведение будет радовать глаз, иначе — может быть ужасным. Разметчик Фибоначчи — отличное подручное средство для проектирования красивых изделий.

Разметчик Фибоначчи, специальный инструмент, назван по имени итальянского математика Фибоначчи, жившего в  XIII веке.  «Фибоначчи» у этого учёного — это псевдоним, происхождение которого не известно он же — Fibonacci, он же — Леона́рдо Пиза́нский, он же — Leonardo Pisano. В честь учёного назван и числовой ряд, в котором каждое последующее число равно сумме двух предыдущих. Эта числовая последовательность носит название чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, …  Хотя этот ряд и был известен ещё в Древней Индии, т.е. задолго до рождения умного Фибоначчи, но, тем не менее, своё нынешнее название числа Фибоначчи получили благодаря исследованию свойств этих чисел, проведённому именно этим учёным в его труде «Книга абака» (Издательство РИМГНИЗ «Римское Государственное Народное Издательство», 1202 г.).  Ряды Фибоначчи, спирали Фибоначчи, уровни Фибоначчи — об этом много можно прочитать.

К чёму всё это? Одна закономерность упомянута, но можно заметить и другую — деление числа в ряду Фибоначчи на предыдущее даёт практически постоянный результат — 1,618 — проверьте, если не лень. С этими последовательностями много чего связано — от биржевых котировок до рубежей разграничения развития человечества на отдельные этапы, которые иногда называют временными ступенями эволюции.

Короче говоря, замечательная последовательность. Ну и к чему же это, нам то, с шипорезками, пилами и стамесками, зачем всё это? Есть в этом большой смысл и для нас, читаем дальше.

Даже если вы одарены превосходным видением, не так-то просто спроектировать предмет мебели без использования основополагающих принципов для определения размеров этого предмета мебели и, главное, пропорций между его элементами. Будет ли это подход к проектированию, который передаётся от мастера к ученику или ваше врожденное чувство равновесия и гармонии, которым обладают лишь некоторые одарённые люди, в любом случае без такой совокупности знаний и опыта вы не сможете создать совершенное изделие, которое будет радовать ваш глаз и вызывать восхизение окружающих и ваших друзей. Можно создать изделие, которое будет прочно и функционально адекватно, но не будет радовать и вызывать приятные чувства. Предмет мебели, который не учитывает проверенные веками правила построения может выглядеть неуклюжим, неуравновешенным или даже ужасным.

Главным среди множества совокупностей фундаментальных установок, сложившихся за сотни лет представлений и понятий, которые разработчики предметов мебели использовали и продолжают использовать  для обеспечения баланса и хороших пропорций в дизайне мебели является золотая пропорция или соотношение (также называемое золотой серединой или золотым сечением). Обозначается эта пропорция греческой буквой ∳ (фи). Золотое соотношение может быть выражено уравнением ∳ (фи)= [1 + √ 5] / 2. Для простоты практического применения, мы можем взять лишь результирующее значение ∳ (фи), равное 1,618. Т.е. одно значение к другому должно относится как 1 к 1,618. Одна длина, к другой, например.

Один из многих замечательных принципов золотой пропорции является то, что коротий отрезок прямой линии по отношению к длинному отрезку этой же линии относится так же, как длинный отрезок линии относится к общей длине линии, и это соотношение равно ∳ (фи) = 1,618:

Именно это соотношение заложено в самой конструкции замечательного разметочного инструмента — Разметчика Фибоначчи:

Исходя из описанного принципа, Золотым (или гармоничным) Прямоугольником является такой, стороны в котором соотносятся как 1 : 1,618, т. е. длина большей стороны прямоугольника равна длине меньшей стороны прямоугольника, умноженной на ∳ (фи)=1,618:

Узнаёте? Это же столешница гармоничного стола! Или фасад тумбы и много чего ещё.

Аналогично, Золотым (или гармоничным) Параллелепипедом является тот, стороны в котором тоже соотносятся как 1 : 1,618, т.е. длина большей стороны параллелепипеда равна высоте параллелепипеда, умноженной на ∳ (фи)=1,618, а ширина параллелепипеда равна высоте параллелепипеда, поделённой на ∳ (фи)=1,618:

Узнаёте? Это же мебельная тумба, пристенный стол (консоль) и т.д.

Золотая Пропорция лежит в основе многих (если не всех) естественных соотношений и даже построения нашей Вселенной. Примеры есть в изобилии на каждом уровне, от размножения кроликов, расположения семян в подсолнухе и орешков в шишке, до астрофизики и квантовой механики. Планетарные орбиты и даже структура человеческой фигуры являются ещё одним подвержедния соблюдения этой замечательной пропорции.

Соотношение между соседними фалангами пальцев — это ∳ (фи) = 1,618, Соотношение между локтем и кистью — это ∳ (фи) = 1,618, соотношение расстояния от макушки до глаз и растояния от глаз до подбородка — это ∳ (фи) = 1,618, соотношение расстояния от макушки до пупка и растояния от пупка до пяток — это опять-таки ∳ (фи) = 1,618:

 

Дистанции между солнцем и первыми пяти планетами в солнечной системе так же соотносятся (примерно) как ∳ (фи) = 1,618, поэтому, как безусловно известно, астронометрия использует золотое соотношение при определении планет на их орбитах:

Будучи столь фундаментальным и столь широко распространённым в природе, это отношение просто призывает нас на подсознательном уровне как абсолютно правильное, которому надо следовать. Как таковое, это соотношение было использовано на протяжении веков дизайнерами и архитекторами, от пирамид до мебельных шедевров.

Большая пирамида в Гиза, как теперь понятно, тоже построена в соответствии с Золотым Сечением: высота стороны пирамиды равна длине основания стороны пирамиды, умноженной на всё ту же величину ∳ (фи) = 1,618:

 

При строительстве Парфенона (древнегреческий храм, расположенный на афинском Акрополе, главный храм в древних Афинах) использовалось соотношение ∳ (фи) = 1,618 при определении внешних размеров и соотношения его частей:

Достоверно не известно, применялись ли при построении Парфенона калькуляторы или Разметчики Фибоначчи, но соотношение точно применялось. Более подробно о соотношении ∳ (фи) = 1,618 в конструкции этого памятника архитектуры сказано в видеоролике, начиная с 48-й секунды:

В вышеприведённом ролике, наконец-то, дело дошло и до предмета мебели, пусть и простого.

Главное — соотношение всё то же — ∳ (фи) = 1,618.

В одном из видов комода с множеством ящиков называемом в разных изданиях как Highboy или Popadour («Высокий парень» или «Помпадур»), сделанном в Филадельфии в промежутке между 1762 и 1790 годами, используется Золотая Пропорция в соотношении размеров многих из его элементов. Каркас — это Золотой прямоугольник, положение сужения («талии» шкафа) определяется делением общей высоты шкафа на ∳ (фи) = 1,618. Высоты нижних ящиков так же соотносятся как ∳ (фи) = 1,618:

 

Золотое Сечение применяется при изготовлении мебели чаще всего в качестве некоего прямоугольника, который строится с помощью ∳ (фи) = 1,618 для двух его измерений, т.е. уже упоминаемого Золотого прямоугольника, где длина в 1,618 раз больше ширины (или наоборот). Эти пропорции могут быть использованы для определения габаритных размеров мебели, а также деталей интерьера, таких как двери и ящики. Можно применять рассчёты, деля и умножая на такое «круглое» и удобное число, как 1,618, но можно просто использовать Разметчик Фибоначчи, просто снимая размеры бОльшего предмета и откладывая после этого размер меньшего предмета.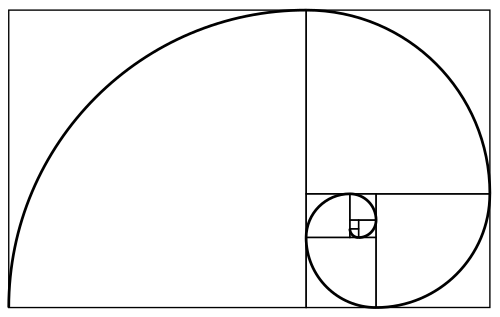

Или наоборот. Быстро, просто и удобно.

Предметы мебели являются трехмерными и Золотое Соотношение может быть применено ко всем трем измерениям, т.е. предмет мебели становится Золотым Параллелепипедом, если сделать его по правилам Золотого Соотношения. К примеру, в простом случае, глядя на предмет мебели сбоку, его высота может быть наибольшим измерением в Золотом  Прямоугольнике. Однако, если смотреть на тот же предмет мебели спереди, та же высота может быть коротким измерением в Золотом Прямоугольнике.

Необходимо отметить, однако, что форма предмета должна следовать за его функцией. Даже превосходные пропорции мебели могут оказаться быть бессмысленными, если этот предмет не может быть использован, например потому, что он слишком маленький или слишком большой или по другим причинам не может быть использован с комфортом. Следовательно, практические соображения должны быть на первом месте. В самом деле, большинство проектов мебели требуют, чтоб вы начали проектирование с некоторых заданных размеров: стол должен быть определенной высоты, шкаф возможно, придется приноравливать к конкретному пространству, а в книжном шкафу может потребоваться определенное количество полок.

 Но почти наверняка вы вынуждены будете определять множество других размеров, в отношении которых можно применить правильные пропорции. Но результат будет стоит затраченных усилий, чтоб в результате увидеть, как Золотое Соотношение может работать для всех этих элементов. Принятие решения о размерах «на глаз» или, что еще хуже, исходя из имеющихся заготовок, не позволит вам получить отлично сбалансированный, с красивыми пропорциями отдельных частей и предмета мебели в целом.

Итак, размеры отдельных частей мебели должны быть пропорциональны в соответствии с Золотым Соотношением. Такие элементы, как ножки стола, относительные размеры элементов каркаса, такие как вертикальные и горизонтальные части фасадов, проноги, царги и т.д., могут быть рассчитаны с применением Золотой Пропорции. Золотое сечение также предлагает один из способов решение проблемы проектирования ящиков в комоде с ступенчатым увеличением высоты ящиков. С помощью Разметчика Фибоначчи легко осуществить такую разметку — надо просто взять размер бОльшего ящика и по разметчику отложить размеры двух соседних ящиков и т. д. После этого, взяв размер ящика, по разметчику отложить расстояние от верха ящика до места расположения его ручки.

Такой метод использования Разметчика Фибоначчи, как инструмента для практического применения Золотого Соотношения будут эффективен для определения и других размеров, таких, как положение полок в шкафу, разделителей между ящиками и т.д. Любые размеры предмета мебели, изначально, определяются функциональными и структурными требованиями, но множество поправок может быть сделано путём применения Золотого Соотношения, что, несомненно, добавит в предмет гармонию. Использование Золотого Соотношения при проектировании мебели позволит вам сделать гармоничным не только предмет в целом, но и позволит вам быть уверенным в том, что все составные части — дверные панели, ящики, ножки, царги и т.д. принципиально, гармонично связаны между собой.

Спроектировать что-то с абсолютно совершенными пропорциями редко удается в реальности. Почти каждый предмет мебели или дерева придётся соотносить с ограничениями, накладываемыми функциональностью, возможностями столярных соединений или  экономией средств.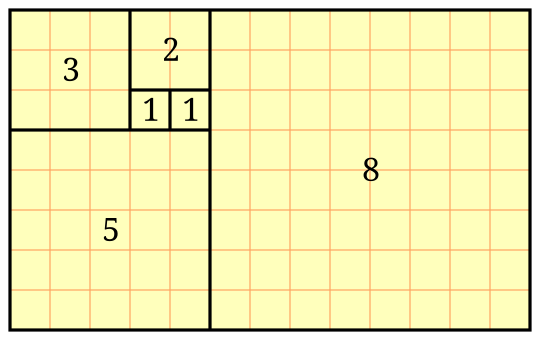 Но даже попытка приблизиться к совершенству, которое может быть определено как размеры, в точности соответствующие Золотому Соотношению гарантирет вам получение лучшего результата по сравнению с разработкой без внимания к этим основополагающим принципам. Даже если вы приблизились к идеальным пропорциям, то глаз зрителя сгладит небольшие недостатки и сознание заполнит некоторые пробелы в дизайте. Желательно, но не обязательно, чтоб всё было идеально и соответственно формуле. Но если предмет вашей мебели абсолютно не соответствует правильным пропорциям, без сомнения, он будет некрасив. Поэтому стремиться к правильным пропорциям необходимо.

Наконец, мы часто корректируем вещи на глаз, чтобы сделать предмет легче и лучше сбалансированным, и делаем мы это с помощью методов, которые являются повседневными в деревообработке. Эти методы включают в себя учёт изменения размеров заготовки, исходя из направления волокон древесины, учёт рисунка древесины, с помощью которого можно предмет мебели сделать более привлекательным, отделку краёв и углов, которая создаст впечатление большей или меньшей толщины элемента изделия, использование молдингов для более точного соответствия изделия Золотому Прямоугольнику или Параллелепипеду, использование сужающихся ножек, чтобы сделать ощущение большего приближения предмета мебели к идеальной пропорции, и, в конце концов, смешивание всех этих методов для достижения идеального дизайна. Использование Золотого Сечения и инструмента для его применения — Разметчика Фибоначчи — начало этого стремления к совершенству.

В статье использованы материалы главы «A Guide to Good Design» из книги «Practical Furniture Design», написанной Graham Blackburn — признанным мебельным мастером, популяризатором деревообработки и издателем.

Евгений Фукс

технический консультант
LeighJigs.ru
[email protected]

Золотое сечение в стоматологии | Клиника биоэстетической стоматологии доктора Даяна

С древних времен человек начал разделять вещи на красивые и не красивые. Уже в Древней Греции античные философы начали выявлять некую формулу, которая раскрыла тайну того, что мы называем гармонией. Так что же такое гармония? Если рассматривать цветок вблизи и аналогично другие естественные и созданные человеком творения, то можно найти единство и порядок, свойственные всем этим предметам.
Этот порядок и единство и есть Гармония, определяющая Красоту.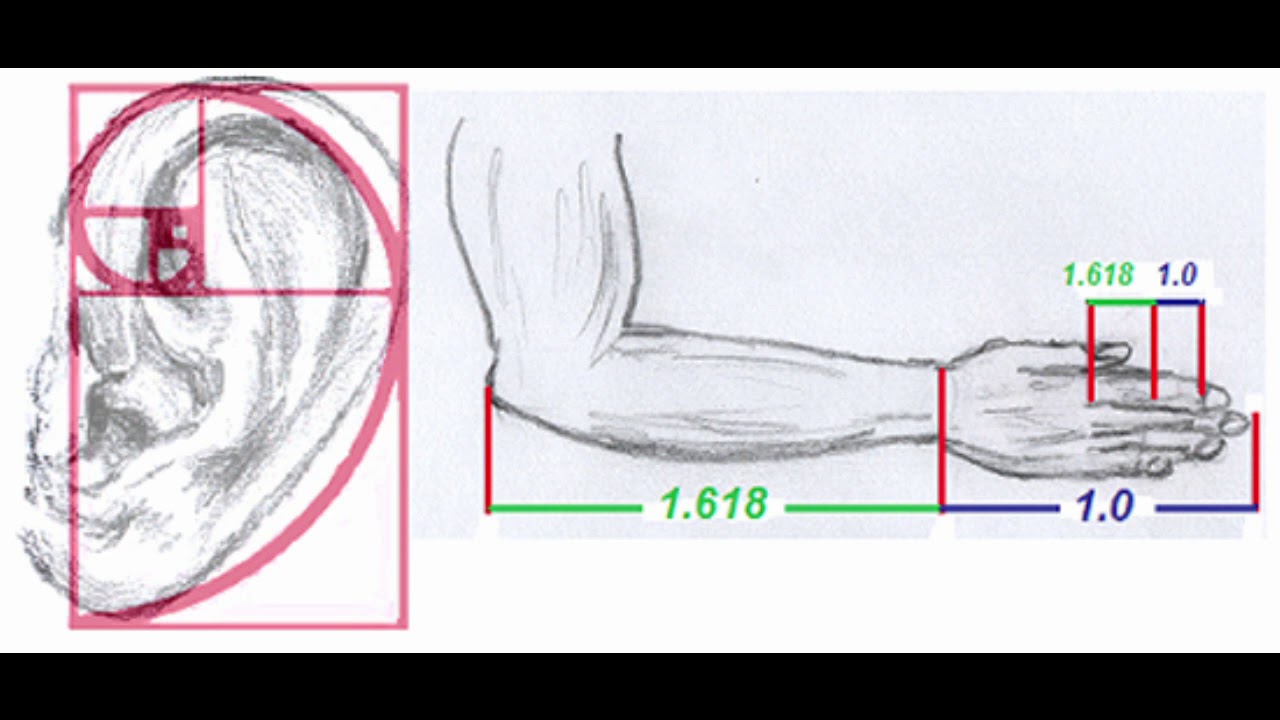

Итак, гармония это красота, а красота, как говорили греки, — это математика, следовательно, гармония это математика. Из многих пропорций, которыми пользовался человек при создании живописи, скульптуры, музыки, поэм, самой главной является одна, и именно она отражает понятие ГАРМОНИИ наилучшим образом. Эту пропорцию называли по-разному: божественной, золотой, золотым сечением, золотой серединой, золотым делением, золотым числом. Но суть ее одна.
Золотое деление — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; другими словами, меньший отрезок так относится к большему, как больший ко всему.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. Термин «золотое сечение» был введён именно Леонардо да Винчи, который использовал золотое сечение как пропорции «идеального человеческого тела».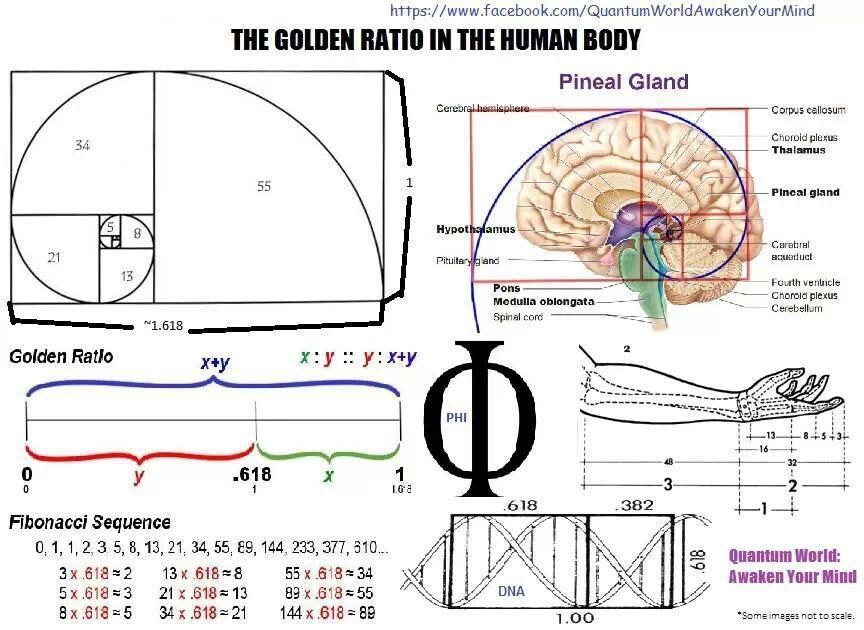
В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.

Было установлено, что числовой ряд чисел Фибоначчи характеризует структурную организацию многих живых систем. Например, винтовое листорасположение на ветке составляет дробь (число оборотов на стебле/число листьев в цикле, например 2/5; 3/8; 5/13), соответствующую рядам Фибоначчи. Хорошо известна «золотая» пропорция пятилепестковых цветков яблони, груши и многих других растений. Носители генетического кода — молекулы ДНК и РНК — имеют структуру двойной спирали; ее размеры почти полностью соответствуют числам ряда Фибоначчи.

Золотое сечение в природе

Все объекты в природе подчиняются золотой пропорции. Значит именно она и позволяет нам восторгаться природой, значит золотая пропорция несет в себе ГАРМОНИЮ. Спиралевидную форму золотой пропорции можно увидеть в расположении семян подсолнечника, в шишках сосны, в ананасах, кактусах, строении лепестков роз и даже в расположении листьев на ветке, энергия закручивается по спирали.
В математике нет более иной формы, которая обладала бы такими же уникальными свойствами как спираль. Спираль — основа всего.

Строение морских раковин, рога и бивни животных, развивающиеся в форме спирали. Бивни слонов и вымерших мамонтов, когти львов, и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль. Пауки всегда плетут свои паутины в виде логарифмической спирали. Строение таких микроорганизмов, как планктоны также имеют форму спирали.

Строение человека

Строение молекулы ДНК: Все сведения о физиологических особенностях живых существ хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра). Так вот 21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотой пропорции 1:1,618!

Если приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг. Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения. Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.

У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи! Американский физик Б.Д.Уэст и доктор А.Л. Гольдбергер во время физико-анатомических исследований установили, что в строении легких человека также существует золотое сечение.

Строение снежинок

Золотое сечение присутствует в строении всех кристаллов. Cнежинки, также представляющие собой водные кристаллы, вполне доступны нашему взору. Все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотой пропорции.

В биологических исследованиях 70-90 гг. показано, что, начиная с вирусов и растений и кончая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем. Можно отметить два вида проявлений золотого сечения в живой природе: иррациональные отношения по Пифагору — 1.62 и целочисленные, дискретные — по Фибоначчи.

Золотое сечение в творениях человека

Формула золотого сечения очень хорошо известна всем людям искусства, ибо это главные правила эстетики. Любое произведение искусства, спроектированное в точном соответствии с пропорциями золотого сечения, являет собой совершенную эстетическую форму.

Записаться на консультацию можно по телефону +7 (499) 322-19-03

Соотношений и методов Фибоначчи в техническом анализе | Мехмет Ата КАРТАЛ

Одним из самых интересных разделов технического анализа являются коэффициенты Фибоначчи.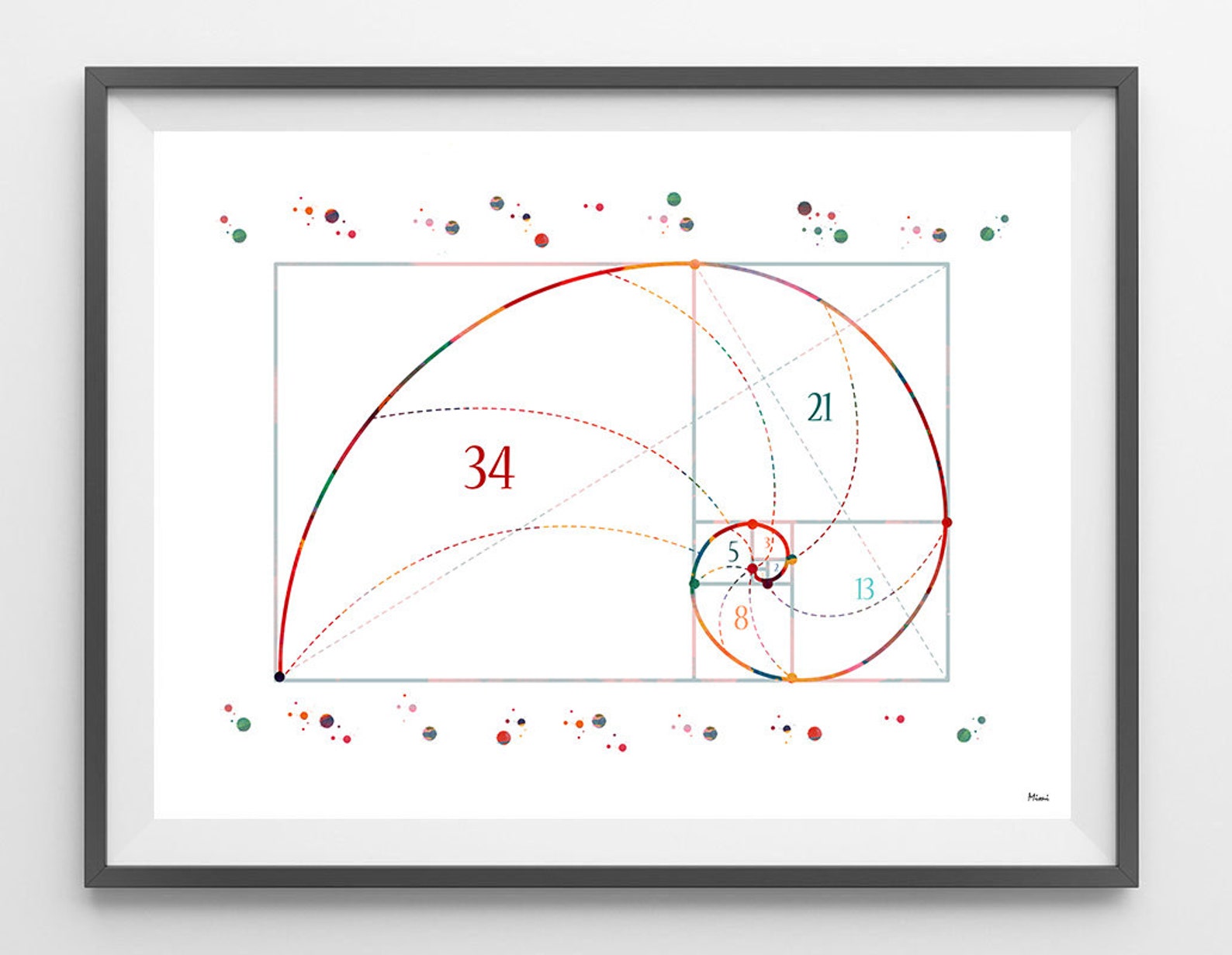 Основная логика метода Фибоначчи заключается в том, что математическая структура, наблюдаемая в естественном порядке, применима и на финансовых рынках. Чтобы лучше понять эту математическую структуру, давайте сначала посмотрим на Леонардо Фибоначчи и числа Фибоначчи:

Леонардо Фибоначчи

Леонардо Фибоначчи родился в Пизе, Италия, в 1170 году. Детство провел в Северной Африке из-за таможенных пошлин своего отца. Он изучал математику в исламском мире, который в то время был намного более развит в математике, чем Европа.

В 12:00 он вернулся в Пизу. В Пизе он написал свой знаменитый труд «Liber Abaci», что означает «Книга исчисления». Эта работа привела западных математиков к открытию арабских цифр и десятичных чисел.

Фибоначчи своими исследованиями, направленными на раскрытие математической структуры природы, стал пионером в разработках, которые можно считать революцией в мире науки и искусства послесмертного периода.

Краеугольным камнем всех теорий Фибоначчи является последовательность чисел. Первым числом в последовательности является 0. В последовательности чисел числа получаются прибавлением предыдущего числа:

0+1=1, 1+1=2, 1+2=3, 3+2=5…

Последовательность чисел Фибоначчи, полученная после вычисления, выглядит следующим образом:

Первые 21 число Фибоначчи Fn для n = 0, 1, 2, …, 20

Последовательность Фибоначчи имеет интересные особенности:

• В последовательности каждое четвертое число можно разделить на 2 , каждое пятое число можно разделить на 5 и каждое восьмое число c делится на 8.
• Умножение любого числа в последовательности чисел Фибоначчи на 1,618 (золотое сечение) приблизительно дает следующее число. По мере роста чисел скорость аппроксимации увеличивается.
• 0,618 умножить на число любого заданного числа приблизительно дает предыдущее число. По мере увеличения числа коэффициент приближения увеличивается.
• 2618 раз любое число, две строки дают следующее число.
• 0,382 умножить на любое число, две строки дают предыдущее число.
• За исключением 1 и 2, все числа Фибоначчи, умноженные на четыре плюс еще одно число Фибоначчи, дают еще одно число Фибоначчи:
  3 х 4 = 12 + 1 = 13, 5 х 4 = 20 + 1 = 21, 8 х 4 = 32 + 2 = 34…

Золотое сечение — это особое соотношение, встречающееся в форме и строении многих живых существ. и неживых существ в природе. Можно увидеть золотое сечение вместе с числовой последовательностью Фибоначчи.

Золотое сечение в природе

Золотое сечение, известное в Древнем Египте и греческой цивилизации, было введено в математическую литературу Фибоначчи. Это соотношение использовалось многими художниками и учеными, особенно Леонардо да Винчи.

Известный немецкий астроном Иоганн Кеплер подчеркнул важность золотого сечения следующим образом:

«Геометрия имеет два великих сокровища; одна — Теорема Фитагора; другой — деление линии на крайнее и среднее отношение. Первую мы можем сравнить с мерой золота; второе мы можем назвать драгоценным камнем». — Иоганн Кеплер

Золотое сечение — иррациональное число. Записывается в десятичной системе как 1.618033988749894 … но в расчетах принимается как 1,6180 .

Золотое сечение

В последовательностях чисел Фибоначчи соотношение между коэффициентом 0,618, полученным путем деления малого числа на большое, и числом 1,618, полученным путем деления большого числа на меньшее, дает отношения Фибоначчи:

• 0,618÷1,618 = 0,382
• 1÷1,618 = 0,618
• 0,618 х 1,618 = 1
• 18 х 19, 1,618
• 1,618 x 1,618 = 2,618
• 2,618 x 1,618 = 4,236
• 4,236 x 1,618 = 6,853

0.382, 0.500 and 0.618 ratios are used frequently in technical analysis. Эти соотношения используются в движениях подъема и коррекции.

Методы коэффициента Фибоначчи в основном используются для определения среднесрочной и долгосрочной поддержки и сопротивления. Однако он также используется для определения поддержки и сопротивления краткосрочных движений.

Существует три способа использования соотношений Fibonacci в техническом анализе:

1. Уровни восстановления Fibonacci [Наиболее распространенные]
2. Fibonacci Time Time Time Zone
. часто используемый метод в техническом анализе. В этом методе анализа уровни поддержки и сопротивления Фибоначчи получаются с помощью линии, проведенной от дна тренда до пикового уровня.
Понимание того, как выглядят максимумы и минимумы колебаний, очень полезно для правильного построения коррекции Фибоначчи.

Этот метод, который не дает отдельных сигналов на покупку и продажу, особенно эффективен при определении среднесрочных и долгосрочных уровней поддержки и сопротивления. Этот метод также может быть использован в течение короткого времени. Однако показатель успеха немного ниже, чем в среднесрочной и долгосрочной перспективе.

Основная логика этого метода заключается в том, что разница между дном и пиком в трендах и деление вертикального расстояния на ключевые коэффициенты Фибоначчи 23,6%, 38,2%, 50%, 61,8% и 100%.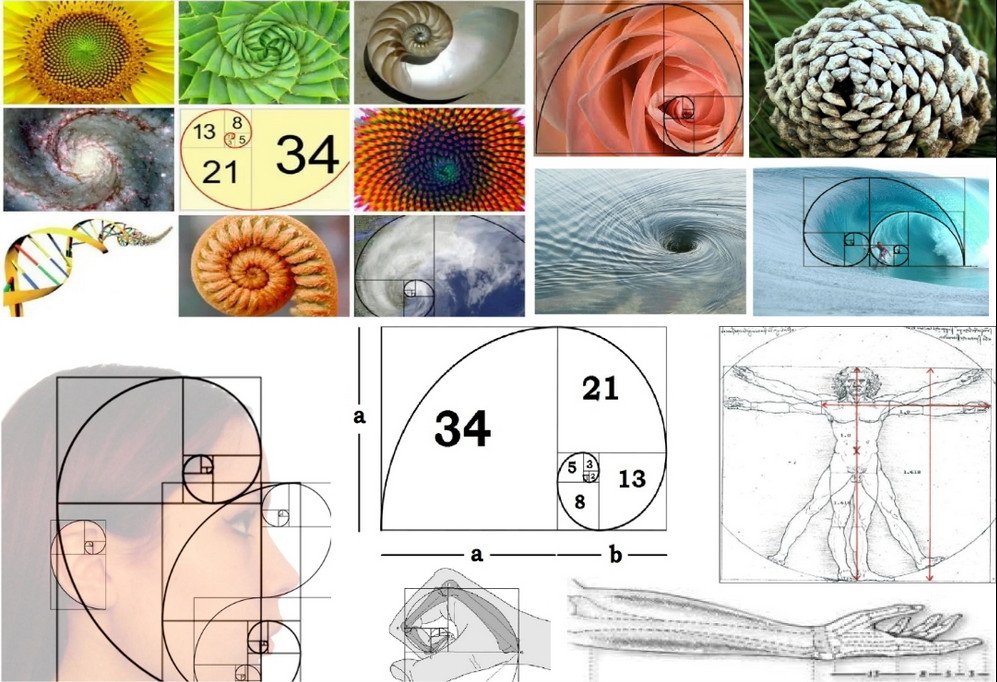 Как только эти уровни определены, горизонтальные линии рисуются и используются для определения возможных уровней поддержки и сопротивления.

Уровни восстановления Фибоначчи и их значение

Уровни восстановления Фибоначчи и их значение для меня Золотой отскок

Как нарисовать восстановление Фибоначчи?

1. Сосредоточьтесь на минимуме колебания и максимуме колебания
2. Рисуйте от точки значимого минимума
3. Перетащите его вверх к следующей важной точке максимума
4. Потяните инструмент вправо, чтобы позволить ценовому движению отыгрываться

Бычий Волна

Колебание от низкого до высокого колебания

Чтобы нарисовать коррекцию Фибоначчи в бычьей волне, вам нужно рисовать от минимума к максимуму. Как вы можете видеть на графике выше, значительный минимум составляет 9850 долларов, а значительный максимум — 12070 долларов.

Цена отскочила от уровня 0,50 , который является средним уровнем отката . После отскока цена достигла первого уровня расширения -0,27.

СОВЕТ: Если вы изо всех сил пытаетесь найти колебания максимума и минимума, вы можете использовать индикатор PivotsHL.

Медвежья волна

Колебание от максимума до минимума

Чтобы нарисовать коррекцию Фибоначчи в медвежьей волне, вам нужно рисовать от максимума к минимуму. Как вы можете видеть на графике выше, значительный минимум составляет 9850 долларов, а значительный максимум — 12070 долларов.

Цена отклонена от уровня 0,382 , который является уровнем быстрого и агрессивного отката . После отклонения цена достигла уровней расширения -0,27, -0,618. Это идеальный пример сильного нисходящего тренда.

СОВЕТ: Если вы изо всех сил пытаетесь найти колебания максимума и минимума, вы можете использовать индикатор PivotsHL.

ПОМНИТЕ: Рынок может двигаться вверх и вниз очень быстро. Всегда наносите уровни поддержки и сопротивления.

2. Временные зоны Фибоначчи

Цена не единственная переменная в техническом анализе. Временная переменная также является важным предметом исследования. По этой причине теории Фибоначчи используются как в ценовых движениях, так и во временных интервалах.

Временные интервалы Фибоначчи состоят из вертикальных линий, проведенных снизу или сверху с помощью чисел Фибоначчи.

На этапе отрисовки дно или пик принимается за 0. Затем на ценовой график наносятся линии временных интервалов, созданные с помощью чисел Фибоначчи.

Согласно основной логике, используемой при использовании чисел Фибоначчи в этом методе, каждое число Фибоначчи представляет количество дней во временном интервале.

Первое число Фибоначчи 1 представляет однодневный временной интервал, второе число Фибоначчи 2 — двухдневный временной интервал и пятое число Фибоначчи 8 — восьмидневный временной интервал: 5, 8, 13 , 21 и 34 дня, чтобы попасть в период.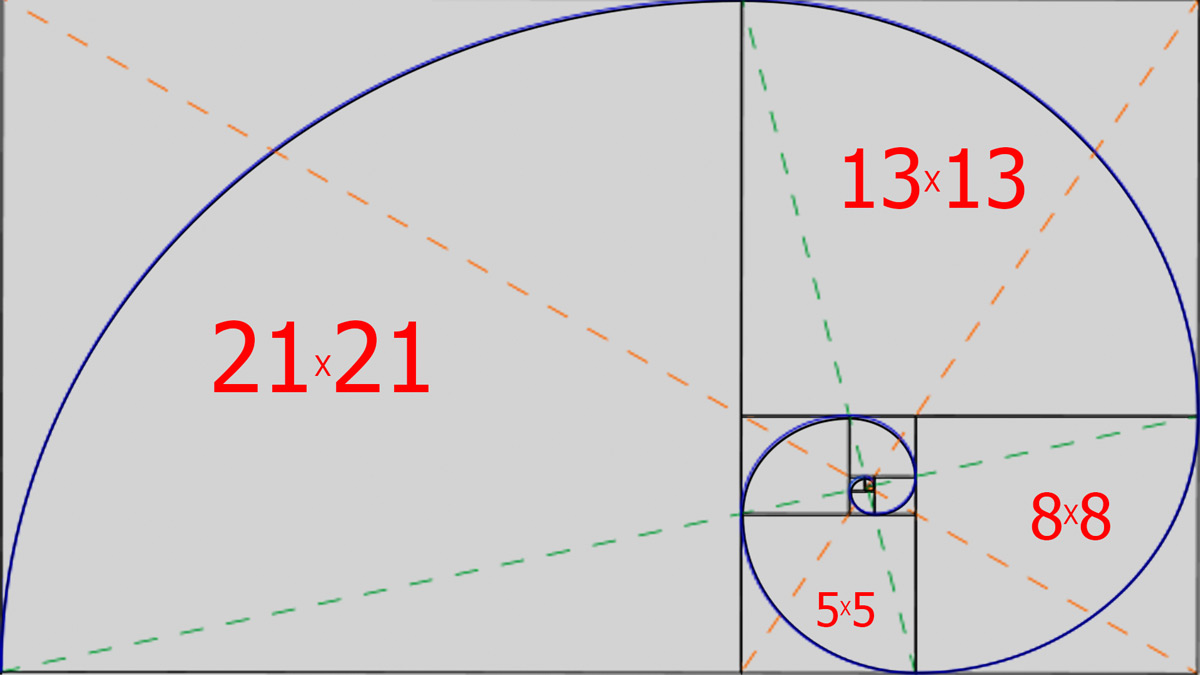

Согласно основной логике этого метода важные движения происходят в каждый временной интервал. Временные интервалы Фибоначчи не дают сигналов на покупку или продажу и в основном используются для определения продолжительности колебаний.

USDTRY Часовой пояс Фибоначчи Еженедельно

3. Вееры Фибоначчи

Соотношения Фибоначчи можно увидеть в Веерах Фибоначчи. Как и в других методах анализа Фибоначчи, веер Фибоначчи сначала проводит контрольную линию между дном и пиком.

Тем не менее, опорная линия, проведенная в этом методе, должна быть проведена к пику промежуточного тренда.

USDTRY Еженедельный веер Фибоначчи

Веер Фибоначчи используется для определения значительных уровней поддержки и сопротивления в возникающих трендах.

Подъем выше линии 38,2 в восходящем тренде означает чрезмерный рост и коррекцию в среднесрочной перспективе.

Интерпретируется, что провисание ниже линии 61,8 слишком сильно упало. Однако неспособность укрепить позиции покупателей на этих уровнях может означать разворот тренда. На этом этапе обычно используются индикаторы.

ВАЖНО: Веер Фибоначчи — это метод анализа, надежность которого вызывает сомнения. Он не работает должным образом в периоды резких движений. Поэтому рекомендуется использовать на рынках, где волатильность ниже.

Я очень давно торгую криптовалютой и товарным рынком. Соотношения Фибоначчи играют большую роль в технике. Большинство индикаторов и торговых ботов используют коэффициенты Фибоначчи. Я думаю, что люди должны понимать красоту золотого сечения и коэффициента Фибоначчи.

Лично я не использую уровни Фибоначчи на рынке криптовалют. Я использую только коэффициенты Фибоначчи в скользящих средних. Они отлично работают, потому что, когда рынок нестабилен, нам нужно динамических уровня поддержки/сопротивления , а не только статические линии.

Кроме того, подкрепите свою предвзятость другими методами технического анализа и фундаментального анализа. Попробуйте научиться торговать по-своему.

Пропорции фибоначчи: Золотое сечение и пропорции Фибоначчи