Как проверить монитор на битые пиксели и все починить
Одна из самых распространенных проблем компьютерного монитора — появление на экране отдельных точек, цвет которых не соответствует картинке. Причина этого заключается в повреждении или неправильной работе матрицы экрана, минимальным по размеру элементом которой считается пиксель. Этим термином называют неделимый прямоугольный или круглый объект, с помощью которого формируется изображение.
Несколько видов проблемы
Такой дефект как битый пиксель может выглядеть по-разному:
- элементы, которые всегда остаются выключенными, называются «мертвыми пикселями» и на светлом фоне будут выглядеть как темные точки;
- пиксели, которые всегда работают, считаются «горячими» — увидеть их можно на темном или полностью черном фоне, где они продолжают оставаться белыми;
- «застрявшими» называют элементы, не меняющие цвет — они становятся заметны только при несовпадении оттенка с основным изображением.

Важно: если вышло из строя сразу несколько пикселей в одной области, такое повреждение называется «группой битых пикселей». Вместе они складываются в прямоугольники размером от 2 х 2 до 10 х 10 элементов или даже в линии по горизонтали или вертикали.
Допустимое количество битых пикселей
Проверять монитор на наличие поврежденных элементов матрицы следует сразу же при покупке. Такая проверка позволит избежать проблем с возвратом товара по гарантии и проведением экспертизы, доказывающей, что причиной неполадок стал заводской брак, а не действия пользователя.
В соответствии со стандартом ISO13406-2 для каждого монитора допускается определенное количество дефектных элементов. Поэтому даже если проверка монитора на битые пиксели показала их наличие, это будет считаться нормой в таких ситуациях:
- изделие относится к 4 классу качества и может иметь до 50 «горячих» пикселей, до 150 «мертвых» и до 500 с другими видами дефектов;
- матрица выпущена по 3 классу, который допускает наличие до 5 постоянно включенных, до 15 все время не работающих элементов, а также до 50 пикселей с другими неполадками;
- класс качества монитора — второй, и на экране может появляться до 2 «горячих» и «мертвых» пикселя и до 5 «застрявших»;
- первый класс монитора — битых пикселей не должно быть вообще.

Рассчитывать на полное отсутствие дефектных элементов можно только при покупке товара первого класса. Однако большинство серийных моделей относится ко второму, а при их проверке можно найти 1-2 и даже 5 неправильно работающих пикселя. Хотя класс монитора и показывает, сколько дефектов не считается браком — на самом деле, у большинства изделий они отсутствуют полностью.
Определять наличие повреждений матрицы рекомендуется в магазине, где вы покупаете монитор. Однако, если такой возможности нет или товар приобретается онлайн, проверку можно провести и в домашних условиях. Для этого применяют онлайн-тест или специальную программу, хотя заметные дефекты можно обнаружить и невооруженным взглядом.
Визуальный способ проверки
Самый простой тест монитора на битые пиксели заключается в выводе на экран однотонного фона стандартных цветов — черного, белого, красного, зеленого и синего. Эти пять вариантов позволят обнаружить «горящие», «мертвые» и «застрявшие» пиксели.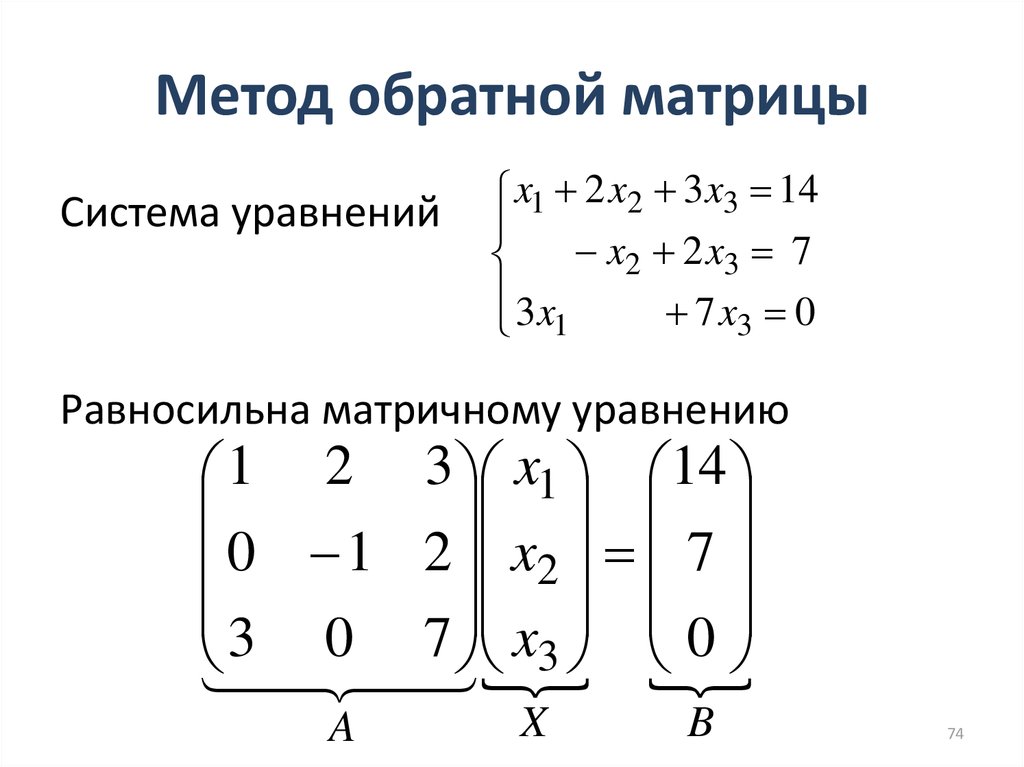
Проверить монитор на дефекты таким способом можно и в домашних условиях, и в магазинах. В последнем случае фоны копируются на флешку и запускаются на подключенном к покупке компьютере. Кроме однотонных изображений можно воспользоваться тестовыми картинками, найдя их в интернете.
Программное обеспечение
Еще один способ найти дефекты — программа для проверки монитора на битые пиксели. Воспользоваться подходящим приложением можно и дома, и в магазине, записав на флешку не тестовые изображения, а одну из проверочных утилит.
Dead Pixel Tester
Одна из самых популярных программ для тестирования монитора — Dead Pixel Tester. Скачать ее можно с официального сайта.
Для проверки следует выполнить такие действия:
- Запустить приложение, которое не требует установки, и выбрать подходящий режим в разделе Pettern и цвет с помощью кнопки Colour Selector.
- При необходимости установить смену режимов, используя опцию Auto Colour Cycle.

- Проверить, не появляются ли на экране точки, не соответствующие по цвету картинке.
Функция Exerciser, включаемая нажатием на соответствующую кнопку, позволяет найти дефекты в определенной части экрана. Она создает прямоугольную область, которую можно перетаскивать по экрану в поисках битых пикселей.
IsMyLcdOk
Еще одна программа, подходящая для диагностики матриц компьютерного монитора — IsMyLcdOk. Ее тоже можно скачать бесплатно и не требуется устанавливать. Инструкция по выполнению проверки появляется на экране после первого запуска.
Проверка запускается 4 клавишами — от F2 до F5. В списке доступных режимов тестирования есть вывод на экран окрашенных полос, прямоугольников, вертикальных или горизонтальных линий. Кроме стандартных тестов, можно вывести однотонную или градиентную картинку.
Онлайн-сервисы для проверки
Если загрузить и запустить утилиту не получается (например, из-за ограничения скачивания и запуска на рабочем ПК), можно выполнить проверку монитора на битые пиксели онлайн. Сайтов, позволяющих найти дефекты, довольно много, но среди них есть два самых простых и удобных для использования.
Сайтов, позволяющих найти дефекты, довольно много, но среди них есть два самых простых и удобных для использования.
Monteon
monteon.ru/
Для проверки дефектов матрицы на этом ресурсе достаточно нажать кнопку начала тестирования и выбрать один из семи видов диагностики и его вариацию.
Важно: в отличие от большинства других сайтов, Monteon.ru использует для тестирования не статическую картинку, а зацикленный видеоролик. Поэтому с его помощью можно не только найти дефекты, но и проконтролировать скорость обновления пикселей на экране.
Vanity Monitor Test
tft.vanity.dk
Еще один популярный сервис, позволяющий быстро обнаружить проблемы с отображением картинки на экране. Для запуска утилиты на ПК понадобится установленный Adobe Flash Player и поддерживающий его браузер. Для начала проверки нажимается надпись HTML Window.
Режимы в онлайн-сервисе выбираются с помощью выпадающего сверху меню. А использовать его для проверки битых пикселей можно не только для компьютерного монитора, но и для экрана ноутбука, планшета и даже смартфона.
А использовать его для проверки битых пикселей можно не только для компьютерного монитора, но и для экрана ноутбука, планшета и даже смартфона.
Восстановление поврежденных областей
- Иногда работоспособность поврежденной матрицы можно восстановить, не обращаясь в сервис. Решить, как убрать битые пиксели на мониторе, можно после того, как вы поймете, откуда они появились. Если вышел из строя управляющий транзистор, убирать поврежденный элемент экрана можно только с помощью специального лазера. Однако если причиной является зависание субпикселя, пользователь может избавится от дефекта, применив программу Bad Crystal.
- Также очень хорошо показывает себя утилита UndeadPixel. Если вы обнаружили ошибку пикселя, запустите приложение, нажав «Start» в разделе «Undead Pixel». На экране отобразится квадрат, который меняет цвета.Используя функцию Drag & Drop, можно перемещать квадрат над дефектной областью. Постоянное изменение цвета должно происходить в течение нескольких часов — после такой процедуры пиксель может быть восстановлен.
 Обратите внимание, что вернуть к жизни полностью черные пиксели уже невозможно.
Обратите внимание, что вернуть к жизни полностью черные пиксели уже невозможно. - Бесплатная программа EIZO Test Monitor (подойдет для любого устройства) содержит 24 тестовых изображения и поможет вам быстро оптимизировать цветовые параметры, а также проверить экран на наличие битых пикселей. Данная утилита не требует установки. Распакуйте ZIP-архив и запустите приложение двойным щелчком мыши. После этого нажмите на кнопку «Start TEST». В утилите доступны восемь сценариев, в том числе калибровка яркости и контрастности. Если возникнет необходимость изменить какие-либо настройки, программа подскажет как это сделать.
- Еще один способ лечения предполагает физическое воздействие. Для удаления повреждения стоит взять ватную палочку и аккуратно надавливать на битый пиксель. Через несколько минут (от 10 до 15) вышедший из строя элемент может заработать. Вылечить матрицу таким способом получится, если пиксели были «застрявшими» или «горячими».
Особенности возврата монитора в магазин
Если ничего не помогло, обнаруживший дефект пользователь имеет право вернуть монитор или обменять его на равноценный товар. В течение 14 дней возврат совершается без указания причины: достаточно всего лишь предоставить товарный или кассовый чек и упаковку возвращаемой техники, на которой не должно остаться следов использования.
В течение 14 дней возврат совершается без указания причины: достаточно всего лишь предоставить товарный или кассовый чек и упаковку возвращаемой техники, на которой не должно остаться следов использования.
Если 2 недели с момента покупки уже прошли, покупатель имеет право рассчитывать на гарантийный ремонт монитора или его возврат, если починить устройство не получилось. Однако в этой ситуации техника сначала отправляется на экспертизу: по ее результатам определяется, за чей счет будет ремонтироваться монитор — покупателя или продавца.
Читайте также:
- Как работает G-Sync compatible: проверяем на мониторе Asus VG278Q
- Какой монитор выбрать для игр: советы и рейтинг 2019
Тест матрицы монитора. Специализированные картинки и видеоролики окажут помощь
В некоторых случаях нам необходимо проверить монитор на работоспособность в режиме онлайн. Это может быть покупка устройства б/у или выявление причин неисправности.
Online Monitor Test — проверяем с помощью тестировшика
Сервис Online Monitor Test – это англоязычный онлайн тестировщик монитора, который имеет несколько вариантов проведения проверки.
Каждый из этих вариантов будет использовать один и тот же алгоритм проверки монитора, выбор любой из этих трех способов на конечный результат не влияет. Первым запустится автоматически тест на способность вашего монитора воспроизводить близкие по оттенкам цвета. Мониторы с качественным отображением оттенков способны различать между темными тонами разницу в два процента. Чтобы отобразились другие тесты на этом сервисе, передвиньте курсоры мыши в верхнюю часть экрана.
Для тех, кто работает с несколькими мониторами одновременно будет полезен специальный тест «Input Lag Html», который отображает задержку вывода информации на другом мониторе.
Monteon — тестируем дисплей компьютера
При помощи теста Monteon вы можете протестировать не только монитор компьютера, но и мобильное устройство. Для этого вам нужно просто набрать в адресной строке адрес сайта Monteon.ru и запустить онлайн тест монитора. Этот сервис имеет большое преимущество в виде русскоязычного интерфейса. Если вам нужен определенный тест, например, на битые пиксели – просто запустите тест, нажав «Начать». Если необходимо подробное описание каждого теста, нажмите «Узнать больше о тестах».
Главная страница сервиса Monteon
Тесты рекомендуется делать в помещении без солнечного света и с минимум освещения для лучшего восприятия событий на мониторе. Сервис вам предложит , перейдите на наго. Чтобы снизу экрана появилось меню управления тестами, пошевелите мышью. Меню тестов позволяет вам пролистывать ненужные тесты, переворачивать (если это позволяет тест), выключить полноэкранный режим и вернуться в начальный экран. По краям монитора отображены стрелки перехода с одного теста в другой. Вы можете заменить стрелки, используемые мышью на стрелки клавиатуры. Действия их равнозначны. Также для теста рекомендуется отключить все программы, корректирующие работу цветопередачи на дисплея. Ими могут быть драйверы на видеокарту. Зайдите в настройки этой программы и деактивируйте на время проведения теста.
Чтобы снизу экрана появилось меню управления тестами, пошевелите мышью. Меню тестов позволяет вам пролистывать ненужные тесты, переворачивать (если это позволяет тест), выключить полноэкранный режим и вернуться в начальный экран. По краям монитора отображены стрелки перехода с одного теста в другой. Вы можете заменить стрелки, используемые мышью на стрелки клавиатуры. Действия их равнозначны. Также для теста рекомендуется отключить все программы, корректирующие работу цветопередачи на дисплея. Ими могут быть драйверы на видеокарту. Зайдите в настройки этой программы и деактивируйте на время проведения теста.
На сервисе Monteon доступны следующие тесты.
Как проверить наличие залипших пикселей?
Запускаем программу. Перед нами будет представлено несколько объектов для тестирования: монитор ПК, мобильное устройство, ЖК устройство для ТВ. Выбираем нужное (в данном случае монитор ПК) и кликаем «Мониторинг дефектных пикселей».
Появится окно программы. Выбираем первую скорость мерцания.
Развернув окно программы, можно увидеть глухие точки, которые не изменяются. Это и есть залипший пиксель.
Для того, чтобы восстановить битый пиксель, нужно программу зарегистрировать, что стоит реальных денег. Согласно отзывам пользователей, Bad Crystal 2.5 FINAL восстанавливает залипшие пиксели только на тех мониторах, срок работы которых не превышает 3-4 лет.
IsMyLcdOK
Программа IsMyLcdOK – простой и понятный инструмент для тестирования ПК мониторов на наличие битых пикселей. Софт бесплатный. Имеет несколько полезных инструментов для проверки. Однако вылечить «залипший» пиксель с его помощью невозможно. Запустить можно со съёмного носителя. Скачивается в виде архива.
Одна из самых частых проблем ЖК-экранов — это «битый пиксель». Это происходит, когда один из миллионов пикселей на мониторе, работает некорректно. Технически этот термин «мертвый пиксель» происходит из-за неисправности производства, где пиксель является черным и нет никакого способа, чтобы заставить его работать должным образом. Также можем говорить, когда белый пиксель застрял в цветах (RGB) и светится более или менее чем другие.
Также можем говорить, когда белый пиксель застрял в цветах (RGB) и светится более или менее чем другие.
Если пиксель неисправен с завода, мы ничего не можем сделать, этот пиксель действительно битый. Однако, если пиксель только «спит», тоесть он остается пустым или фиксированным цветом, его даже можно восстановить, заставив его загружать последовательности цветов до тех пор, пока они не будут повторно активированы.
Разберем серию веб-сайтов, которые позволят определить, есть ли у монитора битые пиксели и попытаться восстановить их бесплатно. Эти сайты также могут использоваться для проверки битых пикселей на мобильных телефонах и телевизоров.
Сайты для проверки битых пикселей на мониторе и LCD дисплеях
Застрявший пиксель можно исправить тестами повторив их несколько раз, если же имеется битый «мертвый» пиксель на мониторе — это производственный дефект. Если монитор на гарантии, то занесите его обратно на замену.
Это простой сайт позволит нам проверить состояние пикселей нашего монитора. Заполнив сплошным цветом весь экран мы сможем выявить битый пиксель и определить его состояние. Просто выберите цвет, который хотите проверить и нажмите клавишу F11 для полноэкранного режима, также можно листать стрелками влево и вправо, меняя цвета на мониторе.
Заполнив сплошным цветом весь экран мы сможем выявить битый пиксель и определить его состояние. Просто выберите цвет, который хотите проверить и нажмите клавишу F11 для полноэкранного режима, также можно листать стрелками влево и вправо, меняя цвета на мониторе.
Более автоматический сервис чем предыдущий. Нажав кнопку «Start test», браузер автоматически отображается в полноэкранном режиме, и мы можем прокручивать цвета нажатием мышки по экрану. Имеются также другие инструменты для анализа мониторов, такие как Dynamic Range Test или Color-shift Test , чтобы видеть точность с которой наш монитор показывает цвета.
Еще одна альтернативная веб-страница для проверки состояния пикселей любого экрана или ЖК-монитора. Этот сервис позволяет нам видеть ответ всех пикселей на белый, черный или красный, зеленый или синие цвета.
Как проверить монитор или телевизор на битые пиксели, засветы и прочие дефекты? Для этих целей существует огромное множество различных способов, и отдельные из них мы рассмотрим в этой статье. Но, друзья, в таком тонком деле, как проверка экрана, большее значение имеет не конкретный способ проверки, не используемые инструменты, а чёткое понимание того, какие возможные дефекты мы ищем. И об этом мы также будем говорить ниже. Итак, вы собираетесь приобрести монитор или телевизор. Как его проверить перед покупкой в магазине или перед принятием почтовой посылки, если это интернет-заказ?
Но, друзья, в таком тонком деле, как проверка экрана, большее значение имеет не конкретный способ проверки, не используемые инструменты, а чёткое понимание того, какие возможные дефекты мы ищем. И об этом мы также будем говорить ниже. Итак, вы собираетесь приобрести монитор или телевизор. Как его проверить перед покупкой в магазине или перед принятием почтовой посылки, если это интернет-заказ?
Инструменты
Для проверки качества и целостности экрана монитора или телевизора существует масса различных Windows-программ и веб-сервисов. В числе первых:
- Утилита в составе программы AIDA64,
- Nokia Monitor Test,
- EIZO Monitortest,
- Monitors Matter CheckScreen,
- PassMark MonitorTest и пр.
Есть узкопрофильные утилиты только для проверки на предмет поиска битых пикселей, например:
- Dead Pixel Tester и
- Pestretsov Dead Pixel Test.
Из веб-сервисов, предлагающих услуги по различным тестам на предмет качества и целостности экранов:
- Monteon.
 Ru,
Ru, - Tft.Vanity.Dk и пр.
У каждой из этих программ, у каждого сервиса, безусловно, свои какие-то преимущества, но я, друзья, скажу вам, что особо витиеватых каких-то инструментов для проверки монитора или телевизора не нужно. Часть тестов в составе таких инструментов нужны не для проверки, а для настройки изображения. Чтобы проверить экран на предмет качества и целостности, можно воспользоваться простыми подручными средствами.
Если мы, например, ищем только битые пиксели, в среде Windows 10 делаем так:
Заходим в раздел «Персонализация» приложения «Параметры»;
В подразделе «Фон» устанавливаем «Сплошной цвет», кликаем «Дополнительный цвет»;
Выбираем белый, светло-серый или красный оттенок на цветовой шкале. Жмём «Готово»;
Опускаемся в последний подраздел и скрываем панель задач Windows;
Наконец, убираем отображение ярлыков на рабочем столе в контекстном меню последнего.
То же самое проделываем в других версиях Windows с учётом отличий в настройках персонализации.
Вот таким простым образом можем проверить монитор на битые пиксели, засветы и качество цветопередачи. Если нужно проверить на засветы, то, соответственно, в качестве фоновой картинки выбираем чёрный цвет. Поведение проблемных пикселей при передаче других цветов, а также качество цветопередачи в целом оцениваем, поочерёдно меняя расцветку фона рабочего стола. Используем синий, зелёный, жёлтый, красный, голубой и фиолетовый цвета.
На предмет прочих нюансов экрана – плавности перехода между цветами, резкости, правильности геометрии, отсутствия размытости границ, отсутствия шлейфов при динамике кадров и т.п. – монитор или телевизор можно проверить с помощью видео на YouTube. Идём на видеохостинг и вводим запрос в поисковик «тест монитора». В результатах поиска обходим всякие обзоры и гайды, запускаем только непосредственно видеотесты.
Видео разворачиваем на весь экран. Где нужно присмотреться, жмём клавишу-пробел для приостановки, а потом продолжения воспроизведения видео.
Видеотесты на YouTube – часто это записанные скринкасты прохождения тестов экрана теми же специализированными программами и веб-сервисами. Но вот, друзья, в чём ещё преимущество видеохостинга, так это то, что с его помощью можно проверить качество экрана на «живых» картинках. Т.е. так, как мы будем использовать монитор или телевизор в обычной жизни. Вот, например, у Samsung есть специальный видеоролик для презентации всех красот продукции компании, отлично демонстрирующий качество цветопередачи и воспроизведение динамичных сцен экранами.
А насколько эффектно монитор отображает видеоряд в высоком разрешении, можем увидеть с помощью художественных видеороликов по поисковым запросам «4К» или «8К».
Чужая территория проверки
Приведённые выше способы тестирования экрана применимы, когда у нас есть Windows-устройство или Интернет. Этих условий не будет на почте. Также не факт, что в магазине электроники нам позволят на их тестовый компьютер какие-то свои программы устанавливать или сёрфить по Интернету. Рассчитывать можно только на воспроизведение универсального формата контента. Если монитор или телевизор нужно проверить на чужой территории, поможет флешка. На неё можно перекинуть тестовые изображения и видеоролики. Практически все современные телевизоры и некоторые функциональные мониторы предусматривают встроенные проигрыватели медийного контента с USB-носителей. Лишь если мы покупаем монитор с базовым функционалом, придётся просить в супермаркете организовать подключение к какому-нибудь источнику изображения. В случае с почтой, конечно, ничего не останется иного, как тащить туда своё устройство и кабель.
Рассчитывать можно только на воспроизведение универсального формата контента. Если монитор или телевизор нужно проверить на чужой территории, поможет флешка. На неё можно перекинуть тестовые изображения и видеоролики. Практически все современные телевизоры и некоторые функциональные мониторы предусматривают встроенные проигрыватели медийного контента с USB-носителей. Лишь если мы покупаем монитор с базовым функционалом, придётся просить в супермаркете организовать подключение к какому-нибудь источнику изображения. В случае с почтой, конечно, ничего не останется иного, как тащить туда своё устройство и кабель.
- Примечание: друзья, предварительно ознакомьтесь с полными характеристиками покупаемого монитора. Если модель предусматривает поддержку технологии MHL – вывод видео и звука с мобильных устройств через порт HDMI или MicroUSB, проверить качество экрана при принятии посылки на почте можно с помощью смартфона. Для этого, естественно, нужен соответствующий кабель подключения, а также приложение или медиаконтент для тестирования экранов.
 То же самое касается технологий беспроводных подключений.
То же самое касается технологий беспроводных подключений.
Где взять медиаконтент для проверки монитора или телевизора, чтобы поместить его на флешку? Картинки и видео нужно скачать в Интернете. Специальную подборку картинок с изображениями для теста экранов я вот, например, нашёл на Рутрекере.
Ну а теперь друзья, давайте о сути. Какие дефекты экрана нужно искать? И как их искать?
Корректность цветопередачи
Корректность цветопередачи — это проверка основных цветов и оттенков, насколько правильно экран отображает их. Проверяется с помощью картинок такого плана.
Такие изображения также можно использовать при настройке монитора или телевизора – тестировать готовые пресеты, накручивать параметры яркости/контраста вручную.
Плавность переходов (градиенты)
Градиенты – переходы цветовых оттенков – должны отображаться плавно, без резких перепадов, без ступенек. Проверяются картинками типа этой.
Также можно просмотреть градиентные заливки для каждого из основных цветов, например, как вот эта картинка для зелёного спектра.
Бандинг
Бандинг – это вертикальные или горизонтальные полосы с отличным оттенком цвета.
Нет ли этого дефекта, проверяется с помощью картинок со сплошной заливкой. Такие картинки с основными цветами (белый, серый, чёрный, жёлтый, синий, зелёный, красный, фиолетовый) обязательно должны быть в составе тестового контента.
Тинт
Тинт – это хаотические участки некорректного отображения белого цвета, обычно с розоватыми или зеленоватыми оттенками. Для поиска этого дефекта используем изображение со сплошной заливкой белого цвета.
Геометрические пропорции
Изображения с сетками разного калибра помогут определить, насколько корректно отображаются геометрические пропорции экрана.
Шлейф при динамичном видеоряде
Тестовая анимация с быстро движущимися объектами позволит выявить, не остаются ли на экране шлейфы – следы от объектов при динамичном воспроизведении видеоряда.
Битые пиксели
При поиске битых пикселей используем однотонное изображение белого, светло-серого или красного цвета. Именно битые, они же мёртвые пиксели можно обнаружить сразу, это тёмные точки на экране. Так называемые застрявшие пиксели могут светиться точками белого, красного, зелёного, фиолетового, жёлтого или прочего цвета. Застрявшие пиксели, соответственно, будут видны при подаче на экран контрастирующей одноцветной картинки.
Именно битые, они же мёртвые пиксели можно обнаружить сразу, это тёмные точки на экране. Так называемые застрявшие пиксели могут светиться точками белого, красного, зелёного, фиолетового, жёлтого или прочего цвета. Застрявшие пиксели, соответственно, будут видны при подаче на экран контрастирующей одноцветной картинки.
Чтобы обнаружить любого рода дефекты пикселей, необходимо с близкого расстояния исследовать экран. Можно использовать увеличительное стекло. Если телевизор или монитор находится на гарантии, на предмет поиска дефектных пикселей его нужно проверить дополнительно, но уже после покупки, когда он проработает пару часов. Проблемные пиксели могут проявиться не сразу, лишь в условиях нагрева матрицы.
Засветы
Засветы – это светлые участки на тёмном фоне по краям экрана.
PLS-матрицы обычно не «болеют» проблемой засветов экрана, у MVA-матриц они встречаются, но редко. А вот матрицам IPS и старым TN, увы, эта проблема присуща. Приобретая IPS- или TN-монитор, особенно модель бюджетного сегмента, нужно обязательно проверить покупку на предмет наличия засветов. Для этого на экран необходимо подать однотонную картинку чёрного цвета и накрутить яркость по максимуму. Сам же тест желательно проводить в затемнённом помещении.
Для этого на экран необходимо подать однотонную картинку чёрного цвета и накрутить яркость по максимуму. Сам же тест желательно проводить в затемнённом помещении.
Вот, друзья, привёл основные проблемы мониторов и телевизоров, которые нужно проверять перед покупкой. Если вам есть что дополнить по теме, пишите в комментариях.
Привет! Для тех, кто проводит много времени за компьютером, комфорт работы имеет особое значение. Я не для кого не «открою Америку», если скажу, что монитор — один из важнейших компонентов комфортной и продуктивной работы. Многие пользователи задаются вопросом, как проверить монитор на битые пиксели, а сделать это проще простого.
Сегодня я расскажу вам способы проверки монитора не только на пиксели, но и на равномерность подсветки и размытие картинки.
Перед тем, как приступать к тестам, сделаем небольшое отступление и ознакомимся с понятием цветовая модель RGB.
RGB — это аббревиатура от английских слов Red Green Blue. Данная модель представляет из себя способ цветовоспроизведения, который нашел широкое применения в технике. Способ основан на особенности восприятия цвета сетчаткой глаза человека. При такой модели все цвета, воспроизводимые монитором, выводятся благодаря сочетанию трех основных цветов — красного
, зеленого
и синего
. Именно поэтому все тесты для мониторов работаю с этими основными цветами.
Способ основан на особенности восприятия цвета сетчаткой глаза человека. При такой модели все цвета, воспроизводимые монитором, выводятся благодаря сочетанию трех основных цветов — красного
, зеленого
и синего
. Именно поэтому все тесты для мониторов работаю с этими основными цветами.
Онлайн тест монитора
Для онлайн тестирования нам нужно перейти на сайт —
http://tft.vanity.dkПереходим в меню HTML window.
В первом же окне перед нами представлена шкала оттенков серого цвета, которая позволяет сравнить близкие тона. Если на вашем мониторе можно рассмотреть темные оттенки с шагом в 2%, тогда это хороший монитор. На самых качественных мониторах можно увидеть различия между светлыми тонами.
Конечно на этой шкале оценка монитора не заканчивается. Если подвести указатель мыши к верхнему краю окна браузера, перед нами раскрывается меню с различными вариантами тестов.
Если вам мешает окно с подсказками на экране, его можно выключить, нажав на кнопку «Info on/off»
в правом верхнем углу всплывающего меню.
Всего в меню представлено 6 тестов, включая главную страницу:
- Color range — цветовая гамма;
- Trailing — тест на размытие в движении;
- Homogenuity — равномерная заливка экрана;
- Pixelmapping — пиксельная карта;
- Text — тесты с текстом
В этих тестах вы можете проверить воспроизведение цвета на вашем мониторе и посмотреть его способность воспроизводить плавность перехода различных оттенков. В меню представлены 9 вариантов цветовых градиентов, чтобы вы могли сравнить плавность перехода для каждого из основных цветов. В пункте Black/White представлена доработанная модель теста на главной странице.
TrailingЗдесь представлен простой тест на размытие объектов в движении. Не путайте его с тестами производительности игр, в которых измеряется FPS — Frames per second — число кадров в секунду.
Чтобы привести объект в движение, нужно нажать кнопку «Start box»
и просто посмотреть на шлейф, который остается за объектом. Чем он короче, тем лучше монитор. В этом же меню представлены и другие тесты, в которых можно перемещать объект указателем мыши.
Чем он короче, тем лучше монитор. В этом же меню представлены и другие тесты, в которых можно перемещать объект указателем мыши.
На этом экране мы можем проверить равномерность подсветки монитора (на черном фоне). Переключая цвета, также можно убедиться, что цвет отображается одинаково на всей поверхности экрана.
Также этот тест сможет помочь в обнаружении так называемых «битых пикселей», так как их становится очень хорошо видно на равномерном фоне.
PixelmappingНа качественном мониторе экран должен быть равномерно заполнен черными/белыми пикселями без каких либо цветных областей. Это говорит о том, что матрица монитора не засвечивает границы перехода цветов. Кроме того тест позволяет определить отсутствие геометрических искажений.
Такой тест часто используют для проверки телевизоров.
TextПозволят оценить отображение различных типов и размеров шрифтов на разных фонах.
Тест монитора с помощью программыКроме теста онлайн существует огромное количество программ для проверки мониторов. В большинстве своем эти программы содержат одинаковый набор тестов. Зачастую различия только в интерфейсе.
В большинстве своем эти программы содержат одинаковый набор тестов. Зачастую различия только в интерфейсе.
Такую программу для тестов предоставляет вышеописанный сервис тестирования. Скачать её можно у них на сайте — http://tft.vanity.dk Возможности и интерфейс данной программы полностью совпадают с описанными выше функциями онлайн проверки.
Возможности программы:
- тест равномерности подсветки матрицы и отсутствия «битых точек»;
- градиент цвета для проверки линейности матрицы;
- окружности для проверки «неродных» разрешений;
- кольцевой градиент для проверки линейности и дискретности матрицы;
- узоры для проверки интерполяции «неродных» разрешений;
- проверка читаемости шрифтов;
- сетка для проверки разборчивости деталей;
- движущийся квадрат;
- движущийся квадрат с масштабной сеткой.
На этом я заканчиваю свою статью и желаю вам легкой работы за компьютером .
P.S. Лучший отдых после напряженной работы — это прогулка на свежем воздухе. Не забывайте делать перерывы, берегите свое зрение и здоровье.
Не забывайте делать перерывы, берегите свое зрение и здоровье.
Как проверить монитор без компьютера при покупке
Когда я собирал сыну компьютер, то стояла задача купить хороший монитор. Чтобы не нарваться на брак, нужно монитор обязательно проверять. В этой статье я поделюсь, как проверить монитор без компьютера, а также расскажу, как с помощью ноутбука проверить матрицу на битые пиксели и засветы.
Содержание статьи:
- 1 Как проверить монитор без компьютера
- 2 Как проверить монитор на битые пиксели
- 2.1 Проверка монитора на битые пиксели онлайн
- 3 Как проверить монитор на засветы
- 4 Как проверить частоту монитора
- 4.1 Проверка герцовки монитора на windows 10
- 4.2 Проверка герцовки монитора онлайн
- 5 Как проверить отклик монитора
- 6 Как проверить инпут лаг монитора
- 7 Как проверить разрешение монитора
- 8 Как проверить монитор на мерцание
- 9 Выводы
Как проверить монитор без компьютера
Сразу скажу, для проверки матрицы монитора без подключения к компьютеру или ноутбуку не получится. Но в целом проверить исправность монитора можно и без компьютера. Для этого нужно сделать следующее:
Но в целом проверить исправность монитора можно и без компьютера. Для этого нужно сделать следующее:
- Осмотреть монитор на отсутствие царапин. Особенно обратите внимание, чтобы царапин не было на матрице экрана.
- Подключите монитор к сети и включите. При включении должен загореться индикатор (светодиодная лампочка) и высветится на экране логотип монитора.
- Если кабель не подключен к ПК, то через несколько секунд на экране высветится надпись: «не подключен кабель, или нет сигнала». Это говорит о том, что монитор в целом исправен. Если при включении монитора, появляется логотип и сразу гаснет и не появляется надпись «кабель не подключен», то это говорит о неисправности подсветки монитора. Чтобы убедиться в этом точно, есть способ описанный в этой статье — как проверить подсветку экрана монитора.
- Попробуйте зайти в меню настроек монитора, с помощью кнопок на мониторе. Заходит в меню — хорошо. Если не заходит, то значит меню настроек работает на мониторе, только при подключении к компьютеру.
- Прислушайтесь к включенному монитору, он не должен издавать странных звуков искрения и гудения.
Чтобы проверить монитор полностью: на битые пиксели, засветы, герцовку и т.д. нужно монитор подключать к компьютеру или ноутбуку.
Как проверить монитор на битые пиксели
Когда иду забирать монитор у продавца, я всегда беру с собой нетбук и кабель VGA.
Для проверки матрицы монитора использую нетбук с кабелем VGAВсегда смотрите есть ли соответствующий вход на мониторе VGA. Если входа VGA на мониторе нет, то понадобится ноутбук с выходом HDMI и сам кабель HDMI.
Далее нам понадобится специальная программа для проверки монитора, которую нужно скачать на ноутбук. Я использую такую — TFT монитор тест.
- Подключаю ноутбук кабелем VGA или HDMI.
- Запускаю программу TFT монитор тест на ноутбуке.
Далее нужно попеременно включать разные цвета и смотреть внимательно на экран в поисках битых точек.
Программа для диагностики монитора на битые пикселиНапример, включаем белый цвет и смотрите. Если на белом цвете, есть точки черного цвета — это битый пиксель. Если такого не замечено, то включаете другой цвет красный, зеленый, синий и т.д. Смотрите внимательно нет ли битых пикселей.
Если на белом цвете, есть точки черного цвета — это битый пиксель. Если такого не замечено, то включаете другой цвет красный, зеленый, синий и т.д. Смотрите внимательно нет ли битых пикселей.
Могу помочь в подборе хорошего монитора для игр. Вступайте в мою группу в ВК, обсудим — https://vk.com/ruslankomp
Помогу решить проблему с ПК или ноутбуком. Вступайте в группу VК — ruslankompБитые пиксели бывают трех типов:
- Горящий пиксель — всегда светится, виден как белая точка на черном фоне.
- Мертвый пиксель — всегда не горит, виден как черная точка на светлом фоне.
- Застрявший пиксель — цветной пиксель, постоянно горящий или мигающий красный, зеленый и голубой пиксель.
Горящий и мертвый пиксель исправить не получится. А вот застрявший цветной пиксель можно убрать с помощью специальных программ или физического воздействия. Поэтому, чтобы таких проблем у вас не возникло, надо проверять монитор перед покупкой на битые пиксели.
Поэтому, чтобы таких проблем у вас не возникло, надо проверять монитор перед покупкой на битые пиксели.
После покупки монитора советую в течение 2-х недель проверять на битые пиксели. Так как бывают случаи, что битые пиксели могут появиться через несколько дней.
Проверка монитора на битые пиксели онлайн
В домашних условиях проверить монитор можно онлайн, без специальных программ.
Перейдите по ссылке — http://monteon.ru/
Запуск онлайн тест Monteon для проверки монитора на битые пикселиМеняем цвет экрана для выявления битых пикселей в онлайн тесте MonteonВторой сервис — тест монитора онлайн
Принцип проверки монитора такой же, запускаете онлайн тест и поочередно меняете цвет экрана и внимательно смотрите нет ли битых пикселей.
Тест монитора онлайнКак проверить монитор на засветы
Я долго не мог понять, есть ли засветы на мониторе, который купил сыну.
После того, как я себе приобрел монитор 144 Гц, то понял, что на моем мониторе есть засвет в левом верхнем углу экрана. А на мониторе сына засветов вообще не было.
А на мониторе сына засветов вообще не было.
Интересно что за монитор? Вот статья — https://ruslankomp.ru/igrovoj-kompjuter-dlya-syna-za-30-tysyach-rublej/
На самом деле найти монитор с IPS матрицей без засветов — большая редкость. Если вам попался монитор без засветов, вам крупно повезло.
Проверять засветы на мониторе нужно в темном помещении. В освещенном помещении засветы не очень заметны. Включите черный цвет на экране, для этого можно использовать программу для проверки битых пикселей — TFT монитор тест
Смотрите по углам и краям экрана. Обычно, где есть засвет, из под рамки экрана виден белый свет.
Я заметил на своем мониторе, где есть засвет, если рамку поджать пальцем, то засвет пропадает. Это говорит о том, что есть зазор там, где не должен быть. Поэтому свет проникает туда, где не нужно.
Чтобы было понятней покажу пару примеров экрана без засветов и с засветами.
Экран монитора без засветовНа экране монитора есть засветы в левом верхнем углу и внизуВстречал такие мониторы, что засветы были по всему периметру экрана. Для работы в интернете сгодится, где больше преобладает белый цвет и засветов не видно. Но если смотреть фильм, играть игру, где есть темные сцены, эти засветы доставят ряд неудобств.
Для работы в интернете сгодится, где больше преобладает белый цвет и засветов не видно. Но если смотреть фильм, играть игру, где есть темные сцены, эти засветы доставят ряд неудобств.
Как проверить частоту монитора
После подключения монитора к компьютеру, возникает вопрос на какой частоте работает монитор. Часто бывает, что 144 Гц монитор работает на стандартных 60 Гц и пользователь даже об этом не догадывается.
Для проверки свойств монитора используйте программу — AIDA64.
В разделе Дисплей — Монитор можно увидеть диапазон всех частот монитора. Например в моем случае монитор Samsung S23C350 поддерживает до 75 Гц.
Aida64 — частота поддерживаемых кадров монитораВ разделе Дисплей — Рабочий стол, показатель Частота регенерации показывает на какой частоте работает монитор. В данном случае — 60 Гц.
Aida64 частота регенерации монитора — 60 ГцПроверка герцовки монитора на windows 10
Кликните правой кнопкой мыши на рабочем столе экрана и в контекстном меню выберите — Параметры экрана.
Далее заходим в — Дополнительные параметры дисплея.
Заходим в дополнительные параметры дисплеяСмотрим частоту обновления 60 Гц — это и есть герцовка монитора, на которой работает в данный момент.
Чуть ниже можно изменять частоту обновления монитора.
Частота обновления монитора 60 ГцПроверка герцовки монитора онлайн
Проверить герцовку своего монитора можно онлайн.
Для этого перейдите по этой ссылке — https://www.testufo.com/
Через 3 секунды узнаете частоту вашего монитора.
Частота монитора в Testufo онлайн показывает 60 ГцЕще один сайт для проверки частоты монитора — https://www.displayhz.com/
Частота монитора в Displayhz — 59,99 ГцЕсли у вас монитор 144 Гц подключен по HDMI или DisplayPort, но при проверке частота монитора показывает 60-75 Гц. То в этом случае вам нужно поменять герцовку в панели управления видеокартой Nvidia, как показано на рисунке ниже.
В панели Nvidia частота обновления 144 Гц будет доступна при условии, что видеокарта игровая, а не бюджетная затычка.
Как проверить отклик монитора
Время отклика монитора важнейший фактор для геймеров. Чем меньше время отклика, тем лучше. Это время измеряется в миллисекундах, например 1 мс, или 4 мс.
Простыми словами отклик — это время, за которое пиксель изменяет цвет и яркость свечения при динамичной сцене.
В характеристиках монитора указывается параметр время отклика. Но как измерить и убедиться в том, что отклик пикселя действительно 1 мс.
Характеристики монитора — отклик пикселя 1 мсНа самом деле измерить время отклика самостоятельно невозможно в домашних условиях. Для этого понадобится специальный станок с двигающейся камерой, чтобы измерить отклик матрицы. Программный способ вряд ли покажет реальную цифру время отклика пикселя.
Как проверить инпут лаг монитора
Инпут лаг — это задержка ввода, не путайте с временем отклика. Инпут лаг или задержка ввода — это когда вы нажимаете клавишу во время игры, например влево, а затем соответствующее действие происходит на экране.
С большой задержкой ввода вы сразу заметите, как неудобно играть. Нажали на кнопку стрелять, а на экране выстрел произойдет не сразу, а чуть позже. Знакомо?
Инпут лаг 26 мс и 65 мсТакая задержка зависит от множества факторов:
- беспроводная мышь, может посылать сигнал больше времени, чем проводная мышь.
- слабый компьютер, которому не хватает мощности обработать информацию быстро.
- скорость передачи кабеля от компьютера к монитору, как правило, самые быстрые HDMI и DisplayPort.
- монитор с большим откликом матрицы, который увеличивает общую задержку.
Задержка ввода измеряется в миллисекундах, но в отличии от времени отклика эти показания будут больше. Например мониторы 144 Гц имеют задержку 9-10 мс, а среднее значение 15-22 мс для игровых мониторов.
С задержкой ввода 40-50 мс вы ощутите проблему с синхронизацией, играть на таких мониторах будет не комфортно.
Проверить инпут лаг на своем мониторе можно на глаз. Включите игру и смотрите, как быстро реагирует на ваши действия монитор. Если играть комфортно, лагов не наблюдается, то значит все нормально.
Включите игру и смотрите, как быстро реагирует на ваши действия монитор. Если играть комфортно, лагов не наблюдается, то значит все нормально.
Если же инпут лаг большой и играть не комфортно, то нужно разбираться. Возможно дело не в мониторе, а в видеокарте, в слабом процессоре или в скорости оперативной памяти.
Как узнать частоту оперативной памяти, читайте здесь — https://ruslankomp.ru/kak-proverit-chastotu-operativnoj-pamyati-na-kompjutere/
Ещё один способ проверить инпут лаг — это подключить второй монитор с быстрой матрицей, запустить игру и сравнить разницу.
Знаете ещё способ, как проверить инпут лаг? Поделитесь в комментариях.
Как проверить разрешение монитора
Разрешение экрана — это количество точек (pixel) по горизонтали и вертикали. Самые распространенные разрешения мониторов:
- HD — 1280 х 720 (720p) часто встречается на бюджетных телевизорах.
- Full HD — 1920 х 1080 (1080p) часто встречающейся разрешение на современных недорогих мониторах.

- 2K — 2560 х 1440
- UltraHD 4K — 3840 х 2160
Чтобы проверить разрешение монитора в Windows 10, нужно зайти в параметры экрана, вызвав меню правой кнопкой мыши.
Заходим в параметры экрана Windows 10В разделе Дисплей видим разрешение экрана, где также можно поменять на другое.
Разрешение экрана в разделе дисплей Windows 10Разрешение экрана можно определить онлайн — https://screenresolution.ru/
Определяем разрешение экрана онлайнКак проверить монитор на мерцание
Мерцание монитора можно проверить с помощью камеры на смартфоне. Включите камеру и посмотрите через экран телефона на монитор, мерцает ли экран.
Есть еще один способ проверить мерцание с помощью карандашного теста. Но я считаю, что с помощью камеры мерцание лучше определить.
Пример проверки монитора на мерцание с помощью карандаша. Суть в том, чтобы перед экраном быстро шевелить карандашом. Если видны очертания карандаша, то значит мерцание есть на экране. Если очертаний карандаша не видно, то значит экран не мерцает.
Если видны очертания карандаша, то значит мерцание есть на экране. Если очертаний карандаша не видно, то значит экран не мерцает.
В этом видео через камеру видно, что экран мерцает. Карандашный тест подтверждает мерцание.
Проверка мерцания экрана онлайн — http://monteon.ru/
Запустите тест, и выберите режим — Мерцание.
Проверка мерцании экрана с помощью онлайн тестаНа большом расстоянии от монитора они должны выглядеть серыми. При близком рассмотрении должен быть четко виден мелкий узор чередующихся контрастных пикселей (черных и белых).
Если изображение мерцает или создается впечатление «бегающих пикселей», или если изображения выглядят сплошным серым цветом (не видно точек даже при близком рассмотрении) или есть черно-белые полосы (вертикальные или изогнутые), то необходима корректировка монитора.
Выводы
Проверяйте всегда монитор перед покупкой. От качества монитора зависит комфортная работа и здоровье ваших глаз.
При покупке монитора проверьте:
- Отсутствие внешних повреждений, царапин на экране.
- Убедитесь, что нет битых пикселей.
- Смотрите, чтобы как можно меньше было засветов по углам и краям.
- С помощью камеры на мобильном телефоне убедитесь, что нет мерцаний экрана.
- Настройте на самую высокую частоту, которую поддерживает монитор.
- Выставьте рекомендуемое разрешение на мониторе.
Нужна помощь, пишите мне в группе ВК — https://vk.com/ruslankomp
Помогу решить проблему с ПК или ноутбуком. Вступайте в группу VК — ruslankompВ свое время стояла задача по созданию проверок в Navisworks по матрице коллизий. Проверок было огромное количество, и простое набивание их наименований, не говоря уже о создании поисковых наборов, выборе типа проверки и назначении допуска, занимало неприлично большое количество времени. Автоматизированных решений подобной задачи найти не удалось, поэтому я написала пару скриптов, позволяющих создавать проверки по заданным правилам и поисковые наборы элементов в Navisworks на основе данных из матрицы коллизий. Возможно, кому-то еще это пригодится, поэтому делюсь своими наработками в этой небольшой статье.
Автоматизированных решений подобной задачи найти не удалось, поэтому я написала пару скриптов, позволяющих создавать проверки по заданным правилам и поисковые наборы элементов в Navisworks на основе данных из матрицы коллизий. Возможно, кому-то еще это пригодится, поэтому делюсь своими наработками в этой небольшой статье.
Материалы можно скачать по ссылке в конце статьи.
Идея
Основная идея очень проста — заполнить матрицу коллизий, собрать из нее данные о проверках, которые нужно провести, внедрить эту информацию в структуру файла XML и импортировать его в Navisworks.
Матрица
Если мы хотим избежать проверки «всего со всем», конкретизировать допуски для каждой пары групп элементов и получить в итоге менее громоздкие отчеты, то матрица коллизий — это удобный инструмент для фиксации таких проверок.
Матрица представляет собой таблицу, в столбцах и строках которой прописаны элементы модели, сгруппированные определенным образом (в моем случае это разделы и категории элементов Revit). На пересечении пар категорий проставляются номера необходимых проверок.
На пересечении пар категорий проставляются номера необходимых проверок.
Порядок работы
1. Расстановка приоритетов разделов. На вкладке «Приоритеты» присвоить порядковые номера разделам по «важности» и гибкости с точки зрения внесения изменений.
Таблица приоритетов разделовРасстановка приоритетов позволяет организовать последовательную работу по поиску и устранению коллизий. Каждый последующий раздел подключается к проверке после устранения коллизий в разделах с более высоким приоритетом. Это позволяет избежать ситуаций, когда одна и та же коллизия устраняется одновременно в нескольких моделях и, в итоге, приводит к образованию новой коллизии.
Проверки в окне Clash Detective структурируются в соответствии с приоритетами.
2. Определение типов проверок и допусков. Для каждой пары категорий актуален определенный тип проверки: пересечение, пересечение (консервативно), просвет или дублирование. Помимо типа, проверки могут отличаться допусками для разных пар категорий.
На вкладке «Мэппинг проверок» необходимо определить перечень проверок, задать допуски. Можно удалить лишние или добавить недостающие проверки, при этом важно использовать только те значения типов, которые представлены в таблице.
Код проверки — цифра, которую мы будем вписывать в матрицу коллизий на пересечениях пар.
Тип проверки — наименование проверки в том виде, в котором оно представлено в файле XML, важно использовать только приведенные наименования типов, создавая новую проверку.
Код типа проверки — сокращение для типа проверки, которое будет указано в наименование проверки в Navisworks.
Допуск — значение в метрах, в пределах которого пересечение не считается коллизией.
3. Заполнение матрицы коллизий. На вкладке «Матрица проверок на коллизии» на пересечениях категорий проставить номера проверок, которые необходимо провести.
Если для пары нужно выполнить несколько проверок, введите двузначное или трехзначное значение без пробелов и запятых. Например, 13 означает проверки 1 и 3, 45 — проверки 4 и 5 и т.п.
Например, 13 означает проверки 1 и 3, 45 — проверки 4 и 5 и т.п.
В таблице настроено условное форматирование для проверок с 1 по 5, дополнительные условия можно настроить самостоятельно.
4. Запуск скрипта по формированию перечня проверок и поисковых наборов по матрице коллизий. Откройте скрипт 00_BIM_Создание перечня проверок по матрице коллизий, задайте путь к файлу с матрицей коллизий и запустите скрипт.
После завершения работы скрипта проверьте вкладки «Проверки» и «Поисковые наборы».
На вкладке «Проверки» получаем список проверок с соответствующими поисковыми наборами, типами проверки и допусками. Наименование в формате Приоритет_Раздел1_Раздел2_Тип проверки и допуск_Категория 1_Категория 2.
Вид таблицы с данными о проверках после завершения работы скриптаВ столбце «Допуск» замените запятые на точки. К сожалению, в Dynamo данную операцию произвести не удалось, поэтому приходится заменять в Excel.
На вкладке «Поисковые наборы» получаем список уникальных поисковых наборов с данными для создания правил их формирования. Я буду искать элементы по коду модели, в которой они находятся, и по их категориям, поэтому создаю и заполняю соответствующие столбцы.
Я буду искать элементы по коду модели, в которой они находятся, и по их категориям, поэтому создаю и заполняю соответствующие столбцы.
Поисковые наборы могут иметь большее количество правил, их можно добавить уже в Нэвисе и обновить наборы, либо откорректировать скрипты для автоматического формирования правил по своим критериям.
5. Сохранение файл Excel. Файл можно не закрывать, но обязательно сохранить. Важно не забыть это сделать, иначе изменения о замене запятых на точки в допуске не сохранятся, и файл XML не загрузиться в Нэвис.
6. Запуск скрипта по формированию XML файла с проверками. Откройте скрипт 00_BIM_Создание файла XML с проверками по перечню проверок и поисковых наборов.
1 — задайте имя файла XML.
2 — скопируйте путь, куда будет сохранен созданный файл, замените бэкслеши в пути на двойные бэкслеши. Путь к файлу должен заканчиваться именем файла с расширением, как указано на скриншоте.
3 — задайте путь к матрице коллизий.
После завершения всех настроек запустите скрипт. В указанной папке появится файл XML с заданным именем.
6. Загрузка файла XML в Navisworks. Загрузите файл XML, используя кнопку импорта в окне Clash Detective, проверьте правильность созданных проверок и поисковых наборов.
Наименование проверок, правила формирования поисковых наборов, кодировки и прочие частные нюансы можно настроить под себя. Так же, вероятно, скрипты можно оптимизировать. Надеюсь, что кому-то данная информация упростит жизнь и создаст почву для дальнейшей автоматизации.
Скрипты собраны в версии Dynamo 2.0.3. Использованы ноды из пользовательских пакетов Clockwork и Zhukoven.com.
Скачать материалы можно по ссылке.
Как проверить матрицу монитора на работоспособность
Содержание
- Простыми словами о ремонте телевизоров и домашней бытовой техники своими руками
- Устройство и порядок работы
- Характерные неисправности
- Что такое матрица и за что она отвечает
- Основные неисправности матрицы
Простыми словами о ремонте телевизоров и домашней бытовой техники своими руками
Основной элемент LCD-панели или попросту монитора – жидкокристаллическая матрица, представляющая собой законченный функциональный модуль с набором входных сигналов, определяемых его архитектурой. Поэтому все образцы этих устройств построены примерно одинаково, а их проверка и ремонт проводятся в виде стандартных процедур.
Поэтому все образцы этих устройств построены примерно одинаково, а их проверка и ремонт проводятся в виде стандартных процедур.
Устройство и порядок работы
Матрица представляет собой комбинацию большого числа жидких кристаллических ячеек, располагающихся системно. Характерным для нее является то, что положение каждого из этих элементов описывается двумя координатами: номерами строк и столбцов.
С другой стороны, в ее конструкции предусмотрены следующие модули (смотрите фото ниже):
- Рабочий интерфейс LVDS.
- Микроконтроллер TCON.
- Плата управления (ПУ) питающими напряжениями.
- Модуль задней подсветки (инвертор).
Обратите внимание: Последний компонент имеется не у всех моделей LCD-панелей.
Первый из модулей (интерфейс LVDS) обеспечивает высокую скорость приема данных и существенное снижение линейных помех. Благодаря этому узлу панель приобретает универсальные свойства, позволяющие эксплуатировать ее с любой управляющей платой, имеющей аналогичный интерфейс.
При его использовании информация на ЖК-панель передается в последовательном виде – поэтому в ее составе предусмотрен специальный чип, преобразующий данные в параллельный код. Он представляет собой интегральную микросхему, выполняющую функцию приемника. Далее данные в параллельном коде поступают на микросхему контроллера TCON.
Вторая составляющая матрицы обеспечивает выполнение следующих операций:
- Управление синхронизацией и приемом данных.
- Распределение ее по драйверам строк и столбцов.
- Выдача управляющих сигналов на выход.
На выходном шлейфе контроллера формируется столько сигналов, сколько необходимо для управления транзисторами, встроенными в панель. Общее их количество определяется разрешением, которое поддерживается данным конкретным образцом матрицы. При разрешении 1600х1200, например, на экране будет 1200 строк и 4800 столбцов (1600х3).
Дополнительная информация: Умножение на 3 означает, что каждый цветной элемент формируется на базе трех располагающихся рядом точек.
В панелях большинства марок используется полосковая топология, называемая Stripe. Пример расположения точек на поверхности матрицы приводится на фото снизу.
Характерные неисправности
К числу основных проблем, чаще всего возникающих при эксплуатации матриц, следует отнести:
- Монитор не включается, а светодиод индикатора питания не светится.
- Слишком низкая или очень высокая яркость картинки.
- Изображение на экране мигает (все или только один край).
- Темный экран (индикатор питания горит).
- Экранная подсветка гаснет через какое-то время.
- Отсутствует один цвет.
Рассмотрим каждую из неисправностей более подробно.
В первом случае, возможно, вышел из строя внутренний источник питания, который можно попробовать отремонтировать. Однако специалисты советуют при наличии возможностей сразу заменить его новым изделием (сделать это можно, если он оформлен как отдельный модуль). В ситуации, когда источник входит в состав управляющей платы – придется полностью обновить этот узел. Причиной этой неполадки также могут быть:
Причиной этой неполадки также могут быть:
- Выход из строя сетевого адаптера (в моделях, где он имеется).
- Неисправность кнопки включения.
- Неполадки в самой ПУ.
Для устранения этих нарушений сначала нужно проверить «подозрительную» деталь, модуль или плату с помощью тестера (на предмет наличия нужных напряжений и отсутствия обрывов в рабочих цепях). При обнаружении поврежденных узлов или элементов плату, адаптер или кнопку придется заменить.
При выявлении неисправности второго рода (изменился уровень яркости) причину следует искать в нарушениях в работе инвертора, лампочек задней подсветки или ПУ. После проверки импульсных напряжений на выходе инвертора и управляющей платы можно будет убедиться в их состоянии.
Важно! Для получения полной картины с управляющими сигналами удобнее всего воспользоваться цифровым осциллографом.
Если нужные импульсные напряжения на выходе этих узлов отсутствуют – потребуется заменить их исправными. При наличии всех сигналов можно попробовать обновить лампочки подсветки. В ряде моделей следует начинать с проверки соединительного шлейфа между инвертором и ПУ на предмет его целостности.
При наличии всех сигналов можно попробовать обновить лампочки подсветки. В ряде моделей следует начинать с проверки соединительного шлейфа между инвертором и ПУ на предмет его целостности.
При мигающем экране неисправными могут быть инвертор или лампа задней подсветки. Для устранения этой неисправности придется проделать все те же операции, что и в предыдущем случае. При обнаружении нарушений в формировании импульсных сигналов или обрыва шлейфа – необходимо заметь эти элементы новыми изделиями. Неисправную лампочку подсветки также потребуется обновить.
При наличии опыта соответствующих работ можно попытаться отремонтировать инвертор своими руками. Однако в этом случае надеяться на положительный результат можно не всегда. Если экран потемнел и ни изменяет свое состояние (фото ниже) – нужно проверить преобразователь в плате ПУ или инвертор.
В первом случае следует убедиться с помощью тестера в наличии напряжений у всех стабилизаторов и при обнаружении нарушений заменить неисправный элемент новой деталью. При выявлении отклонений в работе инвертора проще всего заменить его рабочим аналогом.
При выявлении отклонений в работе инвертора проще всего заменить его рабочим аналогом.
Если экран выключается через неопределенное время – нарушение, скорее всего, кроется в срабатывании токовой защиты инвертора. Другой причиной может быть неисправность лампочки задней подсветки. Для решения вопроса в этом случае рекомендуется заменить оба узла.
В ситуации, когда отсутствует один из цветов в изображении – неисправность может скрываться в нарушении работы интерфейса или ПУ. Если их проверка подтвердила эти предположения – вышедшие из строя узлы следует заменить. В заключение отметим, что к самостоятельному ремонту матрицы монитора не следует приступать, если вы полностью не уверены в своих силах.
Основным компонентом в телевизоре или мониторе является матрица. Именно она отвечает за качество изображения, а также за яркость, контрастность и четкость картинки. Для того, чтобы устройство работало как можно дольше, а его параметры были наилучшими, при выборе монитора в первую очередь внимание следует обращать именно на матрицу.
Что такое матрица и за что она отвечает
Матрица — это основная и самая важная деталь монитора. Именно на ней формируется изображение, и его качество зависит именно от матрицы. Она же является и самым дорогим компонентом в устройстве. Зачастую пользователю дешевле купить новое устройство, чем заниматься заменой именно этой составляющей.
Для того, чтобы проверить данный элемент, следует в первую очередь разобрать корпус. Самой простой проверкой работоспособности этого компонента, будет подключение мультиметра к специальному шлейфу на плате. Это позволит проверить работоспособность контактов и наличие питания между элементами.
СПРАВКА! Проверка работоспособности составляющих позволит найти неисправность или исключить рабочие составляющие.
Если каждый компонент обеспечивается достаточным напряжением и неисправностей не обнаружено, возможно, проблема в дешифраторе. Для того, чтобы проверить это, следует припаять входу питания дополнительный источник энергии. После этого необходимо включить монитор в «тестовый режим». Если в этом режиме будут наблюдаться полосы или искажения — значит матрица неисправна. В обратном случае, если тестовый режим показал правильное изображение, проблема может заключаться в нарушении целостности контактов или шлейфа.
После этого необходимо включить монитор в «тестовый режим». Если в этом режиме будут наблюдаться полосы или искажения — значит матрица неисправна. В обратном случае, если тестовый режим показал правильное изображение, проблема может заключаться в нарушении целостности контактов или шлейфа.
Основные неисправности матрицы
Зачастую это повреждение поверхности с ЖК кристаллами. В данном случае изображение искажается, а экран «течет». В данном случае наилучшим решением будет либо замена этого компонента, либо замена всего устройства в целом.
Экран не загорается. Причин этому есть две:
- Отсутствие питание на элементах. Чтобы это проверить достаточно подключиться мультиметром ко всем контактам и посмотреть питающее напряжение.
- Неработающая подсветка. Чтобы исключить данный вариант достаточно посветить направленным светом на монитор. Под определенным углом появится изображение. Если этого не произошло неисправность заключается в другом.
Изображение рябит, видны полосы. Данная проблема свидетельствует о неисправности в дешифраторе. При обладании достаточными знаниями и навыками можно произвести замену вручную, но лучше воспользоваться помощью компетентного специалиста.
Данная проблема свидетельствует о неисправности в дешифраторе. При обладании достаточными знаниями и навыками можно произвести замену вручную, но лучше воспользоваться помощью компетентного специалиста.
LCD монитор — скалер, инвертор, CCFL лампы,матрица
Одним из важных аспектов ремонта, является скорость ремонта, если в любительском варианте ремонта, это вообще не критичный параметр, то в профессиональном ремонте, чем быстрее отремонтируется монитор, тем дешевле выходит себестоимость ремонта. Хороший инженер за 4 часа ремонтирует 8 мониторов из 10, правда без тех прогона. А если учесть, что ремонты до такого инженера доходят уже после конденсаторно-предохранительной диагностики, то становится понятно, что не только наработки помогают ремонтировать – но и технология поиска дефекта играет значительную роль.
Немного теории.
Другим важным аспектом ремонта, является максимальное ограничение области поиска неисправности, что само по себе не только косвенно уменьшает время на ремонт, но и дает максимальный выход исправного оборудования по завершению ремонтных работ.
Блок схема работы ЖК монитора.
Из блоксхемы можно увидеть самый сложный модуль в диагностике – это инвертор, его работа зависит от работы трех блоков: скалера, блока питания, ламп(ы) CCFL.
Давайте рассмотрим распространенную ошибку при диагностике дефекта монитора. Рассматривать будем в разрезе отсутствия наработок, то есть, например, за ремонт взялся инженер ранее не занимавшийся ремонтом монитора, но разбирающийся в электронике, и соответственно не может сказать, что неисправно, только по названию монитора. Большинство специалистов более менее ознакомившись с устройством монитора, делают диагностику так – отключают скалер и подают внешний сигнал включения на инвертор, а сам инвертор нагружают заведомо исправными лампами CCFL.
Блок схема диагностики ЖК монитора, с не самой лучшей эффективностью, но с максимальной простотой.
Не смотря на кажущуюся простоту, данный метод имеет существенные минусы
низкую скорость диагностики
очень широкий диапазон возможных неисправных блоков
в некоторых случаях, в инверторах не реализован режим прямого включения
не дают общую картину стоимости ремонта.
Блок схема диагностики ЖК монитора, с максимальной эффективностью диагностики.
Не можем сказать, что данный вариант диагностики не лишен недостатков, но эффективность впечатляет. Мы сразу можем оценить общую картину поломки монитора, например если неисправна ЖК панель, то большинстве в случаев, это выявится на начальном этапе без всяких ремонтных работ.
Немного практики.
Первый способ диагностики требует минимальных ремонтных работ, замены всех полярных конденсаторов. И его основным тонким местом является зависимость работы блока питания от исправности инвертора. Для принудительного запуска инвертора требуется отключить скалер, подключить заведомо исправные лампы, и пинцетом замыкаем сигнал ON на+5В. Как правило такие контакты подписаны на плате инвертора.
Разъем управления инвертором BN44-000123 E установленного в мониторе Samsung 940 N.
В приведенном примере, для запуска инвертора необходимо отключить разъем от скалера (на фото он подключен), подать на блок питания 220В и замкнуть пинцетом контакты +5В(6,7) с контактом ON/OFF(9). При размыкании контактов – инвертор отключается, соответсвенно лампы CCFL гаснут. При положительных результатах проверки, подключаем все в обратном порядке, родные лампы, проверяем работу инвертора, потом подключаем скалер и проверяем работу монитора в целом. Как можно понять. При выходе из строя только конденсаторов блока питания и инвертора – о неисправной ЖК панели мы узнаем только в конце ремонтных работ. Если учесть, что большинство владельцев мониторов отказываются от замены ЖК панели, то время затраченное на поиск неисправного блока оказывается безрезультатно утерянным.
При размыкании контактов – инвертор отключается, соответсвенно лампы CCFL гаснут. При положительных результатах проверки, подключаем все в обратном порядке, родные лампы, проверяем работу инвертора, потом подключаем скалер и проверяем работу монитора в целом. Как можно понять. При выходе из строя только конденсаторов блока питания и инвертора – о неисправной ЖК панели мы узнаем только в конце ремонтных работ. Если учесть, что большинство владельцев мониторов отказываются от замены ЖК панели, то время затраченное на поиск неисправного блока оказывается безрезультатно утерянным.
Второй способ диагностики требует дополнительного оборудования.
Подключение внешнего блока питания для проверки.
В качестве внешнего блока питания желательно использовать блок питания от компьютера, на нем присутствуют и 12Вольт и 5Вольт (иногда 3,3Вольт) необходимые для работы монитора и его довольно легко найти, в крайнем случае подойдет даже частично неисправный блок питания, лишь бы выдавал требуемые два напряжения. Как правило длины провода не хватает поэтому необходимо землю, +12Вольт, +5Вольт несколько удлинить проводами, ну и не стоит забывать что бы запустить ATX блок питания, необходимо замкнуть черный и зеленый провод на основном разъеме блока питания. В этом случае, если виноваты только конденсаторы, вы уже увидите картинку на экране монитора, а значит, можете в целом оценить состояние и стоимость ремонта монитора.
Как правило длины провода не хватает поэтому необходимо землю, +12Вольт, +5Вольт несколько удлинить проводами, ну и не стоит забывать что бы запустить ATX блок питания, необходимо замкнуть черный и зеленый провод на основном разъеме блока питания. В этом случае, если виноваты только конденсаторы, вы уже увидите картинку на экране монитора, а значит, можете в целом оценить состояние и стоимость ремонта монитора.
Пример.
Самый наглядный пример — ремонт монитора Benq Q7T4 с неисправным конденсатором в цепи обратной связи ламп CCFL. Монитор пришел в мастерскую с заключением от предыдущей мастерской, ремонту не подлежит. Монитор имел следующую неисправность, включается – с прогревом минут через 5-7 выключается. От предыдущих механиков осталось в наследие измененная цепь обратной связи в цепи блока питания. Блок питания выдавал на инвертор 21Вольт, которые периодически проваливались до 8вольт, блок питания «гуляет» по питанию инвертора.
Схема блока питания монитора Benq Q7T4
Предыдущий ремонтник сделал ошибочные выводы о неисправности блока питания и пытался цепью обратной связи R711 (10k) поднять напряжение на выходе блока питания, тем самым механик пошел по тупиковому пути. При подключении внешнего блока питания сразу выявился дефект инвертора, ну дальше, зная, что именно инвертор неисправен, а так же типовые поломки для этого класса инвертора – неисправность была быстро выявлена.
При подключении внешнего блока питания сразу выявился дефект инвертора, ну дальше, зная, что именно инвертор неисправен, а так же типовые поломки для этого класса инвертора – неисправность была быстро выявлена.
Схема инвертора монитора Benq Q7T4
Неисправность заключалась в еле видном дефекте пайки конденсатора C826 (0,22мкФ*160В), который довольно сложно увидеть, но так как поломка конденсатора 826 (0,22мкФ*160В) характерна для этого типа инвертора, то при проверке и был обнаружен дефект пайки.
Но даже если не знать о типовой поломке, визуальный осмотр сузился до цепей инвертора, а значит шанс найти дефект пайки для неопытного механика вырос почти в два раза.
Ремонт монитора без учета разборки — сборки занял 20 минут и тех. прогон 3 часа.
Как проверить бу монитор при покупке — совет от EUROPC
Качество картинки, которую мы видим на экране монитора, во многом зависит от его возможностей и технического состояния. Поэтому комплексная проверка монитора — обязательная процедура перед покупкой. Особенно, если вы хотите купить стоковую технику, побывавшую в эксплуатации. Лучше осуществить диагностику в магазине, до оформления покупки. Но если на бу монитор есть гарантия, его можно проверить и дома. Ниже мы расскажем, как осуществить комплексную диагностику бу экрана, и какие характеристики необходимо проверить при покупке.
Особенно, если вы хотите купить стоковую технику, побывавшую в эксплуатации. Лучше осуществить диагностику в магазине, до оформления покупки. Но если на бу монитор есть гарантия, его можно проверить и дома. Ниже мы расскажем, как осуществить комплексную диагностику бу экрана, и какие характеристики необходимо проверить при покупке.
Что включает комплексная проверка бу монитора
В магазине, прежде, чем вы оформите покупку, или дома, после распаковки и подключения устройства, его нужно протестировать по параметрам:
- наличие и число битых точек;
- наличие засветки;
- корректность цветовой передачи;
- градиенты;
- мерцание;
- настройки резкости, яркости и контрастности;
- геометрия экрана;
- бандинг.
Это несложно сделать при помощи определенных утилит, или набора тестовых картинок, которые находятся в сети интернет в свободном доступе.
Проверка матрицы бу монитора
Картинка на экране формируется из пикселей — крохотных по размеру квадратов или точек круглой формы. В случае повреждения матрицы, на дисплее могут появиться точки, которые по цвету выбиваются из общей картинки.
В случае повреждения матрицы, на дисплее могут появиться точки, которые по цвету выбиваются из общей картинки.
”Битыми” пикселями называют:
- темные точки, заметные на белом фоне — это “мертвые”, выключенные пиксели;
- бесцветные точки, что светятся на темном — это “горячие” пиксели;
- разноцветные точки, что не меняют окраску при любой заливке экрана — “застрявшие” пиксели.
По производственным стандартам, мониторы делятся на 4 класса. Для каждого из них допускается определенное число дефектных точек:
- 4 класс — до 50 белых, до 150 черных, и до пятисот цветных точек;
- 3 класс — до 5 “горячих”, до 15 “мертвых”, и до пятидесяти “застрявших” пикселей;
- 2 класс — до 2 белых и черных пикселей, и до 5 цветных;
- на мониторах 1 класса битых точек быть не должно.
Таким образом, при диагностике матрицы, учитывайте класс бу монитора.
Как проверить бу монитор на битые пиксели
Существует два основных способа проверки:
- вручную;
- с использованием утилиты или онлайн-сервиса.

Проверка вручную. Большую группу битых точек можно увидеть сразу. Чтобы найти отдельные точки, нужно поочередно вывести на экран 5 однотонных картинок, залитых стандартными цветами RGB, а также черной и белой краской. При смене фона, осматривайте экран, и вы сможете обнаружить все дефектные пиксели. Чтобы этим методом проверить дисплей в магазине, заранее сохраните картинки на флешке.
Проверка с использованием программного обеспечения или онлайн-сервисов.
Для диагностики монитора бу дома, просто скачайте и запустите подходящее приложение. Они основаны на том же принципе смены картинок, только это происходит в автоматическом режиме. Чтобы провести диагностику в магазине, сохраните утилиту на флеш-карту, и запустите ее перед оформлением покупки.
Какие есть сервисы для проверки монитора на битые пиксели
Среди популярных утилит, стоит отметить эти 2:
- Dead Pixel Tester. Ее легко найти на официальном вебсайте.
Как выполнить диагностику:
- запустите программу;
- в закладке Pettern выберите нужный режим;
- выберите цвет заливки;
- установите автоматическую смену режимов;
- проверьте матрицу на наличие дефектов.

Рекомендуем воспользоваться функцией Exerciser. Кликнув на кнопку с соответствующей командой, вы увидите на экране прямоугольную рамку, которую можно перетаскивать при помощи мышки. Она “работает” как увеличительное стекло, и позволяет быстрее заметить выбивающиеся по цвету точки.
- IsMyLcdOk — аналогичная утилита, которая также есть в сети в свободном доступе.
После запуска, на экране появится инструкция пользователя. В ней подробно описаны возможности программы, и алгоритм действий. Удобные онлайн — ресурсы для проверки на битые пиксели:
- Monteon, ресурс monteon.ru/.
На этом сайте вы найдете 7 видов диагностики дисплея, и разные их вариации. Для начала тестирования нужно выбрать соответствующий тип проверки, и кликнуть кнопку запуска. При этом на экран будет выведен зацикленный видеоролик с однотонными картинками, рассмотрев которые вы сможете обнаружить дефекты.
- Vanity Monitor Test, ресурс tft.
 vanity.dk.
vanity.dk.
Эту онлайн-утилиту можно задействовать для диагностики дисплея лэптопа, планшетного ПК и мобильного телефона. Для запуска проверки на ПК нужно будет установить Adobe Flash Player (если он не установлен на вашем ПК), и поддерживающий его веб-обозреватель. Для старта диагностики, нажмите кнопку “HTML Window”, предварительно выбрав нужный режим из пунктов меню.
Как проверить монитор бу на засветы
Засветы — это дефект, который бывает на матрицах IPS и TN. Причина — слишком плотное прилегание матрицы и подсветки. Засветы могут появиться из-за заводского брака, или вследствие неосторожного обращения с монитором.
Этот дефект можно заметить при среднем или темном освещении комнаты, и почти невозможно при ярком дневном свете. Чтобы обнаружить засветы, загрузите на экран фото или картинку с темным фоном. Если обнаружите на экране белые, подсвеченные пятна, значит у монитора есть этот дефект.
Цветопередача бу монитора
Корректная цветопередача экрана позволяет видеть картинку с теми же цветами, которые будут на распечатанном изображении. Правильная настройка цветопередачи особенно важна для фотографов и видеооператоров. Определить правильность цветопередачи помогут специальные тестовые картинки с разноцветными полосами или цифрами, которые можно скачать в сети. К каждому такому тесту есть инструкция. В ней подробно описано, как должна выглядеть картинка на правильно откалиброванном экране.
Правильная настройка цветопередачи особенно важна для фотографов и видеооператоров. Определить правильность цветопередачи помогут специальные тестовые картинки с разноцветными полосами или цифрами, которые можно скачать в сети. К каждому такому тесту есть инструкция. В ней подробно описано, как должна выглядеть картинка на правильно откалиброванном экране.
Проверка градиентов бу монитора
Этот тест позволит узнать, насколько качественно на экране отображаются оттенки цветов. Правильная передача оттенков важна при просмотре кинофильмов, играх в современные видеоигры с хорошей графикой, при работе в фото- и видеоредакторах.
Для диагностики по этому показателю, воспользуйтесь упомянутым выше сервисом Монтеон. Здесь вы найдете коллекцию цветных и черно-белых тестовых шаблонов с плавным градиентом. Для диагностики нужно вывести изображение на весь экран. На хорошем бу мониторе переходы между цветами будут плавными, без полосок и резких смен цвета.
Проверка мерцания монитора
Просто посмотрев на экран, этот дефект заметить сложно. Мерцать могут и новые, и бу мониторы, так как этот дефект не зависит от типа и года выпуска подсветки. Причины мерцания экрана:
Мерцать могут и новые, и бу мониторы, так как этот дефект не зависит от типа и года выпуска подсветки. Причины мерцания экрана:
- неправильная настройка, когда обновление экрана происходит с маленькой частотой;
- поломка графического адаптера или матрицы;
- неустановленный драйвер графического адаптера.
Если вы много времени проводите за компьютером, мерцание экрана может со временем привести к снижению зрения, сухости и хронической боли в глазах, а также быстрой утомляемости.
Чтобы диагностировать мерцание дисплея, скачайте несколько тестовых картинок. Развернув изображение, рассмотрите его с разного расстояния. На хорошем экране при близком рассмотрении вы увидите на картинке четкий узор из черных и белых точек. На расстоянии рисунок будет выглядеть равномерно серым. На мерцающем дисплее картинка будет отличаться — вблизи вы не сможете увидеть точки, а при удалении от экрана на нем могут появиться прямые или гнутые полоски. Это — верный признак того, что вам необходимо откорректировать синхронизацию фазы, или обратиться к специалистам для более детальной диагностики устройства.
Это — верный признак того, что вам необходимо откорректировать синхронизацию фазы, или обратиться к специалистам для более детальной диагностики устройства.
Как проверить настройки резкости бу монитора
Если уровень резкости недостаточный, вы будете видеть на экране размытое изображение или расплывшиеся буквы, так как граница между темными и светлыми цветами в этом случае будет нечеткой. При этом, от чрезмерно резкого изображения может сильно уставать зрение.
Для диагностики резкости, выберите соответствующий режим проверки в сервисе Монтеон, или скачайте такую тестовую картинкку. Развернув ее, внимательно рассмотрите изображение. Если резкость выставлена правильно, вы увидите квадраты с мелкими узорами, размещенные в шахматном порядке, и четкий серый кружок посередине.
Контрастность и яркость монитора бу
Неправильно отрегулированные яркость и контрастность влияют на зрение так же негативно, как мерцание экрана. Чтобы определить, насколько корректно настроены эти показатели, загрузите с вебсайта monteon. ru/ полноразмерное изображение этого теста:
ru/ полноразмерное изображение этого теста:
Развернув картинку, рассмотрите ее. На качественном мониторе вы рассмотрите четкие границы между разноцветными квадратиками, и разные уровни яркости внутри каждого квадрата.
Геометрия бу монитора
С помощью этой диагностики, можно выявить наличие искажений изображения, что выводится на экран. Чтобы проверить геометрию, скачайте утилиту Nokia monitor test, и запустите ее, предварительно прочитав инструкцию. Как диагностировать монитор на геометрию “вручную”:
- откройте картинку с сеткой из четких линий;
- приложите к экрану лист А4;
- проверьте, все ли линии ровные.
Выпуклые линии говорят о том, что у этого монитора есть экранное искажение.
Бандинг
Этот дефект можно обнаружить на ЖК мониторах. Он проявляется в виде ступенчатого градиента по всему экрану, или полос с размытой границей.
Причины проявления бандинга:
- давление внутри матрицы;
- производственный брак;
- дефекты подсветки;
- попадание пыли между слоями матрицы.

Исправить бандинг при помощи настроек невозможно, поэтому не забудьте протестировать бу монитор на наличие этого дефекта перед покупкой. Для этого можно использовать те же тесты, что вы применяли для диагностики на битые пиксели. На исправном экране одноцветные картинки будут отображаться равномерно, без полосок и градиентных переходов цвета.
Почему бу монитор лучше купить в специализированном магазине
Как видите, проверка работоспособности бу монитора занимает определенное время, и требует предварительной подготовки. Некоторые дефекты можно выявить только в определенных условиях освещенности. Поэтому в момент покупки не всегда удается составить полную картину о работоспособности устройства. Особенно, если вы покупаете его с рук.
Поэтому мы рекомендуем делать такие покупки в магазинах, что специализируются на реализации стоковой техники. Они обычно предоставляют две недели для тестирования купленного товара, и гарантию сроком от 6 до 12 месяцев. Если в течение этого времени обнаружатся поломки, вы сможете вернуть или бесплатно отремонтировать бу монитор.
Если в течение этого времени обнаружатся поломки, вы сможете вернуть или бесплатно отремонтировать бу монитор.
8.4: Матрицы проверки на четность и генератора
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 81086
- Томас В. Джадсон
- Государственный университет Стивена Ф. Остина via Abstract Algebra: Theory and Applications
Нам нужно найти систематический способ генерации линейных кодов, а также быстрые методы декодирования. Изучая свойства матрицы \(H\) и тщательно выбирая \(H\text{,}\), можно разработать очень эффективные методы кодирования и декодирования сообщений. С этой целью мы введем стандартный генератор и канонические матрицы проверки на четность.
Предположим, что \(H\) является матрицей \(m \times n\) с элементами в \({\mathbb Z}_2\) и \(n \gt m\text{.}\). Если последняя \ (m\) столбцов матрицы образуют \(m \times m\) единичную матрицу, \(I_m\text{,}\) тогда матрица представляет собой каноническая матрица проверки на четность . Более конкретно, \(H= (A \mid I_m)\text{,}\), где \(A\) — матрица \(m \times (n-m)\)
\[ \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1,n-m} \\ a_{21} & a_{22} & \cdots & a_{2,n-m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{m,n-m} \end{pmatrix} \nonumber \]
и \(I_m\) — это \(m \times m\) единичная матрица
\[ \begin{pmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \ конец {pmatrix}\text{.} \nonumber \]
С каждой канонической проверочной матрицей мы можем связать \(n \times (n-m)\) стандартную порождающую матрицу
\[ G = \left( \frac{I_{n-m}}{A} \right)\text{. } \nonumber \]
} \nonumber \]
Нашей целью будет показать, что \(\mathbf x\), удовлетворяющий \(G {\mathbf x} = {\mathbf y}\), существует тогда и только тогда, когда \(H{\mathbf y} = {\mathbf 0}\text{.}\) Если задан блок сообщений \({\mathbf x}\), который необходимо закодировать, матрица \(G\) позволит нам быстро закодировать его в линейное кодовое слово \({\mathbf y }\текст{.}\)
Пример \(8.23\)
Предположим, что у нас есть следующие восемь слов для кодирования:
\[ (000), (001), (010), \ldots, (111)\text{.} \nonumber \]
Для
\[ A = \begin{pmatrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix}\text{,} \nonumber \]
соответствующий стандартный генератор и канонические матрицы проверки на четность: \ 1 & 1 & 0 \\ 1 & 0 & 1 \end{pmatrix} \nonumber \]
и
\[ H = \begin{pmatrix} 0 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 1 & 0 & 0 & 1 \end{pmatrix}\text{,} \nonumber \]
соответственно.
Решение
Обратите внимание, что строки в \(H\) представляют проверки четности на определенных битовых позициях в \(6\)-кортеже. \(1\) в единичной матрице служат проверкой четности для \(1\) в той же строке. Если \({\mathbf x} = (x_1, x_2, x_3, x_4, x_5, x_6)\text{,}\), то
\(1\) в единичной матрице служат проверкой четности для \(1\) в той же строке. Если \({\mathbf x} = (x_1, x_2, x_3, x_4, x_5, x_6)\text{,}\), то
\[ {\mathbf 0} = H{\mathbf x} = \begin{pmatrix} x_2 + x_3 + x_4 \\ x_1 + x_2 + x_5\\ x_1 + x_3 + x_6 \end{pmatrix}\text{, } \nonumber \]
что дает систему уравнений:
\begin{align*} x_2 + x_3 + x_4 & = 0\\ x_1 + x_2 + x_5 & = 0\\ x_1 + x_3 + x_6 & = 0 \text{.} \end{align*}
Здесь \(x_4\) служит контрольным битом для \(x_2\), а \(x_3\text{;}\) \(x_5\) является контрольным битом для \(x_1\) и \(x_2\text{;}\) и \(x_6\) является контрольным битом для \(x_1\) и \(x_3\text{.}\) Единичная матрица сохраняет \( x_4\text{,}\) \(x_5\text{,}\) и \(x_6\) от необходимости проверять друг друга. Следовательно, \(x_1\text{,}\) \(x_2\text{,}\) и \(x_3\) могут быть произвольными, но \(x_4\text{,}\) \(x_5\text{,} \) и \(x_6\) должны быть выбраны для обеспечения четности. Нуль-пространство \(H\) легко вычислить как
\[ \begin{array}{cccc} (000000) & (001101) & (010110) & (011011) \\ (100011) & (101110) & (110101) & (111000). \end{array} \nonumber \]
\end{array} \nonumber \]
Еще проще вычислить нулевое пространство с помощью порождающей матрицы \(G\) (таблица \(8.24\)).
\(Таблица \текст { } 8.24\). Сгенерированный матрицей код
| Слово сообщения \(\mathbf x\) | Кодовое слово \(G \mathbf x\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(000\) | \(000000\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(001\) | \(001101\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(010\) | \(010110\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(011\) | \(011011\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(100\) | \(100011\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(101\) | \(101110\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| \(110\) | 9n\) , чьи первые \(n-m\) битов произвольны, а последние \(m\) битов определяются \(H{\mathbf x} = {\mathbf 0}\text{.} \) Каждый из последних \(m\) бит служит битом проверки четности для некоторых из первых \(n-m\) бит.
| Feature | Implementation |
|---|---|
| Manually running a workflow from the UI: | workflow_dispatch |
| Triggering a workflow to run automatically: | pull_request |
| Запуск рабочего процесса через равные промежутки времени: | расписание |
| Установка разрешений для токена: | Разрешения |
| Контроль, сколько рабочих процессов или задания могут выполняться в одно и то же время: | . |
| Предотвращение запуска задания, если не выполняются определенные условия: | , если |
| Использование матрицы для создания различных тестовых конфигураций: | matrix |
| Cloning your repository to the runner: | actions/checkout |
Installing node on the runner: | actions/setup-node |
| Caching dependencies : | действия/кэш |
| Запуск тестов на бегуне: | npm test |
Пример рабочего процесса
0031 Команда GitHub Docs Engineering создала следующий рабочий процесс. Чтобы просмотреть последнюю версию этого файла в репозитории github/docs , см. test.yml .
Примечание . Каждая строка этого рабочего процесса объясняется в следующем разделе «Понимание примера».
Понимание примера
В следующей таблице объясняется, как каждая из этих функций используется при создании рабочего процесса GitHub Actions.
| Код | Пояснение |
|---|---|
|
Имя рабочего процесса, которое будет отображаться на вкладке «Действия» репозитория GitHub. |
|
|
Ключевое слово |
|
|
Добавьте событие |
|
|
Добавьте событие |
|
|
Добавить |
|
|
Изменяет разрешения по умолчанию, предоставленные |
|
|
Создает группу параллелизма для определенных событий и использует |
|
|
Отменяет любое выполняющееся в данный момент задание или рабочий процесс в той же группе параллелизма. |
|
|
Группирует вместе все задания, выполняемые в файле рабочего процесса. |
|
|
Определяет задание с идентификатором |
|
|
Настраивает задание для запуска в исполнителе, размещенном на GitHub, или в локальном исполнителе, в зависимости от репозитория, в котором запущен рабочий процесс. В этом примере задание будет выполняться на локальном исполнителе, если репозиторий называется |
|
|
Устанавливает максимальное количество минут, в течение которого задание может выполняться, прежде чем оно будет автоматически отменено. |
|
| В этом разделе определяется матрица построения для ваших должностей. | |
|
Установка |
|
|
Создает матрицу с именем |
|
|
Группирует вместе все шаги, которые будут выполняться как часть задания |
|
|
|
|
|
Если текущим репозиторием является репозиторий |
|
|
Если текущим репозиторием является репозиторий | |
|
Если текущим репозиторием является репозиторий |
|
|
На этом этапе выполняется команда для извлечения объектов LFS из репозитория. |
|
|
На этом шаге используется |
|
|
На этом этапе выполняется команда оболочки, которая использует выходные данные предыдущего шага для создания файла, содержащего список файлов, измененных в запросе на вытягивание. |
|
|
На этом шаге используется действие |
|
|
На этом этапе выполняется команда оболочки |
|
|
На этом шаге используется |
|
|
На этом этапе выполняется сценарий сборки. |
|
|
На этом шаге тесты выполняются с использованием |
Следующие шаги
- Дополнительные сведения о концепциях GitHub Actions см. в разделе «Общие сведения о GitHub Actions».

- Дополнительные пошаговые инструкции по созданию базового рабочего процесса см. в разделе «Краткое руководство по действиям GitHub».
- Если вы знакомы с основами GitHub Actions, вы можете узнать о рабочих процессах и их функциях в разделе «О рабочих процессах».
Многоязычный матричный тест: принципы, применение и сравнение языков: обзор
Сохранить цитату в файл
Формат: Резюме (текст) PubMedPMIDAbstract (текст) CSV
Добавить в коллекции
- Создать новую коллекцию
- Добавить в существующую коллекцию
Назовите свою коллекцию:
Имя должно содержать менее 100 символов
Выберите коллекцию:
Не удалось загрузить коллекцию из-за ошибки
Повторите попытку
Добавить в мою библиографию
- Моя библиография
Не удалось загрузить делегатов из-за ошибки
Повторите попытку
Ваш сохраненный поиск
Название сохраненного поиска:
Условия поиска:
Тестовые условия поиска
Эл. адрес:
(изменить)
адрес:
(изменить)
Который день? Первое воскресеньеПервый понедельникПервый вторникПервая средаПервый четвергПервая пятницаПервая субботаПервый деньПервый день недели
Который день? воскресеньепонедельниквторниксредачетвергпятницасуббота
Формат отчета: SummarySummary (text)AbstractAbstract (text)PubMed
Отправить не более: 1 шт. 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
Отправить, даже если нет новых результатов
Необязательный текст в электронном письме:
Создайте файл для внешнего программного обеспечения для управления цитированием
Полнотекстовые ссылки
Тейлор и Фрэнсис
Полнотекстовые ссылки
Обзор
. 2015;54 Приложение 2:3-16.
2015;54 Приложение 2:3-16.
дои: 10.3109/149.2015.1020971. Epub 2015 18 сентября.
Биргер Коллмайер 1 2 3 4 , Анна Варжибок 1 2 , Сабина Хохмут 1 2 , Мелани Зоколл 1 2 , Верена Услар 1 2 3 , Томас Брэнд 1 2 , Кирстен С Вагенер 1 4
Принадлежности
- 1 Кластер передового опыта Hearing4all, Ольденбург, Германия.

- 2 b Медицинская физика, Ольденбургский университет, Германия.
- 3 c HörTech gGmbH, Ольденбург, Германия.
- 4 d Hörzentrum Oldenburg GmbH, Ольденбург, Германия.
- PMID: 26383182
- DOI: 10.3109/149 .2015.1020971
Обзор
Birger Kollmeier et al. Int J Audiol. 2015.
. 2015;54 Приложение 2:3-16.
дои: 10. 3109/149.2015.1020971.
Epub 2015 18 сентября.
3109/149.2015.1020971.
Epub 2015 18 сентября.
Авторы
Биргер Коллмайер 1 2 3 4 , Анна Варжибок 1 2 , Сабина Хохмут 1 2 , Мелани Зоколл 1 2 , Верена Услар 1 2 3 , Томас Брэнд 1 2 , Кирстен С Вагенер 1 4
Принадлежности
- 1 Кластер передового опыта Hearing4all, Ольденбург, Германия.

- 2 b Медицинская физика, Ольденбургский университет, Германия.
- 3 c HörTech gGmbH, Ольденбург, Германия.
- 4 d Hörzentrum Oldenburg GmbH, Ольденбург, Германия.
- PMID: 26383182
- DOI: 10.3109/149 .2015.1020971
Абстрактный
Задача:
Представлен обзор разработки, оценки и применения так называемого «теста матричных предложений» для проверки разборчивости речи в многоязычном обществе. Формат допускает повторное использование с одним и тем же пациентом на его или его родном языке, даже если экспериментатор не понимает этого языка.
Формат допускает повторное использование с одним и тем же пациентом на его или его родном языке, даже если экспериментатор не понимает этого языка.
Дизайн: Используя закрытый формат, синтаксически фиксированные, семантически непредсказуемые предложения (например, «Петр купил восемь белых кораблей») обеспечивают словарь из 50 слов (10 альтернатив для каждой позиции в предложении). Рассмотрены принципы (т. е. построение, оптимизация, оценка и проверка) для 14 различных языков. Сообщается об исследованиях влияния говорящего, языка, шума, тренировочного эффекта, открытого и закрытого проведения теста и владения языком испытуемых, а также обсуждаются примеры применения.
Полученные результаты:
Принципы оптимизации приводят к резкой функции разборчивости и высокой однородности представленных речевых материалов и используемых тестовых списков, что обеспечивает высокую эффективность и отличную сопоставимость между языками. Характеристики носителей обычно доминируют в различиях между языками.
Характеристики носителей обычно доминируют в различиях между языками.
Вывод: Формат матричного теста с изложенными здесь принципами рекомендуется для получения эффективных, надежных и сравнимых порогов приема речи на разных языках.
Ключевые слова: Разборчивость речи в шуме; влияние языка; порог приема речи.
Похожие статьи
-
Влияние говорящего и языка на разборчивость речи в шуме, оцененное двуязычными говорящими: какой язык более устойчив к шуму и реверберации?
Хохмут С., Юргенс Т., Бранд Т., Коллмайер Б. Хохмут С. и соавт. Int J Audiol. 2015; 54 Приложение 2:23-34. дои: 10.3109/149
.2015.1088174. Epub 2015 21 октября.
Int J Audiol. 2015.
PMID: 26486466
-
Влияние типа шума на пороги восприятия речи на четырех языках, измеренное с помощью матричных тестов предложений.

Хохмут С., Коллмайер Б., Бранд Т., Юргенс Т. Хохмут С. и соавт. Int J Audiol. 2015; 54 Дополнение 2:62-70. дои: 10.3109/149
.2015.1046502. Epub 2015 22 июня.
Int J Audiol. 2015.
PMID: 26097982
-
Разработка и оценка теста предложений по турецкой матрице.
Зоколл М.А., Фидан Д., Тюркилмаз Д., Хохмут С., Эргенч И., Сеннароглу Г., Коллмайер Б. Зоколл М.А. и соавт. Int J Audiol. 2015; 54 Дополнение 2:51-61. дои: 10.3109/149
.2015.1074735. Epub 2015 7 октября.
Int J Audiol. 2015.
PMID: 26443486
-
[Характеристики, преимущества и ограничения матричных тестов].
Марка T, Wagener KC. Брэнд Т и др. ХНО. 2017 март; 65(3):182-188. doi: 10.1007/s00106-016-0224-9. ХНО. 2017. PMID: 27538937 Обзор.
 Немецкий.
Немецкий. -
Синтезированный речевой вывод и дети: предварительный обзор.
Драгер К.Д., Райхле Дж., Пинкоски К. Драгер К.Д. и др. Am J Speech Ланг Патол. 2010 авг;19(3): 259-73. doi: 10.1044/1058-0360 (2010/09-0024). Epub 2010 11 июня. Am J Speech Ланг Патол. 2010. PMID: 20543017 Обзор.
Посмотреть все похожие статьи
Цитируется
-
Последовательная двусторонняя кохлеарная имплантация: долгосрочное восприятие речи приводит к тому, что дети впервые имплантируются в раннем возрасте.
Форли Ф., Брускини Л., Франциози Б., Берреттини С., Лаццерини Ф. Форли Ф. и др. Eur Arch Оториноларингол. 3 августа 2022 г. doi: 10.1007/s00405-022-07568-4. Онлайн перед печатью.
4 Eur Arch Оториноларингол. 2022.
PMID: 35
Eur Arch Оториноларингол. 2022.
PMID: 35 -
Нормативные данные для взрослых по адаптации теста «Слух в шуме» на европейском французском языке (СОВЕТ-5 мин).
Буиссон Савин Дж., Рейнард П., Байи-Массон Э., Джозеф С., Джоли К.А., Буате С., Тай-Ван Х. Buisson Savin J, et al. Здравоохранение (Базель). 2022 14 июля; 10 (7): 1306. doi: 10.3390/healthcare10071306. Здравоохранение (Базель). 2022. PMID: 35885831 Бесплатная статья ЧВК.
-
Интратимпанальные кортикостероиды при внезапной сенсоневральной тугоухости.
Плонтке С.К., Мейснер С., Агравал С., Кайе-Томасен П., Гэлбрейт К., Микулек А.А., Парнес Л., Премакумар Ю., Рейбер Дж., Шильдер А.Г., Либау А. Плотке С.К. и соавт. Cochrane Database Syst Rev.
 2022 Jul 22;7(7):CD008080. doi: 10.1002/14651858.CD008080.pub2.
Кокрановская система базы данных, ред. 2022 г.
PMID: 35867413
Бесплатная статья ЧВК.
Обзор.
2022 Jul 22;7(7):CD008080. doi: 10.1002/14651858.CD008080.pub2.
Кокрановская система базы данных, ред. 2022 г.
PMID: 35867413
Бесплатная статья ЧВК.
Обзор. -
Активность MEG в зрительной и слуховой коре представляет собой акустическую информацию, связанную с речью, во время молчаливого чтения по губам.
Броль Ф., Кейтель А., Кайзер К. Брель Ф. и соавт. eNeuro. 27 июня 2022 г.; 9(3):ENEURO.0209-22.2022. doi: 10.1523/ENEURO.0209-22.2022. Печать 2022 май-июнь. eNeuro. 2022. PMID: 35728955 Бесплатная статья ЧВК.
-
Прогнозирование разборчивости речи по откликам ЭЭГ на предложения в шуме.
Мунке Дж., Курувила И., Хоппе У. Манке Дж. и соавт. Фронтальные нейроски. 2022 1 июня; 16:876421. doi: 10.
 3389/fnins.2022.876421. Электронная коллекция 2022.
Фронтальные нейроски. 2022.
PMID: 35720724
Бесплатная статья ЧВК.
3389/fnins.2022.876421. Электронная коллекция 2022.
Фронтальные нейроски. 2022.
PMID: 35720724
Бесплатная статья ЧВК.
Просмотреть все статьи "Цитируется по"
Типы публикаций
термины MeSH
Полнотекстовые ссылки
Тейлор и Фрэнсис
Укажите
Формат: ААД АПА МДА НЛМ
Отправить на
Как проверить (быстро) умножение матриц | by Haris Angelidakis
Спойлер: случайность помогает (еще раз)
Умножение двух N x N матриц A и B является фундаментальной операцией, которая проявляется как подпрограмма во всех видах приложений. Поиски алгоритма, способного умножать две матрицы за время O( N ²), все еще продолжаются, причем самый быстрый асимптотический алгоритм разработан Джошем Алманом и Вирджинией Василевской Уильямс (2021), время выполнения которых в настоящее время равно
Поиски алгоритма, способного умножать две матрицы за время O( N ²), все еще продолжаются, причем самый быстрый асимптотический алгоритм разработан Джошем Алманом и Вирджинией Василевской Уильямс (2021), время выполнения которых в настоящее время равно
. отмечено в этой статье Википедии, этот алгоритм является галактическим алгоритмом из-за больших констант и не может быть реализован на практике. Если вам интересно узнать о первом алгоритме, нарушившем наивный O( N ³) барьер для умножения матриц, вы можете взглянуть на мою предыдущую статью о классическом алгоритме Штрассена.
Однако в сегодняшней статье мы рассмотрим другой, связанный с этим вопрос. Предположим, что кто-то дает нам N x N матрицы A, B и C, и, кроме того, предположим, что они утверждают, что C есть произведение A и B , т.е. = АБ . Вопрос теперь в следующем. Можем ли мы проверить, является ли C действительно является произведением A и B без умножения A на B с нуля? Другими словами:
Учитывая N x N матриц A , B и C , как быстро мы можем проверить, является ли C =
Тривиальным тестом на приведенный выше вопрос было бы просто умножить A на B и проверить, равно ли произведение С . Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь — разработать алгоритм O( N ²), который проверяет, является ли C = AB . Для этого мы прибегаем к случайности.
Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь — разработать алгоритм O( N ²), который проверяет, является ли C = AB . Для этого мы прибегаем к случайности.
Примечание: Прежде чем продолжить, мы заявляем, что изложение следует главе 11 прекрасной книги «Тридцать три миниатюры: математические и алгоритмические приложения линейной алгебры» Иржи Матусека.
Основная идея — выбрать случайные N -мерный {0,1} вектор x , где каждая координата независимо установлена в 0 или 1 с вероятностью 0,5, и умножьте оба C и AB на x. Если C = AB , то мы будем иметь Cx = (AB)x, для любого вектора x. Однако, если C не равно AB, , то мы надеемся, что существует много векторов, для которых Cx не равно ( AB)x. Формально предлагаемый тест выглядит следующим образом.
Базовый тест
- Выберите N -мерный {0,1} вектор x равномерно случайным образом.
- Вычислить y = Cx и z = ( AB ) x .
- Если y = z , то вернуть «РАВНО», иначе вернуть «НЕ РАВНО».
Очень легко увидеть, что тест всегда будет возвращать «EQUAL», если C действительно равно AB . Итак, единственный интересный случай для анализа — это когда C не равно AB . Но прежде чем сделать это, мы должны уточнить следующее. Предлагаемая идея требует вычисления произведения (AB)x . Здесь мы должны быть немного осторожны, так как хотим избежать вычисления произведения AB . Чтобы решить эту проблему, мы используем тот факт, что умножение матриц является ассоциативным, и сначала вычисляем Bx , затем умножаем A на результат Bx для общего времени работы O( N ²).
Возвращаясь к анализу, предположим, что C не равно AB . Пусть D = C-AB. Ясно, что хотя бы одна запись D будет отличной от нуля. Обозначим элемент в i -й строке и j -м столбце D как d(i,j) , и пусть k , t таковы, что d(k, t) не равно нулю. Пусть x(j) обозначает j -ю координату вектора x, а q= Dx . Заметьте, что q = y-z . Теперь у нас есть
Поскольку каждая координата x выбирается случайным образом независимо, мы можем предположить, что координата x(t) является последней, которая будет установлена в 0 или 1. Итак, предположим, что все остальные координаты x за исключением координаты x(t) . Когда мы собираемся решить, равно ли x(t) 0 или 1, подбрасывая правильную монету, мы уже определили значение выражения
Обратите внимание, что для S есть две опции; он либо равен нулю, либо отличен от нуля. Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая:
Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая:
- с вероятностью 0,5, x(t) = 1, и поэтому q(k) = S + d(k,t) .
- с вероятностью 0,5, x(t) = 0, поэтому q(k) = S .
Поскольку d(k,t) не равно нулю, это означает, что S + d(k,t) не равно S . Таким образом, по крайней мере одно из S и S+ d(k,t) не равно нулю, и поэтому мы заключаем, что q(k) не равно нулю с вероятностью не менее 0,5, из чего следует, что y не равно z с вероятностью не менее 0,5. Мы заключаем, что с вероятностью не менее 0,5 наш тест правильно определит, что C не равно AB .
Тем не менее, можно сказать, что вероятность успеха в 50% не очень удовлетворительна. И, действительно, это справедливое беспокойство. Но мы можем использовать стандартный прием, используемый для таких алгоритмов, которые попадают в широкий класс алгоритмов Монте-Карло, а именно повторить их несколько раз. Точнее, окончательный алгоритм, который мы будем использовать, следующий.
Точнее, окончательный алгоритм, который мы будем использовать, следующий.
Окончательный тест
- Выполнить базовый тест M раз независимо.
- Если все выполнения базового теста вернули «РАВНО», верните «РАВНО», в противном случае верните «НЕ РАВНО».
Легко видеть, что Final Test всегда завершается успешно, если C = AB . В случае, когда C не равно AB , тогда мы знаем, что однократное выполнение базового теста удается с вероятностью не менее 0,5 . Таким образом, чтобы получить неправильный ответ, все M выполнения базового теста должны завершиться неудачно. Поскольку эти исполнения независимы, это происходит с вероятностью не более 1/2 ᴹ .
Например, если мы зададим M = 10, то вероятность неудачи меньше 0,001, или другими словами вероятность успеха не менее 99,9%, что совсем неплохо! Что касается времени работы, то в него будет включено M , а общее время работы O( М Н ²). Поскольку M является константой, это по-прежнему равно O( N ²) и намного быстрее, чем современные лучшие алгоритмы умножения матриц. Мы сделали!
Поскольку M является константой, это по-прежнему равно O( N ²) и намного быстрее, чем современные лучшие алгоритмы умножения матриц. Мы сделали!
- Тридцать три миниатюры: математические и алгоритмические приложения линейной алгебры», Иржи Матоусек. Издатель: Американское математическое общество
- https://en.wikipedia.org/wiki/Matrix_multiplication_algorithm
Проверить, является ли двумерный массив NumPy или матрица симметричным — thisPointer
В этой статье мы узнаем, как проверить симметричность двумерного массива или матрицы NumPy.
Учитывая массив NumPy, нам нужно проверить, является ли он симметричным. Это означает, что если данный массив и его транспонирование равны, то мы можем сказать, что данный массив симметричен. Транспонирование матрицы вычисляется путем замены ее строк на столбцы или столбцов на строки.
Например: Образец матрицы или двумерного массива NumPy выглядит следующим образом:
a = [[ 1, 3, 5 ]
[ 3, 2, 4 ]
[ 5, 4, 1 ]] Транспонировать эту матрицу,
b = [[ 1, 3, 5 ]
[ 3, 2, 4 ]
[ 5, 4, 1 ]] И 2D-массив, и его транспонирование равны, поэтому мы можем сказать, что данная матрица является симметричной матрицей.
Объявления
Существует несколько способов проверить, является ли двумерный массив или матрица NumPy симметричным или нет. Давайте обсудим все методы один за другим с правильным подходом и примером рабочего кода.
1.) Использование оператора ==, методов all() и transpose()
Массив Numpy имеет метод transpose(). Метод transpose() используется для транспонирования массива. Затем данный массив и транспонирование проверяются на равенство.
Два пустых массива при сравнении с использованием оператора == возвращают массив логических значений с такой же длиной, что и сравниваемые массивы. Логический массив представляет, в каких позициях элементы в обоих массивах равны. Значение True означает, что элементы в обоих массивах равны в этой конкретной позиции, а значение False означает, что соответствующие элементы в обоих массивах не равны.
Метод all() используется для проверки того, что все элементы, присутствующие в массиве, равны True. Метод all() принимает массив в качестве входного параметра и возвращает логическое значение.
Метод all() принимает массив в качестве входного параметра и возвращает логическое значение.
Синтаксис all()
numpy.all(массив, ось = Нет)
Параметры:
array = Массив, который будет передан в функцию.
ось = значение по умолчанию, ось = нет
Возвращает:
Возвращает логическое значение.
Синтаксис транспонирования()
numpy.transpose(a, axes=None)
Параметры:
array = Массив, который будет передан в функцию.
ось = значение по умолчанию, ось = нет
Возвращает:
Возвращает транспонирование массива.
Подход
- Импортировать библиотеку numpy и создать массив numpy
- Используя метод transpose(), получить транспонирование данного массива
- Проверить, имеют ли оба массива одинаковую форму, используя метод shape()
- Сравнить массивы используя оператор ==, и он возвращает логический массив
- Применить метод all() к логическому массиву, если он возвращает true, тогда напечатайте Массив симметричен, иначе напечатайте массив несимметрично.

Исходный код
импортировать numpy как np
# создание пустого массива
а = np.массив ([[ 1, 3, 5],
[ 3, 2, 4 ],
[ 5, 4, 1 ]])
# Транспонировать заданный массив
б = а.транспонировать()
# проверяем, имеют ли оба массива одинаковый размер
если a.shape == b.shape:
# сравнение массивов с помощью метода == и all()
если (а == б).все():
print("Массив или матрица симметричны")
еще:
print("Массив/матрица не симметричны")
еще:
print("Массив/матрица не симметричны")
ВЫВОД:
Массив или матрица симметричны
2.
 ) Использование метода array_equal() и transpose()
) Использование метода array_equal() и transpose() Метод transpose() используется для транспонирования массива. Затем данный массив и транспонирование
проверяются на равенство. Метод array_equal() является встроенным методом numpy, он принимает два массива в качестве аргументов и возвращает логическое значение
, True означает, что массивы равны, а false означает, что массивы не равны.
Синтаксис array_equal()
numpy.array_equal(array_1, array_2)
Синтаксис transpose()
numpy.transpose(a, axes=None)
Параметры:
array = Массив, который будет передан в функцию. ось = значение по умолчанию, ось = нет
Возвращает:
Возвращает транспонирование массива.
ось = значение по умолчанию, ось = нет
Возвращает:
Возвращает транспонирование массива.
Подход
- импортировать библиотеку numpy и создать массив numpy
- Использование метода transpose() получить транспонирование данного массива
- Проверить, имеют ли оба массива одинаковую форму, используя метод shape()
- Если форма двух массивов не одинакова, то вывести массивы не равны, иначе перейти к следующему шагу
- Передать два массива методу array_equal(), если он возвращает значение true, затем выведите, что массив симметричен, иначе выведите, что массив не симметричен.
Исходный код
импортировать numpy как np
# создание пустого массива
а = np.массив ([[ 1, 3, 5],
[ 3, 2, 4 ],
[ 5, 4, 1 ]])
# Транспонировать заданный массив
б = а. транспонировать()
# Сравнение обоих массивов с помощью метода array_equal()
если np.array_equal (а, б):
print("Массив симметричен")
еще:
print("Массив несимметричен")
транспонировать()
# Сравнение обоих массивов с помощью метода array_equal()
если np.array_equal (а, б):
print("Массив симметричен")
еще:
print("Массив несимметричен")
ВЫВОД:
Массив симметричен
3.) Использование функции transpose() и сглаживания массивов и сравнения элементов один за другим
Метод transpose() используется для транспонирования массива. Затем данный массив и транспонирование
проверяются на равенство. Метод flatten() — это встроенный метод numpy, он принимает массив в качестве аргументов и возвращает сглаженный массив, то есть массив
1d. И массив, и транспонирование массива сглаживаются. Теперь эти сглаженные массивы можно легко повторять и сравнивать.
Синтаксис flatten()
ndarray.flatten()
Подход
- импортировать библиотеку numpy и создать массив numpy
- Использование метода transpose() получить транспонирование данного массива одинаковая форма с использованием метода shape()
- если форма двух массивов не равна, то выведите неравные массивы, иначе перейдите к следующему шагу
- Инициализируйте как логический флаг и установите для него значение False.
- Свести оба массива с помощью метода flatten()
- Итеративно сравнить каждый элемент обоих массивов, используя цикл for
- , если какой-либо из элементов не равен, тогда установите флаг not_equal в True и прервите цикл Массив симметричен, иначе напечатайте Массив не симметричен.
Исходный код
импортировать numpy как np # создание пустого массива а = np.массив ([[ 1, 3, 5], [ 3, 2, 4 ], [ 5, 4, 1 ]]) # Транспонировать заданный массив б = а.транспонировать() #инициализировать логический флаг не_равно = Ложь если a.shape == b.shape: # сглаживание обоих массивов с помощью метода flatten() а = а.flatten () b = b.flatten () # перебор элементов из обоих массивов одновременно с помощью zip() для i, j в zip (a, b): если я != j: # если какой-либо элемент не равен, установить флаг not_equal в true и сломать не_равно = Истина ломать если не не равно: print("Массив симметричен") еще: print("Массив НЕ симметричен") еще: print("Массив НЕ симметричен")
ВЫВОД:
Массив симметричен
4.) Использование методов transpose() и ravel()
Этот подход почти аналогичен предыдущему, но единственное отличие состоит в том, что мы используем метод ravel() для выравнивания массив и остальные остаются прежними. Метод ravel() — это встроенный метод numpy, он принимает массив в качестве аргументов и возвращает сглаженный массив, то есть массив 1d
Метод ravel() — это встроенный метод numpy, он принимает массив в качестве аргументов и возвращает сглаженный массив, то есть массив 1d
. Теперь эти сглаженные массивы можно легко повторять и сравнивать.
Синтаксис ravel()
ndarray.ravel()
Approach
- импортировать библиотеку numpy и создать массив numpy
- Использование метода transpose() получить транспонирование данного массива
- Проверить, имеют ли оба массива одинаковую форму, используя метод shape()
- если форма двух массивов не одинакова, тогда выведите неравные массивы, в противном случае перейдите к следующему шагу
- Инициализируйте как логический флаг и установите для него значение False.
- Свести оба массива с помощью метода ravel()
- Итеративно сравнить каждый элемент обоих массивов, используя цикл for
- Если какой-либо из элементов не равен, установите флаг not_equal в True и прервите цикл
- Вне цикла проверьте флаг not_equal и, если он равен true, напечатайте Массив симметричен, иначе напечатайте Массив не симметричен.

Исходный код
импортировать numpy как np
# создание пустого массива
а = np.массив ([[ 1, 3, 5],
[ 3, 2, 4 ],
[ 5, 4, 1 ]])
# Транспонировать заданный массив
б = а.транспонировать()
#инициализировать логический флаг
не_равно = Ложь
# проверяем, имеют ли оба массива одинаковый размер
если a.shape == b.shape:
# выравниваем оба массива с помощью метода ravel()
а = а.ravel()
b = b.ravel()
# перебор элементов из обоих массивов одновременно с помощью zip()
для i, j в zip (a, b):
если я != j:
# если какой-либо элемент не равен, установить флаг not_equal в true и сломать
не_равно = Истина
ломать
если не не равно:
print("Массив симметричен")
еще:
print("Массив НЕ симметричен")
еще:
print("Массив НЕ симметричен") ВЫВОД:
Массив симметричен
5.
 ) Использование array_equiv() для проверки симметричности матрицы
) Использование array_equiv() для проверки симметричности матрицы Используйте метод transpose() для получения транспонирования заданного метода, затем проверьте оба массивы равны. Метод array_equiv() является встроенным методом numpy, он принимает два массива в качестве аргументов и возвращает логическое значение, True означает, что массивы равны, а False означает, что массивы не равны.
Синтаксис array_equiv()
numpy.array_equiv(array_1, array_2)
Подход
- импортировать библиотеку numpy и создать массив numpy
- Использование метода transpose() получить транспонирование обоих массивов Проверить, равны ли массивы 0 900 форма с использованием метода shape()
- если форма двух массивов не равна, тогда выведите массивы, не равные иначе перейдите к следующему шагу
- передайте два массива в метод array_equiv(), если он возвращает true print Массив симметричен иначе print The массив не является симметричным.

Исходный код
импортировать numpy как np
# создание пустого массива
а = np.массив ([[ 1, 3, 5],
[ 3, 2, 4 ],
[ 5, 4, 1 ]])
# Транспонировать заданный массив
б = а.транспонировать()
если np.array_equiv (а, б):
print("Массив симметричен")
еще:
print("Массив НЕ симметричен") ВЫВОД:
Массив симметричен
6.) Использование метода allclose()
Используйте метод transpose(), чтобы получить транспонирование данного метода, затем проверьте, равны ли оба массива. Метод allclose() является встроенным методом numpy, он принимает два массива в качестве аргументов и atol (абсолютный допуск), rtol (относительный допуск) в качестве необязательных аргументов, которые используются для указания допуска, то есть значения, на которое могут отличаться значения. Он возвращает логическое значение, True означает, что элементы в массивах очень близки друг к другу (т.е. равны), а False означает, что массивы не равны.
Он возвращает логическое значение, True означает, что элементы в массивах очень близки друг к другу (т.е. равны), а False означает, что массивы не равны.
ПРИМЕЧАНИЕ:
В случае проверки равенства двух массивов устанавливаем atol=0 и rtol=0. Так что allclose() вернет true только тогда, когда все элементы обоих массивов точно равны.
Синтаксис allclose()
np.allclose(a, b,rtol=0, atol=0)
Подход
- импортировать библиотеку numpy и создать массив numpy
- Используя метод transpose(), получить транспонирование заданный массив
- Проверить, имеют ли оба массива одинаковую форму, используя метод shape()
- если форма двух массивов не одинакова, то вывести массивы не равны иначе перейти к следующему шагу
- передать два массива в метод allclose(), если он возвращает true print Массив симметричен, иначе print Массив не симметричен.

Исходный код
импортировать numpy как np
# создание пустого массива
а = np.массив ([[ 1, 3, 5],
[ 3, 2, 4 ],
[ 5, 4, 1 ]])
# Транспонировать заданный массив
б = а.транспонировать()
если np.allclose(a, b,rtol=0, atol=0):
print("Массив симметричен")
еще:
print("Массив НЕ симметричен") ВЫВОД:
Массив симметричен
Резюме
Мы узнали, как проверить, являются ли два массива NumPy симметричными или нет.
Учебные пособия по Pandas — изучение анализа данных с помощью Python
-
Учебное пособие по
Pandas, часть №1 — Введение в анализ данных с помощью Python
-
Pandas Tutorial Часть №2 — Основы серии Pandas
-
Учебное пособие
Pandas, часть № 3.
 Получение и установка значений серии г.
Получение и установка значений серии г.
-
Pandas Tutorial Part #4 — Атрибуты и методы Pandas Series
-
Учебное пособие по Pandas, часть № 5. Добавление или удаление элементов серии Pandas
-
Учебное пособие
Pandas, часть № 6 — Введение в DataFrame
-
Учебное пособие по Pandas, часть № 7 — DataFrame.loc [] — выбор строк/столбцов путем индексирования
-
Учебное пособие по Pandas, часть № 8 — DataFrame.iloc [] — выбор строк/столбцов по именам меток
-
Учебное пособие Pandas, часть № 9 — фильтрация строк DataFrame
-
Учебное пособие по Pandas, часть № 10. Добавление и удаление строк и столбцов DataFrame
-
Учебное пособие по Pandas, часть № 11 — атрибуты и методы DataFrame
-
Учебное пособие по Pandas, часть № 12. Обработка отсутствующих данных или значений NaN
-
Pandas Tutorial, часть № 13 — перебор строк и столбцов DataFrame
-
Pandas Tutorial Part #14 — Сортировка DataFrame по строкам или столбцам
г. Проверка матрицы: Тест монитора онлайн — monteon
Проверка матрицы: Тест монитора онлайн — monteon
