Прямоугольник фибоначчи: Прямоугольники Фибоначчи — Числа Фибоначчи

Правило Золотого сечения: руководство для дизайнера

Правило Золотого сечения это чудесная штука из математической теории, которая поможет придать вашему дизайну ощущение пропорциональности и стать приятным глазу. Здесь мы объясняем как его использовать.

Существует общее математическое соотношение, встречающееся в природе, и которое может быть использовано для создания приятной естественной композиции в ваших дизайнерских работах. Мы называем его — правило Золотого сечения, хотя оно также известно как — Золотая середина, Золотое соотношение или греческая буква «Фи».

 

Действуя на основе последовательности Фибоначчи (которую вы, вероятно, помните из школьных уроков математики, или романа Дэна Брауна «Код да Винчи»), Золотое сечение описывает отношения между двумя пропорциями.

 

 

 

 

Числа Фибоначчи, как и многие элементы, встречающиеся в природе, следуют соотношению 1:1.61 — это то, что мы называем Золотым соотношением, и то, как оно формирует общую закономерность в природе, так что оно воспринимается приятным для глаз и когда мы используем это же соотношение в наших дизайнерских работах.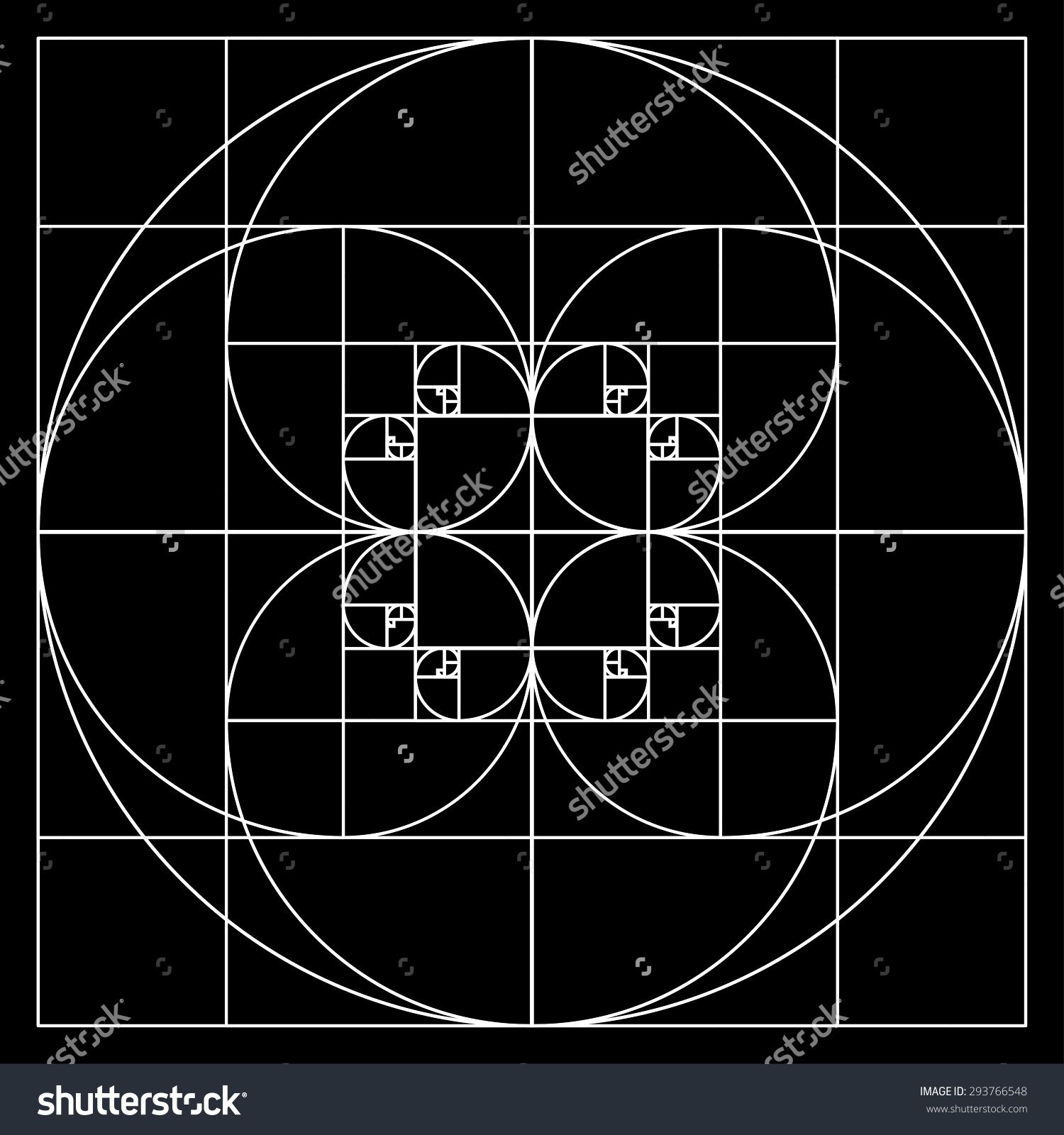

 

 Золотое сечение — это соотношение двух чисел из последовательности Фибоначчи…

 

 …а построение этих соотношений в масштабе дает нам спираль, которую можно увидеть вокруг нас повсюду в природе

 

 

 

 

Считается, что Золотое соотношение используется в искусстве и дизайне уже в течение, по крайней мере, 4000 лет, но этот период может быть даже больше: некоторые люди утверждают, что древние египтяне использовали принцип Золотого сечения для построения пирамид. В наше время Золотое соотношение можно наблюдать в музыке, искусстве, дизайне и во всем вокруг нас.

 

Примеры Золотого сечения

Использование Золотого соотношения хорошо задокументировано в области искусства и дизайна на протяжении всей истории, и его можно увидеть во всем — от архитектуры до великих шедевров искусства. Применяя аналогичную методику, вы можете привнести ту же дизайнерскую чувственность в вашу собственную работу.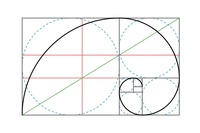

Вот лишь несколько примеров, чтобы вдохновить вас:

 

Парфенон

Древнегреческая архитектура использовала Золотое соотношение, чтобы определить приятные размерные соотношения между шириной здания и его высотой, размерами портика и даже положением колонн, поддерживающих строение. Конечный результат представляет собой здание, которое ощущается полностью пропорциональным. Нео-классические движения в архитектуре также повторили эти принципы Золотого сечения.

 

 

 

 

«Тайная вечеря»

Леонардо да Винчи, как и многие другие художники на протяжении веков, широко использовал Золотое соотношение для создания приятных композиций. В «Тайной вечери» фигуры расположены в нижних двух третях (большая из двух частей Золотого соотношения), а положение Иисуса прекрасно расположено, организуя золотые прямоугольники по холсту.

 

Золотое сечение в природе

Золотое соотношение можно увидеть во всем вокруг нас в природе: от ракушек до цветов

 

Есть множество примеров Золотого сечения в природе, где вы можете наблюдать это соотношение повсюду вокруг вас! Цветы, ракушки, ананасы, и даже соты — все они демонстрируют в своем составе одно и то же соотношение принципа Золотого сечения.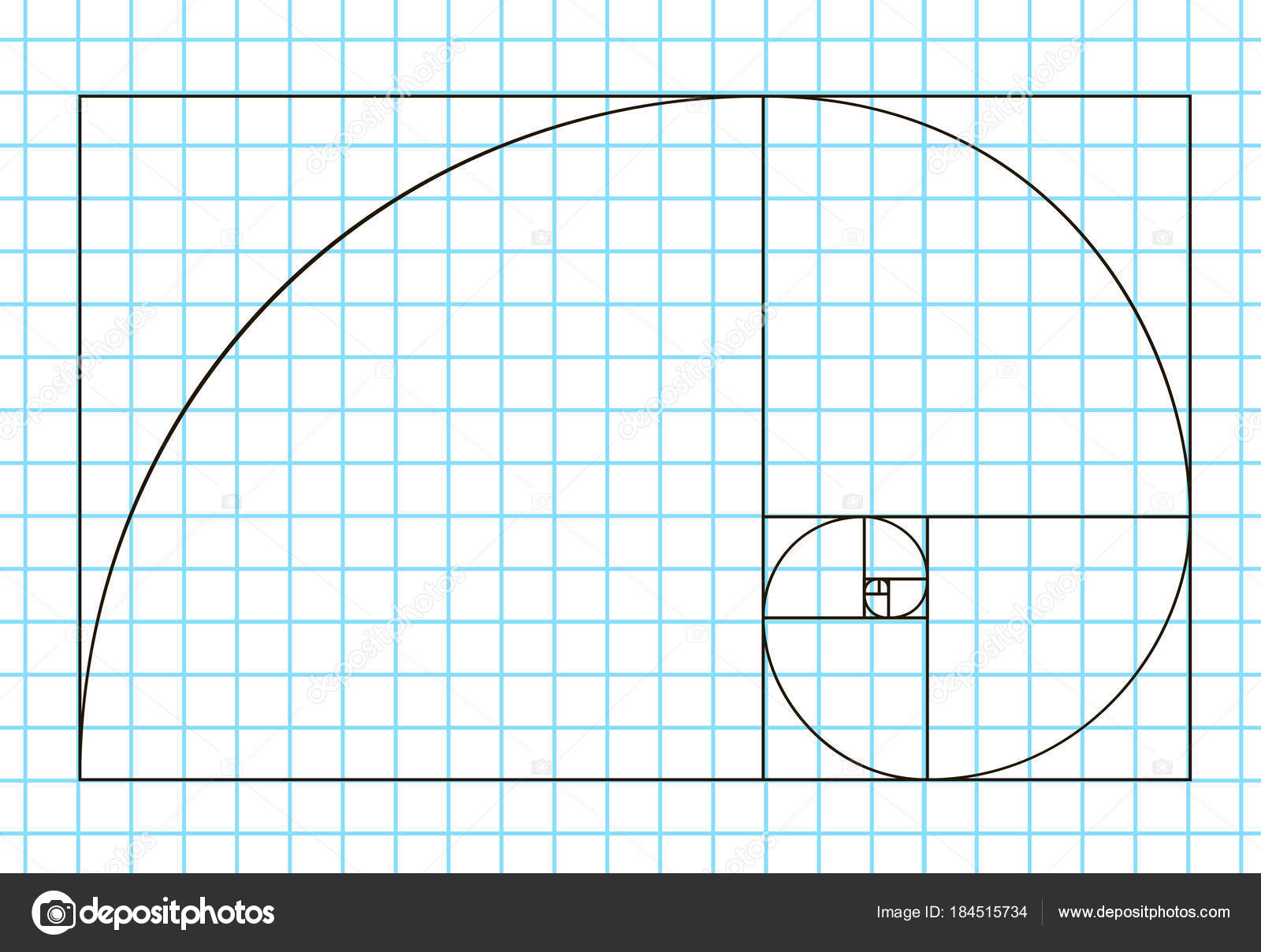 Таким образом, использование Золотого соотношения в ваших дизайнерских работах не только уместно, но и обусловлено нашим повседневным окружением.

 

Как построить прямоугольник Золотого сечения

Создание Золотого прямоугольника довольно просто, и начинается с основного квадрата. Выполните следующие шаги для создания собственного Золотого соотношения:

 

Шаг 01: Нарисуйте квадрат. Это позволит сформировать длину «короткой стороны» прямоугольника.

 

Шаг 02: Разделите квадрат пополам вертикальной линией, дающей вам два прямоугольника.

 

Шаг 03: В одном прямоугольнике нарисуйте линию из одного угла в противоположный угол.

 

Шаг 04: Поверните эту линию так, чтобы она легла горизонтально рядом с первым прямоугольником.

 

Шаг 05: Достройте прямоугольник с помощью новой горизонтальной линии, используя имеющийся прямоугольник в качестве направляющего.

 

Применение Золотого сечения в вашей дизайнерской работе

Применение Золотого сечения проще, чем вы думаете! Есть несколько быстрых приемов, которые можно использовать, чтобы оценить при его помощи свои макеты, или вы можете затеять немного больше, и полностью изменить концепцию дизайна!

 

Быстрый способ

Если вы когда-либо сталкивались Правилом третей, то вы знакомы с идеей, что, разделив площадь на равные трети как вертикально, так и горизонтально, полученные пересечения линий обеспечивают естественную фокусную точку всей площади.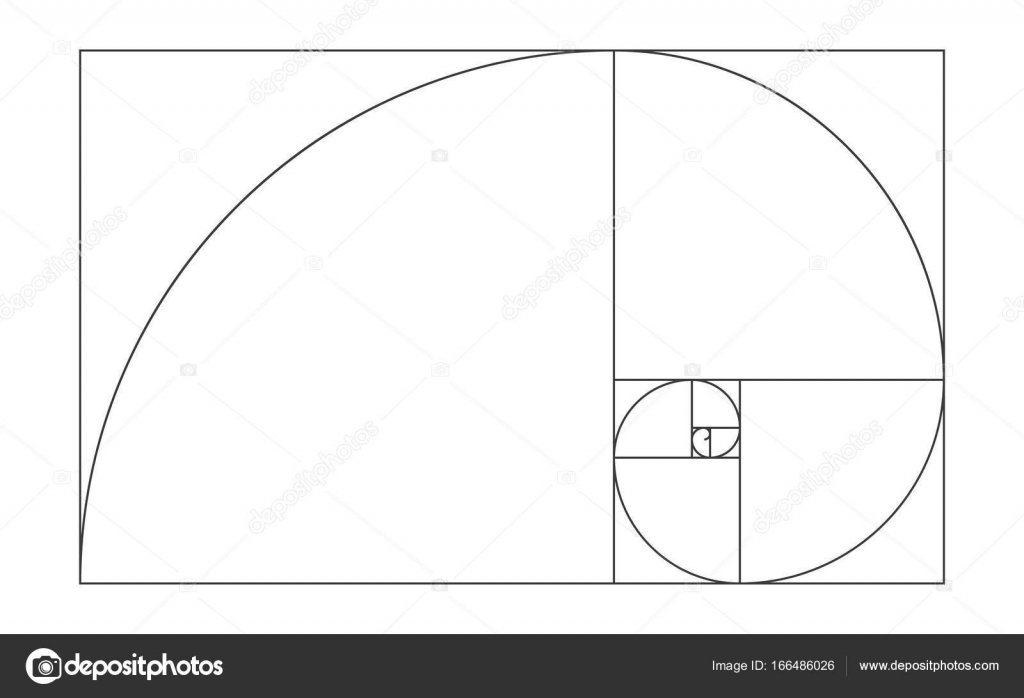

 

Фотографов учили позиционировать свой ключевой объект на одной из этих пересекающихся линий для достижения приятной композиции, и тот же принцип может быть использован в ваших макетах страниц, веб-макетах, а также стендовых конструкциях.

 

Правило третей может быть применено к любой форме, и если вы примените его в прямоугольнике с пропорциями примерно 1:1.6, то Вы получите что-то очень близкое к Золотому прямоугольнику, который делает композицию еще более приятной для глаз.

 

Полная реализация

Если вы хотите в полной мере реализовать Золотое соотношение в вашем проекте, вы можете это легко сделать, обеспечивая, чтобы отношение между вашей областью контента и боковой панелью (в дизайне сайта, например) придерживалось соотношения 1:1.61.

 

Нормальным будет округлить его в большую, или в меньшую сторону на точку или две, чтобы сделать эти числа соответствующими пикселям или точкам. Так что если у вас есть область контента размером 640px, то боковая панель в 400px будет достаточно хорошо соответствовать Золотому соотношению, хотя на самом деле это соотношение — 1:1,6.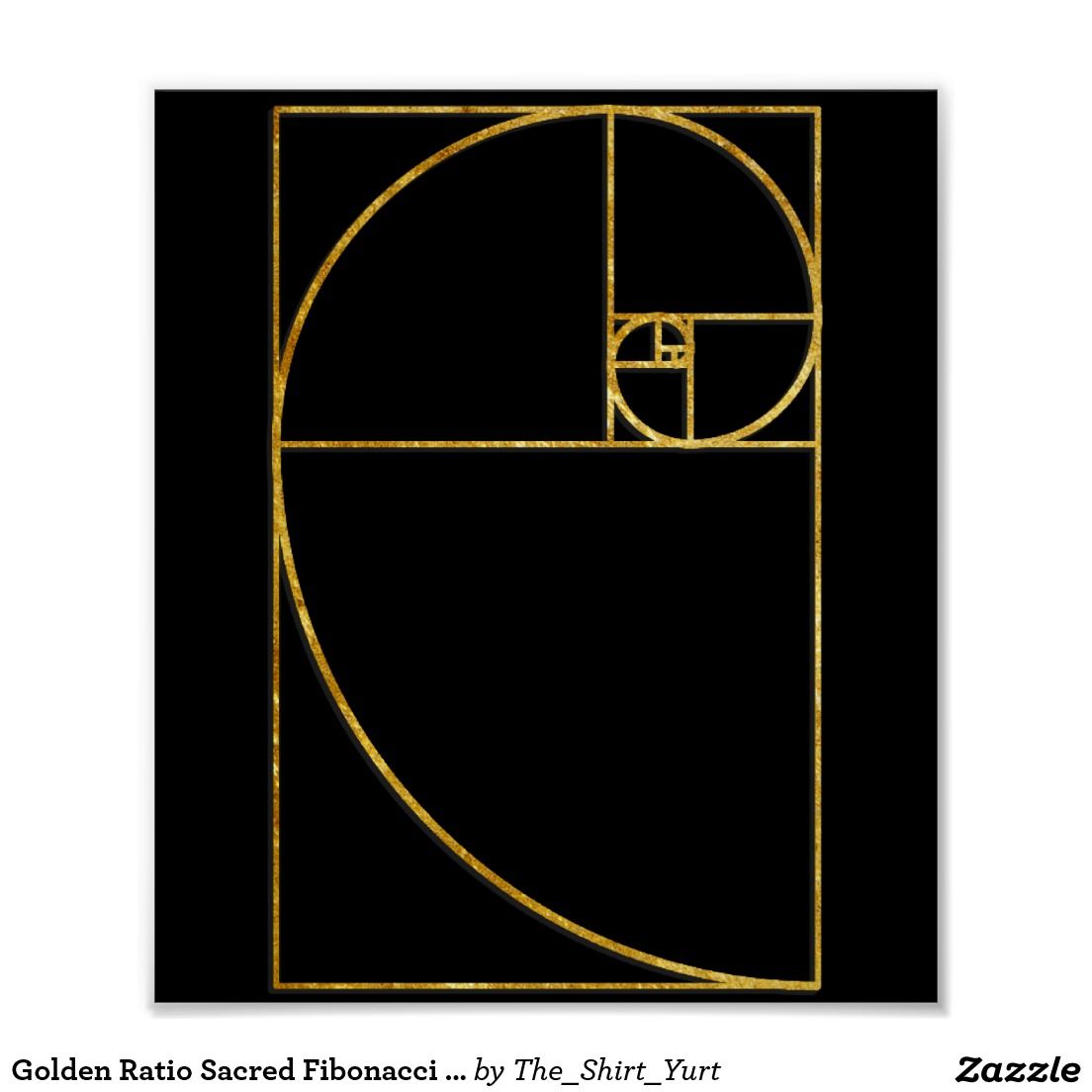

Применение Золотого сечения на макете веб-страницы обеспечивает естественный, приятный для глаз результат.

 

Конечно, вы можете также разделить контент и боковую область с использованием тех же пропорций, а соотношения между заголовком веб-страницы, областью контента, футером и навигацией также могут быть разработаны с использованием тех же основ применения Золотого сечения.

 

Вы увидели прекрасный пример Золотого сечения в применении? Дайте нам знать в комментариях ниже!

Что такое «золотое сечение»?. На протяжении веков «золотое сечение»… | by Сергей Базанов | Paradox Review

«Золотое сечение», называемое также «золотая пропорция» или «золотое соотношение», было обнаружено во многих самых знаменитых творениях человечества — от древнегреческого Парфенона до творений Сальвадора Дали. Возможно, вы уже читали на эту тему статью «Нереализованное влияние золотого сечения».

Не важно, считаете ли вы, что эта божественная пропорция является поистине знамением красоты или просто предвзятым выбором, но, без сомнения, это одно из самых интригующих чисел в мире. Поэтому, сейчас мы поговорим о математической основе «золотого сечения».

Впервые о «золотом сечении» упоминает древнегреческий математик Евклид около 300 лет до нашей эры. В шестой книге своего трактата «Начала» Евклид дает определение «золотого сечения». Он поручает нам взять отрезок линии и разделить его на два меньших сегмента так, что отношение всей линии (a + b) к отрезку a будет таким же, как отношение отрезка a к сегменту b:

Что эквивалентно пропорции:

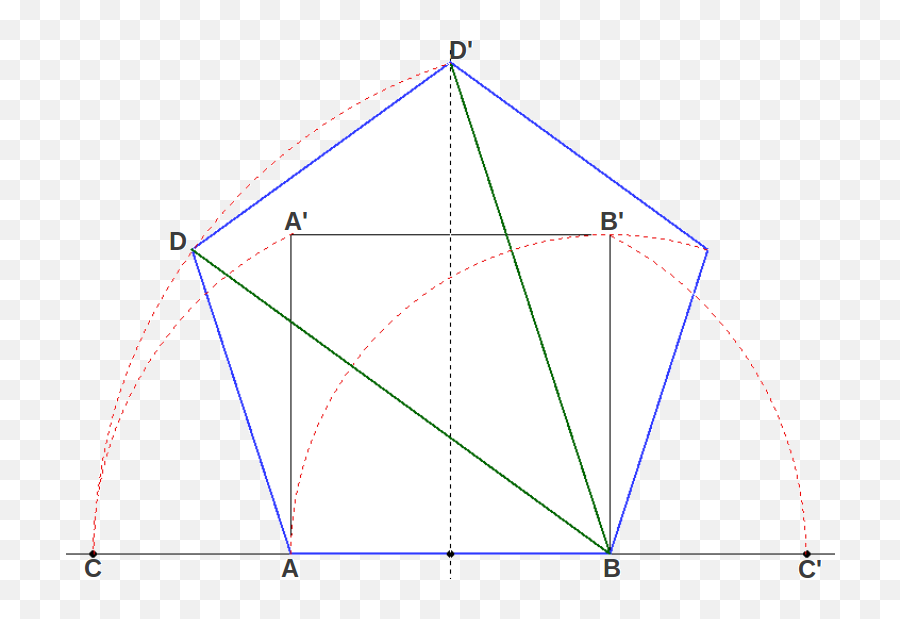
Евклид использовал «золотое сечение» для построения правильного пятиугольника. Отношение диагонали правильного пятиугольника к его стороне равно золотому сечению. Правильный пятиугольник (пентагон) еще называют «золотой пятиугольник».

«Золотое сечение» часто представляют как «Золотой прямоугольник» — прямоугольник с отношением длин сторон примерно 1,618:1.

Этот прямоугольник обладает тем свойством, что если от него отрезать квадрат, то снова получится золотой прямоугольник меньшего размера и так до бесконечности.

Золотой прямоугольник.

На самом деле, соотношение сторон «золотого прямоугольника» — это иррациональное значение 1,618034…, т.е. бесконечная десятичная дробь, не имеющая периода.

Это число и есть пропорция «золотого сечения», оно обозначается греческой буквой Фи в честь древнегреческого скульптора и архитектора Фидия, мастера, воплотившего его в своих работах.

Чтобы найти значение 1,618034…, мы должны решить пропорцию, показанную выше. Для простоты предположим, что b = 1 и a = x и найдем решение для x.

a = x, b = 1

Шаг 1. Сделаем перекрестное умножение:

Шаг 2. Приведем уравнение к 0:

Шаг 3. Решим квадратное уравнение:

Поскольку мы работаем с длинами, нам нужно только положительное решение:

Решение найдено! «Золотое сечение» выражается, как дробь.
Для проверки подставим a = 1.618 и b = 1, чтобы убедиться, что наша пропорция верная:

Обратите внимание, как интересно: мы можем написать «золотое соотношение» при помощи самого себя. Это потрясающе!

Что эквивалентно:

Пойдем дальше… Заменим φ = 1 + 1 / φ для φ в знаменателе:

И еще дальше!

Мы могли бы продолжать делать это бесконечно. Оказывается, «Золотое сечение» может быть записано как бесконечная цепная дробь.

Мы можем использовать непрерывную дробь, чтобы раскрыть связь «золотого сечения» с последовательностью Фибоначчи.

Для начала мы немного изменим нашу бесконечную дробь — добавим индексы, чтобы показать, как следующее значение φ(n+1) может быть получено из предыдущего значения φ(n).

Так как это бесконечная цепная дробь, с ростом n искомое значение приближается к истинному значению φ.

Теперь допустим, что φ(0) = 1 и найдем φ(1).

Продолжим вычислять следующеезначение — φ(2)

И далее… φ(3), φ(4)…

Посмотрите! Это же последовательность Фибоначчи! Каждое приближение — это отношение двух соседних чисел Фибоначчи.

По мере продвижения к каждому новому последовательному вычислению мы обнаруживаем, что наше искомое значение все ближе и ближе приближается к его истинному «Золотому сечению».

На девятом члене последовательности Фибоначчи мы уже получаем значения «золотого сечения», с тремя верными цифрами после запятой.

В самом деле, limit F(n+1)/F(n) при n→∞ (где F(n) и F(n+1) представляют n и n+1 числа в последовательности Фибоначчи) сходится к φ.

Если визуализировать этот процесс, то мы увидим, как последовательность Фибоначчи создает прямоугольники всё ближе и ближе к «Золотому прямоугольнику».

Прямоугольник Фибоначчи.

Хотя в мире дизайна продолжаются споры о том, является ли «золотое сечение» оптимальной пропорцией или нет, можно с уверенностью сказать, что оно математически совершенно и не перестает нас удивлять.

Фибоначчи повсюду!. Числа Фибоначчи названы в честь… | by Сергей Базанов | Paradox Review

Числа Фибоначчи и золотое сечение

Как известно, последовательность Фибоначчи начинается с 1 и 1, после чего каждое новое число является результатом сложения двух предыдущих чисел:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …

Если разделить два последовательных числа в этом ряду, например 144/89, в конечном итоге получится число 1,618, которое называется «Золотое число» или «Золотое сечение».

Последовательное приближение соотношения двух соседних чисел ряда Фибоначчи к Золотому сечению.

Пропорция золотого сечения считается эстетически приятной и из-за этого многие художники и архитекторы, в том числе Сальвадор Дали и Ле Корбюзье использовали её в своих работах.

Последовательность Фибоначчи и Золотое сечение тесно взаимосвязаны. Отношение последовательных чисел Фибоначчи сходится и приближается к золотому сечению, а выражение замкнутой формулы для последовательности Фибоначчи включает Золотое сечение.

Золотой прямоугольник (розовый) с длинной стороной a и короткой стороной b, и находящийся рядом с ним квадрат со стороной длиной a, создадут подобный золотой прямоугольник с длинной стороной а + b и короткой стороной a. Это изобажение иллюстрирует взаимосвязь отношений (a+b)/a = a/b.

Спираль Фибоначчи или золотая спираль — это последовательность соединенных четвертей окружностей, вписанных внутри массивов квадратов со сторонами равными числам Фибоначчи. Квадраты идеально подходят друг к другу из-за природы последовательности Фибоначчи, в которой следующее число равно сумме двух перед ним (см.предыдущий рисунок). Любые два последовательных числа Фибоначчи имеют отношение, очень близкое к золотому сечению, которое составляет примерно 1.618034. Чем больше пара чисел Фибоначчи, тем ближе это приближение. Спираль и результирующий прямоугольник называются золотым прямоугольником.

Золотое сечение в дизайне

Говорят, что “божественная пропорция” заложена в природе, и во многих вещах вокруг нас. Вы можете найти ее в цветах, ульях, морских раковинах, и даже нашем теле.

Эта божественная пропорция, также известная как золотое сечение, божественное сечение, или золотая пропорция может быть применена к различным видам искусства и обучения. Ученые утверждают, что чем ближе объект к золотому сечению, тем лучше человеческий мозг воспринимает его.

С тех пор как это соотношение было открыто, многие художники и архитекторы применяли его в своих работах.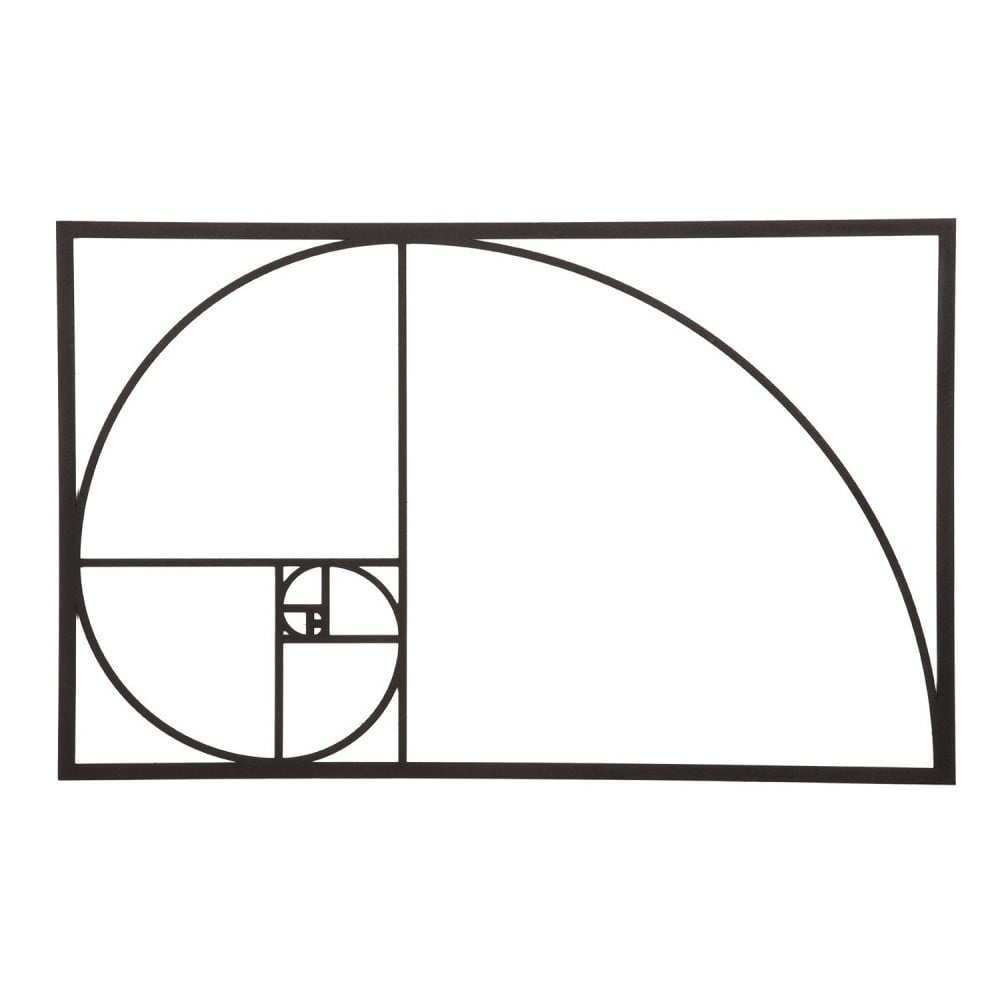 Вы можете найти золотое сечение в нескольких шедеврах эпохи Возрождения, архитектуре, живописи, и многом другом. В результате – красивый и эстетически приятный шедевр.

Немногие знают, в чем заключается тайна золотого сечения, что так радует наши глаза. Многие полагают, что то, что она появляется везде и является “универсальной” пропорцией, заставляет нас принять ее как что-то логическое, гармоничное и органичное. Другими словами, оно просто “чувствует” то, что нам нужно.

Итак, что такое золотое сечение?

Золотое сечение, также известное как “фи” по-гречески, это математическая константа. Оно может быть выражено уравнением a/b=a+b/a=1,618033987, где a больше, чем b. Это также можно объяснить последовательностью Фибоначчи, другой божественной пропорцией. Последовательность Фибоначчи начинается с 1 (некоторые говорят с 0) и добавляет к нему предыдущее число, чтобы получить последующее (т.е. 1, 1, 2, 3, 5, 8, 13, 21 …)

Если вы попытаетесь найти частное от деления двух последующих чисел Фибоначчи (т.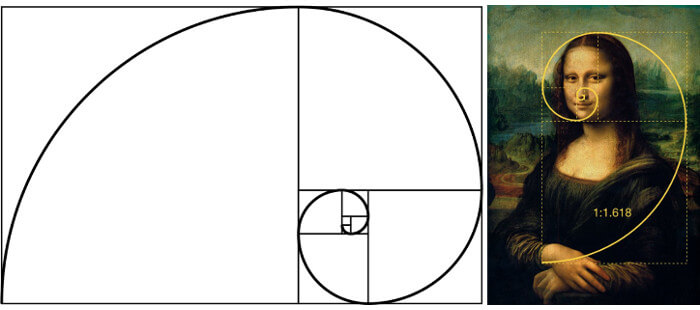 е. 8/5 или 5/3), результат очень близок к золотому сечению 1,6 или φ (фи).

Золотая спираль создается с помощью золотого прямоугольника. Если у вас есть прямоугольник из квадратов 1, 1, 2, 3, 5 и 8 соответственно, как показано на рисунке выше, вы можете приступить к строительству золотого прямоугольника. Используя сторону квадрата, как радиус, вы создаете дугу, которая касается точек квадрата по диагонали. Повторите эту процедуру с каждым квадратом в золотом треугольнике, и в конечном итоге вы получите золотую спираль.

Где мы можем увидеть его в природе

Золотое сечение и последовательность Фибоначчи можно найти в лепестках цветов. У большинства цветков количество лепестков сводится к двум, трем, пяти или больше, что походит на золотое сечение. Например, у лилий 3 лепестка, у лютиков 5, у цветков цикория 21, а у ромашек 34. Вероятно, семена цветков также следуют золотому сечению. Например, семена подсолнечника прорастают из центра и растут к внешней стороне, заполняя головку семени.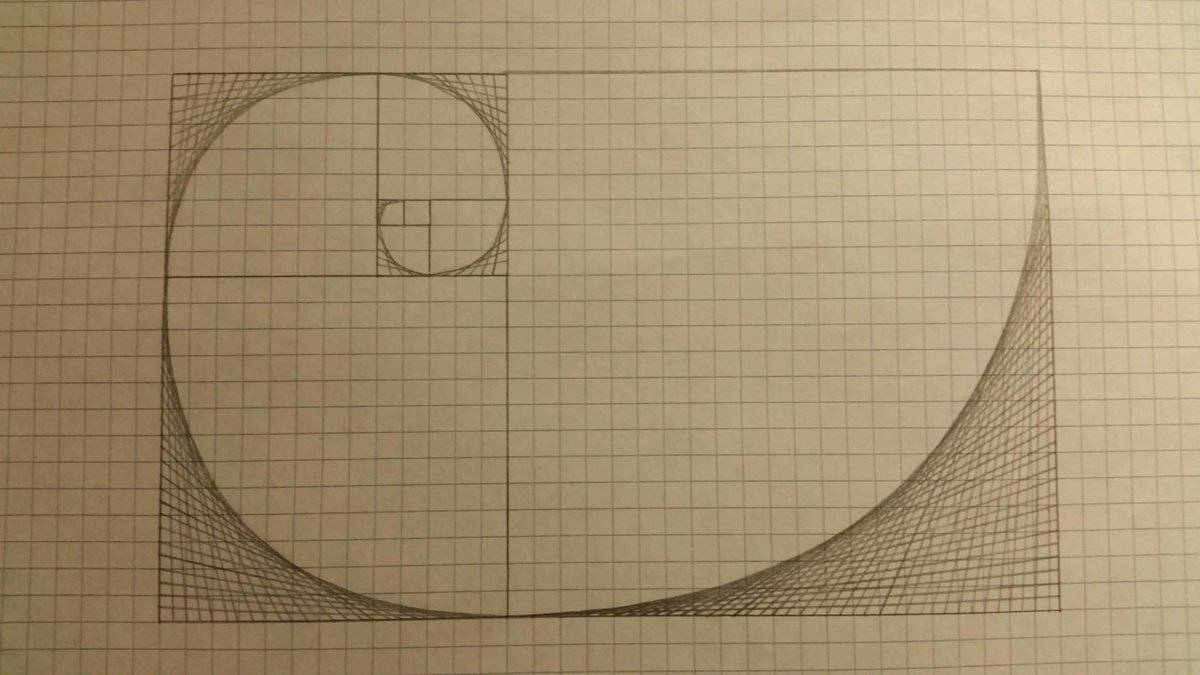 Обычно они спиралевидные и имеют сходство с золотой спиралью. Более того, количество семян, как правило, сводится к числам Фибоначчи.

Руки и пальцы также являются примером золотого сечения. Посмотрите ближе! Основание ладони и кончик пальца разделен частями (костьми). Соотношение одной части в сравнении к другой всегда 1,618! Даже предплечья с руками находятся в таком же соотношении. И пальцы, и лицо, и можно продолжать список…

Применение в искусстве и архитектуре

Парфенон в Греции, как утверждается, был построен с использованием золотых пропорций. Считается, что размерные соотношения высоты, ширины, колонн, расстояния между столбами, и даже размер портика близки к золотому сечению. Это возможно потому, что здание выглядит пропорционально идеально, и оно было таким с древних времен.

Леонардо Да Винчи был также поклонником золотого сечения (и многих других любопытных предметов, собственно говоря!). Дивная красота Мона Лизы может быть связана с тем, что ее лицо и тело представляют собой золотое сечение, как и реальные человеческие лица в жизни.

Кроме того, цифры в картине “Тайная вечеря” Леонардо Да Винчи расположены в порядке, который используется в золотом сечении. Если начертить золотые прямоугольники на холсте, Иисус окажется как раз в центральной доле.

Применение в дизайне логотипов

Неудивительно, что вы также можете найти использование золотого сечения во многих современных проектах, в частности, дизайне. Сейчас давайте сосредоточимся на том, как это может быть использовано в дизайне логотипа. Во-первых, рассмотрим некоторые из самых известных в мире брендов, которые использовали золотое сечение для совершенствования своих логотипов.

Видимо, Apple использовал круги из чисел Фибоначчи, соединив и обрезав формы для получения логотипа Apple. Неизвестно, было ли это сделано намеренно или нет. Тем не менее, в результате получился идеальный и визуально эстетичный дизайн логотипа.

Логотип Toyota использует соотношение a и b, формируя сетку, в которой образуются три кольца. Обратите внимание, как этот логотип использует прямоугольники вместо кругов для создания золотого сечения.

Логотип Pepsi создан двумя пересекающимися кругами, один больше другого. Как показано на рисунке выше, больший круг пропорционален в соотношении к меньшему – вы уже догадались! Их последний нерельефный логотип – простой, эффектный и красивый!

Кроме Toyota и Apple, логотипы некоторых других компаний, таких как, BP, iCloud, Twitter, и Grupo Boticario, как полагают, также использовали золотое сечение. И мы все знаем, насколько известны эти логотипы – все потому, что изображение сразу всплывает в памяти!

Как вы можете применить его в своих проектах?

Создайте эскиз золотого прямоугольника, как показано выше желтым цветом. Этого можно достичь путем построения квадратов с высотой и шириной из чисел, принадлежащих золотому сечению. Начните с одного блока и поместите другой рядом с ним. А другой квадрат, чья площадь равна тем двум, поместите над ними. Вы автоматически получите сторону из 3 блоков. После построения этой конструкции из трех блоков, в конечном итоге у вас будет сторона из 5 четырехугольников, из которой можно сделать другую (площадью в 5 блоков) коробку. Это может продолжаться сколько угодно, пока вы не найдете тот размер, который вам нужен!

Прямоугольник может перемещаться в любом направлении. Выделите мелкие прямоугольники и используйте каждый из них, чтобы собрать макет, который будет служить в качестве сетки дизайна логотипа.

Если логотип более округлый, то вам потребуется круговая версия золотого прямоугольника. Вы можете добиться этого начертанием кругов, пропорциональных числам Фибоначчи. Создайте золотой прямоугольник, используя только круги (это означает, что самый большой круг будет иметь диаметр 8, а у круга поменьше будет диаметр 5, и так далее). Теперь разделите эти круги и разместите их так, чтобы вы могли сформировать основную схему для вашего логотипа. Вот пример логотипа Twitter:

Примечание: Вам не обязательно чертить все круги или прямоугольники золотого сечения.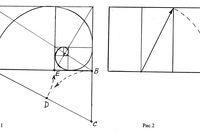 Вы также можете использовать один размер неоднократно.

Как применять его в дизайне текста

Это проще, чем проектирование логотипа. Простое правило для применения золотого сечения в тексте заключается в том, что последующий больший или меньший текст должен соответствовать Фи. Давайте разберем этот пример:

Если размер моего шрифта – 11, то подзаголовок должен быть написан в более крупном шрифте. Умножаю шрифт текста на число золотого сечения, чтобы получить большее число (11*1,6=17). Значит подзаголовок должен быть написан в 17 размере шрифта. А теперь заголовок или название. Умножу подзаголовок на пропорцию и получу 27 (1*1,6=27). Вот так! Ваш текст теперь пропорционален золотому сечению.

Как применить его в веб-дизайне

А здесь немного сложнее. Вы можете оставаться верными золотому сечению даже в веб-дизайне. Если вы опытный веб-дизайнер, вы уже догадались, где и как ее можно применить. Да, мы можем эффективно использовать золотое сечение и применить его к сеткам наших веб-страниц и макетам пользовательского интерфейса.

Возьмите общее число сетки пикселей за ширину или высоту и используйте его для построения золотого прямоугольника. Разделите наибольшую ширину или длину для получения меньших чисел. Это может быть шириной или высотой вашего основного контента. То, что осталось, может быть боковой панелью (или нижней панелью, если вы применили его к высоте). Теперь продолжайте использовать золотой прямоугольник для дальнейшего применения его к окнам, кнопкам, панелям, изображениям и тексту. Вы также можете построить полную сетку, основанную на маленьких версиях золотого прямоугольника расположенных как горизонтально, так и вертикально для создания более маленьких объектов интерфейса, которые пропорциональны золотому прямоугольнику. Для получения пропорций вы можете использовать этот калькулятор.

Спираль

Вы также можете использовать золотую спираль, чтобы определить, где разместить контент на вашем сайте. Если ваша домашняя страница загружается с графическим контентом, как, например, на веб-сайте онлайн магазина или блога фотографий, вы можете воспользоваться золотым методом спирали, который используют многие художники в своих работах.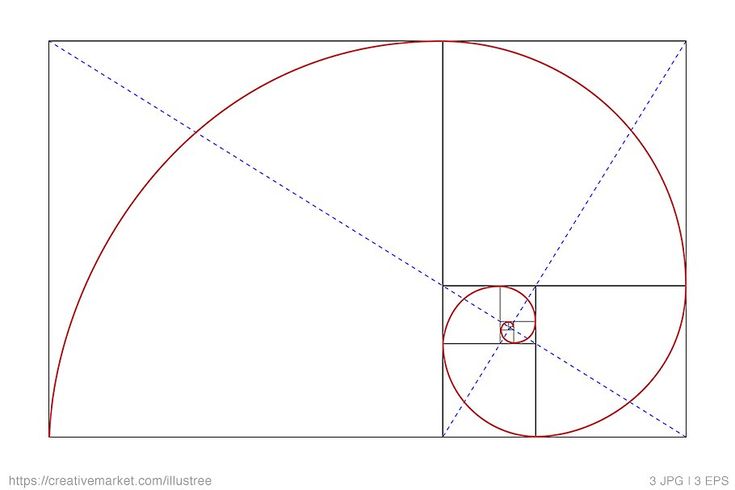 Задумка в том, чтобы поместить наиболее ценный контент в центре спирали.

Контент со сгруппированным материалом тоже может быть размещен при помощи золотого прямоугольника. Это означает, что чем ближе спираль движется к центральным квадратам (к одному квадратному блоку), тем “плотнее” там содержимое.

Вы можете использовать эту технику, чтобы обозначить расположение вашего заголовка, изображений, меню, панели инструментов, окна поиска и других элементов. Twitter славится не только использованием золотого прямоугольника в дизайн логотипа, но и задействовал его в веб-дизайне. Как? Благодаря использованию золотого прямоугольника, или, другими словами концепцией золотой спирали, в странице профиля пользователей.

Но нелегко будет проделать такое на платформах CMS, где автор материала определяет расположение вместо веб-дизайнера. Золотое сечение подходит WordPress и другим дизайнам блога. Это, вероятно, потому, что боковая панель почти всегда присутствует в дизайне блога, который хорошо вписывается в золотой прямоугольник.

Правило третей

Для тех, кто не очень понимает язык математики, есть более простой способ. Он известен как правило третей. Оно не включает в себя точные математические вычисления, но помогает достигнуть правильных пропорций.

Все, что требуется – это разделить первоначальный эскиз на девять равных частей: 

Точки, где встречаются линии в сетке, будут основными точками вашего дизайна, от которых вы будете в дальнейшем отталкиваться. Вы можете поместить ключевую тему или основные элементы на одну или все точки пересечения. Фотографы также используют эту концепцию.

Если Вы разделите каждую колонку в сетке так, чтобы получились две равные половины, то Вы получите сетку для работы с дизайном сайта. Например, Вы можете разместить эмблему или логотип в верхнем правом квадрате в левой части. Менее важная информация, которая будет располагаться вертикально сверху вниз, может брать свое начало верхнем правом квадрате.

Чем ближе прямоугольники к соотношению 1:1,6, тем приятнее воспринимается картина человеческим мозгом (так как это ближе к золотому сечению).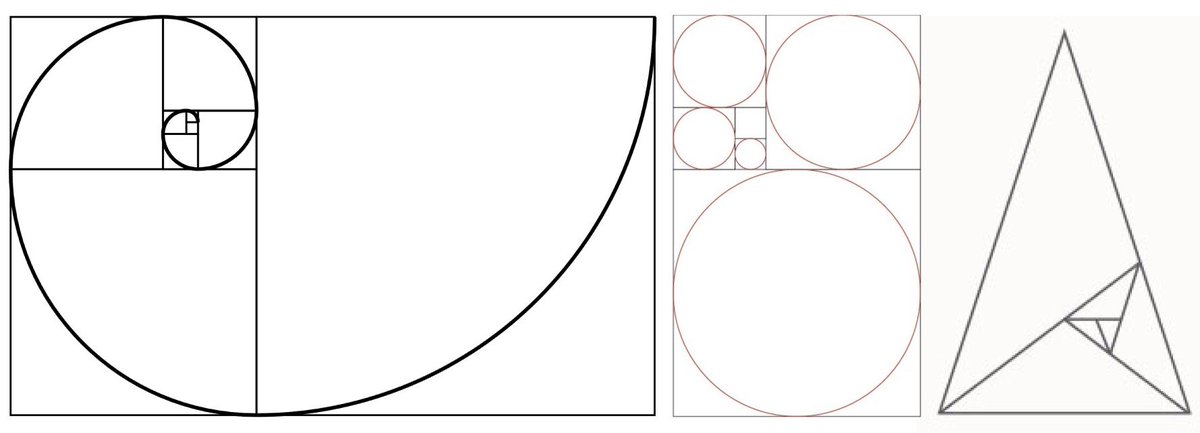  Если вы не любите математику и не хотите считать, то достаточно использовать отношение 3:5 при расчете золотого отношения. Результат будет не таким точным, но он будет близок к пропорциям, которые применяются в работе с дизайном.

Пример того, как можно использовать сечение в веб-дизайне, описан ниже. 

Золотое сечение на примере

Ширина вашего макета может быть фиксированная или гибкая, но прежде чем применить золотое отношение, вам нужно определить число, чтобы начать с ним работать. Для веб-дизайна это число будет равно числу пикселей в ширине лэйаута.

Если вы, например, работаете на лэйауте в 1200 пикселей, то нужно разделить это число на Phi. Для упрощения задачи, число Phi можно сократить до 1.62. При делении 1200 на 1.62, Вы получаете ширину основной колонны, что в нашем случае составит 740 пикселей.

Чтобы определить ширину второй колонки, просто вычтите ширину главной колонки от общей ширины. В этом примере получается 460 пикселей.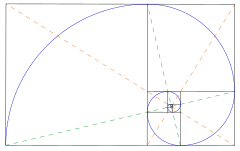

Теперь у вас есть две колонки в 740 пикселей и 460. При помощи этого простого вычисления, вы всегда сможете определить идеальные пропорции для колонок вашего сайта.

Для гибкого лэйаута нужно брать расчеты в процентах. Делим 100% на 1.62 и получаем основную колонку, которая займет 62%, а вторая – 38% соответственно. Далее вы сможете работать исходя из этого соотношения.

Золотое отношение может эффективно использоваться, при создании маленьких прямоугольников в пределах общего дизайна. Это пространство может быть использовано для кнопок навигации, заголовков изображений, пространства для объявлений или для текста, который располагается вокруг изображения. Как бы их не использовали, эти мини золотые прямоугольники будут пропорциональны и законченный вид дизайна, будет приятным завершением работы.

Золотое сечение – не панацея

Использование золотого сечения в дизайне не гарантирует успех вашего лендинга.

В то же время изображения, блоки текста и врезок могут быть хорошо представлены в маленьких золотых прямоугольниках, которые формируют красивый, сбалансированный вид, но число прямоугольников на каждой странице должно быть ограниченным. Ничто в веб-дизайне не должно быть в слишком большом количестве.

Также важно помнить о том, что есть много других факторов, которые нужно учитывать при создании дизайна, и которые будут соответствовать общей цели проекта.

Инструменты для дизайнеров

Калькулятор Phi

Когда вы вводите число в этот веб-инструмент, он рассчитывает результат, необходимый для золотого сечения. Этот сервис бесплатный и очень простой в использовании.

Типографический калькулятор Pearsonified

Это онлайн инструмент с кнопкой ‘Set My Type’. Вы просто нажимаете на нее после того, как введете ширину контента и/или размер шрифта, и сервис сам подберет лучшее типографическое решение. У Вас также есть возможность ввести значение CPL. Он оптимизирует размер знаков по линиям.

Сервис золотого отношения UX Triggers

Вы можете проверить любой сайт с помощью этого бесплатного сервиса и быстро определить использована ли последовательность Фибоначчи в дизайне.

Заключительные мысли

Веб-страницы выглядят более гармонично, когда они сделаны с использованием принципов золотого сечения. Это единственное соотношение, которое использовалось еще две тысячи лет назад, для тех же целей, что и сегодня. Посетителя интуитивно будут чувствовать комфорт гармоничного интерфейса, потому что им уже знакомы классические пропорции архитектурных строений и других произведений искусства.

Использование золотых прямоугольников дает чувство упорядоченности вашему лендингу. Но вы должны быть аккуратны, и избегать злоупотребления ими. Слишком большое их количество произведет обратный эффект и сделает дизайн приторным и менее привлекательным.

Сочетание математических вычислений и органической структуры в веб-дизайне может дать отличный результат. Необязательно, чтобы весь дизайн опирался на все упомянутые принципы, иногда достаточно правила третей, которое поможет вам правильно соблюсти пропорции и расположить элементы на свои места.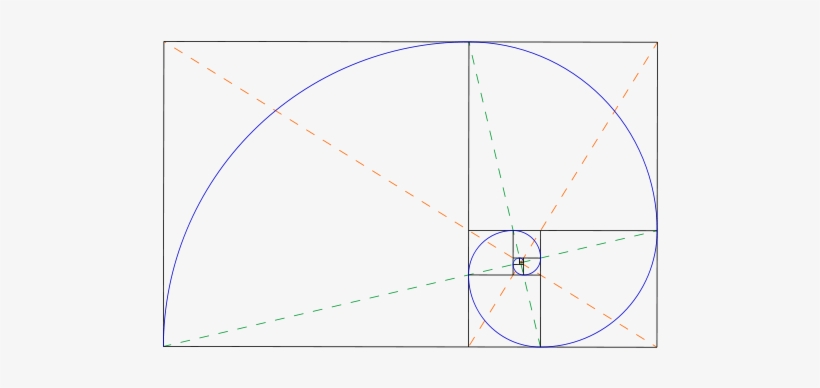

Готовы проверить полученные знания на лендинге? Вы можете выбрать подходящий шаблон и настроить его под себя в конструкторе LPgenerator, или, если у вас нет времени разбираться в тонкостях лендостроения, но при этом вам нужна уникальная страница с гарантированно высокой конверсией, подать заявку на индивидуальный дизайн. 

Он будет выполнен с учетом всех ваших пожеланий, подчеркнет особенности оффера и позиционирование бренда, а еще — легко масштабируется по мере необходимости.

Высоких конверсий!

12-03-2016

Последовательность Фибоначчи

Последовательность Фибоначчи, известная всем по фильму «Код Да Винчи» — ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII веке. Вкратце суть загадки:
Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

 
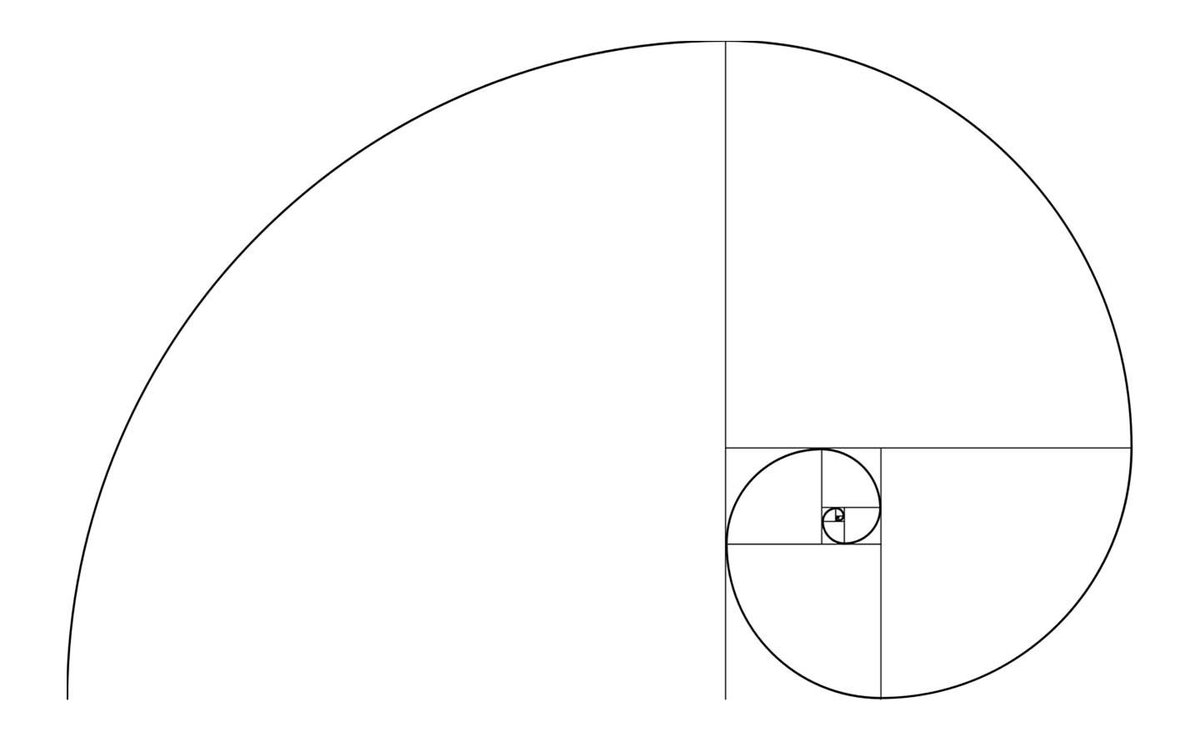
В итоге получается такая последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, где через запятую показано количество пар кроликов в каждом из двенадцати месяцев. Эту последовательность можно продолжать бесконечно долго. Её суть в том, что каждое следующее число является суммой двух предыдущих.
У этой последовательности есть ряд математических особенностей, которых обязательно нужно коснуться. Данная последовательность асимптотически (приближаясь все медленнее и медленнее) стремится к некоторому постоянному соотношению. Однако, это соотношение иррационально, то есть представляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифр в дробной части. Его невозможно выразить точно.
Так отношение какого-либо члена последовательности к предшествующему ему колеблется около числа 1,618, через pаз то превосходя, то не достигая его. Отношение к следующему аналогично приближается к числу 0,618, что обратно пропорционально 1,618. Если мы будем делить элементы последовательности через одно, то получим числа 2,618 и 0,382, которые так же являются обратно пропорциональными. Это так называемые коэффициенты Фибоначчи.
К чему всё это? Так мы приближаемся к одному из самых загадочных явлений природы. Фибоначчи по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.
Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым. Золотое сечение  — высшее проявление совершенства целого и его частей в науке, искусстве и природе.
Если на простом примере, то Золотое Сечение — это деление отрезка на две части в таком соотношении, при котором большая часть относится к меньшей, как их сумма (весь отрезок) к большей.

Если мы примем весь отрезок c за 1, то отрезок a будет равен 0,618, отрезок b — 0,382, только так будет соблюдено условие Золотого Сечения (0,618/0,382=1,618; 1/0,618=1,618). Отношение c к a равно 1,618, а с к b2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.
Разумеется есть золотой прямоугольник, золотой треугольник и даже золотой кубоид. Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.

Изображение: marcus-frings.de

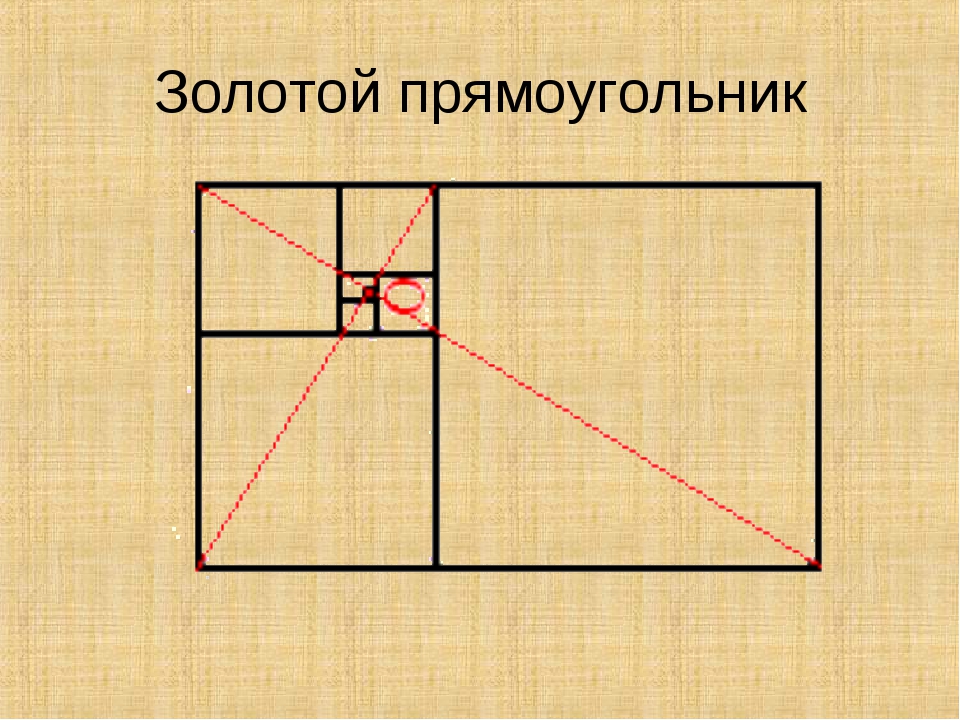
Но самое интересное начинается, когда мы объединим полученные знания. На рисунке наглядно показана связь между последовательностью Фибоначчи и Золотым сечением. Мы начинаем с двух квадратов первого размера. Сверху добавляем квадрат второго размера. Подрисовываем рядом квадрат со стороной, равной сумме сторон двух предыдущих, третьего размера. По аналогии появляется квадрат пятого размера. И так далее пока не надоест, главное, чтобы длина стороны каждого следующего квадрата равнялась сумме длин сторон двух предыдущих. Мы видим серию прямоугольников, длины сторон, которых являются числами Фибоначчи, и, как не странно, они называются прямоугольниками Фибоначчи.
Если мы проведём плавную линий через углы наших квадратов, то получим ни что иное, как спираль Архимеда, увеличение шага которой всегда равномерно.

Ничего не напоминает?

Фото: ethanhein on Flickr
И не только в раковине моллюска можно найти спирали Архимеда, а во многих цветах и растениях, просто они не такие явные.
Алое многолистный:

Фото: brewbooks on Flickr
Броколи романеско:

Фото: beart. org.uk
Подсолнечник:

Фото: esdrascalderan on Flickr
Сосновая шишка:

Фото: mandj98 on Flickr
А если взглянуть чуть подальше, то можно разглядеть последовательность Фибоначчи в недосягаемых галактиках.

И тут самое время вспомнить о Золотом Сечении! Ни одни ли из самых прекрасных и гармоничных творений природы изображены на этих фотографиях? И это далеко не все. Присмотревшись, можно найти похожие закономерности во многих формах.
Конечно заявление, что все эти явление построены на последовательности Фибоначчи звучит слишком громко, но тенденция на лицо. Да и к тому же сама последовательность далека от совершенства, как и всё в этом мире.
Есть предположение, что последовательность Фибоначчи — это попытка природы адаптироваться к более фундаментальной и совершенной золотосечённой логарифмической последовательности, которая практически такая же, только начинается из ниоткуда и уходит в никуда. 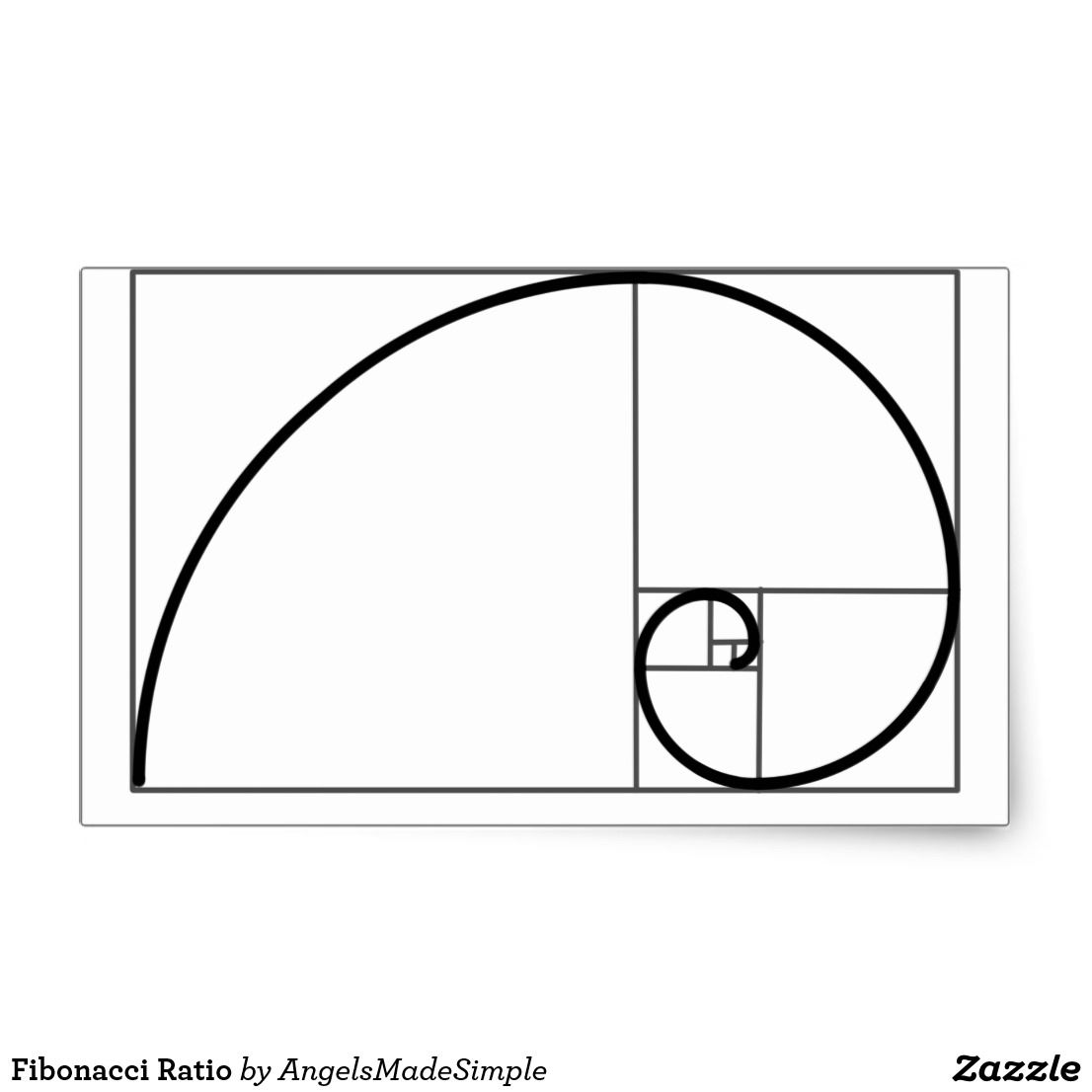Природе же обязательно нужно какое-то целое начало, от которого можно оттолкнуться, она не может создать что-то из ничего. Отношения первых членов последовательности Фибоначчи далеки от Золотого Сечения. Но чем дальше мы продвигаемся по ней, тем больше эти отклонения сглаживаются. Для определения любой последовательности достаточно знать три её члена, идущие друг за другом. Но только не для золотой последовательности, ей достаточно двух, она является геометрической и арифметической прогрессией одновременно. Можно подумать, будто она основа для всех остальных последовательностей.
Каждый член золотой логарифмической последовательности явлется степенью Золотой Пропорции (z). Часть ряда выглядит примерно так: … z^-5; z^-4; z^-3; z^-2; z^-1; z⁰; z¹; z²; z³; z⁴; z⁵ … Если мы округлим значение Золотой пропорции до трёх знаков, то получим z=1,618, тогда ряд выглядит так: … 0,090 0,146; 0,236; 0,382; 0,618; 1; 1,618; 2,618; 4,236; 6,854; 11,090 . .. Каждый следующий член может быть получен не только умножением предыдущего на 1,618, но и сложением двух предыдущих. Таким образом экспоненциальный рост в последовательности обеспечивается путем простого сложения двух соседних элементов. Это ряд без начала и конца, и именно на него пытается быть похожей последовательность Фибоначчи. Имея вполне определённое начало, она стремится к идеалу, никогда его не достигая. Такова жизнь.
И всё-таки, в связи со всем увиденным и прочитанным, возникают вполне закономерные вопросы:
От куда взялись эти числа? Кто этот архитектор вселенной, попытавшийся сделать её идеальной? Было ли когда-то всё так, как он хотел? И если да, то почему сбилось? Мутации? Свободный выбор? Что же будет дальше? Спираль скручивается или раскручивается?
Найдя ответ на один вопрос, получишь следующий. Разгадаешь его, получишь два новых. Разберёшься с ними, появится ещё три. Решив и их, обзаведёшься пятью нерешёнными. Потом восьмью, потом тринадцатью, 21, 34, 55. ..

Источник: http://greenword.ru/

Калькулятор золотого сечения (золотой пропорции) онлайн

Золотое сечение — это особое соотношение сторон фигуры, которое наиболее приятно для созерцания. Это число известно с античных времен, а ученые эпохи Возрождения называли его божественной пропорцией. Число Фи — золотое сечение, приблизительно равное 1,618.

История

Особую красоту деления отрезка на стороны в соотношении 1/1,618 заметили еще античные ученые. Евклид в своих началах использовал этот метод при построении пентагона, а пифогорейцы рассматривали весь мир как царство математической гармонии и уделяли большое внимание соотношению 1/1,618. В 1202 году Леонардо Фибоначчи вывел особую последовательность, отношение членов которой стремилось к числу Фибоначчи. Лука Пачоли, один из величайших алгебраистов Италии, назвал это соотношение божественной пропорцией, связав свойства бога с числом Фи. Именно с этого момента золотое сечение начало активно использоваться в работах художников эпохи Возрождения и получило буквально мистический статус. По словам Кеплера, число Фи — бесценная жемчужина математики.

Число Фи в математике

Золотое сечение часто встречается в геометрии. Золотой прямоугольник — фигура на плоскости, длина и ширина которой соотносятся как 1/1,618. Примечательное свойство такого прямоугольника состоит в том, что при удалении из фигуры любого квадрата образуется новый прямоугольник с точно таким же соотношением сторон. Стоит упомянуть и пентаграмму — звездчатый многоугольник, стороны которого пересекаются в соответствии с правилом золотого сечения.

В арифметике число Фи встречается в упоминаемой выше последовательности Фибоначчи, так как lim(Fn/Fn-1) -> Фи. Кроме того, золотое сечение имеет интересное представление в других формах записи. Так, Фи представляется как бесконечная цепочка квадратных корней из единицы. А если привести Фи к цепному виду, то получится бесконечная дробь вида [1; 1, 1, 1, 1, 1…]

Число Фи в реальности

Мистический ореол вокруг золотого сечения возник благодаря такому явлению как «золотой числизм». Энтузиасты, задавшиеся целью найти эту пропорцию в как можно большем количестве реальных объектов или явлений, часто подгоняли результаты. К примеру, храм Парфенон всегда присутствует в списке объектов, которые построены с учетом божественной пропорции. Однако на деле соотношение ширины храма к его высоте составляет 1,74, а если исключить фронтон, то и вовсе 3.

После придания числу божественных свойств, многие художники и музыканты начали сознательно использовать это соотношение в своих работах. Леонардо да Винчи, Альбрехт Дюрер, Иоганн Бах, Ле Корбюзье, Густав Фехнер намеренно придавали своим произведениям форму, соответствующую числу Фи. Одним из современных примеров использования золотого сечения является мозаика Пенроуза — метод непериодического разбиения плоскости.

Несмотря на явное преувеличение свойств золотой пропорции, она все же встречается в реальности. Большинство спиралевидных объектов связны с числом Фи: раковины моллюсков, атмосферные вихри и даже галактики действительно соответствуют божественной пропорции.

Калькулятор золотого сечения

Если вы хотите использовать божественную пропорцию в своей работе, то наш калькулятор к вашим услугам. Для определения сторон золотого прямоугольника вам понадобится ввести одну из сторон, а программа определит вторую, соответствующую правилу золотого сечения. Прелесть калькулятора состоит в том, что он не просто умножает сторону на 1,618, а подбирает целое значение. Именно поэтому вам потребуется оперировать целыми числами, что удобно на практике.

Пример из реальной жизни

Живопись

Допустим, вы хотите сделать приятную с точки зрения математики картину, следовательно, вам нужно нарисовать ее на золотом прямоугольнике. Вам потребуется заказать холст определенного размера, и чтобы определить его размеры, используйте наш калькулятор. Пусть вы хотите писать на холсте, длина которого составит 120 см. Как узнать необходимую ширину? Введите это значение в ячейку A и получите ответ, равный 74 см.

Заключение

Божественная пропорция — мистическое соотношение, которое занимает умы математиков уже несколько тысячелетий. Возможно, именно число Фи содержит ответы на вечные вопросы о тайнах мироздания. Если вам потребуется создать объекты, соответствующие золотому сечению, используйте наш калькулятор, при помощи которого вы сможете подобрать целые числа.

Золотое сечение: Самый раздутый миф в дизайне

Золотое сечение – это полный нонсенс в дизайне. И вот почему.

В мире искусства, архитектуры и дизайна золотое сечение завоевало потрясающую репутацию. Великие гении, включая Корбюзье и Сальвадора Дали, использовали эту пропорцию в своих работах. Парфенон, Пирамиды в Гизе, полотна Микелянджело, Мона Лиза и даже логотип Apple якобы построены на его основе.

Это бред. Эстетика золотого сечения – это просто современная байка, миф. Многие дизайнеры им пренебрегают, а если и используют, то не стесняются преуменьшать его значение. Кроме того, у этой пропорции нет никакой научной подоплеки. Те, кто верят, что за красотой золотого сечения кроется математика, попались на крючок 150-летней давности.

Пользователь FlickrSébastien Bertrand

Что такое золотое сечение?

Изначально описанный в Элементах Эвклида 2300 лет назад, этот термин гласит: два объекта находятся в золотой пропорции, если соотношение между ними идентично отношению их суммы к большему из двух элементов. Обычно эта пропорция составляет 1.6180. Самое известное применение золотого сечения – так называемый золотой прямоугольник, который может быть разделен на идеальный квадрат и меньший прямоугольник тех же пропорций, что и “родительский” прямоугольник. Вы можете применить эту теорию к большему разнообразию объектов, также разделяя их на компоненты.

Золотое сечение всегда немного неточное.

Простым языком: если у вас есть два объекта (или один объект, который можно разделить на два, по аналогии с золотым прямоугольником), и если после вышеописанной математики, вы получите число 1.6180, обычно считается, что два объекта демонстрируют золотое сечение. Но есть одна проблема.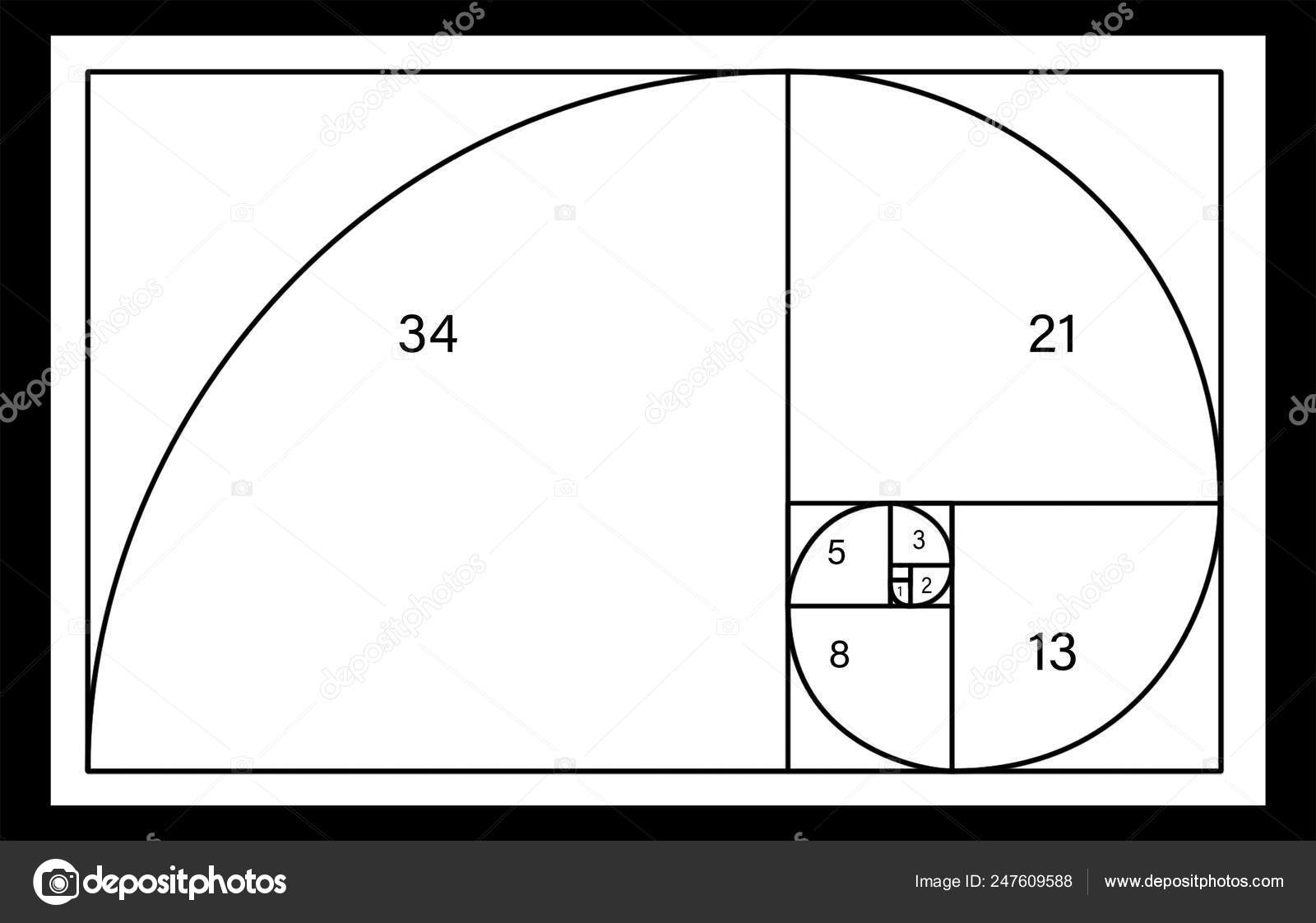 Когда вы все-таки посчитаете, то сама пропорция не равна 1.6180. Она равна 1.6180339887… И десятичная часть уходит в бесконечность.

“Собственно говоря, невозможно подобрать примеры золотого сечения в реальном мире, потому что это иррациональное число”, – заявляет Кит Девлин, профессор математики Стэнфордского университета. Вы можете только приблизиться к более стандартным пропорциям. Стороны экрана iPad соотносятся как 3:2, пропорция HDTV составляет 16:9, и все это “вокруг да около”, по словам Девлина. Но само золотое сечение – это как число “пи”. Как нельзя найти идеальный круг в реальном мире, так и нельзя применить точное золотое сечение к любому объекту в реальном мире. Оно всегда будет немного смещаться.

Золотое сечение – это как эффект Моцарта

Конечно, это педантизм. Неужели 1.6180 – недостаточно точно? Возможно, и достаточно, если бы было какое-то научное обоснование того, что именно золотое сечение позволяет нам считать объекты вроде Парфенона или Моны Лизы эстетически приятными.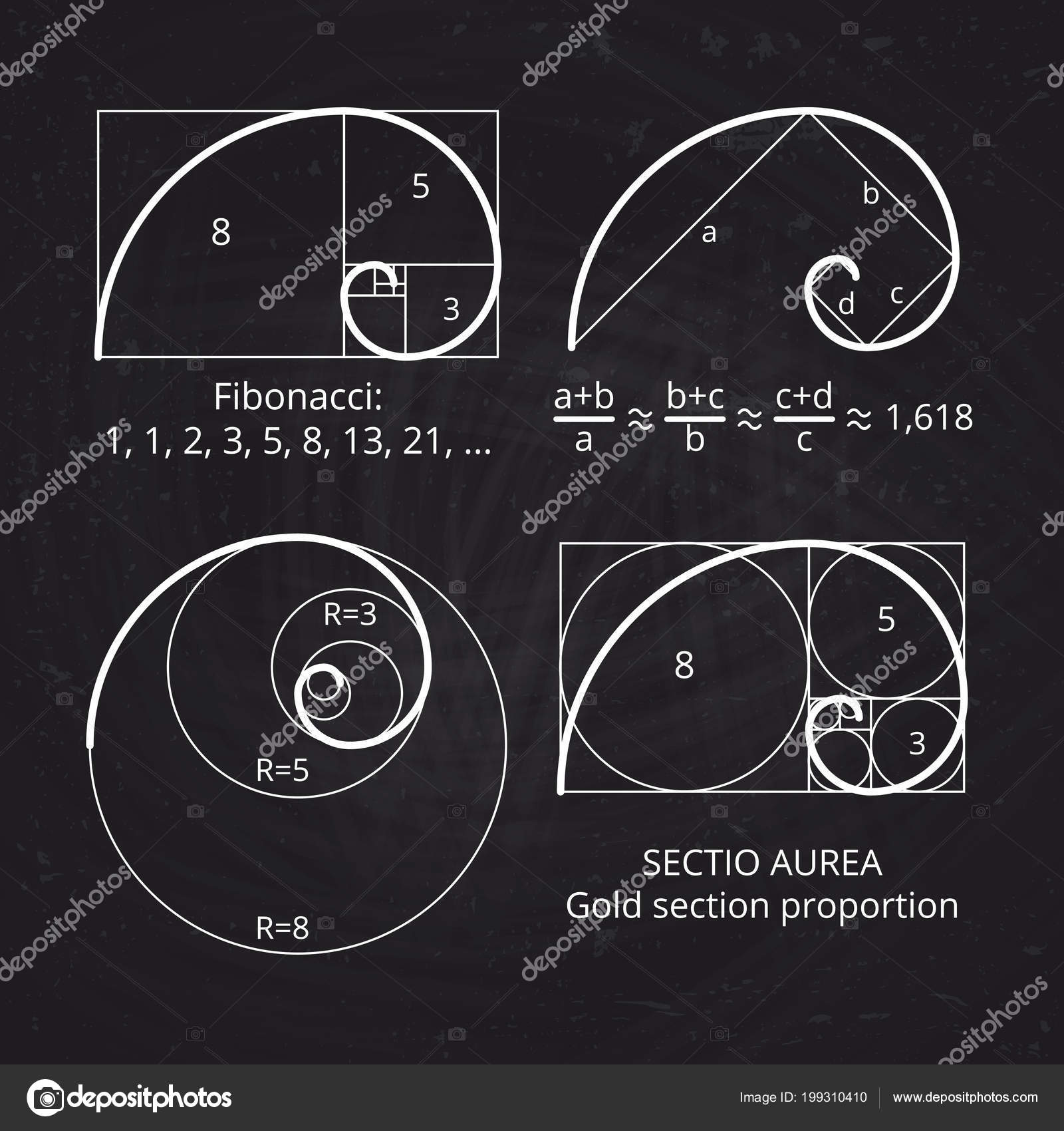

Но это не так. Девлин считает, что сама идея, будто золотое сечение имеет какое-то отношение к эстетике, исходит от двух людей, один из которых был неправильно истолкован, а второй это толкование и обнародовал.

Первый человек – Лука Пачоли, францисканский монах, который написал книгу под названием De Divina Proportione в далком 1509 году, и она была названа в честь золотого сечения. Примечательно то, что в своей книге Пачоли не отстаивал теорию эстетики этого сечения в отношении к искусству, архитектуре и дизайну: вместо этого он поддерживал Витрувианскую систему рациональных пропорций, основанную римским архитектором первого века, Витрувием. Золотое сечение ошибочно было приписано Пачоли в 1799 году, согласно Марио Ливио, который буквально написал книгу по золотому сечению. Но Пачоли был близким другом Леонардо да Винчи, чьи работы получили огромное признание и популярность в 19 веке. Так как Да Винчи проиллюстрировал De Divina Proportione, вскоре начали говорить, что и сам Да Винчи применил золотое сечение как секретную математику в своих восхитительно красивых творениях.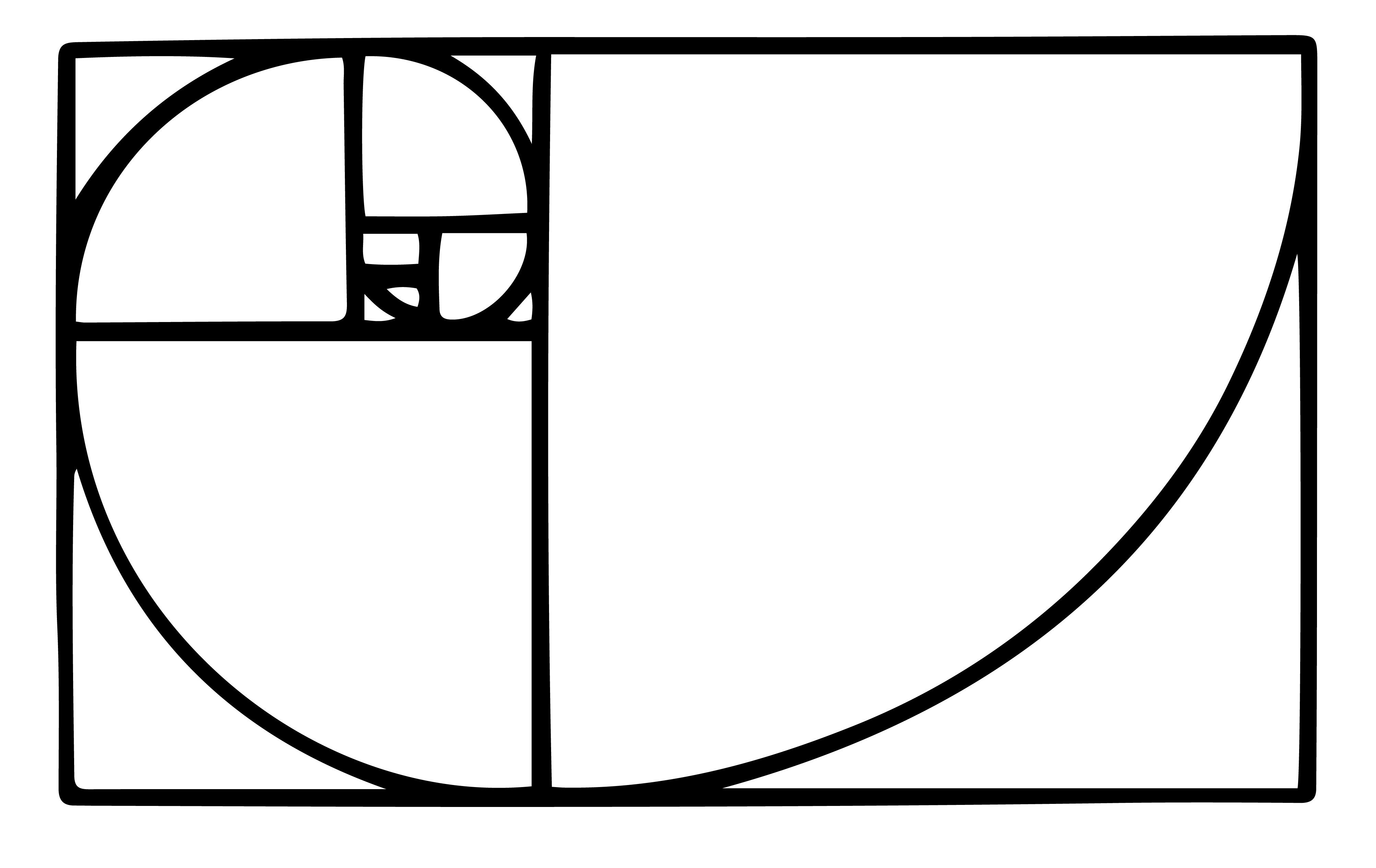

Адольф Цейзинг был тем, кто в это поверил. “Это человек, который хотел сжечь себя на костре во имя репутации золотого сечения” – шутит Девлин. Цейзинг был немецким психологом, который отстаивал идею, что золотое сечение является универсальным законом, описывающим “красоту и завершенность в природе и в искусстве… оно проходит красной нитью как первостепенный духовный идеал во всех структурах, формах и пропорциях, космических и индивидуальных, органических и неорганических, акустических или оптических”.

Он был очень многословным. Единственной проблемой Цейзинга было то, что он видел закономерности там, где их не было. Например, Цейзинг доказывал, что золотое сечение можно применить к человеческому телу, взяв рост человека от пупка до пальцев ног, поделив его на полный рост. По словам Девлина, это всего лишь произвольные части тела, слепленные в формулу. Он говорит: “При замерах чего-то столь сложного, как человеческое тело, очень легко найти примеры разных пропорций, близких к 1. 6”.

В моей собственной работе я даже не найду примера использования золотого сечения.

Но это не имеет никакого значения. Теории Цейзинга стали невероятно популярны, и Девлин называет их “эквивалентом эффекта Моцарта 19-го века”. Эффект Моцарта гласит, что прослушивание классической музыки повышает интеллект. В 20 веке известный швейцарско-французский архитектор Ле Корбузье положил золотое сечение в основу своей системы антропометрических пропорций “Модулора”. Дали нарисовал свой шедевр “Тайная вечеря” на холсте в форме золотого прямоугольника. Тем временем историки искусства начали просматривать и другие шедевры, пытаясь отыскать золотое сечение в Стоунхендже, полотнах Рембранта, Шартрском соборе и работах Сёра. Связь между золотым сечением и красотой превратилась в самую раздутую утку в мире искусства, архитектуры и дизайна.

Ian Yen на Yanko Design

На самом деле, вы не очень-то и предпочитаете золотое сечение

В реальном мире людям не особо необходимо золотое сечение.

Девлин совместно с кафедрой психологии Стенфордского университета в течение многих лет опрашивал сотни студентов, какой прямоугольник их любимый. Он показывал разные прямоугольники студентам, а затем просил их выбрать наиболее понравившийся. Если бы оды золотому сечению были оправданы, студенты бы выбирали прямоугольники, близкие к золотому. Но это было не так. Они выбирают их произвольно. И если вы попросите их повторить свой выбор, они выберут другие прямоугольники. “Это очень полезный пример для демонстрации сложности человеческого восприятия”. Кроме того, это отличная демонстрация того, что золотое сечение не является более приятным для людей с эстетической точки зрения.

Эксперименты Девлина не единственные в исследовании золотого сечение. Исследование, проведенное специалистами Школы бизнеса имени Уолтера Хааса в Беркли, показало, что в среднем потребители предпочитают прямоугольники, пропорция которых между 1.414 и 1.732. Золотое сечение входит в этот диапазон, но не является явным “любимчиком” публики.

Многие современные дизайнеры не считают его полезным

Дизайнеры, с которыми мы обсуждали золотое сечение, не видят в нем особой пользы.

Ричард Мейер, легендарный архитектор, автор Центра Гетти и Музея современного искусства в Барселоне, отмечает, что в начале своей карьеры у него был архитекторский треугольник, который соответствовал золотому сечению, но он никогда не создавал свои здания по золотому сечению. “В мире такое множество других чисел и формул, которые важнее при проектировании зданий”, – говорит Мейер, ссылаясь на формулы по расчету максимальных допустимых размеров пространств зданий, или на формулы расчета структурной нагрузки.

Алиса Андрасек, дизайнер из Biothing, онлайн-репозитория машинного проектирования, соглашается с этим: “В своей работе я даже не найду примера использования золотого сечения. Я могу представить, что эту пропорцию можно встроить в разные системы в качестве ‘изюминки’, но мне сложно вообразить, чтобы весь дизайн был построен именно на золотом сечении, как это случалось в истории… это слишком уж упрощенно”.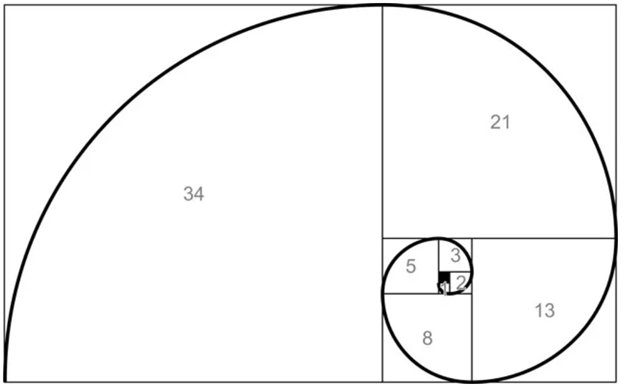

Джорджия Лупи из Accurat, итальянской дизайн-фирмы, говорит, что в лучшем случае золотое сечение так же важно для дизайнеров, как и любое другое композиционное правило, например, правило третей: отличное распространенное правило, которое хорошие дизайнеры могут с таким же успехом проигнорировать. “Я не знаю, сколько дизайнеров на практике специально внедряют золотое сечение в свои работы. Лично я никогда не работала с этой пропорцией в своих проектах”.

Из всех опрошенных дизайнеров, индустриальный дизайнер Ив Бехар из Fuseproject теплее всех относится к золотому сечению: “Иногда я действительно вижу золотое сечение в пропорциях продуктов и графики, которую мы создаем, но это скорее просто случайность, чем догма. Это важный инструмент, но не правило”.

Даже дизайнеры, которые по совместительству являются математиками, скептически относятся к использованию золотой пропорции в дизайне. Эдмуд Харрис – клинический доцент кафедры математики в Университете Арканзаса, который использует множество формул для создания новых произведений искусства. Но и Харрис говорит, что золотое сечение, в лучшем случае, всего лишь один из множества инструментов в руках дизайнеров, склонных к математике: “Во многих смыслах это просто число, и оно, как и другие числа, часто встречается в разных местах… [Но] это точно не универсальная формула эстетической красоты”.

Тайная вечеря, 1955, Сальвадор Дали

Почему этот миф так популярен?

Если ценность золотого сечения так незначительна, почему же этот миф процветает?

Девлин поясняет это просто: “Мы создания, генетически запрограммированные видеть паттерны и искать смысл. В нашей ДНК не зашифрована способность мириться с условными вещами вроде эстетики, поэтому мы пытаемся доказать их с помощью нашего часто ограниченного математического видения. Большая часть людей не понимает математику, и даже не может понять, как формула вроде золотого сечения применяется к сложной системе, так что и проверить себя они не могут. Люди думают, что повсюду видят золотое сечение, в природе и в любимых объектах, но они не могут это обосновать. Они – жертвы своего природного желания найти смысл в разных объектах вселенной, но из-за недостаточной математической грамотности они не могут понять, что обнаруживаемые закономерности иллюзорны”.

Золотое сечение в дизайне интерфейсов

Последовательность Фибоначчи | Блог по математике ∞

Каждое существо на Земле разделяет определенную общую связь. Это не сложный, глубоко скрытый элемент или какая-то потусторонняя связь; это просто правда. Мы все входим в существование в какой-то момент, и все мы покидаем свое существование в другой точке вниз по линии.

Между этими начальными и конечными точками у каждого из нас есть свой собственный опыт. Некоторые делятся с другими людьми, тогда как другие являются чисто внутренними, но все они так или иначе влияют на нас.Являются ли все эти события чисто случайными или за ними стоит какая-то рифма и причина?

Многие философы, учителя, математики и любители жизни в целом считают, что нет ничего случайного. В эту категорию попадает мужчина, родившийся в Италии более 800 лет назад. Его звали Леонардо Пизано Боголло, но сегодня мы знаем его как Фибоначчи. В юном возрасте он развил любовь к числам, и эта страсть привела к открытию, способному изменить то, как люди смотрят на жизнь и мир вокруг них.

Оживление последовательности Фибоначчи

Некоторые считают, что если присмотреться, можно найти узор в чем угодно.Это вполне может быть правдой, но Фибоначчи смог извлечь конкретную закономерность из своего знания чисел и доказать, что она, возможно, может продолжаться вечно. Он указал на последовательность Фибоначчи в своей первой книге, Liber abacci , где он поставил математически обоснованную словесную задачу для всеобщего размышления.

«Один человек посадил пару кроликов на место, обнесенное стеной. Сколько пар кроликов можно произвести от этой пары за год, если предполагается, что каждый месяц каждая пара порождает новую пару, от которой второй месяц становится продуктивным? »

Это может быть хорошее время, чтобы заварить кофе и определить местонахождение аспирина, потому что ваш разум вот-вот взорвется!

Хорошо, поехали! Видите ли, Фибоначчи рассуждал, что кролики достигнут зрелости и спариваются примерно через месяц, поэтому по прошествии одного месяца осталась только одна пара кроликов.Поскольку срок их беременности также составляет месяц, второй месяц подошел к концу, и у них осталась только одна пара. Однако в конце третьего месяца появилась вторая пара. Кролики-самки должны иметь возможность рожать один раз в месяц после получения первого помета, поэтому на четвертом месяце первая пара родила еще одну.

Месяц пятый прокатился, и первая пара воспроизвелась снова, а вторая пара сделала то же самое. На данный момент общее количество составляло пять пар. Короче говоря, в конце года в пределах стены проживало 377 пар.

Заглянем глубже

Конечно, Фибоначчи сделал несколько довольно смелых скачков, прежде чем предсказал плодотворность этого вздора. Его сценарий вращался вокруг некоторых строго контролируемых условий. Например,

• Каждый новый помет состоял из двух кроликов: самца и самки
• Все были физически способны к воспроизведению
• Каждая самка смогла начать репродуктивный процесс в возрасте одного месяца и после этого рожать новый помет каждый месяц
• Все прожили год, не умерли от болезней и не были выгнаны из фермы другими кроликами

По правде говоря, некоторым кроликам может потребоваться четыре месяца или больше, чтобы достичь зрелости.В одном помете может родиться до 12 потомков, и не всем гарантировано выживание. Однако если серьезно подумать, неконтролируемые числа и естественный отбор, безусловно, могут компенсировать друг друга. Хорошо продуманные условия Фибоначчи могут легко учесть все возможности и уравновесить весы.

Разборка

В письменной форме все эти идеи могут звучать несколько абстрактно. Конечно, математика Фибоначчи точна. Как только вы поставите числа на место слов, станет немного понятнее.В последовательности Фибоначчи вы начинаете с 0 и 1 и двигаетесь оттуда. Проще говоря, это выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и так далее.

Каждое новое число в последовательности создается путем сложения двух предыдущих чисел.

0 + 1 = 1

1 + 1 = 2

1 + 2 = 3

2 + 3 = 5

3 + 5 = 8

5 + 8 = 13

8 + 13 = 21

13 + 21 = 34

21 + 34 = 55

34 + 55 = 89

Вы можете продолжать бесконечно, складывая последние два числа в последовательности, чтобы получить следующее.Хотя объяснение кажется запутанным и сложным, на самом деле оно довольно простое. Однако с этого момента дела становятся более сложными.

Концепция принимает форму

Мы собираемся вывести это дело на совершенно новый уровень. Представьте себе числа в последовательности Фибоначчи, представленные квадратами, как на миллиметровой бумаге. Найдите начальную точку где-нибудь в центре страницы и раскрасьте один квадрат, представляющий первое число в последовательности (1).Рядом сделайте то же самое в честь второго. Затем, когда два — третье число, используйте другой цвет, чтобы заштриховать квадрат 2 на 2. Оттуда найдите другой оттенок для окрашивания в пространстве размером 3 на 3 квадрата и так далее. У вас получится яркая версия этого примера:

.

Вы замечаете, как они идеально сочетаются друг с другом, как кусочки пазла? Следующее число в серии будет 13, а фигура, которая здесь обретает форму, имеет размер 13 квадратов в поперечнике.По мере того, как вы перебираете большие числа, узор остается прежним. Каждый новый квадрат будет больше следующего, но, следуя числам в последовательности Фибоначчи, они всегда будут аккуратно встать на место в точной пропорции с предыдущими.

Теперь, если вы следите за бумагой, возьмите ручку. Начните с верхнего угла вашего первого отдельного квадрата и нарисуйте первую ступень спирали, ведущую к его противоположному углу, разрезая квадрат пополам. Продолжайте линию через следующий одиночный блок и через следующие, проводя спираль по диагональному центру каждого большего квадрата.В итоге вы получите что-то вроде этого:

Спираль Фибоначчи и прямоугольник, образованный его последовательностью чисел, известны как золотой прямоугольник из-за их связи с золотым сечением. В качестве числа эта магическая фигура — 1.61803 и представлена ​​греческой буквой Фи (Φ). Может показаться, что мы немного прыгаем, но все это действительно актуально.

В геометрии золотое сечение создается, когда вы делите линию на две части, а не только на любые две части.Линия должна быть разделена в нужном месте, где вся линия, разделенная на длину самой длинной части ее деления, точно равна самому длинному сегменту, разделенному на самый короткий. Вы угадали: обе цифры должны равняться 1,61803.

прямоугольника, созданного с использованием золотого сечения, считаются самыми приятными из тех, что вы когда-либо видели. Это возвращает нас к Фибоначчи. Оказывается, когда вы берете любые два последовательных числа в его последовательности и находите их отношение, разделив большее на меньшее, это очень близко к древнему золотому стандарту.Смотри!

21/13 = 1,61538

89/55 = 1,47272

121393/75025 = 1,61803

Посмотрите на это! Мы нашли победителя! Сказав все это, следует отметить, что последовательность Фибоначчи, золотой прямоугольник и присущая ему спираль — все вокруг нас. Вы вот-вот узнаете, как и где.

По спирали в полный контроль

Прежде чем читать дальше, вы должны быть абсолютно уверены, что готовы к этому прыжку. Это всего лишь небольшой дружеский совет.Как только вы это увидите, вы не сможете не увидеть это, и это изменит вашу жизнь!

Золотой прямоугольник, образованный последовательностью Фибоначчи, веками появлялся по всему миру. Одним из главных образцов является Парфенон в Греции. Многочисленные примеры золотого сечения и прямоугольника встречаются внутри и снаружи как в большом, так и в маленьком масштабе.

Мона Лиза Леонардо да Винчи может считаться еще одним проявлением почти золотого сечения в действии. Его размеры составляют 30 на 21 дюйм.Если следовать стандартному плану, большая часть прямоугольника, разделенная на меньшую, составляет 1,42857. Совпадение не точное, но очень близкое.

Направляясь в Египет, мы находим еще один возможный пример в Великой пирамиде в Гизе. Эта самая большая из трех пирамид имеет ширину 756 футов и высоту 481 фут. Когда вы делаете математику, соотношение будет 1,57172; опять же, это прямо на границе.

Художник Пит Мондриан также вставляет последовательность Фибоначчи в некоторые из своих картин.Вы можете ясно видеть квадраты из кусочков пазла, составляющие Золотой прямоугольник в некоторых примерах его работ. Если вы посмотрите на это достаточно долго, ваш мысленный взор может даже начать рисовать спираль.

Это лишь несколько широко известных примеров использования этого узора в искусстве, архитектуре и инженерии на протяжении веков. Многие люди настаивают на том, что это простое совпадение, ссылаясь на тот факт, что вы можете найти закономерности практически во всем, если ищете их. В том же духе некоторые из этих примеров возникли задолго до самого Фибоначчи.

Многие списывают все на очевидное. За созданием этих постановок стоят одни из самых ярких и эстетически склонных умов в истории. Чистая логика подсказывает, что они должны включать в свою работу наиболее визуально приятные аспекты, даже если это на подсознательном уровне.

Вы можете рационализировать ситуацию по-разному, но она еще глубже. Некоторые вещи нельзя игнорировать или объяснять.

Это только натуральное

Если вы выйдете на улицу и осмотритесь, вы также найдете Фибоначчи в природе, а не только в одном или двух разных местах.Подсолнухи — яркий тому пример. Эти блестящие желтые лепестки окружают большую массу семян, но они не расположены случайным образом; они изящно изгибаются из центра семенной головки.

Сосновые шишки — еще один широко используемый пример. Вы заметите, что их шипы расположены по спирали как по часовой, так и против часовой стрелки. То же самое и с ананасами. Если поблизости есть куст падуба или другой подобный кустарник, взгляните на него. Сначала кажется, что листья растут беспорядочно или даже по кругу.При ближайшем рассмотрении вы увидите, что они на самом деле немного пошатнулись, бегая по спирали от кончика к стволу.

Человечество также демонстрирует маленькие фрагменты Золотого Прямоугольника. Средние размеры лица взрослого человека составляют от восьми до девяти дюймов в длину и от шести до семи дюймов в ширину. Если вы вычислите соотношение двух крайностей, оно составит 1,5, что находится в пределах доли золотого сечения. Человеческие волосы имеют тенденцию расти наружу по спирали из центральной точки. С этого момента вы начнете видеть версию последовательности везде, куда бы ни посмотрели.Не говорите, что мы вас не предупреждали заранее!

Делаем математику

Как и в большинстве математических ситуаций, в этом ряду есть правила вычисления чисел. Он поставляется со своим разнообразием формул. Прежде всего, давайте посмотрим на демонстрацию общего правила, связанного с последовательностью Фибоначчи:

.

x _n = x _n-1 + x _n-2

Здесь «n» дает каждому числу в ряду Фибоначчи соответствующее число в нашей традиционной последовательности: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10…

«Xn» представляет числа в последовательности Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…

Используя правило, мы можем вычислить число в последовательности.Попробуем седьмой:

x ₇ = x _7-1 + x _7-2

x ₇ = x ₆ + x ₅

х ₇ = 8 + 5

х ₇ = 13

На самом деле это просто еще один способ сказать: «Определенное число в последовательности Фибоначчи равно сумме двух чисел перед ним».

Отсюда все становится только сложнее и запутаннее. Вы найдете любое количество уравнений и объяснений, связанных с математической индукцией, линейным повторением, построением последовательности на графиках и т. Д.

Эти формулы — греческие, если простите за каламбур, для тех, кто пытается прыгнуть головой вперед в продвинутый конец спектра. Если у вас нет опыта в реальных методах решения проблем, которые здесь используются, лучше разобраться в ситуации. Как только вы поймете основы, подобные приведенной выше формуле, вам будет достаточно просто делать маленькие шаги в дальнейшем.

Всего

У всех нас общие узы. Являются ли они случайными и случайными или являются продуктом лежащих в основе математических последовательностей и таинственно упорядоченного хаоса, это в значительной степени вопрос мнения.Независимо от того, где вы стоите в вопросе, определенные закономерности нельзя упускать из виду или легко игнорировать. Фибоначчи видел это даже в детстве, и работа его жизни породила непреодолимую последовательность событий.

7.2: Золотое сечение и последовательность Фибоначчи

В этом разделе мы обсудим очень особое число, называемое золотым сечением. Это иррациональное число, немного больше 1,6, и оно (что несколько удивительно) имело огромное значение в мире науки, искусства и музыки.Также было обнаружено, что это число имеет удивительную связь с так называемой последовательностью Фибоначчи, первоначально изученной в контексте биологии много веков назад. Эта неожиданная связь между алгеброй, биологией и искусством предполагает математическое единство мира и иногда также обсуждается в философии.

Золотое сечение

Для одного числа \ (a \) и другого меньшего числа \ (b \) соотношение этих двух чисел находится путем их деления. Их соотношение равно \ (a / b \).Другое соотношение получается сложением двух чисел \ (a + b \) и делением их на большее число \ (a \). Новое соотношение — \ ((a + b) / a \). Если эти два соотношения равны одному и тому же числу, то это число называется золотым соотношением. Греческая буква \ (\ varphi \) (фи) обычно используется для обозначения золотого сечения.

Например, если \ (b = 1 \) и \ (a / b = \ varphi \), то \ (a = \ varphi \). Второе соотношение \ ((a + b) / a \) тогда будет \ ((\ varphi + 1) / \ varphi \). Поскольку эти два соотношения равны, это верно:

\ [\ varphi = \ dfrac {\ varphi + 1} {\ varphi} \ nonumber \]

(У этого уравнения есть два решения, но только положительное решение называется золотым сечением \ (\ varphi \)).

Один из способов написать это число —

\ [\ varphi = \ dfrac {1+ \ sqrt {5}} {2} \ nonumber \]

\ (\ sqrt {5} \) — положительное число, которое при умножении само на себя дает \ (5: \ sqrt {5} \ times \ sqrt {5} = 5 \).

Золотое сечение — иррациональное число. Если человек попытается записать его десятичное представление, оно никогда не остановится и никогда не создаст шаблон, но начнется так: 1.6180339887 … Интересная особенность этого числа заключается в том, что вы можете вычесть из него 1 или разделить 1 по нему, и результат будет таким же.

\ [\ varphi-1 = 1,6180339887 \ ldots-1 = 0,6180339887 \ nonumber \]

\ [1 / \ varphi = \ frac {1} {1.6180339887} = 0,6180339887 \ nonumber \]

Золотой прямоугольник

Если длина прямоугольника, деленная на его ширину, равна золотому сечению, то прямоугольник называется «золотым прямоугольником». Если квадрат отрезан от одного конца золотого прямоугольника, то другой конец будет новым золотым прямоугольником. На картинке большой прямоугольник (синий и розовый вместе) представляет собой золотой прямоугольник, потому что \ (a / b = \ varphi \).{2} \). Тогда мы получим \ (\ dfrac {a} {b} = \ dfrac {b} {a-b} \). Обе стороны \ (\ varphi \) .

Последовательность Фибоначчи

Последовательность Фибоначчи — это список чисел. Начните с 1, 1, а затем вы сможете найти следующее число в списке, сложив два последних числа вместе. Результирующая (бесконечная) последовательность называется последовательностью Фибоначчи. Поскольку мы начинаем с 1, 1, следующее число будет 1 + 1 = 2. Теперь у нас есть 1, 1, 2. Следующее число 1 + 2 = 3. Теперь у нас есть 1, 1, 2, 3. Следующее число 2 + 3 = 5.Следующее — 3 + 5 = 8 и так далее. Каждое из этих чисел называется числом Фибоначчи. Первоначально Фибоначчи (Леонардо Пизанский, живший около 800 лет назад) придумал эту последовательность для изучения популяций кроликов! Он, вероятно, понятия не имел, что произойдет, если вы разделите каждое число Фибоначчи на предыдущее, как показано ниже.

Таблица \ (\ PageIndex {1} \):

Число Фибоначчи	делится на число до	соотношение
1
1	1/1	= 1.0000
2	1/2	= 2,0000
3	3/2	= 1,5000
5	5/3	= 1.6667
8	8/5	= 1,6000
13	13/8	= 1,6250
21	21/13	= 1.6154 …
34	34/21	= 1,6190 …
55	55/34	= 1,6177 …
89	89/55	= 1.6182 …
…	…	…
		= 1,6180 …

Вот очень удивительный факт:

Примечание

Отношение двух последовательных чисел Фибоначчи приближается к золотому сечению.

Оказывается, числа Фибоначчи довольно часто встречаются в природе. Некоторые примеры — узор листьев на стебле, части ананаса, цветение артишока, распускание папоротника и расположение сосновой шишки. Числа Фибоначчи также встречаются в генеалогическом древе пчел.

Между тем, многие художники и исследователи музыки изучали художественные произведения, в которых золотое сечение играет важную роль. К ним относятся работы Микеланджело, Да Винчи и Моцарта.Заинтересованные читатели могут найти в Интернете множество ресурсов и видео. Возможно, неудивительно, что числа вроде 3, 5, 8 и 13 довольно важны в теории музыки; просто взгляните на клавиши пианино!

Номер ссылки

1. Список литературы (17)

Авторы и авторство

Fabulous Fibonacci

Введение

Числа Фибоначчи — интересная математическая идея. Хотя обычно они не преподаются в школьной программе, особенно в младших классах, преобладание их внешнего вида в природе и легкость их понимания делают их отличным принципом для обучения детей младшего возраста.

Цели обучения

После завершения уроков этого раздела учащиеся смогут:

• Объясните числа Фибоначчи и их происхождение.
• Определите числа Фибоначчи в природе и искусстве.
• Сгенерировать следующие числа в последовательности Фибоначчи.
• Создайте исходную номерную серию.
• Создайте прямоугольник и спираль Фибоначчи.
• Напишите стихотворение акростиха Фибоначчи.

Препарат

• Внимательно прочтите уроки.
• Соберите материалы.
• Распечатайте уроки на цветном принтере.

Урок 1: Введение в числа Фибоначчи

Вы когда-нибудь отрывали лепестки от ромашки? Если вы внимательно посмотрите на центр ромашки, вы обнаружите, что желтый центр не сплошной. Он состоит из наборов спиралей, выходящих из центра. Это не только ромашки! Природа — это математика.

Посмотрите фотографии сосновой шишки. У него такие же спирали.Они не ходят по кругу — они гаснут, как фейерверк. Посмотрите на изображения ниже, чтобы увидеть, как это выглядит. Сколько спиралей идет по часовой стрелке (зеленые линии)? Сколько спиралей идет против часовой стрелки (желтые линии)? Разве это не странно? Разве вы не ожидали, что они будут такими же?

Чтобы понять спирали в сосновых шишках, ананасах, маргаритках и многих других вещах в природе, нам нужно встретиться с математиком по имени Леонардо де Пиза. Большинство людей называют его Фибоначчи (произносится как фиб-о-науч-и).Около 800 лет назад он написал книгу, в которую включил математическую задачу следующего вида:

«Некий человек посадил пару кроликов на место, обнесенное стеной. Сколько пар кроликов можно произвести от этой пары за год, если предполагается, что каждый месяц каждая пара порождает новую пару, от которой второй месяц становится продуктивным? »
(Liber abbaci, стр. 283-284)

(Разве не странно, что 800 лет назад у них были проблемы со словами?) Работа Фибоначчи над этой проблемой привела его к следующей последовательности чисел:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

Можете ли вы определить, какое будет следующее число в последовательности?

Мы называем это последовательностью Фибоначчи, а числа — числами Фибоначчи.Чтобы получить следующее число в последовательности, вы складываете два предыдущих числа вместе. Теперь вернитесь и посмотрите на эти спирали из шишек. Что вы заметили в количестве спиралей в каждом направлении, теперь, когда вы знаете о числах Фибоначчи?

Урок 2: Нахождение Фибоначчи

Теперь, когда вы знаете, что такое числа Фибоначчи, вы готовы к охоте на Фибоначчи.

Цветы
Посмотрите на этот цветок (это лилейник Blizzard Bay, изображение любезно предоставлено Barossa Daylilies).Сколько у него лепестков? Вы видите шесть? Вы думаете, что шесть — это не число Фибоначчи? Посмотри внимательнее. Вы видите, что на самом деле есть два набора по три лепестка? Внешние лепестки с прямыми краями на самом деле не являются лепестками. Их называют чашелистиками. Так сколько же настоящих лепестков?

Не все цветы имеют по три лепестка. У некоторых есть намного больше. Некоторых сложно сосчитать, потому что лепестков слишком много или они расположены рядами. И есть несколько цветов, для лепестков которых нет чисел Фибоначчи.Посмотри, сможешь ли ты найти рисунок ромашки. Являются ли лепестки числом Фибоначчи?

Семенные головки
Семенные головки цветов расположены в виде спиралей последовательности Фибоначчи, как вы видели в шишках. Посмотрите на семенную головку этого подсолнуха. Вы видите, как упакованы семена? Но ни один из них не разбит. Спиральный узор позволяет цветку поместиться в большинство семенных головок на минимальном пространстве.

Как вы думаете, вы могли бы использовать эту информацию в своей жизни? Как вы думаете, сработает ли попытка упаковать такой чемодан? Почему или почему нет?

Еда
Посмотрите на это изображение фиолетовой цветной капусты.Если вы посмотрите внимательно, вы можете увидеть его центр, где начинаются маленькие цветочки (соцветия).

Вы видите спираль?

Природа полна чисел Фибоначчи и последовательностей Фибоначчи. Взгляните на плакат Лесной службы с изображением полевых цветов. Сколько примеров чисел Фибоначчи вы можете найти на плакате? (Не беспокойтесь, что слова расплывчаты; просто посмотрите на изображения цветов.)

Урок 3: Работа с Фибоначчи

Материалы

• Большой лист бумаги
• Миллиметровая бумага (Если вам нужна миллиметровая бумага, распечатайте ее на enchantedlearning.com / math / graphs / graphpaper)
• Линейка
• Компас
• Карандаши цветные

Прямоугольники Фибоначчи
Давайте нарисуем несколько прямоугольников, используя числа Фибоначчи. Это приведет нас в удивительное место. Завершите последовательность Фибоначчи ниже (попробуйте сделать это без посторонней помощи!):

0, 1, 1, 2, 3, 5, __, __, __, __,

Отлично! Вы готовы начать. Во-первых, мы собираемся сделать простую задачу на миллиметровой бумаге.

В создании таких прямоугольников интересно то, что соотношение (число, показывающее, как стороны соотносятся друг с другом) остается неизменным, независимо от того, насколько большим становится прямоугольник.Это соотношение дает нам прямоугольники, которые мы называем «золотым прямоугольником», потому что они считаются самыми красивыми прямоугольниками для его внешнего вида. Это соотношение называется золотым сечением. Вы можете найти его, разделив длинную сторону на короткую. Итак, если у вас есть прямоугольник 3 × 5, вы должны разделить 5 на 3. Это даст нам число примерно 1,61. (Узнайте больше о золотом сечении.)

Можете ли вы найти вокруг себя золотые прямоугольники? Как насчет этой бумажки?

Теперь вы создадите золотой прямоугольник самостоятельно (на большом листе бумаги, а не на миллиметровой бумаге) и увидите что-то действительно удивительное!

1. Сначала нарисуйте два квадрата рядом.С помощью линейки сделайте из них квадрат 0,5 см.
2. Теперь создайте квадрат 2 × 2 поверх первого квадрата. Итак, если бы первый квадрат был 0,5 см, квадрат 2 × 2 был бы квадратом 1 см, верно?
3. Продолжайте эту модель, делая каждый квадрат следующего размера в последовательности Фибоначчи. Итак, после квадрата 2 × 2 вы должны сделать квадрат 3 × 3 (1,5 см × 1,5 см), затем квадрат 5 × 5 (2,5 см × 2,5 см) и так далее. Это похоже на то, что вы делали с миллиметровой бумагой, только с помощью линейки. Продолжайте идти, пока не получите квадрат 21 × 21 (10.5 см × 10,5 см).
4. У каждого квадрата будет край, который представляет собой сумму двух квадратов перед ним, как и в последовательности Фибоначчи.
5. См. Схему ниже, чтобы узнать, как это должно выглядеть. Последнее еще не сделано. Вы видите, куда он пойдет?

Теперь с помощью циркуля нарисуйте дугу из квадратов с радиусом, равным размеру края квадрата. Не волнуйтесь из-за этих громких слов; они просто означают, что дуга будет составлять четверть круга.Дуги в первых квадратах будут действительно очень маленькими. Но посмотрите, как они растут!

Посмотрите на это изображение раковины наутилуса. Что ты заметил?

Art Connection
А теперь посмотрите на эту картину Мондриана:

Какие связи вы обнаруживаете между тем, что вы рисовали, и тем, что рисовал Мондриан? Все ли его прямоугольники выглядят для вас как прямоугольники, основанные на Фибоначчи?

добавочный номер

Оценка

Фибоначчи

Фибоначчи

Энди Нортон

Отделение Математическое образование

Университет Джорджии

---

* см. Другие примеры

---

Фибоначчи и золотое сечение

Связь между последовательностью Фибоначчи и Золотое сечение удивительно.У нас есть два, казалось бы, не связанных между собой темы, производящие такое же точное количество. Учитывая, что это число (или золотое сечение) нерационально, происшествие выходит за рамки совпадение. Это требует дальнейшего изучения …

---

Золотое сечение = (sqrt (5) + 1) / 2 или около 1,618 Золотое сечение, пожалуй, лучше всего отображается визуально. в золотом прямоугольнике. Этот прямоугольник обладает тем свойством, что его длина находится в соотношении Голена с шириной. Как следствие, мы можем разделить этот прямоугольник на квадрат и прямоугольник меньшего размера что похоже на первое.Пусть следующий набросок GSP проиллюстрирует:

---

Последовательность Фибоначчи — это последовательность, в которой определяется каждый член. как сумма двух предыдущих условий: Мы можем легко создать эту последовательность в электронной таблице, используя формулу выше. Это было сделано в центральной колонке. таблицы ниже:690

1	1
2	1	1
3	2	2
4	3	1.5
5	5	1.66666666666667
6	8	1,6
7	13	1,625
8	21	1,61538461538462
9	34	1,6112
10	55	1.61764705882353
11	89	1,61818181818182
12	144	1,61797752808989
13	233	1.61805555555556
14	377	1.61802575107296
15	610	1.61803713527851
16	987	1.61803278688525
17	1597	1.61803444782168
18	2584	1.61803381340013
19	4181	1.61803405572755
20	6765	1.61803396316671
21	10946	1.6180339985218
22	17711	1.61803398501736
23	28657	1.6180339 6
24	46368	1.61803398820533
25	75025	1.6180339889579
26	121393	1.61803398867044
27	196418	1.61803398878024
28	317811	1.6180339887383
29	514229	1.61803398875432
30	832040	1.6180339887482
31	1346269	1.61803398875054
32	2178309	1.61803398874965
33	3524578	1.61803398874999
34	5702887	1.61803398874986
35	9227465	1.61803398874991
36	14930352	1.61803398874989
37	24157817	1.6180339887499
38	3
1.61803398874989
39	63245986	1.6180339887499
40	102334155	1.61803398874989
41	165580141	1.6180339887499
42	267914296	1.6180339887499
43	433494437	1.6180339887499
44	701408733	1.6180339887499
45	1134	1.6180339887499
46	1836311903	1.6180339887499
47	2971215073	1.6180339887499
48	4807526976	1.6180339887499
49	7778742049	1.6180339887499
50	12586269025	1.6180339887499

Мы также взяли соотношение каждых двух последовательных термины в правом столбце.Если взять предел этого отношения по мере того, как условия становятся больше … Золотое сечение!

---

Понимание отношений Помните, теперь золотой прямоугольник можно разделить в квадрат и еще один золотой прямоугольник. Фактически, мы можем повторить этот процесс снова и снова. Предположим, мы начинаем с прямоугольника длиной Y и шириной X. Когда мы разделим этот прямоугольник на квадрат и новый золотой прямоугольник, получаем длину X и ширину Y-X для нового прямоугольника. Поскольку стороны прямоугольников равны в той же пропорции (а именно 1.618 …), получаем: Теперь вернемся к последовательности Фибоначчи. Соотношение последовательных терминов образует саму последовательность. Предположим, мы знаем что эта последовательность сходится к некоторому действительному числу (мы можем доказать это в уроке по геометрическим последовательностям). Тогда для больших значений из n: Но так И, если мы заменим на Y и с X мы имеем Коэффициент Голена!

φ Геометрические конструкции с участием Фи ★ Фибоначчи

Это отрывок из книги «Мастер Фибоначчи: человек, изменивший математику».Все цитаты занесены в каталог на странице «Цитаты».

ЧИСЛА ФИБОНАЧЧИ

(Предыдущий раздел: Золотое сечение )

Купить сейчас на Amazon

Прямоугольники со сторонами, равными длинам чисел Фибоначчи, сохраняют постоянное соотношение (длинная сторона делится на короткую) независимо от того, как прямоугольник большой. Прямоугольники, созданные с использованием золотого сечения, называются «золотыми прямоугольниками», потому что многие люди считают, что у них самые эстетичные пропорции.Например, прямоугольник со сторонами 8 × 5 имеет отношение 1,6.

Золотой прямоугольник

Золотые прямоугольники можно «клонировать» путем разделения квадрата со стороной, равной длине короткой стороны прямоугольника (Зевальда), как показано ранее на изображении Золотой спирали.

Золотой треугольник

Купить сейчас на Amazon

Другой геометрический вариант — золотой треугольник, также известный как возвышенный треугольник, который представляет собой равнобедренный треугольник, в котором отношение стороны к основанию равно Фи.В золотом треугольнике базовый угол 72 ° можно разделить пополам, чтобы создать два дополнительных самоподобных треугольника (внутренние углы и отношения между сторонами идентичны, независимо от длины сторон).

Golden Gnomon

В результате получается острый равнобедренный треугольник тех же размеров, что и исходный, и тупой равнобедренный треугольник, в котором длина равных (более коротких) сторон к длине третьей стороны создает соотношение, которое является величиной, обратной золотому сечению.Этот тупой равнобедренный треугольник известен как «гномон». Таким же образом могут быть созданы пятиугольники, пентаграммы и декагоны (Зевальд).

Золотая спираль

Ученые и математики изучили эти логарифмические спирали (названные в честь того, как увеличивается радиус спирали при движении вокруг нее по часовой стрелке), потому что они распознают узоры в объектах биологии и природы, полученные от животных. и растения в обширные галактики (Зевальд). Они также очевидны в гармонии и соотношении искусства и архитектуры.Золотая спираль использовалась в дизайне некоторых видов современного искусства и архитектуры, но вопрос о том, преднамеренно ли использовали золотое сечение древние художники и архитекторы (такие как Фидий, архитектор Парфенона), все еще обсуждается.

Сад золотого сечения — как использовать золотой прямоугольник в дизайне сада

Используя элементы золотого прямоугольника и золотого сечения, вы можете создать привлекательные и расслабляющие сады, независимо от того, какие растения вы выберете.Узнайте больше о планировании сада с золотым прямоугольником в этой статье.

Использование геометрии в садах

На протяжении веков дизайнеры использовали золотой прямоугольник в дизайне сада, иногда даже не осознавая этого. Если вам интересно, как это могло быть, взгляните на свой собственный сад. Сколько групп из 3, 5 и 8 человек вы видите? Вы посадили их таким образом, потому что нашли группу такого размера визуально привлекательной, не зная, что группы такого размера являются неотъемлемой частью золотого сечения.Многие японские сады известны своим успокаивающим дизайном, который, конечно же, выполнен в золотых прямоугольниках и пропорциях.

Что такое золотой прямоугольник?

Сад золотого сечения начинается с прямоугольника соответствующих размеров. Определите размер коротких сторон золотого прямоугольника, умножив длину длинных сторон на 0,618. В результате должна получиться длина ваших коротких сторон. Если вы знаете размер коротких сторон и вам нужно определить длину длинных сторон, умножьте известную длину на 1.618.

Создание сада золотого сечения

Другой аспект золотого сечения — последовательность Фибоначчи, которая выглядит так:
0, 1, 1, 2, 3, 5, 8…

Чтобы получить следующее число в последовательности, сложите два последних числа вместе или умножьте последнее число на 1,618 (Узнаете это число?). Используйте эти числа, чтобы определить, сколько растений поместить в каждую группу. По совпадению (или нет) в каталогах и садовых магазинах вы найдете множество цветочных луковиц, упакованных в группы по 3, 5, 8 и так далее.

Вы также можете использовать это соотношение для определения высоты растений, которые будут расти вместе. 6-футовое дерево, три 4-футовых куста и восемь 2,5-футовых многолетних растений — образец, повторяющийся в самых красивых садах.

Я дал вам множители, которые вы можете использовать для вычисления длин сторон золотого прямоугольника, но если вам нравится красота и элегантность математики, вам может понравиться вычисление размеров с помощью небольшого геометрического упражнения.

При рисовании на миллиметровой бумаге вы можете использовать рисунок для расчета размеров, назначив единицу измерения, например футы или дюймы, для каждого квадрата.Вот как:

• Нарисуйте квадрат.
• Нарисуйте линию, чтобы разделить квадрат пополам, так чтобы у вас была верхняя половина и нижняя половина.
• Проведите диагональную линию, чтобы разделить верхнюю половину квадрата на два треугольника. Измерьте длину диагональной линии. Это измерение будет радиусом дуги, которую вы собираетесь нарисовать.
• Используя простой циркуль, как вы использовали в начальной школе, нарисуйте ковчег с радиусом, который вы определили на шаге 3. Дуга должна касаться нижнего левого и верхнего левого углов квадрата.Самая высокая точка дуги — это длина вашего золотого прямоугольника.

Золотая спираль

Золотая спираль

ЗОЛОТАЯ СПИРАЛЬ, СПИРАЛЬ ФИБОНАЧЧИ
и натуральные спирали

Фигура начинается с золотого прямоугольника ABCD , с AB = 1 и = золотое сечение; рисуем квадрат ABA’D ‘и получаем золотой прямоугольник A’B’C’D ‘ длина сторон которых и 1. Этот процесс повторяется для получения прямоугольника A»B»C»D » и так далее, и так далее, а также внешние квадраты; золотой спираль состоит из следующих друг за другом четвертей окружностей, вписанных в каждый квадрат. Пунктирные диагонали BD и CD ‘ пересекаются в точке O , которая является асимптотической точкой спирали, называемой «око Бога» (золотое сечение также называют «божественной пропорцией»!) Линии АА ‘ и A’A » ‘ перпендикулярны и пересекаются в точках O .

Указанные числа — длины сторон квадратов.

Если вместо золотого прямоугольника мы начнем с прямоугольником Фибоначчи, с AB = F n-1 и BC = F n , где F n-1 и F n — два последовательных Фибоначчи чисел, мы получаем спираль, состоящую из четверти окружностей, которая называется Фибоначчи. спираль , которая приближается к золотой спирали, но не имеет Имущество «eadem mutata resurgo».

См. Также Падован спираль, коэффициент увеличения на каждом витке которой составляет шестую степень числа Падована, то есть около 5,4.

На этом сайте, можно найти объяснение того, что оболочка наутилус предположительно приближается к золотой спирали, но это очевидно противоречит прямому наблюдению: спираль наутилуса намного более точные и экспериментальные измерения показывают, что его коэффициент увеличения составляет около 3, что явно меньше 6.9 золотой спирали …

Аммонит: явно меньший коэффициент увеличения ….

Усик зеленой фасоли предположительно приближается к треугольная золотая спираль …

Сравните построение золотой спирали с тем, что спирали с n центров, что приближается к спирали Архимеда.

Швейцарская марка 1987 г.