Размеры матрицы фотоаппарата: Правильный выбор техники

Фотоаппараты Nikon, бюджетные и зеркальные

Японская компания Nikon является производителем оптики и устройств для обработки изображений. Была основана в 1917 году. Занималась производством оптики для флота Японии. После Второй Мировой войны переквалифицировались на производство продукции для населения. В 1946 году выпустили первый фотоаппарат Nikon. С тех пор компания стала совершенствовать свои технологии и производить новые фотоаппараты.

С 2006 года компания практически прекратила производство пленочных фотоаппаратов, и сконцентрировалась на производстве цифровых фотокамер. Кроме того Nikon производит фото-принадлежности, бинокли, сканеры и микроскопы. Под торговой маркой Nikkor выпускаются объективы для фотоаппаратов.

Компания Nikon одна из самых успешных компаний на рынке фотоаппаратуры. Их основными конкурентами являются Canon и Sony.

Модельная линейка фотоаппаратов компании Nikon довольно широка. Для любителей классики на данный момент выпускается пеленочная зеркальная усовершенствованная фотокамера F6.

Цифровые фотоаппараты делятся на три основные категории: зеркальные, серия COOLPIX и серия Nikon 1.

Зеркальные фотокамеры SLR разделяют на два вида: любительские и профессиональные. Зеркальные фотоаппараты отличаются уникальной системой позволяющей видеть предмет съемки, через объектив, используемый для выполнения снимка. Среди профессиональных очень популярна модель D700 а так же новинка D4.

Любительские зеркальные фотокамеры сейчас на гребне волны популярности. В топе продаж интернет магазинов такие модели как D7000, D3100, D5100 и конечно же D90. Любительские камеры отличаются от профессиональных тем, что они более компактные и несколько ограниченные в возможностях.

Серия COOLPIX это обычные компактные камеры с зуммированием. В свою очередь эта серия делится на три группы. Группа S (Style), отличаются компактностью, современным и красочным дизайном и невысокой стоимостью. Популярна модель S2600.

Группа L (Life) — это практичные фотокамеры с зуммированием. В модельной линейки представлены как суперзумы так и камеры с широкоугольным объективом. В группе L популярна модель L25.

Группа P (Performance) разработана специально для тех, кто хочет многофункциональную камеру, идущую в ногу со временем по доступной цене. Это гибридные камеры внешне похожие на зеркальные фотокамеры. Одной из самых популярных моделей является P510.

Компания Nikon производит и специализированную камеру для людей ведущих активный образ жизни COOLPIX AW100. Модель водонепроницаема, морозостойка и прочна, оснащена встроенным компасом и GPS с картой мира.

Серия Nikon 1 — это компактные камеры со съемным объективом. Пока что представлены всего три модели: J1, J2, V1. Отличаются интеллектуальным выбором снимка, режимом моментальной съемки. Делает до 60 кадров в секунду.

Nikon продолжает искать новые технологии для внедрения в фотокамеры. Основные тенденции в развитии компании это усовершенствование оптики и фотоаппаратов.

Размер матрицы цифрового фотоаппарата — Fantastic Factory

Каждый начинающий фотограф-любитель при приобретении цифровой фотокамеры, как правило, руководствуется рядом параметров, среди них на одном из первых мест стоит разрешение матрицы — количество пикселей, расположенных на ее поверхности. Продвинутые пользователи и профессионалы обязательно перед покупкой поинтересуются физическим размером матрицы. То есть реальной площадью, на которой будут размещены активные пиксели.

Производители часто не указывают физический размер матрицы цифрового фотоаппарата, по неизвестной для меня причине, а продавцы обычно об этой величине ничего сказать не могут, однако если вы планируете подходить к приобретению фотокамеры (или фотокамер) профессионально, вы сможете физический размер матрицы рассчитать. Единственное, что вы можете найти в спецификации к камере, это размер, указанный в обратном количестве дюймов, к примеру, 1/3.2 это матрица с физическими размерами примерно 3.4Х4.5 мм. Размеры матриц, которые сейчас выпускаются, их отношение к полному кадру 35мм, а так же кроп фактор вы можете увидеть на рисунке.

Почему же профессионалы так трепетно относятся к физическому размеру матрицы цифрового фотоаппарата? Да потому что от него зависит ряд важнейших параметров. Во-первых, это шум — цифровые помехи на изображении и всевозможные искажения, во-вторых, это глубина резкости изображаемого пространства, или ГРИП, ну и, в-третьих, конечно, габариты, и вес самой камеры.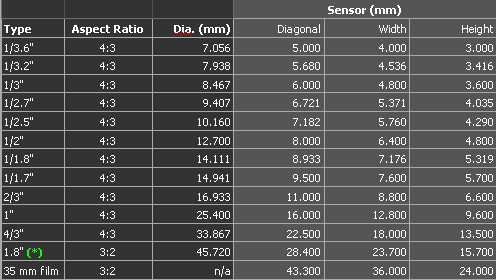

Начнем по-порядку. Цифровой шум — это искажения на изображении, он выглядит так, будто на снимке лежит пленка, на которую нанесены разноцветные точки. Количество «цифрового шума» на матрицах большего размера обусловлено тем, что пиксели “не наползают” друг не друга, между ними надежнее слой изоляции. Конечно, сам размер имеет значение — чем больше площадь, тем больше света может принять матрица за единицу времени, и тем сильнее полезный сигнал матрицы, тем меньше шума. Сигнал, полученный матрицей небольшого размера, приходится усиливать, конечно, пропорционально полезному сигналу усиливаются и становятся видимыми и шумы. Следует учитывать и возможности зарядов пробивать изоляцию между пикселями, получаются так называемые токи утечки, которые так же ведут к образованию шумов.

Далее, следует сказать о влиянии физического размера матрицы на глубину резкости изображаемого пространства (ГРИП). Какую бы формулу для расчета ГРИП вы не использовали, вы будете задействовать кроп фактор, то есть соотношение диагонали кадра соответствующего 35мм пленки и диагонали физического размера матрицы.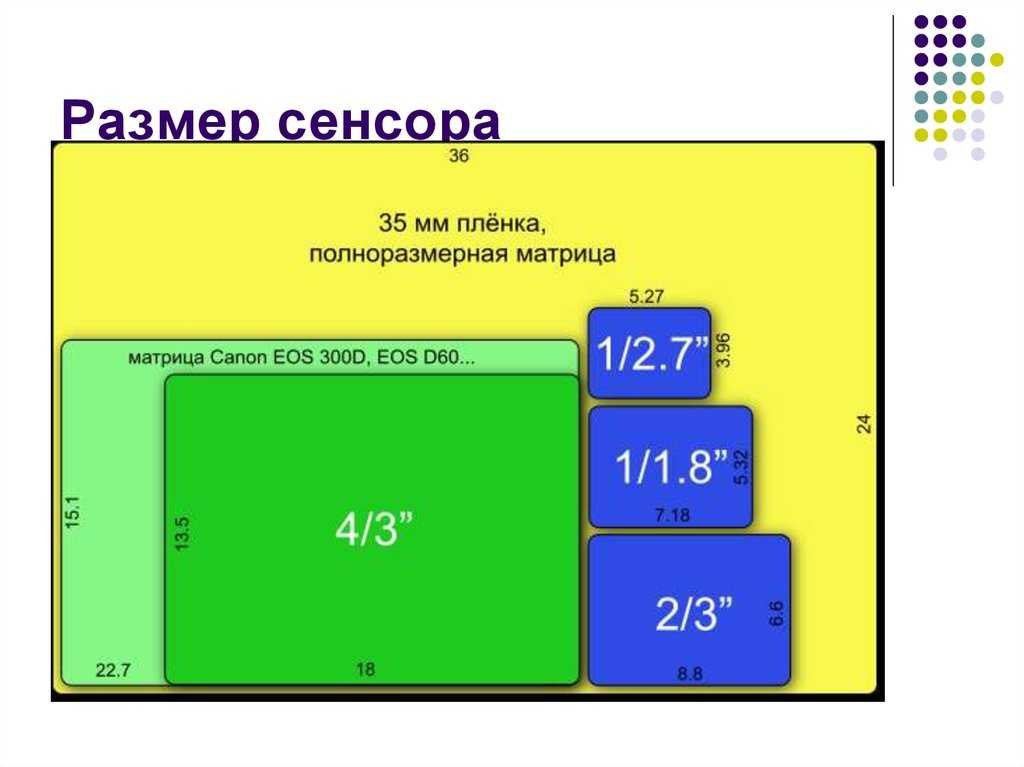 Другими словами, для 35мм кадра или матрицы кроп фактор будет равен единице. На практике, это означает, что чем меньше физический размер матрицы фотоаппарата, тем показатель ГРИП будет выше, а портретную съемку с размытым фоном лучше выполнять, используя камеры с большим физическим размером матрицы, так как при небольшой матрице задний фон будет прорабатываться и становиться четким, вопреки вашему желанию.

Ну и напоследок о габаритах. Логично предположить, что чем больше площадь матрицы, тем большее «пятно» света на нее должно попасть, соответственно должен использоваться объектив больший, по размерам, что влечет увеличение размера и веса самой камеры.

Внутренняя матрица камеры

с примером на Python | by Neeraj Krishna

Часть 3 обширной серии руководств по формированию изображения и калибровке камеры в Python

В предыдущей статье мы узнали о внешних свойствах камеры, которые должны смотреть на мир с точки зрения камеры. В этой статье мы увидим, как изображение формируется камерой, и узнаем о ее внутренних параметрах.

Фундаментальная идея формирования изображения заключается в захвате проекции точки на плоскость изображения камеры. Пиксели изображения соответствуют проекциям на плоскость изображения. Помните, что плоскость изображения похожа на пленку, которая захватывает световые лучи, отражающиеся от точек. Посмотрим, как это работает:

Проекция точки

На приведенном выше рисунке центр камеры расположен в начале координат 𝑂, а плоскость изображения находится на расстоянии 𝑓 от начала координат по направлению к оси Z -ve. 𝑓 называется фокусным расстоянием и обычно известен для камеры. Проекция точки 𝑃 на плоскость изображения равна 𝑃′. Координаты 𝑃 равны (𝑥, 𝑦, 𝑧), а координаты 𝑃′ равны (𝑥′, 𝑦′, 𝑓). Наша цель — найти координаты 𝑃′.

 из рисунка, 
 △OMP и △OO′P′ — подобные треугольники. 
 ⟹ х'/х = у'/у = f/z 
 ⟹ x′ = x ∗ f/z и y′ = y ∗ f/z 

Мы нашли координаты 𝑃′. Из приведенного выше уравнения видно, что по мере того, как точка 𝑃 удаляется от камеры, ее координата 𝑧 увеличивается, а ее проекция становится меньше.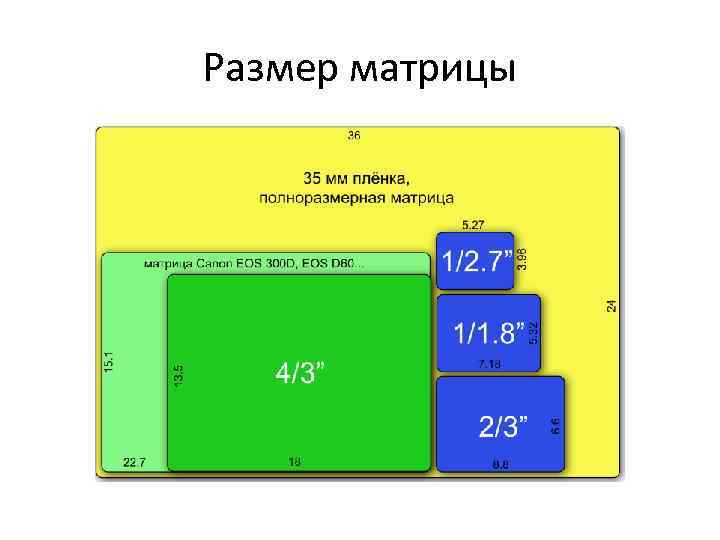 Таким образом, чем дальше объект от камеры, тем меньше он будет отображаться на изображении.

Чтобы получить пиксели изображения, мы просто берем координаты проекции, отбрасываем последнее измерение и наносим точки.

Например, мы нашли координаты 𝑃′ как (𝑥𝑓/𝑧, 𝑦𝑓/𝑧, 𝑓). Его координаты изображения будут (𝑥𝑓/𝑧, 𝑦𝑓/𝑧). Представим координаты изображения в виде (𝑢,𝑣), Тогда:

 (u, v) = (xf/z, yf/z) 

Итак, мы увидели, как камера формирует изображение. Итак, мы закончили со встроенными функциями камеры? Нет. В реальном мире все идет не так, как ожидалось, и на формирование образа влияют другие параметры.

Давайте рассмотрим каждый из них.

Масштаб

Когда вы покупаете камеру, ее регулируемое фокусное расстояние будет указано в ее описании, и обычно оно указывается в миллиметрах, но пространство, с которым вы работаете, может использовать другие единицы измерения, такие как пиксели. Поэтому нам нужно включить коэффициент масштабирования, который нормализует единицы измерения.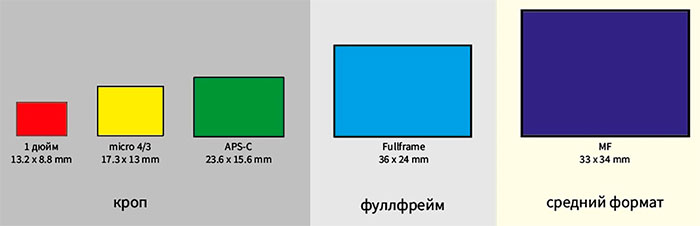

 (u, v) = (𝛼 *x/z, 𝛼 * y/z) 

Здесь вы можете представить 𝛼 как масштабированное фокусное расстояние или коэффициент преобразования.

Прямоугольные пиксели

В идеале мы предполагаем, что пиксели квадратные, но в реальном мире они могут быть прямоугольными с разной высотой и шириной. Из-за этого нам необходимо включить отдельные коэффициенты масштабирования для каждого измерения.

 (u, v) = (𝛼 * x/z, 𝛽 * y/z) 

Здесь 𝛼 — коэффициент масштабирования для измерения ширины, а 𝛽 — коэффициент масштабирования для измерения высоты.

Смещение

Перпендикулярная линия от центра камеры к плоскости изображения называется оптической осью. Точка пересечения этой оси с плоскостью изображения называется оптическим центром. Обычно оптический центр и начало плоскости изображения совпадают друг с другом, но в реальном мире они могут быть разнесены, как показано на рисунке ниже:

Оптический центр и начало координат могут не совпадать

Поэтому мы включаем смещение в уравнение чтобы учесть это:

 (u, v) = (𝛼 * x/z + x0, 𝛽 * y/z + y0) 

Здесь (𝑥0, 𝑦0) — смещение.

Наклон

До сих пор мы изображали плоскость изображения в виде прямоугольника, ширина и высота которого перпендикулярны друг другу. Но в реальном мире плоскость изображения может быть перекошена и напоминать параллелограмм, как показано на рисунке ниже:

Плоскость идеального изображения против плоскости перекошенного изображения

Так что же нам делать с этим? Мы предположили, что оси перпендикулярны друг другу, а на самом деле они расположены под углом. Если подумать, это проблема смены базиса. Учитывая точку 𝑃 относительно стандартных ортонормированных осей, нам нужно выразить ее относительно наклонных осей. Пусть (𝑥, 𝑦) — координаты 𝑃 относительно стандартного ортонормированного базиса, а (𝑥′, 𝑦′) — его координаты относительно асимметричного базиса. Наша цель — найти (𝑥′, 𝑦′).

 На приведенном выше рисунке 
 cos(90−θ) = y/y′ 
 ⟹ sinθ = y/y′ 
 ⟹ y = y’sinθ 
 ⟹ y′= y / sinθтакже 
 sin(90−θ) = (x - x')/y' 
 ⟹ y'cosθ = x - x' 
 ⟹ x' = x - y'cosθ 
 но, y'= y / sinθ 
 ⟹ x' = x - ycosθ / sinθ 
 ⟹ x′ = x - ycotθ 

Теперь, когда мы нашли (𝑥′, 𝑦′), давайте включим их в уравнение. Нам просто нужно заменить старые координаты этими новыми координатами.

 u = 𝛼 * (x - ycotθ)/z + x0 
 v = 𝛽 * (y / sinθ)/z + y0⟹ u = 𝛼x/z - (𝛼y/z)cotθ + x0 
 ⟹ v = (𝛽y / zsinθ) + y0 

Наконец, после учета параметров, влияют на формирование изображения, координаты изображения задаются как:

 (u, v) = [𝛼x/z - (𝛼y/z)cotθ + x0, (𝛽y / zsinθ) + y0] 

Мы можем представить это как матрицу умножение с использованием однородных координат:

Приведенная выше матрица называется внутренней матрицей камеры и обозначается 𝜅. Учитывая координаты точки мира относительно камеры, мы можем умножить их на внутреннюю матрицу камеры, чтобы получить однородные координаты точки на изображении.

 Здесь, 
 𝑃′ - Однородные координаты точки на изображении 
 𝜅 - Внутренняя матрица камеры 
 𝑃𝑐 - Однородные координаты точки мира относительно камеры 

Для преобразования из однородных координат просто делим на последний элемент :

Здесь (𝑢, 𝑣) представляют собой евклидовы координаты точки на изображении или положение пикселя.

Если вы заметили, последний столбец внутренней матрицы камеры является нулевым столбцом, и мы можем удалить его, поскольку он ни на что не влияет, и еще больше упростить матрицу следующим образом:

Теперь матричное уравнение можно переписать так:

Здесь не требуется представлять координаты точек в их однородном виде.

 Здесь, 
 𝑓 - фокусное расстояние 
 𝑠 - коэффициент наклона 
 𝑐𝑥,𝑐𝑦 - смещение 
 𝑎 - соотношение сторон 

Как видите, в собственной матрице камеры пять степеней свободы.

Вся эта теория может вас немного запутать. Итак, давайте сделаем практический пример, чтобы прояснить ситуацию.

Настройка

Репозиторий GitHub со всем кодом можно найти здесь.

Предполагая, что вы не настраивали среду ранее, вы можете сделать это сейчас, выполнив следующие команды:

 # создать виртуальную среду в anaconda 
 conda create -n camera-caulication-python python=3.6 anaconda 
 conda активировать камера-калибровка-python# клонировать репозиторий и установить зависимости 
 git clone https://github. com/wingedrasengan927/Image-formation-and-camera-dication.git 
 cd Формирование изображения и калибровка камеры 
 pip install -r requirements.txt 

Примечание: Предполагается, что вы установили Anaconda.

Мы будем использовать две основные библиотеки:

• pytransform3d: Эта библиотека имеет отличные функции для визуализации и преобразования в трехмерном пространстве.
• ipympl: Это меняет правила игры. Это делает график matplotlib интерактивным, позволяя нам выполнять панорамирование, масштабирование и вращение в режиме реального времени в блокноте, что полезно при работе с 3D-графиками.

Пример Интуиция

В этом примере мы рассмотрим простую установку, в которой камера расположена в начале координат, а плоскость изображения находится над ней вдоль +ve оси Z (мы будем работать с левой ручная система координат). Далее наносим несколько точек так, чтобы все они лежали в одной плоскости, параллельной плоскости изображения и вершине ее. Таким образом, легко визуализировать проекции и формирование изображения. Затем мы создаем внутреннюю матрицу камеры и используем ее для проецирования точек на плоскость изображения и формирования изображения. Наконец, мы преобразуем плоскость изображения, используя эту матрицу. Подробное пошаговое объяснение приведено ниже.

Записная книжка встроена ниже:

Пройдемся по ней пошагово:

• Сначала импортируем необходимые библиотеки. Файл utils.py содержит все необходимые вспомогательные функции. Волшебная команда %matplotlib widget включает бэкэнд ipympl, который позволяет нам играть с графиками.
• Далее мы определяем параметры плоскости изображения и точек. Здесь я взял 6 точек на высоте z=5 равномерно между пределами XY (-5, 5). Плоскость изображения находится на высоте z=2. Наконец, мы построим их все.

• Затем мы создаем внутренние матрицы камеры, которые позволяют нам проецировать точки на плоскость изображения и формировать изображение. Здесь мы создали четыре матрицы с разными параметрами, чтобы проиллюстрировать влияние каждой из них.

• Итак, мы поработали с параметрами и увидели их влияние на изображение. Теперь можно ли визуализировать, как будет выглядеть плоскость изображения в каждом случае? внутренняя матрица камеры представляет собой изменение базовой матрицы, и ее функция заключается в выборке точек из плоскости изображения. Теперь мы увидели, что можем получить матрицу преобразования, если возьмем обратную матрицу изменения базиса. Итак, давайте возьмем обратную внутреннюю матрицу камеры и применим результат к плоскости изображения. Тем не менее, мы должны удалить фокусное расстояние из сценария, так как он имеет дело с возвышением плоскости изображения, а мы хотим, чтобы возвышение было постоянным. Мы просто хотим увидеть влияние других параметров на плоскость изображения.

• На приведенном выше изображении показана плоскость изображения, если для параметра перекоса s установлено значение 2, изображение которого показано в правом верхнем углу предыдущего рисунка. Обратите внимание, как изображение и плоскость изображения ориентированы в противоположных направлениях.

Надеюсь, вам понравилась статья. Я призываю вас поиграть с блокнотом, повозиться с параметрами и посмотреть, как они влияют на изображение. Если у вас есть какие-либо сомнения или вопросы, пожалуйста, дайте мне знать в комментариях ниже.

1. Введение в компьютерное зрение — Udacity

Все изображения и рисунки в этой статье, если их источник явно не указан в подписи, принадлежат автору.

opencv — Расчет изображения в пикселях на мм с использованием матрицы калибровки камеры и расстояния до объекта не совпадает с размером объекта в пикселях в MS Paint

Я хочу рассчитать количество пикселей на сетку (т.е. пикселей на 11 мм) шахматной доски . Я делаю это, чтобы убедиться, что вычисление мм/пиксель, которое я получаю, используя калибровочную матрицу и формулу (ниже), совпадает с тем, что я увижу, когда открою изображение в MS Paint.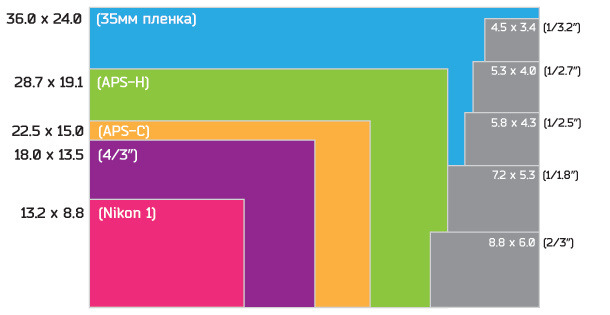

Для изображения шахматной доски (разрешение 1920×1080): размер сетки 11 x 7, каждая сетка 11x 11 мм, на расстоянии 500 мм (рисунок ниже).

Я вычисляю калибровочную матрицу, используя код:

 import cv2
импортировать numpy как np
импортировать pathlib
#из импорта утилит *
импортировать глобус
из argparse импортировать ArgumentParser
topview_image_path = 'шахматная_верхняя часть\*.png'
camera_orientation = 'вид сверху'
если camera_orientation == 'вид сверху':
    image_path = topview_image_path
def calibrate_chessboard (папка):
# Определение размеров шахматной доски
    ШАХМАТНАЯ ДОСКА = (6,9)
    критерии = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0,001)
    # Создание вектора для хранения векторов 3D-точек для каждого изображения шахматной доски
    точки объекта = []
    # Создание вектора для хранения векторов 2D точек для каждого изображения шахматной доски
    Имгпоинты = []
    # Определение мировых координат для 3D точек
    objp = np.  zeros((1, CHECKERBOARD[0] * CHECKERBOARD[1], 3), np.float32)
    objp[0,:,:2] = np.mgrid[0:CHECKERBOARD[0], 0:CHECKERBOARD[1]].T.reshape(-1, 2)
    prev_img_shape = Нет
    # Извлечение пути к отдельному изображению, хранящемуся в заданном каталоге
    print("путь к изображению:", путь_изображения)
    изображения = glob.glob(image_path)
    
    #images = glob.glob(f'{папка}/*.png')
    # если len(изображения) == 0:
    # изображения = glob.glob(f'{папка}/*.jpg')
    # печать (изображения)
    для fname в изображениях:
        img = cv2.imread(fname)
        серый = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
        # Найдите углы шахматной доски
        # Если на изображении найдено нужное количество углов, то ret = true
        ret, углы = cv2.findChessboardCorners(серый, CHECKERBOARD, cv2.CALIB_CB_ADAPTIVE_THRESH + cv2.CALIB_CB_FAST_CHECK + cv2.CALIB_CB_NORMALIZE_IMAGE)
        """
        Если желаемое количество углов обнаружено,
        уточняем координаты пикселей и отображаем
        их на изображения шахматной доски
        """
        если рет == Истина:
            objpoints.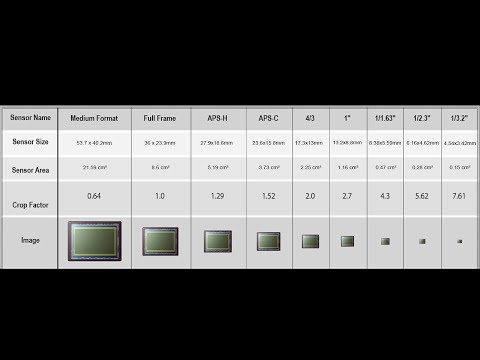
  append(objp)
            # уточнение координат пикселей для заданных 2d точек.
            углов2 = cv2.cornerSubPix (серый, углы, (11,11), (-1,-1), критерии)
            
            imgpoints.append (уголки2)
            # Рисуем и отображаем углы
            img = cv2.drawChessboardCorners(img,ШАХМАТНАЯ ДОСКА,углы2,рет)
        
        cv2.imshow('img',img)
        cv2.waitKey(0)
    cv2.destroyAllWindows()
    ч, ш = изображение.форма[:2]
    """
    Выполнение калибровки камеры с помощью
    передача значения известных 3D точек (objpoints)
    и соответствующие пиксельные координаты
    обнаруженные углы (imgpoints)
    """
    ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, grey.shape[::-1], None, None)
    вернуть [рет, мтх, дист, rvecs, tvecs]
если __name__ == '__main__':
    синтаксический анализатор = синтаксический анализатор()
    parser.add_argument('--type', dest='type',type=str, default='topview',help='это изображение сверху или сбоку?')
    parser.  add_argument('--folder', dest='folder',type=str, default='cal_images/checkerboard_topview',help='это изображение сверху или сбоку?')
    аргументы = парсер.parse_args()
    ШИРИНА = 6
    ВЫСОТА = 9# Калибровка
    ret, mtx, dist, rvecs, tvecs = calibrate_chessboard (args.folder)
    печать (мтх)
    печать (расстояние)
    mtx_list = ["матрица калибровки:\n", str(mtx),
                "\nматрица искажения:", str(dist)]
    txt_file = "matrix_" + camera_orientation +".txt"
    
    с open(txt_file, mode='wt', encoding='utf-8') как myfile:
        myfile.write('\n'.join(mtx_list))
 

и получить калибровочную матрицу как:

 M = [[2,86276094e+03 0,00000000e+00 8,23315889e+02]
 [0,00000000e+00 2,86846709е+03 5.80987675е+02]
 [0,00000000e+00 0,00000000e+00 1,00000000e+00]]
 

Это дает мне фокусное расстояние ( f ) в пикселях (M[0][0]), то есть 2862.

Затем я вычисляю размер в пикселях ( X_sizepx ) сетки шахматной доски 11 мм ( X_sizemm ) объект на расстоянии Z (в моем случае 500 мм) по формуле:

 X_sizepx = (f/Z) * X_sizemm
 

Подстановка всех значений: f = 2862 , Z = 500 , X_sizemm = 11 , получаю 62,94.