Уровни Фибоначчи в трейдинге и как их применяют
10 декабря 2021
10.12
6 минут
6 мин.
28 282
943
В природе все движения объектов на земле и в космосе подчинены невидимым законам. Это может быть направление, по которому растет лист дерева или закручиваются в спираль рукава галактики. Характерно то, что в обоих описанных случаях присутствует последовательность Фибоначчи и золотое сечение.
Неудивительно, что рано или поздно биржевые аналитики попытались применить “золотые стандарты” к движению биржевых графиков. В результате появились интересные стратегии, которые могут спрогнозировать поведение тренда.
В статье расскажем, что такое последовательность Фибоначчи, когда ее необходимо применять, покажем самые популярные методы и выясним, в чем кроятся их главные недостатки и риски.
Статьи
Содержание статьи
Последовательность Фибоначчи
Золотое сечение Фибоначчи
Числа Фибоначчи в трейдинге
Уровни Фибоначчи
Как строить уровни Фибоначчи
Торговля по уровням Фибоначчи
Волны Эллиотта
Веер Фибоначчи
Дуги Фибоначчи
Временные зоны (периоды) Фибоначчи
Другие инструменты Фибоначчи
Частые вопросы
Последовательность Фибоначчи
Числа Фибоначии получили свое название по имени математика из Италии Леонардо Фибоначчи.
Если быть точнее, его настоящее имя Леонардо Пизанский (1170-1250). В своем труде по арифметике “Книга абака” (лат. Liber abaci) он изложил особую последовательность чисел, которая и получила название “последовательность Фибоначчи”. Кроме этого, числа Фибоначчи тесно связаны с золотым сечением.
Последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т.д., можно продолжать до бесконечности. На этом этапе стоит отметить, что первые два значения могут быть 1 и 1 либо 0 и 1.
Структура последовательности состоит в том, что каждое следующее число является суммой сложения двух предыдущих чисел. Например, 3 это сумма 2 и 1, 5 это сумма 2 и 3, 8 сумма 5 и 3 и т.д. Однако это не самое интересное.
Золотое сечение Фибоначчи
Главной особенностью чисел, которой нашлось применение в трейдинге, является следующее. Если вы возьмете любое число в последовательности и поделите на предыдущее, результат всегда будет 1,618. Здесь оговоримся, что при делении чисел из начала последовательности значение будет приближено к 1,618.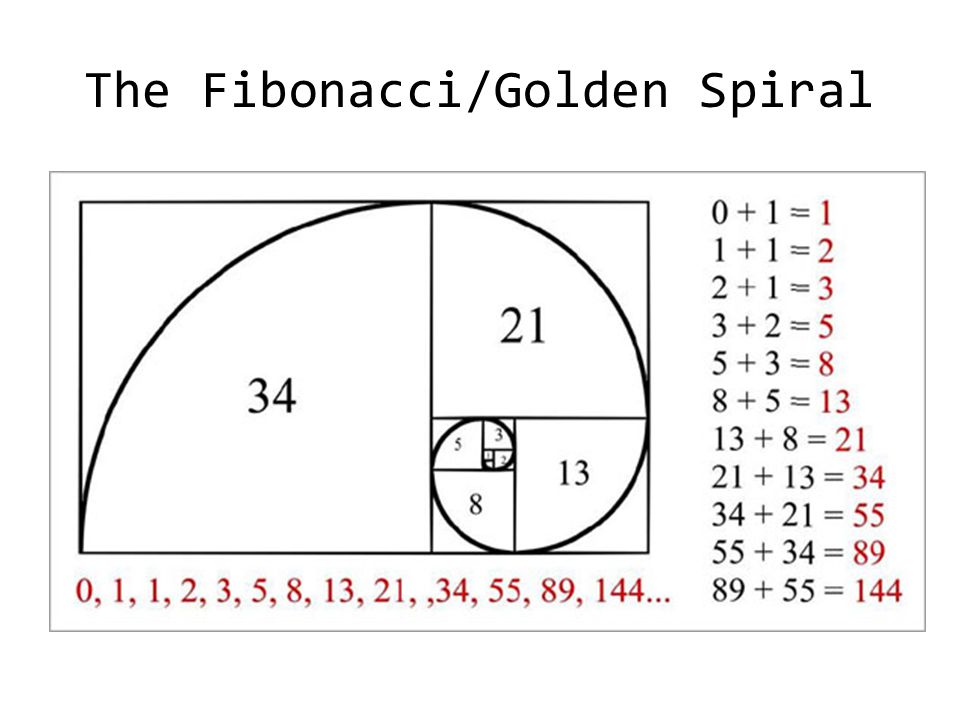
И чем дальше числа, тем точнее результат.
Само число 1,618 интересно тем, оно имеет прямое отношение к “золотому сечению”. Иногда его называют “золотой серединой”. Как мы уже отметили, чем дальше мы идем по последовательности, то ближе результат к значению “золотого сечения”.
Другая особенность заключается в обратном. При делении любого числа на следующее вы получите значение 0.618. Возьмите калькулятор и разделите 89 на 144 или 34 на 55. Если же вы поделите число на следующее через одно, то результат будет всегда стремиться к 0.382. Например, 34 поделить на 89.
Подобное соотношение чисел как раз и называется золотым сечением. В природе оно встречается повсеместно. Например, расположение каждого семени на подсолнухе составляет 0,618 оборота от предыдущего семени. Форма ракушки улитки также стремится к золотому сечению. Даже развитие человеческого тела не прошло мимо. Соотношение длины предплечья к длине руки стремится к значению 1,618. Данное движение известно как кривая Фибоначчи.
В целом, золотое сечение было известно в естественных и гуманитарных науках с древнейших времен. Развитие математики лишь подтвердило существование такого явления. Но как оно проникло в биржевую торговлю?
Из всего сказанного необходимо сделать вывод, что ключ в значениях, которые выражают результат соотношения одних чисел к другим. Пока мы привели всего два результата: 0.382 и 0.618.
Числа Фибоначчи в трейдинге
Первым решил применить законы золотого сечения к движению биржевых графиков американец Ральф Hельсон Эллиотт. Будучи инженером и управленцем, он решил изучить биржевые графики разных временных отрезков: годы, месяцы, недели, дни, даже часы и по 30 минут. Это позволило ему выделить закономерности, которые наблюдаются в ритмике падения и роста котировок. Связаны они были с числом 1,618 и соотношениями чисел, что мы описали выше.
Свои измышления Эллиот описал в труде “Закон природы — секрет вселенной”. Так появилась на свет волновая теория Эллиотта (о ней мы скажем позже отдельно).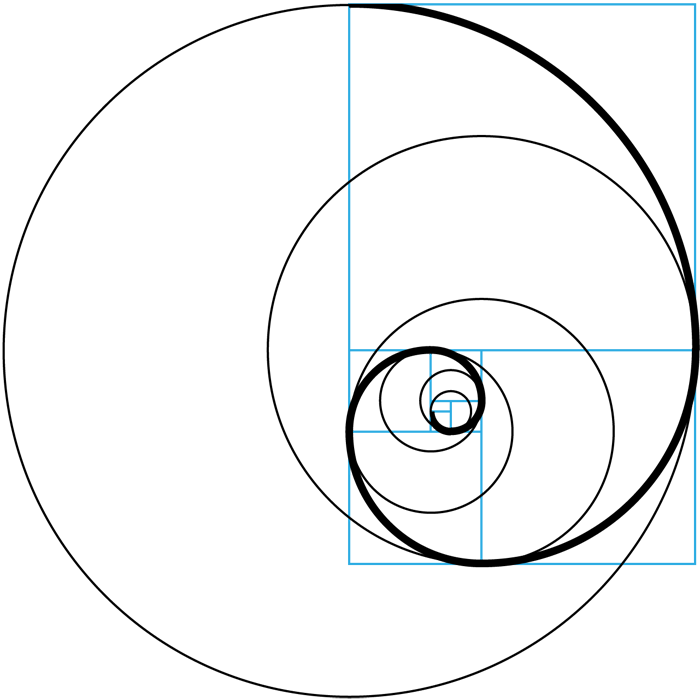
После этого биржевые аналитики разработали новые методы анализа, связанные с числами Фибоначчи. Анализ трейдеров помог выявить, что моменты, в которых чаще всего происходит движение графиков, связаны со значениями Фибоначчи. Суть в следующем.
Так, моменты коррекции актуальных трендов представляют собой процентное выражение от текущего движения цены. Данные события подозрительно часто происходят на значениях, связанных с последовательностью Фибоначчи. Иначе говоря, коррекции завершаются чаще всего на уровнях 23,6%, 38,2%, 50,0%, 61,8% и 76,4% в пределах выделенного отрезка. Здесь можно вспомнить числа 0,382 и 1,618 (остальные мы опустили).
Отметим, что значение 50 не имеет связи с последовательностью Фибоначчи. Это дополнительно введенный уровень, который связан с теорией Чарльза Доу, одного из основателей индекса Доу Джонса. Она гласит, что зачастую предел коррекции занимает 50% от первого импульса. При этом значения 23,6, 38,2, 61,8 и 76,4 зеркальны по отношению друг к другу от уровня 50.
Так, уровень 38,2 находится от уровня 50 на таком же расстоянии, что и 61,8 от 50 (23,6 и 76,4 аналогично).
В дальнейшем, на основе представленной закономерности, было построено несколько популярных способ анализа текущих трендов: уровни, веер, дуги и временные зоны Фибоначчи. Все они прогнозируют будущее движение и помогают подобрать момент для входа в тренд — откаты. Рассмотрим их.
Читайте также Что такое индекс Доу Джонса
Уровни Фибоначчи
Честно говоря, ответ на вопрос о том, что такое уровни Фибоначчи, уже наполовину описан в предыдущем блоке. Данный метод также называется как уровни коррекции или коррекция по Фибоначчи. Он позволяет выделить границы поддержки и сопротивления. Смысл процесса заключается в следующем.
Как правило, график в тренде периодические делает паузу, который называется откатом. При этом он немного проседает. После небольшой “передышки” тренд продолжает свое движение. Такие моменты служат хорошим сигналом трейдерам для входа в сделку, чтобы заработать на дальнейшем развитии.
Как строить уровни Фибоначчи
Сначала рассмотрим процесс построения уровней на примере популярного в России торгового терминала QUIK. Для начала в окне с графиком нам нужно выбрать инструмент “Уровни Фибоначчи”. Далее если тренд восходящий, то соединяем минимальную и максимальную цены. Если тренд нисходящий, то соединяем максимальную отметку с минимальной.
Как только вы соедините значения, будут отображены те самые линии Фибоначчи. Выделенный вами интервал следует понимать как диапазон “0-100%”. В свою очередь уровни Фибоначчи отображаются на отметках 23,6%, 38,2%, 50%, 61,8% выделенного диапазона 0-100%. Напоминаем, что 50 не имеет отношения к последовательности.
Торговля по уровням Фибоначчи
Итак, уровни выставлены. Они нам помогут выявить завершение коррекции или определить дальнейшие действия.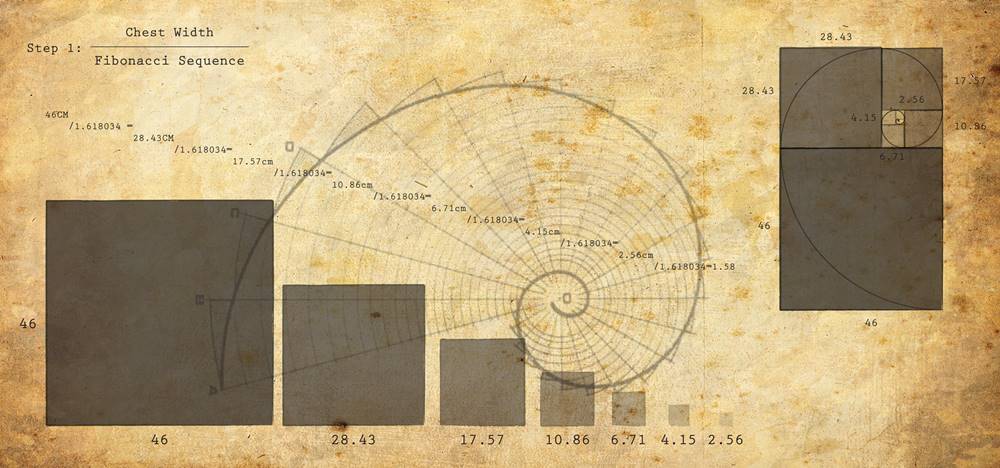
Для начала рассмотрим пример при растущем тренде.Пример 1 Восходящий тренд достиг определенного уровня и оттолкнулся от него. Это сигнал отката, тренд вошел в коррекцию. Трейдер приобретает актив и ставит ордер на продажу выше.
Пример2 Восходящий тренд игнорирует уровень коррекции и идет дальше. Трейдер ничего не приобретает, потому что момент для входа в сделку не был создан. Его задачей становится дождаться очередной коррекции.
График отскочил от уровня 38,2, трейдер открыл сделку. При этом движение проигнорировало в дальнейшем 23,6.
Уровни Фибоначчи применимы и при нисходящем тренде. В данном случае трейдеры шортят активы и зарабатывают на понижении цены. Рассмотрим два примера.
Пример 1 Возникшая коррекция дошла до уровня и отскочила от него по направлению тренда. Трейдер продает актив. Защитный ордер устанавливается за текущим максимумом цены, который находится около уровня.
Пример 2 Тренд проходит мимо уровня, трейдеру следует его игнорировать, ожидая следующего отскока на уровне.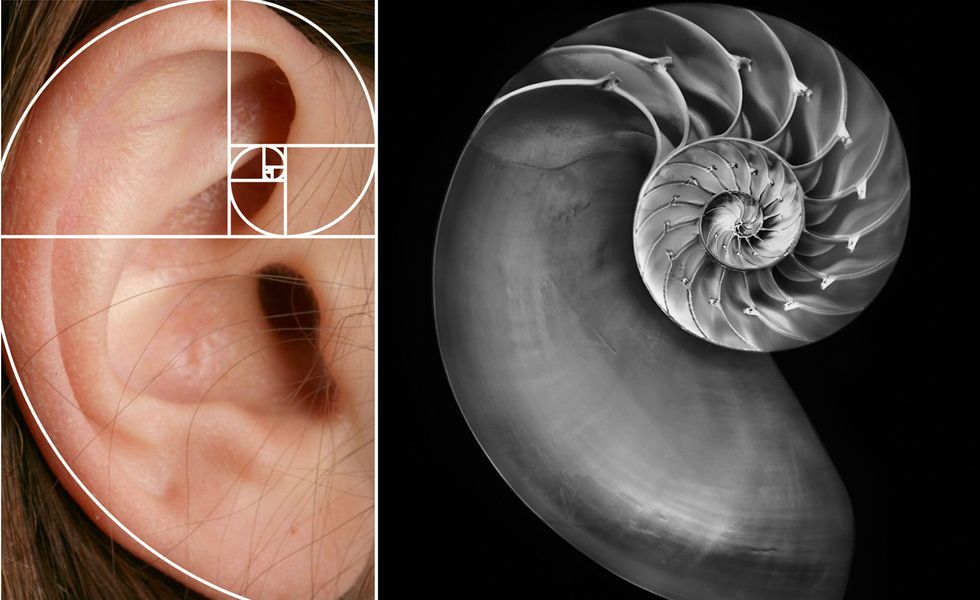
График пробил значения 23,6 и 38,2. Отскок от уровня 50% позволил принять решение о продаже.
Таким образом, уровни Фибоначчи позволяют спрогнозировать возможный момент окончания коррекции, а также направление развития тренда. Как видите, не всегда уровни коррекции срабатывают, поэтому данный метод (и все остальные) используют как дополнение к классическим индикаторам.
Не используйте уровни как самостоятельный индикатор, комбинируйте их с другими инструментами анализа. Кроме этого, сетка Фибоначчи накладывается на сформированный тренд, в котором прослеживается импульс.
Волны Эллиотта
Уровни коррекции Фибоначчи зачастую применяются с волновой теорией Эллиота, которую мы упоминали в начале. Из-за этого последняя порой именуется как волны Фибоначчи. Сначала разберем саму теорию. Она гласит о том, что весь путь тренда возможно разбить на 5 крупных волн: 3 импульсные и 2 коррекционные, идущие против тренда. Волны 1, 3 и 5 — импульсные, а 2 и 4 — коррекционные, т.
е. они сменяют друг друга. После них следуют три волны A, B и C, которые следуют в противоположном от тренда направлении.
В то же время эти волны (5 восходящих и 3 нисходящие) являются частью более крупной волны, которая, в свою очередь, действует по такому же принципу. Это значит, что если вы заметили пять волн как на примере выше, то, скорее всего, перед вами одна большая первая волна. Далее все волны складываются как фрактал, и вот во что они превращаются:
Таким образом, если мы узнаем, к какой волне сейчас относится текущая цена, то сможем спрогнозировать ее дальнейшее движение.
Для трейдеров особо интересна волна 3, т.к. она лидирует по длине и скорости. Поэтому по теории Эллиота трейдеру следует открыть сделку под конец 2-й волны и закрыть ее в конце третьей. Но как ее увидеть? Здесь и пригодятся линии Фибоначчи, о которых говорили ранее.
Теория Эллиота утверждает, что 3-ая волна по своей высоте относится к 1-ой как 1,618. Соответственно, если 1 и 2 волны уже видны на графике, уровни Фибоначчи рассчитают нам высоту третьей.
Для этого в терминалах существует функция “расширение Фибоначчи”. Нам нужны три точки: начало 1-й волны, конец 1-й и 2-й. После этого отобразятся наши фибо-уровни и прогнозируемая отметка со значением 1,618 — это предполагаемый конец 3-й волны.
Соотношение других волн выглядит так:
- волна 1 формируется сама;
- волна 2 часто завершается на уровнях 50,0 и 61,8;
- волна 3, как мы выяснили, обычно составляет 1,618 от 1-й;
- волна 4 завершается между 38,2 и 50,0, часто в форме флэта;
- волна 5 имеет диапазон 61,8-100% от интервала от начала 1-й и до конца 3-й.
Даже если каждый раз удачно определять текущую волну, метод не гарантирует 100% совпадения. Третья волна (1,618) может не дойти до значения или пробить его, разброс допустим. Сами волны не всегда легко определить на графике.
Веер Фибоначчи
Данный метод тесно связан с уровнями и позволяет определить, в какой момент произойдет коррекция или же разворот тренда.
Инструмент встроен во многие терминалы.
Рассмотрим на примере восходящего тренда. От минимальной цены (А), начала движения импульса, ведем линию до максимальной цены (Б). От точки Б ведем вертикальную линию вниз, которая пересекает все ключевые уровни: 38,2, 50,0 и 61,8 (они устанавливаются автоматически). Появляются точки пересечения уровней и вертикальной линии.
Теперь снова от точки А проводим линии, но уже через возникшие точки пересечения. В итоге возникает фигура, похожая на веер. Лучи получившегося веера обозначают предполагаемые точки завершения коррекции. В них возможен вход в торги.
Важно! Не применяйте данный метод как самостоятельный. Он используется как дополнение к техническому анализу.
Дуги Фибоначчи
Дуги отличаются тем, что используются не только для прогнозирования движения тренда, но и определения времени этого движения. Это значит, что у нас появляется значение времени.
Для построения графика точка начала тренда и его конца соединяются прямой.
Далее требуется построить три полукруга (дуги), центром которых выступает конец тренда. Каждая из дуг должна пересекать нашу начерченную линию на уровнях 23,6, 38,2, 50, 61,8 и 78,6. Порой трейдеры вырабатывают стратегии, основываясь лишь на уровнях 38,2, 50 и 61,8.
То, какие получатся дуги, зависит от размеров нашего графика. Чем длиннее нарисованная нами линия, тем шире получится каждый полукруг.
Обратите внимание! Из-за субъективного выбора диапазона графика и привязки ко времени дуги Фибоначчи считаются спорным методом. Как и другие методики, его следует использовать в связке с классическими индикаторами.
Временные зоны (периоды) Фибоначчи
Временные периоды Фибоначчи позволяют спрогнозировать время, в которое произойдет некоторое событие: коррекция, разворот или достижение максимума и минимума. В основу метода заложена сама последовательность чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13 и т.д.
Для построения периодов в качестве отсчетной точки нужно выбрать локальный максимум или минимум, она отмечается как 0.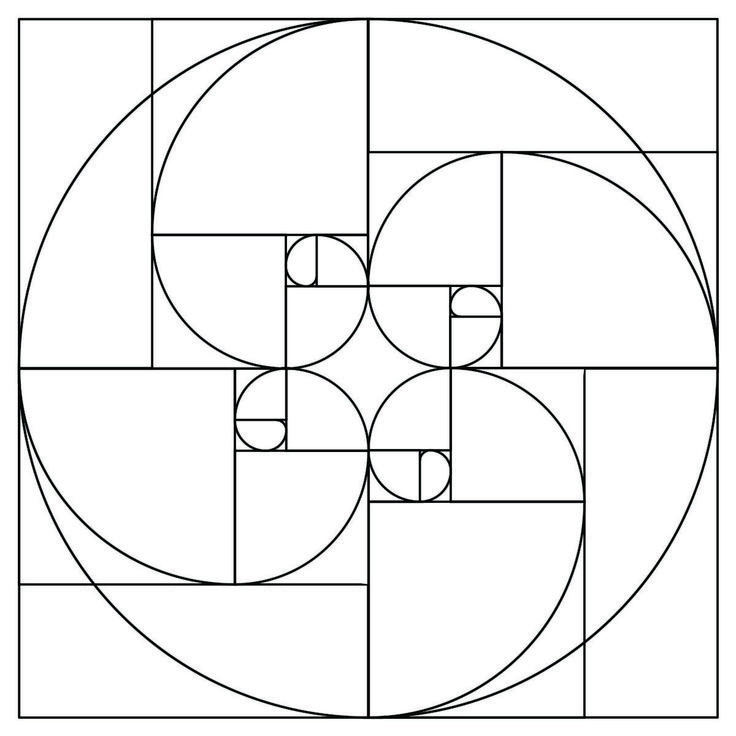
Вторая выбранная отметка укажет на конец построения расчета. В результате получается диапазон, на котором будет расположена наша последовательность. Далее на графике появятся вертикальные линии, каждая из них соответствует своему числу в последовательности. В момент времени, на котором находится вертикальная линия, возможна коррекция.
При достижении графика одной из вертикальных линий следует привлечь дополнительные аналитические инструменты. Из-за субъективного выбора начальной точки расчета прогнозирование не лишено погрешностей.
Первые пять периодов, отмеченные вертикальными линиями, часть трейдеров игнорирует. Связано это с высокой долей ненадежности. Точно также в последовательности чем дальше числа, тем точнее значение 1,618 при делении.
Другие инструменты Фибоначчи
На основе последовательности Фибоначчи созданы и другие методы построения расчетов и прогнозирования. Например, спираль, канал, клин, окружность Фибоначчи и многие другие. Как понятно из названия, они различаются по способу анализа, но цель у всех одна — нахождение точки для выгодного открытия сделки.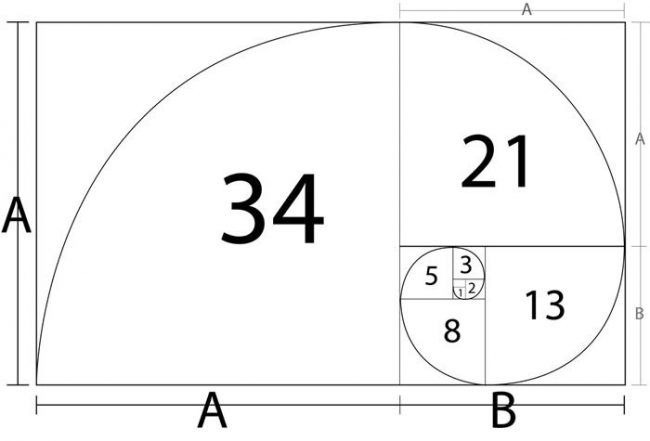
Применение последовательности Фибоначчи в трейдинге для начинающих трейдеров может показаться обычным поклонением мистике. Однако опытные трейдеры выстраивают собственные стратегии с привлечением подобных инструментов. Важным моментом является то, что методы, построенные на последовательности Фибоначчи, должны выступать дополнительным индикатором, но никак не основным или самостоятельным.
Частые вопросы
Насколько торговля по Фибоначчи принимается в биржевой среде?
+
Подобные инструменты внедрены в торговые терминалы. Это значит, что от них не отказываются. Однако использовать фибо-уровни следует как дополнительные индикаторы.
Гарантирует ли какой-либо уровень коррекцию?
+
Тренд вошел в коррекцию на одном из уровней. Это значит, что нужно входить в сделку?
+
Невозможно дать верный ответ лишь на основании уровня. Все существующие биржевые инструменты дают представление о текущей ситуации и варианты развития тренда.
Решение принимает трейдер.
Когда лучше всего использовать методы Фибоначчи?
+
Они применимы только к выраженному тренду.
Публикуем только проверенную информацию
Автор статьи
Анастасия Чернова Налоговый консультант
стаж: 10 лет
консультаций: 3930
Составляет налоговые декларации 3-НДФЛ для физлиц. Помогает клиентам получить вычет даже в сложных случаях, защищает интересы клиентов на камеральных проверках, составляет претензии в отношении результатов проверки, оказывает устные и письменные консультации
Поделиться:
351
Золотое сечение Фибоначчи
Фибоначчи (1170—1250) — настоящее имя — Леонардо из Пизы — считается крупнейшим математиком средневековой Европы.
Фибоначчи был родом из купеческой семьи, и отец, желая, чтобы сын изучил математику, отправил его учиться в Алжир. Потом юноша не раз сопровождал отца в деловых поездках, побывал в Византии, Сирии, Египте, где немало общался с местными учеными.
Кролики помогли Фибоначчи проиллюстрировать ряд, позднее названный его именем. В этом ряду каждый член — сумма двух предыдущих
На молодого человека большое впечатление произвели позиционная система счисления и арабские, они же индийские, цифры. В то время в Европе мало кто знал об этой системе. Фибоначчи стал распространять ее. Особенно он хвалит позиционную систему и арабские цифры в своей работе «Книга абака», которая была написана в 1202 г. В этой книге он также приводит любопытный пример с постоянно размножающимися кроликами.
«Человек посадил пару кроликов в загон, окруженный со всех сторон стеной. Сколько пар кроликов за год может произвести на свет эта пара, если известно, что каждый месяц, начиная со второго, каждая пара кроликов производит на свет одну пару?»
Число пар в каждый из двенадцати последующих месяцев будет соответственно 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144.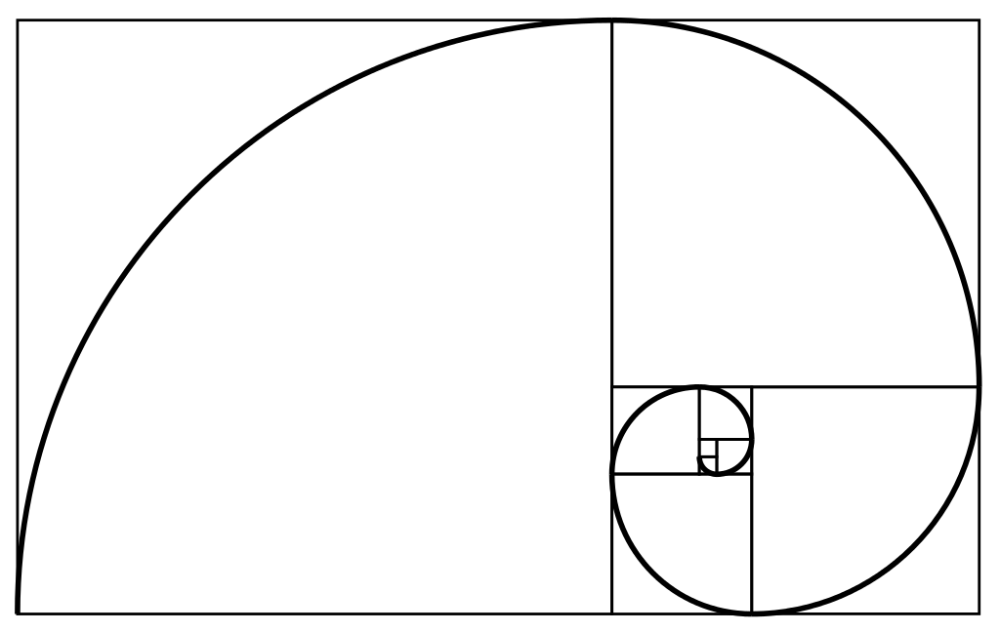
.. Таким образом, кролики создают ряд, каждый член в котором — сумма двух предыдущих. Он известен как ряд Фибоначчи, а сами числа называют числами Фибоначчи. По этим числам можно изобразить спираль, выстраивая квадраты с соответствующими сторонами.
Спираль Фибоначчи
У этой последовательности есть несколько любопытных свойств. Например, если последующий член разделить на предыдущий, то получается число, примерно равное 1,618. Правда, для первых чисел эта закономерность почти не работает. Если 5 разделить на 3, получится 1,66. Но чем больше числа, тем точнее ответ. А коэффициент 1,618 — это знаменитое золотое сечение. Такая пропорция считается наиболее гармоничной в архитектуре и живописи. Таким образом, спираль Фибоначчи близка к золотому сечению, хотя полностью таковым не является.
Кроме того, последовательность Фибоначчи встречается в природе. Например, если вы рассмотрите семечки в подсолнухе, то убедитесь, что они расположены в два ряда спиралей: одна закручена по часовой стрелке, другая — против.
Причем в одной такой спирали 55 семян, в другой — 34. А это — числа Фибоначчи.
Семечки в подсолнухе располагаются в соответствии со спиралью Фибоначчи
Подобные пропорции встречаются в соотношении длин фаланг пальцев, в чертах лица, в молекуле ДНК и в расположении листьев и веток у растений.
Надо сказать, по справедливости, что эти пропорции были известны на Востоке задолго до Фибоначчи, но сложилось так, что они обрели его имя.
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или, другими словами, меньший отрезок так относится к большему, как больший ко всему. Золотое сечение было известно с глубокой древности и считалось залогом гармонии и красоты.
Золотое сечение на примере античной статуи
Античные статуи имеют именно такие пропорции. Однако сам термин ввел Леонардо да Винчи. Он говорил: «Если человеческую фигуру — самое совершенное творение Вселенной — перевяжем поясом и отмерим потом расстояние от пояса до ступней, то эта величина будет относиться к расстоянию оттого же пояса до макушки, как весь рост человека относится к длине от пояса до ступней».
Поделиться ссылкой
Фибоначчи и Золотое сечение
Патрик Марсолек (4/2013)
В 2011 году Американский музей естественной истории наградил юного ученого 7-го класса Эйдена Дуайера премией «Молодой натуралист» за предложение устройства солнечных батарей на основе Фибоначчи. серии. Эйден заметил, что естественная схема расположения листьев дерева вокруг ствола, которая соответствует ряду Фибоначчи, будет более эффективной, чем традиционные массивы солнечных батарей. Точно так же в области биомимикрии компания PAX Scientific из Сан-Рафаэля, Калифорния, разрабатывает технологии движения воздуха и жидкости, также основанные на рядах Фибоначчи. Их «принцип оптимизации» применяется к вентиляторам, смесителям, крыльчаткам и т. д., которые более эффективно перемещают воздух и жидкости в системах. Использование чуда ряда Фибоначчи и его коррелята, золотого сечения, происходит уже тысячи лет. Признавая это сознательно или нет, люди имеют удивительные отношения с рядами Фибоначчи и золотым сечением.
Что такое ряд Фибоначчи? Хотя Леонардо Пизанский, он же Фибоначчи, не открыл эту серию, он прославился благодаря ей. Хотя этот числовой ряд был записан индийскими математиками по крайней мере еще в 6 веке, Фибоначчи сделал его широко известным примерно в 1202 году, когда он опубликовал свой математический трактат Liber Abaci. В почти сноске в своей книге он предложил задачу подсчета числа пар репродуктивных кроликов, которые будут получаться из месяца в месяц от одной стартовой пары кроликов. Ряд продолжается таким образом: 1,1,2,3,5,8,13,21,34… и так до бесконечности. Каждое последующее число в ряду является суммой двух предыдущих чисел. Ряд Фибоначчи — это самовоспроизводящийся ряд, растущий из самого себя, как растение.
Ряд Фибоначчи связан с золотым сечением, потому что по мере увеличения чисел в ряду отношение любых двух соседних чисел становится все ближе и ближе к золотому сечению, также называемому золотым сечением или греческой буквой фи ( е). Мы говорим, что отрезок делится в точке Фи, если большая часть, деленная на меньшую часть, равна всей прямой, деленной на большую часть.
Соотношение Фи — это отношение большей части к меньшей, что примерно равно 1,6180339.887 …, и чаще всего приближается к 1,618.
Это число не является рациональным, то есть десятичные дроби никогда не повторяются, и его нельзя записать в виде дроби двух целых чисел. Некоторые математики утверждают, что число Фи может быть самым иррациональным известным числом. Это записывается алгебраически как f = (1 + ÷5)/2. Интересно отметить, что f2 = 2,61803… и 1/f = 0,61803… Каждый показатель степени имеет одинаковые цифры после запятой. Число Фи действительно самоподобно и возникает само по себе, как ряд Фибоначчи.
Прямоугольник, стороны которого пропорциональны фи, является золотым прямоугольником. Если мы отрежем квадрат от прямоугольника, у нас останется еще один золотой прямоугольник. Размеры меньшего прямоугольника меньше размеров «родительского» прямоугольника ровно в f раз. Начертите две диагонали любой пары прямоугольников «мать-дочь» в ряду, и все они пересекутся в одной точке.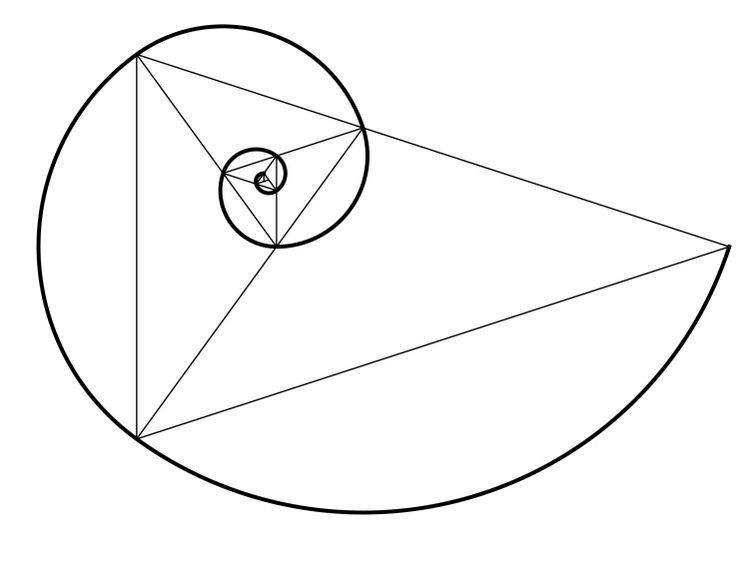
Ряд непрерывно уменьшающихся прямоугольников сходится к этой недостижимой точке. Клиффорд А. Пиковер предложил называть эту точку «Глазом Бога».
Многие исследователи и историки утверждают, что Золотой прямоугольник и Золотая пропорция включены во многие священные структуры, такие как Стоунхендж, древние индийские храмы, египетские пирамиды, пирамиды в Америке и Парфенон в Греции. Например, исследователи недавно искали Фи в Великой мечети в Кайруане в Тунисе, строительство которой началось в 670 году нашей эры и видоизменялось в течение нескольких сотен лет. План мечети не идеально квадратный из-за условий местности. Принимая это во внимание, исследователи все же пришли к выводу, что общий прямоугольник плана здания, отношение внутреннего открытого двора ко всему зданию, расположение башни, а также высота и пропорции различных ступеней башни — все это использует Пропорция Фи.
Скептики утверждений о наличии золотого сечения в большинстве архитектурных сооружений заявляют, что очень легко жонглировать числами, чтобы найти близкие соотношения, и что люди часто упускают из виду неточности в измерениях.
В одном критическом взгляде на появление золотого сечения в Парфеноне золотое сечение часто рисуется поверх изображения фасада храма. Исследователи отметили, что части структуры неизменно выходят за пределы нарисованных золотых прямоугольников и что размеры варьируются от источника к источнику. Скептики также заявляют, что можно нарисовать всевозможные геометрические фигуры на любом плане участка или возвышении памятника, но если их главные вершины не попадают в реальную физическую точку, пересечение или угол, выводы, сделанные из такого цифры «в лучшем случае произвольны, а в худшем – бессмыслица».
Точно так же вопрос о том, была ли построена Великая пирамида в Египте с использованием соотношения Фи, также был предметом многочисленных споров. Некоторые исследователи утверждают, что наклон сторон Великой пирамиды очень близок к наклону Золотой пирамиды, которая имеет отношение f как неотъемлемую часть своей геометрии. Поскольку нет никаких исторических свидетельств того, что египтяне знали о Фи или даже могли вычислить угол наклона Великой пирамиды, многие считают ее присутствие в их архитектуре случайным.
Шваллер де Любич, французский оккультист, интересовавшийся сакральной геометрией, считал, что египтяне знали о f. Он много лет изучал Луксорский храм в Египте. Он написал обширный том под названием «Храм человека», в котором поделился своими исследованиями. В своих трудах де Любич утверждает, что Фи закодирована по всему храму и что храм демонстрирует своего рода гномонический рост, который подобен геометрической прогрессии в ряду Фибоначчи и выражается в человеческом теле.
Гномон — это фигура, которая при добавлении к исходной фигуре дает большую фигуру аналогичной формы. Это качество спиралей и прямоугольников ряда Фибоначчи и золотого сечения. (изображение) Таким же образом развиваются твердые ткани в телах животных, такие как кости, зубы, панцири и рога. В «Храме человека» ДеЛюбиц демонстрирует, как секции Луксорского храма отображают эту гномоническую прогрессию, очень похожую на некоторые индуистские храмы, которая соответствует росту человеческого тела. Каждая часть храма строится на предыдущей части в соответствии с пропорциями Фи.
Он считает, что весь храм представляет собой полноценного человека.
Хотя скептики снова заявляют, что ДеЛюбич жонглировал числами, чтобы проиллюстрировать свои теории, ДеЛюбич отмечает, что, хотя он мог измерить существование Фи в пропорциях храма, Фи также обладает универсальным символическим качеством, которого нет физически. Аналогия, которую он предлагает, состоит в том, чтобы представить себе вращающуюся сферу, которая дает нам представление об оси. Мы воображаем эту ось, но она не имеет объективного существования. Мы используем эту воображаемую ось для вычисления свойств, движения и массы сферы. Де Любич утверждает, что камни Храма Луксора являются записью числового выражения Фи, как и измеримых свойств сферы. Фи в своем универсальном аспекте непроявлен, но очень сильно пронизывает храм, как и ось сферы.
ДеЛюбич не первый, кто видит Фи в таком виде. Немецкий математик и астроном XVII века Иоганн Кеплер считал, что золотое сечение служит фундаментальным инструментом Бога при создании Вселенной.
Швейцарский архитектор Ле Корбюзье сосредоточился на системах гармонии и пропорции. Он описывал свойства золотого сечения как «ритмы, кажущиеся глазу и ясные в своих отношениях друг к другу. И эти ритмы лежат в самом корне человеческой деятельности. Они звучат в человеке органической неизбежностью, той самой тонкой неизбежностью, которая вызывает вычерчивание золотого сечения детьми, стариками, дикарями и учеными».
Как и Золотой прямоугольник, Фи является неотъемлемой частью математики всех пятиугольников. В отличие от трех-, четырех- и шестисторонних правильных многоугольников, пятиугольник не проявляется в кристаллических структурах, потому что его форму нельзя плотно склеить. Пятиугольник лучше сочетается с асимметричными формами и живым ростом. Из-за этого некоторые люди связывают пятиугольник и фи с живыми существами. Многие растения, по-видимому, предпочитают пятиугольную симметрию.
Числа Фибоначчи встречаются во многих спиралевидных расположениях листьев на ветках растений и деревьев.
(изображения) От любого листа на ветке, если вы подсчитаете количество листьев вокруг стебля, пока не дойдете до листа прямо над ним, количество листьев часто является числом Фибоначчи, обычно 3, 5 или 8. Количество витков от начального листа до конечного также обычно является числом Фибоначчи. Отношение числа витков к числу листьев называется филлотактическим коэффициентом дерева. Хотя филлотактический коэффициент не всегда соответствует ряду Фибоначчи, он часто соответствует ему: у липы и вяза он равен 1/2; для бука и лещины – 1/3; для абрикоса, вишни и дуба — 2/5; для груши и тополя – 3/8; а для миндаля и ивы — 5/13. Это все чередующиеся числа Фибоначчи. Эту схему предложил семиклассник Эйден Двайер, чтобы сделать свои солнечные батареи более эффективными.
Точно так же спиралевидные узоры на сосновых шишках, артишоках и ананасах являются отличными примерами чисел Фибоначчи. Если вы посчитаете спирали, идущие в обоих направлениях на этих растениях, они часто являются соседними числами Фибоначчи.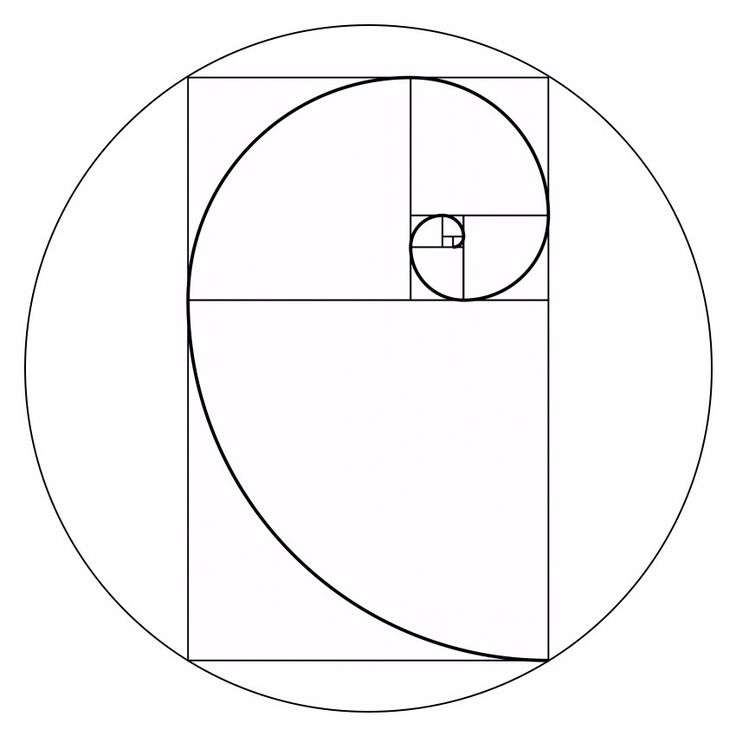
Некоторые шишки имеют три спирали по часовой стрелке и пять спиралей против часовой стрелки, некоторые имеют 5 и 8, а некоторые имеют 8 и 13. Некоторые сосновые шишки и ананасы имеют три различных спиральных узора, которые являются соседними числами Фибоначчи, такими как 5, 8 и 13. спирали в подсолнухах также показывают пары Фибоначчи 21 и 34, 34 и 55, 55 и 89, или даже 89 и 144. Если вы измерите углы между каждым листом, почкой или чешуей у этих растений, вы найдете Фи.
Одна интересная боковая касательная здесь, круги на полях, похожие на подсолнухи, появились на холме Вуборо в графстве Уилтшир, Англия, в 2000 году. натуральный цветок с его отношениями Phi.
Как предположил Шваллер де Любич, соотношение Фи также присутствует в организме человека. Пупок (верхняя часть бедер на скелете) делит тело по золотому сечению. Принимая полный рост за 1, тело от ступней до пупка равно 1/f, а часть от пупка до макушки равна 1/f2. Однако эта пропорция не постоянна. При рождении пупок находится в центре, и его положение на теле меняется по мере взросления.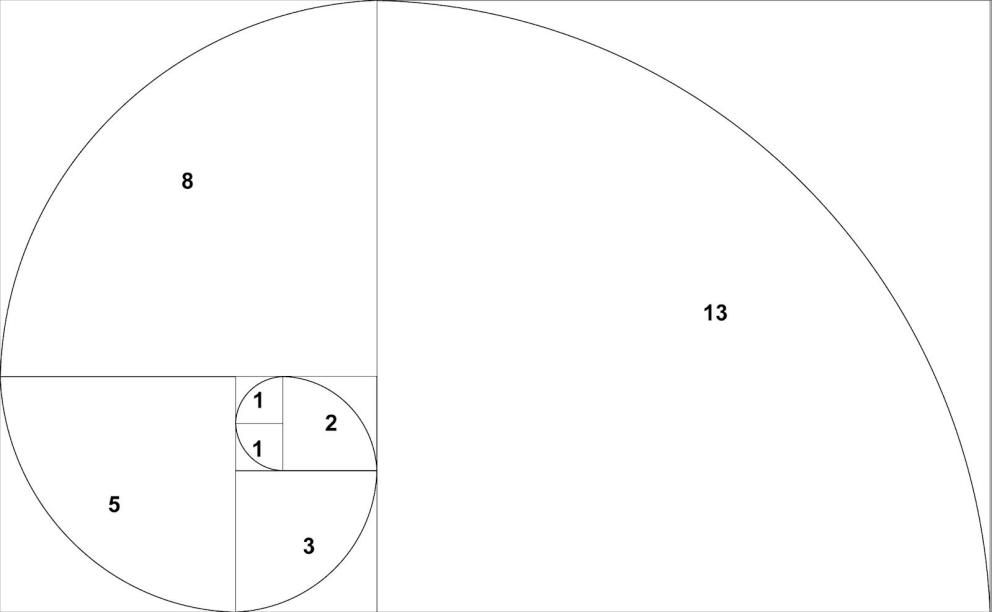
У взрослой женщины пупок обычно находится немного выше золотого сечения, а у мужчин — немного ниже. Аналогичные отношения возникают между участками ног и рук. Вы можете посмотреть на свой указательный палец и увидеть соотношение Фи. Соотношение первых двух сегментов к полной длине пальца близко к золотому сечению. Согните указательный палец, как будто сжимая его в кулак, и вы увидите прямоугольник, близкий к Фи, на согнутом пальце. Аналогичные соответствия происходят в лице и голове.
От жуков до бабочек, от лошадей до лягушек исследователи отмечают, что взаимосвязь их различных частей тела часто близка к Phi. Следует отметить, что размеры этих разных животных и частей тела не совсем соответствуют золотому сечению. Однако, когда кто-то усредняет измерения, они часто очень близки. Живые, растущие формы танцуют внутри и вокруг этого идеального соотношения.
Золотая Спираль, которая может быть образована из Золотого Треугольника или Золотого Прямоугольника, также является отражением самой распространенной спирали, встречающейся в природе.
Это логарифмическая спираль, которую мы видим в папоротниках, раковинах наутилуса, бараньих рогах, ураганах и даже в галактиках. Подобно Золотому сечению или Золотому прямоугольнику, эти спирали имеют одинаковую пропорцию независимо от масштаба, который, как некоторые утверждают, является выражением бесконечности.
Люди живут в теле и мире, начертанном буквой Фи. Кажется естественным, что мы стремимся найти его выражение в нашей архитектуре, искусстве, музыке и языке. Мы уже видели, как Золотая пропорция может быть в некоторых священных зданиях. Числа Фибоначчи также фигурировали в Матра-виттах санскритской и пракитской поэзии 7-го века. Один автор дает специальное правило для создания измерителей путем добавления двух предыдущих измерителей и вычисляет серию измерителей 1, 2, 3, 5, 8, 13, 21…, которая является последовательностью Фибоначчи.
Другие предполагают, что Леонардо да Винчи использовал эту пропорцию в некоторых своих картинах, таких как Мона Лиза и Тайная вечеря.
Пол Ларсон из Университета Темпл утверждал, что он обнаружил золотое сечение в некоторых из самых ранних григорианских песнопений, известных как Liber Usualis. Музыка, кажется, состоит из фраз на некоторых из Золотых Пропорций. Другие проанализировали некоторые произведения Белы Бартока, в частности его «Музыку для струнных, перкуссии и челесты». Эта музыка показывает дивизии в 89, 55, 34, 21, 13 и 8 тактов, все числа Фибоначчи. Принято считать, что Барток сознательно не пытался использовать числа Фибоначчи в своей музыке, по крайней мере, он не делал записей об этом.
Густав Фехнер измерил размеры тысяч печатных книг, рамок для картин в галереях, окон и других обычных прямоугольных объектов, таких как игральные карты. Результаты варьировались по-разному, но средние значения многих из этих объектов действительно приближались к соотношению Фи. Интересно, что многие книги, выпущенные между 1550 и 1770 годами, имели соотношение Фи с точностью до миллиметра.
Ясно, что если зайти достаточно далеко, то можно найти Золотое сечение, куда бы ни посмотрели.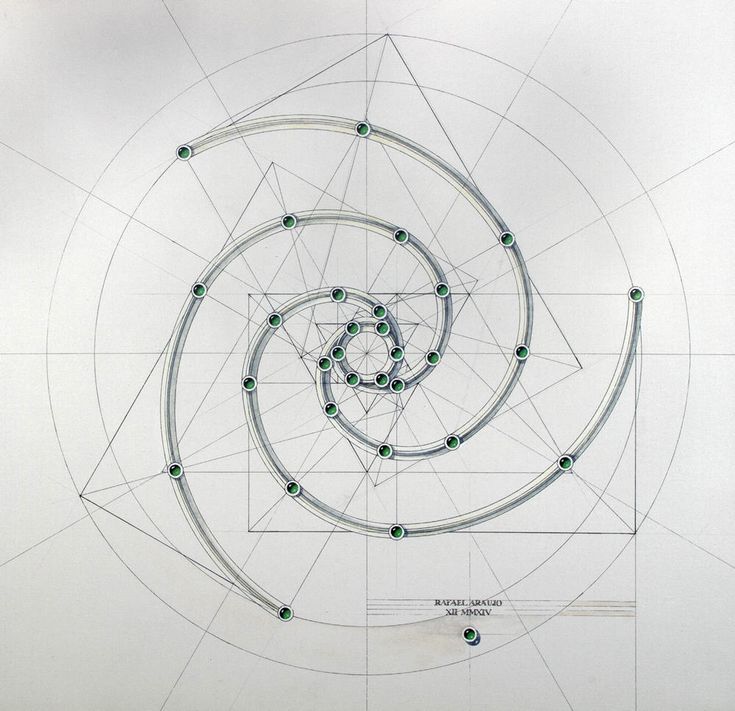
Мы можем видеть это в древней архитектуре, искусстве, поэзии и сделать поспешный вывод, что наши предки знали об этой пропорции и использовали ее. Тем не менее, существует очень мало фактических свидетельств того, что у древних народов была математика, которую мы имеем сегодня, чтобы понимать число Фи, или что даже исторические художники и музыканты сознательно использовали ее.
Тем не менее, в нашем отношении к этому соотношению происходит что-то любопытное. Оно снова и снова проявляется в вещах, которые мы создаем, и может продолжать давать нам новые элегантные решения современных проблем. Возможно, как предполагает Шваллер де Любич, соотношение Фи является в некотором роде базовой константой мира, в котором мы живем. Когда древние люди были в гармонии с миром природы и строили священное пространство, им не нужно было знать формулу Фи — соотношение было встроено в эту структуру как отражение их самих и их связи с миром природы.
Патрик Марсолек — писатель, танцор, фасилитатор, клинический гипнотерапевт и директор отдела внутренних рабочих ресурсов.
Он ведет группы и проводит занятия по расширенным человеческим возможностям, исследованию сознания, личностному развитию и сострадательному общению. Он предлагает свои услуги предприятиям, отдельным лицам и семьям, а также проводит семинары по расширению возможностей. Он является автором книг «Преобразуйте себя: руководство по самогипнозу» и «Радостная интуиция». См. www.PatrickMarsolek.com для получения дополнительной информации.
Что такое последовательность Фибоначчи и почему она является секретом музыкального величия?
20 мая 2022, 16:37
Последовательность Фибоначчи часто появляется в музыке и искусстве. Картина: Getty Images / Классика FMСофия Рицци
гения от Моцарта до Леонардо да Винчи использовали последовательность Фибоначчи. Но что это такое и почему из него получается отличная музыка?
Последовательность Фибоначчи получила прозвище «код природы», «божественная пропорция», «золотое сечение», «спираль Фибоначчи» и другие.
Что такое последовательность Фибоначчи?
Проще говоря, это ряд чисел:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
Следующий номер в последовательности получается сложением двух чисел перед ним . Соотношение для этой последовательности составляет 1,618 . Это то, что некоторые люди называют «Божественной пропорцией» или «Золотым сечением».
Подробнее: НАСА выпускает жуткое «пение» черной дыры — послушайте здесь
Если из этих значений сделать квадраты, получится красивая спираль:
Спираль Фибоначчи. Картина: Классика FMКажется знакомым? Вы, наверное, видели это раньше…
Басовый ключ и спираль Фибоначчи. Картина: классический FMЭта последовательность, узор и спираль проявляются во многих вещах, которые вы, возможно, никогда не замечали. Используется в искусстве и музыке; просто посмотрите, как Леонардо да Винчи использовал его в одной из своих самых известных картин, Моне Лизе:
Использование Леонардо да Винчи последовательности Фибоначчи в «Джоконде» (Мона Лиза).
Картина:
Getty Images / Классика FMПоследовательность Фибоначчи в музыке
Последовательность Фибоначчи играет большую роль в западной гармонии и музыкальных гаммах. Вот факты:
- Октава на фортепиано состоит из 13 нот. Восемь белых клавиш и пять черных клавиш.
- Гамма состоит из восьми нот, из которых третья и пятая составляют основу основного аккорда
- В гамме доминирующей нотой является пятая нота, которая также является восьмой нотой из всех 13 нот, составляющих октаву.
- Восемь разделить на 13 равно 0,61538 … приблизительно Золотое сечение )
Начинаете видеть закономерность? Это все числа в последовательности Фибоначчи: 3, 5, 8, 13.
Последовательность Фибоначчи можно увидеть на клавиатуре фортепиано. Картина: Классика FMКто использовал последовательность Фибоначчи?
Композиторы и производители инструментов использовали последовательность Фибоначчи и золотое сечение на протяжении сотен лет для сочинения и создания музыки.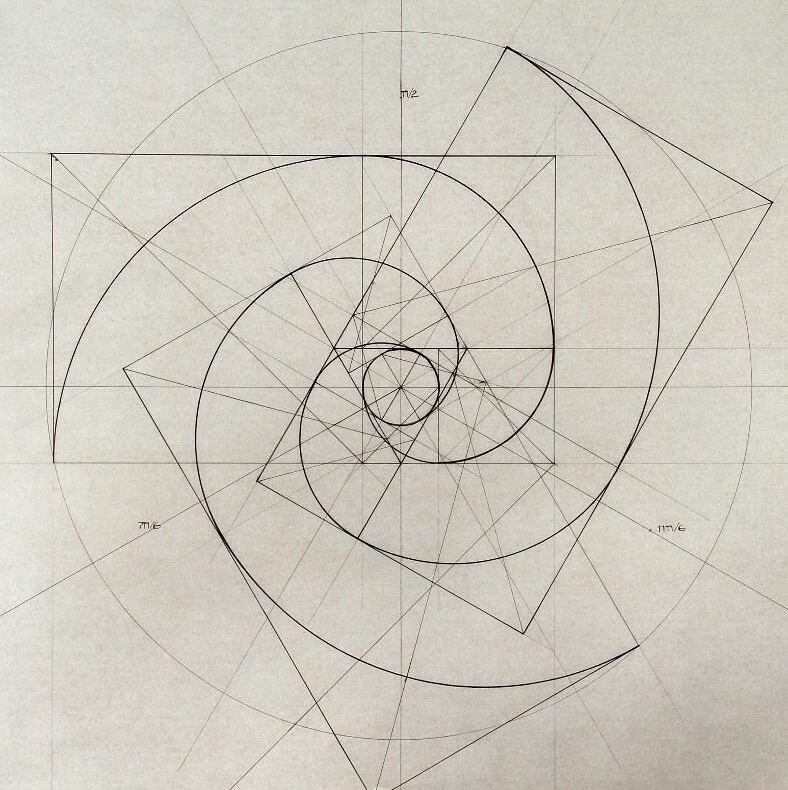
Моцарт, например, основывал многие свои произведения на золотом сечении, особенно его фортепианные сонаты.
- Традиционная соната состоит из двух частей:
Экспозиция – где вводится музыкальная тема - Развитие и реприза – где тема развивается и повторяется
А вот и интересное…
Моцарт аранжировал свои сонаты для фортепиано так, чтобы количество тактов в развитии и репризе , деленное на количество тактов в экспозиции , равнялось примерно 1,618 , Золотая Соотношение.
Возьмем в качестве примера первую часть Сонаты для фортепиано Моцарта № 1 до мажор.
Золотое сечение в Сонате для фортепиано № 1 Моцарта. Картина: Классика FMНа приведенной выше диаграмме C — первая часть сонаты в целом, B — 9-я часть.0117 развитие и резюмирование, и экспозиция .
экспозиция состоит из 38 тактов, а разработка и реприза состоит из 62.