Сферическая аберрация | это… Что такое Сферическая аберрация?
У этого термина существуют и другие значения, см. Аберрация.
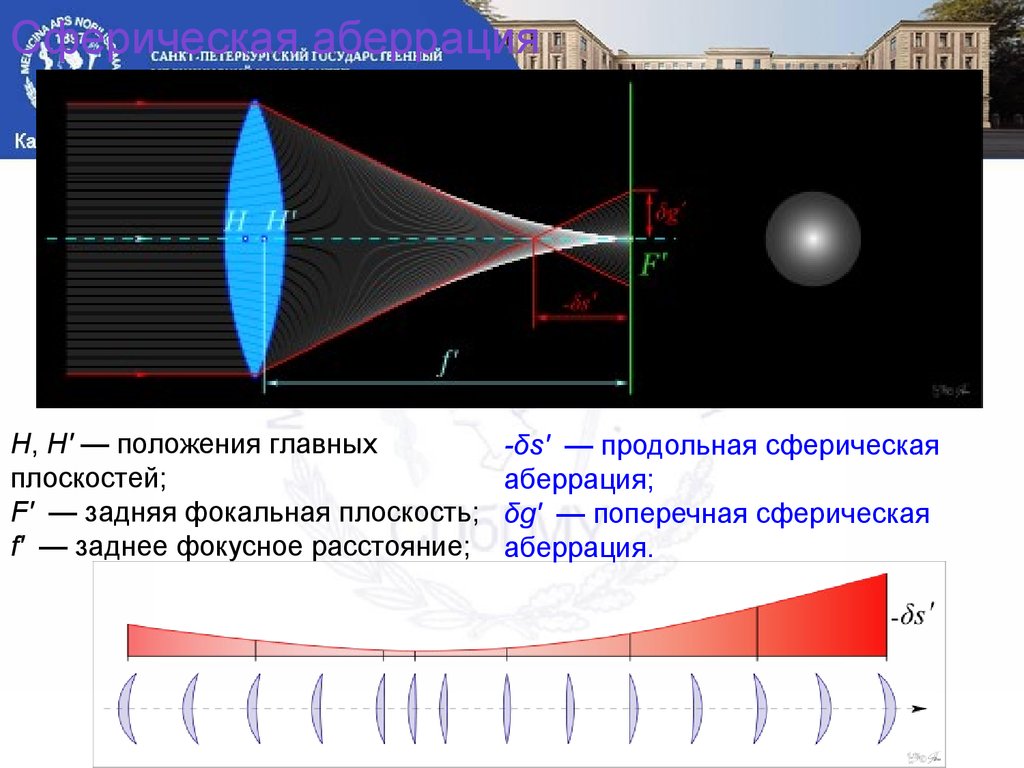
Схема сферической аберрации, где
H, H’ — положения главных плоскостей;
F’ — задняя фокальная плоскость;
f’ — заднее фокусное расстояние;
-δs’ — продольная сферическая аберрация;
δg’ — поперечная сферическая аберрация.
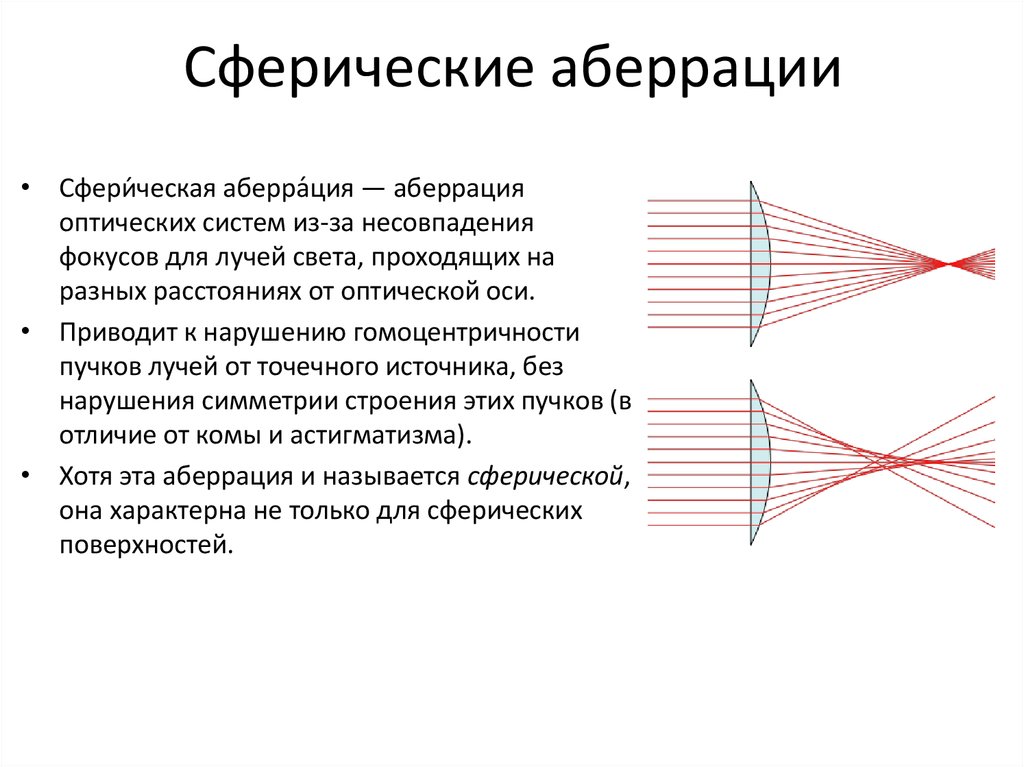
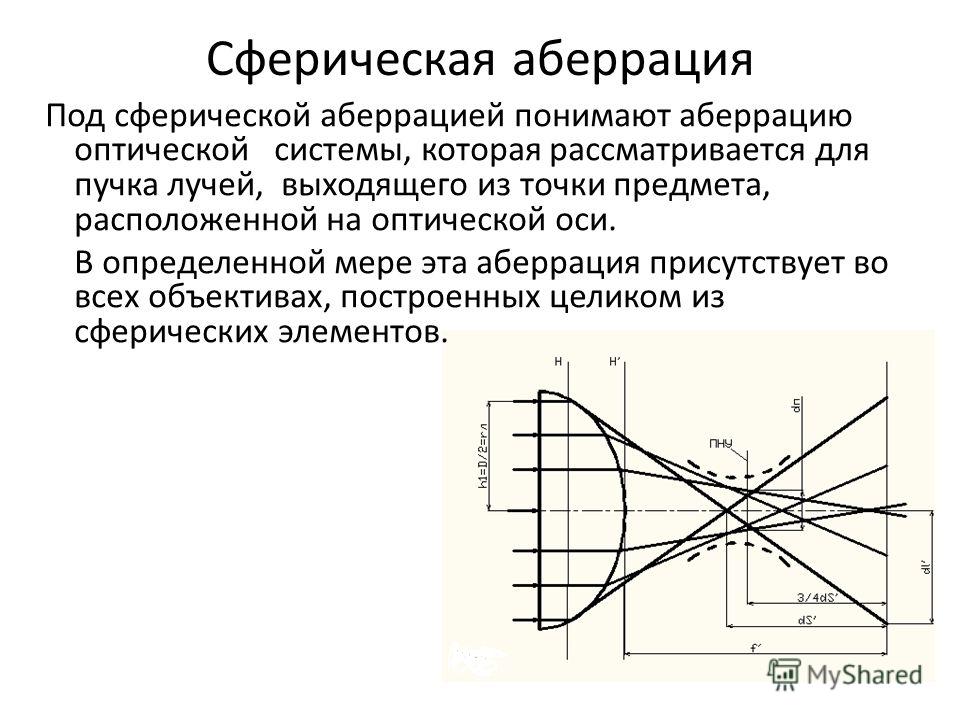
Сфери́ческая аберра́ция — аберрация оптических систем; нарушение гомоцентричности пучков лучей от точечного источника, прошедших через оптическую систему без нарушения симметрии строения этих пучков (в отличие от комы и астигматизма).
Содержание
|
Условия рассмотрения
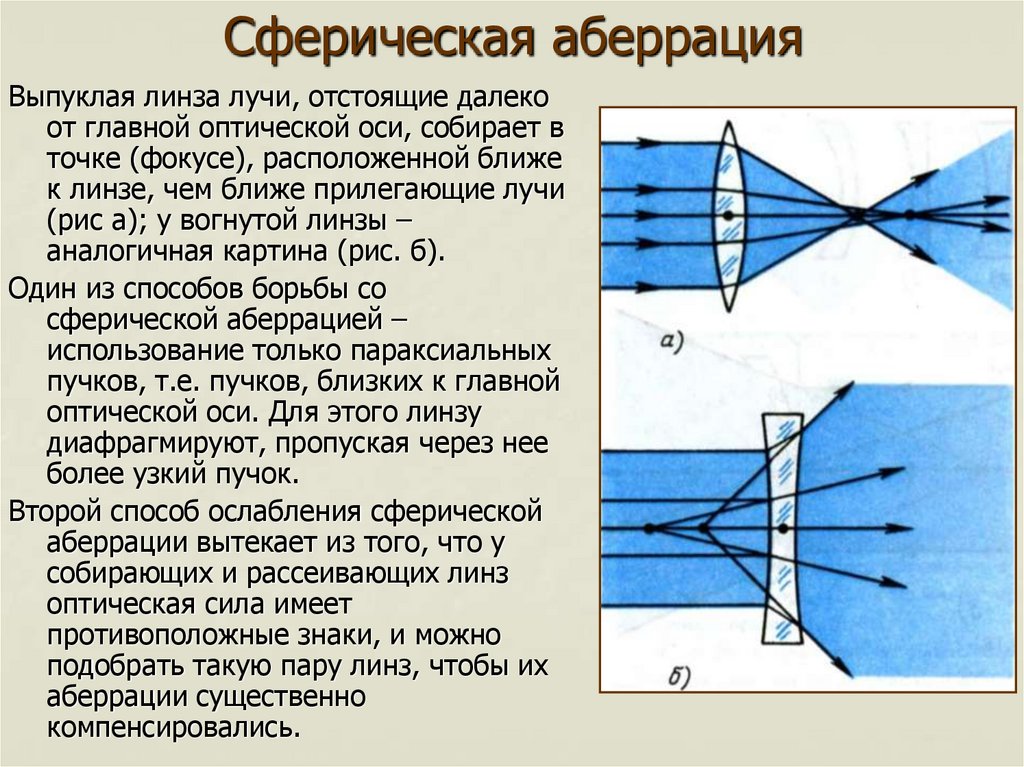
Сферическую аберрацию принято рассматривать для пучка лучей, выходящего из точки предмета, расположенной на оптической оси.
Однако, сферическая аберрация имеет место и для других пучков лучей, выходящих из точек предмета, удаленных от оптической оси, но в таких случаях она рассматривается как составная часть аберраций всего наклонного пучка лучей. Причём, хотя эта аберрация и называется сферической, она характерна не только для сферических поверхностей.
В результате сферической аберрации цилиндрический пучок лучей, после преломления линзой (в пространстве изображений) получает вид не конуса, а некоторой воронкообразной фигуры, наружная поверхность которой, вблизи узкого места, называется каустической поверхностью. При этом изображение точки имеет вид диска с неоднородным распределением освещённости, а форма каустической кривой позволяет судить о характере распределения освещённости. В общем случае, фигура рассеяния, при наличии сферической аберрации, представляет собой систему концентрических окружностей с радиусами пропорциональными третьей степени координат на входном (или выходном) зрачке.
Сферическая аберрация линзы (системы линз) объясняется тем, что её преломляющие поверхности встречают отдельные лучи сколько-нибудь широкого пучка под различными углами.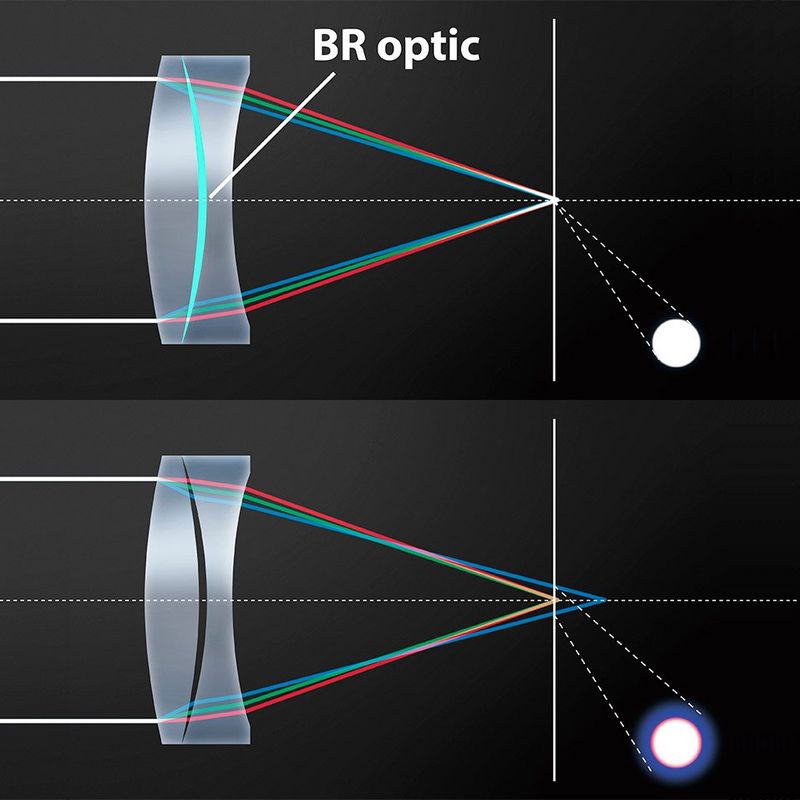
[1] Вследствие чего, более удалённые от оптической оси лучи преломляются сильнее, нежели нулевые[2] лучи, и образуют свои точки схода удалённые от фокальной плоскости.
Расчётные значения
Расстояние δs’ по оптической оси между точками схода нулевых и крайних лучей называется
Диаметр δ’ кружка (диска) рассеяния при этом определяется по формуле
,
где
- 2h1 — диаметр отверстия системы;
- a’ — расстояние от системы до точки изображения;
- δs’ — продольная аберрация.
Для объектов расположенных в бесконечности
,
где
- f’ — заднее фокусное расстояние.
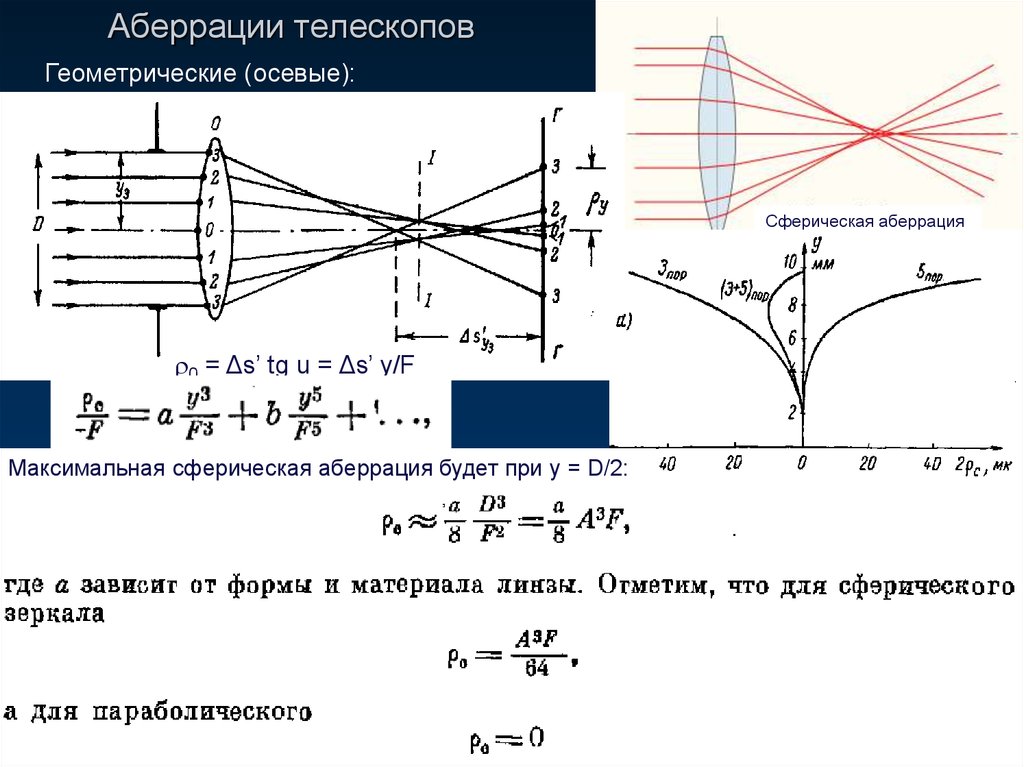
Для наглядности сферическую аберрацию, как правило, представляют не только в виде таблиц, но и графически.
Графики сферической аберрации:
1a. — продольная сферическая аберрация плоско-выпуклой линзы,
1b.
— продольная сферическая аберрация плоско-вогнутой линзы,
2. — поперечная сферическая аберрация.
Графическое представление
Обычно приводят графики продольной δs’ и поперечной δg’
сферической аберраций, как функций координат лучей.Для построения характеристической кривой продольной сферической аберрации по оси абсцисс откладывают продольную сферическую аберрацию δs’, а по оси ординат — высоты лучей на входном зрачке h. Для построения аналогичной кривой для поперечной аберрации по оси абсцисс откладывают тангенсы апертурных углов в пространстве изображений, а по оси ординат радиусы кружков рассеяния δg’
Положительные (собирательные) линзы создают отрицательную сферическую аберрацию, то есть δs’ < 0 для всех зон. Поэтому, на графике, характеристическая кривая продольной аберрации для такой линзы находится слева от оси ординат. Отрицательные (рассеивающие) линзы имеют аберрацию противоположного знака, и соответствующая кривая продольной аберрации будет справа от оси ординат.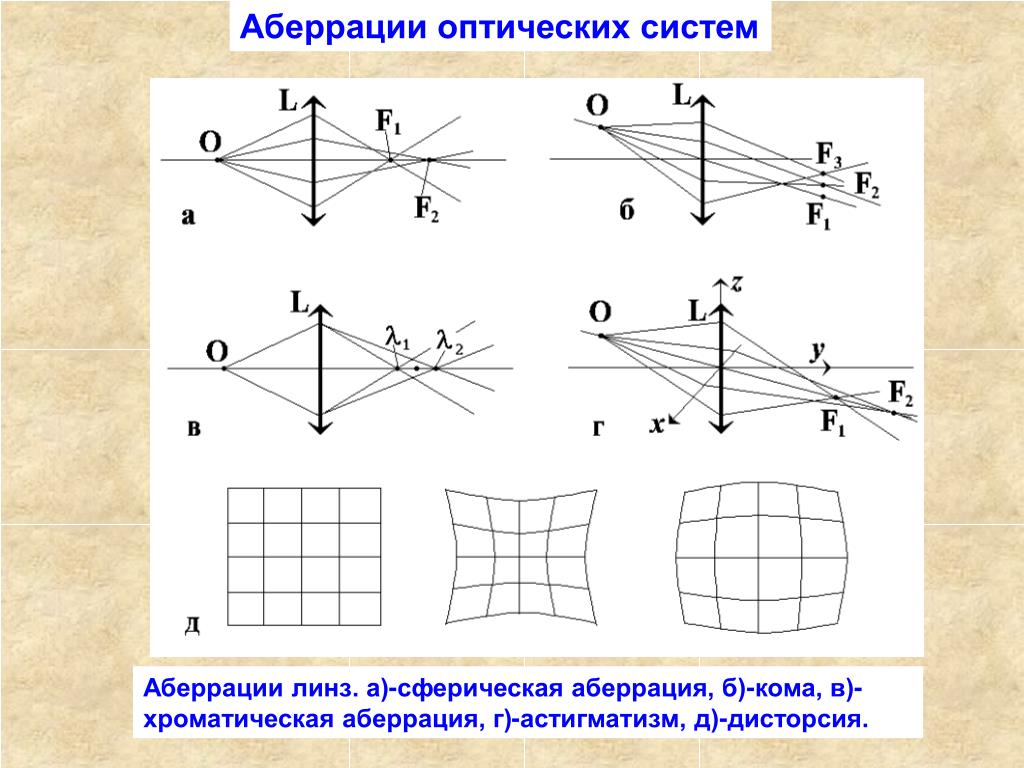
Комбинируя такие простые линзы, можно значительно исправить сферическую аберрацию.
Зависимость величины продольной сферической аберрации (δs’ ) от формы линзы.
Уменьшение и исправление
Как и другие аберрации третьего порядка, сферическая аберрация зависит от кривизны поверхностей и оптической силы линзы. Поэтому применение оптических стёкол с высокими показателями преломления позволяют уменьшить сферическую аберрацию, посредством увеличения радиусов поверхностей линзы при сохранении её оптической силы.
Уменьшение влияния сферической аберрации
1. диафрагмированием;
2. с помощью дефокусировки.
К тому же, для линз с разной кривизной поверхностей будет иметь значение ориентация линзы относительно хода светового луча. Так, например, сферическая аберрация для плоско-выпуклой линзы, обращенной навстречу лучу своей плоской поверхностью, будет иметь величину бо́льшую, нежели для той же линзы, но встречающей луч своей выпуклой поверхностью.
Заметное влияние на сферическую аберрацию оказывает диафрагмирование объектива (или иной оптической системы), так как при этом отсекаются краевые лучи широкого пучка. Очевидно, что этот способ непригоден для оптических систем, требующих высокой светосилы.
В отдельных случаях небольшая величина сферической аберрации третьего порядка может быть исправлена за счёт некоторой дефокусировки[4] объектива. При этом плоскость изображения смещается к, так называемой, «плоскости лучшей установки», находящейся, как правило, посередине, между пересечением осевых и крайних лучей, и не совпадающей с самым узким местом пересечения всех лучей широкого пучка (диском наименьшего рассеяния)[5]
То есть, можно сказать, что «диск» представляет из себя яркое кольцо с центральной точкой. Поэтому, разрешение оптической системы, в плоскости совпадающей с с диском наименьшего рассеяния, будет ниже, несмотря на меньшую величину поперечной сферической аберрации. Пригодность этого метода зависит от величины сферической аберрации, и характера распределения освещённости в диске рассеяния. Пересечения лучей возле точки заднего фокуса при остаточной сферической аберрации, соответствующие им диски рассеяния и графики продольной сферической аберрации:
1. — при исправленной сферической аберрации для нулевых и крайних лучей;
2. и 3. — при «переисправленной» сферической аберрации.
δs’ — расстояние от точки заднего фокуса до точки схода краевых лучей,
— δs’0,7h’ — расстояние от точки заднего фокуса до точки схода «среднезонных» лучей.
Достаточно успешно сферическая аберрация исправляется при помощи комбинации из положительной и отрицательной линз.
Причём, если линзы не склеиваются, то, кроме кривизны поверхностей компонентов, на величину сферической аберрации будет влиять и величина воздушного зазора (даже в том случае, если поверхности, ограничивающие этот воздушный промежуток, имеют одинаковую кривизну). При этом способе коррекции, как правило исправляются и хроматические аберрации.
Строго говоря, сферическая аберрация может быть вполне исправлена только для какой-нибудь пары узких зон, и притом лишь для определенных двух сопряженных точек. Однако, практически исправление может быть весьма удовлетворительным даже для двухлинзовых систем.
Обычно сферическую аберрацию устраняют для одного значения высоты h0 соответствующего краю зрачка системы. При этом наибольшее значение остаточной сферической аберрации ожидается на высоте he определяемой по простой формуле
Остаточная сферическая аберрация приводит к тому, что изображение точки так и не станет точечным. Оно останется диском, хотя и значительно меньшего размера, чем в случае не исправленной сферической аберрации.
Для уменьшения остаточной сферической аберрации часто прибегают к рассчитанному «переисправлению» на краю зрачка системы, придавая сферической аберрации краевой зоны положительное значение (δs’ > 0). При этом, лучи, пересекающие зрачок на высоте he[6], перекрещиваются ещё ближе к точке фокуса, а краевые лучи, хотя и сходятся за точкой фокуса, не выходят за границы диска рассеяния. Таким образом, размер диска рассеяния уменьшается и возрастает его яркость. То есть улучшается, как детальность, так и контраст изображения. Однако, в силу особенностей распределения освещённости в диске рассеяния, объективы с «переисправленной» сферической аберрацией, часто, обладают «двоящим» размытием вне зоны фокуса.
В отдельных случаях допускают значительное «переисправление». Так, например, ранние «Планары» фирмы Carl Zeiss Jena имели положительное значение сферической аберрации (δs’ > 0), как для краевых, так и для средних зон зрачка. Это решение несколько снижает контраст при полном отверстии, но заметно увеличивает разрешение при незначительном диафрагмировании.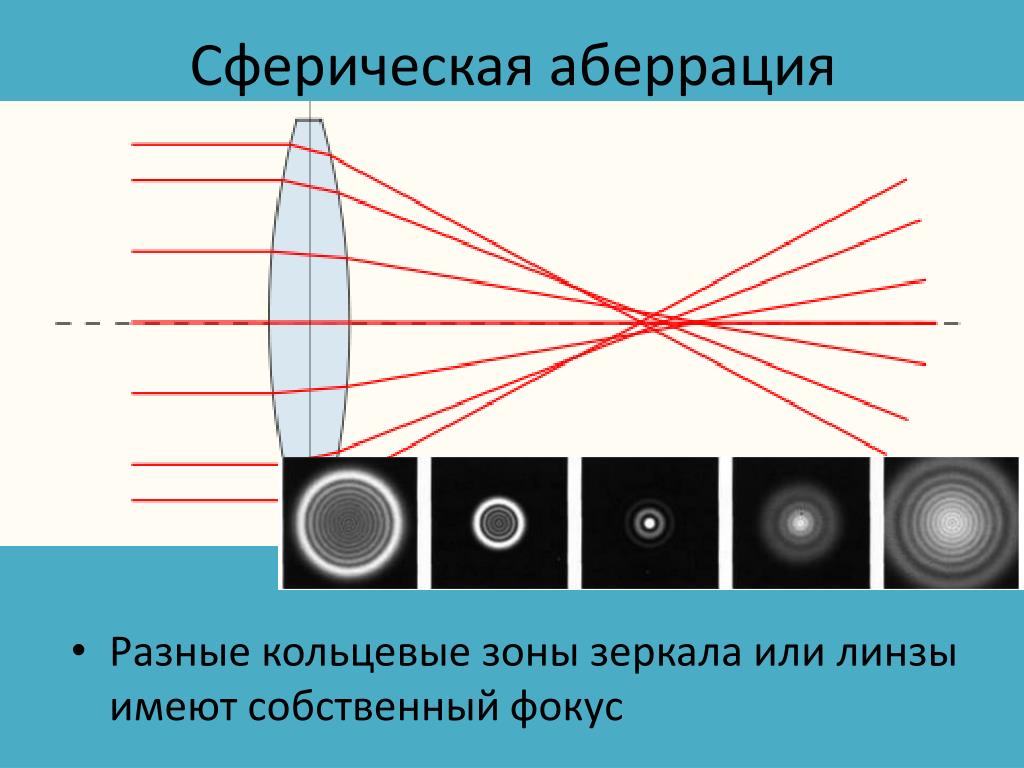
Примечания
- ↑ Или же можно сказать, что оптическая сила сферической линзы неоднородна, и возрастает по мере удаления от оптической оси.
- ↑ Эти лучи, так же, именуются параксиальными лучами.
- ↑ Согласно правилам знаков и ГОСТ 7427-76, преломляющие и отражающие поверхности и разделяющие их среды нумеруются по порядку их следования в направлении распространения света.
- ↑ Согласно теории аберраций, дефокусировка — это аберрация первого, то есть более низкого, порядка.
- ↑ Самое узкое место пересечения всех лучей широкого пучка, проходящего через собирающую линзу, находится слева от точки фокуса на расстоянии ¾δs’.
- ↑ Эти лучи иногда именуются среднезонными лучами.
Литература
- Бегунов Б. Н. Геометрическая оптика, Изд-во МГУ, 1966.
- Волосов Д. С., Фотографическая оптика. М., «Искусство», 1971.
- Заказнов Н. П. и др., Теория оптических систем, М.
, «Машиностроение», 1992. - Ландсберг Г. С. Оптика. М.,ФИЗМАТЛИТ, 2003.
- Чуриловский В. Н. Теория оптических приборов, Л., «Машиностроение», 1966.
- Smith, Warren J. Modern optical engineering, McGraw-Hill, 2000.
, «Машиностроение», 1992.Сферическая аберрация | это… Что такое Сферическая аберрация?
У этого термина существуют и другие значения, см. Аберрация.
Схема сферической аберрации, где
H, H’ — положения главных плоскостей;
F’ — задняя фокальная плоскость;
f’ — заднее фокусное расстояние;
-δs’ — продольная сферическая аберрация;
δg’ — поперечная сферическая аберрация.
Сфери́ческая аберра́ция — аберрация оптических систем; нарушение гомоцентричности пучков лучей от точечного источника, прошедших через оптическую систему без нарушения симметрии строения этих пучков (в отличие от комы и астигматизма).
Содержание
|
Условия рассмотрения
Сферическую аберрацию принято рассматривать для пучка лучей, выходящего из точки предмета, расположенной на оптической оси.
Однако, сферическая аберрация имеет место и для других пучков лучей, выходящих из точек предмета, удаленных от оптической оси, но в таких случаях она рассматривается как составная часть аберраций всего наклонного пучка лучей. Причём, хотя эта аберрация и называется сферической, она характерна не только для сферических поверхностей.
В результате сферической аберрации цилиндрический пучок лучей, после преломления линзой (в пространстве изображений) получает вид не конуса, а некоторой воронкообразной фигуры, наружная поверхность которой, вблизи узкого места, называется каустической поверхностью. При этом изображение точки имеет вид диска с неоднородным распределением освещённости, а форма каустической кривой позволяет судить о характере распределения освещённости. В общем случае, фигура рассеяния, при наличии сферической аберрации, представляет собой систему концентрических окружностей с радиусами пропорциональными третьей степени координат на входном (или выходном) зрачке.
Сферическая аберрация линзы (системы линз) объясняется тем, что её преломляющие поверхности встречают отдельные лучи сколько-нибудь широкого пучка под различными углами.
[1] Вследствие чего, более удалённые от оптической оси лучи преломляются сильнее, нежели нулевые[2] лучи, и образуют свои точки схода удалённые от фокальной плоскости.
Расчётные значения
Расстояние δs’ по оптической оси между точками схода нулевых и крайних лучей называется продольной сферической аберрацией.
Диаметр δ’ кружка (диска) рассеяния при этом определяется по формуле
,
где
- 2h1 — диаметр отверстия системы;
- a’ — расстояние от системы до точки изображения;
- δs’ — продольная аберрация.
Для объектов расположенных в бесконечности
,
где
- f’ — заднее фокусное расстояние.
Для наглядности сферическую аберрацию, как правило, представляют не только в виде таблиц, но и графически.
Графики сферической аберрации:
1a. — продольная сферическая аберрация плоско-выпуклой линзы,
1b.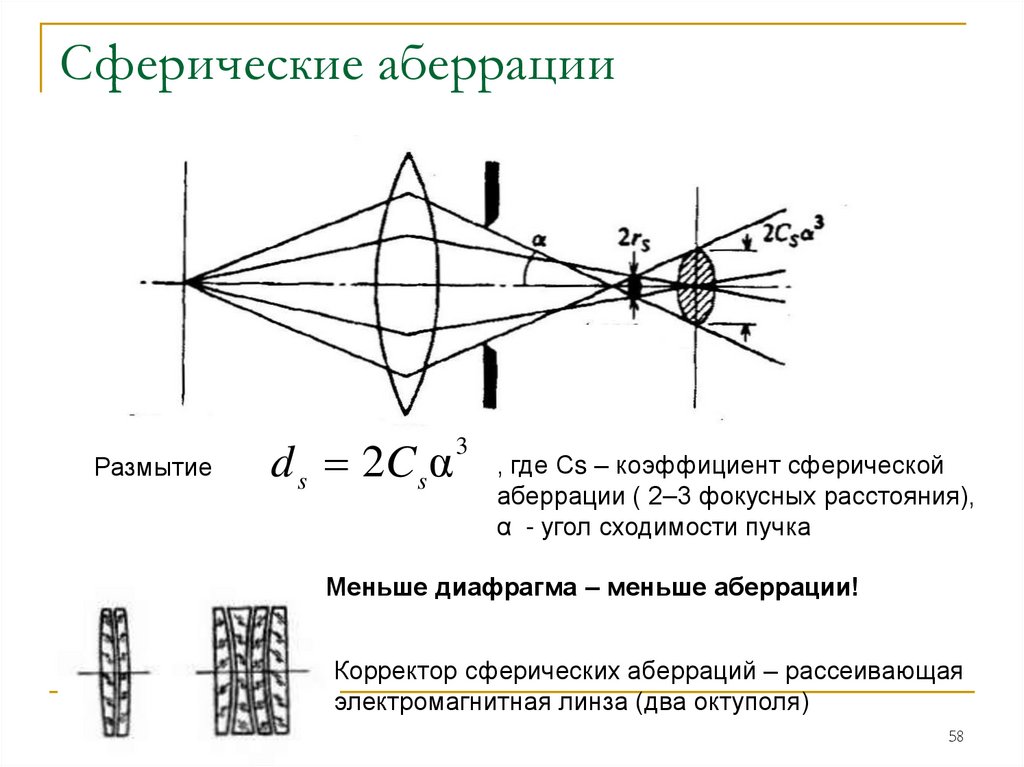
— продольная сферическая аберрация плоско-вогнутой линзы,
2. — поперечная сферическая аберрация.
Графическое представление
Обычно приводят графики продольной δs’ и поперечной δg’ сферической аберраций, как функций координат лучей.
Для построения характеристической кривой продольной сферической аберрации по оси абсцисс откладывают продольную сферическую аберрацию δs’, а по оси ординат — высоты лучей на входном зрачке h. Для построения аналогичной кривой для поперечной аберрации по оси абсцисс откладывают тангенсы апертурных углов в пространстве изображений, а по оси ординат радиусы кружков рассеяния δg’
Положительные (собирательные) линзы создают отрицательную сферическую аберрацию, то есть δs’ < 0 для всех зон. Поэтому, на графике, характеристическая кривая продольной аберрации для такой линзы находится слева от оси ординат. Отрицательные (рассеивающие) линзы имеют аберрацию противоположного знака, и соответствующая кривая продольной аберрации будет справа от оси ординат.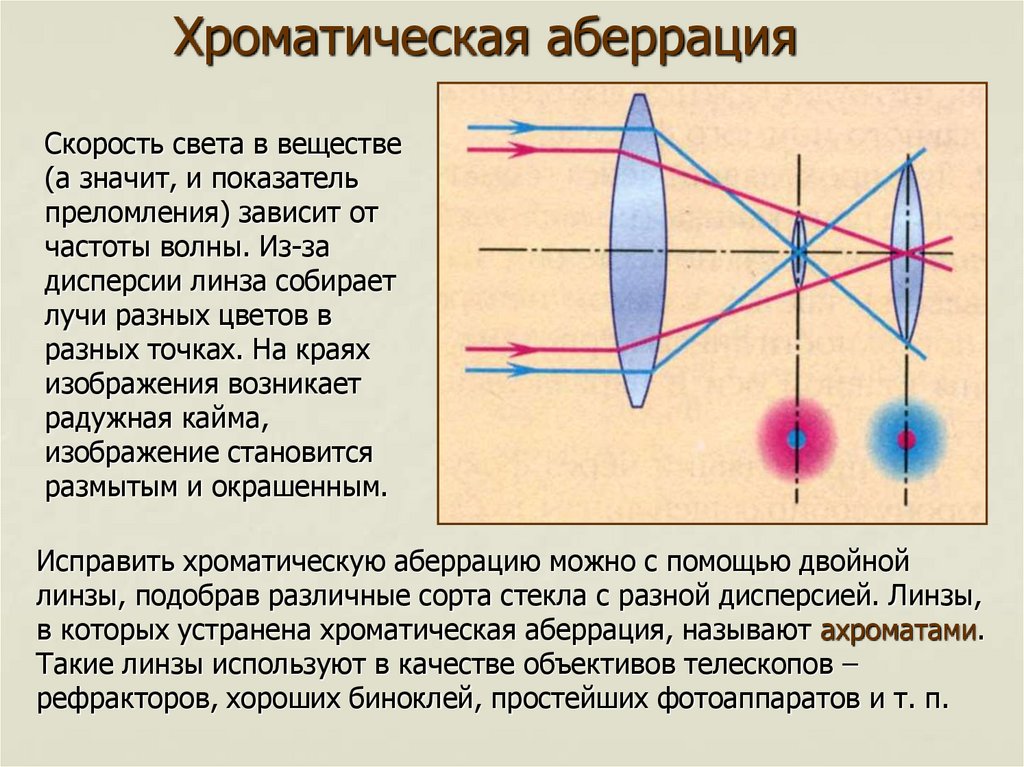
Комбинируя такие простые линзы, можно значительно исправить сферическую аберрацию.
Зависимость величины продольной сферической аберрации (δs’ ) от формы линзы.
Уменьшение и исправление
Как и другие аберрации третьего порядка, сферическая аберрация зависит от кривизны поверхностей и оптической силы линзы. Поэтому применение оптических стёкол с высокими показателями преломления позволяют уменьшить сферическую аберрацию, посредством увеличения радиусов поверхностей линзы при сохранении её оптической силы.
Уменьшение влияния сферической аберрации
1. диафрагмированием;
2. с помощью дефокусировки.
К тому же, для линз с разной кривизной поверхностей будет иметь значение ориентация линзы относительно хода светового луча. Так, например, сферическая аберрация для плоско-выпуклой линзы, обращенной навстречу лучу своей плоской поверхностью, будет иметь величину бо́льшую, нежели для той же линзы, но встречающей луч своей выпуклой поверхностью.
Таким образом, выбор отношения кривизны первой[3] поверхности линзы, к её второй поверхности, так же, будет одним из средств уменьшающих сферическую аберрацию.
Заметное влияние на сферическую аберрацию оказывает диафрагмирование объектива (или иной оптической системы), так как при этом отсекаются краевые лучи широкого пучка. Очевидно, что этот способ непригоден для оптических систем, требующих высокой светосилы.
В отдельных случаях небольшая величина сферической аберрации третьего порядка может быть исправлена за счёт некоторой дефокусировки[4] объектива. При этом плоскость изображения смещается к, так называемой, «плоскости лучшей установки», находящейся, как правило, посередине, между пересечением осевых и крайних лучей, и не совпадающей с самым узким местом пересечения всех лучей широкого пучка (диском наименьшего рассеяния)[5]. Это несовпадение объясняется распределением световой энергии в диске наименьшего рассеяния, образующей максимумы освещённости не только в центре, но и на краю.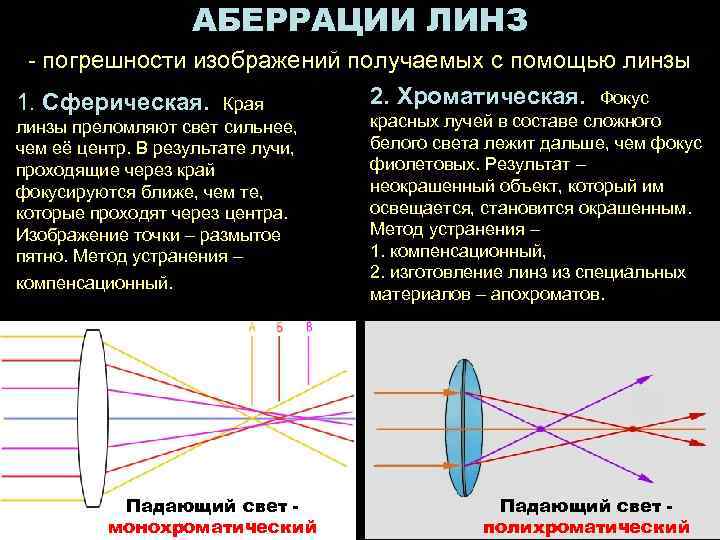
То есть, можно сказать, что «диск» представляет из себя яркое кольцо с центральной точкой. Поэтому, разрешение оптической системы, в плоскости совпадающей с с диском наименьшего рассеяния, будет ниже, несмотря на меньшую величину поперечной сферической аберрации. Пригодность этого метода зависит от величины сферической аберрации, и характера распределения освещённости в диске рассеяния.
Пересечения лучей возле точки заднего фокуса при остаточной сферической аберрации, соответствующие им диски рассеяния и графики продольной сферической аберрации:
1. — при исправленной сферической аберрации для нулевых и крайних лучей;
2. и 3. — при «переисправленной» сферической аберрации.
Где F’ — задняя фокальная плоскость,
δs’ — расстояние от точки заднего фокуса до точки схода краевых лучей,
— δs’0,7h’ — расстояние от точки заднего фокуса до точки схода «среднезонных» лучей.
Достаточно успешно сферическая аберрация исправляется при помощи комбинации из положительной и отрицательной линз.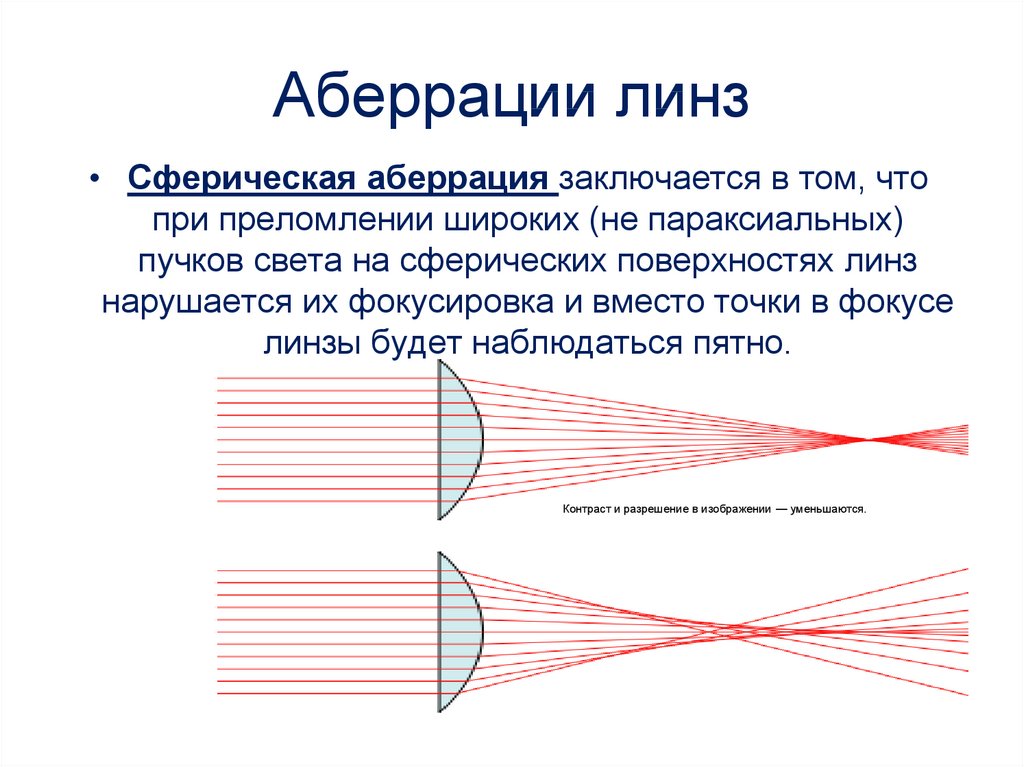
Причём, если линзы не склеиваются, то, кроме кривизны поверхностей компонентов, на величину сферической аберрации будет влиять и величина воздушного зазора (даже в том случае, если поверхности, ограничивающие этот воздушный промежуток, имеют одинаковую кривизну). При этом способе коррекции, как правило исправляются и хроматические аберрации.
Строго говоря, сферическая аберрация может быть вполне исправлена только для какой-нибудь пары узких зон, и притом лишь для определенных двух сопряженных точек. Однако, практически исправление может быть весьма удовлетворительным даже для двухлинзовых систем.
Обычно сферическую аберрацию устраняют для одного значения высоты h0 соответствующего краю зрачка системы. При этом наибольшее значение остаточной сферической аберрации ожидается на высоте he определяемой по простой формуле
Остаточная сферическая аберрация приводит к тому, что изображение точки так и не станет точечным. Оно останется диском, хотя и значительно меньшего размера, чем в случае не исправленной сферической аберрации.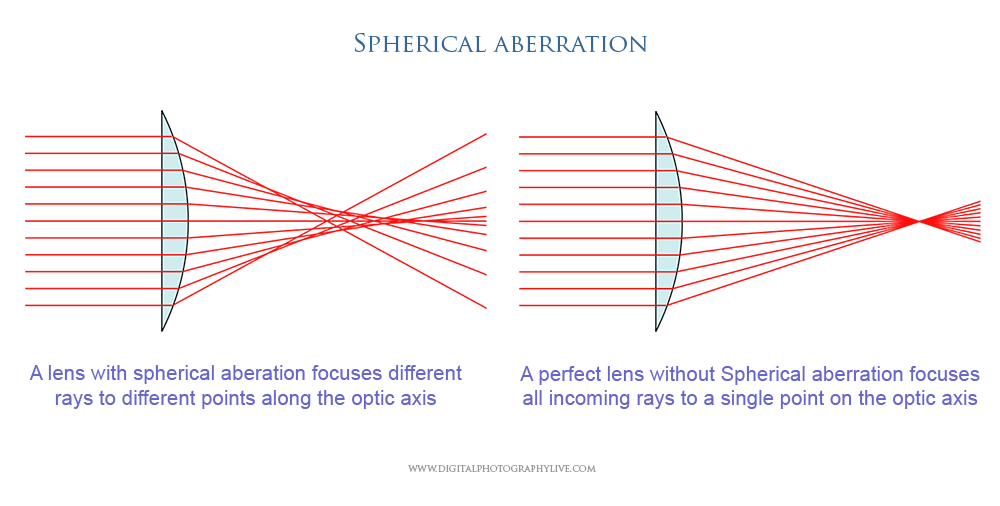
Для уменьшения остаточной сферической аберрации часто прибегают к рассчитанному «переисправлению» на краю зрачка системы, придавая сферической аберрации краевой зоны положительное значение (δs’ > 0). При этом, лучи, пересекающие зрачок на высоте he[6], перекрещиваются ещё ближе к точке фокуса, а краевые лучи, хотя и сходятся за точкой фокуса, не выходят за границы диска рассеяния. Таким образом, размер диска рассеяния уменьшается и возрастает его яркость. То есть улучшается, как детальность, так и контраст изображения. Однако, в силу особенностей распределения освещённости в диске рассеяния, объективы с «переисправленной» сферической аберрацией, часто, обладают «двоящим» размытием вне зоны фокуса.
В отдельных случаях допускают значительное «переисправление». Так, например, ранние «Планары» фирмы Carl Zeiss Jena имели положительное значение сферической аберрации (δs’ > 0), как для краевых, так и для средних зон зрачка. Это решение несколько снижает контраст при полном отверстии, но заметно увеличивает разрешение при незначительном диафрагмировании.
Примечания
- ↑ Или же можно сказать, что оптическая сила сферической линзы неоднородна, и возрастает по мере удаления от оптической оси.
- ↑ Эти лучи, так же, именуются параксиальными лучами.
- ↑ Согласно правилам знаков и ГОСТ 7427-76, преломляющие и отражающие поверхности и разделяющие их среды нумеруются по порядку их следования в направлении распространения света.
- ↑ Согласно теории аберраций, дефокусировка — это аберрация первого, то есть более низкого, порядка.
- ↑ Самое узкое место пересечения всех лучей широкого пучка, проходящего через собирающую линзу, находится слева от точки фокуса на расстоянии ¾δs’.
- ↑ Эти лучи иногда именуются среднезонными лучами.
Литература
- Бегунов Б. Н. Геометрическая оптика, Изд-во МГУ, 1966.
- Волосов Д. С., Фотографическая оптика. М., «Искусство», 1971.
- Заказнов Н. П. и др., Теория оптических систем, М. , «Машиностроение», 1992.
- Ландсберг Г. С. Оптика. М.,ФИЗМАТЛИТ, 2003.
- Чуриловский В. Н. Теория оптических приборов, Л., «Машиностроение», 1966.
- Smith, Warren J. Modern optical engineering, McGraw-Hill, 2000.
, «Машиностроение», 1992.Что такое сферическая аберрация?
Сферическая аберрация — это оптическая проблема, возникающая, когда все входящие световые лучи фокусируются в разных точках после прохождения через сферическую поверхность. Световые лучи, проходящие через линзу вблизи ее горизонтальной оси, преломляются меньше, чем лучи ближе к краю или «периферии» линзы, и в результате попадают в разные точки поперек оптической оси. Другими словами, параллельные световые лучи падающего света не сходятся в одной и той же точке после прохождения через линзу. Из-за этого сферическая аберрация может влиять на разрешение и четкость, затрудняя получение четких изображений. Вот иллюстрация, показывающая сферическую аберрацию:
Как показано выше, лучи света преломляются или изменяют свой угол при прохождении через линзу.
Те, что ближе к верхней и нижней части иллюстрации, в конечном итоге сходятся на меньшем расстоянии вдоль оптической оси (черная/красная пунктирная линия), а те, что ближе к оптической оси, сходятся на большем расстоянии, создавая разные точки фокусировки вдоль та самая ось. Точка наилучшего фокуса с «кругом наименьшего замешательства» показана толстой зеленой линией. Сферическая аберрация вызвана не только конструкцией линзы, но и качеством материала линзы. Линзы из некачественного материала и большие пузыри могут сильно повлиять на преломление света.
У идеальной линзы все лучи света должны сходиться в одной фокусной точке, как показано ниже:
Таким образом, лучшая точка фокусировки с кругом наименьшего нерезкости находится прямо в этой фокусной точке. Однако конструкция обычной сферической линзы не позволила бы вышеперечисленному произойти, поэтому производители разработали специализированные точные методы для уменьшения эффекта сферической аберрации.
Способы уменьшения сферической аберрации
В современных объективах используются различные методы значительного уменьшения сферической аберрации.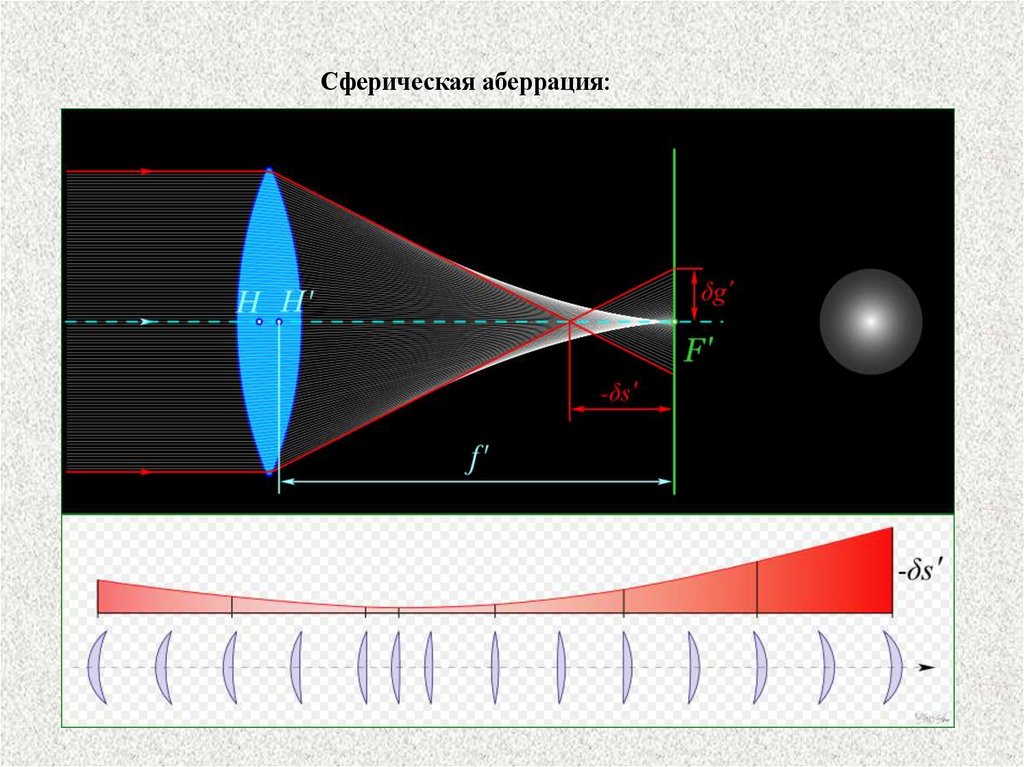
В одном из методов используется специальная асферическая (то есть несферическая) поверхность линзы, изогнутая наружу с одной стороны с единственной целью — сводить световые лучи в единую фокальную точку, как показано ниже:
Сферическая аберрация наиболее выражена при полностью открытой диафрагме объектива (максимальная диафрагма). Закрытие объектива даже на один стоп резко снижает сферическую аберрацию, поскольку лепестки диафрагмы блокируют внешние края сферических линз. Наглядный пример этого можно найти в статье о смещении фокуса.
Если вам интересно узнать больше, ниже приведен список статей о других типах аберраций и проблемах, которые мы ранее публиковали на сайте Photography Life:
- Кривизна поля
- Кома
- Хроматическая аберрация
- Дисторсия
- Виньетирование
- Двоение / Блики
- Дифракция 5 03 0 900
Раскрытие информации, условия и варианты поддержки
Рубрики: Учебники по фотографии Tagged With : Дополнительные советы по фотосъемке, терминология камеры, объективы, оптика, сферическая аберрация
сферическая аберрация
сферическая аберрацияДля линз со сферическими поверхностями лучи, параллельные оптической оси, но находящиеся на разном расстоянии от оптической оси, не сходятся в одной и той же точке.
Для одиночной линзы сферическую аберрацию можно свести к минимуму, согнув линзу в наилучшую форму. Для нескольких объективов сферические аберрации можно устранить путем чрезмерной коррекции некоторых элементов. Использование симметричных дублетов, таких как ортоскопический дублет, значительно снижает сферическую аберрацию.Когда используется понятие главного фокусного расстояния, предполагается, что все параллельные лучи фокусируются на одном и том же расстоянии, что, конечно, верно только при отсутствии аберраций. Использование уравнения линзы также предполагает идеальную линзу, и это уравнение практически верно только для лучей, близких к оптической оси, так называемых параксиальных лучей. Для объектива со сферической аберрацией наилучшее приближение фокусного расстояния — это расстояние, на котором разница между параксиальным и краевым лучами наименьшая. Это не идеально, но отклонение от идеального фокуса образует то, что называется «кругом наименьшего беспорядка».
Сферическая аберрация — одна из причин, по которой меньшая апертура (большее число f) объектива камеры дает более четкое изображение и большую глубину резкости, поскольку разница между параксиальными и маргинальными лучами меньше.Аберрации объектива Index Концепции линз
Концепции толстых линз
HyperPhysics***** Light and Vision R Nave Вернуться Величина сферической аберрации линзы, изготовленной из сферических поверхностей, зависит от ее формы. Изгиб линзы также может дать частичную коррекцию аберрации комы.
Аберрации объектива Минимизация сферической аберрации с помощью формы Index Концепции объективов
«Reference
Jenkins & White
p 156 ffHyperPhysics***** 907 Light and Vision 9000 Вернуться Хотя сферическая аберрация не может быть устранена для одной линзы, ее можно свести к минимуму путем соответствующего изгиба линзы в ее наилучшую форму.
Сферическая аберрация: Сферическая аберрация. Большая российская энциклопедияПролистать наверх
Для одиночной линзы сферическую аберрацию можно свести к минимуму, согнув линзу в наилучшую форму. Для нескольких объективов сферические аберрации можно устранить путем чрезмерной коррекции некоторых элементов. Использование симметричных дублетов, таких как ортоскопический дублет, значительно снижает сферическую аберрацию.
Сферическая аберрация — одна из причин, по которой меньшая апертура (большее число f) объектива камеры дает более четкое изображение и большую глубину резкости, поскольку разница между параксиальными и маргинальными лучами меньше.