Сигма 0 2: Условный предел текучести

Условный предел текучести. Сигма ноль-два ? : Механика и Техника

Neuter	Условный предел текучести. Сигма ноль-два ? 26.01.2014, 21:11
02/01/13 79	Господа ! Есть вопрос на который не могу найти понятного ответа Почему условный предел текучести принято определять именно по 0,2% остаточной деформации ? (можно было бы выбрать 0,1% или скажем 0,5%, чем обоснован такой выбор. ..именно 0,2% ?) (подскажите где можно найти, или выскажите своё видение)

angor6	Re: Условный предел текучести. Сигма ноль-два ? 26.01.2014, 23:11
11/03/12 586 Беларусь, Минск	Neuter, насколько мне известно, для материалов, диаграмма растяжения которых не имеет площадки текучести, за величину предела текучести условно принято такое напряжение, при котором остаточное относительное удлинение образца достигает примерно той же величины, что и для материалов, диаграмма растяжения которых имеет площадку текучести. Это остаточное удлинение составляет 0,2 … 0,3 %.

Neuter	Re: Условный предел текучести. Сигма ноль-два ? 27.01.2014, 03:29
02/01/13 79	angor6, спасибо за ответ. Но получается всё-таки что принято 0,2% чисто «условно» !? Просто для большого числа материалов (металлов) это удачный выбор (или совпадение). …

angor6	Re: Условный предел текучести. Сигма ноль-два ? 27.01.2014, 06:46
11/03/12 586 Беларусь, Минск	Neuter, да, 0,2 % приняты условно. Исходя из результатов испытаний образцов, изготовленных из материалов, для которых характерна площадка текучести. А почему это так беспокоит Вас?

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 4 ]

Модераторы: photon, profrotter, Парджеттер, Супермодераторы

Прочность | Материаловедение

Прочность — свойство материалов сопротивляться разрушению или пластической деформации под действием внешней нагрузки.

Наиболее простым и распространенным методом определения прочности материала является испытание его на растяжение (рисунок 1). Концы образца металла круглого сечения зажимают в разрывной машине и подвергают действию растягивающей нагрузки Р.

Рисунок 1 — Метод определения прочности на растяжение. ι_о — начальная длина; F₀— начальная площадь поперечного сечения; Δι — удлинение; ι_к — конечная длина образца в момент разрыва; F_к — площадь поперечного сечения образца в месте разрыва

Диаграмму растяжения можно построить в координатах «нагрузка Р -удлинение Δι» или в координатах «напряжение σ — относительная деформация ε». σ= Р/F₀ а ε= Δι/ι₀ ×100% (рисунок 2).
Под действием нагрузки в материале возникают деформации. Деформацией называется изменение размеров и формы тела, она может быть упругой и пластической. Упругой называют деформацию, влияние которой на форму, структуру и свойства тела полностью устраняется после прекращения действия внешней силы Р.

На рисунке 2 упругая деформация характеризуется прямолинейным участком ОА. При упругой деформации изменяется расстояние между атомами в кристаллической решетке. При снятии нагрузки атомы становятся на прежние места и деформация исчезает.

Рисунок 2 — Диаграмма растяжения

Оценить свойства материала в пределах упругих деформаций можно с помощью коэффициента, получившим название модуля упругости Е (Гука). Это отношение напряжения к вызванной им деформации:
Значение модуля упругости определяется силами межатомного взаимодействия, оно постоянно и характеризует жесткость материала. Чем меньшую деформацию вызывает напряжение, тем выше жесткость. Угол а на диаграмме есть геометрическое выражение жесткости и модуля упругости. Чем угол больше, тем выше жесткость материала. Пластическая деформация наступает, когда напряжение превышает предел упругости (выше точки А) и после снятия нагрузки форма, структура и свойства тела не восстанавливаются полностью, т.е. имеет место остаточная деформация.

На практике напряжение, при котором начинается пластическая деформация, оценивается пределом текучести σ_T . Его легко определить, если на диаграмме растяжения имеется площадка текучести (горизонтальный участок). Однако, многие материалы имеют диаграмму растяжения без площадки текучести (медь, латуни, алюминий и др.), тогда за предел текучести принимают напряжение, которое вызывает остаточное удлинение 0,2 % и обозначают σ _0,2. σ_T называют физическим, а σ_0.2 условным пределом текучести. Предел текучести используют в качестве одного из показателей прочности материала.
Напряжение, соответствующее наибольшей нагрузке, предшествующей разрушению, называется временным сопротивлением (σ_B) или чаще пределом прочности, оно измеряется в МПа. На рисунке 2 это максимальная точка на кривой σ-ε.

ОБРАТИТЕ ВНИМАНИЕ! На нашем сайте Вы можете заказать любые решения по всем разделам материаловедение. Решение предоставляется в печатном виде (в Word) с детальными комментариями.

Каноническая и стандартная форма — Geeksforgeeks

Напишите статью

• Напишите опыт интервью

Комбинационные схемы

последовательные схемы

Репрезентация и компьютерный авиаммеческий

Сохранить статью

• Уровень сложности: Easy
• Последнее обновление: 23 фев, 2022
• Читать
• Обсудить

Улучшить статью

Сохранить статью

Каноническая форма – В булевой алгебре логическая функция может быть выражена в виде канонической дизъюнктивной нормальной формы, известной как minterm , а некоторые выражаются в виде канонической конъюнктивной нормальной формы, известной как maxterm .
В Minterm мы ищем функции, результатом которых является «1», а в Maxterm мы ищем функцию, результатом которой является «0».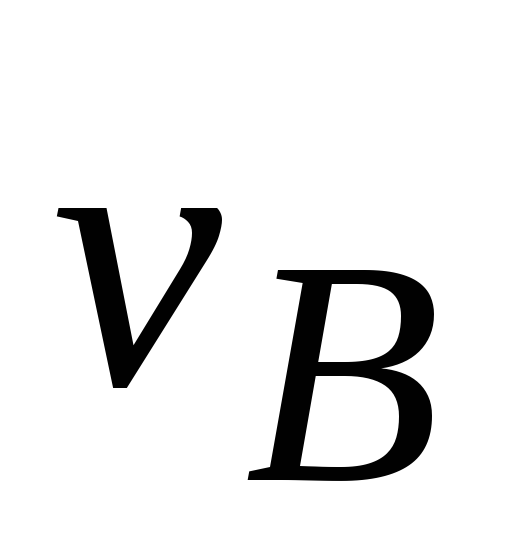
Выполняем Сумма minterm , также известный как Сумма произведений (СОП).
Мы выполняем Продукт Maxterm

также известный как Продукт суммы (POS).
Булевы функции, выраженные в виде суммы minterms или произведения maxterms, называются каноническими.

Стандартная форма – Логическая переменная может быть выражена как в истинной, так и в дополненной форме. В стандартной форме булева функция будет содержать все переменные либо в истинной форме, либо в дополненной форме, тогда как в канонической форме количество переменных зависит от вывода SOP или POS.

Булева функция может быть выражена алгебраически из заданной таблицы истинности путем формирования : 

• минтерма для каждой комбинации переменных, которая дает 1 в функции, а затем выполнения операции ИЛИ всех этих термов.
• maxterm для каждой комбинации переменных, которая дает 0 в функции, а затем выполняет И всех этих условий.

Таблица истинности, представляющая minterm и maxterm –  
 

Из приведенной выше таблицы видно, что minterm выражается в формате произведения, а maxterm выражается в формате суммы. 9н)). Иногда бывает удобно выразить булеву функцию в виде суммы minterm.
 

• Пример – Выразите логическую функцию F = A + B’C в виде стандартной суммы minterms.
• Решение –  
  A = A(B + B’) = AB + AB’
  В этой функции по-прежнему отсутствует одна переменная, поэтому
  A = AB(C + C’) + AB'(C + C’) = ABC + ABC’+ AB’C + AB’C’
  Во втором члене B’C отсутствует одна переменная; следовательно,
  B’C = B’C(A + A’) = AB’C + A’B’C 
  Объединив все термины, мы получим
  F = A + B’C = ABC + ABC’ + AB’C + AB’C’ + AB’C + A’B’C 
  Но AB’C встречается дважды, и
  соответственно теореме 1 (x + x = x) можно удалить одно из этих вхождений. Переставляя minterms в порядке возрастания, окончательно получаем
  F = A’B’C + AB’C’ + AB’C + ABC’ + ABC
  = m1 + m4 + m5 + m6 + m7
  SOP представлен как Sigma( 1, 4, 5, 6, 7)

Статьи по теме

Что нового

Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство просмотра нашего веб-сайта. Используя наш сайт, вы подтверждаете, что вы прочитали и поняли наши Политика в отношении файлов cookie и Политика конфиденциальности

Введение K-Map (карты Карно)

Во многих цифровых схемах и практических задачах нам нужно найти выражение с минимальным количеством переменных. Мы можем очень легко минимизировать булевы выражения с 3, 4 переменными, используя K-карту, не используя никаких теорем булевой алгебры. K-map может принимать две формы: сумма продукта (SOP) и продукт суммы (POS) в зависимости от необходимости проблемы. K-map представляет собой табличное представление, но дает больше информации, чем TRUTH TABLE. Мы заполняем сетку K-карты нулями и единицами, а затем решаем ее, создавая группы.

Шаги для решения выражения с использованием K-карты-  

1. Выберите K-карту в соответствии с количеством переменных.
2. Идентифицируйте minterms или maxterms, указанные в задаче.
3. Для SOP поставьте 1 в блоках K-карты, соответствующих minterms (0 в других местах).
4. Для POS поместите 0 в блоки K-карты, соответствующие maxterms (1 в других местах).
5. Составьте прямоугольные группы, содержащие общее количество членов в степени двойки, например 2,4,8 ..(кроме 1), и постарайтесь охватить как можно больше элементов в одной группе.
6. Из групп, созданных на шаге 5, найдите условия продукта и суммируйте их для формы СОП.

ФОРМА СОП:

6,7) 

Из группы красный мы получаем условия продукта— 

 A'C  

0037 Окончательное выражение (A’C+AB)  
 

2. К-карта для 4-х переменных –

К-карта 4-х переменная СОП форма

 F(P,Q,R,S)=∑ (0,2,5,7,8,10,13,15) 

Из группы красный получаем товарный термин—

 QS 

Из зеленый группа получаем товарный термин—

Q’S»

Суммируя эти условия продукта, мы получаем- Окончательное выражение (QS+Q’S’)  

 

ФОРМА POS:

7)

Из Red Group Мы находим термины

 A B 

Сделайте дополнение этих двух

 A 

Из группы коричневый находим термины

 B   C  

Дополняя эти два термина

 B' C' 

Теперь суммируем их

 (B'+C') 

Из группы желтый находим термины

 A' B' C' 0 
 A' B' C' 3 дополнение этих двух 
 
 A B C 
 Теперь  суммируем 
 (A + B + C) 
 Возьмем произведение этих трех членов:  Конечное выражение – 
 ') (A (В' + С') (А + В + С)    
   2.
Сигма 0 2: Условный предел текучести