Числа Фибоначчи и золотое сечение: взаимосвязь
Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Золотое сечение
Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.
В основе его лежит теория о пропорциях и соотношениях делений отрезков, которое было сделано еще древним философом и математиком Пифагором. Он доказал, что при разделении отрезка на две части: X (меньшую) и Y (большую), отношение большего к меньшему будет равно отношению их суммы (всего отрезка):
X : Y = Y : X+Y.
В результате получается уравнение: х2 – х – 1=0, которое решается как х=(1±√5)/2.
Если рассмотреть соотношение 1/х, то оно равно 1,618…
Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.
Числа Фибоначчи
Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Также ученый привел ряд закономерностей:
- Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618.
Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным. - Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.
- Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.
Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.
Спираль Архимеда и золотой прямоугольник
Спирали, очень распространенные в природе, были исследованы Архимедом, который даже вывел ее уравнение. Форма спирали основана на законах о золотом сечении. При ее раскручивании получается длина, к которой можно применить пропорции и числа Фибоначчи, увеличение шага происходит равномерно.
Параллель между числами Фибоначчи и золотым сечением можно увидеть и построив «золотой прямоугольник», у которого стороны пропорциональны, как 1,618:1.
Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.
История применения золотых пропорций
Многие древние памятники архитектуры Египта возведены с использованием золотых пропорций: знаменитые пирамиды Хеопса и др. Архитекторы Древней Греции широко использовалиих их при возведении архитектурных объектов, таких как храмы, амфитеатры, стадионы. Например, были применены такие пропорции при строительстве античного храма Парфенон, театра Диониса (Афины) и других объектов, которые стали шедеврами древнего зодчества, демонстрирующими гармонию, основанную на математической закономерности.
В более поздние века интерес к золотому сечению поутих, и закономерности были забыты, однако опять возобновился в эпоху Ренессанса вместе с книгой францисканского монаха Л.
Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».
Витрувианский человек Леонардо
Рисунок, которым Леонардо да Винчи в 1492 г. проиллюстрировал книгу Витрувия, изображает фигуру человека в 2-х позициях с руками, разведенными в стороны. Фигура вписана в круг и квадрат. Этот рисунок принято считать каноническими пропорциями человеческого тела (мужского), описанными Леонардо на основе изучения их в трактатах римского архитектора Витрувия.
Центром тела как равноудаленной точкой от конца рук и ног считается пупок, длина рук приравнивается к росту человека, максимальная ширина плеч = 1/8 роста, расстояние от верха груди до волос = 1/7, от верха груди до верха головы =1/6 и т.д.
С тех пор рисунок используется в виде символа, показывающего внутреннюю симметрию тела человека.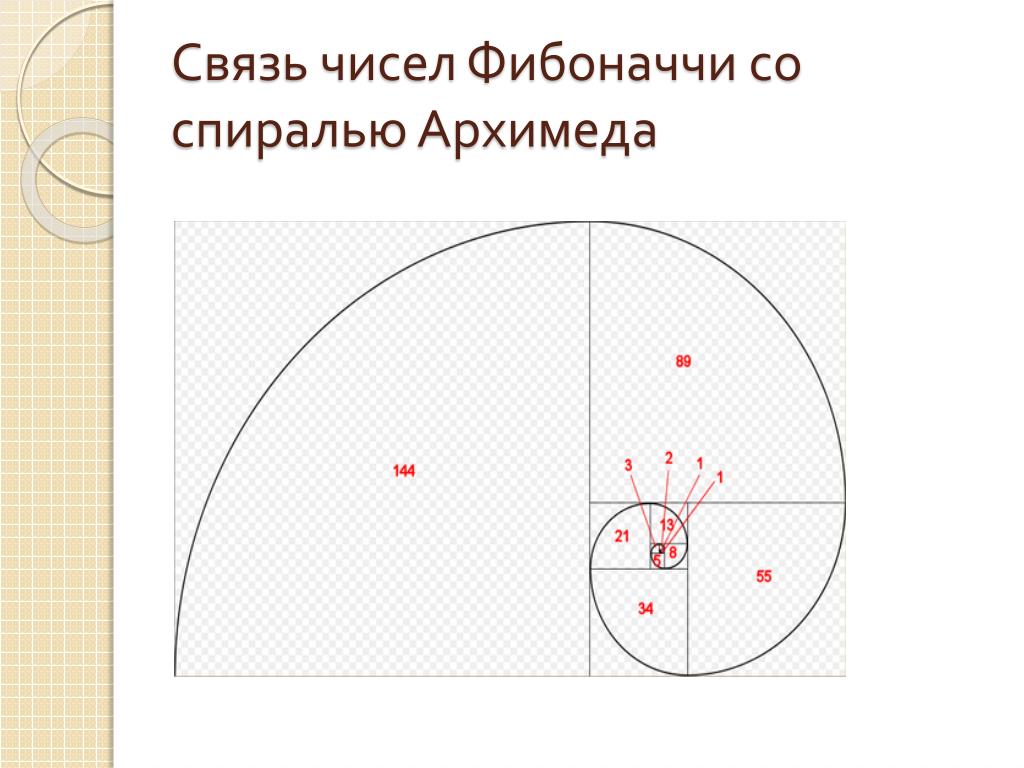
Термин «Золотое сечение» Леонардо использовал для обозначения пропорциональных отношений в фигуре человека. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.
Все эти гармоничные пропорции часто используются деятелями искусства для создания красивых и впечатляющих произведений.
Исследования золотого сечения в 16-19 веках
Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.
В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.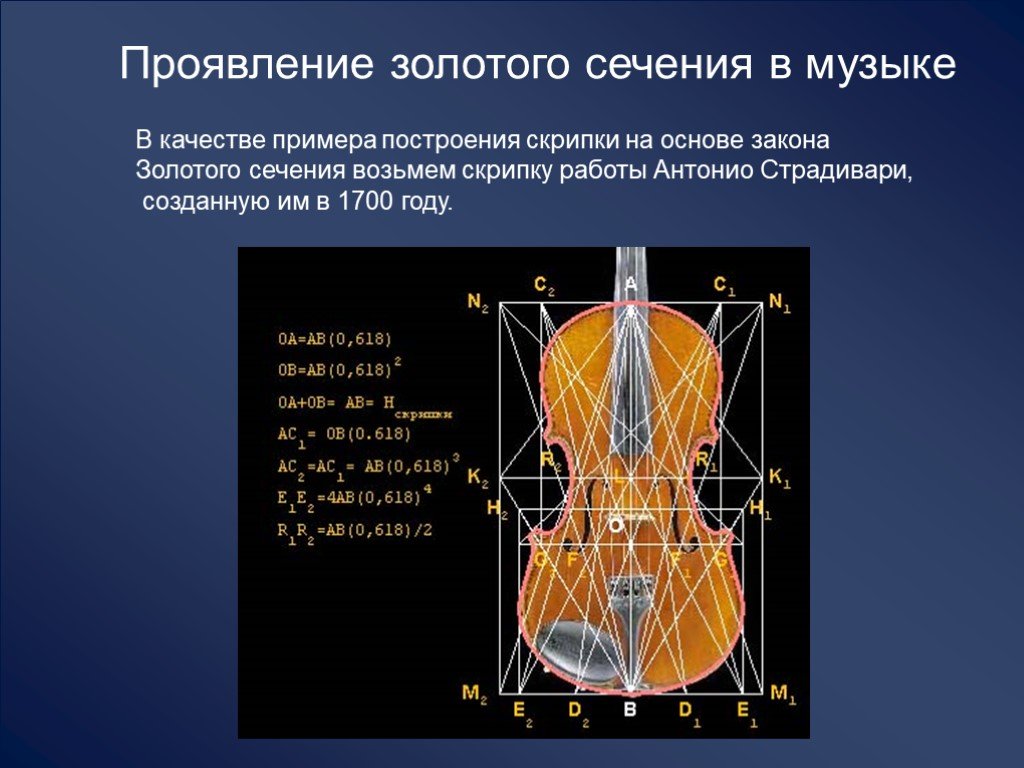
Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.
Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.
Число Фибоначчи и золотое сечение в природе
В растительном и животном мире существует тенденция к формообразованию в виде симметрии, которая наблюдается в направлении роста и движения.
Деление на симметричные части, в которых соблюдаются золотые пропорции, — такая закономерность присуща многим растениям и животным.
Природа вокруг нас может быть описана с помощью чисел Фибоначчи, например:
- расположение листьев или веток любых растений, а также расстояния соотносятся с рядом приведенных чисел 1, 1, 2, 3, 5, 8, 13 и далее;
- семена подсолнуха (чешуя на шишках, ячейки ананаса), располагаясь двумя рядами по закрученным спиралям в разные стороны;
- соотношение длины хвоста и всего тела ящерицы;
- форма яйца, если провести линию условно через широкую его часть;
- соотношение размеров пальцев на руке человека.
И, конечно, самые интересные формы представляют закручивающиеся по спирали раковины улиток, узоры на паутине, движение ветра внутри урагана, двойная спираль в ДНК и структура галактик — все они включают в себя последовательность чисел Фибоначчи.
Использование золотого сечения в искусстве
Исследователи, занимающиеся поиском в искусстве примеров использования золотого сечения, подробно исследуют различные архитектурные объекты и произведения живописи.
Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.
Одно из творений Леонардо да Винчи — «Портрет Моны Лизы» — уже многие годы является предметом исследований ученых. Ими было обнаружено, что композиция работы целиком состоит из «золотых треугольников», объединенных вместе в правильный пятиугольник-звезду. Все работы да Винчи являются свидетельством того, насколько глубоки были его познания в строении и пропорциях тела человека, благодаря чему он и смог уловить невероятно загадочную улыбку Джоконды.
Золотое сечение в архитектуре
В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618.
Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.
Применение пропорций в дизайне
В дизайне одежды все модельеры делают новые образы и модели с учетом пропорций человеческого тела и правил золотого сечения, хотя от природы не все люди имеют идеальные пропорции.
При планировании ландшафтного дизайна и создании объемных парковых композиций с помощью растений (деревьев и кустарников), фонтанов и малых архитектурных объектов также могут применяться закономерности «божественных пропорций».
Ведь композиция парка должна быть ориентирована на создание впечатления на посетителя, который свободно сможет ориентироваться в нем и находить композиционный центр.
Все элементы парка находятся в таких соотношениях, чтобы с помощью геометрического строения, взаиморасположения, освещения и света, произвести на человека впечатление гармонии и совершенства.
Применение золотого сечения в кибернетике и технике
Закономерности золотого сечения и чисел Фибоначчи проявляются также в переходах энергии, в процессах, происходящих с элементарными частицами, составляющих химические соединения, в космических системах, в генной структуре ДНК.
Аналогичные процессы происходят и в организме человека, проявляясь в биоритмах его жизни, в действии органов, например, головного мозга или зрения.
Алгоритмы и закономерности золотых пропорций широко используются в современной кибернетике и информатике. Одна из несложных задач, которую дают решать начинающим программистам, — написать формулу и определить, сумму чисел Фибоначчи до определенного числа, используя языки программирования.
Современные исследования теории о золотой пропорции
Начиная с середины 20 века, интерес к проблемам и влиянию закономерностей золотых пропорций на жизнь человека, резко возрастает, причем со стороны многих ученых различных профессий: математиков, исследователей этноса, биологов, философов, медицинских работников, экономистов, музыкантов и др.
В США с 1970-хгодов начинает выпускаться журнал The Fibonacci Quarterly, где публикуются работы на эту тему. В прессе появляются работы, в которых обобщенные правила золотого сечения и ряда Фибоначчи используют в различных отраслях знаний. Например, для кодирования информации, химических исследований, биологических и т.д.
Все это подтверждает выводы древних и современных ученых о том, что золотая пропорция многосторонне связана с фундаментальными вопросами науки и проявляется в симметрии многих творений и явлений окружающего нас мира.
Золотые числа Фибоначчи . ? – Число Бога [Золотое сечение – формула мироздания]
Снова рассмотрим последовательность Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 – и на сей раз посмотрим на отношения последовательных членов этого ряда (вычислять будем до шестого знака после запятой):
1/1 = 1,000000
2/1 = 2,000000
3/2 = 1,500000
5/3 = 1,666666
8/5 = 1,6000001
3/8 = 1,625000
21/13 = 1,615385
34/21 = 1,619048
55/34 = 1,617647
89/55 = 1,6180561
44/89 = 1,617978
233/144 = 1,618056
377/233 = 1,618026
610/377 = 1,618037
987/610 = 1,618033
Узнаете это число? Чем дальше мы продвинемся по последовательности Фибоначчи, тем ближе отношение двух соседних чисел Фибоначчи будет колебаться (то чуть больше, то чуть меньше) вокруг золотого сечения, неуклонно приближаясь к нему.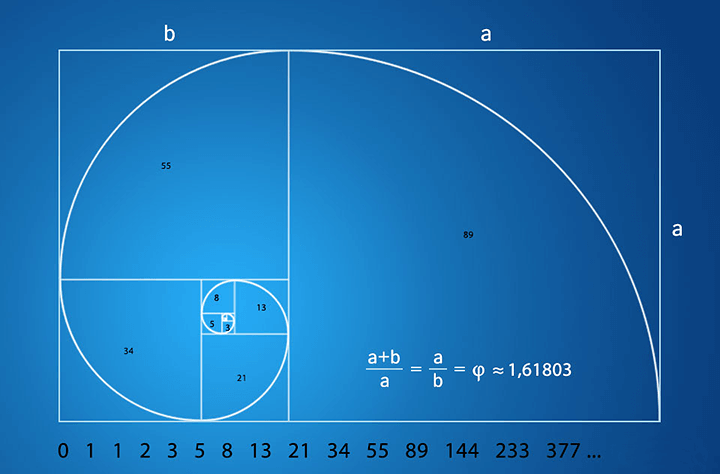
Если обозначить n-ный член последовательности Фибоначчи как
Но почему члены последовательности, выведенной из схемы разведения кроликов, подводят нас к соотношению, выведенному из деления отрезка? Чтобы понять эту связь, придется вернуться к поразительной непрерывной дроби, с которой мы познакомились в главе 4.
В принципе, можно вычислить значение ? методом последовательных приближений: прерывая непрерывную дробь все ниже и ниже. Предположим, мы именно так и поступим. Тогда у нас получится целый ряд значений (напомню: 1 к a/b – это все равно, что b/a).
Иными словами, последовательные приближения, при помощи которых мы ищем золотое сечение, в точности равны соотношениям чисел Фибоначчи. Ничего удивительного, что чем дальше мы продвигаемся по последовательности, тем ближе они сходятся к золотому сечению. Это качество прекрасно описано в книге «О росте и форме» знаменитого натуралиста сэра Д’Арси Уэнтворта Томпсона (1860–1948) (Sir D’Arcy Wentworth Thompson. On Growth and Form). Вот как он пишет о числах Фибоначчи: «Один мой друг, сведущий в математике, пишет мне б этих прославленных, поразительных числах: “Вся романтика непрерывных дробей, линейных рекурретнтых последовательностей… все это есть в них, и они – источник бесконечного интереса; как увлекательно наблюдать, с каким рвением они стремятся достичь недостижимого – например, золотого сечения; а ведь это всего лишь одно из сотен подобных соотношений”».
Числа Фибоначчи, подобно «предмету устремлений» их отношений – золотому сечению, – обладают поистине поразительными свойствами. Перечень математических закономерностей, связанных с числами Фибоначчи, буквально бесконечен. Приведу лишь несколько из них.
Что такое золотое сечение и как оно связано с последовательностью Фибоначчи?
Некоторая математика работает. Немного математики весело. А какая-то математика просто ошеломляет. Если это последнее описание кажется вам невероятным, то сегодня вы можете изменить свое мнение.
Потому что теперь, когда мы рассмотрели достаточно материала, мы собираемся взглянуть на некоторые из удивительных, элегантных и совершенно загадочных способов, которыми последовательность Фибоначчи проявляется в окружающем вас мире.
Резюме последовательности Фибоначчи
В прошлой статье мы говорили о том, как, казалось бы, невинный вопрос о росте популяции кроликов привел Фибоначчи к последовательности чисел, которая теперь носит его имя, — последовательности Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, …
Каждое последующее число в этой последовательности получается путем сложения двух предыдущих чисел. И, за исключением нескольких усложняющих деталей, таких как тот факт, что кролики в конце концов стареют и умирают, эта последовательность прекрасно моделирует рост популяции. Но у чисел в последовательности Фибоначчи есть жизнь далеко за пределами кроликов, и они появляются в самых неожиданных местах.
Что такое золотое сечение?
Одно из таких мест особенно увлекательно: золотое сечение.
Так что же это за золотое сечение? Ну, это число равно примерно 1,618. Это число теперь часто называют «фи» и выражается в письменной форме с использованием символа буквы фи из греческого алфавита. Фи не равно точно 1,618, поскольку, как и его знаменитый двоюродный брат пи, фи является иррациональным числом, а это означает, что его десятичные цифры продолжаются вечно без повторения шаблона. Если вам интересно узнать, как получается фактическое значение числа фи, ознакомьтесь с выпуском Math Dude «Video Extra!» на этой неделе. эпизод на ютубе. Но как это число стало таким важным? Как ни странно, все началось с вопроса эстетики.
Золотой прямоугольник
Какой самый красивый прямоугольник? Более конкретно: каково отношение высоты этого «самого красивого» прямоугольника к его ширине? Этот вопрос кажется странным, но это не безумие. Мы не будем сейчас вдаваться в подробности, но есть свидетельства того, что люди склонны воспринимать одну конкретную форму прямоугольника как наиболее приятную для глаз.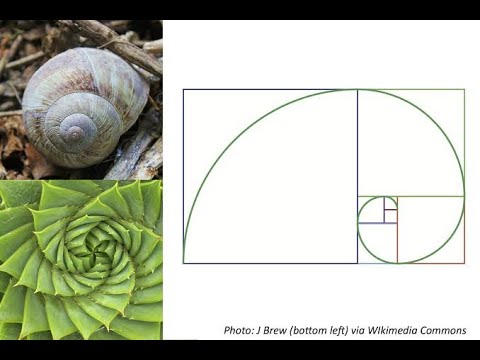
Конечно, греки знали об этом задолго до того, как это проверили современные психологи, поэтому они использовали золотые прямоугольники, а также другие золотые формы и пропорции, придерживающиеся золотого сечения, в своей архитектуре и искусстве.
Например, считается, что почти 2500 лет назад греческий скульптор и архитектор по имени Фидий использовал золотое сечение для проектирования статуй, которые он изваял для Парфенона (обратите внимание на слово «фи» в имени Фидия — это не совпадение и фактически вдохновило название числа в 20-м веке). А со времен Фидия многие художники и музыканты также использовали золотое сечение в своих работах — Леонардо да Винчи, Сальвадор Дали, Клод Дебюсси и многие другие.
Но вернемся к проблеме определения формы самого приятного прямоугольника. Если вы просто нарисуете то, что считаете самым красивым прямоугольником, затем измерите длины каждой стороны и, наконец, разделите самую длинную длину на самую короткую, вы, вероятно, обнаружите, что соотношение составляет где-то около 1,6, что является золотым сечением.
, фи, округленное до десятых. Это будет не совсем 1,6, но должно быть довольно близко. Помимо того, что она «красива», получившаяся форма обладает интригующей характеристикой: если вы нарисуете золотой прямоугольник, а затем проведете внутри него линию, чтобы разделить этот прямоугольник на квадрат и еще один меньший прямоугольник, этот меньший прямоугольник удивительным образом станет еще одним золотым прямоугольником! Вы можете сделать это снова с этим новым золотым прямоугольником, и вы снова получите квадрат и еще один золотой прямоугольник.
Связь между золотым сечением и последовательностью Фибоначчи
Хорошо, но как насчет последовательности Фибоначчи? Как это фигурирует в этом? Я знаю, что это может показаться совершенно не связанным, но проверьте это. Давайте создадим новую последовательность чисел, разделив каждое число в последовательности Фибоначчи на предыдущее число в последовательности. Помните, последовательность
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Таким образом, деление каждого числа на предыдущее дает: 1 / 1 = 1 , 2/1 = 2, 3/2 = 1,5 и так далее до 144/89= 1,6179….
В результате получается последовательность:
1, 2, 1,5, 1,666…, 1,6, 1,625, 1,615…, 1,619…, 1,6176…, 1,6181…, 1,6179…
Но заметили ли вы что-нибудь в этих числах? Возможно, из-за того, что они продолжают колебаться и дразняще приближаться все ближе и ближе к 1,618? — значению фи: золотому сечению! Действительно, без ведома Фибоначчи его решение проблемы роста популяции кроликов имеет глубокую связь с золотым сечением, которое художники и архитекторы использовали на протяжении тысячелетий!
Применение золотого сечения
Но золотое сечение предназначено не только для математиков, греческих скульпторов и художников эпохи Возрождения — его можно использовать и в жизни. На самом деле, в следующей статье мы поговорим о том, как вы можете использовать золотое сечение, чтобы делать более качественные снимки. И даже больше. Эти приятные формы проявляются не только в человеческом искусстве, но и в «искусстве» мира природы — во всем, от ракушек до подсолнухов! Обо всем этом мы тоже поговорим в следующий раз.
Подведение итогов
Это все математические расчеты, на которые у нас есть время на сегодня. Еще раз спасибо нашему спонсору на этой неделе, Go To Meeting. Посетите GoToMeeting.com/podcast и подпишитесь на бесплатную 45-дневную пробную версию их службы онлайн-конференций.
Пожалуйста, присылайте свои математические вопросы и комментарии по адресу , получайте обновления о шоу и моих повседневных размышлениях о математике, науке и жизни в целом, следуя за мной в Твиттере, и присоединяйтесь к нашему растущему сообществу поклонников математики в социальных сетях с помощью станьте поклонником Math Dude на Facebook — это отличное место, чтобы задавать вопросы и общаться с другими любителями математики.
Если вам понравилось то, что вы прочитали, и у вас есть несколько свободных минут, я был бы очень признателен за ваш отзыв в iTunes. И пока вы там, пожалуйста, подпишитесь на подкаст, чтобы не пропустить новый выпуск Math Dude.
До встречи в следующий раз, это Джейсон Маршалл с «Быстрыми и грязными советами чувака-математика, чтобы сделать математику проще».
Спасибо за внимание, любители математики!
Фибоначчи
Фибоначчи*см. другие примеры
| 1 | 1 | |||
| 2 | 1 | 1 | ||
| 3 | 2 | 2 | ||
| 4 | 3 | 1,5 | ||
| 5 | 5 | 1.66666666666667 | ||
| 6 | 8 | 1,6 | ||
| 7 | 13 | 1,625 | ||
| 8 | 21 | 1. 61538461538462 | ||
| 9 | 34 | 1.61 | 1 | 2 |
| 10 | 55 | 1.61764705882353 | ||
| 11 | 89 | 1.61818181818182 | ||
| 12 | 144 | 1.61797752808989 | ||
| 13 | 233 | 1.61805555555556 | ||
| 14 | 377 | 1.61802575107296 | ||
| 15 | 610 | 1.61803713527851 | ||
| 16 | 987 | 1.61803278688525 | ||
| 17 | 1597 | 1.61803444782168 | ||
| 18 | 2584 | 1.61803381340013 | ||
| 19 | 4181 | 1.61803405572755 | ||
| 20 | 6765 | 1.61803396316671 | ||
| 21 | 10946 | 1. 6180339985218 | ||
| 22 | 17711 | 1.61803398501736 | ||
| 23 | 28657 | 1.6180339 | 6||
| 24 | 46368 | 1.61803398820533 | ||
| 25 | 75025 | 1.6180339889579 | ||
| 26 | 121393 | 1.61803398867044 | ||
| 27 | 196418 | 1.61803398878024 | ||
| 28 | 317811 | 1.6180339887383 | ||
| 29 | 514229 | 1.61803398875432 | ||
| 30 | 832040 | 1.6180339887482 | ||
| 31 | 1346269 | 1.61803398875054 | ||
| 32 | 2178309 | 1.61803398874965 | ||
| 33 | 3524578 | 1. 61803398874999 | ||
| 34 | 5702887 | 1.61803398874986 | ||
| 35 | 9227465 | 1.61803398874991 | ||
| 36 | 14930352 | 1.61803398874989 | ||
| 37 | 24157817 | 1.6180339887499 | ||
| 38 | 39088169 | 1.61803398874989 | ||
| 39 | 63245986 | 1.6180339887499 | ||
| 40 | 102334155 | 1.61803398874989 | ||
| 41 | 165580141 | 1.6180339887499 | ||
| 42 | 267914296 | 1.6180339887499 | ||
| 43 | 433494437 | 1.6180339887499 | ||
| 44 | 701408733 | 1.6180339887499 | ||
| 45 | 1134 | 0 1. 6180339887499 | ||
| 46 | 1836311903 | 1.6180339887499 | ||
| 47 | 2971215073 | 1.6180339887499 | ||
| 48 | 4807526976 | 1.6180339887499 | ||
| 49 | 7778742049 | 1.6180339887499 | ||
| 50 | 12586269025 | 1.6180339887499 |
