Теория фибоначчи: Числа Фибоначчи — что это и для чего они нужны

Что такое последовательность Фибоначчи и как ее использовать в трейдинге

Опытные трейдеры знают, что большое количество рыночных ордеров скапливаются близко к уровням и влияют на рыночную цену бумаг. Чтобы прогнозировать эти уровни, используют последовательность Фибоначчи, которую видно на графиках. 

На основе этих чисел сформировано громадное количество стратегий. Они делятся на две большие группы — коррекцию и расширение.

Теория Фибоначчи создана итальянским математиком 12 века Леонардо Пизанским и в то время никакого отношения к биржевым операциям не имела — такая последовательность чисел встречается даже в живой природе. В биржевой технический анализ метод пришел аж через 5 веков.

Определение золотого сечения

Леонардо Фибоначчи из Пизы обнаружил некую числовую последовательность, которая встречается везде и универсальна для большинства природных явлений.

Вот эта последовательность чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

В этой цепочке каждое следующее число — это сумма двух предыдущих значений. Можете пересчитать сами и убедиться в этом. 

Попробуйте разделить 34 на 55, 21 на 34 или 8 на 13. То есть два любых числа, которые стоят рядом — делите предыдущее число на следующее. У вас получится одно и то же значение — округленное в чуть большую сторону. 

34 / 55 = 21 /34 = 8 /13 = примерно 0, 625 или 0, 618.

Но это только начало. Если мы будем делить числа через одно, то также получим одно и то же значение — 0, 382. Никакой магии — простая математика. Эти постоянные значения дробей называют «золотым сечением», эффект которого часто демонстрируют на примере спиралей внутри подсолнуха.  

 

Под золотым сечением подразумевают идеальную гармоничную пропорцию отношения части к целому.  Как раз это число — 1,618 — наблюдается в различных природных формах — раковины улитки, расстояние между листьями на одной ветке и даже соотношение частей тела человека. Это примеры того, как выглядит спираль Фибоначчи. Ученые, которые изучали формы золотого сечения в природе, замечали, что все живое стремится занять место в пространстве и для него характерны пропорции золотого сечения.

Вы спросите, при чем тут трейдинг?

А при том, что эти же значения дробей используются в качестве главного коэффициента при построении графиков!

Уровни фибоначчи используются для того, чтобы прогнозировать дальнейшее движение цены инструмента. Работа с этими числами привязывается к уже существующему тренду, чтобы в дальнейшем прогнозировать коррекцию или развитие. Алгоритм задает ориентиры — до какого уровня дойдет цена, где возможен разворот и прочее. Благодаря этим расчетам трейдеры могут устанавливать отложенные ордера, стопы и профиты. 

Первым додумался искать золотое сечение числа фибоначчи на биржевых графиках американский инженер Ральф Hельсон Эллиотт. В начале 30-х годов ХХ века он серьезно заболел и от нечего делать стал изучать графики фондовых индексов за последние 75 лет существования бирж.

Он отследил, что индексы двигаются волнообразно — в определенном ритме. И там тоже прослеживается та же пропорция — с числом 1,618. Так родилась теория волнового анализа, которую ученый описал в нескольких серьезных трудах, включая книгу «Закон природы — секрет вселенной». Но четкого ответа на вопрос — в какой волне в конкретный момент находится цена — теория не дает. Это упирается в параметры определения точки отсчета первой волны — страсти кипят по сей день, и к единому мнению биржевики так и не пришли.

Практичнее всего было бы применить принцип «Не торгуй, если не уверен».  Но есть инструменты, в которых волны на определенной стадии четко вырисовываются и их легко идентифицировать. 

На некоторых инструментах вычислить волны невозможно, приходится регулярно наблюдать и находить те из них, где волны ходят понятным трейдеру образом. И потом торговать исключительно на них. 

Что такое числа Фибоначчи в трейдинге и как это выглядит на графиках

Для определения ценовых ориентиров и понимания того, когда выгоднее продавать/покупать бумаги, в каком месте цена сменит направление, трейдеры применяют старый проверенный инструмент — уровни поддержки и сопротивления. Но к сожалению, не всегда можно вычислить, какой из них будет работать, а какой цена может не заметить — как раз этот вопрос и помогает разрешить метод Фибоначчи.

Что такое линии Фибоначчи?

На биржевых графиках это сетка из линий, которые расположены друг от друга на определенном расстоянии — его рассчитывают с применением уже известного коэффициента. Чаще всего рыночная цена стремится к этим линиям, приближаясь к уровням, и часто меняет направление. А если она его пробивает — то это признак сильного тренда.

Когда чертят линии, привязку делают к последнему явно выраженному тренду. Сетка Фибоначчи растягивается от начала до конца тренда. И уровни внутри диапазона будут ориентирами в случае возможной коррекции. А те, что лежат вне диапазона, — это ориентиры возможного продолжения тренда.

Открывая сделку по тренду, на внешние уровни можно ставить тейки, а на внутренние — стопы. При коррекции целями трейдера будут внутренние уровни. Возможно открытие сделок на пробой уровней и установка на них отложенных ордеров.

Временные зоны 

Они дают возможность спрогнозировать время очередной трендовой или коррекционной волны — за основу берется протяженность предыдущего сигнала.  

От линий временные зоны отличаются тем, что их растягивают от точки начала тренда до точки разворота.

Но используют их крайне редко— на отдельных таймфреймах у любой валютной пары будет своя длина волны. А значит, конкретного правила на вход не бывает. И торговать отложенными ордерами не получится.

Канал 

В отличие от горизонтальных линий канал может выглядеть на графике наклонно — и сетка линий тренда при определении цели для цены учитывает угол наклона тренда. При восходящем текущем тренде точки привязываются к минимумам, при нисходящем — к максимумам. После чего выстраивают первую линию тренда — она и будет основной поддержкой или сопротивлением. Передвигая следующую линию, настраивают всю остальную сетку. 

Дуги 

Эффективны, когда цена движется во флэте. Их применяют, чтобы уловить коррекцию. При этом дуги растягивают от начала до конца тренда и наоборот в соответствии с направлением закругления.

Классический вариант — когда на графике присутствуют три дуги внутри амплитуды движения тренда. Чем дальше цена движется от ключевых точек, тем сильнее расходятся линии дуг, расширяя при этом диапазон. 

Веер 

Это когда на графике из одной точки несколько лучей расходятся в разные стороны — рисунок действительно напоминает веер. Его растягивают по двум точкам тренда и начинают всегда с первой, из которой и выстраиваются лучи.

Когда тренд восходящий, веер выстраивается под графиком цены, а когда он нисходящий — веер располагается над ним и дает ориентиры для коррекции.

Еще его используют, когда работают с динамичным стопом — ордер при этом передвигают на одной из веерных линий, следуя за движением цены. 

Расширения

Часто применяют во время волнового анализа. Для построения нужны три точки, образующие коррекционную и трендовую волны. Расширения дают возможность увидеть новые цели по направлению тренда и помогают выставлять тейк-профиты.  

Дуги, веера и временные зоны — слишком специфические инструменты и применяются редко. Разве что в торговых системах, которые специально разрабатывались под них. В принципе, фигура Фибоначчи — популярный базовый инструмент, используемый в сочетании с другими элементами (поиск или подтверждение дополнительных сигналов, и других).

В популярном терминале для российских трейдеров Quik есть 4 инструмента — уровни, дуги, веер и временные зоны.

Что такое коррекция в трейдинге и как выставлять уровни коррекции Фибоначчи

В соответствии с правилами их растягивают от точки начала тренда к его окончанию (в терминале Quik можно растягивать и наоборот — на результат это не повлияет). Образовавшиеся уровни будут возможными целями коррекции — от них можно входить по тренду.

Уровни коррекции Фибоначчи:

0.236, 0.382, 0.500, 0.618, 0.764

Уровни расширения Фибоначчи:

0, 0.382, 0.618, 1.000, 1.382, 1.618

При выстраивании уровней коррекции и расширения считать дроби нет необходимости — для этого существуют калькуляторы, да и на живых графиках они вырисовываются автоматически.

Почему уровни основаны на дробях?

Опытные трейдеры вполне резонно полагают, что если внутри подсолнуха расстояние между линиями спирали из семечек можно просчитать этими дробями, то и уровни ретрейсмента по аналогии можно использовать в качестве поддержки и сопротивления.

С их помощью также открывают сделки и размещают стопы на форексе. А уровни расширения помогают корректно устанавливать тейк-профиты — часто цена доходит до них, и это надо учитывать.

Всегда ли ряд Фибоначчи поможет трейдеру

Если цена может пробить уровень сопротивления или поддержки, то аналогично она способна пробить и линии Фибоначчи. Поэтому их нельзя считать окончательной гарантией того, что произойдет откат или отскок — просто они дают высокую степень вероятности.

Как и любой другой аспект технического анализа, уровни Фибоначчи надо тщательно отрабатывать, постоянно уточнять и фильтровать. Собственно говоря, на вероятностях построен теханализ. И об этом нельзя забывать — ведь цена не всегда будет взаимодействовать с ними так, как вы предполагаете. Она может перемещаться от уровня к уровню — и какой из них она посчитает более значимым, это только ей одной известно. И поэтому во время применения стратегии уровней Фибоначчи придется использовать все доступные инструменты, совмещая их с линиями Фибоначчи, а также с поддержкой и сопротивлением.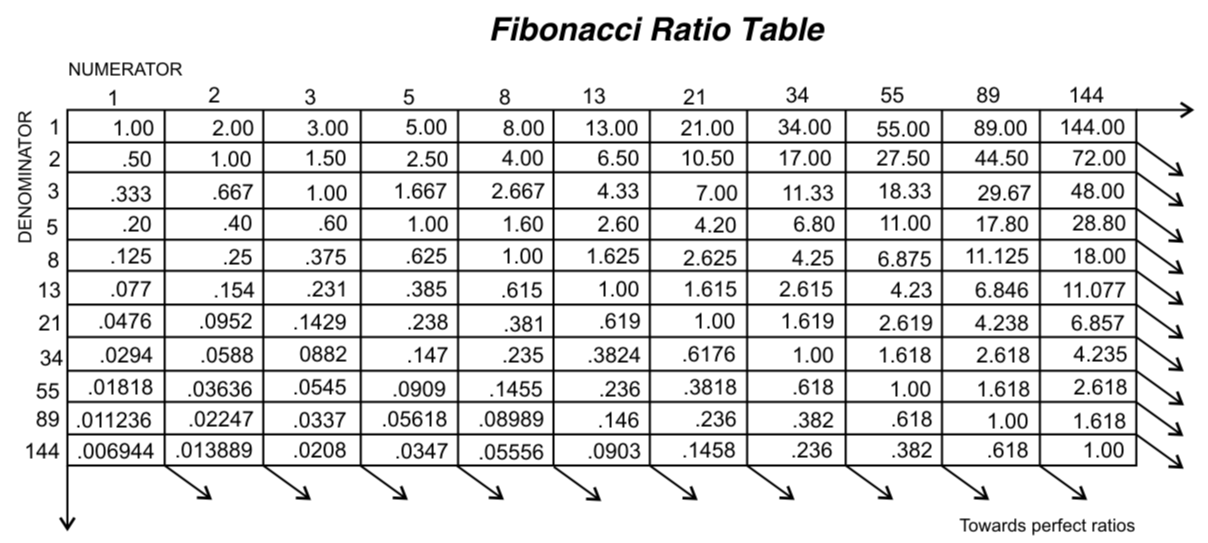

Каждый трейдер сам решает, применять ли данный метод. 

Преимущества и недостатки метода

Плюсы инструмента:

• Главный жирный плюс — универсальность инструмента, подтвержденная сотнями лет применения в разных сферах, в том числе и трейдинге. Уже лет пятьдесят их применяют в анализе фондовых рынков, Форекса, а также крипторынка. Именно поэтому трейдинг по Фибоначчи остается востребованным, независимо от того, как сильно меняется рынок от волатильности к спокойствию и наоборот.
• Спектр применения метода весьма широк — с ним можно открывать новые ордера, искать точки входа и выхода из рынка.

Минус:

• До того, как устанавливать уровни, нужен предварительный анализ. Если другие компьютерные ориентиры можно только запустить, и они на графике установятся автоматически, то уровни Фибоначчи надо устанавливать вручную — в этом случае трейдеру придется самому выбирать, от каких точек строить линии.

Книги по теме 

•  А. Фроста и Р. Пректер «Волновой принцип Эллиотта» — там хорошо описаны принципы классической волновой теории Эллиота в ее изначальном виде..
• Б. Мендельброт и Р. Хадсон «(Не)послушные рынки» — современный взгляд на теорию волн Эллиотта.
• Б. Вильямс «Торговый хаос» — подробное знакомство с методикой подсчета волн в доступной форме.
• Р. Фишеp «Последовательность Фибоначчи: приложения и стратегии для трейдеров»  — еще один нестандартный взгляд на применение последовательности Фибоначчи для подсчета волн.

Выводы

Последовательность Фибоначчи напрямую связана с термином «золотое сечение», которому соответствует число 1,618. Отношение каждого следующего числа к предшествующему стремится к этой величине.

Работая с этим методом, трейдеры могут прогнозировать, куда двинется тренд, неважно, на каком рынке — Форексе, фондовом или криптовалюты.

У любого тренда всегда будут наблюдаться циклы повышения, коррекции, спада, снова коррекции и последующего роста. И линии Фибоначчи нужны, чтобы прогнозировать направление движения тренда, опираясь на цифры.

Несколько полученных значений биржевики связывают в неровную линию и подвергают анализу, чтобы найти некие ориентиры, которые позволят уверенно входить в рынок.

Опытному трейдеру уровни Фибоначчи сэкономят время и силы на утомительные детальные расчеты и послужат отличным инструментом получения прибыли. 

Новичкам в этом деле следует начать с изучения волнового анализа и базовых навыков торговли от уровней. И только потом переходить к освоению метода Фибоначчи. 

Но как бы в разных трейдерских блогах ни нахваливали этот продвинутый инструмент, следует знать, что его абсолютная эффективность до конца не доказана — поэтому результаты применения целиком зависят от степени подготовки и опыта трейдера.

Это сложная тема. Ее невозможно детально разобрать в рамках одной статьи. Поэтому приглашаем на наш базовый курс.

Math.ru

Николай Николаевич Воробьев

М. : Наука, 1978. 144 с.
Тираж 100000 экз.
Серия Популярные лекции по математике, выпуск 6

Загрузить (Mb) djvu (0.95) pdf (-) ps (-) html (-) tex (-)

Первый вариант текста этой книжки писался почти тридцать лет тому назад. С тех пор изменилось очень многое.

Прежде всего, и это главное, изменился математический уровень основного круга читателей популярных математических книг: интересующихся математикой школьников старших классов и их преподавателей. Созданная сеть специализированных математических и физико-математических школ и классов предопределила существенное расширение математического кругозора соответствующего контингента учащихся, которых теперь можно заинтересовать скорее не забавными элементарными фактами, а уже достаточно глубокими и сложными результатами.

Кроме того, и это является фундаментальным фактом истории математики нашего времени, существенно сместился центр тяжести математических исследований в целом. В частности, утратила свои доминирующие позиции теория чисел, и резко повысился удельный вес экстремальных задач. В самостоятельную отрасль математики сложилась теория игр. По существу возникла вычислительная математика. Все это не могло не сказаться и на содержании научно-популярной литературы по математике.

Далее, числа Фибоначчи проявили себя еще в нескольких математических вопросах, среди которых в первую очередь следует назвать решение Ю. В. Матиясевичем десятой проблемы Гильберта и далеко не столь глубокую, но приобретшую широкую известность теорию поиска экстремума унимодальной функции, построенную впервые, по-видимому, Р. Беллманом.

Наконец, было установлено довольно большое количество ранее неизвестных свойств чисел Фибоначчи, а к самим числам существенно возрос интерес.

Значительное число связанных с математикой людей в различных странах приобщились к благородному хобби «фибоначчизма». Наиболее убедительным свидетельством этому может служить журнал The Fibonacci Quarterly, издаваемый в США с 1963 г.

Все сказанное определило изменения содержания книги от издания к изданию и тот вид, в котором она предлагается читателю сейчас. Во втором издании был добавлен параграф о фибоначчиевых планах поиска экстремума унимодальной функции вместе с возникающими при этом общематематическими и вычислительными вопросами. В третьем издании была расширена теоретико-числовая тематика, и этот материал из § 2 оказался полезной информацией при решении десятой проблемы Гильберта. Наконец, в настоящем издании «подтягиваются» до общего уровня и объема § 3 и 4. В § 3 приводятся ставшие классическими теоремы о точности приближений подходящими дробями и описывается роль чисел Фибоначчи в этих фактах, а в § 4 рассматривается игра «цзяньшицзы», теоретико-игровой анализ которой опирается на детальное рассмотрение фибоначчиевых представлений натуральных чисел.

Книга по-прежнему не требует от читателя знаний, выходящих за пределы школьного курса. Более трудные ее места выделены мелким шрифтом и могут быть при чтении пропущены без ущерба для понимания остального материала.

Вырица 1
Н. Н. Воробьев
1978 г.

---

Содержание

Предисловие к первому изданию

Предисловие к четвертому изданию

Введение

§ 1. Простейшие свойства чисел Фибоначчи

§ 2. Теоретико-числовые свойства чисел Фибоначчи

§ 3. Числа Фибоначчи и непрерывные дроби

§ 4. Числа Фибоначчи и геометрия

§ 5. Числа Фибоначчи и теория поиска

---

Загрузить (Mb) djvu (0. 95) pdf (-) ps (-) html (-) tex (-)

Постоянный адрес этой страницы: http://math.ru/lib/plm/6

последовательность Фибоначчи | Определение, формула, числа, соотношение и факты

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Этот день в истории
• Викторины
• Подкасты
• Словарь
• Биографии
• Резюме
• Популярные вопросы
• Обзор недели
• Инфографика
• Демистификация
• Списки
• #WTFact
• Товарищи
• Галереи изображений
• Прожектор
• Форум
• Один хороший факт

• Развлечения и поп-культура
• География и путешествия
• Здоровье и медицина
• Образ жизни и социальные вопросы
• Литература
• Философия и религия
• Политика, право и правительство
• Наука
• Спорт и отдых
• Технология
• Изобразительное искусство
• Всемирная история

• Britannica объясняет
  В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.
• Britannica Classics
  Посмотрите эти ретро-видео из архивов Encyclopedia Britannica.
• #WTFact Видео
  В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти.
• На этот раз в истории
  В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории.
• Demystified Videos
  В Demystified у Britannica есть все ответы на ваши животрепещущие вопросы.

• Студенческий портал
  Britannica — это главный ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д.
• Портал COVID-19
  Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня.
• 100 женщин
  Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
• Britannica Beyond
  
  Мы создали новое место, где вопросы находятся в центре обучения. Вперед, продолжать. Просить. Мы не будем возражать.
• Спасение Земли
  Британника представляет список дел Земли на 21 век. Узнайте об основных экологических проблемах, стоящих перед нашей планетой, и о том, что с ними можно сделать!
• SpaceNext50
  Britannica представляет SpaceNext50. От полёта на Луну до управления космосом — мы исследуем широкий спектр тем, которые подпитывают наше любопытство к космосу!

Содержание

• Введение

Краткие факты

• Факты и сопутствующий контент

Викторины

• Интересные факты об измерениях и математике
• Числа и математика

Теория Фибоначчи | FOREX.

com

Немного истории Фибоначчи

Прежде чем мы слишком углубимся в то, что такое Фибоначчи, давайте сначала ответим на вопрос «кто такой Фибоначчи?» Леонардо Пизано, или Леонардо Фибоначчи, как он наиболее широко известен, был европейским математиком в средние века, написавшим Liber Abaci (Книгу вычислений) в 1202 году нашей эры. В этой книге он обсуждал различные темы, в том числе способы конвертации валют и измерений для торговли, расчеты прибыли и процентов, а также ряд математических и геометрических уравнений. Однако есть две вещи, которые выходят на передний план нашего обсуждения в современном мире. Во-первых, в начальных частях Liber Abaci он обсуждал преимущества использования арабской системы счисления. В то время влияние несуществующей Римской империи было еще сильным, и большинство граждан Европы предпочитали использовать римские цифры. Однако в Liber Abaci Фибоначчи предоставил очень мощный, влиятельный и простой для понимания аргумент в пользу использования арабской системы счисления. С этого момента арабская система счисления прочно закрепилась в европейском сообществе и вскоре стала доминирующим методом математики в регионе, а затем и во всем мире. Оно было настолько сильным, что мы до сих пор пользуемся арабской системой счисления.

Вторым важным разделом Liber Abaci, который мы используем сегодня, является последовательность Фибоначчи. Последовательность Фибоначчи — это ряд чисел, где каждое число в ряду эквивалентно сумме двух предшествующих ему чисел.

Как видно из этой последовательности, нам нужно начать с двух «начальных» чисел, 0 и 1. Затем мы добавляем 0 и 1, чтобы получить следующее число в последовательности, то есть 1. Затем вы берете это значение и добавить его к числу, предшествующему ему, чтобы получить следующее число в последовательности. Если мы продолжим следовать этому шаблону, мы получим это:

Последовательность Фибоначчи очень важна для этого обсуждения, потому что нам нужны эти числа, чтобы получить коэффициенты Фибоначчи. Без последовательности Фибоначчи коэффициенты Фибоначчи не существовали бы.

Из чего состоит коэффициент Фибоначчи?

С появлением Интернета появилось много дезинформации о том, какие значения составляют коэффициенты Фибоначчи. Распространение анализа Фибоначчи, особенно в сфере трейдинга, способствовало неправильному толкованию и непониманию того, как и что составляет отношение Фибоначчи. Давайте посмотрим, что такое отношение Фибоначчи, как оно создается, и некоторые примеры тех, которые на самом деле вообще не являются отношениями Фибоначчи.

Коэффициенты Фибоначчи

Математика, связанная с коэффициентами Фибоначчи, довольно проста. Все, что нам нужно сделать, это взять определенные числа из последовательности Фибоначчи и следовать образцу деления по всей ней. В качестве примера возьмем число в последовательности и разделим его на число, следующее за ним.

0 ÷ 1 = 0
1 ÷ 1 = 1
1 ÷ 2 = 0,5
2 ÷ 3 = 0,67
3 ÷ 5 = 0,6
5 ÷ 8 = 0,625
8 ÷ 13 = 0,615
13 ÷ 21 = 0,619
. 21 ÷ 34 = 0,618
34 ÷ 55 = 0,618
55 ÷ 89 = 0,618

Заметили, что здесь развивается закономерность? Начиная с деления 21 на 34 и до бесконечности, вы ВСЕГДА получите 0,618!

Мы могли бы сделать это и с другими числами в последовательности Фибоначчи. Например, взяв число в последовательности и разделив его на число, которое ему предшествует, мы увидим еще одно постоянное число, которое развивается.

1 ÷ 0 = 0
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 2 = 1,5
5 ÷ 3 = 1,67
8 ÷ 5 = 1,6
13 ÷ 8 = 1,625
21 ÷ 13 = 1,615
34 ÷ 21 = 1,619
55 ÷ 34 = 1,618
89 ÷ 55 = 1,618
144 ÷ 89 = 1,618

. Другое рисунок разрабатывает числа из чисел. Теперь 1,618 на самом деле имеет еще большее значение, потому что его также называют золотым сечением, золотым числом или божественным соотношением, но я мог бы продолжить еще много страниц на эту тему.

Вот еще несколько примеров паттернов, которые развиваются, если брать числа из последовательности Фибоначчи и делить их по паттерну с другими числами в последовательности.

Разделить на 2 после	Разделить на 2 перед	Разделить на 3 после	Разделить на 3 перед
0 ÷ 1 = 0	1 ÷ 0 = 0	0 ÷ 2 = 0	2 ÷ 0 = 0
1 ÷ 2 = 0,5	2 ÷ 1 = 2	1 ÷ 3 = 0,33	3 ÷ 1 = 3
1 ÷ 3 = 0,33	3 ÷ 1 = 3	1 ÷ 5 = 0,2	5 ÷ 1 = 5
2 ÷ 5 = 0,4	5 ÷ 2 = 2,5	2 ÷ 8 = 0,25	8 ÷ 2 = 4
3 ÷ 8 = 0,375	8 ÷ 3 = 2,67	3 ÷ 13 = 0,231	13 ÷ 3 = 4,33
5 ÷ 13 = 0,385	13 ÷ 5 = 2,6	5 ÷ 21 = 0,238	21 ÷ 5 = 4,2
8 ÷ 21 = 0,381	21 ÷ 8 = 2,625	8 ÷ 34 = 0,235	34 ÷ 8 = 4,25
13 ÷ 34 = 0,382	34 ÷ 13 = 2,615	13 ÷ 55 = 0,236	55 ÷ 13 = 4,231
21 ÷ 55 = 0,382	55 ÷ 21 = 2,619	21 ÷ 89 = 0,236	89 ÷ 21 = 4,231
34 ÷ 89 = 0,382	89 ÷ 34 = 2,618	34 ÷ 144 = 0,236	144 ÷ 34 = 4,235
55 ÷ 144 = 0,382	144 ÷ 55 = 2,618	55 ÷ 233 = 0,236	233 ÷ 55 = 4,236
89 ÷ 233 = 0,382	233 ÷ 89 = 2,618	89 ÷ 377 = 0,236	377 ÷ 89 = 4,236
144 ÷ 377 = 0,382	377 ÷ 144 = 2,618	144 ÷ 610 = 0,236	610 ÷ 144 = 4,236

Как видите, мы могли бы получить множество различных чисел, просто взяв числа из последовательности Фибоначчи и разработав в ней разделяющий паттерн. Однако это не единственный способ получить коэффициенты Фибоначчи. Получив числа от деления, мы можем извлечь квадратные корни из каждого из этих чисел, чтобы получить больше чисел. См. диаграмму ниже для некоторых примеров этих значений.

Коэффициент Фибоначчи	Операция	Результат
0,236	Квадратный корень из 0,236	0,486
0,382	Квадратный корень из 0,382	0,618
0,618	Квадратный корень из 0,618	0,786
1.618	Квадратный корень из 1,618	1,272
2,618	Квадратный корень из 2,618	1,618
4,236	Квадратный корень из 4,236	2,058

Последним этапом преобразования этих чисел в коэффициенты Фибоначчи является простое преобразование их в проценты. Используя это обоснование, 0,236 становится 23,6%, 0,382 становится 38,2% и т. д. Итак, глядя на наш анализ, мы видим, что 23,6%, 38,2%, 48,6%, 61,8%, 78,6%, 127,2%, 161,8%, 205,8%, 261,8 %, а 423,6% — наши достоверные коэффициенты Фибоначчи.

А как насчет 50%?

Хотя коэффициент 50% часто используется в анализе Фибоначчи, он не является коэффициентом Фибоначчи. Некоторые говорят, что уровень 50% — это коэффициент Ганна, созданный У. Д. Ганном в начале 1900-х годов. Другие называют уровень 50% обратным «священному соотношению». Как и в случае с отношениями Фибоначчи, многие люди будут либо брать обратный, либо квадратный корень из «священных отношений», чтобы получить больше значений. Некоторые примеры можно найти в таблице ниже.

Священное отношение	Операция	Результат	Инверсия священного соотношения
1	Квадратный корень из 1	1	1
2	Квадратный корень из 2	1. Теория фибоначчи: Числа Фибоначчи — что это и для чего они нужны Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Пролистать наверх