Угол 20 градусов рисунок: Поворот и отражение надписи, фигуры, объекта WordArt или рисунка

Поворот и отражение надписи, фигуры, объекта WordArt или рисунка

Положение надписи (и текста в ней), фигуры, объекта WordArt или рисунка можно изменять, поворачивая или переворачивая их. 

Если вы работаете в электронной почте, см. статью Поворот рисунка в Outlook.

Щелкните заголовок раздела ниже, чтобы открыть подробные инструкции.

1. Выберите объект, который вы хотите повернуть.

2. Щелкните маркер поворота сверху объекта и перетащите его в нужном направлении.

   • org/ListItem»>

     Чтобы выполнять поворот с шагом в 15 градусов, перетаскивайте маркер поворота, удерживая нажатой клавишу SHIFT.

   • При повороте нескольких фигур каждая из них поворачивается по отдельности относительно своего центра.

1. Щелкните объект, который нужно повернуть.

2. В разделе Средства рисования (или Работа с рисунками, если вы поворачиваете рисунок) откройте вкладку Формат, в группе Упорядочение нажмите кнопку Повернуть, а затем выберите пункт Другие параметры поворота.

3. В открывшейся области или диалоговом окне введите требуемую величину угла поворота объекта в поле Поворот. Вы также можете использовать стрелки, чтобы повернуть объект точно так, как хотите.

Если в разделе Средства рисования или Работа с рисунками не отображается вкладка «Формат», выделите надпись, фигуру или объект WordArt. Для открытия вкладки

Формат может потребоваться дважды щелкнуть объект.

1. Выберите объект, который вы хотите повернуть.

2. org/ListItem»>

   В разделе Средства рисования (или Работа с рисунками, если вы поворачиваете рисунок) откройте вкладку Формат, в группе Упорядочить нажмите кнопку Повернуть, а затем сделайте следующее:

   • Чтобы повернуть объект на 90° вправо, выберите пункт Повернуть вправо на 90°.

   • Чтобы повернуть объект на 90° влево, выберите пункт Повернуть влево на 90°.

Если в разделе Средства рисования или Работа с рисунками не отображается вкладка «Формат», выделите надпись, фигуру, объект WordArt или рисунок. Для открытия вкладки Формат может потребоваться дважды щелкнуть объект.

Вы можете зеркально отразить объект или перевернуть его вверх ногами с помощью переворачивания.

1. Выберите объект, который вы хотите повернуть.

2. В разделе Средства рисования (или Работа с рисунками, если вы поворачиваете рисунок) откройте вкладку Формат, в группе Упорядочить нажмите кнопку Повернуть, а затем сделайте следующее:

   • Чтобы перевернуть объект вверх ногами, щелкните Отразить сверху вниз.

   • Чтобы зеркально отразить объект, щелкните Отразить слева направо.

Если в разделе Средства рисования или Работа с рисунками не отображается вкладка «Формат», выделите надпись, фигуру, объект WordArt или рисунок. Для открытия вкладки Формат может потребоваться дважды щелкнуть объект.

Совет: Если вы просто хотите зеркально отразить текст в документе, см. статью Создание зеркального отражения текста.

При повороте объекта текст внутри него также поворачивается. Однако текст внутри перевернутого объекта не переворачивается вместе с ним. Чтобы отразить текст вместе с объектом, содержащим его, вы можете сделать следующее в Outlook, Excel и PowerPoint:

org/ItemList»>

1. Выберите и щелкните правой кнопкой мыши объект, который вы хотите отразить, и выберите команду Формат фигуры.

2. В области Формат фигуры в разделе Параметры фигуры откройте вкладку Эффекты.

3. В разделе Поворот объемной фигуры введите 180 в одном из полей Вращение вокруг оси (X, Y или Z в зависимости от того, как вы хотите повернуть текст).

   Примечания: 

   • Вращение может повлиять на цвет заливки. Вы можете настроить цвет заливки в области Формат фигуры на вкладке Заливка и границы .

   • Если щелкнуть объект, чтобы изменить текст, он временно вернется к прежнему виду. Он будет снова отражен, когда вы завершите изменение текста и щелкнете за пределами объекта.

Важно:  Office 2010 больше не поддерживается. Перейдите на Microsoft 365, чтобы работать удаленно с любого устройства и продолжать получать поддержку.

Повысить статус

Щелкните заголовок раздела ниже, чтобы открыть подробные инструкции.

1. Выберите объект, который вы хотите повернуть.

2. Щелкните маркер поворота сверху объекта и перетащите его в нужном направлении.

   Примечание: Чтобы выполнять поворот с шагом в 15 градусов, перетаскивайте маркер поворота, удерживая нажатой клавишу SHIFT.

1. Щелкните объект, который нужно повернуть.

2. В разделе Средства рисования (или Работа с рисунками, если вы поворачиваете рисунок) откройте вкладку Формат, в группе Упорядочение нажмите кнопку Повернуть, а затем выберите пункт Другие параметры поворота.

   Если вкладка Работа с рисунками, Средства рисования или Формат не отображается, выделите рисунок. Для открытия вкладки Формат может потребоваться дважды щелкнуть рисунок.

3. В открывшейся области или диалоговом окне введите требуемую величину угла поворота объекта в поле Поворот. Вы также можете использовать стрелки, чтобы повернуть объект точно так, как хотите.

Вы можете зеркально отразить объект или перевернуть его вверх ногами с помощью переворачивания.

1. Выберите объект, который вы хотите повернуть.

2. В разделе Средства рисования (или Работа с рисунками, если вы поворачиваете рисунок) откройте вкладку Формат, в группе Упорядочить нажмите кнопку Повернуть, а затем сделайте следующее:

   • Чтобы перевернуть объект вверх ногами, щелкните Отразить сверху вниз.

   • Чтобы зеркально отразить объект, щелкните Отразить слева направо.

Если в разделе Средства рисования или Работа с рисунками не отображается вкладка «Формат», выделите надпись, фигуру, объект WordArt или рисунок. Для открытия вкладки Формат может потребоваться дважды щелкнуть объект.

Совет: Если вы просто хотите зеркально отразить текст в документе, см. статью Создание зеркального отражения текста.

При повороте объекта текст внутри него также поворачивается. Однако текст внутри перевернутого объекта не переворачивается вместе с ним. Чтобы отразить текст вместе с объектом, содержащим его, вы можете сделать следующее в Outlook, Excel и PowerPoint:

1. Выберите и щелкните правой кнопкой мыши объект, который вы хотите отразить, и выберите команду Формат фигуры.

2. В левой области диалогового окна Формат фигуры щелкните Поворот объемной фигуры.

3. Введите 180 в одном из полей Вращение вокруг оси (X, Y или Z в зависимости от того, как вы хотите повернуть текст).

   Примечания: 

   • Вращение может повлиять на цвет заливки. Вы можете настроить цвет заливки в диалоговом окне Формат фигуры на вкладке Заливка.

   • Если щелкнуть объект, чтобы изменить текст, он временно вернется к прежнему виду. Он будет снова отражен, когда вы щелкнете за его пределами.

org/ItemList»>

1. Выберите объект, который вы хотите повернуть.

2. Щелкните маркер поворота сверху объекта и перетащите его в нужном направлении.

   • Чтобы выполнять поворот по 15 градусов, перетаскивайте маркер поворота, удерживая нажатой клавишу SHIFT.

   • При повороте нескольких фигур каждая из них поворачивается по отдельности относительно своего центра.

   • Кроме того, вы можете выделить объект, нажать и удерживать клавишу OPTION, а затем нажимать клавиши со стрелками влево или вправо, чтобы выполнить поворот.

1. Щелкните объект, который нужно повернуть.

2. На вкладке Формат фигурыФормат рисунка в группе Упорядочить нажмите кнопку Повернуть.

   • org/ListItem»>

     Если вы не видите вкладку Формат фигуры или Формат рисунка, убедитесь, что выбрана надпись, фигура, объект WordArt или рисунок.

   • Кнопка Повернуть может быть скрыта, если у вас маленький экран. Если вы не видите кнопку Повернуть, щелкните Упорядочить, чтобы просмотреть скрытые кнопки в группе Упорядочить.

3. Нажмите кнопку Другие параметры поворота.

4. org/ListItem»>

   В открывшемся диалоговом окне или области введите требуемую величину угла поворота объекта в поле Поворот. Вы также можете использовать стрелки, чтобы повернуть объект точно так, как хотите.

1. Щелкните объект, который нужно повернуть.

2. На вкладке Формат фигурыФормат рисунка в группе Упорядочить нажмите кнопку Повернуть.

   • org/ListItem»>

     Если вы не видите вкладку Формат фигуры или Формат рисунка, убедитесь, что выбрана надпись, фигура, объект WordArt или рисунок.

   • Кнопка Повернуть может быть скрыта, если у вас маленький экран. Если вы не видите кнопку Повернуть, щелкните Упорядочить, чтобы просмотреть скрытые кнопки в группе Упорядочить.

3. Чтобы повернуть объект на 90 градусов вправо, щелкните Повернуть вправо на 90°. Для поворота влево щелкните Повернуть влево на 90°.

Вы можете зеркально отразить объект или перевернуть его вверх ногами с помощью переворачивания.

1. Выберите объект, который вы хотите повернуть.

2. На вкладке Формат фигурыФормат рисунка в группе Упорядочить нажмите кнопку Повернуть.

   • Если вы не видите вкладку Формат фигуры или Формат рисунка, убедитесь, что выбрана надпись, фигура, объект WordArt или рисунок.

   • Кнопка Повернуть может быть скрыта, если у вас маленький экран. Если вы не видите кнопку Повернуть, щелкните Упорядочить, чтобы просмотреть скрытые кнопки в группе Упорядочить.

3. Выполните одно из указанных ниже действий.

   • Чтобы перевернуть объект вверх ногами, щелкните Отразить сверху вниз.

   • org/ListItem»>

     Чтобы зеркально отразить объект, щелкните Отразить слева направо.

1. Щелкните объект, который нужно переместить.

2. Перетащите объект в нужное место.

   • Чтобы переместить несколько объектов, удерживайте нажатой клавишу SHIFT при выделении объектов.

   • org/ListItem»>

     Чтобы переместить объект вверх, вниз или вбок с небольшим шагом, щелкните объект и нажмите клавишу со стрелкой, удерживая нажатой клавишу COMMAND. Обратите внимание, что в Word это действие можно использовать только для перемещения вверх или вниз.

   • Чтобы объект перемещался только по горизонтали или по вертикали, при его перетаскивании удерживайте нажатой клавишу SHIFT.

При группировании объекты объединяются, и их можно форматировать, перемещать и копировать как группу.

1. Удерживая нажатой клавишу SHIFT, щелкните объекты, которые нужно сгруппировать, а затем (в зависимости от типа выбранных объектов) откройте вкладку Формат фигуры или Формат рисунка.

2. Щелкните значок Группа и выберите параметр Группировать.

Совет: Если параметр Группировать затенен или недоступен, обычно это вызвано тем, что вы еще не выбрали два или более объектов для группировки.

Дополнительные сведения

Вставка рисунков в Office для Mac

Обрезка рисунка

Поворот на любой угол

org/ItemList»>

1. Выберите объект, который вы хотите повернуть.

2. Щелкните маркер поворота сверху объекта и перетащите его в нужном направлении.

Отражение текста

См. статью Зеркальное отражение текста.

Поворот таблицы или графического элемента SmartArt

Скопируйте таблицу или графический элемент SmartArt, вставьте как рисунок, а затем поверните рисунок.

Дополнительные сведения

Обтекание текста вокруг круга или другой фигуры

Обрезка рисунка

Группировка и отмена группировки фигур, рисунков и других объектов

Трапеция: свойства, признаки, площадь, средняя линия

Углы при параллельных прямых и секущей

Пусть прямая пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.

Углы 1 и 3 — вертикальные. Очевидно, вертикальные углы равны, то есть

Конечно, углы 5 и 7, 6 и 8 — тоже вертикальные.

Углы 1 и 2 — смежные, это мы уже знаем. Сумма смежных углов равна .

Углы 3 и 5 (а также 1 и 7, 2 и 8, 4 и 6) — накрест лежащие.

Накрест лежащие углы равны.

,

,

,

.

Углы 1 и 6 — односторонние. Они лежат по одну сторону от всей «конструкции». Углы 4 и 7 — тоже односторонние. Сумма односторонних углов равна , то есть

,

.

Углы 2 и 6 (а также 3 и 7, 1 и 5, 4 и 8) называются соответственными.

Соответственные углы равны, то есть

,

.

Углы 3 и 5 (а также 2 и 8, 1 и 7, 4 и 6) называют накрест лежащими.

Накрест лежащие углы равны, то есть

,

,

,

.

Чтобы применять все эти факты в решении задач по геометрии, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть две параллельных прямые и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это – один из шагов, из которых и состоит решение.

В этой статье – полезные теоремы и примеры решения задач ЕГЭ и ОГЭ по теме «Углы при параллельных прямых и секущей».

Этот материал можно использовать для проектов по геометрии, в работе на уроке и самостоятельно.

Теорема 1.

Углы с соответственно параллельными сторонами равны, если они оба острые или тупые.

Доказательство:

Дано два острых угла: и Известно, что их стороны параллельны: и

Докажем, что

Пусть

Тогда как соответственные углы при параллельных прямых CA и NF и секущей CB.

как соответственные углы при параллельных прямых CB и NM и секущей NF.

Отсюда следует, что что и требовалось доказать.

Аналогично и для тупых углов.

Теорема 2.

Углы с соответственно параллельными сторонами в сумме составляют если один из них острый, а другой тупой.

Доказательство:

Дано: – острый, а – тупой. Известно, что их стороны параллельны: и

Докажем, что сумма углов и равна

Пусть Продолжим луч NM за точку N и получим прямую MK.

Получили два острых угла, и с параллельными сторонами. Согласно теореме 1, они равны, т. е.

как смежные. Значит,

Теорема доказана.

Теорема 3.

Если накрест лежащие углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей AB накрест лежащие углы равны:

Докажем, что Если углы 1 и 2 прямые, то прямые и перпендикулярны к прямой AB и, следовательно, параллельны.

Рассмотрим случай, когда углы 1 и 2 не прямые.

Из середины О отрезка АВ проведем перпендикуляр OH к прямой

На прямой от точки В отложим отрезок равный отрезку AH

по двум сторонам и углу между ними, поэтому и Из равенства следует, что точка лежит на продолжении луча OH, т. е. точки H, O и лежат на одной прямой, а из равенства следует, что угол 6 – прямой (так как угол 5 – прямой). Итак, прямые и перпендикулярны к прямой поэтому они параллельны. Теорема доказана.

Теорема 4.

Если соответственные углы равны, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей соответственные углы равны, например

Так как углы 2 и 3 – вертикальные, то Из этих двух равенств следует, что . Но углы 1 и 3 – накрест лежащие, поэтому прямые и параллельны. Теорема доказана.

Теорема 5.

Если сумма односторонних углов равна 180 градусов, прямые параллельны.

Доказательство:

Пусть при пересечении прямых и секущей сумма односторонних углов равна например

Так как углы 3 и 4 – смежные, то Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые и параллельны. Теорема доказана

И самое главное. Подборка примеров заданий ОГЭ и ЕГЭ по темам: углы при параллельных прямых и секущей, внешние накрест лежащие и внутренние накрест лежащие углы, односторонние углы.

Задачи ОГЭ по теме: Свойства параллельных прямых и секущей, углы при пересечении параллельных прямых секущей

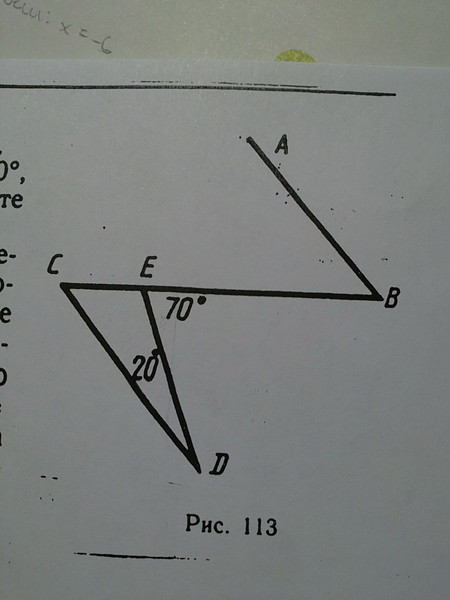
Задача 1. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.

Решение:

Стороны BC и AD параллелограмма параллельны, АК – секущая. Углы и равны как накрест лежащие.

– равнобедренный треугольник.

Мы доказали важное утверждение.

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

AB=BK=5.

Ответ: 48.

Задача 2. Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F.

Найдите AB, если AF=24, BF=10.

Решение:

Основания трапеции АD и ВС параллельны, поэтому углы BAD и АВС – односторонние при параллельных прямых АD и ВС и секущей АВ. Сумма односторонних углов равна

Сумма углов, прилежащих к боковой стороне трапеции, равна

Мы получили, что

AF — биссектриса угла А,

BF — биссектриса угла В, поэтому

тогда

Из треугольника AFB получим, что

Мы доказали теорему:

Биссектрисы углов трапеции, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AFB – прямоугольный.

По теореме Пифагора,

Ответ: 26.

Задача 3. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=28, AC=16, MN=12. Найдите AM.

Решение:

Пусть М – середина АВ, N – середина ВС. Тогда MN – средняя линия треугольника АВС,

Значит, как односторонние углы при параллельных прямых и и секущей АВ.

по двум углам.

Отсюда ;

Ответ: 21.

Задача 4. Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 108 Найдите угол B этой трапеции. Ответ дайте в градусах.

Решение:

ABCD – трапеция, – основания, AB – секущая.

Значит, и – внутренние односторонне углы.

Отсюда

Ответ:

 

Задача 5. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=7, а расстояние от точки K до стороны AB равно 4.

Решение:

Сумма углов, прилежащих к боковой стороне параллелограмма, равна

Это значит, что

AК — биссектриса угла А,

BК — биссектриса угла В, поэтому

тогда

Из треугольника AKB получим, что

Мы доказали теорему:

Биссектрисы углов параллелограмма, прилежащих к боковой стороне, перпендикулярны.

Значит, треугольник AKB – прямоугольный.

Расстояние от точки K до стороны AB – это длина перпендикуляра, проведенного из точки на прямую АВ, т.е.

по гипотенузе и острому углу

Аналогично, по гипотенузе и острому углу

Получили:

Тогда ;

Ответ: 56.

Задача 6. На плоскости даны четыре прямые. Известно, что Найдите Ответ дайте в градусах.

Решение:

и – это внутренние односторонние углы,

Отсюда следует, что прямые параллельны, т.е.

Рассмотрим углы при параллельных прямых и секущей d.

и – это односторонние углы, а значит, они равны:

Ответ:

Задача 7. Прямые m и n параллельны. Найдите если Ответ дайте в градусах.

Решение:

как односторонние углы.

Сумма углов треугольника равна

Для треугольника на рисунке:

Ответ: 86.

Задача 8. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30 и 45 Найдите больший угол параллелограмма. Ответ дайте в градусах.

Решение:

и – это внутренние односторонние углы при параллельных прямых.

и секущей АВ, их сумма равна

Тогда

Это и есть наибольший угол параллелограмма.

Ответ: 105.

Задача 9. Найдите величину тупого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15 Ответ дайте в градусах.

Решение:

AK – биссектриса угла А параллелограмма ABCD,

и – внутренние односторонние углы при параллельных прямых.

и секущей АВ. Их сумма равна значит,

Ответ: 150.

Задача 10. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и Найдите меньший угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение: тогда – равнобедренный, в нем Значит,

Ответ: 5,5.

Задачи ЕГЭ по теме: Углы при параллельных прямых и секущей

Задача 1, ЕГЭ. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Решение:

Напомним, что биссектриса угла – это луч, выходящий из вершины угла и делящий угол пополам.

Пусть BM – биссектриса тупого угла B. По условию, отрезки MD и AB равны 3x и 4x соответственно.

Рассмотрим углы CBM и BMA. Поскольку AD и BC параллельны, BM – секущая, углы CBM и BMA являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник ABM – равнобедренный, следовательно, AB = AM = 4x.

Периметр параллелограмма – это сумма всех его сторон, то есть

7x+7x+4x+4x=88.

Отсюда

Ответ: 28.

Задача 2, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Решение:

Мы знаем, что равнобедренной (или равнобокой) называется трапеция, у которой боковые стороны равны. Следовательно, равны углы при верхнем основании, а также углы при нижнем основании.

Давайте посмотрим на рисунок. По условию, то есть

Углы и – односторонние при параллельных прямых и секущей, следовательно,

по свойству односторонних углов.

Итак,

тогда

Ответ: 115.

Задача 3, ЕГЭ. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Решение:

и – внутренние односторонние углы и при параллельных прямых

и и секущей BC; их сумма равна

BE – биссектриса угла В, значит как накрест лежащие углы при и секущей BE. Тогда – равнобедренный,

Аналогично, CE – биссектриса угла С, значит как накрест лежащие углы при и секущей CE. Тогда – равнобедренный и

Значит

Ответ : 10.

Задача 4, ЕГЭ. В ромбе ABCD угол ABC равен 122 Найдите угол ACD. Ответ дайте в градусах.

Решение:

и – это внутренние односторонние углы при параллельных прямых.

и секущей BC, их сумма равна

Значит,

– ромб, диагонали ромба делят его углы пополам.

Тогда

Ответ: 29.

Задача 5, ЕГЭ. Угол между стороной и диагональю ромба равен Найдите острый угол ромба.

Решение:

Диагональ ромба делит его угол пополам, то есть является биссектрисой угла ромба. Поэтому один из углов ромба равен градусов, и это тупой угол ромба. Тогда острый угол ромба равен

Ответ: 72.

Задача 6, ЕГЭ. Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 Найдите площадь трапеции.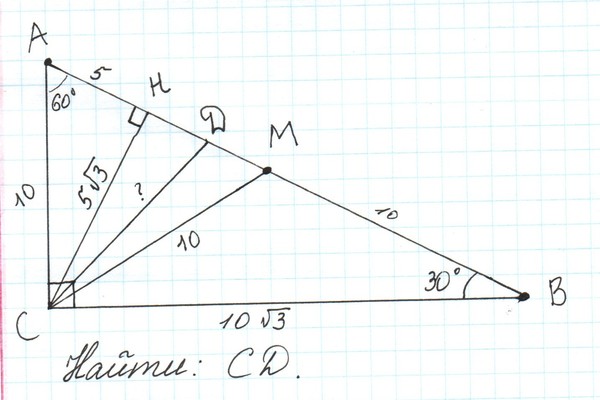

Решение:

Пусть

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними при и секущей BC. Их сумма равна

Тогда Построим высоту из вершины Получим прямоугольный треугольник с острым углом в 30

Высота трапеции DH – это катет, лежащий напротив угла в и равный половине гипотенузы, т. е.

Отсюда

Ответ: 42.

Задача 7, ЕГЭ. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Решение:

У равнобедренной трапеции углы при основании равны т.е.

По условию,

и прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых
и и секущей BC. Их сумма равна

Получили:

Сложив два уравнения, получим: тогда

Ответ: 115.

Задания ЕГЭ Базового уровня, геометрия. Свойства углов при параллельных прямых и секущей.

Задание 1.  Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол Найдите площадь трапеции.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных основаниях трапеции и секущей. Их сумма равна Значит, острый угол трапеции равен 30 Построив высоту, мы увидим, что она лежит против прямого угла в прямоугольном треугольнике. Значит, высота равна половине боковой стороны, т.е.

Отсюда

Ответ: 60.

Задание 2. В прямоугольной трапеции основания равны 4 и 7, а один из углов равен Найдите меньшую боковую сторону.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна Значит, острый угол равен

Вторая высота отсекает равнобедренный прямоугольный треугольник с катетом, равным разности оснований. Значит, высота равна: 7–4=3.

Отсюда

Ответ: 16,5.

Задание 3. В трапеции ABCD известно, что AB = CD, и Найдите угол ABD. Ответ дайте в градусах.

Решение:

Углы, прилежащие к боковой стороне трапеции, являются внутренними односторонними углами при параллельных прямых и секущей. Их сумма равна Значит, острый угол равен

Нам дана трапеция, в которой Очевидно, что это боковые стороны, и трапеция равнобедренная с основаниями и .

и параллельны, BD секущая, тогда

Ответ: 70.

Задание 4. В параллелограмме ABCD проведена биссектриса угла A, пересекающая сторону BC в точке K. Найдите KC, если AB = 4, а периметр параллелограмма равен 20.

Решение:

ABCD – параллелограмм, тогда AB = DC = 4.

AK – биссектриса угла А, значит,

как накрест лежащие углы при параллельных прямых и и секущей AK.

Получили, что – равнобедренный и

значит

Ответ: 2.

Задание 5. Прямые m и n параллельны (см. рисунок). Найдите если Ответ дайте в градусах.

Решение:

(как накрест лежащие углы).

(развернутый угол).

Тогда

Ответ: 39.

Задание 6. В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.

Решение:

Пусть диагонали пересекаются в точке О, т.е.

и параллельны, АС – секущая,

– равнобедренный, отсюда угол между диагоналями равен:

Ответ: 38.

Если вам понравился наш материал на тему «Углы при параллельных прямых и секущей» — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

 

Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 08.04.2023

Углы луча света

и классификация NEMA

A: Классификация света NEMA берет угол луча света и группирует его в одну из 7 категорий от очень узкого прожектора до очень широкой диаграммы направленности. Это помогает определить типы света и их идеальное использование.

Угол луча NEMA Классификация Название

От 10° до 18° I (один или 1) Очень узкий

От 18° до 29° II (также известный как два или 2) Узкий

От 29° до 46° III ( также три или 3) Средне-узкий

От 46° до 70° IV (то есть четыре или 4) Средний

От 70° до 100° V (также известный как пять из 5) Средне-широкий

От 100° до 130° VI  (также известный как шесть или 6) Широкий

От 130°+ VII (также известный как семь или 7) Очень широкий

Эти классификации NEMA часто сокращаются, чтобы выглядеть примерно как 5H5V. Это соответствует 5 горизонтальным и 5 вертикальным из шаблона выше. Многие огни, такие как спортивные, стадионные и высокие мачты, просто указаны как NEMA 3, что указывает на круглую форму.

Официальное правило расчета светового луча: освещенность составляет 10% или выше в процентах от максимума; Итак, если его угол луча 30 градусов, но 9% шире, это все еще 30-градусный луч. Кровотечение в пределах спецификации. Это правило также верно для паттернов H + V, где каждое направление должно соответствовать этому числу.

ОПИСАНИЕ ОБЫЧНОГО РАССЕЯНИЯ ЛУЧА

Ультрапрожектор 1х2В или просто NEMA I

Традиционно очень сложно сделать, это не было обычным явлением до появления более новых светодиодных фонарей для стадионов. В фонариках часто использовался трюк с вогнутой выпуклостью для создания этого узора, но не настоящий NEMA из-за неточного рисунка. Современные светодиоды могут создавать диаграмму направленности 12, 15 или 20 градусов с очень высокой степенью точности. Они используются для очень дальних приложений.

 

Прожектор 3х4В или просто NEMA III

Самая распространенная 1500-ваттная спортивная зажигалка HID за последние 40 лет, а теперь в эту категорию попадают и 500-ваттные стадионные светильники. NEMA III было довольно легко создать с помощью большого металлического отражателя вокруг газоразрядной лампы. Этот луч отлично работает на высоте 40-60 футов, что делает его таким популярным. См. руководство покупателя и видео о светодиодных светильниках для стадионов здесь

 4h5V или NEMA IV

Общий угол луча в различных светильниках. 60-градусные лучи можно найти как в высоких пролетах, так и в некоторых спортивных светильниках;

 

H5V3 широкий, короткий Рисунок

Увеличение горизонтального рисунка при сохранении вертикального начинает формировать свет. Наиболее распространенным выражением этого является уличное освещение. Похож на широкий свет Типа II вверх и вниз по улице, но немного вперед, чтобы не ослеплять соседей.

 

h4V5 УЗКИЙ ВЫСОКИЙ

Перевернутый с высоким рисунком для поражения зданий и знаков. Не распространен, и обычно его нужно заказывать, но все же имеет свое применение.

 

ШИРОКИЙ РАСПРЕДЕЛЕНИЕ ПОТОКА H5V5

Часто встречающийся под углом 90 градусов, это популярный угол освещения склада для высоты около 30-40 футов, чтобы направить больше света на землю.

 H6V6 ULTRA WIDE FLOOD

Самый распространенный широкоугольный прожектор, обеспечивающий широкий охват. Ожидайте этого на большинстве жилых настенных светильников и небольших прожекторах. Популярные идут в охват.

СРАВНЕНИЕ С МОДЕЛЯМИ СВЕТА IES

В таблице ниже представлена ​​классификация светильников IES. Почти все наши светодиодные фонари для парковки относятся к типу III или T3. T3 очень эффективен, потому что он широкий, и вы можете наклонить его, чтобы увеличить бросок вперед

Можно заказать любой из этих шаблонов. Обычно мы не рекомендуем тип V, так как большая часть света падает на веху или крепление. Лучше использовать 2 небольших светильника.

НАИЛУЧШИЕ ПРАКТИКИ ДЛЯ ПРОЕКТИРОВАНИЯ ОСВЕЩЕНИЯ

• Более узкие лучи для дальних лучей
• Средние лучи для стандартного освещения
• Широкий угол для близких расстояний
• Всегда думайте об однородности как вертикальных, так и горизонтальных фут-кандел 9 0074
• Будьте вежливы с соседями и темнотой соответствие небу, когда это возможно
• Будьте в курсе рейтингов BUG и того, как они могут или не могут повлиять на ваш проект

Позвоните любому из наших экспертов сегодня для бесплатной консультации по световому дизайну.

Натяжные, синусоидальные и брызговые формы

«» Многие факторы будут определять форму капли крови, включая гравитацию, силу и поверхность, на которую она приземлится. Как это работает

При анализе рисунка пятен крови эксперт опирается на три основных взаимосвязанных элемента: размер, форму и распределение пятен крови. Поскольку мы уже обсудили размер пятна, давайте сразу перейдем к форме. Капли крови, падающие прямо вниз, на которые мало влияет сила тяжести и сопротивление воздуха, образуют круглые пятна. Однако кровь, движущаяся под углом и ускоряющаяся под действием некоторой силы, имеет тенденцию оставлять продолговатые следы, особенно когда она попадает на непористую поверхность.

Как правило, если следовать по длинной оси пятна от более тупого конца к более острому и неровному краю, можно определить направление движения крови. Если несколько пятен исходят наружу, аналитики могут провести линии вдоль этих осей в обратном направлении к области конвергенции . Но это дает им площадь только в двух измерениях. Следователи также должны определить угол падения крови [источник: Dutelle].

Реклама

Чем меньше угол падения крови на поверхность, тем тоньше и вытянутее пятно. Верно и обратное. Например, если капля крови имеет угол падения 10 градусов, она образует сильно вытянутое пятно, а капля крови 9 градусов.Падение под углом 0 градусов (вертикальное) оставляет круглое пятно [источник: Dutelle]. Измеряя ширину и длину пятна, аналитики используют следующую математическую формулу для расчета угла падения:

угол падения = arcsin (ширина пятна/длина пятна)

«» Капли крови удлиняются по мере увеличения угла, под которым они ударяются о поверхность.

HowStuffWorks

Чем больше разница между шириной и длиной, тем острее угол удара [источник: Dutelle]. Например, представьте себе пятно крови шириной 0,08 дюйма и длиной 0,16 дюйма (2 на 4 миллиметра). Ширина, деленная на длину, равна 0,5. ArcSin 0,5 равен 30, что означает, что кровь попала на поверхность под углом 30 градусов. В пятне крови размером 0,04 на 0,16 дюйма (1 на 4 миллиметра) угол удара составляет около 14,5 градусов.

Если пятно крови имеет хвост, как это бывает при попадании капель на поверхность под определенным углом и с определенной скоростью, его следует исключить из этого расчета [источники: Dutelle, Eckert and James].

Как только аналитики узнают все три ракурса, они могут перейти к самой визуально яркой части процесса и, следовательно, к той, которая чаще всего фигурирует в таких шоу, как «Декстер», — к технике нанизывания . Натягивание включает в себя протягивание нитей от задних краев пятен крови вверх под соответствующими углами, чтобы найти, где они примерно сходятся — район происхождения . Однако этот метод дает лишь приблизительное представление и в основном используется для установления того, сидела ли жертва, стояла или лежала, когда произошло событие. Наличие или отсутствие крови на других поверхностях в сочетании со здравым смыслом также помогает в этом анализе [источник: Dutelle].

Аналитики все чаще используют компьютерные программы, которые позволяют им сохранять данные о разбрызгивании, вычислять такие значения, как угол удара, и отображать информацию в полезных трехмерных изображениях. Первоначально это программное обеспечение требовало ручного ввода данных, что было утомительно, но, возможно, не так утомительно, как ввод строк.

«» Натягивание включает в себя протягивание нитей от задних краев пятен крови вверх под соответствующими углами, чтобы определить, где они примерно сходятся, что также известно как область конвергенции.