Условия дифракции: 43. Дифракция света. Условие возникновения дифракционных картин. — Главная

Содержание

43. Дифракция света. Условие возникновения дифракционных картин.

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий. Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени. Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Одномерная дифракционная решетка представляет собой систему из большого числа N одинаковых по ширине и параллельных друг другу щелей в экране, разделенных также одинаковыми по ширине непрозрачными промежутками (рис. 9.6).

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.

е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Обозначим: b – ширина щели решетки; а – расстояние между щелями; – постоянная дифракционной решетки.

Линза собирает все лучи, падающие на нее под одним углом и не вносит никакой дополнительной разности хода.


Рис. 9.6	Рис. 9.7

Пусть луч 1 падает на линзу под углом φ (угол дифракции). Световая волна, идущая под этим углом от щели, создает в точке максимум интенсивности. Второй луч, идущий от соседней щели под этим же углом φ, придет в ту же точку .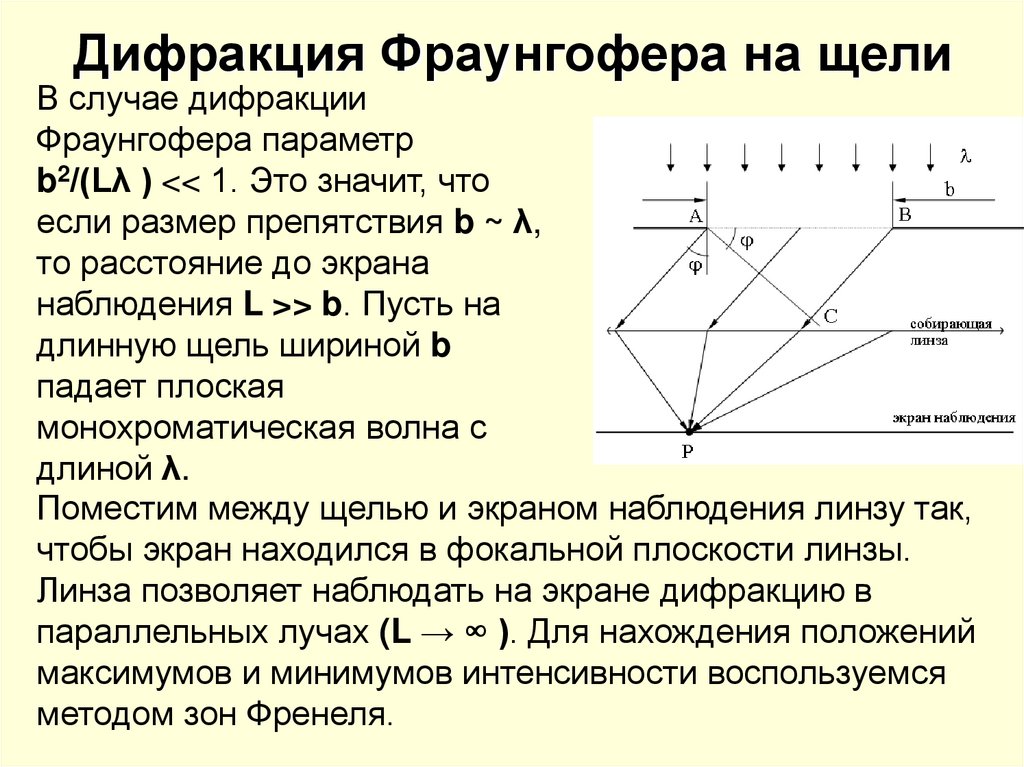

Оба эти луча придут в фазе и будут усиливать друг друга, если оптическая разность хода будет равна mλ:

Условие максимума для дифракционной решетки будет иметь вид:

(9.4.4)

где m = ± 1, ± 2, ± 3, … .

Максимумы, соответствующие этому условию, называются главными максимумами. Значение величины m, соответствующее тому или иному максимуму называется порядком дифракционного максимума.

В точке F

0 всегда будет наблюдаться нулевой или центральный дифракционный максимум.

Так как свет, падающий на экран, проходит только через щели в дифракционной решетке, то условие минимума для щели и будет условием главного дифракционного минимума для решетки:

(9.4.5)

Конечно, при большом числе щелей, в точки экрана, соответствующие главным дифракционным минимумам, от некоторых щелей свет будет попадать и там будут образовыватьсяпобочные дифракционные максимумы и минимумы (рис. 9.7). Но их интенсивность, по сравнению с главными максимумами, мала (≈ 1/22).

При условии ,

волны, посылаемые каждой щелью, будут гаситься в результате интерференции и появятся дополнительные минимумы.

Условие возникновения дифракционных картин.

Законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны:

Дифракция происходит в том случае, когда размеры препятствий (А) соизмеримы с длиной волны () : А ~ λ.

Дифракционная картина, полученная на экране, расположенном за различными преградами, представляет собой результат интерференции: чередование светлых и темных полос (для монохроматического света) и разноцветных полос (для белого света) .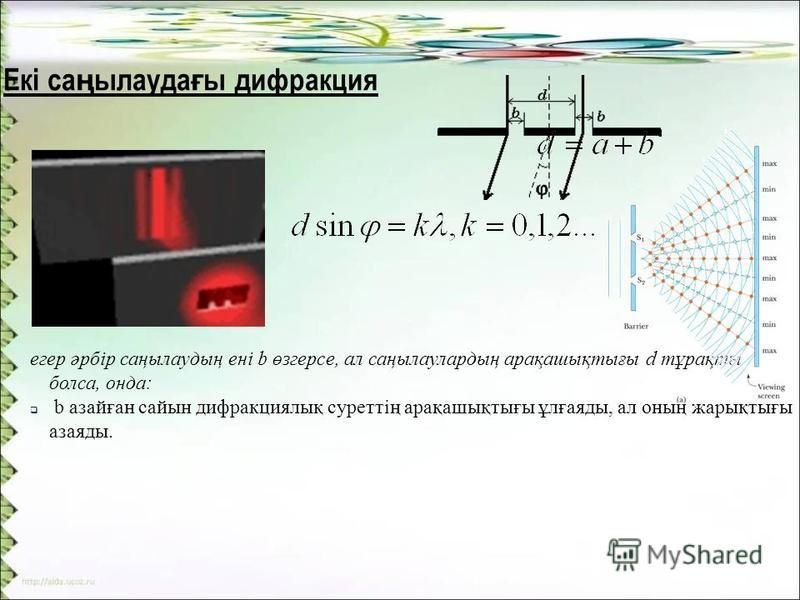 Дифракционная решетка — оптический прибор, представляющий собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками. Число штрихов у хороших дифракционных решеток доходит до нескольких тысяч на 1 мм.

Дифракция света, волн. Дифракционная щель, решётка. Максимум

В рамках геометрической оптики, распространение луча в оптически однородной среде — прямолинейное, однако в природе существует ряд явлений, где можно наблюдать отклонение от этого условия.

Дифракция – явление огибания световыми волнами встреченных препятствий. В школьной физике изучаются две дифракционные системы (системы, при прохождении луча в которых наблюдается дифракция):

дифракция на щели (прямоугольном отверстии)
дифракция на решётке (набор равноотстоящих друг от друга щелей)

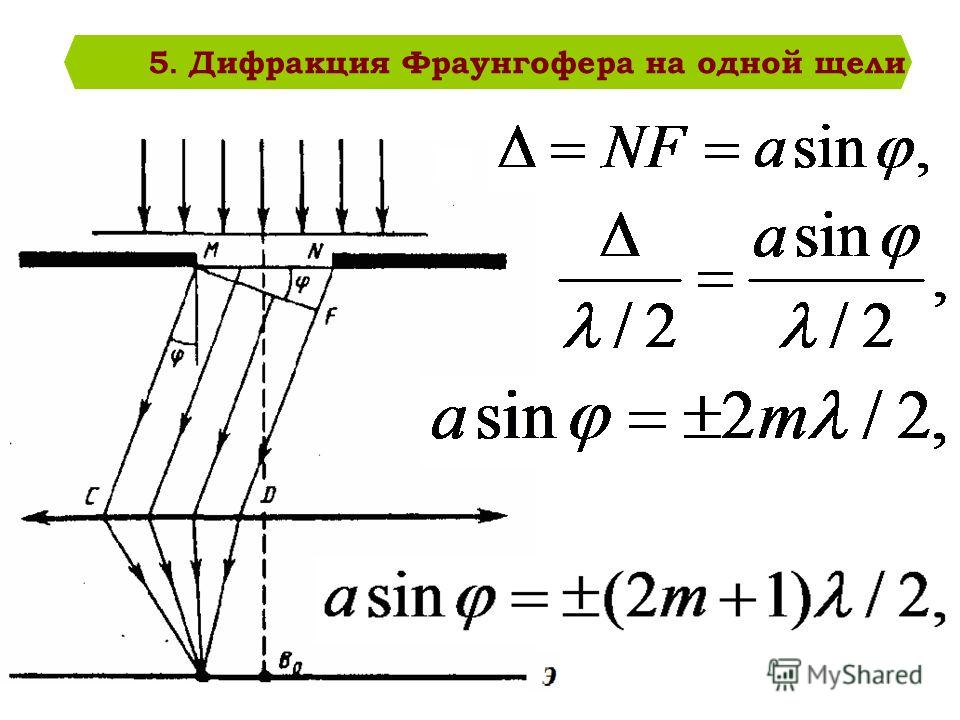
Дифракция на щели — дифракция на прямоугольном отверстии (рис. 1).

Рис. 1. Дифракция на щели

Пусть дана плоскость со щелью, шириной

, на которую под прямым углом падает пучок света А. Большинство света проходит на экран, однако часть лучей дифрагирует на краях щели (т.е. отклоняется от своего первоначального направления). Далее эти лучи интерферируют друг с другом с образованием дифракционной картины на экране (чередование ярких и тёмных областей). Рассмотрение законов интерференции достаточно сложно, поэтому ограничимся основными выводами.

Полученная дифракционная картина на экране состоит из чередующихся областей с дифракционными максимумами (максимально светлыми областями) и дифракционными минимумами (максимально тёмными областями). Эта картина симметрична относительно центрального светового пучка. Положение максимумов и минимумов описывается углом относительно вертикали, под которым они видны, и зависит от размера щели и длины волны падающего излучения. Положение этих областей можно найти используя ряд соотношений:

для дифракционных максимумов

(1)

где
- — ширина щели,
- — угол между вертикалью и направлением на максимум,
- — порядок максимума (счётчик),
- — длина волны света.

Нулевым максимумом дифракции называется центральная точка на экране под щелью (рис. 1).

для дифракционных минимумов

(2)

где
- — ширина щели,
- — угол между вертикалью и направлением на минимум,
- — порядок минимума (счётчик),
- — длина волны света.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (1) или (2).

Дифракция на дифракционной решётке.

Дифракционной решёткой называется система, состоящая из чередующихся щелей, равноотстоящих друг от друга (рис. 2).

Рис. 2. Дифракционная решётка (лучи)

Так же, как и для щели, на экране после дифракционной решётки будет наблюдаться дифракционная картина: чередование светлых и тёмных областей. Вся картина есть результат интерференции световых лучей друг с другом, однако на картину от одной щели будет воздействовать лучи от других щелей. Тогда дифракционная картина должна зависеть от количества щелей, их размеров и близкорасположенности.

Введём новое понятие — постоянная дифракционной решётки:

(3)

где
- — постоянная дифракционной решётки,
- — расстояние между щелями,
- — ширина щели.

Тогда положения максимумов и минимумов дифракции:

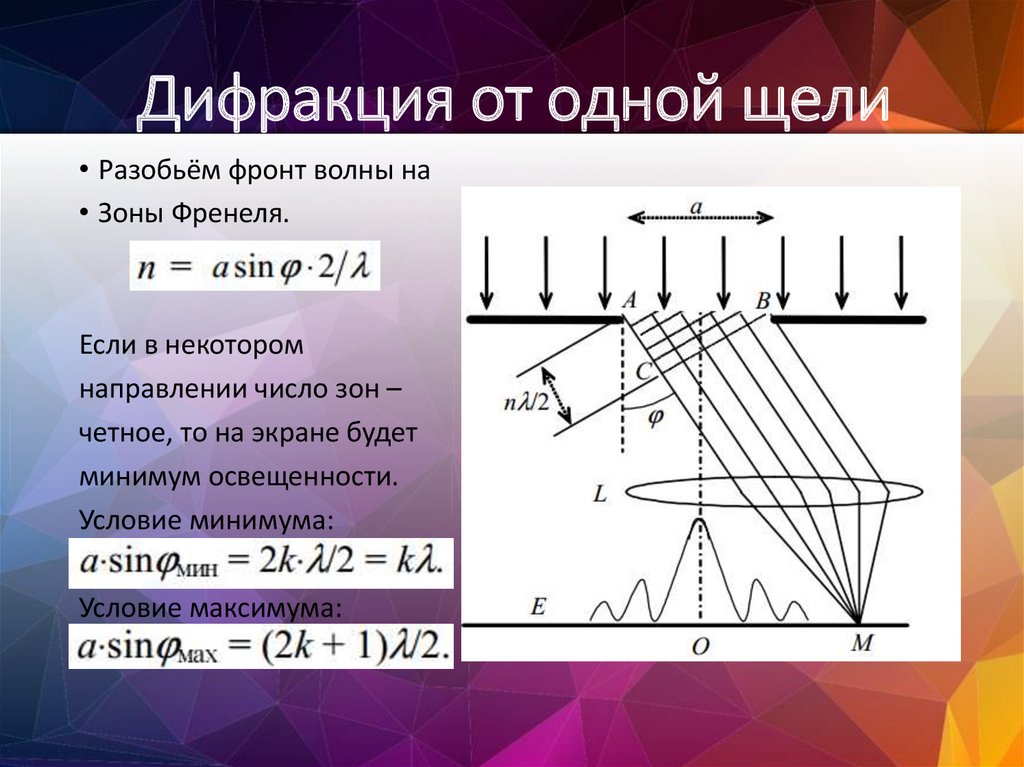
для главных дифракционных максимумов (рис. 3)

(4)

где
- — постоянная дифракционной решётки,
- — угол между вертикалью и направлением на максимум.
- — порядок максимума (счётчик),

Рис. 3. Дифракционная решётка (максимумы)

для дифракционных минимумов

(5)

где
- — ширина щели,
- — угол между вертикалью и направлением на минимум,
- — порядок минимума (счётчик),
- — длина волны света.

Отдельным вопросом задач на дифракцию является вопрос о наибольшем количестве максимумов, которые можно наблюдать в текущей системе. Наибольший угол, под которым можно наблюдать максимум —

, тогда, исходя из (4):

(6)

Главное помнить, что число максимумов — число, т.е. от полученного ответа необходимо брать только целую часть.

Вывод: по условиям задачи необходимо выяснить: максимум или минимум дифракции необходимо найти и использовать соответствующее соотношение (4) или (5).

Общий вывод: задачи на дифракцию должны содержать в себе словосочетания, связанные с «дифракцией». Далее разбираемся с объектом: щель или дифракционная решётка и используем соответствующие соотношения для минимума или максимума.

Понравилось это:

Нравится Загрузка…

Рентгеновская дифракция, закон Брэгга и уравнение Лауэ

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 320

В ноябре 1895 года Вильгельм Рентген открыл рентгеновские лучи, работая в Вюрцбургском университете в Германии.

Рентген исследовал катодные лучи в различных типах вакуумированных стеклянных трубок и пытался определить их диапазон в воздухе. Он заметил, что во время образования лучей экран, покрытый флуоресцентным платиноцианидом бария, светился. Он был заинтригован тем, что экран находился слишком далеко от трубки, чтобы на него могли воздействовать катодные лучи.

Он предположил, что неизвестные рентгеновские лучи испускаются стенками трубки во время работы электронно-лучевой трубки. К своему изумлению, Рентген обнаружил, что лучи могут проходить прямо через его руку и отбрасывать тени его костей на флуоресцентный экран. Он провел несколько недель, исследуя лучи в частном порядке, прежде чем опубликовать свои результаты в конце года.

Закон Брэгга

Закон Брэгга является результатом экспериментов, полученных физиком сэром Уильямом Лоуренсом Брэггом в 19{[1]}\) Уильям Лоуренс Брэгг и его отец, сэр Уильям Генри Брэгг, были удостоены Нобелевской премии по физике в 1915 году за их работу по определению кристаллических структур, начиная с NaCl, ZnS и алмаза.

После того, как Вильгельм Рентген открыл рентгеновские лучи в 1895 году, Уильям Генри Брэгг впервые определил кристаллическую структуру методами дифракции рентгеновских лучей, начал всю жизнь исследовать природу излучения, главным образом рентгеновских лучей, а также альфа- и бета-частиц и гамма-излучения. лучи. После открытия дифракции рентгеновских лучей на кристаллах в 19 в.12, Брэгг и его сын Уильям Л. вывели закон Брэгга, который связывает длину волны рентгеновских лучей с углом скользящего отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.

Уильям Лоуренс Брэгг стал директором Кавендишской лаборатории в Кембридже, Англия. {[2]}\) 9{[3]}\)

В 1915 году Уильям Генри Брэгг и Уильям Лоуренс Брэгг были удостоены Нобелевской премии за вклад в анализ структуры кристаллов. Они были первой и (пока) единственной командой отца и сына, которая вместе выиграла приз. Среди других лауреатов отцов и сыновей Нильс и Оге Бор, Манн и Кай Зигбан, Дж. Дж. Томсон и Джордж Томсон, Ганс фон Эйлер-Хелпин и Ульф фон Эйлер, а также Артур и Роджер Корнберги были удостоены премии за отдельные вклады.

В то время У. Л. Брэггу было 25 лет, что делало его самым молодым лауреатом Нобелевской премии на сегодняшний день.

У.Х. Брэгг (1862-1942) и У.Л. Брэгг (1890-1971) на шведской почтовой марке.

1.2 Закон Брэгга и дифракция рентгеновских лучей

\[\begin{align} n\lambda=2d\cdot\sin\theta \end{align} \label{1}\]

где
• n — целое число, определяемое заданным порядком,
• λ — длина волны рентгеновского излучения и движущихся электронов, протонов и нейтронов, 9{[2]}\)

Рассмотрим условия, необходимые для совпадения фаз лучей при равенстве угла падения и угла отражения. Лучи падающего луча всегда совпадают по фазе и параллельны до точки, в которой верхний луч падает на верхний слой в атоме z. Второй луч переходит на следующий слой, где он рассеивается атомом B. Второй луч должен пройти дополнительное расстояние AB + BC, если два луча должны продолжать двигаться рядом и параллельно. Это дополнительное расстояние должно быть целым ($n$) кратным длине волны (\лямбда\), чтобы фазы двух лучей были одинаковыми:

\begin{align} n\lambda=AB+BC \end{align}

Признав d гипотенузой прямоугольного треугольника Abz, мы можем использовать тригонометрию, чтобы связать d и (\theta\) с расстоянием (AB + БК). Расстояние AB противоположно (\theta\), поэтому

\begin{align} AB=d\sin\theta \end{align}

Поскольку $AB = BC$, уравнение (2) становится

\begin{align} n\lambda=2AB \end{align}

Подставив уравнение (3) в уравнение (4), мы получим

\begin{align} n\lambda=2d\cdot\sin\theta \end {выравнивание}

и был получен закон Брэгга.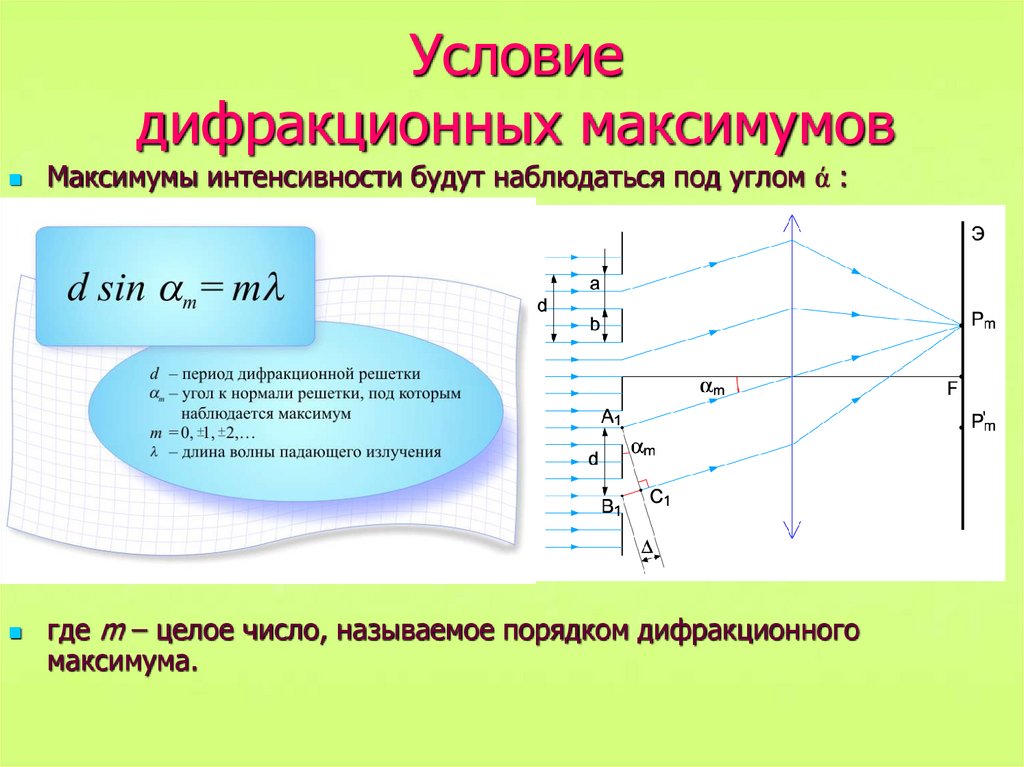

Обратите внимание, что если задействованы только два ряда атомов, переход от конструктивной интерференции к деструктивной по мере изменения $\тета$ будет постепенным. Однако, если возникает интерференция из многих рядов, то пики конструктивной интерференции становятся очень острыми, а между ними в основном деструктивная интерференция. Такое заострение пиков при увеличении числа рядов очень похоже на заострение дифракционных пиков от дифракционной решетки при увеличении числа щелей. 9{‘}}+\overrightarrow{g} \end{align}

, поэтому

\begin{align} |\overrightarrow{g}|=2|\overrightarrow{k}|\sin\theta \end{align}

Чтобы обеспечить соблюдение закона Брэгга, $\overrightarrow{g}$ должно быть установлено равным $\overrightarrow{G}$, где

\begin{align} |\overrightarrow{G}|=2\ pi/d_{h,k,l} \end{align}

Сравните уравнения (7) и (8), мы имеем

\begin{align} \lambda=2/d_{h,k,l}\ sin\theta \end{align}

Итак, только если

\begin{align} \overrightarrow{g}=\overrightarrow{G} \end{align} 9{[9]}\)

Определение обратной решетки можно увидеть следующим образом:

В кристаллографии обратной решеткой решетки Браве называется набор всех векторов $\overrightarrow{k}$, таких что:

\begin{align} \exp({i}\overrightarrow{k}\cdot\overrightarrow{r})=1 \end{align}

Эта обратная решетка сама по себе является решеткой Браве, а обратная решетка — исходная реальная решетка.

1.3 Применение закона Брэгга — дифракция Брэгга

Дифракция Брэгга (также известная как дифракция рентгеновских лучей по Брэггу) была впервые предложена Уильямом Лоуренсом Брэггом и Уильямом Генри Брэггом в 1913 году в ответ на их открытие, что кристаллические твердые тела производят удивительные картины отраженных рентгеновских лучей (в отличие от к, скажем, жидкости). Они обнаружили, что в этих кристаллах при определенных длинах волн и углах падения возникают интенсивные пики отраженного излучения (известные как пики Брэгга). В. Л. Брэгг объяснил этот результат, моделируя кристалл как набор дискретных параллельных плоскостей, разделенных постоянным параметром d. Было высказано предположение, что падающее рентгеновское излучение будет давать пик Брэгга, если его отражения от различных плоскостей конструктивно интерферируют, как мы показали выше.

Концепция дифракции Брэгга в равной степени применима к процессам дифракции нейтронов и электронов.

1.3.

{[7]}\) 9{[8]}\)

1.5 Каталожные номера

W.L. Брэгг, «Дифракция коротких электромагнитных волн на кристалле», Труды Кембриджского философского общества, 17 (1913), 43–57.
ru.Wikipedia.org/wiki/Брэгг%27s_law
http://nobelprize.org/nobel_prizes/p…915/index.html
Рисунок взят из работы Джеффа Даля, а рисунок взят с сайта www.goiit.com/posts/list/comm…tion-83055.htm
Эта часть получена от Пола Дж. Шилдса, Центр исследований высоких давлений, Департамент наук о Земле и космосе, Государственный университет Нью-Йорка в Стони-Брук, Стоуни-Брук, Нью-Йорк 1179.4-2100.
G. Prado, E. Suard, L. Fournes и C. Delmasb, «Распределение катионов в электродных материалах Li1-z(Ni1-yFey)1+zO2», J. of Mater. хим. 10 (2000) 2553
«Принципы и практика электронной микроскопии», Ян М. Ватт, 1997, Cambridge University Press
perso.fundp.ac.be/%7Ejwouters. ..ffraction.html

Для получения дополнительной информации о реальной и обратной кристаллической решетке см. также веб-страницу Fangxiao: http://electrons.wikidot.com/paraelectric-and-antiferroelectric-properties 9{[1]}\)

С 1909 по 1912 год Лауэ был приват-доцентом в Институте теоретической физики под руководством Арнольда Зоммерфельда Мюнхенского университета Людвига-Максимилиана (LMU). Во время рождественских каникул 1911 года и в январе 1912 года Пол Питер Эвальд заканчивал написание своей докторской диссертации под руководством Зоммерфельда. Во время прогулки по Английскому саду в Мюнхене в январе Эвальд рассказал Лауэ о теме своей диссертации. Волны волн, интересующие Эвальда, находились в видимой области спектра и, следовательно, намного превышали расстояние между резонаторами в кристаллической модели Эвальда. Лауэ казался отвлеченным и хотел знать, какой будет эффект, если рассматривать гораздо меньшие длины волн. В июне Зоммерфельд сообщил в Physikalische Gesellschaft в Геттингене об успешной дифракции рентгеновских лучей, проведенной Лауэ, Паулем Книппингом и Вальтером Фридрихом в LMU, за которую Лауэ будет удостоен Нобелевской премии по физике в 1919 году. 14. Находясь в Мюнхене, он написал первый том своей книги по теории относительности в период с 1910 по 1911 год. Нобелевская премия по физике 1914 года: «за открытие дифракции рентгеновских лучей на кристаллах»

После открытия при дифракции рентгеновских лучей на кристаллах в 1912 г. Брэгг и его сын Уильям Л. вывели закон Брэгга, связывающий длину волны рентгеновских лучей с скользящим углом отражения. В 1913 году Брэгг-старший построил первый рентгеновский спектрометр, который он первоначально использовал для изучения спектральных распределений рентгеновского излучения. В течение нескольких лет они смогли использовать этот прибор и закон Брэгга для определения структуры кристаллов и точного положения атомов. Впоследствии они продемонстрировали, что свойства и поведение большого количества веществ могут быть связаны с положением составляющих их атомов.

Уильям Лоуренс Брэгг стал директором Кавендишской лаборатории в Кембридже, Англия. Именно в этой лаборатории, когда он был директором, в начале 1950-х годов Дж. {[2]}\)

2.2 Принцип уравнения Лауэ

2.2.1 Обратное пространство

Все точки обратной решетки могут быть описаны линейной комбинацией кратных двух базисных векторов: $\vec{b_1},\vec{b_2}, \vec{b_3}$. Его определение эквивалентно следующим соотношениям:

\[\begin{align} \vec{b_{1}}=\frac{\vec{a_{2}}\times\vec{a_{3}}}{ \vec{a_{1}}\cdot(\vec{a_{2}}\times\vec{a_{3}})} \end{align}\]

\[\begin{align} \vec{ b_{2}}=\frac{\vec{a_{3}}\times\vec{a_{1}}}{\vec{a_{1}}\cdot(\vec{a_{2}}\times \vec{a_{3}})} \end{align}\] 9{\ast} = 1\) также верно.

Теперь мы можем определить вектор обратной решетки $\vec{h}$ линейной комбинацией целых чисел, кратных трем векторам обратной решетки:

\[\begin{align} \vec{h}=h\ vec{b_{1}}+k\vec{b_{2}}+l\vec{b_{3}} \end{align}\]

Позже мы увидим, что обратные векторы играют важную роль в дифракции . Прежде свяжем векторы обратной решетки с некоторыми макроскопическими свойствами кристаллов.

Индексы Миллера

По построению каждый вектор обратной решетки нормальен к ряду плоскостей решетки. Мы также знаем, что грани кристалла параллельны плоскостям решетки и, следовательно, нормальны к обратным векторам. Таким образом, мы можем однозначно характеризовать каждую грань кристалла целочисленными компонентами обратного вектора с одной важной тонкостью. Грань, нормаль к вектору $\vec{h}$, нельзя отличить от нормали к вектору $n\vec{h}$. Поэтому будем характеризовать каждую грань кристалла тремя целыми компонентами, но без общего знаменателя. Тройка (h,k,l), удовлетворяющая этому условию, называется индексами Миллера грани. С этой спецификацией мы понимаем, что индексы Миллера являются лишь подмножеством возможных векторов обратной решетки.

Рисунок выше представляет собой абстракцию кристаллической структуры, где даны только узлы решетки. Мы также сообщили ряд плоскостей решетки с расстояниями $d_i$ и соответствующей нормалью $\vec{h_i}$ к ряду плоскостей. Без дальнейшей демонстрации мы приводим здесь важное соотношение между расстояниями d и вектором обратной решетки $\vec{h}$, нормальным к ряду равноудаленных плоскостей:

\[\begin{align} d=\frac{1 }{|\vec{h}|} \end{align}\] 9{[3]}\)

Предположим, что имеется ряд рассеивателей, разделенных постоянным повторением, a. Излучение с длиной волны $\lambda$ падает на этот ряд под углом $\alpha_{0}$. Изучите разброс из этого ряда под углом $\alpha_{n}$. Разность хода лучей, рассеянных в точках A и D, равна просто AB-CD. Если входящие лучи находятся в фазе, разность хода должна быть некоторым целым кратным длины волны, чтобы возникла конструктивная интерференция. Это приводит к первому уравнению Лауэ:

\begin{align} (AB-CD)=a(\cos(\alpha_{n}-\cos\alpha_{0}))=n_{x}\lambda \end{align}

Этот результат справедливо для любого рассеянного луча, составляющего угол $\alpha_{n}$ с осью элементарной ячейки. Таким образом, условие Лауэ согласуется с конусом рассеянных лучей с центром вокруг оси а.

Это уравнение можно переформулировать в векторной форме. Расстояние повторения a становится вектором элементарной ячейки $\vec{a}$. Назовите единичный вектор, параллельный входящим лучам, $\vec{S_{0}}$, и один, параллельный рассеянным лучам, $\vec{S}$. Тогда есть несколько простых векторных точечных произведений:

\begin{align} \vec{a}\cdot\vec{S}=a\cos\alpha_{n} \end{align}

\begin{align} \vec{a}\cdot\vec{ S_{0}}=a\cos\alpha_{0} \end{align}

\begin{align} a\cos(\alpha_{n}-\cos\alpha_{0})=\vec{a} \cdot(\vec{S}-\vec{S_{0}})=n_{x}\lambda \end{align}

2.

2.4 Уравнение Лауэ в трех измерениях

Для кристалла с ячейкой параметры $\vec{a},\vec{b},\vec{c}$, мы имеем три уравнения Лауэ:

\begin{align} a\cos(\alpha_{n}-\cos\alpha_ {0})=ч\лямбда\конец{выравнивание} 9{2}\gamma_{n}=1 \end{align}

Исходя из того, что угол между падающим и отраженным лучом равен $2\theta$

\begin{align} \cos2\theta=\cos\ alpha_{n}\alpha_{0}+\beta_{n}\beta_{0}+\gamma_{n}\gamma_{0} \end{align}

Возьмите $\vec{k_{i}}\ ) — волновой вектор для входящего (падающего) луча, а \(\vec{k_{o}}$ — волновой вектор для выходящего (дифрагированного) луча. $\vec{k_{o}}-\vec{k_{i}}=\Delta\vec{k}$ — это вектор рассеяния, измеряющий изменение между двумя волновыми векторами. Возьмем $\vec{a_{1}},\vec{a_{2}},\vec{a_{3}}$ за примитивные векторы кристаллической решетки. Три условия Лауэ для вектора рассеяния, или уравнения Лауэ, для целых значений индексов обратной решетки отражения (h,k,l) можно также записать следующим образом:

\begin{align} \vec{a_{1}}\cdot\Delta\vec{k}=2\pi h \end{align}

\begin{align} \vec{a_{2}}\ cdot\Delta\vec{k}=2\pi k \end{align}

\begin{align} \vec{a_{3}}\cdot\Delta\vec{k}=2\pi l \end{ align}

Эти условия говорят о том, что вектор рассеяния должен быть ориентирован в определенном направлении по отношению к примитивным векторам кристаллической решетки. {[1]}\)

2.3 Связь уравнения Лауэ с законом Брэгга

Если $\vec{G}=h\vec{b_{1}}+k\vec{b_{2}}+l\vec{b_{3} }$ — вектор обратной решетки, мы знаем:

\begin{align} \vec{G}\cdot(h\vec{a_{1}}+k\vec{a_{2}}+l\vec {a_{3}})=2\pi(h+k+l) \end{align}

Уравнения Лауэ определяют:

\begin{align} \Delta\vec{k}\cdot(h\vec {a_{1}}+k\vec{a_{2}}+l\vec{a_{3}})=2\pi(h+k+l) \end{align}

, где

\begin {align} \vec{k_{o}}-\vec{k_{i}}=\vec{G} \end{align} 9{[2]}\)

2.4 Ссылки

en.Wikipedia.org/wiki/Max_von_Laue
Другая веб-страница Джиалана: http://electrons.wikidot.com/x-ray-diffraction-and-bragg-s-law
стручковый перец.me.utexas.edu/ChE386…_equations.htm
Киттель, К. (1976). Введение в физику твердого тела, Нью-Йорк: John Wiley & Sons. ISBN 0-471-49024-5
В.Л. Брэгг, «Дифракция коротких электромагнитных волн на кристалле», Труды Кембриджского философского общества, 17 (19). 13), 43–57.

Авторы и ссылки

ContribMSE5317

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Лицензия
CC BY-SA
Показать оглавление
нет
Теги
1. Закон Брэгга
2. Уравнение Лауэ

Дифракция Фраунгофера

Хотя формальным требованием дифракции Фраунгофера является бесконечное расстояние до экрана, обычно разумные результаты дифракции получаются, если расстояние до экрана D >> a. Но дополнительным требованием является D >> a ² /λ, которое вытекает из критерия Рэлея применительно к одиночной щели. Если условия дифракции Фраунгофера не выполняются, необходимо использовать метод дифракции Френеля.

Дифракционная картина справа получена с помощью гелий-неонового лазера и узкой одиночной щели. Рисунок ниже был сделан с помощью зеленой лазерной указки.

Примечание. Чтобы получить приведенное выше выражение для смещения y, использовалось приближение малого угла.

Расчет для одной щели	Интенсивность для одной щели
Двухщелевая интерференция	Сравнение с двухщелевым
Проверить приближение	Вариант с шириной щели

Индекс

Дифракционные концепции

Дифракция Fraunhofer

Oxford Optics

74747474747474744447474747474744474747474744474474747474744474474474747444747474744474747н

Hyperphysics ***** Light and Vision	97	Hyperphysics ***** Light and Vision	798 44474747474748
Назад

Эти дифракционные картины с одной щелью были сфотографированы с использованием гелий-неонового лазера в качестве источника света и одиночной щели, контролируемой микрометром.

Условия дифракции: 43. Дифракция света. Условие возникновения дифракционных картин.