В чем измеряется разрешение: Разрешение изображения — что это такое?

Разрешение растровых изображений

Главная

»

Инструкции

»

Разрешение растрового изображения

Цифровые технологии все больше завоевывают рынок. Резко удешевились сканеры и цифровые камеры, почти все издательства перешли на компьютерную обработку изображений. В итоге технологии, ранее применяемые лишь в специализированных репроцентрах, стали доступны всем. Однако здесь есть немало секретов. В этой статье дается обзор такого параметра как разрешение.

 

Все изображения, с точки зрения количества градаций, можно поделить на тоновые и штриховые. Тоновые иллюстрации содержат различные градации цветов (в случае цветных иллюстраций) или градации серого (в случае черно-белых иллюстраций). Штриховые иллюстрации содержат только два цвета: собственно краски и носителя. На практике наиболее часто приходится сталкиваться с тоновыми изображениями, о них и пойдет речь в статье.

 

Изображение, представленное в цифровой форме, состоит из мельчайших дискретных элементов — пикселей. Последовательность пикселей формирует строку, последовательность строк — все изображение. Пиксел – величина виртуальная, и может быть характеризован своим цветом, имеющим самые разнообразные форматы представления.

 

Количество элементов (пикселей) на единицу длины называется – разрешением. Оно измеряется в распространенном программном обеспечении в dpi, сокращенное от dot per inch (точек на дюйм) или ppi, сокращенное от pixel per inch (пиксел на точку). Часто эти понятия смешиваются, потому что отображают одно и тоже. Разница лишь в том, что в первом случае единичный элемент изображения назван точкой (dot), а во втором — пикселем (pixel). Всем известная программа PhotoShop оперирует термином dpi, в то время как более верным было бы назвать единичный элемент изображения в цифровой форме — пикселем. Программное обеспечение сканеров также должно было бы оперировать термином ppi, а вот разрешение выводных устройств — всегда измеряется в dpi и в данном случае использование понятия «точка» верно.

В целом термин dpi более прижился для обозначения разрешения устройств «ввода/вывода» и цифровых иллюстраций.

 

Разрешение цифровых изображений – понятие запутанное, поскольку каждая стадия процесса воспроизведения накладывает свои требования и ограничения. Рассмотрим этапы последовательно.

 

На этапе сканирования мы переводим изображение из аналоговой формы в цифровую. Разрешение, установленное в программном обеспечении сканера, обозначает, сколько пикселей будет получено на один дюйм реального оригинала. К примеру, если разрешение сканирования установлено, как 300 dpi, а оригинальная иллюстрация имеет десять дюймов в длину и пять дюймов в ширину, то полученное изображение будет содержать 3000×1500 пикселей.

 

Разрешение – один из важнейших параметров сканера. Оно бывает физическое и интерполяционное. Первое зависит от конструкции устройства и в ряде случаев может быть переменным, например как в Linotype-Hell Topaz, где количество различаемых точек на дюйм меняется в зависимости от положения оригинала на рабочем столе сканера. Практически во всех моделях сканеров (особенно недорогих) существует и второй тип разрешения ѕѕ интерполяционное. Дополнительное количество точек на дюйм в этом случае получается методом интерполяции. Суть его в том, что на некотором участке по имеющимся цифровым данным полиномом необходимой степени воспроизводится функция, в приближении отражающая существовавший аналоговый сигнал. Затем по этой функции производится перевыборка (изменение шага дискретизации). Таким образом, можно получить любое количество точек, то есть повысить разрешение сканера.

 

Разрешение цифровых камер дает понятие о том, из скольких точек будет состоять полученное изображение. На этапе преобразования цифрового изображения в компьютере понятие «разрешающая способность» весьма эфемерно. Фактически, это величина, которая показывает, какого размера будет иллюстрация в случае ее вывода. Ни на какие цифровые преобразования разрешение не влияет. Если изображение имеет 3000×1500 пикселей и разрешение 300 dpi, то оно будет выведено размером 10×5 дюймов. Однако если изменить разрешающую способность на 3000 dpi, то оно будет выведено размером 1×0,5 дюйма. При этом файл по-прежнему будет содержать 3000×1500 пикселей. Все цифровые преобразования производятся над пикселями, поэтому на этапе обработки на компьютере, значение разрешения роли не играет.

 

На этапе вывода мы сталкиваемся с огромным количеством разнообразных устройств. Все они связаны с разрешением. В этом случае под разрешением понимают количество точек, которое может «поставить» то или иное устройство на единицу длины.

 

Рассмотрим, например, вывод черно-белого тонового изображения. Для того чтобы воспроизвести черный цвет, нужно ставить черные точки подряд. Для воспроизведения белого — их не надо ставить вовсе. Все промежуточные тона воспроизводятся большим или меньшим количеством точек на единицу площади. Для воспроизведения серого 50 % поля площадь черных точек и пустого пространства должна быть одинакова. Чем светлее поле, тем меньше точек будет ставить выводное устройство.

 

Принтер, как правило, ставит точки случайным образом, но в его программном обеспечении заложено, что для воспроизведения определенного оттенка, надо поставить соответствующее количество точек на единицу площади. Поэтому, пиксел цифрового изображения, характеризующийся многими оттенками, при выводе отображается некоторым количеством черных точек на единицу площади. Вот почему один пиксел иллюстрации в цифровом виде не равен одному пикселю устройства вывода. Процесс преобразования тонового изображения в массу одноцветных точек, расставленных определенным образом по площади листа, называют растрированием.

 

Итак, для воспроизведения оттенков устройство вывода (например, принтер) вынуждено ставить определенное количество черных дискретных точек на единицу площади, которая называется растровой точкой (ячейкой). Если точки в пределах единичной области ставятся случайным образом, то это стохастическое растрирование. Если точки образуют круги или, например, эллипсы, то такой растр называют регулярным. Понятно, что каждая растровая точка образована большим количеством единичных точек. Считается, что растровая ячейка должна состоять из 16×16 единичных точек. В этом случае количество воспроизводимых оттенков составит 16×16 = 256. Такое же количество градаций имеет каждый пиксел в стандартном черно-белом тоновом изображении цифрового формата Grayscale.

 

Растровые точки составляют линии. Совокупность всех линий составляет изображение. Количество линий на единицу длины называют линиатурой (рис. 1). Обычно в программном обеспечении линиатура измеряется в линиях на дюйм или lpi (lines per inch).

 

Линия растровых точек

 

В принципе, каждая растровая точка выводимого изображения может соответствовать одному пикселю цифрового формата. То есть линиатура вывода может соответствовать разрешению цифрового изображения. Но для достижения наилучшего качества, разрешение должно быть вдвое большее линиатура или, другими словами, для формирования одной растровой точки следует взять 4 пикселя.

Эту зависимость можно представить в виде формулы

 

d = l х Qf [1],

 

где d – разрешение цифрового файла, l – линиатура вывода, Qf – коэффициент качества, изменяющийся от 1 для малозначимых иллюстраций до 2 для высококачественной продукции. Если исходить из того, что растровая точка состоит из 16×16 единичных точек, то по формуле [1], приняв Qf = 2, получим, что разрешение цифрового файла должно быть в 8 раз меньше, чем разрешение выводного устройства.

 

Для того чтобы проиллюстрировать эту зависимость приведем четыре одинаковых изображения Рис 2.1, 2.2, 2.3 и 2.4. Для первого коэффициент качества равен 0,5, для второго — 1, для третьего — 2, для четвертого — 4. Линиатура, с которой печатается журнал «РТ», составляет 150 lpi. Исходя из этого, получаем, что для иллюстраций разрешение будет равно 75 dpi, 150 dpi, 300 dpi, 600 dpi соответственно. По приведенным примерам видно, что качество передачи мелких деталей возрастает при изменении Qf от 0,5 до 2.

Иллюстрация с Qf = 4 неотличима от той, что имеет Qf = 2.

 

В практике полиграфического производства для печати журнальной продукции и художественных альбомов в большинстве случаев используются три линиатуры: 133, 150, 175 lpi. Иные значения крайне редки. Практически всегда одна растровая точка составляется как минимум из 16×16 единичных точек, поскольку разрешение фотовыводных устройств высоко и может достигать 5000 dpi. Производители драйверов (RIP – Raster Image Processor) подобных устройств также прибегают к некоторым уловкам для улучшения передачи мелких деталей, оставляя линиатуру прежней. Например, можно сместить центр растровой точки для лучшего подчеркивания контура. В силу этого, для определения максимально необходимого разрешения цифрового файла возможно применять формулу [1], приняв Qf = 2.

 

Итак, если вы планируете разместить иллюстрацию размером в страницу А4 в журнале, использующем линиатуру 175 lpi, то максимальный размер цифрового файла составит 2891×4186 точек (8,26 дюймов x 350 точек/дюйм и 11,69 дюймов x 350 точек/дюйм).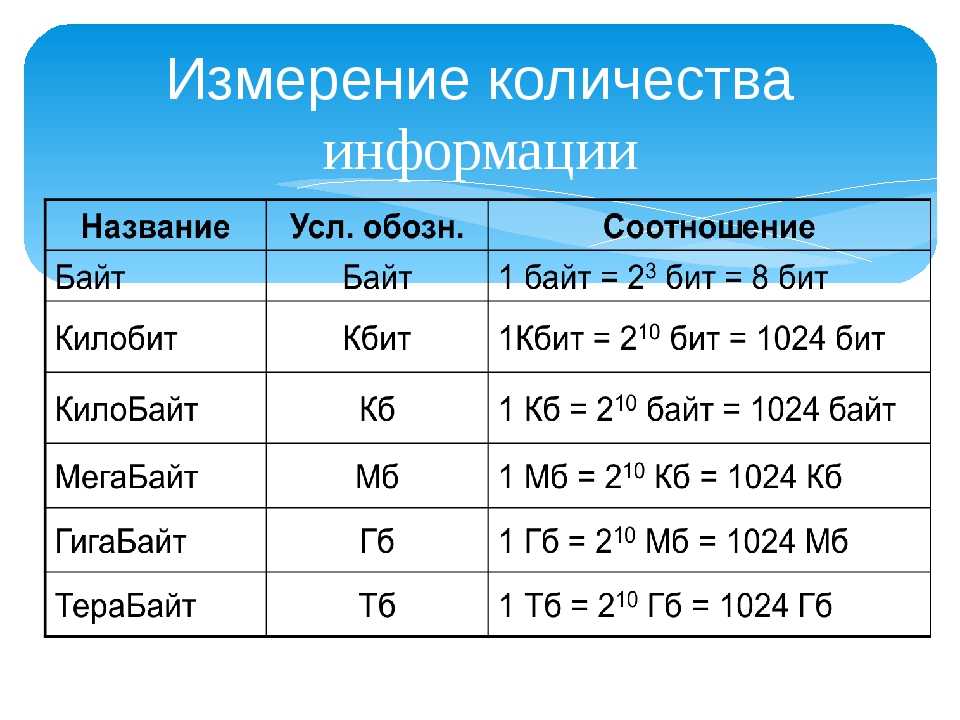 Для журнала с линиатурой 150 lpi он составит 2478 x 3507 точек.

 

В газетном производстве значение используемой линиатуры изменяется от 85 до 100 lpi. Таким образом, для вывода изображения форматом А4 потребуется цифровая иллюстрация, состоящая максимум из 1652×2338 точек.

 

В качестве примера мы привели максимальный размер цифрового файла при Qf = 2. Также возможно принять Qf = 1, тогда размер файлов уменьшится в 4 раза, но оптимальное качество достигнуто не будет.

 

Теперь поговорим о цифровом разрешении аналоговой пленки. Хотелось бы разделить эту задачу на две:

 

1. Всю информацию, находящуюся на кадре пленки, нужно сохранить в цифровом виде.

 

2. Необходимо создать цифровой файл максимального качества.

 

Первая задача может возникнуть при необходимости сохранить какой-нибудь фотошедевр навечно, не потеряв ни одной мелкой детали. Требования, предъявляемые к процессу сканирования, будут соответствующие.

 

Как известно, разрешение пленки и объектива оценивается функцией передачи модуляции. Оба эти звена одинаково важны. Для оценки информационной емкости важна максимальная пространственная частота системы «объектив-пленка», т. е. максимальная разрешающая способность. Этот параметр в большинстве случаев колеблется в пределах 80-120 лин/мм.

 

Для того чтобы понять, сколько же точек на миллиметр понадобится для сохранения такого количества информации, вспомним теорему Котельникова. Она может быть сформулирована следующим образом: имеется сигнал с ограниченным спектром, например F(t), есть последовательность отсчетов F(t1), F(t2)…F(n). Для того чтобы исходный сигнал можно было бы восстановить абсолютно точно, частота отсчета должна быть вдвое больше, чем максимальная частота исходного сигнала. Ее следствием является то, что для передачи пространственной частоты (скажем, 100 лин/мм) потребуется сканирование с вдвое большей частотой (200 линий на мм). Это легко представить практически. Если бы мы сканировали миру с разрешением 100 лин/мм с таким же шагом в 100 линий на мм, то можно было бы сохранить ее полностью, если каждая линия миры попадет на каждую линию сканирующего устройства. Но если каждая линия миры попадет между сканирующими линиями, то получится серое поле (рис. 3). Пространственная частота устройства считывания (сканера) в 200 лин/мм, означает, что имеется 400 переходов черное/белое или 400 элементов, т.е. для создания такой пространственной частоты потребуется 400 считывающих элементов на мм. Получаем, что для сканирования миры с разрешением 100 лин/мм необходимо взять разрешение сканирующего устройства как минимум 400 точек на мм.

 

Если разрешение совокупности пленки и объектива составляет 80 лин/мм (что понимается как 80 пар линий или 160 переходов черное/белое), то для того, чтобы без потерь сохранить такое количество информации в цифровой форме, потребуется 320 точек на мм или 8128 точек на дюйм. Для формата 24×36 мм это равняется 7680×11520 точек.

 

Таким образом, для считывания всей информации с пленки потребуется разрешение сканирования около 8000 dpi. При таком значении фактически каждое зернышко фотошедевра будет сохранено в цифровом формате. На практике такая задача встречается редко.

 

Рассмотрим задачу получения цифрового файла максимального качества. В данном случае цель состоит в том, чтобы перенести в цифровое изображение только то, что реально сохранено на пленке. Предположим, что разрешающая способность пленки и объектива составляет 80 лин/мм. По теореме, обратной теореме Котельникова получаем, что у существовавшего в плоскости пленки изображения реально сохранена пространственная частота 40 лин/мм. Для восстановления такой частоты необходимо будет сканировать с разрешением 80 точек на мм или 2032 dpi. Получаем, что для создания цифрового файла максимально качества необходимо разрешение сканера в пределах 2000-2500 dpi. Сканеры с таким параметром вполне доступны.

 

Используя разрешение, скажем, в 2000 dpi, мы получим из одного кадра формата 24×36 мм файл, размером 1890×2834 пикселей. Если вернуться к рассмотренному вопросу о необходимой информации для публикации в журнале, то, приняв Qf = 2 и линиатуру журнала равной 150 lpi один кадр узкой пленки может быть напечатан с максимальным качеством форматом 16×24 см, то есть чуть больше, чем половина полосы. Примерно до этого формата не имеет значения, возьмем мы узкую пленку или широкую. Как известно, кадр с узкого формата все же можно поместить на целую полосу (Qf будет равен примерно 1,5), но отличие от среднего формата уже будет заметно.

 

Если пересчитать максимальное разрешение цифрового изображения, полученного с кадра 24×36 мм в мегапикселы, получается 1890 x 2834 = = 5356260 (~ 5,3 мегапикселей). Примерно таким разрешением должна обладать цифровая камера, чтобы сравниться с пленочным аналогом.

 

В заключение хотелось бы отметить, что все приведенные значения не следует понимать буквально. Отличие разрешающей способности пар «объектив – пленка» может быть велико и колеблется от 40 до 150 лин/мм. Поэтому размер полученного цифрового файла с максимальным качеством будет различным. Все рекомендации относительно разрешения цифрового файла для печати могут незначительно меняться, в частности, в зависимости от алгоритма растрирования.

 

Смотрите также:

 

Принтер останавливается во время печати

Защита от неприятностей

Что делать если произошло загрязнение печатающей головки или помпы Вашего струйного принтера

Взаимосвязанное расположение картриджа и печатающей головки струйного принтера

Подходы к фотопечати с помощью струйных принтеров.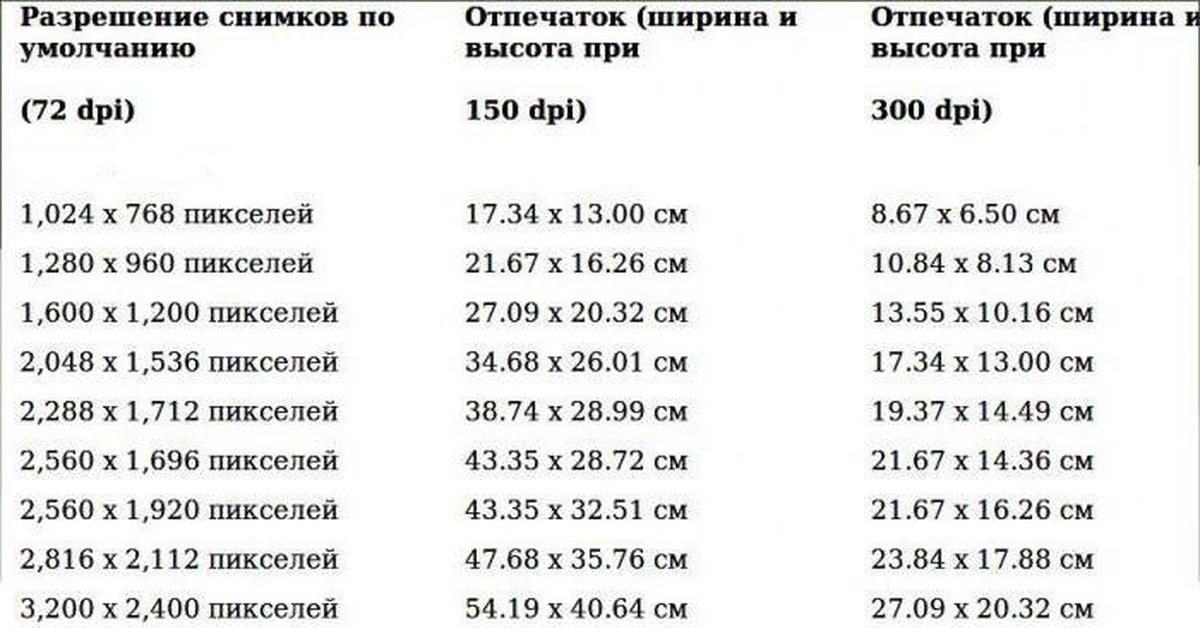 Управление размером точки

Склеивание трубок-капиляров в шлейф. Изготовление многоканального шлейфа для СНПЧ

Разрешение изображения и его размер

Лекция 3

Основные понятия КГ

Разрешение изображения и его размер

Следует четко различать разрешение экрана, разрешение печатающего устройства и разрешение изображения. Все эти понятия относятся к разным объектам. Друг с другом эти виды разрешения никак не связаны, пока не потребуется узнать, какой физический размер будет иметь картинка на экране монитора, отпечаток на бумаге или файл на жестком диске.

Разрешение экрана – свойство компьютерной видеосистемы (зависит от параметров монитора и видеокарты) и операционной системы (зависит от настроек Windows). Разрешение экрана измеряется в пикселах на дюйм (ppi — pixel per inch) и определяет размер изображения, которое может быть размещено на экране целиком.

Разрешение принтера – свойство принтера, выражающее количество отдельных точек, которые могут быть напечатаны на участке единичной длины. Оно измеряется в единицах dpi (dots per inch – точки на дюйм) и определяет размер изображения при заданном качестве или, наоборот, качество изображения при заданном размере.

Разрешение изображения – свойство самого изображения. Оно  измеряется в точках на дюйм (dpi) и задается при создании изображения в графическом редакторе или с помощью сканера. Значение разрешения изображения хранится в файле изображения и неразрывно связано с другим свойством изображения – его физическим размером.

Физический размер изображения. Может измеряться как в пикселах, так и в единицах длины (миллиметрах, сантиметрах, дюймах). Он задается при создании изображения и хранится вместе с файлом.

Если изображение готовят для демонстрации на экране, то его ширину и высоту задают в пикселах, чтобы знать, какую часть экрана оно занимает. Если изображение готовят для печати, то его размер задают в единицах длины, чтобы знать, какую часть листа бумаги оно займет. Нетрудно пересчитать размер изображения из пикселов в единицы длины и наоборот, если известно разрешение изображения (см. таблицу).

Связь между размером иллюстрации (в пикселах) и размером
 отпечатка (в мм) при разных разрешениях отпечатка

Понятие растра

Появление и широкое использование растра основано на свойстве человеческого зрения воспринимать изображение, состоящее из отдельных точек, как единое целое. Эту особенность зрения с давних пор использовали художники. На ней основана и технология полиграфической печати.

Изображение проецируется на светочувствительную пластину через стекло, на которое равномерно нанесена непрозрачная растровая решетка. В результате непрерывное полутоновое изображение оказывается разбитым на отдельные ячейки, которые называются элементами растра. Растр получил широкое распространение при изготовлении различного рода печатной продукции: газет, журналов, книг.

Понятие непрерывного полутонового изображения пришло из фотографии. На самом деле фотографический отпечаток при просмотре его через оптический прибор с очень большим увеличением тоже состоит из отдельных элементарных точек. Однако они настолько малы, что неразличимы невооруженным глазом.

Другие методы представления изображений: полиграфия, распечатка на принтере, вывод на монитор – используют сравнительно большие по размеру элементы растра.

Методы растрирования

В полиграфии плотность заполнения элемента растра черной краской определяет восприятие данной точки на отпечатке как более светлой или темной. Таким образом, интенсивность тона регулируют изменением размера растровой точки: чем темнее точка на отпечатке, тем больше степень заполнения черной краской ячейки растра. Такой метод называют растрированием с амплитудной модуляцией.

Интенсивность тона можно регулировать за счет изменения числа черных точек одинакового размера, размещаемых в растровой ячейке. Такой метод называют растрированием с частотной модуляцией.

Если черные точки расположены внутри растровой ячейки случайным образом, метод называют стохастическим растрированием.

Интенсивность тона (светлоту) принято подразделять на 256 уровней, т. е. для воспроизведения всего полутонового диапазона достаточно, чтобы размер растровой ячейки составил 16х16 точек. Таких ячеек, накладываемых на изображение, должно быть столько, чтобы не пропали какие-то мелкие детали изображения. Следовательно, чем больше ячеек растра содержится в каждой строке, тем более высокое качество мы получим при печати изображения.

Расстояние между центрами растровых ячеек одинаково, их число на единицу длины называется линиатурой растра и измеряется в линиях на дюйм (lpi — lines per inch). Чем выше значение lpi растра, тем более четким выглядит изображение, так как мелкие детали попадают в несколько ячеек растра. Современное качественное полиграфическое оборудование может иметь линиатуру растра до 300 lpi. При печати на принтере линиатура растра составляет порядка 65-90 lpi.

В полиграфической печати растровую сетку принято поворачивать на угол 45˚ (для черной краски). Это связано с особенностью человеческого глаза фиксировать линии, близкие к вертикали или горизонтали. При использовании цветной печати угол поворота может быть иным, в зависимости от количества цветов.

Линиатуру растра необходимо учитывать при печати изображения на принтере. Для получения качественного изображения надо знать зависимость между линиатурой, разрешением и тоновым диапазоном.

В настоящий момент для ввода изображения используются, в основном, цифровые устройства (сканеры, фото- и видеокамеры). Эти устройства характеризуются постоянным размером пятна. Следовательно, чтобы заполнить растровую ячейку, попавшую в темную область изображения, в ней размещают много пятен одинакового размера. Такие пятна называют точками. Максимальное число точек одинакового размера, которые могут поместиться в отрезке фиксированной длины (по вертикали или горизонтали) отпечатка, называют разрешающей способностью печатающего устройства. В качестве единицы измерения используется  dpi. Например, разрешение принтера 600×1200 dpi (разрешение по горизонтали – 600, по вертикали – 1200).

Тоновый диапазон, линиатура растра и разрешающая способность печатающего устройства связаны следующим соотношением:

Основы теории цвета

При работе с цветом используют понятия цветовое разрешение (его еще называют глубиной цвета) и цветовая модель.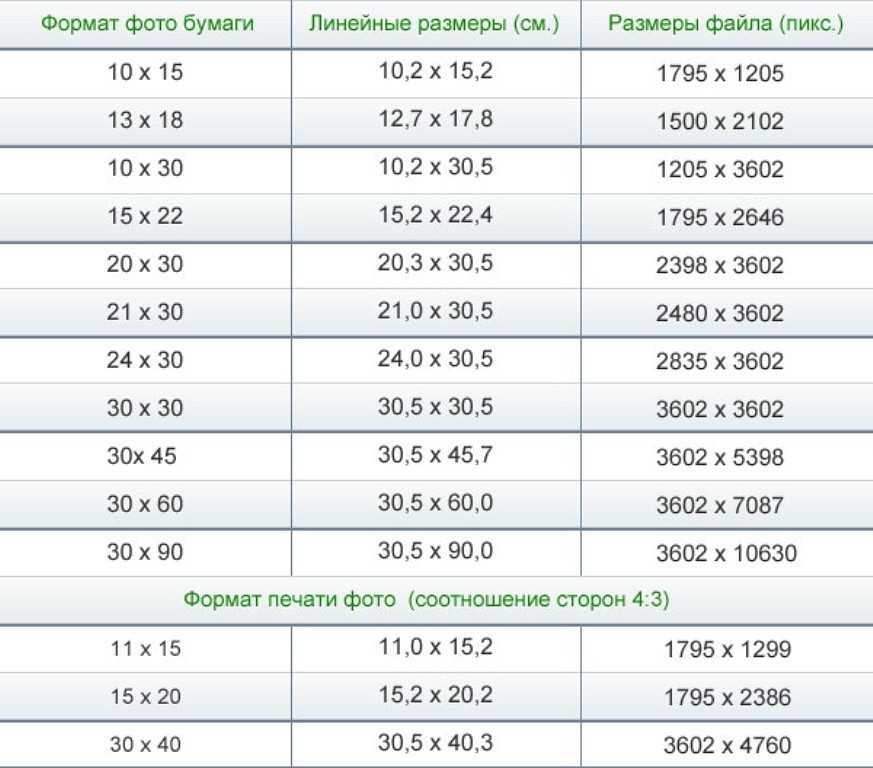 Цветовое разрешение определяет метод кодирования цветовой информации, и от него зависит то, сколько цветов на экране может отображаться одновременно. Для кодирования двухцветного (черно-белого) изображения достаточно выделить по одному биту на представление цвета каждого пиксела. Выделение одного байта позволяет закодировать 256 различных цветовых оттенков. Два байта (16 битов) позволяют определить 65536 различных цветов. Этот режим называется High Color. Если для кодирования цвета используется три байта (24 бита), возможно одновременное отображение 16,5 млн цветов. Этот режим называется True Color.

Цвета в природе редко являются простыми. Большинство цветовых оттенков образуется смешением основных цветов. Способ разделения цветового оттенка на составляющие называется цветовой моделью. Существует много различных типов цветовых моделей, но в компьютерной графике, как правило, применяется не более трех. Эти модели известны под названиями RGB, CMYK и HSB.

Цвет – один из факторов нашего восприятия светового излучения. Для характеристики цвета используются следующие атрибуты.

Цветовой тон. Можно определить преобладающей длиной волны в спектре излучения. Цветовой тон позволяет отличить один цвет от другого, например, зеленый от красного, желтого и других.

Яркость. Определяется энергией, интенсивностью светового излучения. Выражает количество воспринимаемого света.

Насыщенность или чистота тона. Выражается долей присутствия белого цвета. В идеально чистом цвете примесь белого отсутствует. Если, например, к чистому красному цвету добавить в определенной пропорции белый цвет (у художников это называется разбелом), то получится светлый бледно-красный цвет.

Указанные три атрибута позволяют описать все цвета и оттенки. То, что атрибутов именно три, является одним из проявлений трехмерных свойств цвета.

Наука, которая изучает цвет и его измерения, называется колориметрией. Она описывает общие закономерности цветового восприятия света человеком.

Одними из основных законов колориметрии являются законы смешивания цветов.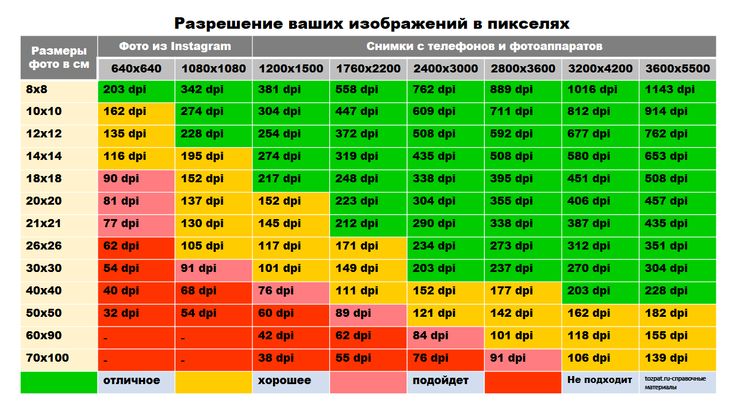 Эти законы в наиболее полном виде были сформулированы в 1853 г. немецким математиком Германом Грассманом:

1.Цвет трехмерен — для его описания необходимы три компоненты. Любые четыре цвета находятся в линейной зависимости, хотя существует неограниченное число линейно независимых совокупностей из трех цветов.

Иными словами, для любого заданного цвета (Ц) можно записать такое цветовое уравнение, выражающее линейную зависимость цветов:

Лекция «Лекция 9» также может быть Вам полезна.

Ц = к₁ Ц₁ + к₂ Ц₂ + к₃ Ц₃,

где Ц₁, Ц₂, Ц₃ – некоторые базисные, линейно независимые цвета, коэффициенты к₁, к₂, и к₃ – количество соответствующего смешиваемого цвета. Линейная независимость цветов Ц₁, Ц₂, Ц₃ означает, что ни один из них не может быть выражен взвешенной суммой (линейной комбинацией) двух других.

Первый закон можно трактовать и в более широком смысле, а именно в смысле трехмерности цвета. Необязательно для описания цвета применять смесь других цветов, можно использовать и другие величины, но их обязательно должно быть три.

2.Если в смеси трех цветовых компонентов один меняется непрерывно, в то время как два других остаются постоянными, цвет смеси также изменяется непрерывно.

3.Цвет смеси зависит только от цветов смешиваемых компонентов и не зависит от их спектральных составов.

Смысл третьего закона становится более понятным, если учесть, что один и тот же цвет (в том числе и цвет смешиваемых компонентов) может быть получен различными способами. Например, смешиваемый компонент может быть получен, в свою очередь, смешиванием других компонентов.

Измерьте разрешение вашего экрана

Под «разрешением» я подразумеваю значение PPI (пикселей на дюйм). Как ни странно, есть два определения слова «разрешение» — одно относится к PPI, а другое — к размерам в пикселях, которые вы, наверное, уже знаете — у меня экран 1280×1024.

Очень легко измерить PPI вашего экрана:

1. Создайте новый пустой документ в Photoshop и установите его размер 1000 пикселей в ширину . (Не обязательно 1000 — если у вас экран меньшего размера, используйте 700 или 800. Если у вас очень большой экран или экран с очень высоким разрешением, используйте 1500 или 2000.)
2. Когда откроется пустой документ, убедитесь, что вы просматриваете его в масштабе 100% (при необходимости нажмите Ctrl +). Возможно, вам придется нажать клавишу Tab, чтобы временно скрыть все ваши палитры.
3. Измерьте ширину документа, поднеся линейку или рулетку к экрану. (Будьте осторожны, чтобы не поцарапать его!) Запишите размер в дюймах.
4. Тогда просто возьмите свой калькулятор и разделите 1000 (или что вы использовали) на ширину в дюймах. Полученное значение является разрешением вашего экрана.

Я сделал на своем экране изображение размером 1000 пикселей, и оно имело ширину 11,575 дюймов. 1000/11,575 = 86,4 точек на дюйм .

Готов поспорить на десять баксов, что разрешение вашего ЖК-экрана намного выше, чем 72ppi. 72 — устаревший стандарт, но многие упорно за него цепляются.

Хорошо, так в чем смысл?

У этого есть только одна цель, которую я могу придумать, но она удобная. Вы когда-нибудь посещали View > Print Size и были разочарованы тем, что Photoshop на самом деле не показал вам изображение нужного размера?

Если вы перейдете в «Редактирование» > «Установки» > «Единицы и линейки» в Photoshop, вы сможете ввести точное значение в поле «Разрешение экрана».

Затем, когда у вас открыто изображение и вы выбираете Размер печати в меню «Вид», это даст вам точное представление размера вашего изображения на экране.

К тому же, если вы такой же зануда, как и я, то возможность сказать: «Я знаю точное разрешение моего экрана, а вы?» — дает теплое удовлетворение.

Как насчет «Шаг пикселя»?

Как ни странно, производители экранов мало говорят о PPI. Если вы когда-нибудь тратили время на поиски нового экрана, вы видели, как они говорят о «шаге пикселя», который измеряется в миллиметрах.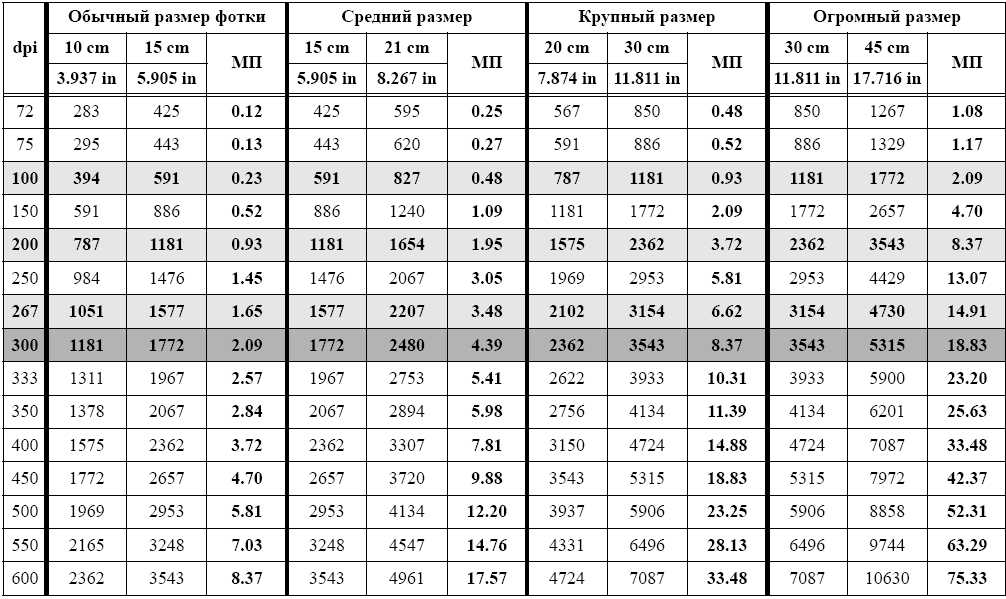 Например, это снимок экрана со страницы характеристик экрана Dell, на который я смотрел:

.

Если вы хотите узнать шаг пикселя вашего экрана, это очень просто — вы делаете это почти точно так же. Вы создаете в Photoshop пустой документ шириной 1000 пикселей, затем просматриваете его в масштабе 100% и измеряете в миллиметрах. Затем разделите миллиметры на 1000, чтобы получить шаг пикселя. На моем старом экране мой 1000-пиксельный файл равен 29.Ширина 4 мм, поэтому шаг пикселя равен 0,294.

(Как упоминалось ранее, он не обязательно должен быть шириной 1000 пикселей. Он может быть любого размера. Если вы разделите миллиметры на пиксели, вы получите правильный результат. И помните, это миллиметры. /px для получения шага пикселя, тогда как px/in для получения PPI.)

 

Если у вас есть вопросы по этой статье, задайте их в разделе «Спросите Дэмиена».

экранов | Wellesley College

Для изображений, отображаемых на экране, более высокое разрешение не означает лучшей четкости, как это происходит с распечатанными изображениями. Для экранных изображений разрешение означает просто размер. Если ваше разрешение выше, размеры изображения будут больше. Большие изображения могут выглядеть более четкими, но есть компромисс в площади экрана. Хотя очень маленькие изображения часто кажутся «нечеткими» при просмотре в большем масштабе, разница в качестве по мере увеличения изображений едва заметна, когда они просматриваются в предполагаемых размерах.

Что такое пиксели и ppi?

При работе с изображением и разрешением экрана мы говорим о пикселях. Пиксели — это просто блоки цвета, расположенные в сетке. Сетка составляет любое изображение, на которое вы смотрите. Экран и изображение можно измерять в пикселях. Мы используем термин ppi или пикселей на дюйм. Это указывает, сколько пикселей представляет собой линейный дюйм изображения или экрана монитора.

При сканировании фотографии размером 3×5 дюймов с разрешением 100 пикселей на дюйм результирующее изображение становится размером 300×500 пикселей, поскольку каждый дюйм представлен 100 отдельными пикселями.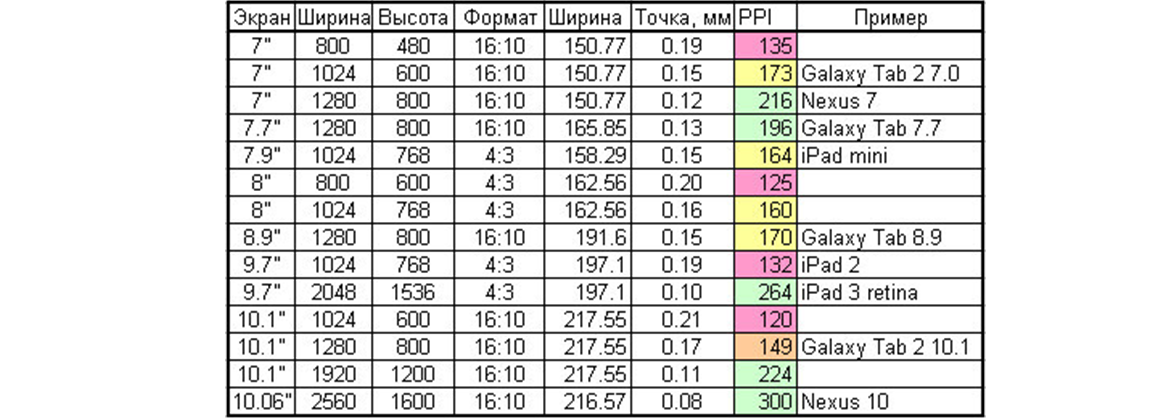 Сканирование изображения с более высоким разрешением приведет к увеличению изображения. Например, при сканировании той же фотографии размером 3×5 дюймов с разрешением 200 пикселей на дюйм результирующее изображение становится размером 600×1000 пикселей, поскольку каждый дюйм изображения представлен 200 пикселями.

Экран компьютера имеет собственное разрешение. Разрешение задается в Панели управления монитором (или дисплеем) путем выбора размеров экрана. Вы можете выбрать один из размеров, таких как 640×480 пикселей или 800×600 пикселей. Предположим, что экран настроен на 800×600 пикселей.

Поскольку экран может отображать только 800×600 пикселей, изображение 300×500 займет почти половину ширины и почти всю высоту. Если бы размер экрана был установлен на 640×480 пикселей, то же самое изображение 300×500 было бы выше всего экрана, и вам пришлось бы прокручивать вниз, чтобы увидеть его нижнюю часть.

Итак, какое разрешение следует использовать при сканировании?

По умолчанию большинство сканеров в кампусе, если в программном обеспечении TWAIN установлено значение «Экран», будут устанавливать разрешение примерно 72 или 75. (Обычно вы выбираете параметр «Экран» в меню «Назначение» или «Разрешение» в окне TWAIN. ) Поскольку увеличение разрешения не улучшает качество изображения, лучше оставить разрешение по умолчанию и изменить размер с помощью функции масштабирования в окне TWAIN. Если это все, что вам интересно знать, прекратите чтение. Если вы хотите узнать подробности о 72 ppi, это объясняется ниже.

Почему 72 ppi является стандартом? (иначе известный как мельчайший)

Чтобы ответить на этот вопрос, вам нужно больше узнать о разрешении экрана вашего монитора. Как упоминалось ранее, вы можете изменить разрешение экрана, изменив размеры в Панели управления монитором (или дисплеем). Разрешение экрана определяется путем деления ширины экрана в пикселях на видимую ширину экрана в дюймах.

Например: установите размер экрана 800×600 пикселей в панели управления монитором (или дисплеем). 17-дюймовый монитор имеет видимую область шириной около 12,5 дюймов. Чтобы найти разрешение экрана, разделите 800 на 12,5, и вы получите разрешение 64 ppi.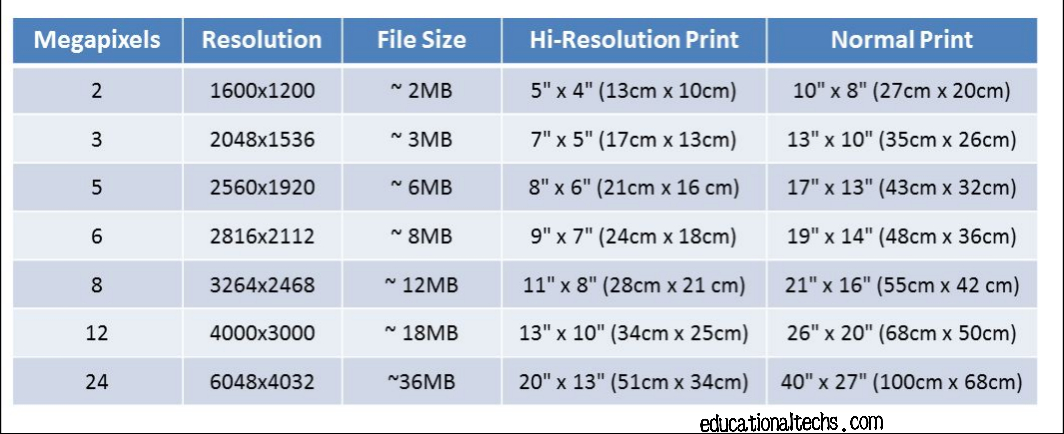 Ниже приведены несколько других расчетов для разрешения экрана. Как правило, мониторы имеют разрешение экрана от 60 до 100 пикселей на дюйм.

Размеры экрана с панели управления монитора (или дисплея)	Видимая ширина монитора	Разрешение экрана
800×600 пикселей	Монитор 12,5 дюймов (17 дюймов)	800/12,5 = 64 точки на дюйм
1024×768 пикселей	12,5 дюйма	1024/12,5 = 82 точки на дюйм
1024×768 пикселей	Монитор 14,6 дюйма (19 дюймов)	1024/14,6 = 70 пикселей на дюйм
1280×1024 пикселей	14,6 дюйма	1280/14,6 = 87 пикселей на дюйм

Что это значит? Почти ничего. Вот пример, который иллюстрирует, как разрешение экрана влияет на отображение изображения.

Скан изображения размером 3×5 дюймов с разрешением 72 ppi. Предположим, что ваш монитор также имеет разрешение экрана 72 ppi. Это означает, что когда вы смотрите на изображение на своем мониторе, оно отображается в размере, близком к исходному. (Я говорю близко к, потому что изображения отображаются на мониторах немного увеличенными.) Если бы разрешение экрана вашего монитора составляло 64 ppi, изображение было бы немного больше (как если бы это было изображение размером 3,4×5,6). Если бы ваш монитор имел разрешение экрана 82 ppi, изображение отображалось бы меньше (как если бы это было изображение 2,6×4,4).

Вот математика, если вам интересно…

    Мое исходное изображение 3×5 дюймов, я отсканировал его с разрешением 72 ppi
    3×72 на 5×72 = 216×360 пикселей
    На мониторе 72 ppi 216/72 на 360/72 = 3×5 дюймы
    На мониторе с плотностью пикселей 64 ppi 216/64 на 360/72 составляет прибл. 3,4 x 5,6 дюйма
    На мониторе с плотностью пикселей 82 ppi 216/82 на 306/82 составляет прибл. 2,6×4,4 дюйма

Это явление можно наблюдать при изменении настроек на панели управления монитором (или дисплеем). Если вы измените размер экрана с 800×600 на 1024×832 (более высокое разрешение), внезапно все ваши окна и значки станут намного меньше!

Таким образом, поскольку вы не можете определить разрешение всех экранов, на которых будет отображаться ваше изображение, лучше просто выбрать число, а именно 72 или 75. Это «достаточно хорошая» оценка разрешения экрана.

Это зависит от модели вашего компьютера для ноутбуков и типа монитора, который вы используете для настольных компьютеров (некоторые настольные компьютеры имеют встроенные мониторы, например, iMac или определенные модели ПК). Большинство современных экранов обычно можно найти с одним из следующих разрешений по умолчанию:

Чтобы узнать разрешение экрана на компьютере под управлением macOS, щелкните значок Apple, затем нажмите «Option» + «Об этом Mac» (удерживая «Option», вместо этого будет написано «Информация о системе…»). В разделе «Оборудование» нажмите «Графика/дисплеи». На всех подключенных экранах будут отображаться их исходное и текущее разрешения.