Гистограмма — QUORACE
Гистограммы позволяют сделать при контроле качества предварительную оценку закона распределения случайной величины, т.е. понять, как происходит разброс значений, есть ли влияющие факторы и как они влияют на измеряемый результат.
Гистограмма является столбчатым графиком и позволяет наглядно представить характер распределения случайной величины
Построение гистограммы происходит следующим образом
1. Создаётся план исследования, проводятся измерения, результаты заносятся в таблицу. Результатом может быть, как фактическое измеренное значение, например, момент затяжки 20 Н*м, так и отклонение от требуемого значения, например, запись отклонения в 0,05 мм при оценке диаметра изделия.
В Таблице 1 приведён пример для 40 результатов измерений момента силы (Н*м).
Заданный момент силы равен 25,5 Н*м, отклонения ±1,5 Н*м. Он будет рассмотрен для построения гистограмм.
Таблица 1.
2. В полученной выборке находят минимальное и максимальное значение 
3. Вычисляют разницу R=Xmax-Xmin (Таблица 2).
4. Разницу R разбивают на z равных интервалов (L), где z=√N, N – объём всей выборки (количество измеренных значений параметра) (Таблица 2). Для точного анализа выборка должна быть представительной, т.е. быть достаточной для проведения анализа и его точной интерпретации. Представительной считается выборка от 35 до 100 значений, обычно N=100. Длина интервала L=R/x должна быть больше цены деления шкалы измерительного устройства, которым выполнялись измерения.
Таблица 2.
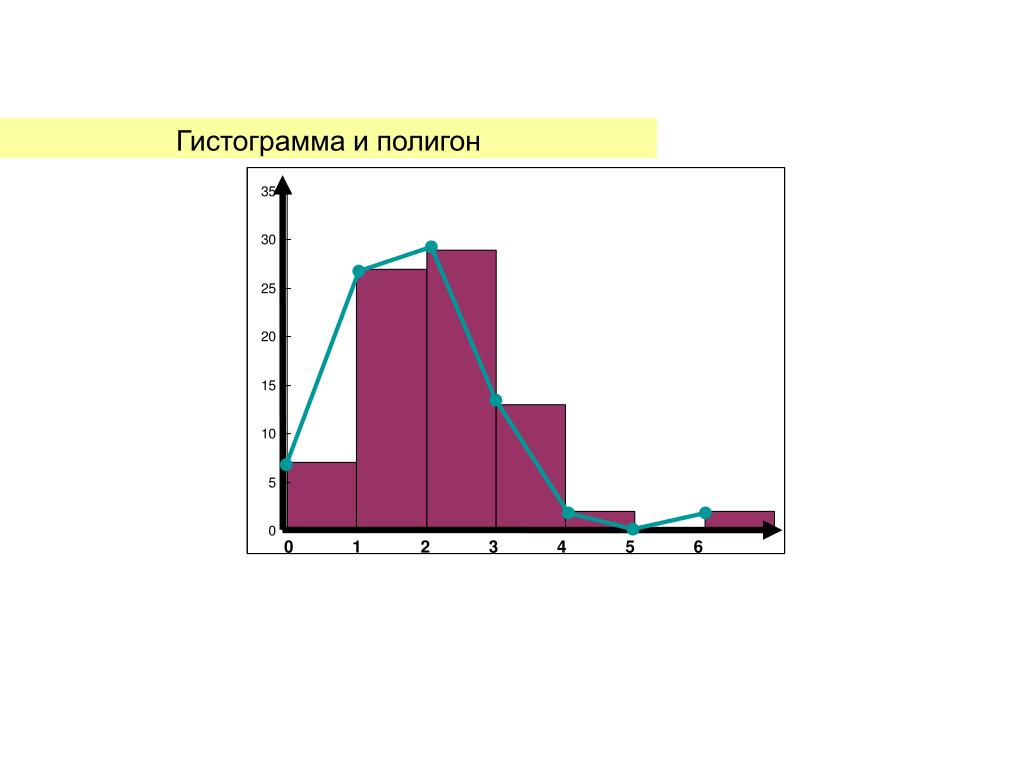
5. Подсчитываются частоты попадания значений в интервалы, составляется таблица распределения и строится его графическое изображение. При этом частоты значений, оказавшиеся на границе интервалов, поровну распределяют между соседними интервалами (Рис.1)
Рис.1
Имея таблицу распределения значения X(среднее арифметическое) и S2 (стандартное отклонение) можно рассчитать по формулам
Где xi – среднее значение i-го интервала
Или воспользовавшись соответствующими функциями в MS Excel
СРЗНАЧ() для X
СТАНДОТКЛОН.
 В() или СТАНДОТКЛОН.Г() для S2
В() или СТАНДОТКЛОН.Г() для S2Зная X и S2 можно оценить индекс воспроизводимости процесса (Ср), который будет рассмотрен в другой статье.
Исходя из гистограммы, рассмотренной в примере, можно сделать вывод о том, что часть значений находится вне допусков и большинство значений уходят в сторону двух пиков по левую и правую границу допусков, что характерно для выборки, объединяющей результаты двух процессов, когда происходит смешивание двух распределений с далеко отстоящими средними значениями. В данном случае необходимо применить метод стратификации и провести анализ ещё раз. В данном случае можно предположить, что измерения проводились двумя различными ключами, что и дало такой результат. Разделение данных по различным ключам позволит исключить двойные пики в гистограмме.
Существует восемь основных типов гистограмм:
- Нормальное распределение. Обычный тип. Форма колокола.
Симметричная форма с пиком примерно в центре интервала характерна для нормального распределения. Отклонения от данной формы могут указывать на наличие различных причин, влияющих на распределение. -
Распределение с двумя пиками.
В центре интервала низкая частота попадания, зато есть два пика по левую и правую стороны интервала. Подобное распределение говорит о том, что в выборку включены значения, объединяющие различные процессы, например, смешаны результаты контроля двух станков или была произведена различная настройка контролирующего инструмента. - Плато
При подобном распределении можно говорить о влиянии условий, аналогичных предыдущей гистограмме, отличие в том, что средние значения нескольких распределений отличаются незначительно. Необходимо провести расслоение данных, снизить вариабельность процессов.
- Распределение гребенчатого типа.
Чередующиеся высокие и низки значения обычно указывают на ошибки измерений или ошибки в способе группировки данных, также на систематическую погрешность в способе округления данных. Существуют незначительная вероятность того, что это распределение типа плато. Если значения в таблицу заносятся человеком, то наличие пиков на целых числах может быть обусловлено влиянием человека при округлении значений. Человеку свойственно отдавать предпочтения при записи круглым числам - Положительно или отрицательно скошенное распределение.
Среднее значение гистограммы локализовано слева или справа от центра размаха. Частоты резко спадают к противоположному от пика концу. Форма ассиметрична. Подобное распределение возможно, когда невозможно получение значений больше или меньше определённой величины, либо при наличии одностороннего поля допуска, также это может быть влияние точности заготовок при их механической обработке.
- Усечённое распределение, с обрывом справа или слева.
Среднее арифметическое гистограммы локализовано далеко слева или справа от центра размаха, частоты резко спадают в противоположном от пика направлении. Подобные распределения встречаются при стопроцентном просеивании изделий из-за плохой воспроизводимости процессов, т.е., например, часть распределения изъята при контроле качества. - Распределение с изолированным пиком.
На ряду с обычным распределением любого типа по одну сторону от распределения находится маленький пик. Причиной может быть включение данных из другого распределения или появление ошибки измерения. Стоит перепроверить измерения и вычисления, может возможно выделить условия (оборудование, время), которые могут служить причиной образования изолированного пика. - Распределение с пиком на краю.
Имеется большой пик по одну из сторон размаха. Подобное распределение может быть при объединении всех несоответствий, близких к одному из концов размаха в одну категорию, либо на неаккуратную запись данных.
Если существуют границы допуска, то следует нанести их на гистограммы. Исходя из положения распределения относительно границ допуска на гистограмме можно делать выводы о необходимости принятия решений.
Есть пять типичных случаев расположения распределения относительно границ допуска
- Гистограмма находится в допуске.
Состояние процесса стабильно, необходимо поддерживать процесс в данном состоянии - Гистограмма находится в допуске, но вплотную к границам.
Необходимо уменьшить разброс до меньшего значения. - Гистограмма за границами допуска слева (или справа).
Необходимо сместить среднее значение ближе к центру. - Гистограмма за границами допуска слева и справа.
Необходимы действия, направленные на снижение вариаций процесса. - Гистограмма за границами допуска слева и справа, пик смещён вправо (или влево).
Необходимо провести действия, аналогичные для 3 и 4 случая одновременно, для снижения вариаций и смещения среднего.
Поделиться:
QUORACE — эволюция бизнеса
Изучение распределений
Раздел 1. Распределение дискретных переменных.
Раздел 2. Распределения непрерывных переменных – гистограммы.
Раздел 3. Распределения непрерывных переменных – диаграммы размаха.
В этом модуле вы продолжите совершенствовать свои навыки работы с данными и узнаете о распределениях данных, а также о том, как графически представлены эти распределения.
Видео 1
Видео 2
Цели
По завершении этого модуля вы сможете:
- Различать частотное и пропорциональное распределение для дискретных переменных.
- Определять формы распределений для непрерывных переменных.
-
Понимать гистограммы и диаграммы размаха.

Раздел 1, Распределение дискретных переменных
Модуль «Распознавание хорошо структурированных данных» объясняет, как данные организованы в столбцах, полях и строках. В хорошо структурированных данных каждая переменная (поле) находится в своем собственном столбце, а каждое отдельное наблюдение этой переменной (значения) находится в отдельной строке. Модуль «Изучение переменных поля и типов полей» показывает, что переменные могут быть дискретными или непрерывными. Дискретные переменные имеют значения, которые являются отдельными и разными, тогда как непрерывные переменные имеют значения, которые образуют неразрывное целое.
При работе с данными иногда может возникнуть желание увидеть распределения набора данных. Распределение показывает все возможные значения данных и частоту (количество) их появления. Другими словами, распределение описывает, сколько раз встречается каждое значение данных. То, что вы видите на организованном распределении, зависит от того, является ли переменная дискретной или непрерывной.
То, что вы видите на организованном распределении, зависит от того, является ли переменная дискретной или непрерывной.
Распределение дискретных переменных
Когда мы смотрим на распределения дискретных переменных, мы видим частоту (общее количество) или пропорцию (проценты). Давайте посмотрим на пример, взятый из главы Дэвида М. Лейна и Хайди Цимер о распределении в онлайн-статье Введение в статистику.
Представьте, что у вас есть мешок с конфетами шести разных цветов. Рассмотрим переменную цвет. Это номинальная качественная переменная, поэтому вы знаете, что она будет дискретной.
Дискретные переменные можно подсчитывать отдельно. Вы высыпаете содержимое мешка с конфетами и быстро подсчитываете их количество. Как видите, из 55 конфет у нас 17 коричневых, 18 красных, 7 желтых, 7 зеленых, 2 синих и 4 оранжевых.
Этот быстрый подсчет дает вам частотное распределение цветов в вашем мешке с конфетами.
Вы можете составить следующую таблицу частот, чтобы описать это распределение.
|
Цвет |
Частота |
|---|---|
|
Коричневый |
17 |
|
Красный |
18 |
|
Желтый |
7 |
|
Зеленый |
7 |
|
Синий |
2 |
|
Оранжевый |
4 |
Вы также можете использовать график, чтобы показать это частотное распределение. Следующая столбиковая диаграмма показывает частотное распределение цветов конфет, или, другими словами, сколько конфет каждого цвета было в вашем мешке.
Столбиковая диаграмма, которая показывает частотное распределение цветов конфет
Распределение по пропорциональным долям
Частотное распределение в предыдущем примере касалось только вашего мешка с конфетами. Что, если вам понадобится узнать о распределении цветов для всех мешков с конфетами такого типа?
Производитель конфет предоставляет некоторую информацию, но не указывает точно, сколько конфет каждого цвета они когда-либо производили.
Вместо частоты (общее количество когда-либо созданных цветов) они показывают пропорциональные доли для каждого из цветов. Вы можете думать о пропорциональных долях как о процентах каждого произведенного цвета, выраженных в десятичных дробях. Например, доля красных конфет составляет 0,20, и это означает, что 20% произведенных конфет являются красными.
Каждая конфета имеет один из шести цветов, поэтому, если сложить все пропорциональные доли, общая сумма составит 1,00 (или 100%).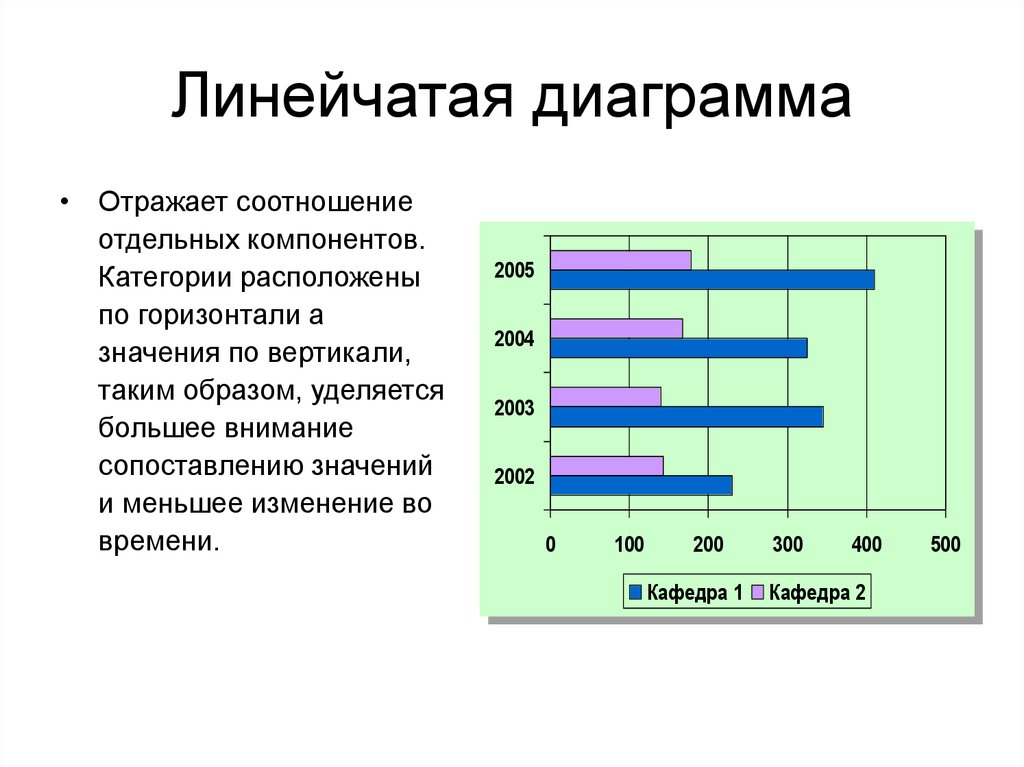
График, показывающий эти пропорциональные доли, называется пропорциональным распределением. На следующей гистограмме показано пропорциональное распределение цветов конфет или, другими словами, какой процент имеет каждый цвет от общего количества произведенных конфет.
Столбиковая диаграмма, показывающая пропорциональное распределение цветов конфет
Проверка знаний
Дети из третьего класса каждый день выбирают на завтрак яблоко, банан или сливу. Вы хотите показать, сколько детей выбрало каждый из этих фруктов.
Что бы вы использовали, чтобы представить такую информацию?
- Частотное распределение
- Пропорциональное распределение
Резюме
Итак, здесь вы узнали о двух типах распределений дискретных переменных: частотном и пропорциональном. На следующем уроке вы узнаете, как показать распределение для непрерывных переменных.
Раздел 2. Распределения непрерывных переменных – гистограммы
На предыдущем уроке вы рассмотрели распределения дискретной переменной (цвет конфет). Как вы помните, дискретные переменные имеют отдельные различающиеся значения, тогда как непрерывные переменные имеют значения, которые образуют неразрывное целое. На этом уроке вы изучите распределения непрерывных переменных в целом и использование гистограмм в частности.
Следующий пример вы взяли из главы Дэвида М. Лейна и Хайди Цимер о распределении в онлайн-статье «Введение в статистику». Один из авторов записывал время своей реакции при перемещении курсора над целью в серии из 20 опытов. Переменная «время ответа» является непрерывной. Когда время измерялось в миллисекундах, двух одинаковых значений времени отклика не было.
На диаграмме ниже показано время отклика в миллисекундах.
|
Номер опыта |
Время ответа в миллисекундах |
Номер опыта |
Время ответа в миллисекундах |
|
1. |
568 |
11. |
720 |
|
2. |
577 |
12. |
728 |
|
3. |
581 |
13. |
729 |
|
4. |
640 |
14. |
777 |
|
5. |
641 |
15. |
808 |
|
6. |
645 |
16. |
824 |
|
7. |
657 |
17. |
825 |
|
8. |
673 |
18. |
865 |
|
9. |
696 |
19. |
875 |
|
10. |
703 |
20. |
1007 |
Сгруппированные частотные распределения
Вспомните, что вы узнали о частотном распределении на предыдущем уроке. Если представить значения времени ответа из показанной выше таблицы в виде частотного распределения, результаты не будут информативными. Было бы 20 различных значений, каждое с частотой в 1.
Чтобы решить эту задачу, мы создадим сгруппированное частотное распределение, в котором сведем в таблицу время отклика, попадающее в различные интервалы одинакового размера (диапазоны значений), как показано в таблице ниже.
|
Интервал (в миллисекундах) |
Частота |
|---|---|
|
500-600 |
3 |
|
600-700 |
6 |
|
700-800 |
5 |
|
800-900 |
5 |
|
900-1000 |
0 |
|
1000-1100 |
1 |
Сгруппированные частотные распределения можно показать графически. График, представленный ниже, называется гистограммой. Метки на оси X – это средние значения интервалов, которые они представляют. Чуть позже мы рассмотрим гистограммы более подробно.
График, представленный ниже, называется гистограммой. Метки на оси X – это средние значения интервалов, которые они представляют. Чуть позже мы рассмотрим гистограммы более подробно.
Столбиковая диаграмма сгруппированного частотного распределения интервалов времени отклика
Формы распределений
Распределения бывают разных форм. Распределения могут быть симметричными, со значениями, равномерно распределенными по центру. Также они могут иметь положительный перекос с большим количеством значений, сгруппированных справа, или отрицательный перекос с большим количеством значений, сгруппированных слева.
Представьте, что вы измерили рост людей из 3 разных групп и создали гистограмму для каждой группы, чтобы показать распределение роста людей в этой группе.
Величина интервала составляет 2,95 дюйма, поэтому рост людей составляет 59-61,95 дюйма, 62-64,95 дюйма и так далее.
Теперь вы хотите по отдельности изучить форму каждого распределения.
Три гистограммы, которые показывают распределение роста, по одной для каждой группы
Симметричные распределения
В нашем примере с данными о росте людей, распределение роста для одной из наших групп почти симметрично. Если сложить его пополам, две стороны будут почти идеально соответствовать друг другу.
В полностью симметричном распределении центр данных является и средним, и медианным, поскольку эти значения равны. Центр данных представлен обоими значениями, а разброс данных составляет одинаковую величину по обе стороны от центра.
Положительные асимметричные распределения
Некоторые распределения не симметричны. Если данные в распределении расходятся в положительном направлении дальше, чем в отрицательном, то такое распределение – распределение с положительным перекосом.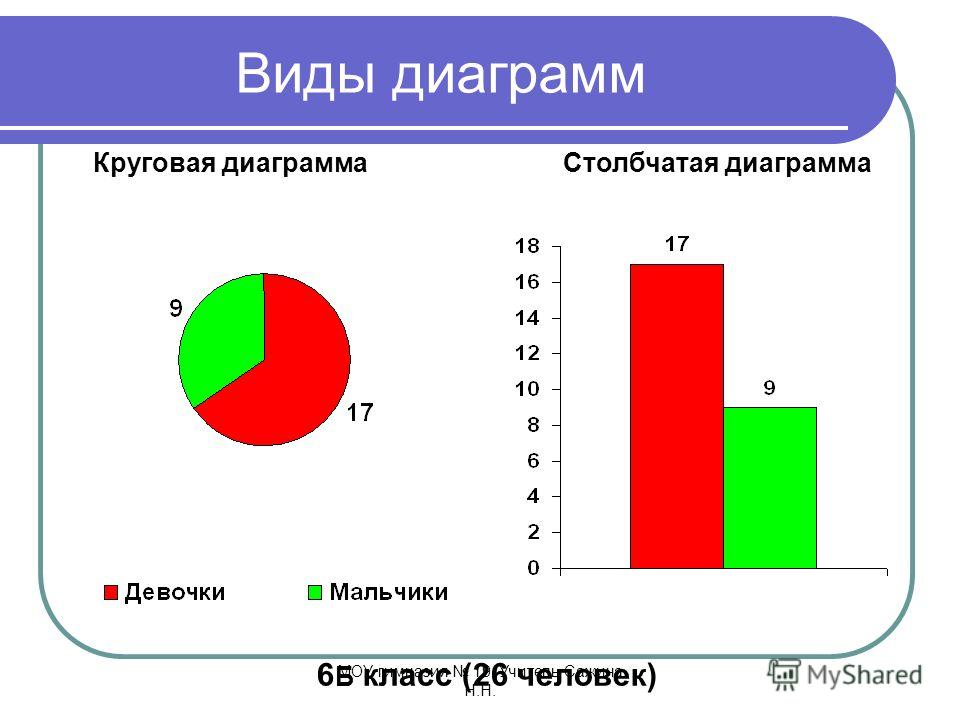 Положительный перекос также называется перекосом вправо, потому что данные оттягиваются вправо. Правый «хвост» длиннее. Когда распределение имеет положительный перекос, медиана будет меньше среднего.
Положительный перекос также называется перекосом вправо, потому что данные оттягиваются вправо. Правый «хвост» длиннее. Когда распределение имеет положительный перекос, медиана будет меньше среднего.
Представьте себе город, в котором живут несколько миллиардеров. Высокие доходы этих миллиардеров исказили бы средний доход города. Среднее значение дохода будет выше чем фактическое. Чтобы реально отразить экономическое состояние всех жителей города, лучше выбрать медианный доход.
Точно так же, глядя на наши данные о росте, одна группа показывает положительный перекос из-за присутствия в ней трех человек, рост которых близок или превышает 72 дюйма (6 футов). Их высокий рост делает среднее значение выше. Поэтому лучше будет использовать медиану для получения общей картины роста в группе.
Отрицательные асимметричные распределения
Еще одно асимметричное распределение – это отрицательное асимметричное распределение.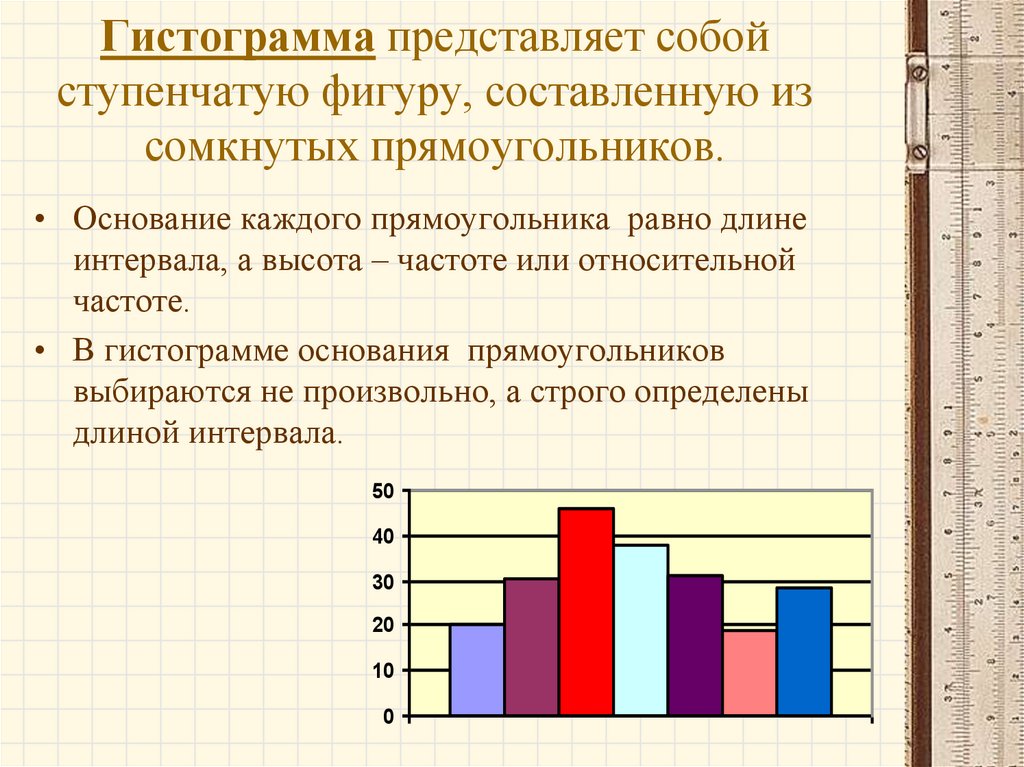 Данные в отрицательном асимметричном распределении расходятся дальше в отрицательном направлении, чем в положительном. Отрицательный перекос также называется перекосом влево, потому что данные оттягиваются влево. Левый «хвост» длиннее. Когда распределение имеет отрицательный перекос, медиана будет больше среднего.
Данные в отрицательном асимметричном распределении расходятся дальше в отрицательном направлении, чем в положительном. Отрицательный перекос также называется перекосом влево, потому что данные оттягиваются влево. Левый «хвост» длиннее. Когда распределение имеет отрицательный перекос, медиана будет больше среднего.
Например, представьте себе класс, в котором есть 20 учеников. В этом классе есть двое, которые никогда не посещали занятий и не выполняли никаких заданий. Эти ученики получили итоговую оценку «0». Их нули будут искажать результаты средней оценки в классе, из-за чего средняя успеваемость ученика будет казаться ниже чем есть на самом деле. Чтобы действительно отразить успехи учащихся в этом классе, лучше выбрать медианный балл.
Точно такая же ситуация с нашими данными о росте, где одна группа показывает отрицательный перекос из-за присутствия людей, рост которых меньше 60 дюймов (5 футов). Их низкий рост делает среднее значение меньшим.
Проверка знаний
В каком из распределений среднее значение и медиана будут равны?
- Симметричное распределение
- Положительное неравномерное распределение
- Отрицательное распределение перекоса
- Сгруппированное частотное распределение
Гистограммы
Гистограмма похожа на столбиковую диаграмму, но она группирует значения для непрерывной переменной в диапазоны или интервалы равного размера.
Эта гистограмма использует набор данных с информацией об олимпийских спортсменах. Одна из переменных в наборе данных содержит возраст спортсменов от 18 до 90. Гистограмма позволяет увидеть, как спортсмены делятся на разные возрастные группы.
Интервалы – каждый интервал определяется четырехлетним периодом, например, 12–15, 16–19, 20–23, 24–27 и т. д. Этот интервал представляет возрастной диапазон от 16 до 19 лет.
Столбцы – каждая точка данных помещается в соответствующую ячейку, которая доходит до нижнего предела следующей ячейки, но не включает ее, и ячейка представлена столбцом.
Каждый столбец представляет собой количество элементов, соответствующих критериям интервала. Этот столбец показывает, что 48 спортсменов попадают в интервал возрастного диапазона 32–35 лет.
Проверка знаний
Посмотрите еще раз на гистограмму возрастных диапазонов олимпийских спортсменов. В какой возрастной группе больше всего людей? Помните, что столбцы соответствуют нижнему пределу следующего интервала, но не включают его.
В какой возрастной группе больше всего людей? Помните, что столбцы соответствуют нижнему пределу следующего интервала, но не включают его.
Кликните на изображение, чтобы увеличить его.
- 20-23
- 24-27
- 28-31
- 32-35
Резюме
Итак, вы ознакомились с распределениями непрерывных переменных, организованными в виде гистограмм. На следующем уроке вы узнаете о просмотре распределений непрерывных переменных с помощью диаграмм размаха.
Раздел 3. Распределения непрерывных переменных
В этом модуле мы рассмотрим несколько способов представления распределения переменных. На этом уроке вы узнаете о другом важном графике, который называется диаграмма размаха (в Tableau) или блочная диаграмма (в Qlik Sense). Диаграммы размаха – это визуально сжатый способ увидеть и сопоставить распределения данных.
Прямоугольники на диаграмме размаха показывают средние 50% данных. Эти данные находятся в пределах от 25-го до 75-го процентиля с медианным значением 50-го процентиля.
Процентиль показывает, как оценка сравнивается с другими оценками в том же наборе данных. Например, вы проходите тест, чтобы измерить свой уровень интроверсии. Ваш показатель интроверсии сам по себе будет довольно трудно интерпретировать. Будет гораздо более информативно узнать процент людей с более низким показателем интроверсии, чем ваш. Этот процент является процентилем. Если 65% других испытуемых оказались менее застенчивыми, чем вы, ваш результат – 65-й процентиль.
«Усы» – это вертикальные линии, которые заканчиваются горизонтальной чертой. Их добавляют к прямоугольникам диаграммы, чтобы показать дополнительную информацию о распределении данных. Усы наносят нестандартно. Они дают представление о значениях, которые не находятся в пределах этих средних 50% данных (поле), в том числе указывают на выбросы. Выбросы можно интерпретировать, как нетипичные наблюдения или как значения, которые имеют крайнее отклонение от центра распределения.
Выбросы можно интерпретировать, как нетипичные наблюдения или как значения, которые имеют крайнее отклонение от центра распределения.
Мы рассмотрим все эти концепции более подробно позже в этом уроке.
Создание диаграммы размаха
Следующий пример диаграммы размаха взят из главы Дэвида М. Лейна о диаграммах размаха в онлайн-статье «Введение в статистику».
Автор использовал аудиторный эксперимент с 31 студентом. Каждому студенту выдали 30 цветных прямоугольников, и их задача заключалась в том, чтобы как можно быстрее называть цвета.
Их время в секундах записано в следующей таблице:
|
|
||||||
|
14 |
17 |
18 |
19 |
20 |
21 |
29 |
|
15 |
17 |
18 |
19 |
20 |
22 |
|
|
16 |
17 |
18 |
19 |
20 |
23 |
|
|
16 |
17 |
18 |
20 |
20 |
24 |
|
|
17 |
18 |
18 |
20 |
21 |
24 |
|
Мы будем использовать этот набор данных, чтобы проиллюстрировать, как создать диаграмму размаха. Создание диаграммы размаха выполняется следующим образом:
Создание диаграммы размаха выполняется следующим образом:
- Рассчитать процентили.
- Построить прямоугольник в соответствии с процентилями.
- Определить размер шага.
- Добавить усы.
- Добавить внешнее значение.
Рассчитать процентили
Помните, что прямоугольники на диаграммах размаха простираются от 25-го до 75-го процентиля данных. В них отображается 50-й процентиль. Нижняя часть прямоугольника (нижний ящик) – это 25-й процентиль, а верхняя часть поля (верхний ящик) – 75-й процентиль.
Чтобы увидеть процентили мы будет использовать числовую линию, как показано в следующих шагах:
- Составим список значений от наименьшего к наибольшему.
31 значение на числовой прямой от наименьшего к наибольшему.
-
Определим медиану или центральное значение. Среднее значение отображается на полпути между началом и концом последовательности чисел.

Для последовательности из 31 значения, медиана будет означать, что есть 15 значений до медианы и 15 значений после нее. Таким образом, медианное значение равно 19.
31 значение на числовой прямой от наименьшего к наибольшему с указанием медианной оценки.
- Определим 25-й процентиль. Значение 25-го процентиля появляется на полпути между началом последовательности и медианным значением.
В нашем примере с 31 значением, у этого промежуточного местоположения будет 7 значений перед ним и 7 значений между ним и медианой. Таким образом, значение 25-го процентиля равно 17.
31 значение на числовой прямой от наименьшего к наибольшему с указанием 25-го процентиля и среднего значения.
- Определим 75-й процентиль. Значение 75-го процентиля появляется на полпути между медианой и концом последовательности.
Для нашего списка из 31 значения, в этом промежуточном положении будет 7 значений между ним и медианой и 7 значений между ним и концом последовательности. Таким образом, значение 75-го процентиля равно 20.
Таким образом, значение 75-го процентиля равно 20.
31 значение на числовой прямой от наименьшего к наибольшему с указанием 75-м процентилем и иедианным значением
Построим диаграмму размаха в соответствии с процентилями
На диаграммах размаха нижняя часть прямоугольника (нижний ящик) – это 25-й процентиль, а верхняя часть прямоугольника (верхний ящик) – это 75-й процентиль. 50-й процентиль (медиана) проведен через их границу.
Для нашего набора из 31 значения мы определили, что:
- 25-й процентиль равен 17.
- 50-й процентиль (или медиана) равен 19.
- 75-й процентиль равен 20.
Итак, рисуем диаграмму следующим образом:
Прямоугольник простирается от 25-го до 75-го процентиля.
- 25-й процентиль (нижний ящик) совпадает с 17-м по оси y.
- 50-й процентиль (медиана) совпадает с 19 на оси ординат.
-
75-й процентиль (верхний ящик) совпадает с 20 по оси y.

Примечание. В поле отображаются средние 50% значений данных.
Определим размер шага
Теперь подготовимся к нанесению усов над и под прямоугольником, чтобы предоставить дополнительную информацию о разбросе данных. Размещение усов определяется по шагам, где шаг определяется как 1,5 x IQR, а IQR – это межквартильный диапазон.
Звучит сложно, но IQR просто означает разницу между значением верхней петли (75-й процентиль) и значением нижней петли (25-й процентиль). Помните, что средние 50% значений данных находятся в поле, ограниченном этими значениями.
В нашем наборе оценок значение верхней петли равно 20, а значение нижней петли – 17. Итак, IQR составляет 20—17, или 3.
Чтобы определить размер нашего шага, умножаем 3 (IQR) на 1,5, чтобы получить размер шага 4,5.
Добавим усы
Чтобы понять, как будут отображаться наши усы, давайте сначала рассмотрим некоторые термины и то, как они применяются к оценкам в нашем примере.
Так куда же девать усы?
Усы проводят от верхнего ящика к верхнему предельному значению и от нижнего ящика к нижнему предельному значению.
Хотя мы не прорисовываем усы полностью до внешних значений, мы все же представляем их в виде диаграмм размаха. Внешнее значение представлено маленьким o, а дальнее значение – звездочкой (*).
Для наших данных усы простираются от верхнего значения петли (20) до верхнего предельного значения (24) и от нижнего значения петли (17) до нижнего предельного значения (14).
График 3 Усы проходят от нижнего ящика до нижнего предельного значения и от верхнего ящика до верхнего предельного значения. Они не распространяются на границы.
Они не распространяются на границы.
Добавим внешнее значение
Значение за пределами внутренней границы, но не за пределами внешней границы, является внешним значением. В нашем наборе оценок есть одно из этих значений – 29, которое совпадает со значением внешней границы, но не превышает ее. Мы будем использовать маленькую букву o, чтобы обозначить это значение.
Все, на этом наше построение диаграммы размаха закончено!
Проверка знаний
Усы на диаграмме размаха простираются от верхнего и нижнего ящика до чего еще?
- Верхние и нижние внутренние границы.
- Верхние и нижние внешние границы.
- Верхнее и нижнее предельное значения
- Внешние и дальние значения
Диаграмма размаха против гистограммы
Вам может быть интересно, чем диаграммы размаха отличаются от гистограмм при отображении распределений.
- Гистограммы используют интервалы для отображения частоты значений.
- В диаграммах размаха средние 50% данных отображаются в ящике, а выбросы (если таковые имеются) представлены в виде усов.
Чтобы понять, как это выглядит, вернемся к данным, показывающим распределения роста людей. Мы увидим, как данные для каждой группы выглядят на гистограмме, и на диаграмме размаха.
Гистограммы и диаграммы размаха, показывающие распределение роста по группам
Обратите внимание, насколько меньше места занимает диаграмма размаха, что позволяет упростить сравнение распределений. Три параллельных распределения легче сравнивать на диаграммах размаха, чем на гистограммах.
Смотрите каждую вкладку ниже, чтобы увидеть распределения, представленные обоими типами диаграмм.
Симметричные распределения
Вот как выглядит почти симметричное распределение высот для одной из наших групп данных по росту на гистограмме в сравнении с диаграммой размаха. Обратите внимание, что на диаграмме размаха выбросов нет.
Обратите внимание, что на диаграмме размаха выбросов нет.
Положительные асимметричные распределения
Вот как выглядит положительно искаженное распределение высот для одной из наших групп данных по росту, когда оно отображается на гистограмме и на диаграмме размаха. Оба графика демонстрируют центр и разброс данных, но диаграмма разброса показывает выбросы более явно.
Отрицательные асимметричные распределения
Вот как отображается отрицательно искаженное распределение высот для одной из наших групп данных по росту, когда оно отображается на гистограмме и на диаграмме размаха. Оба графика демонстрируют центр и разброс данных, но диаграмма размаха более очевидно показывает то, что есть только один выброс.
Проверка знаний
Рассмотрим гистограмму, показанную здесь. Какая у нее форма (симметричная или перекошенная)?
Посмотрите на эту гистограмму, прежде чем отвечать на вопрос проверки знаний ниже.
Затем выберите, какая диаграмма размаха соответствует распределению, представленному на гистограмме.
Какой из этих трех диаграмм размаха соответствует распределение, представленное на гистограмме, которую вы видите выше?
- Диаграмма размаха A
- Диаграмма размаха B
- Диаграмма размаха C
Резюме
Итак, теперь вы понимаете, как распределения могут помочь вам исследовать, оценивать и взаимодействовать с данными.
#dataliteracy, #информационная грамотность, #DataLiteracyProject
Следующая статья Исследование хорошо структурированных данных
Построить графики в Python
Данная статья является переводом. Ссылка на оригинал.
Гистограмма – это двухмерный график с прямоугольными столбцами по оси X или Y. Мы используем эти столбцы для сравнения значений, принадлежащих дискретным категориям, сравнивая высоту или ширину соответствующих столбцов. Такие графики часто используются для визуализации данных, поскольку их нетрудно создать и просто понять.
Такие графики часто используются для визуализации данных, поскольку их нетрудно создать и просто понять.
Однако в некоторых ситуациях, таких, как создание инфографики или когда необходимо привлечь внимание публики к данным, гистограмма может быть недостаточно привлекательной. Иногда слишком большое количество гистограмм может сделать презентацию скучной.
Визуализация данных включает множество видов графиков. Эта статья продемонстрирует девять идей, которые можно использовать не только для разнообразия, но и для улучшения внешнего вида полученных результатов.
Два примера визуализаций из этой статьи, которые можно использовать вместо гистограмм для привлечения внимания. Изображение автора.Предупреждение. Целью этой статьи не является опорочить гистограммы. Каждый вид графиков имеет свои преимущества. Эта статья всего лишь демонстрирует виды визуализации, привлекающие внимание больше, чем гистограммы.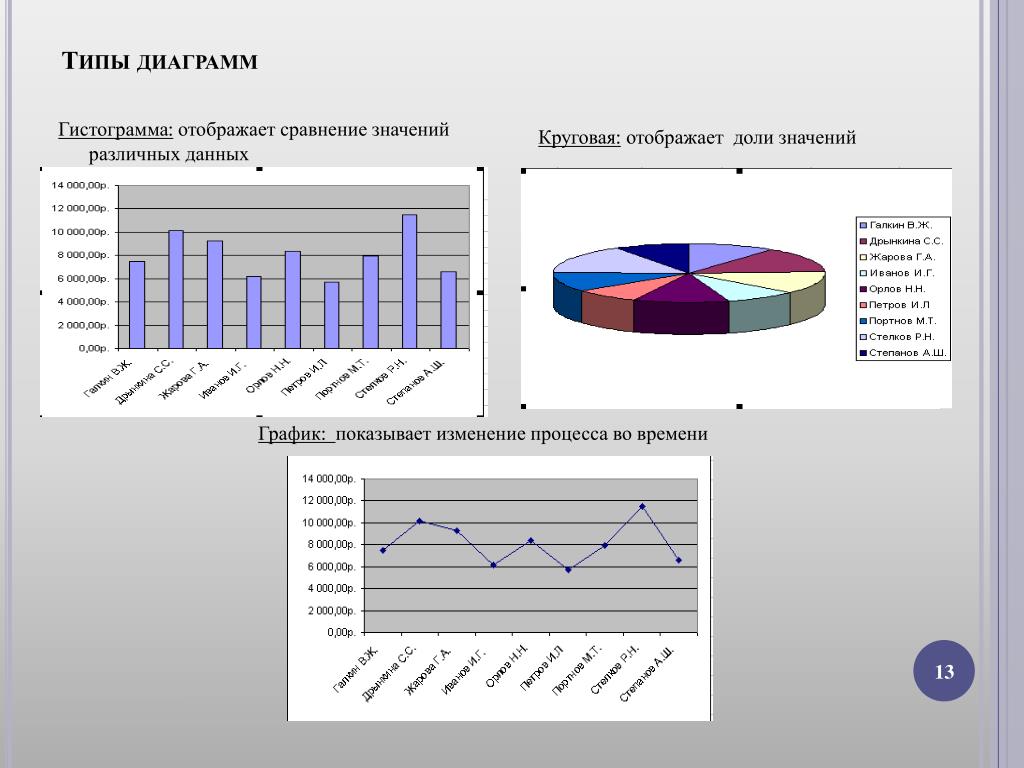 Разумеется, они не идеальны – каждый из них имеет свои преимущества и недостатки.
Разумеется, они не идеальны – каждый из них имеет свои преимущества и недостатки.
Давайте приступим к делу.
Получаем данные
Начнем с импортирования библиотек.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
Чтобы продемонстрировать, что методы, используемые в этой статье, можно применять к реальным данным, мы используем данные из Списка стран по выбросам углекислого газа из Википедии. Эта статья содержит список суверенных государств и территорий и их выбросы углекислого газа в 2018 году.
Мы используем эти данные из Википедии в соответствии с лицензией. Я использовал следующие шаги из статьи «Получение данных из Интернета – из таблицы Википедии в DataFrame»:
import requests from bs4 import BeautifulSoup wikiurl='https://en.wikipedia.org/wiki/List_of_countries_by_carbon_dioxide_emissions' table_class='wikitable sortable jquery-tablesorter' response=requests.get(wikiurl) #status 200: Сервер успешно ответил на запрос http print(response.status_code)
Используем BeautifulSoup для разбора полученных данных:
soup = BeautifulSoup(response.text, 'html.parser')
table = soup.find('table',{'class':"wikitable"})
df2018 = pd.read_html(str(table))[0]
df2018
В качестве примера я выберу последний столбец, «Выбросы углекислого газа в 2018 / Общие, за исключением изменения методов использования земель и лесного хозяйства» и отфильтрую только страны с выбросами от 200 до 1000 MTCO2e (Метрических тонн эквивалента углекислого газа).
Приведенный ниже код можно изменять, если вы хотите использовать другие столбцы или другой диапазон выбросов CO2.
# Получаем списки данных
emi_ = df2018[('2018 CO2 emissions[21]', 'Total excluding LUCF[23]')]
country_ = list(df2018[('Country[20]', 'Country[20]')])
country_mod = [i.replace('\xa0',' ') for i in country_]
# Создаем DataFrame
df = pd.DataFrame(zip(country_mod,emi_), columns = ['countries', 'emission_2018'])
# Убираем строку о стране, которую нельзя конвертировать
df = df[df['countries']!='Serbia & Montenegro']
df.iloc[:,1] = df.iloc[:,1].astype('float')
df = df[(df['emission_2018']>200) & (df['emission_2018']<1000)]
df['percentage'] = [i*100/sum(df['emission_2018']) for i in df['emission_2018']]
df.head(9)
После получения DataFrame мы отсортируем выбросы углекислого газа, чтобы получить новую DataFrame. Оба DataFrame, обычный и отсортированный, будут использованы позже для прорисовки. Мы создаем два DataFrame для того, чтобы продемонстрировать, что результаты могут быть различными.
df_s = df.sort_values(by='emission_2018', ascending=False) df_s.head(9)
Теперь, когда все готово, давайте нарисуем гистограмму для будущего сравнения с другими методами визуализации.
plt.figure(figsize=(15,6.5))
sns.set_style('darkgrid')
g = sns.barplot(data=df, x='countries', y='emission_2018', ci=False, palette='viridis_r')
g.set_xticklabels(df['countries'], rotation=55, fontdict={'fontsize':10})
plt.show()
Гистограмма, показывающая выбросы CO2 между 200 и 1000 MTCO2e в 2018 году по странам. Данные взяты из Википедии. Изображение автора.Прежде чем продолжить, определим функцию, возвращающую список цветов, которую мы будем использовать в каждой визуализации.
def get_color(name, number):
pal = list(sns.color_palette(palette=name, n_colors=number).as_hex())
return pal
Используем эту функцию для получения нескольких списков цветов:
pal_vi = get_color('viridis_r', len(df))
pal_plas = get_color('plasma_r', len(df))
pal_spec = get_color('Spectral', len(df))
pal_hsv = get_color('hsv', len(df))
Визуализации
В этой статье рассматривается 9 видов визуализации, которые можно разделить на две группы: изменение прямоугольных столбцов и изменение форм.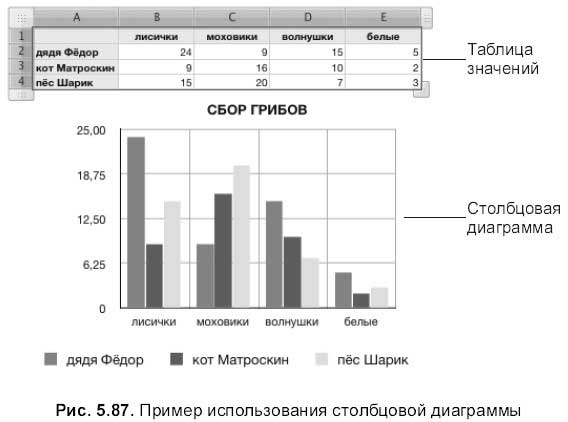
Изменение прямоугольных столбцов:
- Круговая диаграмма
- Радиальная гистограмма
- Древовидная диаграмма
- Вафельная диаграмма
- Интерактивная гистограмма
Изменение форм:
- Секторная диаграмма
- Лепестковая диаграмма
- Пузырьковая диаграмма
- Упаковка кругов
Больше полезных материалов вы найдете на нашем телеграм-канале «Библиотека data scientist’а»
Интересно, перейти к каналу
1. Изменение направления с помощью Круговой диаграммы (также известной как Гоночная диаграмма)
Концепция Круговой диаграммы заключается в «закрутке» столбцов диаграммы вокруг центра круга. Каждый столбец начинается с одного и того же градуса и движется в одном и том же направлении. Максимальное значение соответствует тому столбцу, который заполняет большую часть своего круга.
Максимальное значение соответствует тому столбцу, который заполняет большую часть своего круга.
Это хорошая идея для привлечения внимания зрителей. Но при этом столбцы, заканчивающиеся на половине круга, трудно распознавать. Имейте в виду, что длина столбцов не одинакова: столбцы, находящиеся ближе к центру круга, короче столбцов, находящихся дальше.
Давайте нарисуем Круговую диаграмму для нашего DataFrame.
import math
plt.gcf().set_size_inches(12, 12)
sns.set_style('darkgrid')
# Установим максимальное значение
max_val = max(df['emission_2018'])*1.01
ax = plt.subplot(projection='polar')
# Зададим внутренний график
ax.set_theta_zero_location('N')
ax.set_theta_direction(1)
ax.set_rlabel_position(0)
ax.set_thetagrids([], labels=[])
ax.set_rgrids(range(len(df)), labels= df['countries'])
# Установим проекцию
ax = plt.subplot(projection='polar')
for i in range(len(df)):
ax.barh(i, list(df['emission_2018'])[i]*2*np.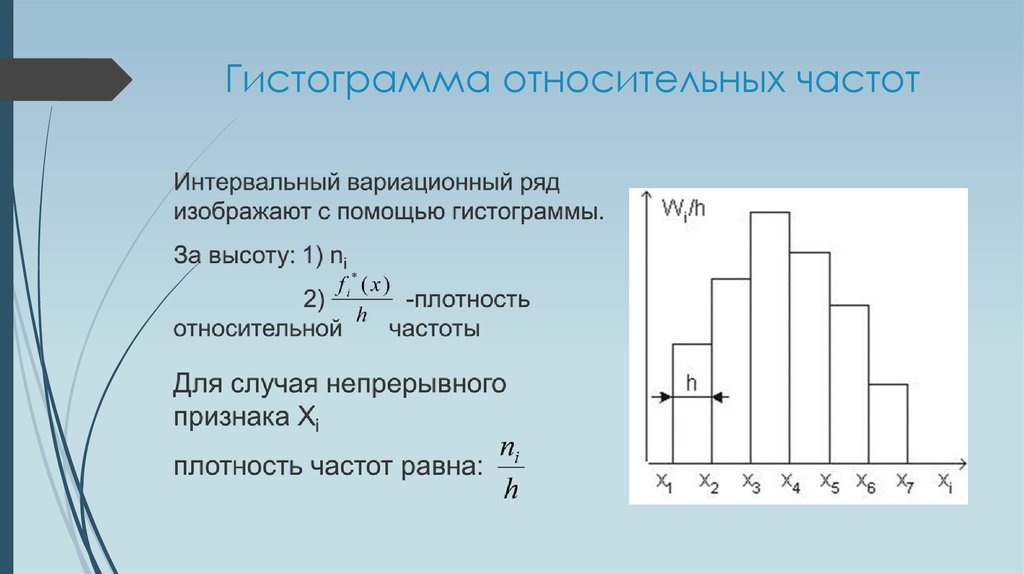 pi/max_val,
label=list(df['countries'])[i], color=pal_vi[i])
plt.legend(bbox_to_anchor=(1, 1), loc=2)
plt.show()
pi/max_val,
label=list(df['countries'])[i], color=pal_vi[i])
plt.legend(bbox_to_anchor=(1, 1), loc=2)
plt.show()
Круговая диаграмма, показывающая выбросы между 200 и 1000 MTCO2e в 2018 году по странам. Изображение автора.Нарисуем круговую диаграмму для отсортированного DataFrame.
import math
plt.gcf().set_size_inches(12, 12)
sns.set_style('darkgrid')
# Установим максимальное значение
max_val = max(df_s['emission_2018'])*1.01
ax = plt.subplot(projection='polar')
for i in range(len(df)):
ax.barh(i, list(df_s['emission_2018'])[i]*2*np.pi/max_val,
label=list(df_s['countries'])[i], color=pal_plas[i])
# Зададим внутренний график
ax.set_theta_zero_location('N')
ax.set_theta_direction(1)
ax.set_rlabel_position(0)
ax.set_thetagrids([], labels=[])
ax.set_rgrids(range(len(df)), labels= df_s['countries'])
# Установим проекцию
ax = plt.subplot(projection='polar')
plt.legend(bbox_to_anchor=(1, 1), loc=2)
plt. show()
show()
Круговая диаграмма, показывающая выбросы между 200 и 1000 MTCO2e в 2018 году по странам. Изображение автора. 2. Начинаем от центра – Радиальная гистограмма
Концепция радиальной гистограммы заключается в изменении направления столбцов. Прежде все наши столбцы имели одно и то же направление, а теперь каждый столбец начинается от центра круга и движется в своем направлении к краю круга.
Пожалуйста, имейте в виду, что сравнивать столбцы, не находящиеся рядом, может быть трудно. Метки столбцов будут располагаться под разным углом, что может быть неудобно для зрителей.
Нарисуем Радиальную гистограмму для нашего исходного DataFrame.
plt.figure(figsize=(12,12)) ax = plt.subplot(111, polar=True) plt.axis() # Установим минимальное и максимальное значение lowerLimit = 0 max_v = df['emission_2018'].max() # Установим высоту и ширину heights = df['emission_2018'] width = 2*np.Радиальная гистограмма, показывающая выбросы между 200 и 1000 MTCO2e в 2018 году по странам. Изображение автора.pi / len(df.index) # Установим индекс и угол indexes = list(range(1, len(df.index)+1)) angles = [element * width for element in indexes] bars = ax.bar(x=angles, height=heights, width=width, bottom=lowerLimit, linewidth=1, edgecolor="white", color=pal_vi) labelPadding = 15 for bar, angle, height, label in zip(bars,angles, heights, df['countries']): rotation = np.rad2deg(angle) alignment = "" # Разберемся с направлением if angle >= np.pi/2 and angle < 3*np.pi/2: alignment = "right" rotation = rotation + 180 else: alignment = "left" ax.text(x=angle, y=lowerLimit + bar.get_height() + labelPadding, s=label, ha=alignment, va='center', rotation=rotation, rotation_mode="anchor") ax.set_thetagrids([], labels=[]) plt.show()
Теперь нарисуем радиальную гистограмму для отсортированного DataFrame
plt.Радиальная гистограмма, показывающая выбросы между 200 и 1000 MTCO2e в 2018 году по странам. Изображение автора.figure(figsize=(12,12)) ax = plt.subplot(111, polar=True) plt.axis() # Установим минимальное и максимальное значение lowerLimit = 0 max_v = df_s['emission_2018'].max() # Установим высоту и ширину heights = df_s['emission_2018'] width = 2*np.pi / len(df_s.index) # Установим индекс и угол indexes = list(range(1, len(df_s.index)+1)) angles = [element * width for element in indexes] bars = ax.bar(x=angles, height=heights, width=width, bottom=lowerLimit, linewidth=1, edgecolor="white", color=pal_plas) labelPadding = 15 for bar, angle, height, label in zip(bars,angles, heights, df_s['countries']): rotation = np.rad2deg(angle) alignment = "" # Разберемся с направлением if angle >= np.pi/2 and angle < 3*np.pi/2: alignment = "right" rotation = rotation + 180 else: alignment = "left" ax.text(x=angle, y=lowerLimit + bar.get_height() + labelPadding, s=label, ha=alignment, va='center', rotation=rotation, rotation_mode="anchor") ax.
set_thetagrids([], labels=[]) plt.show()
3. Используем для сравнения площадь в древовидной диаграмме
Древовидная диаграмма изображает иерархические данные в виде площадей прямоугольников. Несмотря на то, что наши данные не имеют иерархии, мы все-таки можем применить древовидную диаграмму, показав только один уровень иерархии.
При отрисовке древовидной диаграммы данные обычно сортируются по убыванию – от максимальных к минимальным. Если прямоугольников много, имейте в виду, что самые мелкие из них может быть трудно заметить или отделить друг от друга.
Создадим интерактивную древовидную диаграмму с помощью Plotly.
import plotly.express as px
fig = px.treemap(df, path=[px.Constant('Countries'), 'countries'],
values=df['emission_2018'],
color=df['emission_2018'],
color_continuous_scale='Spectral_r',
color_continuous_midpoint=np. average(df['emission_2018'])
)
fig.update_layout(margin = dict(t=50, l=25, r=25, b=25))
fig.show()
average(df['emission_2018'])
)
fig.update_layout(margin = dict(t=50, l=25, r=25, b=25))
fig.show()
Древовидная диаграмма, показывающая выбросы CO2 между 200 и 1000 MTCO2e в 2018 году по странам. Изображение автора. 4. Собираем Вафельную диаграмму из маленьких квадратов
Вафельная диаграмма не только имеет забавное название – это очень хорошая идея для создания инфографики. Она состоит из множества маленьких квадратиков, вместе образующих большой прямоугольник – итоговый результат похож на вафлю.
Обычно прямоугольники выстраиваются квадратами 10*10, чтобы показать процент прогресса. Между прочим, количество квадратов можно менять, чтобы оно соответствовало данным.
Нарисуем вафельную диаграмму, изображающую выбросы CO2 для каждой страны.
#!pip install pywaffle from pywaffle import Waffle fig = plt.Вафельная диаграмма, показывающая выбросы CO2 между 200 и 1000 MTCO2e в 2018 году по странам. Изображение автора.figure(FigureClass=Waffle, rows=20, columns=50, values=list(df_s['emission_2018']), colors=pal_spec, labels=[i+' '+format(j, ',') for i,j in zip(df_s['countries'], df_s['emission_2018'])], figsize = (15,6), legend={'loc':'upper right', 'bbox_to_anchor': (1.26, 1) }) plt.tight_layout() plt.show()
Этот результат может выглядеть цветным и привлекательным, но очень трудно различать похожие оттенки цветов. Это можно считать ограничением вафельной диаграммы. Поэтому считается, что вафельную диаграмму лучше всего использовать для небольшого количества категорий.
Чтобы избежать сложностей восприятия, давайте покажем каждую страну по одной, против всех остальных стран, а потом соберем коллаж. При работе со следующим кодом, пожалуйста, имейте в виду, что графики будут экспортированы на ваш компьютер для дальнейшего импорта. Нарисуем вафельные диаграммы для каждой страны.
При работе со следующим кодом, пожалуйста, имейте в виду, что графики будут экспортированы на ваш компьютер для дальнейшего импорта. Нарисуем вафельные диаграммы для каждой страны.
save_name = []
for i,p,n,c in zip(df_s['emission_2018'], df_s['percentage'], df_s['countries'], pal_hsv):
fig = plt.figure(FigureClass=Waffle,
rows=10, columns=20,
values=[i, sum(df_s['emission_2018'])-i],
colors=[c,'gainsboro'],
labels=[n + ' ' + str(round(p,1)) +' %','Other countries'],
figsize = (8,8),
legend={'loc':'upper right', 'bbox_to_anchor': (1, 1), 'fontsize':24}
)
save_name.append('waffle_'+ n + '.png')
plt.tight_layout()
plt.savefig('waffle_'+ n + '.png', bbox_inches='tight') #export_fig
plt.show()
Пример вафельной диаграммы, показывающей выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора.
Изображение автора.Теперь, когда у нас есть вафельные диаграммы для каждой страны, давайте определим функцию для создания фотоколлажа. Я нашел отличный код для объединения графиков на StackOverflow (ссылка):
from PIL import Image
def get_collage(cols_n, rows_n, width, height, input_sname, save_name):
c_width = width//cols_n
c_height = height//rows_n
size = c_width, c_height
new_im = Image.new('RGB', (width, height))
ims = []
for p in input_sname:
im = Image.open(p)
im.thumbnail(size)
ims.append(im)
i, x, y = 0,0,0
for col in range(cols_n):
for row in range(rows_n):
print(i, x, y)
try:
new_im.paste(ims[i], (x, y))
i += 1
y += c_height
except IndexError:
pass
x += c_width
y = 0
new_im.save(save_name)
Применим эту функцию, чтобы получить фотоколлаж.
# Чтобы создать фотоколлаж:
# width = number of columns * figure width
# height = number of rows * figure height
get_collage(5, 5, 2840, 1445, save_name, 'Collage_waffle.png')
Часть фотоколлажа, комбинирующая вафельные диаграммы для каждой страны. Изображение автора.Больше полезных материалов вы найдете на нашем телеграм-канале «Библиотека питониста»
Интересно, перейти к каналу
5. Ничего не меняем, но делаем гистограмму интерактивной
Мы можем сделать обычную гистограмму интерактивной. Это отличная идея, если вы собираетесь продолжать использовать эту гистограмму. С полученным результатом можно играть или фильтровать его любым удобным для вас способом. Plotly – это полезная библиотека, которая позволит легко создавать интерактивные гистограммы.
Единственная проблема – это научить конечных пользователей использовать интерактивную гистограмму – придется предоставить инструкцию, объясняющую, как использовать гистограмму. Давайте создадим интерактивную гистограмму.
Давайте создадим интерактивную гистограмму.
import plotly.express as px
fig = px.bar(df, x='countries', y='emission_2018', text='emission_2018',
color ='countries', color_discrete_sequence=pal_vi)
fig.update_traces(texttemplate='%{text:.3s}', textposition='outside')
fig.update_layout({'plot_bgcolor': 'white',
'paper_bgcolor': 'white'})
fig.update_layout(width=1100, height=500,
margin = dict(t=15, l=15, r=15, b=15))
fig.show()
Пример интерактивной диаграммы, показывающей выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора. 6. Показываем проценты в секторной диаграмме
Секторная диаграмма – это еще один привычный вид графика в визуализации данных. Это кругообразный статистический график, разделенный на секторы, чтобы показать числовые пропорции. Обычную секторную диаграмму можно сделать интерактивной, чтобы результат можно было настроить или отфильтровать.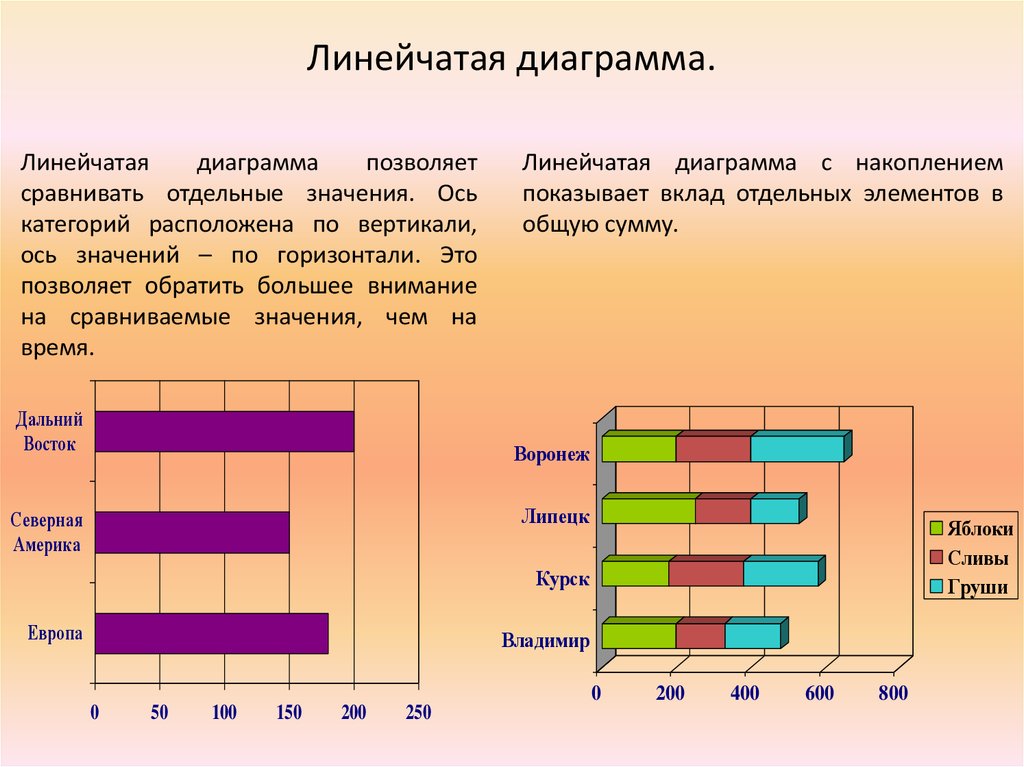 Для создания интерактивной секторной диаграммы можно использовать Plotly.
Для создания интерактивной секторной диаграммы можно использовать Plotly.
import plotly.express as px
fig = px.pie(df_s, values='emission_2018', names='countries',
color ='countries', color_discrete_sequence=pal_vi)
fig.update_traces(textposition='inside',
textinfo='percent+label',
sort=False)
fig.update_layout(width=1000, height=550)
fig.show()
Интерактивная секторная диаграмма, показывающая выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора. 7. Чертим Лепестковую диаграмму внутри круга
Лепестковая диаграмма – это графический метод изображения многовариантных данных. Для сравнения, гистограммы обычно используются для категориальных данных. Чтобы создать лепестковую диаграмму, можно считать каждую категорию переменной в многовариантных данных. Значение каждой категории будет чертиться от центра.
Если категорий много, зрителям может быть трудно сравнивать данные, не расположенные рядом друг с другом. Эту проблему можно решить, рисуя лепестковую диаграмму для отсортированных данных. При этом зрители смогут определить, какие значения больше или меньше прочих.
Эту проблему можно решить, рисуя лепестковую диаграмму для отсортированных данных. При этом зрители смогут определить, какие значения больше или меньше прочих.
Давайте нарисуем лепестковую диаграмму для нашего DataFrame.
import plotly.express as px
fig = px.line_polar(df, r='emission_2018',
theta='countries', line_close=True)
fig.update_traces(fill='toself', line = dict(color=pal_spec[5]))
fig.show()
Лепестковая диаграмма, показывающая выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора.Теперь нарисуем лепестковую диаграмму для отсортированного DataFrame
import plotly.express as px
fig = px.line_polar(df_s, r='emission_2018',
theta='countries', line_close=True)
fig.update_traces(fill='toself', line = dict(color=pal_spec[-5]))
fig.show()
Лепестковая диаграмма, показывающая выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора.
Изображение автора. 8. Пузырьковая диаграмма: много-много кружков
Теоретически, пузырьковая диаграмма – это диаграмма рассеяния с различными размерами точек, представляющих данные. Это идеальный график для представления трехмерных данных: X, Y и размеры точек данных.
При создании пузырьковых диаграмм для категориальных данных хорошо то, что у них нет координат X и Y, и мы можем расположить кружки данных так, как захотим. Например, следующий код показывает, как разместить кружки данных вертикально.
Создайте список значений X, значений Y и меток. Затем добавьте их в качестве столбцов DataFrame. Если вы хотите разместить кружки горизонтально, поменяйте местами значения столбцов X и Y.
# Столбцы по осям X и Y
df_s['X'] = [1]*len(df_s)
list_y = list(range(0,len(df_s)))
list_y.reverse()
df_s['Y'] = list_y
# Столбец меток
df_s['labels'] = ['<b>'+i+'<br>'+format(j, ",") for i,j in zip(df_s['countries'], df_s['emission_2018'])]
df_s
Теперь нарисуем нашу пузырьковую диаграмму.
import plotly.express as px
fig = px.scatter(df_s, x='X', y='Y',
color='countries', color_discrete_sequence=pal_vi,
size='emission_2018', text='labels', size_max=30)
fig.update_layout(width=500, height=1100,
margin = dict(t=0, l=0, r=0, b=0),
showlegend=False
)
fig.update_traces(textposition='middle right')
fig.update_xaxes(showgrid=False, zeroline=False, visible=False)
fig.update_yaxes(showgrid=False, zeroline=False, visible=False)
fig.update_layout({'plot_bgcolor': 'white',
'paper_bgcolor': 'white'})
fig.show()
Вертикальная пузырьковая диаграмма, показывающая выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора.Чтобы продемонстрировать, что мы можем изображать пузыри в различных формах, давайте попробуем расположить их по кругу.
Чтобы сделать это, нам нужно рассчитать координаты X и Y. Начнем с деления 360 градусов на количество строк в таблице данных. Затем получим координаты X и Y из градусов с помощью функций синуса и косинуса.
Начнем с деления 360 градусов на количество строк в таблице данных. Затем получим координаты X и Y из градусов с помощью функций синуса и косинуса.
# Создаем координаты X и Y по кругу
e = 360/len(df)
degree = [i*e for i in list(range(len(df)))]
df_s['X_coor'] = [math.cos(i*math.pi/180) for i in degree]
df_s['Y_coor'] = [math.sin(i*math.pi/180) for i in degree]
df_s
Теперь нарисуем пузырьковую диаграмму по кругу.
import plotly.express as px
fig = px.scatter(df_s, x='X_coor', y='Y_coor',
color="countries", color_discrete_sequence=pal_vi,
size='emission_2018', text='labels', size_max=40)
fig.update_layout(width=800, height=800,
margin = dict(t=0, l=0, r=0, b=0),
showlegend=False
)
fig.update_traces(textposition='bottom center')
fig.update_xaxes(showgrid=False, zeroline=False, visible=False)
fig.update_yaxes(showgrid=False, zeroline=False, visible=False)
fig. update_layout({'plot_bgcolor': 'white',
'paper_bgcolor': 'white'})
fig.show()
update_layout({'plot_bgcolor': 'white',
'paper_bgcolor': 'white'})
fig.show()
Пузырьковая диаграмма по кругу, показывающая выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора.Можно заметить, что чем сложнее мы располагаем пузыри, тем больше места они занимают. Вертикальная или горизонтальная пузырьковые диаграммы помогут сэкономить пространство для других визуализаций.
9. Размещаем пузыри с Упаковкой круга
Наконец, давайте сгруппируем пузыри без перекрытий. Упаковка круга – это хорошая идея для рисования пузырей, не тратя лишнего пространства. Нам нужно рассчитать позиции и размеры каждого пузыря. К счастью, существует библиотека circlify, делающая эти расчеты простыми.
Недостаток Упаковки круга в том, что может быть трудно определить разницу между кругами, имеющими похожие размеры. Его можно устранить, помечая каждый круг его значением.
Его можно устранить, помечая каждый круг его значением.
import circlify
# Рассчитываем позиции кругов:
circles = circlify.circlify(df_s['emission_2018'].tolist(),
show_enclosure=False,
target_enclosure=circlify.Circle(x=0, y=0)
)
circles.reverse()
Нарисуем круг, упакованный кругами.
fig, ax = plt.subplots(figsize=(14, 14), facecolor='white')
ax.axis('off')
lim = max(max(abs(circle.x)+circle.r, abs(circle.y)+circle.r,) for circle in circles)
plt.xlim(-lim, lim)
plt.ylim(-lim, lim)
# Рисуем круги
for circle, label, emi, color in zip(circles, df_s['countries'], df_s['emission_2018'], pal_vi):
x, y, r = circle
ax.add_patch(plt.Circle((x, y), r, alpha=0.9, color = color))
plt.annotate(label +'\n'+ format(emi, ","), (x,y), size=15, va='center', ha='center')
plt.xticks([])
plt.yticks([])
plt.show()
Упаковка круга, показывающая выбросы CO2 одной страны по сравнению с другими странами между 200 и 1000 MTCO2e в 2018 году. Изображение автора.
Изображение автора. Заключение
В гистограммах нет ничего плохого. Они просты в понимании, и их легко построить. Однако разные виды графиков лучше подходят для различных целей. Иногда визуализация данных создается с целью привлечь внимание – например, при создании инфографики, и для этой цели гистограммы не очень подходят.
В этой статье показаны девять видов визуализации, использующих те же данные, на основе которых мы построили гистограмму, но привлекающих намного больше внимания. У этих видов также есть свои недостатки. Имейте в виду, что их может быть сложно интерпретировать, и они могут не годиться для официального отчета.
Спасибо за внимание!
***
Материалы по теме
- 🐍📈 Как «оживлять» графики и впечатлять всех красивыми анимациями с помощью Python
- Анимация графиков в Python за 4 шага
- 🎞️ Как с помощью Python делать красивые математические анимации
5 популярных способов визуализации данных
Барчарт (bar chart) Гистограмма (histogram) Пайчарт (круговая диаграмма) Линейная диаграмма (line chart, график) Скаттерплот (scatter plot, диаграмма рассеяния)
Читайте наc в Telegram
Разбираемся, что происходит в мире рассылок и digital-маркетинга. Публикуем анонсы статей, обзоры, подборки, мнения экспертов.
Публикуем анонсы статей, обзоры, подборки, мнения экспертов.
Смотреть канал
Станьте email-рокером 🤘
Пройдите бесплатный курс и запустите свою первую рассылку
Подробнее
Статья написана совместно с экспертом — Анастасией Кузнецовой, аналитиком и преподавателем, автором телеграм-канала «настенька и графики» и онлайн-курса «Визуализация данных и основы работы в Tableau».
Разбираться в данных легче, когда изучаешь картинку, а не всматриваешься в длинный текст или большую эксельку. Если у вас маленькая пошаговая инструкция или пара статистических фактов, достаточно ёмко сформулировать главное и добавить иллюстрацию. Но если нужно наглядно и красиво донести большой объем информации, — плюс поискать интересные инсайты и паттерны, — потребуется визуализация.
В отличие от интеллект-карт, списков или презентаций, которые допускают свободу творчества, у диаграмм чёткие принципы построения. В них всегда есть система координат, шкала значений и отметки по этой шкале, которые как раз и несут в себе информацию.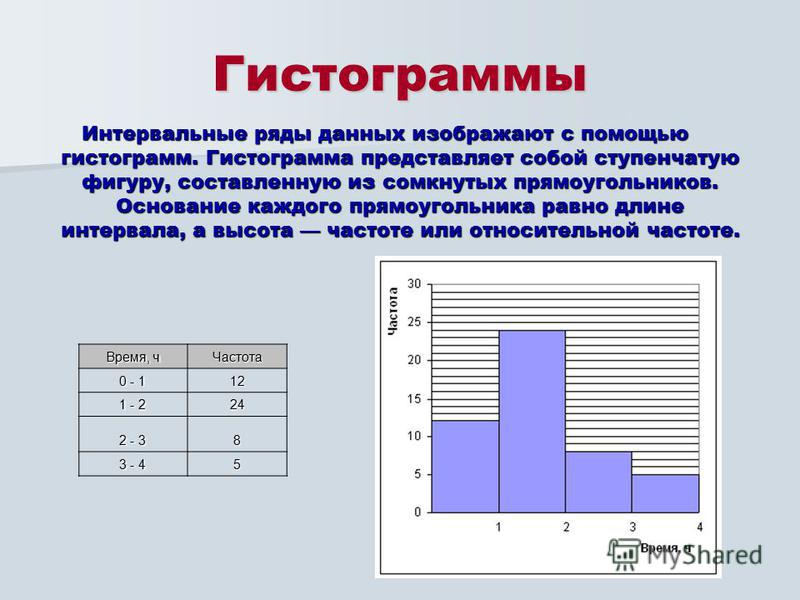
Рассмотрим самые популярные базовые виды диаграмм, которые могут пригодиться для отчетов, статей или рассылок.
| Что нужно показать | Что для этого подходит |
| Сравнение нескольких категорий | Барчарт (bar chart) |
| Распределение одной переменной | Гистограмма (histogram) |
| Доли от целого | Пайчарт (круговая диаграмма) |
| Развитие, динамику во времени | Линейная диаграмма (line chart, график) |
| Корреляцию между двумя переменными | Скаттерплот (scatter plot, диаграмма рассеяния) |
Барчарт (bar chart)
С такой диаграммой вы наверняка уже сталкивались — она состоит из нескольких вертикальных или горизонтальных полосок разной длины. Вертикальные диаграммы ещё называют столбчатыми, а горизонтальные — линейчатыми.
Линейчатый барчарт (CFR), который показывает примерную стоимость проведения Олимпиады в разных городах мира
Столбчатый барчарт (Справка Google Docs) визуализирует результаты опросов, оценку пользователей
Для чего нужно. Барчарт позволяет сравнивать несколько категорий по какой-то числовой переменной. Каждый столбик — это категория, а его длина отвечает на вопрос «Сколько?» — чем длиннее, тем больше значение.
Барчарт позволяет сравнивать несколько категорий по какой-то числовой переменной. Каждый столбик — это категория, а его длина отвечает на вопрос «Сколько?» — чем длиннее, тем больше значение.
Так можно визуализировать, в каком вузе выпускники быстрее трудоустраиваются, какое животное выше всех прыгает или какой источник приносит больше трафика на сайт.
Сортировка категорий от большего к меньшему облегчает восприятие данных. Получается рейтинг — сразу видно, где значения максимальные и минимальные. Если в категории есть какая-то внутренняя иерархия (например, дни недели), то лучше сортировать в рамках неё, а не по количеству значений.
Вообще в барчартах можно показывать как положительные, так и отрицательные значения.
Барчарт с позитивными и негативными значениями (ТАСС)
Особенности. Столбчатые и линейчатые барчарты взаимозаменяемы: они выполняют одинаковую функцию. Единственный нюанс: если длинные названия категорий, лучше сделать горизонтальную диаграмму. Так для текста будет достаточно места, не придется его сокращать или переворачивать. Плюс читать так тоже сильно проще.
Так для текста будет достаточно места, не придется его сокращать или переворачивать. Плюс читать так тоже сильно проще.
Линейчатый барчарт с длинными названиями категорий (Infogram)
Важный момент: ось в барчарте всегда начинается с нуля. Читатель может ошибочно сравнить категории и сделать неправильные выводы, если обрезать столбцы — начать ось с большего значения.
Гистограмма (histogram)
Эта диаграмма внешне очень похожа на барчарт. Но она не сравнивает разные категории, а показывает распределение переменной. Каждый столбик — частотность в определенном интервале.
Для чего нужно. Визуализировать, как часто какие значения встречаются в наборе данных. Например, чтобы показать, какой размер обуви чаще покупают, по какой стоимости в основном продают дома, сколько времени чаще всего проводят на сайте.
Пример гистограммы (FlowingData) — она показывает, в каком возрасте женщины чаще всего впервые выходят замуж
Ещё примеры гистограмм (FlowingData). Они показывают средний доход в разных штатах
Они показывают средний доход в разных штатах
Особенности. Важно не путать гистограмму с барчартом. Дополнительные отличительные признаки:
- гистограмма всегда вертикальная;
- значения по оси X у гистограммы — последовательные;
- между столбцами обычно нет промежутка или он совсем небольшой — это показывает непрерывность числового ряда;
- чаще всего гистограмма работает с одной переменной, тогда как барчарт — с двумя: числовой и категориальной.
Пайчарт (круговая диаграмма)
Эта визуализация в виде круга, разделенного на несколько частей (секторов). Напоминает то, как мы режем круглый пирог — отсюда и название.
Пайчарт (Influencer Marketing Hub). Показывает результаты опроса: кто измеряет рентабельность инвестиций (ROI), а кто нет
Даже так — пайчарт в виде настоящей еды (Data-comics), который показывает, как pie chart переводится на разные языки
Для чего нужно. Чтобы показать доли от целого — пропорцию или процентное соотношение. С помощью пайчарта можно визуализировать соотношение мужчин и женщин, распределение по опыту (junior, middle, senior), результаты опроса по любимым видам кофе или структуру выручки в компании.
Чтобы показать доли от целого — пропорцию или процентное соотношение. С помощью пайчарта можно визуализировать соотношение мужчин и женщин, распределение по опыту (junior, middle, senior), результаты опроса по любимым видам кофе или структуру выручки в компании.
Пример пайчарта-бублика (Think with Google), который визуализирует результаты исследования — немного другая форма, но суть одна
Особенности. С круговыми диаграммами стоит быть осторожными: они красивые с точки зрения дизайна, но не всегда удобные для восприятия.
Из-за сложной формы кусочков «пирога» трудно сравнивать значения на глаз: разница между 70% и 30% будет очевидна, а между 53% и 47% — не совсем. Также в круг нельзя уместить слишком много значений — иначе доли получатся слишком тонкими, их будет совсем трудно различать, плюс будет мало места для подписей.
Ещё важный момент: сумма значений в пайчарте (донате) всегда должна быть 100%, так как диаграмма показывает доли от целого.
Пайчарт можно взять, если хотите визуализировать несколько долей со значительной разницей. В остальных случаях барчарт будет более репрезентативным.
В остальных случаях барчарт будет более репрезентативным.
Линейная диаграмма (line chart, график)
Линейная диаграмма строится по временной оси Х и каким-то значениям по оси Y.
Пример графика (ТАСС) — показывает изменение стоимости строительства «Зенит-Арены»
Для чего нужно. Это идеальный вариант, чтобы показать изменение какого-то показателя во времени. Можно визуализировать динамику трафика, продаж, цен и многих других переменных. Линия хорошо подсвечивает резкие изменения, отклонения.
График роста состояния миллиардеров (Т—Ж)
Особенности. Время всегда на горизонтальной оси и идет слева направо (от старого к новому).
Можно добавить несколько переменных, главное, не увлекаться количеством графиков и цветов. И аккуратнее с пропорциями: линейчатая диаграмма должна хорошо показывать какие-то резкие изменения.
Интересный пример (Datawrapper). Он показывает, сколько наборов Lego выпускали каждый год, а также как менялось среднее количество деталей в комплекте
Скаттерплот (scatter plot, диаграмма рассеяния)
График рассеяния (точечная диаграмма) показывает распределение элементов множества в плоскости между двумя переменными. Это позволяет увидеть возможные связи между ними.
Это позволяет увидеть возможные связи между ними.
Пример скаттерплота (Rockefeller Foundation). Он показывает связь между доходом и потреблением энергии на душу населения
Для чего нужно. Чтобы найти и визуализировать зависимость одной переменной от другой. И оценить силу корреляции через плотность точек на диаграмме. Так, можно определить, как связаны количество съеденных калорий и вес, расходы на рекламу и прямые заходы на сайт, просмотры и позиции в поиске.
Пример скаттерплота (Яндекс), который кодирует больше данных за счет цвета и размера точек. Главное, не увлекаться, иначе читателю будет сложно воспринимать информацию
Особенности. Независимую переменную стоит располагать на горизонтальной оси, а зависимую — на вертикальной.
Важно: correlation != causation. Наличие корреляции необязательно значит, что между переменными действительно есть зависимость. И что одна точно влияет на другую.
Диаграмма рассеяния (Swissinfo): чем выше в горах находится курорт, тем дороже стоит его абонемент
Поделиться
СВЕЖИЕ СТАТЬИ
Другие материалы из этой рубрики
Не пропускайте новые статьи
Подписывайтесь на соцсети
Делимся новостями и свежими статьями, рассказываем о новинках сервиса
Статьи почтой
Раз в неделю присылаем подборку свежих статей и новостей из блога. Пытаемся шутить, но получается не всегда
Пытаемся шутить, но получается не всегда
Наш юрист будет ругаться, если вы не примете 🙁
✓
Спасибо, ждите письмо.
Проверяйте почту — письмо придет в течение 5 минут (обычно мгновенно).
Как запустить email-маркетинг с нуля?
В бесплатном курсе «Rock-email» мы за 15 писем расскажем, как настроить email-маркетинг в компании. В конце каждого письма даем отбитые татуировки об email ⚡️
*Вместе с курсом вы будете получать рассылку блога Unisender
Оставляя свой email, я принимаю Политику конфиденциальностиНаш юрист будет ругаться, если вы не примете 🙁
Как строить линейные графики, гистограммы и диаграммы в Matplotlib
В прошлых материалах вы встречали примеры, демонстрирующие архитектуру библиотеки matplotlib. После знакомства с основными графическими элементами для графиков время рассмотреть примеры разных типов графиков, начиная с самых распространенных, таких как линейные графики, гистограммы и круговые диаграммы, и заканчивая более сложными, но все равно часто используемыми.
После знакомства с основными графическими элементами для графиков время рассмотреть примеры разных типов графиков, начиная с самых распространенных, таких как линейные графики, гистограммы и круговые диаграммы, и заканчивая более сложными, но все равно часто используемыми.
Поскольку визуализация — основная цель библиотеки, то этот раздел является очень важным. Умение выбрать правильный тип графика является фундаментальным навыком, ведь неправильная репрезентация может привести к тому, что данные, полученные в результате качественного анализа данных, будет интерпретированы неверно.
Для выполнения кода импортируйте pyplot и numpy
import matplotlib.pyplot as plt import numpy as np
Линейные графики
Линейные графики являются самыми простыми из всех. Такой график — это последовательность точек данных на линии. Каждая точка состоит из пары значений (x, y), которые перенесены на график в соответствии с масштабами осей (x и y).
В качестве примера можно вывести точки, сгенерированные математической функцией. Возьмем такую:
Возьмем такую: y = sin (3 * x) / x
Таким образом для создания последовательности точек данных нужно создать два массива NumPy. Сначала создадим массив со значениями x для оси x. Для определения последовательности увеличивающихся значений используем функцию np.arrange(). Поскольку функция синусоидальная, то значениями должны быть числа кратные π (np.pi). Затем с помощью этой последовательности можно получить значения y, применив для них функцию np.sin() (и все благодаря NumPy).
После этого остается лишь вывести все точки на график с помощью функции plot(). Результатом будет линейный график.
x = np.arange(-2*np.pi,2*np.pi,0.01) y = np.sin(3*x)/x plt.plot(x,y) plt.show()
Этот пример можно расширить для демонстрации семейства функций, например, такого (с разными значениями n):
x = np.arange(-2*np.pi,2*np.pi,0.01) y = np.sin(3*x)/x y2 = np.sin(2*x)/x y3 = np.sin(x)/x plt.plot(x,y) plt.plot(x,y2) plt.plot(x,y3) plt.show()
Как можно увидеть на изображении, каждой линии автоматически присваивается свой цвет. При этом все графики представлены в одном масштабе. Это значит, что точки данных связаны с одними и теми же осями x и y. Вот почему каждый вызов функции plot() учитывает предыдущие вызовы, так что объект Figure применяет изменения с учетом прошлых команд еще до вывода (для вывода используется show()).
x = np.arange(-2*np.pi,2*np.pi,0.01) y = np.sin(3*x)/x y2 = np.sin(2*x)/x y3 = np.sin(x)/x plt.plot(x,y,'k--',linewidth=3) plt.plot(x,y2,'m-.') plt.plot(x,y3,color='#87a3cc',linestyle='--') plt.show()
Как уже говорилось в прошлых в разделах, вне зависимости от настроек по умолчанию можно выбрать тип начертания, цвет и так далее. Третьим аргументом функции plot() можно указать коды цветов, типы линий и все этой в одной строке. Также можно использовать два именованных аргумента отдельно: color — для цвета и linestyle — для типа линии.
| Код | Цвет |
|---|---|
| b | голубой |
| g | зеленый |
| r | красный |
| c | сине-зеленый |
| m | пурпурный |
| y | желтый |
| k | черный |
| w | белый |
На графике определен диапазон от — 2π до 2π на оси x, но по умолчанию деления обозначены в числовой форме. Поэтому их нужно заменить на множители числа π. Также можно поменять делители на оси y. Для этого используются функции xticks() и yticks(). Им нужно передать список значений. Первый список содержит значения, соответствующие позициям, где деления будут находиться, а второй — их метки. В этом случае будут использоваться LaTeX-выражения, что нужно для корректного отображения π. Важно не забыть добавить знаки $ в начале и конце, а также символ r в качестве префикса.
x = np.arange(-2*np.pi,2*np.pi,0.01)
y = np.sin(3*x)/x
y2 = np.sin(2*x)/x
y3 = np.sin(x)/x
plt.plot(x,y,color='b')
plt.plot(x,y2,color='r')
plt.plot(x,y3,color='g')
plt.xticks([-2*np.pi,-np.pi,0, np.pi, 2*np.pi],
[r'$-2\pi$',r'$-\pi$',r'$0$',r'$+\pi$',r'$+2\pi$'])
plt.yticks([-1,0,1,2,3],
[r'$-1$',r'$0$',r'$+1$',r'$+2$',r'$+3$'])
plt.show()
Пока что на всех рассмотренных графиках оси x и y изображались на краях объекта Figure (по границе рамки). Но их же можно провести так, чтобы они пересекались — то есть, получит декартову система координат.
Для этого нужно сперва получить объект Axes с помощью функцию gca. Затем с его помощью можно выбрать любую из четырех сторон, создав область с границами и определив положение каждой: справа, слева, сверху и снизу. Ненужные части обрезаются (справа и снизу), а с помощью функции set_color() задается значение none. Затем стороны, которые соответствуют осям x и y, проходят через начало координат (0, 0) с помощью функции set_position().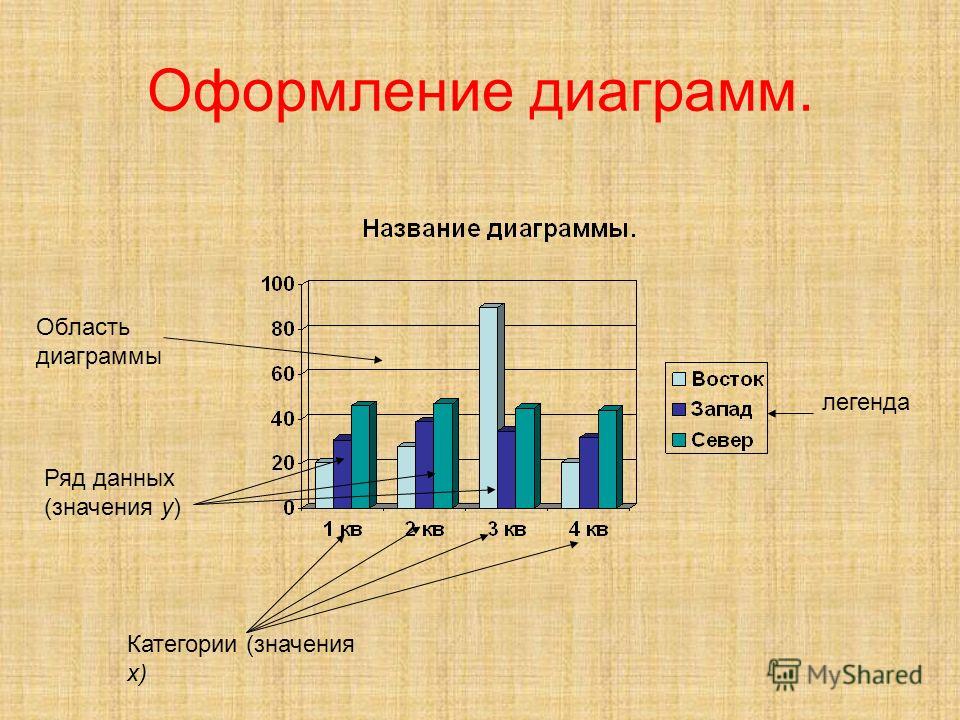
x = np.arange(-2*np.pi,2*np.pi,0.01)
y = np.sin(3*x)/x
y2 = np.sin(2*x)/x
y3 = np.sin(x)/x
plt.plot(x,y,color='b')
plt.plot(x,y2,color='r')
plt.plot(x,y3,color='g')
plt.xticks([-2*np.pi,-np.pi,0, np.pi, 2*np.pi],
[r'$-2\pi$',r'$-\pi$',r'$0$',r'$+\pi$',r'$+2\pi$'])
plt.yticks([-1,0,1,2,3],
[r'$-1$',r'$0$',r'$+1$',r'$+2$',r'$+3$'])
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.show()
Теперь график будет состоять из двух пересекающихся в центре осей, который представляет собой начало декартовой системы координат.
Также есть возможность указать на определенную точку с помощью дополнительных обозначений и стрелки. Обозначением может выступать LaTeX-выражение, например, формула предела функции sinx/x, стремящейся к 0.
Для этого в matplotlib есть функция annotate().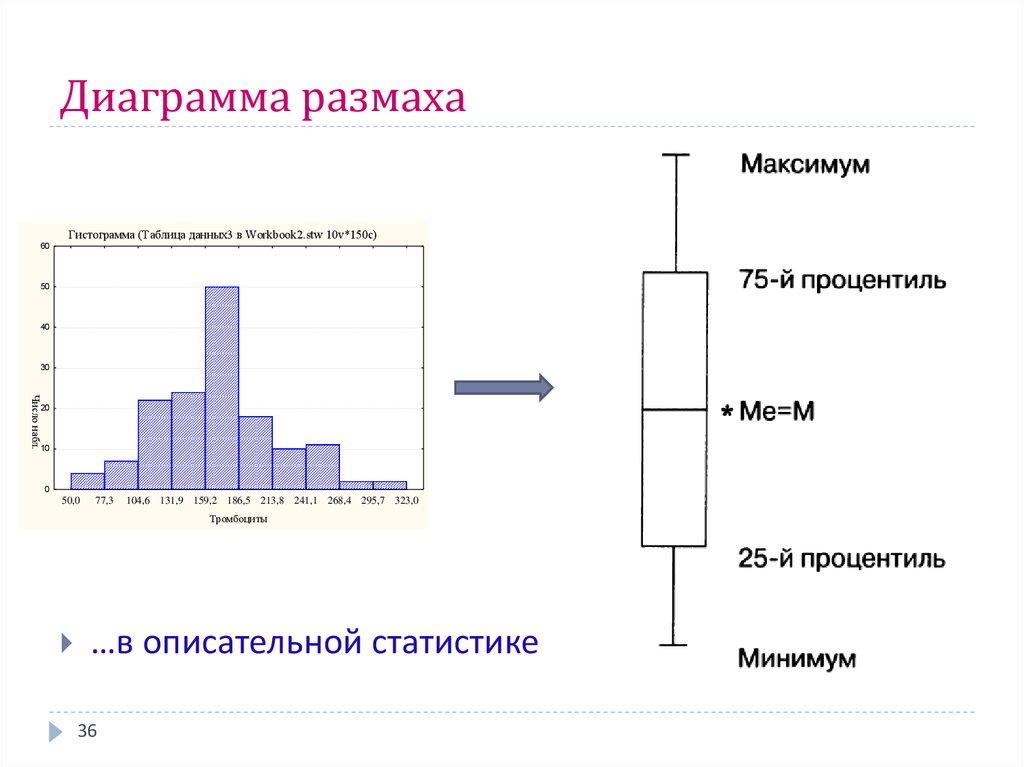 Ее настройка кажется сложной, но большое количество
Ее настройка кажется сложной, но большое количество kwargs обеспечивает требуемый результат. Первый аргумент — строка, представляющая собой LaTeX-выражение, а все остальные — опциональные. Точка, которую нужно отметить на графике представлена в виде списка, включающего ее координаты (x и y), переданные в аргумент xy. Расстояние заметки до точки определено в xytext, а стрелка — с помощью arrowprops.
x = np.arange(-2*np.pi,2*np.pi,0.01)
y = np.sin(3*x)/x
y2 = np.sin(2*x)/x
y3 = np.sin(x)/x
plt.plot(x,y,color='b')
plt.plot(x,y2,color='r')
plt.plot(x,y3,color='g')
plt.xticks([-2*np.pi,-np.pi,0, np.pi, 2*np.pi],
[r'$-2\pi$',r'$-\pi$',r'$0$',r'$+\pi$',r'$+2\pi$'])
plt.yticks([-1,0,1,2,3],
[r'$-1$',r'$0$',r'$+1$',r'$+2$',r'$+3$'])
plt.annotate(r'$\lim_{x\to 0}\frac{\sin(x)}{x}= 1$', xy=[0,1],xycoords='data',
xytext=[30,30],fontsize=16, textcoords='offset points', arrowprops=dict(arrowstyle="->",
connectionstyle="arc3,rad=.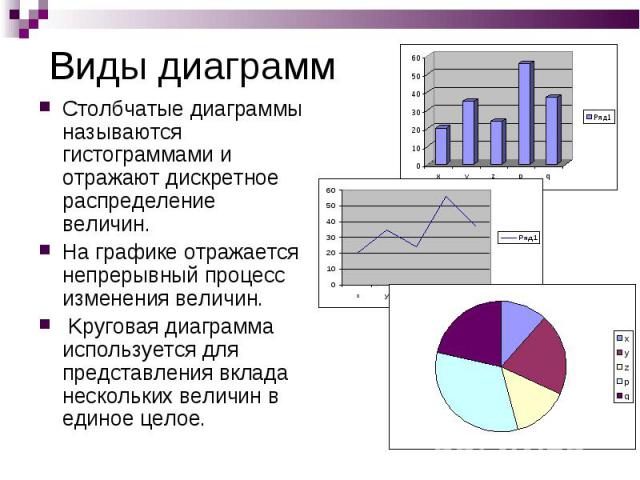 2"))
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.show()
2"))
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.show()
В итоге этот код сгенерирует график с математической формулой предела, представленной точкой, на которую указывает стрелка.
Линейные графики с pandas
Рассмотрим более практический и приближенный к анализу данных пример. С ним будет видно, насколько просто использовать библиотеку matplotlib для объектов Dataframe из библиотеки pandas. Визуализация данных в виде линейного графика — максимально простая задача. Достаточно передать объект в качестве аргумента функции plot() для получения графика с несколькими линиями.
import pandas as pd
data = {'series1':[1,3,4,3,5],
'series2':[2,4,5,2,4],
'series3':[3,2,3,1,3]}
df = pd.DataFrame(data)
x = np.arange(5)
plt.axis([0,5,0,7])
plt. plot(x,df)
plt.legend(data, loc=2)
plt.show()
plot(x,df)
plt.legend(data, loc=2)
plt.show()
Гистограммы
Гистограмма состоит из примыкающих прямоугольников, расположенных вдоль оси x, которые разбиты на дискретные интервалы, их называют bins. Их площадь пропорциональна частоте конкретного интервала. Такой способ визуализации часто используют в статистике для демонстрации распределения.
Для представления гистограммы в pyplot есть функция hist(). У нее также есть особенности, которых не найти у других функций, отвечающих за создание графиков. hist() не только рисует гистограмму, но также возвращает кортеж значений, представляющих собой результат вычислений гистограммы. Функция hist() может реализовывать вычисление гистограммы, чего достаточно для предоставления набора значений и количества интервалов, на которых их нужно разбить. Наконец hist() отвечает за разделение интервала на множество и вычисление частоты каждого. Результат этой операции не только выводится в графической форме, но и возвращается в виде кортежа.
Для понимания операции лучше всего воспользоваться практическим примером. Сгенерируем набор из 100 случайных чисел от 0 до 100 с помощью random.randint().
pop = np.random.randint(0,100,100) pop
array([33, 90, 10, 68, 18, 67, 6, 54, 32, 25, 90, 6, 48, 34, 59, 70, 37,
50, 86, 7, 49, 40, 54, 94, 95, 20, 83, 59, 33, 0, 81, 18, 26, 69,
2, 42, 51, 7, 42, 90, 94, 63, 14, 14, 71, 25, 85, 99, 40, 62, 29,
42, 27, 98, 30, 89, 21, 78, 17, 33, 63, 80, 61, 50, 79, 38, 96, 8,
85, 19, 76, 32, 19, 14, 37, 62, 24, 30, 19, 80, 55, 5, 94, 74, 85,
59, 65, 17, 80, 11, 81, 84, 81, 46, 82, 66, 46, 78, 29, 40])
Дальше создаем гистограмму из этих данных, передавая аргумент функции hist(). Например, нужно разделить данные на 20 интервалов (значение по умолчанию — 10 интервалов). Для этого используется именованный аргумент bin.
n, bin, patches = plt.hist(pop, bins=20) plt.show()
Столбчатые диаграммы
Еще один распространенный тип графиков — столбчатые диаграммы. Они похожа на гистограммы, но на оси x тут располагаются не числовые значения, а категории. В matplotlib для реализации столбчатых диаграмм используется функция
Они похожа на гистограммы, но на оси x тут располагаются не числовые значения, а категории. В matplotlib для реализации столбчатых диаграмм используется функция bin().
index = [0,1,2,3,4] values = [5,7,3,4,6] plt.bar(index,values) plt.show()
Всего нескольких строк кода достаточно для получения такой столбчатой диаграммы.
На последней диаграмме видно, что метки на оси x написаны под каждым столбцом. Поскольку каждый из них относится к отдельной категории, правильнее обозначать их строками. Для этого используется функция xticks(). А для правильного размещения нужно передать список со значениями позиций в качестве первого аргумента в той же функции. Результатом будет такая диаграмма.
index = np.arange(5) values1 = [5,7,3,4,6] plt.bar(index, values1) plt.xticks(index+0.4,['A','B','C','D','E']) plt.show()
Есть и множество других операций, которые можно выполнить для улучшения диаграммы. Каждая из них выполняется за счет добавления конкретного именованного аргумента в bar(). Например, можно добавить величины стандартного отклонения с помощью аргумента
Например, можно добавить величины стандартного отклонения с помощью аргумента yerr вместе с соответствующими значениями. Часто этот аргумент используется вместе с error_kw, который принимает друге аргументы, отвечающие за представление погрешностей. Два из них — это eColor, который определяет цвета колонок погрешностей и capsize — ширину поперечных линий, обозначающих окончания этих колонок.
Еще один именованный аргумент — alpha. Он определяет степень прозрачности цветной колонки. Его значением может быть число от 0 до 1, где 0 — полностью прозрачный объект.
Также крайне рекомендуется использовать легенду, за которую отвечает аргумент label.
Результат — следующая столбчатая диаграмма с колонками погрешностей.
index = np.arange(5)
values1 = [5,7,3,4,6]
std1 = [0.8,1,0.4,0.9,1.3]
plt.title('A Bar Chart')
plt.bar(index, values1, yerr=std1, error_kw={'ecolor':'0.1','capsize':6},alpha=0.7,label='First')
plt.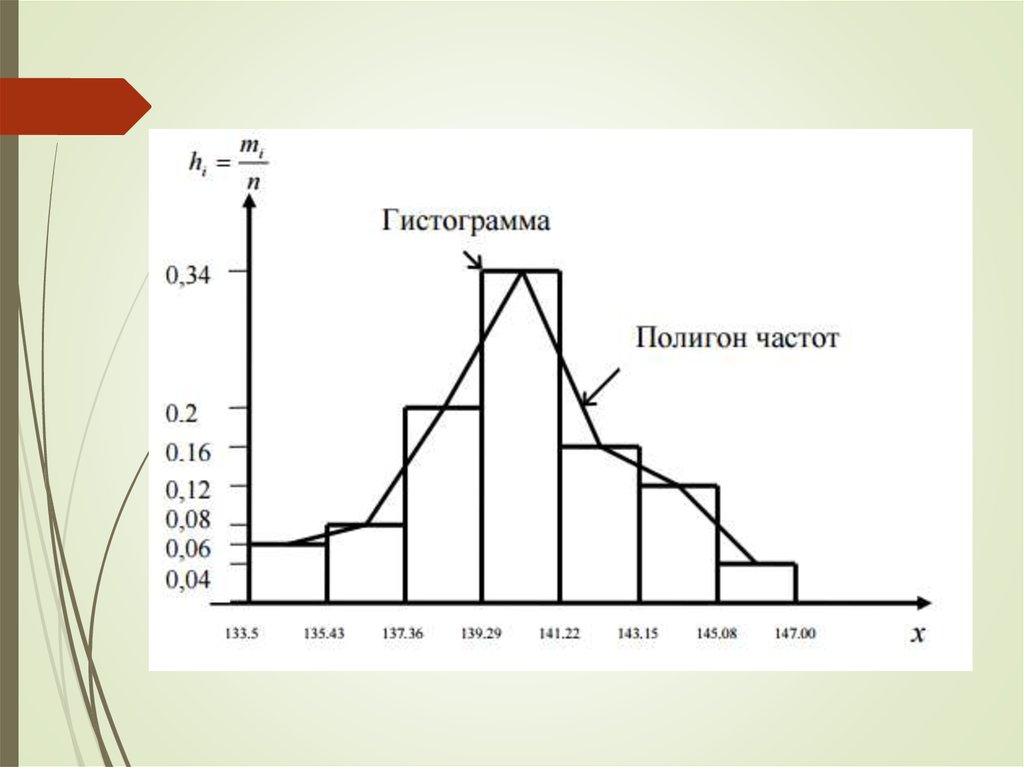 xticks(index+0.4,['A','B','C','D','E'])
plt.legend(loc=2)
plt.show()
xticks(index+0.4,['A','B','C','D','E'])
plt.legend(loc=2)
plt.show()
Горизонтальные столбчатые диаграммы
В предыдущем разделе столбчатая диаграмма была вертикальной. Но блоки могут располагаться и горизонтально. Для этого режима есть специальная функция barh(). Аргументы и именованные аргументы, которые использовались для bar() будут работать и здесь. Единственное изменение в том, что поменялись роли осей. Категории теперь представлены на оси y, а числовые значения — на x.
index = np.arange(5)
values1 = [5,7,3,4,6]
std1 = [0.8,1,0.4,0.9,1.3]
plt.title('A Horizontal Bar Chart')
plt.barh(index, values1, xerr=std1, error_kw={'ecolor':'0.1','capsize':6},alpha=0.7,label='First')
plt.yticks(index+0.4,['A','B','C','D','E'])
plt.legend(loc=5)
plt.show()
Многорядные столбчатые диаграммы
Как и линейные графики, столбчатые диаграммы широко используются для одновременного отображения больших наборов данных. Но в случае с многорядными работает особая структура.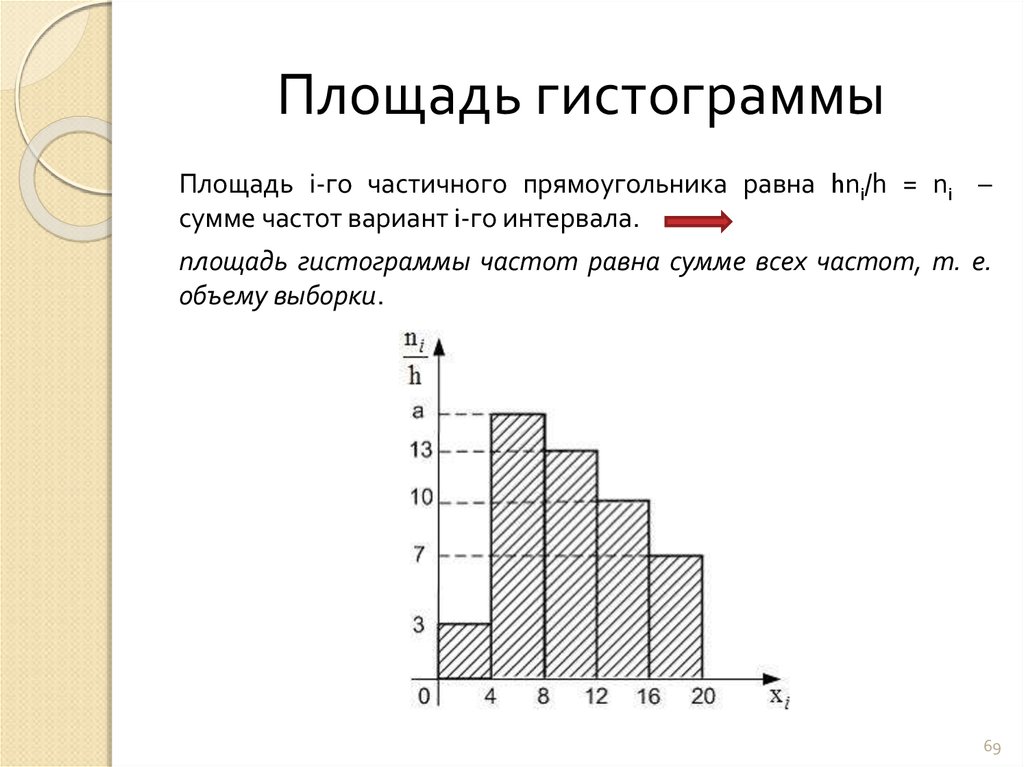 До сих пор во всех примерах определялись последовательности индексов, каждый из которых соответствует столбцу, относящемуся к оси x. Индексы представляют собой и категории. В таком случае столбцов, которые относятся к одной и той же категории, даже больше.
До сих пор во всех примерах определялись последовательности индексов, каждый из которых соответствует столбцу, относящемуся к оси x. Индексы представляют собой и категории. В таком случае столбцов, которые относятся к одной и той же категории, даже больше.
Один из способов решения этой проблемы — разделение пространства индекса (для удобства его ширина равна 1) на то количество столбцов, которые к нему относятся. Также рекомендуется добавлять пустое пространство, которое будет выступать пропусками между категориями.
index = np.arange(5)
values1 = [5,7,3,4,6]
values2 = [6,6,4,5,7]
values3 = [5,6,5,4,6]
bw = 0.3
plt.axis([0,5,0,8])
plt.title('A Multiseries Bar Chart', fontsize=20)
plt.bar(index, values1, bw, color='b')
plt.bar(index+bw, values2, bw, color='g')
plt.bar(index+2*bw, values3, bw, color='r')
plt.xticks(index+1.5*bw,['A','B','C','D','E'])
plt.show()
В случае с горизонтальными многорядными столбчатыми диаграммами все работает по тому же принципу. Функцию bar() нужно заменить на соответствующую barh(), а также не забыть заменить xticks() на yticks(). И нужно развернуть диапазон значений на осях с помощью функции
И нужно развернуть диапазон значений на осях с помощью функции axis().
index = np.arange(5)
values1 = [5,7,3,4,6]
values2 = [6,6,4,5,7]
values3 = [5,6,5,4,6]
bw = 0.3
plt.axis([0,8,0,5])
plt.title('A Multiseries Bar Chart', fontsize=20)
plt.barh(index, values1, bw, color='b')
plt.barh(index+bw, values2, bw, color='g')
plt.barh(index+2*bw, values3, bw, color='r')
plt.yticks(index+0.4,['A','B','C','D','E'])
plt.show()
Многорядные столбчатые диаграммы с Dataframe из pandas
Как и в случае с линейными графиками matplotlib предоставляет возможность представлять объекты Dataframe с результатами анализа данных в форме столбчатых графиков. В этом случае все происходит даже быстрее и проще. Нужно лишь использовать функцию plot() по отношению к объекту Dataframe и указать внутри именованный аргумент kind, ему требуется присвоить тип графика, который будет выводиться. В данном случае это bar. Без дополнительных настроек результат должен выглядеть как на следующем изображении.
import pandas as pd
index = np.arange(5)
data = {'series1': [1,3,4,3,5],
'series2': [2,4,5,2,4],
'series3': [3,2,3,1,3]}
df = pd.DataFrame(data)
df.plot(kind='bar')
plt.show()
Но для еще большего контроля (или просто при необходимости) можно брать части Dataframe в виде массивов NumPy и описывать их так, как в предыдущем примере. Для этого каждый нужно передать в качестве аргумента функциям matplotlib.
К горизонтальной диаграмме применимы те же правила, но нужно не забыть указать значение barh для аргумента kind. Результатом будет горизонтальная столбчатая диаграмма как на следующем изображении.
Многорядные сложенные столбчатые графики
Еще один способ представления многорядного столбчатого графика — сложенная форма, где каждый столбец установлен поверх другого. Это особенно полезно в том случае, когда нужно показать общее значение суммы всех столбцов.
Для превращения обычного многорядного столбчатого графика в сложенный нужно добавить именованный аргумент bottom в каждую функцию bar(). Каждый объект
Каждый объект Series должен быть присвоен соответствующему аргументу bottom. Результатом будет сложенный столбчатый график.
series1 = np.array([3,4,5,3])
series2 = np.array([1,2,2,5])
series3 = np.array([2,3,3,4])
index = np.arange(4)
plt.axis([-0.5,3.5,0,15])
plt.title('A Multiseries Stacked Bar Chart')
plt.bar(index,series1,color='r')
plt.bar(index,series2,color='b',bottom=series1)
plt.bar(index,series3,color='g',bottom=(series2+series1))
plt.xticks(index,['Jan18','Feb18','Mar18','Apr18'])
plt.show()
Здесь для создания аналогичного горизонтального графика нужно заменить bar() на barh(), не забыв про остальные параметры. Функцию xticks() необходимо поменять местами с yticks(), потому что метки категорий теперь будут расположены по оси y. После этого будет создан следующий горизонтальный график.
series1 = np.array([3,4,5,3]) series2 = np.array([1,2,2,5]) series3 = np.array([2,3,3,4]) index = np.arange(4) plt.axis([0,15,-0.5,3.5]) plt.title('A Multiseries Horizontal Stacked Bar Chart') plt.barh(index,series1,color='r') plt.barh(index,series2,color='b',left=series1) plt.barh(index,series3,color='g',left=(series2+series1)) plt.yticks(index,['Jan18','Feb18','Mar18','Apr18']) plt.show()
До сих пор объекты Series разделялись только по цветам. Но можно использовать, например, разную штриховку. Для этого сперва необходимо сделать цвет столбца белым и использовать именованный аргумент hatch для определения типа штриховки. Все они выполнены с помощью символов (|, /, -, \, *), соответствующих стилю столбца. Чем чаще он повторяется, тем теснее будут расположены линии. Так, /// — более плотный вариант чем //, а этот, в свою очередь, плотнее /.
series1 = np.array([3,4,5,3])
series2 = np.array([1,2,2,5])
series3 = np.array([2,3,3,4])
index = np.arange(4)
plt.axis([0,15,-0.5,3.5])
plt.title('A Multiseries Horizontal Stacked Bar Chart')
plt. barh(index,series1,color='w',hatch='xx')
plt.barh(index,series2,color='w',hatch='///',left=series1)
plt.barh(index,series3,color='w',hatch='\\\\\\',left=(series2+series1))
plt.yticks(index,['Jan18','Feb18','Mar18','Apr18'])
plt.show()
barh(index,series1,color='w',hatch='xx')
plt.barh(index,series2,color='w',hatch='///',left=series1)
plt.barh(index,series3,color='w',hatch='\\\\\\',left=(series2+series1))
plt.yticks(index,['Jan18','Feb18','Mar18','Apr18'])
plt.show()
Сложенные столбчатые графики с Dataframe из padans
В случае со сложенными столбчатыми графиками очень легко представлять значения объектов Dataframe с помощью функции plot(). Нужно лишь добавить в качестве аргумента stacked со значением True.
import pandas as pd
data = {'series1': [1,3,4,3,5],
'series2': [2,4,5,2,4],
'series3': [3,2,3,1,3]}
df = pd.DataFrame(data)
df.plot(kind='bar',stacked=True)
plt.show()
Другие представления столбчатых графиков
Еще один удобный тип представления данных в столбчатом графике — с использованием двух Series из одних и тех же категорий, где они сравниваются путем размещения друг напротив друга вдоль оси y. Для этого нужно разместить значения y одного из графиков в отрицательной форме. Также в этом примере показано, как поменять внутренний цвет другим способом. Это делается с помощью задания значения для аргумента
Также в этом примере показано, как поменять внутренний цвет другим способом. Это делается с помощью задания значения для аргумента facecolor.
Также вы увидите, как добавить значение y с меткой в конце каждого столбца. Это поможет улучшить читаемость всего графика. Это делается с помощью цикла for, в котором функция text() показывает значение y. Настроить положение метки можно с помощью именованных аргументов ha и va, которые контролируют горизонтальное и вертикальное выравнивание соответственно. Результатом будет следующий график.
x0 = np.arange(8)
y1 = np.array([1,3,4,5,4,3,2,1])
y2 = np.array([1,2,5,4,3,3,2,1])
plt.ylim(-7,7)
plt.bar(x0,y1,0.9, facecolor='g')
plt.bar(x0,-y2,0.9,facecolor='b')
plt.xticks(())
plt.grid(True)
for x, y in zip(x0, y1):
plt.text(x, y + 0.05, '%d' % y, ha='center', va = 'bottom')
for x, y in zip(x0, y2):
plt.text(x, -y - 0.05, '%d' % y, ha='center', va = 'top')
plt.show()
Круговая диаграмма
Еще один способ представления данных — круговая диаграмма, которую можно получить с помощью функции pie().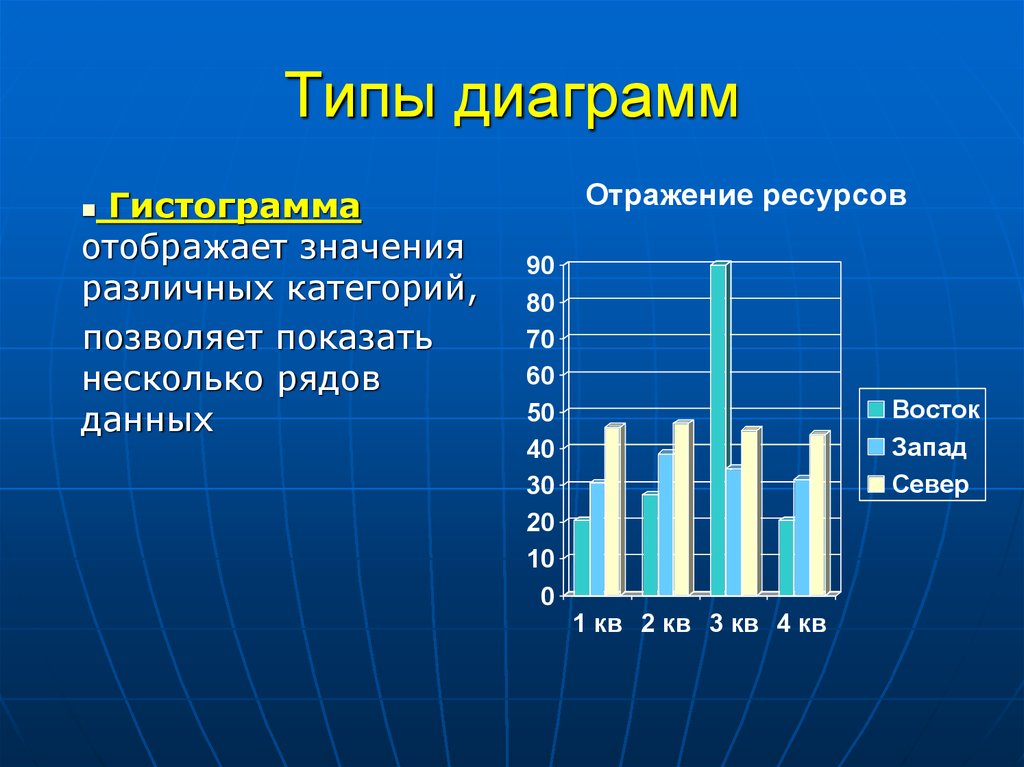
Даже для нее нужно передать основной аргумент, представляющий собой список значений. Пусть это будут проценты (где максимально значение — 100), но это может быть любое значение. А уже сама функция определит, сколько будет занимать каждое значение.
Также в случае с этими графиками есть другие особенности, которые определяются именованными аргументами. Например, если нужно задать последовательность цветов, используется аргумент colors. В таком случае придется присвоить список строк, каждая из которых будет содержать название цвета. Еще одна возможность — добавление меток каждой доле. Для этого есть labels, которой присваивает список строк с метками в последовательности.
А чтобы диаграмма была идеально круглой, необходимо в конце добавить функцию axix() со строкой equal в качестве аргумента. Результатом будет такая диаграмма.
labels = ['Nokia','Samsung','Apple','Lumia'] values = [10,30,45,15] colors = ['yellow','green','red','blue'] plt.pie(values,labels=labels,colors=colors) plt.axis('equal') plt.show()
Чтобы сделать диаграмму более сложной, можно «вытащить» одну из частей. Обычно это делается с целью акцентировать на ней внимание. В этом графике, например, для выделения Nokia. Для этого используется аргумент explode. Он представляет собой всего лишь последовательность чисел с плавающей точкой от 0 до 1, где 1 — положение целиком вне диаграмма, а 0 — полностью внутри. Значение между соответствуют среднему градусу извлечения.
Заголовок добавляется с помощью функции title(). Также можно настроить угол поворота с помощью аргумента startangle, который принимает значение между 0 и 360, обозначающее угол поворота (0 – значение по умолчанию). Следующий график показывает все изменения.
labels = ['Nokia','Samsung','Apple','Lumia']
values = [10,30,45,15]
colors = ['yellow','green','red','blue']
explode = [0.3,0,0,0]
plt.title('A Pie Chart')
plt.pie(values,labels=labels,colors=colors,explode=explode,startangle=180)
plt. axis('equal')
plt.show()
axis('equal')
plt.show()
Но и это не все, что может быть на диаграмме. У нее нет осей, поэтому сложно передать точное разделение. Чтобы решить эту проблему, можно использовать autopct, который добавляет в центр каждой части текст с соответствующим значением.
Чтобы сделать диаграмму еще более привлекательной визуально, можно добавить тень с помощью shadow со значением True. Результат — следующее изображение.
labels = ['Nokia','Samsung','Apple','Lumia']
values = [10,30,45,15]
colors = ['yellow','green','red','blue']
explode = [0.3,0,0,0]
plt.title('A Pie Chart')
plt.pie(values,labels=labels,colors=colors,explode=explode,shadow=True,autopct='%1.1f%%',startangle=180)
plt.axis('equal')
plt.show()
Круговые диаграммы с Dataframe из pandas
Даже в случае с круговыми диаграммами можно передавать значения из Dataframe. Однако каждая диаграмма будет представлять собой один Series, поэтому в примере изобразим только один объект, выделив его через df['series1'].
Указать тип графика можно с помощью аргумента kind в функции plot(), который в этом случае получит значение pie. Также поскольку он должен быть идеально круглым, обязательно задать figsize. Получится следующая диаграмма.
import pandas as pd
data = {'series1': [1,3,4,3,5],
'series2': [2,4,5,2,4],
'series3': [3,2,3,1,3]}
df = pd.DataFrame(data)
df['series1'].plot(kind='pie', figsize=(6,6))
plt.show()
Фотография и гистограмма, определение, гистограмма в фотоаппарате, гистограмма в Adobe Photoshop и Lightroom, недоэкспонированная, переэкспонированный, нормальная гистограмма
Содержание
- Вид — гистограмма
- Гистограмма в фотографии что это такое и как её читать
- Для чего нужна гистограмма кадра
- Другие виды диаграмм
- Столбиковая диаграмма
- Полосовая диаграмма
- Квадратная диаграмма
- Круговая диаграмма
- Секторная диаграмма
- Треугольная диаграмма
- Вид — гистограмма
- Пример гистограммы в условном форматировании
- Гистограмма
Вид — гистограмма
Вид гистограммы зависит от объема выборки, количества интервалов, начала отсчета первого интервала.
|
Статистическая и теоретическая функции распределения случайной. |
По виду гистограммы и графика статистической функции распределения выдвигают гипотезу о законе распределения случайной величины, которую затем проверяют. Прежде всего проверку осуществляют графически путем сопоставления статистической и теоретической функций распределения. На рис. 3 значения статистической функции распределения даны кружками, теоретической — сплошной линией. Графическое сравнение наглядно показывает степень совпадения статистической и теоретической функций распределения. Однако графический способ дает возможность только качественно сопоставить распределения. Для количественной оценки согласия статистического и теоретического распределения используют критерии согласия А. Н. Колмогорова и Пирсона.
|
Гистограмма результатов химического ана. |
Этому виду гистограммы отвечает достаточно представительная выборка результатов анализа, часть из которых отягощена систематической ошибкой, а другая часть лишена ее.
Этому виду гистограммы отвечает достаточно представительная выборка результатов анализа, часть из которых отягощена систематической погрешностью, а другая часть лишена ее. Другой пример — многократный эмиссионный спектральный анализ образца, в ходе которого часть определений проведена с использованием угольных электродов одной, а вторая часть — другой марки. Разность значений A i, 2 2 — х может служить в этих примерах мерой систематической погрешности.
|
Гистограмма результатов химического анализа для случая, когда часть результатов отягощена систематической ошибкой. |
Этому виду гистограммы отвечает достаточно представительная выборка результатов анализа, часть из которых отягощена систематической ошибкой, а другая часть лишена ее.
Она имеет вид гистограммы, на которой даны результаты испытаний последних заправок из серии смесей одного шифра. Данные приведены по порядку номеров заправок; результат испытаний последней заправки приводится в самом низу гистограммы. Нет необходимости испытывать смеси в той последовательности, в которой их приготовляют, так как компьютер перестраивает данные и представляет их по порядку номеров.
Данные приведены по порядку номеров заправок; результат испытаний последней заправки приводится в самом низу гистограммы. Нет необходимости испытывать смеси в той последовательности, в которой их приготовляют, так как компьютер перестраивает данные и представляет их по порядку номеров.
|
Гистограммы, построенные по экспериментальным данным. |
Иногда по виду гистограммы можно с большой уверенностью заключить, что результат измерения подчиняется ( или не подчиняется) нормальному закону распределения вероятности. Если, например, гистограмма имеет вид, показанный на рис. 41, а, то результат измерения определенно не подчиняется нормальному закону. Если же гистограмма имеет вид, показанный на рис. 41, б, то возникает сомнение: достаточно ли хорошо она соответствует теоретической кривой нормального закона распределения плотности вероятности, показанной пунктиром. Для разрешения этого сомнения нужно иметь правило, руководствуясь которым можно было бы принимать то или иное решение.
Цилиндричес — Имеют вид гистограммы со столбцами цилиндрической, конической ] кая ( Cylinder), и пирамидальной формы. Позволяют существенно улучшить внешний i коническая вид и наглядность объемной диаграммы.
Индикатор изображается в виде гистограмм, отдельно сила быков и отдельно медведей.
Например, если по виду гистограммы можно заключить, что случайные погрешности подчиняются равномерному закону распределения вероятностей, то зависимость между А и о определяется следующим образом.
Объем обычно изображают в виде гистограммы — ряда столбиков, высота которых отражает ежедневные объемы. Обычно его рисуют ниже цен.
Гистограмма в фотографии что это такое и как её читать
Фотография для начинающих. Семь шагов по улучшению резкости фотоснимков
3 апреля 2012
Искандер Рубинин
Гистограмма (в фотографии) — это график распределения полутонов изображения, в котором по горизонтальной оси представлена яркость, а по вертикали — относительное число пикселов с данным значением яркости.
Гистограмма всех цветовых каналов
Изучив гистограмму, можно получить общее представление о правильности экспозиции, контрасте и цветовом насыщении снимка, оценить требуемую коррекцию как при съёмке (изменение экспозиции, цветового баланса, освещения либо композиции снимка), так и при последующей обработке.
Обычно на экране цифрового фотоаппарата показывается лишь гистограмма светлоты (исключения составляют дорогостоящие зеркальные камеры), а гистограмма для всех цветовых каналов доступна уже на компьютере, в приложениях для обработки растровой графики. К примеру, в Adobe Photoshop.
В общем случае гистограмма изображения не описывает художественных качеств изображения (например, съёмка силуэта в контровом свете будет на гистограмме выглядеть как недосвеченное (или пересвеченное) изображение), но в большинстве случаев позволяет ориентироваться в «направлении коррекции» изображения (если таковая коррекция требуется).
Многие фоторедакторы (напр. Adobe Photoshop, GIMP) и программы проявки RAW-файлов (UFRAW, PhotoOne, CaptureNX) позволяют осуществлять редактирование уровней изображения. Оно может производиться следующими методами:
Оно может производиться следующими методами:
• Сопоставлением пяти параметров: начального и конечного диапазона начального и итоговых изображений и показателем гамма-кривой (в Photoshop — панель Levels).
Гистограмма уровня света, тени, полутонов
• Заданием кривой функции соответствия точек начальной и конечной гистограмм изображения (функция задаётся чаще всего с помощью точек, через которых производится аппроксимация функции, обычно сплайнами) (в Photoshop — панель Curves).
Корректировка изображения с помощью кривых на гистограмме
• Заданием набора предустановок, осуществляющих ту или иную коррекцию.
• В автоматическом режиме (программа пытается добиться максимума по одному из параметров, например, по максимизации площади кривой)
Часть фотоаппаратов позволяет просматривать гистограмму изображения для отснятых снимков (а некоторые модели с контрастной фокусировкой — и во время фокусировки).
Похожим образом обстоит ситуация с характеристиками изображения — надо просто знать, что оно бывает 8-битным или 16-битным, кодировано в JPEG или RAW, иметь определенное количество пикселов разной яркости в трех цветовых каналах.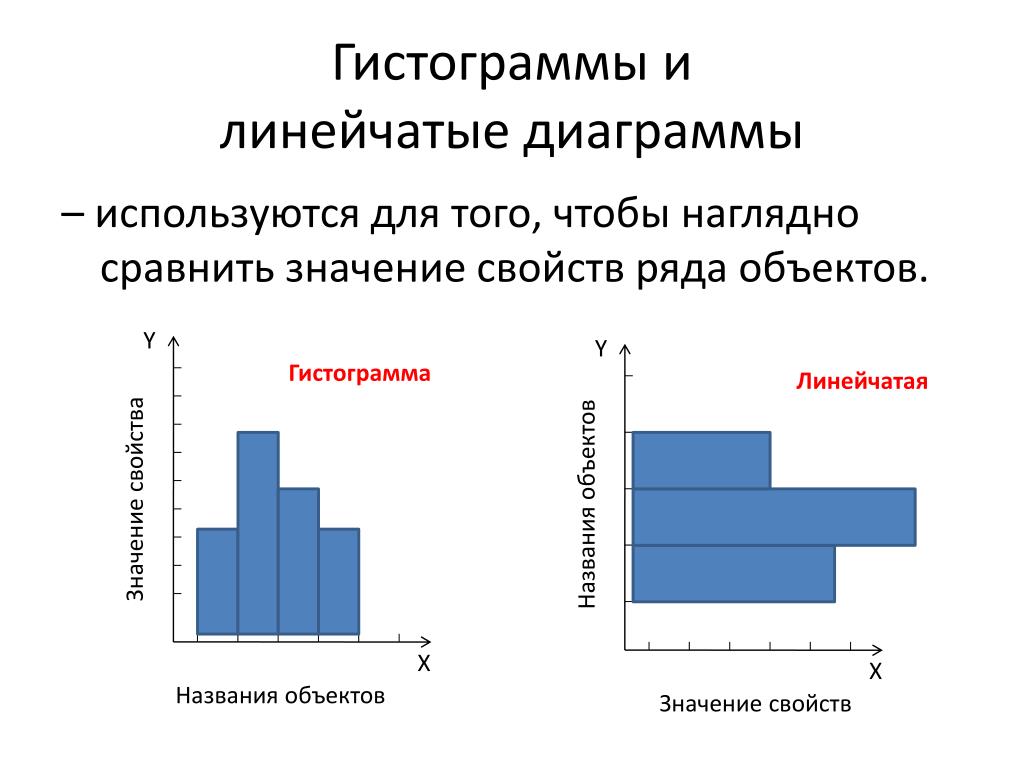 И если первые две характеристики позволяют только два варианта (+ или -), то третья огромное множество — для стандартного изображения это 256 градаций яркости от черного к белому в каждом из трех основных каналов (красный, зеленый, синий, если вы не в курсе) для каждого пиксела. Другими словами, отклониться с пути здесь гораздо проще, чем на неизвестной местности, хотя и с куда меньшим риском для жизни, так что поле для экспериментов тоже открывается огромное.
И если первые две характеристики позволяют только два варианта (+ или -), то третья огромное множество — для стандартного изображения это 256 градаций яркости от черного к белому в каждом из трех основных каналов (красный, зеленый, синий, если вы не в курсе) для каждого пиксела. Другими словами, отклониться с пути здесь гораздо проще, чем на неизвестной местности, хотя и с куда меньшим риском для жизни, так что поле для экспериментов тоже открывается огромное.
Если же подъемы графика смещены относительно центра гистограммы влево или вправо, то фотография отличается слишком темными или засвеченными участками. Конечно, следует отдать должное гистограмме — она способна характеризовать изображение, но стремиться всегда к определенному ее виду, даже если глаза, глядя на изображение, с нужным вам идеальным обликом гистограммы в корне не согласны, наверное, не стоит. К примеру, ниже показана фотография с нормальной гистограммой, в которой свет и тени сбалансированы.
Свет и тени на гистограмме для этого фото сбалансированы
Ниже, мы можем наблюдать пример фотографии сделанной в «высоком ключе» (преобладание света на гистограмме). Однако, эта фотография является исключением потому что если смотреть исключительно на гистограмму, создастся впечатление, что фото пересвечено. Однако, мы видим, что это не так.
Однако, эта фотография является исключением потому что если смотреть исключительно на гистограмму, создастся впечатление, что фото пересвечено. Однако, мы видим, что это не так.
Гистограмма показывает преобладание светлых тонов на фото
Ещё одним примером того, что не стоит полагаться только лишь на гистограмму, является ночная съёмка.
Гистограмма с преобладанием теней
Для чего нужна гистограмма кадра
Значение ЭЛЕКТРОННАЯ ФОТОГРАФИЯ в Большой советской энциклопедии, БСЭ
Для чего же она нужна, и как читать гистограмму? Благодаря данному графику мы можем безошибочно определить, темный кадр или пересвечен.
Прежде всего, надо освоить три важных параметра. Света–это наиболее светлые участки, и располагаются на графике справа. Второй параметр – это тени, соответственно – самые темные, на графике – слева. Ну и полутона — это нейтрально- серые цвета, которые находятся по центру гистограммы. Только здесь надо понимать, что речь идет не о цветах, а о их яркости, поэтому к примеру, оранжевый цвет относится к полутонам.
В некоторых графических редакторах, таких как «лайтрум» или «фотошоп», мы можем поправить экспозицию за счет гистограммы.
Изображение до коррекции гистограммы
Если мы откроем график в одной из этих программ, то увидим три ползунка, которые и отвечают за коррекцию трех основных параметров яркости. Двигая вправо черный ползунок, находящийся в левом нижнем углу, можно заметить, что тени на изображении становятся темнее. При движении светлого ползунка влево, картинка светлеет.
Изображение после коррекции гистограммы
А вот если сдвигать оба треугольника навстречу друг другу, мы получим более контрастную фотографию. Центральную стрелочку мы сдвигаем, если хотим проработать полутона.
кадр недоэкспонирован
Гистограмма на самом фотоаппарате не позволяет так кардинально изменить изображение, но сообщает о недостатках снимка. Когда вы производите фотосъемку при полуденном, ярком солнце, очень сложно рассмотреть на снимке количество пересветов или теней. Здесь просто необходима гистограмма, находящаяся в настройках фотокамеры. Если график на гистограмме смещен влево, то это означает, что кадр недоэкспонированный, нам поможет поправка экспозиции или увеличение длины выдержки.
Здесь просто необходима гистограмма, находящаяся в настройках фотокамеры. Если график на гистограмме смещен влево, то это означает, что кадр недоэкспонированный, нам поможет поправка экспозиции или увеличение длины выдержки.
кадр переэкспонирован
Аналогично, если смещение происходит вправо, то снимок пересвечен. Стоит поправить экспозицию, уменьшить выдержку или чуть прикрыть диафрагму.
Хорошая экспозиция кадра
В идеальном состоянии гистограмма должна выглядеть так, что столбики должны постепенно увеличиваться к центру гистограммы, и также плавно уменьшаться. В таких снимках не произойдет потери света и потери яркости и не будет преобладание темных участков.
Хорошая экспозиция кадра
Но идеальных графиков практически не бывает. Очень многое зависит от задачи и цели фотографа, что именно он хочет получить в итоге на изображении. Стоит лишь запомнить одно правило, что излишне темный кадр очень просто исправить, а вот «пересвеченное» изображение придется долго дорабатывать.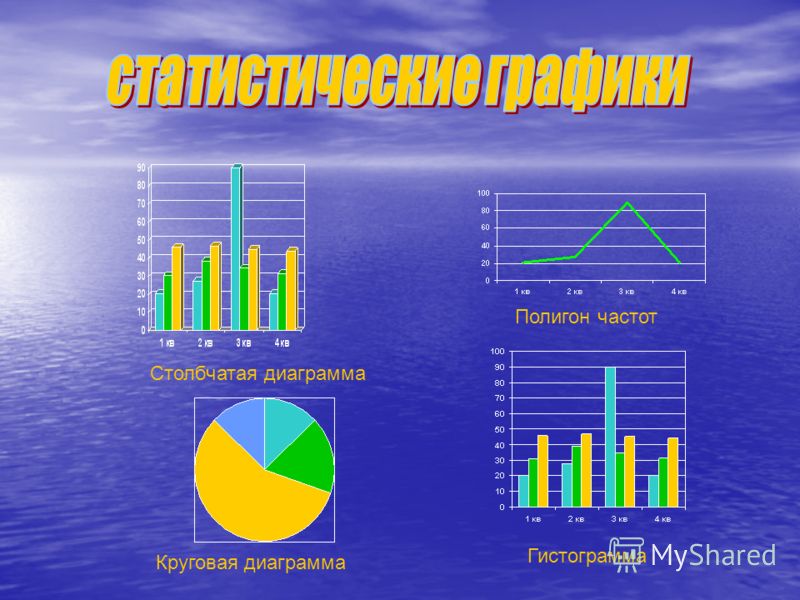
Другие виды диаграмм
Столбиковая диаграмма
Портретная фотография. Удаляем морщины с освещением «бабочка»
Среди плоскостных диаграмм наибольшее распространение получили столбиковые, полосовые или ленточные, треугольные, квадратные, круговые, секторные, фигурные.
Столбиковые диаграммы изображаются в виде прямоугольников (столбиков), вытянутых по вертикали, высота которых соответствует значению показателя (рис. 6.9).
Полосовая диаграмма
Принцип построения полосовых диаграмм тот же, что и столбиковых. Отличие заключается в том, что полосовые (или ленточные) графики представляют значение показателя не по вертикальной, а по горизонтальной оси.
Оба вида диаграмм применяются для сравнения не только самих величин, но и их частей. Для изображения структуры совокупности строят столбики (полосы) одинакового размера, принимая целое за 100%, а величину частей целого — соответствующей удельным весам (рис. 6.10).
Для изображения показателей с противоположным содержанием (импорт и экспорт, сальдо положительное и отрицательное, возрастная пирамида) строят разнонаправленные столбиковые или полосовые диаграммы.
Основу квадратных, треугольных и круговых диаграмм составляет изображение значения показателя величиной площади геометрической фигуры.
Квадратная диаграмма
Для построения квадратной диаграммы устанавливают размер стороны квадрата путем извлечения корня квадратного из значения показателя.
Так, например, для построения диаграммы на рис. 6.11 из объема услуг связи за 1997 г. в России по отправлению телеграмм (73 млн.), пенсионных выплат (392 млн.), посылок (24 млн.) квадратные корни составили соответствено 8,5; 19,8; 4,9.
Круговая диаграмма
Круговые диаграммы строятся в виде площади кругов, радиусы которых равны корню квадратному из значений показателя.
Секторная диаграмма
Для изображения структуры (состава) совокупности используются секторные диаграммы. Круговая секторная диаграмма строится путем разделения круга на секторы пропорционально удельному весу частей в целом. Размер каждого сектора определяется величиной угла расчета (1% соответствует 3,6).
Пример. Доля продовольственных товаров в объеме розничного товарооборота России составила в 1992 г. 55%, а в 1997 г. — 49%, доля непродовольственных товаров составила соответственно 45% и 51%.
Построим два круга одинакового радиуса, а для изображения секторов определим центральные углы: для продовольственных товаров 3,6*55 = 198, 3,6*49 = 176,4; для непродовольственных товаров 3,6*45 = 162; 3,6*51 = 183,6. Разделим круги на соответствующие секторы (рис. 6.12).
Треугольная диаграмма
Разновидностью диаграмм, представляющих структуру (кроме столбиковых и полосовых), является диаграмма треугольная. Она применяется для одновременного изображения трех величин, изображающих элементы или составные части целого. Треугольная диаграмма представляет собой равносторонний треугольник, каждая сторона которого является равномерной масштабной шкалой от 0 до 100. Внутри строится координатная сетка, соответствующая линиям, проводимым параллельно сторонам треугольника. Перпендикуляры из любой точки координатной сетки представляют доли трех компонентов, соответствует в сумме 100% (рис. 6.13). Точка на графике соответствует 20% (по А), 30% (по В) и 50% (по С).
6.13). Точка на графике соответствует 20% (по А), 30% (по В) и 50% (по С).
Рис. 6.13. Треугольная диаграмма
Вид — гистограмма
Сила быков отображается в виде гистограммы во втором окне. Высота этой гистограммы зависит от расстояния между вершиной ценового столбика и ЕМА — это и есть максимальная сила быков. Гистограмма в третьем окне отражает максимальную силу медведей. Ее глубина соответствует расстоянию от нижней точки ценового столбика до ЕМА.
На рис. 2 в виде гистограммы изображен ряд распределения рабочих по коэффициенту эффективности труда. По вертикальной оси указывается число рабочих, имеющих коэффициент эффективности труда в соответствующем интервале. На основании отрезков по горизонтальной оси строится ряд прямоугольников с высотой, равной числу рабочих данной группы. Этот ряд прямоугольников и представляет собой гистограмму распределения рабочих по коэффициенту эффективности труда.
Она рисует эту разницу в виде гистограммы — последовательности вертикальных столбиков. Эта разница может быть очень мала, но компьютер развернет ее на весь экран.
Эта разница может быть очень мала, но компьютер развернет ее на весь экран.
При замене кривой плотности в виде гистограммы кривой в виде полигона правило нормирования выполняется автоматически, так как от каждого большого столбца гистограммы ( см. рис. 5 — 7, б) отсекается и отбрасывается часть площади в виде треугольников, заштрихованных на рис. 5 — 7, б вертикально, а к каждому меньшему столбцу добавляются такие же площади треугольников, заштрихованных горизонтально. В итоге общая площадь под кривой полигона остается равной площади исходной гистограммы.
После измерения электрогранулометр выдает информацию в виде гистограмм и счетных концентраций аэрозольных частиц в каждом канале анализатора.
Мы можем начертить индекс силы в виде гистограммы, на которой положительные значения индекса расположены выше нулевой линии, а отрицательные — ниже. Такая сырая гистограмма выглядит очень неровно, потому что ежедневно скачет вверх-вниз.
Анализ экспериментальных данных, представленных в виде гистограмм, в связи с практическими удобствами использования метода наименьших квадратов широко применяется и в тех случаях, огда такое представление данных приводит к определенной потере полученной в эксперименте информации.
После измерения электрогранулометр выдает информацию в виде гистограмм и счетных концентраций аэрозольных частиц в каждом канале анализатора.
Рассеивание отклонений размера наглядно представляется в виде гистограммы, состоящей из прямоугольников или эмпирической кривой распределения ( фиг.
Результаты ранжировки представлены на рис. III-5 в виде гистограммы. Сопоставление ее с гистограммой рис. 1П — 4 отчетливо показывает основное различие ранжировок, данных специалистами, большинство из которых ( 28 из 35) являются технологами, и специалистами по автоматизации
Последние, естественно, большее значение придавали возможности ( пусть даже и принципиальной) осуществления автоматического контроля ранжируемого параметра, безусловно принимая во внимание и важность поставляемой им информации.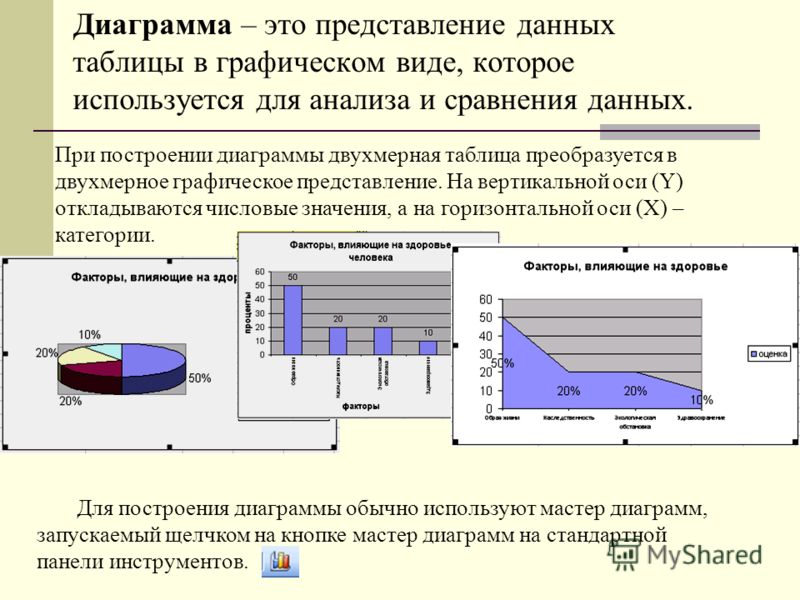 Из гистограммы рис. Ш-5 видно следующее.
Из гистограммы рис. Ш-5 видно следующее.
Ш-5 видно следующее.
Полученные данные могут быть представлены как в виде гистограмм, так и в виде кривых, сглаживающих ступенчатую функцию распределения. Каждая точка на этих кривых дает долю сплавов, заключенных в интервале Ас 5 % в окрестности данной точки.
Задание III уровня требует вывода результатов в виде гистограмм и построения на экране дисплея и на ПУ геометрических фигур.
|
Влияние параметра Р на изыеневие фактора ослабления Q для частиц, взвешенных в нефтепродуктах. д. |
Распределение частиц по размерам можно представить в виде гистограммы ( рис. 4.1, б), где по оси абсцисс откладывают размеры частиц, а по оси ординат их относительное содержание.
Распределение отказов труб правого потока радиантной камеры.| Распределение отказов труб левого потока радиантной камеры. |
Пример гистограммы в условном форматировании
Для наглядного примера возьмем отчет в таблице по прибыльности магазинов за последние 2 года:
Чтобы в столбце D добавить правило основано на гистограмме выделите диапазон ячеек D2:D12 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Гистограммы»-«Градиентная заливка»-«Зеленая гистограмма».
В результате появилась диаграмма в ячейке Excel, которая визуально отображает содержание значения.
Чем больше значение содержит ячейка по отношению к другим ячейкам, тем длиннее ее диаграмма. Положительные значения отображаются зеленым цветом, а отрицательные – красным.
Полезный совет! Уже при наведении мышкой на любой цвет гистограммы диапазон предварительно оформляется соответственному типу. Если среди предложенных вариантов Вы не нашли удовлетворяющий Вашим потребностям выберите нижнюю опцию «Другие правила». Откроется окно с гибкими настройками оформления гистограммы для ячеек.
Так же, как и при других типах правил условного форматирования мы можем изменять и настраивать график в ячейке с помощью диспетчера правил. Для этого:
- Выделите диапазон D2:D12 и выберите инструмент: «ГЛАВНАЯ»-«Стили»-«Условное форматирование»-«Управление правилами».
- Появится окно «Диспетчер правил условного форматирования». В нем выделите текущее правило и нажмите на кнопку «Изменить».
- В появившемся окне «Изменение правила форматирования» из группы параметров «Внешний вид столбца» из выпадающего списка «Граница» выберите опцию «Нет границы». Так мы немного изменим вид шкал под свой вкус.
- Нажмите на кнопку «Отрицательные значения и ось».
- Теперь в новом окне «Настройка отрицательных значений оси» укажите на самую нижнею опцию «Нет (показать отрицательные и положительные значения в одном направлении)». И нажмите ОК на всех открытых окнах.
Обратите внимание! Во окне «Настройка отрицательных значений оси» по умолчанию ось с нулевым значением автоматически смещается в зависимости от размера наибольшего отрицательного значения. Там же есть опция «Середина ячейки» при выборе которой ось с нулевым значением всегда будет находится по середине ячейки в независимости от ее значений
Там же есть опция «Середина ячейки» при выборе которой ось с нулевым значением всегда будет находится по середине ячейки в независимости от ее значений
При этом по умолчанию для положительных значений шкала будет увеличиваться в правую сторону, а для отрицательных – в левую. Хотя направление можно менять в предыдущем окне «Изменение правила форматирования» в правом нижнем углу, выпадающий список «Направление столбца:»
Об этом следует помнить если выбран один и тот же цвет для положительных и отрицательных значений. Как вы заметили настройках отрицательного значения, так же изменяется цвет шкалы для отрицательных чисел.
В окне «Изменение правила форматирования» для пользователя предоставляются широкие возможности для настройки различных параметров. Например, если отметить галочкой пункт «Показать только столбец», то содержимое ячеек будет скрыто, будет видно только шкалы гистограмм.
Ниже нам предоставляется гибкая настройка для минимальных и максимальных значений.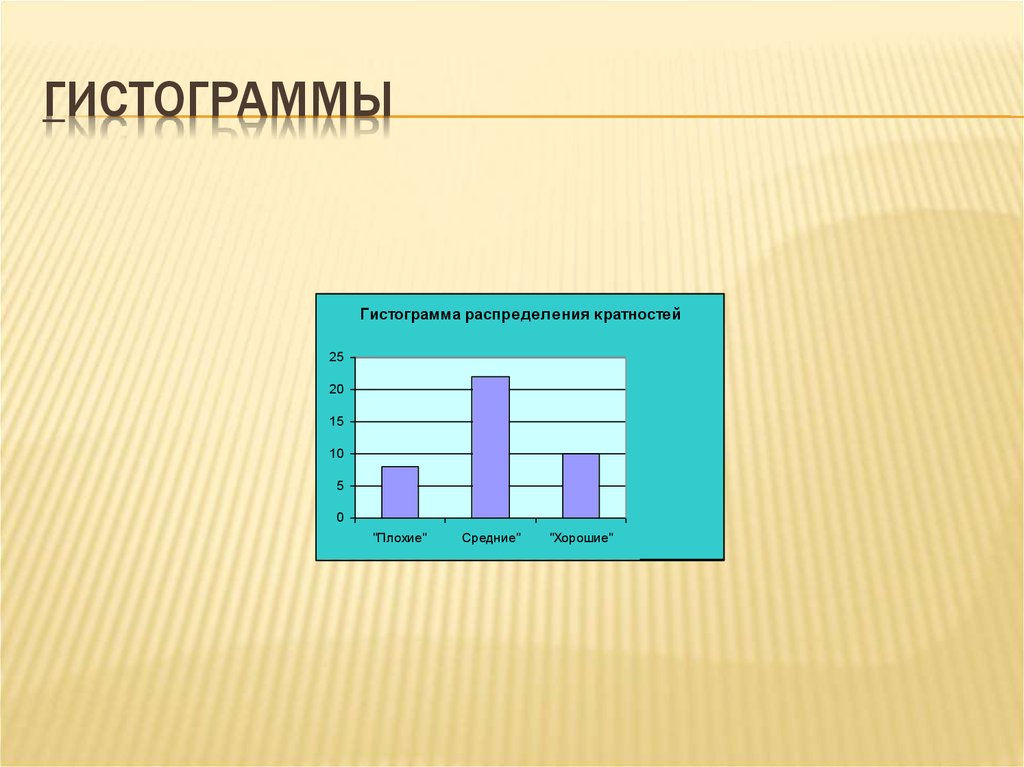 Из выпадающих списков выбираете опции: число, процент. А под ними вводите свои значения. При выборе же опции «формула» мы получаем неограниченные возможности для настройки данного параметра.
Из выпадающих списков выбираете опции: число, процент. А под ними вводите свои значения. При выборе же опции «формула» мы получаем неограниченные возможности для настройки данного параметра.
Гистограмма
Гистограмма – (Histogram) представляет собой график, по которому можно оценить яркость изображения см.Рис.1.
Гистограмму каждого кадра можно посмотреть на дисплее цифровой фотокамеры, как компактного класса, так и зеркальной. Некоторые фотокамеры позволяют просматривать информацию в каждом из трёх цветных каналов RGB.
Гистограмма иллюстрирует распределение пикселей изображения на графике. График показывает соответствие числа пикселей каждому уровню яркости.
Гистограмма отображает, какая часть изображения содержит достаточное количество деталей в тенях (левая часть гистограммы), в средних тонах (середина гистограммы) и в светах (правая часть гистограммы).
Рис.1. Гистограмма типичного фотографического снимка
При помощи гистограммы фотограф может оперативно корректировать результаты съёмки.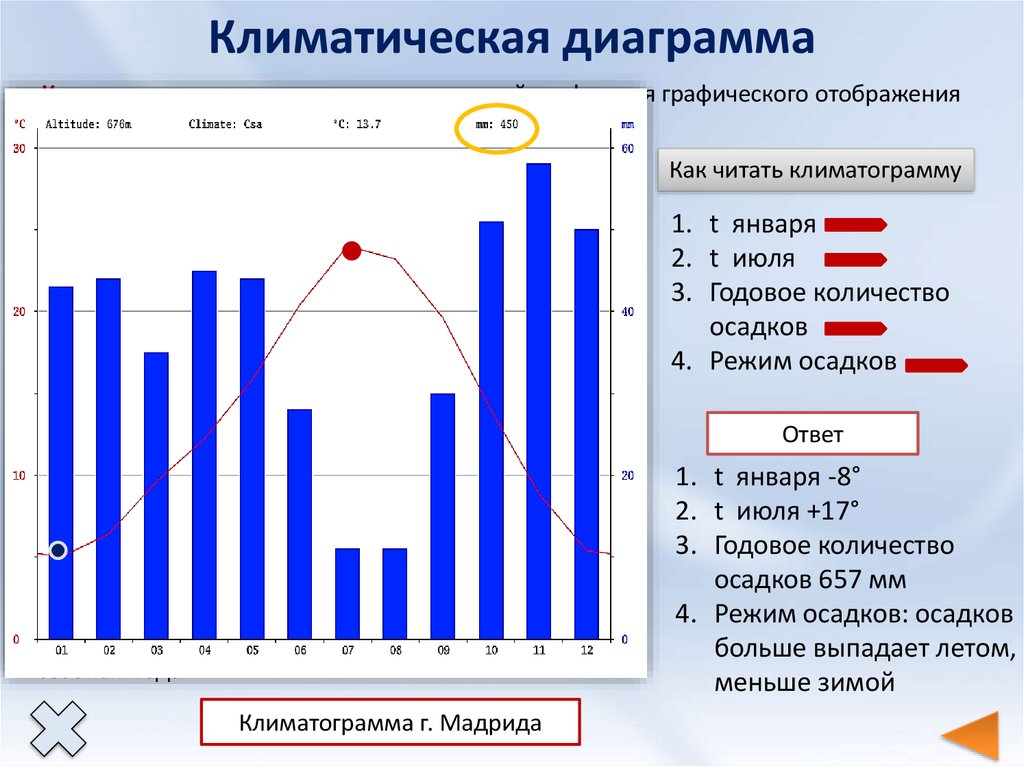
Благодаря тому, что гистограмма показывает распределение числа пикселей в соответствии с каждым уровнем яркости, у фотографа появляется возможность оценить тональность снимка.
Гистограмма также позволяет быстро оценить тональный диапазон фотографии или ключ, в котором выполнен снимок.
Снимок, выполненный в тёмной тональности или в низком ключе, характеризуется концентрацией пикселей в тенях изображения см.Рис.2. Тёмное изображение
Снимок, выполненный в светлой тональности или в высоком ключе, характеризуется концентрацией пикселей в светах изображения см.Рис.2. Светлое изображение
Снимок, выполненный в средней тональности или в среднем ключе, характеризуется концентрацией пикселей в средних тонах изображения.
Снимок, выполненный в полном тональном диапазоне, характеризуется распределением пикселей по всей тональной шкале, т.е. в тенях изображения, в средних тонах изображения и в светах изображения см.Рис.2. Нормальное изображение
Определение тональности снимка помогает установить необходимую тональную коррекцию.
типов гистограмм | Информация и обучение
Информация и обучение. | SPC и статистические методы для улучшения процессов.
Когда вы строите гистограмму, вы обычно ожидаете получить кривую в форме колокола. В таких ситуациях большинство измерений, записанных в ходе анализируемого процесса, будут располагаться в центре. Дальше от центра будет записываться все меньше и меньше измерений. Это распределение настолько распространено, что, когда распределение не соответствует такому «нормальному распределению», вам нужно спросить, почему данные не распределяются нормально? Какие типы гистограмм часто встречаются? SPC и статистические методы для улучшения процессов.
Информационная и обучающая презентация >>>
Бимодальная гистограмма.
Также можно назвать мультимодальным. Этот тип гистограммы имеет два или более пика. В бимодальном или мультимодальном распределении возникают два или более кластера с более высокими частотными числами. Это происходит, когда данные поступают из двух или более дистрибутивов, например, если вы используете два разных станка на одной производственной линии, два источника одного и того же сырья, разные смены и т. д.
Это происходит, когда данные поступают из двух или более дистрибутивов, например, если вы используете два разных станка на одной производственной линии, два источника одного и того же сырья, разные смены и т. д.
Чтобы полностью понять и интерпретировать бимодальную гистограмму, необходимо определить источники двух (или более) распределений, а затем построить отдельные гистограммы.
Также может возникнуть бимодальная гистограмма, когда данные для гистограммы берутся за определенный период времени. В этой ситуации в процессе могло возникнуть изменение, которое вызвало изменение среднего значения данных, что привело к двум пикам данных. В такой ситуации процесс следует исследовать в течение периода времени, связанного со сбором данных, чтобы определить, что могло измениться в процессе, например, были ли данные собраны в течение двух смен с разными операторами процесса. Могли ли измениться условия окружающей среды (теплый день по сравнению с холодным днем), использовались ли различные предметы испытательного оборудования для записи измерений и т. д.
д.
Типы гистограмм — гистограммы с отсутствующими наборами данных.
Если набор данных кажется отсутствующим, рецензент должен спросить, есть ли конкретная причина, например, предубеждение при сборе данных. Возможно, данные поступают из контрольной точки, где незначительное изменение приводит к результату «Годен/Отклонен», и есть тенденция к «Годену», поэтому данные отсутствуют сразу за пределами предела отказа, и выше, чем обычно, наблюдается частота данных. внутри спецификации Pass limit.
SPC и статистические методы для улучшения процессов.
Информационная и обучающая презентация >>>
Гистограмма с положительным и отрицательным перекосом.
Есть ли сортировка данных? Предпринимаются ли попытки уменьшить измеренные значения на гистограмме с положительной асимметрией? Имеются ли на отрицательно скошенной гистограмме противоположные эффекты увеличения измеренных значений?
Искаженные данные часто возникают из-за нижних или верхних границ данных.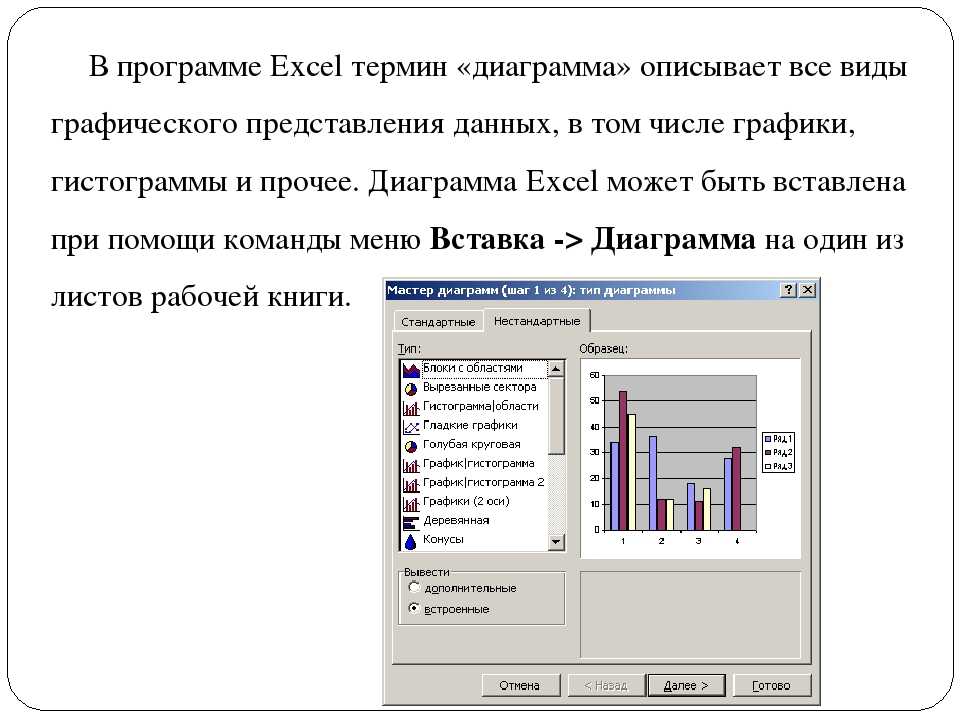 То есть данные, у которых есть нижняя граница, часто искажены вправо, а данные, которые имеют верхнюю границу, часто искажены влево.
То есть данные, у которых есть нижняя граница, часто искажены вправо, а данные, которые имеют верхнюю границу, часто искажены влево.
Другая возможная причина — ранние этапы нового процесса или продукта, когда наблюдается высокий уровень сбоев на ранних стадиях, которые со временем уменьшаются. Альтернативой является процесс, измеряемый во времени, где существует высокий уровень надежности внутри процесса, однако, приближаясь к ситуациям «конца жизни», начинают возникать сбои. Эти два сценария могут привести к положительному и отрицательному перекосу гистограмм.
SPC и статистические методы для улучшения процессов.
Информационная и обучающая презентация >>>
Типы гистограмм – однородная гистограмма.
Равномерная гистограмма может быть распределением с диапазоном мод, т.е. мультимодальным. В этой ситуации может быть ряд независимых влияний на построенную гистограмму.
Такое распределение может быть отражением неточности расчета ширины ячеек.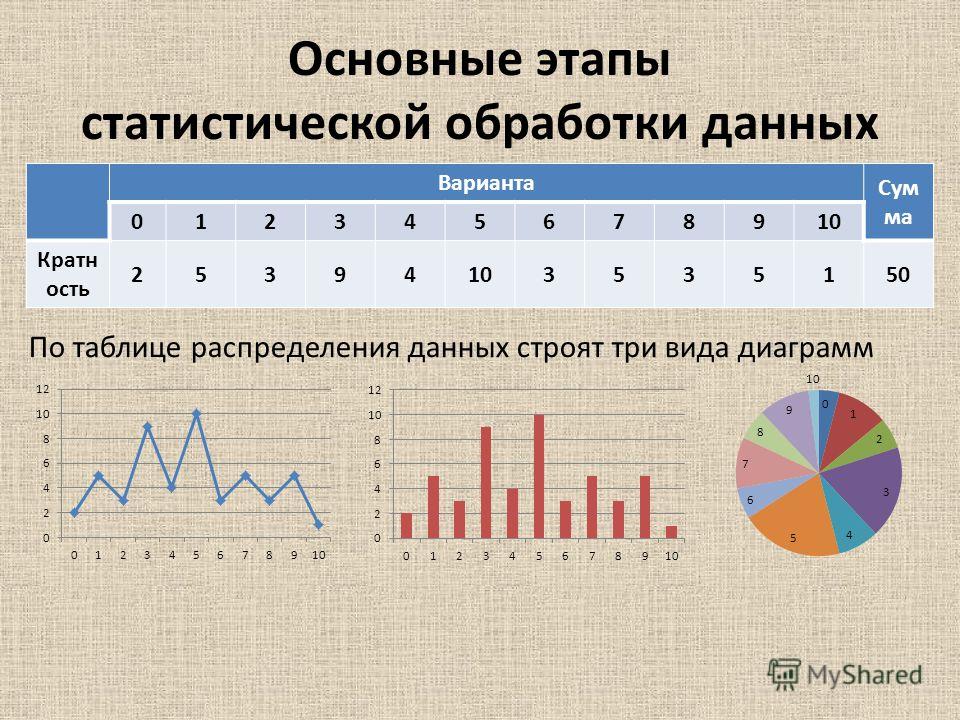 Рецензенту необходимо просмотреть данные и оценить, повлияют ли различные размеры ячеек на гистограмму.
Рецензенту необходимо просмотреть данные и оценить, повлияют ли различные размеры ячеек на гистограмму.
Распределение может демонстрировать, что существуют равные вероятности появления данных в каждой ячейке, например, в ситуации «бросания костей» или лотереи будут равные вероятности. Гистограмма может показывать, что вероятности действительно равны.
Равномерная гистограмма может указывать на то, что процесс не находится под контролем, т.е. инструмент на станке изнашивается, что приводит к тому, что процесс со временем выходит за рамки спецификации. Проведенные измерения могут продемонстрировать, что одни и те же результаты процесса возникают всегда, когда меняются входные данные.
Гистограммы с выбросом.
Выбросы могут возникать из-за ряда факторов, таких как неточное считывание, ошибка ввода данных или другой подобный тип ошибки, эффект запуска, отказ оборудования, изменение ввода, т.е. скачок напряжения и т. д.
Выброс может возникнуть из-за группировки данных, т. е. в верхней части спектра измерений может быть категория «все остальные данные». В этой ситуации в эту категорию может быть включено слишком много точек данных. Решением может быть пересмотр ширины ячеек.
е. в верхней части спектра измерений может быть категория «все остальные данные». В этой ситуации в эту категорию может быть включено слишком много точек данных. Решением может быть пересмотр ширины ячеек.
Необходимо исследовать выбросы, поскольку они могут представлять уникальные группы условий или периодические изменения в производительности процесса.
SPC и статистические методы для улучшения процессов.
Информационная и обучающая презентация >>>
Типы гистограмм – Гребенчатая гистограмма.
В гребенчатом распределении ячейки чередуются между короткими и длинными, каждая со своей кривой нормального распределения. Этот эффект может возникнуть, когда данные округляются, т. е. показания меньше «0,5» округляются до «0», показания выше «0,5» округляются до «1». Во всех ситуациях с непрерывными данными будет элемент округления либо лицом, выполняющим измерение, либо автоматически элементами испытательного оборудования, где округление будет присуще тестовому программному обеспечению. Решение состоит в том, чтобы убедиться, что границы ячеек установлены надлежащим образом, чтобы устранить этот эффект.
Решение состоит в том, чтобы убедиться, что границы ячеек установлены надлежащим образом, чтобы устранить этот эффект.
Информация и обучение.
SPC и статистические методы для улучшения процессов.
- Возможности процесса. Снижение изменчивости. Статистическое управление процессами.
- Предварительный контроль. Исследования R&R.
- Показатели возможностей процесса Cp, Cpk, Cpm, коэффициент производительности.
- Показатели производительности Pp и Ppk.
- Таблицы управления переменными.
- Таблицы атрибутов.
- Диаграммы Парето.
- Индивидуальные – X Графики.
- Гистограммы/анализ возможностей процесса.
- Точечные диаграммы.
- И т. д. … И т. д. …
- Информационная и обучающая презентация >>>
Определение, типы, характеристики, детали и работа
Гистограмма представляет собой представление числовых данных, не точное, а приблизительное.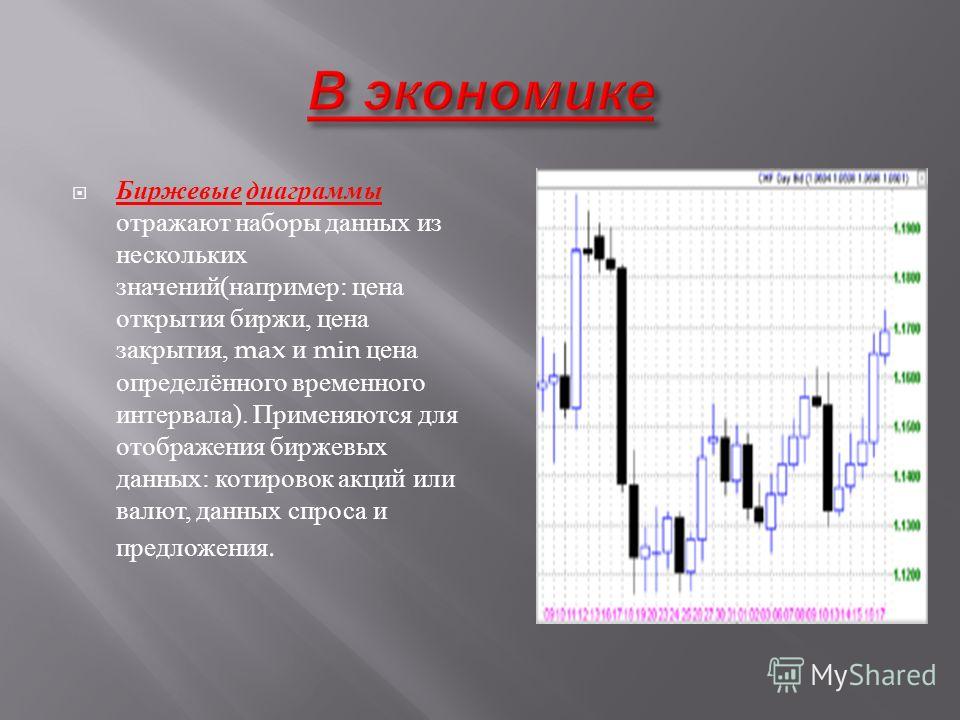 Карл Пирсон был первым, кто представил идею гистограммы. Чтобы создать гистограмму, первым шагом является бинирование, которое также называется бинированием данных, или группированием или дискретным бинированием. На этом этапе данные предварительно обрабатываются и используются для уменьшения влияния незначительных ошибок наблюдения, он делит весь диапазон значений на последовательность интервалов, а затем подсчитывает количество значений, попадающих в каждый из интервалов.
Карл Пирсон был первым, кто представил идею гистограммы. Чтобы создать гистограмму, первым шагом является бинирование, которое также называется бинированием данных, или группированием или дискретным бинированием. На этом этапе данные предварительно обрабатываются и используются для уменьшения влияния незначительных ошибок наблюдения, он делит весь диапазон значений на последовательность интервалов, а затем подсчитывает количество значений, попадающих в каждый из интервалов.
В двух словах, гистограмма помогает суммировать непрерывные данные. И, следовательно, учащимся важно узнать об одном и том же, потому что это помогает учащимся понимать и интерпретировать различные типы данных. Но прежде всего важно знать о гистограмме в целом.
Таким образом, Веданту предоставляет изучающим математику полное объяснение гистограммы вместе с ее определением, типами, характеристиками, частями и работами в простой и ясной форме, понятной всем изучающим.
Значение гистограммы
Значение гистограммы может быть сформулировано как графическое представление, которое сжимает ряд данных в простую интерпретацию числовых данных путем их группировки в логические диапазоны разной высоты, которые также известны как интервалы.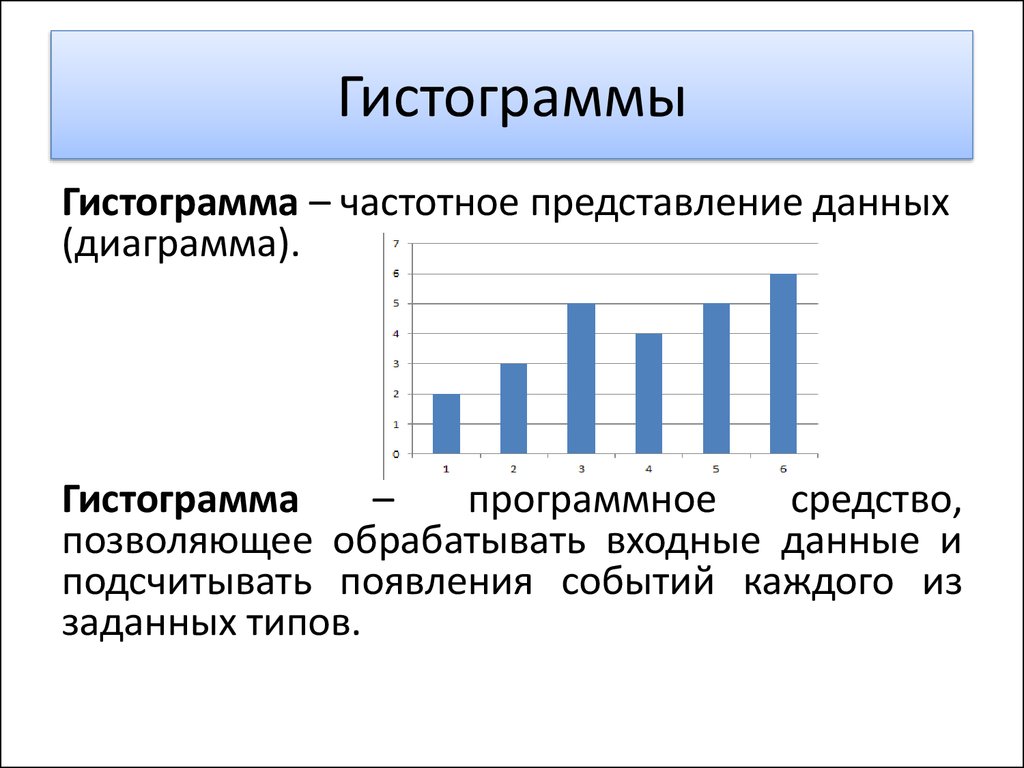 В основном, он суммирует дискретные или непрерывные данные. Мы также можем назвать это графиком частотного распределения, поскольку он похож на график, который позволяет вам обнаружить лежащее в основе частотное распределение.
В основном, он суммирует дискретные или непрерывные данные. Мы также можем назвать это графиком частотного распределения, поскольку он похож на график, который позволяет вам обнаружить лежащее в основе частотное распределение.
Определение гистограммы может быть предложено как инструмент, визуализирующий распределение данных в течение непрерывного интервала или определенного периода времени. Это помогает нам получить оценку того, где сосредоточены значения, каковы крайности, есть ли разрыв или необычные значения. В некоторой степени гистограмма также дает нам краткое представление о распределении вероятностей. Гистограмма очень похожа на вертикальную гистограмму, но разница между ними заключается в том, что между столбцами гистограммы нет промежутка, в отличие от гистограммы.
Части гистограммы.
Ниже приведены основные части гистограммы.
-
Заголовок: Заголовок — это первое и главное, что описывает всю информацию, которая представлена в гистограмме.

-
Ось X: Интервалы, в которые попадает измерение, показаны в интервалах оси X.
-
Ось Y: значения, полученные в пределах интервалов, установленных по оси X, отображаются на оси Y.
-
Полосы: Полосы используются для отображения значения данных. А чтобы узнать общее количество раз, когда значения встречались в интервале, полезна высота столбца, а охваченный интервал показан шириной столбца. И, следовательно, очевидно, что гистограмма, у которой все интервалы равны, должна иметь одинаковую ширину на всех столбцах.
Как работает гистограмма
В статистике Гистограммы, по большей части, широко используются, потому что они показывают, сколько переменных определенного типа встречается в определенном диапазоне. Другими словами, это помогает отображать данные или числа в графическом формате и, следовательно, значительно облегчает нам понимание и интерпретацию данных.
Гистограммы могут работать и служить многим различным целям, например, для переписи населения. Гистограмма может использоваться для отображения диапазона людей в возрасте от eh до определенного возраста, например, сколько людей в стране в возрасте от 10 до 20 лет и т. д. Во многих различных операциях полезны гистограммы.
Кроме того, если вы хотите узнать о гистограмме и гистограмме, поскольку чаще всего их путают друг с другом, вам может оказаться полезной эта ссылка: Гистограммы и гистограмма — определение, типы, использование и ключевые различия (vedantu .com)
Характеристики гистограммы
-
Гистограмма используется для отображения непрерывных данных в виде категорий.
-
На гистограмме нет промежутков между столбцами, в отличие от гистограммы.
-
Ширина ящиков одинаковая.

Именно площадь, а не высота столбцов
В гистограмме именно площадь, а не высота столбца указывает частоту появления каждого бина. Высота столбца не указывает, сколько вхождений оценок имеется в каждом отдельном бине. Произведение высоты и ширины ячейки всегда указывает на частоту появления в этой ячейке.
Как построить график гистограммы частот
Чтобы построить график гистограммы на основе непрерывной переменной, необходимо выполнить несколько шагов. Они приведены ниже;
-
Шаг 1) Во-первых, нам нужно разделить данные на интервалы классов, которые также известны как интервалы и частоты.
-
Шаг 2) На этом шаге мы должны нарисовать график гистограммы с осями X и Y. Затем запишите интервалы классов по оси X и частоты по оси Y.
-
Шаг 3) Нарисуйте вертикальные прямоугольники, используя оси X и оси Y.
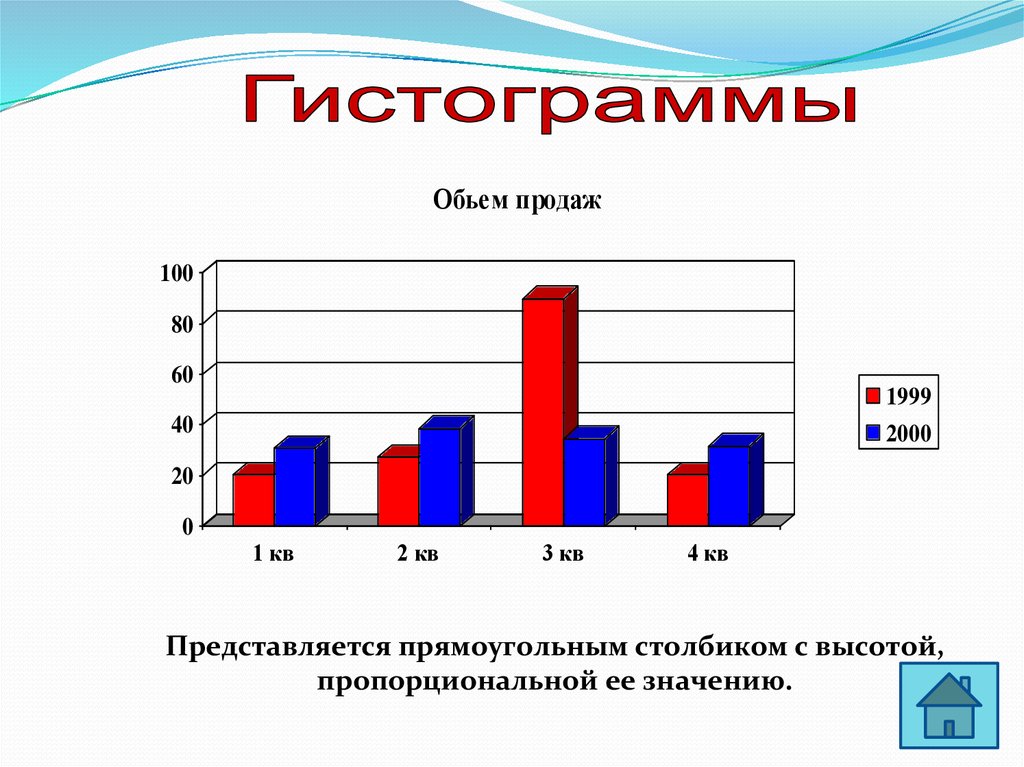
Difference between Bar Graph And Histogram
| | Histogram | Bar Graph |
| Indicates | Distribution of non-discrete variables | Сравнение дискретных переменных |
| Represents | Quantitative data | Categorical data |
| Spaces | No spaces between the bars | Spaces are there between the bars |
| Elements | Элементы сгруппированы вместе | Элементы взяты по отдельности |
| Изменение порядка стержней | No | Yes |
| Width of the bar | Doesn’t need to be same | Has to be same |
A Histogram can be represented по-разному. Некоторые из них также приведены ниже с примером гистограммы.
Некоторые из них также приведены ниже с примером гистограммы.
Типы гистограмм
| Нормальное распределение: | В нормальном распределении точки по обе стороны от среднего одинаковы. |
| Бимодальное распределение: | В бимодальном распределении данные отдельно анализируются как нормальное распределение. Поэтому они представлены как два разных пика. |
| Распределение с асимметрией вправо: | Распределение с асимметрией вправо, также известное как распределение с положительной асимметрией, когда большое количество значений данных встречается в левой части, тогда как меньшее количество значений данных встречается на правой стороне. Правостороннее распределение возникает, когда данные в левой части гистограммы имеют нижнюю границу диапазона, например 0,9. |
| Распределение с асимметрией влево: | Распределение с асимметрией влево также известно как распределение с асимметрией влево. В распределении с асимметрией влево большое количество значений данных появляется с правой стороны, тогда как меньшее количество значений данных появляется с левой стороны. Правостороннее распределение возникает, когда данные имеют нижнюю границу диапазона в правой части гистограммы, например 100. |
| Случайное распределение: | На гистограмме случайного распределения нет шаблона, поэтому она имеет несколько пиков. Причиной этого может быть то, что свойства данных были объединены. |
Приведенная выше таблица научит вас не только различным типам гистограмм, но и тому, как их рисовать.
Примеры, типы + [Учебник по Excel]
Одним из основных недостатков различных методов визуализации данных является то, что их становится все труднее читать с большими наборами данных. Совершенно иначе обстоит дело с гистограммами, которые в основном используются для визуализации больших наборов дискретных и непрерывных данных.
Совершенно иначе обстоит дело с гистограммами, которые в основном используются для визуализации больших наборов дискретных и непрерывных данных.
Гистограммы обеспечивают визуальное представление количественных данных, используя высоту аккуратно соединенных прямоугольных столбцов для указания частоты точек в интервале класса. Этот график можно построить вручную, нарисовав его прямой линейкой, или в цифровом виде с помощью Excel.
Построить гистограмму в цифровом виде очень просто. Поэтому в этой статье мы подробно расскажем о том, что такое гистограмма и как мы можем создать ее в цифровом виде с помощью Excel.
Что такое гистограмма?
График гистограммы — это график, который используется для визуализации частоты дискретных и непрерывных данных с помощью прямоугольных столбцов. Прямоугольные столбцы показывают количество точек данных, попадающих в указанный интервал класса.
Также известная как гистограмма, интервалы классов (или ячейки) не всегда имеют одинаковый размер по горизонтальной оси. При построении диаграммы гистограммы первое, что нужно сделать после сбора данных, — это определить ячейки или интервалы классов.
При построении диаграммы гистограммы первое, что нужно сделать после сбора данных, — это определить ячейки или интервалы классов.
Данные должны быть сгруппированы в соответствии с этим интервалом, затем будет взята частота данных, попадающих в эти группы. Поскольку интервалы классов обычно представляют собой непрерывный диапазон значений, в отличие от гистограмм, прямоугольные части не разнесены (т. е. они касаются друг друга).
Особенности гистограммы
Гистограмма — это популярный графический инструмент, обеспечивающий визуальное представление распределения данных. Чтобы идентифицировать диаграмму гистограммы, вот некоторые качества, на которые вам, возможно, придется обратить внимание.
Название
Название гистограммы — это то, что дает представление о данных, отображаемых на графике. Он суммирует информацию, отображаемую на гистограмме.
Имея заголовок на гистограмме, третья сторона может легко изобразить, о чем идет речь на графике, не углубляясь в чтение самого графика. На приведенном выше рисунке заголовок гистограммы — Histogram.
На приведенном выше рисунке заголовок гистограммы — Histogram.
Оси
Гистограмма имеет две оси: вертикальную и горизонтальную. Вертикальная ось на диаграмме гистограммы указывает частоту, а горизонтальная ось указывает интервалы классов или бины.
Эти две оси обычно помечены тем, что они представляют, что придает больше смысла названию графика гистограммы. Горизонтальная ось (x) показывает шкалу значений, в которой измеряется интервал класса.
Каждая из этих осей обычно имеет метку, описывающую тип данных, отображаемых на каждой оси. В этом случае горизонтальная метка — Bin , а вертикальная метка — Frequency
Bars
Столбцы — это основная часть гистограммы, которая в основном визуализирует набор данных. Полосы на гистограмме имеют прямоугольную форму и показывают, сколько раз значения попадают в каждый интервал класса.
Высота столбцов показывает частоту, а ширина столбцов указывает интервал. Графики гистограмм с равномерными интервалами классов обычно имеют одинаковую ширину.
Графики гистограмм с равномерными интервалами классов обычно имеют одинаковую ширину.
Масштаб
Масштаб гистограммы — это набор чисел, используемый для измерения или количественной оценки набора данных на графике. Это часть того, что определяет ширину и высоту каждого прямоугольного столбца на гистограмме.
Это то, что описывает структуру каждой единицы по горизонтальной и вертикальной осям. На рисунке 1 единица по горизонтальной оси эквивалентна 20, а 2 единицы по вертикальной оси эквивалентны 2.
Гистограммы
Гистограммы представляют собой графики, образованные путем соединения верхних средних точек прямоугольных столбцов на существующей диаграмме гистограммы. Также известные как полигоны частот, они обычно используются при визуализации набора данных непрерывных переменных.
Другими словами, мы можем сказать, что гистограммы представляют собой линейные диаграммы, нарисованные на гистограмме, где точка середины вершины прямоугольных столбцов является точками данных.
Не все гистограммы имеют гистограф. Однако при добавлении к диаграмме гистограммы это очень полезно для предоставления дополнительной информации о наборе данных.
Типы гистограмм
Гистограммы делятся на разные типы в зависимости от распределения прямоугольных столбцов на графике. То есть форма столбцов и вся структура графика.
Различные распределения гистограмм выделены ниже:
Нормальное распределение
Говорят, что гистограмма имеет нормальное распределение, если она имеет форму колокола. Как следует из названия, это нормальная или типичная структура, которую, как ожидается, примет распределение гистограммы, даже если она не является «нормальной».
В некоторых случаях можно сказать, что график гистограммы имеет нормальное распределение, просто взглянув на него. Однако другие распределения подобны нормальному распределению, поэтому необходимо выполнить статистические расчеты, прежде чем можно будет сказать, что распределение является нормальным.
Бимодальное распределение
Бимодальное распределение является результатом объединения двух различных процессов в одном наборе данных. Это распределение содержит два разных нормально распределенных графа.
Например, данные, собранные из двух разделов одного класса (например, класса 1А и класса 1В), могут быть бимодальными. Похожий на спину двугорбого верблюда, его также называют двугорбым распределением.
Распределение с перекосом
Распределение с перекосом — это асимметричный график с нецентральным пиком, стремящимся к границе графика (или от хвоста). Есть два типа асимметричных распределений, а именно; распределения с правым и левым наклоном.
При распределении с асимметрией вправо хвост графика находится справа. Это также известно как положительно асимметричное распределение.
С другой стороны, распределение с асимметрией влево имеет хвост с левой стороны и также известно как распределение с асимметрией с отрицательной асимметрией.
Случайное распределение
В этом типе распределения отсутствует определенный шаблон, и он дает несколько пиков. Следовательно, это также упоминается как мультимодальное распределение.
Случайное распределение обычно создается при объединении набора данных, содержащего переменные с разными свойствами. В этом случае данные должны быть отсортированы и отдельно проанализированы.
Распределение краевых пиков
Распределение краевых пиков очень похоже на нормальное распределение, с тем отличием, что первое имеет большой пик на одном из хвостов.
Такое распределение обычно возникает из-за ошибки в построении графика гистограммы.
Гребенчатое распределение
Как следует из названия, полосы в гребенчатом распределении имеют гребенчатую структуру . Эти полосы чередуются между высокими и короткими, что делает график похожим на расческу.
Гребенчатое распределение обычно создается из-за ошибок округления в наборе данных.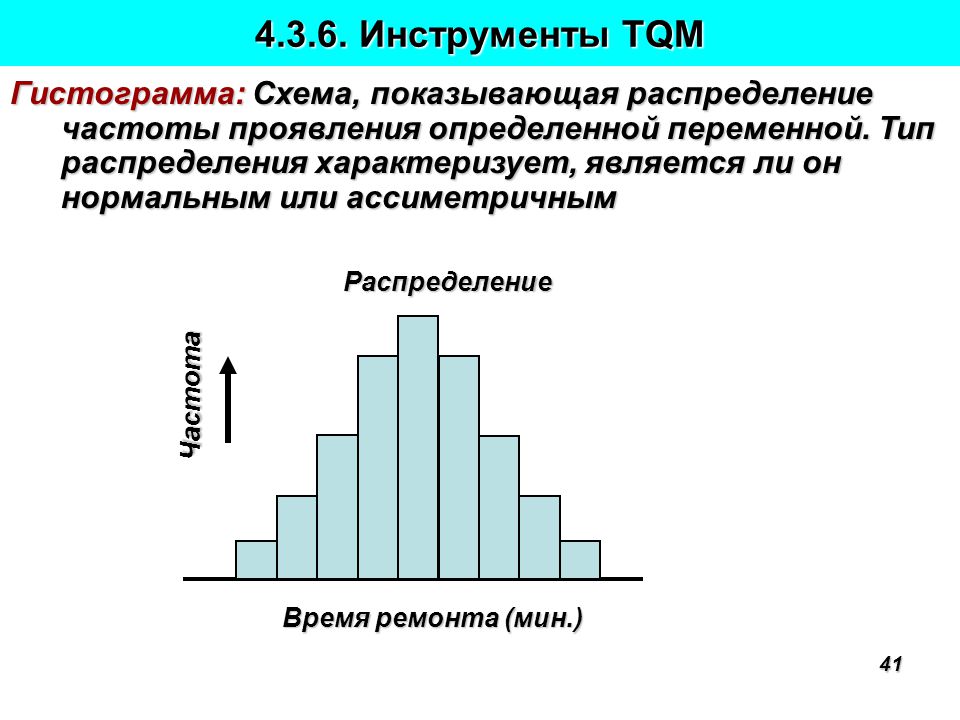
Усеченное распределение
Усеченное распределение создается, когда хвост нормального распределения обрезается на результирующей диаграмме гистограммы. Отрезание хвоста иногда придает ему форму сердца, в результате чего его называют распределением с вырезом в виде сердца.
Примеры графиков гистограмм
Пример 1: Компания ABC пытается сократить время ожидания клиентов в очередях для повышения удовлетворенности клиентов. Для этого они взяли случайного клиента и опросили его о том, сколько времени ему пришлось ждать в очереди за последние 10 дней.
Приведенная ниже таблица является результатом этого интервью. Создайте диаграмму гистограммы, используя эти данные. Отсюда определите, к какому распределению относится график
Решение: Как показано ниже, мы создали гистограмму с 4 интервалами и 4 частотами. Горизонтальная ось показывает диапазон времени ожидания, а вертикальная ось указывает среднее количество клиентов, испытывающих каждый интервал времени ожидания.
Полученная гистограмма имеет рандомизированное распределение.
Пример 2: Филантроп хочет пожертвовать товары менее привилегированному сообществу. Для того, чтобы определить количество и вид предметов для пожертвования, в сообществе был проведен опрос.
Цель этого опроса – выяснить возрастную демографию жителей общины. После проведения этого опроса он был визуализирован на гистограмме для удобства анализа, как показано ниже.
Учитывая, что Число людей , указанное на графике, измеряется сотнями, определите численность населения в каждой возрастной группе, а затем используйте полученный результат, чтобы узнать, в какой из этих групп больше всего населения.
Решение: Поскольку количество людей, указанное на гистограмме, исчисляется сотнями, то количество людей, относящихся к каждой возрастной группе, равно:
0-20: 4*100 = 400 человек
20-40: 7*100 = 700 человек
40-60: 2*100 = 200 человек
40 возрастная категория. Это означает, что большинство жителей этого сообщества в возрасте от 20 до 40 лет. определить наиболее распространенный результат процесса в наборе данных. Визуализируя собранные данные на гистограмме, результат с наибольшей частотой будет легко выделяться как пик графика.
Это означает, что большинство жителей этого сообщества в возрасте от 20 до 40 лет. определить наиболее распространенный результат процесса в наборе данных. Визуализируя собранные данные на гистограмме, результат с наибольшей частотой будет легко выделяться как пик графика.
- Идентификация структуры данных
При чтении гистограммы можно легко определить тенденции в данных. Это может быть полезно для прогнозирования, оптимизации процессов и выявления возможных проблем.
- Обнаружение отклонений в данных
Вы можете легко обнаружить отклонения в данных при визуализации с помощью гистограммы по сравнению с некоторыми другими методами визуализации данных. Это очень полезно в тех случаях, когда вы собираете данные с течением времени.
Немедленное отклонение данных, отклонение заметно на графике гистограммы. Это легко поможет вам проверить процесс сбора данных и внести исправления, если отклонение вызвано человеческим фактором.
Гистограмма и столбчатая диаграмма t
Несмотря на то, что гистограммы и гистограммы обладают очень похожими структурами и характеристиками, они имеют ряд различий. Эти различия помогут нам распознать эти диаграммы, когда мы столкнемся с ними.
Поэтому в этом разделе мы рассмотрим сходства и различия между гистограммами и гистограммами.
Различия
- Характеристики
Прямоугольные столбцы на гистограмме разнесены, а прямоугольные столбцы на гистограмме соединены вместе. Кроме того, горизонтальные метки на гистограмме обычно представляют собой дискретные или номинальные данные.
Оси гистограмм, напротив, помечены бинами или интервалами классов набора данных.
- Использование
При анализе данных гистограммы используются для измерения частоты категориальных данных, а гистограммы измеряют порядковые и количественные (интервал и отношение) данные. Хотя вертикальная ось обоих графиков является дискретной, горизонтальная ось гистограммы является категориальной, а ось гистограммы — числовой.
Хотя вертикальная ось обоих графиков является дискретной, горизонтальная ось гистограммы является категориальной, а ось гистограммы — числовой.
- Заказ
Прямоугольные столбцы на гистограмме обычно располагаются в порядке уменьшения высоты. Гистограммы, с другой стороны, имеют прямоугольные столбцы, упорядоченные в соответствии с их положением в интервале классов.
Хотя интервалы классов расположены в порядке возрастания, это не означает, что прямоугольные столбцы обязательно будут расположены одинаково. Это связано с частотой каждого интервала, которая случайным образом меняется в зависимости от набора данных.
Сходства
- Характеристики
Как гистограммы, так и гистограммы имеют заголовок, оси, масштаб и прямоугольные столбцы. Просто взглянув на оба графика, они очень похожи друг на друга. В основном это связано с тем, что они оба используют прямоугольные столбцы для визуализации данных.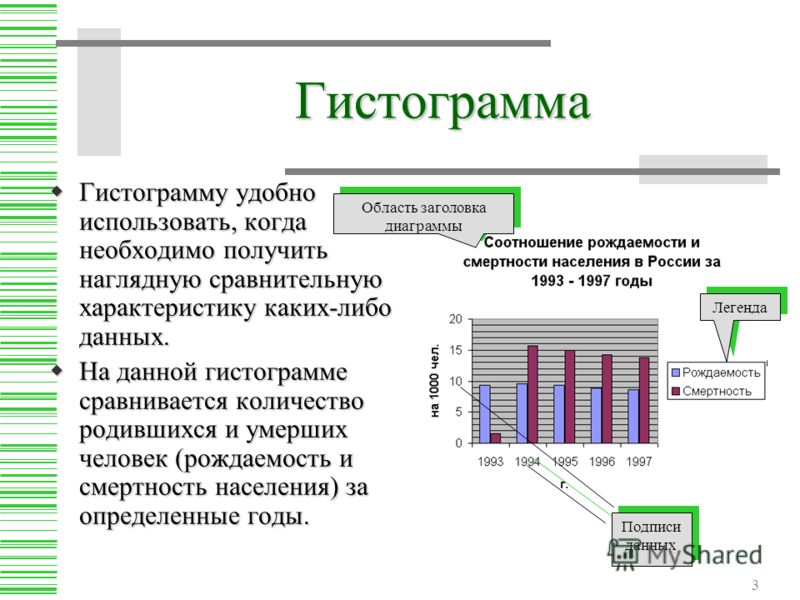
- Использование
Гистограммы и гистограммы используются для определения режима или частоты элементов в наборе данных. Высота прямоугольных полос соответствует частоте определенного элемента в наборе данных.
Простым способом чтения этих двух графиков является следование простому неофициальному правилу, которое гласит: «Чем выше полоса, тем выше частота, и наоборот».
График гистограммы в Excel
Чтобы построить гистограмму с помощью Excel, выполните несколько простых шагов:
- Шаг 1: Введите данные в книгу Excel, как показано на рисунке ниже.
Входные данные — это набор случайных величин, которые мы хотим визуализировать с помощью Excel, Диапазон значений — это диапазон значений, которые вы хотите отобразить на горизонтальной оси. Это то, что определяет ширину прямоугольных полос и масштаб горизонтальной оси.
- Шаг 2: Перейдите к Данные>Анализ|Анализ данных .
 Если вы не можете найти вкладку Data Analysis , это означает, что вы не установили плагин Analysis Toolpak. Чтобы установить плагин, выберите Файл > Параметры . Появится диалоговое окно, подобное приведенному ниже.
Если вы не можете найти вкладку Data Analysis , это означает, что вы не установили плагин Analysis Toolpak. Чтобы установить плагин, выберите Файл > Параметры . Появится диалоговое окно, подобное приведенному ниже.
Нажмите на Analysis Toolpak, , затем на кнопку Go . Появится другое диалоговое окно, похожее на диаграмму ниже.
Отметьте Пакет инструментов анализа и нажмите OK , как показано выше. Вкладка Data Analysis теперь появится в меню Analysis .
- Шаг 3: После нажатия на Data Analysis появится диалоговое окно, подобное показанному ниже.
Щелкните Гистограмма , а затем OK , чтобы перейти к следующему шагу.
- Шаг 4: Введите диапазон ввода и диапазон ячеек, затем отметьте необходимые параметры, как показано на диаграмме ниже.
 Нажмите OK и вы получите гистограмму.
Нажмите OK и вы получите гистограмму.
- Шаг 5: На приведенной ниже диаграмме сгенерированная гистограмма больше похожа на гистограмму с пробелами между столбцами.
Отредактируйте зазор между прямоугольными столбцами, выделив все столбцы, затем перейдите к Формат ряда данных > Параметры ряда . Устраните dap, уменьшив Gap Width до 0%, как показано ниже.
Отделите столбцы друг от друга, добавив к столбцам цвет границы.
- Шаг 6: . Отредактируйте бины или интервалы классов, щелкнув правой кнопкой мыши график и выбрав «Выбор ряда данных». Появится приглашение, подобное приведенному ниже.
Нажмите Edit в метках горизонтальной оси (категории), чтобы изменить маркировку бункера.
Нажмите OK и у вас есть гистограмма.
Просто взглянув на симметрию этого графика, мы можем заключить, что он имеет случайное распределение.
Недостатки графика гистограммы
- Его можно использовать только для визуализации непрерывных данных. Поскольку графики, как правило, склеены между собой, использовать гистограмму для визуализации дискретных данных будет некорректно. Это можно сделать только с помощью гистограммы.
- Поскольку данные сгруппированы по разным категориям, гистограммы не могут считывать точные значения. Вы не можете определить конкретные точки данных на графике, просто прочитав гистограмму.
- Нельзя использовать для сравнения двух наборов данных.
Заключение
Диаграмма гистограммы — отличный инструмент визуализации для изучения изменений больших наборов данных. Это один из наиболее часто используемых методов визуализации данных в статистическом анализе.
Гистограммы являются одним из семи основных инструментов контроля качества благодаря их простоте и способности решать большинство проблем, связанных с качеством.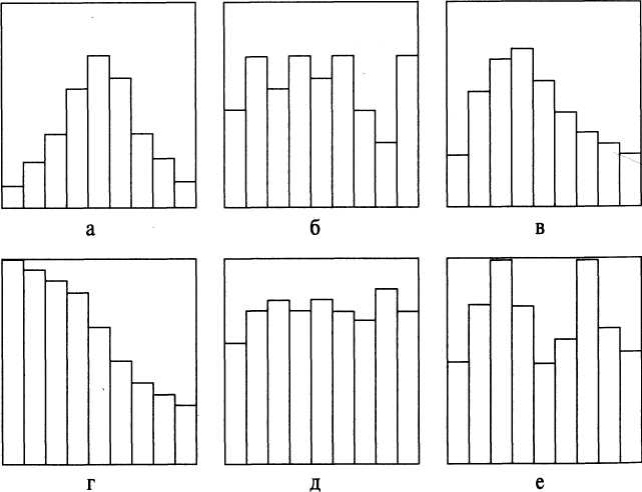 Аналитики по контролю качества изучают различные аспекты гистограммы, в том числе распределение, ширину и высоту прямоугольных столбцов.
Аналитики по контролю качества изучают различные аспекты гистограммы, в том числе распределение, ширину и высоту прямоугольных столбцов.
Хотя обычно говорят, что высота гистограммы указывает на частоту появления в ячейке, это не относится ко всем случаям. В случаях, когда гистограмма не имеет одинаковых интервалов, частота интервала определяется площадью прямоугольных столбцов.
Гистограмма: типы, характеристики и детали
Namrata Das
Мастер по подготовке к экзаменам | Обновлено 5 апреля 2022 г.
Гистограмму можно просто определить как непрерывное графическое представление данных. Их целью является достижение точного распределения вероятностей наряду с его решением. Карл Пирсон открыл эту теорию в 189 г.1, чтобы дать представление о предыдущих или прошлых данных. С гистограммами легко работать, и они используются во многих областях, таких как медицина, гидрология, фондовая биржа и фотография. Здесь мы узнаем больше о гистограмме и обсудим некоторые важные вопросы.
| Таблица содержания
|
Также:
. Также: 9 . 9 9. гистограммы
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Гистограмма — это графическое представление распределения числовых данных до наиболее приблизительного значения. Они имеют форму прямоугольных стержней, расположенных рядом друг с другом. Каждая полоса уникальна и обозначает различный тип числовых данных и частоту. Частота количество раз, когда данные появляются в распределении. Для частотного распределения существует отдельная таблица. Эти стержни или ячейки могут различаться по своей соответствующей ширине.
Они имеют форму прямоугольных стержней, расположенных рядом друг с другом. Каждая полоса уникальна и обозначает различный тип числовых данных и частоту. Частота количество раз, когда данные появляются в распределении. Для частотного распределения существует отдельная таблица. Эти стержни или ячейки могут различаться по своей соответствующей ширине.
Идея гистограммы впервые была предложена английским математиком Карлом Пирсоном. Основная цель гистограммы — оценить вероятностное распределение . Это дает очень четкую картину значений, лежащих в распределении. Они проливают свет на природу данных, например, где они сконцентрированы и где их нет. Он используется во многих программах цифровой обработки изображений. Гистограммы часто используются в отличие от гистограмма . Важно отметить, что данные, присутствующие в гистограмме, являются непрерывными, тогда как на гистограммах они часто отсутствуют. Проще говоря, на гистограмме есть пробелы.
Читайте также:
Характеристики гистограммы
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Гистограмма обладает определенными характеристиками, которые необходимо изучить, чтобы получить о ней больше информации. Они следующие:
- Ширина полос представляет собой интервалы классов.
- Частота указывается высотой столбца на гистограмме.
- В гистограмме нет места или промежутка между двумя столбцами. Данные непрерывны.
- Внутри гистограммы присутствуют неразличимые переменные.
- Столбики гистограммы негибкие, поэтому их нельзя переупорядочить.
Типы гистограмм
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Гистограммы классифицируются по четырем важным разделам в зависимости от типа распределенной частоты.
- Равномерное распределение
- Симметричная гистограмма
- Бимодальная гистограмма
- Гистограмма вероятности
Равномерная гистограмма
Характер данных, представленных в однородной гистограмме, очень последователен. Он обозначает почти одинаковое количество значений в каждом баре. Все столбцы однородной гистограммы имеют почти одинаковый размер или высоту.
Он обозначает почти одинаковое количество значений в каждом баре. Все столбцы однородной гистограммы имеют почти одинаковый размер или высоту.
Симметричная гистограмма
Симметричная гистограмма, более известная как колоколообразная гистограмма, названа в честь ее структуры. Это так, что кажется, что есть центр, и все ценности непрерывно окружают его. По мере того, как мы движемся в стороны от центра, значение кажется уменьшающимся. Гистограмма в форме колокола представляет собой нормальное распределение.
В этом типе гистограммы вертикальная линия рисуется в центре и по бокам, поскольку она продолжает уменьшаться в равной степени. Поэтому они находятся в симметрии.
Симметричная гистограммаБимодальная гистограмма
В бимодальной гистограмме есть два столбца одинаковой высоты или два пика. Поскольку здесь два центра, это означает два типа данных. Данные в этом случае не следует путать и правильно анализировать. Эти гистограммы легко идентифицировать.
Гистограмма с наклоном вправо
Если гистограмма скошена вправо, это означает, что значения положительные. Такое распределение данных обычно происходит в большом количестве в левой части гистограммы. Частота их возникновения очень меньше справа. Когда данные внутри гистограммы имеют низкий диапазон, например 0, имеет место распределение с перекосом вправо. Это означает, что все данные имеют значения больше нуля.
Гистограмма с перекосом вправоГистограмма с перекосом влево
В гистограммах с асимметрией влево распределение происходит влево и считается отрицательно асимметричным. Это совершенно противоположно смещенной вправо гистограмме. Вы можете легко определить этот тип гистограммы, увидев хвост, идущий влево. Мы можем понять, что частота уменьшается по мере того, как мы переходим к меньшим числам. Собранные данные здесь имеют значения меньше 100, что означает, что наблюдений меньше.
Скошенная влево гистограммаЧитайте также:
Части гистограммы
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Гистограмма состоит из 4 основных частей, необходимых для эффективной работы. Каждая из этих частей выполняет определенную функцию, чтобы способствовать достижению конечной цели гистограммы. Они описываются следующим образом:
Каждая из этих частей выполняет определенную функцию, чтобы способствовать достижению конечной цели гистограммы. Они описываются следующим образом:
- Заголовок — Заголовок является самой важной частью гистограммы. Именно по названию читатели получают представление о том, о чем идет речь. Он состоит из общей сути и информации о гистограмме.
- Ось X – Ось X гистограммы указывает масштаб значений, представленных внутри гистограммы. Это интервал по своей природе, и он относится к значениям так, чтобы проложить путь для подпадающих под него измерений.
- Ось Y – это та часть гистограммы, которая представляет количество раз, когда значение или значения встречаются в этих интервалах оси X. Ось Y относится к частоте.
- Столбцы – столбец важен, поскольку его высота определяет частоту значений, встречающихся в интервалах. В этом случае ширина полосы указывает на интервал данных, который уже закончился.
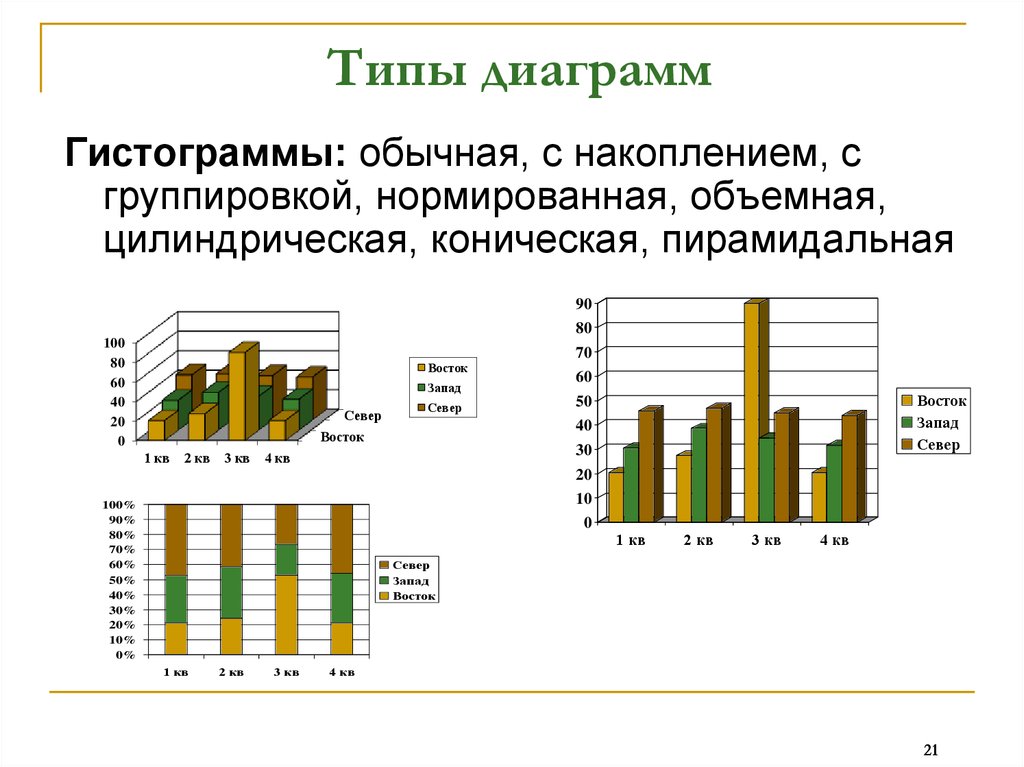
Разница между гистограммой и гистограммой
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Следует помнить о некоторых основных различиях между гистограммой и гистограммой. Давайте посмотрим подробно.
| Гистограмма | Столбчатая диаграмма |
|---|---|
| Гистограмма представляет собой графическое представление данных, которое показывает частоту появления числовых данных в виде столбцов. | Гистограмма или диаграмма — это графическое представление данных, связанных со сравнением различных категорий данных в виде столбцов. |
| Между стержнями нет зазоров. Они непрерывны. | В этом случае между стержнями есть промежутки. |
| Целью гистограммы является распределение недискретных переменных. | Гистограмма предназначена для сравнения дискретных переменных. |
| Характер данных количественный. | Характер данных категоричен. |
| Стержни фиксированы по своей природе, поэтому их нельзя изменить. | Стержни являются гибкими и могут быть легко изменены. |
| Ширина полосы варьируется и может меняться. | Ширина брусков абсолютно одинаковая. |
Что следует помнить
- Гистограмма — это графическое представление данных. Эти данные сгруппированы в столбцы разной высоты, также называемые ячейками. Данные здесь непрерывны, в отличие от гистограмм.
- Гистограммы имеют дело с непрерывными количественными данными. В зависимости от их характера гистограмма была разделена на разные головки. Они называются правосторонней гистограммой, бимодальной гистограммой, левосторонней гистограммой, симметричной гистограммой и однородной гистограммой.
- Различные части гистограммы одинаково важны для ее работы.
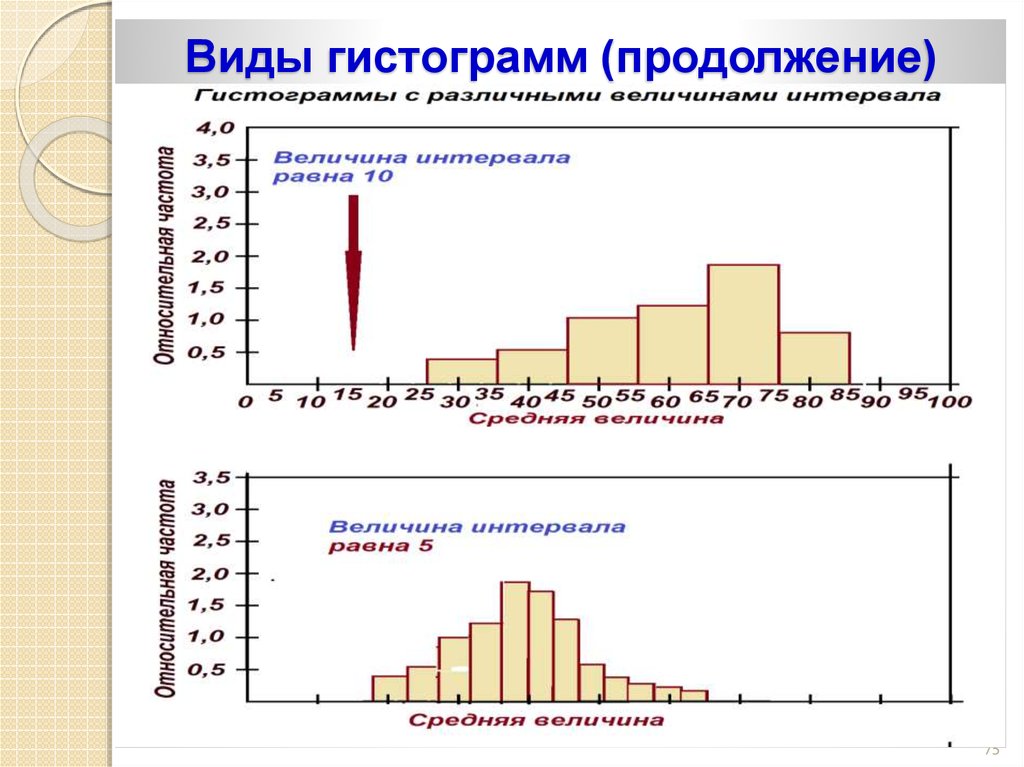 Заголовок, который дает представление о гистограмме, оси x, оси y и столбцах. Каждая часть связана с выполнением определенной функции, которая помогает решить гистограмму.
Заголовок, который дает представление о гистограмме, оси x, оси y и столбцах. Каждая часть связана с выполнением определенной функции, которая помогает решить гистограмму.
- Гистограммы не следует путать с гистограммами. Первое имеет контрастный характер по отношению ко второму. Гистограмма отображает непрерывные данные, в то время как на гистограмме между столбцами присутствуют промежутки. Столбцы на гистограммах не являются гибкими, тогда как на гистограммах их можно изменить.
Читайте также:
Примеры вопросов
Вопросы. Что такое гистограмма? (2 балла)
Отв. Гистограмма – это графическое представление, в котором данные отображаются в виде столбцов, чтобы показать частоту появления числовых данных. Он выполнен в виде стоящих прямоугольных стержней, без промежутков между ними. Гистограмма означает, что данные непрерывны и столбцы не могут быть изменены.
Вопрос. Почему мы используем гистограмму? (5 баллов)
Почему мы используем гистограмму? (5 баллов)
Ответ. В повседневной жизни гистограмма служит нескольким целям. Они перечислены ниже:
- Помощь в вычислении результатов
- Помощь в изучении яркости пикселей
- Используется для расчета функции плотности
- Исследование поведения и частоты
- Помогает в определении симметричных данных
Вопрос. Назовите части гистограммы. (4 балла)
Ответ. Правильная гистограмма состоит из 4 основных частей. Эти части необходимы для бесперебойной работы гистограммы и получения точных результатов. Гистограмма включает:
- Заголовок — Это дает общее представление о гистограмме. Без этой информации трудно двигаться вперед.
- Ось X — Обозначает те значения, которые находятся внутри гистограммы.
- Ось Y — Обозначает частоту значения, которое встречается в интервале оси X.

- Столбики – Высота и частота значений коррелируют друг с другом.
Вопрос. Назовите некоторые приложения гистограммы. (3 балла)
Ответ. Гистограммы все чаще используются на фондовой бирже, поскольку они помогают понять происходящую сделку. Они также используются в области обработки изображений. Он изучает различные виды состояний у людей в медицинском аспекте жизни. Они также разработаны в области гидрологии и шести сигм для более глубокого понимания структуры дефектов образцов.
Вопрос. Что происходит на гистограмме, перекошенной вправо? (3 балла)
Ответ. Гистограмма называется скошенной вправо, если кажется, что вершина или пик смещаются влево. В этом случае значения положительны. Данные распределяются преимущественно по левой стороне. Значения данных больше нуля, а частота меньше справа. Говорят, что нижняя граница, присутствующая в наборе данных, является основной причиной такой гистограммы.
Вопрос. Дайте определение нормальному распределению. (3 балла)
Ответ. Гистограмма нормального распределения является наиболее распространенным типом гистограммы, и ее легко идентифицировать. Эти гистограммы имеют форму колокола и также называются симметричными гистограммами. График симметричен в среднем. В этом случае распределения, среднего, медианы и моды значения всех трех являются одинаковыми значениями. Они считаются более важными, чем другие, потому что они обеспечивают наиболее точные результаты.
Вопрос. Какие существуют типы гистограмм? (4 балла)
Ответ. Гистограмма классифицирована по основным заголовкам, таким как
- Равномерная гистограмма
- Гистограмма с наклоном вправо
- Гистограмма с наклоном влево
- Симметричная/колоколообразная гистограмма
- Бимодальная гистограмма 1 91 Каковы свойства гистограммы? (4 балла)
- Незначительные промежутки между столбцами гистограммы
- Столбцы не могут быть переупорядочены
- Ширина столбца может изменяться
- Данные непрерывны
- Высота столбцов обозначает частоту
- Гистограммы измеряют категориальные данные: данные, которые можно разделить на разные категории или типы
- Гистограммы измеряют непрерывные, количественные данные: данные, которые можно подсчитать
- Среднее представляет собой сумму всех значений в наборе данных, деленную на общее число ценностей. Для этого набора данных среднее значение равно 3,8. Когда упоминается среднее значение без указания, является ли оно средним значением, медианой или значением моды, это почти всегда среднее значение.
- Медиана относится к среднему значению набора данных.
 Если имеется четное количество значений, берется средняя точка между двумя ближайшими значениями. Для этого набора данных среднее значение равно 3,5.
Если имеется четное количество значений, берется средняя точка между двумя ближайшими значениями. Для этого набора данных среднее значение равно 3,5. - Режим — это просто наиболее часто встречающееся значение. Для этого набора данных используется режим 5.
Ответ. Гистограмма включает такие характеристики, как
Гистограмма включает такие характеристики, как
Читайте также:
Гистограммы — отличный способ визуализации данных и отслеживания ключевых показателей эффективности, поскольку они наглядны и просты для чтения. Они являются предпочтительным методом представления больших объемов данных в простой и понятной форме. Что такое гистограмма и как она помогает анализировать данные?
Что такое гистограмма?
Гистограмма — это график, часто используемый в математике и статистике. Гистограммы используются для измерения частоты появления значений или диапазонов значений в наборе данных. Горизонтальная ось обычно отображает измеренное значение — либо непрерывную числовую переменную, такую как высота, расстояние или время, либо дискретное исчисляемое значение, такое как количество предметов. Вертикальная ось показывает частоту , в которой появляется это значение или диапазон значений.
Вертикальная ось показывает частоту , в которой появляется это значение или диапазон значений.
Разделениями гистограммы могут быть блоки дискретных чисел (1, 2, 3) или, в случае диапазона, интервалы классов или интервалов (0-10, 10-20, 20-30). Самое главное помнить, что не должно быть пробелов между числами или диапазонами чисел — каждая секция диапазона значений отображается по горизонтальной оси.
Для непрерывно измеряемой переменной интервалы классов могут быть условными или определяться методом проб и ошибок. Их следует выбирать так, чтобы форма графика напоминала кривую распределения, подобную приведенным выше гистограммам.
Гистограммы и гистограммы: категориальные и количественные
Гистограммы имеют общие характеристики с традиционными гистограммами — они измеряют частоту и используют аналогичную компоновку. Однако есть ключевое отличие:
Гистограммы, безусловно, являются полезным инструментом для визуализации размера каждой категории, но гистограммы являются лучшим способом отображения частотного распределения в диапазоне.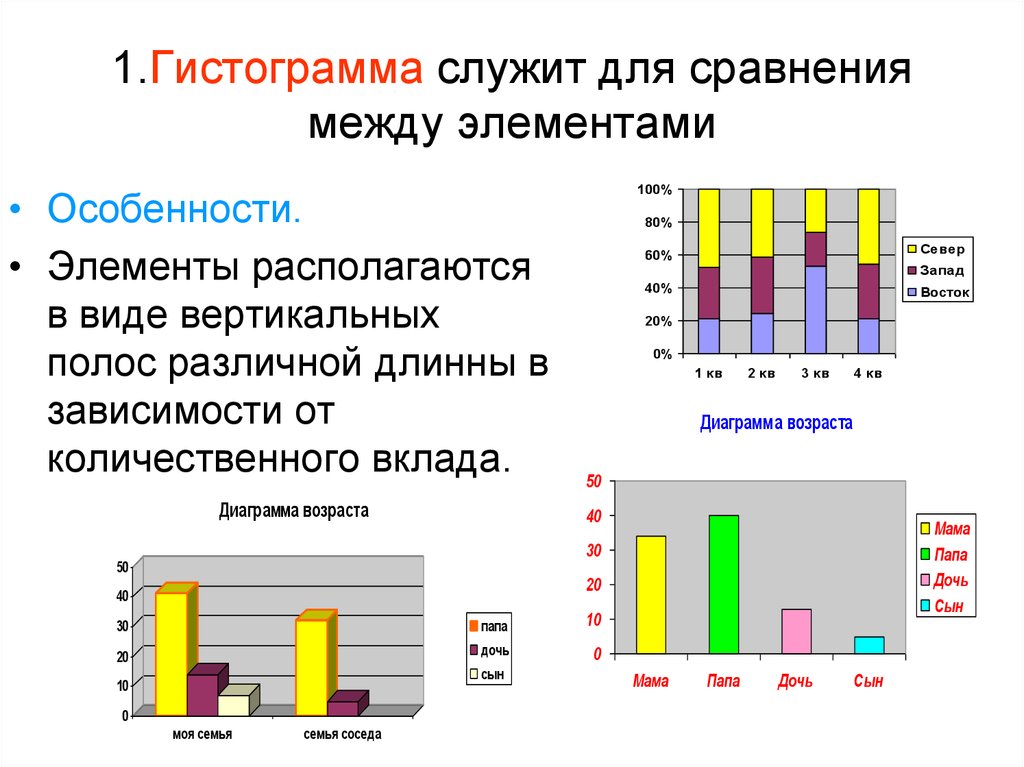 Гистограммы также позволяют нам лучше анализировать набор данных и находить его среднее значение, медиану и моду.
Гистограммы также позволяют нам лучше анализировать набор данных и находить его среднее значение, медиану и моду.
Как читать гистограммы
Мы можем использовать форму гистограммы, чтобы понять, как распределяются наши частотные данные и где находится центральная тенденция набора данных.
Средние значения: среднее, медиана и мода
Средние значения можно рассчитать тремя способами. Различные методы могут давать одинаковые или разные значения в зависимости от используемого набора данных. Рассмотрим этот простой набор данных:
1, 2, 2, 3, 3, 4, 5, 5, 5, 8
Три метода расчета, три разных средних значения. Цель усреднения — определить центральную тенденцию ваших данных — значение, вокруг которого группируются ваши данные. Глядя на форму вашего частотного распределения, вы можете увидеть, какое среднее значение лучше всего отражает эту центральную тенденцию.
Формы частотного распределения
Наиболее распространенным типом частотного распределения является нормальное распределение (также известное как распределение Гаусса или колоколообразная кривая). Эта симметричная форма показывает, что значения сгруппированы вокруг центрального пика с меньшим количеством экземпляров дальше. В нормальном распределении мода, медиана и среднее имеют одно и то же значение.
Наборы данных также могут быть смещены влево (отрицательное значение) или вправо (положительное значение). Вместо симметричной группировки вокруг центрального значения гораздо более высокие или более низкие значения искажают форму графика. В этих случаях мода, медиана и среднее различны. Для искаженных данных лучшим отражением центральной тенденции является медиана.
Некоторые гистограммы показывают два пика. Это известно как бимодальное распределение. Это распределение указывает на то, что в вашем наборе данных есть две перекрывающиеся группы. Мы рекомендуем попытаться разделить группы, чтобы получить более четкое представление о данных.
Одним из важнейших показателей Канбан-метода является продуктивность вашей команды. Он измеряется количеством выполненных работ за период времени (день, неделя, месяц). Этот показатель известен как пропускная способность. Наиболее эффективным способом визуализации изменения пропускной способности во времени является использование гистограммы пропускной способности. Отслеживание производительности вашей команды с течением времени позволит вам измерить и улучшить свои возможности.
Отслеживание производительности вашей команды с течением времени позволит вам измерить и улучшить свои возможности.
Используете ли вы гистограммы для мониторинга KPI? Какие закономерности вы замечаете в своих данных? Расскажите нам о своем опыте в комментариях!
Считаете ли вы эту статью ценной?
Рейтинг: 4,9 звезды (проголосовало 11 читателей)
Гистограмма | Think Design
Гистограмма — это график, который позволяет представлять точки данных, лежащие в диапазоне значений, называемых классами или бинами, создавая частотное распределение непрерывного набора данных. Это позволяет проверять данные на предмет их основного распределения (например, нормального распределения), выбросов, асимметрии и т. д. Будучи одним из семи основных инструментов контроля качества, это один из наиболее широко используемых способов представления любых данных для статистического анализа. .
Краткие сведения
Что: обнаружение изменений, распространение
Зачем: определение согласованности вашего процесса с помощью статистического анализа
История гистограммы
Карл Пирсон представил несколько ставших общепринятыми статистических инструментов. Одной из них была гистограмма, диаграмма, похожая на гистограмму, но представляющая набор непрерывных, а не дискретных данных. По этой причине Пирсон объяснил, что ее можно использовать в качестве инструмента при изучении истории, например, для составления графиков исторических периодов времени, и придумал название «гистограмма» в 189 г.1, чтобы передать его использование в качестве «исторической диаграммы».
Одной из них была гистограмма, диаграмма, похожая на гистограмму, но представляющая набор непрерывных, а не дискретных данных. По этой причине Пирсон объяснил, что ее можно использовать в качестве инструмента при изучении истории, например, для составления графиков исторических периодов времени, и придумал название «гистограмма» в 189 г.1, чтобы передать его использование в качестве «исторической диаграммы».
Гистограмма и гистограмма: Гистограмма представляет категории переменных на оси x. Хотя гистограмма представляет собой непрерывные неперекрывающиеся числовые интервалы в прогрессии, следовательно, ячейки (прямоугольники) являются последовательными.
Источник
Когда использовать гистограмму?
1 Сравните частоту появления количественных данных – Сравните высоту столбцов
Используйте гистограмму, когда весь диапазон значений непрерывных числовых данных может быть разбит на ряд интервалов, а затем сколько значений выпадает в каждом интервале можно посчитать. Ячейки (или интервалы) должны быть смежными и часто (но не обязательно) иметь одинаковый размер. Когда эти интервалы имеют одинаковую ширину, высота столбцов пропорциональна частоте и может использоваться для сравнения данных.
Ячейки (или интервалы) должны быть смежными и часто (но не обязательно) иметь одинаковый размер. Когда эти интервалы имеют одинаковую ширину, высота столбцов пропорциональна частоте и может использоваться для сравнения данных.
Частота появления сотрудников в разных возрастных диапазонах – Одинаковая ширина бина Гистограмма
Источник
2 Сравнить частоту появления количественных данных – Сравнить площадь столбцов при неравных интервалах
Фактически, на гистограмме это площадь полосы, которая указывает частоту появления для каждого бина. Это означает, что высота столбца не обязательно всегда указывает правильную частоту, но произведение высоты, умноженной на ширину ячейки, указывает частоту появления в пределах этой ячейки. Когда столбцы расположены неравномерно, высота бина не отражает частоту и не должна использоваться в качестве критерия для сравнения.
Плотность частоты = Частота/ширина класса; Гистограммы с переменной шириной бина
Источник
3 Обзор статистических аномалий в данных
— на график. Используйте гистограммы, чтобы оценить, где сосредоточены значения, каковы крайности и есть ли пробелы или необычные значения в вашем распределении данных. Определите режим распределения, найдя пик гистограммы как значение, которое встречается чаще всего или имеет наибольшую вероятность появления. Для многих явлений довольно часто распределение значений отклика группируется вокруг одномодового (унимодально-нормальное распределение), а затем распределяется с меньшей частотой в хвосты. Точно так же найдите бимодальные или мультимодальные наборы данных. Это может помочь диагностировать такие проблемы, как неоднородность данных, и изучить причину выбросов.
Используйте гистограммы, чтобы оценить, где сосредоточены значения, каковы крайности и есть ли пробелы или необычные значения в вашем распределении данных. Определите режим распределения, найдя пик гистограммы как значение, которое встречается чаще всего или имеет наибольшую вероятность появления. Для многих явлений довольно часто распределение значений отклика группируется вокруг одномодового (унимодально-нормальное распределение), а затем распределяется с меньшей частотой в хвосты. Точно так же найдите бимодальные или мультимодальные наборы данных. Это может помочь диагностировать такие проблемы, как неоднородность данных, и изучить причину выбросов.
Гистограммы, представляющие различные модели распределения по моде
Источник
4 Представление и обнаружение вероятностных явлений
В гидрологии оценочная функция плотности осадков и данные речного стока анализируются с помощью гистограмм распределения вероятностей. Гистограммы также полезны для получения приблизительного представления о распределении вероятностей и используются для понимания их поведения и частоты возникновения. Используйте гистограммы, чтобы дать приблизительное представление о плотности базового распределения данных для оценки плотности: при оценке функции плотности вероятности базовой переменной. Общая площадь гистограммы, используемой для плотности вероятности, всегда нормируется до 1. Однако для масштаба, который дает нам высоту данного столбца гистограммы, можно использовать только неотрицательные числа.
Гистограммы также полезны для получения приблизительного представления о распределении вероятностей и используются для понимания их поведения и частоты возникновения. Используйте гистограммы, чтобы дать приблизительное представление о плотности базового распределения данных для оценки плотности: при оценке функции плотности вероятности базовой переменной. Общая площадь гистограммы, используемой для плотности вероятности, всегда нормируется до 1. Однако для масштаба, который дает нам высоту данного столбца гистограммы, можно использовать только неотрицательные числа.
Гистограмма, представляющая распределения вероятностей
Источник
Типы гистограмм
1. Одинаковая ширина бина Гистограмма
представляет гистограмму равной ширины бина.
2. Гистограммы переменной ширины бина
Когда бины не имеют одинаковой ширины, площадь возведенного прямоугольника пропорциональна частоте случаев в бине. Вертикальная ось — это не частота, а плотность частоты — частота на единицу ширины класса на горизонтальной оси.
Вертикальная ось — это не частота, а плотность частоты — частота на единицу ширины класса на горизонтальной оси.
3. Нормализованные или кумулятивные гистограммы
Гистограмма также может быть нормализована для отображения «относительных» частот. Затем он показывает долю случаев, попадающих в каждую из нескольких категорий, с суммой высот, равной 1.
Когда не следует использовать гистограмму?
1 Если вам нужно показать распределение по нечисловым категориям
Не используйте гистограмму для построения графика частоты появления оценок в непрерывных наборах данных. Используйте гистограммы для других типов переменных, включая порядковые и номинальные наборы данных, поскольку гистограмма представляет собой график категориальных переменных. На линейчатых диаграммах между прямоугольниками есть промежутки, чтобы прояснить это различие.
2 Когда вам нужно представить и обнаружить корреляции между двумя переменными
Используйте точечный график, когда необходимы корреляции между величинами по осям X и Y, а не для представления и понимания распределения одной переменной между различными интервалы.


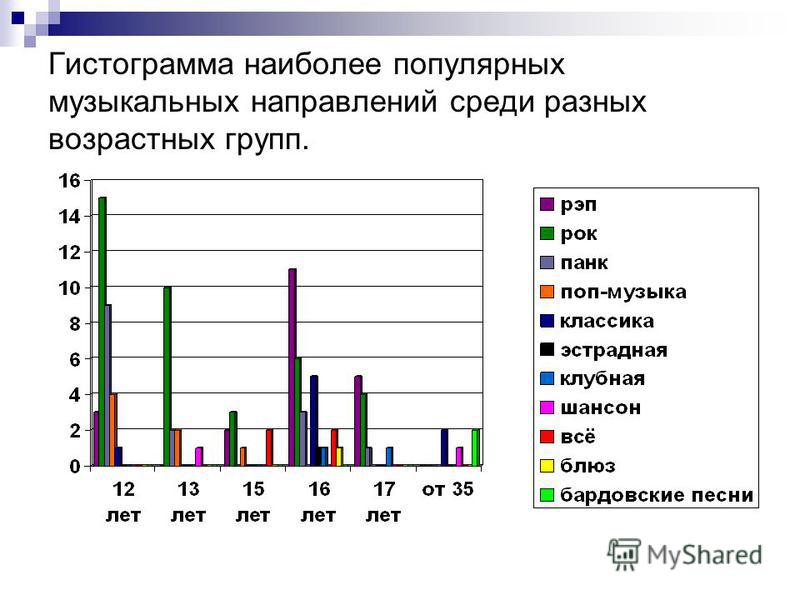
 0010
0010