Закон квадратов
← →
xayam ©
(2013-09-30 12:03) [0]
Есть такой изобретатель Джон Серл, он объясняет всё с помощью квадратов.
Вроде есть книги по этой теме с его авторством, но всё на английском.
кто-нибудь в курсе, что такое Закон квадратов?
PS Тема очень интересная
в магических квадратах как будто зашита какая-то необычная геометрия
вот пример для 3х3 http://ic.pics.livejournal.com/xayam/26173943/17399/17399_original.gif
← →
БарЛог ©
(2013-09-30 12:22) [1]
Гифка красивая, но в чём суть?
← →
xayam ©
(2013-09-30 12:29) [2]
вот суть вроде как в этом законе, а что это такое непонятно
> Гифка
там как раз показан пример для числа 3: три фигуры по три числа в каждой при трансформации (повороте и переносе) дают магический квадрат, нечто подобное явно есть и для больших квадратов 4х4, 5х5 и т.
д.← →
[ВладОшин] ©
(2013-09-30 13:00) [3]
> Джон Серл, он объясняет всё с помощью квадратов.
Дано: Двигатель внутреннего сгорания (или квазиэкспоненциальность:))
пример объяснения с помощью квадратов — в с тудию!
← →
Юрий Зотов ©
(2013-09-30 13:11) [4]
> [ВладОшин] © (30.09.13 13:00) [3]
Нет проблем: двигатель сообщает машине кинетическую энергию, равную эмвэ квадратпополам.
← →
БарЛог ©
(2013-09-30 13:36) [5]
> Джон Серл, он объясняет всё с помощью квадратов.
Почему 1С — УГ? 🙂
← →
[ВладОшин] ©
(2013-09-30 13:56) [6]
Дык очевидно же — потому что оно не развивает >> кинетическую энергию, равную эмвэквадратпополам.
← →
Туповатый ©
(2013-09-30 14:04) [7]
Я могу объяснить все что угодно при помощи кастрюли.
← →
vuk ©
(2013-09-30 14:04) [8]
to БарЛог © (30.09.13 13:36) [5]
> Почему 1С — УГ? 🙂
Потому, что пока в ней разбересся, голова будет — квадратная?
← →
[ВладОшин] ©
(2013-09-30 14:16) [9]
> Туповатый © (30.09.13 14:04) [7]
«А что на свете быстрее всего? Опусти руку, отрок! Эдак ты мне весь закон божий .
.» (с) Анекдот
← →
брат Птибурдукова
(2013-09-30 14:17
> пример объяснения с помощью квадратов — в с тудию!
Разъярённый муж врывается в комнату:
— Я всё знаю!
Жена, продолжая спокойно разгадывать кроссворд:
— Да?.. Ну назови приток Амазонки из девяти букв…
← →
[ВладОшин] ©
(2013-09-30 14:22) [11]
> хотя истинная магия в умножении числа из одних только единичек
> на самое себя.
после 11 разрядов не так смотрится 🙂
← →
Туповатый ©
(2013-09-30 14:24) [12]
> Джон Серл
почитал сейчас про него.
что же касается закона квадрата:
из википедии
Закон квадрата — куба представляет собой принцип, применяемый в технике и биомеханике, и базируется на математическом пересчете размеров. Он был впервые продемонстрирован в 1638 г. Галилео Галилеем в Discorsi e Dimostrazioni Matematiche, intorno a due nuove scienze («Беседы и математические доказательства двух новых наук»), 1638. Он гласит:
Когда объект подвергается пропорциональному увеличению размеров, его новый объём будет пропорционален кубу множителя, а новая площадь его поверхности пропорциональна квадрату множителя.
Всякие красивости с цифрами может найти любой чувак, измыслить из найденого нечто офигительное — любой больной чувак. Как же назвать тех, кто верит в это нечто офигительное?
Впрочем, чем бы дитя не тешилось, лишь бы не стало Крайоном – любящей ангельской сущностью.
← →
Туповатый ©
(2013-09-30 14:25) [13]
> после 11 разрядов не так смотрится 🙂
тогда из одних девяток
← →
Dimka Maslov ©
(2013-09-30 18:31) [14]
Тот удивительный факт, что круглые колёса поездов внезапно стучат по прямым гладким рельсам, легко объясняется тем, что площадь круга равна пи-на-эр-квадрат. Вот эти квадраты и стучат. Этому в любой паровозной школе научить могут.
← →
Inovet ©
(
> [14] Dimka Maslov © (30.09.13 18:31)
А уж квадратные стучат в квадрате, но этому учат в паравозных ВУЗах.
← →
RDen ©
(2013-09-30 18:52) [16]
> Dimka Maslov © (30.09.13 18:31) [14]
>
> Тот удивительный факт, что круглые колёса поездов внезапно
> стучат по прямым гладким рельсам
хм, а где это >по прямым гладким рельсам ?
или ты не про Россию?
← →
Dimka Maslov ©
(2013-09-30 21:45) [17]
> Inovet © (30.09.13 18:41) [15]
Парадокс в том, что квадратные вообще не едут, а поэтому не стучат вообще.
> RDen © (30.09.13 18:52) [16]
Этот анекдот был бояном ещё лет *цать назад. Вообще-то.
Закон квадрата | это… Что такое Закон квадрата?
Закон квадрата — куба представляет собой принцип, применяемый в технике и биомеханике, и базируется на математическом пересчете размеров.
Он был впервые продемонстрирован в 1638 г. Галилео Галилеем в «Discorsi e Dimostrazioni Matematiche, intorno a due nuove scienze («Беседы и математические доказательства двух новых наук»), 1638»;. Он гласит
Когда объект подвергается пропорциональному увеличению размеров, его новый объем будет пропорционален кубу множителя, а новая площадь его поверхности пропорциональна квадрату множителя.
где — объём исходного объекта, — новый объём, — линейный размер исходного объекта, а — новый линейный размер. Заметьте, что не имеет значения, какой линейный размер используется.
где — площадь поверхности исходного объекта, а — новая площадь поверхности.
Например, куб с длиной стороны 1 метр имеет площадь поверхности 6 м² и объём 1 м³. Если длину стороны удвоить, площадь его поверхности увеличится до 24 м², а его объём увеличится до 8 м³. Этот принцип применим ко всем телам.
Содержание
|
1 В живых существахТехника
Если физический объект увеличить в размерах при сохранении неизменной плотности материала, из которого он изготовлен, его масса увеличится пропорционально произведению массы и коэффициента увеличения в третьей степени, в то время как площадь его поверхности — только в квадрате масштабного множителя. Это должно означать, что в том случае, если увеличенному в размерах объекту сообщить то же ускорение, что и оригиналу, на поверхность увеличившегося объекта будет действовать большее давление
Давайте рассмотрим простой пример — тело массой = M имеет ускорение = a и площадь поверхности = A , на которую действует ускоряющая сила.
Сила, вызванная ускорением: F = M*a, а давление на поверхность T = F/A = M*a/A
Теперь рассмотрим объект, размеры которого умножены на коэффициент = x так, чтобы его новая масса M’ = x3*M, а поверхность, на которую действует сила, имеет новую площадь, A’ = x2*A.
Новая сила, вызванная ускорением F’ = x³*M*a и
Результирующее давление на поверхность
T' = F'/A'
= x3*M*a/(x2*A)
= x*(M*a/A)
= x*T
Таким образом, при простом увеличении размеров объекта с сохранением того же самого материала конструкции (плотности), и при том же самом ускорении, давление, производимое им на поверхность, увеличится во столько же раз. Это показывает, что способность сопротивляться напряжению у объекта снизится и он станет более склонен к разрушению в процессе ускорения.
Это и есть объяснение тому, почему большие транспортные средства плохо выдерживают испытания на разрушения при столкновениях и почему есть пределы высоты строительства высотных зданий. Аналогично, чем больше размер объекта, тем меньше другие объекты окажут сопротивление движению, вызывая его замедление
Биомеханика
Если размеры животного значительно увеличить, его мускульная сила серьёзно уменьшится, так как поперечное сечение его мускулов увеличится пропорционально квадрату коэффициента масштабирования, в то время как его масса увеличится пропорционально кубу коэффициента масштабирования.
В результате этого сердечно-сосудистые функции сильно ограничатся. Для летающих животных, если их увеличить в размерах, их нагрузка на крылья должна возрасти, и поэтому им, чтобы сохранять ту же подъемную силу, придется лететь быстрее,. Это будет нелегко ввиду того, что сила мускулов станет меньше. Это также объясняет, почему шмель может иметь большой размер тела относительно размаха его крыльев, что невозможно для большего летающего животного. Для животных малых размеров сопротивление воздуха на единицу массы также выше, что объясняет, отчего маленькое насекомое, такое, как муравей, не погибнет, падая с любой высоты.
По этой причине гигантские насекомые, пауки и другие животные, показываемые в фильмах ужасов — нереальны, поскольку такие крупные размеры вызвали бы их разрушение. Исключением являются гигантские водные животные, поскольку вода способна поддерживать такие огромные существа.
Тепловые процессы
Закон квадрата-куба применим также и к тепловым процессам. Поверхность теплообмена возрастает пропорционально квадрату размера, а объём, содержащий или генерирующий теплоту — пропорционально кубу.
Следовательно, теплопотери в расчёте на единицу объёма объекта уменьшаются при увеличении его размеров и, наоборот, увеличиваются при уменьшении размеров. Поэтому, например, энергия, необходимая для обогрева или охлаждения единицы объёма склада, уменьшается с ростом размеров склада.
В технике
Закон имеет очень широкое применение в технике. К примеру, он является единственной причиной того, что для создания самолетов вдвое бОльшей грузоподъемности было бессмысленно (и никогда не применялось) удвоение всех размеров на всех чертежах самолета — запрет на прямое масштабирование наложен законом квадрата-куба.
Интересным примером непонимания данного закона уже в наше время является история создания двигателя для а/м «Запорожец». Данный двигатель был скопирован удвоением всех основных размеров небольшого двухцилиндрового пускового двигателя с немецких бомбардировщиков времен II Мировой войны. Это безграмотное решение привело к целой лавине негативных эффектов, от несоответствия массы балансиров шатунов требуемой, до большой избыточной толщины стенок цилиндров, впоследствии растачивавшихся любителями до фантастических диаметров.
В живых существах
Данная статья представляет собой несколько доработанный перевод статьи из английской Википедии Square-Cube Law с добавлением текста о тепловых процессах
См. также
Биомеханика
Allometric law (англ.)
On Being the Right Size (англ.)
Ссылки
Wayne Throop. «Sauropods, Elephants, Weightlifters: Miscellaneous Issues» (англ.).
«World Builders: The Limits to Animal Size — Size to Volume Ratio». (англ.)
Michael C. LaBarbera. «The Biology of B-Movie Monsters»(англ.)
Общество SEG | Закон квадратов
Опубликовано в 18:55 в Сообщество, Медиа by admin
История Магических или Латинских квадратов восходит к тысячелетней давности, к пирамидам Древнего Египта и, возможно, даже к первым китайским династиям. На самом деле, сегодня китайцы все еще используют магические квадраты для обрезки и обрезки деревьев бонсай в соответствии с правильными математическими соотношениями природы. Понимая эти законы природы, можно утверждать, что Вселенная существует в соответствии с точными математическими законами.
Закон Квадратов (LOS) или Магические Квадраты — это не новая технология, а старая технология, которая возродилась после того, как Джон Серл в молодом возрасте разработал ее независимо и обнаружил, что его пронумерованная матрица обладает трехмерными свойствами, которые могут моделировать квантовую энергетические состояния массы во времени и пространстве.
Есть три группы квадратов – первая, вторая и третья, других быть не может. Квадраты первой группы состоят из всех нечетных чисел. Все четные числа, которые делятся на четыре, находятся во второй группе. Все остальные четные числа, не делящиеся на четыре, находятся в группе три.
Когда правильная матрица случайных чисел дает в сумме одно и то же значение линии поперек, вниз и по диагонали, тогда она так же верна, как и физика в отношении известных законов сохранения, согласно которым энергия не создается и не уничтожается, но может быть преобразована из одной формы в другую.
Матрица LOS точно демонстрирует эти консервативные законы, правильно трансформируя случайные числа квадратов в линейные значения, которые в сумме дают одно и то же значение в любом направлении, что приводит к неслучайному или единообразному состоянию суммирования без создания большего или меньшего значения чем общая сумма куба.
Технология LOS вместе с соответствующей стимуляцией является трансформационным решением для преобразования случайного квантового энергетического состояния в полезное неслучайное (однородное) состояние резонанса и когерентного движения электронов в атомной решетке или, проще говоря, может формировать электрические токи из хаоса.
Примечание. Первый закон термодинамики утверждает, что и работа, и теплота являются формами энергии и что полная энергия сохраняется, как показывает матрица LOS с ее точным суммированием; SEG функционирует в полном соответствии с этим законом.
Также обратите внимание: Второй закон термодинамики гласит, что в «замкнутой системе» беспорядок возрастает и для работы доступно меньше энергии. SEG функционирует на основе «открытой системы», как и жизнь, ветряные мельницы, гидроэлектростанции, солнечные батареи и т. д.
Дело в том, что 2-й закон НЕ применяется к «открытым системам»; Типичная ошибка самопровозглашенных экспертов — говорить иначе об энергетическом цикле SEG.
Квадрат четыре графически проиллюстрирован в трех измерениях; сложенные в любом направлении суммы 34.
Ядро квадрата — это куб 2×2, который представляет собой ядро квадрата.
Нажмите на изображение или здесь, чтобы просмотреть преобразование случайных результатов в однородные.
Для эффективной работы SEG различные материалы или элементы должны иметь определенную природу, вес и размеры. Кроме того, он должен быть сконфигурирован таким образом, чтобы соответствовать требованиям LOS с высоким уровнем точности материала на основе строгих математических критериев проектирования.
Профессор Джон Серл написал много книг на тему Закона Квадратов, и он использует эти квадратные матрицы и их законы для создания Генератора Эффекта Серла. Он объяснил уникальные свойства Закона Квадрата и много путешествовал, читая лекции о нем в школах, конгрессах и университетах многих стран.
Нажмите здесь, чтобы посмотреть видео, в котором профессор Серл отрабатывает квадраты на конференции Tesla 2010 года.
Колонн и Закон Квадратов – Джорджия Одиссея Разума
Существует обратно пропорциональная квадратичная зависимость между длиной колонны и весом, который она может нести. Если вы разрежете колонну пополам, одна из более коротких частей будет нести в четыре раза больше веса, чем исходная колонна. Это вычисляется следующим образом: возьмите ½ (вы разрезаете столбец пополам) и инвертируйте его, чтобы получить 2. Затем возведите в квадрат 2 (2 x 2), чтобы получить 4. Если вы возьмете столбец и разделите его на трети, одна из более короткие части будут нести в девять раз больше веса. (Переверните 1/3, чтобы получить 3, а затем возведите 3 в квадрат, чтобы получить 9.). Колонна, длина которой составляет одну четвертую (1/4) длины другой колонны, будет нести в 16 раз больший вес. Вы можете только нести это до сих пор. Вы не можете сделать материал прочнее, чем он есть. В этих примерах предполагается, что изменяется только длина столбцов. Если материал столбца каким-либо образом изменится, то примеры не работают.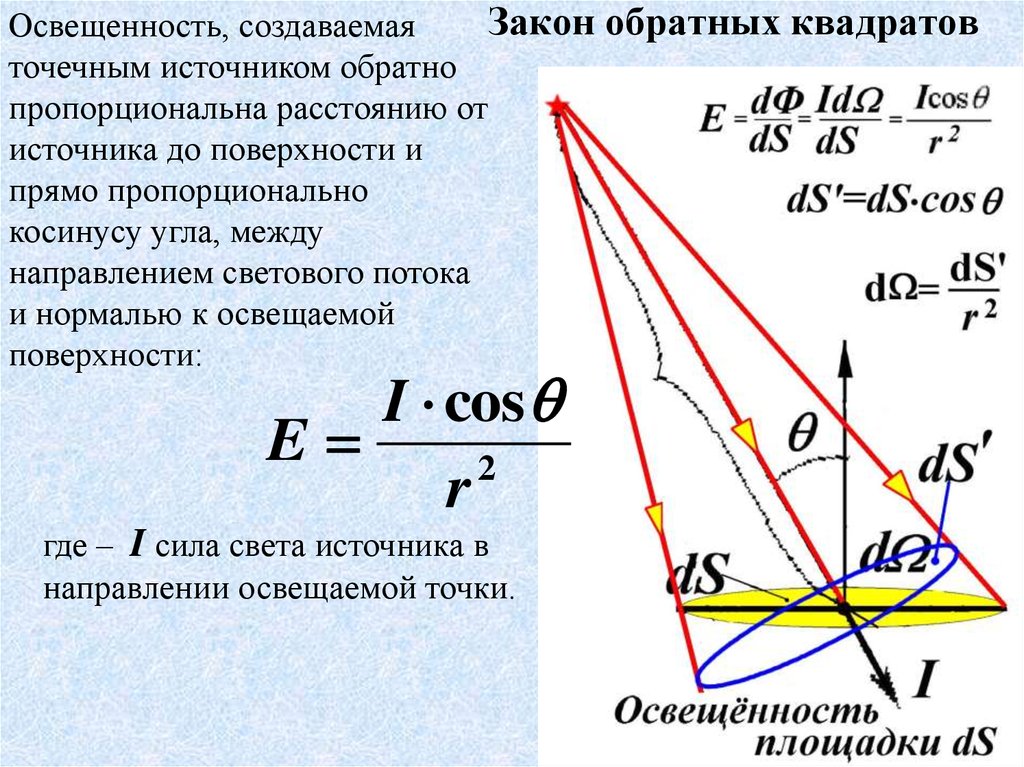
Проще всего посмотреть на это так. Если я разрежу колонну на 2 равные части, более короткая часть выдержит в четыре раза больше веса (2 в квадрате или 2 x 2). Если я разрежу колонну на 3 равные части, короткая часть выдержит в девять раз больший вес (3 в квадрате или 3×3).
Вот 2 простых эксперимента, чтобы продемонстрировать это:
Тест элементарного уровня:
- Возьмите кусок пробкового дерева длиной 1/8″ x 1/8″ x 36″ (не используйте куски большего размера, используйте только бальзовые дерево) .
2. Поставьте деревянный брусок вертикально на стол и слегка надавите на верхнюю часть палочки. Палка должна очень легко гнуться.
3. Затем свободной рукой (примерно 18″) держите палку посередине и нажимайте с таким же усилием. Заметили, что палка стала сильнее и ее труднее согнуть? (каждый так чуть-чуть…)
4. Повторите тест с помощником, держащим его в 2 точках посередине между тем, где вы держите его – примерно в 9″ от стола (1/4 высоты) и 27″ над столом (примерно 3/4 высоты).
путь вверх). Палка должна ощущаться намного прочнее, а не сгибаться так же легко.
Вы можете повторять этот тест снова и снова, разрезая палку пополам. Ключевой вывод заключается в том, чтобы заметить, насколько сильнее ощущается палка каждый раз, когда ее держат (напрягают). Это самый простой тест, который можно представить, чтобы показать концепцию 9.0048 Закон квадратов .
Тест на измеримые результаты
- Возьмите кусок пробкового дерева длиной 1/8″ x 1/8″ x 36″ (не используйте более крупные куски и используйте только пробковое дерево) .
- Положите палочку из бальзы на граммовую шкалу. Весы зарегистрируют некоторый вес дерева. Не снимая бальзовой палочки с весов, тарируйте весы (обнулите). Это удаляет вес палочки из показаний весов.
- Удерживая бальзовую палочку перпендикулярно шкале, поместите палец на верхнюю часть палочки и надавите, пока древесина не начнет гнуться. Запишите показания на весах. Число будет колебаться, поэтому просто выберите число, которое находится в середине показаний.
- Запишите это показание – вы только что рассчитали нагрузку на изгиб (вес) этой конкретной 36-дюймовой деревянной палки.
- Разрежьте 36-дюймовую палку на две 18-дюймовые части.
- Возьмите одну из 18-дюймовых частей и повторите шаги 2, 3 и 4. Теперь вы рассчитали нагрузку на изгиб этой 18-дюймовой части исходной 36-дюймовой колонны. Нагрузка на изгиб 18-дюймовой детали должна быть почти в четыре раза выше, чем на 36-дюймовую деталь.
- Возьмите один из 18-дюймовых кусков и обрежьте его до 12 дюймов в длину. Длина теперь составляет 1/3 длины оригинальной 36-дюймовой детали. Попробуйте предсказать, каков будет изгибающий вес 12-дюймовой детали, умножив изгибающий вес 36-дюймового элемента на 9.. (1/3 в перевернутом виде = 3 * 3 в квадрате = 9).
- Повторите шаги 2, 3 и 4 с 12-дюймовым куском и сравните со своей оценкой.
- Вы можете использовать эти эксперименты, чтобы узнать больше о свойствах дерева. Составьте таблицу и запишите вес каждого бруска бальзы до того, как вы его нарежете, а затем вес каждого куска, когда вы разрезаете его на 18-дюймовые и 12-дюймовые куски. Насколько близки к 1/2 веса 36-дюймовой палки две 18-дюймовые части? Насколько близки к 1/3 веса 36-дюймовой палки три 12-дюймовых клюшки?
Насколько близки к 1/2 веса 36-дюймовой палки две 18-дюймовые части? Насколько близки к 1/3 веса 36-дюймовой палки три 12-дюймовых клюшки?(Примечание: в этой демонстрации используется пробковая древесина 1/8″ x 1/8″, поскольку большинство весов должны быть в состоянии записывать все показания. Проведение эксперимента с более крупными кусками или более тяжелым деревом может быть опасным, поскольку количество сила, необходимая для того, чтобы согнуть детали, может быть чрезмерной, что приведет к поломке дерева и попаданию сломанного острого конца в руку.)
Вы можете задаться вопросом, какая польза от этой информации, потому что высота конструкции должна спецификации проблемы. Нет никакой пользы в том, чтобы знать, что если вы построите конструкцию вдвое меньше требуемой высоты, она выдержит в четыре раза больший вес.
Эта информация является полезной, поскольку при проектировании и строительстве конструкции раскосы делают колонну более короткой.