Закон обратных квадратов | это… Что такое Закон обратных квадратов?
Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.
|
Содержание
|
Обоснование
Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле ) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника. Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Проявления
Гравитация
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
- Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними.
 Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).
Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данное массивное тело, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу
Электростатика
Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними.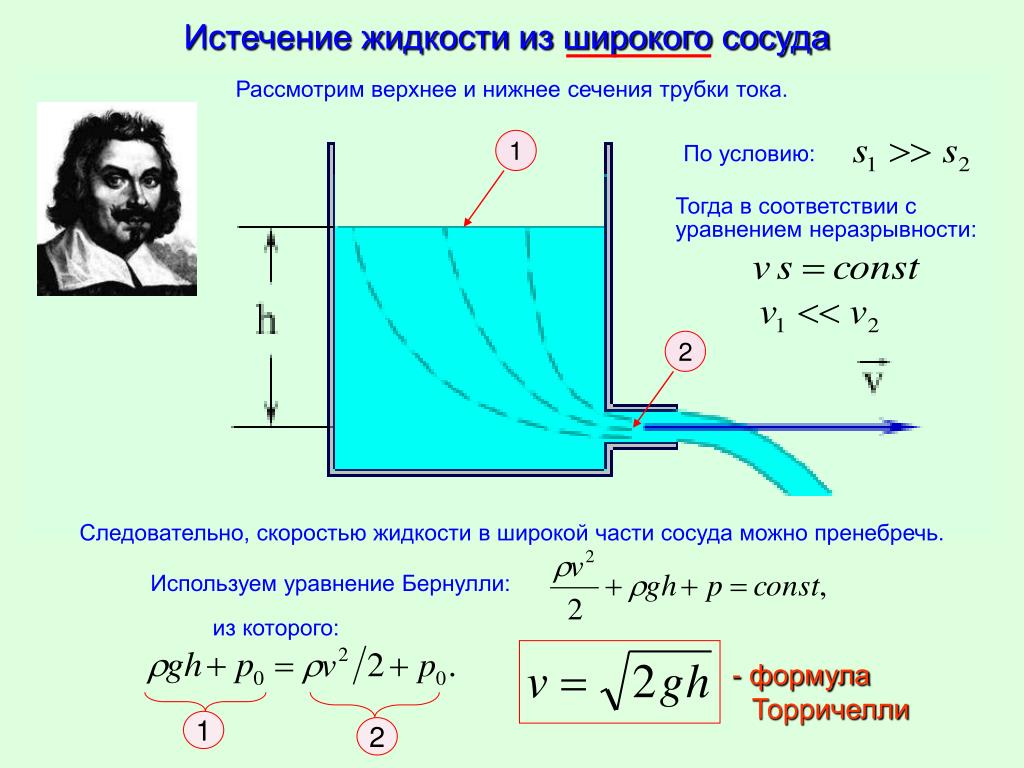 Это утверждение известно под названием закона Кулона.
Это утверждение известно под названием закона Кулона.
Свет и другие виды электромагнитного излучения
Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.
Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.
Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально первой степени расстояния:
Фотографы и театральные мастера по свету используют закон обратных квадратов для выбора оптимального места положения осветительных приборов.
Закон обратных квадратов может быть применён только для точечных источников света; наиболее распространённые в помещениях цилиндрические лампы дневного света не являются точечными источниками, и поэтому к ним нельзя применять закон обратных квадратов, в отличие от большинства других источников искусственного излучения.
Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.
Формулы закона обратных квадратов в рентгенографии имеют вид:
где
- I — интенсивность,
- r — расстояние (радиус).
Приложения в теории поля
Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.
Примечания
- ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.
- ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.
Закон обратных квадратов | это… Что такое Закон обратных квадратов?
Линии обозначают поток, исходящий от источника. Общее количество линий потока зависит от мощности источника и остаётся неизменным с увеличением расстояния от него. Более высокая плотность линий (количество линий на единицу площади) означает более сильное поле. Плотность линий потока обратно пропорциональна квадрату расстояния от источника, так как площадь поверхности сферы растёт пропорционально квадрату радиуса. Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
Таким образом, сила поля обратно пропорциональна квадрату расстояния от источника.
В физике закон обратных квадратов — это закон, утверждающий, что значение некоторой физической величины в данной точке пространства обратно пропорционально квадрату расстояния от источника поля, которое характеризует эта физическая величина.
|
Содержание
|
Обоснование
Закон обратных квадратов в общем случае применим, когда линии действия некоторой силы, или энергия или другая сохраняющая полное значение величина расходится (распространяется) в радиальном направлении от источника. По мере того, как площадь сферы (которая определяется по формуле ) растёт пропорционально квадрату расстояния от источника (радиуса сферы), и как испущенное излучение удаляется всё дальше от источника, это излучение должно проходить через поверхность, площадь которой растёт пропорционально квадрату расстояния от источника.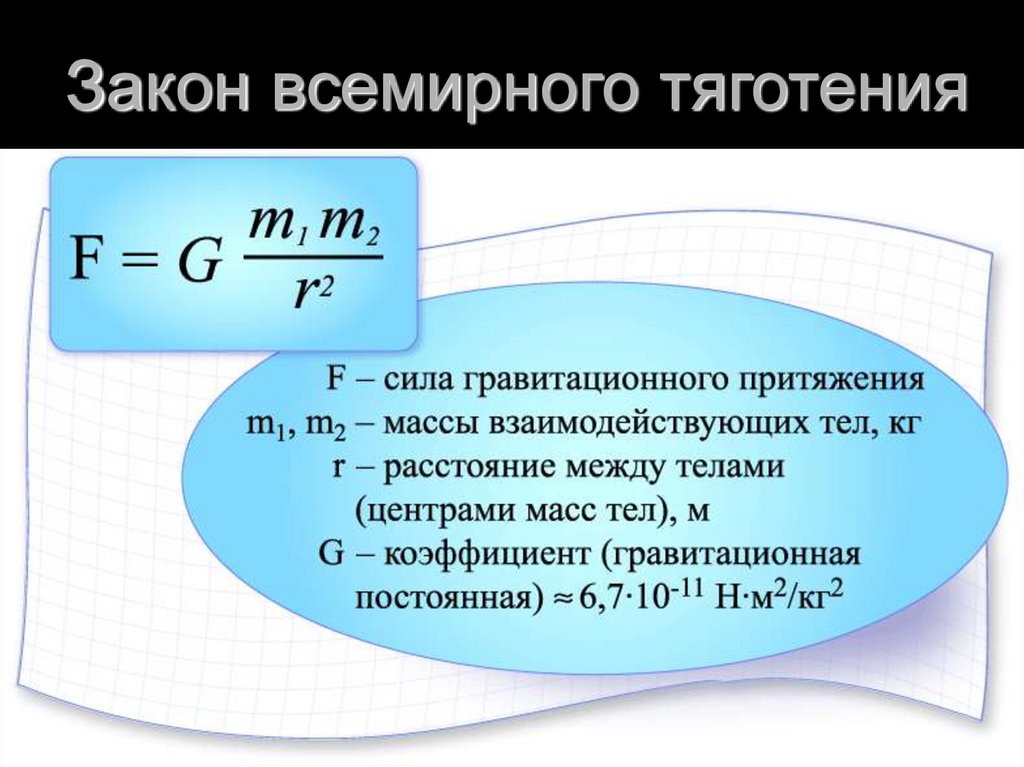 Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Следовательно, интенсивность излучения, проходящего через одну и ту же площадь, обратно пропорциональна квадрату расстояния от источника.
Проявления
Гравитация
Гравитация — это взаимодействие между двумя объектами, обладающими массами. Такие объекты подчиняются закону всемирного тяготения:
- Силы гравитационного взаимодействия между двумя точечными массами прямо пропорциональны произведению этих масс, и обратно пропорциональны квадрату расстояния между ними. Эти силы всегда действуют и направлены вдоль прямой, соединяющей эти точечные массы.
Если распределение масс в некотором материальном неточечном объекте обладает сферической симметрией, то такой объект может рассматриваться как точечная масса (материальная точка).
Однако, если мы хотим рассчитать силу взаимодействия между массивными телами, мы должны сложить векторно силы взаимодействия между всеми парами точечных масс, образующих данное массивное тело, и результирующее взаимодействие может не подчиняться закону обратных квадратов. В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
В то же время, если расстояния между двумя массивными объектами очень велики в сравнении с размерами этих объектов, то целесообразно рассматривать эти объекты как материальные точки при расчёте сил гравитационного взаимодействия между ними.
Как закон обратных квадратов закон всемирного тяготения был сформулирован в 1645 году Исмаэлем Буйо (Булиальдом). Это отличалось от предположения Иоганна Кеплера об обратно пропорциональной зависимости от расстояния. Но Булиальд не признавал справедливость ни второго и третьего законов Кеплера, ни решения Христиана Гюйгенса для движения по окружности. Буллиальд считал, что солнце притягивается в афелии и отталкивается в перигелии.
Роберт Гук и Джованни Альфонсо Борели в 1666 году подробно описали гравитационную силу как притягивающую силу [1]. В лекции в 1670 году Гук объяснил, что гравитация свойственна «всем небесным телам» и ввёл принцип, утверждающий, что сила гравитации убывает с расстоянием. К 1679 году Гук пришёл к выводу, что гравитация имеет обратно пропорциональную зависимость квадрату расстояния. Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы[2]
Он сообщил это в письме к Исааку Ньютону. Гук был достаточно резок, несмотря даже на то, что в своей работе «Начала» Ньютон признал, что Гук наряду с Реном и Галлеем независимо друг от друга применяли закон обратных квадратов для солнечной системы[2]
Электростатика
Сила притяжения или отталкивания, действующая между двумя заряженными частицами, в добавление к прямо пропорциональной зависимости от произведения зарядов, является обратно пропорциональной квадрату расстояния между ними. Это утверждение известно под названием закона Кулона.
Свет и другие виды электромагнитного излучения
Интенсивность света (то есть, энергия, приходящаяся на единицу площади в единицу времени) или других линейных волн, исходящих от точечного источника обратно пропорциональна квадрату расстояния от источника. Это значит, например, что объект, перемещённый на расстояние в 2 раза большее от источника, получает только четверть той мощности, которую он получал в первоначальном положении.
Например, интенсивность солнечных лучей составляет 9140 Вт на квадратный метр на орбите Меркурия, но лишь 1370 Вт на орбите Земли (на ту же площадь) — трёхкратное увеличение расстояния влечёт девятикратное уменьшение интенсивности солнечных лучей.
Следует отметить, что в отличие от интенсивности и от поля в статическом случае, амплитуда напряжённости электрического поля и магнитной индукции в электромагнитной волне от точечного источника падает обратно пропорционально
Фотографы и театральные мастера по свету используют закон обратных квадратов для выбора оптимального места положения осветительных приборов.
Закон обратных квадратов может быть применён только для точечных источников света; наиболее распространённые в помещениях цилиндрические лампы дневного света не являются точечными источниками, и поэтому к ним нельзя применять закон обратных квадратов, в отличие от большинства других источников искусственного излучения.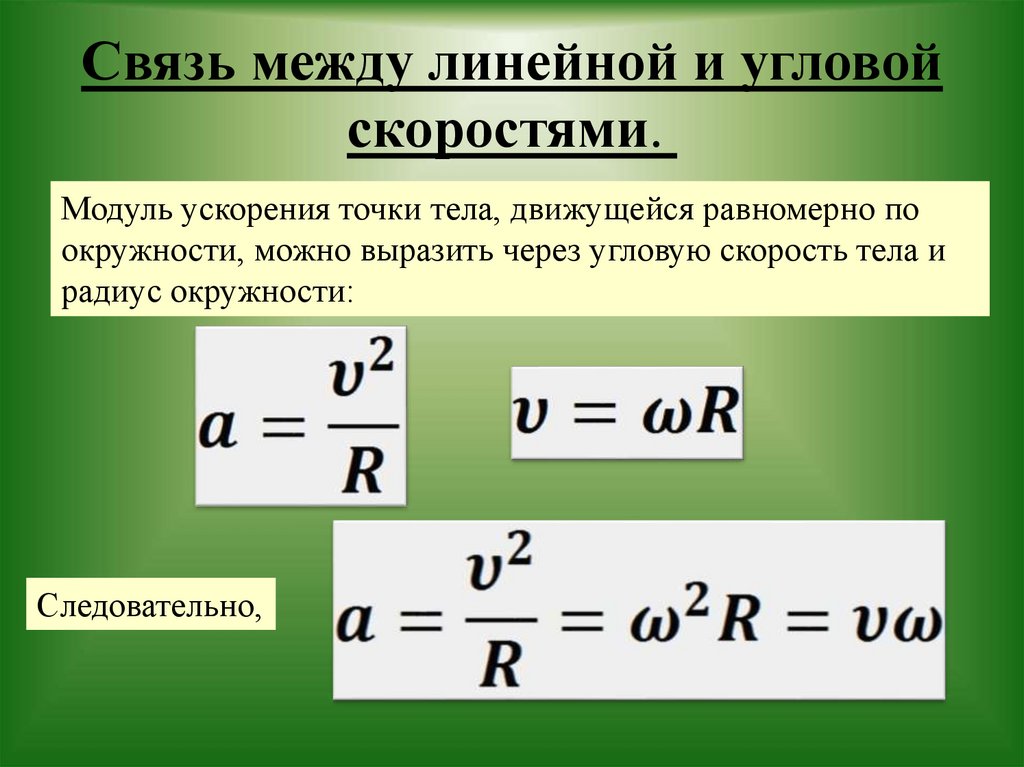
Закон обратных квадратов имеет некоторое значение в диагностической рентгенографии и радиационной терапии для расчёта дозы облучения. Однако эта пропорциональность не соблюдается в практических случаях, несмотря даже на то, что размеры источников облучения намного меньше расстояний до объекта облучения.
Формулы закона обратных квадратов в рентгенографии имеют вид:
где
- I — интенсивность,
- r — расстояние (радиус).
Приложения в теории поля
Для безвихревого векторного поля в трёхмерном пространстве закон обратных квадратов связан с тем свойством, что дивергенция обращается в ноль вне источника.
Примечания
- ↑ Гравитация Гука ещё не была универсальной, хотя она приблизилась к всеобщей универсальности гораздо больше, чем предыдущие гипотезы: См. стр. 239 в Curtis Wilson (1989), «The Newtonian achievement in astronomy», ch.13 (стр. 233—274) в «Planetary astronomy from the Renaissance to the rise of astrophysics: 2A: Tycho Brahe to Newton», CUP 1989.

- ↑ Ньютон признавал роль Рена, Гука и Галлея в этой связи в Scholium to Proposition 4 в книге I (во всех изданиях): см., например, английский перевод «Начал» от 1729 года, на стр. 66.
Яблоко, Луна и закон обратных квадратов
В начале 1600-х годов немецкий математик и астроном Иоганн Кеплер провел математический анализ известных астрономических данных, чтобы разработать три закона для описания движения планет вокруг Солнца. Три закона Кеплера возникли в результате анализа данных, тщательно собранных в течение нескольких лет его датским предшественником и учителем Тихо Браге. Три закона движения планет Кеплера можно кратко описать следующим образом:
- Траектории планет вокруг Солнца имеют эллиптическую форму, при этом центр Солнца находится в одном из фокусов. (Закон эллипсов)
- Воображаемая линия, проведенная от центра Солнца к центру планеты, заметает равные площади за равные промежутки времени. (Закон равных площадей)
- Отношение квадратов периодов любых двух планет равно отношению кубов их средних расстояний от Солнца.
 (Закон Гармоний)
(Закон Гармоний)
(Дальнейшее обсуждение этих трех законов дано в Уроке 4.)
Хотя законы Кеплера обеспечили подходящую основу для описания движения и траекторий планет вокруг Солнца, общепринятого объяснения того, почему такие траектории существуют, не существовало. Причина того, как планеты двигались, так и не была указана. Кеплер мог только предположить, что между Солнцем и планетами существовало какое-то взаимодействие, которое создавало движущую силу для движения планеты. Для Кеплера планеты каким-то образом «магнитно» приводились в движение солнцем по их эллиптическим траекториям. Однако между самими планетами не было взаимодействия.
Ньютон был обеспокоен отсутствием объяснения орбит планет. Для Ньютона должна быть какая-то причина такого эллиптического движения. Еще более тревожным было круговое движение Луны вокруг Земли. Ньютон знал, что должна быть какая-то сила, управляющая небесами; для движения Луны по круговой траектории и планет по эллиптической траектории требовалось наличие направленной внутрь составляющей силы.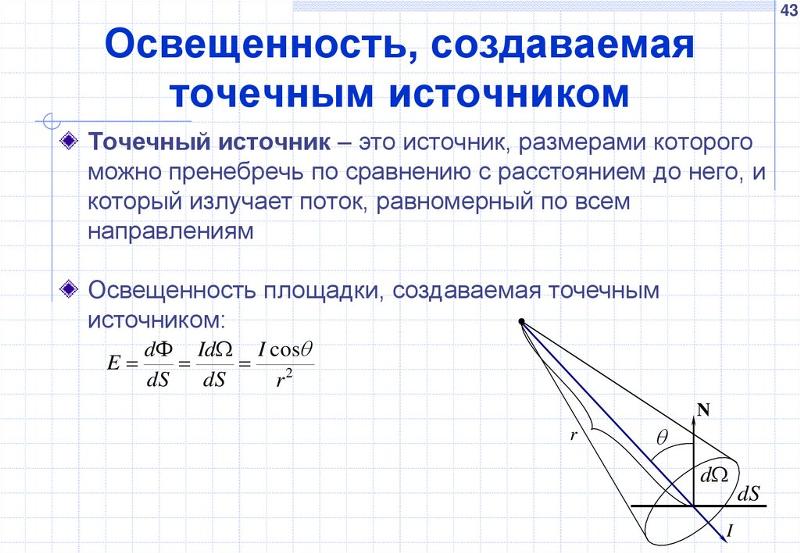 Круговое и эллиптическое движение были явно отклонениями от инерционных траекторий (прямолинейных) объектов. И как таковые, эти небесные движения требовали причины в виде неуравновешенной силы. Как вы узнали из Урока 1, круговое движение (как и эллиптическое движение) требует наличия центростремительной силы. Природа такой силы — ее причина и происхождение — какое-то время беспокоила Ньютона и послужила поводом для долгих умственных размышлений. А по легенде прорыв случился в 24 года в яблоневом саду в Англии. Ньютон никогда не писал о таком событии, однако часто утверждается, что представление о гравитации как причине всех небесных движений возникло, когда он был поражен яблоком по голове, когда лежал под деревом в саду в Англии. Миф это или реальность, но несомненно то, что Ньютон сумел связать причину небесного движения (обращение Луны вокруг Земли) с причиной земного движения (падение яблока на Землю). ), что привело его к понятию всеобщее тяготение .
Круговое и эллиптическое движение были явно отклонениями от инерционных траекторий (прямолинейных) объектов. И как таковые, эти небесные движения требовали причины в виде неуравновешенной силы. Как вы узнали из Урока 1, круговое движение (как и эллиптическое движение) требует наличия центростремительной силы. Природа такой силы — ее причина и происхождение — какое-то время беспокоила Ньютона и послужила поводом для долгих умственных размышлений. А по легенде прорыв случился в 24 года в яблоневом саду в Англии. Ньютон никогда не писал о таком событии, однако часто утверждается, что представление о гравитации как причине всех небесных движений возникло, когда он был поражен яблоком по голове, когда лежал под деревом в саду в Англии. Миф это или реальность, но несомненно то, что Ньютон сумел связать причину небесного движения (обращение Луны вокруг Земли) с причиной земного движения (падение яблока на Землю). ), что привело его к понятию всеобщее тяготение .
Мысленный эксперимент Ньютона в горах
Обзор работ Ньютона обнаруживает иллюстрацию, похожую на показанную справа. Иллюстрация сопровождалась обширным обсуждением движения Луны как снаряда. Рассуждения Ньютона шли следующим образом. Предположим, что пушечное ядро выпущено горизонтально с очень высокой горы в районе, лишенном сопротивления воздуха. В отсутствие гравитации пушечное ядро двигалось бы по прямолинейной траектории. Тем не менее, в присутствии силы тяжести пушечное ядро должно было упасть ниже этой прямолинейной траектории и, в конце концов, упасть на Землю (как в путь A ). Теперь предположим, что пушечное ядро снова летит горизонтально, но с большей скоростью. В этом случае пушечное ядро все равно упадет ниже своей прямолинейной тангенциальной траектории и в конечном итоге упадет на землю. Только на этот раз пушечное ядро пролетело дальше, прежде чем удариться о землю (как в пути B ). Теперь предположим, что существует скорость, с которой пушечное ядро может быть выпущено так, чтобы траектория падающего пушечного ядра соответствовала кривизне земли.
Иллюстрация сопровождалась обширным обсуждением движения Луны как снаряда. Рассуждения Ньютона шли следующим образом. Предположим, что пушечное ядро выпущено горизонтально с очень высокой горы в районе, лишенном сопротивления воздуха. В отсутствие гравитации пушечное ядро двигалось бы по прямолинейной траектории. Тем не менее, в присутствии силы тяжести пушечное ядро должно было упасть ниже этой прямолинейной траектории и, в конце концов, упасть на Землю (как в путь A ). Теперь предположим, что пушечное ядро снова летит горизонтально, но с большей скоростью. В этом случае пушечное ядро все равно упадет ниже своей прямолинейной тангенциальной траектории и в конечном итоге упадет на землю. Только на этот раз пушечное ядро пролетело дальше, прежде чем удариться о землю (как в пути B ). Теперь предположим, что существует скорость, с которой пушечное ядро может быть выпущено так, чтобы траектория падающего пушечного ядра соответствовала кривизне земли. Если бы можно было получить такую скорость, то ядро падало бы вокруг земли, а не в нее. Пушечное ядро упадет на Землю, ни разу не столкнувшись с ней, и впоследствии станет спутником, вращающимся по кругу (как в путь C ). А затем, при еще большей скорости запуска, пушечное ядро снова будет вращаться вокруг Земли, но по эллиптической траектории (как в траектории D ). Движение пушечного ядра по орбите вокруг Земли под действием силы тяжести аналогично движению Луны по орбите вокруг Земли. И если вращающуюся вокруг Луну можно сравнить с падающим пушечным ядром, то ее можно даже сравнить с падающим яблоком. Та же самая сила, которая заставляет объекты на Земле падать на землю, также заставляет объекты в небе двигаться по своим круговым и эллиптическим траекториям. Совершенно удивительно, что законы механики, которые управляют движением объектов на Земле, также управляют движением объектов в небе.
Если бы можно было получить такую скорость, то ядро падало бы вокруг земли, а не в нее. Пушечное ядро упадет на Землю, ни разу не столкнувшись с ней, и впоследствии станет спутником, вращающимся по кругу (как в путь C ). А затем, при еще большей скорости запуска, пушечное ядро снова будет вращаться вокруг Земли, но по эллиптической траектории (как в траектории D ). Движение пушечного ядра по орбите вокруг Земли под действием силы тяжести аналогично движению Луны по орбите вокруг Земли. И если вращающуюся вокруг Луну можно сравнить с падающим пушечным ядром, то ее можно даже сравнить с падающим яблоком. Та же самая сила, которая заставляет объекты на Земле падать на землю, также заставляет объекты в небе двигаться по своим круговым и эллиптическим траекториям. Совершенно удивительно, что законы механики, которые управляют движением объектов на Земле, также управляют движением объектов в небе.
Аргумент Ньютона в пользу того, что гравитация универсальна
Конечно, дилемма Ньютона заключалась в том, чтобы предоставить разумные доказательства распространения силы гравитации от земли до неба. Ключ к этому расширению требовал, чтобы он был в состоянии показать, как влияние гравитации ослабевает с расстоянием. В то время было известно, что сила гравитации заставляет привязанные к земле объекты (например, падающие яблоки) ускоряться по направлению к земле со скоростью 9.8 м/с 2 . Также было известно, что Луна движется к Земле со скоростью 0,00272 м/с 2 . Если та же самая сила, которая вызывает ускорение яблока относительно Земли, также вызывает ускорение Луны относительно Земли, то должно быть правдоподобное объяснение того, почему ускорение Луны намного меньше, чем ускорение яблока. Что такого в силе гравитации, которая заставляет более далекую луну ускоряться с ускорением, примерно равным 1/3600 ускорения яблока?
Ключ к этому расширению требовал, чтобы он был в состоянии показать, как влияние гравитации ослабевает с расстоянием. В то время было известно, что сила гравитации заставляет привязанные к земле объекты (например, падающие яблоки) ускоряться по направлению к земле со скоростью 9.8 м/с 2 . Также было известно, что Луна движется к Земле со скоростью 0,00272 м/с 2 . Если та же самая сила, которая вызывает ускорение яблока относительно Земли, также вызывает ускорение Луны относительно Земли, то должно быть правдоподобное объяснение того, почему ускорение Луны намного меньше, чем ускорение яблока. Что такого в силе гравитации, которая заставляет более далекую луну ускоряться с ускорением, примерно равным 1/3600 ускорения яблока?
Ньютон знал, что сила тяжести должна каким-то образом «разбавляться» расстоянием. Но как? Какая математическая реальность присуща силе гравитации, из-за которой она находится в обратной зависимости от расстояния между объектами?
Загадка решается сравнением расстояния от яблока до центра земли с расстоянием от луны до центра земли. Луна на своей орбите вокруг Земли примерно в 60 раз дальше от центра Земли, чем яблоко. Математическая связь становится ясной. Сила притяжения между Землей и любым объектом обратно пропорциональна квадрату расстояния, отделяющего этот объект от центра Земли. На Луну, находящуюся в 60 раз дальше, чем на яблоко, действует сила тяжести, равная 1/(60)9.0051 2 раза больше, чем у яблока. Сила тяжести подчиняется закону обратных квадратов .
Луна на своей орбите вокруг Земли примерно в 60 раз дальше от центра Земли, чем яблоко. Математическая связь становится ясной. Сила притяжения между Землей и любым объектом обратно пропорциональна квадрату расстояния, отделяющего этот объект от центра Земли. На Луну, находящуюся в 60 раз дальше, чем на яблоко, действует сила тяжести, равная 1/(60)9.0051 2 раза больше, чем у яблока. Сила тяжести подчиняется закону обратных квадратов .
Связь между силой тяжести ( F grav ) между Землей и любым другим объектом и расстоянием, разделяющим их центры ( d ) может быть выражена следующим соотношением
9 Поскольку расстояние d находится в знаменателе этой зависимости, можно сказать, что сила тяжести обратно пропорциональна расстоянию. А так как расстояние возведено во вторую степень, то можно сказать, что сила тяжести обратно пропорциональна квадрату расстояния. Это математическое соотношение иногда называют законом обратных квадратов, поскольку одна величина находится в обратной зависимости от квадрата другой величины. Обратно-квадратичное соотношение между силой гравитации и расстоянием между ними предоставило достаточно доказательств для объяснения Ньютоном того, почему гравитацию можно считать причиной как ускорения падающего яблока, так и ускорения Луны на орбите.
Это математическое соотношение иногда называют законом обратных квадратов, поскольку одна величина находится в обратной зависимости от квадрата другой величины. Обратно-квадратичное соотношение между силой гравитации и расстоянием между ними предоставило достаточно доказательств для объяснения Ньютоном того, почему гравитацию можно считать причиной как ускорения падающего яблока, так и ускорения Луны на орбите.
Использование уравнений как ориентира для размышлений
Закон обратных квадратов, предложенный Ньютоном, предполагает, что сила тяжести, действующая между любыми двумя объектами, обратно пропорциональна квадрату расстояния между центрами объектов. Изменение разделительного расстояния (d) приводит к изменению силы тяжести, действующей между объектами. Поскольку эти две величины обратно пропорциональны, увеличение одной величины приводит к уменьшению значения другой величины. То есть увеличение расстояния разделения вызывает уменьшение силы тяжести, а уменьшение расстояния разделения вызывает увеличение силы тяжести. Кроме того, коэффициент, на который изменяется сила тяжести, равен квадрату коэффициента, на который изменяется разделительное расстояние. Таким образом, если разделительное расстояние удвоить (увеличить в 2 раза), то сила тяжести уменьшится в четыре раза (2 во второй степени). А если расстояние увеличить втрое (увеличить в 3 раза), то сила тяжести уменьшится в девять раз (3 во второй степени). Размышление об отношениях сила-расстояние таким образом предполагает использование математических соотношений в качестве руководства к размышлениям о том, как изменение одной переменной влияет на другую переменную. Уравнения могут быть больше, чем рецепты для решения алгебраических задач; их может быть руководство к мышлению . Проверьте свое понимание закона обратных квадратов как руководства к мышлению, ответив на следующие вопросы ниже. Когда закончите, нажмите кнопку, чтобы проверить свои ответы.
Кроме того, коэффициент, на который изменяется сила тяжести, равен квадрату коэффициента, на который изменяется разделительное расстояние. Таким образом, если разделительное расстояние удвоить (увеличить в 2 раза), то сила тяжести уменьшится в четыре раза (2 во второй степени). А если расстояние увеличить втрое (увеличить в 3 раза), то сила тяжести уменьшится в девять раз (3 во второй степени). Размышление об отношениях сила-расстояние таким образом предполагает использование математических соотношений в качестве руководства к размышлениям о том, как изменение одной переменной влияет на другую переменную. Уравнения могут быть больше, чем рецепты для решения алгебраических задач; их может быть руководство к мышлению . Проверьте свое понимание закона обратных квадратов как руководства к мышлению, ответив на следующие вопросы ниже. Когда закончите, нажмите кнопку, чтобы проверить свои ответы.
Мы хотели бы предложить…
Иногда недостаточно просто прочитать об этом.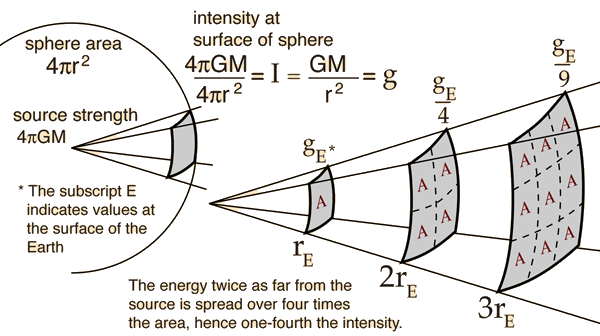 Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Gravitation Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Gravitation Interactive позволяет учащимся в интерактивном режиме исследовать закон обратных квадратов гравитации.
Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашей Gravitation Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Gravitation Interactive позволяет учащимся в интерактивном режиме исследовать закон обратных квадратов гравитации.
Посетите: Gravitation Interactive
Проверьте свое понимание
1 . Предположим, что два объекта притягиваются друг к другу с силой притяжения 16 единиц. Если расстояние между двумя объектами увеличить вдвое, какова новая сила притяжения между двумя объектами?
2. Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если расстояние между двумя объектами утроить, то какова новая сила притяжения между двумя объектами?
3. Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если расстояние между двумя объектами уменьшить вдвое, то какова новая сила притяжения между двумя объектами?
Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если расстояние между двумя объектами уменьшить вдвое, то какова новая сила притяжения между двумя объектами?
4. Предположим, что два объекта притягиваются друг к другу с силой тяжести 16 единиц. Если расстояние между двумя объектами уменьшить в 5 раз, то какова новая сила притяжения между двумя объектами?
5. Недавно завершив свой первый курс физики, Ной Формула разработал новый бизнес-план на основе темы своего учителя «Физика для лучшей жизни ». Ной узнал, что объекты весят разное количество на разном расстоянии от центра Земли. Его план включает в себя покупку золота по весу на одной высоте, а затем продажу его на другой высоте по той же цене за вес. Должен ли Ной покупать на большой высоте и продавать на низкой высоте или наоборот?
Следующий раздел:
Перейти к следующему уроку:
Определение закона обратных квадратов
Не сходите с ума! Для некоторых из вас слова «Закон обратных квадратов» могут вызвать болезненные воспоминания о том уроке математики в старшей школе, который, как вы думали, наконец-то позади, но мы обещаем, что это не так сложно. Мы объясним эту концепцию, используя термины непрофессионала или, как я их называю; «Условия Пимана».
Мы объясним эту концепцию, используя термины непрофессионала или, как я их называю; «Условия Пимана».
Закон обратных квадратов можно легко понять, если помнить об этих двух вещах.
- Ваш свет теряет мощность по мере увеличения расстояния от источника до объекта.
- Вы потеряете этот свет быстрее, чем вы думаете.
Например, если вы установили источник света на расстоянии 1 метра от объекта и получаете 100%-ную мощность вспышки на объект. Вы перемещаете свет на 1 метр назад, и теперь вы находитесь на расстоянии 2 метров. Означает ли это, что вы потеряли половину своего света, около 50%? Вроде бы логично, но это не так. Вы фактически теряете 75% своего света. Мы можем сказать это по-другому. У вас есть только 25% интенсивности вашего света, попадающего на объект, или ¼ вашего света. Ниже диаграмма увеличена, чтобы помочь визуализировать это.
Прежде чем двигаться дальше, давайте быстро взглянем на реальную формулу.
Интенсивность=1/Расстояние²
Почему это называется законом обратных квадратов? Давайте разберем его шаг за шагом:
Проще говоря, инверсия означает противоположность самой себе. Вы переворачиваете его. Например, 2 будет ½, а 4 будет ¼.
Вы переворачиваете его. Например, 2 будет ½, а 4 будет ¼.
Проще говоря, квадрат означает число, умноженное само на себя. Например, 2×2 или 10×10.
Объединив их, мы получим обратный квадрат.
2 обратное равно ½
½ в квадрате равно ½ X ½
А что такое ½ X ½? Это ¼.
Итак, 2 обратно в квадрат равно ¼. Другой способ сказать это с точки зрения фотографии: на расстоянии 2 метров вы получаете ¼ мощности. Это закон обратных квадратов. Вот как вы это понимаете. Если вы знаете расстояние, на котором вы собираетесь находиться от объекта, все, что вам нужно сделать, это подставить это число в формулу, чтобы узнать, сколько света вы потеряете.
Глядя на наш график, вы также замечаете кое-что очень интересное. От 1 метра до 6 метров процент потери света драматичен. А вот от 6 до 7 метров не так драматично, всего 0,6%. Также от 7 метров до 8 метров, это всего около 0,5%.
Зная эти основы, закон обратных квадратов чаще всего используется при съемке больших групповых фотографий. Он имеет практический смысл. Если вы разместите свой источник света впереди и в центре своей группы на расстоянии около 3 метров, основываясь на нашей таблице и формуле, вы можете подумать, что группа будет получать 11,11% вашего света, и вы соответствующим образом отрегулируете (увеличив мощность). Но только человек в центре будет получать 11,11%.
Люди в дальних углах группы будут дальше, чем в центре. Они могут находиться на расстоянии 6 метров от источника света, что дает им только 2,78% мощности. Это создает очень нелестный и неравномерный свет для групповых портретов. Поскольку мы знаем, что интенсивность света имеет менее резкое падение на большем расстоянии, мы должны отодвинуть источник света еще дальше, чтобы обеспечить равномерное освещение всех людей.
Равномерное освещение для семьи
Закон обратных квадратов не так сложен, как кажется, и знание этих основ принесет вам большую пользу.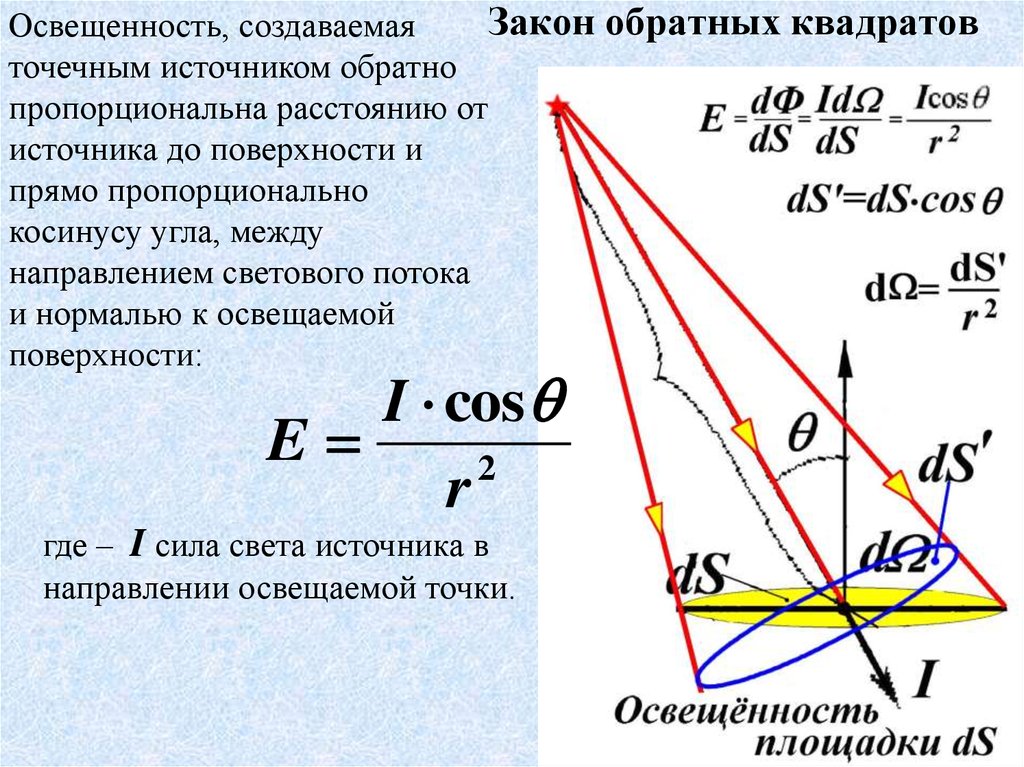
Закон обратных квадратов на практике | Транскрипция
Ниже приведена полная транскрипция видео выше
Это мой любимый слайд. Перевернутый Квадрат Пай-мэн, что-то вроде Пакмана, но я Пай. Ты понял? Хорошо, вы получите это всего за секунду. Эта прекрасная демонстрация в реальном мире, или действительно моя демонстрация в реальном мире, дает вам пример закона обратных квадратов на практике. Это не очень хорошая практика, но она показывает вам пример. У нас есть свет, размещенный здесь, с левой стороны. Это все разные кадры, и в основном здесь мы находимся в одном футе, двух футах, трех футах, четырех футах, пяти футах, шести футах от света.
Допустим, одним футом мы получаем сто процентов желаемого света, которого хотим. Когда мы отойдем на два фута, вы заметите, что я намного темнее, чем на этом снимке. Этот кадр практически на грани провала. Этот выстрел составляет одну четверть интенсивности этого выстрела. Когда мы отходим, ты видишь, как я становлюсь все темнее и темнее.
Интересно отметить, что разница между одним футом и, скажем, тремя футами, чрезвычайно драматична в яркости. Это огромная разница, но разница между пятью и даже семью футами очень мала. Это намного меньше первоначальной разницы. По сути, мы узнаем, что чем дальше мы удаляемся от источника света, тем свет падает гораздо медленнее, чем вблизи этого источника света.
Мы видели это в мире Пая. Давайте посмотрим еще одну демонстрацию в реальном мире с участием жуткого Джозефа. Что мы здесь сделали? Ну, обратная квадратная линия, и практика, и пусть он не сделает такую дерьмовую фотографию на практике. Это просто потому, что я хочу показать вам жуткую, дерьмовую фотографию, но на этом снимке мы сделали то, что в основном поместили вспышку прямо на левую сторону лица Оливии. Джо находится на расстоянии примерно одного фута от Оливии. Расстояние до Оливии составляет примерно один фут от вспышки, и это делает расстояние Джо от вспышки вдвое больше, чем расстояние до Оливии.
Если вы посмотрите на Оливию, она красивая, яркая и с правильной экспозицией, а если вы посмотрите на Джо, то увидите, что он недоэкспонирован примерно на три-четыре шага. Особенно, когда вы начинаете переходить к другой стороне его лица, он становится еще темнее. Теперь Джо немного подкрался к ней, чтобы приблизиться к этому, но здесь вспышка находится в основном в четырех футах от модели. Теперь, что мы сделали здесь, все, что мы делаем, это регулируем мощность вспышки.
Особенно, когда вы начинаете переходить к другой стороне его лица, он становится еще темнее. Теперь Джо немного подкрался к ней, чтобы приблизиться к этому, но здесь вспышка находится в основном в четырех футах от модели. Теперь, что мы сделали здесь, все, что мы делаем, это регулируем мощность вспышки.
Каждый раз, когда мы делаем шаг в сторону, нам приходится увеличивать мощность вспышки, чтобы компенсировать это, потому что теперь расстояние вспышки до объектов становится намного больше. Смотри, в этом Джо был в два раза дальше Оливии от той вспышки. Где, как и на этой стороне, Джо теперь всего на один фут дальше, чем Оливия. Оливия в четырех футах от вспышки, а Джо в пяти футах. Вы заметите, что падение гораздо менее драматично. Джо на самом деле гораздо больше похож на Оливию.
Здесь мы перемещаем вспышку на восемь футов. Мы включили вспышку еще немного выше, и снова Джо оказался в жутких шести дюймах от лица Оливии, и она наслаждается этим. Между прочим, ей все это нравится, но здесь Джо примерно в девяти футах от вспышки, а Оливия примерно в восьми футах. Вы можете видеть, что экспозиции равны. Нам нужно увеличить мощность вспышки, но чем дальше мы удаляемся от источника света, в основном, чем дальше находится группа, тем более похоже относительное расстояние. Сейчас у Оливии всего восемь футов, у Джо девять футов, и мы получаем примерно такое же освещение.
Вы можете видеть, что экспозиции равны. Нам нужно увеличить мощность вспышки, но чем дальше мы удаляемся от источника света, в основном, чем дальше находится группа, тем более похоже относительное расстояние. Сейчас у Оливии всего восемь футов, у Джо девять футов, и мы получаем примерно такое же освещение.
Когда мы высаживаем большую группу, предположим, что группа имеет ширину десять футов. Мне может понадобиться вспышка, может быть, в двадцати или тридцати футах от меня. Опять же, в зависимости от угла этого света от группы, чтобы иметь возможность получить примерно одинаковую яркость для всех, и для этого есть и другие методы, которые мы рассмотрим в Lightning 201 и 301, где мы берем камеру, я хочу снять вспышку с камеры. Теперь, прежде чем мы закончим этот сумасшедший дерьмовый тест, многое было усложнено, закон обратных квадратов. Позвольте мне дать вам четыре простых вывода.
Номер один. Закон обратных квадратов по-прежнему применяется к физическим лицам. То есть снимаю ли я прекрасную модель, будь то парень или девушка.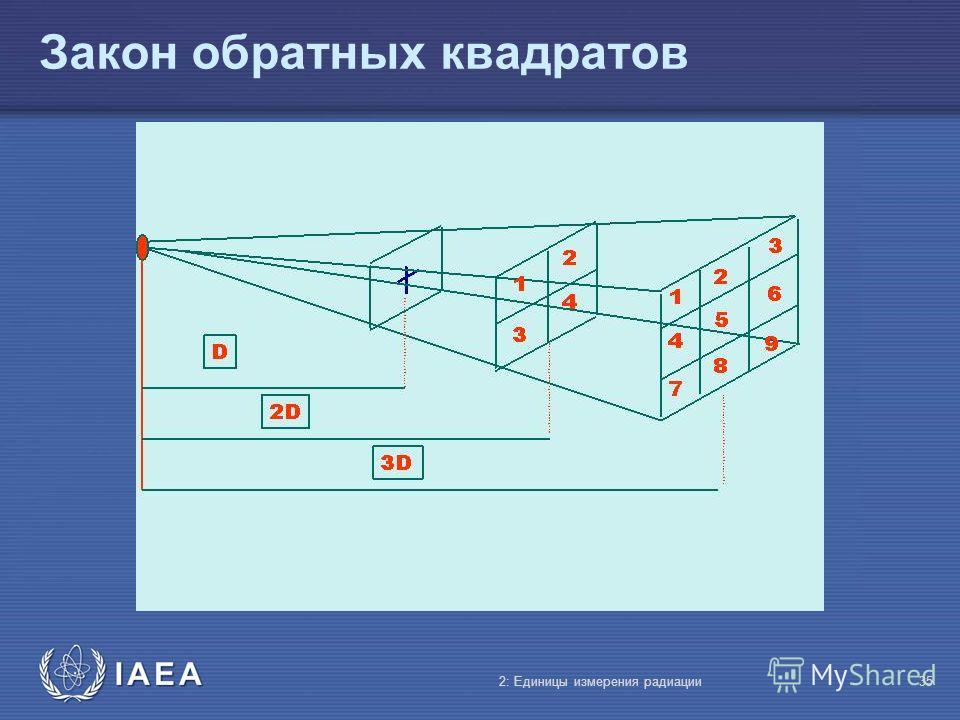 Предположим, что в данном случае это Оливия. В этом кадре я поместил источник света так близко к голове Оливии, что если я снимаю Оливию в полный рост, ее голова будет намного ярче, чем остальная часть ее тела, и вы действительно можете это увидеть.
Предположим, что в данном случае это Оливия. В этом кадре я поместил источник света так близко к голове Оливии, что если я снимаю Оливию в полный рост, ее голова будет намного ярче, чем остальная часть ее тела, и вы действительно можете это увидеть.
Вспышка прямо здесь, и вы даже можете видеть, когда она достигает ее груди, я получаю только двадцать, тридцать процентов света, как я был на ее лице. Если я помещу модификатор света очень близко к кому-то, он все равно будет иметь тот же эффект, даже если я просто снимаю их по отдельности, а не в группе. Помните, если я хочу равномерно освещать все части тела, то этот свет должен быть примерно на одинаковом расстоянии от всего тела, от головы до пяток.
Номер два. Чем больше людей в кадре, тем больше расстояние вы хотите снять. Чем больше группа, просто отодвиньте свет немного дальше, чтобы равномерно осветить всех, а это значит, что вам нужно будет включить свет. Помните, что вы теряете больше света, чем думаете. Каждый раз, когда вы удваиваете расстояние, вы увеличиваете оставшуюся мощность вспышки в четыре раза. Удвоение расстояния означает увеличение мощности на двадцать пять процентов.
Удвоение расстояния означает увеличение мощности на двадцать пять процентов.
Номер три. Основное эмпирическое правило. Когда вы пытаетесь осветить группу людей, скажем, группу из десяти человек, каждый человек в этой группе из десяти человек находится примерно на одинаковом расстоянии от моего источника света. Мой источник света находится на расстоянии пятнадцати футов, двадцати футов, тогда разница в один или два фута между этим относительным расстоянием на самом деле не будет иметь большого значения, но если мы говорим о двадцати футах от источника света с одной стороны. по сравнению с десятью футами от света на другой стороне, да, вы получите двадцать пять процентов вашего света на той стороне, и вы получите сто процентов вашего света на другой стороне. Просто помните, все ли примерно на одинаковом расстоянии от источника света?
Число четыре более драматично, угол вспышки, тем больше расстояние, которое вам нужно, чтобы иметь одинаковое относительное расстояние для всех в группе, и вот что это значит. Все это означает, что моя вспышка находится прямо над моей камерой, что опять же зависит от того, какие у вас есть инструменты и что у вас есть, но давайте просто скажем, что я использую прямую вспышку для группы из пятнадцати человек. Если я стою на расстоянии десяти футов, то мое расстояние до всех пятнадцати человек примерно одинаковое.
Все это означает, что моя вспышка находится прямо над моей камерой, что опять же зависит от того, какие у вас есть инструменты и что у вас есть, но давайте просто скажем, что я использую прямую вспышку для группы из пятнадцати человек. Если я стою на расстоянии десяти футов, то мое расстояние до всех пятнадцати человек примерно одинаковое.
Это может отличаться от шести дюймов до фута или около того, так как эта прямая вспышка находится на моей камере, и она направлена на каждого человека в группе. Очень небольшая разница, я получу примерно одинаковую яркость для каждого человека с этого ракурса, но как только я сниму вспышку с камеры, и, скажем, мне даже не нужно снимать вспышку с камеры. Я могу отражаться от отражателя или чего-то еще. Как только я удаляю основной источник света от камеры, картина становится более драматичной. Мы получаем больше теней.
Теперь этот свет будет благоприятствовать одной стороне группы гораздо сильнее, чем другой стороне. Как только этот свет окажется под углом, группа, которая находится на этой стороне, теперь, вероятно, будет намного ближе, может быть, в десяти футах от вспышки.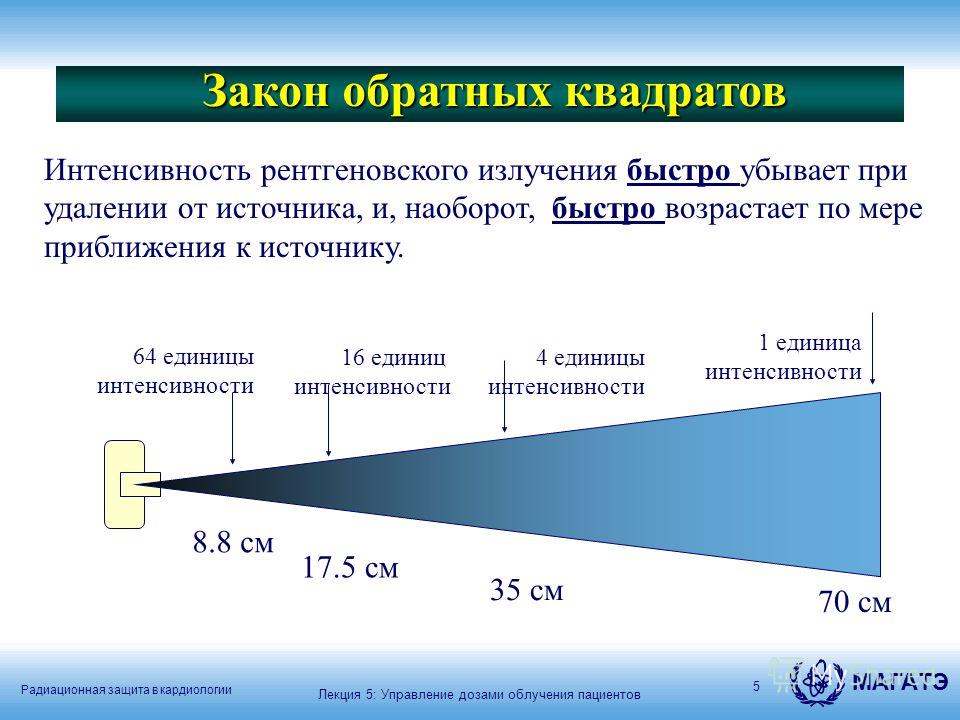

 3 Свет и другие виды электромагнитного излучения
3 Свет и другие виды электромагнитного излучения