Откуда в подсолнухе золотое сечение? / Хабр
Пропорция золотого сечения известна людям уже несколько тысяч лет и всё это время не теряет популярности как в чисто математической среде, так и среди художников, скульпторов, философов, биологов. Золотое сечение можно найти в:
Классической живописи
Скульптуре
Архитектуре
Принципах перспективы и композиции фотографий
Пропорциях человеческого тела
Ракушках
Растениях
Развитии эмбрионов
Ветвях галактик
И во множестве других, подчас весьма необычных, сфер.
Сегодня мы будем говорить о растениях.
Из труда А. Цезинга «Эстетические исследования».Идея золотого сечения очень проста. Возьмем отрезок, и разделим его на две части Существует единственный способ разделить отрезок на две части с длинами , так что отношение длины всего отрезка к большей части равно отношению большей части к меньшей.
В самом деле, пусть длина отрезка ; по условию
Определив и немного преобразовав систему, получим квадратное уравнение:
У этого уравнения единственный положительный корень
Число называется числом Фидия или, попросту, пропорцией золотого сечения.
На заглавной картинке изображен цветок подсолнечника маслянистого — растения, масло из семян которого вы почти наверняка регулярно употребляете в пищу. С точки зрения ботаники, большой красивый цветок подсолнуха называется «соцветием-корзинкой». Желтые лепестки соцветия — видоизмененные листья; они окаймляют корзинку из крошечных желтых цветков, каждому из которых после опыления суждено превратиться в семечко. Рассматривая корзинку подсолнуха, мы можем обнаружить удивительный факт:
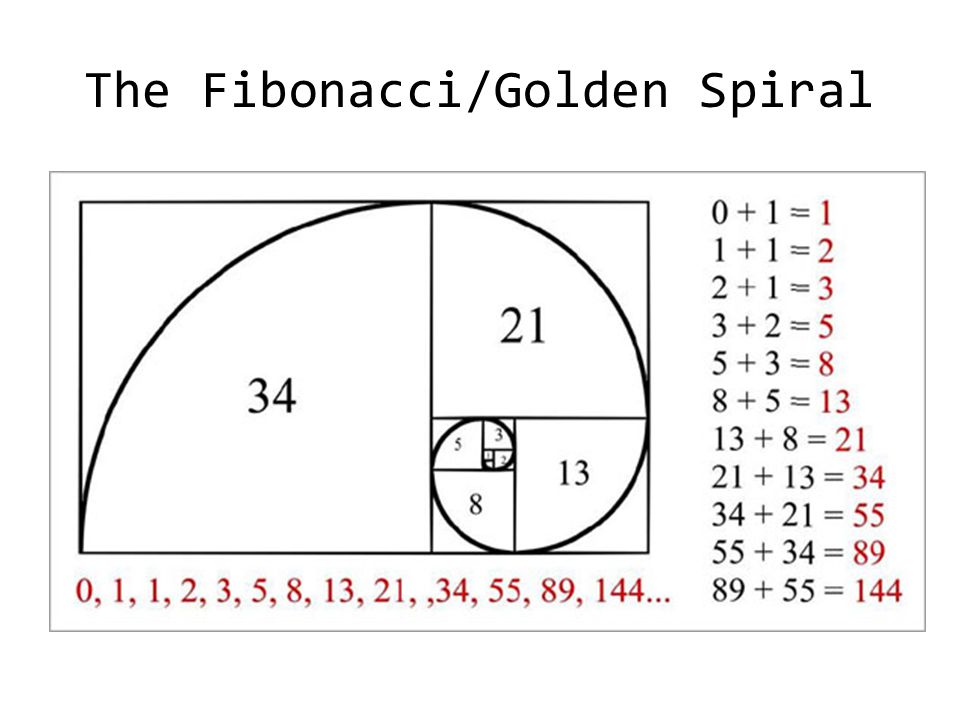
Человеческий глаз легко различает, как семена группируются по спиралям — левым и правым. Их число различно. Приложив усилия, можно сосчитать, что в цветке подсолнуха на фотографии 21 спираль идет по часовой стрелке и 34 спирали — против часовой.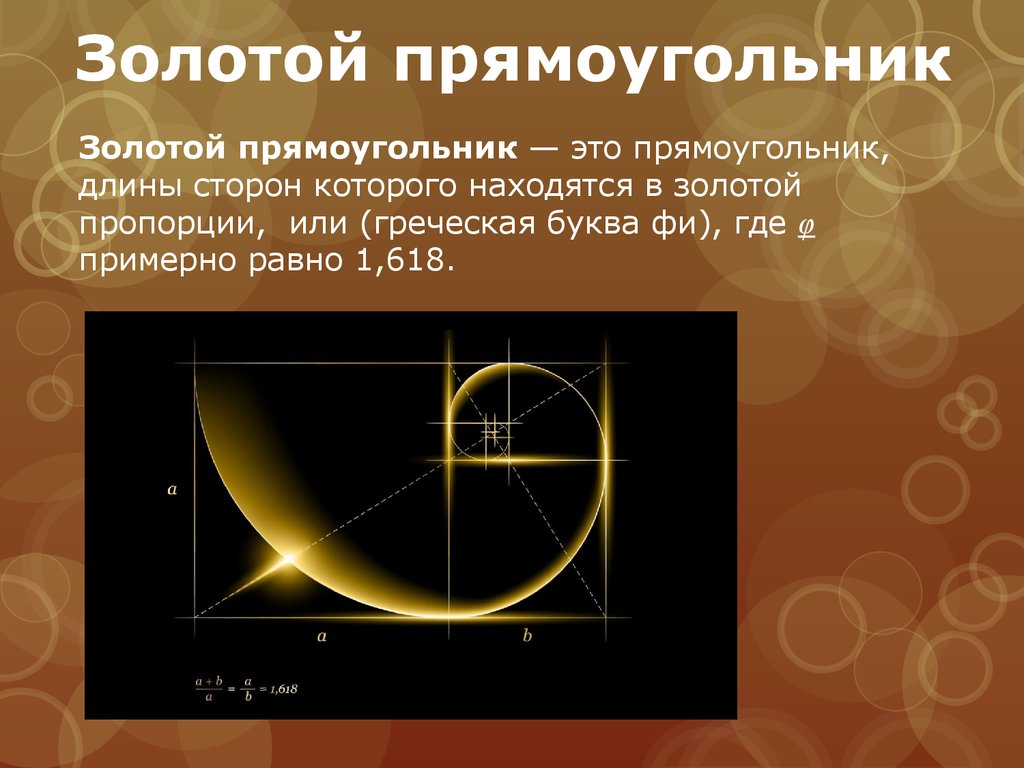
Количества подобных спиралей называются в ботанике парастическими числами (parastichy numbers). Интересно то, что что близко к . Это не случайно.
Оказывается, у множества видов растений у здорового, неповрежденного цветка или розетки имеется тенденция к выбору в качестве парастических чисел двух соседних чисел следующего ряда:
Эта последовательность широко известна как последовательность Фибоначчи. Она начинается с двух единиц; каждое следующее число последовательности — сумма двух предшествующих. У ряда Фибоначчи много замечательных свойств, главным из которых для нас является то, что отношение двух соседних членов стремится к . Этот замечательный факт напрямую вытекает из явной формулы для чисел ряда Фибоначчи, так называемой формулы Бине:
Как можно видеть, отношение двух соседних членов ряда Фибоначчи быстро стремится в . На самом деле, это характерно для любого рекуррентного ряда, строящегося по формуле «каждый следующий член равен сумме двух предыдущих».
Откуда же члены последовательности Фибоначчи взялись в цветке?
Процесс формирования корзинки называется филлотаксисом. Внутри центральной части корзинки подсолнуха — меристемы — происходит деление зародышевых клеток, образующих сначала цветок, а потом и семечко. Сразу после рождения цветок начинает выталкиваться младшими братьями и сестрами в радиальном направлении от центра.
Закон движения единичного цветка в корзинке проще всего описать в радиальной системе координат — по радиусу и углу. Для цветка номер из рожденных меристемой, его радиальные координаты описываются примерно так:
Помимо и мы видим здесь два параметра — и . — некая постоянная величина, связанная с размерами цветка в соцветии.
Закон радиального выталкивания легко обосновать физически, приняв за внимание, что цветки соцветия приблизительно одинакового размера и должны покрывать собой всю свободную площадь корзинки. Интереснее закон направления . Он зависит от константы , которая для подсолнуха с высокой точностью равна
Иными словами, порождая цветок, меристема задает ему направление движения, каждый раз меняя его это направление относительно предшествующего поворотом на .
Это число, , неявным образом закодировано в геноме растения. Для того, что бы понять, что это и откуда оно берется, разделим его на , то есть вычислим, какую долю полного оборота оно составляет:
Вот где прячется золотое сечение! Но зачем оно нужно растению?
Для ответа на этот вопрос, обратимся к уникальному свойству числа- его разложению в цепную дробь.
Любое действительное число можно представить следующим способом:
Где целое число; прочие натуральные числа. Такое представление называется цепной дробью. Если число — рациональное, его представление в виде цепной дроби насчитывает конечное число членов, и вычисляется посредством алгоритма Евклида. В противном случае, представление числа в виде цепной дроби выражается бесконечной последовательностью знаменателей. Например, знаменитое число расписывается в виде цепной дроби вот так:
Наиболее важным свойством цепных дробей для математики является то, что они кодируют наилучшие рациональные приближения данного числа.
В самом деле, попробуем «обрезать» дробь по одной из контурных линий. Мы получим рациональное число, приблизительно равное . Утверждается, что для каждого из них не существует рационального числа с меньшим знаменателем, более близкого к :
Сравните приближение и
И в том и в другом случае мы получили 6 значимых цифр после запятой, но в одном случае знаменатель — 113, а в другом — 10000000. Разница, как говорится, налицо.
Теперь, наконец, разложим в цепную дробь. Получится следующее:
Рациональные приближения, полученные посредством обрезания этого представления, выглядят так:
Легко видеть, что это ни что иное, как отношения соседних членов ряда Фибоначчи. И вот теперь, сравнивая цепочку рациональных приближений числа с аналогичной цепочкой числа мы можем видеть главное математическое свойство пропорции золотого сечения.
Для любого достаточно большого , у больше рациональных приближений со знаменателем меньше чем , чем у любого другого иррационального числа.
В самом деле. Приближая , мы видим, что уже у седьмого приближения знаменатель вырос до 99532. Узнаменатель седьмой дроби — 34. Алгоритм вычисления рационального приближения из частичного представления цепной дроби прост, и мы не будем его здесь приводить. Выведя его, легко видеть, что чем меньше числа в ряду, тем меньше будут представления, а натуральных чисел меньше, чем ряд из последовательных единиц, нельзя и представить. Одновременно с этим, является наиболее плохо приближенным числом из всех, в том смысле, что с ростом знаменателя число угаданных знаков приближения растет максимально медленно, насколько это возможно. Этот факт является прямым следствием из теоремы Гурвинца и его доказательство довольно занудно, так что мы не будем включать его в данную статью.
Суха теория, друзья, но древо жизни пышно зеленеет. Настало время сложить всё вышесказанное, и понять, как связаны: филлотаксис подсолнуха, угол , последовательность Фибоначчи, цепные дроби и рациональные приближения.
И вместо того, что бы рассказать, лучше показать:
Интерактивное онлайн-демо, иллюстрирующее процесс филлотаксиса
Перейдя по ссылке, вы увидите небольшую онлайн-демонстрацию процесса формирования корзинки подсолнуха. Вы можете регулировать угол порождения меристемой цветков и их количество, или изучать спирали, полученные путем выделения каждого ного зерна, начиная с первого, где n (ранг) — знаменатель одно из рациональных приближений для выставленного вами угла. Вы увидите, что при углах и некоторых других зерна в корзинке распределены почти равномерно, а число рациональных приближений с небольшим основанием максимально; для других углов число рациональных приближений невелико, а зерна подсолнуха четко группируются в спирали, причем их число соответствует знаменателю дроби того или иного рационального приближения выставленного угла. И глядя на это, даже не оперируя сложной математикой вы можете дать правильный ответ на поставленный в заголовке вопрос:
Золотое сечение в подсолнухе обеспечивает наиболее равномерное распределение семян в корзинке за счет наихудшего его приближения рациональными числами и максимизации числа спиралей небольшого ранга, вдоль которых упорядочены семена.
Настоящая статья написана по мотивам кружковых занятий Малого Мехмата МГУ для старших классов. В статье использованы следующие источники:
А. Цезинг «Эстетические исследования»
В. Арнольд «Цепные дроби»
А. Щетников «Загадки филлотаксиса» (видео)
«Математическая составляющая / Филлотаксис» — энциклопедия по популярной математике
«Special Topics — Lessons from Biology for Engineering Tiny Devices / Lessons 12: Spirals and phyllotaxis» — цикл популярных лекций Принстонского университета, посвященных спиралям.
Takuya Okabe, Atsushi Ishida and Jin Yoshimura — The unified rule of phyllotaxis explaining both spiral and non-spiral arrangements — более строгое математическое описание процесса развития цветка.
Математика листьев: как один необычный куст изменил уравнение модели роста растений — статья на habr.com с прелестными анимироваными иллюстрациями.
Wikipedia: Golden ratio, Continued fraction, Fibonacci number, Hurwitz’s theorem.
Интерактивное онлайн-демо, иллюстрирующее процесс филлотаксиса
Читать онлайн «φ – Число Бога. Золотое сечение – формула мироздания», Марио Ливио – Литрес
Права на перевод получены соглашением с Broadway Books (Crown Publishing Group, Random House LLC., A Penguin Random House Company) и литературным агентством «Синопсис».
Mario Livio THE GOLDEN RATIO:
The Story of PHI, the World’s Most Astonishing Number
© Mario Livio, 2002
© Бродоцкая А., перевод на русский язык, 2014
© ООО «Издательство АСТ», 2021
⁂
CЕКРЕТ ГАРМОНИИ ВО ВСЕМЯвляются ли некоторые числа более значимыми, чем другие? Конечно же, да! Если уж у простых людей, далеких от науки или мистики, есть свои любимые и нелюбимые числа, что же говорить про математиков и физиков? Число – такой же важный компонент культуры, как слово. Нет человека, которому бы ни о чем не говорили числа 7, 13 или 666. Но есть числа, которые влияют на нашу жизнь, даже если мы о них не знаем.
Таково число фи, в котором кроется секрет гармонии во всем. Марио Ливио написал эту книгу, чтобы мы не были так слепы и не думали, что нумерология – это предрассудки.
ИЗ ЧЕГО СКЛАДЫВАЕТСЯ КРАСОТАТимоти Хью, Коннектикут
Книга Марио Ливио полна увлекательнейших цифровых трюков, но, чтобы понять их, вовсе не нужно иметь математический склад ума. Все мы сталкиваемся с тем, что называют красотой. Но кто скажет, из чего складывается красота? Почему нам так нравится смотреть на картины старых мастеров, любоваться спиральными галактиками или разглядывать сосновую шишку? В своей книге Ливио раскрывает секреты красоты и уводит читателя в увлекательный мир математики – науки, которая объясняет все.
ПОТРЯСАЮЩЕЕ ИССЛЕДОВАНИЕЭлис Хоул, Лос-Анджелес
Я даю этой книге пять звезд из пяти! Эта книга – и для математиков, и для тех, кто не дружит с цифрами.
Если вы любите науку, вас захватит потрясающее исследование, которое автор предпринимает в своем труде, если вы любитель беллетристики – эта книга станет для вас тем же, что и хороший детектив.
ФОРМУЛА ВСЕЛЕНСКОЙ ГАРМОНИИРэндом Уэсли, Сан-Франциско
Марио Ливио написал прекрасную работу, в которой дается подробный исторический обзор того, как на протяжении веков люди старались открыть универсальную формулу вселенской гармонии. Оказалось, что все гораздо проще – все сводится к одному-единственному числу, известному как золотое сечение, или число Бога. Вы можете быть математиком или всего лишь человеком, которого чуть-чуть интересует мистика. Если вам интересен окружающий мир, книга приведет вас в восторг!
ХОРОШАЯ ЛИТЕРАТУРАКристофер Паркер, Кембридж
«Золотое сечение» – это настоящий шедевр талантливого автора. Я был впечатлен той четкой и захватывающей манерой, которая делает научный труд книгой не только для ума, но и для отдыха.
В этой книге Марио Ливио одновременно отвечает на самые актуальные вопросы современной науки и рассказывает удивительную историю, увлечься которой способен каждый. Это хорошая литература во всех отношениях.
Мишель Тернер, Колд Спринг Харбор
Памяти моего отца Робина Ливио
Предисловие
«Золотое сечение» – это книга об одном-единственном числе, однако число это совершенно особое. Это число – 1,61803… – встречается и в лекциях по истории искусств, и в перечнях «любимых чисел», которые составляют математики. Не менее поразительно, что оно было предметом множества экспериментов по психологии.
Так называемое «золотое сечение» заинтересовало меня пятнадцать лет назад, когда я готовился к лекции об эстетике в физике (представьте себе, это отнюдь не оксюморон), и с тех пор оно не идет у меня из головы.
В создании этой книги прямо и косвенно поучаствовало столько моих коллег, друзей и учеников, что всех и не перечислишь.
Здесь я хотел бы выразить особую благодарность Иву-Алену Буа, Митчу Фейгенбауму, Гиллелю Гаухману, Теду Хиллу, Рону Лифшицу, Роджеру Пенроузу, Джоанне Постма, Полу Стейнхардту, Пат Тиль, Анне ван дер Хельм, Дивакару Вишванату и Стивену Вольфраму – за бесценные сведения и крайне продуктивные споры.
Я благодарен своим коллегам Даниэле Кальцетти, Стефано Казертано и Массимо Стиавелли за помощь с переводами с латыни и итальянского, Клаусу Лейтереру и Эрмине Ландт за помощь с переводами с немецкого, а Патрику Годону – за помощь с переводами с французского. Сара Стивенс-Рейберн, Элизабет Фрэзер и Нэнси Хэнкс очень посодействовали мне во всем, что касалось лингвистики и библиографии. Особенно я благодарен Шэрон Тулан за содействие в подготовке рукописи.
Искренне благодарю своего литературного агента Сьюзен Рабинер за то, что она не давала мне опустить руки до начала и во время работы над книгой. Я в огромном долгу перед Джеральдом Ховардом, моим редактором из издательства «Doubleday Broadway», за то, что он так тщательно вычитывал рукопись и делал такие точные, глубокие замечания.
Также я благодарен Ребекке Холланд, выпускающему редактору в «Doubleday Broadway», за постоянное содействие в то время, пока книга была в печати.
И, наконец, эта книга вообще была написана исключительно благодаря постоянной помощи, терпению и поддержке Софи Ливио.
Прелюдия к числу
Много есть чудес на свете.
Софокл (495–405 гг. до н. э.)(Пер. С. Шервинского, Н. Познякова)
Знаменитый английский физик лорд Кельвин (Уильям Томпсон, 1824–1907), в честь которого назван градус абсолютной температурной шкалы, во время одной своей лекции сказал: «Если знание невозможно выразить численно, значит, оно поверхностно и недостаточно». Разумеется, Кельвин имел в виду то знание, которое необходимо для научного прогресса. Однако числа и математика удивительным образом предрасположены к тому, чтобы способствовать пониманию даже того, что крайне далеко от науки – или, по крайней мере, представляется таким на первый взгляд.
Даже если вы не слишком любите шоколад, то все равно понимаете, что этот пример демонстрирует простой математический закон, который можно применить и во многих других случаях.
Однако математические свойства, формулы и законы (многие из которых не задерживаются у нас в памяти) – это далеко не все; существуют еще и особые числа, которые настолько вездесущи, что не устают нас изумлять. Самое прославленное из них – число π (пи), отношение длины окружности к ее диаметру. Значение π – 3,14159… – завораживало много поколений математиков. Хотя изначально число π было определено в геометрии, оно очень часто и неожиданно всплывает при вычислении вероятности. Знаменитый пример – так называемая игла Бюффона, названная в честь французского математика Жоржа-Луи Леклерка, графа де Бюффона (1707–1788), который поставил и решил эту вероятностную задачу в 1777 году. Леклерк задал следующий вопрос: представьте себе, что у вас на полу лежит большой лист бумаги, разлинованный параллельными линиями через равные заданные промежутки. На лист совершенно случайным образом бросают иглу, длина которой в точности равна промежутку между линиями. Какова вероятность, что игла упадет так, что пересечет одну из линий (то есть как на рис.
Менее знаменито другое число – φ (фи), а между тем, во многих отношениях оно даже интереснее. Вот, скажем, представьте себе, что я спрашиваю у вас, что общего у изумительного расположения лепестков алой розы, композиции знаменитой картины Сальвадора Дали «Тайная вечеря», чудесного рисунка спиральной раковины и статистики размножения кроликов? Трудно поверить, что у столь разнородных явлений действительно есть нечто общее – и это некое число или геометрическая пропорция, известная человечеству еще со времен античности, число, которому в XIX веке дали почетное называние «золотое число» или «золотое сечение».
В повседневной жизни мы применяем слово «пропорция» для обозначения соотношения между частями целого по размеру или количеству – или когда хотим подчеркнуть гармоничные отношения между разными частями. В математике термин «пропорция» применяется для описания равенства следующего типа: девять относится к трем, как шесть к двум. Как мы увидим, золотое сечение дарит нам чарующее сочетание этих определений: хотя определяется оно строго математически, однако считается, что оно обладает свойствами, обеспечивающими приятную гармонию.
Рис. 1
Первое четкое определение соотношения, которое впоследствии станет известно как золотое сечение, дал примерно в 300 году до н. э. Евклид Александрийский, основатель геометрии как формальной дедуктивной системы. К Евклиду и его фантастическим достижениям мы еще вернемся в главе 4, а пока позвольте отметить, что Евклид вызывает столь сильное восхищение, что поэтесса Эдна Сент-Винсент Миллей в 1923 году даже посвятила ему стихотворение под названием «На обнаженность красоты Евклид взглянул» ( пер.
Л. Мальцевой). Эдна даже сохранила свою школьную тетрадь по евклидовой геометрии. Евклид определил пропорцию, выведенную из простого деления линии (отрезка), по его выражению, «в крайнем и среднем отношении»: «Прямая линия называется рассеченною в крайнем и среднем отношении, когда как целая прямая к большему отрезку, так больший к меньшему» (пер. Ф. Петрушевского) (рис. 2).
Иначе говоря, если мы посмотрим на рис. 2, то увидим, что отрезок АВ определенно длиннее отрезка АС, в то же время АС длиннее СВ. Если отношение длины АС к длине СВ такое же, как отношение длины АВ к длине АС, значит, отрезок поделен «в крайнем и среднем отношении» – или в золотом сечении.
Рис. 2
Кто бы мог подумать, что такое на первый взгляд невинное разделение отрезка, которое Евклид определил в чисто геометрических целях, окажет влияние на самые разные разделы знания – от положения листьев в ботанике до структуры галактик, состоящих из миллиардов звезд, от математики до искусства? Следовательно, золотое сечение – прекрасный пример того самого крайнего изумления и восторга, которые так высоко ценил великий физик Альберт Эйнштейн (1879–1955).
Вот как он об этом писал: «Самое прекрасное, что только может выпасть нам на долю, – это тайна. Стремление разгадать ее стоит у колыбели подлинного искусства и подлинной науки. Тот, кто не знает этого чувства, утратил любопытство, не способен больше удивляться, – все равно что мертвый, все равно что задутая свеча».
Как мы еще увидим, когда проследим на страницах этой книги все необходимые вычисления, точное значение золотого сечения (то есть отношение АС к СВ на рис. 2) – бесконечное непериодическое число 1,6180339887…, а такие бесконечные неповторяющиеся числа интересовали людей со времен античности. Рассказывают, что когда греческий математик Гиппас из Метапонта в V веке до н. э. обнаружил, что золотое сечение – это и не целое число (подобное нашим добрым знакомым 1, 2, 5 и т. д.), и даже не отношение двух целых чисел (подобное дробям вроде 1/2, 2/3, 3/4, которые в совокупности называются рациональными числами), это привело остальных пифагорейцев – то есть последователей знаменитого математика Пифагора – в полнейшее смятение.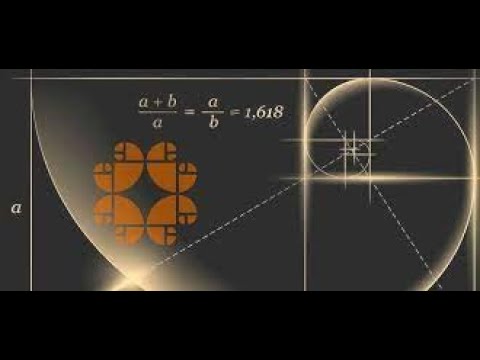
Предметом поклонения для пифагорейского мировоззрения (о котором мы подробно поговорим в главе 2) был arithmos – то есть имманентные качества целых чисел и их отношений и их предполагаемая роль в мироздании. А открытие, что существуют числа вроде золотого сечения, которые все тянутся и тянутся вечно и при этом в них нет никаких следов повторяемости, никакой закономерности, вызвало самый настоящий философский кризис. Легенда даже утверждает, будто пифагорейцы, совершенно потрясенные этим открытием колоссальной важности, устроили гекатомбу – пожертвовали сто быков, – хотя это вряд ли, учитывая, что пифагорейцы были строгими вегетарианцами. Тут я вынужден подчеркнуть, что большинство подобных историй основаны на недостоверном историческом материале. Так или иначе, мы даже приблизительно не знаем, когда именно были открыты числа, которые не являются ни целыми, ни дробями – так называемые
Очевидно одно: пифагорейцы в общем и целом считали, что существование подобных чисел так ужасно, что это, должно быть, своего рода ошибка мироздания, которую надо замолчать и держать в тайне. Тот факт, что золотое сечение невозможно выразить в виде дроби (как рациональное число), попросту означает, что нельзя выразить в виде дроби соотношение длин АС и СВ на рис. 2. Иначе говоря, как бы мы ни трудились, мы не найдем единицы измерения, которая, скажем, укладывалась бы 51 раз в АС и 19 раз в СВ. Две длины, у которых нет подобной единицы измерения, называются несоизмеримыми. В своем труде «Жизнь Пифагора» (ок. 300 г. н. э.) философ и историк Ямвлих из аристократического сирийского семейства так описывает бурную реакцию на это открытие: будто бы тот, кто открыл эту тайну непосвященным, «вызвал, как говорят, такую ненависть, что его не только изгнали из общины и отлучили от пифагорейского образа жизни, но и соорудили ему надгробие, как будто действительно ушел из жизни тот, кто некогда был их товарищем» (пер.
В профессиональной математической литературе золотое сечение принято обозначать греческой буквой τ (тау) – от греческого слова τομή (читается «томэ»), которое означает «сечение» или «разрез». Однако в начале ХХ века американский математик Марк Барр предложил обозначать золотое сечение буквой φ – по первой букве имени великого древнегреческого скульптора Фидия, жившего примерно в 490–430 гг. до н. э. Величайшие шедевры Фидия – Афина Партенос в Афинах и Зевс в Олимпии. Кроме того, полагают, что он отвечал и за другие скульптуры в Парфеноне, хотя весьма вероятно, что их создали его ученики и помощники. Барр решил, что надо почтить память скульптора, поскольку многие искусствоведы полагают, что Фидий часто и весьма точно применял золотое сечение в своих творениях (эту и подобные гипотезы мы очень дотошно разберем в нашей книге). Я буду называть его и золотым сечением, и числом φ, поскольку именно такие обозначения чаще всего встречаются в популярной математической литературе.
Величайшие математические умы в истории – и древнегреческие мудрецы Пифагор и Евклид, и средневековый итальянский ученый Леонардо Пизанский по прозвищу Фибоначчи, и астроном эпохи Возрождения Иоганн Кеплер, и современные научные светила, например, физик из Оксфорда Роджер Пенроуз, немало часов провели в размышлениях над этим простым соотношением и его свойствами. Однако золотое сечение чарует отнюдь не только математиков. Биологи, художники, историки, музыканты, архитекторы, психологи и даже мистики – все они размышляли над тем, почему это число столь вездесуще и в чем его притягательность. По сути дела, можно, пожалуй, сказать, что золотое сечение вдохновляло мыслителей из всех отраслей знания – и в этом с ним не в силах сравниться никакое другое число в истории математики.
Даже простому вопросу о происхождении названия «золотое сечение» посвящено огромное количество исследований, а особенно глубоко этим интересовался канадский математик и писатель Роджер Герц-Фишлер, о чем и рассказано в его превосходной книге «A Mathematical History of the Golden Number» («Математическая история золотого сечения»).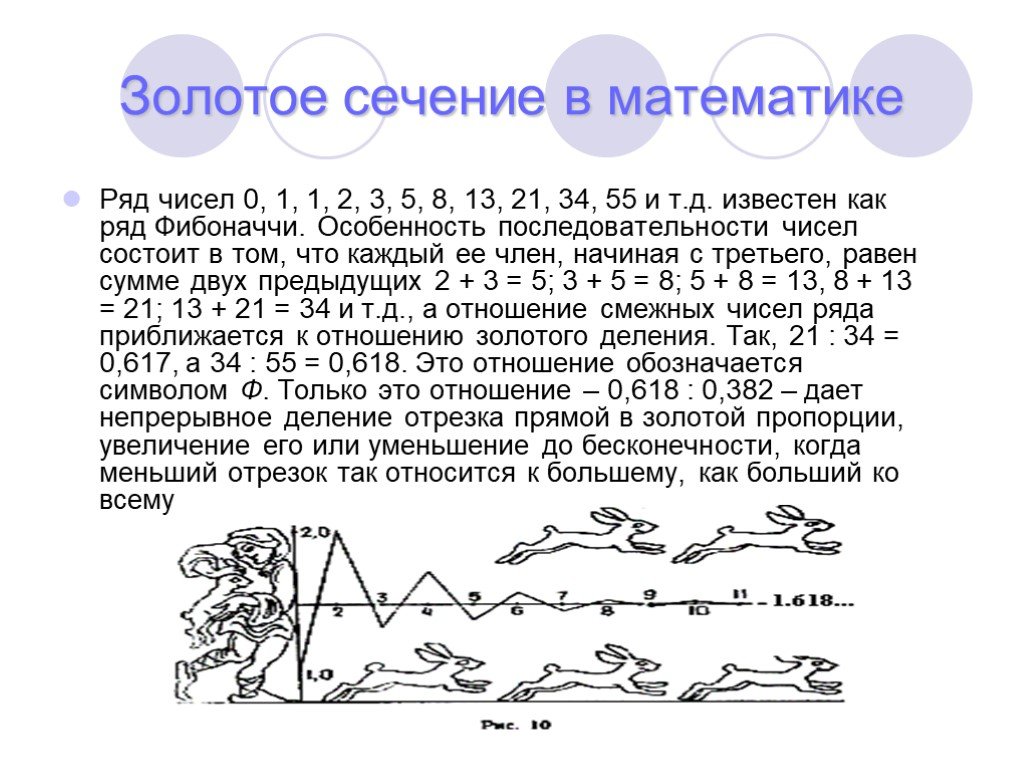
Учитывая, какой пристальный интерес вызывало это число еще со времен античности, можно было бы подумать, что и название это античного происхождения. И в самом деле, некоторые авторитетные труды по истории математики, например, «Рождение математики во времена Платона» Франсуа Ласерре (François Lasserre. «The Birth of Mathematics in the Age of Plato») и «История математики» Карла Б. Бойера (Carl B. Boyer. «History of Mathematics»), возводят это название, соответственно, к XVI и XVII векам. Однако дело, скорее всего, не в этом. Насколько я могу судить по обширным источниковедческим данным, впервые это словосочетание применил в 1835 году немецкий математик Мартин Ом (брат знаменитого физика Георга Симона Ома, в честь которого назван закон Ома в электромагнетизме) во втором издании своей книги «Чистая элементарная математика» (Martin Ohm. «Die Reine Elementar-Mathematik»). В одной сноске Ом пишет: «Подобное разделение произвольного отрезка на две части принято также называть золотым сечением».
Формулировка Ома однако создает впечатление, что он не сам придумал этот термин, а скорее привел уже принятое название. Тем не менее, в первом издании книги, опубликованном в 1826 году, Ом этого названия не приводит, а это заставляет сделать по крайней мере тот вывод, что выражение «золотое сечение» (нем. «der Goldene Schnitt») завоевало популярность лишь к 1835 году. Вероятно, ранее это было лишь разговорное выражение, применявшееся преимущественно в математических кругах. Однако нет никаких сомнений, что после книги Ома термин «золотое сечение» стал часто повторяться в немецкой литературе по математике и искусствоведению. А в англоязычной печати это выражение, по всей видимости, дебютировало в статье Джеймса Салли (James Sully) по эстетике, которая появилась в девятом издании Британской энциклопедии в 1875 году. Салли описывает «интересное экспериментальное исследование… проведенное Густавом Теодором Фехнером (известным немецким физиком и первопроходцем в области психологии, жившим в XIX веке) о том, что «золотое сечение» первоначально было именно зримой пропорцией» (об экспериментах Фехнера мы подробно поговорим в главе 7).
В математическом контексте этот термин впервые встретился в англоязычной литературе, по всей видимости, в статье Э. Эккерманна, которая так и называлась «Золотое сечение» (E. Ackermann. «The Golden Section») и была напечатана в журнале «American Mathematical Monthly» в 1895 году, а также – примерно в это же время, в 1898 году – в книге «Введение в алгебру» известного преподавателя и писателя Дж. Кристала (1851–1911). Позвольте мне отметить любопытства ради, что единственное определение «золотого числа», появившееся в издании французской энциклопедии «Nouveau Larousse Illustré» 1900 года, гласит: «Число, определяющее каждый год лунного цикла». Это относится к положению календарного года в пределах 19-летнего цикла, после которого фазы луны снова приходятся на те же даты. Очевидно, во французскую математическую номенклатуру «золотое число» и тем более «золотое сечение» проникало гораздо дольше.
Однако почему это вообще так важно? Из-за чего, собственно, это число или геометрическая пропорция так сильно нас интересуют? Привлекательность золотого сечения в первую очередь коренится в том факте, что оно обладает прямо-таки пугающим свойством вылезать там, где его никак не ожидаешь.
Возьмем, к примеру, самое обычное яблоко – фрукт, который часто и, вероятно, ошибочно ассоциируется с древом познания, играющим столь заметную роль в библейском рассказе о грехопадении – и разрежем его поперек. И мы увидим, что яблочные семечки образуют пятиконечную звезду – она же пентаграмма (рис. 3). Каждый из пяти равнобедренных треугольников, составляющих лучи пентаграммы, обладает таким свойством, что соотношение длины его длинной стороны к короткой, то есть к основанию, равно золотому сечению – 1,618… Правда, вы, вероятно, решите, что это не так уж и удивительно. В конце концов, золотое сечение и определяется в первую очередь как геометрическая пропорция, так что, вероятно, не надо так уж поражаться, если эта пропорция встречается в некоторых геометрических фигурах.
Рис. 3
Однако это лишь верхушка айсберга. Согласно буддистской традиции, Будда во время одной своей проповеди не проронил ни слова, а всего-навсего показал слушателям цветок. Чему может научить нас цветок? Скажем, роза часто служит примером природной симметрии, гармонии, любви и хрупкости.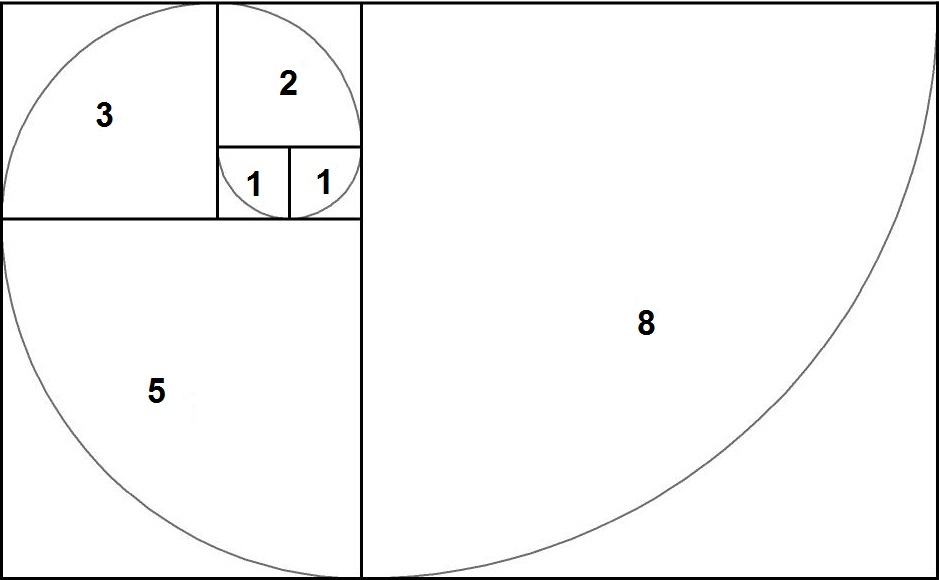
Индийский поэт Рабиндранат Тагор (1861–1941) в своей «Религии человека» пишет: «Нам почему-то кажется, что роза – это язык, который нашла любовь, чтобы достичь наших сердец». Предположим, вам нужно качественно оценить симметричное устройство розы. Возьмите розу и препарируйте ее, чтобы разобраться, каким образом ее внешние лепестки накладываются на внутренние. Как я показываю в главе 5, вы обнаружите, что лепестки расположены в соответствии с математическим законом, основанном на золотом сечении.
Теперь обратимся к царству животных: все мы хорошо знакомы с чарующе прекрасными спиральными структурами многих раковин моллюсков, например, вида Nautilus pompilius (рис. 4). Между прочим, такую раковину держит в руке танцующий Шива из индийских легенд – это символ одного из орудий творения. Кроме того, структура этих раковин вдохновляла и многих зодчих. Например, американский архитектор Фрэнк Ллойд Райт (1869–1959) положил эту структуру в основу здания музея Гуггенхайма в Нью-Йорке.
Попав в музей, посетители поднимаются по спиральному пандусу, насыщая воображение созерцанием произведений искусства – точно так же, как моллюск выстраивает новые спиральные камеры, заполняя свое физическое пространство. В главе 5 мы увидим, что рост спиральных раковин также подчиняется правилу, основанному на золотом сечении.
Рис. 4
Рис. 5
Пожалуй, не нужно быть особым поклонником нумерологии – мистики чисел, чтобы уже сейчас почувствовать некоторый душевный трепет: столь поразительна способность золотого сечения проявляться в самых разных ситуациях, в самых разных феноменах, казалось бы, совершенно не связанных друг с другом. Более того, как я уже отметил в начале главы, золотое сечение обнаруживается не только в природных явлениях, но и в самых разных рукотворных предметах и произведениях искусства. Например, на рис. 5 мы видим картину Сальвадора Дали «Тайная вечеря», написанную в 1955 году (она хранится в Национальной галерее в Вашингтоне): соотношение сторон этой картины – ее размеры 167 на 268 см – приблизительно равно золотому сечению.
Более того, над столом, словно охватывая композицию, парит фрагмент огромного додекаэдра – правильного двенадцатигранника, каждая грань которого представляет собой правильный пятиугольник. Как мы увидим в главе 4, правильные многогранники, например, куб, которые можно вписать в сферу (т. е. сделать так, чтобы все их углы лежали на сфере), а особенно додекаэдр, тесно связаны с золотым сечением. Почему Дали решил так явно подчеркнуть золотое сечение в своей картине? Художник отмечал, что «Композиция Тайной Вечери должна быть симметричной» – но это лишь начало ответа на наш вопрос. Как я показываю в главе 7, золотое сечение появляется – или по крайней мере, должно появляться по замыслу создателя – в работах многих других художников, архитекторов, дизайнеров и даже в знаменитых музыкальных произведениях. Говоря обобщенно, золотое сечение применяется в некоторых произведениях искусства с целью достичь определенного зрительного или слухового эффекта. Подобный эффект вызывается, в частности, особым соотношением размеров отдельных частей и целого, особыми пропорциями.
История искусств показывает, что в результате долгих поисков неуловимого канона «совершенных» пропорций – такого, чтобы любое произведение искусства при его применении автоматически становилось эстетичным и приятным – выяснилось, что этим требованиям лучше всего удовлетворяет именно золотое сечение. Но почему?
Если подробнее рассмотреть примеры из мира природы и из мира искусства, окажется, что они заставляют задаваться вопросами на трех уровнях глубины. Прежде всего, это непосредственные вопросы: (а) все ли случаи появления числа φ в природе и искусстве, описанные в литературе, действительно имеют место или некоторые из них – всего лишь результаты неверных интерпретаций и всякого рода натяжек? (б) Если число φ и правда появляется в этих и других обстоятельствах, можем ли мы как-то это объяснить? Далее, если учесть, что мы придерживаемся определения «красоты», подобного, скажем, тому, которое дано в словаре Уэбстера: «Качество, которое делает объект приятным или приносит определенное удовлетворение» – возникает вопрос: есть ли у математики эстетическая составляющая? Если да, какова сущность этой составляющей? Это серьезный вопрос, поскольку, как заметил однажды американский архитектор, математик и инженер Ричард Бакминстер Фуллер (l895–l983): «Когда я работаю над какой-то задачей, то никогда не думаю о красоте.
Думаю я только о том, как решить эту задачу. Но если я решу ее и решение окажется некрасивым, я буду знать, что ошибся». И, наконец, самый интересный вопрос звучит так: почему, собственно, математика столь могущественна и столь вездесуща? Благодаря чему математика и численные константы вроде золотого сечения играют столь важную роль во всем на свете – от фундаментальных теорий происхождения Вселенной до рынка ценных бумаг? Существует ли математика и ее принципы независимо от людей, которые ее открыли или обнаружили? Математична ли Вселенная по своей природе? Последний вопрос можно задать, переформулировав известный афоризм английского физика сэра Джеймса Джинса (1847–1946): может быть, и сам Бог – математик?
В этой книге я постараюсь обсудить все эти вопросы более или менее подробно с точки зрения увлекательной истории числа φ. История этой константы, временами запутанная, насчитывает тысячелетия и разворачивается на всех материках. Но при этом я надеюсь рассказать вам еще и интересную историю о человеческой психологии.
Наш сюжет отчасти повествует о тех временах, когда физиками и математиками называли себя люди, которых попросту интересовали различные вопросы, разжигавшие в них любознательность. Зачастую подобные люди трудились и умирали, не зная, удастся ли результатам их трудов изменить ход научной мысли или они просто канут в Лету, не оставив и следа.
Однако прежде чем пуститься в этот путь, нам придется поближе познакомиться с числами вообще и с золотым сечением в частности. Откуда, в сущности, появилась сама идея золотого сечения? Что именно заставило Евклида задуматься о том, чтобы разделить отрезок именно в таком соотношении? Моя цель – помочь вам заглянуть в подлинные истоки, так сказать, «золотого исчисления». Для этого мы и предпримем краткую ознакомительную экскурсию во времена зарождения математики.
Золотое сечение — определение, формула, примеры
Золотое сечение, которое часто называют золотым сечением, божественной пропорцией или золотым сечением, представляет собой особый атрибут, обозначаемый символом ϕ, и примерно равен 1,618.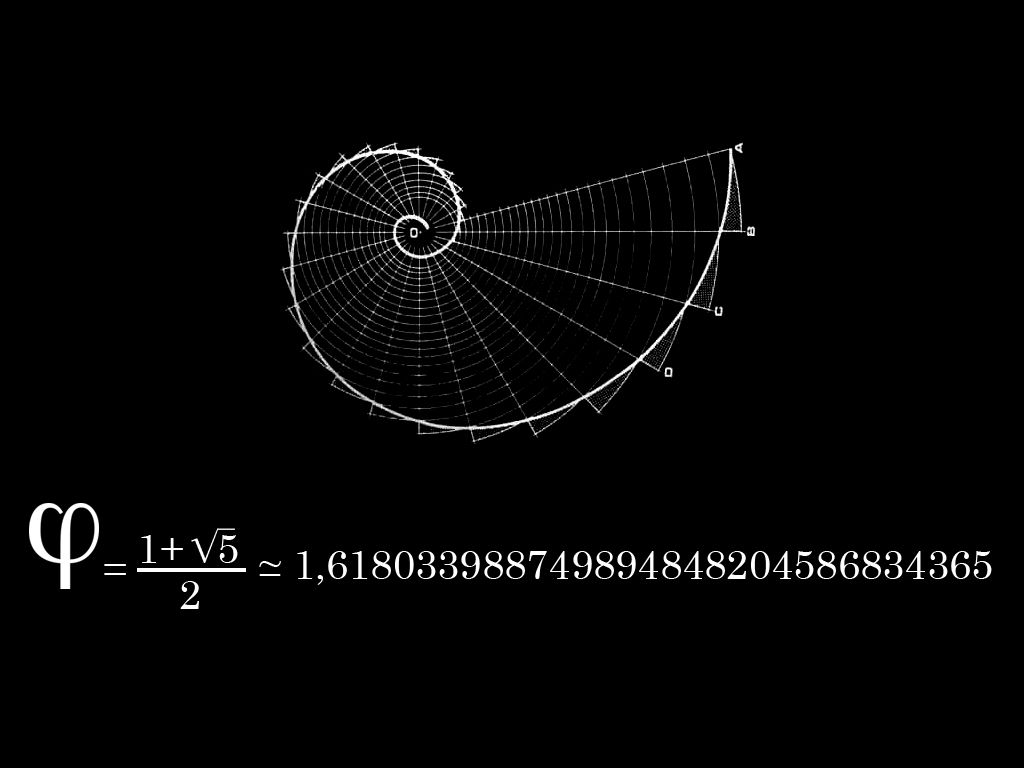
Изучение многих специальных формаций может быть выполнено с использованием специальных последовательностей, таких как последовательность Фибоначчи, и атрибутов, таких как золотое сечение.
Это соотношение встречается в различных искусствах, архитектуре и дизайне. Многие замечательные архитектурные сооружения, такие как Великая пирамида Египта, Парфенон, были частично или полностью спроектированы так, чтобы отражать в своей структуре золотое сечение. Великие художники, такие как Леонардо да Винчи, использовали золотое сечение в нескольких своих шедеврах, и в 1500-х годах оно было известно как «Божественная пропорция». Давайте узнаем больше о золотом сечении в этом уроке.
| 1. | Что такое золотое сечение? |
| 2. | Формула золотого сечения |
| 3. | Как рассчитать золотое сечение? |
| 4. | Что такое золотой прямоугольник? |
5. | Что такое последовательность Фибоначчи? |
| 6. | Часто задаваемые вопросы о золотом сечении |
Что такое золотое сечение?
Золотое сечение, также называемое золотым сечением, божественной пропорцией или золотым сечением, существует между двумя величинами, если их отношение равно отношению их суммы к большей величине между ними. Со ссылкой на это определение, если мы разделим линию на две части, части будут в золотом сечении, если:
Отношение длины более длинной части, скажем, «а», к длине более короткой части, скажем, «b» равно отношению их суммы «(a + b)» к большей длине.
Обратитесь к следующей диаграмме для лучшего понимания вышеуказанной концепции:
Обозначается греческой буквой ϕ, произносимой как «фи». Приблизительное значение ϕ равно 1,61803398875 . Оно находит применение в геометрии, искусстве, архитектуре и других областях. Таким образом, следующее уравнение устанавливает соотношение для расчета золотого сечения: два.
Определение золотого сечения
Когда линия делится на две части, длинная часть, которая делится на короткую часть, равна всей длине, деленной на длинную часть, определяется как золотое сечение. Ниже приведены примеры золотого сечения в архитектуре и искусстве.
Существует множество применений золотого сечения в области архитектуры. Многие архитектурные чудеса, такие как Великая мечеть Кайруана, были построены с учетом золотого сечения в их структуре. Такие художники, как Леонардо да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах.
Формула золотого сечения
Формулу золотого сечения можно использовать для расчета значения золотого сечения. Уравнение золотого сечения выведено, чтобы найти общую формулу для расчета золотого сечения.
Уравнение золотого сечения
Из определения золотого сечения
a/b = (a + b)/a = ϕ
Из этого уравнения получаем два уравнения:
a/b = ϕ → ( 1)
(а + b)/а = ϕ → (2)
Из уравнения (1)
a/b = ϕ
⇒ a = b
Подставить это в уравнение (2):
(bϕ + b)/bϕ = ϕ
b( ϕ + 1)/ bϕ = ϕ
(ϕ + 1)/ϕ = ϕ
1 + 1/ϕ = ϕ
1 + 1/ϕ = ϕ
Как рассчитать золотое сечение?
Значение золотого сечения можно рассчитать разными методами.
Начнем с основного.
Метод проб и ошибок
Мы угадаем произвольное значение константы, а затем выполним следующие шаги, чтобы вычислить более близкое значение на каждой итерации.
- Вычислите мультипликативную обратную величину угаданного вами значения, т. е. 1/значение. Это значение будет нашим первым термином.
- Вычислите другой член, добавив 1 к мультипликативному, обратному этому значению.
- Оба условия, полученные на предыдущих шагах, должны быть равны. Если нет, мы будем повторять процесс, пока не получим примерно равное значение для обоих членов.
- Для второй итерации мы будем использовать предполагаемое значение, равное члену 2, полученному на шаге 2, и так далее.
Например,
Поскольку ϕ = 1 + 1/ϕ, оно должно быть больше 1. Начнем со значения 1,5 в качестве нашего первого предположения.
- Член 1 = Мультипликативное обратное 1,5 = 1/1,5 = 0,6666…
- Член 2 = мультипликативный, обратный 1,5 + 1 = 0,6666. . + 1 = 1,6666…
. + 1 = 1,6666… Поскольку оба термина не равны, мы повторим этот процесс снова, используя предполагаемое значение, равное термину 2 .
В следующей таблице приведены данные расчетов для всех принятых значений, пока мы не получим желаемые равные условия:
| Итерация | Предполагаемое значение | Термин 1 (1/значение) | Термин 2 (1/значение + 1) |
|---|---|---|---|
| 1. | 1,5 | 11,511,5 = 0,6666.. | 0,6666.. + 1 = 1,6666.. |
| 2. | 1.6666.. | 11,666..11,666.. = 0,6 | 0,6 + 1 = 1,6 |
| 3. | 1,6 | 11,611,6 = 0,625 | 0,625 + 1 = 1,625 |
| 4. | 1,625 | 11,62511,625 = 0,61538.. | 0,61538.. + 1 = 1,61538.. |
| 5. | 1. 61538.. | .. | .. и так далее |
Чем больше итераций вы выполните, тем ближе приблизительное значение будет к точному. Другие методы обеспечивают более эффективный способ вычисления точного значения. 92 — 4ac}}{2a}\)
Подставляя значения a = 1, b = -1 и c = -1, получаем
ϕ = \(\frac{1 \pm \sqrt{( 1 + 4 )}}{2}\)
Решение можно упростить до положительного значения, что даст:
ϕ = 1/2 + √5/2
Обратите внимание, что мы не рассматриваем отрицательное значение, так как \( \phi\) — это отношение длин, и оно не может быть отрицательным.
Следовательно, ϕ = 1/2 + √5/2
Что такое золотой прямоугольник?
В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.
Построение золотого прямоугольника
Мы можем построить золотой прямоугольник, выполнив следующие шаги:
- Шаг 1: Сначала мы нарисуем квадрат со стороной 1 единица. На одной из его сторон нарисуйте точку посередине. Теперь мы проведем линию от этой точки до угла другой стороны.
- Шаг 2: Используя эту линию в качестве радиуса и точку, проведенную посередине, в качестве центра, нарисуйте дугу, идущую вдоль стороны квадрата. Длину этой дуги можно рассчитать с помощью теоремы Пифагора: √(1/2) 2 + (1) 2 = √5/2 шт.
- Шаг 3: Используйте пересечение этой дуги и стороны квадрата, чтобы нарисовать прямоугольник, как показано на рисунке ниже:
Это золотой прямоугольник, потому что его размеры находятся в золотом сечении. т. е. ϕ = (√5/2 + 1/2)/1 = 1,61803
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это особый ряд чисел, в котором каждый член (начиная с третьего члена) является суммой двух предыдущих членов.
Для нахождения последовательности Фибоначчи можно использовать следующие шаги:
- Начнем с того, что возьмем 0 и 1 в качестве первых двух членов.
- Таким образом, третий член 1 вычисляется путем сложения 0 и 1.
- Точно так же следующий член = 1 + 2 = 3 и так далее.
Последовательность Фибоначчи задается как 0, 1, 1, 2, 3, 5, 8, 13, 21,… и так далее. Последовательность Фибоначчи и золотое сечение имеют между собой особую связь. Когда мы начинаем вычислять отношения двух последовательных членов ряда Фибоначчи, значение каждого последующего отношения становится ближе к точному значению ϕ.
Например,
В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ. В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ.
| Срок 1 | Срок 2 | Соотношение = Клемма 2 / Клемма 1 |
|---|---|---|
| 2 | 3 | 1,5 |
| 3 | 5 | 1. 6666.. |
| 5 | 8 | 1,6 |
| 8 | 13 | 1,625 |
| 13 | 21 | 1.61538 |
☛Связанные темы
Ниже приведен список тем, тесно связанных с золотым сечением. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.
- Среднее
- Соотношение
- Числа Фибоначчи
- Квадратные уравнения
- Соотношение, доля, процентные формулы
Часто задаваемые вопросы о золотом сечении
Что такое золотое сечение простыми словами?
Золотое сечение — это математическое отношение, которое существует между двумя величинами, если их отношение равно отношению их суммы к большей из них величин. Другими словами, когда линия разделена на две части и более длинная часть «а», разделенная на меньшую часть «b», равна сумме (а + b), деленной на «а», это означает, что линия отражая золотое сечение, которое равно 1,618.
Что вы подразумеваете под золотым прямоугольником?
В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.
Почему золотое сечение красиво?
Золотое сечение — это соотношение, которое при использовании в различных областях для проектирования объектов делает объекты эстетически привлекательными и приятными на вид. Поэтому золотое сечение называют красивым атрибутом. Его можно заметить в различных узорах природы, например, в спиралевидном расположении цветов и листьев. Есть много применений золотого сечения в области архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре, например, Великая пирамида Египта и Великая мечеть Кайруана.
Почему золотое сечение важно?
Золотое сечение — это математическое соотношение, которое часто встречается в природе и используется в различных областях.
Он используется в нашей повседневной жизни, искусстве и архитектуре. Объекты, созданные с учетом золотого сечения в своей структуре и дизайне, более приятны и эстетичны для глаз. Это можно заметить по спиралевидному расположению цветков и листьев.
Где в реальной жизни используется золотое сечение?
Существует множество применений золотого сечения в области искусства и архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре. Такие художники, как Лео да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах. Его можно использовать для изучения структуры многих объектов в нашей повседневной жизни, которые напоминают определенный узор.
Кто открыл золотое сечение?
Древнегреческие математики первыми упомянули о золотом сечении в своих работах. Математики V века до нашей эры Гиппакус и Евклид внесли большой вклад в свои исследования по этому вопросу.
Что такое формула золотого сечения?
Формулу золотого сечения можно использовать для расчета значения золотого сечения.
Формула для расчета золотого сечения дается как
1 + 1/ϕ = ϕ
, где ϕ обозначает золотое сечение.
Калькулятор золотого сечения
Калькулятор золотого сечения рассчитает длину частей, на которые нужно разделить отрезок, чтобы получить золотое сечение . Прежде чем мы перейдем к вычислению золотого сечения, давайте обсудим, что такое золотое сечение. В дальнейшем вы можете найти все необходимые знания!
Вы также можете воспользоваться калькулятором пропорций, если хотите узнать о пропорциях в целом.
Определение золотого сечения
Золотое сечение (также известное как золотое сечение или золотая пропорция ) возникает, когда отрезок делится на две части — соотношение более длинной части к более короткой должно быть таким же, как пропорция весь сегмент к более длинной части. То есть, если более длинная часть имеет длину aaa, а более короткая часть имеет длину bbb, формула золотого сечения будет выглядеть так:
a+ba=ab\small \frac{a+b}{a} = \frac abaa+b =ba
Чтобы вычислить значение золотого сечения, вам нужно решить приведенное выше уравнение для a/ba/ba/b.
Удобно переставить его как 92-х-1=0х2-х-1=0. Делаем это стандартными методами и обнаруживаем, что значение золотого сечения равно 12(1+5)\frac 12 (1+\sqrt{5})21(1+5), что примерно равно 1,61803398875. ..1,61803398875…1,61803398875…. Это число часто обозначается греческой буквой ϕ\phiϕ.
🙋 Золотое сечение 1,618…1,618…1,618… совпадает с пределом отношения последовательных чисел Фибоначчи! Это магический ? Узнайте больше с калькулятором последовательности Фибоначчи!
Теперь мы знаем, что такое золотая пропорция и как вычислить ее значение, поэтому давайте обсудим, как проверить, подчиняются ли некоторые две заданные длины этой божественной пропорции.
Как проверить, находятся ли два сегмента в золотом сечении?
Вот пошаговые инструкции, которые помогут вам выяснить, находятся ли два отрезка в золотом сечении:
- Найдите длину более длинного отрезка и обозначьте его
a. - Найдите длину более короткого сегмента и обозначьте его как
b. - Вычислить
a/b. - Если пропорция (приблизительно) равна
1,618, ваши сегменты находятся в золотой пропорции.
Вы также можете использовать калькулятор золотого сечения Omni для выполнения этой работы. Хотя любой калькулятор пропорций может помочь вам в этом, наш калькулятор золотого сечения специально занимается этим вопросом, поэтому лучшего инструмента вы не найдете!
Как использовать этот калькулятор золотого сечения?
Калькулятор золотого сечения Omni не может быть более удобным и простым. Он имеет три поля , соответствующие три длины , которые входят в формулу золотой пропорции. И вам нужно всего лишь ввести один из них , чтобы оставшиеся два были рассчитаны автоматически. Разве это не потрясающе?
Золотой прямоугольник
Золотой прямоугольник — это прямоугольник, длины сторон которого подчиняются золотому сечению, т.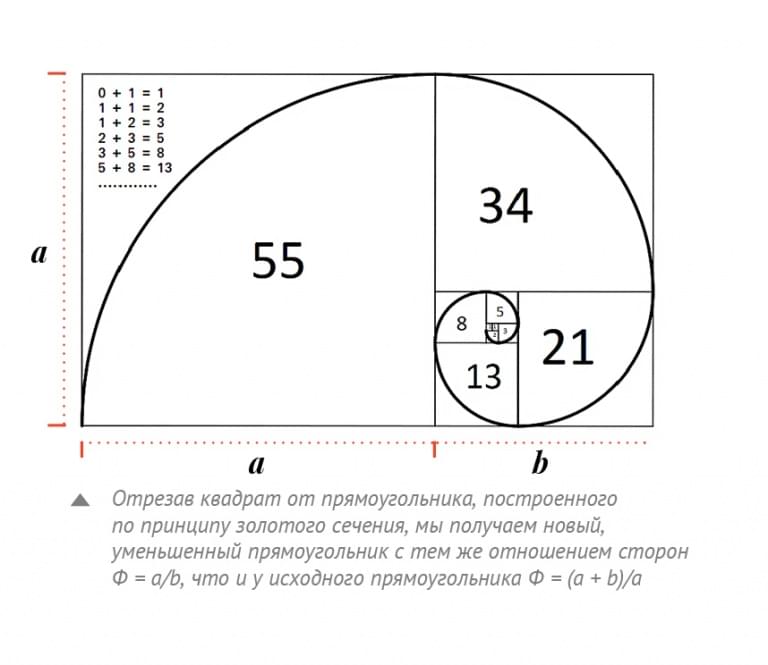
е. отношение длины к ширине равно 1,6181,6181,618. Этот прямоугольник часто можно увидеть в искусстве, так как он считается самым приятным для человеческого глаза из всех прямоугольников. Калькулятор золотого прямоугольника — это удобный способ найти стороны золотого прямоугольника вместо того, чтобы вычислять их вручную.
Почему золотое сечение важно?
Золотое сечение всегда имело особое значение в науке и искусстве благодаря своим свойствам и внешнему виду. К слову о математике:
- Золотой прямоугольник можно разделить на два меньших золотых прямоугольника (при этом пропорции сохраняются).
- Золотое сечение тесно связано с числом
5. Это число появляется в его определении (φ = (1 + √5)/2) и пятиугольника как отношение диагонали к стороне.
В искусстве золотое сечение появилось совсем недавно: Дали, например, использовал это соотношение во многих своих работах.
Где найти золотое сечение в природе?
Многие исторические и современные источники утверждают, что золотое сечение довольно распространено в природе. Некоторые примеры:
- Модель роста оставляет ;
- Геометрические поверхности некоторых овощей и ракушек ;
- Пропорции костей некоторых животных .
Однако, хотя мы не можем отрицать наличие геометрических узоров в природе, мы не можем подтвердить точность пропорций приведенных выше примеров: некоторые из них имеют огромные вариации, а другие лишь приближаются к золотому сечению.
Часто задаваемые вопросы
Что такое золотое сечение?
Золотое сечение — это соотношение между двумя величинами, которое мы также можем найти, вычислив отношение между суммой этих величин и большей из двух . Численно говоря, числа a и b находятся в золотом сечении, если:
a/b = (a + b)/a
Значение этого отношения приблизительно равно 1,618 .