Золотое сечение в цифрах: Правило третей и золотое сечение — как это работает | Статьи | Фото, видео, оптика — Главная

Содержание

ЧТО ТАКОЕ ЗОЛОТОЕ СЕЧЕНИЕ

Что такое Золотое Сечение? Что такое Золотая Пропорция? Это одно и то же, просто кто и как больше любит называть.

Попробую в публицистической манере, просто, по-житейски ответить на вопросы, которые часто задают люди, в частности слушатели моих курсов.

Для начала просто полезно знать, что в интернете, объективно, запросов на Золотое Сечение в десять раз больше чем на Золотую Пропорцию, но при этом есть специалисты, которые считают определение — Золотое Сечение — вообще ошибочным, искажающим суть данной пропорции и не имеющее права на жизнь.

Что такое Золотое Сечение или Золотая Пропорция простыми словами? В примитиве, это отношение одной части, чего либо, к другой с коэффициентом 1,618 (это 61,8%), или 62% на 38%, грубо принято округлять 60% на 40%.

Важно понимать, что в Золотой Пропорции «части» всегда три, третье – это целое (100%).

Классическое определение Золой Пропорции: меньшее относится к большему так, как большее относится к целому, с коэффициентом 1,618.

Что такое число ФИ? Это и есть этот самый коэффициент 1,618 между двумя частями. Он показывает, на сколько одна часть отличается от другой. Золотое Число — так часто называют этот коэффициент.

Золотое Сечение – Пропорция Гармонии Природы. Золотое Сечение в Природе проявится во всём, если поискать. Даже можно сказать, если есть Золотая Пропорция с рядом проявлений своих свойств, то есть «жизнь», и есть Природная красота.

Формула Золотого Сечения, Золотое Сечение в математике – это раскрытие в цифрах закономерностей проявлений отношения частей в Природе. Основные формулы проявлений Золотого Сечения есть даже в детских учебниках.

Гуманитарных объяснений смысла Золотого Сечения, в глубоком смысле, значительно меньше и они часто овеяны вековыми тайнами, но это время осталось в прошлой эпохе, теперь выявлена простота на уровне букваря.

Золотое Сечение Фибоначчи, Золотая пропорция Фибоначчи, или Ряд Фибоначчи. Это проявление шагов Золотой пропорции в целых числах, которая становится точной 62% на 38%, или 1,618 — только к десятому шагу.

По шагу Фибоначчи изменяется вся Природа, растут веточки, листики, плодятся кролики, насекомые и т.д.

Опять уточню, что детские учебники красочно показывают это.

Главное надо знать, что начиная с 0 и 1, все дальнейшие цифры – это сумма двух последних… 0,1,1,2,3,5,8,13,21,34,55…

Поскольку в Природе всё начинается с двух единиц, то соответственно к любому числу из ряда надо прибавлять – 1, например, 21 – это не 21, а 21 +1 (коварное очко и не только очко, но и любое число из ряда). То есть, если нам надо 21 яблоко, то с точки зрения Природы, по ряду Фибоначчи, их надо взять 22 = 21 + 1. Всегда на одну единицу больше.

Эта, на первый взгляд, странная тонкость, имеет принципиальное значение для поиска «постоянных» и «переменных» состояний. Например, какая зарплата нас удовлетворит, или сколько яблок надо купить, чтобы быть довольным. Купив «постоянное» количество (из ряда Фибоначчи) – будешь удовлетворён, даже если купил меньше планируемого.

Золотое Сечение Леонардо да Винчи. Так часто люди отождествляют гения и пропорцию. Да, это справедливо, хотя, намного раньше, по ходу истории, разные цивилизации использовали Пропорцию Бога, это и шумеры, и египтяне…

Мы привыкли, что Золотое Сечение в архитектуре, это удел специалистов, и то редких, или сумасшедших гениев. Это ошибка. Любому человеку, даже детям, надо знать элементарные проявления закона Золотого Сечения – базовые приёмы Природоподобных Технологий, как таблицу умножения.

Это позволит в психологии понимать причино-следственность поступка в программном смысле, а также это позволит легко ориентироваться в городе на предмет зданий, несущих положительные состояния или за городом, на дачном участке на предмет получения удовлетворения от пребывания на природе и от ведения хозяйства. Золотое Сечение в Природе и Золотое Сечение в доме, станут одинаково положительно влиять на ощущения.

Теперь пару слов о Золотом Сечении в искусстве. Хорошо когда произведение искусства завораживает. Завораживать может только «жизнь», проявленная в произведении, которая включается исключительно проявлениями Золотого Сечения, то есть Природоподобия.

Есть интересный пример проявления Золотого Сечения в фотографии. Стоит взять по Природоподобию «правильные» размеры рамки, самой фотографии и изображения, то одна и та же фотография, которая только что была скучной, вдруг заживёт притягательной магией.

В итоге, еще раз повторю, Золотая Пропорция – это выключатель или включатель всей полноты Природоподобия, Гармонии, Красоты, Жизни — с больших букв: равновесия, сил, здоровья, удовлетворения, доходности, счастья и любви. Собственно, это и есть маркер Любви. Причина этого в том, что правило Золотой Пропорции отражает мирозданческий принцип Триединства, но об этом я расскажу в другой статье.

Полезные статьи:

— Человек в золотом сечении;

— Метод Аркадия Осипова;

— Заказать индивидуальный проект;

— Что такое Закон Триединства;

— Улей для пчел по Золотому Сечению;

— Отзывы;

— Семинары;

— На главную

Читать онлайн «φ – Число Бога.

Золотое сечение – формула мироздания», Марио Ливио – Литрес

Права на перевод получены соглашением с Broadway Books (Crown Publishing Group, Random House LLC., A Penguin Random House Company) и литературным агентством «Синопсис».

Mario Livio THE GOLDEN RATIO:

The Story of PHI, the World’s Most Astonishing Number

⁂

CЕКРЕТ ГАРМОНИИ ВО ВСЕМ

Являются ли некоторые числа более значимыми, чем другие? Конечно же, да! Если уж у простых людей, далеких от науки или мистики, есть свои любимые и нелюбимые числа, что же говорить про математиков и физиков? Число – такой же важный компонент культуры, как слово. Нет человека, которому бы ни о чем не говорили числа 7, 13 или 666. Но есть числа, которые влияют на нашу жизнь, даже если мы о них не знаем. Таково число фи, в котором кроется секрет гармонии во всем. Марио Ливио написал эту книгу, чтобы мы не были так слепы и не думали, что нумерология – это предрассудки.

Тимоти Хью, Коннектикут

ИЗ ЧЕГО СКЛАДЫВАЕТСЯ КРАСОТА

Книга Марио Ливио полна увлекательнейших цифровых трюков, но, чтобы понять их, вовсе не нужно иметь математический склад ума. Все мы сталкиваемся с тем, что называют красотой. Но кто скажет, из чего складывается красота? Почему нам так нравится смотреть на картины старых мастеров, любоваться спиральными галактиками или разглядывать сосновую шишку? В своей книге Ливио раскрывает секреты красоты и уводит читателя в увлекательный мир математики – науки, которая объясняет все.

Элис Хоул, Лос-Анджелес

ПОТРЯСАЮЩЕЕ ИССЛЕДОВАНИЕ

Я даю этой книге пять звезд из пяти! Эта книга – и для математиков, и для тех, кто не дружит с цифрами. Если вы любите науку, вас захватит потрясающее исследование, которое автор предпринимает в своем труде, если вы любитель беллетристики – эта книга станет для вас тем же, что и хороший детектив.

Рэндом Уэсли, Сан-Франциско

ФОРМУЛА ВСЕЛЕНСКОЙ ГАРМОНИИ

Марио Ливио написал прекрасную работу, в которой дается подробный исторический обзор того, как на протяжении веков люди старались открыть универсальную формулу вселенской гармонии. Оказалось, что все гораздо проще – все сводится к одному-единственному числу, известному как золотое сечение, или число Бога. Вы можете быть математиком или всего лишь человеком, которого чуть-чуть интересует мистика. Если вам интересен окружающий мир, книга приведет вас в восторг!

Кристофер Паркер, Кембридж

ХОРОШАЯ ЛИТЕРАТУРА

«Золотое сечение» – это настоящий шедевр талантливого автора. Я был впечатлен той четкой и захватывающей манерой, которая делает научный труд книгой не только для ума, но и для отдыха. В этой книге Марио Ливио одновременно отвечает на самые актуальные вопросы современной науки и рассказывает удивительную историю, увлечься которой способен каждый.

Это хорошая литература во всех отношениях.

Мишель Тернер, Колд Спринг Харбор

Памяти моего отца Робина Ливио

Предисловие

«Золотое сечение» – это книга об одном-единственном числе, однако число это совершенно особое. Это число – 1,61803… – встречается и в лекциях по истории искусств, и в перечнях «любимых чисел», которые составляют математики. Не менее поразительно, что оно было предметом множества экспериментов по психологии.

Так называемое «золотое сечение» заинтересовало меня пятнадцать лет назад, когда я готовился к лекции об эстетике в физике (представьте себе, это отнюдь не оксюморон), и с тех пор оно не идет у меня из головы.

В создании этой книги прямо и косвенно поучаствовало столько моих коллег, друзей и учеников, что всех и не перечислишь. Здесь я хотел бы выразить особую благодарность Иву-Алену Буа, Митчу Фейгенбауму, Гиллелю Гаухману, Теду Хиллу, Рону Лифшицу, Роджеру Пенроузу, Джоанне Постма, Полу Стейнхардту, Пат Тиль, Анне ван дер Хельм, Дивакару Вишванату и Стивену Вольфраму – за бесценные сведения и крайне продуктивные споры.

Я благодарен своим коллегам Даниэле Кальцетти, Стефано Казертано и Массимо Стиавелли за помощь с переводами с латыни и итальянского, Клаусу Лейтереру и Эрмине Ландт за помощь с переводами с немецкого, а Патрику Годону – за помощь с переводами с французского. Сара Стивенс-Рейберн, Элизабет Фрэзер и Нэнси Хэнкс очень посодействовали мне во всем, что касалось лингвистики и библиографии. Особенно я благодарен Шэрон Тулан за содействие в подготовке рукописи.

Искренне благодарю своего литературного агента Сьюзен Рабинер за то, что она не давала мне опустить руки до начала и во время работы над книгой. Я в огромном долгу перед Джеральдом Ховардом, моим редактором из издательства «Doubleday Broadway», за то, что он так тщательно вычитывал рукопись и делал такие точные, глубокие замечания. Также я благодарен Ребекке Холланд, выпускающему редактору в «Doubleday Broadway», за постоянное содействие в то время, пока книга была в печати.

И, наконец, эта книга вообще была написана исключительно благодаря постоянной помощи, терпению и поддержке Софи Ливио.

Прелюдия к числу

Много есть чудес на свете.
Софокл (495–405 гг. до н. э.)
(Пер. С. Шервинского, Н. Познякова)

Знаменитый английский физик лорд Кельвин (Уильям Томпсон, 1824–1907), в честь которого назван градус абсолютной температурной шкалы, во время одной своей лекции сказал: «Если знание невозможно выразить численно, значит, оно поверхностно и недостаточно». Разумеется, Кельвин имел в виду то знание, которое необходимо для научного прогресса. Однако числа и математика удивительным образом предрасположены к тому, чтобы способствовать пониманию даже того, что крайне далеко от науки – или, по крайней мере, представляется таким на первый взгляд. В «Тайне Мари Роже» Эдгара Аллана По знаменитый детектив Огюст Дюпен замечает: «Мы превращаем случайность в предмет точных исчислений. Мы подчиняем непредвиденное и невообразимое научным математическим формулам» (

пер. И. Гуровой). Можно пояснить это и на более простом примере. Представьте себе, что вы готовитесь к приему гостей и столкнулись со следующей задачей: у вас есть шоколадка, состоящая из двенадцати долек – сколько раз нужно ее разломить, чтобы разделить все части? Ответ куда проще, чем вы думали, и почти не требует вычислений. Каждый раз, когда вы ломаете шоколадку, у вас получается на один кусок больше, чем раньше. Следовательно, если вам нужно получить двенадцать кусков, придется ломать шоколадку одиннадцать раз (убедитесь сами). А если обобщить, то количество разломов всегда будет на один меньше, чем требуемое количество кусков, независимо от того, из скольких частей состоит шоколадка.

Даже если вы не слишком любите шоколад, то все равно понимаете, что этот пример демонстрирует простой математический закон, который можно применить и во многих других случаях. Однако математические свойства, формулы и законы (многие из которых не задерживаются у нас в памяти) – это далеко не все; существуют еще и особые числа, которые настолько вездесущи, что не устают нас изумлять. Самое прославленное из них – число π (пи), отношение длины окружности к ее диаметру. Значение π – 3,14159… – завораживало много поколений математиков. Хотя изначально число π было определено в геометрии, оно очень часто и неожиданно всплывает при вычислении вероятности. Знаменитый пример – так называемая игла Бюффона, названная в честь французского математика Жоржа-Луи Леклерка, графа де Бюффона (1707–1788), который поставил и решил эту вероятностную задачу в 1777 году. Леклерк задал следующий вопрос: представьте себе, что у вас на полу лежит большой лист бумаги, разлинованный параллельными линиями через равные заданные промежутки. На лист совершенно случайным образом бросают иглу, длина которой в точности равна промежутку между линиями. Какова вероятность, что игла упадет так, что пересечет одну из линий (то есть как на рис. 1)? Как ни странно, ответ, оказывается, 2/π. То есть в принципе возможно даже вычислить π, если повторить этот эксперимент много раз и понаблюдать, какая доля бросков заканчивается пересечением иглы с линией (правда, есть и другие методы вычисления π, не такие скучные).

Словосочетание «число π» настолько вошло в обиходный лексикон, что кинорежиссер Даррен Аронофски в 1998 году даже снял психологический триллер под таким названием.

Менее знаменито другое число – φ (фи), а между тем, во многих отношениях оно даже интереснее. Вот, скажем, представьте себе, что я спрашиваю у вас, что общего у изумительного расположения лепестков алой розы, композиции знаменитой картины Сальвадора Дали «Тайная вечеря», чудесного рисунка спиральной раковины и статистики размножения кроликов? Трудно поверить, что у столь разнородных явлений действительно есть нечто общее – и это некое число или геометрическая пропорция, известная человечеству еще со времен античности, число, которому в XIX веке дали почетное называние «золотое число» или «золотое сечение». А в начале XVI века в Италии вышла книга, в которой это число называлось «Божественной пропорцией» – не более и не менее.

В повседневной жизни мы применяем слово «пропорция» для обозначения соотношения между частями целого по размеру или количеству – или когда хотим подчеркнуть гармоничные отношения между разными частями. В математике термин «пропорция» применяется для описания равенства следующего типа: девять относится к трем, как шесть к двум. Как мы увидим, золотое сечение дарит нам чарующее сочетание этих определений: хотя определяется оно строго математически, однако считается, что оно обладает свойствами, обеспечивающими приятную гармонию.

Рис. 1

Первое четкое определение соотношения, которое впоследствии станет известно как золотое сечение, дал примерно в 300 году до н. э. Евклид Александрийский, основатель геометрии как формальной дедуктивной системы. К Евклиду и его фантастическим достижениям мы еще вернемся в главе 4, а пока позвольте отметить, что Евклид вызывает столь сильное восхищение, что поэтесса Эдна Сент-Винсент Миллей в 1923 году даже посвятила ему стихотворение под названием «На обнаженность красоты Евклид взглянул» (пер. Л. Мальцевой). Эдна даже сохранила свою школьную тетрадь по евклидовой геометрии. Евклид определил пропорцию, выведенную из простого деления линии (отрезка), по его выражению, «в крайнем и среднем отношении»: «Прямая линия называется рассеченною в крайнем и среднем отношении, когда как целая прямая к большему отрезку, так больший к меньшему» (пер. Ф. Петрушевского) (рис. 2).

Иначе говоря, если мы посмотрим на рис. 2, то увидим, что отрезок АВ определенно длиннее отрезка АС, в то же время АС длиннее СВ. Если отношение длины АС к длине СВ такое же, как отношение длины АВ к длине АС, значит, отрезок поделен «в крайнем и среднем отношении» – или в золотом сечении.

Рис. 2

Кто бы мог подумать, что такое на первый взгляд невинное разделение отрезка, которое Евклид определил в чисто геометрических целях, окажет влияние на самые разные разделы знания – от положения листьев в ботанике до структуры галактик, состоящих из миллиардов звезд, от математики до искусства? Следовательно, золотое сечение – прекрасный пример того самого крайнего изумления и восторга, которые так высоко ценил великий физик Альберт Эйнштейн (1879–1955). Вот как он об этом писал: «Самое прекрасное, что только может выпасть нам на долю, – это тайна. Стремление разгадать ее стоит у колыбели подлинного искусства и подлинной науки. Тот, кто не знает этого чувства, утратил любопытство, не способен больше удивляться, – все равно что мертвый, все равно что задутая свеча».

Как мы еще увидим, когда проследим на страницах этой книги все необходимые вычисления, точное значение золотого сечения (то есть отношение АС к СВ на рис. 2) – бесконечное непериодическое число 1,6180339887…, а такие бесконечные неповторяющиеся числа интересовали людей со времен античности. Рассказывают, что когда греческий математик Гиппас из Метапонта в V веке до н. э. обнаружил, что золотое сечение – это и не целое число (подобное нашим добрым знакомым 1, 2, 5 и т. д.), и даже не отношение двух целых чисел (подобное дробям вроде 1/2, 2/3, 3/4, которые в совокупности называются рациональными числами), это привело остальных пифагорейцев – то есть последователей знаменитого математика Пифагора – в полнейшее смятение. Предметом поклонения для пифагорейского мировоззрения (о котором мы подробно поговорим в главе 2) был arithmos – то есть имманентные качества целых чисел и их отношений и их предполагаемая роль в мироздании. А открытие, что существуют числа вроде золотого сечения, которые все тянутся и тянутся вечно и при этом в них нет никаких следов повторяемости, никакой закономерности, вызвало самый настоящий философский кризис. Легенда даже утверждает, будто пифагорейцы, совершенно потрясенные этим открытием колоссальной важности, устроили гекатомбу – пожертвовали сто быков, – хотя это вряд ли, учитывая, что пифагорейцы были строгими вегетарианцами. Тут я вынужден подчеркнуть, что большинство подобных историй основаны на недостоверном историческом материале. Так или иначе, мы даже приблизительно не знаем, когда именно были открыты числа, которые не являются ни целыми, ни дробями – так называемые иррациональные числа. Однако некоторые ученые датируют это открытие V веком до н. э., что, по крайней мере, соответствует только что рассказанным легендам. Очевидно одно: пифагорейцы в общем и целом считали, что существование подобных чисел так ужасно, что это, должно быть, своего рода ошибка мироздания, которую надо замолчать и держать в тайне.

Тот факт, что золотое сечение невозможно выразить в виде дроби (как рациональное число), попросту означает, что нельзя выразить в виде дроби соотношение длин АС и СВ на рис. 2. Иначе говоря, как бы мы ни трудились, мы не найдем единицы измерения, которая, скажем, укладывалась бы 51 раз в АС и 19 раз в СВ. Две длины, у которых нет подобной единицы измерения, называются несоизмеримыми. В своем труде «Жизнь Пифагора» (ок. 300 г. н. э.) философ и историк Ямвлих из аристократического сирийского семейства так описывает бурную реакцию на это открытие: будто бы тот, кто открыл эту тайну непосвященным, «вызвал, как говорят, такую ненависть, что его не только изгнали из общины и отлучили от пифагорейского образа жизни, но и соорудили ему надгробие, как будто действительно ушел из жизни тот, кто некогда был их товарищем» (пер. И. Ю. Мельниковой).

В профессиональной математической литературе золотое сечение принято обозначать греческой буквой τ (тау) – от греческого слова τομή (читается «томэ»), которое означает «сечение» или «разрез». Однако в начале ХХ века американский математик Марк Барр предложил обозначать золотое сечение буквой φ – по первой букве имени великого древнегреческого скульптора Фидия, жившего примерно в 490–430 гг. до н. э. Величайшие шедевры Фидия – Афина Партенос в Афинах и Зевс в Олимпии. Кроме того, полагают, что он отвечал и за другие скульптуры в Парфеноне, хотя весьма вероятно, что их создали его ученики и помощники. Барр решил, что надо почтить память скульптора, поскольку многие искусствоведы полагают, что Фидий часто и весьма точно применял золотое сечение в своих творениях (эту и подобные гипотезы мы очень дотошно разберем в нашей книге). Я буду называть его и золотым сечением, и числом φ, поскольку именно такие обозначения чаще всего встречаются в популярной математической литературе.

Величайшие математические умы в истории – и древнегреческие мудрецы Пифагор и Евклид, и средневековый итальянский ученый Леонардо Пизанский по прозвищу Фибоначчи, и астроном эпохи Возрождения Иоганн Кеплер, и современные научные светила, например, физик из Оксфорда Роджер Пенроуз, немало часов провели в размышлениях над этим простым соотношением и его свойствами. Однако золотое сечение чарует отнюдь не только математиков. Биологи, художники, историки, музыканты, архитекторы, психологи и даже мистики – все они размышляли над тем, почему это число столь вездесуще и в чем его притягательность. По сути дела, можно, пожалуй, сказать, что золотое сечение вдохновляло мыслителей из всех отраслей знания – и в этом с ним не в силах сравниться никакое другое число в истории математики.

Даже простому вопросу о происхождении названия «золотое сечение» посвящено огромное количество исследований, а особенно глубоко этим интересовался канадский математик и писатель Роджер Герц-Фишлер, о чем и рассказано в его превосходной книге «A Mathematical History of the Golden Number» («Математическая история золотого сечения»). Учитывая, какой пристальный интерес вызывало это число еще со времен античности, можно было бы подумать, что и название это античного происхождения. И в самом деле, некоторые авторитетные труды по истории математики, например, «Рождение математики во времена Платона» Франсуа Ласерре (François Lasserre. «The Birth of Mathematics in the Age of Plato») и «История математики» Карла Б. Бойера (Carl B. Boyer. «History of Mathematics»), возводят это название, соответственно, к XVI и XVII векам. Однако дело, скорее всего, не в этом. Насколько я могу судить по обширным источниковедческим данным, впервые это словосочетание применил в 1835 году немецкий математик Мартин Ом (брат знаменитого физика Георга Симона Ома, в честь которого назван закон Ома в электромагнетизме) во втором издании своей книги «Чистая элементарная математика» (Martin Ohm. «Die Reine Elementar-Mathematik»). В одной сноске Ом пишет: «Подобное разделение произвольного отрезка на две части принято также называть золотым сечением». Формулировка Ома однако создает впечатление, что он не сам придумал этот термин, а скорее привел уже принятое название. Тем не менее, в первом издании книги, опубликованном в 1826 году, Ом этого названия не приводит, а это заставляет сделать по крайней мере тот вывод, что выражение «золотое сечение» (нем. «der Goldene Schnitt») завоевало популярность лишь к 1835 году. Вероятно, ранее это было лишь разговорное выражение, применявшееся преимущественно в математических кругах. Однако нет никаких сомнений, что после книги Ома термин «золотое сечение» стал часто повторяться в немецкой литературе по математике и искусствоведению. А в англоязычной печати это выражение, по всей видимости, дебютировало в статье Джеймса Салли (James Sully) по эстетике, которая появилась в девятом издании Британской энциклопедии в 1875 году. Салли описывает «интересное экспериментальное исследование… проведенное Густавом Теодором Фехнером (известным немецким физиком и первопроходцем в области психологии, жившим в XIX веке) о том, что «золотое сечение» первоначально было именно зримой пропорцией» (об экспериментах Фехнера мы подробно поговорим в главе 7). В математическом контексте этот термин впервые встретился в англоязычной литературе, по всей видимости, в статье Э. Эккерманна, которая так и называлась «Золотое сечение» (E. Ackermann. «The Golden Section») и была напечатана в журнале «American Mathematical Monthly» в 1895 году, а также – примерно в это же время, в 1898 году – в книге «Введение в алгебру» известного преподавателя и писателя Дж. Кристала (1851–1911). Позвольте мне отметить любопытства ради, что единственное определение «золотого числа», появившееся в издании французской энциклопедии «Nouveau Larousse Illustré» 1900 года, гласит: «Число, определяющее каждый год лунного цикла». Это относится к положению календарного года в пределах 19-летнего цикла, после которого фазы луны снова приходятся на те же даты. Очевидно, во французскую математическую номенклатуру «золотое число» и тем более «золотое сечение» проникало гораздо дольше.

Однако почему это вообще так важно? Из-за чего, собственно, это число или геометрическая пропорция так сильно нас интересуют? Привлекательность золотого сечения в первую очередь коренится в том факте, что оно обладает прямо-таки пугающим свойством вылезать там, где его никак не ожидаешь.

Возьмем, к примеру, самое обычное яблоко – фрукт, который часто и, вероятно, ошибочно ассоциируется с древом познания, играющим столь заметную роль в библейском рассказе о грехопадении – и разрежем его поперек. И мы увидим, что яблочные семечки образуют пятиконечную звезду – она же пентаграмма (рис. 3). Каждый из пяти равнобедренных треугольников, составляющих лучи пентаграммы, обладает таким свойством, что соотношение длины его длинной стороны к короткой, то есть к основанию, равно золотому сечению – 1,618… Правда, вы, вероятно, решите, что это не так уж и удивительно. В конце концов, золотое сечение и определяется в первую очередь как геометрическая пропорция, так что, вероятно, не надо так уж поражаться, если эта пропорция встречается в некоторых геометрических фигурах.

Рис. 3

Однако это лишь верхушка айсберга. Согласно буддистской традиции, Будда во время одной своей проповеди не проронил ни слова, а всего-навсего показал слушателям цветок. Чему может научить нас цветок? Скажем, роза часто служит примером природной симметрии, гармонии, любви и хрупкости. Индийский поэт Рабиндранат Тагор (1861–1941) в своей «Религии человека» пишет: «Нам почему-то кажется, что роза – это язык, который нашла любовь, чтобы достичь наших сердец». Предположим, вам нужно качественно оценить симметричное устройство розы. Возьмите розу и препарируйте ее, чтобы разобраться, каким образом ее внешние лепестки накладываются на внутренние. Как я показываю в главе 5, вы обнаружите, что лепестки расположены в соответствии с математическим законом, основанном на золотом сечении.

Теперь обратимся к царству животных: все мы хорошо знакомы с чарующе прекрасными спиральными структурами многих раковин моллюсков, например, вида Nautilus pompilius (рис. 4). Между прочим, такую раковину держит в руке танцующий Шива из индийских легенд – это символ одного из орудий творения. Кроме того, структура этих раковин вдохновляла и многих зодчих. Например, американский архитектор Фрэнк Ллойд Райт (1869–1959) положил эту структуру в основу здания музея Гуггенхайма в Нью-Йорке. Попав в музей, посетители поднимаются по спиральному пандусу, насыщая воображение созерцанием произведений искусства – точно так же, как моллюск выстраивает новые спиральные камеры, заполняя свое физическое пространство. В главе 5 мы увидим, что рост спиральных раковин также подчиняется правилу, основанному на золотом сечении.

Рис. 4

Рис. 5

Пожалуй, не нужно быть особым поклонником нумерологии – мистики чисел, чтобы уже сейчас почувствовать некоторый душевный трепет: столь поразительна способность золотого сечения проявляться в самых разных ситуациях, в самых разных феноменах, казалось бы, совершенно не связанных друг с другом. Более того, как я уже отметил в начале главы, золотое сечение обнаруживается не только в природных явлениях, но и в самых разных рукотворных предметах и произведениях искусства. Например, на рис. 5 мы видим картину Сальвадора Дали «Тайная вечеря», написанную в 1955 году (она хранится в Национальной галерее в Вашингтоне): соотношение сторон этой картины – ее размеры 167 на 268 см – приблизительно равно золотому сечению. Более того, над столом, словно охватывая композицию, парит фрагмент огромного додекаэдра – правильного двенадцатигранника, каждая грань которого представляет собой правильный пятиугольник. Как мы увидим в главе 4, правильные многогранники, например, куб, которые можно вписать в сферу (т. е. сделать так, чтобы все их углы лежали на сфере), а особенно додекаэдр, тесно связаны с золотым сечением. Почему Дали решил так явно подчеркнуть золотое сечение в своей картине? Художник отмечал, что «Композиция Тайной Вечери должна быть симметричной» – но это лишь начало ответа на наш вопрос. Как я показываю в главе 7, золотое сечение появляется – или по крайней мере, должно появляться по замыслу создателя – в работах многих других художников, архитекторов, дизайнеров и даже в знаменитых музыкальных произведениях. Говоря обобщенно, золотое сечение применяется в некоторых произведениях искусства с целью достичь определенного зрительного или слухового эффекта. Подобный эффект вызывается, в частности, особым соотношением размеров отдельных частей и целого, особыми пропорциями. История искусств показывает, что в результате долгих поисков неуловимого канона «совершенных» пропорций – такого, чтобы любое произведение искусства при его применении автоматически становилось эстетичным и приятным – выяснилось, что этим требованиям лучше всего удовлетворяет именно золотое сечение. Но почему?

Если подробнее рассмотреть примеры из мира природы и из мира искусства, окажется, что они заставляют задаваться вопросами на трех уровнях глубины. Прежде всего, это непосредственные вопросы: (а) все ли случаи появления числа φ в природе и искусстве, описанные в литературе, действительно имеют место или некоторые из них – всего лишь результаты неверных интерпретаций и всякого рода натяжек? (б) Если число φ и правда появляется в этих и других обстоятельствах, можем ли мы как-то это объяснить? Далее, если учесть, что мы придерживаемся определения «красоты», подобного, скажем, тому, которое дано в словаре Уэбстера: «Качество, которое делает объект приятным или приносит определенное удовлетворение» – возникает вопрос: есть ли у математики эстетическая составляющая? Если да, какова сущность этой составляющей? Это серьезный вопрос, поскольку, как заметил однажды американский архитектор, математик и инженер Ричард Бакминстер Фуллер (l895–l983): «Когда я работаю над какой-то задачей, то никогда не думаю о красоте. Думаю я только о том, как решить эту задачу. Но если я решу ее и решение окажется некрасивым, я буду знать, что ошибся». И, наконец, самый интересный вопрос звучит так: почему, собственно, математика столь могущественна и столь вездесуща? Благодаря чему математика и численные константы вроде золотого сечения играют столь важную роль во всем на свете – от фундаментальных теорий происхождения Вселенной до рынка ценных бумаг? Существует ли математика и ее принципы независимо от людей, которые ее открыли или обнаружили? Математична ли Вселенная по своей природе? Последний вопрос можно задать, переформулировав известный афоризм английского физика сэра Джеймса Джинса (1847–1946): может быть, и сам Бог – математик?

В этой книге я постараюсь обсудить все эти вопросы более или менее подробно с точки зрения увлекательной истории числа φ. История этой константы, временами запутанная, насчитывает тысячелетия и разворачивается на всех материках. Но при этом я надеюсь рассказать вам еще и интересную историю о человеческой психологии. Наш сюжет отчасти повествует о тех временах, когда физиками и математиками называли себя люди, которых попросту интересовали различные вопросы, разжигавшие в них любознательность. Зачастую подобные люди трудились и умирали, не зная, удастся ли результатам их трудов изменить ход научной мысли или они просто канут в Лету, не оставив и следа.

Однако прежде чем пуститься в этот путь, нам придется поближе познакомиться с числами вообще и с золотым сечением в частности. Откуда, в сущности, появилась сама идея золотого сечения? Что именно заставило Евклида задуматься о том, чтобы разделить отрезок именно в таком соотношении? Моя цель – помочь вам заглянуть в подлинные истоки, так сказать, «золотого исчисления». Для этого мы и предпримем краткую ознакомительную экскурсию во времена зарождения математики.

Золотой коэффициент калькулятора

, созданный Piotr Małek и Mateusz Muga

, просмотрено Bogna Szyk and Jack Bowater

Последнее обновление: 04 февраля 2023

СОДЕРЖА

Калькулятор золотого сечения рассчитает более короткую сторону, более длинную сторону и общую длину двух сторон, чтобы вычислить золотое сечение. Прежде чем мы сможем рассчитать золотое сечение, важно ответить на вопрос «что такое золотое сечение?». В следующем разделе мы надеемся дать вам ответ.

Вы также можете воспользоваться калькулятором пропорций, если хотите анализировать пропорции в целом.

Что такое золотое сечение

Золотое сечение, также известное как золотое сечение или золотая пропорция, получается, когда две длины сегмента имеют такое же отношение, как отношение их суммы к большей из двух длин. Значение золотого сечения, которое является пределом соотношения последовательных чисел Фибоначчи, составляет примерно 1,6181,6181,618.

Формула золотого сечения выглядит следующим образом. Пусть больший из двух отрезков будет aaa, а меньший обозначим как bbb. Тогда золотое сечение равно (a+b)/a=a/b(a+b)/a = a/b(a+b)/a. =a/b Любой старый калькулятор пропорций справится с этой задачей за вас, но этот калькулятор золотого сечения решает эту проблему специально, так что вам не о чем беспокоиться!

Вот пошаговый метод решения соотношения вручную.

Найдите более длинный сегмент и назовите его aaa
Найдите более короткий сегмент и назовите его bbb
Введите значения в формулу.
Возьмите сумму aaa и bbb и разделите на aaa
Разделить aaa на bbb
Если пропорция находится в золотом сечении, она будет равна примерно 1,6181,6181,618
Используйте калькулятор золотого сечения, чтобы проверить свой результат

Калькулятор постулата сложения сегментов можно использовать для нахождения одной из длин сегментов, когда 3 точки лежат на одной прямой и известны два расстояния.

Золотой прямоугольник

Золотой прямоугольник — это прямоугольник длиной a+ba+ba+b и шириной aaa. Этот прямоугольник часто можно увидеть в искусстве, так как было сказано, что он самый приятный для глаз из всех подобных прямоугольников. Калькулятор золотого прямоугольника — это удобный способ найти золотой прямоугольник вместо того, чтобы работать с ним вручную.

Золотое сечение встречается во многих формах архитектуры и в некоторых природных узорах, например, в расположении листьев у некоторых растений. Золотая пропорция также наблюдается в правильных пятиугольниках. Вы можете найти больше информации об этой форме в калькуляторе пятиугольника.

Часто задаваемые вопросы

Что такое золотое сечение?

Золотое сечение — это отношение между двумя величинами, которое мы также можем найти, вычислив отношение между суммой этих величин и большей из двух .0058 . Численно говоря, числа a и b находятся в золотом сечении, если:
a/b = (a+b)/a
Это отношение имеет определенное значение, обозначаемое греческой буквой φ :
φ = 1,618033988749
Золотое сечение высоко ценится, поскольку фигуры, построенные по этим пропорциям, выглядят особенно приятно для человеческого глаза.

Какова длина сторон золотого прямоугольника с диагональю 1?

Стороны золотого прямоугольника с диагональю d = 1 равно a = 0,850651 и b = 0,525731 . Чтобы найти эти результаты:

Используйте теорему Пифагора, чтобы найти длину стороны b как функцию a :
`b = sqrt(1 — a²).
Вычислите длину стороны a , зная, что a/b = φ :
a/b = φ
a/sqrt(1 - a²) - φ
a = sqrt(φ/² 1 + φ²)) = 0,850651
Вычислить длину стороны b по следующей формуле:
b = a/φ = 0,525731

Вот оно!

Почему золотое сечение важно?

Золотое сечение всегда имело особое значение в науке и искусстве благодаря своим свойствам и внешнему виду. К слову о математике:

Золотой прямоугольник (прямоугольник, стороны которого находятся в золотом сечении) можно разделить на два меньших золотых прямоугольника (он сохраняет свои пропорции).
Золотое сечение глубоко коррелирует с числом 5 . Это число появляется в его определении ( φ = (1 + √5)/2 ) и пятиугольника как отношение между диагональю и стороной.

В искусстве золотое сечение появилось сравнительно недавно: Дали, например, использовал это соотношение в своих работах.

Где я могу найти золотое сечение в природе?

Многие источники, как исторические, так и современные, утверждают, что золотое сечение довольно распространено в Природе. Некоторые примеры:

Характер роста листьев;
Геометрические поверхности некоторых овощей и ракушек;
Пропорции костей некоторых животных.

Однако, хотя мы не можем отрицать наличие геометрических узоров в Природе, мы не можем подтвердить точность пропорций приведенных выше примеров: некоторые из них имеют огромные вариации, а другие лишь приближаются к золотому сечению.

Петр Малек и Матеуш Муха

Длинная часть (a)

Короткая часть (b)

Целиком (a+b)

Посмотреть 18 похожих калькуляторов дробей 🍕

Сложение дробейСравнение дробейДесятичная дробь… Еще 15

Золотое сечение — самое иррациональное число.

Гетти Изображений Плюс
Эта статья адаптирована из Форма: скрытая геометрия информации, биологии, стратегии, демократии и всего остального Джордана Элленберга. © Penguin Press 2021.
Одна из величайших прелестей теории чисел — существование иррациональные числа — числа, подобные квадратному корню из 2 или π, которые нельзя выразить как отношение любых двух целых чисел, какими бы большими они ни были. Легенда гласит — возможно, ложная, но, эй, она доказывает, — что открытие иррациональности √2 настолько смутило пифагорейцев, которые хотели, чтобы все числа были рациональными, что они бросили первооткрывателя в океан.
Среди загадок иррациональности особое место занимает одно число: так называемое золотое сечение .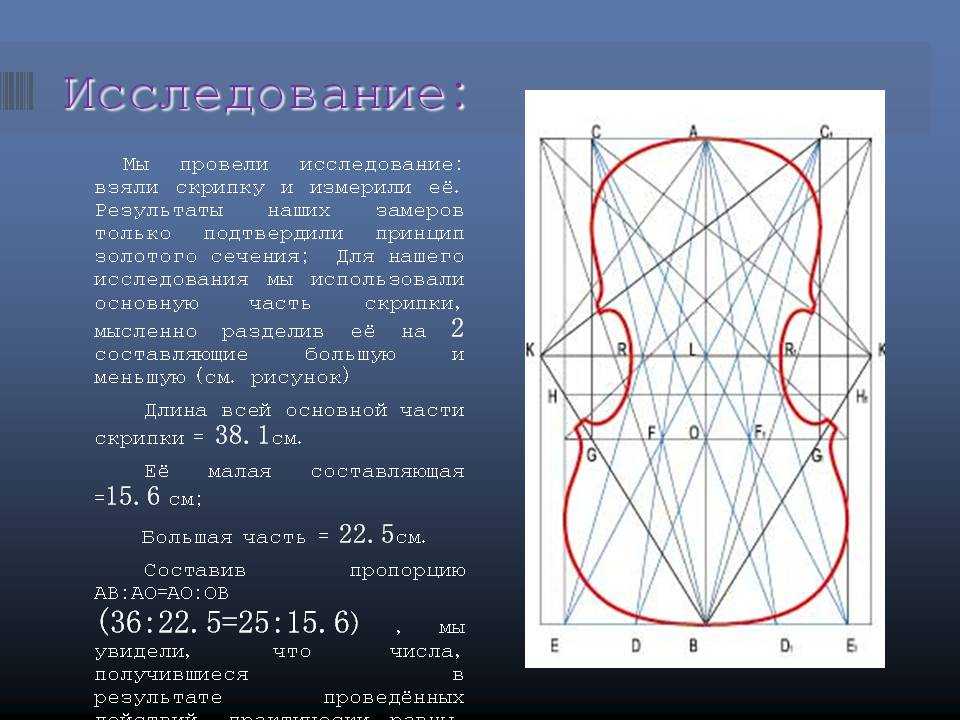 Значение золотого сечения составляет около 1,618 (но не точно 1,618, так как тогда это было бы соотношение 1,618/1,000 и, следовательно, не иррационально), и оно также обозначается греческой буквой φ, которая произносится как «плата», если вы ты математик и «тьфу», если ты в братстве. Если вам нужно точное описание, золотое сечение можно выразить как (1/2)(1+√5.)
Люди веками поднимали шум вокруг этого числа. У Евклида эта пропорция носит более приземленное название «деление на крайнее и среднее». Он понадобился ему для построения правильного пятиугольника, так как золотое сечение — это пропорция между диагональю такого пятиугольника и его стороной. Золотой прямоугольник — это прямоугольник, длина которого в φ умножается на ширину; у него приятное качество: если разрезать его поперек, так что один из двух кусков будет квадратом, а другой будет меньшим золотым прямоугольником.
Вы можете сделать то же самое с этим меньшим прямоугольником, чтобы сделать новый меньший золотой прямоугольник, затем отрезать квадрат от этого маленького золотого мальчика, чтобы сделать золотой прямоугольник еще меньше, и так далее и тому подобное; в результате получается что-то вроде прямоугольной спирали:
Википедия
Золотое сечение возникает не только в геометрии; в последовательности Фибоначчи, где каждое число является суммой двух предыдущих (1, 1, 2, 3, 5, 8, 13, 21, 34, …), отношения между последовательными членами приближаются к φ все больше и больше по мере термины становятся все больше и больше. (Но, конечно, эти соотношения никогда не0166 прибывают в φ, потому что, опять же, иррационально!)
com/_components/slate-paragraph/instances/ckpo8csmo001p3g6cal645iv2@published»> Вокруг золотого сечения уже давно витают миазмы мистицизма. Теоретик чисел Джордж Баллард Мэтьюз жаловался на это еще в 1904 году, написав, что «божественная пропорция» или «золотое сечение» поражала невежественных и даже ученых людей, таких как Кеплер, чувством тайны и повергала их в мечтательность. видов фантастического символизма». Иногда говорят, что фигуры, длина которых находится в золотой пропорции друг к другу, по своей природе являются самыми красивыми, хотя утверждения о том, что Великая пирамида в Гизе, Парфенон и Мона Лиза были спроектированы по этому принципу, недостаточно обоснованы. В влиятельной статье 1978 года в Журнале ортопедической стоматологии говорится, что набор искусственных зубов для максимальной привлекательности улыбки должен иметь центральный резец в 1,618 раза шире бокового резца, который, в свою очередь, должен быть в 1,618 раза шире клыка. Существует небольшая, но настойчивая школа финансового анализа, которая считает, что колебания на фондовом рынке управляются золотым сечением; Ваш терминал Bloomberg, если у вас достаточно флеша, чтобы иметь его, нарисует для вас маленькие «линии Фибоначчи» на биржевых графиках.
Однажды в 90-х я ужинал с другом моего друга в закусочной Galaxy Diner в Нью-Йорке. Он сказал, что снимает фильм о математике и хочет поговорить с практикующим о том, на что на самом деле похожа математическая жизнь. Мы ели лепешки, я рассказывал ему истории, я забыл об этом, прошли годы. Друга друга звали Даррен Аронофски, а его фильм Pi вышел в 1998 году. Главный герой фильма — теоретик чисел по имени Макс Коэн, который очень напряженно думает и много крутит пальцами в волосах. Он встречает хасида, который заинтересовывает его еврейской нумерологией, практикой под названием 9.0166 гематрия , где слово превращается в число путем сложения числового значения содержащихся в нем еврейских букв. Еврейское слово, обозначающее «восток», дает в сумме 144, объясняет хасид, а «Древо жизни» — 233. Теперь Максу интересно, потому что это числа Фибоначчи. Он рисует еще несколько чисел Фибоначчи на страницах газеты, посвященных фондовому рынку. «Я никогда раньше такого не видел», — говорит впечатленный хасид. Макс лихорадочно программирует свой компьютер, который называется Евклид, рисует спирали золотых прямоугольников и довольно долго смотрит на такие же спирали молока в своем кофе. Он вычисляет 216-значное число, которое, кажется, является ключом к прогнозированию цен на акции, а также, возможно, тайным именем Бога. Он много играет в го со своим научным руководителем. («Перестань думать, Макс. Всего чувствовать . Используй свою интуицию».) У него сильно болит голова, и он еще сильнее накручивает волосы. Красивая женщина в соседней квартире заинтригована. Я забыл упомянуть, но этот фильм черно-белый. Кто-то пытается его похитить. Наконец, он просверливает дыру в собственном черепе, чтобы выпустить часть математического давления, и фильм приходит к тому, что кажется счастливым концом.
Не помню, что я говорил Аронофски о математике, но это было не то.
Золотая нумерация действительно стала популярной в 2003 году, когда Дэн Браун опубликовал свой мегахитовый роман 9.0166 Код да Винчи , история «религиозного символиста» и профессора Гарварда, который использует последовательность Фибоначчи и золотое сечение, чтобы раскрыть заговор с участием рыцарей-тамплиеров и современных потомков Иисуса. После этого «поставить φ» было просто хорошим маркетингом. Вы могли купить джинсы, золотые пропорции которых льстили вашей задней части (они идут к вашим вставным зубам!). Существовал «Кодекс диеты», в котором утверждалось, что Леонардо хотел, чтобы вы похудели, употребляя белки и углеводы в пропорции золотого сечения. И был, пожалуй, величайший из когда-либо созданных мистических геометрических чудаков: маркетинговая фирма Arnell Group на 27 страницах объяснила новый логотип Pepsi в виде земного шара, который она разработала в 2008 году. Документ назывался «ЗАХВАТЫВАЮЩИЙ». В презентации объясняется, что Pepsi и золотое сечение являются естественными партнерами, потому что, как вы, несомненно, знаете, «словарь истины и простоты — повторяющееся явление в истории бренда». Хронология показывает, что открытие нового логотипа Pepsi является кульминацией 5000 лет науки и дизайна, включая Пифагора, Евклида, да Винчи и каким-то образом ленту Мёбиуса. Новый логотип Pepsi будет построен из дуг кругов, радиусы которых находятся в золотом сечении друг к другу, соотношение, которое, как заявляет поле, теперь, в действительно впечатляющем предложении по ребрендингу, будет известно как «Коэффициент Pepsi».
Но моя любимая вещь о золотом сечении не имеет ничего общего с пятиугольниками или пепси. Дело в том, что золотое сечение среди всех иррациональных чисел — это самое иррациональное.
com/_components/slate-paragraph/instances/ckpo8csnp001u3g6cdqovvd3k@published»> Что это может означать? Либо число является отношением двух целых чисел, либо нет*.
Оказывается, есть способы говорить о том, насколько иррационально иррациональное число. В конце концов, тот факт, что такое число, как φ, иррационально, не означает, что рядом с ним нет рациональных дробей. Конечно есть! В конце концов, десятичное расширение — это способ записи дробей, близких к числу:
16/10 = 1,6 (довольно близко)
161/100 = 1,61 (близко)
1618/1000 = 1,618 (еще ближе)
Десятичное расширение дает дробь со знаменателем 1000, которая находится в пределах 1/1000 от золотое сечение; если мы допустим, что знаменатель равен 10 000, мы можем получить в пределах 1/10 000 и так далее.
Мы можем сделать лучше, чем десятичные дроби! Помните, что отношения между числами Фибоначчи также являются дробями, которые все ближе и ближе приближаются к золотому сечению:
8/5 = 1,6
13/8 = 1,625
21/13 = около 1,615
Пройдите дальше по последовательности, и вы получите:
233/144 = 1,6180555555…
… что всего лишь около 2 из 100 000 от золотого сечения, что значительно лучше приближения, чем 1,618/ 1000, со значительно меньшим знаменателем.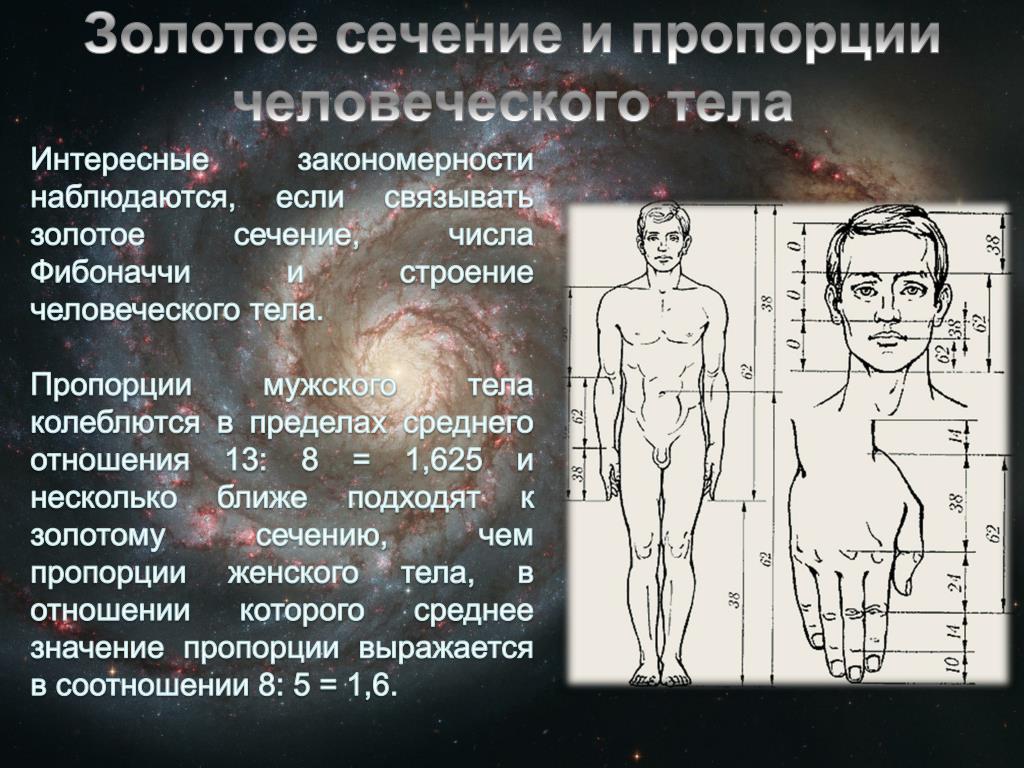
Мой предок с психическим заболеванием родился во времена, когда еще не было приютов. Вот как он жил.
19Мультфильм MTV 90-х с удивительно современным взглядом на слежку
Худые люди принимают Ozempic, чтобы похудеть. Я принимаю это по медицинским показаниям.
Я развязал А.И. о мужчинах в Tinder. То, что произошло, меня удивило.
Некоторые иррациональные образы знаменитостей могут быть аппроксимированы еще точнее. Цзу Чунчжи, астроном пятого века из Нанкина, заметил, что простая дробь 355/113 невероятно близка к π, всего лишь 2 из 10 миллионов. Он назвал это milü («очень близкое соотношение»).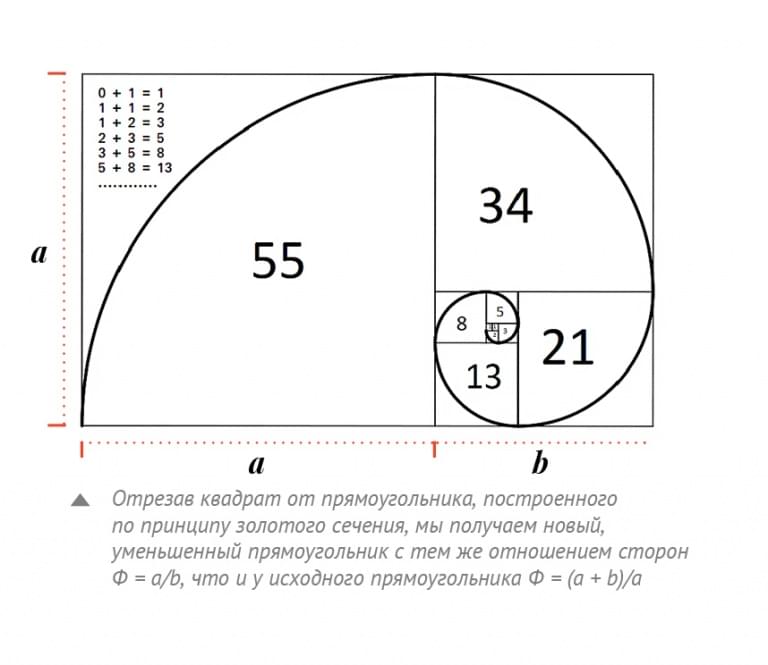 Книга Зу по математическим методам утеряна, поэтому мы не знаем, как он придумал милю. Но это была не простая находка; прошло 1000 лет, прежде чем это приближение было заново открыто в Индии, еще 100 лет, прежде чем оно стало известно в Европе, и еще столетие после этого, прежде чем было окончательно доказано, что число π на самом деле иррационально.
Один из способов получить представление о том, насколько хорошо число может быть аппроксимировано рациональными числами, — нарисовать рисунок, который я называю «штрих-код». Вот как его сделать: если х — число, посмотрите на первые, скажем, 300 кратных х — х, 2х, 3х, 4х и т. д. — и для каждого из этих кратных сделайте небольшую вертикальную отметку. в его «дробной части», которая является частью числа после запятой. То есть это число от 0 до 1; дробная часть φ, например, составляет около 0,618.
com/_components/slate-paragraph/instances/ckpo8csns00293g6cxbqeshbu@published»> Понял? Возможно нет. Вот пример. Предположим, вы начинаете с рационального числа, например 1/7. Я получаю картинку, которая выглядит как семь тактов; потому что на что бы я ни умножал 1/7, я получаю некоторое количество седьмых, дробная часть которого равна 0, 1/7, 2/7, 3/7, 4/7, 5/7 или 6/7.
То же самое для любого рационального числа; мы можем рассматривать все больше и больше множителей, но столбцы будут ограничены конечным набором, равномерно расположенным от 0 до 1.
А как насчет π? Вот его первые 300 множителей:
Много баров. Но не 300. На самом деле, если бы вы посчитали видимые здесь полосы, вы бы увидели, что их ровно 113. То, что вы видите здесь, является подписью milü. Поскольку число π очень близко к 355/113, его первые триста кратных также очень близки к некоторому числу 113-х, а это означает, что эти столбцы будут оставаться очень близко к числам 0, 1/113, 2/113, ( сделай вид, что я записал все 113 вариантов), и 112/113. Поскольку π не совсем равно милу, его кратные числа не бьют по носу эти дроби; полосы на картинке, которые выглядят немного толще и темнее, на самом деле представляют собой несколько полос, сгруппированных так близко друг к другу, что на странице они выглядят как одна.
Что возвращает нас к золотому сечению. Штрих-код, образованный первыми 300 множителями φ, хорошо распределен, а не сгруппирован, как штрихи π:
.
com/_components/slate-paragraph/instances/ckpo8enhm003z3g6ceycahgir@published»> Нарисуйте тысячу кратных, и это та же история, только с большим количеством полос:
И независимо от того, сколько кратных золотому сечению я возьму — тысячу, миллиард или больше — эти полосы никогда не выстроятся вдоль небольшого набора равномерно расположенных позиций, как штрих-код рационального числа. , или даже сгруппироваться рядом с этими позициями, как это делает штрих-код для π. Милю для φ не существует.
Вот прекрасный факт, который слишком сложно доказать здесь: вы не найдете каких-либо лучших рациональных приближений к φ, чем те, которые дает последовательность Фибоначчи. На самом деле, таким образом, который можно сделать достаточно точным (но не здесь), φ из всех чисел наименее хорошо аппроксимируется дробями; в этом смысле это число — самое иррациональное число .
Золотое сечение в цифрах: Правило третей и золотое сечение — как это работает | Статьи | Фото, видео, оптика