Геометрическая композиция в рисунке: Врезки геометрических фигур, архитектурная композиция

Врезки геометрических фигур, архитектурная композиция

1. Баланс и вес композиции

Самая тяжелая часть композиции должна быть сосредоточена чуть ниже центра всего объема. Чем выше мы поднимаемся по листу, тем легче композиция должна восприниматься.

Вес объектов зависит от:
Силуэта (чем больше площадь тем тяжелее)
От тона (чем темнее тем тяжелее)
От абриса: прямые и тупые углы призм/кубов воспринимаются более весомо чем острые углы конусов или пирамид или вообще отсутствие углов у сферы.

Чтобы почувствовать вес в композиции можно повернуть ее на 90 градусов и посмотреть какая часть тяжелее. Посмотрите на рисунок ниже: левая часть перевернутой композиции сильно перевешивает правую. Если в вертикальном положении это придавало композиции устойчивость, то при повороте на 90 градусов это стало причиной дисбаланса.

Какие инструменты лучше для рисунка и черчения?

Ответьте на 1 вопрос и получите проверенный список инструментов, которые точно подойдут.

Ответить на 1 вопрос
и получить список

2. Абрис композиции

Абрис композиции имеет свои правила и сильно влияет на вес. Пирамиды, конусы, сферы обычно завершают абрис сверху; кубы, призмы, цилиндры составляют «устойчивое основание» по центру и снизу. Но это не значит, что вы не имеете право использовать пирамиды, конусы и сферы снизу, а кубы, призмы и цилиндры сверху. Фигуры верха могут быть врезаны снизу композиции, если они могут составить красивую врезку. Фигуры низа могут быть врезаны сверху по той же причине.

3. Площадь врезаемой фигуры накладывается на площадь существующей фигуры минимум на 1/3

4. Фигуры удлиненного модуля (1,5-2 размера куба: призмы, пирамиды, конусы, цилиндры) не врезаются параллельно друг другу, только крест-накрест.

5. Врезки не должны оставлять маленьких «хвостиков».

6. Грани фигур не должны сливаться в одну плоскость, ребра фигур не должны сливаться в один отрезок.

7.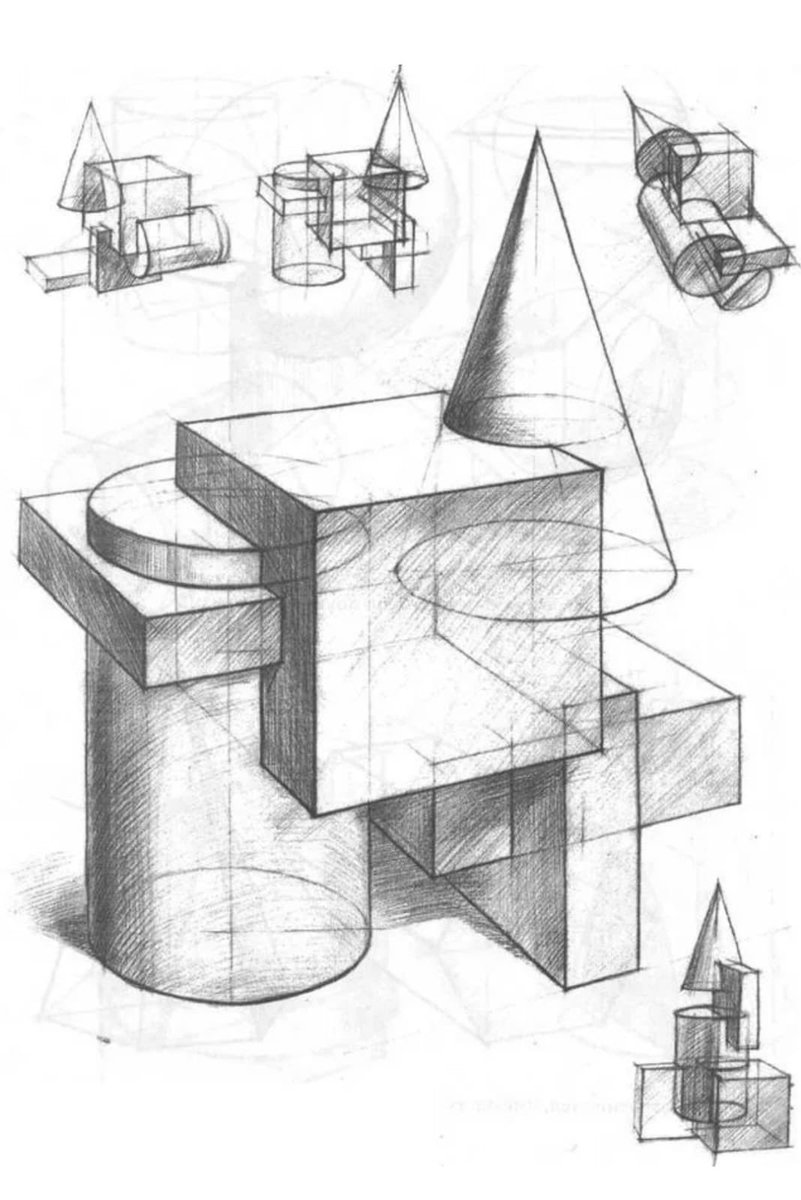 Модульность.
Врезки геометрических фигур в композиции МАрхИ могут строиться только из тел определенного размера. В качестве строительной единицы берется куб, а остальные тела меняют свои размеры кратно его размерам. Например, пирамида должна быть с квадратным основанием такого же размера, как и у куба. Ее высота кратна высоте куба: либо 0,5, либо 1, либо 1,5, либо 2. Так же и для остальных фигур.

8. Билеты
Билет по композиции МАрхИ включает 2 соприкасающиеся (но не врезанные) фигуры — первоначальную связку. Вид спереди на связку (фасад) изображен вверху, а вид сверху (план) — под фасадом. На этой связке двумя стрелками задано:

• А) положение горизонта на виде спереди
  
• Б) направление взгляда на виде сверху

Положение горизонта бывает только 2 видов: вы смотрите на композицию либо снизу, либо сверху. Причем третьего варианта, когда линия горизонта находится на самом листе в экзаменационных билетах, не существует.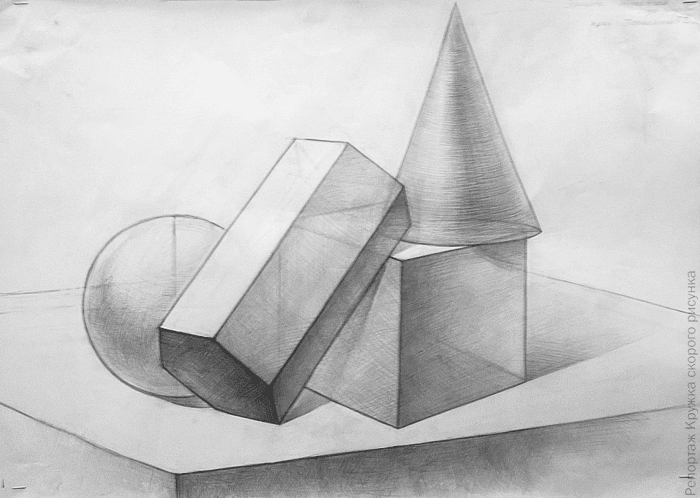

Направление взгляда всегда проходит через переднее вертикальное ребро куба и через середину боковой грани за ним. Это значит, что вам нужно нарисовать куб именно в таком повороте к зрителю, чтобы переднее ребро оказалось по центру задней грани. Опять же тут есть 2 варианта, зависящие от положения стрелки в билете. Либо геометрическая фигура раскрывается больше правой стороной, либо левой. Выше пример одного из билетов, который мы используем для тренировки.

9. Что нужно сделать
Нужно придумать композицию из геометрических тел, причем их должно быть не меньше 9 и не более 15. В рисунок нужно включить первоначальную связку с того ракурса, как указано в билете. Экзамен идет 4 часа. Формат листа всегда вертикальный А3.

Курс
Композиция МАрхИ

Курс
Композиция МАрхИ

(открыт) Перспектива, линия горизонта, точки схода

(открыт) Куб — построение из эллипса

(открыт) Сфера — построение

(открыт) Шестигранная призма — построение

(открыт) Построение сетки (вид сверху)

Все видеоуроки >>

Ответьте на 3 вопроса и узнайте, сколько занятий вам понадобится, чтобы поступить в ваш ВУЗ

Получите чек-лист из 3-5 важнейших действий, которые приводили учеников к поступлению, а также ошибок, из-за которых они оставались на второй год.

Ответить на 3 вопроса
и получить чек-лист

Подготовьтесь к МАрхИ, ГУЗ, МГСУ за 6 месяцев в мини-группах до 6 человек

5 из 6 наших учеников поступают
через 6 месяцев обучения

• Обучение рисунку, композиции, черчению от 2-х месяцев для поступления в региональные ВУЗы, от 6 месяцев — в МАрхИ, ГУЗ, МГСУ
• До 3-х раз больше времени на ученика: индивидуальное обучение в группах до 6 человек
• Ваш прогресс виден в цифрах. Ежемесячный экзамен по 100-балльной шкале

Бесплатное 1-ое занятие

Посмотрите как мы учим

Подготовьтесь к МАрхИ, ГУЗ, МГСУ за 6 месяцев в мини-группах до 6 человек

5 из 6 наших учеников поступают
через 6 месяцев обучения

• Обучение рисунку, композиции, черчению от 2-х месяцев для поступления в региональные ВУЗы, от 6 месяцев — в МАрхИ, ГУЗ, МГСУ
  
• До 3-х раз больше времени на ученика: индивидуальное обучение в группах до 6 человек
  
• Ваш прогресс виден в цифрах. Ежемесячный экзамен по 100-балльной шкале

Бесплатное 1-ое занятие

Композиционный рисунок — 82 фото

Врезки МАРХИ пирамида в шар

Геометрический натюрморт

Врезка фигур МАРХИ

Archineo

Композиция из геометрических фигу

Натюрморт из геометрических фигур (куб, Призма)

Линейно-конструктивный рисунок геометрических тел МАРХИ

МАРХИ черчение вступительный экзамен

Компоновка предметов в натюрморте

Композиция в рисунке примеры

Композиция для поступления в МАРХИ

МАРХИ композиция Асейкина

Композиция рисунок

Объемно-пространственная композиция рисунок

Статика и динамика беспредметная композиция

МАРХИ черчение вступительный экзамен

МАРХИ объемно пространственная композиция

Архитектурная композиция из геометрических фигур

Врезки геометрических тел аксонометрия

Фигуры карандашом

Московский архитектурный институт МАРХИ : «архитектура»

Объемная архитектурная композиция вступительный экзамен СПБГАСУ

Врезки геометрических фигур МАРХИ

Объемно-пространственная композиция рисунок

Врезки композиция МАРХИ

Композиция из объемных фигур

Объемно-пространственная композиция рисунок

МАРХИ архитектура вступительные экзамены

Геометрические фигуры для экзамена МАРХИ

Гризайль Академия художеств Репина

Статика динамика ритм

Натюрморт с овощами карандашом

Варианты композиции в рисунке

Бионика клаузура

Композиция эмоции

Контрастность в композиции

Светотень шар, конус, цилиндр, куб

Пропедевтика основы композиции

Линейная композиция

Композиция для скетча

Композиция из геометрических фигур

Компоновка натюрморта на листе

Композиция из геометрических фигу

Композиция из линий и пятен

Композиционные зарисовки

Человек ракурс снизу референс

Вступительные в архитектурный

Глубинно пространственная композиция эскиз

Графическая композиция

Академический натюрморт

Врезки геометрических фигур МАРХИ

Композиционные Наброски будущего рисунка

Построение композиции

Основы графической композиции

ТГАСУ олимпиада по рисунку

Экзамены на архитектурный Факультет

Вдохновение для рисования

Этапы построения натюрморта

Композиция из геометрических тел МАРХИ

Врезка фигур МАРХИ

Перспективная композиция

Средства композиции симметрия асимметрия статика динамика ритм

Осенние скетчи акварелью

Композиция в архитектуре для поступления

Геометрическая композиция

Графический натюрморт

Рисование геометрических тел

Архитектурная композиция

Академический Строгановка линейно конструктивный натюрморт

МАРХИ вступительные экзамены

Арт композиция

Геометрические фигуры в перспективе

Этапы рисования натюрморта

Композиция из геометрических фигур

Горизонтальная композиция из геометрических фигур

Врезки композиция МАРХИ

Простые предметы для рисования

Комментарии (0)

Написать

Информация
Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Геометрия в композиции

Первый урок, Правило третей, представил широко используемый принцип, который помогает решить *куда поместить предмет*. Вторая, «Простота», заключалась в том, чтобы убрать ненужное и сконцентрироваться на важном.

Предыдущие аспекты более или менее воспринимали предмет или основной интерес фотографии как данность. Этот другой: его цель — дать представление о том, «что фотографировать», не с точки зрения предметов, а с точки зрения того, что искать в предметах или композициях. Чтобы выйти за пределы трех «К» (что изображения с детьми, животными или красивыми женщинами обычно побеждают изображения без них; спросите Чака, что означает «К»), мы остаемся на несколько абстрактном уровне. Геометрия играет важную роль в фотографии, так как помогает создавать интересные композиции и придает изображениям ощущение баланса. Понимая, как использовать основные геометрические формы и линии, фотографы могут добавлять эффектные визуальные элементы к своим фотографиям.

Теперь мы рассмотрим геометрические элементы и то, как их использовать в композиции.

Для чего это нужно?

Геометрические элементы редко бывают очень хорошими предметами, начальными или второстепенными. Вместо этого они выполняют вспомогательную роль, помогая собрать картину воедино. Они имеют как минимум три общих и очень важных применения:

Ведущая линия

Ведущая линия делает то, о чем говорит: она ведет взгляд от одной части изображения к другой: от переднего плана к заднему, второстепенному подчинены основному предмету (но очень редко наоборот). Ведущая линия добавляет движения статичному изображению и связывает вместе различные элементы. Диагонали и дуги или другие незамкнутые кривые являются хорошими направляющими линиями.

Пространственный разделитель

Пространственный разделитель делит изображение на отдельные области, которые вместе образуют композицию. Не все изображения основаны на областях, но иногда области могут создавать сильную композицию даже при отсутствии четких точек интереса. Треугольники особенно полезны в качестве пространственных разделителей, но и другие элементы (диагонали, незамкнутые кривые) также могут выполнять эту роль.

Элемент обрамления

Элемент обрамления служит для фокусировки внимания на главном объекте. Обычно он закрывает как минимум два края изображения и может сильно вторгаться в него, иногда занимая большую часть его пространства. Чтобы это работало, обрамляющий элемент должен иметь некоторые собственные интересные характеристики: цвет, текстуру или форму. Смелые геометрические формы могут очень хорошо работать в качестве элементов обрамления: особенно хорошо работают треугольники или дуги. Обычно элементы обрамления должны быть в более низком ключе и более приглушенными, чем основной объект: они предназначены не для отвлечения, а для фокусировки, даже если фактическая точка изображения является элементом обрамления, например, в некоторых примерах Фальшивого Субъекта. .

Что это значит?

Это не математика, поэтому мы упрощаем. Геометрические элементы — это простые узнаваемые формы, такие как квадраты, круги, треугольники, линии и кривые. Композиционно одни геометрические формы имеют больше возможностей, чем другие: квадраты и круги, например, более статичны и поэтому менее интересны, чем треугольники или незамкнутые кривые.

Некоторые геометрические фигуры имеют особенно большой композиционный потенциал:

• Диагонали
• Треугольники
• Дуги
• S-кривые

Мы сосредоточимся на этих формах и их использовании.

Диагональ

Изображение с диагональным элементом почти всегда динамичнее и сильнее, чем такое же изображение без него. В то время как вертикали и горизонтали обычно делят пространство на области, диагонали соединяют. Действительно, одним из наиболее распространенных и эффективных способов использования диагонали является «ведущая линия» — то, что соединяет главный объект с второстепенным, заставляя глаз двигаться внутри кадра. В этой роли диагонали могут быть сильными компонентами перспективы и глубины, придающими изображению трехмерность.

Вот картина, составленная из диагоналей, используемых в качестве направляющих линий и для создания трехмерности:

Линии чугунных перил, трамвайных путей и тросов ведут взгляд от статуи к приближающемуся трамваю. Ощущение глубины усиливается малой глубиной резкости.

Вот изображение, составленное вокруг диагонали, используемой в качестве направляющей линии и разделителя пространства, но не в первую очередь как показатель перспективы:

Простая диагональ — одна из самых универсальных геометрических фигур, используемых в композициях. Ищите их и делайте из них лучшее. Однако, поскольку диагональ представляет собой линию и часто одновременно входит и выходит из кадра, важно положить на нее что-нибудь, чтобы взгляд не убегал за пределы кадра. Использование его в качестве ведущей линии, например, от главного объекта к второстепенному или от переднего плана к заднему, — хороший способ организовать это.

Треугольник

Треугольник — это замкнутая кривая, имеющая хотя бы одну диагональ. Будучи закрытым, он не будет уводить взгляд за пределы кадра. Тем не менее, особенно равносторонний треугольник намного более статичен, чем диагональ. Сам по себе, и особенно в середине кадра, он может сделать композицию статичной и скучной. Иногда треугольные области могут создавать необычные изображения, как, например, это:

Однако настоящие треугольники встречаются довольно редко. Вместо того, чтобы искать их, треугольник можно использовать более абстрактно: для размещения основного и второстепенного объектов в кадре или с помощью трех дополнительных точек интереса, чтобы сформировать «рамку» для вашего основного объекта.

Дуга

Дуга может быть прекрасным композиционным элементом. В незамкнутом виде может служить ведущей линией, притягивающей взгляд к главному объекту (фото Шоста Сулонена)…

…пространственным разделителем. ..

… или обрамляющим элементом, фокусирующим внимание на основной предмет:

Особенно если он асимметричный, он может создать динамичную и интересную композицию. Если вы видите дугу, внимательно изучите сцену и найдите элементы, которые сбалансируют (обычно) асимметричную композицию, созданную дугой, и попытайтесь найти способ наилучшим образом использовать дугу — не просто включайте ее, сконцентрируйтесь. на него и его назначение в композиции: ведущая линия, связующее звено, разделитель пространства или обрамляющий элемент?

S-образная кривая

S-образная кривая — это кривая в форме буквы S. Это композиционное золото. Если вы его видите, вы *знаете*, что это хорошая картина. S-образная кривая — едва ли не единственная геометрическая форма, которая может стоять отдельно в качестве основного объекта, но ее также можно использовать в качестве направляющей линии, элемента кадра или чего-либо еще.

Обе фотографии Мелани Кипп.

Подводя итог, можно сказать, что геометрия является важным аспектом фотографии, поскольку ее можно использовать для создания интересных композиций и визуального интереса к фотографии, а также для исправления искажений перспективы и создания баланса и симметрии в сцене. Короче говоря, геометрию можно использовать в фотографии для создания интересных композиций, добавления визуального интереса, исправления искажений перспективы и создания баланса и симметрии. Понимая основные принципы, фотографы могут сделать свои фотографии более эстетичными и визуально привлекательными.

Что такое геометрические фигуры? Определение, типы, свойства, факты

Геометрические фигуры Определение

Геометрические фигуры — это замкнутые фигуры, созданные с использованием точек, отрезков, окружностей и кривых. Такие формы можно увидеть повсюду вокруг нас.

Примерами геометрических фигур являются круг, прямоугольник, треугольник и т. д. Пицца круглая, а ее ломтики треугольные. Точно так же двери и окна являются примерами прямоугольников.

У правильной формы все стороны равны. Например, квадрат или правильный шестиугольник. Неправильные формы имеют стороны разной величины. Например, разносторонний треугольник.

Некоторые из самых популярных форм описаны ниже:

1. Прямоугольник

Прямоугольник — это фигура, полученная в результате соединения четырех разных точек четырьмя разными линиями. В прямоугольнике противоположные стороны параллельны и равны по длине. Все углы в прямоугольнике прямые. Отличие прямоугольника от квадрата в том, что в прямоугольнике два параллельных отрезка длиннее двух других, а в квадрате все отрезки имеют одинаковую длину.

Примерами прямоугольных объектов являются экраны ноутбуков, мобильные экраны и т. д.

2. Квадрат

Квадрат — это четырехсторонняя геометрическая фигура, образованная путем соединения четырех отрезков равной длины. Подобно прямоугольнику, отрезки, образующие квадрат, лежат под прямым углом друг к другу. Примерами квадратных объектов являются кубик Рубика, игральные кости, шахматные доски и т. д.

3. Круг

Круг — это геометрическая фигура, состоящая из прямых линий. Можно считать, что окружность составлена ​​из бесчисленных точек, расположенных на одинаковом расстоянии от центральной точки.

Примерами круглых объектов являются целые пиццы и колеса.

4. Треугольник

Треугольник состоит из трех соединенных отрезков. Это сложная геометрическая фигура, поскольку она может иметь переменные углы и размеры.

Примерами треугольных объектов являются кусочки пиццы, начос, праздничные шапочки и т. д.

Примечательно, что название треугольника меняется в зависимости от его углов и размера сторон. Например, когда два отрезка треугольника образуют прямой угол, такой треугольник называется прямоугольным. Вот как это выглядит:

Любой треугольник с углами меньше 90 градусов называется остроугольным. Точно так же треугольник с одним углом больше 90 градусов называется тупоугольным треугольником. В равноугольном треугольнике все внутренние углы равны 60 градусов, а все стороны равны по длине. Обратитесь к диаграмме ниже, чтобы лучше понять.

Родственные игры

Применение геометрических фигур в реальной жизни

Геометрия — это наука о форме и пространстве. Это помогает нам понять другие математические концепции, а также приложения в реальной жизни. Геометрию можно использовать для проектирования зданий, мостов, автомобилей и даже одежды. Принципы геометрии также используются в других разделах математики, таких как тригонометрия и исчисление.

Ниже приведены некоторые из реальных применений:

Квадраты: Квадраты можно найти в природе, например, кристаллы квадратной формы. Квадраты также используются в искусстве. Ярким примером является известная картина Пита Мондриана «Композиция с красным, синим и желтым».

Прямоугольники: Многие искусственные объекты, такие как телевизоры, книги и компьютерные мониторы, имеют прямоугольную форму. Есть много реальных примеров прямоугольников, таких как банкноты, сотовые телефоны и обложки книг.

Круги: Круги можно увидеть повсюду вокруг нас, от пиццы, которую мы едим, до циферблата часов.

Треугольники: Треугольники можно найти во многих местах. Большинство крыш имеют треугольную форму, называемую фронтонами. Треугольники могут помочь поддерживать такие конструкции, как мосты и здания. Есть даже некоторые чипы, которые имеют форму треугольников.

Овалы/эллипсы: Овал или эллипс представляет собой вытянутый круг (яйцевидной формы), длина которого больше ширины.

Связанные рабочие листы

Примеры трехмерных фигур

Трехмерные фигуры представляют собой группу вершин, линий, соединяющих вершины, и граней, заключенных в эти линии.

Они имеют длину, ширину и высоту и занимают некоторый объем. Для многих трехмерных фигур грани двумерны. Кроме того, некоторые фигуры в трех измерениях имеют криволинейные поверхности.

В трех измерениях основными фигурами являются:

• Кубик: Кубик Рубика, кубик сахара
• Конус: Конус для мороженого, пирамидка
• Кубовидный: Деревянная прямоугольная коробка, спичечный коробок
• Цилиндр: Рулон туалетной бумаги; банка газировки
• Сфера: Футбол, Баскетбол

Решенные примеры 

Пример 1. Сколько сторон у десятиугольника?

Решение : У десятиугольника десять сторон и десять вершин.

Пример 2: Как называется треугольник, у которого только две равные стороны?

Решение : Треугольник, у которого только две равные стороны, называется равнобедренным.

Пример 3: конус имеет двумерную или трехмерную форму?
Решение : Конус представляет собой трехмерную фигуру.

Практические задачи

1

Квадрат имеет _________.

Две равные стороны

Четыре равные стороны

Четыре неравные стороны

Ни одна из этих

Правильный ответ: Четыре равные стороны
Квадрат в геометрии — это плоская фигура, имеющая четыре равные стороны и четыре прямых угла.

2

Расстояние от центра круга до его внешней границы называется _________.

радиус

кривая

диаметр

хорда

Правильный ответ: радиус
Расстояние от центра круга до его внешней границы называется радиусом круга. Диаметр круга всегда вдвое больше его радиуса.

3

Куб – это _________.

одномерная фигура

трехмерная фигура

двумерная фигура

Ничего из перечисленного

Правильный ответ: трехмерная фигура
Куб – трехмерная фигура. У него шесть граней, восемь вершин и двенадцать ребер. Каждая грань куба представляет собой квадрат, и все ребра имеют одинаковую длину. У куба шесть квадратных граней.

4

Равносторонний треугольник _________.

открытая форма

неправильная форма

правильная форма

замкнутая кривая

Правильный ответ: правильная форма
Стороны равностороннего треугольника имеют одинаковую длину. Итак, равносторонний треугольник – это правильная фигура.

Заключение

Геометрические фигуры являются частью нашей повседневной жизни. Учащимся они помогают заложить основу для более сложных понятий, таких как пространственные отношения.

Часто задаваемые вопросы

Основные геометрические фигуры?

Основными геометрическими формами являются круг, квадрат, прямоугольник, треугольник и т. д. Эти формы могут быть расположены в различных комбинациях.

Как образуются геометрические фигуры?

Геометрические фигуры формируются с помощью линий, точек или кривых.