Использование частотного разложения в Photoshop
В этой статье будет только практическая работа. Теоретические знания прошу черпать в бесплатно доступных источниках, которые указаны в конце статьи. Не вижу смысла переписывать уже и без того прекрасно изложенный материал. Предлагаю сосредоточиться на том, как на практике применяются теоретические знания, на автоматизации (создание экшенов) частотного разложения и на том, как можно ускоренно применять эту технику в своей реальной работе.
Начнем с общего алгоритма действий. Нам требуется разделить изображение на частоты: слой низких частот, где будет размытое изображение, в котором можно легко исправлять крупные детали (менять в основном цвет, менять яркость крупных областей), и слой высоких частот, где можно корректировать мельчайшие элементы (дефекты кожи, волосинки, лишние мелкие детали).
Итак, открываем любое изображение, не обязательно портрет, и создаем самый простой и быстрый экшен для этого:
1. В палитре Actions создаем экшен Split Frequency Easy.
2. Создаем 2 копии слоя Background. Для этого Layer->New->Layer, имя слоя — LOW. Далее Image->Apply Image (Layer=Merged, Blending=Multiply). Далее, Layer->Duplicate Layer, имя слоя — HIGH.
3. У слоя HIGH отключаем видимость, выбираем слой LOW.
4. Для слоя LOW запускаем фильтр Filter->Blur->Gaussian Blur, подбираем радиус такой, чтобы пропала мелкая фактура (кожи, любых других поверхностей), которую необходимо исправить или наоборот сохранить. Для точного подбора следует увеличить изображение.
5. Включаем слой HIGH и для него запускаем фильтр Filter->Other->High Pass. Указываем тот же радиус, что и в Gaussian Blur. Режим наложения слоя HIGH — Linear Light. Fill — 50%. Можно вместо Fill использовать кривые с обтравочной маской, где черная точка Input=0, Output=64, белая точка Input=255,Output=192.
6. В палитре Actions для действий Gaussian Blur и High Pass нужно поставить признак отображения диалогов, чтобы управлять значениями радиуса.
В этом экшене есть огромный недостаток: нужно запоминать радиус и вводить его повторно при вызове High Pass. Кроме того, High Pass имеет незначительную ошибку в своих вычислениях и потому использование этого фильтра нежелательно. Впрочем, второй недостаток настолько незначительный, что им можно и пренебречь.
Итак, удаляем только, что созданный экшен, и создаем два новых. Два — потому, что для 8-битных и 16-битных изображений алгоритмы различаются. Я приведу единое описание, в котором лишь один пункт будет отличаться.
Split Frequency Easy
1. В палитре Actions создаем экшен Split Frequency Easy 16.
2. Создаем копию исходного слоя. Для этого Layer->New->Layer, имя слоя — High. Далее Image->Apply Image (Layer=Merged, Blending=Multiply).
3. Дублируем слой Layer->Duplicate Layer, имя слоя — Low.
4. Для слоя Low применяем фильтр Gaussian Blur, радиус подбираем такой, чтобы размылась вся детализация.
5. Перемещаем слой Low вниз (Ctrl+[). Выделяем слой High (Alt+])
Выделяем слой High (Alt+])
6. На слое High применяем команду Image->Apply Image. Выбираем слой Low. Остальные параметры для 16-битных изображений: Blending=Add, Invert=true, Scale=2, Offset=0. Для 8-битных изображений: Blending=Subtract, Invert=false, Scale=2, Offset=128.
7. Для слоя High устанавливаем режим наложения Linear Light.
В палитре слоев должен получиться такой сэндвич.
Все, первый экшен готов. Остается продублировать созданный экшен, назвав его Split Frequency Easy 8 и изменить в нем параметры на шаге 6. Обычно радиусы задаются в диапазоне 3-10 пикселей в зависимости от детализации. По большому счету слой Background уже не нужен, его можно удалить для экономии размера файла.
Как ретушировать? Исправлять детализацию нужно на слое High инструментом Clone Stamp с жесткими краями и непрозрачностью 100%. Ретушировать при помощи Healing Brush или Spot Healing Brush я бы не советовал, ими имеет смысл пользоваться когда без частотного разложения необходимо быстро убрать проблемные детали со снимка.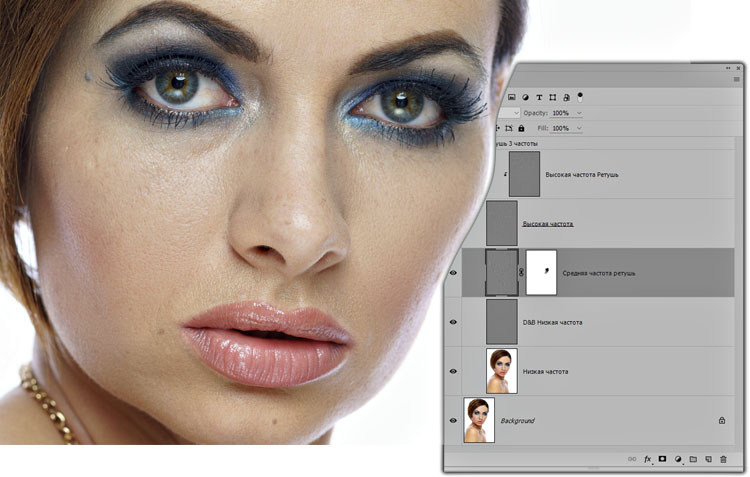 На слое Low кистью (Brush) или штампиком (Clone Stamp) с маленькой (10-20%) непрозрачностью можно исправить тон крупных объектов и даже исправить светотеневой рисунок.
На слое Low кистью (Brush) или штампиком (Clone Stamp) с маленькой (10-20%) непрозрачностью можно исправить тон крупных объектов и даже исправить светотеневой рисунок.
Прежде чем перейти к созданию более продвинутого экшена, предлагаю обсудить недостатки созданных экшенов (Split Frequency Easy 16/8).
1. Экшен не следует принципу неразрушающей обработки поскольку работа производится прямо в слоях High и Low и возможности вернуть «как было» только часть своей работы нет. То есть, этот экшен подходит для максимально быстрой ретуши, когда на всю работу тратится не более 1-10 минут.
2. Фильтр Gaussian Blur создает характерные для него ореолы на контрастных границах, что делает неудобным ретушь в этих областях. В качестве альтернативы может выступать фильтр Surface Blur, но он сильно задействует ресурсы компьютера и на слабых машинах его использование нежелательно.
Попробуем избавиться от этих недостатков и создадим для этого еще два экшена.
Split Frequency
1. В палитре Actions создаем экшен Split Frequency 16.
В палитре Actions создаем экшен Split Frequency 16.
2. Создаем копию исходного слоя. Для этого Layer->New->Layer, имя слоя — High. Далее Image->Apply Image (Layer=Merged, Blending=Multiply).
3. Дублируем слой Layer->Duplicate Layer, имя слоя — Low.
4. Дублируем слой Layer->Duplicate Layer, имя слоя — Low_temp. (Порядок слоев временно перевернут, это нужно для минимизации операций, далее этот порядок будет инвертирован)
5. Инвертируем слой Low_temp через Image->Adjustments->Invert (Ctrl+I) и задает параметр слоя Fill=50%.
6. Создаем корректирующий слой Low_invert через Layer->New Adjustment Layer->Invert.
7. Выделяем слой Low, созданный на шаге 3. Применяем фильтр Surface Blur. Threshold выставить сперва нужно в 255 и подобрать радиус такой, что была видна фактура, но еще не видны объемы (обычно в пределах 4-12). Затем снизить Threshold до уровня когда пропадут ореолы на контрастных границах (обычно 14-24). На этом шаге мы устраняем недостаток 2, используя вместо Gaussian Blur фильтр Surface Blur.
8. Удаляем слои Low_temp и Low_invert, т.к. они были нужны лишь для визуализации работы фильтра Surface Blur.
9. Слой Low пермещаем на 1 позицию вниз, под слой High (Ctrl+[)
10. Создаем пустой слой. Для этого Layer->New->Layer, имя слоя — Low_Retouch. В этом слое будет происходить ретушь низких частот (устраняем недостаток 1).
11. Для слоя High (нужно выделить через Alt+]) применяем команду Image->Apply Image. Выбираем слой Low. Остальные параметры для 16-битных изображений: Blending=Add, Invert=true, Scale=2, Offset=0. Для 8-битных изображений: Blending=Subtract, Invert=false, Scale=2, Offset=128.
12. Создаем группу Layer->New->Group from Layers, имя группы High_group.
13. Создаем пустой слой. Для этого Layer->New->Layer, имя слоя — High_Retouch. В этом слое будет происходить ретушь верхних частот (устраняем недостаток 1).
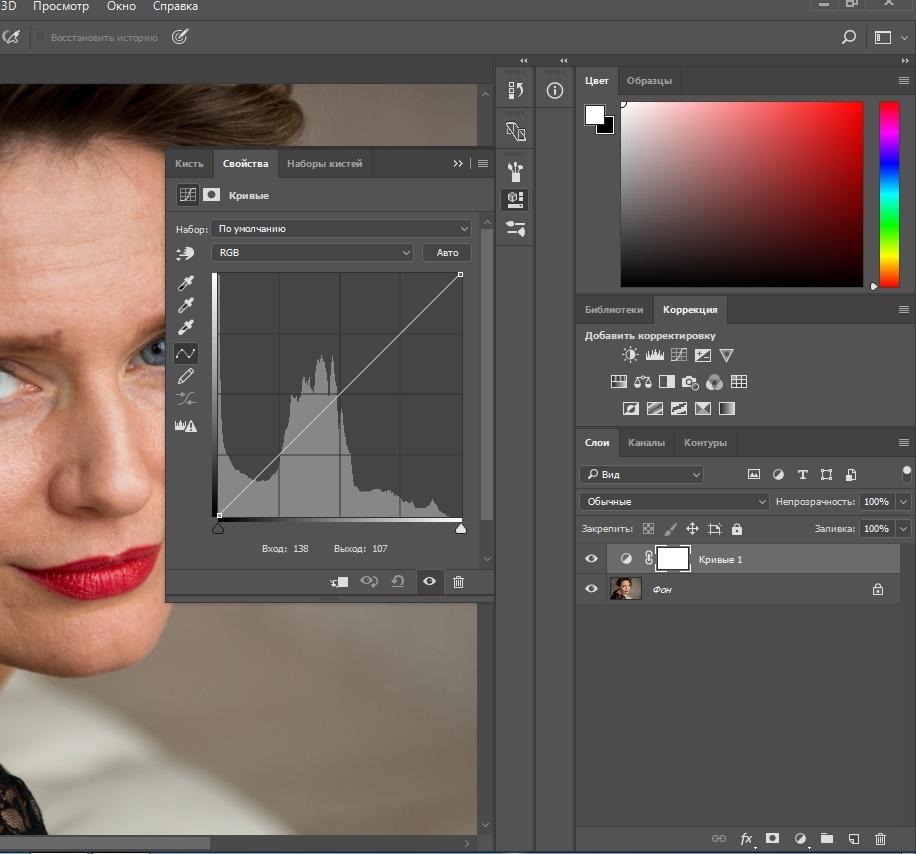
14. Для усиления видимости детализации создаем корректирующий слой кривых Layer->New Adjustment Layer->Curves.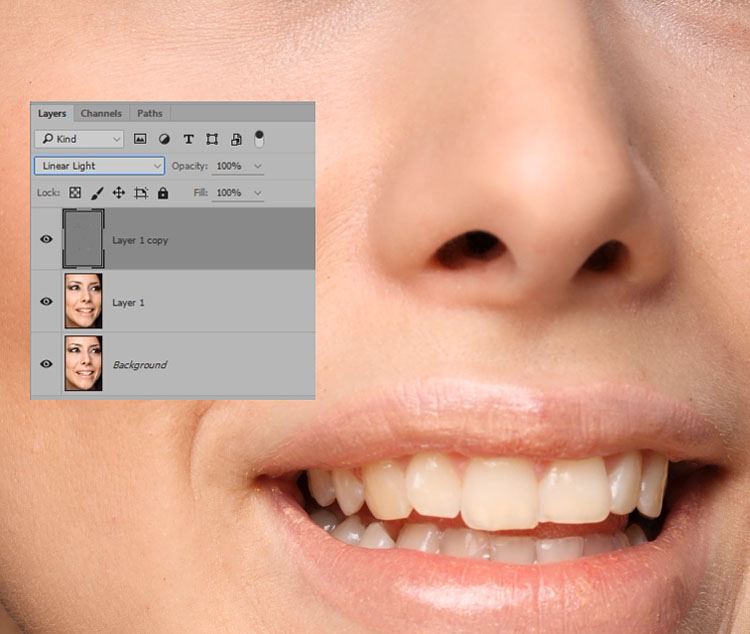 Зададим черную точку Input=64, Output=0, белая точка Input=192,Output=255. Этот слой создаст контраст, который проявит все недостатки на слое верхних частот.
Зададим черную точку Input=64, Output=0, белая точка Input=192,Output=255. Этот слой создаст контраст, который проявит все недостатки на слое верхних частот.
Все, Остается выбрать нужный слой (мне удобно сразу выбирать слой High_Retouch для ретуши верхних частот) и интрумент (в моем случае Clone Stamp). Почему задаются на шаге 11 указанные параметры, подробно объясняется в материалах Андрея Журавлева, ссылки на которые можно найти в конце статьи.
Создав экшен Split Frequency 16 можно легко создать Split Frequency 8 для 8-битных изображений, продублировав его и изменив параметры шага 11.
В результате работы экшена будет построена следующая структура слоев.
Итак, у нас уже есть четыре рабочих экшена. Более сложный случай возникает, когда нужно разложить изображение на три частоты. На три частоты обычно раскладывают, чтобы выделить в средние частоты нежелательную детализацию, часто это бывают веснушки или мелкие волосы. С разложением на более чем 3 частоты я лично не сталкивался и думаю, что необходимости в таких сложных манипуляциях на самом деле нет.
Triple Split Frequency
1. В палитре Actions создаем экшен Triple Split Frequency 16.
2. Создаем копию исходного слоя. Для этого Layer->New->Layer, имя слоя — High. Далее Image->Apply Image (Layer=Merged, Blending=Multiply).
3. Дублируем слой Layer->Duplicate Layer, имя слоя — Medium.
4. Дублируем слой Layer->Duplicate Layer, имя слоя — Low. (Порядок слоев временно перевернут, это нужно для минимизации операций, далее этот порядок будет инвертирован)
5. Для слоя Low применяем фильтр Gaussian Blur, радиус подбираем такой, чтобы размыть всю детализацию, оставить нужно только объемы (6-10).
6. Для слоя Medium выполнить Image->Apply Image. Выбираем слой Low. Остальные параметры для 16-битных изображений: Blending=Add, Invert=true, Scale=2, Offset=0. Для 8-битных изображений: Blending=Subtract, Invert=false, Scale=2, Offset=128.
7. Перемещаем слой Low под слой High. Сделать это можно через Ctrl+[ (т.е. перемещаем слой вниз, для перемещения вверх используется Ctrl+], для выделения верхнего слоя Alt+], для выделения нижнего слоя Alt+[). Слой High перемещаем на самый вверх.
Сделать это можно через Ctrl+[ (т.е. перемещаем слой вниз, для перемещения вверх используется Ctrl+], для выделения верхнего слоя Alt+], для выделения нижнего слоя Alt+[). Слой High перемещаем на самый вверх.
9. Для слоя High применяем фильтр High Pass, в котором радиус подбираем таким образом, чтобы оставить только мелкую фактуру без средних частот (1-4).
10. Для слоя High применяем кривые, где черная точка Input=0, Output=64, белая точка Input=255,Output=192.
11. Для слоя Medium применяем Image->Apply Image. Выбираем слой High. Остальные параметры: Blending=Subtract, Invert=false, Scale=1, Offset=128.
12. Ретушь будет проводиться на отдельном слое. Для этого дублируем слой Medium, имя Medium_Retouch. Применяем команду Layer->Create Clipping Mask.
13. Слоям Medium и High необходимо задать режим наложения Linear Light.
Радиусы не должны отличаться более чем в три раза, это чревато появлением разного рода пятен и прочих артефактов. В результате работы экшена будет создана следующая структура слоев:
Остается продублировать экшен и изменить параметры на шаге 6. В итоге получим экшен для разложения на три частоты для 8-битных изображений.
В итоге получим экшен для разложения на три частоты для 8-битных изображений.
И в завершение хочется рассмотреть такой популярный метод как Inverted High Pass. Это ни что иное, как очень упрощенный метод только, что рассмотренной техники разложения на три частоты, в котором просто удалена средняя частота.
Inverted High Pass
1. Копируем слой через уже традиционный способ: Layer->New->Layer, имя слоя — InvHP. Далее Image->Apply Image (Layer=Merged, Blending=Multiply).
2. Применяем фильтр High Pass. Радиус подобрать такой, чтобы осталась вся детализация, но без объемов (частот 5-10), т.е. нужно отсечь низкие частоты. Режим наложения Linear Light, Fill=50%. Инвертируем через Image->Adjustments->Invert.
3. Применяем фильтр Gaussian Blur с радиусом (1-4) таким, чтобы отсечь средние частоты (размыть их). В результате останутся только верхние и низкие частоты.
4. Остается добавить маску Layer->Layer Mask->Hide All.
В результате будет создан один единственный слой. Ретушировать нужно по маске белой кисточкой с мягкими краями и убирать нужно только точечные дефекты, не стоит проходить большой кистью по поверхности, сглаживая все на своем пути, такой подход просто превратит кожу в гладкую резину. Впрочем существуют задачи, когда такой подход актуален.
Ретушировать нужно по маске белой кисточкой с мягкими краями и убирать нужно только точечные дефекты, не стоит проходить большой кистью по поверхности, сглаживая все на своем пути, такой подход просто превратит кожу в гладкую резину. Впрочем существуют задачи, когда такой подход актуален.
Остается добавить одно замечание. Экшенами для 8-битных изображений я не пользуюсь по одной простой причине, если и случается открыть изображение в 8-битном представлении (например, jpeg), я сразу же его перевожу в 16-битное и перед сохранением, после всей проделанной работы снова перевожу его в 8-битное. Поэтому все 8-битные экшены, созданные по рецептам из этой статьи можно смело удалить или не создавать. Будем считать, что информация дана ради общего развития.
Теперь в вашем арсенале есть семь экшенов (я использую только 4 из них), которые помогут при ретушировании. Вооружившись ими можно совершенно спокойно обходиться без каких либо ретушерских плагинов типа портретуры и подобных. На этом все. Желаю качественной ретуши и творческих побед!
Желаю качественной ретуши и творческих побед!
Ссылка на скачивание экшенов, созданных в этой статье:
kapankov.ru/downloads/kapankov.rar
Дополнительные материалы:
Ретушь портрета на основе частотного разложения изображения
Частотное разложение 2. Проблема High Pass
Частотное разложение 4. Конспект занятия
Частотное разложение. Ultimate. Конспект и видео
Частотное разложение в Фотошопе. Уроки Фотошопа для начинающих
Эта статья предназначена для «чайников». В ней метод частотного разложения описан как можно более детально и подробно и предпринята попытка ответить на основные вопросы по этому поводу. Кроме того, в статью вставлены фишки и лайфхаки не только для ретуши фотографий в «Фотошопе», но и в общем для работы с программой.
Частотное разложение в «Фотошопе» вызывает много вопросов. И если еще два года назад информации по этому поводу было мало, то сейчас ответы в Сети, конечно, есть, однако все они даны обрывочно и не всегда понятно. Именно из-за этого новичкам разобраться в частотном разложении в «Фотошопе» сложно.
Именно из-за этого новичкам разобраться в частотном разложении в «Фотошопе» сложно.
Туториалы от профессионалов в Интернете даны не просто так. Многие компании выставляют к вакансии ретушера требование знать, как сделать частотное разложение в «Фотошопе» хотя бы на минимальном уровне. Но даже фрилансерам техника придется кстати — увеличит и скорость, и качество работы.
Частотное разложение — это разложение по частотам. Термин применяется не только в области обработки портретов, но и в математике, музыке и др. Для ретушера это значит, что фотографию раскладывают на несколько слоев (частот), например, слой деталей и слой тона, каждый из которых редактируется отдельно от остальных.
Так как эта статья включается в уроки «Фотошопа» для начинающих, в ней будет уделено внимание как объяснению непосредственно принципов частотного разложения, так и мелочам, с которыми профессионалы давно знакомы.
Компьютерная графика и обработка основана на математических законах, хотя творцам порой до них нет никакого дела. Таким образом и частотное разложения пошло от разложения Фурье на частоты: вначале математический метод позаимствовали радиотехники, затем — музыканты и, наконец, ретушеры.
Таким образом и частотное разложения пошло от разложения Фурье на частоты: вначале математический метод позаимствовали радиотехники, затем — музыканты и, наконец, ретушеры.
В этой статье пойдем сверху вниз, то есть начнем с «Низких».
На слой «Низкие» накладывается «Размытие по Гауссу». В отличие от метода разложения на два слоя, параметр размытия может доходить до 30. Главное — подобрать число, при котором тон кожи будет равномерным.
Для слоя «Высокие» выбирается фильтр «Цветовой Контраст». Значение «Цветового Контраста» должно быть в три раза меньше «Размытия по Гауссу».
Лайфак: записывать значения параметров слоев в их названии. Если числа 30-10, их легко запомнить, но, работая с 12,7, лучше все-таки записать.
Слой «Низкие» будет содержать и блур (размытие) и контрастность. Значение блур равняется значению «Цветового Контраста» в слое «Высокие» (в рассматриваемом примере, 30), а значение контрастности значению размытие в «Низких» (10).
Для всех трех слоев создается группа. Разложение готово, можно приступать к редактированию.
Разложение готово, можно приступать к редактированию.
Для чего нужны каждые из частот
Слой «Средние» содержит все дефекты. Удалять его полностью нежелательно. Чтобы убрать неровности, необходимо создать маску (Alt+иконка маски в низу окошка слоев), а затем черной кистью провести по портрету в местах, где имеются неровности.
Таким же образом можно обработать слой «Высокие», чтобы повысить равномерность тона кожи. На этом же слое работают с цветовой гаммой — затемняют и тонируют необходимые участки, выравнивают цвета.
Возможности применения
Кроме студийных портретов, в которых требуется убрать пару прыщиков, перед ретушью методом частотного разложения в «Фотошопе» будут ставиться совсем другие цели. Так, оно может быть применено в таких случаях:
- Необходимо исправить топорную работу визажиста — проще говоря, переделать макияж. Также возможно нанесение мейк-апа с нуля. В последнем случае рекомендуется иметь при работе фотографию той же модели с любым другим макияжем для достоверности нанесения.

- Мягкое приглушение фактуры кожи — легкая и аккуратная ретушь, без вмешательства точечной кисти и «замыленного» блура.
- Побрить мужчину — требуется комбинация методов частотного разложения, при кропотливой работе получается неплохой результат.
Скорость работы
Несмотря на то что способ кажется простым, после того как само разложение выполнено, работа над всеми тремя слоями-частотами продолжает быть кропотливой. Опытный ретушер работает над такими «мелочами», как тени и блики, объем изображения. Частотное разложение — не способ в один клик преобразить фотографию, но, наоборот, техника ее глубинной проработки.
Тем не менее математическая база способа наводит на мысль о том, как его можно автоматизировать.
Программные способы
Для «Фотошопа» (и для «Гимпа», его «Линуксовского» брата, кстати, тоже) существуют специальные плагины, а также экшены. Все они не автоматизируют полностью ретушь фотографии (в конечном итоге, это все-таки творческий процесс), однако программно выполняют действия для создания необходимых слоев и их настроек. Это значительно упрощает частотное разложение в «Фотошопе».
Это значительно упрощает частотное разложение в «Фотошопе».
Экшен (action — действие, операция) — это файл с расширением ANT, представляющий собой набор операций в «Фотошопе». Его даже можно назвать мини-программой. Уже имеющийся файл экшена открывается при помощи вкладки «Окно»-«Операции».
Экшен для частотного разложения при желании можно создать самостоятельно — вручную произвести все вышеперечисленные действия и перейти на все ту же вкладку «Операции», а далее нажать на пиктограмму создания новой операции. Для удобства также рекомендуется создать несколько экшенов для создания отдельно первого, второго и третьего слоев.
Экшены для скачивания доступны на интернет-ресурсах, однако рекомендуется все же создавать их самостоятельно — сперва опробовать частотное разложение вручную, затем понять, как им пользоваться, и затем автоматизировать этот процесс для последующего применения. Кроме того, скачивание из Интернета всегда предполагает возможность загрузки вируса.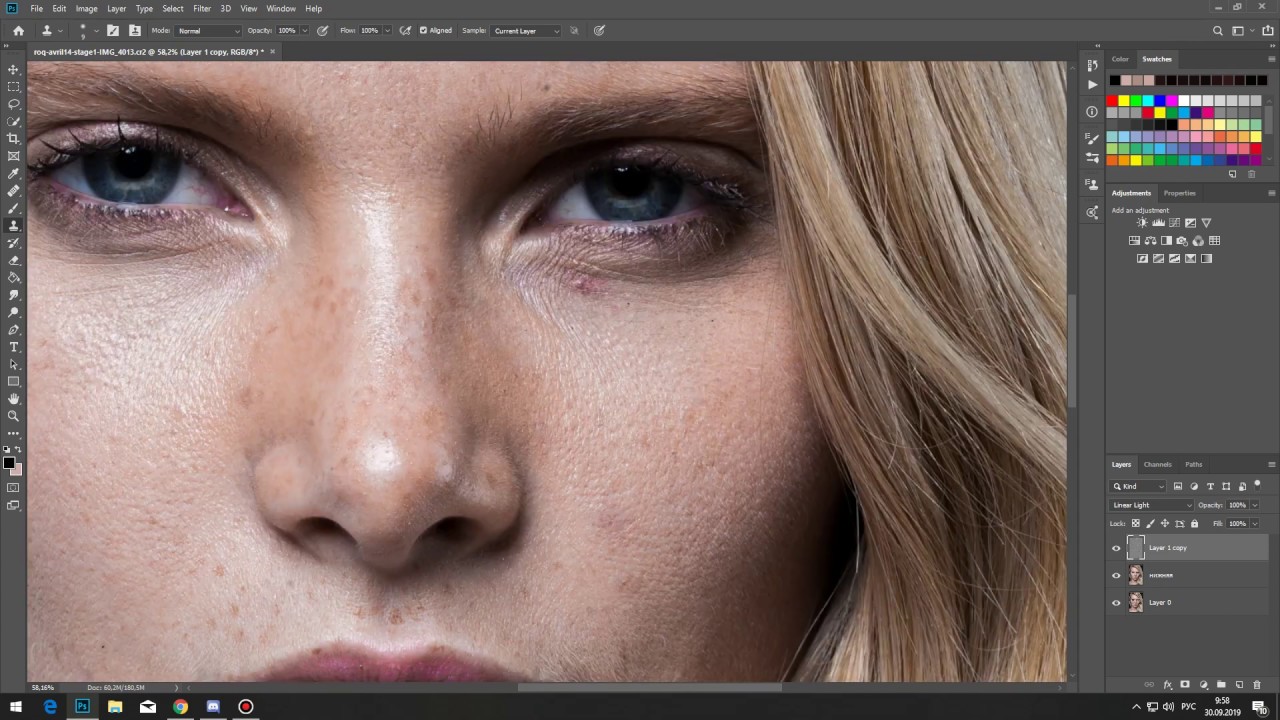 Так что лучше перестраховаться.
Так что лучше перестраховаться.
Как любые программы, экшены доступны для редактирования, а редактировать то, что было написано кем-то другим, — сложнее. К тому, что каждый автор делает операцию, прежде всего, «под себя», и только затем в порыве щедрости выкладывает в Интернет на всеобщее обозрение.
Выводы
Вообще, частотное разложение — очень мощный инструмент. Первый метод, при котором процесс производится в два слоя, больше приближен к обычной ретуши и лишь немного приоткрывает завесу использования разложения. Второй же, представляя собой модифицированную математическую операцию, дает огромный простор для творчества. В статье были описаны минимальные возможности использования, поскольку ее цель — рассказать о самом разложении, что оно собой представляет и как его сделать. А углубившись в тему чуть больше, можно найти куда больше «фишек».
Напоследок также стоит сказать, что одно владение частотным разложением не сделает никого гениальным ретушером. Как любой инструмент, он имеет силу лишь в опытных руках. Так, нужно видеть конечный результат еще до того, как сделан первый шаг, замечать мелочи и только затем выбирать, при помощи какого инструмента их лучше всего исправить.
Так, нужно видеть конечный результат еще до того, как сделан первый шаг, замечать мелочи и только затем выбирать, при помощи какого инструмента их лучше всего исправить.
|
Перед тем как перейти к основному описанию, сразу предупрежу, предполагается, что вы уже знакомы с частотным разложением, а в частности, со статьей Андрея Журавлева «Ретушь портрета на основе частотного разложения изображения». Кстати, именно мастер-классы Андрея по частотному разложению и экшенописанию, натолкнули в своё время на идею экшена, речь о котором пойдет ниже. Что требовалось от экшена? О частотном разложении уже столько всего написано, и, казалось бы, сложно придумать что-то новое. В интернете встречается множество реализаций этой техники, многочисленные авторские Actions. Каждый из них, хоть в чем-то, но обязательно казался мне неудобным, ограничивал в свободе и с трудом вписывался в привычный рабочий поток. Вот подробный список всего, что хотелось получить от экшена:
Что получилось, или «инструкция к применению» Скачать Action По ссылке находится Set c четырьмя вариациями экшена, как говориться, на вкус и цвет: Суть у всех четырех сценариев одна, различия только в применяемом фильтре размытия и визуализации подбора радиуса: экшены SF_GaussianBlur и SF_SurfaceBlur при настройке радиуса отображают размытое изображения (НЧ составляющую), а эти же экшены, но с припиской «High_Pass_preview» в названии, будут показывать ВЧ-составляющую, на подобии того, как это делает фильтр High Pass. Примечательно, что даже с экшенами «High_Pass_preview», все равно остается возможность одновременно видеть размытую версию изображения в небольшом окне: Пользоваться всем этим просто: встаем в палитре Layers на слой, требующий ретуши частотным разложением, запускаем любой экшен, подбираем параметры размытия и готово.  В результате мы получаем группу, в которой находятся слои с низкочастотной («Low») и высокочастотной («High») составляющими, а также копии этих слоёв, предназначенные непосредственно для ретуши («Low_Retouch» и «High_Retouch»). Плюс к этому добавлен дополнительный слой кривых «High_Contrast_Booster«, его удобно включать при работе на слое «High_Retouch», когда требуется подчеркнуть детализацию для более явного отображения недостатков. Получившаяся структура группы сделана по образу и подобию экшена Андрея Журавлева: В результате мы получаем группу, в которой находятся слои с низкочастотной («Low») и высокочастотной («High») составляющими, а также копии этих слоёв, предназначенные непосредственно для ретуши («Low_Retouch» и «High_Retouch»). Плюс к этому добавлен дополнительный слой кривых «High_Contrast_Booster«, его удобно включать при работе на слое «High_Retouch», когда требуется подчеркнуть детализацию для более явного отображения недостатков. Получившаяся структура группы сделана по образу и подобию экшена Андрея Журавлева:При желании, слой «Low_Retouch» можно заново разложить на частоты с большим радиусом размытия, в этом случае мы получаем дробление уже не на 2 полосы, а на 3 и больше. Для ретуши High-cлоя прекрасно подходят Healing Brush Tool, Spot Healing Brush Tool, Patch Tool и Stamp Tool с жесткими краями. Для слоя Low, в принципе, применимо тоже самое, но особенно успешно здесь можно использовать Mixer Brush Tool, Stamp Tool c мягкими границами и сниженной непрозрачностью, или обычную кисть. Action предназначен для RGB-файлов, хотя и в CMYK он тоже работает. Оптимизирован для 16-битных картинок, слой можно раскладывать хоть 100 раз подряд, никаких погрешностей расчетов заметно не будет. Локализация и версия фотошопа значения не имеет.
После работы экшена, не важно, прошло ли всё правильно или вы прервали его на этапе подбора радиуса, нажав Cancel, всё равно будет создана папка SF, которую вы тут же можете удалить, вернувшись к исходному состоянию файла. Всё, что нужно знать для пользования экшеном, рассказал, ниже будет описание устройства сценария, которое вряд ли большинству будет интересно, только самым пытливым умам. [Как экшен устроен?]Как экшен устроен? Возьмем для примера любой экшен, скажем SF_GaussianBlur, и быстренько пробежимся по шагам, на самых интересных остановимся подробнее. Шаги 1, 3, 4, 5, 6 – обычная «защита от дурака», на всякий случай сбрасывается активное выделение и снимаются Lock’и с копии слоя (если таковые имелись), режим наложения устанавливается в normal, а Opacity=100%. Чтобы экшен срабатывал и на смарт-объектах, дополнительно введено растрирование копии слоя.  Для большей стабильности экшена, можно было бы встроить проверку типа слоя, который выбран для разложения (действительно ли он пиксельный?), проверку наличия маски слоя, или текущей цветовой модели документа, но такого типа условия появились в Photoshop недавно, на более старых версиях экшен станет «спотыкаться». Из соображений совместимости сценария проверку вышеперечисленных условий оставил на совести пользователя. Для большей стабильности экшена, можно было бы встроить проверку типа слоя, который выбран для разложения (действительно ли он пиксельный?), проверку наличия маски слоя, или текущей цветовой модели документа, но такого типа условия появились в Photoshop недавно, на более старых версиях экшен станет «спотыкаться». Из соображений совместимости сценария проверку вышеперечисленных условий оставил на совести пользователя.На шаге 2 делается копия исходного слоя, если он имел над собой Clipping Mask, то произойдет автоматический Release Clipping Mask. Копия слоя сразу помещается в группу (шаг 7), в ней и будет проходить всё разложение, при любом исходе работы экшена, удачном или неудачном, группу можно быстро удалить. Не будем терять время на шаги, которые и так очевидны (переходы по слоям, выделение, копирования), а перейдем непосредственно к процессу частотного разложения. На то, чтобы не использовать пару High Pass и Gaussian Blur у меня было несколько причин: во-первых, это необходимость дважды вводить радиус размытия (об этом уже вспоминали выше), во-вторых, невозможность использования фильтра размытия, отличного от Gaussian Blur, и в-третьих, всё та же пресловутая ошибка High Pass. «Source_Copy (Temp)» здесь это неразмытый исходный слоя, а «Low (Temp)» – слой инвертированный и размытый (на шаге 10) в режиме наложения Add. Чтобы эта последовательность слоёв после сложения представляла из себя низкочастотную составляющую (High-слой), её нужно доработать кривыми (слои «Scale_Offset (Temp)»). Так как итоговый High-слой в последствии будет накладываться в режиме Linear Light, то вся детализация, представленная в виде отклонений яркости, должна «вращаться» вокруг средне-серого, а контраст понижен в два раза (для компенсация удвоения контраста, заложенного в Linear Light). В Apply Image такая коррекция в паре с режимом наложения Subtract реализуется параметрами Offset=128, Scale=2.  Наши две кривые «Scale_Offset (Temp)», имитирующие эту же коррекцию, приняли бы вид: Наши две кривые «Scale_Offset (Temp)», имитирующие эту же коррекцию, приняли бы вид:Черная точка опущена на 128 – контраст понижен в два раза, а отклонения яркостей на итоговом High-cлое станут откладываются от 128. Но проблема в том, такая коррекция идеально подойдет только для 8-битных изображений. Средне-серый цвет у 16-битных изображений, а именно для таких в первую очередь рассчитан экшен, не выражается 8-битным значением 128. Именно поэтому частотное разложение в Apply Image через Subtract: Offset=128, Scale=2 даёт небольшую погрешность на 16-битных картинках, тогда как на 8-битных работает прекрасно. Средне-серый в 16 битах можно было бы записать как 127.5, но дробные значения нельзя вводить ни в Apply Image, ни в интерфейсе кривых. Если в Apply Image из этой ситуации выходят использованием режима Add, то при раскладывании на слоях к нам на помощь приходит параметр Opacity. Посмотрим как это работает на примере: Опускание черной точки до значения 0 (кривая в горизонтальном положение) совместно с уменьшенной в два раза непрозрачностью будет аналогично смещению черной точки на полпути к самому нижнему положению.  Другими словами, уменьшение непрозрачности аналогично подтягиванию кривой в исходное положение. Очевидно, что используя непрозрачность слоя, можно получать и дробные значения сдвига точки на кривой: Другими словами, уменьшение непрозрачности аналогично подтягиванию кривой в исходное положение. Очевидно, что используя непрозрачность слоя, можно получать и дробные значения сдвига точки на кривой:Сдвиг черной точки вниз до значения 1 и Opacity=50% дают нам желаемый эффект аналогичного сдвига черной точки до 127,5. Именно такая комбинация непрозрачности и формы кривой используется в слоях «Scale_Offset (Temp)», что позволяет экшену очень точно раскладывать 16-битные изображения. Для 8-битных картинок можно было бы сделать отдельный экшен, сначала я так и поступил, но потом осознал бессмысленность затеи: те, кто обрабатывают картинки в 8 битах, вряд ли сильно задумываются о погрешностях разложения, а от 2-3 запусков экшена и так ничего страшного не случиться. Напоследок еще нужно упомянуть, как сделан предпросмотр ВЧ-слоя при подборе радиуса в экшенах «High_Pass_preview». Про этот способ мне напомнил deffar, а впервые про него услышал от Евгения Карташова на мастер-классе Андрея Журавлева. где, «Source_Copy (Temp)» — исходный неразмытый слой, а слой «Low», подвергаемый размытию, инвертирован и накладывается в режиме normal с 50% непрозрачностью на исходник. Слой «High_Contrast_Boost» не обязателен, он просто увеличивает контраст деталей на средне-сером фоне, что делает подбор радиуса более комфортным. Инвертирование слоя «Low» применено не напрямую, а через корректирующий слой «Invert (Temp)», это сделано для того, чтобы в маленьком окошке предпросмотра фильтра размытия мы могли видеть неинвертированное изображение. Казалось бы, используя эту последовательность слоёв, мы также получаем высокочастотную составляющую, причем эта структура не в пример проще той, что описана выше (через режим Add и хитрые слои кривых). Но, как оказалось, этот способ прекрасно подходит только для предпросмотра, а в качестве High-слоя при честном разложении почему-то получается заметная погрешность, причем как в 8, так и в 16 битах. На этом всё. Пробуйте экшен, комментируйте, спрашивайте. |
Журнальная ретушь
Макросы для ретуши с частотным разделением.
Скачать их можно здесь, пока выкладываю только трёхчастотный способ. Средне-серую кисть 30% надо прописать в палитре инструментов самостоятельно, где макрос остановится на её вызове.
Этот продвинутый и
очень практичный способ портретной ретуши я нашёл на
http://zhur74.livejournal.com/998.html, там доходчиво объясняется теория
процесса частотного разложения. Несмотря на кажущуюся громоздкость, метод очень
интересный и легкий в применении, даёт очень большую экономию времени при
качественном результате. Степень воздействия ретуши можно плавно регулировать. При практической отладке этой технологии ретуши я
составил 2 набора экшенов с полным согласованием экшенов внутри каждого набора
между собой, чтобы использование данного способа стало удобным, простым и
быстрым делом. Вот это — результат всего лишь двух минут работы:
Вот это — результат всего лишь двух минут работы:
В работе требуется именно система экшенов в двух наборах, а не
один-единственный экшен, как это обычно встречается в Интернет-источниках (что совершенно не годится для употребления). На точках останова в макросах всё написано, что надо делать, а здесь объясняется теория того, что в них запрограммировано.
Самый первый экшен в наборах делает сведение имеющихся слоёв и затем
первоначальную расстановку всех необходимых слоёв для производства ретуши
средних частот по серому Фурье-образу изображения, автоматически для закрашивания дефектов включается
также средне-серая кисть по её имени в палитре Tools (кисть надо подгружать или
прописывать новую). От себя я добавил ещё один слой Curves на самый верх стопки
слоёв для сильного временного повышения визуального контраста дефектов и
автоматическое включение-выключение в нужные моменты ещё двух слоёв Curves -
ретушь сильно облегчается, зрение уже не придётся портить, как с
распространёнными версиями таких экшенов. Вторым экшеном в наборах идёт
приводка изображения к обычному виду для его просмотра и регулировки степени
воздействия ретуши прозрачностью рисованного слоя (обычно до 50 процентов). Третий
экшен в наборах делает возврат снова на продолжение процесса ретуши без
сведения слоёв. В наборе «3F» есть экшен перехода к обработке мелкой
фактуры (или по-другому — высоких частот). В наборе «2F» есть ещё
экшены перемены параметра. Есть экшен правильного сведения слоёв в конце
работы. Теоретики пишут, что можно таким способом делать также ретушь низких
частот, что-то в этом есть, но мне для таких дел в практической работе больше
нравится классический способ ретуши притемнением-осветлением (кистью большого
размера для низких частот, экшен в наборе тоже прилагаю). Применяются смарт-объекты,
поэтому Фотошоп должен быть не ниже версии CS3.
Вторым экшеном в наборах идёт
приводка изображения к обычному виду для его просмотра и регулировки степени
воздействия ретуши прозрачностью рисованного слоя (обычно до 50 процентов). Третий
экшен в наборах делает возврат снова на продолжение процесса ретуши без
сведения слоёв. В наборе «3F» есть экшен перехода к обработке мелкой
фактуры (или по-другому — высоких частот). В наборе «2F» есть ещё
экшены перемены параметра. Есть экшен правильного сведения слоёв в конце
работы. Теоретики пишут, что можно таким способом делать также ретушь низких
частот, что-то в этом есть, но мне для таких дел в практической работе больше
нравится классический способ ретуши притемнением-осветлением (кистью большого
размера для низких частот, экшен в наборе тоже прилагаю). Применяются смарт-объекты,
поэтому Фотошоп должен быть не ниже версии CS3. В более ранних версиях (если
это кому-то нужно) способ сработает и без смарт-объектов, но для регулировки
силы воздействия ретуши наверх надо ставить копию исходного изображения с
начальной непрозрачностью 0%. Способ «2F» — двухчастотный — хорошо
подходит для восстановления старых фотографий — отчётливо видны дефекты снимка
и улучшается результат работы, основной рабочий инструмент здесь Healing Brush.
Способ «3F» — трёхчастотный — самый для ретушёров полезный,
применяется для «журнальной» ретуши портретов, работа проводится в
основном на средних частотах, дефекты кожи быстро и эффективно убираются
средне-серой кистью, а на высоких частотах дефекты устраняются применением
Healing Brush в режиме Current & Below. Источник фактуры (только самый первый раз) берётся со
смарт-слоя, а ретушь делается на вышележащем прозрачном слое.
В более ранних версиях (если
это кому-то нужно) способ сработает и без смарт-объектов, но для регулировки
силы воздействия ретуши наверх надо ставить копию исходного изображения с
начальной непрозрачностью 0%. Способ «2F» — двухчастотный — хорошо
подходит для восстановления старых фотографий — отчётливо видны дефекты снимка
и улучшается результат работы, основной рабочий инструмент здесь Healing Brush.
Способ «3F» — трёхчастотный — самый для ретушёров полезный,
применяется для «журнальной» ретуши портретов, работа проводится в
основном на средних частотах, дефекты кожи быстро и эффективно убираются
средне-серой кистью, а на высоких частотах дефекты устраняются применением
Healing Brush в режиме Current & Below. Источник фактуры (только самый первый раз) берётся со
смарт-слоя, а ретушь делается на вышележащем прозрачном слое. Если на
высокочастотном слое применить серую кисть, то мелкая фактура исчезнет совсем.
На смарт-слоях рисовать нельзя, иначе они тут же превращаются в обычные слои.
Но их параметры изменить можно и для этого даже легко по образцу составить свой
экшен (лучше параметр менять в начале работы).
Если на
высокочастотном слое применить серую кисть, то мелкая фактура исчезнет совсем.
На смарт-слоях рисовать нельзя, иначе они тут же превращаются в обычные слои.
Но их параметры изменить можно и для этого даже легко по образцу составить свой
экшен (лучше параметр менять в начале работы).
Применяются смарт-объекты, поэтому Фотошоп должен
быть не ниже версии CS3. Есть также макрос без смарт-объектов для более ранних
версий Фотошопа, но в нём нет такой же возможности регулировать степень частотного разделения, а для регулировки воздействия ретуши вверху стопки слоёв есть копия нижнего слоя с начальной
непрозрачностью 0%. Есть 2 набора макросов – один воздействует сразу на мелкую
и среднюю фактуру, другой позволяет делать это раздельно (Retouch 1F и Retouch
3F). То есть можно быстро убрать крупные дефекты кожи, не затрагивая её мелкую
фактуру, что очень важно на практике. Получается так называемая «журнальная»
ретушь. В наборах для этого вида ретуши есть макрос «Просмотр» для возвращения
обычного (не серого) вида изображениям для контроля изменений и ослабления
степени воздействия ретуши регулировкой прозрачности того слоя, на котором
производилось рисование. Данный макрос выставляет непрозрачность слоя для
рисования по средним частотам в 50%, так результат ретуши выглядит
естественнее, это значение можно изменить. Если снова после выхода на просмотр
запустить главный макрос в наборе, то сведением слоёв изменения запомнятся и
обработка продолжится. В каждом наборе есть также макрос для продолжения
обработки без сведения слоёв с возможностью отмены первоначальных изменений. Есть
макрос перехода к ретуши мелкой фактуры. Во время просмотра для выхода из
обработки можно вручную сделать сведение слоёв и прекратить ретушь, но удобнее
и более правильно это делается специальным макросом.
Получается так называемая «журнальная»
ретушь. В наборах для этого вида ретуши есть макрос «Просмотр» для возвращения
обычного (не серого) вида изображениям для контроля изменений и ослабления
степени воздействия ретуши регулировкой прозрачности того слоя, на котором
производилось рисование. Данный макрос выставляет непрозрачность слоя для
рисования по средним частотам в 50%, так результат ретуши выглядит
естественнее, это значение можно изменить. Если снова после выхода на просмотр
запустить главный макрос в наборе, то сведением слоёв изменения запомнятся и
обработка продолжится. В каждом наборе есть также макрос для продолжения
обработки без сведения слоёв с возможностью отмены первоначальных изменений. Есть
макрос перехода к ретуши мелкой фактуры. Во время просмотра для выхода из
обработки можно вручную сделать сведение слоёв и прекратить ретушь, но удобнее
и более правильно это делается специальным макросом. К работе макрос готовит 2
рабочих инструмента – включает лечилку и настраивает серую 30% кисть, делает
активным слой для рисования по средним частотам. Особенность работы лечилки:
источник фактуры берётся на смарт-слое, а для работы этим инструментом надо
сделать активным вышележащий прозрачный слой (задавать источник фактуры с
другого слоя позволяет режим кисти Current&
Below). Что интересно, в данном режиме только самый первый щелчок с нажатой
клавишей Alt надо делать для взятия фактуры со смарт-слоя, в дальнейшем
переключаться на смарт-слой для перемены фактуры уже не надо, можно оставаться
на прозрачном слое для взятия новой фактуры. Для обычной серой рисующей кисти переход
с одного слоя на другой делать не надо, рисование проводится на прозрачных
слоях. Основная обработка делается серой кистью, кое-что можно доработать
лечилкой.
К работе макрос готовит 2
рабочих инструмента – включает лечилку и настраивает серую 30% кисть, делает
активным слой для рисования по средним частотам. Особенность работы лечилки:
источник фактуры берётся на смарт-слое, а для работы этим инструментом надо
сделать активным вышележащий прозрачный слой (задавать источник фактуры с
другого слоя позволяет режим кисти Current&
Below). Что интересно, в данном режиме только самый первый щелчок с нажатой
клавишей Alt надо делать для взятия фактуры со смарт-слоя, в дальнейшем
переключаться на смарт-слой для перемены фактуры уже не надо, можно оставаться
на прозрачном слое для взятия новой фактуры. Для обычной серой рисующей кисти переход
с одного слоя на другой делать не надо, рисование проводится на прозрачных
слоях. Основная обработка делается серой кистью, кое-что можно доработать
лечилкой. Главный макрос делает вход на обработку дефектов средней величины, а
для перехода к работе с мелкой фактурой есть отдельный макрос (смена параметра).
Макросы между собой согласованы, то есть их можно запускать в произвольном
порядке после запуска первоначального. Обычно непрозрачность нарисованного слоя
приходится снижать примерно до 50% (в режиме просмотра), чтобы не было избытка
ретуши.
Главный макрос делает вход на обработку дефектов средней величины, а
для перехода к работе с мелкой фактурой есть отдельный макрос (смена параметра).
Макросы между собой согласованы, то есть их можно запускать в произвольном
порядке после запуска первоначального. Обычно непрозрачность нарисованного слоя
приходится снижать примерно до 50% (в режиме просмотра), чтобы не было избытка
ретуши.
А это ссылка с 1 Гб полезной для фотографов информации: http://depositfiles.com/files/qhrbi0024CRC32 CRC32 53F34B52
MD5 565FC1F86F55026D7F6D55DD52547E93
SHA-1 647FC931CCD206360F3540E9817F4224070633AC
Что такое экшен в Фотошоп. Как использовать экшен в ретуши изображений через частотное разложений. Часть 9. | Cardio
Создание и использование экшенов в ФотошопеСоздание и использование экшенов в Фотошопе
Экшен-это набор операций, которые мы делаем в Фотошопе с изображением, записанные в память компьютера, котрые мы можем запустить к любой фотографии открытой в программе. Если говорить более понятно, то, приведем пример, представьте себе что у вас есть 100 изображений, размер которых вам надо уменьшить на 50%, каждое фото сделать черно-белым и более контрастным. Если обрабатывать каждое изображение последовательно, то на это уйдет масса времени, но мы можем записать порядок действий в отношении одной фотографии в память программы (в экшен или, как это еще называют — операция), и затем применить данную операцию ко всем оставшимся изображениям, что будет происходить очень быстро.
Если говорить более понятно, то, приведем пример, представьте себе что у вас есть 100 изображений, размер которых вам надо уменьшить на 50%, каждое фото сделать черно-белым и более контрастным. Если обрабатывать каждое изображение последовательно, то на это уйдет масса времени, но мы можем записать порядок действий в отношении одной фотографии в память программы (в экшен или, как это еще называют — операция), и затем применить данную операцию ко всем оставшимся изображениям, что будет происходить очень быстро.
Операции в Фотошоп для создания частотного разложения
Скачать данный экшен вы можете по ссылке здесь.
Как работать с экшенами, вы можете посмотреть у меня на сайте (ссылки в статье ведут на мой-же канал, но там все популярно написано) — здесь.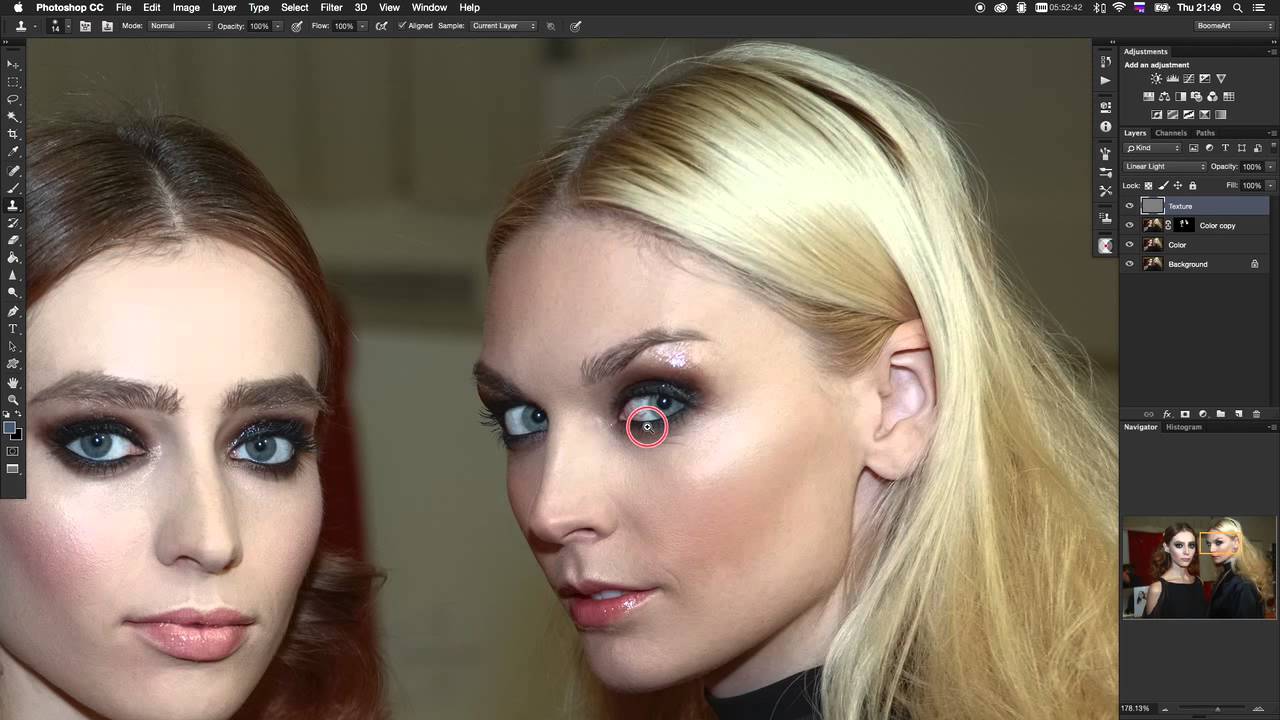
Все предыдущие уроки из серии по ретуши методом частотного разложения, все этапы, вы можете посмотреть по ссылкам ниже:
1. Оценка размеров изображения для ретуши
2. Пластика лица в ретуши портретной фотографии
3. Инструмент заплатка в ретуши портретной фотографии
4. Палитра история в Фотошоп. Сравниваем результаты до и после ретуши
5. Восстанавливающая кисть в ретуши портретного снимка
6. Точечная восстанавливающая кисть в ретуши портретов
7. Инструмент штамп в ретуши портрета
8. Что такое частотное разложение в ретуши портретного фото. Создаем разложение по частотам в Фотошопе
Наши курсы по Adobe Photoshop, проводимые в очном и дистанционном форматах:
Базовый курс по Adobe Photoshop для начинающих
Ретушь в Фотошоп
Фотошоп для фотографов
#Урокифотошоп #Ретушьфото #Частотноеразложение
تحميل Экшен для разглаживания кожи mp3 — mp4
Экшен для разглаживания кожи
Ретушь в Фотошопе БЕСПЛАТНЫЕ ЭКШЕНЫ
The BEST Automatic Skin Softening Photoshop Action
Добавление текстуры кожи чтобы убрать волоски добавить текстуру кожи Пошагово Экшен в Фотошоп
РЕТУШЬ КОЖИ ЗА 1 МИНУТУ В PHOTOSHOP CC
ЧАСТОТНОЕ РАЗЛОЖЕНИЕ Профессиональная ретушь кожи быстро и просто
ЭКШЕНЫ это НЕ пресеты Гайд по лучшим экшенам для обработки
СУПЕР ЭКШЕН ДЛЯ БЫСТРОЙ И КАЧЕСТВЕННОЙ РЕТУШИ ФОТО
5 интересных возможностей частотного разложения разбор и бесплатный экшен
High End Skin Softening In 1 Minute Or Less In Photoshop
Частотное разложение Секреты фишки лайфхаки для идеальной ретуши
Супер Экшены для обработки кожи в Photoshop Important Actions For Portrait Retouching In Photoshop
Раздаю экшены для Фотошопа частотка резкость насыщенность яркость Инструкция по применению
Разглаживание кожи с сохранением текстуры в фотошоп Photoshop
5 способов ретуши кожи экшен
Ретушь кожи в фотошоп через экшен
Фотошоп экшен кисть для работы с кожей чистка пятен и пигментации не мылят структуру кожи
Photoshop S NEW In Built Skin Softening Any Good
1 Click Skin Retouching Free Photoshop Actions By Shazim Creations
Экшен для ускорения ретуши кожи – Мир в кадре
Предлагаю вашему вниманию экшен для ускорения процесса ретуши. Он построен на основе методики упрощенного метода частотного разложения с подавлением средних частот. В зарубежных источниках данный метод называется Inverted High Pass.
Он построен на основе методики упрощенного метода частотного разложения с подавлением средних частот. В зарубежных источниках данный метод называется Inverted High Pass.
Скачать экшен fastretouch
Я несколько усовершенствовал данный метод. Это касается выбора фильтров для размытия. Можно выбирать Размытие по Гауссу (Gaussian Blur), Размытие по поверхности (Surface Blur) и Медиану (Median). Это позволяет использовать различные методы для фильтрации разных пространственных частот.
Например, метод с Размытием по Гауссу, на мой взгляд, подходит для мелкой и средней текстуры кожи, но не подходит для работы вблизи контрастных границ. Для этого лучше использовать фильтры Размытие по поверхности или Медиана.
Принцип работы с экшеном:
- Сначала удаляем явные дефекты с помощью обычной восстанавливающей кисти (Healing Brush). Это нужно сделать на пустом слое. Если вы не знаете, как это делается, лучше сначала изучить основы работы в программе, например, с помощью видеокурса “Photoshop CS5 от А до Я”.

- Далее запускаем экшен из палитры Операции. Отличительной особенностью работы экшена является то, что он использует информацию со всех предыдущих слоев изображения, то есть, создает слой на основе всех предыдущих и выполняет операцию частотного разложения с заранее выбранным фильтром. Нужный фильтр можно выбирать путем его включения в экшене. Это нужно сделать ДО запуска экшена.
Можно также включать два или все три фильтра. Попробуйте сами, возможно, вам понравится использовать один фильтр или два.
- После того, как вы подобрали необходимые параметры фильтров (это потребует некоторой практики), экшен выполняет несколько операций и создает структуру слоев.
- Теперь выбираем мягкую белую кисть, непрозрачность кисти регулируем в процессе работы, в зависимости от нужной степени подавления дефектов. Кистью работаем по маске слоя. При фильтрации дефектов больших размеров кистью можно работать “по площадям”.

- Поработав с крупными дефектами, запускаем экшен еще раз. Перед этим можно переключиться на другой фильтр. При удалении средних и мелких дефектов кистью нужно работать точечно, иначе результатом работы будет “пластиковая” кожа с излишне мелкой текстурой.
- Следует также помнить, что данный экшен является всего лишь инструментом для ускорения работы. Как и всякий “ускоритель”, он имеет свои достоинства, недостатки и область применения. Используя только его, вам не удастся сделать ретушь High-End качества, но никто не запрещает применять его для отдельных этапов работы.
Частотная декомпозиция и фазовая синхронизация зрительного вызванного потенциала с использованием эмпирической модовой декомпозиции
Список литературы
1. Башар Э. Динамика ЭЭГ-мозга: связь между ЭЭГ и вызванными потенциалами мозга . Амстердам: издательство Elsevier-North-Holland Biomedical Press; 1980. Искать в Google Scholar
.
2. Варела Ф., Лашо Дж., Родригес Э., Мартинери Дж. Фазовая синхронизация и крупномасштабная интеграция. Nat Rev Neurosci 2001; 2: 229–39.https://doi.org/10.1038/35067550. Искать в Google Scholar
3. Лайт Г.А., Уильямс Л.Е., Миноу Ф., Спрок Дж., Рислинг А., Шарп Р. и др. Электроэнцефалография (ЭЭГ) и связанные с событиями потенциалы (ERP) с участниками-людьми. Curr Protoc Neurosci 2010; 6:25. 1-6. 4. https://doi.org/10.1002/0471142301.ns0625s52. Искать в Google Scholar
4. Мисулис К.Э., Фахури Т. Праймер с вызванным потенциалом Спельмана . Соединенное Королевство: Баттерворт-Хайнеманн; 2001. Искать в Google Scholar
.5.Ключевые APF, Dove GO, Maguire MJ. Связь мозговых волн с мозгом: учебник по ERP. Dev Neuropsychol 2005; 27: 183–215. https://doi.org/10.1207/s15326942dn2702_1. Искать в Google Scholar
6. Арбиб М.А. Справочник по теории мозга и нейронным сетям . Кембридж: пресса Массачусетского технологического института; 2003. Искать в Google Scholar
Искать в Google Scholar
7. Уильямс Н., Насуто С.Дж., Сэдди Д.Д. Оценка разложения эмпирических мод для анализа потенциала, связанного с событием. EURASIP J Adv Sig Pr 2011; 2011: 1–11.https://doi.org/10.1155/2011/965237. Искать в Google Scholar
8. Ли ГБ, Чо Б.Дж. Классификация сердечной аритмии на основе EMD с использованием мультиклассовой SVM. J Korea Inst Inf Commun Eng 2010; 14: 16–22. https://doi.org/10.6109/jkiice.2010.14.1.016. Искать в Google Scholar
9. Пачори Р.Б., Баджадж В. Анализ сигналов ЭЭГ нормальных и эпилептических припадков с использованием эмпирической разложения по модам. Программы вычислительных методов Biomed 2011; 104: 373–81. https://doi.org/10.1016/j.cmpb.2011.03.009. Искать в Google Scholar
10. Хуан Н.Э., Шен З., Лонг С.Р., Ву М.К., Ши Х.Х., Чжэн Кью и др., Редакторы. Разложение по эмпирическим модам и спектр Гильберта для нелинейного и нестационарного анализа временных рядов. In: Proceedings of the Royal Society of London a: Mathematical Physical Engineering Sciences . Королевское общество, Лондон; 1998. Поиск в Google Scholar
Королевское общество, Лондон; 1998. Поиск в Google Scholar
11. Суини-Рид К.М., Насуто С.Дж. Новый подход к обнаружению синхронизации в ЭЭГ, основанный на разложении эмпирических мод. Дж. Comput Neurosci 2007; 23: 79–111. https://doi.org/10.1007/s10827-007-0020-3. Искать в Google Scholar
12. Риллинг Г., Фландрин П., Гонсалвес П., редакторы. Об эмпирической модовой декомпозиции и ее алгоритмах. В: Семинар IEEE-EURASIP по нелинейным сигналам и обработке изображений . IEEER, Градо, Италия; 2003. Искать в Google Scholar
.13. Торрес М.Э., Коломинас М.А., Шлоттауэр Г., Фландрин П., редакторы. Разложение полного ансамбля на эмпирические моды с адаптивным шумом.В: 2011 Международная конференция IEEE по акустике, речи и обработке сигналов (ICASSP) . IEEE, Прага, Чехия; 2011. Искать в Google Scholar
. 14. Лабате Д., Фореста Флорида, Оккиуто Дж., Морабито Ф. К., Лей-Экуакилле А., Вергалло П. Разложение эмпирических мод и вейвлет-разложение для извлечения респираторного сигнала из одноканальной ЭКГ: сравнение. IEEE Sens J 2013; 13: 2666–74. https://doi.org/10.1109/JSEN.2013.2257742. Искать в Google Scholar
IEEE Sens J 2013; 13: 2666–74. https://doi.org/10.1109/JSEN.2013.2257742. Искать в Google Scholar
15.Ким ВС, Хан СК. Фазовый анализ однократных ЭЭГ: фазовый сброс альфа- и тета-ритмов. Neurocomputing 2006; 69: 1337–40. https://doi.org/10.1016/j.neucom.2005.12.103. Искать в Google Scholar
16. Рэй В.Дж., Коул Х.В. Альфа-активность ЭЭГ отражает требования к вниманию, а бета-активность отражает эмоциональные и когнитивные процессы. Наука 1985; 228: 750. https://doi.org/10.1126/science.39. Искать в Google Scholar
17. Фогель EK, Luck SJ. Визуальный компонент N1 как показатель процесса распознавания. Психофизиология 2000; 37: 190–203. https://doi.org/10.1111/1469-8986.3720190. Искать в Google Scholar
18. Freunberger R, Klimesch W, Doppelmayr M, Höller Y. Визуальный компонент P2 связан с тета-фазовой синхронизацией. Neurosci Lett 2007; 426: 181–6. https://doi.org/10.1016/j.neulet.2007.08.062. Искать в Google Scholar
19. Буркитт Г.Р., Зильберштейн Р.Б., Кадуш П.Дж., Вуд А.В. Устойчивые визуальные вызванные потенциалы и бегущие волны. Clin Neurophysiol 2000; 111: 246–58.https://doi.org/10.1016/S1388-2457(99)00194-7. Искать в Google Scholar
Буркитт Г.Р., Зильберштейн Р.Б., Кадуш П.Дж., Вуд А.В. Устойчивые визуальные вызванные потенциалы и бегущие волны. Clin Neurophysiol 2000; 111: 246–58.https://doi.org/10.1016/S1388-2457(99)00194-7. Искать в Google Scholar
20. Ито Дж., Николаев А.Р., Ван Левен С. Пространственно-временная структура фазовой синхронизации спонтанной альфа-активности ЭЭГ. Biol Cybern 2005; 92: 54–60. https://doi.org/10.1007/s00422-004-0533-z. Искать в Google Scholar
Сравнительное исследование методов частотно-временной декомпозиции для обнаружения неисправностей в асинхронных двигателях с использованием анализа вибрации во время переходных процессов при запуске
Асинхронные двигатели являются критически важными компонентами для большинства отраслей промышленности, и для обнаружения неисправностей необходим мониторинг состояния.Существует несколько методов диагностики неисправностей асинхронных двигателей, и анализ переходных сигналов вибрации при запуске не так широко используется, как другие методы, такие как анализ сигнатуры тока двигателя.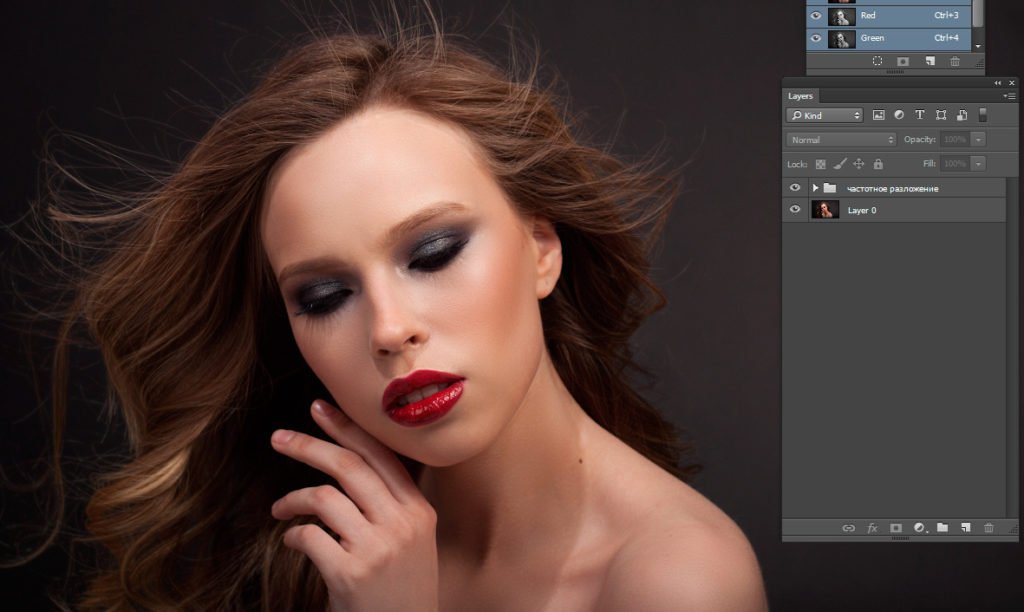 Анализ вибрации дает диагностику неисправностей, сосредоточенную на локализации спектральных компонентов, связанных с неисправностями. Таким образом, в данной статье представлено сравнительное исследование различных методологий частотно-временного анализа, которые могут быть использованы для обнаружения неисправностей в асинхронных двигателях, анализируя сигналы вибрации во время переходного процесса при запуске.Изучаемые методологии — это частотно-временное распределение Габора (TFDG), частотно-временная скалограмма Морле (TFMS), классификация множественных сигналов (MUSIC) и быстрое преобразование Фурье (FFT). Анализируемые вибрационные сигналы — это один сломанный стержень ротора, два сломанных стержня, неуравновешенность и дефекты подшипников. Полученные результаты показали возможность обнаружения неисправностей в асинхронных двигателях с помощью частотно-временного спектрального анализа, применяемого к сигналам вибрации, и предложенная методика применима, когда она не имеет сигналов тока, а имеет только сигналы вибрации.
Анализ вибрации дает диагностику неисправностей, сосредоточенную на локализации спектральных компонентов, связанных с неисправностями. Таким образом, в данной статье представлено сравнительное исследование различных методологий частотно-временного анализа, которые могут быть использованы для обнаружения неисправностей в асинхронных двигателях, анализируя сигналы вибрации во время переходного процесса при запуске.Изучаемые методологии — это частотно-временное распределение Габора (TFDG), частотно-временная скалограмма Морле (TFMS), классификация множественных сигналов (MUSIC) и быстрое преобразование Фурье (FFT). Анализируемые вибрационные сигналы — это один сломанный стержень ротора, два сломанных стержня, неуравновешенность и дефекты подшипников. Полученные результаты показали возможность обнаружения неисправностей в асинхронных двигателях с помощью частотно-временного спектрального анализа, применяемого к сигналам вибрации, и предложенная методика применима, когда она не имеет сигналов тока, а имеет только сигналы вибрации. Кроме того, методика применяется в двигателях, которые не питаются напрямую от линии питания, в таких случаях анализ токовых сигналов не рекомендуется из-за плохого качества токовых сигналов.
Кроме того, методика применяется в двигателях, которые не питаются напрямую от линии питания, в таких случаях анализ токовых сигналов не рекомендуется из-за плохого качества токовых сигналов.
1. Введение
Асинхронные двигатели — одно из наиболее часто используемых машин в мире. Применения разнообразны, а преимущества их использования многочисленны. Около половины электроэнергии, потребляемой промышленностью в США, используется асинхронными двигателями; Фактически, 89% двигателей в производстве — электродвигатели [1].Они также присутствуют в различных видах транспорта. В результате они являются основными элементами в современном индустриальном мире. Отсюда возникает необходимость в быстрой и точной диагностике неисправностей для предупреждения остановки работы в процессах, в которых используются эти машины. Отказ асинхронных двигателей может происходить в любом из трех основных компонентов: роторе, статоре и подшипниках [2]. Фактически, 38% отказов происходит в статоре, 10% — в роторе и около 40% представляют собой механические отказы, включая повреждение подшипников, перекос, эксцентриситет и изгиб вала [3].
Самыми популярными методами обнаружения неисправностей в асинхронных двигателях являются анализ сигнатур тока двигателя (MCSA) и анализ вибрации. MCSA позволяет неинвазивную диагностику неисправностей в режиме онлайн [4]. В этом методе используется датчик на эффекте Холла для измерения сигналов тока статора и система сбора данных для регистрации сигнала [5]. Затем этот токовый сигнал анализируется для определения характерных черт и характеристик компонентов, связанных с различными неисправностями, которые могут усиливаться во время переходного процесса при запуске, поскольку двигатель работает в напряженных условиях [6].С другой стороны, методы анализа вибрации используются для диагностики неисправностей асинхронных двигателей с использованием сигналов вибрации по трем пространственным осям [7]; этот метод особенно подходит для определения механических неисправностей. Измерение вибрации производится с использованием акселерометров в качестве основных датчиков. Затем сигналы вибрации регистрируются системой сбора данных [5]. На вибрации асинхронного двигателя влияют изменения магнитодвижущих сил, вызванные неисправностями в машине или неисправностями, вызывающими ненормальное вращение двигателя.Это неинвазивный метод, который позволяет легко найти место неисправности [8]. Эти два метода могут использоваться как во время переходного режима запуска, так и в установившемся режиме работы. В зависимости от того, какой режим работы используется для контроля состояния двигателя, существуют определенные характеристики, связанные с различными состояниями неисправности.
На вибрации асинхронного двигателя влияют изменения магнитодвижущих сил, вызванные неисправностями в машине или неисправностями, вызывающими ненормальное вращение двигателя.Это неинвазивный метод, который позволяет легко найти место неисправности [8]. Эти два метода могут использоваться как во время переходного режима запуска, так и в установившемся режиме работы. В зависимости от того, какой режим работы используется для контроля состояния двигателя, существуют определенные характеристики, связанные с различными состояниями неисправности.
Набор методов диагностики неисправностей асинхронных двигателей путем анализа переходных вибрационных сигналов при запуске не так широко используется по сравнению с методами, которые анализируют токовые сигналы.Анализ вибрации и MCSA дают диагностику неисправностей, сфокусированную на местоположении спектральных компонентов, связанных с неисправностями, с использованием преобразования Фурье, которое переводит сигнал из временной области в частотную область, отображая все частотное содержание сигнала, но не позволяет наблюдать эволюции частотного содержания сигнала во времени. Это является причиной расширения возможностей преобразования Фурье, таких как линейное частотно-временное разложение (кратковременное преобразование Фурье и вейвлет-преобразование), квадратичное частотно-временное разложение и распределения время-частотной энергии, которые позволяют эволюцию частотного содержания на всем протяжении длительность сигнала во времени.Это очень полезно для нестационарных сигналов, например, полученных из переходного процесса запуска двигателя, потому что сигнатуры, связанные с неисправностями, развиваются со временем, и их частотный состав не остается постоянным, а изменяется во время переходного процесса при запуске. Чтобы найти признаки, связанные с неисправностями двигателя, на MCSA использовались различные инструменты для частотно-временного разложения, позволяющие отслеживать эволюцию таких частот во времени. Примерами таких разложений являются кратковременное преобразование Фурье [9–12], дискретное вейвлет-преобразование [12–15], непрерывное вейвлет-преобразование [16–19], преобразование Гильберта [20, 21], преобразование Гильберта-Хуанга [ 20, 21], распределение Вигнера-Вилля [22–27], распределение Чоя – Вильямса [26–28] и классификация множественных сигналов (MUSIC) [5].
Это является причиной расширения возможностей преобразования Фурье, таких как линейное частотно-временное разложение (кратковременное преобразование Фурье и вейвлет-преобразование), квадратичное частотно-временное разложение и распределения время-частотной энергии, которые позволяют эволюцию частотного содержания на всем протяжении длительность сигнала во времени.Это очень полезно для нестационарных сигналов, например, полученных из переходного процесса запуска двигателя, потому что сигнатуры, связанные с неисправностями, развиваются со временем, и их частотный состав не остается постоянным, а изменяется во время переходного процесса при запуске. Чтобы найти признаки, связанные с неисправностями двигателя, на MCSA использовались различные инструменты для частотно-временного разложения, позволяющие отслеживать эволюцию таких частот во времени. Примерами таких разложений являются кратковременное преобразование Фурье [9–12], дискретное вейвлет-преобразование [12–15], непрерывное вейвлет-преобразование [16–19], преобразование Гильберта [20, 21], преобразование Гильберта-Хуанга [ 20, 21], распределение Вигнера-Вилля [22–27], распределение Чоя – Вильямса [26–28] и классификация множественных сигналов (MUSIC) [5]. Некоторые из этих инструментов работают вместе с классификаторами искусственного интеллекта для принятия решений о компонентах или сигнатурах, которые присутствуют в сигналах для определения ошибок и их серьезности, таких как искусственные нейронные сети (ИНС), нечеткая логика, нечеткие нейронные сети и генетические алгоритмы [6, 10, 14, 16, 17, 24, 29]. Гарсия-Перес и др. [5] представили исследование по обнаружению множественных неисправностей в асинхронном двигателе путем применения MUSIC к токовому сигналу в установившемся режиме.Впоследствии Гарсия-Перес и др. [30] расширил метод обнаружения множественных неисправностей в асинхронном двигателе с помощью MUSIC, включая звуковые сигналы наряду с сигналами вибрации, также в установившемся режиме. Родригес-Донате и др. [31] разработали метод идентификации множественных неисправностей в асинхронном двигателе, напрямую подключенном к электросети, на основе дискретного вейвлет-преобразования (DWT), применяемого к переходному процессу вибрации при запуске.
Некоторые из этих инструментов работают вместе с классификаторами искусственного интеллекта для принятия решений о компонентах или сигнатурах, которые присутствуют в сигналах для определения ошибок и их серьезности, таких как искусственные нейронные сети (ИНС), нечеткая логика, нечеткие нейронные сети и генетические алгоритмы [6, 10, 14, 16, 17, 24, 29]. Гарсия-Перес и др. [5] представили исследование по обнаружению множественных неисправностей в асинхронном двигателе путем применения MUSIC к токовому сигналу в установившемся режиме.Впоследствии Гарсия-Перес и др. [30] расширил метод обнаружения множественных неисправностей в асинхронном двигателе с помощью MUSIC, включая звуковые сигналы наряду с сигналами вибрации, также в установившемся режиме. Родригес-Донате и др. [31] разработали метод идентификации множественных неисправностей в асинхронном двигателе, напрямую подключенном к электросети, на основе дискретного вейвлет-преобразования (DWT), применяемого к переходному процессу вибрации при запуске. Pilloni et al. [19] представили сравнительное исследование различных методологий, включая быстрое преобразование Фурье (FFT), преобразование Гильберта (HT), DWT, непрерывное вейвлет-преобразование (CWT) и распределение Вигнера-Вилля (WVD), применяемое к сигналу тока статора в асинхронные двигатели для обнаружения неисправностей как в установившемся, так и в переходном режимах.Гарсия-Перес и др. [32] представили экспериментальное исследование частотно-временных характеристик эволюции во время пускового переходного процесса токового сигнала в асинхронном двигателе с частично сломанной штангой ротора при подаче непосредственно в электросеть с использованием MUSIC. Большинство этих методов использовалось для анализа сигналов тока статора. В случае вибрационных сигналов не проводится много исследований по применению методов частотно-временного разложения для анализа, где в основном используются БПФ [33] и распределение Чжао-Атласа-Маркса (ZAM) [34] для частотно-временного разложения. был использован.
Pilloni et al. [19] представили сравнительное исследование различных методологий, включая быстрое преобразование Фурье (FFT), преобразование Гильберта (HT), DWT, непрерывное вейвлет-преобразование (CWT) и распределение Вигнера-Вилля (WVD), применяемое к сигналу тока статора в асинхронные двигатели для обнаружения неисправностей как в установившемся, так и в переходном режимах.Гарсия-Перес и др. [32] представили экспериментальное исследование частотно-временных характеристик эволюции во время пускового переходного процесса токового сигнала в асинхронном двигателе с частично сломанной штангой ротора при подаче непосредственно в электросеть с использованием MUSIC. Большинство этих методов использовалось для анализа сигналов тока статора. В случае вибрационных сигналов не проводится много исследований по применению методов частотно-временного разложения для анализа, где в основном используются БПФ [33] и распределение Чжао-Атласа-Маркса (ZAM) [34] для частотно-временного разложения. был использован. Следовательно, существует необходимость исследовать пригодность методов частотно-временного разложения для выявления неисправностей двигателя во время переходного процесса при запуске с использованием сигналов вибрации, применяя спектральный анализ с высоким разрешением в качестве метода MUSIC.
Следовательно, существует необходимость исследовать пригодность методов частотно-временного разложения для выявления неисправностей двигателя во время переходного процесса при запуске с использованием сигналов вибрации, применяя спектральный анализ с высоким разрешением в качестве метода MUSIC.
Вклад этой работы — сравнительное исследование различных методологий частотно-временного анализа, которые могут быть использованы для обнаружения неисправностей в асинхронных двигателях, анализирующих сигналы вибрации во время переходного процесса запуска. Предлагаемые методики — это частотно-временное распределение Габора (TFDG), частотно-временная скалограмма Морле (TFMS), MUSIC и FFT.Выбор TFDG и TFMS основан на их способности уменьшать помехи, также известные как перекрестные члены между параллельными развивающимися гармониками. MUSIC — это техника, используемая в MCSA, которая дала наилучшие результаты благодаря очень хорошему разрешению по частоте. БПФ используется в качестве эталона для сравнения с другими методологиями. Анализируемые вибрационные сигналы в данной статье связаны со следующими неисправностями двигателя: поломка одного стержня ротора, поломки двух стержней, дисбаланса и дефектов подшипников.
Анализируемые вибрационные сигналы в данной статье связаны со следующими неисправностями двигателя: поломка одного стержня ротора, поломки двух стержней, дисбаланса и дефектов подшипников.
2.Описание устраняемых неисправностей
В этой статье рассматриваются три распространенных неисправности асинхронных двигателей: состояние дисбаланса (UNB), неисправности подшипников (BDF) и поломка стержней ротора (BRB).
2.1. Дисбаланс (UNB)
Механическая балансировка в асинхронном двигателе включает в себя всю конструкцию ротора, которая состоит из множества частей, включая вал, пластинки ротора, концевые головки, стержни ротора, концевые соединители, стопорные кольца и вентиляторы. Эти многие элементы должны быть спроектированы и изготовлены для конечного узла, обеспечивающего стабильную прецизионную балансировку.Когда двигатель правильно сбалансирован и выровнен, амплитуда частоты, связанная с неисправностью дисбаланса, практически не изменяется и остается ограниченной до определенного уровня. Однако механический дисбаланс в асинхронном двигателе вызывает небольшую радиальную вибрацию конструкции статора. Уровень вибрации достигает максимума, когда частота вращения равна собственной частоте системы, определяемой выражением, где — коэффициент жесткости, а — масса дисбаланса [35, 36]. Кроме того, этот вибрационный сигнал колеблется с частотой вращения, уровень вибрации увеличивается, как и амплитуда частоты вращения, и то же самое происходит с его гармониками [37].Анализ сигналов вибрации может обеспечить быстрый и простой способ получения информации, позволяющей диагностировать наличие дисбаланса в асинхронном двигателе. Номинальная скорость двигателя, обычно выражаемая в оборотах в минуту, предоставляется производителем. В асинхронных двигателях эта скорость немного ниже синхронной скорости, которая связана с частотой электрического питания следующим образом: где — число полюсов двигателя, а константа «120» используется для выражения синхронной скорости двигателя в оборотах.
Однако механический дисбаланс в асинхронном двигателе вызывает небольшую радиальную вибрацию конструкции статора. Уровень вибрации достигает максимума, когда частота вращения равна собственной частоте системы, определяемой выражением, где — коэффициент жесткости, а — масса дисбаланса [35, 36]. Кроме того, этот вибрационный сигнал колеблется с частотой вращения, уровень вибрации увеличивается, как и амплитуда частоты вращения, и то же самое происходит с его гармониками [37].Анализ сигналов вибрации может обеспечить быстрый и простой способ получения информации, позволяющей диагностировать наличие дисбаланса в асинхронном двигателе. Номинальная скорость двигателя, обычно выражаемая в оборотах в минуту, предоставляется производителем. В асинхронных двигателях эта скорость немного ниже синхронной скорости, которая связана с частотой электрического питания следующим образом: где — число полюсов двигателя, а константа «120» используется для выражения синхронной скорости двигателя в оборотах. -поминутные единицы.
-поминутные единицы.
2.2. Неисправности подшипников (BDF)
Некоторые авторы [38] дают обзор причин и ожидаемых частот вибрации из-за подшипников качения. Различные частоты, связанные с вращением двигателя, могут быть рассчитаны на основе геометрии подшипника, например, частоты прохождения элементов внутреннего и внешнего кольца, частота вращения сепаратора и частота вращения тел качения. Дефект на внешнем кольце вызывает импульс каждый раз, когда тела качения соприкасаются с дефектом.Скорость ротора () — это частота вращения внутренней дорожки качения, которая должна быть частотой вала. Физическое явление вибрации, генерируемой в телах качения, таких как подшипники, в исправном состоянии можно объяснить как комбинацию различных источников, таких как модуляция из-за неравномерной нагрузки, изгибные режимы подшипников, а также вибрации и шум, вызванные оборудованием. Предполагается, что нагрузка на подшипник представляет собой неуравновешенную силу. Следовательно, радиальная нагрузка перемещается по окружности внешнего кольца при вращении вала. Одиночная радиальная нагрузка преобразуется в распределенную нагрузку, поскольку внутреннее кольцо находится в контакте с более чем одним шариком во время вращения. Однако в случае неисправности подшипника, когда дефект одной поверхности подшипника ударяется о сопрягаемую поверхность, создается импульс, который вызывает резонансы в системе. В этот момент дефект находится в контакте с одним из тел качения и находится в центре зоны нагрузки на линии действия приложенной радиальной нагрузки. Механическая система симметрична относительно линии приложенной нагрузки.При вращении подшипника удары происходят с частотой внешней дорожки качения (), определяемой формулой [39], где — угол контакта между поверхностями подшипника, — диаметр сепаратора подшипника и измеряется от центра шарика до противоположного шарика. центр, — диаметр шарика, — количество шариков в подшипнике.
Одиночная радиальная нагрузка преобразуется в распределенную нагрузку, поскольку внутреннее кольцо находится в контакте с более чем одним шариком во время вращения. Однако в случае неисправности подшипника, когда дефект одной поверхности подшипника ударяется о сопрягаемую поверхность, создается импульс, который вызывает резонансы в системе. В этот момент дефект находится в контакте с одним из тел качения и находится в центре зоны нагрузки на линии действия приложенной радиальной нагрузки. Механическая система симметрична относительно линии приложенной нагрузки.При вращении подшипника удары происходят с частотой внешней дорожки качения (), определяемой формулой [39], где — угол контакта между поверхностями подшипника, — диаметр сепаратора подшипника и измеряется от центра шарика до противоположного шарика. центр, — диаметр шарика, — количество шариков в подшипнике.
2.3. Сломанные стержни ротора (BRB)
В случае стержней ротора известно, что симметричные токи в симметричном роторе асинхронного двигателя индуцируют результирующее прямое вращающееся магнитное поле с синхронной скоростью со здоровыми стержнями ротора. Сломанные стержни ротора приводят к асимметрии ротора; тогда возникает вращающееся назад поле с частотой скольжения по отношению к ротору. Взаимодействие вращающегося в обратном направлении поля ротора с полем статора вызывает колебательный момент и колебательную скорость, и частота этого колебания равна, где это колебание действует как частотная модуляция на частоте вращения, а частота неисправности () появляется в спектре колебаний. [40]: где — частота питания, — это скольжение двигателя на единицу, — это скорость ротора, и — положительные целые числа.Скольжение определяется как относительная механическая скорость двигателя по отношению к синхронной скорости двигателя следующим образом:
Сломанные стержни ротора приводят к асимметрии ротора; тогда возникает вращающееся назад поле с частотой скольжения по отношению к ротору. Взаимодействие вращающегося в обратном направлении поля ротора с полем статора вызывает колебательный момент и колебательную скорость, и частота этого колебания равна, где это колебание действует как частотная модуляция на частоте вращения, а частота неисправности () появляется в спектре колебаний. [40]: где — частота питания, — это скольжение двигателя на единицу, — это скорость ротора, и — положительные целые числа.Скольжение определяется как относительная механическая скорость двигателя по отношению к синхронной скорости двигателя следующим образом:
3. Теоретические основы
3.1. Музыкальный алгоритм
Методы подпространства известны как методы высокого разрешения, которые обнаруживают частоты с низким отношением сигнал / шум. Методы подпространства предполагают, что сигнал с дискретным временем может быть представлен комплексными синусоидами в шуме [5], поскольку где — количество выборочных данных, — комплексная амплитуда комплексной синусоиды th, — ее частота и является последовательностью белого шума. с нулевым средним и дисперсией.Этот метод использует разложение по собственным векторам для получения двух ортогональных подпространств. Матрица автокорреляции зашумленного сигнала представляет собой сумму матриц автокорреляции сигнала и шума (и, соответственно): где — количество частот, а показатель степени обозначает эрмитово транспонирование. — единичная матрица, а — вектор сигнала, заданный формулой Из условия ортогональности обоих подпространств псевдоспектр MUSIC задается формулой где — собственный вектор шума. Это выражение показывает пики, которые точно соответствуют частотам основных синусоидальных компонентов, где.
с нулевым средним и дисперсией.Этот метод использует разложение по собственным векторам для получения двух ортогональных подпространств. Матрица автокорреляции зашумленного сигнала представляет собой сумму матриц автокорреляции сигнала и шума (и, соответственно): где — количество частот, а показатель степени обозначает эрмитово транспонирование. — единичная матрица, а — вектор сигнала, заданный формулой Из условия ортогональности обоих подпространств псевдоспектр MUSIC задается формулой где — собственный вектор шума. Это выражение показывает пики, которые точно соответствуют частотам основных синусоидальных компонентов, где.
3.2. Частотно-временное распределение Габора
Расширенная версия STFT (кратковременное преобразование Фурье) представляет собой частотно-временное распределение Габора (TFDG), которое использует тип окна Гаусса и FT (преобразование Фурье) для достижения времени -частотный анализ [41]. У TFDG есть недостаток компромисса, как у STFT, вызванный фиксированной шириной окна, но он имеет лучшее разрешение по частоте, чем STFT.
TFDG описывается следующим уравнением: Как и в непрерывном случае, дискретный TFDG идентичен дискретному STFT с конкретной характеристикой окна Гаусса.Дискретный TFDG может расширяться как линейная комбинация коэффициентов Габора и базовых функций [42, 43]. Для конечного набора данных расширение Габора получается из того, где массив является периодическим по периоду и с периодом. Последовательность известна как окно синтеза. Массив коэффициентов Габора можно найти через TFDG: где последовательность — это окно анализа. Преобразование Зака используется для получения коэффициентов Габора. Дискретное преобразование Зака периодизированного окна определяется как одномерное дискретное преобразование Фурье последовательности: где и — параметры настройки, — период и — длина выборки.
3.3. Скалограмма Морле
Поскольку непрерывное вейвлет-преобразование ведет себя как разложение ортонормированного базиса, можно показать, что оно сохраняет энергию: где — энергия. Это приводит нас к определению скалограммы как квадрата модуля непрерывного вейвлет-преобразования. Это распределение энергии сигнала на шкале времени, связанное с мерой.
Это распределение энергии сигнала на шкале времени, связанное с мерой.
Что касается вейвлет-преобразования, временное и частотное разрешение скалограммы связаны через принцип Гейзенберга-Габора: временное и частотное разрешение зависят от рассматриваемой частоты [44].
Разрешение по частоте явно зависит от частоты, поскольку оно увеличивается с. Интерференционные составляющие скалограммы ограничены теми областями частотно-временной плоскости, где перекрываются соответствующие автоскалограммы (составляющие сигнала). Следовательно, если два компонента сигнала находятся достаточно далеко друг от друга в частотно-временной плоскости, их перекрестная скалограмма по существу равна нулю.
Вейвлет Морле является наиболее популярным комплексным вейвлетом, используемым на практике, чей материнский вейвлет определяется как где — центральная частота материнского вейвлета.Обратите внимание, что этот термин используется для исправления ненулевого среднего комплексной синусоиды, и им можно пренебречь, когда. Поэтому в некоторых исследованиях определение материнского вейвлета вейвлета Морле дается где центральная частота. Вейвлет Морле имеет форму, очень похожую на преобразование Габора. Важное отличие состоит в том, что оконная функция также масштабируется параметром масштабирования, в то время как размер окна в преобразовании Габора является фиксированным [45].
Поэтому в некоторых исследованиях определение материнского вейвлета вейвлета Морле дается где центральная частота. Вейвлет Морле имеет форму, очень похожую на преобразование Габора. Важное отличие состоит в том, что оконная функция также масштабируется параметром масштабирования, в то время как размер окна в преобразовании Габора является фиксированным [45].
4. Проверка предлагаемых методов
Для проверки предложенной методологии генерируется синтетический сигнал, как указано в (17), с целью имитации некоторых гармоник вибрации, присутствующих в реальных сигналах электродвигателя.Синусоидальный сигнал состоит из трех чистых синусоидальных сигналов с постоянной частотой 80, 670 и 700 Гц, а также синусоидального сигнала с переменной частотой в диапазоне от 0 Гц до 56,7 Гц от 0 до 2 с, а затем остается с постоянной частотой. К сигналу также добавляется нормально распределенный случайный шум. Компоненты постоянной частоты, расположенные на 670 и 700 Гц, используются для оценки производительности метода для различения близких компонентов. Синусоида с переменной частотой имитирует пусковой переходный процесс, достигающий установившегося состояния на 56.7 Гц, что близко к постоянной составляющей частоты 80 Гц. Наконец, добавляется гауссов шум (), чтобы оценить поведение обрабатываемого метода для сигналов с низким отношением сигнал / шум. Синтетический сигнал квантуется с частотой дискретизации 1,5 кГц, что составляет 4096 отсчетов с общим временем работы 2,73 с. Также синтетический сигнал имеет отношение сигнал / шум, равное SNR = -3,6 дБ: где — синтетический сигнал,,,, и На рисунке 1 показаны результаты процесса проверки для синтетического сигнала во временной области и во временной области. частотное разложение, полученное обработанными методами.На рисунке 1 (а) изображен синтетический сигнал во временной области. Истинное (теоретическое) частотно-временное разложение показано на рисунке 1 (b). Частотно-временное разложение обработанных методов показано на рисунке 1 (c) для STFT, на рисунке 1 (d) для TFDG, на рисунке 1 (e) для TFMS и на рисунке 1 (f) для MUSIC.
Синусоида с переменной частотой имитирует пусковой переходный процесс, достигающий установившегося состояния на 56.7 Гц, что близко к постоянной составляющей частоты 80 Гц. Наконец, добавляется гауссов шум (), чтобы оценить поведение обрабатываемого метода для сигналов с низким отношением сигнал / шум. Синтетический сигнал квантуется с частотой дискретизации 1,5 кГц, что составляет 4096 отсчетов с общим временем работы 2,73 с. Также синтетический сигнал имеет отношение сигнал / шум, равное SNR = -3,6 дБ: где — синтетический сигнал,,,, и На рисунке 1 показаны результаты процесса проверки для синтетического сигнала во временной области и во временной области. частотное разложение, полученное обработанными методами.На рисунке 1 (а) изображен синтетический сигнал во временной области. Истинное (теоретическое) частотно-временное разложение показано на рисунке 1 (b). Частотно-временное разложение обработанных методов показано на рисунке 1 (c) для STFT, на рисунке 1 (d) для TFDG, на рисунке 1 (e) для TFMS и на рисунке 1 (f) для MUSIC.
Как видно из рисунка 1 (c), поведение STFT не является хорошим методом частотно-временного разложения, когда отношение сигнал / шум низкое; Также очень трудно различить две близкие частоты на 670 и 700 Гц, тогда как синусоида переменной частоты едва видна, а в установившемся состоянии она неотличима от спектральной составляющей 80 Гц.С другой стороны, другие предложенные методы позволяют отличить спектральные составляющие от фонового шума. Эти три метода четко определяют временную эволюцию синусоиды переменной частоты, и также отчетливо видна составляющая 80 Гц. Тем не менее, методы TFDG и MUSIC обнаруживают близкие спектральные компоненты, расположенные на 670 и 700 Гц, но метод TFMS не может дать четкий результат в этой области, и MUSIC может отображать три частоты без какого-либо шума в своем спектре.Наконец, делается вывод, что MUSIC является лучшим частотно-временным разложением из четырех протестированных методов, в которых полученный спектр менее подвержен низкому отношению сигнал / шум.
5. Экспериментальная установка
Испытательный стенд, используемый для тестирования двигателей с различными типами неисправностей, и система сбора данных, используемая для регистрации сигналов, показаны на рисунке 2. Несколько асинхронных двигателей с короткозамкнутым ротором, модель WEG 00136APE48T, из 1 л.с. (745,7 Вт) используются для проверки исправных и неисправных состояний двигателя.Двигатели имеют два полюса, 28 бар, они питаются напряжением 220 В переменного тока при 60 Гц, а приложенная нагрузка представляет собой обычный генератор переменного тока. Сигналы вибрации регистрируются с помощью трехосного акселерометра на базе микроэлектромеханических систем (модель LIS3L02AS4) от STMicroelectronics. Для сбора данных (DAS) используется 12-битный четырехканальный аналого-цифровой преобразователь с последовательным выходом (ADS7841). Эта система сбора данных использует частоту дискретизации 1,5 кГц, и во время переходного процесса при запуске получается 4096 отсчетов. На рисунках 2 (b) и 2 (c) представлены вид спереди и сбоку асинхронного двигателя, соответственно, с указанием положения акселерометра и ориентации его осей.
На рисунках 2 (b) и 2 (c) представлены вид спереди и сбоку асинхронного двигателя, соответственно, с указанием положения акселерометра и ориентации его осей.
5.1. Неисправности двигателя
Состояние UNB возникает, когда механическая нагрузка асинхронного двигателя распределяется неравномерно, из-за чего центр масс выходит за пределы вала двигателя. На рисунке 3 показан шкив со смещенной от центра массой, используемый для создания состояния UNB на асинхронном двигателе. Сигнатура UNB в сигнале вибрации обычно имеет форму увеличенной амплитуды вдоль частоты ротора, находясь в данном случае на 56.7 Гц.
Для проведения теста на неисправность подшипника его искусственно повреждают путем просверливания отверстия диаметром 1,191 мм на его внешнем кольце с помощью вольфрамового сверла. На рисунке 4 показан искусственно поврежденный подшипник модели 6203-2ZNR, использованный в этом эксперименте. Частота характерных дефектов вибрации наружного кольца подшипника качения рассчитывается по формуле (2). Исследуемый асинхронный двигатель имеет частоту ротора Гц, а испытательный подшипник имеет восемь шариков по 6 штук.Диаметр 5 мм и диаметр сепаратора подшипника 28 мм с углом контакта; таким образом, дефект частоты внешней дорожки качения шарового паса () составляет 174,1 Гц.
Исследуемый асинхронный двигатель имеет частоту ротора Гц, а испытательный подшипник имеет восемь шариков по 6 штук.Диаметр 5 мм и диаметр сепаратора подшипника 28 мм с углом контакта; таким образом, дефект частоты внешней дорожки качения шарового паса () составляет 174,1 Гц.
Как уже упоминалось, частоты, характерные для BRB, зависят от колебания скорости с частотой 2. Состояние сломанного стержня создается искусственно путем сверления одного отверстия диаметром 7,938 мм без повреждения вала ротора. На рисунке 5 изображен используемый ротор с одним BRB. Двигатель работает со скоростью 3402 об / мин в системе 60 Гц.Гармоники, характерные для неисправности BRB, получаются сначала путем включения фактических значений данных скорости двигателя в (4), чтобы найти значение скольжения (), которое можно использовать в (3) для получения частот гармоник, связанных с BRB.
5.2. Методология
На рисунке 6 изображена блок-схема предлагаемой методологии. Во-первых, испытательный стенд устанавливается с асинхронным двигателем в различных условиях: исправный, один и два сломанных стержня ротора, неуравновешенный шкив и неисправность подшипника на внешнем кольце.Затем начинается процесс сбора данных, чтобы получить начальный переходный процесс вибраций через трехосный акселерометр. Во время переходного процесса при запуске регистрируется 4096 отсчетов на частоте 1,5 кГц за время сбора данных 2,73 с. После завершения процесса регистрации переходного процесса при запуске полученные сигналы вибрации обрабатываются и анализируются. На этом этапе применяются методологии частотно-временного разложения TFDG, TFMS и MUSIC, которые сравниваются с STFT. Наконец, по результатам спектрограмм частотно-временного разложения определяется состояние двигателя.Кроме того, проводится качественная и количественная оценка распределений, используемых для оценки их производительности, по сравнению с STFT.
Во-первых, испытательный стенд устанавливается с асинхронным двигателем в различных условиях: исправный, один и два сломанных стержня ротора, неуравновешенный шкив и неисправность подшипника на внешнем кольце.Затем начинается процесс сбора данных, чтобы получить начальный переходный процесс вибраций через трехосный акселерометр. Во время переходного процесса при запуске регистрируется 4096 отсчетов на частоте 1,5 кГц за время сбора данных 2,73 с. После завершения процесса регистрации переходного процесса при запуске полученные сигналы вибрации обрабатываются и анализируются. На этом этапе применяются методологии частотно-временного разложения TFDG, TFMS и MUSIC, которые сравниваются с STFT. Наконец, по результатам спектрограмм частотно-временного разложения определяется состояние двигателя.Кроме того, проводится качественная и количественная оценка распределений, используемых для оценки их производительности, по сравнению с STFT.
6. Результаты и обсуждение
В этом разделе представлены результаты, полученные после анализа сигналов вибрации с помощью методов частотно-временного разложения, TFDG, TFMS и MUSIC, включая сравнение с STFT. Эти вибрационные сигналы регистрируются при переходных процессах запуска двигателей в пяти различных условиях, а именно: исправное состояние, сломанная штанга ротора, две сломанные штанги ротора, дисбаланс и дефекты подшипников.Наилучшие результаты получаются из сигнала вибрации по оси, и это связано с тем, что вибрации в асинхронном двигателе обычно являются радиальными колебаниями (вертикальными или осевыми) из-за радиальных сил, действующих на статор и ротор, связанных с магнитными потоками. вход или выход из металлических поверхностей в асинхронном двигателе, а также наличие компонентов спектрального потока, создаваемых распределениями плотности тока, пазами статора и ротора, а также магнитное насыщение, которое вносит дополнительные нежелательные компоненты в радиальные силы [7].Результаты представлены в четырех случаях исследования и дан качественный анализ состояния работы двигателя.
Эти вибрационные сигналы регистрируются при переходных процессах запуска двигателей в пяти различных условиях, а именно: исправное состояние, сломанная штанга ротора, две сломанные штанги ротора, дисбаланс и дефекты подшипников.Наилучшие результаты получаются из сигнала вибрации по оси, и это связано с тем, что вибрации в асинхронном двигателе обычно являются радиальными колебаниями (вертикальными или осевыми) из-за радиальных сил, действующих на статор и ротор, связанных с магнитными потоками. вход или выход из металлических поверхностей в асинхронном двигателе, а также наличие компонентов спектрального потока, создаваемых распределениями плотности тока, пазами статора и ротора, а также магнитное насыщение, которое вносит дополнительные нежелательные компоненты в радиальные силы [7].Результаты представлены в четырех случаях исследования и дан качественный анализ состояния работы двигателя.
Пример исследования: Здоровый . На рисунке 7 представлено частотно-временное разложение STFT, TFDG, TFMS и MUSIC сигнала для здорового случая. Для этого случая исследования полоса частот между 400 Гц и 700 Гц имеет некоторые едва заметные изменения, связанные с ранее существовавшими эксцентриситетами в двигателе, которые заметны только после переходного процесса запуска, когда достигается установившийся режим.В спектрограммах для исследуемого случая нет других значимых частотных компонентов, и эти спектрограммы становятся эталоном для сравнения неисправных состояний двигателя.
Для этого случая исследования полоса частот между 400 Гц и 700 Гц имеет некоторые едва заметные изменения, связанные с ранее существовавшими эксцентриситетами в двигателе, которые заметны только после переходного процесса запуска, когда достигается установившийся режим.В спектрограммах для исследуемого случая нет других значимых частотных компонентов, и эти спектрограммы становятся эталоном для сравнения неисправных состояний двигателя.
Пример исследования: сломанные стержни ротора . Как упоминалось ранее, неисправность в сломанных стержнях ротора можно обнаружить, наблюдая за изменением частоты на спектрограмме. Из (3) и полученных спектрограмм видно, что существует гармоника (617,1 Гц) неисправности частоты BRB, близкая к частоте 640 Гц, показанная на спектрограммах здорового случая.На рисунке 8 (a) показана спектрограмма STFT, и имеется значительная полоса частот в районе 620–655 Гц, но гармоника (617,1 Гц) неисправности частоты BRB четко не обнаруживается. На рисунке 8 (b) представлена спектрограмма TFDG, значимая частота составляет около 640 Гц, поэтому гармоника не обнаруживается. На рисунке 8 (c) показана спектрограмма TFMS, и это наихудший метод, потому что значительная полоса частот находится в районе 610–690 Гц, поэтому ошибка частоты BRB не обнаруживается. На рисунке 8 (а) показана спектрограмма MUSIC, где гармоника (617.1 Гц) неисправности частоты BRB четко определяется, когда режим запуска заканчивается и начинается установившееся состояние (отмечено белым).
На рисунке 9 показаны спектрограммы частотно-временного разложения STFT, TFDG, TFMS и MUSIC для случая стержня с двумя сломанными роторами. Для этого случая исследования ошибка частоты BRB, когда и (87 Гц), и другая гармоника и (263,7 Гц) присутствуют в большинстве полученных спектрограмм (отмечены белым цветом). На рисунке 9 (а) показана спектрограмма STFT; однако неисправность частоты BRB и гармоники в 87 Гц и 263.7 Гц не наблюдаются четко, как в других методах. На рисунке 9 (b) показаны спектрограммы TFDG, но в этом методе обе частоты лучше наблюдаются с меньшими шумовыми помехами, и эти частоты показывают лучшее разрешение как STFT. На рисунке 9 (c) показана спектрограмма TFMS, где во время запуска в установившемся режиме немного наблюдается только сбой частоты BRB. На рисунке 9 (d) представлена спектрограмма MUSIC, и этот метод обеспечивает лучший просмотр для исследуемого случая с ошибкой частоты BRB и его гармониками (87 Гц и 263.7 Гц) во время завершения запуска и устойчивых запусков. Но также гармоника в 617,1 Гц немного обнаруживается в начале установившегося режима.
Пример исследования: дисбаланс . На рисунке 10 показан анализ STFT, TFDG, TFMS и MUSIC для несбалансированного случая. В этом случае скорость двигателя в оборотах в минуту соответствует частотной составляющей в Гц.
Как видно из рисунка 10, имеется четко выраженная частотная составляющая около 56,7 Гц.Эта частотная составляющая связана со скоростью ротора, и ее повышенное значение указывает на наличие дисбаланса в рабочем состоянии. Обратите внимание, что в здоровом случае нет значимых частотных компонентов на 56,7 Гц на частотно-временных спектрограммах, демонстрирующих наличие этой неисправности. Для всех методов анализа: STFT, TFDG, TFMS и MUSIC, соответствующая частота с этой ошибкой четко видна (отмечена белым цветом). Эта неисправность также способствует образованию пиков в полосе частот, связанных с эксцентриситетом двигателя, но то, что делает возможной идентификацию, — это увеличение амплитуды спектральной составляющей, которая связана с вращением ротора, и MUSIC обеспечивает лучшая визуализация частотной составляющей, связанной с неисправностью.
Пример исследования: дефекты подшипников . На рисунке 11 показаны спектрограммы частотно-временного разложения STFT, TFDG, TFMS и MUSIC для случая дефектов подшипников. Как упоминалось ранее, дефект на внешнем кольце вызывает импульс каждый раз, когда элемент качения контактирует с дефектом. Таким образом, частота, связанная с этой неисправностью, связана с вращением вала, а частота, связанная с неисправностью внешней дорожки качения (), составляет 174,1 Гц. MUSIC — единственный метод, способный обнаружить эту частоту в 3-й гармонике (522 Гц) в конце переходного процесса запуска и начале установившегося режима (отмечено белым).
Для количественной оценки эффективности различных методов спектральной оценки представлено сравнение обнаруживаемости в децибелах. Обнаруживаемость рассчитывается как среднее отношение амплитуд между пиковой амплитудой для исправных и неисправных состояний спектральных частот, присутствующих в области эволюции. Сравнительное исследование обобщено в таблице 1, и в исследовании оценивается эффективность метода спектральной оценки MUSIC при обнаружении сломанной шины ротора, механического дисбаланса и неисправностей подшипников по сравнению с другими методами.
| ||||||||||||||||||||||||||||||||
Таблица 1 показывает, что MUSIC обеспечивает лучшую обнаруживаемость трех изученных неисправностей в асинхронном двигателе во время переходного режима запуска, поскольку обеспечивает большую обнаруживаемость для все условия.
7. Выводы
Была показана возможность обнаружения неисправностей в асинхронных двигателях с использованием методов частотно-временного спектрального анализа, предложенных в этой статье, применительно к сигналам вибрации. Методология, предложенная в этой статье, применима, когда она не имеет сигналов тока, а имеет только сигналы вибрации. Эта методология также применяется в двигателях, которые не питаются напрямую от линии питания; в таких случаях анализ текущих сигналов не рекомендуется из-за плохого качества текущего сигнала.Точно так же с использованием этой методологии могут быть обнаружены неисправности, так как MCSA выполняется при мониторинге тока асинхронного двигателя. Метод частотно-временного разложения, который обеспечивает лучшие результаты, — это MUSIC, который имеет более высокое разрешение по частоте и способен обнаруживать частоты и их гармоники, связанные с устраненными неисправностями в сильно зашумленном вибрационном сигнале. Для дальнейшего развития может быть включена система классификации для автоматического обнаружения неисправностей. Кроме того, анализ, применяемый к объединению данных от датчиков ускорения и тока, может дать улучшенную методологию обнаружения неисправностей в асинхронных двигателях.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Благодарности
Это исследование было частично поддержано стипендией CONACYT 237491, грантом Университета Гуанахуато SEP PIFI 2014 и Университетом Вальядолида, проект 061/130251.
A Примечание по частотно-временному анализу постукивания пальцами
J Mot Behav. Авторская рукопись; доступно в PMC 19 апреля 2009 г.
Опубликован в окончательной редакции как:
PMCID: PMC2670435
NIHMSID: NIHMS14285
Кафедра физиотерапии и реабилитации, Школа медицины, Университет Мэриленда, Балтимор Адрес для корреспонденции
: Вэй Лю, факультет физиотерапии и реабилитации, Мэрилендский университет, 100 Penn Street, Baltimore, MD 21201, США.Адрес электронной почты: ude.dnalyramu.mos@uilw См. Другие статьи в PMC, в которых цитируется опубликованная статья.Abstract
Постукивание пальцем включает 3 важных функции: время, пространственную амплитуду и частоту. В классическом анализе исследователи исследуют временные параметры; в спектральном анализе они исследуют частотные параметры. Оба типа анализа основаны на информации о стационарных отводах. Авторы полагают, что частотно-временной анализ является полезным инструментом для анализа нестационарного постукивания пальцем.Они описывают метод и приводят примеры частотной модуляции, разницы в возрасте и скорости перехода, которые демонстрируют дополнительные идеи, которые можно получить с помощью этого анализа.
Ключевые слова: постукивание пальцем, быстрое преобразование Фурье (БПФ), время-частота
Один из методов оценки целостности нервно-мышечной системы и изучения проблем управления моторикой — это измерение способности человека постукивать пальцем. Постукивание пальцами имеет то преимущество, что является относительно чистой двигательной задачей, управляемой неврологически, поскольку инерционные и межсегментарные взаимодействия настолько малы, что биомеханические воздействия на движение снижаются (Collyer, Broadbent, & Church, 1994).Стабильное постукивание пальцами также относительно не зависит от когнитивных и перцептивных требований или культурного опыта, хотя может присутствовать музыкальное влияние и влияние клавишных. Кроме того, легко обнаруживаются тенденции развития и клинические нарушения, что делает изменения в поведении четким сигналом изменений в некоторых аспектах нейромоторной системы. В таком случае, как характеристики постукивания связаны с основными нейромоторными процессами, является важным вопросом. В этой заметке мы предлагаем, чтобы классические методы измерения постукивания пальцем во временной или частотной области могли быть дополнены или, возможно, заменены частотно-временным аналитическим методом, который может обеспечить дополнительное понимание основных процессов.
Исторически измеряемыми характеристиками повторяющегося одностороннего нарезания резьбы были скорость и постоянство. Скорость обычно измеряется как средний интервал между ответами или ответами (ITI или IRI, соответственно) между последовательными ответами в течение испытания. Согласованность измеряется как коэффициент вариации или стандартное отклонение среднего ITI (например, CV ITI, SD ITI). Второй классический метод описания постукивания пальцем — это спектральный анализ кинематического временного ряда, который выявляет различные частотные компоненты постукивания.В этом подходе сигнал разлагается на различные частотные компоненты, используя быстрое преобразование Фурье (БПФ) для вычисления дискретного преобразования Фурье (ДПФ), необходимого для получения спектра частотных компонентов. В обоих типах анализа спектр заданного сигнала представлен так, как если бы постукивание пальцем было неизменным во времени (то есть спектральные характеристики не меняются с течением времени). В действительности, однако, нейромоторные сигналы находятся под влиянием многих внутренних и внешних ограничений, которые могут вызывать быстрые и резкие изменения сигнала, которые нельзя игнорировать или сглаживать как шум.
У этой записки двоякая цель. Во-первых, мы описываем два классических метода анализа и показываем, как выводятся частотно-временные инструменты, которые можно применять к данным, полученным путем касания пальцем. Во-вторых, мы проиллюстрировали потенциальную полезность частотно-временного метода в анализе отдельных испытаний в различных экспериментальных условиях и в разных популяциях.
Описание методов измерения
Анализ во временной области
В наиболее фундаментальных подходах к анализу постукивания пальцами исследователи сосредоточили свое внимание на времени и постоянстве времени, которое измеряется дискретным событием, обычно моментом контакта с поверхностью, для обозначения граница между одним циклом постукивания и следующим.Один метод декомпозиции изменчивости времени был первоначально предложен Wing и Kristofferson (1973), которые использовали автокорреляцию ITI для разложения общей наблюдаемой дисперсии постукивания на центральные часы по сравнению с периферическими моторными источниками (подробнее см. Wing & Kristofferson). Следует отметить, что довольно часто предположения модели Винга и Кристофферсона не выполняются (особенно у детей), поскольку модель требует стационарных данных. Нестационарность постукивания давно признана проблемой для анализа.Средние данные с большой вероятностью искажают реальную производительность. Альтернативный метод борьбы с нестационарностью заключается в выполнении корректировок с помощью апостериорной обработки. Например, существуют различные методы устранения тренда данных, обычно включающие подгонку к данным линейной или криволинейной функции (Robertson et al., 1999).
Анализ частотной области
Методы БПФ долгое время были стандартным инструментом для определения доминирующих частот в стационарных периодических сигналах (Oppenheim & Schafer, 1989).БПФ является основой для спектрального анализа, который предоставляет ценное окно для повторяющегося поведения постукивания, выявляя присутствие частотных составляющих, которые не обязательно находятся на основной движущей частоте постукивания пальцем и которые не могут быть обнаружены только измерениями во временной области. . Хотя БПФ является простым и быстрым в вычислительном отношении, его производительность весьма неэффективна из-за предвзятости для коротких последовательностей данных и «эффекта утечки» даже с помощью передовых методов работы с окнами (Welch, 1967).Кроме того, его удаление временной области исключает потенциальные идеи, которые могут быть получены из привязки спектральной информации к динамике поведения постукивания во времени. Поэтому было бы полезно иметь метод, объединяющий временной и спектральный анализ, чтобы можно было увидеть изменения частотного разложения в ходе испытания.
Частотно-временной анализ
В методе частотно-временного анализа допускаются нестационарные сигналы; поэтому его можно использовать для количественной оценки изменений спектральных характеристик сигнала с течением времени (в зависимости от времени).Двумя широко используемыми частотно-временными представлениями являются подходы кратковременного преобразования Фурье (STFT) и обобщенного частотно-временного распределения (TFD) (Cohen, 1989).
STFT — это просто результат умножения временного ряда на короткое временное окно и последующего выполнения БПФ. Действие этого окна заключается в количественной оценке спектров в пределах более узких периодов поведения, что приводит к серии локальных спектров, которые определяются для всех времен. Отображение локальных спектров мощности называется спектрограммой .Эта схема управления окнами может быть описана как управление окнами постоянной ширины . Временное разрешение одинаково для всех спектральных составляющих. Величина для любого заданного спектрального компонента TFD дает среднее значение по оконному временному ряду. Выбор размера окна несколько произвольный. Иногда необходимо выполнить два STFT с разными размерами окна, чтобы достичь адекватного разрешения по времени и частоте. Однако при выборе размера окна исследователь будет искать компромисс между разрешением по времени и разрешением по частоте.Класс частотно-временного анализа Коэна (Cohen, 1989) — это более точный подход, который решает проблему размера окна.
Класс Коэна (1989) — это очень общий подход к разработке совместной функции времени и частоты, которая будет описывать плотность энергии или интенсивность сигнала одновременно по времени и частоте. В этой статье мы исследуем применение преобразования Чоя – Вильямса (1989) в качестве ядра для анализа данных касания пальцем. Наиболее важным свойством класса Коэна является билинейное частотно-временное преобразование, инвариантное к временному и частотному сдвигу, которое вызывает ограничение этого класса, называемое интерференционным членом или перекрестным членом .В этом исследовании мы использовали функцию преобразования Гильберта (Oppenheim & Schafer, 1989) для преобразования наших кинематических данных касания пальца в аналитический сигнал. Аналитический сигнал определяется как комплексный сигнал, спектр которого идентичен спектру реального сигнала для положительных частот и равен нулю для отрицательных частот. Одна из основных причин использования аналитического сигнала в TFD заключается в том, что он не содержит отрицательных частотных составляющих; отсутствуют перекрестные члены, возникающие как интерференция между отрицательной частотой и положительной частотной составляющими; таким образом, структура TFD более читабельна и понятна.Следует отметить, что существует несколько ядер. Например, мы сравнили ядро Чоя – Вильямса с ядром конической формы (Zhao, Atlas, & Marks, 1990) и обнаружили, что использование аналитического сигнала было достаточным для устранения перекрестных членов и связанных с ними артефактов. Более того, сравнение ядер не имело особого значения для тех, кто использует данные. Поэтому мы выполнили автономный анализ, используя MATLAB с набором инструментов для обработки сигналов (MathWorks, Natick, MA) и ядром Чоя – Вильямса (Auger, Flandrin, Goncalves, & Lemoine, 1996).
Демонстрация БПФ и TFD: анализ синусоидальных волн
Чтобы проиллюстрировать взаимосвязи и различия между подходами время, частотный спектр и время-частота, мы сначала представляем демонстрацию искусственно сгенерированного синусоидального сигнала с частотой 1,6 Гц за 15 с. Синусоидальная волна аппроксимирует пространственно-временную картину непрерывного сигнала касания пальца в пространстве. Синусоидальная волна является стационарным сигналом, если его основная частота постоянна во времени.
Синусоидальная волна, сгенерированная MATLAB, а также БПФ и TFD синусоидальной волны показаны на.БПФ синусоидальной волны показывает, что пиковая мощность спектра соответствует 1,6 Гц, как это также показано в TFD синусоидальной волны. Это наблюдение подтверждает, что синусоидальная волна имеет постоянную частоту.
Компьютерная синусоида с частотой 1,6 Гц, быстрое преобразование Фурье (FFT) и обобщенное частотно-временное распределение (TFD) этой синусоидальной волны. Величина мощности TFD проиллюстрирована цветовым градиентом, при этом красный и синий обозначают наивысшую и самую низкую мощности, соответственно.
Чтобы проиллюстрировать устойчивость алгоритмов TFD к аддитивному шуму, мы добавили случайный шум к исходному 1.Синусоидальный сигнал с частотой 6 Гц, генерируемый MATLAB. Результаты FFT и TFD показаны в. БПФ синусоидальной волны по-прежнему показывает, что пиковая мощность спектра соответствует 1,6 Гц, но по оси частот распределено больше частотных составляющих. TFD синусоидальной волны также показывает более сильную полосу частот 1,6 Гц по оси времени. Этот вывод подтверждает, что при использовании подхода TFD синусоидальная волна имеет относительно постоянную частоту при добавлении шума. Хотя этот пример чрезмерно упрощает вероятную природу шума при постукивании пальцем, он все же иллюстрирует способность алгоритма справляться со случайным шумом.
Компьютерная синусоида с частотой 1,6 Гц, полученная путем добавления случайного шума, а также БПФ и ТФД этой синусоидальной волны со случайным шумом; обратите внимание, что частотная шкала БПФ совпадает с частотной шкалой TFD. БПФ = быстрое преобразование Фурье; TFD = обобщенное частотно-временное распределение.
Демонстрация частотно-временного анализа в отдельных испытаниях постукивания пальцами
Метод
Для всех испытаний мы измеряли постукивание пальцами с помощью системы Motion Monitor (Иннспорт, Чикаго, Иллинойс), системы магнитного отслеживания, которая обеспечивает трехмерное пространственное данные о положении.Данные о движении доминирующего указательного пальца регистрировались с частотой 100 Гц в течение 15 с. Испытания проводились либо с предпочтительной скоростью, либо с помощью звуковых сигналов, генерируемых с помощью генератора сигналов Hewlett Packard (установленный на 0,4, 1,2 и 1,6 Гц), подключенного к усилителю и динамику. Данные представлены от взрослых участников ( n = 3) и типично развивающегося ребенка ( n = 1). Участники принимали участие в эксперименте, который был одобрен Наблюдательным советом Университета Мэриленда; либо они, либо их родители, либо опекун подписали форму согласия.
Пример 1: TFD постукивания пальцем взрослого при 1,6 и 0,4 Гц
Для демонстрационных целей показаны пространственно-временные данные, FFT и TFD постукивания пальцем для испытаний, проведенных здоровым взрослым участником при 1,6 Гц. При такой скорости TFD постукивания пальцем показывает полосу пропускания от 1,5 до 1,8 Гц с течением времени, а также изменчивость изменения частоты во времени отображается в. По сравнению с TFD показывает изменение полосы частот со временем, указывая на управление, которое отличается от машинного пальца (Deutsch & Newell, 2003; Riley & Turvey, 2002; Sternad, Dean, & Newell, 2000), производящего синусоидальную волну. движение.В отличие от обычных пространственно-временных результатов, на рисунке мы видим свидетельства изменчивости, обычно связанной с движением человека.
Постукивание пальцами взрослого при частоте 1,6 Гц. ( A ) БПФ и TFD постукивания пальцем. ( B ) Оценка гистограммы и функции плотности ядра IMF. БПФ = быстрое преобразование Фурье; TFD = обобщенное частотно-временное распределение; IMF = мгновенная средняя частота.
В дополнение к просмотру временной и частотной составляющих на одном графике мы извлекли два параметра для количественной оценки TFD постукивания пальцем.TFD ( t, f ) представляет собой трехмерную матрицу, которая включает в себя временной индекс, частотный индекс и величину мощности. Частотная составляющая, изменяющаяся с течением времени, или величина изменения мощности с течением времени — это два способа разложения этой трехмерной матрицы. Расчет мгновенной средней частоты (IMF) является стандартным способом разложения TFD ( t, f ) (Choi & Williams, 1989), и он дает больше информации об изменениях параметров спектра во времени. Дополнительным способом изображения сигнала IMF является отображение его в виде гистограммы и сглаженного приближения, которое можно получить, используя оценку плотности ядра (Bowman & Azzalini, 1997).
Показываем МВФ в рублях. Гистограмма и оценка функции плотности ядра указывают на унимодальный характер распределения с пиком, соответствующим 1,6 Гц, и высокой вероятностью того, что частота будет соответствовать внешнему управляющему сигналу.
Результаты прослушивания 0,4 Гц от одного и того же взрослого показаны в аналогичном формате в формате. Интересное отличие состоит в том, что на медленной скорости TFD постукивания пальцем не был просто уменьшенной картой той же структуры от быстрой скорости; скорее, он показал отчетливую подпись для медленного нажатия пальцем с широкой полосой пропускания.Из гистограммы и оценки функции плотности ядра в, мы видим признаки бимодального паттерна с двумя пиками (0,20 и 0,70 Гц) и одной впадиной (0,45 Гц). Это наблюдение предполагает, что при более низкой частоте ответвлений высока вероятность того, что спектральные компоненты не будут полностью соответствовать внешнему управляющему сигналу. Действительно, помимо внешней частоты есть еще одна важная частотная составляющая. Можно предположить, что сложность частотных составляющих на низкой скорости является функцией времени задержки между ответвлениями.Наличие бимодального, а не унимодального паттерна указывает на возможные различия в стратегиях контроля для двух частот. Однако мы не можем сделать вывод о линейности или нелинейности лежащего в основе процесса управления.
Постукивание пальцами взрослого с частотой 0,4 Гц. ( A ) БПФ и TFD постукивания пальцем. ( B ) Оценка гистограммы и функции плотности ядра IMF. БПФ = быстрое преобразование Фурье; TFD = обобщенное частотно-временное распределение; IMF = мгновенная средняя частота.
Пример 2: TFD постукивания пальцем взрослого и ребенка с частотой 1,2 Гц
Временно-пространственные данные, FFT и TFD постукивания пальцем для испытаний от взрослых и детей показаны в и. Данные МВФ по тем же испытаниям показаны в и. Мы выбрали эти испытания, потому что временной анализ испытаний показал, что они имели одинаковый ITI (0,83 с) и CV ITI (6,96 взрослых; 6,39 детей). То есть анализ, основанный на времени, не выявит различий между взрослым и ребенком; но мы можем видеть из анализа TFD различные закономерности при аналогичных условиях ITI и CV ITI.В частности, когда мы сравнивали среднее значение IMF с течением времени, постукивание пальцами взрослого показало стабильную картину (1,19 ± 0,05 Гц), тогда как постукивание пальцами ребенка показало нестабильную картину (1,04 ± 0,20 Гц). К тому же вероятность МВФ была разной. Эти различия демонстрируют возможность использования МВФ в качестве количественных изменений в индивидуальных показателях деятельности, которые можно использовать для будущего статистического анализа. Также возможно установить критерии на основе уровня мощности, чтобы можно было обнаружить разницу в разбросе полосы пропускания, как показано на и.
Постукивание пальцем при частоте 1,2 Гц для взрослого. ( A ) БПФ и TFD постукивания пальцем. ( B ) Оценка гистограммы и функции плотности ядра IMF. БПФ = быстрое преобразование Фурье; TFD = обобщенное частотно-временное распределение; IMF = мгновенная средняя частота.
Постукивание пальцем с частотой 1,2 Гц для ребенка. ( A ) БПФ и TFD постукивания пальцем. ( B ) Оценка гистограммы и функции плотности ядра IMF. БПФ = быстрое преобразование Фурье; TFD = обобщенное частотно-временное распределение; IMF = мгновенная средняя частота.
Пример 3: TFD постукивания пальцем взрослого с изменением частоты в середине испытания
В этом примере участника попросили постучать указательным пальцем правой руки синхронно со слуховым сигналом при двух условиях: (а) внезапное переключение с медленного (0,667 Гц) на быструю (2,8 Гц) частоту и (б) внезапный переход от быстрой (2,8 Гц) к медленной (0,667 Гц) частоте. Пространственно-временные данные, БПФ и TFD для пробного перехода от медленной к быстрой стимуляции и наоборот показаны в и.Данные МВФ по тем же испытаниям показаны в и. В этом случае TFD предоставил информацию о том, как преднамеренные изменения были внесены в ходе исследования. Как и ожидалось, относительно постоянная частота поддерживалась в течение каждого периода постоянной стимуляции. Между этими периодами устойчивого состояния TFD показывает, как палец адаптировался к внезапному изменению звукового управляющего сигнала. Паттерны частотной адаптации выявили тонкие различия в том, как участник отреагировал на изменение внешних временных ограничений.Переход от быстрого к медленному выглядит как более плавный и стабильный паттерн в TFD, в отличие от более разрозненного паттерна во время перехода от медленного к быстрому. Таким образом, анализ TFD может выявить особенности перехода, и в этом случае он предполагает, что увеличение периода содержит больше частотных компонентов, чем уменьшение периода. Эти особенности могут иллюстрировать характеристики эффекта гистерезиса при двунаправленном частотном масштабировании.
Постукивание пальцем с пробным изменением частоты у взрослого человека (с медленной на быструю скорость).( A ) БПФ и TFD постукивания пальцем. ( B ) Оценка гистограммы и функции плотности ядра IMF. БПФ = быстрое преобразование Фурье; TFD = обобщенное частотно-временное распределение; IMF = мгновенная средняя частота.
Постукивание пальцем с промежуточным изменением частоты у взрослого (с быстрой на медленную). ( A ) БПФ и TFD постукивания пальцем. ( B ) Оценка гистограммы и функции плотности ядра IMF. БПФ = быстрое преобразование Фурье; TFD = обобщенное частотно-временное распределение; IMF = мгновенная средняя частота.
Обсуждение
Мы продемонстрировали, как можно использовать частотно-временной анализ, чтобы потенциально помочь в понимании нейромоторного процесса, лежащего в основе повторяющегося постукивания пальцами. Сила этого подхода заключается в том, что частотные составляющие движения фиксируются с течением времени, что устраняет необходимость в стационарных данных. Во-первых, во время различных частотных протоколов анализ IMF показал нам одномодальный образец на частоте 1,6 Гц и бимодальный образец на частоте 0,4 Гц. Во-вторых, с аналогичным условием ITI и CV ITI у взрослого была другая картина TFD, чем у ребенка.В-третьих, мы обнаружили в этом подходе тонкие различия в переходе в условиях сдвига периода.
Для иллюстрации мы использовали данные одного испытания, но также можно было бы усреднить непрерывные пространственно-временные данные, а затем отобразить TFD группы. Одним из ограничений этого подхода является то, что вычисления занимают больше времени, чем для временного или частотного анализа. В будущем этот подход можно будет расширить для анализа касания двумя пальцами, посмотрев на согласованность в области TFD.Можно также использовать анализ TFD, чтобы посмотреть на продолжающийся электромиографический сигнал постукивания пальцами, который обеспечивает метод сочетания поведения и мышечной активности.
Частотно-временной анализ использовался в других моторных областях, включая мышечную усталость во время динамического сокращения (Bonato & Knaflitz, 1999) и контроль баланса (Schumann, Redfern, & Furman, 1995). Насколько нам известно, исследователи впервые использовали его для иллюстрации повторяющихся данных касания пальцами. Таким образом, основным преимуществом этого подхода является его способность обнаруживать тонкие изменения, вызванные сигналом, на основе нестационарности, что позволяет получить больше информации из сигнала.
ПОДТВЕРЖДЕНИЕ
Гранты от Национального института исследований в области инвалидности и реабилитации (h233G10111), присужденные Джилл Уитолл, от VA R&D (# B3390K), присужденные Ларри Форрестеру, и от Национального института по проблемам старения (P60AG12583), предоставленные Джилл Уитолл и Ларри Форрестер поддержал это исследование.
ПРИЛОЖЕНИЕ
Временной анализ
Рассмотрим анализ постукивания пальцем во временной области. Средние значения ITI и CV ITI обозначаются следующими уравнениями:
MeanITI = 1N − 1∑i = 1N − 1ITI,
(A1)
CVITI = 1N − 1∑i = 1N − 1 (ITI −1N − 1∑i = 1N − 1ITI) 21N − 1∑i = 1N − 1ITI,
(A2)
, где N — количество ответвлений, а i — индекс отдельного ответвления.
Рассмотрим декомпозицию изменчивости времени; метод был первоначально предложен Wing и Kristofferson (1973), которые использовали автокорреляцию ITI для разложения общей наблюдаемой дисперсии утечки. Уравнение:
var ( C ) = var ( I ) + 2 ∗ cov ( I j I j −1 ),
(A3)
, где C — интервал хронометриста, I — интервал между ответами, а j — индекс отдельного ответвления.
Анализ частотного спектра
Рассмотрим анализ частотного спектра постукивания пальцем. Преобразование Фурье — основа спектрального анализа; он связывает частотную область (уравнение A4) и временную область (уравнение A5).
H (f) = ∫ − ∞∞h (t) e − i2πftdt,
(A4)
h (t) = ∫ − ∞∞H (f) e2πiftdf,
(A5)
где H (f) — это ряд Фурье в частотной области, h (t) обозначает сигнал во временной области, t — временной индекс, а f — частотный индекс.
При работе с фактическим дискретным временным рядом уравнение модифицируется как дискретное преобразование Фурье (ДПФ) следующим образом:
H (nNT) = 1N∑k = 0N − 1h (kT) e − i2πnkN,
(A6)
h (kT) = ∑n = 0N − 1H (nNT) e − i2πnkN,
(A7)
, где N — количество точек во временном ряду, а T — это интервал выборки.
Частотно-временной анализ
Рассмотрим частотно-временной анализ постукивания пальцем; Двумя широко используемыми частотно-временными представлениями являются подходы кратковременного преобразования Фурье (STFT) и обобщенного частотно-временного распределения (TFD) (Cohen, 1989).STFT — это наиболее распространенное частотно-временное представление.
H [n, λ] = ∑m = −∞∞h [n + m] w [m] e − jλm.
(A8)
Одномерная последовательность h [n] преобразуется в двумерную функцию временной переменной n , которая является дискретной. Частотная переменная λ является непрерывной, тогда как Вт [м] — это последовательность окон, которая ограничивает размер последовательности, которая должна быть преобразована, так что спектральные характеристики являются достаточно стабильными на протяжении всего окна.
Класс Коэна — это очень общий подход к разработке совместной функции времени и частоты, которая будет описывать плотность энергии или интенсивность сигнала одновременно по времени и частоте. Эту совместную функцию можно получить из общей формулировки Коэна:
TFD (t, f) = ∭x (t ′ + τ / 2) x * (t′ − τ / 2) * ϕ (θ, τ) e − jθ (t − t ′) — jτfdt′dτdθ.
(A9)
TFD ( t, f ) — частотно-временной спектр класса Коэна, x (t) — реальный сигнал, x * ( t ) — комплексное сопряжение x (t) , t — временной индекс, f — частотный индекс, τ — временная задержка, θ — частотная задержка, а ϕ (θ, τ) называется ядром .Разные выборки ядра могут иметь разные свойства распределения TFD. В этой заметке мы исследовали применение преобразования Чоя – Вильямса (1989) в качестве ядра для анализа данных касания пальцем. Ядро Чоя-Вильямса определяется как
ϕ (θ, τ) = e — j θ 2 τ 2 / σ . f ( х) = 1N∑i = 1N1hK (х — xih).
(A12)
Оценка плотности ядра — это непараметрический метод оценки плотности, в котором усредняется известная функция плотности (ядро) по наблюдаемым точкам данных для создания гладкого приближения. При оценке плотности ядра x i (от x 1 до x n ) — это n независимых наблюдений от случайной величины x, K (●) обозначает так называемый функция ядра, а h обозначает пропускную способность.
СПРАВОЧНЫЕ МАТЕРИАЛЫ
- Оже Ф, Фландрин П., Гонсалвес П., Лемуан О. Набор инструментов «Время-частота» — для использования с MATLAB, справочное руководство. Париж, Франция: Национальный центр научных исследований; 1996. [Google Scholar]
- Bonato P, Knaflitz M. Частотно-временные методы, применяемые для оценки мышечной усталости во время динамических сокращений. Журнал электромиографии и кинезиологии. 1999; 9: 337–350. [PubMed] [Google Scholar]
- Bowman AW, Azzalini A. Прикладные методы сглаживания для анализа данных.Оксфорд, Англия: Издательство Оксфордского университета; 1997. [Google Scholar]
- Choi HI, Williams WJ. Улучшенное частотно-временное представление многокомпонентных сигналов с использованием экспоненциальных ядер. Транзакции IEEE по акустике, речи и обработке сигналов. 1989; 37: 862–871. [Google Scholar]
- Коэн Л. Частотно-временное распределение: обзор. Труды IEEE. 1989; 77: 941–981. [Google Scholar]
- Collyer CE, Broadbent HA, Church RM. Предпочтительные скорости повторного постукивания и категориального времени производства.Восприятие и психофизика. 1994; 55: 443–453. [PubMed] [Google Scholar]
- Deutsch KM, Newell KM. Детерминированные и стохастические процессы в изменчивости изометрической силы у детей. Психобиология развития. 2003. 43: 335–345. [PubMed] [Google Scholar]
- Оппенгейм А.В., Шафер Р.В. Обработка сигналов в дискретном времени. Река Аппер Сэдл, Нью-Джерси: Прентис-Холл; 1989. [Google Scholar]
- Riley MA, Turvey MT. Вариабельность и детерминизм двигательного поведения. Журнал моторного поведения.2002; 34: 99–125. [PubMed] [Google Scholar]
- Робертсон С.Д., Желязник Х.Н., Лантеро Д.А., Бойчик К.Г., Спенсер Р.М., Доффин Дж. Г. и др. Корреляции для согласованности синхронизации между задачами постукивания и рисования: свидетельство против единого процесса синхронизации для управления двигателем. Журнал экспериментальной психологии: человеческое восприятие и производительность. 1999; 25: 1316–1330. [PubMed] [Google Scholar]
- Шуман Т., Редферн М., Фурман Дж. Частотно-временной анализ постурального колебания. Журнал биомеханики. 1995; 28: 603–607.[PubMed] [Google Scholar]
- Штернэд Д., Дин В.Дж., Ньюэлл К.М. Изменчивость силы и времени при ритмичном монимануальном постукивании. Журнал моторного поведения. 2000. 32: 249–267. [PubMed] [Google Scholar]
- Welch PD. Использование быстрого преобразования Фурье для оценки спектров мощности: метод, основанный на усреднении по времени по коротким модифицированным периодограммам. IEEE Transactions по аудио и электроакустике. 1967; AU-15: 70–73. [Google Scholar]
- Wing AM, Kristofferson AB. Задержки отклика и время дискретных двигательных реакций.Восприятие и психофизика. 1973; 14: 5–12. [Google Scholar]
- Чжао Ю., Atlas LE, Marks RJ. Использование конических ядер для обобщенного частотно-временного представления нестационарных сигналов. Транзакции IEEE по акустике, речи и обработке сигналов. 1990; 38: 1084–1091. [Google Scholar]
Метод на основе разложения эмпирических мод для обнаружения потенциала действия в исходных нейронных данных
Авторы: Саджад Фараши, Мохаммаджавад Аболхассани, Мостафа Тагави Кани
Аннотация:
Информация в нервной системе кодируется как образцы возбуждения электрических сигналов, называемые потенциалом действия или спайком, поэтому важным шагом в анализе нервного механизма является обнаружение потенциалов действия, встроенных в нейронные данные.Для этой цели в литературе предлагается несколько методов. В этой статье был разработан новый метод, основанный на разложении по эмпирическим модам (EMD). EMD — это метод разложения, который выделяет колебания с различным частотным диапазоном в форме волны. Метод является адаптивным и не требует априорных знаний о данных или настройке параметров. Результаты моделирования данных показывают, что предлагаемый метод сопоставим с методами обнаружения всплесков на основе вейвлетов. Для нейронных сигналов с отношением сигнал / шум около 3 предложенных методов позволяет точно обнаруживать более 95% потенциалов действия.
Ключевые слова: EMD, обработка нейронных данных, обнаружение пиков, вейвлет-разложение.
Идентификатор цифрового объекта (DOI): doi.org/10.5281/zenodo.10
Процедуры APA BibTeX Чикаго EndNote Гарвард JSON ГНД РИС XML ISO 690 PDF Загрузок 2062Артикул:
[1] Кён Х.Ким, Сунг Дж. Ким, «Метод на основе вейвлетов для обнаружения потенциала действия по записи внеклеточного нейронного сигнала с низким соотношением сигнал / шум», IEEE Trans. биомед. англ., т. 50, нет. 8. С. 999-1011, 2003.
[2] И. Обейд и П. Вольф, «Оценка алгоритмов обнаружения всплесков для приложения интерфейса мозг-машина», IEEE Trans Biomed Eng, том 51, № 6, стр. 905–911, 2004.
[3] Р. Чандра и Л. М. Оптикан, «Обнаружение, классификация и разрешение наложения потенциалов действия в многоканальных одноканальных записях с помощью нейронной сети в режиме реального времени», IEEE Trans.Биомед. Англ., Т. 44. С. 403–412, 1997.
[4] Сунган Ким, Джеймс МакНеймс, «Автоматическое обнаружение спайков на основе адаптивного сопоставления шаблонов для внеклеточных нейронных записей», J. Neurosci. Методы, том 165, стр. 165–174, 2007.
[5] Роберт Дж. Брихта и др., «Вейвлет-методы для обнаружения спайков в активности почечных симпатических нервов мышей», IEEE Trans. Biomed Eng., Том 54 (1), стр. 82–93, январь 2007 г.
[6] Шахджахан Шахид, Жаклин Уокер и Лесли С. Смит, «Новый алгоритм обнаружения спайков для внеклеточных нейронных записей», IEEE Trans.Биомед Инж., Т. 57, pp.853-866, 2010.
[7] Левицки. M. S, «Обзор методов сортировки спайков: обнаружение и классификация потенциалов нейронного действия», Network, Vol. 9, pp. 53-78, 1998.
[8] Хуанг Н., З. Шен, С. Лонг, М. Ву, Э. Ши, К. Чжэн, Ч. Тунг и Х. Лю, «Метод эмпирического разложения мод и спектр Гильберта для не -стационарный анализ временных рядов, Труды Лондонского королевского общества, том 454, стр. 903–995, 1998.
[9] П. Фландрин, Г. Риллинг и П.Гонцалвес, «Разложение эмпирических мод как банк фильтров», Письма об обработке сигналов IEEE, том 11, № 2, часть 1, стр. 112–114, 2004.
[10] Чжаохуа Ву, Норден Э. Хуанг, «Исследование характеристик белого шума с использованием метода эмпирического разложения мод», Королевское общество Лондонских слушаний, серия A, том 460, выпуск 2046, стр. 1597-1611, 2004 г.
[11] Кайс Халди и др., «Улучшение речи с помощью EMD», журнал Eurasip о достижениях в обработке сигналов, том 8, стр. 1-8, 2008 г.
[12] Д.Л. Донохо и И. М. Джонстон, «Адаптация к неизвестной гладкости с помощью вейвлет-сжатия», Журнал Американской статистической ассоциации, том 90, № 432, стр. 1200–1424, 1995.
[13] Лесли С. Смит, Нхамойнсу Мтетва, «Инструмент для синтеза цепочек спайков с реалистичной интерференцией», J. Neurosci. Методы, том 159, стр. 170–180, 2007. Обнаружение, обработка, классификация и приложения
Реферат
Электромиографические (ЭМГ) сигналы могут использоваться для клинических / биомедицинских приложений, разработки Evolvable Hardware Chip (EHW) и взаимодействия современного человека с компьютером.Для сигналов ЭМГ, полученных от мышц, требуются передовые методы обнаружения, разложения, обработки и классификации. Цель этой статьи — проиллюстрировать различные методологии и алгоритмы анализа сигналов ЭМГ, чтобы обеспечить эффективные и действенные способы понимания сигнала и его природы. Мы также указываем на некоторые аппаратные реализации, использующие EMG, с упором на приложения, связанные с управлением протезами руки, распознаванием захвата и взаимодействием человека с компьютером. Также дано сравнительное исследование, чтобы показать эффективность различных методов анализа сигналов ЭМГ.Эта статья дает исследователям хорошее представление об ЭМГ-сигнале и процедурах его анализа. Эти знания помогут им разрабатывать более мощные, гибкие и эффективные приложения.
Ключевые слова: Электромиография, анализ Фурье, мышцы, нервная система
Введение
Биомедицинский сигнал означает коллективный электрический сигнал, полученный от любого органа, который представляет интересующую физическую переменную. Этот сигнал обычно является функцией времени и может быть описан в терминах его амплитуды, частоты и фазы.Сигнал ЭМГ — это биомедицинский сигнал, который измеряет электрические токи, генерируемые в мышцах во время их сокращения, представляющие нервно-мышечную активность. Нервная система всегда контролирует мышечную активность (сокращение / расслабление). Следовательно, сигнал ЭМГ — это сложный сигнал, который контролируется нервной системой и зависит от анатомических и физиологических свойств мышц. Сигнал ЭМГ приобретает шум при прохождении через разные ткани. Более того, детектор ЭМГ, особенно если он находится на поверхности кожи, одновременно собирает сигналы от разных двигательных единиц, которые могут генерировать взаимодействие разных сигналов.Обнаружение сигналов ЭМГ с помощью мощных и передовых методик становится очень важным требованием в биомедицинской инженерии. Основная причина интереса к анализу сигналов ЭМГ заключается в клинической диагностике и биомедицинских приложениях. Сфера лечения и реабилитации двигательной инвалидности определена как одна из важных областей применения. Формы и частота активации потенциалов действия двигательных единиц (MUAP) в сигналах ЭМГ являются важным источником информации для диагностики нервно-мышечных расстройств.Как только соответствующие алгоритмы и методы для анализа сигнала ЭМГ становятся легкодоступными, природа и характеристики сигнала могут быть правильно поняты, и могут быть реализованы аппаратные средства для различных приложений, связанных с сигналами ЭМГ.
До сих пор в этой области были предприняты исследования и обширные усилия, направленные на разработку лучших алгоритмов, обновление существующих методологий, улучшение методов обнаружения для уменьшения шума и получения точных сигналов ЭМГ. Было сделано несколько аппаратных реализаций для управления протезами руки, распознавания захвата и взаимодействия человека с машиной.Очень важно провести исследование, чтобы классифицировать актуальные проблемы анализа сигналов ЭМГ и обосновать принятые меры.
Технология записи ЭМГ относительно новая. Все еще существуют ограничения в обнаружении и характеристике существующих нелинейностей в сигнале поверхностной электромиографии (sEMG, специальный метод исследования мышечных сигналов), оценке фазы, получении точной информации из-за вывода из нормальности (1, 2) Традиционные алгоритмы реконструкции системы имеют различные ограничения и значительную вычислительную сложность, а многие из них демонстрируют высокую дисперсию (1).Последние достижения в технологиях обработки сигналов и математических моделей сделали практическую разработку передовых методов обнаружения и анализа ЭМГ. Широкое распространение получили различные математические методы и искусственный интеллект (ИИ). Математические модели включают вейвлет-преобразование, частотно-временные подходы, преобразование Фурье, распределение Вигнера-Вилля (WVD), статистические меры и статистику более высокого порядка. Подходы ИИ к распознаванию сигналов включают искусственные нейронные сети (ИНС), динамические рекуррентные нейронные сети (DRNN) и систему нечеткой логики.Генетический алгоритм (GA) также был применен в эволюционируемом аппаратном чипе для сопоставления входных сигналов ЭМГ с желаемыми действиями рук.
Вейвлет-преобразование хорошо подходит для нестационарных сигналов, таких как ЭМГ. Частотно-временной подход с использованием аппаратного WVD может позволить создать инструмент в реальном времени, который можно использовать для тренировки определенных двигательных единиц в ситуациях биологической обратной связи. Статистические методы более высокого порядка (HOS) могут использоваться для анализа сигнала EMG из-за уникальных свойств HOS, применяемых к случайным временным рядам.Биспектр или спектр третьего порядка имеет то преимущество, что подавляет гауссов шум.
В этой статье сначала дается краткое объяснение сигнала ЭМГ и краткая историческая справка по анализу сигнала ЭМГ. Далее следует описание современных методов обнаружения, разложения, обработки и классификации сигнала ЭМГ, а также сравнительное исследование. Наконец, были обсуждены некоторые аппаратные реализации и приложения EMG.
Материалы и методы
ЭМГ: анатомо-физиологические предпосылки
EMG — электромиография.Это исследование электрических сигналов мышц. ЭМГ иногда называют миоэлектрической активностью. Мышечная ткань проводит электрические потенциалы так же, как нервы, и название, данное этим электрическим сигналам, — потенциал действия мышц. Поверхностная ЭМГ — это метод записи информации, содержащейся в этих потенциалах действия мышц. При обнаружении и записи сигнала ЭМГ есть две основные проблемы, которые влияют на точность сигнала. Первый — это отношение сигнал / шум.То есть отношение энергии сигналов ЭМГ к энергии шумового сигнала. В общем, шум определяется как электрические сигналы, которые не являются частью желаемого сигнала ЭМГ. Другой проблемой является искажение сигнала, что означает, что относительный вклад любой частотной составляющей в сигнал ЭМГ не должен изменяться. Для получения мышечного сигнала использовались два типа электродов: инвазивный электрод и неинвазивный электрод. Когда ЭМГ получают от электродов, установленных непосредственно на коже, сигнал представляет собой совокупность всех потенциалов действия мышечных волокон, возникающих в мышцах, лежащих под кожей.Эти потенциалы действия возникают через случайные промежутки времени. Таким образом, в любой момент сигнал ЭМГ может быть как положительным, так и отрицательным напряжением. Потенциалы действия отдельных мышечных волокон иногда измеряются с помощью проволочных или игольчатых электродов, помещаемых непосредственно в мышцу. Комбинация потенциалов действия мышечных волокон от всех мышечных волокон одной двигательной единицы представляет собой потенциал действия двигательной единицы (MUAP), который может быть обнаружен поверхностным электродом кожи (неинвазивным), расположенным рядом с этим полем, или иглой. электрод (инвазивный) вставлен в мышцу (3).Уравнение 1 показывает простую модель сигнала ЭМГ:
где, x (n) , смоделированный сигнал ЭМГ, e (n) , обработанная точка, представляет импульс стрельбы, ч (r) , представляет MUAP, w (n) , нулевое среднее вызывающий привыкание белый гауссовский шум и N — количество срабатываний моторных единиц.
Сигнал улавливается электродом и усиливается. Обычно в качестве усилителя первой ступени используется дифференциальный усилитель.Могут последовать дополнительные стадии усиления. Перед отображением или сохранением сигнал можно обработать для устранения низкочастотного или высокочастотного шума или других возможных артефактов. Часто пользователя интересует амплитуда сигнала. Следовательно, сигнал часто выпрямляется и усредняется в некотором формате, чтобы указать амплитуду ЭМГ.
Нервная система является одновременно управляющей и коммуникационной системой тела. Эта система состоит из большого количества возбудимых связанных клеток, называемых нейронами, которые общаются с различными частями тела с помощью электрических сигналов, которые являются быстрыми и специфическими.Нервная система состоит из трех основных частей: головного мозга, спинного мозга и периферических нервов. Нейроны являются основной структурной единицей нервной системы и значительно различаются по размеру и форме. Нейроны — это узкоспециализированные клетки, которые передают сообщения в виде нервных импульсов от одной части тела к другой.
Мышца состоит из пучков специализированных клеток, способных сокращаться и расслабляться. Основная функция этих специализированных клеток — генерировать силы, движения и способность общаться, например речь, письмо или другие способы выражения.Мышечная ткань обладает растяжимостью и эластичностью. Он способен принимать раздражители и реагировать на них, его можно сокращать или сокращать. Мышечная ткань выполняет четыре ключевые функции: движение, перемещение вещества внутри тела, стабилизация и выработка тепла. На основании структуры, сократительных свойств и механизмов контроля можно выделить три типа мышечной ткани: (i) скелетная мышца, (ii) гладкая мышца и (iii) сердечная мышца. ЭМГ применяется для исследования скелетных мышц.Ткань скелетных мышц прикреплена к кости, и ее сокращение отвечает за поддержку и движение скелета. Сокращение скелетных мышц инициируется импульсами нейронов к мышце и обычно находится под произвольным контролем. Волокна скелетных мышц хорошо снабжены нейронами для их сокращения. Этот конкретный тип нейрона называется «двигательным нейроном», и он приближается к мышечной ткани, но на самом деле не связан с ней. Один мотонейрон обычно стимулирует множество мышечных волокон.
Человеческое тело в целом электрически нейтрально; у него одинаковое количество положительных и отрицательных зарядов. Но в состоянии покоя мембрана нервной клетки поляризована из-за различий в концентрациях и ионном составе на плазматической мембране. Между внутриклеточными и внеклеточными жидкостями клетки существует разность потенциалов. В ответ на стимул от нейрона мышечное волокно деполяризуется, поскольку сигнал распространяется по его поверхности, и волокно дергается.Эта деполяризация, сопровождаемая движением ионов, создает электрическое поле около каждого мышечного волокна. Сигнал ЭМГ — это последовательность потенциала действия двигательных единиц (MUAP), показывающая мышечный ответ на нервную стимуляцию. Сигнал ЭМГ выглядит случайным по своей природе и обычно моделируется как отфильтрованный импульсный процесс, где MUAP является фильтром, а импульсный процесс обозначает импульсы нейрона, часто моделируемые как процесс Пуассона (3). На рисунке показан процесс получения сигнала ЭМГ и его разложение для достижения MUAP.
ЭМГ-сигнал и разложение MUAP.
EMG: история
Разработка EMG началась с документации Франческо Реди в 1666 году. В документе сообщается, что узкоспециализированная мышца рыбы с электрическим скатом генерирует электричество (3). К 1773 году Уолш смог продемонстрировать, что мышечная ткань рыбы-угря может генерировать искру электричества. В 1792 г. вышло издание «De Viribus Electricitatis in Motu Musculari Commentarius», написанное А.Гальвани, где автор показал, что электричество может инициировать сокращение мышц (4). Шесть десятилетий спустя, в 1849 году, Дубиос-Раймонд обнаружил, что можно также регистрировать электрическую активность во время произвольного сокращения мышц. Первая запись этой активности была сделана Марей в 1890 году, который также ввел термин электромиография (5). В 1922 году Гассер и Эрлангер использовали осциллограф, чтобы показать электрические сигналы от мышц. Из-за стохастической природы миоэлектрического сигнала при его наблюдении можно было получить только приблизительную информацию.Возможности обнаружения электромиографических сигналов неуклонно улучшались с 1930-х по 1950-е годы, и исследователи начали более широко использовать улучшенные электроды для исследования мышц (1). Клиническое использование поверхностной ЭМГ для лечения более специфических заболеваний началось в 1960-х годах. Хардик и его исследователи были первыми (1966) практиками, использовавшими sEMG (5). В начале 1980-х годов Крам и Стегер представили клинический метод сканирования различных мышц с помощью устройства измерения ЭМГ (5).
Только в середине 80-х годов прошлого века методы интеграции электродов были достаточно развиты, чтобы позволить серийное производство необходимых небольших и легких приборов и усилителей. В настоящее время имеется в продаже ряд подходящих усилителей. В начале 1980-х годов стали доступны кабели, которые создают артефакты в желаемом диапазоне микровольт. В течение последних 15 лет исследования привели к лучшему пониманию свойств записи поверхностной ЭМГ.В последние годы поверхностная электромиография все чаще используется для записи данных с поверхностных мышц в клинических протоколах, где внутримышечные электроды используются только для глубоких мышц (2, 4).
Есть много приложений для использования EMG. ЭМГ используется в клинической практике для диагностики неврологических и нервно-мышечных проблем. Он используется для диагностики в лабораториях по изучению ходьбы и врачами, обученными использованию биологической обратной связи или эргономической оценки. ЭМГ также используется во многих типах исследовательских лабораторий, включая лаборатории, занимающиеся биомеханикой, двигательным контролем, нервно-мышечной физиологией, двигательными расстройствами, контролем позы и физиотерапией.
Электрический шум и факторы, влияющие на сигнал ЭМГ
Диапазон амплитуды сигнала ЭМГ составляет 0-10 мВ (от +5 до -5) до усиления. Сигналы ЭМГ приобретают шум при прохождении через различные ткани. Важно понимать характеристики электрического шума. Электрический шум, который влияет на сигналы ЭМГ, можно разделить на следующие типы:
-
Собственный шум в электронном оборудовании : Все электронное оборудование генерирует шум.Этот шум невозможно устранить; использование высококачественных электронных компонентов может только уменьшить его.
-
Окружающий шум: Источником такого шума является электромагнитное излучение. Поверхности наших тел постоянно залиты электромагнитным излучением, и избежать его воздействия на поверхности земли практически невозможно. Окружающий шум может иметь амплитуду на один-три порядка больше, чем сигнал ЭМГ.
-
Артефакт движения: Когда артефакт движения вводится в систему, информация искажается. Артефакт движения вызывает искажения в данных. Существует два основных источника артефактов движения: 1) интерфейс электрода и 2) кабель электрода. Артефакты движения могут быть уменьшены за счет правильной разработки электронных схем и настроек.
-
Собственная нестабильность сигнала : Амплитуда ЭМГ носит случайный характер.На сигнал ЭМГ влияет частота срабатывания моторных единиц, которые в большинстве случаев срабатывают в диапазоне частот от 0 до 20 Гц. Этот вид шума считается нежелательным, и его устранение важно.
Факторы, которые в основном влияют на сигнал ЭМГ, также могут быть классифицированы. Такая классификация устанавливается таким образом, чтобы алгоритмы анализа сигналов ЭМГ могли быть оптимизированы, а оборудование могло быть спроектировано согласованным образом. Факторы, влияющие на сигнал ЭМГ, делятся на три основные категории:
-
Причинные факторы: Это прямое влияние на сигналы.Причинные факторы можно разделить на два класса:
-
Внешний : Это связано со структурой и расположением электродов. Такие факторы, как площадь поверхности обнаружения, форма электрода, расстояние между поверхностью обнаружения электродов, расположение электрода по отношению к двигательным точкам в мышце, расположение электрода мышцы на поверхности мышцы по отношению к боковому краю мышцы, ориентация поверхностей обнаружения по отношению к мышечным волокнам в основном влияет на сигнал ЭМГ.
-
Внутренний : Физиологические, анатомические и биохимические факторы зависят от количества активных двигательных единиц, состава волокон, кровотока, диаметра волокна, глубины и расположения активных волокон, а также количества ткани между поверхностью мышцы и электродом.
-
-
Промежуточные факторы: Промежуточные факторы — это физические и физиологические явления, на которые влияют один или несколько причинных факторов.Причинами этого могут быть аспекты полосовой фильтрации только электрода с его объемом обнаружения, суперпозиция потенциалов действия в обнаруженном ЭМГ-сигнале, скорость проведения потенциала действия, который распространяется вдоль мембраны мышечных волокон. Даже перекрестные помехи от ближайшей мышцы могут вызвать промежуточные факторы.
-
Детерминированные факторы : На них влияют промежуточные факторы. Количество активных двигательных единиц, частота двигательных импульсов и механическое взаимодействие между мышечными волокнами имеют прямое отношение к информации в сигнале ЭМГ и регистрируемой силе.Амплитуда, продолжительность и форма потенциала действия двигательной единицы также могут быть ответственными.
Максимизировать качество сигнала ЭМГ можно следующими способами:
-
Отношение сигнал / шум должно содержать максимально возможное количество информации из сигнала ЭМГ и минимальное количество шумовых помех.
-
Искажение сигнала ЭМГ должно быть минимальным, без ненужной фильтрации, искажения пиков сигнала и режекторных фильтров не рекомендуется.
Во время обработки сигнала ЭМГ анализируются только положительные значения. Когда выполняется полуволновое выпрямление, все отрицательные данные отбрасываются, а положительные данные сохраняются. Абсолютное значение каждой точки данных используется во время двухполупериодного выпрямления. Обычно для выпрямления предпочтительнее двухполупериодное выпрямление.
Обнаружение сигнала ЭМГ
Точное обнаружение дискретных событий в пЭМГ (например, изменение фазы в паттерне активности, связанное с инициированием быстрой двигательной реакции) является важной задачей при анализе двигательной системы.Было предложено несколько методов для определения времени включения и выключения мышцы.
Наиболее распространенный метод определения событий, связанных с двигателем, по сигналам ЭМГ состоит в визуальном осмотре обученными наблюдателями. «Однопороговый метод», который сравнивает сигнал ЭМГ с фиксированным порогом, является наиболее интуитивным и распространенным компьютерным методом определения времени начала мышечной активности (6). Этот метод основан на сравнении выпрямленных необработанных сигналов и порога амплитуды, значение которого зависит от средней мощности фонового шума (7).Этот метод может быть полезен для преодоления некоторых проблем, связанных с визуальным осмотром. Однако такой подход обычно не является удовлетворительным, поскольку результаты измерений сильно зависят от выбора порогового значения. Этот вид метода часто полагается на критерии, которые являются слишком эвристическими и не позволяют пользователю независимо устанавливать вероятности обнаружения и ложной тревоги (8). В «однопороговом методе» соотношение между вероятностью обнаружения P dk и вероятностью P γ того, что выборка шума превышает пороговое значение γ, определяется уравнением 2.
В 1984 году Винтер (9) заметил, что этот подход в целом неудовлетворителен, поскольку он сильно зависит от выбора порога. Чтобы преодолеть «однопороговые» проблемы, Борнато и др. . (8) представили метод «двухпорогового обнаружения» в 1998 году. Двухпороговые детекторы превосходят однопороговые, потому что они дают более высокую вероятность обнаружения. Двухпороговые детекторы позволяют пользователю установить связь между ложной тревогой и вероятностью обнаружения с большей степенью свободы, чем однопороговые.Пользователь может настроить детектор в соответствии с различными оптимальными критериями, таким образом, адаптируя его характеристики к характеристикам каждого конкретного сигнала и приложения (8).
Сигнал пЭМГ, записанный во время произвольных динамических сокращений, можно рассматривать как гауссовский процесс с нулевым средним с (t) εN (0, σ с ) , модулируемый мышечной активностью и искаженный независимой гауссовой добавкой с нулевым средним шум n (t) εN (0, σ n ) . Если вероятность обнаружения равна P d , то метод двойного порога определяется уравнением 3.
Поведение двухпорогового детектора фиксируется параметрами: порог r o и длина окна наблюдения м . Их значения выбраны так, чтобы минимизировать значение вероятности ложной тревоги и максимизировать P d для каждого конкретного отношения сигнал / шум (SNR) (8). В 2004 году Ланьи и Адлер (10) обнаружили, что метод двойного порога, предложенный Борнато, сложен и требует больших вычислительных затрат и требует отбеливания сигнала.Это тоже не очень чувствительно. Ланьи и Энди предложили новый алгоритм, основанный на методе двойного порога, который является более чувствительным, стабильным и эффективным с уменьшенными вычислительными затратами. Для конкретных приложений, помимо точности обнаружения, важным фактором может быть скорость алгоритма. Алгоритмы с большим временем вычисления не подходят для онлайн-обнаружения. Один специфический недостаток метода Борнато и др. . (8) вероятность обнаружения будет максимальной, когда P fa фиксировано, второй порог должен быть выбран равным «1.«Второй порог фиксируется во время обнаружения, что означает, что двухпороговый детектор фактически становится однопороговым детектором. Этот метод не требует этапа отбеливания сигнала, который требовался ранее. Процесс отбеливания занимает много времени вычислений. Кроме того, процесс отбеливания снижает вероятность сигнала. Эта функция приведет к тому, что при обнаружении будет пропущена часть интервала активации. Методы, предложенные Lanyi и Adler (10), обеспечивают быстрое и более надежное обнаружение включения-выключения мышц.В таблице показано сравнение различных методов обнаружения, основанное на исследованиях Мерло и Фарина (11) в 2003 году.
Таблица 1
Сравнение трех основных методов обнаружения ЭМГ.
| SNR (дБ) | |||||||||
| 2 | 4 | 6 | 8 | ||||||
| Метод | Смещение | Std | Смещение | Std | Смещение | Std | Смещение | Std | Замечание |
| Улучшенный метод (11) | -39 | 26 | -22 | 25 | -12 | 22 | -3 | 17 | Порог Best |
| Двойной | 41 | 68 | 21 | 69 | 12 | 47 | 0 | 53 | Хорошо |
| Одиночный порог (11) | 55 | 154 14 | 909135 | 72 | 139 | Хуже | |||
Разложение сигнала ЭМГ
ЭМГ-сигналы представляют собой суперпозицию действий нескольких двигательных единиц.Необходимо разложить сигнал ЭМГ, чтобы выявить механизмы, относящиеся к мышечному и нервному контролю. Были разработаны различные методы разложения ЭМГ.
Декомпозиция сигнала ЭМГ была произведена путем согласования вейвлет-спектра и анализа основных компонентов вейвлет-коэффициентов. Согласно Jianjung et al . (12), потенциал более одной моторной единицы (SMU) будет регистрироваться одновременно, перекрывая друг друга, особенно во время сильного мышечного сокращения.В 1997 году они разработали методику с использованием вейвлет-преобразования для классификации потенциалов SMU и разложения сигналов ЭМГ на составляющие их потенциалы SMU. Отличие этого метода в том, что он измеряет подобие формы волны потенциалов SMU из вейвлет-области, что очень выгодно. Этот метод основан на согласовании спектра в вейвлетной области. Метод согласования спектра иногда считается более эффективным, чем методы согласования формы сигнала, особенно когда помехи вызваны низкочастотным дрейфом базовой линии или высокочастотным шумом.Методика, разработанная для разложения многоэлементного ЭМГ сигнала, состоит из четырех отдельных процедур: процедуры устранения шума, процедуры обнаружения пиков, процедуры классификации пиков и процедуры разделения пиков. Согласно Даниэлю и др. . (13), только вейвлет-коэффициенты более низких частотных диапазонов более важны для дифференциации характеристики потенциала действия (AP), чем более высокие диапазоны. Эта концепция субъективна и разработана эмпирически. Экспериментальные результаты Ри Ямада и др. .(14) в 2003 году показали, что высокочастотная информация, которая не учитывалась, также важна при классификации MUAP. Чтобы преодолеть субъективный критерий выбора характеристик, они предложили другой метод, использующий анализ основных компонентов (PAC) для вейвлет-коэффициентов. Алгоритм декомпозиции состоит из четырех этапов обработки: сегментация, вейвлет-преобразование, PCA и кластеризация. Преимущество этого метода заключается в том, что он не требует ручного выбора коэффициентов и учитывает всю частотную информацию.
Разложение сигнала ЭМГ с использованием оптимизации нелинейных наименьших средних квадратов (LMS) кумулянтов более высокого порядка было предложено Эриком и Дамджаном (15) в 2002 году. Их разложение основано на кумулянтах третьего порядка, значения которых входят в качестве коэффициентов нелинейная система уравнений. Система решена путем нелинейной оптимизации LMS. Для этого метода использовалась модель с множеством входов и множеством выходов, поскольку она может описывать несколько наложений MUAP сигнала ЭМГ.
Обработка сигналов ЭМГ
Raw EMG предлагает нам ценную информацию в особенно бесполезной форме.Эта информация полезна только в том случае, если ее можно определить количественно. К необработанному ЭМГ применяются различные методы обработки сигналов для получения точного и фактического сигнала ЭМГ. В этом разделе дается обзор обработки сигналов ЭМГ с использованием различных методов.
Вейвлет-анализ
В прошлом предпринимались попытки использовать подходы как во временной, так и в частотной области. Вейвлет-преобразование (WT) — это эффективный математический инструмент для локального анализа нестационарных и быстрых переходных сигналов.Одним из основных свойств WT является то, что он может быть реализован с помощью банка фильтров дискретного времени. Преобразования Фурье вейвлетов называются фильтрами WT. WT представляет собой очень подходящий метод для классификации сигналов ЭМГ.
Гульельминотти и Мерлетти (16) предположили, что если вейвлет-анализ выбран так, чтобы соответствовать форме MUAP, полученный WT дает наилучшую возможную локализацию энергии в плоскости шкалы времени (16). В 1997 г. Laterza и Olmo (17) обнаружили, что WT является альтернативой другим частотно-временным представлениям с тем преимуществом, что он является линейным, дает представление с множественным разрешением и не зависит от перекрестных терминов; это особенно актуально при работе с многокомпонентными сигналами.При определенных условиях сигнал ЭМГ можно рассматривать как сумму масштабированных задержанных версий одного прототипа. Основываясь на теории Гульельминотти, Laterza и Olmo (17) использовали вейвлет-анализ, чтобы сопоставить форму MUAP. Для униполярного записанного сигнала и при определенных гипотезах, представленных Габором в 1946 году (18), типичная форма MUAP может быть аппроксимирована как производная второго порядка от гауссова распределения. В результате было предложено использовать хорошо известный вейвлет мексиканской шляпы, который действительно является производной второго порядка от гауссова распределения.Сравнение между вейвлетом мексиканской шляпы и типичной униполярной формой MUAP показано на рисунке. Основываясь на исследовании, Laterza и Olmo пришли к выводу, что WT особенно полезен для обнаружения MUAP в присутствии аддитивного белого шума. В этой ситуации вклад шума распространяется по всей плоскости шкалы времени, независимо от используемого вейвлета. Недостатком этого предложения (17) было то, что вейвлет мексиканской шляпы не идеально соответствовал форме MUAP. Следовательно, полученные результаты, вероятно, будут подлежать дальнейшему улучшению, если будет выполнено идеальное согласование.В 1998 году Исмаил и Асфур (19) выдвинули теорию, согласно которой наиболее распространенным методом, используемым для определения частотного спектра ЭМГ, являются быстрые и краткосрочные преобразования Фурье (БПФ и SFT). Но они также пришли к выводу, что основным недостатком этих методов преобразования является то, что они предполагают, что сигнал является стационарным. Однако сигналы ЭМГ нестационарны.
Сравнение между вейвлетом мексиканской шляпы и типичной униполярной формой MUAP.
В 1999 году Паттихис и Паттихис (20) обнаружили, что WT также может использоваться для анализа сигналов с различными уровнями разрешения.Согласно теории, процесс анализа сигналов с разным уровнем разрешения известен как анализ с несколькими разрешениями. Они проанализировали взаимосвязь между вейвлет-коэффициентами и частотно-временной плоскостью. Алгоритм WT состоит из фазы декомпозиции и фазы реконструкции. Паттихис и Паттихис кратко описывают, как коэффициенты из каждого этапа WT могут быть использованы для построения функционального приближения к исходному сигналу. Данные отсчеты сигнала x 0 , x 1 , x 2 …, соответствующий непрерывный сигнал времени задается уравнением 4:
, где ø (t-k) называется функцией масштабирования. Это предполагает, что выборки сигнала представляют собой средневзвешенные значения непрерывного сигнала.
Снова в 2003 году Кумар и др. . (21) пришли с аналогичным предложением, в котором говорится, что WT разлагает сигнал на несколько компонентов с разным разрешением в соответствии с базовой функцией, называемой «вейвлет-функцией» (WF).WF расширяется и транслируется во времени, обеспечивая двумерную взаимную корреляцию с сигналом sEMG во временной области. Этот метод можно рассматривать как математический микроскоп, который предоставляет инструмент для обнаружения и характеристики кратковременной составляющей в нестационарном сигнале. Это метод, который предоставляет информацию, относящуюся к частотно-временному изменению сигнала. Кумар и др. . также пришел к выводу, что короткое преобразование Фурье (SFT) с относительно короткими временными окнами может пытаться отслеживать спектральные изменения во времени, но не принимает оптимальное разрешение по времени или частоте для нестационарного сигнала.В (21) sEMG была разложена с использованием WT с различными WF, и выходной сигнал области преобразования мощности вычисляется и используется в качестве решающего параметра при выборе WF, который обеспечивает лучший контраст между случаями sEMG. В результате их исследовательской деятельности можно сказать, что с помощью sEMG и вейвлет-преобразований можно определить состояние мышечной усталости (мышечная недостаточность), просто определив вейвлет-разложение Sym4 или Sym5 сигнала на уровне 8 и 9 ( из 10 уровней).На рисунке показана экспериментальная процедура.
Блок-схема методики эксперимента.
Частотно-временной подход
Попытки получить количественную информацию из записей ЭМГ были широко исследованы, когда сигнал представлен как функция времени (временная область). Преобразование класса Коэна, распределение Вигнера-Вилля (WVD) и распределение Чоя-Вильямса — вот некоторые из частотно-временных подходов, используемых для обработки сигналов ЭМГ.
Piper (22) показал в начале этого столетия (1912), что во время длительного сокращения мышц спектральные компоненты поверхностного миоэлектрического сигнала сжимаются в сторону более низких частот. Механизмы, регулирующие это явление, выяснились только за последние два десятилетия. Когда пЭМГ записывается в условиях динамических сокращений, предположение о стационарности не выполняется, потому что частотная составляющая сигнала непрерывно изменяется во времени. Нестационарные состояния поверхностного миоэлектрического сигнала можно разделить на медленные и быстрые.Медленные нестационарные реакции возникают в основном из-за накопления метаболитов, вызывающих электрические проявления мышечной усталости. Быстрые нестационарности в основном связаны с биомеханикой задачи. Вариации мышечной силы вызывают изменение частотной составляющей сигнала.
Преобразование классов Коэна, предложенное Коэном в 1995 г. (23), привлекло значительное внимание, особенно в области обработки биомедицинских сигналов. Класс частотно-временного представления особенно подходит для анализа поверхностных миоэлектрических сигналов, зарегистрированных во время динамических сокращений, которые могут быть смоделированы как реализации нестационарного стохастического процесса.Предыдущие работы Мартина и Фландрина (24), Амина (25) и Сайида и Джонса (26) продемонстрировали, что любой частотно-временной спектр S (t, f) класса Коэна может быть записан как уравнение 5:
, где E {} — оператор математического ожидания, x (t) — реализация рассматриваемого случайного процесса, x * (t) — комплексное сопряжение, g (θ, τ) — ядро трансформации.
Коэн в 1995 г. также пришел к выводу, что при выборе г (θ, τ) = 1, результирующее распределение называется распределением Вигнера-Вилля (23).WVD оптимален для анализа сигналов, состоящих из одного компонента. Однако он не подходит для применения к многокомпонентным сигналам, поскольку билинейность преобразования вызывает присутствие интерференционных членов. Syeed и Jones (26) также продемонстрировали, что формулировка, представленная в уравнении 5, также может быть использована, когда доступна единственная реализация анализируемого стохастического процесса, как в случае обработки поверхностных миоэлектрических сигналов, регистрируемых динамическими сокращениями.
WVD — это время-частота, которая может отображать частоту как функцию времени, таким образом используя всю доступную информацию, содержащуюся в сигнале EMG.Хотя сигнал ЭМГ часто можно рассматривать как квазистационарный, все же передается важная информация, которую можно различить только с помощью WVD. Ricamato и др. . (27) в 1992 году обнаружили, что WVD можно использовать для отображения частотных диапазонов моторного блока. Можно показать закономерности набора по мере того, как мышца выполняет сложные задачи. Распределение Вигнера-Вилля дается уравнением 6:
, где x (t) и x ’(t) — сигнал и его комплексное сопряжение соответственно.
Для реализации WVD с помощью цифрового компьютера требуется дискретная форма. Это позволяет использовать быстрое преобразование Фурье (БПФ), которое дает представление с дискретным временем и дискретной частотой. Распространенным типом частотно-временного распределения является кратковременное преобразование Фурье (STFT). Согласно Дэвису и Райсману (28) (1994), основная трудность с распределением STFT состоит в том, что оно не удовлетворяет четырем важным свойствам, которые требуются для частотно-временных распределений. Два свойства — это предельные значения времени и частоты, а два других — поддержка времени и частоты.Они также сообщают, что общий спектр плотности, создаваемый WVD, очень зашумлен, но демонстрирует очень хорошие свойства локализации и обычно сосредоточен вокруг мгновенной частоты сигнала. Метод Чоя-Вильямса, предложенный в 1993 г., является примером уменьшенного распределения помех (29). Дэвис и Райсман (28) обнаружили, что, хотя распределение Чоя-Вильямса не удовлетворяет всем желаемым свойствам частотно-временного распределения, оно удовлетворяет одному важному критерию, уменьшающему помехи.STFT не удовлетворяет маржинальным свойствам. Этот коэффициент означает, что когда берется временной интервал распределения STFT, он не равен спектру плотности мощности в этот момент времени. То же самое верно и для частотного среза распределения. Свойство поддержки времени не выполняется, потому что распределение не обязательно равно нулю до начала сигнала или после его окончания. Для частотно-временных методов требуется очень чистый сигнал. Есть много других частотно-временных распределений. Дэвис и Райсман (28) выбрали распределения STFT и Вигнера-Вилля, поскольку они широко использовались в прошлом.Согласно их исследованиям, STFT наиболее четко показывает сжатие спектра как мышечную усталость. WVD имеет перекрестные члены и, следовательно, не является точным представлением изменения частотных составляющих при утомлении. Когда в распределении Чоя-Уильяма появляются стены, в исходном сигнале наблюдается всплеск. Он решит, содержат ли стены какую-либо важную информацию для исследования мышечной усталости.
Модель авторегрессии
Модель временных рядов авторегрессии (AR) использовалась для изучения сигнала ЭМГ.Поверхностный электрод улавливает активность ЭМГ от всех активных мышц в непосредственной близости от него, в то время как внутримышечная ЭМГ очень чувствительна, с минимальными перекрестными помехами от соседних мышц. Таким образом, чтобы объединить удобство и точность, существует большая потребность в разработке методики оценки внутримышечной ЭМГ и их спектральных свойств на основе измерения поверхности. Исследователи представили сигнал пЭМГ как модель AR с задержанной внутримышечной ЭМГ в качестве входа.
В 1975 году Грауп и Клайн (30) впервые представили модель авторегрессионного скользящего среднего (ARMA) для представления сигналов ЭМГ.Эмпирический результат Граупа и Клайна показывает, что ЭМГ можно считать стационарной в течение достаточно коротких интервалов времени. Шериф (31) заменил эту модель в 1980 году, поскольку электрическое поведение медицинской дельтовидной мышцы было нестационарным. Шериф в своей диссертации подчеркнул нестационарный характер EMG и использовал AR — представление интегрированного скользящего среднего (ARIMA). Он охарактеризовал нестационарный характер ЭМГ в разные фазы мышечной активности. Doerschuk и др. .В 1983 году (32) подошли к проблеме, подобной Graupe и Cline, а именно к управлению протезами по сигналам ЭМГ с помощью моделей AR множественных сигналов ЭМГ. В 1986 году Чжоу и др. . (33) представили поверхностную ЭМГ как модель AR с задержанным внутримышечным ЭМГ-сигналом в качестве входа. Модель, называемая «тканевым фильтром», связывает форму сигнала внутримышечной ЭМГ с поверхностной ЭМГ. Предполагая, что прототипы внутримышечных и поверхностных сигналов ЭМГ доступны, идентифицируются параметры модели временного ряда, которая преобразует внутримышечные сигналы в сигналы поверхности.Идентифицированная модель затем используется для оценки внутримышечного сигнала по поверхностному сигналу. Эта модель проиллюстрирована с использованием реальных сигналов ЭМГ. Хеффтнер и др. . В 1988 г. (34) оценили предыдущие модели и выбрали модель AR для распознавания сигнатуры ЭМГ из-за ее вычислительной скорости. Бернатос и др. . В 1986 г. (35) использовали статический нелинейный элемент с моделью нестационарного авторегрессионного скользящего среднего (ARMA), а Мозер и Грауп в 1989 г. (36) предложили нестационарный идентификатор изменяющихся во времени параметров AR.В 1992 г. Тору (37) считал, что более точная модель, такая как ARMA или ARIMA, не нужна для динамических движений мышц. Стоимость вычислений модели ARIMA высока, а определение порядка модели является сложным, а иногда и трудным. Модель AR была выбрана Тору (37) в основном из-за ее вычислительной стоимости, которая является проблемой при моделировании. Их исследование было основано на параметрах модели AR, вычисленных с помощью квазистационарной обработки.
Искусственный интеллект
Некоторые методы искусственного интеллекта, в основном основанные на нейронных сетях, были предложены для обработки сигнала ЭМГ.Этот вид техники очень полезен для приложений в реальном времени, таких как запись и анализ сигналов ЭМГ.
Приложение искусственной нейронной сети в реальном времени, которое может точно распознавать миоэлектрический сигнал (MES), было предложено Del и Park (38) в 1994 году. Согласно их исследованиям, MES-характеристики сначала извлекаются с помощью анализа Фурье и группируются с использованием нечетких c-означает алгоритм. Нечеткое c-средство (FCM) — это метод кластеризации, который позволяет данным принадлежать двум или более кластерам.Выходные данные нейронной сети представляют собой степень желаемой мышечной стимуляции по сравнению с синергической, но ослабленной мышцей. Работа в реальном времени достигается за счет использования аппаратных умножителей, присутствующих в процессорах цифровой обработки сигналов (DSP), для выполнения быстрого преобразования Фурье для извлечения признаков и интеграции ввода нейродов для классификации признаков. Адаптивные интерфейсы — это естественный и важный класс приложения для искусственной нейронной сети (ИНС). Метод обратного распространения ошибок используется в качестве процедуры обучения для многослойной нейронной сети с прямой связью.С помощью этой процедуры сеть может научиться сопоставлять набор входов с набором выходов. Выбранная топология сети представляла собой разновидность прямой связи с одним входным слоем, содержащим 64 входных нейрод, один скрытый слой с двумя нейродами и один выходной нейрод (38). Модель с использованием ИНС — это не только прогресс в распознавании сигналов MES в реальном времени, но также она сокращает обучение субъектов до минимума. Архитектура нейронных сетей обеспечивает двойное решение: быстрый способ настройки системы для пациента и лучшее принятие пациентом системы, что снижает скорость принятия устройств.Метод, предложенный Делом и Парком, может решить проблемы (приемлемые критерии стоимости и производительности), которые обычные статистические методы не могут.
Другой подход на основе ИНС был разработан в 1996 году Чероном и др. . (39) с целью разработки альтернативного подхода, основанного на искусственных динамических рекуррентных нейронных сетях (DRNN), для определения взаимосвязи между мышечной ЭМГ-активностью и кинематикой руки. Его цель состояла в том, чтобы доказать, что эта идентификация DRNN является биомеханически правдоподобной.Нейронная сеть состоит из полностью связанных между собой нейроноподобных единиц с двумя типами адаптивных параметров: классическими весами между единицами и постоянными времени, связанными с каждым нейроном. В частности, эта сеть определяет некоторые сложные отношения между ЭМГ мышечной активности и кинематикой верхних конечностей во время сложных движений. Согласно методу, предложенному Перлмуттером в 1989 году, искусственная нейронная сеть представляет собой полностью связанную сеть из 20 нейронов. Метод используется Cheron и др. .(39), что регулируется уравнением 7:
где, y i — уровень активации состояния устройства I, F (α) — функция сжатия F (α) = (1 + e -α ) -1 и x i дается уравнением 8.
Основная особенность предлагаемой DRNN состоит в том, что ее моделируемые движения являются результатом взаимодействия необработанных сигналов ЭМГ без каких-либо теоретических предположений относительно типа управления.Пригодность DRNN в основном обусловлена адаптивными постоянными времени, связанными с каждой нейроноподобной единицей.
Системы нечеткой логики полезны при обработке и классификации биомедицинских сигналов. Биомедицинские сигналы, такие как сигналы ЭМГ, не всегда строго воспроизводимы, а иногда даже могут быть противоречивыми. По данным Чана и др. . Согласно (40), одно из наиболее полезных свойств систем нечеткой логики состоит в том, что противоречия в данных допускаются. Кроме того, используя обучаемые нечеткие системы, можно обнаруживать закономерности в данных, которые нелегко обнаружить другими методами, как это также можно сделать с помощью нейронной сети.Наконец, можно использовать опыт медицинских экспертов. Это неполное, но ценное знание можно интегрировать в систему нечеткой логики благодаря стилю рассуждений системы, аналогичному человеческому. Это значительное преимущество перед искусственной нейронной сетью (ИНС). Системы нечеткой логики более точно имитируют процесс принятия решений, чем ИНС. Ядром нечеткой системы является механизм нечеткого вывода. Знания эксперта или хорошо классифицированные примеры выражаются или передаются в набор «нечетких производственных правил» в форме IF-THEN, что приводит к алгоритмам, описывающим, какое действие или выбор следует предпринять на основе наблюдаемой в настоящее время информации ( 40).
Метод слепого разделения источников (BSS), предложенный в 2001 году Белушрани и др. . (41) — это метод на основе нейронной сети, который разделяет линейную смесь стационарных независимых источников, полученных разными датчиками, с помощью статистических моментов более высокого порядка в алгоритме обучения. В 2004 г. Фарина и др. . (42) обнаружили, что сигналы ЭМГ, генерируемые разными мышцами, могут перекрываться во временной и частотной областях, поэтому классические подходы линейной фильтрации не могут применяться с целью разделения источников.Она сообщила, что предыдущие исследования, направленные на применение подходов BSS к сигналам sEMG, не предоставили никакой проверки производительности и не обсудили предположения и ограничения метода BSS для анализа сигналов sEMG. Чтобы преодолеть эти проблемы, был применен подход, основанный на пространственных частотно-временных распределениях, для разделения как смоделированных, так и экспериментальных нестационарных сигналов sEMG (42). В таблице показаны характеристики диагностики временной области, частотной области и вейвлет-коэффициентов с использованием искусственных нейронных сетей.
Таблица 2
Диагностика производительности временной области, частотной области и вейвлет-коэффициентов с использованием искусственных нейронных сетей.
| Набор функций | Среднее% |
| Временная область | 78,3 |
| Частотная область | 62,5 |
| Вейвлет DAU4 | 66.2 |
| Вейвлет DAU20 | 59,6 |
| Вейвлет CH | 63,3 |
| Вейвлет BL | 65,8 |
Статистика высшего порядка
Статистика высшего порядка (HOS) — это метод анализа и интерпретации характеристик и природы случайного процесса. Предмет HOS основан на теории ожидания (теории вероятностей).Из-за ограничений:
-
Обнаружение и определение характеристик существующих нелинейностей в сигнале sEMG;
-
Оценить фазу; и
-
Точная информация из-за вывода из нормальности. HOS были введены в 1960-х и применялись в 1970-х.
Статистический метод оценки амплитуды и количества новых MUAP был предложен Kanosue et al. . В 1974 г. (43). В методе используются моменты второго и четвертого порядка с параметрической моделью элементарных сигналов MUAP.Модели низкого порядка получаются с использованием статистики второго порядка (SOS) и обеспечивают скупое описание реальных данных. В последнее время наблюдается рост интереса к использованию статистики более высокого порядка (HOS). Статистика высшего порядка (HOS) — это метод анализа и интерпретации характеристик и природы случайного процесса. Предмет HOS основан на теории ожидания (теории вероятностей) (1). В 1991 году Гианнакис и Цацанис (44) использовали HOS для анализа сигналов ЭМГ. Согласно Гианнакису и Цацанису, SOS не зависит от фазы, но имеет оценки с низкой дисперсией и, будучи ограниченными линейно-гауссовскими процессами, дает модели, эффективные с точки зрения вычислений и статистики.В 1995 году Яна и др. . (45) обобщил метод оценки форм сигналов MUAP и их частоты без каких-либо предположений для сигналов MUAP. Этот метод был использован как неинвазивный метод для анализа четвертого производственного механизма мышцы. Согласно его теории, H (w) и λ, соответственно, представляют собой одну форму волны MUAP, а частота ее появления определяется уравнениями 9 и 10.
Согласно уравнению 11, φ (ω) = arg H (ω).φ (ω) оценивается по биспектру с использованием алгоритма оценки фазы. Формы сигналов MUAP можно найти с помощью уравнений (9) — (11). Их исследования показывают, что амплитуда MUAP увеличивается с увеличением веса груза.
С 1987 по 1993 годы такими исследователями, как Никиас, Мендал, Рагхувеер и Петропулу, были разработаны методы анализа сигналов на основе HOS для детерминированных и недетерминированных фазовых сигналов, проверки гауссовости и линейности, когерентности и связи сигнала и т. Д. .В 1990-е годы Никиас и др. . (2, 46, 47) обнаружили, что главное преимущество HOS перед SOS состоит в том, что HOS может подавлять гауссов шум при обнаружении, оценке параметров и классификации. Никиас сообщает, что HOS не видит никаких гауссовских процессов; ненулевое измерение HOS может обеспечить проверку степени негауссовости сигнала. Другой особенностью HOS является то, что спектр HOS суммы двух или более статистически независимых случайных процессов равен сумме их индивидуальных спектров HOS, поэтому HOS может извлекать информацию из-за производной от гауссовости и обеспечивает подходящее измерение степени статистической зависимость во временном ряду.Кроме того, биспектр, первый член спектров HOS, несет информацию об амплитуде и фазе, которая позволяет восстанавливать как величину Фурье, так и значение фазы импульсной характеристики системы с ожиданием линейного фазового члена. В 2000 году Капланис и др. . (48) представили свою теорию анализа сигналов пЭМГ с использованием HOS. Согласно их теории, для количественной оценки негауссовости случайного процесса нормализованный биспектр или бикогерентность оценивается в соответствии с уравнением 12:
где, P (.) — спектр мощности.
Тест на гауссовость основан на средней мощности бикогерентности, определенной в уравнении 13, с суммированием, выполняемым по неизбыточной области.
Индекс бикогерентности использовался для характеристики гауссовости сигнала. Результаты показывают, что распределение сигнала пЭМГ сильно негауссово при низком и высоком уровнях силы, тогда как распределение имеет максимальную гауссовость на среднем уровне максимального уровня произвольного сокращения (MVC).Мера линейности сигнала, основанная на выборе погоды или нет, оценка бикогерентности является постоянной, следует обратной схеме с мерой гауссовости. Средняя частота спектра мощности уменьшается с увеличением силы.
В 2004 году Шахджахан Шахид (1) применил HOS для анализа и характеристики сигналов ЭМГ из-за его преимуществ перед SOS. Он предложил «Биспектр линейной системы ». Моделирование биспектра сигнала временного ряда как выходного сигнала линейной системы позволяет применять полезные методы для идентификации и характеристики системы, которая создает выходной сигнал системы.Пусть e (n) будет стационарным случайным сигналом с нулевым средним, применяемым к системе LTI в соответствии с рисунком, частотная характеристика которого равна H (k) (где отклик системы во временной области h (n) , является причинным и стабильный). Предположим, что w (n) — это независимый одинаково распределенный случайный гауссовский белый шум, который представляет системный шум, а x (n) — это выходной сигнал системы. Согласно теореме свертки для системы LTI выход x (n) может быть записан как уравнение 14.
Модель системы LTI.
С помощью бицепстра можно восстановить систему по ее выходному сигналу после восстановления фазовых компонентов системы. Поскольку выходной сигнал системы LTI несет в себе всю информацию о системе плюс шум, при рассмотрении выходных сигналов системы как негауссовского шума можно оценить импульсную характеристику системы с помощью алгоритма восстановления системы.Могут быть разработаны алгоритмы для характеристики входного импульса системы, чтобы можно было получить фактический сигнал ЭМГ от мышцы. По словам Шахджахана Шахида, традиционные алгоритмы реконструкции системы имеют различные ограничения и значительную вычислительную сложность, а многие демонстрируют высокую дисперсию. Наиболее распространенный алгоритм реконструкции системы на основе биспектра был улучшен путем выделения параметра асимметрии. Кроме того, Шахджахан Шахид разработал кепстр из Bispectrum — новую ветвь кепстра — для выполнения реконструкции импульсной функции системы простым в вычислительном отношении способом.Разработанный алгоритм показывает лучшую производительность, чем традиционные алгоритмы. Кепстр биспектра также используется для разработки алгоритма восстановления последовательности входных импульсов системы из выходного сигнала системы LTI. Результаты показали, что ЭМГ покоящихся мышц содержит серию импульсных ПДЕ, пики которых ориентированы по обе стороны от нулевого уровня. Это означает, что в покоящейся мышце не задействованы двигательные единицы. С другой стороны, MUAP обычно ориентированы на одну сторону от нулевого уровня, когда мышца сокращается.На рисунке показан образец необработанного сигнала ЭМГ и его биспектральная кривая.
Пример сигнала ЭМГ и его биспектральной кривой.
Другие методы
Существуют и другие модели, предложенные различными исследователями для обработки сигналов ЭМГ. Некоторые из этих моделей кратко описаны здесь.
В 1969 году Розенфальк (49) математически сформулировал g (z) = 96x 3 e -z -90 на основе экспериментальных работ Людина на межреберных мышцах.Нандедкар и Стальберг (50) изменили выражение в 1983 году с g (z) до e (z) = g (2z) , чтобы соответствовать лучшим экспериментальным данным, что привело к e (z) = 768z 3. e -2z — 90. Это принято в качестве внутриклеточного состава по умолчанию для моделирования потенциала действия одного волокна.
Нандердар и Баркхаус (51) предложили в 1992 г. модель, основанную на простом принципе векторного суммирования. Согласно теории Slawnych, Laszlo и Hershler (1990), модель Nandedkar предполагает, что амплитуда MUAP алгебраически складывается для генерации амплитуды комплексного мышечного протенциала (CAMP).Поскольку формы сигналов MUAP не возникают синхронно, это предположение неверно. Если суммировать два MUAP с амплитудой A 1 и A 2 , то амплитуда полученного сигнала не равна A 1 + A 2 . Другими словами, вклад MUAP в амплитуду CMAP меньше, чем его амплитуда, это явление называется подавлением фазы. Согласно (51) амплитуда их суммы обозначена как A 12 ниже A 1+ A 2 .Это выражается в уравнении 15.
В 1994 г. , Энглхарт и Паркер (52) рассмотрели два типа моделей функции плотности вероятности (pdf) с межимпульсным интервалом (IPI). Последовательность разряда в виде серии IPI, оценка среднего IPI, дисперсия и функция плотности вероятности (pdf) использовались в качестве дескрипторов активности двигательных нейронов. Функция плотности Гаусса выражается уравнением 16:
, где μ x — среднее значение, а σ x 2 — дисперсия.
Функция плотности гамма выражается уравнением 17:
где α — параметр местоположения, β — параметр масштаба, ρ — параметр формы, а Γ () — гамма-функция.
Согласно модели, оценки моментов и pdf последовательности нейронных разрядов подвержены смещению, если данные нестационарны. Некоторые факторы, которые могут повлиять на степень стационарности экспериментальных данных IPI, — это продолжительность сокращения, средства создания силы и уровень сокращения.
Аналитическое выражение для миоэлектрического сигнала было получено с использованием модели интегральной частоты импульса и амплитудной модуляции (IPFAM) Zhang et al . (53) в 1995 г. Модель состоит из трех основных элементов: амплитудно-импульсной модуляции (PAM), частотно-импульсной модуляции (PFM) и линейной системы. PAM описывает связь амплитуды ЭМГ с вариациями мышечной силы, PFM описывает вариации сигнала ЭМГ, вызванные изменениями скорости нервных импульсов и линейной системы, p (t), представляет собой сложное действие двигательных единиц. потенциал, включая эффекты рассеивания распространения и тканевой фильтрации.В этой модели потенциал возрастает до тех пор, пока не будет достигнут заранее установленный порог, что вызывает возникновение потенциала действия или события. Таким образом, модель IPFAM включает в себя наиболее важные функции, связанные с генерацией реальных сигналов ЭМГ.
Система реального времени для анализа сигналов ЭМГ была создана Карлссоном и Нистромом в 1995 г. (54). Целью было разработать систему для клинического использования с характеристиками графической обратной связи, гибким выбором параметров, стандартным методом и гибкой обработкой добавления.Для получения частотно-временного представления сигнала было предложено использовать кратковременное преобразование Фурье. Основным недостатком этого метода было то, что предполагался стационарный сигнал. Даже когда нет произвольного изменения состояния мышц, миоэлектрические сигналы нестационарны просто из-за внутренней физиологии органов.
Модель EMG предложена Duchene и Hogrel (55) в 2000 году. Согласно Duchene и Hogrel, любой новый алгоритм обработки должен быть оптимизирован путем сравнения его результата с исходными значениями параметров, чтобы получить оптимизированный критерий.Эта оптимизация может быть проведена только в том случае, если известны все фактические значения. Только комплексная имитационная модель может помочь выполнить это требование. Потенциал внеклеточного действия рассчитывается после потенциала внутриклеточного действия для моделирования потенциала действия одного волокна. Согласно первоначальной работе де Лоренте (56), потенциал в точке наблюдения [z 0 , y 0 ] можно выразить уравнением 18:
, где z и y — осевое и радиальное направления соответственно, S1 и S2 — участки волокна на концах волокна и r — расстояние между элементами поверхности dS и точка наблюдения.
Гамильтон и Сташук (57) предложили новейшее моделирование клинических сигналов ЭМГ в 2005 году. Согласно предложению, первое требование для моделирования сигналов ЭМГ — создание модели структуры мышцы. Это выполняется в следующие этапы:
-
Расчет диаметра территории мышечно-двигательной единицы;
-
MY территориальное расположение центра;
-
Схема и назначение оптоволокна;
-
Обновление территориальных центров МО;
-
Расчет фактических территориальных центров МО;
-
Назначение диаметров волокна; и
-
Назначение расположения нервно-мышечных соединений.
Эта модель уникальна, поскольку включает в себя следующее:
-
Пространственное соотношение между мышечными волокнами, MU, которые они составляют, и морфологией мышц на макроуровне;
-
Расчеты MUP, объединяющие клинические измерения кончика иглы и обнаруженных канюлей напряжений, вносимых физиологически позиционированными и активированными отдельными волокнами;
-
Изменчивость обнаруженных MUAP из-за изменчивости задержки передачи NMJ;
-
Новый механизм рекрутирования MU, полностью основанный на морфологии мышц; и
-
Клинически реалистичное размещение иглы.
Классификация сигналов ЭМГ
Общей чертой для классификации внутримышечного сигнала ЭМГ является евклидово расстояние между формами волны MUAP. Для клинических интересов основной характеристикой сигнала ЭМГ является количество активных двигательных единиц (MU), формы волны MUAP и статистика времени иннервации. Согласно Wellig и Moschytz (58), определение формы волны MUAP и количества активных MU можно рассматривать как проблему классификации.
Представление синхронизированных по времени и неперекрывающихся MUAP создает мерцание. На мерцание MUAP влияет временной сдвиг дискретизированных сигналов, локальные колебания базовой линии и фоновый шум. На мерцание MUAP также могут влиять все шумы, которые отличаются как от фонового шума, так и от шума, вызванного смещениями. Помимо фонового шума и эффектов смещения, на классификацию влияет белый шум. Если классификация должна выполняться в области вейвлета, следует избегать использования вейвлет-коэффициентов, которые относятся к полосам частот, лежащим ниже 150 Гц.Классификация с вейвлет-коэффициентом требует вейвлет-коэффициента ( F f [m, n] ) для четырех полос частот ( m = 2, 3, 4, 5 ). Эффективность классификации зависит не только от мерцания MUAP от дисперсии внутри класса, но и от расстояния между средними классами. Следовательно, лучший выбор этих четырех частотных диапазонов зависит от преобразования Фурье самих сигналов MUAP. Буалем и Питер (59) предположили, что частотно-временное представление WVD обеспечивает характеристику сигнала с высоким разрешением в частотно-временном пространстве и хорошие характеристики подавления шума.Эта теория может быть очень полезна для классификации сигналов ЭМГ. Для классификации паттернов ЭМГ используется параметрическая модель AR. В 1991 году Чжан и др. . (60) извлекли и сравнили два типа характеристик на основе обработки сигналов с целью классификации паттернов ЭМГ. Двумя характеристиками были коэффициенты параметрических моделей AR и компоненты частотных спектров Фурье. Метод показал лучшие результаты при описании линейных огибающих (LE) ЭМГ.
В 1995 году Христодулу и Паттихис (61) предложили, чтобы процедура классификации с использованием ИНС проводилась в три этапа:
-
На первом этапе применяется обучение без учителя на основе одномерной самоорганизующейся карты признаков и конкурентного обучения.
-
На втором этапе, чтобы улучшить характеристики классификации, применяется метод обучения с самоконтролем, квантование вектора обучения.
-
На третьем этапе происходит фактическая классификация.
Классификация реальных данных ЭМГ на их составляющие Потенциал действия двигательного блока часто является сложной задачей из-за изменчивости формы сигнала MUAP, дрожания потенциалов одиночного волокна и суперпозиции MUPA.Согласно Христодулу и Паттичису, ИНС представляется привлекательной для решения такой проблемы из-за их способности принимать и создавать сложные границы классификации. На рисунке 6 показана стратегия классификации ЭМГ с использованием подхода ИНС.
Стратегия классификации ЭМГ с использованием подхода ИНС.
DRNN, предложенный Чаном и др. . (40) гораздо более адаптируется к временной обработке, чем классическая сеть прямой связи, которая больше предназначена для задач классификации.Их результат показывает, что он успешно идентифицирует сложное отображение между двухполупериодными выпрямленными сигналами ЭМГ и траекторией верхних конечностей. Процесс обучения и результаты классификации метода нечеткой логики Черона и др. . (39) превосходят подходы на основе нейронных сетей; прежде всего в том, что нечеткая система дает более последовательные результаты классификации и нечувствительна к перетренированию. Типичная точность классификации ЭМГ приведена в таблице.
Таблица 3
Типичный уровень точности классификации ЭМГ.
| Метод | Кучность |
| Коэффициенты AR | 99% |
| Нейронные сети | 84% |
| Нечеткая система | 85% |
Оценка количества моторных агрегатов (MUNE)
Точная оценка шаблонов MUAP при наличии фоновой активности ЭМГ и шума приборов является важным требованием количественного клинического анализа ЭМГ, особенно если используется декомпозиция сигнала ЭМГ.MUNE — это процедура, используемая для оценки количества моторных аксонов, подключенных к мышце. Все методы MUNE основаны на предположениях, которые должны быть выполнены для получения достоверной оценки.
В 1971 году МакКомас предложил простой нейрофизиологический метод оценки количества двигательных единиц в мышце (62). Максимальный биоэлектрический ответ мышцы регистрировали с помощью пЭМГ после сверхмаксимальной электрической стимуляции нерва мышцы. Затем максимальный отклик ЭМГ был разделен на оценку среднего отклика одной двигательной единицы.Результатом была оценка количества ответов отдельных двигательных единиц, которые составили максимальный ответ ЭМГ.
По данным Сташука и др. . (63) количество двигательных единиц в мышце можно оценить путем деления значений параметров, связанных с размером, измеренных от максимальной М-волны, на соответствующие значения параметров, измеренные на основе среднего потенциала действия двигательных единиц, обнаруживаемого на поверхности (S-MUAP). Точность оценки зависит от того, насколько репрезентативен средний S-MUAP для популяции S-MUAP, которые внесли вклад в максимальную M-волну.Было показано, что ответы F-Wave представляют полный диапазон размеров S-MUAP. Была разработана автоматизированная система для получения максимальной M-волны, для извлечения выборки ответов F-волны, для вычисления среднего S-MUAP и для оценки количества MU в мышце.
В 1998 г. Zhengquan Xu и Shaojun Xiao (64) представили метод оценки среднего и стандартного отклонения межимпульсных интервалов (IPI) отдельных последовательностей MUAP. Посредством взвешенного соответствия между наблюдаемой функцией плотности вероятности IPI и смоделированной функцией оцениваются параметры срабатывания.Взвешенная функция используется для аппроксимации достоверности данных IPI, чтобы вся достоверная информация, предоставляемая данными IPI, использовалась в максимально возможной степени. По этой причине метод может обеспечить надежные оценки, даже если поезда MUAP извлекаются со значительными ошибками. Таким образом, этот метод очень полезен для оценки статистики стрельбы наземной ЭМГ, когда отдельные поезда MUAP трудно точно идентифицировать.
Учитывая, что MUAP возникает на некотором расстоянии ниже стандартного электрода sEMG, основные формы поверхностных MUAP в идеале могут быть представлены только очень небольшим количеством форм сигналов или вейвлет-функций.Основываясь на этом определении, Ping и Rymer (65) в 2003 году оценили способы оценки количества MUAP, присутствующих в стандартных записях поверхностной ЭМГ, с использованием методов сопоставления на основе вейвлетов для идентификации случаев MUAP. Причина этого подхода заключается в том, что оценки количества MUAP, вероятно, будут более точным отражением нейронной команды для мышцы. Методы согласования вейвлетов с использованием еще более селективного поверхностного электрода могут правильно оценить количество MUAP в сигналах поверхностной ЭМГ при более высоких уровнях силы.Однако максимальное количество MUAP, правильно оцененное в поверхностной ЭМГ, не может быть значительно увеличено.
Недавно, в 2005 году, Major и Jones (66) использовали эту модель для моделирования четырех техник MUNE (инкрементная стимуляция, пересмотренная инкрементальная стимуляция, многоточечная стимуляция и усреднение с запуском спайков) и сравнили надежность каждого из них. Они также сравнили относительную полезность использования ЭМГ по сравнению с силой в качестве измерения выходной мощности мышцы. Использование моделей позволяет детально протестировать методологические допущения в различных техниках MUNE, что приведет к более точному и надежному методу выполнения MUNE.Это приведет к более ранней диагностике и улучшенной оценке лечения пациентов с нервно-мышечными заболеваниями. Основной принцип, лежащий в основе четырех методов MUNE, которые они моделировали, — это деление общего мышечного ответа на расчетный средний ответ одиночной двигательной единицы (SMUP). Мышечные реакции можно измерить с помощью ЭМГ или силы. Поверхностный ЭМГ-ответ нескольких двигательных единиц на электрический стимул, приложенный к нерву, известен как составной потенциал действия мышцы (CMAP). Таким образом, расчетное количество функциональных двигательных единиц в мышце (или группе мышц) определяется уравнением 19.
Аппаратные модели
В связи с передовым развитием биомедицинской науки применение биомедицинских инструментов становится важным в повседневной жизни. В последнее время большое значение приобретает разработка специализированных интегральных схем для биомедицинских инструментов. Для разработки протезов рук для людей с ограниченными возможностями внедрено различное оборудование. Аппаратные микросхемы также были разработаны для фильтрации сигнала ЭМГ для получения точного сигнала для управления протезом руки и других приложений, таких как распознавание захвата и взаимодействие человека с компьютером.
Микропроцессорная система для идентификации миоэлектрического сигнала, предложенная Граупе и др. . (67) основан на микропроцессоре 8080 Intel Corporation, который представляет собой 8-битный параллельный центральный процессор. Он изготовлен на одной микросхеме крупномасштабной интеграции (LSI) с использованием N-канальных кремниевых затворов и представлен в 40-контактном двухрядном керамическом корпусе, имеющем время инструкции 2 мкс. Затем микропроцессор сопрягается со своими портами ввода-вывода и с полупроводниковой памятью размером 4 Кбайт.Кроме того, для увеличения скорости микропроцессор сопряжен с блоком аппаратного умножения на основе модулей умножителя 4×2 бит Fairchild 9344, где время умножения составляет 350 нс против 1 мкс в самом микропроцессоре.
Микросхема аналогового процессора может быть разработана для обработки физиологических сигналов. Поскольку сигнал ЭМГ имеет характеристики очень низкой амплитуды напряжения и несет в себе низкочастотный синфазный шум, Yen et al . (68) интегрировали инструментальный усилитель, каскад регулировки усиления и фильтры в микросхему для обработки сигнала ЭМГ с получением соответствующей амплитуды и ограниченной полосы пропускания.Он разделен на три части: блок обработки аналоговых сигналов, блок беспроводной передачи данных и блок цифровой обработки. Их исследования были сосредоточены на конструкции системы передачи. Благодаря концепции системы на кристалле, микросхема достигла целей низкой стоимости, низкого энергопотребления и минимизации площади компоновки.
Для улучшения жизни людей, потерявших руку, протезы рук существуют уже давно. Чип Evolvable Hardware (EHW) был реализован для применения в миоэлектрических протезах руки.Чип EHW для автономного мобильного робота и миоэлектрической искусственной руки был также разработан в апреле 1998 года, чтобы служить готовым устройством для оценки аппаратного обеспечения на уровне ворот. Чип состоит из трех компонентов: 1) PLA; 2) аппаратные средства GA с памятью хромосом 2K слов и памятью обучающих шаблонов 2K слов; и 3) 16-битное ядро ЦП 33 МГц (NEC V30; совместимость с 8086). Произвольные логические схемы можно динамически реконфигурировать на компоненте PLA в соответствии с хромосомами, полученными аппаратным обеспечением GA.Ядро ЦП взаимодействует со средой микросхемы и при необходимости поддерживает расчет пригодности. Размер аппаратного обеспечения GA, без учета памяти, составляет около 16K гейтов. Что касается размера ворот, это почти одна десятая от 32-разрядного ядра процессора (например, NEC V830). Однако генетические операции, выполняемые этим чипом, в 62 раза быстрее, чем на Sun Ultra2 (200 МГц). Чип реализован Kajitani et al . В 1999 (69) состоит из аппаратного обеспечения GA (генетического алгоритма), реконфигурируемой аппаратной логики, памяти хромосом, памяти обучающих данных и 16-битного ядра процессора (NEC V30).Миоэлектрические протезы рук управляются сигналами, генерируемыми мышечными движениями. Предлагаемая микросхема EHW состоит из семи функциональных блоков, блока GA, блока PLA (2 массива), центрального процессора, файла регистров, генератора случайных чисел, памяти хромосом и памяти обучающих данных. Рабочий процесс микросхемы EHW можно разделить на два этапа. Первый этап — это создание двух детей и этап оценки, а второй этап — этап «выбора двух хромосом». GA адаптивно реализует схему на PLA в контроллере EHW.
В 2001 году Торресен описал двухэтапную инкрементную оценку контроллера протеза руки, для которого требуется ЦП с плавающей запятой или микросхема нейронной сети (70). Используя EHW на уровне ворот, можно обеспечить гораздо более компактное исполнение, что делает его более удобным для установки внутри протеза руки. Такой сложный контроллер, вероятно, можно было бы спроектировать только путем адаптации контроллера к каждому конкретному пользователю. Он состоит из ворот И, за которыми следуют ворота ИЛИ. Одна из основных проблем в развитии аппаратной системы заключается в том, что, по-видимому, существует ограничение на длину строки хромосомы.Для представления сложной системы обычно требуется длинная строка. По мере увеличения строки генетическим алгоритмам (ГА) требуется большое количество поколений. Основное преимущество метода заключается в том, что эволюция не выполняется за одну операцию над всем изменяемым аппаратным блоком; вместо этого он выполняется снизу вверх. Архитектура контроллера протеза руки, основанная на цифровых воротах, показана на рисунке. . Он состоит из одной подсистемы для каждого из шести движений протеза.В каждой подсистеме двоичные входы x 0 . . . x 15 обрабатываются несколькими разными блоками, начиная с блока И-ИЛИ. Это слой вентилей И, за которым следует слой логических элементов ИЛИ. Каждый вентиль имеет одинаковое количество входов, и их можно выбрать два, три или четыре. Выходы логических элементов ИЛИ направляются в Селектор. Этот блок выбирает, какие из этих выходов будут подсчитаны последующим счетчиком. То есть для каждого нового входа счетчик считает, что количество выбранных выходов равно «1» из соответствующего блока И-ИЛИ.Наконец, детектор максимума выводит счетчик, соответствующий одному конкретному движению, имеющему наибольшее значение. Каждый выход датчика Max Detector подключен к соответствующему двигателю протеза. Если счетчик, имеющий наибольшее значение, соответствует правильному движению руки, вход был правильно классифицирован.
Архитектура контроллера протеза руки, основанная на цифровых воротах.
В ЭМГ-сигнале от электрически стимулированной мышцы обычно существуют два типа артефактов: артефакты стимуляции и M-волна.В 2000 году Писгуд и его исследователи (71) предположили, что М-волна является стационарной, и поэтому использовали фиксированный гребенчатый фильтр. Но M-волна, несомненно, является нестационарным сигналом в статистическом смысле, в основном из-за того, что ее временные изменения зависят от многих факторов, таких как интенсивность стимуляции, утомляемость, уровень сокращения мышцы и т. Д. Адаптивный прогноз. фильтр ошибок (PEF), основанный на алгоритме Грама-Шмидта (GS), представлен в 2004 г. Yeom et al . (72) для подавления М-волн.Представленный фильтр реализован на программируемой вентильной матрице (FPGA). Реализация выполняется с использованием 6 PEF -го порядка GS с использованием микросхемы FPGA Xilinx XC2S200pq208-6. Дизайн был синтезирован с использованием Xilinx ISE 5.2i и проверен с помощью ModelSim XE 5.6a. Одним из основных преимуществ аппаратного разделения вычислений корреляции и фильтрации является то, что система фильтрации не связана со сложным конечным автоматом. На рисунке показана схема основного процессора, реализованного на ПЛИС.М-волны должны быть удалены, чтобы использовать произвольную ЭМГ от электрически стимулированной мышцы. Предлагаемая система подавления M-волн, основанная на GS PEF, не только эффективна для устранения периодических сигналов, таких как M-волны, но также подходит для реализаций FPGA, чем традиционный линейный PEF (72).
Схема блока обработки ядра, реализованного на ПЛИС.
Приложения EMG
ЭМГ-сигналы могут использоваться для различных приложений, таких как клинические / биомедицинские приложения, разработка микросхем EHW, взаимодействие человека с машиной и т. Д.Клиническое применение ЭМГ в качестве диагностического инструмента может включать нервно-мышечные заболевания, оценку боли в пояснице, кинезиологию и нарушения моторного контроля. Сигналы ЭМГ могут быть использованы для разработки чипа EHW для управления протезами руки. Распознавание захвата (73) — это усовершенствованное приложение для управления протезом руки.
ЭМГ можно использовать для определения изометрической мышечной активности (типа мышечной активности, которая не переводится в движение). Эта функция позволяет определить класс незаметных неподвижных жестов для управления интерфейсом незаметно и без нарушения окружающей среды.Устройство для этой цели включает в себя усилитель с высоким входным сопротивлением, подключенный к электродам, фильтр сглаживания, микроконтроллер для выборки и обработки сигнала ЭМГ и модуль связи Bluetooth для передачи результатов обработки. При обнаружении активации контроллер отправляет сигнал по беспроводной сети на основной носимый процессор, например на мобильный телефон или КПК. Используя EMG, пользователь может тонко реагировать на сигналы, не нарушая своего окружения и не касаясь интерфейса руками.Контроллер EMG не занимает рук пользователя и не требует от него работы; следовательно, это « без помощи рук » (74).
Интерактивные компьютерные игры предлагают еще одно интересное применение интерфейсов на основе биосигналов. Игровая система будет иметь доступ к сигналам частоты пульса, гальванической реакции кожи и движению глаз, чтобы игра могла реагировать на эмоциональное состояние игрока или угадывать его или ее уровень осведомленности о ситуации, отслеживая движения глаз. Интерактивный игровой персонаж может реагировать на пользователя, который смотрит или смотрит вокруг, в зависимости от обстоятельств.Такое использование отслеживания взгляда проще, чем использование глаз в качестве точного указательного устройства, что затруднительно, поскольку глаза постоянно исследуют окружающую среду и не обеспечивают стабильной точки отсчета для указателя на экране. Чтобы обеспечить больше удовольствия и стратегии, в файтингах обычно возможны два стиля атаки. Один из них — слабая атака, а другой — сильная атака. Обычными устройствами ввода для боевых действий являются джойстик и джойстик . Они используют палку для перемещения персонажа и кнопку для выполнения определенного типа атаки, например, удара кулаком или ногой.Чтобы совершить сильную атаку, пользователь должен ввести сложную последовательность клавиш, которая затрудняет выполнение этого движения, тем самым достигая баланса между двумя типами атаки. Хотя эти устройства дешевы и просты в использовании, у них есть недостатки. Эти интерфейсы не интуитивно понятны для управления движением человека во время боя, и пользователю нужно многое запомнить, например, значение кнопки и последовательность ввода для сильного атакующего движения. Устройство интерфейса «человек-компьютер», предназначенное для игры в жанре файтинг « Muscleman» , было разработано Д.Г. Пак и Х. К. Ким в Корее. Игровые персонажи обычно изображаются в изометрическом сжатии рук, что выражает концентрацию силы, чтобы совершить сильную атаку, как огненный шар (75).
Для измерения силы изометрического сокращения мышц использовалась поверхностная ЭМГ. Кроме того, для получения более точной информации о движении предплечья пользователя в игровой системе установлен акселерометр. Анализируя запись данных об ускорении, полученную от акселерометра, можно узнать, в каком направлении движется предплечье.Кроме того, возможна классификация атакующего движения в таких случаях, как то, было ли движение прямым ударом или движением верхнего удара. Беспроводная передача используется, чтобы не мешать движению пользователя. Приняв беспроводную передачу, этап игры может быть увеличен практически без ограничений в пространстве. На рисунке показана блок-схема системы « Muscleman».
Блок-схема системы «Muscleman».
В Центре исследований вооружений НАСА в Моффетт-Филд, Калифорния, расширение Human Senses Group использует интерфейсы систем биоконтроля.Они использовали сигнал ЭМГ / ЭЭГ в своей программе исследований взаимодействия человека с летными системами. Группа стремится продвигать человеко-машинные интерфейсы, напрямую подключая человека к компьютеру через электрическую нервную систему человека. Это исследование, основанное на сигналах ЭМГ и ЭЭГ, применяет систему распознавания образов для интерпретации этих сигналов как команд компьютерного управления. Эти исследователи НАСА использовали сигнал ЭМГ, чтобы заменить механические джойстики и клавиатуры. В качестве примера они разработали метод пилотирования высокоточного имитатора полета транспортного самолета с использованием джойстика на основе ЭМГ.На рисунке показано управление полетом с использованием технологии EMG. Виртуальный джойстик приводился в действие через повязку, имплантированную с восемью электродами, подключенными к датчикам, когда пилот жестом приземлял самолет. Пилот также мог совершить аварийную посадку моделируемого самолета, который был поврежден. Чарльз Йоргенсен, глава лаборатории нейроинженерии Эймса НАСА, утверждает, что это принципиально новый способ общения с машинами. Его исследовательская группа отходит от идеи управления машинами с помощью рычагов и ручек.Вместо этого они планируют, чтобы машины реагировали непосредственно на человеческие жесты. Помимо управления самолетом, эта технология может также помочь астронавтам в громоздких скафандрах управлять электроинструментами, используемыми для работы вне космического корабля, например, при ремонте или строительстве. Более амбициозная идея для реконфигурируемых самолетов и другой транспортной техники — виртуальная носимая кабина или командный центр. Военно-воздушные силы США и другие военные подразделения все чаще используют беспилотные автомобили для миссий по наблюдению.Одним из способов управления этими системами с места является носимая кабина. Можно использовать носимый компьютер с беспроводной связью и защитными очками, а затем использовать жесты на основе ЭМГ для управления переключателями и ручками управления, необходимыми для полета. Бесконтактные датчики ЭМГ, вшитые в полевую униформу, могли затем определять движения, когда действующий пилот делал вид, что манипулирует управляющими сигналами. Космическое приложение могло позволять космонавтам набирать текст на компьютере, несмотря на то, что его ограничивал скафандр. Если во время долгосрочной космической миссии произошла авария с разгерметизацией, и астронавтам потребовался доступ к бортовым компьютерам, они могли бы использовать электроды ЭМГ в своих скафандрах для имитации компьютерного интерфейса (76).
Распознавание глухой речи — Mime Speech Recognition — распознает речь, наблюдая за мышцами, связанными с речью. Он основан не на голосовых сигналах, а на ЭМГ. Он будет реализовывать беззвучное общение, что является новым стилем общения. Поскольку голосовые сигналы не используются, его можно применять в шумной среде; он может поддерживать людей без голосовых связок и людей с афазией (77).
Связь с компьютером посредством определенных мышечных сокращений позволит выполнять все виды управляемых компьютером действий с помощью ЭМГ.Сокращения мышц могут быть надежно обнаружены, почти нечувствительны к любому виду шума, поэтому интерфейсное устройство, основанное на мышечном тонусе, также может использоваться для управления движущимися объектами, такими как мобильные роботы или электрическое кресло-коляска, что может быть большим подспорьем. для людей с ограниченными возможностями. Конечно, это могло бы стать альтернативой для здоровых людей, а также для управления домашними развлекательными устройствами. Постоянный поток сигналов ЭМГ, связанных с любой произвольной мышцей водителя-коляски, отслеживается и сводится к потоку сокращений.Уменьшенный поток влияет на внутреннее состояние программы, которое преобразуется в соответствующие команды, понятные электронике кресла-коляски. Стандартный способ управления электрическим инвалидным креслом включает использование одной руки для управления каким-то двумерным джойстиком.
Обсуждение
Исследование показывает, что двухпороговые детекторы лучше однопороговых из-за их более высокой вероятности обнаружения. Они также позволяют пользователю установить связь между ложной тревогой и вероятностью обнаружения с большей степенью свободы, чем однопороговые.Разложение сигнала ЭМГ путем согласования вейвлет-спектра показывает, что этот метод точен, надежен и быстр. Этот метод очень полезен при изучении механизмов управления моторикой на уровне SMU. С другой стороны, нелинейный метод декомпозиции оптимизации LMS на основе HOS также надежен в бесшумном случае. Тестирование с различными уровнями аддитивного гауссовского шума показало, что хорошо известная устойчивость HOS приводит к удовлетворительным результатам также в шумной среде. Для обработки сигналов EMG WT является альтернативой другим частотно-временным представлениям.Преимущество WT состоит в том, что он линейный, что дает представление с несколькими разрешениями. Кросстермы не влияют на WT при работе с многокомпонентными сигналами. Мы видим, что основным недостатком SFT является то, что предполагается наличие стационарного сигнала. Спектр совместной плотности, полученный с помощью распределения Вигнера-Вилля, демонстрирует очень хорошие свойства локализации и, как правило, сосредоточен вокруг мгновенной частоты сигнала. Недостаток WVD в том, что он очень шумный. Хотя Чой-Вильямс снижает помехи, он не удовлетворяет всем другим желаемым свойствам частотно-временного распределения.Изучая свойства систем нечеткой логики, мы обнаруживаем, что противоречия в данных допускаются, что является преимуществом. Также ясно, что с помощью обучаемых нечетких систем можно обнаруживать закономерности в данных, которые нелегко обнаружить другими методами, как это также можно сделать с помощью нейронной сети. В результате системы нечеткой логики более точно имитируют процесс принятия решений, чем ИНС. Статистические методы высшего порядка (HOS) используются для анализа сигнала ЭМГ. Это возможно благодаря уникальным свойствам HOS, которые можно применять к случайным временным рядам.Исследование показывает, что гауссов шум можно подавить с помощью биспектра или спектра третьего порядка. Более того, он несет информацию как об амплитуде, так и о фазе, которую можно использовать для восстановления импульсной функции системы и входной импульсной последовательности из линейного не зависящего от времени (LTI) выходного сигнала системы. Основное преимущество HOS перед SOS заключается в том, что HOS может подавлять гауссов шум при обнаружении, оценке параметров и проблемах классификации. Поскольку HOS не учитывает какой-либо гауссовский процесс, ненулевое измерение HOS может обеспечить проверку степени негауссовости сигнала.Сводка основных методов приведена в таблице.
Таблица 4
Краткое изложение основных методов.
| Метод | Преимущество / Недостаток |
| Двухпороговое обнаружение |
|
| Вейвлет-преобразование |
|
| Распределение Вигнера-Вилля |
|
| Метод Чоя-Вильямса | |
| Искусственные нейронные сети (ИНС) |
|
| Нечеткая логика |
|
| Статистика высшего порядка (HOS) |
|
Если требуется количественное соотношение между сигналом ЭМГ и силой, то сокращение должно быть изометрическим. Однако даже при этом ограничении связь между силой и сигналом ЭМГ остается проблематичной. Принято считать, что, когда сигнал ЭМГ достаточно сглажен, взаимосвязь является монотонной, но линейность, по-видимому, различается для разных мышц (при условии, что нет технических и других мешающих факторов, таких как перекрестные помехи).Однако, поскольку амплитуда сигнала поверхностной ЭМГ является случайной величиной, мгновенное значение амплитуды не является монотонным по отношению к значению силы. Кроме того, оценка амплитуды сигнала будет изменяться в зависимости от силы из-за внутренних анатомических и физиологических факторов. На рисунке показано соотношение силы и сигнала ЭМГ.
Соотношение нормализованной силы и сигнала ЭМГ для трех разных мышц.Данные были сильно сглажены с шириной окна 2 с.Обратите внимание на разницу в линейности взаимоотношений между мышцами (78).
Физиологи привыкли использовать выходное усилие мышцы в качестве показателя мышечного утомления. В частности, точка, в которой сокращение больше не может поддерживаться (точка отказа), обычно обозначается как точка, в которой мышца утомляется. Этот подход подразумевает, что утомление возникает в определенный момент времени; понятие, которое несовместимо с концепцией усталости, принятой инженерами и учеными-физиками.На рисунке показан сигнал ЭМГ в виде индекса усталости.
Схематическое объяснение спектральной модификации, которая происходит в сигнале ЭМГ во время длительных сокращений.Индекс мышечной усталости представлен средней частотой спектра (78).
При рассмотрении аппаратных реализаций мы понимаем, что, хотя реконфигурируемые аппаратные устройства, такие как FPGA и PLD, быстро распространяются, а полезность реконфигурируемого оборудования получает все большее признание, реконфигурация в FPGA не является автономной и требует вмешательства человека.Таким образом, EHW указывает на новое направление в реконфигурируемом оборудовании, выходящем за рамки FPGA.
Периодический сигнал — обзор
Пример 5.1-15
Рассмотрим T -периодических сигналов, x (t) ↔Xm и w (t) ↔Wm, где w (t) равно окну Хеннинга, определенному в примере 5.1 -13. Используйте свойство 7, чтобы вычислить коэффициент ряда Фурье y (t) = w (t) x (t). Объединение (5.1-74) и (5.1-75) в примере 5.1-13 дает коэффициенты ряда Фурье, Wm,
(5.1-102) Wm = {12m = 014m = ± 10 | m |> 1
Умножение свойство ведет к
(5.1-103) Ym = ∑n = −∞∞Wm − nXn = 14Xm − 1 + 12Xm + 14Xm + 1
Следовательно, умножение x (t) на окно Хэннинга эквивалентно 3-точечному средневзвешенному значению его Фурье коэффициент серии.
Свойство 8 является следствием свойств умножения и сопряжения. Поскольку y¯ (t) ↔Y¯ − m, из свойства 7 следует
(5.1-104) 1T∫ − T / 2T / 2x (t) y¯ (t) e − im ω0tdt = ∑n = −∞∞XnY ¯n − m
Установка m = 0 приводит к теореме Парсеваля, которая устанавливает эквивалентность внутреннего произведения во временной области и внутреннего произведения коэффициентов Фурье.Если y (t) = x (t), мы получаем аналог теоремы Планшерала, известный как тождество Парсеваля ,
(5.1-105) 1T∫ − T / 2T / 2 | x (t) | 2dt = ∑m = −∞∞ | Xm | 2
Это приравнивает средний квадрат x (t) к сумме квадратов его коэффициентов Фурье. Мы будем называть периодические сигналы интегрируемыми с квадратом, если их средний квадрат за период конечен.
Подводя итог, интеграл ряда Фурье, уравнение. (5.1-66) связывает периодический сигнал x (t) с уникальной последовательностью его коэффициентов Фурье.Тождество Парсеваля подразумевает, что каждый квадратично интегрируемый периодический сигнал имеет коэффициенты Фурье, суммируемые с квадратом. И наоборот, уравнения. Из (5.1-105) и (5.1-65) следует, что любая суммируемая с квадратом последовательность {Xn} связана с уникальным интегрируемым с квадратом периодическим сигналом. Устанавливая эквивалентность скалярных произведений интегрируемых с квадратом периодических сигналов и суммируемых с квадратом последовательностей, теорема Парсеваля утверждает, что геометрия этих двух пространств одинакова, то есть они равны изометрии .
Набор всех квадратично интегрируемых периодических сигналов с периодом T образует линейное векторное пространство, известное как гильбертово пространство . Гильбертовы пространства — это бесконечномерные обобщения конечномерных векторных пространств со скалярными произведениями, которые определяют их геометрию. Гильбертово пространство H обладает бесконечным ортонормированным базисом {um} m = 1∞, так что каждый вектор x∈H может быть представлен суммой базисных векторов
(5.1-106) x = ∑m = 1∞ξmunandξm = 〈x, um〉
Скаляры, ξm, являются координатами x относительно базиса.Ортонормированность базисных векторов означает, что попарные скалярные произведения удовлетворяют
(5.1-107) 〈um, un〉 = {1m = n0m ≠ n
. Рассмотрим векторы x и y с координатами ξm и ηm соответственно. Тогда ортонормированность означает, что
(5.1-108) 〈x, y〉 = ∑m = 1∞ξmη¯m
Следовательно, если x = y, мы получаем
(5.1-109) x‖2 = 〈x , x〉 = ∑m = 1∞ | ξm | 2
В контексте периодических квадратично интегрируемых сигналов и рядов Фурье ортонормированный базис равен {eim ω0t} m = −∞∞, а скалярное произведение двух сигналов, x (t) и y (t), определяется по
(5.1-110) 〈x, y〉 = 1T∫ − T / 2T / 2x (t) y¯ (t) dt
Следовательно, коэффициенты ряда Фурье — это просто координаты периодического сигнала относительно орторнормального базиса, а ряд Фурье — это представление сигнала относительно этого базиса. Также обратите внимание, что в условиях гильбертова пространства теорема и тождество Парсеваля являются непосредственными следствиями (5.1-108) и (5.1-109) соответственно. Дополнительные сведения о гильбертовых пространствах см. В Reed and Simon, 1980; Рудин, 1973.
Пусть x (t) — периодический сигнал с периодом, равным T.Мы рассмотрим связь между коэффициентом ряда Фурье для x (t) и его преобразованием Фурье. Прежде всего отметим, что периодическая функция не является абсолютно интегрируемой, следовательно, ее преобразование Фурье определяется в смысле распределения, как мы обсуждали в предыдущем разделе. Начнем с представления x (t) как репликации периода T (Briggs and Henson, 1995) базового сигнала , x0 (t),
(5.1-111) x (t) = ℜT {x0 (t)} = ∑n = −∞∞x0 (t + nT)
Мы часто будем называть ℜ {x0 (t)} T -репликацией x0 (t).Обратите внимание, что операция репликации T производит сигнал, который является периодическим с периодом, равным T. Мы будем предполагать, что x0 (t) достаточно уменьшается при t → ± ∞, так что бесконечная сумма сходится. Обратите внимание, что x0 (t) не уникален. Например, рассмотрим функции y (t) и z (t),
(5.1-112) y (t) = {x (t) 0 Тогда мы могли бы определить x0 (t) как T -репликацию либо y (t), либо z (t). Затем мы устанавливаем связь между коэффициентом ряда Фурье x (t) и преобразованием Фурье x0 (t), т.е.е., (5.1-113) Xm = 1T∫ − T / 2T / 2x (t) e − im ω0tdt, ω0 = 2πT = 1T∫ − T / 2T / 2 (∑n = −∞∞x0 (t + nT)) e − im ω0tdt = 1T∑n = −∞∞∫ − T / 2T / 2×0 (t + nT) e − im ω0tdt = 1T∑n = −∞∞eim ω0 (nT) ∫nT − T / 2nT + T / 2×0 (τ) e − im ω0τdτ = 1T∑n = −∞∞∫nT − T / 2nT + T / 2×0 (τ) e − im ω0τdτ = 1T∫ − ∞∞x0 (τ) e − im ω0τdτ = X0 (mω0) T Это замечательный результат, учитывая, что существует бесконечно много базовых сигналов, которые могут давать одинаковую репликацию T . Предположим, что x0 (t) и y0 (t) — два разных базовых сигнала с равными T -повторениями, (5.1-114) x (t) = ∑n = −∞∞x0 (t + nT) = ∑n = −∞∞y0 (t + nT) Поскольку x0 (t) ≠ y0 (t), их преобразования Фурье также не равны, т. е. X0 (ω) ≠ Y0 (ω). Уравнение Из (5.1-113) следует, что, поскольку x0 (t) и y0 (t) имеют одинаковую репликацию T , их преобразования Фурье, хотя и разные, должны быть одинаковыми на дискретных частотах, ωm = mω0. Ур. (5.1-113) и разложение x (t) в ряд Фурье приводят нас к следующей интересной теореме: Теорема 5.7 (обратная формула суммирования Пуассона) Предположим, что для непрерывного сигнала времени x0 (t), ℜT {x0 (t)} сходится и конечно.Пусть ω0 = 2π / T, тогда (5.1-115) ℜT {x0 (t)} = 1T∑m = −∞∞X0 (mω0) eim ω0t Приведенная выше теорема утверждает, что дискретное обратное преобразование Фурье X0 (ω) дает T -репликацию x0 (t). Мы обсудим двойную версию теоремы 5.7 в следующем разделе, посвященном дискретизации во временной области. Из пары преобразований Фурье, eim ω0t↔2π δ (ω − mω0) и (5.1-115) следует, что x (t) имеет преобразование Фурье, (5.1-116) ℜT {x0 (t)} = 1T∑ m = −∞∞X0 (mω0) eim ω0t↔ω0∑m = −∞∞X0 (mω0) δ (ω − mω0) Следовательно, уравнения(5.1-115) и (5.1-116) приводят к (5.1-117) ℜT {x0 (t)} = ∑n = −∞∞x0 (t + nT) ↔ω0∑m = −∞∞X0 ( mω0) δ (ω − mω0) То есть репликация во временной области эквивалентна дискретизации преобразования Фурье в частотной области, где X0 (mω0) — значения выборки X0 (ω). TM-SP использует очень простую архитектуру, включающую временную дискретизацию коротких импульсов и дисперсионную задержку, в соответствии с расчетные условия подробно описаны ниже и показаны на рис.2. Эта схема формирует выходной временной сигнал, который следует за полным комплексным STFT (по амплитуде и фазе) входного сигнала, исключительно в реальном времени и с задержкой, которая ограничивается только задержкой распространения через систему аналоговой обработки. Комбинация временной дискретизации и дисперсионной задержки выполняет «виртуальное» временное оконное управление входной SUT и последующее вычисление FT без необходимости реализовывать фактическое высокоскоростное временное усечение входящего сигнала. Это выполняется таким образом, что временные окна последовательного анализа сильно перекрываются по интересующему сигналу, таким образом гарантируя, что информация о сигнале не будет потеряна (работа без пауз). Схема включает в себя (i) временную единицу выборки (первый заштрихованный прямоугольник), где тестируемый сигнал (SUT) со сложной временной огибающей, определяемой s ( t 1 ), модулируется повторяющаяся последовательность коротких импульсов с периодом выборки, определяемым параметром T R . Временная выборка генерирует сдвинутые по частоте копии входной SUT, где каждая спектральная копия сдвигается на ω R = 2 π / T R .За временной выборкой следует (ii) частотно-зависимый (дисперсионный) блок временной задержки (второй заштрихованный прямоугольник), τ ( ω 1 ), где спектральные копии со сдвигом частоты (на ω R ) задерживаются друг относительно друга на сумму T R . 2/2 \ pi \) (дисперсия) по всей полосе частот импульсов дискретизации.Как проиллюстрировано в верхней части рисунка, интерференция между одновременно отложенными по времени и сдвинутыми по частоте копиями SUT создает временную структуру g ( t 2 ) вдоль каждого слота периода дискретизации ( T R ), который пропорционален FT соответствующего участка входного сигнала с временным окном, таким образом реализуя непрерывное временное отображение кратковременного преобразования Фурье или спектрограммы сигнала. В показанном здесь примере SUT представляет собой синусоидальную функцию с частотой, линейно возрастающей во времени, так называемый линейно-частотный ЛЧМ-сигнал.Таким образом, на выходе предложенной схемы FT соответствующего участка SUT с временным окном, а именно два импульса конечной длительности, соответствующие двухстороннему спектру одночастотной синусоидальной функции, отображаются во времени домена в течение каждого периода анализа длительностью T R . Полученный FT изменяет период за периодом, то есть с интервалом между импульсами 2 × Δ t 2 (пропорционально удвоенной соответствующей синусоидальной частоте), которая увеличивается линейно период за периодом, поскольку окно временного анализа «виртуально» сдвигается с той же задержкой ( T R ).{\ left ({i \ omega _0t_1} \ right)} \), где t 1 — временная переменная, с ( t 1 ) — сложная временная огибающая сигнала, i — мнимая единица, а ω 0 — центральная (или несущая) частота сигнала. Предполагается, что ТУС имеет ограниченную полосу пропускания с полной полосой частот, обозначенной Δ ω s . Никаких дополнительных ограничений на длительность сигнала не накладывается (например,г., ТРИ может быть бесконечно длинным). FT комплексной огибающей сигнала s ( t 1 ) определяется как S ( ω 1 ) = FT { s ( t 1 )}, где ω 1 выполняется для переменной радиальной частоты. {\ left ({- i \ omega _1t_1} \ right)} dt_1, $$
(1)
, где h ( t ) — это ограниченная по времени функция, которая служит временным окном для вычисления STFT.Тогда SP сигнала будет: SP s ( τ , ω 1 ) = | STFT s ( τ , ω 1 ) | 2 . Как показано на рисунке 2, предлагаемый метод TM-SP включает в себя каскад из (i) обычного блока временной выборки для модуляции огибающей SUT, s ( t 1 ) с периодической последовательностью короткие импульсы, и (ii) частотно-зависимый блок временной задержки, который может быть практически реализован, e.г., используя хроматическую дисперсию 30,31,32,33,34 . Импульсы выборки в блоке (i) определяются ограниченной по времени функцией p ( t 1 ) (индивидуальная форма импульса), повторяющейся с периодом T R = 2 π / ω R , где ω R — частота дискретизации. 2}} {{2 \ pi}}.$
(2)
Система создает помехи из последовательных задержанных и сдвинутых по частоте копий исходного сигнала, в результате чего форма волны во временной области следует STFT входящего ТУС, см. Общую концепцию, показанную на рис. 1c, и детали реализации на рис. 2. В частности, эта самоиндуцированная волновая интерференция приводит к вычислению FT последовательных секций SUT с временным окном таким образом, что результирующие спектры отображаются на последовательных временных интервалах, каждый с длительностью, равной период выборки, T R .Вкратце, как показано на рисунке 2, набор гармонически связанных частотных компонентов когерентно складывается вдоль каждого интервала периода дискретизации, T R таким образом, что эти различные частотные компоненты взвешиваются по амплитуде и фазе набор последовательных выборок SUT, приводящий к вычислению FT соответствующего временного окна входного сигнала с ( t 1 ). Секция анализируемого сигнала сдвигается на T R из каждого интервала периода дискретизации в следующий.В результате эта схема создает временную форму выходного сигнала, которая следует за сигналом STFT. Дополнительный рисунок 1 показывает более подробную иллюстрацию математических соотношений, которые приводят к аналоговым вычислениям и временному отображению STFT сигнала, как описано ниже. Мы повторяем, что процессы временного оконного управления и вычисления FT по своей сути обеспечиваются комбинацией дискретизации и дисперсионной задержки при заданных проектных условиях. Подробный математический анализ предложенной схемы приведен в разделе «Методы».Для этого анализа мы рассматриваем выходной временной сигнал по последовательным временным интервалам длительностью T R , где n -й временной интервал (с n = 0, ± 1, ± 2…,) определяется как \ (nT _ {\ mathrm {R}} — \ frac {{T _ {\ mathrm {R}}}} {2} \, \ le \, t_2 \, <\, nT _ {\ mathrm {R}} + \ frac {{T _ {\ mathrm {R}}}} {2} \), где t 2 = t 1 — Δ t L — временная переменная на выходе системы, просто задерживается относительно ввода ( t 1 ) на общую задержку системы, Δ t L .В соответствии с иллюстрациями на дополнительном рисунке 1, наши математические выводы доказывают, что сложная временная огибающая выходного сигнала в интервале времени n -й может быть записана следующим образом (с использованием определения STFT в уравнении (1)): $$ g_n \ left ({t_2} \ right) \ propto {\ mathrm {FT}} \ left \ {{h \ left ({t_1 — nT _ {\ mathrm {R}}} \ right) s \ left ( {t_1} \ right)} \ right \} \ Equiv {\ mathrm {STFT}} _ s \ left ({nT _ {\ mathrm {R}}, \ omega _1} \ right), $$
(3)
с \ (\ omega _1 = \ frac {{t_2 — nT _ {\ mathrm {R}}}} {{\ ddot \ phi}} \) и \ (h \ left (t \ right) \ Equiv {\ mathrm {FT}} \ left \ {{p (t_1)} \ right \} _ {\ omega _1 = \ frac {{- t}} {{\ ddot \ phi}}} \).Следовательно, уравнение. (3) указывает на то, что предлагаемая система по своей сути вычисляет STFT анализируемой формы волны, s ( t 1 ), а именно FT версии SUT с временным окном, с центральным расположением временного окно анализа, ч ( t ), работает как nT R , с n = 0, ± 1, ± 2,…. Кроме того, полученный STFT напрямую отображается во временной области последовательно в каждом из интервалов периода выборки анализа.В частности, выходной временной сигнал вдоль интервала периода дискретизации с центром в нТ R , [ g n ( t 2 )] является просто TM-копией соответствующего STFT входной сигнал, то есть STFT, вычисленный с временным окном, центрированным вокруг t 1 = нТл R . Как показано формулой. (3) коэффициент преобразования частоты во время (Δ t 2 ← Δ ω 1 ) определяется коэффициентом дисперсии \ (\ ddot \ phi \), т.е.е., \ (\ frac {{\ Delta t_2}} {{\ Delta \ omega _1}} = \ ddot \ phi \), так что весь частотный спектр усеченного сигнала будет TM в пределах соответствующего периода анализа (длительность Т R ). Временное разрешение ( δt r ) полученного распределения STFT 47,48 продиктовано длительностью оконной функции временного анализа ч ( t ). Как определено формулой. (3) длительность окна анализа (Δ t h ) задается полосой частот импульсов дискретизации (Δ ω P ), масштабированной по временной области с коэффициентом \ ( \ ddot \ phi \), так что \ (\ delta t _ {\ mathrm {r}} \ приблизительно \ Delta t_h \ приблизительно \ left | {\ ddot \ phi} \ right | \ times \ Delta \ omega _p \).Принцип неопределенности FT предполагает, что частотное разрешение полученного STFT напрямую задается обратной величиной временного разрешения 47,48 , \ (\ delta \ omega _ {\ mathrm {r}} \ приблизительно \ Delta t_p / \ left | {\ ddot \ phi} \ right | \). Эти оценки показывают, что разрешение TM-SP (по оси времени) напрямую определяется временной шириной импульсов дискретизации, Δ t P . Учитывая, что полная полоса частот анализа отображается на одном временном периоде дискретизации, T R , каждый оконный спектр Фурье разрешается во времени с общим числом характеристик, заданным коэффициентом M ≈ T R / Δ т P .Более того, можно легко сделать вывод, что временное разрешение вычисленного STFT (длительность временного окна анализа, ч ( t )) примерно в M раз больше, чем период дискретизации, т. Е. δt r ≈ Δ t h ≈ M × T R . Учитывая, что временной сдвиг между последовательными окнами анализа в вычислении SP определяется периодом выборки T R , см.(3) это означает, что последовательные окна временного анализа сильно перекрываются, что гарантирует отсутствие пропусков в проводимой RT-SA и отсутствие мертвых времен при получении или вычислении FT. Фактически, оконный спектр TM остается примерно одинаковым (то есть повторяющимся) в течение временного разрешения реализованного SP, что соответствует примерно M последовательных периодов представления (каждый с длительностью T R ). Это приводит к эффективной передискретизации информации STFT, которая может быть использована для ослабления спецификаций этапа обнаружения, используемого для захвата распределения TM-SP (дальнейшее обсуждение ниже). Чтобы экспериментально проверить предложенную концепцию TM-SP, мы разработали простую фотонную платформу для RT-SA без зазоров микроволновых сигналов с полосой пропускания ГГц, используя широко доступные готовые компоненты фотоники. Индивидуальные высокоскоростные микроволновые сигналы были сгенерированы с помощью электронного генератора сигналов произвольной формы (AWG). Общая схема экспериментальной установки представлена на рис. 3а. Последовательность пикосекундных оптических импульсов, повторяющихся с частотой 4.86 ГГц ( T R = 205,76 пс), модулирует микроволновую SUT в электрооптическом модулятора Маха – Цендера (MZM), реализуя блок временной дискретизации. Линейная дисперсионная задержка реализуется длиной волокна с компенсацией дисперсии (DCF) с общим значением дисперсии ∼6825 пс 2 рад -1 . Форма выходного сигнала фиксируется электронным осциллографом в реальном времени после преобразования оптического сигнала в электрический в фотодетекторе с частотой 50 ГГц. Мы повторяем, что предлагаемая концепция не налагает каких-либо фундаментальных ограничений на длительность сигнала: содержание Фурье сигнала по своей природе непрерывно отображается во времени по мере его распространения через систему TM-SP.Продолжительность каждой из изученных форм сигналов в наших экспериментальных примерах была ограничена доступной памятью инструментов, используемых для генерации (AWG) и измерения (в режиме реального времени) сигналов. Кроме того, таким образом, весь выходной сигнал может быть захвачен осциллографом в реальном времени для последующего автономного анализа и представления обнаруженных данных (например, для двумерных частотно-временных графиков). a Схема экспериментальной установки TM-SP на основе фотоники для спектрального анализа широкополосных микроволновых сигналов в реальном времени. Тестируемый микроволновый сигнал (SUT) дискретизируется с помощью последовательности пикосекундных оптических импульсов, генерируемой волоконным лазером с синхронизацией мод, в модулятор Маха – Цендера (MZM). Оптические образцы распространяются по волокну с компенсацией дисперсии (DCF) с полной дисперсией \ (\ ddot \ phi \), а выходной сигнал TM-SP регистрируется в осциллографе в реальном времени после фото-обнаружения. b Временная диаграмма тестируемого микроволнового сигнала (SUT) с линейно возрастающей частотой от 500 МГц до 2 ГГц в течение 2 мкс. c Временная форма выходного сигнала фото-детектирования (сигнал напряжения), которая фиксируется непосредственно в осциллографе в реальном времени, в течение той же длительности 2 мкс. На вложенных графиках показано увеличение выходного сигнала для трех разных временных интервалов, каждый из которых охватывает один период анализа ( T R = 205,6 пс). Временная кривая в течение каждого последовательного периода анализа, T R , является отображенной во времени копией FT входной SUT, эффективно обработанной окном вокруг соответствующего времени анализа.Верхняя горизонтальная ось соответствует шкале частот, полученной с помощью закона отображения \ (\ Delta t_2 \ leftarrow \ Delta \ omega _1 \ ddot \ phi \). Мгновенный спектр входного сигнала в любой данный момент времени состоит из двух отдельных импульсов, соответствующих частоте сигнала, ± ω RF ( t 1 ), линейно возрастающих со временем. Наблюдаемый фон сигнала (в том числе в месте, соответствующем постоянному току) объясняется нежелательными изменениями в состоянии смещения процесса электрооптической модуляции по сравнению с оптимальной конструкцией. d Двумерное представление совместного частотно-временного распределения энергии сигнала (спектрограмма), которое непосредственно восстанавливается из выходной временной кривой. В первом примере (результаты показаны на рис.3) мы представляем анализ микроволнового сигнала длительностью 2 мкс с мгновенной частотой ω RF ( t 1 ), линейно возрастающей от 500 МГц до 2 ГГц, рис. 3b. График на рис. 3c показывает напряжение выходного электрического временного сигнала, которое непосредственно фиксируется осциллографом в реальном времени.Измеренная временная форма выходного сигнала вдоль каждого слота длительностью T R (период выборки) отображается на эквивалентную частотную ось с использованием определенного закона отображения: \ (\ Delta t_2 \ leftarrow \ Delta \ omega _1 \ ddot \ phi \ ). Мгновенный спектр входного ТРИ в любой данный момент времени состоит из двух отдельных импульсов, соответствующих мгновенной частоте сигнала, ± ω RF ( t 1 ), линейно возрастающих со временем.На рисунке 3d показано двумерное представление совместного частотно-временного распределения энергии (SP) сигнала, которое непосредственно восстанавливается из выходной временной кривой. Как и ожидалось, экспериментально восстановленный SP следует теоретическому линейному частотному чирпу входного SUT (пунктирные серые линии). Отклонения двумерного распределения вдоль вертикальной оси частот относительно теоретического линейного частотного чирпа, которые наблюдаются на рис. 3d, объясняются конечным временным джиттером в пикосекундных оптических импульсах, используемых для временной дискретизации.Важно подчеркнуть, что изменение масштаба не применялось для представления оси времени на двумерном графике время-частота на рис. 3d, что указывает на то, что форма выходного сигнала передает SP входного сигнала исключительно в реальном времени. В частности, изменяющийся сигнал FT вычисляется каждые T R ≈ 205,76 пс, то есть при скорости 4,86 × 10 9 FT / с, что значительно превосходит характеристики существующих приборов. Для сравнения: современный анализатор радиочастотного спектра в реальном времени, основанный на DSP, Keysight N9040B-RT2, обеспечивает максимум 292969 дискретных FT в секунду 22 .Результаты на рис. 3 подтверждают способность продемонстрированной установки обеспечивать RT-SA без пропусков сигналов с мгновенной полосой частот, приближающейся к 5 ГГц, что выходит за рамки возможностей современных электронных платформ на основе DSP. Приведенная выше оценка разрешения по частоте действительна при условии, что ширина полосы обнаружения достаточно высока для разрешения импульсов дискретизации; в противном случае для этой оценки лучше учитывать временную ширину обнаруженных импульсов (Δ t d ← Δ t p ).В нашей конкретной экспериментальной реализации полная ширина на полувысоте (FWHM) импульсов дискретизации составляла Δ t p ∼ 7 пс, тогда как измеренная ширина на полувысоте после фотодетектирования (то есть по интенсивности) составляла быть примерно в два раза больше этого значения, Δ t d ∼ 14,4 пс, см. дополнительный рис. 2. Это соответствует теоретическому разрешению по частоте \ (\ delta \ omega _ {\ mathrm {r}} \ приблизительно \ Delta t_ { \ mathrm {d}} / \ left | {\ ddot \ phi} \ right | \) ~ 2 π × 340.3 МГц. Обратите внимание, что ограниченная полоса обнаружения не изменяет временное разрешение вычисленной SP, амплитуда которой на полувысоте задается как \ (\ delta t _ {\ mathrm {r}} \ приблизительно \ left | {\ ddot \ phi} \ right | \ times \ Delta \ omega _p \ sim 5.9 \, {\ mathrm {ns}} \). Таким образом, более длительное временное разрешение может быть получено за счет использования импульса выборки с более широкой полосой частот, практически ограниченной только рабочей полосой пропускания дисперсионной линии, используемой в системе. Как уже упоминалось, разрешение по частоте останется ограниченным полосой обнаружения.Наивысшее частотное разрешение, предлагаемое системой (обратное временному разрешению SP), может быть использовано только в том случае, если доступен каскад обнаружения с достаточно большой полосой пропускания для захвата длительности импульса дискретизации (без искажений). Дополнительные эксперименты представлены на дополнительном рисунке 3, которые дополнительно подтверждают полученные оценки частотно-временного разрешения. На рисунке 4 представлены результаты RT-SA без промежутков для двух дополнительных, более сложных микроволновых сигналов с полосой пропускания ГГц с использованием описанной платформы фотоники: сигнал, состоящий из двух наложенных синусоидальных сигналов с точно противоположными квадратичными частотными чирпами (левые графики), и несущая с синусоидальной частотной модуляцией (правые графики).Для каждого из этих тестовых случаев верхний график (a, d) показывает измеренную временную форму входного сигнала; график в центре (b, e) показывает численно вычисленную SP цифровой версии входной SUT с использованием окна временного анализа, которое соответствует тому, которое реализовано платформой фотоники в реальном времени, т. е. 5,9-нс (FWHM ) Гауссов импульс; а график внизу (c, f) показывает двумерное представление SP, непосредственно восстановленное из измеренной выходной временной кривой. Как и ожидалось, во всех случаях наблюдается отличное согласие между измеренной в реальном времени SP и численно рассчитанной.Для числового SP потребовались тяжелые цифровые вычисления, основанные на алгоритмах БПФ, и, в частности, с учетом спецификаций универсальной вычислительной платформы, используемой для этих вычислений, это было получено при расчетной скорости ~ 6 футов / с (подробности см. В разделе «Методы. »). В отличие от этого, заявленная платформа анализа на основе фотонов обеспечивает распределение SP чисто в реальном времени, примерно на уровне ∼5 × 10 9 FTs / s. a — c Результаты, соответствующие анализу испытуемого микроволнового сигнала (SUT) длительностью 2 мкс, который состоит из двух наложенных синусоид с частотным чирпом, а именно синусоиды с возрастающим квадратичным частотным чирпом, от 500 МГц до 2 ГГц и синусоиды с таким же, но противоположным частотным чирпом. Сигнал показывает две отдельные полосы частот в каждый момент времени. d — f Результаты, соответствующие анализу тона 2 МГц, частотно модулированного на 1.СВЧ-несущая 215 ГГц с максимальным отклонением частоты ± 1,215 ГГц. Для каждого из проанализированных сигналов верхний график ( a ) и ( d ), соответственно, показывает измеренную временную форму волны (напряжение) входного микроволнового SUT; график в середине ( b ) и ( e ), соответственно, показывает численно вычисленное распределение спектрограммы (SP) измеренного входного сигнала, рассчитанное с использованием гауссова импульса длительностью 5,9 нс в качестве временного окна анализа. ; а нижний график показывает распределение 2D TM-SP, которое непосредственно восстанавливается из измеренной временной трассы на выходе экспериментальной схемы фотонной выборки и дисперсии.Для облегчения интерпретации полученных результатов в каждом представлении спектрограммы представлена только положительная ось частот. Как упоминалось выше, существует сильное перекрытие между последовательными окнами виртуального временного анализа, что изначально реализовано процессом TM-SP. В результате оконный спектр TM остается почти идентичным в течение ряда примерно M последовательных периодов представления, каждый с длительностью T R , где мы напоминаем, что M ≈ T R / Δ t p ( M ∼29 в нашей экспериментальной схеме).Используя это свойство, полученный SP может быть полностью извлечен путем дискретизации выходного сигнала со значительно ослабленной частотой, немного ниже исходной частоты дискретизации, например, с периодом, равным T R + T R / М . Это интересное свойство было подтверждено численным понижением частоты дискретизации выходных сигналов, захваченных осциллографом в реальном времени в описанных экспериментах, см. Примеры, показанные на дополнительном рисунке 4. Наконец, непрерывная RT-SA без зазоров для широкополосных сигналов с наносекундным разрешением также демонстрируют экспериментальные результаты, показанные на рис.5. Анализируемые здесь ТРИ включают быстрые случайные или изолированные события и частотные переходные процессы с длительностью до 5 нс. Опять же, это выходит за рамки возможностей существующих схем RT-SA на основе DSP, которые обычно ограничиваются обеспечением 100% вероятности перехвата характеристик сигнала с длительностью, по крайней мере, в диапазоне микросекунд 21,22 . На рисунке 5a показана временная диаграмма последовательности быстрой перестройки частоты микроволн, специально разработанной для проверки производительности установки TM-SP. В частности, ТУС состоит из сегментов длительностью 5 нс с линейно возрастающей частотой от 0.От 4 до 2 ГГц. На рисунке 5b показано двумерное распределение SP, которое непосредственно восстанавливается из измеренной временной трассы на выходе установки TM-SP, показывая спроектированную последовательность скачков в частотно-временной плоскости. На рисунке 5c показано увеличение временной формы выходного сигнала по временному окну 5 нс, соответствующему присутствию тона 0,4 ГГц. Этот график показывает, что спектр TM этого события генерируется повторно в течение этого 5-нсекундного окна в каждый период выборки (то есть примерно 25 раз), гарантируя, что событие будет перехвачено со 100% вероятностью.В качестве другого примера на рис. 5d, e показаны результаты (входная временная диаграмма и восстановленная SP, соответственно) анализа микроволнового сигнала, состоящего из линейно увеличивающейся частотной ЛЧМ вместе со случайными изолированными переходными процессами частоты помех, каждый из которых имеет длительность 5 нс. На рисунке 5f также показано увеличение выходной временной кривой по временному окну 5 нс, соответствующему событию интерференции на частоте 1,6 ГГц, что снова показывает особенности передискретизации проводимой RT-SA. Эти результаты ясно подтверждают, что платформа TM-SP на основе фотонов позволяет перехватывать частотное содержание любого случайного или изолированного сигнального события в режиме реального времени, если это происходит в течение порядка (или дольше) временное разрешение проводимой ИП ∼5.Ширина на полувысоте 9 нс в указанной экспериментальной конфигурации. a Временная диаграмма тестируемого микроволнового сигнала (SUT), состоящая из последовательности быстрой скачкообразной перестройки частоты, разработанная для проверки производительности метода временной спектрограммы (TM-SP). Последовательность состоит из последовательных тонов длительностью 5 нс с линейно увеличивающимися частотами скачкообразной перестройки, т.е.е., 0,4, 0,8, 1,2, 1,6 и 2 ГГц. b Распределение 2D спектрограммы, которое непосредственно восстанавливается из измеренной временной кривой на выходе установки TM-SP, включая фотонную выборку и дисперсию с параметрами, указанными в тексте. Скорость скачкообразной перестройки частоты, которую можно зафиксировать с помощью этой установки, ограничена только временным разрешением вычисленного TM-SP, ширина которого на полувысоте составляет 5,9 нс в этих экспериментах. c Увеличение временной формы выходного сигнала по временному окну 5 нс, соответствующему присутствию 0.Тональный сигнал 4 ГГц, подтверждающий, что результирующая отображенная во времени спектральная форма повторно восстанавливается через каждые T R (= 205,6 пс) вдоль этого окна анализа. d Временная диаграмма микроволнового ТРИ, состоящая из (i) линейно возрастающей формы волны ЛЧМ-сигнала от 500 МГц до 2 ГГц, и (ii) изолированных переходных процессов мешающей частоты с той же амплитудой, что и у частотного ЛЧМ-сигнала, каждый длительностью 5 нс. Спектральный анализ динамических сигналов без пропусков в реальном времени с наносекундным разрешением посредством обработки аналоговых сигналов
Концепция и принцип работы
Экспериментальная демонстрация

 Если коротко, то мне нужен был экшен, который честно разложит на две (а при необходимости и больше) полосы конкретный растровый слой. Не схлопнутую версию изображения, а именно конкретный слой, это важная условие. Такой экшен наверняка оценили бы те, кто занимается коллажированием: в сложной структуре файла, где множество элементов изображения разнесены по разным группам и слоям, очень важно иметь возможность быстро и безболезненно разложить конкретный слой, требующий ретуши. Но даже если ваш файл имеет всего один пиксельный и несколько корректирующих слоёв, то даже в этом случае экшен будет полезен – один клик и нужный слой готов к ретуши, при этом остальные никак не пострадали.
Если коротко, то мне нужен был экшен, который честно разложит на две (а при необходимости и больше) полосы конкретный растровый слой. Не схлопнутую версию изображения, а именно конкретный слой, это важная условие. Такой экшен наверняка оценили бы те, кто занимается коллажированием: в сложной структуре файла, где множество элементов изображения разнесены по разным группам и слоям, очень важно иметь возможность быстро и безболезненно разложить конкретный слой, требующий ретуши. Но даже если ваш файл имеет всего один пиксельный и несколько корректирующих слоёв, то даже в этом случае экшен будет полезен – один клик и нужный слой готов к ретуши, при этом остальные никак не пострадали.
 Хотя все эти ошибки незначительны и на практике сильных проблем не создают, нам всё же будет приятно если и такие погрешности удастся избежать.
Хотя все эти ошибки незначительны и на практике сильных проблем не создают, нам всё же будет приятно если и такие погрешности удастся избежать. Настройка Sample, если таковая имеется у инструмента, в этих случаях должна иметь значение Current Layer.
Настройка Sample, если таковая имеется у инструмента, в этих случаях должна иметь значение Current Layer. В его задачу не входит предусмотреть все ошибки пользователя, он просто выполняет рутинные операции, которые до этого приходилось выполнять руками.
В его задачу не входит предусмотреть все ошибки пользователя, он просто выполняет рутинные операции, которые до этого приходилось выполнять руками. Какие еще есть варианты? Команда Apply Image, при её использовании, низкочастотную составляющую мы можем получить любым фильтром из группы размытия (и не только размытия, например Median, Dust & Scratches), а высокочастотную составляющую вычислить честным вычитанием из исходного слоя. И всем Apply Image хорош, но в экшене он может сыграть злую шутку: проблема в том, что однозначно выбрать можно только слой Merged, а это, согласно требованиям к экшену, нам не подходит. При выборе слоя, отличного от Merged, его имя жестко запишется в сценарий, и если это название слоя уже повторяется в структуре файла (например после нескольких запусков экшена), то для Photoshop возникает неопределенность – какой именно из слоев с одинаковым названием выбрать для смешивания? «Это слабое место Apply Image, и дабы сохранить стабильность экшена, от данной команды придется отказаться», — именно так я рассуждал, когда мысленно отбросил Apply Image и искал другой способ разложения на частоты.
Какие еще есть варианты? Команда Apply Image, при её использовании, низкочастотную составляющую мы можем получить любым фильтром из группы размытия (и не только размытия, например Median, Dust & Scratches), а высокочастотную составляющую вычислить честным вычитанием из исходного слоя. И всем Apply Image хорош, но в экшене он может сыграть злую шутку: проблема в том, что однозначно выбрать можно только слой Merged, а это, согласно требованиям к экшену, нам не подходит. При выборе слоя, отличного от Merged, его имя жестко запишется в сценарий, и если это название слоя уже повторяется в структуре файла (например после нескольких запусков экшена), то для Photoshop возникает неопределенность – какой именно из слоев с одинаковым названием выбрать для смешивания? «Это слабое место Apply Image, и дабы сохранить стабильность экшена, от данной команды придется отказаться», — именно так я рассуждал, когда мысленно отбросил Apply Image и искал другой способ разложения на частоты. Но когда я понял, что с Apply Image всё-таки можно стабильно работать, было поздно: экшен готов, а переделывать совсем не хочется. Теперь собственно о том, как конкретно реализовано частотное разложение в этом экшене. Вся суть заключается в вычислении низкочастотной составляющей на слоях, сделать это можно создав, к примеру, такую структур:
Но когда я понял, что с Apply Image всё-таки можно стабильно работать, было поздно: экшен готов, а переделывать совсем не хочется. Теперь собственно о том, как конкретно реализовано частотное разложение в этом экшене. Вся суть заключается в вычислении низкочастотной составляющей на слоях, сделать это можно создав, к примеру, такую структур: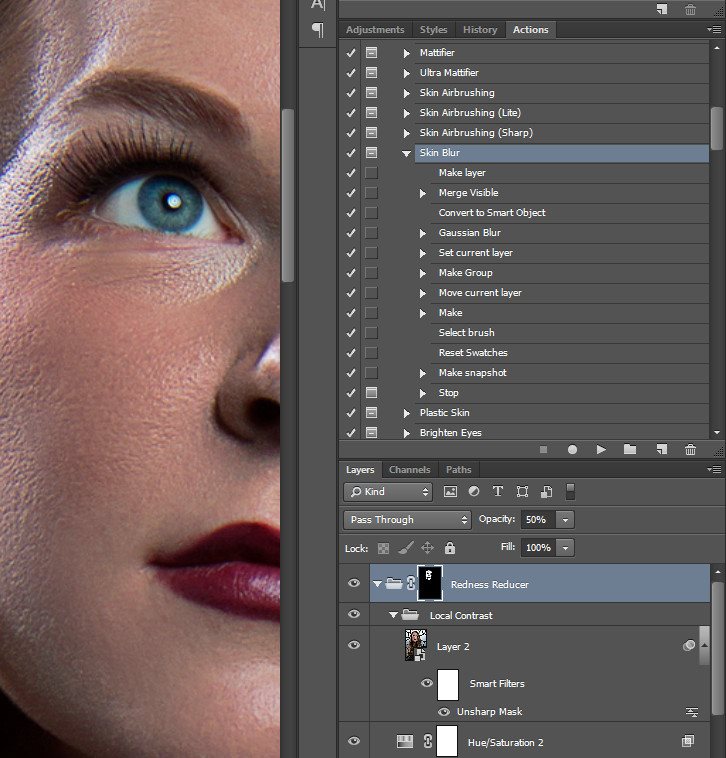 Хитрость заключается в том, что на момент вызова фильтра размытия, мы создаём такую структуру:
Хитрость заключается в том, что на момент вызова фильтра размытия, мы создаём такую структуру: