Числа Фибоначчи и золотое сечение: взаимосвязь
Во вселенной еще много неразгаданных тайн, некоторые из которых ученые уже смогли определить и описать. Числа Фибоначчи и золотое сечение составляют основу разгадки окружающего мира, построения его формы и оптимального зрительного восприятия человеком, с помощью которых он может ощущать красоту и гармонию.
Золотое сечение
Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.
В основе его лежит теория о пропорциях и соотношениях делений отрезков, которое было сделано еще древним философом и математиком Пифагором. Он доказал, что при разделении отрезка на две части: X (меньшую) и Y (большую), отношение большего к меньшему будет равно отношению их суммы (всего отрезка):
X : Y = Y : X+Y.
В результате получается уравнение: х2 – х – 1=0, которое решается как х=(1±√5)/2.
Если рассмотреть соотношение 1/х, то оно равно 1,618…
Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.
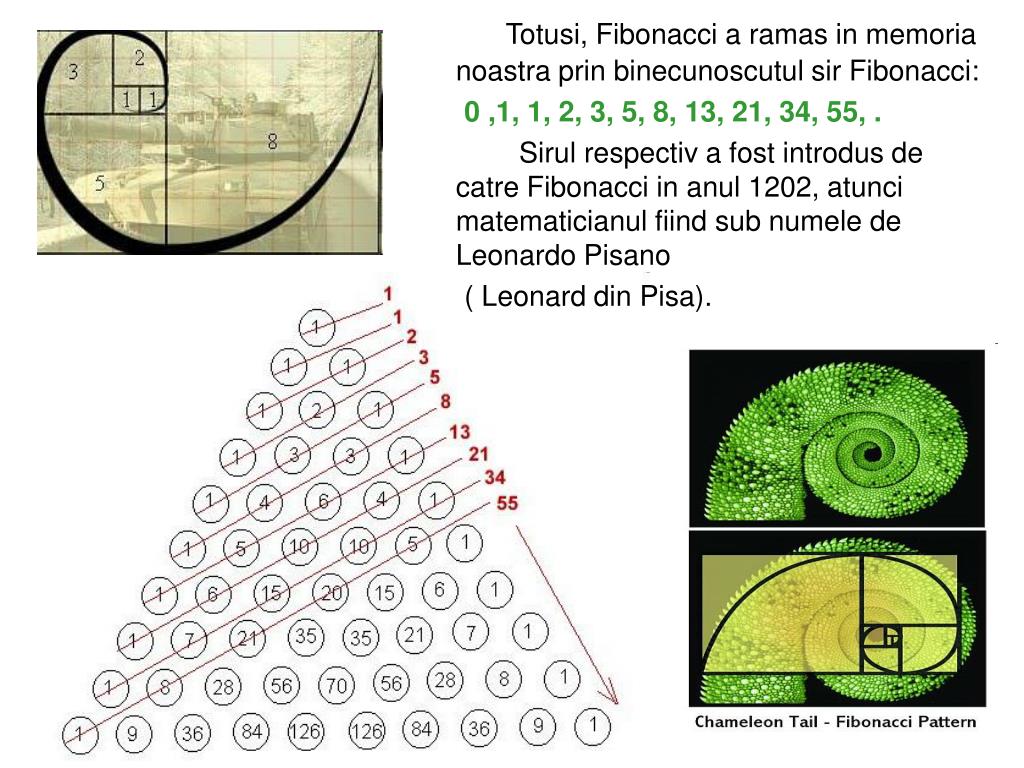
Числа Фибоначчи
Знаменитая книга Liber abaci математика из Италии Леонардо Пизанского, который в последующем стал известен, как Фибоначчи, увидела свет в 1202 г. В ней ученый впервые приводит закономерность чисел, в ряду которых каждое число является суммой 2-х предыдущих цифр. Последовательность чисел Фибоначчи заключается в следующем:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Также ученый привел ряд закономерностей:
- Любое число из ряда, разделенное на последующее, будет равно значению, которое стремится к 0,618.
 Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным.
Причем первые числа Фибоначчи не дают такого числа, но по мере продвижения от начала последовательности это соотношение будет все более точным. - Если же поделить число из ряда на предыдущее, то результат устремится к 1,618.
- Одно число, поделенное на следующее через одно, покажет значение, стремящееся к 0,382.
Применение связи и закономерностей золотого сечения, числа Фибоначчи (0,618) можно найти не только в математике, но и в природе, в истории, в архитектуре и строительстве и во многих других науках.
Спираль Архимеда и золотой прямоугольник
Спирали, очень распространенные в природе, были исследованы Архимедом, который даже вывел ее уравнение. Форма спирали основана на законах о золотом сечении. При ее раскручивании получается длина, к которой можно применить пропорции и числа Фибоначчи, увеличение шага происходит равномерно.
Параллель между числами Фибоначчи и золотым сечением можно увидеть и построив «золотой прямоугольник», у которого стороны пропорциональны, как 1,618:1. Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.
Он строится, переходя от большего прямоугольника к малым так, что длины сторон будут равны числам из ряда. Построение его можно сделать и в обратном порядке, начиная с квадратика «1». При соединении линиями углов этого прямоугольника в центре их пересечения получается спираль Фибоначчи или логарифмическая.
История применения золотых пропорций
Многие древние памятники архитектуры Египта возведены с использованием золотых пропорций: знаменитые пирамиды Хеопса и др. Архитекторы Древней Греции широко использовалиих их при возведении архитектурных объектов, таких как храмы, амфитеатры, стадионы. Например, были применены такие пропорции при строительстве античного храма Парфенон, театра Диониса (Афины) и других объектов, которые стали шедеврами древнего зодчества, демонстрирующими гармонию, основанную на математической закономерности.
В более поздние века интерес к золотому сечению поутих, и закономерности были забыты, однако опять возобновился в эпоху Ренессанса вместе с книгой францисканского монаха Л. Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».
Пачоли ди Борго «Божественная пропорция» (1509 г.). В ней были приведены иллюстрации Леонардо да Винчи, который и закрепил новое название «золотое сечение». Также были научно доказаны 12 свойств золотой пропорции, причем автор рассказывал о том, как проявляется она в природе, в искусстве и называл ее «принципом построения мира и природы».
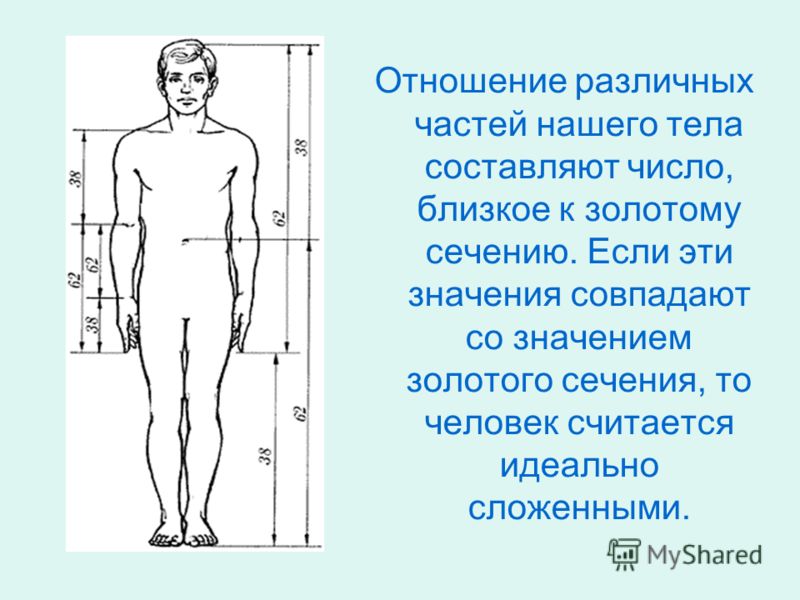
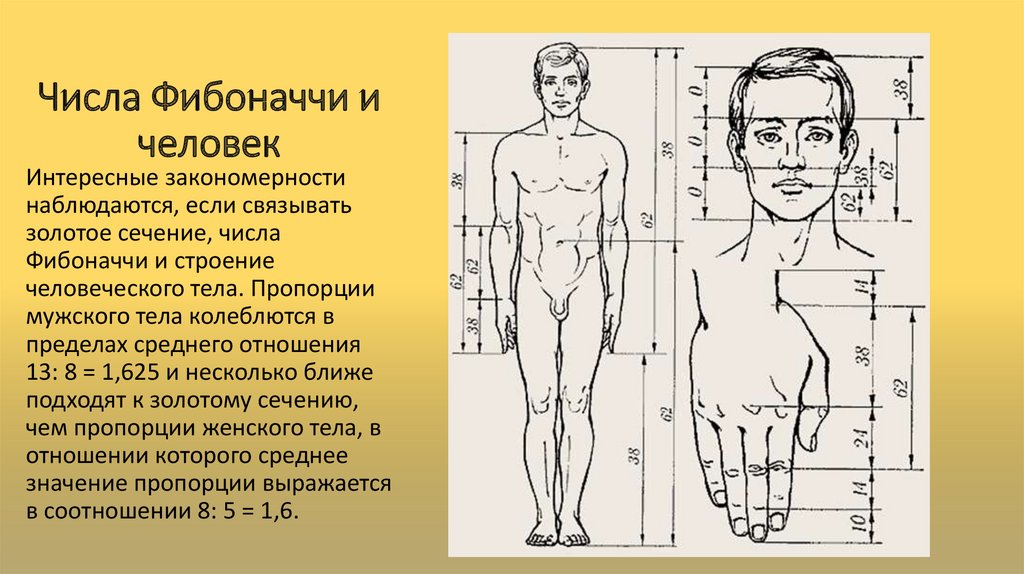
Витрувианский человек Леонардо
Рисунок, которым Леонардо да Винчи в 1492 г. проиллюстрировал книгу Витрувия, изображает фигуру человека в 2-х позициях с руками, разведенными в стороны. Фигура вписана в круг и квадрат. Этот рисунок принято считать каноническими пропорциями человеческого тела (мужского), описанными Леонардо на основе изучения их в трактатах римского архитектора Витрувия.
Центром тела как равноудаленной точкой от конца рук и ног считается пупок, длина рук приравнивается к росту человека, максимальная ширина плеч = 1/8 роста, расстояние от верха груди до волос = 1/7, от верха груди до верха головы =1/6 и т.д.
С тех пор рисунок используется в виде символа, показывающего внутреннюю симметрию тела человека.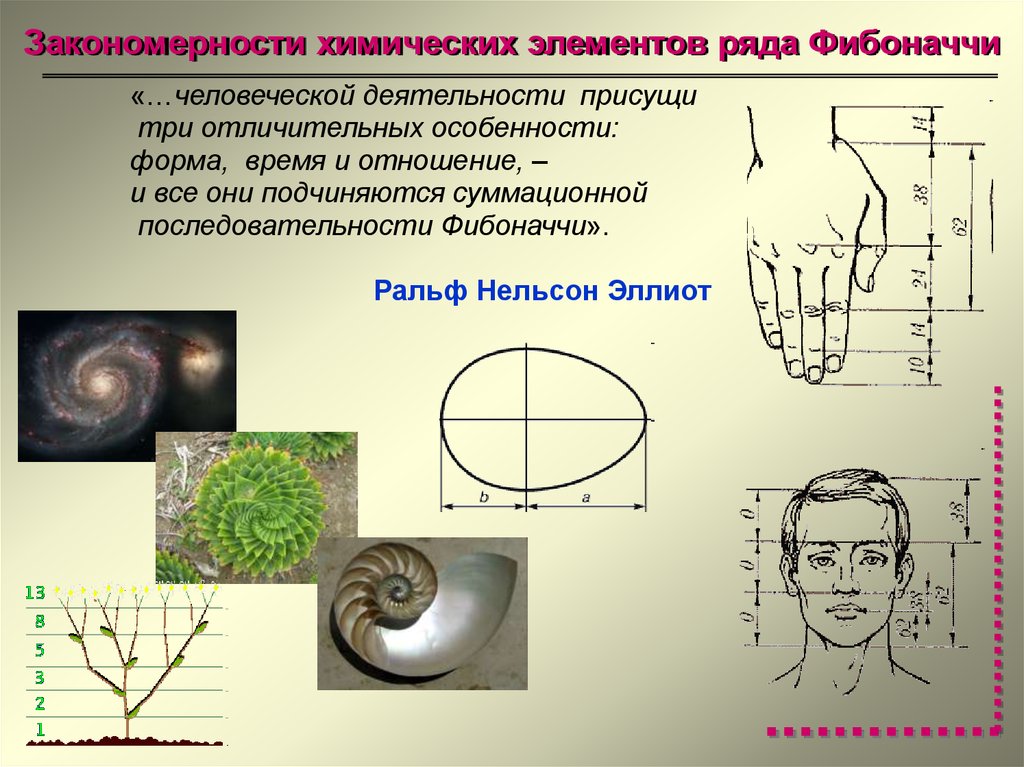
Термин «Золотое сечение» Леонардо использовал для обозначения пропорциональных отношений в фигуре человека. Например, расстояние от пояса до ступней ног соотносится к аналогичному расстоянию от пупка до макушки так же, как рост к первой длине (от пояса вниз). Эти вычисление делается аналогично соотношению отрезков при вычислении золотой пропорции и стремится к 1,618.
Все эти гармоничные пропорции часто используются деятелями искусства для создания красивых и впечатляющих произведений.
Исследования золотого сечения в 16-19 веках
Используя золотое сечение и числа Фибоначчи, исследовательскую работу по вопросу о пропорциях продолжают уже не одно столетие. Параллельно с Леонардо да Винчи немецкий художник Альбрехт Дюрер также занимался разработкой теории правильных пропорций тела человека. Для этого им даже был создан специальный циркуль.
В 16 в. вопросу о связи числа Фибоначчи и золотого сечения были посвящены работы астронома И. Кеплера, который впервые применил эти правила для ботаники.
Новое «открытие» ожидало золотое сечение в 19 в. с опубликованием «Эстетического исследования» немецкого ученого профессора Цейзига. Он возвел эти пропорции в абсолют и объявил о том, что они универсальны для всех природных явлений. Им были проведены исследования огромного количества людей, вернее их телесных пропорций (около 2 тыс.), по итогам которых сделаны выводы о статистических подтвержденных закономерностях в соотношениях различных частей тела: длины плеч, предплечий, кистей, пальцев и т.д.
Были исследованы также предметы искусства (вазы, архитектурные сооружения), музыкальные тона, размеры при написании стихотворений — все это Цейзиг отобразил через длины отрезков и цифры, он же ввел термин «математическая эстетика». После получения результатов выяснилось, что получается ряд Фибоначчи.
Число Фибоначчи и золотое сечение в природе
В растительном и животном мире существует тенденция к формообразованию в виде симметрии, которая наблюдается в направлении роста и движения. Деление на симметричные части, в которых соблюдаются золотые пропорции, — такая закономерность присуща многим растениям и животным.
Деление на симметричные части, в которых соблюдаются золотые пропорции, — такая закономерность присуща многим растениям и животным.
Природа вокруг нас может быть описана с помощью чисел Фибоначчи, например:
- расположение листьев или веток любых растений, а также расстояния соотносятся с рядом приведенных чисел 1, 1, 2, 3, 5, 8, 13 и далее;
- семена подсолнуха (чешуя на шишках, ячейки ананаса), располагаясь двумя рядами по закрученным спиралям в разные стороны;
- соотношение длины хвоста и всего тела ящерицы;
- форма яйца, если провести линию условно через широкую его часть;
- соотношение размеров пальцев на руке человека.
И, конечно, самые интересные формы представляют закручивающиеся по спирали раковины улиток, узоры на паутине, движение ветра внутри урагана, двойная спираль в ДНК и структура галактик — все они включают в себя последовательность чисел Фибоначчи.
Использование золотого сечения в искусстве
Исследователи, занимающиеся поиском в искусстве примеров использования золотого сечения, подробно исследуют различные архитектурные объекты и произведения живописи. Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.
Известны знаменитые скульптурные работы, создатели которых придерживались золотых пропорций, — статуи Зевса Олимпийского, Аполлона Бельведерского и Афины Парфенос.
Одно из творений Леонардо да Винчи — «Портрет Моны Лизы» — уже многие годы является предметом исследований ученых. Ими было обнаружено, что композиция работы целиком состоит из «золотых треугольников», объединенных вместе в правильный пятиугольник-звезду. Все работы да Винчи являются свидетельством того, насколько глубоки были его познания в строении и пропорциях тела человека, благодаря чему он и смог уловить невероятно загадочную улыбку Джоконды.
Золотое сечение в архитектуре
В качестве примера ученые исследовали шедевры архитектуры, созданные по правилам «золотого сечения»: египетские пирамиды, Пантеон, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Парфенон — одно из красивейших зданий в Древней Греции (5 в. до н.э.) — имеет 8 колонн и 17 по разным сторонам, отношение его высоты к длине сторон равно 0,618. Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Выступы на его фасадах сделаны по «золотому сечению» (фото ниже).
Одним из ученых, который придумал и успешно применял усовершенствование модульной системы пропорций для архитектурных объектов (так называемый «модулор»), — был французский архитектор Ле Корбюзье. В основу модулора положена измерительная система, связанная с условным делением на части человеческого тела.
Русский архитектор М. Казаков, построивший несколько жилых домов в Москве, а также здания сената в Кремле и Голицынской больницы (сейчас 1-я Клиническая им. Н. И. Пирогова), — был одним из архитекторов, которые использовали при проектировании и строительстве законы о золотом сечении.
Применение пропорций в дизайне
В дизайне одежды все модельеры делают новые образы и модели с учетом пропорций человеческого тела и правил золотого сечения, хотя от природы не все люди имеют идеальные пропорции.
При планировании ландшафтного дизайна и создании объемных парковых композиций с помощью растений (деревьев и кустарников), фонтанов и малых архитектурных объектов также могут применяться закономерности «божественных пропорций».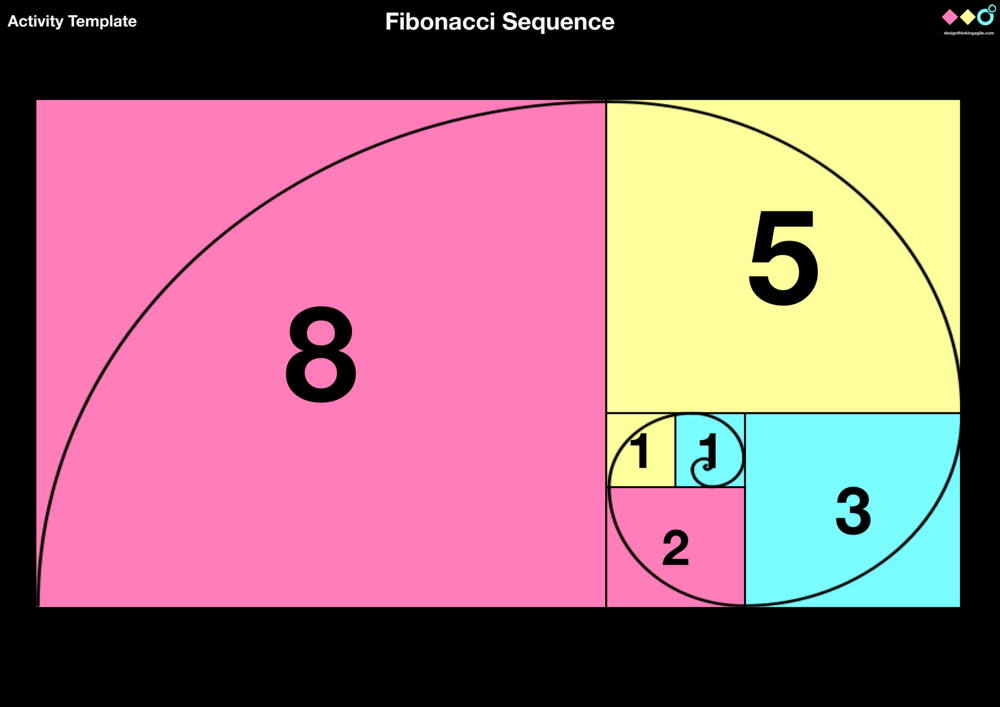 Ведь композиция парка должна быть ориентирована на создание впечатления на посетителя, который свободно сможет ориентироваться в нем и находить композиционный центр.
Ведь композиция парка должна быть ориентирована на создание впечатления на посетителя, который свободно сможет ориентироваться в нем и находить композиционный центр.
Все элементы парка находятся в таких соотношениях, чтобы с помощью геометрического строения, взаиморасположения, освещения и света, произвести на человека впечатление гармонии и совершенства.
Применение золотого сечения в кибернетике и технике
Закономерности золотого сечения и чисел Фибоначчи проявляются также в переходах энергии, в процессах, происходящих с элементарными частицами, составляющих химические соединения, в космических системах, в генной структуре ДНК.
Аналогичные процессы происходят и в организме человека, проявляясь в биоритмах его жизни, в действии органов, например, головного мозга или зрения.
Алгоритмы и закономерности золотых пропорций широко используются в современной кибернетике и информатике. Одна из несложных задач, которую дают решать начинающим программистам, — написать формулу и определить, сумму чисел Фибоначчи до определенного числа, используя языки программирования.
Современные исследования теории о золотой пропорции
Начиная с середины 20 века, интерес к проблемам и влиянию закономерностей золотых пропорций на жизнь человека, резко возрастает, причем со стороны многих ученых различных профессий: математиков, исследователей этноса, биологов, философов, медицинских работников, экономистов, музыкантов и др.
В США с 1970-хгодов начинает выпускаться журнал The Fibonacci Quarterly, где публикуются работы на эту тему. В прессе появляются работы, в которых обобщенные правила золотого сечения и ряда Фибоначчи используют в различных отраслях знаний. Например, для кодирования информации, химических исследований, биологических и т.д.
Все это подтверждает выводы древних и современных ученых о том, что золотая пропорция многосторонне связана с фундаментальными вопросами науки и проявляется в симметрии многих творений и явлений окружающего нас мира.
Числа Фибоначчи,золотое сечение,последовательность Фибоначчи и Иллюминаты.: kamburina — LiveJournal
Леонардо Фибоначчи – один из величайших математиков Средневековья. В одном и своих трудов «Книга вычислений” Фибоначчи описал индо-арабскую систему исчисления и преимущества ее использования перед римской.
В одном и своих трудов «Книга вычислений” Фибоначчи описал индо-арабскую систему исчисления и преимущества ее использования перед римской.Определение
Числа Фибоначчи или Последовательность Фибоначчи — числовая последовательность, обладающая рядом свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.), что подтверждает существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений.
Последовательност Фибоначчи начинается так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…
Свойства последовательности Фибоначчи
1. Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числе к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют (ФИ).
2. При делении каждого числа на следующее за ним, через одно получается число 0.382; наоборот – соответственно 2.618.
3. Подбирая таким образом соотношения, получаем основной набор фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236.
Связь последовательности Фибоначчи и «золотого сечения»
Последовательность Фибоначчм асимптотически (пpиближаясь все медленнее и медленнее) стpемится к некотоpому постоянному соотношению. Однако, это соотношение иppационально, то есть пpедставляет собой число с бесконечной, непредсказуемой последовательностью десятичных цифp в дpобной части. Его невозможно выразить точно.
Если какой-либо член последовательности Фибоначчи pазделить на пpедшествующий ему (напpимеp, 13:8), pезультатом будет величина, колеблющаяся около иppационального значения 1.61803398875… и чеpез pаз то пpевосходящая, то не достигающая его. Hо даже затpатив на это Вечность, невозможно узнать сотношение точно, до последней десятичной цифpы. Kpаткости pади, мы будем пpиводить его в виде 1.618. Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (сpедневековый математик) назвал его Божественной пpопоpцией. Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи
Cpеди его совpеменных названий есть такие, как Золотое сечение, Золотое сpеднее и oтношение веpтящихся квадpатов. Kеплеp назвал это соотношение одним из «сокpовищ геометpии». В алгебpе общепpинято его обозначение гpеческой буквой фи
Ф=1.618
Представим золотое сечение на примере отрезка.
Рассмотрим отрезок с концами A и B. Пусть точка С делит отрезок AB так что,
AC/CB = CB/AB или
AB/CB = CB/AC.
Представить это можно примерно так: A——C———B
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.
Отрезки золотой пропорции выражаются бесконечной иррациональной дробью 0,618…, если AB принять за единицу, AC = 0,382.. Kак мы уже знаем числа 0.618 и 0.382 являются коэффициентами последовательности Фибоначчи.
Пропорции Фибоначчи и золотого сечения в природе и истории
Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи. Просто удивительно, сколько постоянных можно вычислить пpи помощи последовательности Фибоначчи, и как ее члены проявляются в огромном количестве сочетаний. Однако не будет преувеличением сказать, что это не просто игра с числами, а самое важное математическое выражение природных явлений из всех когда-либо открытых.
Пpиводимые ниже примеры показывают некоторые интересные приложения этой математической последовательности.
1. Pаковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см.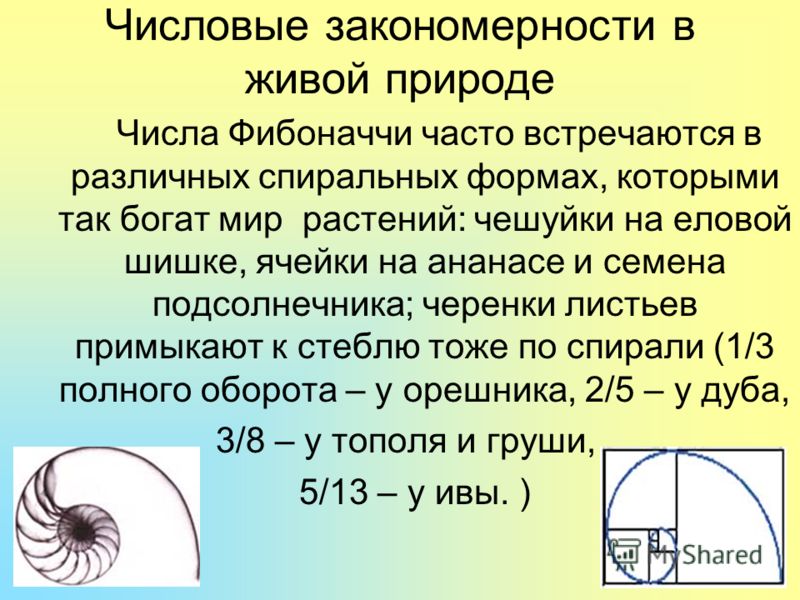 Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618. Архимед изучал спираль раковин и вывел уравнение спирали. Cпираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618. Архимед изучал спираль раковин и вывел уравнение спирали. Cпираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.
2. Растения и животные. Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Cпираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Cовместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Cпиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».
Молекула ДНK закручена двойной спиралью. Гете называл спираль «кривой жизни».
Cреди придорожных трав растет ничем не примечательное растение — цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.
Ящерица живородящая. В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38.
И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.
Пьер Kюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды. Закономерности золотой симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.
3. Космос. Из истории астрономии известно, что И. Тициус, немецкий астроном XVIII в., с помощью этого ряда (Фибоначчи) нашел закономерность и порядок в расстояниях между планетами солнечной системы
Однако один случай, который, казалось бы, противоречил закону: между Марсом и Юпитером не было планеты. Cосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в.
Cосредоточенное наблюдение за этим участком неба привело к открытию пояса астероидов. Произошло это после смерти Тициуса в начале XIX в.
Pяд Фибоначчи используют широко: с его помощью представляют архитектонику и живых существ, и рукотворных сооружений, и строение Галактик. Эти факты — свидетельства независимости числового ряда от условий его проявления, что является одним из признаков его универсальности.
4. Пирамиды. Многие пытались разгадать секреты пирамиды в Гизе. В отличие от других египетских пирамид это не гробница, а скоpее неразрешимая головоломка из числовых комбинаций. Замечательные изобpетательность, мастерство, время и труд аpхитектоpов пирамиды, использованные ими пpи возведении вечного символа, указывают на чрезвычайную важность послания, которое они хотели передать будущим поколениям. Их эпоха была дописьменной, доиероглифической и символы были единственным средством записи открытий. Kлюч к геометро-математическому секрету пирамиды в Гизе, так долго бывшему для человечества загадкой, в действительности был передан Геродоту храмовыми жрецами, сообщившими ему, что пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты.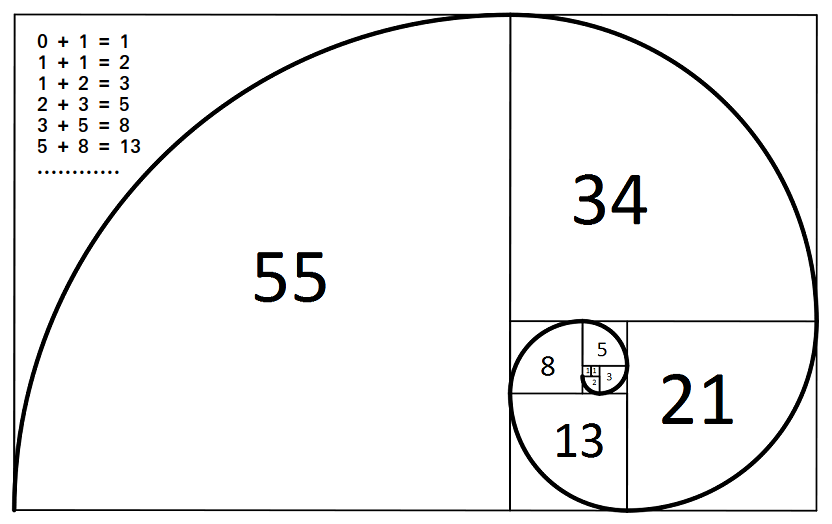
Площадь тpеугольника
356 x 440 / 2 = 78320
Площадь квадpата
280 x 280 = 78400
Длина ребра основания пирамиды в Гизе равна 783.3 фута (238.7 м), высота пирамиды -484.4 фута (147.6 м). Длина ребра основания, деленная на высоту, приводит к соотношению Ф=1.618. Высота 484.4 фута соответствует 5813 дюймам (5-8-13) — это числа из последовательности Фибоначчи. Эти интересные наблюдения подсказывают, что конструкция пирамиды основана на пропорции Ф=1,618. Некоторые современные ученые склоняются к интерпретации, что древние египтяне построили ее с единственной целью — передать знания, которые они хотели сохранить для грядущих поколений. Интенсивные исследования пирамиды в Гизе показали, сколь обширными были в те времена познания в математике и астрологии. Во всех внутренних и внешних пропорциях пирамиды число 1.618 играет центральную роль.
Пирамиды в Мексике. Hе только египетские пиpамиды постpоены в соответствии с совеpшенными пpопоpциями золотого сечения, то же самое явление обнаpужено и у мексиканских пиpамид. Возникает мысль, что как египетские, так и мексиканские пиpамиды были возведены пpиблизительно в одно вpемя людьми общего происхождения.
Возникает мысль, что как египетские, так и мексиканские пиpамиды были возведены пpиблизительно в одно вpемя людьми общего происхождения.
О последовательности Фибоначчи ордена Иллюминатов.
Это по сути, хранящийся в некогда секретных записях общества Иллюминатов, основанному в 1776 году профессором Адамом Вейсгауптом, последовательность чисел Фибоначчи, записанная в ряд:
58683436563811772030917
98057628621354486227052
60462818902449707207204
18939113748475408807538
68917521266338622235369
31793180060766726354433
38908659593958290563832
26613199282902678806752
08766892501711696207032
22104321626954862629631
36144381497587012203408
05887954454749246185695
36486444924104432077134
49470495658467885098743
39442212544877066478091
58846074998871240076521
70575179788341662562494
07589069704000281210427
62177111777805315317141
01170466659914669798731
76135600670874807101317
95236894275219484353056
78300228785699782977834
78458782289110976250030
26961561700250464338243
77648610283831268330372
42926752631165339247316
71112115881863851331620
38400522216579128667529
46549068113171599343235
97349498509040947621322
29810172610705961164562
99098162905552085247903
52406020172799747175342
77759277862561943208275
05131218156285512224809
39471234145170223735805
77278616008688382952304
59264787801788992199027
07769038953219681986151
43780314997411069260886
74296226757560523172777
52035361393621076738937
64556060605921658946675
95519004005559089502295
30942312482355212212415
44400647034056573479766
39723949499465845788730
39623090375033993856210
24236902513868041457799
56981224457471780341731
26453220416397232134044
44948730231541767689375
21030687378803441700939
54409627955898678723209
51242689355730970450959
56844017555198819218020
64052905518934947592600
73485228210108819464454
42223188913192946896220
02301443770269923007803
08526118075451928877050
21096842493627135925187
60777884665836150238913
49333312231053392321362
43192637289106705033992
82265263556209029798642
47275977256550861548754
35748264718141451270006
02389016207773224499435
30889990950168032811219
43204819643876758633147
98571911397815397807476
15077221175082694586393
20456520989698555678141
06968372884058746103378
10544439094368358358138
11311689938555769754841
49144534150912954070050
19477548616307542264172
93946803673198058618339
18328599130396072014455
95044977921207612478564
59161608370594987860069
70189409886400764436170
93341727091914336501371
57660114803814306262380
51432117348151005590134
56101180079050638142152
70930858809287570345050
78081454588199063361298
27981411745339273120809
28972792221329806429468
78242748740174505540677
87570832373109759151177
62978443284747908176518
09778726841611763250386
12112914368343767023503
71116330725869883258710
33632223810980901211019
89917684149175123313401
52733843837234500934786
04979294599158220125810
45982309255287212413704
36149102054718554961180
87642657651106054588147
56044317847985845397312
86301625448761148520217
06440411166076695059775
78325703951108782308271
06478939021115691039276
83845386333321565829659
77310343603232254574363
72041244064088826737584
33953679593123221343732
09957498894699565647360
07295999839128810319742
63125179714143201231127
95518947781726914158911
77991956481255800184550
65632952859859100090862
18029775637892599916499
46428193022293552346674
75932695165421402109136
30181947227078901220872
87361707348649998156255
47281137347987165695274
89008144384053274837813
78246691744422963491470
81570073525457070897726
75469343822619546861533
12095335792380146092735
10210119190218360675097
30895752895774681422954
33943854931553396303807
29169175846101460995055
06480367930414723657203
98600735507609023173125
01613204843583648177048
48181099160244252327167
21901893345963786087875
28701739359303013359011
23710239171265904702634
94028307668767436386513
27106280323174069317334
48234356453185058135310
85497333507599667787124
49058363675413289086240
63245639535721252426117
02780286560432349428373
01725574405837278267996
03173936401328762770124
36798311446436947670531
27249241047167001382478
31286565064934341803900
41017805339505877245866
55755229391582397084177
29833728231152569260929
95942240000560626678674
35792397245408481765197
34362652689448885527202
74778747335983536727761
40759171205132693448375
29916499809360246178442
67572776790019191907038
05220461232482391326104
32719168451230602362789
35454324617699757536890
41763650254785138246314
65833638337602357789926
72988632161858395903639
98183845827644912459809
37043055559613797343261
34830494949686810895356
96348281781288625364608
42033946538194419457142
66682371839491832370908
57485026656803989744066
21053603064002608171126
65995419936873160945722
88810920778822772036366
84481532561728411769097
92666655223846883113718
52991921631905201568631
22282071559987646842355
20592853717578076560503
67731309751912239738872
24682580571597445740484
29878073522159842667662
57807706201943040054255
01583125030175340941171
91019298903844725033298
80245014367968441694795
95453045910313811621870
45679978663661746059570
00344597011352518134600
65655352034788811741499
41274826415213556776394
03907103870881823380680
33500380468001748082205
91096844202644640218770
53401003180288166441530
91393948156403192822785
48241451050318882518997
00748622879421558957428
20216657062188090578088
05032467699129728721038
70736974064356674589202
58656573978560859566534
10703599783204463363464
85489497663885351045527
29824229069984885369682
80464597457626514343590
50938321243743333870516
65714900590710567024887
98580437181512610044038
14880407252440616429022
47822715272411208506578
88387124936351068063651
66743222327767755797399
27037623191470473239551
20607055039920884426037
08790843334261838413597
07816482955371432196118
95037977146300075559753
79570355227144931913217
25564401283091805045008
99218705121186069335731
53895935079030073672702
33141653204234015537414
42687154055116479611433
23024854404094069114561
39873026039518281680344
82525432673857590056043
20245372719291248645813
33441698529939135747869
89579864394980230471169
67157362283912018127312
91658995275991922031837
23568272793856373312654
79985912463275030060592
56745497943508811929505
68549325935531872914180
11364121874707526281068
69830135760524719445593
21955359610452830314883
91176930119658583431442
48948985655842508341094
29502771975833522442912
57364938075417113739243
76014350682987849327129
97512286881960498357751
58771780410697131966753
47719479226365190163397
71284739079336111191408
99830560336106098717178
30554354035608952929081
84641437139294378135604
82038947912574507707557
51030024207266290018090
42293424942590606661413
32287226980690145994511
99547801639915141261252
57282806643312616574693
88195106442167387180001
10042184830258091654338
37492364118388856468514
31500637319042951481469
42431460895254707203740
55669130692209908048194
52975110650464281054177
55259095187131888359147
65996041317960209415308
58553323877253803272763
29773721431279682167162
34421183201802881412747
44316884721845939278143
54740999990722332030592
62976611238327983316988
25393126200650370288447
82866694044730794710476
12558658375298623625099
98232335971550723383833
24408152577819336426263
04330265895817080045127
88731159355877472172564
94700051636672577153920
98409503274511215368730
09121996295227659131637
09396860727134269262315
47533043799331658110736
96431421719794340563915
51210810813626268885697
48068060116918941750272
29874158699179145349946
24441940121978586013736
60828690722365147713912
68742096651378756205918
54328888341742920901563
13328319357562208971376
56309785015631549824564
45865424792935722828750
60848145335135218172958
79329911710032476222052
19464510536245051298843
08713444395072442673514
62861799183233645983696
37632722575691597239543
83052086647474238151107
92734948369523964792689
93698324917999502789500
06045966131346336302494
99514808053290179029751
82515875049007435187983
51183603272277260171740
45355716588555782972910
61958193517105548257930
70910057635869901929721
79951687311755631444856
48100220014254540554292
73458837116020994794572
08237804368718944805636
89182580244499631878342
02749101533579107273362
53289069334741238022220
11626277119308544850295
41913200400999865566651
77566409536561978978183
80451030356510131589458
90287186108690589394713
68014845700183664956472
03294334374298946427412
55143590584348409195487
01523614031739139036164
40198455051049121169792
00120199960506994966403
03508636929039410070194
50532016234872763232732
44943963048089055425137
97233147518520709102506
36859816795304818100739
42453170023880475983432
34504142584314063612721
09602282423378228090279
76596077710849391517488
73168777135223900911711
73509186006546200990249
75852779254278165970383
49505801062615533369109
37846597710529750223173
07412177834418941184596
58610298018778742744563
86696612772450384586052
64151030408982577775447
41153320764075881677514
97553804711629667771005
87664615954967769270549
62393985709255070274069
97814084312496536307186
65337180605874224259816
53070525738345415770542
92162998114917508611311
76577317209561565647869
54744892713206080635457
79462414531066983742113
79816896382353330447788
31693397287289181036640
83269856988254438516675
86228993069643468489751
48408790396476042036102
06021717394470263487633
65439319522907738361673
89811781242483655781050
34169451563626043003665
74310847665487778012857
79236454185224472361713
74229255841593135612866
37167032807217155339264
63257306730639108541088
68085742838588280602303
34140855039097353872613
45119629264159952127893
11354431460152730902553
82710432596622674390374
55636122861390783194335
70590038148700898661315
39819585744233044197085
66967222931427307413848
82788975588860799738704
47020316683485694199096
54802982493198176579268
29855629723010682777235
16274078380743187782731
82119196952800516087915
72128826337968231272562
87000150018292975772999
35790949196407634428615
75713544427898383040454
70271019458004258202120
23445806303450336581472
18549203679989972935353
91968121331951653797453
99111494244451830338588
41290401817818821376006
65928494136775431745160
54093871103687152116404
05821934471204482775960
54169486453987832626954
80139150190389959313067
03186616706637196402569
28671388714663118919268
56826919952764579977182
78759460961617218868109
45465157886912241060981
41972686192554787899263
15359472922825080542516
90681401078179602188533
07623055638163164019224
54503257656739259976517
53080142716071430871886
28598360374650571342046
70083432754230277047793
31118366690323288530687
38799071359007403049074
59889513647687608678443
23824821893061757031956
38032308197193635672741
96438726258706154330729
63703812751517040600505
75948827238563451563905
26577104264594760405569
50959840888903762079956
63880178618559159441117
В самих записях членов этого секретного общества, данный набор цифр занимает очень важную роль. Но какую? Что скрывали Иллюминаты за этими цифрами?
Но какую? Что скрывали Иллюминаты за этими цифрами?
Дело в том, что по сохранившимся данным Иллюминаты обладали обширными познаниями не только в области оккультных наук, но и математики, астрономии, астрологии, химии и алхимии, медицине и психологии. Также им были доступны некоторые древние источники знаний.
Многие исследователи считают что за этими цифрами может скрываться универсальный код жизни, рецепт филосовского камня и т.п…
Последовательность Фибоначчи | Imagination Station
Последовательность Фибоначчи
23 сентября 2021 г.
Последовательность Фибоначчи — это последовательность чисел, в которой каждое число представляет собой сумму двух предыдущих чисел. Например,
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, …
Математически мы можем описать это как:
xn= xn-1 + xn-2
История
Многие источники утверждают, что эта последовательность была впервые обнаружена или «изобретена» Леонардо Фибоначчи.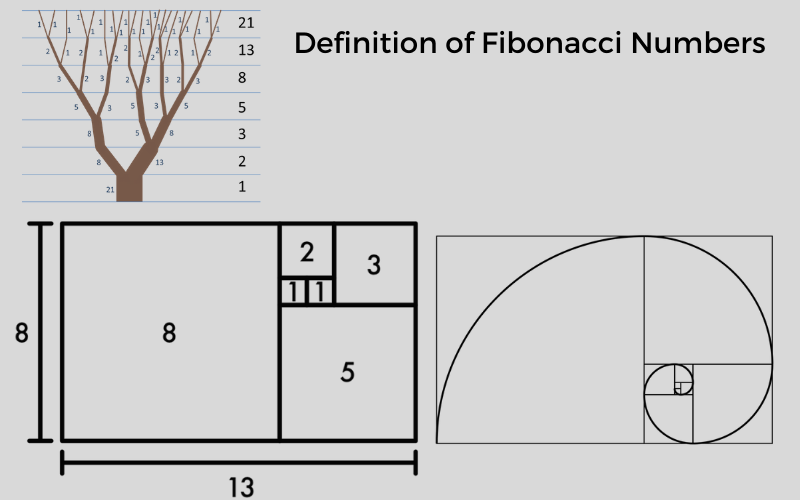 Итальянский математик, родившийся около 1170 года нашей эры, первоначально был известен как Леонардо Пизанский. В 19века историки придумали прозвище Фибоначчи (примерно означающее «сын клана Боначчи»), чтобы отличить математика от другого знаменитого Леонардо Пизанского.
Итальянский математик, родившийся около 1170 года нашей эры, первоначально был известен как Леонардо Пизанский. В 19века историки придумали прозвище Фибоначчи (примерно означающее «сын клана Боначчи»), чтобы отличить математика от другого знаменитого Леонардо Пизанского.
Другие говорят, что он этого не делал. Кит Девлин, автор книги «В поисках Фибоначчи: поиски нового забытого математического гения, изменившего мир», говорит, что существуют древние санскритские тексты, в которых используется индуистско-арабская система счисления, предшествовавшая Леонардо Пизанскому на несколько столетий.
Но в 1202 году Леонардо Пизанский опубликовал математический текст Liber Abaci. Это была «поваренная книга», написанная для торговцев о том, как делать вычисления. В тексте изложена индийско-арабская арифметика, полезная для отслеживания прибылей, убытков, остатков кредита и т. д., знакомящая западный мир с последовательностью Фибоначчи.
Примеры последовательности Фибоначчи:
Кролики
В книге Леонардо задумался над вопросом: при идеальных условиях, сколько пар кроликов может быть произведено из одной пары кроликов за один год? Ответ, как оказалось, равен 144 ¬— и соотношение, используемое для получения этого ответа, как вы уже догадались, представляет собой последовательность Фибоначчи. Этот мысленный эксперимент искусственно диктует, что самки кроликов всегда рождают пары, состоящие из одного самца и одной самки.
Этот мысленный эксперимент искусственно диктует, что самки кроликов всегда рождают пары, состоящие из одного самца и одной самки.
¬В начале двух новорожденных кроликов помещают в огороженный двор и оставляют для размножения. После первого месяца остается только первоначальная пара, поскольку кролики не могут размножаться, пока им не исполнится хотя бы один месяц. К концу второго месяца рождается первая пара, теперь остается две пары крольчат. На третий месяц исходная пара кроликов производит еще одну пару новорожденных, в то время как их более раннее потомство вырастает до зрелого возраста. В результате остаются три пары кроликов, две из которых рожают еще две пары в следующем месяце.
Общее количество кроликов соответствует последовательности Фибоначчи. Через 12 месяцев будет 144 пары кроликов. Через два года это число увеличилось до 46 368 пар!
Спирали
Существует особая связь между числами Фибоначчи и золотым сечением, которое описывает, когда линия делится на две части и длинная часть (а) делится на меньшую часть (б) равно сумме (a) + (b), деленной на (a), что равно 1,618. Обозначается греческой буквой (φ). Отношение любых двух последовательных чисел Фибоначчи приблизительно соответствует значению золотого сечения ( φ = 1,6180339887…). Чем больше пара чисел Фибоначчи, тем точнее приближение. Отсюда математики могут рассчитать так называемую золотую спираль или логарифмическую спираль, коэффициент роста которой равен золотому сечению.
Обозначается греческой буквой (φ). Отношение любых двух последовательных чисел Фибоначчи приблизительно соответствует значению золотого сечения ( φ = 1,6180339887…). Чем больше пара чисел Фибоначчи, тем точнее приближение. Отсюда математики могут рассчитать так называемую золотую спираль или логарифмическую спираль, коэффициент роста которой равен золотому сечению.
Используя значения последовательности в качестве длины ребер квадратов, расположенных, как показано ниже, создается спираль.
В природе
Существует много примеров чисел Фибоначчи (числа, которые появляются в последовательности), появляющихся в естественном мире. Однако тот факт, что ряд чисел может быть применен к объекту, не означает, что существует корреляция между математикой и реальностью.
Числа Фибоначчи появляются в природе достаточно часто, чтобы доказать, что они отражают некоторые естественные закономерности. Обычно их можно заметить, изучая способ роста различных растений.
На многих семенных головках, сосновых шишках, фруктах и овощах изображены спиральные узоры, которые при подсчете выражают числа Фибоначчи. Посмотрите на спирали семян в центре подсолнуха, и вы увидите узоры, изгибающиеся влево и вправо. Если вы посчитаете эти спирали, ваша сумма будет числом Фибоначчи. Разделите спирали на заостренные влево и вправо, и вы получите два последовательных числа Фибоначчи. Таким образом вы можете расшифровать спиральные узоры в сосновых шишках, ананасах и цветной капусте, которые также отражают последовательность Фибоначчи.
Фото: https://momath.org/home/fibonacci-numbers-of-sunflower-seed-spirals/
Подробнее
The Fibonacci Quarterly — это научный журнал на математические темы, связанные с Числа Фибоначчи, публикуемые четыре раза в год. Это основное издание Ассоциации Фибоначчи, которая издает его с 1963 года.
В популярной музыке песня «Lateralus» американской прогрессив-метал-группы Tool включает последовательность Фибоначчи. Слоги в стихах песни следуют числам в последовательности Фибоначчи, возрастая и убывая в порядке 1-1-2-3-5-8-5-3-2-1-1-2-3-5-8- 13-8-5-3.
Слоги в стихах песни следуют числам в последовательности Фибоначчи, возрастая и убывая в порядке 1-1-2-3-5-8-5-3-2-1-1-2-3-5-8- 13-8-5-3.
Ссылки
Последовательность Фибоначчи (https://www.mathsisfun.com/numbers/fibonacci-sequence.html)
Природа, Золотое сечение и числа Фибоначчи (https://www.mathsisfun.com) /numbers/nature-golden-ratio-fibonacci.html)
Заблуждения о золотом сечении (https://www.jstor.org/stable/2686193?origin=JSTOR-pdf)
Фибоначчи | Биография, последовательность и факты Британника (https://www.britannica.com/biography/Fibonacci#ref2359)46)
Миф, который не исчезнет (https://www.maa.org/external_archive/devlin/devlin_05_07.html)
Что такое последовательность Фибоначчи? | Живая наука (https://www.livescience.com/37470-fibonacci-sequence.html)
Числа Фибоначчи для спиралей семян подсолнуха — Национальный музей математики (https://momath.org/home/fibonacci-numbers-of -sunflower-seed-spirals/)
Числа Фибоначчи — Список, Значение, Формула, Примеры
Числа Фибоначчи образуют последовательность чисел, где каждое число является суммой двух предыдущих чисел. Он начинается с 0 и 1 как первых двух чисел. Эта последовательность является одной из самых известных формул в математике. Вы можете найти числа Фибоначчи в структурах растений и животных. Эти числа также называют универсальным законом природы или секретным кодом природы.
Он начинается с 0 и 1 как первых двух чисел. Эта последовательность является одной из самых известных формул в математике. Вы можете найти числа Фибоначчи в структурах растений и животных. Эти числа также называют универсальным законом природы или секретным кодом природы.
В этой статье давайте подробно узнаем о числах Фибоначчи. Мы обсудим их правила, свойства и концепцию золотого сечения и его связь с числами Фибоначчи. Мы будем решать различные примеры, основанные на концепции для лучшего понимания.
| 1. | Что такое числа Фибоначчи? |
| 2. | Формула Фибоначчи |
| 3. | Правила для чисел Фибоначчи |
| 4. | Как найти числа Фибоначчи? |
| 5. | Список чисел Фибоначчи |
| 6. | Свойства чисел Фибоначчи |
| 7. | n th Числа Фибоначчи и золотое сечение |
8. |
Числа Фибоначчи в природе |
| 9. | Часто задаваемые вопросы о числах Фибоначчи |
Что такое числа Фибоначчи?
Числа Фибоначчи представляют собой последовательность целых чисел, расположенных как 0, 1, 1, 2, 3, 5, 8, 13, 21, 34,… Каждое число является суммой двух предыдущих чисел. Вот некоторые интересные факты о числах Фибоначчи:
- Эта последовательность называется последовательностью Фибоначчи, и это бесконечная последовательность.
- Каждое число в ряду или последовательности Фибоначчи представлено как F п .
Как показано ниже, числа Фибоначчи можно представить в виде спирали, если мы создадим квадраты с такой шириной. На приведенном рисунке мы видим, как квадраты аккуратно стыкуются друг с другом. Например, 5 и 8 в сумме дают 13, 8 и 13 в сумме дают 21, и так далее.
Значение Фибоначчи
В математике Фибоначчи — это понятие, которое может быть представлено в виде чисел, последовательностей или рядов, где каждый член представляет собой сумму двух предшествующих ему членов, а первые два члена равны 0 и 1. Число Фибоначчи обычно обозначается F n , где n — натуральное число. Последовательность Фибоначчи задается как 0, 1, 1, 2, 3, 5 и так далее.
Число Фибоначчи обычно обозначается F n , где n — натуральное число. Последовательность Фибоначчи задается как 0, 1, 1, 2, 3, 5 и так далее.
Формула Фибоначчи
Числа Фибоначчи следуют определенной схеме. Чтобы найти числа Фибоначчи в последовательности, мы можем применить формулу Фибоначчи. Соотношение между последующим числом и двумя предыдущими числами можно использовать в формуле для вычисления любого конкретного числа Фибоначчи в ряду с учетом его положения.
Формула для нахождения чисел Фибоначчи
Формула для вычисления (n + 1) -го -го числа в последовательности чисел Фибоначчи может быть представлена следующим образом: ,
п > 1
F n-1 → n th Число Фибоначчи
F n-2 → (n — 1) th Число Фибоначчи
Правила для чисел Фибоначчи
Правила для чисел Фибоначчи даны как:
- Первое число в списке чисел Фибоначчи выражается как F 0 = 0, а второе число в списке чисел Фибоначчи выражается как F 1 = 1.
- Числа Фибоначчи следуют правилу, согласно которому F n = F n-1 + F n-2 , где n > 1,
- Третье число Фибоначчи задается как F 2 = F 1 + F 0 . Как мы знаем, F 0 = 0 и F 1 = 1, значение F 2 = 0 + 1 = 1.
- Последовательность чисел Фибоначчи выглядит так: 0, 1, 1, 2 и так далее.
Правило для чисел Фибоначчи, если объяснить его простыми словами, гласит, что каждое число в последовательности является суммой двух предшествующих ему чисел в последовательности.
Как найти числа Фибоначчи?
Давайте рассчитаем числа Фибоначчи, используя правило из предыдущего раздела. Последовательность задается как 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89., 144 и так далее. Давайте посмотрим, как появляются в последовательности первые десять членов. Если свести расчет в таблицу, то получим:
| n | Срок | Ф н-1 | Ф н-2 | F n = F n-1 + F n-2, |
|---|---|---|---|---|
| 0 | Первый | — | — | Ф 0 = 0 |
| 1 | Второй | Ф 0 = 0 | — | Ф 1 = 1 |
| 2 | Третий | Ф 1 = 1 | Ф 0 = 0 | F 2 = 0 + 1 = 1 |
| 3 | Четвертый | Ф 2 = 1 | Ф 1 = 1 |
F 3 = 1 + 1 = 2 |
| 4 | Пятый | Ф 3 = 2 | Ф 2 = 1 | F 4 = 2 + 1 = 3 |
| 5 | Шестой | Ф 4 = 3 | Ф 3 = 2 | F 5 = 3 + 2 = 5 |
| 6 | Седьмой | Ф 5 = 5 | Ф 4 = 3 | F 6 = 5 + 3 = 8 |
| 7 | Восьмой | Ф 6 = 8 | Ф 5 = 5 | F 7 = 8 + 5 = 13 |
| 8 | Девятый | Ф 7 = 13 | Ф 6 = 8 | F 8 = 13 + 8 = 21 |
| 9 | Десятый | Ф 8 = 21 | Ф 7 = 13 | F 9 = 21 + 13 = 34 |
Из приведенной выше таблицы мы можем сделать вывод, что:
- В последовательности, образованной числами Фибоначчи, первый член всегда равен 0, а второй член всегда равен 1.

- Результат, полученный в столбце 5 th , представляет собой сумму значений в столбцах 3 rd и 4 th , которые представляют два предыдущих числа.
Список чисел Фибоначчи
Используя формулу чисел Фибоначчи и метод нахождения последовательных членов в последовательности, образованной числами Фибоначчи, описанный в предыдущем разделе, мы можем сформировать список чисел Фибоначчи, как показано ниже.
| F 0 = 0 | Ф 10 = 55 |
| Ф 1 = 1 | Ф 11 = 89 |
| Ф 2 = 1 | Ф 12 = 144 |
| Ф 3 = 2 | Ф 13 = 233 |
| Ф 4 = 3 | Ф 14 = 377 |
| Ф 5 = 5 | Ф 15 = 610 |
| Ф 6 = 8 | Ф 16 = 987 |
| Ф 7 = 13 | Ф 17 = 1597 |
| Ф 8 = 21 | Ф 18 = 2584 |
| Ф 9 = 34 | Ф 19 = 4181 |
Свойства чисел Фибоначчи
Числа Фибоначчи используются во многих компьютерных алгоритмах, таких как кубы Фибоначчи, структура данных кучи Фибоначчи и техника поиска Фибоначчи. Давайте посмотрим на различные свойства чисел Фибоначчи в зависимости от положения числа выше и ниже нуля.
Давайте посмотрим на различные свойства чисел Фибоначчи в зависимости от положения числа выше и ниже нуля.
Первые 10 чисел Фибоначчи в последовательности могут быть представлены как:
| F 0 | Ф 1 | Ф 2 | Ф 3 | Ф 4 | Ф 5 | Ф 6 | Ф 7 | Ф 8 | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 |
- Последовательность чисел Фибоначчи может быть расширена до отрицательного индекса n также перестановкой рекуррентного соотношения F n-2 = F n — F n-1 .
- Это дает последовательность чисел NegaFibonacci, которая имеет соотношение F -n =(-1) n+1 × F n .
Таким образом, для чисел Фибоначчи двунаправленная последовательность выглядит так:
| F -5 | Ф -4 | Ф -3 | Ф -2 | Ф -1 | Ф 0 | Ф 1 | Ф 2 | Ф 3 | Ф 4 | Ф 5 |
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | -3 | 2 | -1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 |
Из приведенной выше таблицы видно, что числа Фибоначчи ниже нуля такие же, как числа Фибоначчи выше нуля, с той лишь разницей, что они следуют схеме + — + -. Интересно отметить, что числа Фибоначчи используются при планировании игр в покер.
Интересно отметить, что числа Фибоначчи используются при планировании игр в покер.
n-е число Фибоначчи и золотое сечение
Когда берутся любые два последовательных числа Фибоначчи, их отношение очень близко к 1,618034. Возьмем случайный пример двух последовательных чисел:
- Пусть A = 13, B = 21 и, давайте разделим B на A. Получим 21 ÷ 13 = 1,615.
- Это соотношение последовательных чисел Фибоначчи известно как Золотое сечение.
Мы можем вычислить любое число Фибоначчи, используя это Золотое сечение по следующей формуле: F n = ((ɸ) n − (1−ɸ) n ) ÷ √5. Здесь ɸ = 1,618034. Рассчитаем F 6 = ((1,618034) 6 − (1− 1,618034) 6 ) ÷ √5. Когда этот расчет производится с помощью калькулятора, мы получаем значение F 6 как 8,00000033, которое при округлении до ближайшего целого числа становится 8.
Числа Фибоначчи в природе
Мы можем найти числа Фибоначчи повсюду в природе. Вот некоторые из наиболее распространенных моделей и последовательностей чисел Фибоначчи в природе:
Вот некоторые из наиболее распространенных моделей и последовательностей чисел Фибоначчи в природе:
- Лепестки некоторых растений, таких как подсолнухи, лилии, розы и лютики, следуют схеме Фибоначчи, и эти цветы называются цветами Фибоначчи.
- Спирали, которые встречаются на сосновой шишке, равны числам Фибоначчи.
- Говорят, что даже семена подсолнуха следуют схеме Фибоначчи.
- Морские ракушки и морские звезды, которых мы находим на берегу моря, следуют схеме чисел Фибоначчи.
Одним из практических применений концепции чисел Фибоначчи является то, что она применялась при строительстве Великой пирамиды в Гизе.
Статьи по теме:
Ознакомьтесь со следующими страницами, посвященными числам Фибоначчи в математике.
- Калькулятор чисел Фибоначчи
- Арифметическая прогрессия
- Калькулятор последовательности
- Калькулятор арифметической последовательности
Важные примечания о числах Фибоначчи:
Вот список нескольких моментов, которые следует помнить при изучении чисел Фибоначчи.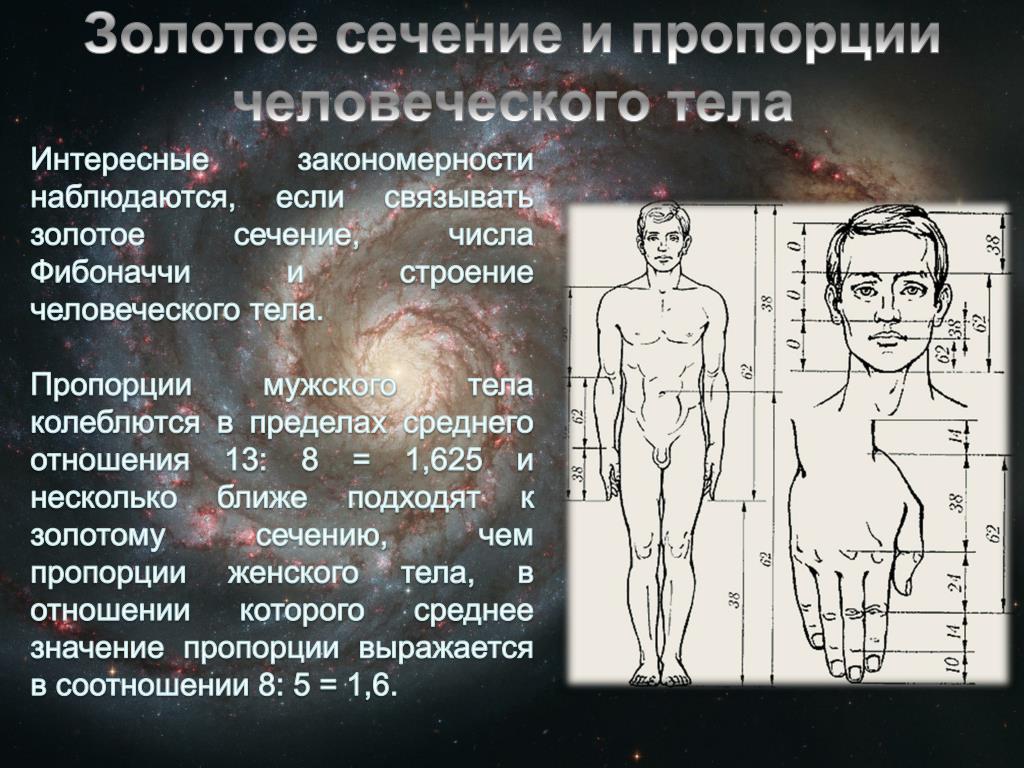
- Концепция чисел Фибоначчи применима только к целым числам и десятичным числам с финансовой точки зрения.
- Последовательность чисел Фибоначчи также применима к числам ниже нуля.
- Первое число Фибоначчи всегда равно 0, а второе число Фибоначчи всегда равно 1.
Числа Фибоначчи Примеры
-
Пример 1: Найдите сумму первых десяти чисел Фибоначчи.
Решение:
Список чисел Фибоначчи задается как 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.
Суммируя числа в последовательности, мы получаем,
Сумма = 0 + 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 = 88.
Таким образом, сумма первых десяти чисел Фибоначчи равна 88.
-
Пример 2: Рассчитайте значение 12 -е и 13-е -е числа Фибоначчи. 9-й и 10-й члены последовательности равны 21 и 34.
Решение:
Мы можем вычислить 12 и 13 числа Фибоначчи следующим образом:
11 сложив члены 9 th и 10 th как 21 + 34 = 55
0005
Таким образом, числа Фибоначчи 12 th и 13 th равны 89 и 144 соответственно.

перейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Записаться на бесплатный пробный урок
Вопросы по числам Фибоначчи
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о числах Фибоначчи
Что такое числа Фибоначчи?
Числа Фибоначчи образуют последовательность чисел, в которой каждое число является суммой двух предыдущих чисел. Он начинается с 0 и 1 как первых двух чисел.
Почему числа Фибоначчи так важны?
Числа Фибоначчи имеют множество практических применений в компьютерных технологиях, музыке, финансовых рынках и многих других областях. Числа Фибоначчи существуют в природе в различных формах и формах.
Является ли 0 числом Фибоначчи?
Да, 0 — это число Фибоначчи, и это первое число Фибоначчи. Обозначается F 0 .
Обозначается F 0 .
Бесконечны ли числа Фибоначчи?
Да, список Фибоначчи состоит из бесконечных чисел Фибоначчи, где каждое число вычисляется простым сложением двух предшествующих ему чисел. Каждое число в последовательности чисел Фибоначчи представлено как F n .
Существует ли формула для нахождения чисел Фибоначчи?
Да, есть формула для нахождения чисел Фибоначчи. Числа Фибоначчи следуют этой формуле, согласно которой F n = F n-1 + F n-2 , где F n — это (n + 1) -й член и n > 1. первое число Фибоначчи выражается как F 0 = 0, а второе число Фибоначчи выражается как F 1 = 1.
Как рассчитать числа Фибоначчи?
Числа Фибоначчи в зависимости от их положения в ряду могут быть рассчитаны с использованием общей формулы для чисел Фибоначчи, представленной как F n = F n-1 + F n-2 , где F n — (n + 1) th член и n > 1.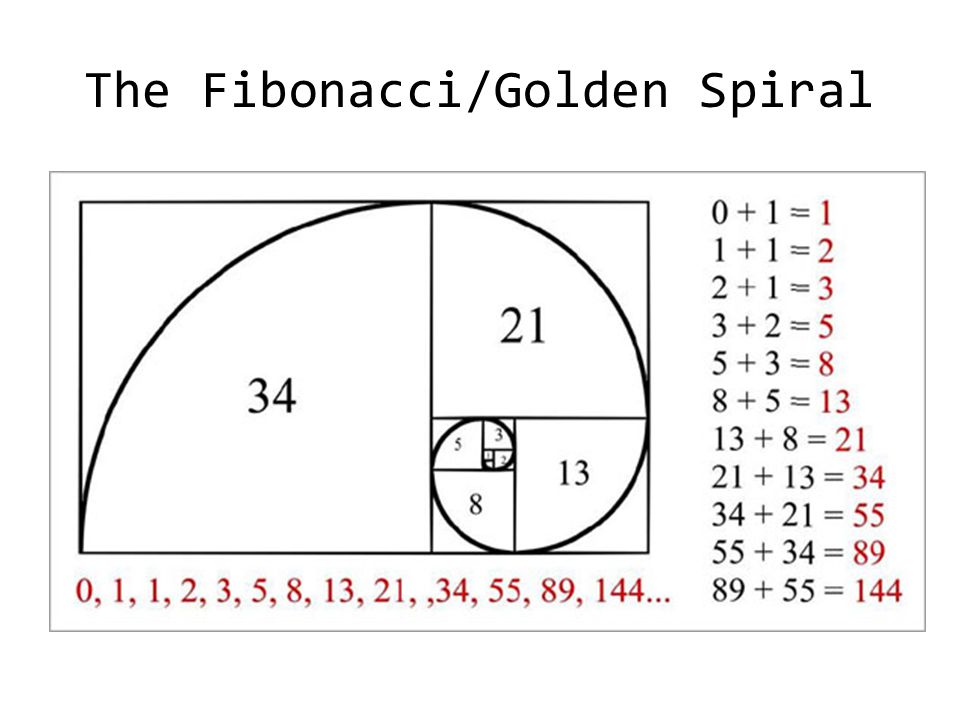
Какова формула для нахождения чисел Фибоначчи?
Формула для нахождения (n + 1) -го члена в последовательности, образованной числами Фибоначчи, может быть представлена как F n = F n-1 + F n-2 , где n > 1.
Каковы применения чисел Фибоначчи?
Числа Фибоначчи имеют различные применения в области математического и финансового анализа. Мы используем числа Фибоначчи в вычислительном анализе времени выполнения алгоритма Евклида, чтобы найти HCF. Кроме того, многие закономерности в природе можно изучать с помощью чисел Фибоначчи.
Каковы первые 10 чисел Фибоначчи?
Первые 10 чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34. Здесь мы видим, что первое число Фибоначчи всегда равно 0, а второе число Фибоначчи всегда равно 1.
Что такое числа Фибоначчи в природе?
Мы можем найти числа Фибоначчи повсюду в природе. Вот некоторые из наиболее распространенных моделей и последовательностей чисел Фибоначчи в природе:
- Лепестки некоторых растений, таких как подсолнухи, лилии, розы и лютики, следуют схеме Фибоначчи, и эти цветы называются цветами Фибоначчи.
 Числа фибоначчи и золотое сечение взаимосвязь: Золотое сечение и пропорции Фибоначчи
Числа фибоначчи и золотое сечение взаимосвязь: Золотое сечение и пропорции Фибоначчи
