Числа фибоначчи и золотое сечение: Золотое сечение и пропорции Фибоначчи — Главная

Содержание

Числа Фибоначчи и золотое сечение. А при чем здесь стоматология? |

Эстетическое направление в стоматологии развивается стремительно. Но, как и в любой другой сфере, так или иначе связанной с красотой, здесь тоже есть принципы, над которыми не властно время. Одним из таких принципов является принцип золотого сечения, описанный в XIII веке средневековым математиком Леонардо Фибоначчи. Хотя поначалу этот концепт окружал некий ореол мистицизма, сейчас ни у кого не возникает сомнений по поводу релевантности золотого сечения.

Задолго до Фибоначчи древние греки пользовались этим принципом, чтобы создавать произведения искусства. Сам Леонардо Да Винчи прибегал к золотой пропорции практически во всех своих творениях. Этим же принципом руководствуются и современные автомобильные дизайнеры.

Ряд Фибоначчи

Последовательность Фибоначчи встречается в природе практически на каждом шагу – в количестве лепестков розы или кроликов, родившихся за год. Кстати, последний пример особенно волновал Фибоначчи в 1202 году.

Ряд Фибоначчи представляет собой числовую последовательность, первые значения которого равны 0 или 1, а каждое последующее равно сумме двух предыдущих.

Выглядит это следующим образом: 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 и т.д.. В конечном счете получается последовательность: 1, 1, 2, 3, 5, 8, 13 …

Золотое сечение

Если поделить одно число из последовательности на предшествующее ему, то получится значение, близкое к 1,618. С развитием последовательности частное, которое еще называют числом Фи, становится все более точным. А его инверсия – 0,618 или число фи – как раз считается золотым сечением.

Числа Фибоначчи лежат в основе золотого сечения (1:1,618) и, как следствие, золотой спирали и золотого прямоугольника. Кредитная карта представляет собой идеальный пример золотого прямоугольника. Ее измерения равны 53 мм и 86 мм. Умножив 53 на число Фи или 1,618, получаем 86.

Лучше всего представить себе золотую спираль на примере раковины моллюска наутилуса. Золотая спираль основывается на квадратах из числа последовательности Фибоначчи, начиная с 1×1.

Связь со стоматологией

Золотое сечение используется при определении размера зуба.

Средняя ширина центрального резца составляет примерно 8 мм. Ширина двух центральных резцов будет равняться 16 мм. Если мы хотим определить идеальную эстетическую длину этих самых резцов, мы можем поделить 16 на 1,618 и получится 9,89 мм. Такие расчеты помогают при восстановлении зубов.

Приведем еще один пример. Ширина центральных резцов является хорошей отправной точкой в расчетах. Поэтому допустим, что 8,5 мм является идеальной шириной для конкретного пациента. Ширина обоих центральных резцов составляет 17, а идеальная эстетическая длина — 10,5 мм (17 / 1,618 = 10,5). Если мы разделим ширину этого центрального резца на число Фи, у нас получится результат, с помощью которого можно вернуть идеальную эстетическую визуальную ширину зуба позади него (боковой резец). Следовательно, 8,5 мм / 1,618 = 5,3 мм, и в этом случае это идеальная визуальная ширина бокового резца.

Стоит учитывать, что речь идет именно о визуальной, а не фактической ширине бокового резца. Можно посчитать все еще раз, определяя идеальную ширину клыка: 5,3 мм / 1,618 = 3,3 мм, первого премоляра позади него: 3,3 мм / 1,618 = 2,0 мм, второго премоляра: 2,0 мм / 1,618 = 1,2 мм и т.д..

Таким образом у нас вырисовывается вполне конкретный план реставрации.

Использование золотого сечения — это всего лишь инструмент для создания идеальной эстетической улыбки. Оно может предоставить стоматологу информацию, которая поможет начать разработку новой улыбки пациента. Золотое сечение не является единственным залогом успеха, поскольку есть много других факторов, которые необходимо учитывать.

Поделиться ссылкой:

The following two tabs change content below.

Автор и редактор блога Стомдевайс. Специализируется на стоматологии, медицине и маркетинге. В 2018 году стажировалась в отделе локализации Google. В 2017 и 2018 году стала призером Международной научной конференции молодых ученых в МГУ. С 2015 года профессионально занимается переводами с английского языка.

Что такое числа Фибоначчи, золотое сечение? ⋆ FutureNow

Последовательность Фибоначчи – одна из самых известных формул математики. Так, что такое числа Фибоначчи, золотое сечение и какая их интересная стория?

Что такое числа Фибоначчи?

Каждое число в последовательности Фибоначчи – это сумма двух чисел, предшествующих ему.

Итак, последовательность выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. Математическое уравнение, описывающее число Фибоначчи: Xn + 2 = Xn + 1 + Xn

Фибоначчи числа иногда называют “секретным кодом природы” и “общем правилом природы”. Говорят, что данная последовательность руководит размерами всего сущего, в том числе обьясняет Великую пирамиду в Гизе, так и многие вещи, с которыми мы сталкиваемся каждый день.

Числа Фибоначчи: богатая история

Поэтому какова реальная история стоит за этой знаменитой последовательностью?

Многие источники утверждают, что ее впервые обнаружил или “изобрел” Леонардо Фибоначчи.

Итальянский математик, родился около 1170 года нашей эры и первоначально был известен как Леонардо из Пизы. Лишь в 19 веке историки придумали прозвище Фибоначчи, чтобы отличить математика от другого известного Пизарського Леонардо.

Но Леонардо из Пизы на самом деле не изобрел последовательность. Ее впервые упоминают древние санскритские тексты, в которых использовалась индуистско-арабская система числения, еще много веков до Леонардо Пизы.

Однако в 1202 Леонардо из Пизы опубликовал большой том “Liber Abaci,” книгу по математике “о том, как производить вычисления”. “Liber Abaci”, написанная для торговцев, где изложена индуистско-арабский арифметика, которая является полезной для отслеживания прибыли, убытков, остатков по кредитам и тому подобное.

ЧТО ТАКОЕ ШАРОВАЯ МОЛНИЯ: СУЩЕСТВУЕТ ЛИ ОНА?

В книге Леонардо из Пизы вводит последовательность с задачей о кроликах. Проблема заключается в следующем: начнем с самца и самки кролика. Через месяц они созревают и дают помет в результате которого мы имеем еще самца и самку кролика. Через месяц эти кролики размножаются и получается – вы догадались – еще один самец и самка, которые также могут спариваться через месяц. Через год сколько бы у вас было кроликов? Ответ, 144, спрятан в формуле, которая сейчас известна как последовательность Фибоначчи.

“Liber Abaci” впервые представила эту последовательность западному миру. Но после нескольких скудных абзацев о разведении кроликов Леонардо из Пизы больше никогда не вспоминал ее.

На самом деле эти числа Фибоначчи были забыты до 19 века, когда математики подробнее изучили математические свойства последовательности. В 1877 году французский математик Эдуард Лукас официально назвал задачу о кроликах “последовательностью Фибоначчи”.

Числа Фибоначчи и золотое сечение

Мы узнали что такое числа Фибоначчи, но какое же значение имеет последовательность Фибоначчи?

Кроме как учебный инструмент, она проявляется во многих случаях в природе. Однако, это не какой-то секретный код, который руководит архитектурой Вселенной.

Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как “золотое сечение”. Проще говоря, отношение чисел в последовательности, поскольку последовательность идет к бесконечности, приближается к золотому сечению, который составляет +1,6180339887498948482 … Оттуда математики могут вычислить то, что называется золотой спиралью, или логарифмической спирали, коэффициент роста которой равен золотому сечению.

Золотое сечение объясняет рост некоторых растений. Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Но есть также растения, которые не соблюдают этого правила.

Мистификации и выдумки

Когда люди начинают связывать человеческое тело, искусство и архитектуру, много вымышленных теорий и мистификаций ссылаются на последовательность Фибоначчи.

“Понадобится большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, многие из которой – это просто повторение одних и тех же фантазий разных авторов”, – написал Джордж Марковский, математик из университета Мэн в 1992 году.

Значительная часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Зейзинга. Он утверждал, что пропорции человеческого тела основана на золотом сечении.

Золотое соотношение проросло в “золотые прямоугольники”, “золотые треугольники” и всевозможные теории об этих знаковых размерах.

С тех пор люди говорят, что золотое соотношение или золотое сечение можно найти в размерах Пирамиды в Гизе, Парфеноне, “Витрувийським человеке” Леонардо да Винчи и ренессансных сооружениях.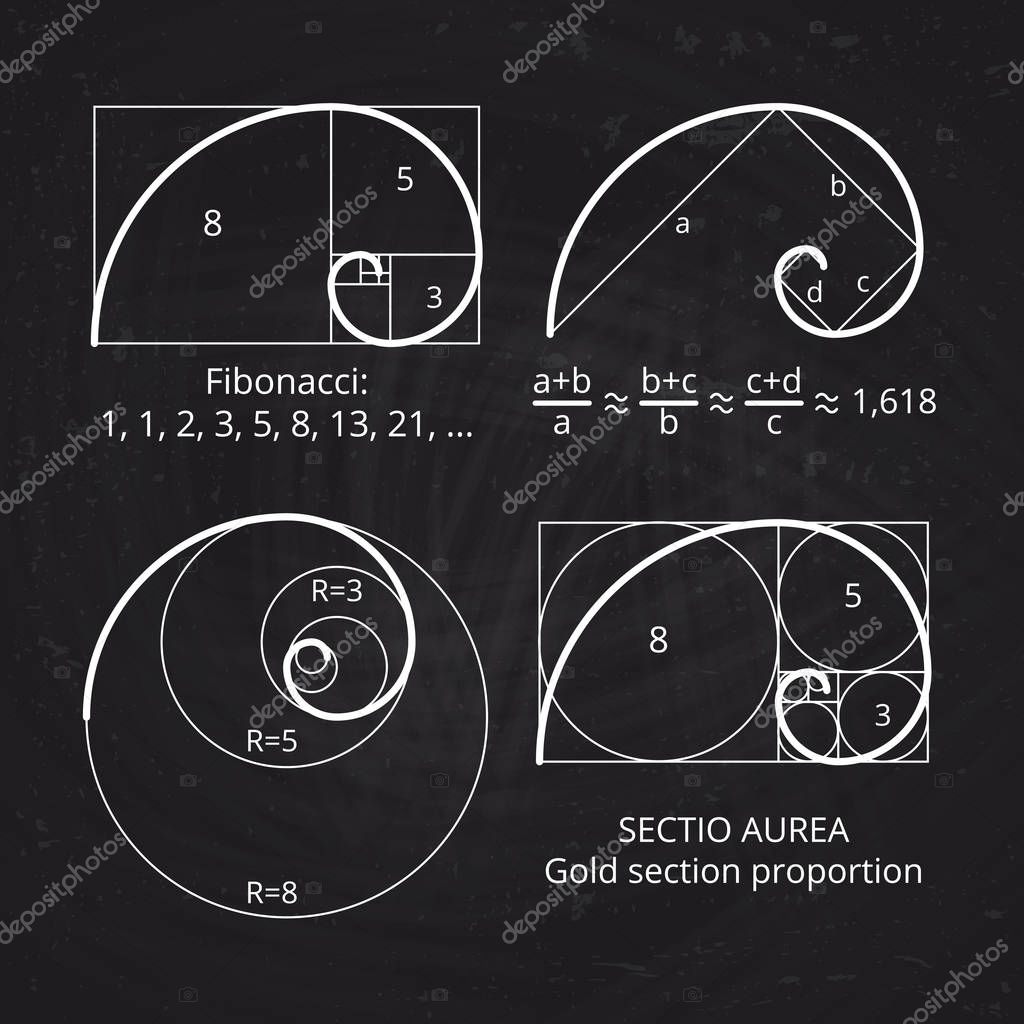

Под сомнение можно поставить и беспрекословное утверждение о том, что золотое сечение является “однозначно приятным” для человеческого глаза – на чем часто настаивают фотографы.

Часто все эти утверждения, когда их проверяют, являются ошибочными. Люди часто выдают желаемое за действительное.

Источник: www.livescience.com/

Числа Фибоначчи и золотое сечение окружают нас повсюду. Вот примеры | Хакнем Школа

Дэн Браун «Код да Винчи»

#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳

Недавно, читая роман Дэна Брауна «Код да Винчи», я по-новому посмотрела на известные со школы: последовательность чисел Фибоначчи, «золотое сечение» и число Фи. Герой романа использует в качестве кода несколько чисел этого ряда.

Своими новыми для себя открытиями я решила поделиться с нашими читателями.

Удивительную последовательность чисел открыл итальянский математик Леонардо Пизанский, более известный под именем Фибоначчи (родился около 1170 — умер после 1228).

Числа, образующие последовательность:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, … называются «числами Фибоначчи», а сама последовательность — последовательностью Фибоначчи. Что же в них такого удивительного?

Числовая последовательность Фибоначчи в задачке с размножением кроликов

1) В этой последовательности первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число получается из суммы двух предыдущих чисел: 1 = 0 +1, 2 = 1 + 1, 3 = 1 +2, 5 = 2 + 3, 8 = 3 +5, и т. д.

2) Ещё одна особенность в том, что при делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом будет величина, колеблющаяся около иррационального значения 1. 61803398875… и через раз то — превосходящая, то — не достигающая его. После 13-ого числа этот результат деления становится постоянным до бесконечности ряда.

Именно это постоянное число деления в средние века было названо Божественной пропорцией, а в наши дни именуется, как золотое сечение. В алгебре это число обозначается греческой буквой фи (φ).

Итак, Золотая пропорция = 1 : 1,618

233 / 144 = 1,618

377 / 233 = 1,618

610 / 377 = 1,618 и т.д., можете проверить сами…

Но самое интересное, что меня поразило, это то, что золотая пропорция есть как в нашем теле, так и в природе.

Тело человека и золотое сечение«Витрувиа́нский человек» — изображение, созданное Леонардо да Винчи

«Витрувиа́нский человек» — изображение, созданное Леонардо да Винчи

Оказывается, художники, учёные, модельеры и дизайнеры делают свои расчёты, чертежи или наброски, исходя из соотношения золотого сечения, так как пропорции различных частей нашего тела составляют число, очень близкое к золотому сечению.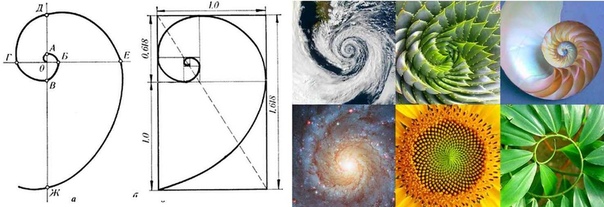

Если эти пропорции совпадают с формулой золотого сечения, то внешность или тело человека считается идеально сложенным.

Несколько основных золотых пропорций нашего тела:

· расстояние от кончиков пальцев до запястья равно 1:1,618;

· расстояние от уровня плеча до макушки головы и размера головы равно 1:1,618;

· расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы равно 1:1,618;

· расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей равно 1:1,618 и др.

Формулу золотого сечения можно найти в других частях тела человека: и в руках человека, и ушах, и в строении лёгких и даже в строении молекулы ДНК (если интересно, можно найти информацию самостоятельно).

Золотой прямоугольникЗолотой прямоугольник

Золотой прямоугольник

В геометрии есть такой прямоугольник, который называют золотым прямоугольником, его длинные стороны соотносятся с короткими сторонами в соотношении 1,168:1.

Он обладает удивительными свойствами — отрезав от золотого прямоугольника квадрат, строна которого равна меньшей стороны прямоугольника, мы снова получим золотой прямоугольник, но меньшего размера. Продолжая отрезать квадраты, мы будем получать всё меньшие и меньшие золотые прямоугольники.

Причём, располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов (например, раковинах улиток).

ПРИРОДАИдеальную пропорцию создала сама природа

Идеальную пропорцию создала сама природа

В природе, лежащее в основе строения спирали, правило золотого сечения встречается в природе очень часто в бесподобных по красоте творениях:

числа спиралей на большинстве шишек и ананасах равны числам Фибоначчи;
расположение листьев и ветвей на стеблях многих растений соответствуют числам Фибоначчи;
семена в центре подсолнуха организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки;
у большинства улиток, которые обладают раковинами, раковина растёт в форме логарифмической спирали.

Наутилус раковина

Оказывается, числа Фибоначчи повсюду вокруг нас!

#хакнем_математика 👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳

Автор: #ирина_чудневцева 41 год, город Ярославль, мама 16-летнего подростка.

как оно стало божественной пропорцией

В XIII веке один из выдающихся математиков Европы Леонардо Пизанский, более известный нам как Фибоначчи, задался следующим вопросом: сколько будет кроликов через год, если изначально их была одна пара, а природа их такова, что любая пара кроликов производит на свет другую пару каждый месяц?

При решении этой весьма практичной задачи Фибоначчи заметил одну интересную закономерность. Ответ ниже, а о том, как мы и Фибоначчи к нему пришли, попробуйте решить сами.

Фибоначчи заметил, что каждое последующее значение (количество) кроликов равно сумме двух предыдущих значений.

Забавный, на первый взгляд, вывод имеет отношение к золотому сечению. Но для начала вспомним, что изначально значение ϕ было получено, как корень квадратного уравнения . Которое мы можем преобразовать в , откуда следует . Далее подставим вместо значения x в знаменателе выражение и так далее:

Что же интересного в этой красивой и бесконечной дроби?

Если брать х=1 в правой части дроби, то мы получим в итоге дробь, состоящую из отношения чисел Фибоначчи, в то же время это соотношение служит приближением золотого сечения, чем больше n, тем точнее приближение. Так как само значение золотого числа есть иррациональное число, а любое деление в этой пропорции может быть достаточно сложной процедурой. В этом случае нам как раз помогут числа Фибоначчи, которые уже указывают нам соотношение (причём в целых числах), например, золотым сечением числа 8 будет 3 и 5, числа 13 будет 5 и 8 и так далее.

Золотое сечение является одной из любимых тем мистиков и любителей загадок. Ведь, как было сказано выше, в природе оно встречается достаточно часто. Возможно, принцип самоорганизации материи (в том числе и живых существ) основан на принципах подобия её частей. Тогда неудивительна повсеместность золотого сечения. Но ведь существуют и другие удивительные числа, которые вы сможете найти везде, например число π, соотношение длины любой окружности к длине её диаметра. Математика — язык, придуманный для описания Вселенной. Он не всегда отвечает на вопрос “почему?”, а скорее: “как это происходит?”. Закономерности вроде золотого сечения и числа π являются одними из множества красивых проявлений природы на языке математики.

Золотое сечение и числа Фибоначчи

Людей с давних времён волновал вопрос, подчиняются ли такие
неуловимые вещи, как красота и гармония, каким-либо
математическим расчётам.
Можно ли «поверить алгеброй гармонию?» — как сказал
А.С. Пушкин.
Конечно, все законы красоты невозможно вместить в несколько
формул, но математика может открыть нам некоторые
слагаемые прекрасного.

Познакомимся с одним из таких математических соотношений.
Там, где оно присутствует, ощущается гармония и красота.
Рассмотрим отрезок АВ.
Его можно разделить точкой С на две части бесконечным множеством способов.
Говорят, что точка С производит золотое сечение отрезка АВ, если выполняется
пропорция: длина всего отрезка так относится к длине большего отрезка, как
длина большего относится к длине меньшего отрезка, то есть
Найдём коэффициент золотого сечения:
1,618… = Ф (фи)
Такое обозначение принято в честь
древнегреческого скульптора
Фидия, жившего в V веке до н.э.
Он прославился удивительно
гармоничными статуями и
архитектурными сооружениями.
Итак, золотое сечение – это иррациональное число, оно приблизительно равно
1,618.
Части золотого сечения составляют приблизительно 62% и 38% всего отрезка.
Термин «золотое сечение»

ввёл Леонардо да Винчи.
Число 1,618 играет по-своему
уникальную роль, роль
кирпичика в фундаменте
построения всего живого на
земле.

Пропорции различных частей нашего
тела составляют число, очень близкое к
золотому сечению.
Число Фи не только является критерием
прекрасного для человека.
Этот принцип соблюдается в строении
животных, в форме яйца и развитии
побегов растений.
В древности считалось, что именно эта пропорция, соблюденная
в архитектурных сооружениях, больше всего радует глаз.
Парфенон. Западный фасад (447-438 до н.э.).
Архитектор Фидий.
С историей золотого сечения связано имя итальянского математика
монаха Леонардо из Пизы, более известного под именем Фибоначчи.
Ряд чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд
Фибоначчи.
Каждый его член, начиная с третьего, равен сумме двух предыдущих
2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21; 13 + 21 = 34 и т.д.
А отношение смежных чисел ряда приближается к отношению
золотого деления.
Так, 34:21 = 1,619, 55:34 = 1,617.
Еще Гёте подчеркивал тенденцию природы к спиральности.

Спираль увидели в расположении семян подсолнечника, в
шишках сосны, ананасах, кактусах и т.д.
Паук плетет паутину спиралеобразно.
Совместная работа ботаников и математиков пролила свет
на эти удивительные явления природы.
Выяснилось, что в расположении листьев на ветке, семян
подсолнечника, шишек сосны проявляет себя ряд
Фибоначчи, а стало быть, проявляет себя закон золотого
сечения.
По золотой спирали свёрнуты раковины
многих улиток и моллюсков.
Природа повторяет свои находки, как
в малом, так и в большом.
По золотым спиралям закручиваются
многие галактики.
Рассмотрим расположение семечек в корзине
подсолнуха. Они выстраиваются вдоль спиралей,
которые закручиваются как слева направо, так и
справа налево.
В одну сторону у среднего подсолнуха закручено 13
спиралей, в другую – 21 . Отношение 21/13 равно Фи.
А каково же число семян в соцветии
подсолнуха?
По 34 и 55 в спиралях по часовой
стрелке и против соответственно.

Это числа из ряда Фибоначчи.
В Ботаническом саду Британского
университета Леcтера выложены
мозаикой три площадки,
символизирующие домик улитки,
сосновую шишку и первые
двенадцать чисел из
последовательности
Фибоначчи.
Золотое сечение – не середина, а пропорция – несложное математическое
соотношение, содержащее в себе “закон звезды и формулу цветка”, рисунок на
хитиновом покрове животных, длину ветвей дерева, пропорции человеческого тела.
Видишь гармоничную композицию, пропорциональное телосложение или здание,
радующее глаз, – измерь и придёшь к одной и той же формуле.
www.goldenmuseum.com/index_rus.html
Материалы с сайта «Музей гармонии»

Золотое сечение в архитектуре: принцип проектирования зданий

Почему нас так привлекают строения древней архитектуры, при виде которых мы испытываем гармонию и умиротворение? Все они были построены на основе золотого сечения, данная зависимость прослеживается и в средневековье, и в современном мире. Математическая пропорция встречается повсеместно: это и ракушки моллюсков, и знаменитые картины художников, и строение человеческого тела, и даже египетские пирамиды. Сегодня об обзоре редакции Homius.ru расскажем простыми словами, как и, самое главное, зачем нужно использовать божественную гармонию чисел, и как она поможет в строительстве собственного дома и оформлении интерьера.

Винтовая лестница построена по принципу золотого сечения

Содержание статьи

Просто о сложном: что это такое – правило золотого сечения

Золотое сечение –это правило общей пропорции, которая создает универсальную композицию. Математики называют её формулой божественной гармонии или асимметричной симметрией.

Это интересно! Общее определение правила ЗС –меньшая величина относится к большей, как большая к целому. Было рассчитано приблизительное число, равное 1,6180339887, это и есть коэффициент золотого сечения. Если смотреть в процентном соотношении, то в одном целом меньшая величина занимает 38%, большая – 62%.

Признано считать, что ЗС пришло к нам еще с древней Греции, но есть и такое мнение, что его греки подсмотрели у египтян. Если проанализировать архитектуру Египта того времени, можно чётко проследить соблюдение математической гармонии. Необычные свойства числовой зависимости стали причиной мистического отношения к золотому сечению:

практически все живые организмы можно привести к принципу числовой зависимости. Например, тело человека, количество семечек в подсолнухе, структуру ДНК, произведения искусства и вирусную бактерию;
данная зависимость чисел характерна только для биологических существ и кристаллов, все остальные неживые объекты природы крайне редко обладают золотой пропорцией;
именно математическая пропорция в строении биологических объектов оказалась оптимальной для выживания.

Идеальный пример ЗС в природе — раковина морского моллюска

Экскурс в историю: кто придумал золотое сечение

Представление о золотой пропорции имели и древние греки, и египтяне, известно было о ней и на Руси. Но впервые ещё в 1509 году в книге «Божественная Пропорция», иллюстрации к которой принадлежат Леонардо да Винчи, монах Лука Пачоли дал научное определение правилу. Он видел в золотом сечении божественное единство:

маленький отрезок – это сын;
большой – отец;
весь отрезок – это святой дух.

Это интересно! Историки присваивают Леонардо да Винчи определение термина ЗС, поскольку он долгое время изучал божественную закономерность и воплощал её принцип в своих творениях.

Вторую жизнь ЗС получило в 1855 году благодаря философу Адольфу Цейзингу. Он доработал теорию до абсолютного идеала, и она стала универсальной для всех проявлений. Все это он описал в своей книге «Математическое Эстетство», на которое в свое время обрушилось много негатива и критики.

Золотое сечение в божественной пропорции

Принцип расчета и построения золотого сечения

Примеры пропорции золотого сечения можно видеть при строительстве многих архитектурных сооружений, только нужно знать, как правильно его увидеть. Для этого достаточно посмотреть на строение всего 5 минут.

Как определить число золотого сечения

С пропорцией ЗС связывают астронома из Италии Фибоначчи, он вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Сегодня эта закономерность известна как ряд Фибоначчи:

0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и так до бесконечности;
если выполнить деление последующего числа на предыдущее – получится коэффициент ЗС.

Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленные значения 0,62 и 0,38.

Ряд Фибоначчи в церкви Покрова на Нерли

Как рассчитать золотое сечение на простейшем примере

Проще всего объяснить гармонию ЗС можно на примере обычного куриного яйца, точнее на удалении всех точек скорлупы от центра тяжести. Именно форма оболочки, а не её прочность, обеспечила выживаемость птиц столь долгое время и в любых условиях.

Если взять обычный отрезок, который состоит из нескольких маленьких, их длины относятся к большей величине как 0,62. Это показывает, как можно разбить целую линию для получения идеальной пропорции.

Простой пример золотого сечения в курином яйце

Как построить золотое сечение на примере прямоугольника и спирали

Если построить золотой прямоугольник, используя ряд Фибоначчи, он будет выглядеть как единое целое. Рассмотрим зависимость на примере:

нужно нарисовать квадрат со стороной 1 и рядом ещё один аналогичный;
над ними разместить квадрат со стороной 2;
слева гармонично помещается квадрат с гранью 3;
ниже – квадрат со стороной 5;
справа пространство займет квадрат с гранью 8;
площадь прямоугольника 8×13, в котором 13 — это следующее число ряда;
если разделить на калькуляторе следующее число на предыдущее, получится значение золотого сечения 1,62, причём, чем больше числа, тем меньшая погрешность в их отношении;
если по этому принципу построить спираль, каждую четверть витка она будет расширяться именно на значение ЗС.

Принцип золотого сечения в прямоугольникеПостроение золотой спирали из прямоугольника

На видео можно более подробно узнать про магию чисел Фибоначчи:

Божественная гармония золотого сечения в архитектуре: фото древних построек и примеры современного строительства

Многие древние здания, которые сохранились до наших времен, подтверждают мнение, что они были построены по правилам идеальной пропорции. Это резиденции королей, церкви, общественные сооружения. Рассмотрим на примерах принцип золотого сечения в разных странах.

Тайны древнеегипетской архитектуры

В архитектуре Древнего Египта по правилам золотой пропорции была построена пирамида Хеопса. Глядя на творение строителей, можно увидеть треугольник с прямым углом, один катет которого является высотой, второй – половиной длины основания. Если взять отношение гипотенузы к меньшей стороне, получим идеальное значение 1,61950 или 1,62.

Это интересно! Форма пирамиды имеет ещё одно неоспоримое свойство. В нём сталь становится прочнее, вода дольше сохраняет свежий вкус, и быстрее растут живые растения. Много лет ученые пытаются разгадать этот феномен, но пока его научное решение не найдено.

Было замечено, что пирамида улучшает психоэмоциональное состояние человека, в её области уменьшаются вредоносные излучения, пропадают геопатогенные зоны.

Идеальная пропорция золотого сечения в пирамиде

Идеальные пропорции в древней Греции

Идеальная пропорциональность делает архитектурные объекты запоминающимися. Яркий представитель ЗС из древней Греции – Парфенон, который возведен в 5 веке до нашей эры. Если взять отношение его высоты к ширине, получится практически идеальное число 0,618.

Ученые определили, что для абсолютного золотого числа нужно отнять от высоты 14 см и прибавить их к ширине. Учитывая строение сооружения, очень похоже, что это было сделано древними архитекторами Иктином и Калликратом намеренно, поскольку фасад немного сужается в верхней части и отклоняется от золотого прямоугольника. Но общие пропорции ЗС соблюдены.

Принцип идеальной пропорции в древнегреческом Парфеноне:

Памятники архитектуры средневековья

Прекрасным памятником истории архитектуры средневековья, сохранившимся до нашего времени, является собор Парижской Богоматери или Нотр-Дам де Пари.

В здании очень заметно желание архитектора соблюсти гармонию и целостностьАнализируя строение, принцип ЗС можно видеть на нескольких участках

Архитектура России

Ряд Фибоначчи – это своеобразная матрица, с помощью которой анализируют любое архитектурное сооружение. Чтобы было проще ориентироваться, можно построить на принципе золотого сечения циркуль Фибоначчи.

Разметчик Фибоначчи построен по правилу золотого сеченияИспользовать циркуль можно практически на любом архитектурном сооруженииЧтобы исследовать большие объекты, нужно отойти на некоторое расстояние и приложить циркуль

Золотое сечение в архитектуре Москвы

Выдающееся здание МГУ на Воробьевых горах было построено в послевоенное время. В те годы это было самое высокое строение, состоящее из пяти композиционных групп, которые венчает центральная башня. Здесь чётко прослеживается треугольник с прямым углом, гипотенуза которого захватывает пристройки и проходит через угол здания.

В МГУ золотому сечению подчиняются высоты

Золотые пропорции прослеживаются и в работах русского зодчего Матвея Казакова.

Кремлевское здание сенатаПречистенский дворецГолицынская больницаДом союзов — благородное собрание

Использовал это прием и архитектор Василий Баженов, его здания причислены к историческим памятникам

Дом Пашкова

Архитектура в Санкт-Петербурге

Живым примером золотого сечения является Исаакиевский собор.

ЗС в Исаакиевском соборе

В первую очередь можно проанализировать его ширину, равную 400 единицам:

при делении числа 400 на значение золотого сечения получим приблизительно 248;
при дальнейшем делении 248/1,618=153;
основная часть собора вписывается в золотой прямоугольник, длинная сторона которого равна 400, ширина – 248.

По высоте здания ЗС можно видеть у купола, благодаря этому внешнее восприятие памятника архитектуры становится гармоничным.

На фото чётко прослеживаются золотой треугольник и прямоугольник в Исаакиевском соборе

Приведем ещё несколько примеров золотого сечения в архитектуре Санкт-Петербурга.

Кунсткамера

Кунсткамера была построена ещё в 1718 году, руководил строительством немецкий архитектор Георг Маттарнови. Она представляет собой 2 корпуса по 3 этажа, между ними возведена куполообразная многоярусная конструкция в виде башни.Золотое сечение в соотношении сторон можно наблюдать в длине корпусов и в высотах разных уровней.

В башне по всей высоте четко прослеживается равнобедренный треугольник, а это значит, что Кунсткамера построена по общему принципу ЗС

Торговый дом Эсдерс и Схейфальс

ЗС в здании, возведенном в 1907 году, наблюдается в следующих размерах:

671, 414, 256, 98, 60, 37 и 23.

Композиция смотрится гармонично благодаря золотому соблюдению высотных величин.

Основной элемент здания — шпиль

Дом Советов

Дом Советов был возведен по проекту Троцкого в 1941 году, основной акцент выполняют портик по центру с 14 колоннами и скульптурный ансамбль. По обе стороны расположены два корпуса высотой в 5 этажей. Длина здания – 1472 единицы, если разделить его на значение Ф = 1,618, получим размерный ряд:

1472, 909, 562, 347, 214, 132, 81, 50. К ним относятся высота входа, всего сооружения, различных элементов.

Анализ длин и высот Дома Советов

Золотой прямоугольный треугольник идеально вписывается в центр здания, его вершина совпадает с вершиной Дома Советов, а гипотенуза заканчивается в конце бокового крыла. Если построить равнобедренный золотой треугольник, его грани будут проходить через точки в верхней части основного входа.

Очевидная пропорциональность Дома Советов

Примеры золотого сечения в современной архитектуре

В современной архитектуре формула расчёта золотого сечения позволяет проектировать уникальные формы, которые несут прочность, спокойствие и красоту.

Правило золотого сечения при строительстве частного дома

Многие архитекторы, которые разрабатывают проекты частных домов, используют правило золотого сечения. У клиентов создается ощущение, что все детали проработаны для максимально комфортного проживания. При грамотном выборе площадей жильцы на психологическом уровне ощущают умиротворение и успокоение.

Что нужно знать при проектировании фасада

В современном строительстве при проектировании домов кроме ряда Фибоначчи используют ещё один метод, основоположником которого был архитектор из Франции Ле Корбюзье. Он принимал за основу рост будущих владельцев усадьбы и, исходя их этого, рассчитывал параметры строения и комнат. Благодаря такому подходу дом получался не только гармоничный, но и максимально комфортный с индивидуальными чертами хозяев.

Идеальные пропорции частного дома

Золотое сечение в оформлении интерьера

Даже если дом возведен по типовому проекту, можно внутри его создать интерьер, максимально приближенный к идеальной пропорции 1:1,62. Например, благодаря дополнительным перегородкам или расположению мебельных групп, а также можно изменить дверные или оконные проемы, чтобы соотношение ширины к высоте было в золотом сечении.

Аналогичная ситуация и с цветовым оформлением интерьера, здесь действует упрощенное правило:

60% — основная палитра;
30% — дополнительный оттенок;
10% — близкий тон, который усиливает восприятие основного и дополнительного.

Правило 1/1,62 в интерьере должно сопровождаться во всем: в соотношении мебели к общей площади, в ее высоте по отношению к параметрам комнаты.

Заключение

Принцип золотого сечения не является новым в архитектуре, поскольку в прежние времена здания строились не по типовым проектам, а с учетом индивидуальных особенностей будущих владельцев. Такие строения выглядят даже спустя многие года гармоничными и привлекательными. Интерьер, оформленный по правилам идеальной пропорции, позволяет грамотно использовать все площади.

Теперь вы сможете самостоятельно и правильно применить божественную гармонию математических цифр, планируя строительство дома или оформляя свой интерьер. Более того, интересную комбинацию цифр можно использовать и в экономике, и в расчете инвестиций и во всех деталях, с которыми соприкасается человек ежедневно.

Если у вас ещё остались вопросы, предлагаем посмотреть видео, в котором простыми словами разъяснен принцип действия золотого сечения:

Новинки рынкаОт теории к практике: самостоятельная регулировка окон к зиме

Новинки рынкаБалкон и лоджия: в чём разница, о каких нюансах стоит знать, если вы решились на переделку?

Понравилась статья? Сохраните, чтобы не потерять!

ТОЖЕ ИНТЕРЕСНО:

ВОЗМОЖНО ВАМ ТАКЖЕ БУДЕТ ИНТЕРЕСНО:

Золотое сечение как объяснение пропорций красоты

Над чем работают лучшие умы современной стоматологической науки? Над идеальной улыбкой, воплотившей в себе красоту и здоровье.

Что такое «красота»? Почему лицо и облик одного человека нам нравится, а другого — нет?

На эти вопросы пытались ответить учёные ещё тогда, когда не было ни только стоматологии как направления медицины, но и сама медицина находилась в стадии зарождения.

Оказывается, наше лицо и тело имеет определённые пропорции, кажущиеся на первый взгляд почти мистическими.

Хотя в наш просвещённый век многому можно найти научное и даже математическое объяснение.

Принято считать, что впервые закономерности соотношение размеров тела человека и отдельных его частей обобщил и сформулировал в 1855 г. немецкий исследователь Цейзинг в своём научном труде «Эстетические исследования». За основу своей теории он взял учение о «золотом сечении».

Ещё в VI веке до н.э. древнегреческий философ и математик Пифагор ввёл в научный обиход понятие «золотое деление». «Золотое деление» — это пропорциональное деление отрезка на неравные части. При этом меньший отрезок так относится к большему, как больший отрезок относится ко всему отрезку. a : b = b : c или с : b = b : а.

Так что же особенного в этом соотношении?

Оказывается, что всегда меньший отрезок относится к большему, как 0,382: к 0,618:

То есть, если АВ принять за единицу, АЕ/ЕВ=0,62/0,32 (в практических целях используют приближённые значения).

Один из примеров «золотого деления», с которым наверняка все знакомы, это — пентаграмма и, как представители её, так любимые людьми старшего поколения, «знак качества» и «звезда».

Все диагонали пятиугольника (пятиугольная звезда) делят друг друга на отрезки, связанные между собой «золотой пропорцией».

В настоящее время эта математическая закономерность носит название «золотое сечение», которое ввел в обиход ещё Леонардо да Винчи, который проводил сечения стереометрического тела, образованного правильными пятиугольниками. И каждый раз он получал соотношение сторон в «золотом делении». Он дал этому делению название «золотое сечение», принятое до сих пор.

Но не Пифагор впервые обнаружил закономерность «золотого сечения». Ещё древние египтяне и вавилоняне использовали эти знания в строительстве пирамид и изготовлении предметов обихода. Древние греки при проектировании своих зданий использовали пропорции «золотого сечения». В эпоху возрождения интерес к «золотому сечению» усилился. Художники нашли применение ему в искусстве. Учение о «золотом сечении» связано с именем гениального итальянского математика и монаха Луки Пачоли. В 1509 г. Была издана его книга «Божественная пропорция» с иллюстрациями Леонардо да Винчи (предположительно). Он причислял золотую пропорцию к «божественной сути» через триединство: бог сын, бог отец и святой дух, находящихся между собой в «золотой пропорции».

История «золотого сечения» связана ещё с одним известным итальянским математиком Фибоначчи. До наших времён дошёл ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д., известный, как ряд Фибоначчи.

Особенность последовательности данных чисел заключается в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих (2+3=5, 3+5=8), а отношение смежных чисел ряда приближается к отношению «золотого сечения» (21:34=0,617, а 34:55=0,618). В последствии все исследователи «золотого сечения» в растительном и животном мире, искусстве и анатомии приходили к этому ряду, как арифметическому выражению закона золотого деления. Интересно, что свой закон Фибонначи вывел, подсчитывая количество рождённых кроликов от пары кроликов за год.

Так в чём же ореол таинственности «золотого сечения»?

Всё, что растёт и приобретает какую-либо форму в живом мире нашей планеты — растёт вверх или закручивается по спирали. Спираль (например, морская раковина) — пример соотношения в пропорциях «золотого сечения». Спирали прослеживаются в расположении семян в шишках хвойных деревьев, в семенах подсолнечника и др.

Паук плетёт паутину по спирали, ДНК человека закручено по спирали.

А рост вверх? Растение живёт по тем же законам «золотого сечения». Самый большой участок стебля — до первого листочка. Затем следующие сегменты уменьшаются в пропорции «золотого сечения»: с : в = в : а

Удивительно то, что и человек в соотношении отдельных частей тела и расстояний между ними, подчиняется законам «золотого сечения».

Немецкий учёный Альберт Дюрер доказал, что рост человека делится в золотых пропорциях линией, проходящей через пупок и линией, проходящей через кончики средних пальцев опущенных рук.

Его труды продолжил Цейзинг. Он выяснил, что пропорции мужского тела колеблются в пределах 13 : 8 = 1, 625.

А пропорции женского тела в среднем находятся в соотношении 8 : 5 = 1,6.

Пропорции «золотого сечения» проявляются в отношении длины плеча, предплечья, кисти и пальцев и т.д.

Поразительно, но в лице человека можно проследить множество пропорций, подчиненных «золотому сечению». Причем, чем больше в лице человека соотношений в этой пропорции, тем красивее нам он кажется. Есть лица, при характеристике которых употребляют выражение «правильные черты лица». У этих людей основные пропорции наиболее близки к соотношению 1, 618: или 62 : 38.

Какие же пропорции в лице человека стремятся к «золотому сечению»?

Прежде всего, у людей с красивыми лицами наблюдается:

Идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это соотношение называется «динамической симметрией» или «динамическим равновесием».
Соотношение высоты верхней и нижней губы будет 1,618.
Высота надгубной складки (расстояние между верхней губой и нижней границей носа) и высота губ будут составлять соотношение 62 : 38.
Ширина одной ноздри суммарно с шириной переносицы относится к ширине другой ноздри в пропорции «золотого сечения».
Ширина ротовой щели также относится к ширине между наружными краями глаз, а расстояние между наружными уголками глаз — к ширине лба на уровне линии бровей, как все пропорции «золотого сечения».
Расстояние между линии смыкания губ до крыльев носа относится к расстоянию от линии смыкания губ до нижней точки подбородка, как 38 : 62: И к расстоянию от крыльев носа до зрачка — как 38 : 62 = 0.
Расстояние между линией верхней части лба до линии зрачков и расстояние между линией зрачков и линией смыкания губ имеет пропорцию «золотого сечения».

Можно продолжить этот список соотношения размеров гармоничного лица. Получается, правильную красоту можно математически просчитать и даже прибегнуть к хирургической корректировке с целью совершенствования внешности.

В настоящее время стоматология, наряду с пластической хирургией, занимается не только лечением заболеваний полости рта, но и эстетической медициной.

Удивительно, но и в стоматологии можно проследить пропорции «золотого сечения».

Красивая улыбка — это не только белоснежные здоровые ровные зубы, но и их правильное соотношение и расположение. И здесь мы опять сталкиваемся с закономерность «золотого сечения».

Вот некоторые примеры соотношений размеров и расстояний между зубами:

Ширина верхнего центрального резца относится к ширине нижнего центрального резца, как 62 : 38, т.е. 1, 618:, в соотношении «золотого сечения».
В этой же пропорции находится ширина двух верхних резцов к ширине двух нижних.
Расстояние между премолярами верхней челюсти относится к ширине четырёх верхних резцов, как 62 : 38.
Расстояние между дистальными поверхностями нижних клыков и щечными фиссурами моляров — пропорция 38 : 62.

И этот список можно продолжить.

Как же на практике можно использовать знание о «золотом сечении» и его влиянии на параметры в стоматологии?

Разумеется, искать применение золотых пропорций в эстетической стоматологии.

Расположение, размер и взаимное соотношение зубов в полости рта — всё это подчинено общему закону — «золотому сечению».

Вольно или невольно, осознанно или неосознанно врач использует эти пропорции при восстановлении коронковой части зуба, при протезировании или ортодонтических мероприятиях. Лучше, конечно, чтобы врач применял математическую составляющую в формировании вашей красоты и здоровья.

А мы теперь знаем, что человек — только часть живого мира на нашей планете, подчиняющийся общим законам мироздания. И доказательство тому — учение о «золотом сечении», дошедшее до нас уже даже не из предыдущего тысячелетия.

Время работы

Пн-Пт	10:00 — 22:00
Сб-Вс	10:00 — 20:00

Векслер Вера Марковна Главный врач, врач-стоматолог терапевт

Фибоначчи и золотое сечение

Существует уникальное соотношение, которое можно использовать для описания пропорций всего, от мельчайших строительных блоков природы, таких как атомы, до самых сложных структур во Вселенной, таких как невообразимо большие небесные тела. Природа полагается на эту врожденную пропорцию для поддержания баланса, но финансовые рынки, похоже, также соответствуют этому «золотому сечению». Здесь мы рассмотрим некоторые инструменты технического анализа, которые были разработаны для использования этого паттерна.

Ключевые выводы

Золотое сечение описывает предсказуемые закономерности на всем, от атомов до огромных звезд на небе.
Это отношение получено из так называемой последовательности Фибоначчи, названной в честь ее итальянского основателя Леонардо Фибоначчи.
Природа использует это соотношение для поддержания баланса, и финансовые рынки, похоже, тоже.
Последовательность Фибоначчи может применяться к финансам с использованием четырех основных методов: ретрейсментов, дуг, вееров и часовых поясов.

Математика

Математики, ученые и естествоиспытатели знали о золотом сечении на протяжении веков. Оно получено из последовательности Фибоначчи, названной в честь ее итальянского основателя Леонардо Фибоначчи (чье рождение предполагается примерно в 1175 году нашей эры, а смерть — примерно в 1250 году нашей эры). В этой последовательности каждое число представляет собой просто сумму двух предыдущих чисел ( 1, 1, 2, 3, 5, 8, 13 и т. Д.).

Но эта последовательность не так уж и важна; скорее, существенная часть — это частное соседнего числа, которое имеет удивительную пропорцию, примерно 1.618 или его обратное 0,618. Эта пропорция известна под многими именами: золотое сечение, золотая середина, PHI и божественная пропорция, среди других. Итак, почему это число так важно? Что ж, почти все имеет размерные свойства, которые соответствуют соотношению 1,618, так что кажется, что оно имеет фундаментальную функцию для строительных блоков природы.

Докажи это

Не верите? Возьмем, к примеру, пчел. Если вы разделите пчел-самок на пчел-самцов в любом конкретном улье, вы получите 1.618. У подсолнухов, у которых есть противоположные спирали семян, соотношение диаметров каждого вращения составляет 1,618. Это же соотношение можно увидеть во взаимоотношениях между различными компонентами в природе.

Вы все еще не можете в это поверить? Вам нужно что-то, что легко измерить? Попробуйте измерить расстояние от плеча до кончиков пальцев, а затем разделите это число на длину от локтя до кончиков пальцев. Или попробуйте измерить расстояние от головы до ног и разделить его на длину от пупка до ступней.Результаты такие же? Где-то в районе 1.618? Казалось бы, золотое сечение неизбежно.

Но означает ли это, что это работает в сфере финансов? На самом деле, финансовые рынки имеют ту же математическую основу, что и эти природные явления. Ниже мы рассмотрим некоторые способы применения золотого сечения к финансам и покажем несколько диаграмм в качестве доказательства.

Исследования Фибоначчи и финансы

При использовании в техническом анализе золотое сечение обычно переводится в три процента: 38.2%, 50% и 61,8%. Однако при необходимости можно использовать больше кратных, например 23,6%, 161,8%, 423% и т. Д. Между тем, есть четыре способа применения последовательности Фибоначчи к графикам: ретрейсменты, дуги, вееры и часовые пояса. Однако не все могут быть доступны в зависимости от используемого графического приложения.

1. Уровни коррекции Фибоначчи

При коррекции Фибоначчи горизонтальные линии используются для обозначения областей поддержки или сопротивления. Уровни рассчитываются с использованием точек максимума и минимума графика.Затем рисуются пять линий: первая — 100% (максимум на графике), вторая — 61,8%, третья — 50%, четвертая — 38,2% и последняя — 0% (минимум на графике). ). После значительного движения цены вверх или вниз новые уровни поддержки и сопротивления часто оказываются на этих линиях или около них.

2. Дуги Фибоначчи

Поиск максимума и минимума графика — это первый шаг к построению дуг Фибоначчи. Затем движением, похожим на компас, рисуем три изогнутые линии в точке 38.2%, 50% и 61,8% от желаемой точки. Эти линии предполагают уровни поддержки и сопротивления, а также торговые диапазоны.

3. Веера Фибоначчи

Веера Фибоначчи состоят из диагональных линий. После определения максимума и минимума графика через крайнюю правую точку проводится невидимая горизонтальная линия. Затем эта невидимая линия делится на 38,2%, 50% и 61,8%, и линии проводятся от крайней левой точки через каждую из этих точек.Эти линии указывают на области поддержки и сопротивления.

4. Часовые пояса Фибоначчи

В отличие от других методов Фибоначчи, часовые пояса представляют собой серию вертикальных линий. Они состоят из разделения диаграммы на сегменты с вертикальными линиями, разнесенными друг от друга с шагом, соответствующим последовательности Фибоначчи (1, 1, 2, 3, 5, 8, 13 и т. Д.). Каждая линия указывает время, в которое можно ожидать значительного движения цены.

Золотое сечение можно применить ко всему: от природы до анатомии человека и финансов.

Итог

Исследования Фибоначчи не предназначены для предоставления основных указаний для определения времени входа и выхода из позиции; однако числа полезны для оценки областей поддержки и сопротивления. Многие люди используют комбинации исследований Фибоначчи для получения более точного прогноза. Например, трейдер может наблюдать точки пересечения в сочетании дуг Фибоначчи и сопротивлений.

Исследования Фибоначчи часто используются в сочетании с другими формами технического анализа.Например, исследования Фибоначчи в сочетании с волнами Эллиотта могут использоваться для прогнозирования степени восстановления после различных волн. Надеюсь, вы сможете найти свое собственное нишевое применение для исследований Фибоначчи и добавить его в свой набор инвестиционных инструментов.

10.4: Числа Фибоначчи и золотое сечение

Известной и важной последовательностью является последовательность Фибоначчи, названная в честь итальянского математика Леонардо Пизано по прозвищу Фибоначчи, жившего с 1170 по 1230 год.Эта последовательность:

\ [\ {1,1,2,3,5,8,13,21,34,55, \ ldots \ ldots \ ldots \} \]

Эта последовательность определяется рекурсивно. Это означает, что каждый термин определяется предыдущими терминами.

и так далее.

Последовательность Фибоначчи определяется, для всех, когда и.

Другими словами, чтобы получить следующий член в последовательности, добавьте два предыдущих члена.

\ [\ {1,1,2,3,5,8,13,21,34,55,55 + 34 = 89,89 + 55 = 144, \ cdots \} \]

Обозначения, которые мы будем использовать для представления последовательности Фибоначчи, следующие:

\ [f_ {1} = 1, f_ {2} = 1, f_ {3} = 2, f_ {4} = 3, f_ {5} = 5, f_ {6} = 8, f_ {7} = 13, f_ {8} = 21, f_ {9} = 34, f_ {10} = 55, f_ {11} = 89, f_ {12} = 144, \ ldots \]

Пример \ (\ PageIndex {1} \): Рекурсивный поиск чисел Фибоначчи

Найдите 13, 14 и 15 числа Фибоначчи, используя приведенное выше рекурсивное определение последовательности Фибоначчи.

Во-первых, обратите внимание, что уже есть 12 чисел Фибоначчи, перечисленных выше, поэтому, чтобы найти следующие три числа Фибоначчи, мы просто складываем два предыдущих члена, чтобы получить следующий член, как указано в определении. {n} \ right]} {\ sqrt {5}} \]

Формула

Бине является примером последовательности , явно определенной .Это означает, что условия последовательности не зависят от предыдущих условий.

Иногда вместо приведенной выше формулы иногда используется несколько более удобная и упрощенная версия формулы Бине.

Упрощенная формула Бине : n-е число Фибоначчи определяется по следующей формуле:

Примечание. Символ означает «округление до ближайшего целого числа.”

Пример \ (\ PageIndex {2} \): поиск явно

Найдите ценность использования упрощенной формулы Бине.

Рисунок \ (\ PageIndex {1} \): Работа калькулятора для

Пример \ (\ PageIndex {3} \): Поиск Явно

Найдите значение , используя упрощенную формулу Бине.

Рисунок \ (\ PageIndex {2} \): Работа калькулятора для

Пример \ (\ PageIndex {4} \): Поиск Явно

Найдите значение , используя упрощенную формулу Бине.

Рисунок \ (\ PageIndex {3} \): Работа калькулятора для

Мы можем найти числа Фибоначчи в природе повсюду вокруг нас. Количество ветвей на некоторых деревьях или количество лепестков некоторых ромашек часто являются числами Фибоначчи

Рисунок \ (\ PageIndex {4} \): числа Фибоначчи и ромашки

а. Ромашка с 13 лепестками б. Ромашка с 21 лепестком

а. б.

(Маргаритки, н.о.)

Числа Фибоначчи также появляются в спиральных структурах роста, таких как количество спиралей на кактусе или на грядках с семенами подсолнечника.

Рисунок \ (\ PageIndex {5} \): числа Фибоначчи и спиральный рост

а. Кактус с 13 спиралями по часовой стрелке b. Подсолнечник с 34 спиралями по часовой стрелке и 55 спиралями против часовой стрелки

а. б.

(Кактус, н.о.) (Подсолнечник, н.о.)

Другой интересный факт возникает при рассмотрении соотношений последовательных чисел Фибоначчи.

Похоже, что эти отношения приближаются к цифре. Число, к которому эти соотношения приближаются, — это особое число, называемое золотым соотношением, которое обозначается (греческой буквой фи).Вы видели это число в формуле Бине.

Золотое сечение:

\ [\ phi = \ frac {1+ \ sqrt {5}} {2} \]

Золотое сечение имеет десятичное приближение \ (\ phi = 1,6180339887 \).

Золотое сечение — это особое число по разным причинам. Его также называют божественной пропорцией, и он проявляется в искусстве и архитектуре.Некоторые утверждают, что это самое приятное для глаз соотношение. Чтобы найти это соотношение, греки разрезали отрезок на две части и позволили меньшему отрезку равняться одной единице. Самый приятный крой — это когда отношение полной длины к длинной части такое же, как отношение длинной части к короткой 1.

перемножим, чтобы получить

переставить, чтобы получить

решите это квадратное уравнение, используя формулу корней квадратного уравнения.

Золотое сечение — это решение квадратного уравнения, означающее, что оно обладает свойством. Это означает, что если вы хотите возвести золотое сечение в квадрат, просто добавьте к нему единицу. Чтобы проверить это, просто подключите.

Сработало!

Еще одна интересная связь между золотым сечением и последовательностью Фибоначчи возникает при использовании степеней.

И так далее.

Обратите внимание, что коэффициенты и числа, добавленные к члену, являются числами Фибоначчи.{n} = f_ {n} \ phi + f_ {n-1} \)

, где \ (f_ {n} \) — n-е число Фибоначчи, а \ (\ phi \) — золотое сечение .

Пример \ (\ PageIndex {5} \): Степени золотого сечения

Найдите следующее, используя правило золотой силы: a. и б.

золотого сечения | Примеры, определение и факты

Золотое сечение , также известное как золотое сечение , золотая середина или божественная пропорция , в математике иррациональное число (1 + квадратный корень из √5) / 2 , часто обозначается греческой буквой ϕ или τ, что приблизительно равно 1.618. Это отношение отрезка прямой, разрезанного на две части разной длины, при котором отношение всего отрезка к таковому более длинного сегмента равно отношению более длинного отрезка к более короткому отрезку. Происхождение этого числа можно проследить до Евклида, который упоминает его как «крайнее и среднее соотношение» в Элементах . С точки зрения современной алгебры, если длина более короткого сегмента равна одной единице, а длина более длинного сегмента — x единицы, возникает уравнение ( x + 1) / x = x / 1; это может быть преобразовано в квадратное уравнение x ² — x — 1 = 0, для которого положительным решением будет x = (1 + квадратный корень из √5) / 2, золотое сечение.

Древние греки признали это свойство «разделения» или «разделения на части», фраза, которая в конечном итоге была сокращена до просто «раздел». Прошло более 2000 лет, когда и «сечение», и «сечение» были названы «золотыми» немецким математиком Мартином Омом в 1835 году. Греки также заметили, что золотое сечение обеспечивает наиболее эстетичную пропорцию сторон прямоугольника. , понятие, которое было усилено в эпоху Возрождения, например, благодаря работе итальянского эрудита Леонардо да Винчи и публикации De divina пропорционально (1509; Божественная пропорция ), написанной итальянским математиком Лукой Пачоли и проиллюстрированной Леонардо.

Витрувианский человек, рисунок Леонардо да Винчи ( ок. 1509), иллюстрирующий пропорциональный канон, установленный классическим римским архитектором Витрувием; в Академии изящных искусств Венеции.
Foto Marburg / Art Resource, New York
Золотое сечение встречается во многих математических контекстах. Его геометрически можно построить с помощью линейки и циркуля, и это происходит при исследовании архимедовых и платоновых тел. Это предел соотношений последовательных членов последовательности чисел Фибоначчи 1, 1, 2, 3, 5, 8, 13,…, в котором каждый член после второго является суммой двух предыдущих, а также значение самой основной из непрерывных дробей, а именно 1 + 1 / (1 + 1 / (1 + 1 / (1 + ⋯.
В современной математике золотое сечение встречается при описании фракталов, фигур, которые проявляют самоподобие и играют важную роль в изучении хаоса и динамических систем.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Последовательность Фибоначчи влияет на фондовый рынок | Наука
В пятницу, 20 марта, когда фондовый рынок США завершил свою худшую неделю с 2008 года из-за беспорядков, связанных с коронавирусом (до некоторого восстановления на следующей неделе), перед инвесторами встал вопиющий вопрос: все ли идет под откос? В условиях такой экономической нестабильности некоторые исследователи рынка обращаются к знакомому мощному набору чисел для предсказания будущего.
«Коррекция Фибоначчи» — это инструмент, который технические аналитики используют для определения своих взглядов на поведение покупателей и продавцов на рынках. Этот метод назван в честь известной последовательности Фибоначчи, набора чисел, свойства которой связаны со многими природными явлениями. Хотя использование этих чисел для прогнозирования рыночных движений гораздо менее надежно, чем их использование для расчета структуры семян подсолнечника, появление последовательности в области финансов является еще одним свидетельством ее способности захватывать человеческое воображение.
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это известная группа чисел, начинающаяся с 0 и 1, в которой каждое число является суммой двух перед ним. Он начинается с 0, 1, 1, 2, 3, 5, 8, 13, 21 и продолжается бесконечно. Этот шаблон скрывает мощный секрет: если вы разделите каждое число в последовательности на его предшественник (кроме 1, деленного на 0), то по мере продвижения к более высоким числам результат сходится к константе phi , или приблизительно 1.61803, иначе известное как золотое сечение.
Последовательность имеет долгую историю. В Европе это было решение проблемы разведения кроликов, описанной в книге Liber Abaci итальянского математика Леонардо Пизанского в 1202 году нашей эры.Но этот образец был известен в Индии гораздо раньше, возможно, даже в седьмом веке. Название последовательности происходит от прозвища Фибоначчи, что означает «сын Боначчи», данного Леонардо в 19 веке, согласно книге Кейта Девлина В поисках Фибоначчи: В поисках заново забытого математического гения, изменившего мир .Затем математик Эдуоард Лукас в 1870-х годах дал название «последовательность Фибоначчи» последовательности, полученной из сценария с кроликом. (Это также проявилось при подсчете количества пчел в последовательных поколениях).
Между тем, золотое сечение может быть записано как половина суммы 1 плюс квадратный корень из 5. И хотя фи не дает такого праздника, как пи, такая константа появляется в природных явлениях. Число спиралей в шишках — это числа Фибоначчи, как и количество лепестков в каждом слое определенных цветов.У спиралевидных растений каждый лист растет под углом по сравнению с его предшественником, равным 360 / phi ², и семена подсолнечника упакованы в спиралевидное образование в центре своего цветка, геометрия которого также регулируется золотым сечением.

«Привлекательность золотого сечения проистекает в первую очередь из того факта, что оно имеет почти сверхъестественный способ появляться там, где его меньше всего ожидают», — пишет Марио Ливио в книге «Золотое сечение: история о Фи, самом удивительном числе в мире» .
Но почему эта последовательность так повсеместна? «Многие вещи в математике и, вероятно, в реальном мире регулируются простыми рекурсивными правилами, где каждое вхождение регулируется простой формулой с точки зрения предыдущего вхождения», — сказал Кен Рибет, профессор математики Калифорнийского университета. Беркли. «А у числа Фибоначчи есть простейшая из возможных формул, просто сумма двух предыдущих».
Фибоначчи выходит на рынок
Люди запрограммированы на идентификацию закономерностей, и когда дело доходит до чисел Фибоначчи, мы не ограничиваемся поиском и восприятием последовательности в природе.Фибоначчи и фи можно найти в некоторых произведениях искусства, архитектуры и музыки (хотя это миф, что пирамиды Египта имеют к этому какое-то отношение). И хотя поведение покупателей и продавцов в значительной степени непредсказуемо, некоторые финансовые аналитики клянутся, что они тоже могут увидеть эти цифры в игре, в том числе в нынешнем экономическом кризисе.
Крупный план подсолнечника (Wiki Commons / Alex M3rcer)
Инвестиционные исследователи, которых называют «техническими аналитиками», изучают исторические формы графиков, чтобы определить, будет ли текущая тенденция покупки или продажи продолжаться или измениться.Некоторые делают свои прогнозы, используя «уровни восстановления Фибоначчи», полученные из известной последовательности.
Технические аналитики могут смотреть на целый набор чисел, соответствующих соотношениям чисел в последовательности Фибоначчи, но есть пара важных — 61,8% и 38,2%. Любое данное число Фибоначчи, деленное на его преемник, составляет приблизительно 1 / фи, или 0,618. Число Фибоначчи, деленное на число на два разряда выше в последовательности, приблизительно равно 0.382.
Например, рассмотрим S&P 500. В разгар рецессии 2008 года индекс достиг своей самой низкой точки в 2009 году — 666 пунктов. С тех пор он, как правило, находится на длительном подъеме, достигнув пика в 3393 человека до резкого падения, вызванного коронавирусом в последние недели.
Чтобы понять тенденции нынешнего спада, Кэти Стоктон, основатель и управляющий партнер фирмы технического анализа Fairlead Strategies, LLC в Стэмфорде, штат Коннектикут, изучает, пробиваются ли ключевые индексы и акции через различные уровни.Если вы возьмете минимум 2009 года в 666 в качестве нижней (0 процентов) и максимум 2020 года в 3393 в качестве верхней (100 процентов), Стоктон будет следить за тем, закрывается ли S&P 500 две пятницы подряд ниже того, что она определяет как « уровень поддержки »38,2 процента. Этот уровень соответствует максимуму 3393 минус 1042 (38,2 процента разницы между максимумом и минимумом), что составляет 2351.
Пока что во время кризиса цены не падали так низко две пятницы подряд, хотя 20 марта индекс закрылся на мрачном уровне 2304.92. Если 27 марта цена закроется ниже этого уровня Фибоначчи 2351, это будет второй страйк подряд. Для таких аналитиков, как Стоктон, это будет указывать на то, что S&P рискует упасть ниже уровня 61,8%, или около 1708 года, что, согласно этой точке зрения, делает сейчас менее оптимальным временем для покупок.
Самореализующееся пророчество?
Рибет, математик, отвергает идею поиска паттернов, связанных с последовательностью Фибоначчи, для прогнозирования рынков.Но даже если это неправда, что числа Фибоначчи связаны с фундаментальными рыночными силами, рынки по своему замыслу реагируют на убеждения своих игроков. Так что, если инвесторы массово покупают из-за анализа Фибоначчи, они все равно создают восходящий тренд; аналогично для продажи.
Стоктон признает, что это, по крайней мере, частично объясняет движение золота в прошлом году, когда инвесторы внимательно отслеживали, поднимется ли цена унции выше определенного уровня Фибоначчи. Цены на золото значительно упали с 2012 по 2015 год, затем колебались в пределах от 1200 до 1400 долларов за унцию в течение четырех лет до июня 2019 года, когда, похоже, цена снова начала расти.
«Это был большой прорыв Фибоначчи, за которым наблюдали многие люди, даже до такой степени, что он стал настолько широко отслеживаемым уровнем, что, я думаю, он становится неким самореализующимся свойством», — сказал Стоктон.
Идея о том, что числа Фибоначчи управляют торговлей акциями людей, может быть волшебным мышлением, но достаточное количество людей с таким же магическим мышлением может двигать рынки. Когда мы готовимся к еще большему хаосу, по крайней мере, мы все можем успокоиться, зная, что сами числа Фибоначчи вечны.
Золотое сечение — что это такое и как его использовать в дизайне
Хороший дизайн обсуждался с тех пор, как мы создаем. Существуют бесконечные форумы, обсуждения в социальных сетях и личные беседы о том, что делает отличный дизайн, и каждый высказывает свою точку зрения.
В этом же прелесть дизайна, правда? Каждый может интерпретировать это по-своему.
Хотя универсального подхода к дизайну никогда не будет, существует конкретный математический подход, который может помочь нам каждый раз на шаг приближаться к созданию потрясающих дизайнерских впечатлений: золотое сечение.
Золотое сечение — это математическое соотношение, которое вы можете найти практически везде, например, в природе, архитектуре, живописи и музыке. Когда он применяется конкретно к дизайну, он создает органичную, сбалансированную и эстетически приятную композицию.
В этой статье мы подробно рассмотрим, что такое золотое сечение, как его рассчитать и как использовать в дизайне, включая удобный список инструментов.
Что такое золотое сечение?
Золотое сечение, также известное как золотое сечение, золотое сечение, божественная пропорция или греческая буква фи, — это особое число, которое приблизительно равно 1.618. Само соотношение происходит от последовательности Фибоначчи, естественной последовательности чисел, которые можно найти везде, от количества листьев на дереве до формы морской ракушки.
Последовательность Фибоначчи — это сумма двух чисел перед ней. Это идет: 0, 1,1, 2, 3, 5, 8, 13, 21 и так далее до бесконечности. На основе этого шаблона греки разработали золотое сечение, чтобы лучше выразить разницу между любыми двумя числами в последовательности.
Как это связано с дизайном? Вы можете найти золотое сечение, если разделите линию на две части, и более длинная часть (a), разделенная на меньшую часть (b), равна сумме (a) + (b), деленной на (a), которые оба равно 1.618. Эта формула может помочь вам при создании фигур, логотипов, макетов и т. Д.
Вы также можете воспользоваться этой идеей и создать золотой прямоугольник. Возьмите квадрат и умножьте одну сторону на 1,618, чтобы получить новую форму: прямоугольник с гармоничными пропорциями.
Если вы положите квадрат на прямоугольник, соотношение между двумя фигурами даст вам золотое сечение.
Если вы продолжите применять формулу золотого сечения к новому прямоугольнику справа, вы получите изображение, состоящее из все более мелких квадратов.
Если вы нарисуете спираль над каждым квадратом, начиная с одного угла и заканчивая в противоположном, вы создадите первую кривую последовательности Фибоначчи (также известную как Золотая спираль).
Как использовать золотое сечение в дизайне
Теперь, когда урок математики окончен, как вы можете применить эти знания в повседневной работе?
Вот четыре способа использования золотого сечения в дизайне:
1. Типографика и определение иерархии
Золотое сечение может помочь вам выяснить, какой размер шрифта вы должны использовать для заголовков и основного текста на веб-сайте, целевой странице, в блоге или даже в печатной кампании.
Допустим, размер вашего основного текста составляет 12 пикселей. Если вы умножите 12 на 1,618, вы получите 19,416, то есть размер текста заголовка 19 или 20 пикселей будет соответствовать золотому сечению и сбалансировать размер основного шрифта 12 пикселей.
Если вы хотите выяснить, насколько большим должен быть размер вашего основного текста, вы можете сделать наоборот. Если размер вашего заголовка составляет 25 пикселей, вы можете разделить его на 1,618, чтобы найти основной текст (15 или 16 пикселей).
2. Обрезка и изменение размера изображений
При кадрировании изображения легко выделить белое пространство, которое нужно вырезать.Но как сделать так, чтобы изображение оставалось сбалансированным после изменения его размера? Вы можете использовать Золотую спираль в качестве ориентира для композиции изображения.
Например, если вы наложите Золотую спираль на изображение, вы можете убедиться, что точка фокусировки находится в середине спирали.
3. Планировка
Использование золотого сечения может помочь вам разработать визуально привлекательный пользовательский интерфейс, привлекающий внимание пользователя к тому, что наиболее важно. Например, страница, которая выделяет широкий блок контента слева и более узкий столбец справа, может соответствовать пропорциям золотого сечения и помочь вам решить, где разместить наиболее важный контент.
4. Разработка логотипа
Если вы разрабатываете новый логотип и чувствуете себя застрявшим, обратитесь к золотому сечению, чтобы набросать пропорции и формы. Многие популярные логотипы следуют золотому сечению, например Twitter, Apple и Pepsi.
Дизайнер Кази Мохаммед Эрфан даже поставил перед собой задачу создать 25 новых логотипов, полностью основанных на золотом сечении. Результат? Простые, сбалансированные и красивые иконки.
Инструменты, которые помогут вам использовать золотое сечение
Вам не нужно выламывать карандаш и бумагу, чтобы вычислить золотое сечение — есть ряд приложений, которые сделают это за вас.
Вот пять инструментов, которые помогут вам использовать золотое сечение в ваших проектах:
Калькулятор золотого сечения: Вычислите более короткую сторону, длинную сторону и общую длину двух сторон, чтобы вычислить золотое сечение.
goldenRATIO: Это приложение, созданное для дизайнеров и разработчиков, позволяет легко создавать веб-сайты, интерфейсы, макеты и многое другое в соответствии с золотым сечением. Он включает в себя встроенный калькулятор с визуальной обратной связью и функциями для хранения положения и настроек экрана, поэтому вам не нужно менять золотое сечение для каждой задачи.
Калькулятор типографики золотого сечения: Найдите идеальную типографику для своего веб-сайта, указав размер и ширину шрифта. Вы можете оптимизировать на основе размера шрифта, высоты строки, ширины и символов в строке.
PhiMatrix : Это программное обеспечение для проектирования и анализа Золотого сечения содержит настраиваемые сетки и шаблоны, которые можно накладывать на любое изображение. Его можно использовать для дизайна и композиции, дизайна продукта, разработки логотипа и многого другого.
Ресурс эскиза золотого сечения : Загрузите бесплатный файл эскиза золотой спирали, чтобы помочь с компоновкой изображения и макета.
Начало работы с золотым сечением
Как только вы узнаете, что искать, вы начнете замечать золотое сечение повсюду. (Не верите? Посмотрите на свои руки. Даже ваши пальцы следуют золотому сечению.) Человеческий глаз привык видеть это магическое число, и мы подсознательно положительно на него реагируем.
Как дизайнеры, мы можем использовать это число в своих интересах. Даже небольшие изменения в способе обрезки изображения или разработки макета могут значительно улучшить взаимодействие пользователей с вашим дизайном.
Повсеместность чисел Фибоначчи — NCJS
Введение
На протяжении всей истории люди были поглощены неустанным поиском закономерностей в физическом мире. Одним из источников естественных закономерностей является последовательность Фибоначчи и связанные с ней числа Фибоначчи. Последовательность Фибоначчи оказалась повсеместной не только в естественном мире, но и в некоторых структурах человеческого тела, таких как улитка (Pietsch et al., 2017).
Последовательность Фибоначчи и соответствующие числа Фибоначчи определяются следующим уравнением:
F _n = F _n-1 + F _n-2 для всех n ≥ 3, где F ₁ = 1; F ₂ = 1
, где Fn представляет собой n-е число Фибоначчи. Последовательность Фибоначчи может быть записана как {1,1,2,3,5,8,13,21,34,55,89,144,233…}.
Золотое сечение — это концепция, которая имеет прочную связь с последовательностью Фибоначчи. Термин «золотое сечение» часто используется взаимозаменяемо с термином «золотое сечение», хотя некоторые ученые обозначили термин «золотое сечение» как аналог золотого сечения.Считается, что золотое сечение пришло от Евклида, в частности из его знаменитой книги Elements , где он попытался решить проблему, касающуюся разделения отрезка прямой на две неравные части, и отметил соотношение размеров полученных частей. Эта проблема более известна как «проблема разделения отрезка прямой в крайнем и среднем соотношении » (Benavoli et al., 2019).
Эта статья предназначена для того, чтобы выделить и подробно рассказать о происхождении и возникновении последовательности Фибоначчи и чисел Фибоначчи, а также о важности золотого сечения не только в природе, но и в таких областях науки, как инженерия.
История последовательности Фибоначчи
Считается, что числа Фибоначчи были созданы итальянским математиком Леонардо Пизано, также известным как Фибоначчи. Фибоначчи преподавал математику в Буджиа, где его отец, который был трейдером, занимал дипломатический пост (Gies, 2020). За это время Фибоначчи путешествовал по Средиземному морю, чтобы получить опыт в древних системах счета, уделяя особое внимание индуистско-арабской системе, которая позже послужит основой его книги Liber Abaci ( The Book of Calculations ).В дополнение к числам Фибоначчи он также включал число Zephirum, которое переводится в ноль (Ballieu, 2009). Число ноль, первоначально служившее заполнителем, позже послужит основой для десятичной системы. Liber abaci также включает в себя предыдущие открытия Пифагора, Евклида и Диофанта, включая алгоритмические методы, полученные из арабских источников. Книга, как и книга Евклида Elements , стала объектом восхищения и была широко воспроизведена и распространена в Европе после того, как Фибоначчи закончил ее писать (Waerden & Baitak, 2019).Многие люди рассматривают Liber Abaci как величайшее произведение Фибоначчи из-за включения не только чисто математических элементов, таких как индуистско-арабская система, но также из-за введения прикладных математических элементов, таких как стоимость и прибыль, бартер, партнерство, инвестиции , утверждение и измерение — измерение геометрических величин (Swetz, 2007).
Одним из важных элементов Liber Abaci было то, что он предлагал Западу индуистско-арабскую систему счисления.Фибоначчи начинает с заявления: «Девять индийских цифр: 9, 8, 7, 6, 5, 4, 3, 2, 1. С этими цифрами и знаком 0… может быть написано любое число» (Tesch, 2018 ).
Механические счеты, которые использовались долгое время, были одним из самых популярных способов выполнения расчетов. Он состоял из бусинок, которые скользили по четырем проволокам. Каждая бусинка представляет собой единицу. Основным недостатком этого метода расчета было то, что оказалось трудно выполнять сложные вычисления, что приводило к арифметическим ошибкам.Эти ошибки не удалось отследить, поскольку на счетах не записаны предыдущие вычисления. Затем появилась индийско-арабская система счисления, которая дала решение проблемы, с которой столкнулись абакисты. Этот новый метод счета рассматривался как ересь, потому что счеты так хорошо подходили для счета римских цифр. Это вызвало споры среди абакистов и алгоритмистов — тех, кто выступал за новую индуистско-арабскую систему счисления (Allen, 2019).
Компульсивное содержание — Золотое сечение и последовательность Фибоначчи в искусстве
Итальянскому математику конца XI века Фибоначчи приписывают то, что он принес арабскую систему счисления в Европу и очень быстро его одноименную последовательность, комбинацию чисел, происходящих от сумма двух предыдущих чисел (например, 1, 1, 2, 3, 5, 8, 13, 21, 34 и т. д.).Во времена итальянского Возрождения эта идея, в частности, позволила более склонным к визуальному восприятию представить числовую последовательность как узор, несколько напоминающий раковину — что-то, что приравнивается к очень эстетически приятной пропорции.
Его раковинная форма чудесным образом нашла свое отражение во многих естественных явлениях и, как таковая, была принята во многих известных художественных произведениях, возможно, больше всего в «Моне Лизе» . Он тесно связан с золотым сечением, также известным как божественное сечение, его можно увидеть в цветах, человеческом лице, великолепной геометрии цветущего артишока и соотношении самцов и самок пчел, присутствующих в их генеалогическом древе (т.е. сколько самок и самцы присутствуют в родословной одной конкретной пчелы).Во многих отношениях он, кажется, не поддается объяснению, и поэтому он получил прозвище «ривин», которое многие называют.
Художники, особенно те, кто настолько хорошо разбирался в мультидисциплинарном подходе, провозглашенном в то время классическим искусством и искусством Возрождения, заметили, что этот принцип, хотя и приятен во всех других аспектах жизни, должен как особенность и в их картинах.
Числа фибоначчи и золотое сечение: Золотое сечение и пропорции Фибоначчи