Золотое сечение: Как это работает?
- Дизайн
- 4 мин на чтение
- 151617
Золотое сечение — это универсальное проявление структурной гармонии. Оно встречается в природе, науке, искусстве — во всем, с чем может соприкоснуться человек. Однажды познакомившись с золотым правилом, человечество больше ему не изменяло.
Определение
Наиболее емкое определение золотого сечения гласит, что меньшая часть относится к большей, как большая — ко всему целому. Приблизительная его величина — 1,6180339887. В округленном процентном значении пропорции частей целого будут соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Древние видели в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одним из сокровищ геометрии.
Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом, отражающим структуру и порядок нашего мироустройства.
История
Представление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научно золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации к которой предположительно сделал Леонардо да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой — Отца, а целое — Святой дух.
Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач ученый вышел на последовательность чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».
Сейчас ряд Фибоначчи — это арифметическая основа для расчетов пропорций золотого сечения во всех его проявлениях.
Леонардо да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего, именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Со временем правило золотого сечения превратилось в академическую рутину, и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечения, сделав их универсальными для всех явлений окружающего мира. Впрочем, его «математическое эстетство» вызывало много критики.
Природа
Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.
Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.
Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.
Человек
Модельеры и дизайнеры одежды все расчеты делают, исходя из пропорций золотого сечения. Человек — это универсальная форма для проверки законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции идеальны, что создает определенные сложности с подбором одежды.
В дневнике Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека, находящегося в двух наложенных друг на друга позициях. Опираясь на исследования римского архитектора Витрувия, Леонардо подобным образом пытался установить пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье, используя «Витрувианского человека» Леонардо, создал собственную шкалу «гармонических пропорций», повлиявшую на эстетику архитектуры XX века.
Адольф Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он измерил порядка двух тысяч человеческих тел, а также множество античных статуй и вывел, что золотое сечение выражает среднестатистический закон. В человеке ему подчинены практически все части тела, но главный показатель золотого сечения это деление тела точкой пупа.
В результате измерений исследователь установил, что пропорции мужского тела 13:8 ближе к золотому сечению, чем пропорции женского тела — 8:5.
Искусство пространственных форм
Художник Василий Суриков говорил, «что в композиции есть непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже лишнюю точку поставить нельзя, это настоящая математика».
Долгое время художники следовали этому закону интуитивно, но после Леонардо да Винчи процесс создания живописного полотна уже не обходится без решения геометрических задач. Например, Альбрехт Дюрер для определения точек золотого сечения использовал изобретенный им пропорциональный циркуль.
Искусствовед Ф. В. Ковалев, подробно исследовав картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает, что каждая деталь полотна, будь то камин, этажерка, кресло или сам поэт, строго вписаны в золотые пропорции.
Исследователи золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая, что они стали таковыми, потому что созданы по золотым канонам: в их списке Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного, Парфенон.
И сегодня в любом искусстве пространственных форм стараются следовать пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают восприятие произведения и формируют у зрителя эстетическое ощущение.
Слово, звук и кинолента
Формы временно?го искусства по-своему демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили внимание, что наиболее популярное количество строк в стихотворениях позднего периода творчества Пушкина соответствует ряду Фибоначчи — 5, 8, 13, 21, 34.
Действует правило золотого сечения и в отдельно взятых произведениях русского классика. Так кульминационным моментом «Пиковой дамы» является драматическая сцена Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а кульминация приходится на 535 строке (853:535=1,6) — это и есть точка золотого сечения.
Советский музыковед Э. К. Розенов отмечает поразительную точность соотношений золотого сечения в строгих и свободных формах произведений Иоганна Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически выверенному стилю мастера. Это справедливо и в отношении выдающихся творений других композиторов, где на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.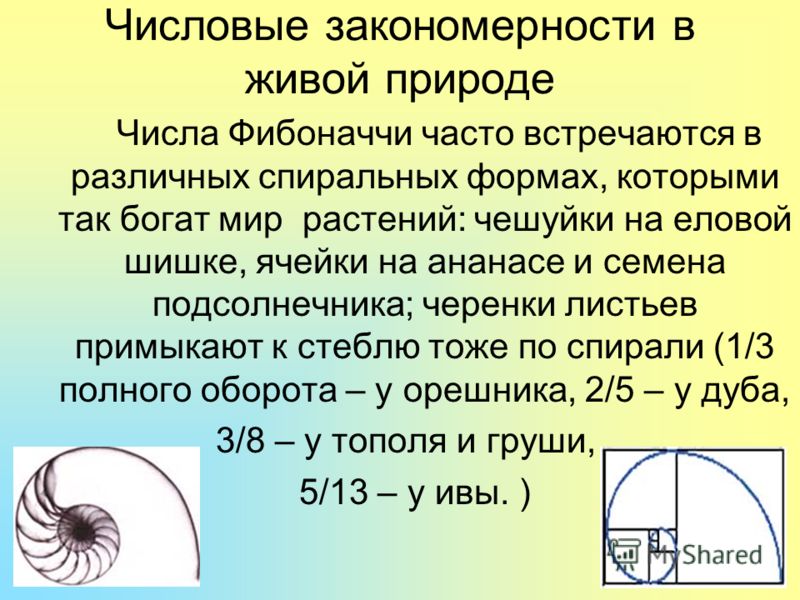
Кинорежиссер Сергей Эйзенштейн сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с правилом золотого сечения, разделив ленту на пять частей. В первых трех разделах действие разворачивается на корабле, а в последних двух — в Одессе. Переход на сцены в городе и есть золотая середина фильма.
Источник: Academic Painting
- #дизайн
- #статья
- 1
Золотое сечение и числа Фибоначчи — Денис Войков на vc.ru
Введение
15 141 просмотров
Человек стремится к знаниям, пытается изучить мир, который его окружает.
В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно, требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы.
Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
История происхождения чисел Фибоначчи и Золотого сечения
Леонардо был рожден в Пизе. Впоследствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Когда Леонардо жил со своим отцом в странах Северной Африки, он изучал математику с арабскими учителями. Получив весь необходимый материал, он создал собственную книгу – «Книгу абака». Именно этот человек становится первым средневековым учёным, познакомившим Европу с арабской системой счисления, которой мы пользуемся всю нашу жизнь[1].
Основная задача, поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара через месяц рождает ещё одну пару, а по природе кролики начинают объектом рождать потомство на второй месяц после своего рождения. Автор даёт нам решение задачи. Получается, что в первый месяц первая пара родит ещё одну. Во второй месяц первая пара родит ещё одну – будет три пары. В третий месяц родят две пары — изначально данная и рождённая в первый месяц. Получается пять пар. И так далее. Используя такую же логику в рассуждении, мы получим, что в четвёртый месяц будет 8 пар, в пятый– 13, в шестой – 21, в седьмой 34, в восьмой — 55, в девятый — 89, в десятый 144, в одиннадцатый – 233, в двенадцатый — 377[2](рис. 1).
Рисунок 1. Задача о кроликах (Павел Малахов, 2017)
Из этой задачи и можно вывести саму последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… В основе этой последовательности лежит алгоритм: начиная с «1, 1» следующим числом будет сумма двух предыдущих чисел.
Золотое сечение в живописи
В эпоху Возрождения художники открыли некие зрительные центры, которые, влияя на психику человека, невольно приковывают наше внимание. Данные точки не зависят от формата картины. Их всего четыре, они делят картину в пропорциях Золотого сечения- примерно 3/8 и 5/8 (рис.2).
Для того чтобы привлечь внимание зрителя к определенному элементу картины, необходимо совместить его с одним из зрительных центров. Данное открытие назвали «золотое сечение картины»[4].
Рисунок 2. Золотое сечение картины (Войков Денис, 2020)
Золотое сечение в медицине
Правило золотого сечения используется в стоматологии, именно они используются при художественной реставрации зубов, их восстановлении. Рассмотрим эстетическое восстановление передних зубов, фронтального зубного ряда (рис.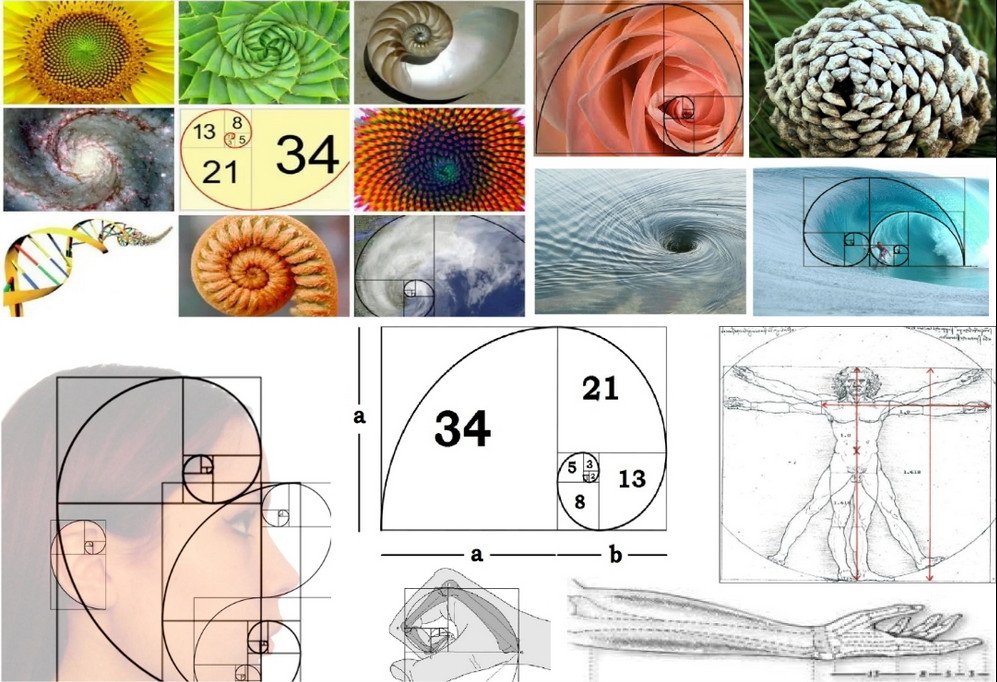
3)[5].
Золотые пропорции включают в себя такие моменты:
— как ширина верхнего переднего зуба относится к ширине нижнего;
— как соотносятся между собой по ширине:
2 резца в нижнем фронтальном ряду;
двое резцов в верхнем ряду;
4 резца вверху;
— какое имеется расстояние между премолярами и т.д.
Рисунок 3. Золотое сечение на зубах (Стас Козловский, 2004)
Так же правило золотого сечения используется в косметологии и пластической хирургии. У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка. Это явление называется «динамической симметрией» или «динамическим равновесием».
Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1: 1,618. Ещё существует множество соотношений на лице, которые представлены на рисунке 4[6].
Рисунок 4.
Золотая пропорция на лице человека (Joaquim Alves Gaspar, 2011)
Золотое сечение в психологии
Числа Фибоначчи и Золотое сечение чтобы также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека. Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества [7].
Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:
• 0 —начало отсчета — ребёнок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;
• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;
• 2 — понимает речь и действует, пользуясь словесными указаниями;
• 3 — действует посредством слова, задаёт вопросы;
• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребёнку охватить мир во всей его целостности;
• 8 — на передний план выходят чувства.
Заключение
Закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
В заключении отмечу, что данная работа является законченным исследованием и при этом имеет ряд перспектив. В дальнейшем возможно исследовать как числа Фибоначчи используются в биологии, химии, как это можно использовать и применять на практике в бытовых условиях.
Список источников информации
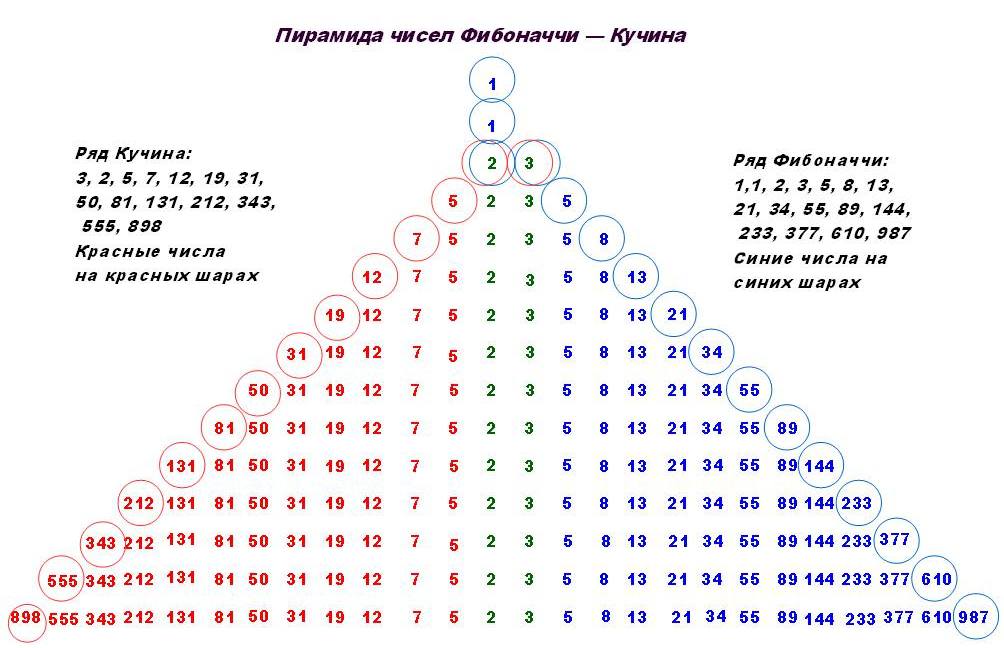
1. Воробьев Н.Н. Числа Фибоначчи. – 5-е изд. – М.: Наука, 1978 – 144с.
2. Загадки природы и числа Фибоначчи – [Электронный ресурс]. – URL: https://www.liveinternet.ru/users/4506755/post186633412 (дата обращения 23.08.2018)
3.
Золотое сечение. – [Электронный ресурс]. – URL: https://ru.wikipedia.org/wiki% D0%97%D0%B% D0%B% D0%B% D1%82%D0%B% D0%B5% D1%81%D0%B5%D1%87%D0%B5%D0%B% D0%B8%D0%B5 (дата обращения 07.09.2018)
4. Правило золотого сечения в живописи – [Электронный ресурс] – URL: https://izo-life.ru/pravilo-zolotogo-secheniya/ (дата обращения 26.02.2021)
5. Золтое сечение в стоматологии – [Электронный ресурс] — URL: http://h809274671.nicwebsite.ru/blog/золотое-сечение-и-числа-фибоначчи-в-стоматологии (дата обращения 09.09.2019).
6. Идеальные пропорции лица – [Электронный ресурс] — URL: https://iakosmetolog.ru/interesno/idealnye-proporcii-lica.html (дата обращения 26.02.2021)
7. Числа Фибоначчи в психологии — [Электронный ресурс] — URL: https://megaobuchalka.ru/1/22657.html (дата обращения 09.09.2019).
Золотое сечение — простая английская Википедия, бесплатная энциклопедия
Английский язык, используемый в этой статье или разделе , может быть не всем легко понять . |
Вы можете помочь Википедии, прочитав Wikipedia:Как писать страницы на простом английском, а затем упростив статью. (сентябрь 2022 г.) С числом, а именно a и другим меньшим числом b , отношение двух чисел находится путем их деления. Их соотношение равно а / б . Другое отношение находится путем сложения двух чисел и деления их на большее число на . Новое соотношение равно ( a + b )/ a . Если эти два соотношения равны одному и тому же числу, то это число называется золотым сечением . Греческая буква φ{\displaystyle \varphi} (фи) обычно используется как название золотого сечения. [1] [2]
Например, если b = 1 и a / b = φ{\displaystyle \varphi}, затем a = φ{\displaystyle \varphi}. Второе отношение ( a + b ) / a тогда равно (φ + 1) / φ {\ displaystyle (\ varphi +1) / \ varphi}.
Поскольку эти два отношения равны, это верно:
φ = φ + 1φ {\ displaystyle \ varphi = {\ frac {\ varphi +1} {\ varphi}}}
Один из способов записать этот номер:
.φ = 1 + 52 = 1,618 … {\ displaystyle \ varphi = {\ frac {1 + {\ sqrt {5}}} {2}} = 1,618 …} [1] [2]
5{\displaystyle {\sqrt {5}}} — это число, которое при умножении само на себя дает 5: 5×5=5{\displaystyle {\sqrt {5}}\times {\sqrt {5} }=5}.
Золотое сечение называется иррациональным числом. Это означает, что если человек попытается написать его, он никогда не остановится и никогда не создаст закономерности, а начнет так: 1,6180339887… Важным моментом в этом числе является то, что если вы вычтете из него 1 или разделите 1 на это, вы получите тот же номер. 9, 6180339887…-1&=&0,6180339887…\\1/\varphi &=&{\frac {1}{1,6180339887…}}&=&0,6180339887…\end{массив}}}
Большой прямоугольник BA — золотой прямоугольник; то есть пропорция b: a равна 1: φ {\ displaystyle \ varphi}.
Для любого такого прямоугольника и только для прямоугольников этой конкретной пропорции, если мы удалим квадрат B , что осталось, A , еще один золотой прямоугольник; то есть с теми же пропорциями, что и исходный прямоугольник.
Если длина прямоугольника, деленная на его ширину, равна золотому сечению, то прямоугольник является «золотым прямоугольником». Если от одного конца золотого прямоугольника отрезать квадрат, то другой конец будет новым золотым прямоугольником. На картинке большой прямоугольник (синий и розовый вместе) является золотым прямоугольником, потому что a/b=φ{\displaystyle a/b=\varphi}. Синяя часть (B) представляет собой квадрат, а розовая часть сама по себе (A) представляет собой еще один золотой прямоугольник, потому что b/(a−b)=φ{\displaystyle b/(a-b)=\varphi}. Большой прямоугольник и розовый прямоугольник имеют одинаковую форму, но розовый прямоугольник меньше и перевернут.
Числа Фибоначчи представляют собой список чисел. Человек может найти следующий номер в списке, сложив два последних числа вместе.
Если человек делит число в списке на число, которое стояло перед ним, это соотношение все больше и больше приближается к золотому сечению.
| Число Фибоначчи | разделить на предыдущее | соотношение|
|---|---|---|
| 1 | ||
| 1 | 1/1 | = 1.0000 |
| 2 | 2/1 | = 2,0000 |
| 3 | 3/2 | = 1,5000 |
| 5 | 5/3 | = 1,6667 |
| 8 | 8/5 | = 1,6000 |
| 13 | 13/8 | = 1,6250 |
| 21 | 21/13 | = 1,6154… |
| 34 | 34/21 | = 1,6190… |
| 55 | 55/34 | = 1,6177… |
| 89 | 89/55 | = 1,6182… |
| … | . .. | … |
| φ{\ Displaystyle \ varphi} | = 1,6180… |
Использование золотого угла позволит оптимально использовать солнечный свет. Это вид сверху.
Лист обыкновенного плюща, показывающий золотое сечение
В природе золотое сечение часто используется для расположения листьев или цветов. В них используется золотой угол примерно 137,5 градусов. Листья или цветы, расположенные под таким углом, лучше всего используют солнечный свет.
Кроме того, расстояние между центром тела человека и полом и расстояние между макушкой головы и основанием позвоночника соответствуют золотому сечению. [3] Несмотря на отсутствие общих архитектурных и дизайнерских моделей, открытие Леонардо Фибоначчи широко признано новаторским. Он может принимать форму ураганов, бивней слона, муравьев, морских ежей, морских звезд, пчел и многих других существ.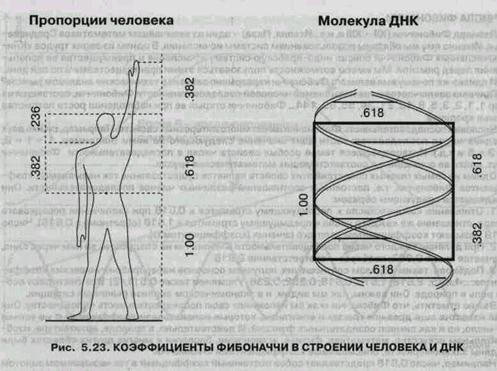
Последовательность Фибоначчи начинается с 0 и продолжается бесконечно: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Перед каждой цифрой стоит сумма двух цифр. Сам узор довольно элементарный и ничем не примечательный.
Так будет до тех пор, пока вы не узнаете, что это соотношение лежит в основе красоты Моны Лизы, человеческих конечностей, шифрования данных и даже количества спиралей на головке подсолнуха. Похоже, что у Вселенной есть естественный способ отслеживать числа.
Цветы всегда имеют нечетное количество лепестков, соответствующих последовательности Фибоначчи. Например, у мирной лилии три лепестка, у лютика — пять, у цикория — 21, у маргаритки — 34 и так далее.
Вот еще несколько естественных проявлений золотого сечения:
Семенные головки. Цветы производят семена в своей сердцевине, которые затем закручиваются наружу, заполняя головку цветка.
Ананасы, цветная капуста и брокколи романеско. Точно так же они соответствуют последовательности Фибоначчи.
Сосновые шишки. Сосновые шишки имеют спиралевидные узоры на своих семенных коробочках, причем две спирали на каждой шишке растут в противоположных направлениях по мере их роста.
Ветви дерева. В природе эта закономерность наблюдается, когда дерево развивает ветвь, а затем разделяется на две новые точки роста. Тогда только один из двух новых стеблей будет активно расти, а другой будет бездействовать.
Способы полета птиц. Лучший угол атаки ястреба перпендикулярен траектории полета цели, что совпадает с шагом спирали.
Спиральные галактики. В Млечном Пути есть несколько спиральных рукавов, каждый с логарифмической спиралью около 12 градусов.
- Числа Фибоначчи
- Phi
- ↑ 1.0 1.1 «Сборник математических символов». Математическое хранилище . 01.03.2020. Проверено 10 августа 2020 г. .
- ↑ 2.0 2.1 Вайсштейн, Эрик В.
«Золотое сечение». mathworld.wolfram.com . Проверено 10 августа 2020 г. . - ↑ «Золотое сечение: величайшая тайна природы». Goodreads . Проверено 2022-09.-26.
«Золотое сечение». mathworld.wolfram.com . Проверено 10 августа 2020 г. . - Простая для понимания статья о золотом сечении
- Золотое сечение -Citizendium
- Золотое сечение в творчестве современного художника Сликара Альфреда Ф. Крупа, YouTube-видео
Золотое сечение — простая английская Википедия, бесплатная энциклопедия
009 май не всем будет легко понять . Вы можете помочь Википедии, прочитав Wikipedia:Как писать страницы на простом английском, а затем упростив статью. (сентябрь 2022 г.) |
Имея число, а именно a и другое меньшее число b , отношение двух чисел находится путем их деления. Их соотношение равно к / к . Другое отношение находится путем сложения двух чисел и деления их на большее число на .
Новое соотношение равно ( a + b )/ a . Если эти два отношения равны одному и тому же числу, то это число называется 9.0009 золотое сечение . Греческая буква φ{\displaystyle \varphi} (фи) обычно используется как название золотого сечения. [1] [2]
Например, если b = 1 и a / b = φ{\displaystyle \varphi}, то a = φ {\ Displaystyle \ varphi} . Второе отношение ( a + b ) / a тогда равно (φ + 1) / φ {\ displaystyle (\ varphi +1) / \ varphi}. Поскольку эти два отношения равны, это верно:
φ = φ + 1φ {\ displaystyle \ varphi = {\ frac {\ varphi +1} {\ varphi}}}
Один из способов записать этот номер:
.φ = 1 + 52 = 1,618 … {\ displaystyle \ varphi = {\ frac {1 + {\ sqrt {5}}} {2}} = 1,618 …} [1] [2]
5{\displaystyle {\sqrt {5}}} — это число, которое при умножении само на себя дает 5: 5×5=5{\displaystyle {\sqrt {5}}\times {\sqrt {5} }=5}.
Золотое сечение называется иррациональным числом. Это означает, что если человек попытается это написать, он никогда не остановится и никогда не создаст шаблон, а начнет так: 1.6180339887 . Важным моментом в этом числе является то, что если вы вычтете из него 1 или разделите на него 1, вы получите то же самое число.
- . 6180339887…-1&=&0,6180339887…\\1/\varphi &=&{\frac {1}{1,6180339887…}}&=&0,6180339887…\end{массив}}}
Большой прямоугольник BA — золотой прямоугольник; то есть пропорция b: a равна 1: φ {\ displaystyle \ varphi}. Для любого такого прямоугольника и только для прямоугольников этой конкретной пропорции, если мы удалим квадрат B , что осталось, A , еще один золотой прямоугольник; то есть с теми же пропорциями, что и исходный прямоугольник.
Если длина прямоугольника, деленная на его ширину, равна золотому сечению, то прямоугольник является «золотым прямоугольником».
Если от одного конца золотого прямоугольника отрезать квадрат, то другой конец будет новым золотым прямоугольником. На картинке большой прямоугольник (синий и розовый вместе) является золотым прямоугольником, потому что a/b=φ{\displaystyle a/b=\varphi}. Синяя часть (B) представляет собой квадрат, а розовая часть сама по себе (A) представляет собой еще один золотой прямоугольник, потому что b/(a−b)=φ{\displaystyle b/(a-b)=\varphi}. Большой прямоугольник и розовый прямоугольник имеют одинаковую форму, но розовый прямоугольник меньше и перевернут.
Числа Фибоначчи представляют собой список чисел. Человек может найти следующий номер в списке, сложив два последних числа вместе. Если человек делит число в списке на число, которое стояло перед ним, это соотношение все больше и больше приближается к золотому сечению.
| Число Фибоначчи | разделить на предыдущее | соотношение|
|---|---|---|
| 1 | ||
| 1 | 1/1 | = 1. 0000 |
| 2 | 2/1 | = 2,0000 |
| 3 | 3/2 | = 1,5000 |
| 5 | 5/3 | = 1,6667 |
| 8 | 8/5 | = 1,6000 |
| 13 | 13/8 | = 1,6250 |
| 21 | 21/13 | = 1,6154… |
| 34 | 34/21 | = 1,6190… |
| 55 | 55/34 | = 1,6177… |
| 89 | 89/55 | = 1,6182… |
| … | … | … |
| φ{\ Displaystyle \ varphi} | = 1,6180… |
Использование золотого угла позволит оптимально использовать солнечный свет. Это вид сверху.
Лист обыкновенного плюща, показывающий золотое сечение
В природе золотое сечение часто используется для расположения листьев или цветов.
В них используется золотой угол примерно 137,5 градусов. Листья или цветы, расположенные под таким углом, лучше всего используют солнечный свет.
Кроме того, расстояние между центром тела человека и полом и расстояние между макушкой головы и основанием позвоночника соответствуют золотому сечению. [3] Несмотря на отсутствие общих архитектурных и дизайнерских моделей, открытие Леонардо Фибоначчи широко признано новаторским. Он может принимать форму ураганов, бивней слона, муравьев, морских ежей, морских звезд, пчел и многих других существ.
Последовательность Фибоначчи начинается с 0 и продолжается бесконечно: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Перед каждой цифрой стоит сумма двух цифр. Сам узор довольно элементарный и ничем не примечательный.
Так будет до тех пор, пока вы не узнаете, что это соотношение лежит в основе красоты Моны Лизы, человеческих конечностей, шифрования данных и даже количества спиралей на головке подсолнуха. Похоже, что у Вселенной есть естественный способ отслеживать числа.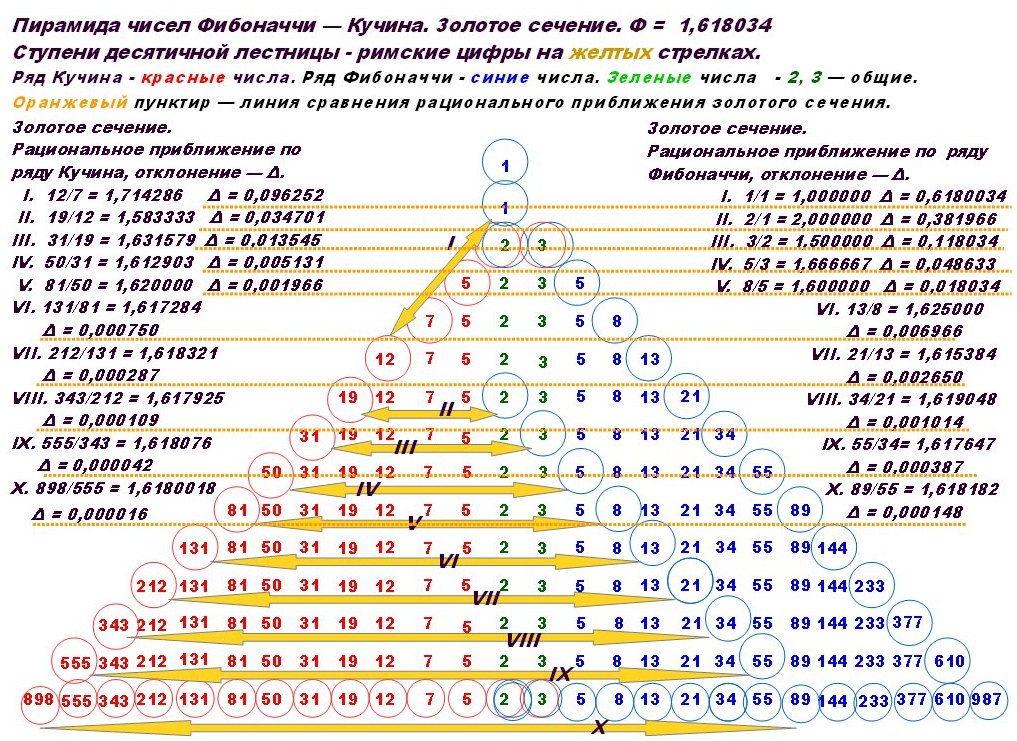
Цветы всегда имеют нечетное количество лепестков, соответствующих последовательности Фибоначчи. Например, у мирной лилии три лепестка, у лютика — пять, у цикория — 21, у маргаритки — 34 и так далее.
Вот еще несколько естественных проявлений золотого сечения:
Семенные головки. Цветы производят семена в своей сердцевине, которые затем закручиваются наружу, заполняя головку цветка.
Ананасы, цветная капуста и брокколи романеско. Точно так же они соответствуют последовательности Фибоначчи.
Сосновые шишки. Сосновые шишки имеют спиралевидные узоры на своих семенных коробочках, причем две спирали на каждой шишке растут в противоположных направлениях по мере их роста.
Ветви дерева. В природе эта закономерность наблюдается, когда дерево развивает ветвь, а затем разделяется на две новые точки роста. Тогда только один из двух новых стеблей будет активно расти, а другой будет бездействовать.
Способы полета птиц.