числа Фибоначчи и золотое сечение — поразительные закономерности, сопровождающие нас повсюду
Числа Фибоначчи — это интересная математическая последовательность, которая наблюдается во всем, что окружает нас. Так сразу этого и не увидеть, но если присмотреться, все станет очевидно.
Из истории феномена
Математик из Италии XIII века Леонардо Фибаначчи заметил необычную закономерность первым. Фибоначчи, или, как его еще звали, Леонардо Пизанский придумал интересную задачку, в которой нужно было провести подсчет обычных кроликов, исходя из условий. Та, последовательность в числах, которую ему удалось обнаружить и доказать, очень проста, но факт в том, что встречается она везде, будь то природа или человек, предметы, произведения искусства.
Элементарная математика — основа чисел Фабоначчи и золотого сечения
В чем же она заключается? В том, что если взять всего два числа, а это 0 и 1 или 1 и 1, и все последующие числа будут равняться сумме предыдущих. Все это очень подробно известный математик описал в своем труде «Книга абака». В Индии очень активно использовали данную последовательность, как оказалось, еще с древних времен. И применялась она в стихосложении. Написанные в соответствии с этой закономерностью стихи действительно отличаются по восприятию.
Все это очень подробно известный математик описал в своем труде «Книга абака». В Индии очень активно использовали данную последовательность, как оказалось, еще с древних времен. И применялась она в стихосложении. Написанные в соответствии с этой закономерностью стихи действительно отличаются по восприятию.
Математика повсюду
После того как человек узнает о числах Фибоначчи, оглянувшись вокруг, он начинает понимать, что они есть повсюду. Та же природа, которая окружает нас и существует уже миллионы лет. Стоит всмотреться в расположение листьев на растениях, лепестков на цветах, семян в подсолнухе. Есть последовательность в ячейках такого фрукта как ананас, в шишках хвойных.
Раковины моллюсков сконструированы по спирали, которая соотносится с рядом чисел, открытым математиком. В общем, очень многое в пространстве и вокруг него подчиняется числам Фибоначчи. Так было изначально в природе, просто математик смог это увидеть и открыть миру. Даже пауки плетут свои паутины в соответствии с числами Фибоначчи. Даже в человеческом теле присутствует данная последовательность, в костяшках пальцев на руках. А если собрать кисть в кулак, как раз получается спираль сечения.
Даже в человеческом теле присутствует данная последовательность, в костяшках пальцев на руках. А если собрать кисть в кулак, как раз получается спираль сечения.
Последоватеность чисел есть даже в расположении лепестков и соцветий
Золотое сечение
Такое понятие, как золотое сечение с числами Фибоначчи очень тесно связано. Если поделить два последовательных числа из ряда, к примеру 144/89, то получится в результате 1,618 — а это число называется золотым сечением. И оно тоже присутствует вокруг нас и даже есть в космосе.
Золотое сечение похоже на спираль, и чем больше пара из чисел Фибоначчи, тем более близко приближение к золотому сечению. В искусстве оно очень часто используется в работах художников и скульпторов, есть в архитектуре. Что касается космоса, взгляните на Млечный Путь и все станет ясно. У человека золотым сечением считается деление пупком всего тела. Да просто можно взглянуть на все окружающее, чтобы удостовериться — эти две закономерности предусмотрены самой природой.
Nurqanat Baizaq
Красота и математика
Золотое сечение и числа Фибоначчи — мостик между естественными и гуманитарными науками, царством чисел и миром искусства.
Что такое золотое сечение? Научно-технический энциклопедический словарь даёт такое определение: «Золотое сечение — это пропорциональное деление отрезка на две неравные части, при котором меньший отрезок так относится к большему, как больший ко всему». Считается, что эта пропорция является проявлением гармонии и порядка мирового устройства, идеальной моделью Вселенной. Золотое сечение встречается и в природе, и в науке, и в технике.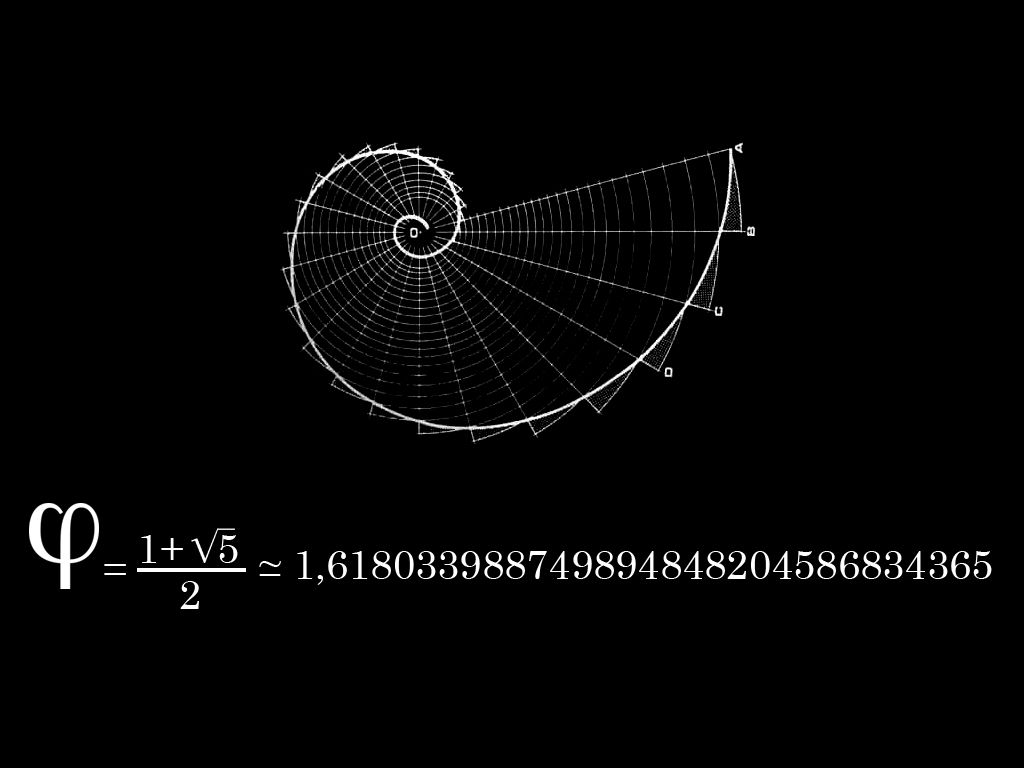
Самый известный пример красоты и совершенства в природе — это структура спирали, которая подчиняется математическому закону золотого сечения и находит воплощение, например, в форме рогов горных козлов или раковинах моллюсков. Принципы золотого сечения можно найти в древней архитектуре, например, египетской. Одним из последователей этого правила считается Леонардо да Винчи — на многих его картинах искусствоведы находят проявление золотого сечения.
Числа Фибоначчи — это частный случай принципа золотого сечения. Последовательность Фибоначчи выглядит так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711…
Здесь каждое последующее число равно сумме двух предыдущих. Эту последовательность первым открыл европейцам математик и путешественник Леонардо Пизанский по прозвищу Фибоначчи. В 1202 году он опубликовал сборник по алгебре и арифметике «Книга абака», основанный на математических знаниях индусов и арабов.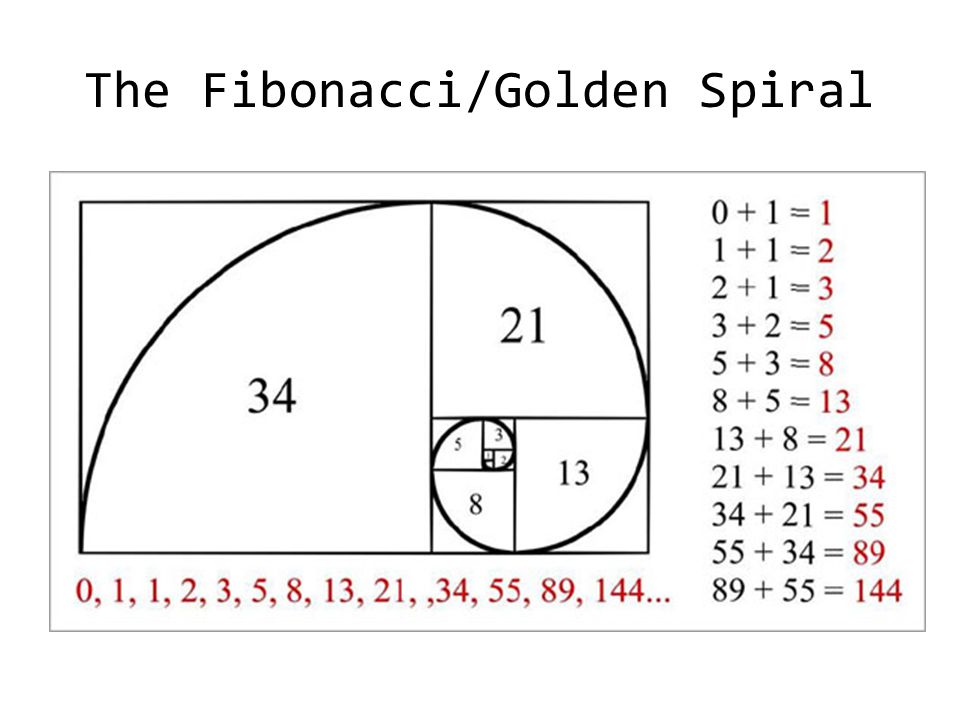
У последовательности Фибоначчи имеется много интересных свойств. Каждое третье число — чётное, каждое четвёртое кратно трём; каждое пятнадцатое оканчивается нулём. Если взять пару соседних чисел из этого ряда и разделить большее число на меньшее, результат будет постепенно приближаться к числу золотого сечения. Это предельное число, примерно равное 1,618 — число Фи. Названо в честь древнегреческого скульптора Фидия, чьи скульптуры считаются эталоном красоты.
Числа Фибоначчи можно найти даже у себя. Посмотрите на свои руки: на обеих по пять пальцев. Два из них (большие) состоят из двух фаланг, а у остальных восьми — по три фаланги. 2, 3, 5, 8 — это одни из первых чисел последовательности Фибоначчи. Математики считают, что это закономерно — правило золотого сечения действует повсюду.
Даже в космосе можно найти число идеальной пропорции. В Солнечной системе планеты вращаются по траектории эллипса, а значит, у их траекторий есть минимальный и максимальный радиус. Удивительно, но соотношение этих радиусов у всех планет Солнечной системы совпадает с числом золотого сечения, погрешность составляет доли процента. В то же время соотношение орбит планет нашей Солнечной системы очень близко к коэффициенту золотого сечения. Этот факт был известен еще Кеплеру, и, опираясь на него, он пытался построить некую универсальную систему мироздания.
Удивительно, но соотношение этих радиусов у всех планет Солнечной системы совпадает с числом золотого сечения, погрешность составляет доли процента. В то же время соотношение орбит планет нашей Солнечной системы очень близко к коэффициенту золотого сечения. Этот факт был известен еще Кеплеру, и, опираясь на него, он пытался построить некую универсальную систему мироздания.
По материалам naukatv.ru, aif.ru
Фото: pixabay
числа Фибоначчи золотое сечение
Последовательность Фибоначчи и Золотое сечение
Последовательность Фибоначчи
Последовательность Фибоначчи, возможно, является самым простым рекуррентным соотношением, встречающимся в природе. Это 0,1,1,2,3,5,8,13,21,34,55,89, 144… каждое число равно сумме двух предшествующих ему чисел и разности двух следующих за ним чисел. Это бесконечная последовательность, которая продолжается вечно по мере своего развития.
Золотое сечение/Божественное отношение или Золотое сечение
Частное любого числа Фибоначчи и его предшественника приближается к фи, представленному как ϕ (1,618), золотому сечению. Золотое сечение лучше всего геометрически понимается золотым прямоугольником.
Прямоугольник, разделенный неравномерно на один квадрат и один прямоугольник, стороны квадрата будут иметь отношение 1:1, а новый прямоугольник будет точно пропорционален исходному прямоугольнику — 1:1,618.
Эта итерация может продолжаться в обе стороны бесконечно. Если вы начертите четверть круга внутри каждого из повторяющихся квадратов, получится золотая спираль. Золотая спираль, возможно, является самым простым математическим узором, встречающимся в природе, таким как раковины улиток, морские раковины, рога, цветы, растения. Числа — это только то, что мы используем для организации количественной информации.
Золотое сечение можно увидеть от Наутилуса с камерами до спиральной галактики. Золотое сечение можно применять к любому количеству геометрических форм, включая круги, треугольники, пирамиды, призмы и многоугольники.
Золотое сечение образовано третями внутри третей, шестыми, связью между двумя и тремя, включая каждое четное и нечетное число. Само соотношение представляет трансцендентность чисел, понимание нашего мира — это не числа, а то, что числа представляют.
Соотношение по спирали показывает, как числа, все количества являются качеством. В конце концов, любое качество можно представить через количество. Качественные и количественные свойства – это всего лишь ярлыки информации, наш собранный неоспоримый факт.
Подсолнухи имеют расположение семян «Золотая спираль». Это обеспечивает биологическое преимущество, поскольку максимизирует количество семян, которые могут быть упакованы в семенную головку. Если построить график любой системы счисления, в конце концов появятся закономерности. В математике числа и их закономерности не только продолжаются бесконечно линейно, но и во всех направлениях. Например, учитывая бесконечное десятичное расширение, даже самые короткие сегменты имеют бесконечное количество точек.
Наша вселенная и числа не только бесконечно линейны, но даже ее короткие отрезки имеют бесконечные точки.
(Красивый короткометражный фильм о последовательности Фибоначчи в «Природе» — «Природа в цифрах»)
Золотое сечение — не единственная математическая закономерность, достигающая бесконечности, существует множество других закономерностей, достигающих бесконечности. Зная это, спросите себя, как бесконечность могла произойти дважды? Если что-то должно было происходить бесконечно, как это могло произойти дважды?
Ответ прост, бесконечность представляет то, что вечно, что истинно целостно. Например, если бы бесконечность использовалась в качестве переменной в математике, как и все другие числа, она обозначалась бы как 1∞, 2∞, 3∞, 4∞ и т. д.
д.
Единство всего фактического — это то, что вы знаете, то, что вы воспринимаете, что вы осознаете, и есть вся вселенная, смотрящая на себя. Это вселенная, даже ты вселенная, мы и все, что мы знаем, это одно и то же.
Поскольку цифры повсюду, все является частью шаблона. Отражения отражений, колеса внутри колес. Жизнь сама по себе является фракталом.
Источник изображения
Phi Золотое сечение
Пожалуйста, поделитесь, это действительно помогает! 🙂
Latest for Members
You May Like
For Members
Load more
Week 1: Fibonacci Sequence and the Golden Ratio
Использование файлов Python В прошлый раз мы записали наши команды Python непосредственно в оболочку, набрав в командной строке ( В меню IDLE выберите Файл -> Новое окно. В новом окне введите Вы можете запустить свою программу (т. е. выполнить команды в файле Python в том порядке, в котором они появляются), нажав F5 в IDLE или выбрав пункт меню «Выполнить» -> «Выполнить модуль». Теперь вы должны увидеть свое приветствие в оболочке Python. Вы также можете запустить свою программу непосредственно из командной строки, набрав С этого момента я предлагаю вам сохранять (Ctrl-S) ваши команды Python в файлах и запускать их с помощью F5 в ПРАЗДНЫЙ. В конце этой страницы я прикрепил несколько примеров файлов Python, которые вы, возможно, захотите изучить. Последовательность Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, и т. д. … Как видите, следующее значение в списке находится путем сложения двух предыдущих значений. Например, 13 = 8 + 5, 21 = 13 + 8, 34 = 21 + 13 и т. д. Математически мы можем определить последовательность с рекуррентным соотношением : F(n+1) = F(n ) + F(n-1) и два начальных «начальных значения», F(0) = 0 и F(1) = 1 . Леонардо Пизанский, известный как Фибоначчи, ввел эту последовательность в европейскую математику в своей книге 1202 года Liber Abaci. Считается, что он возник еще раньше в индийской математике. Давайте посмотрим на простой код из официального руководства по Python, который генерирует последовательность Фибоначчи. Я поместил эти команды в файл В этом примере представлены некоторые новые команды Python, которые объясняются здесь. Давайте рассмотрим каждую строку по очереди:
Итерационный методСуществует множество способов для сопоставления с помощью FibOnCACCACCACCACCACCACCACCACCACCACCACCACCACCACCACCACCACCACCACCACCAC Одним из возможных вариантов является следующий код: Это итеративный метод, как и в предыдущем примере — он использует цикл. Основное отличие состоит в том, что я сохраняю значения в списке и «добавляю» новые значения в конец списка. Видите, как мы можем получить отдельные элементы списка? Здесь Рекурсивный метод Числа Фибоначчи определяются математически (выше) с помощью (i) рекуррентного соотношения F(n+1) = F(n) + F(n-1) и (ii) базового случая F( 1) = 1, F(0) = 0. Вместо использования итеративного метода с циклом мы можем вместо этого определить «рекурсивную» функцию, которая по духу ближе к этому математическому определению. Золотое сечениеТеперь давайте подумаем об отношении последовательных элементов последовательности, то есть F(n+1) / F(n). Оказывается, это отношение стремится к фиксированному значению, так как числа Фибоначчи становятся больше. Более того, это конкретное значение очень хорошо известно математикам на протяжении веков. Он известен как золотое сечение и определяется как Попробуйте вычислить отношение последовательных членов в списке чисел Фибоначчи с помощью следующего утверждения: Что вы видите? Насколько близко вы можете подобраться к точному значению золотого сечения? (Этот код можно найти в Графическое представлениеЧисла Фибоначчи могут быть представлены графически в виде длин плеч по спирали или в виде квадратов, образующих прямоугольник, как показано ниже. В ближайшие недели я покажу, как рисовать такие паттерны с помощью модуля Золотое сечение находится в прямоугольнике особого типа. Когда прямоугольник помещается рядом с квадратом, как показано на рисунке, получается второй прямоугольник. Золотое сечение имеет место, когда два прямоугольника равны 9.0120 подобны , а это значит, что отношение длин их сторон такое же, Формула Бине На самом деле существует простая математическая формула для вычисления n -го числа Фибоначчи, которая не требует вычисления предыдущих чисел. Это называется Формула Бине . Мы можем реализовать формулу Бине в Python, используя функцию: def fibBinet(n): phi = (1 + 5**0,5)/2,0 return int(round((phi**n - (1-phi)**n) / 5* *0,5)) Обратите внимание, что Этот код может показаться немного хитрым. Например, как мы можем быть уверены, что квадратный корень будет взят за до деления? Здесь мы полагаемся на тот факт, что Python (как и большинство языков) выполняет операторы в определенном фиксированном порядке приоритета. Число фибоначчи золотое: Золотое сечение и пропорции Фибоначчи Пролистать наверх
|

 Это нормально для простых команд, но быстро становится громоздким. Особенно, если вы, как и я, ошибаетесь при вводе кода. Кроме того, когда вы выходите из Python, ваши драгоценные строки кода могут быть забыты! С этого момента мы будем хранить наши программы в файлах Python.
Это нормально для простых команд, но быстро становится громоздким. Особенно, если вы, как и я, ошибаетесь при вводе кода. Кроме того, когда вы выходите из Python, ваши драгоценные строки кода могут быть забыты! С этого момента мы будем хранить наши программы в файлах Python. 

 комментарий просто
человекочитаемый текст, который компьютер проигнорирует. Добавление комментариев к
ваш код — очень хорошая идея, особенно если, как и я, у вас есть
короткая память.
комментарий просто
человекочитаемый текст, который компьютер проигнорирует. Добавление комментариев к
ваш код — очень хорошая идея, особенно если, как и я, у вас есть
короткая память.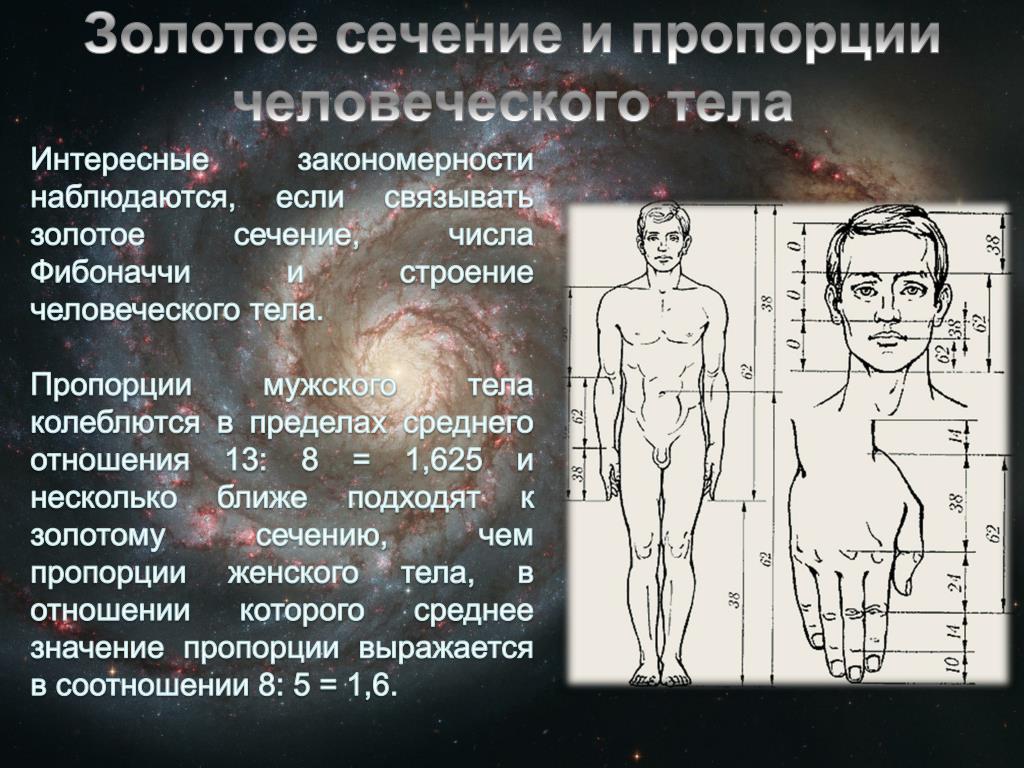 е. сначала присваивать значение b к a, а затем присвойте значение a+b переменной b. Но это неправильно. На самом деле это множественное присвоение . Правильная интерпретация состоит в том, чтобы составить пару значений из b и a+b. Затем назначьте их одновременно a и b. Таким образом, значение a не заменяется до последнего шага. Того же результата можно было бы добиться с помощью трех строк кода:
е. сначала присваивать значение b к a, а затем присвойте значение a+b переменной b. Но это неправильно. На самом деле это множественное присвоение . Правильная интерпретация состоит в том, чтобы составить пару значений из b и a+b. Затем назначьте их одновременно a и b. Таким образом, значение a не заменяется до последнего шага. Того же результата можно было бы добиться с помощью трех строк кода: 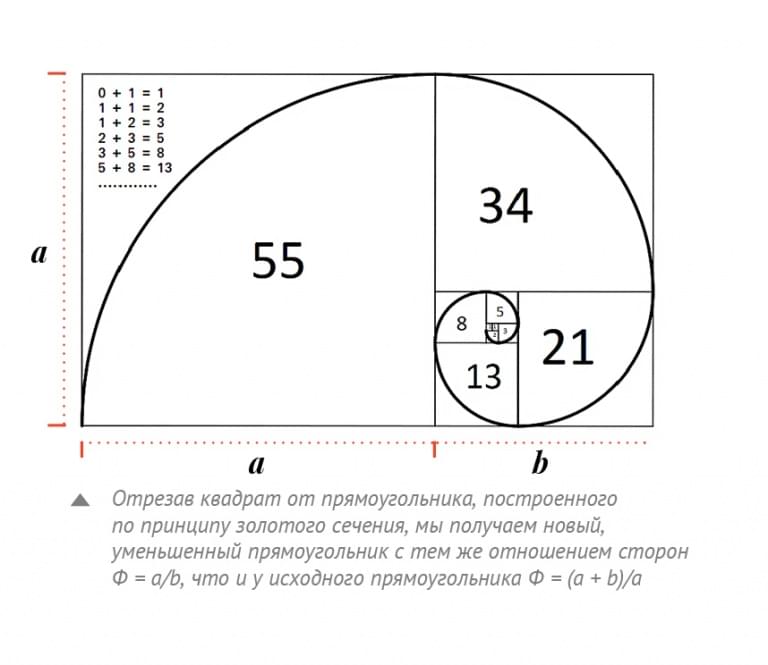 append(fiblist[i] + fiblist[i+1])
append(fiblist[i] + fiblist[i+1])  Повторно вызывая себя, повторение продолжается вниз, пока не будет достигнут базовый случай.
Повторно вызывая себя, повторение продолжается вниз, пока не будет достигнут базовый случай.  py
py  Он имеет золотое сечение:
Он имеет золотое сечение: